1. 서 론
2. 연구 방법
2.1 연구 절차
2.2 대상 관측소
2.3 전지구모형
2.4 분위사상법
2.5 역거리가중치법
3. 결 과
3.1 전망기간의 편이보정결과
3.2 불확실성 비교
3.3 고찰
4. 결 론
1. 서 론
기후변화 연구를 수행하는 연구자들은 대부분 전지구모형(General circulation models, GCMs)을 사용하여 통계학적으로 기후의 변동성과 기상 이변에 대한 연구를 수행한다(Hwang, 2014; Mgangira, 2009). CMIP (Coupled Model Intercomparison Project)은 전세계 30여개 기관들이 참여하여 GCM의 장기적인 미래기후 예측과 불확실성을 평가하고, 모든 결과를 저장하여 활용한다. 온실가스 배출시나리오인 representative concentration pathways (RCP)를 기반으로한 5th Assessment Report (AR5)를 토대로 60여개의 GCMs 이 존재한다. GCM은 과거 강수량 재현을 위해 GCM의 불확실성을 평가하기 위하여 격자기반 평가접근법을 제시한 연구(Ines et al., 2006)와 전망 기간의 다양한 수문학적 요소들을 예측(Im et al., 2006; Pang et al., 2017) 하기 위해 많이 사용되고 있다.
GCM의 원시 강수 자료는 관측소에서 측정된 강수량과 차이가 발생한다. 이러한 차이를 줄이기 위해서 편이보정(Bias correction)방법이 사용된다. 현재 다양한 편이보정방법이 사용되며, 대표적으로 함수를 이용한 편이보정방법, 분위사상법(Quantile mapping) 등이 사용된다(Grillakis et al, 2013; Moon et al., 2013; Song et al., 2019).
GCM을 사용해서 미래기후를 예측할때 존재하는 다양한 불확실성의 원인을 파악하기 위한 연구가 지속적으로 수행되었다. Wilby and Harris (2006)는 GCM에 의해 발생하는 불확실성의 주요 원인을 제시하였으며, Andreas et al. (2018)은 불확실성에 대해 네 가지 관점에서 원인을 제시하고 있는데 첫 번째로 GCM 자체에 내포된 불확실성, 두 번째는 기후 시나리오에 따라 내포된 불확실성, 세 번째는 편이보정 방법별 발생하는 불확실성, 네 번째는 수문 모형에서 내포된 불확실성이다. 불확실성을 파악하기 위한 연구뿐만 아니라, 내포된 불확실성을 줄이기 위해서 다양한 방법들이 제시되었는데 (Patricia and Chung, 2019), 대표적으로는 multi-model ensemble (MME) 방법이 많이 사용되고 있다(Hori and Ueda, 2006; Wang, 2013). MME는 다중 GCM과 배출시나리오를 사용하여 불확실성을 대폭 줄일 수 있으나, 적합하지 않은 GCM도 함께 사용된다. 이에 따라 선정된 연구 지점에 평가지표를 사용하여 적합한 GCM을 사용하거나(Shiru et al., 2019a) 선정된 GCM을 MME로 재구성하는 방법이 있다(Ahmed et al., 2019; Shiru et al., 2019b). GCM을 사용하는 연구에서는 GCM의 모의값과 관측값의 차이를 줄이기 위하여 다양한 편이보정 방법들이 사용되고 있으며, 선정된 편이보정방법에 따라 서로 다른 결과가 도출되기도 한다.
따라서 본 연구는 지점별 9개의 GCM의 과거기간(1970-2005)에 적용된 9개(Bernoulli-Gamma (BG), Bernoulli-LogNormal (BL), Bernoulli-Weibull (BW), Robust Linear (RL), Robust Tricub (RT), 스플라인 평활함수(Smoothing Spline, SSPLIN), 지수점근선변환함수방법(P-EAT), Linear (PL), Scale (PS))의 분위사상법을 사용하여 RCP 4.5 시나리오를 대상하여 전망기간을 3개의 구간(2011-2040년, 2041-2070년, 2071-2100년)으로 나누어 월 강수량을 산정하였다. 산정된 월 강수량을 구간별 평균하여 GCM을 기준으로 산정된 결과와, 편이보정을 기준으로 산정된 결과를 강수량의 표준편차와 1분위와 3분위의 변위(inter-quartile range, IQR)를 사용하여 GCM과 편이보정 방법의 선택으로 인해 발생할 수 있는 불확실성을 정량적으로 비교하였다.
2. 연구 방법
2.1 연구 절차
본 연구는 전망 기간(2011-2100년)의 GCM 기준과 편이보정 방법 기준을 토대로 불확실성을 분석하기 위해 3개(2011-2040년, 2041-2070년, 2071-2100년)의 구간으로 나누어서 평균 강수량을 산정하였으며, 이를 토대로 표준편차와 IQR을 계산하였다. 본 연구는 총 다섯 단계로 구성되어 있다. 첫 번째는 연구에 사용될 GCM을 선정하는 것으로 본 연구에서는 9개의 GCM을 선택하였다. 두 번째는 연구에 사용될 편이보정방법을 선정하는 단계로 본 연구에는 9종류의 분위사상법을 사용하였다. 세 번째는 GCM의 과거기간(1970-2005년)에 편이보정방법을 적용하여 강수량을 산정한다. 네 번째는 과거에 적용한 편이보정방법을 전망기간에 적용하여 3개의 구간별 (2011-2040년, 2041-2071년, 2071-2100년) 강수량을 산정한다. 다섯 번째는 산정된 구간별 월 강수량을 토대로 표준편차와 IQR를 계산하여 불확실성을 정량화한다.
2.2 대상 관측소
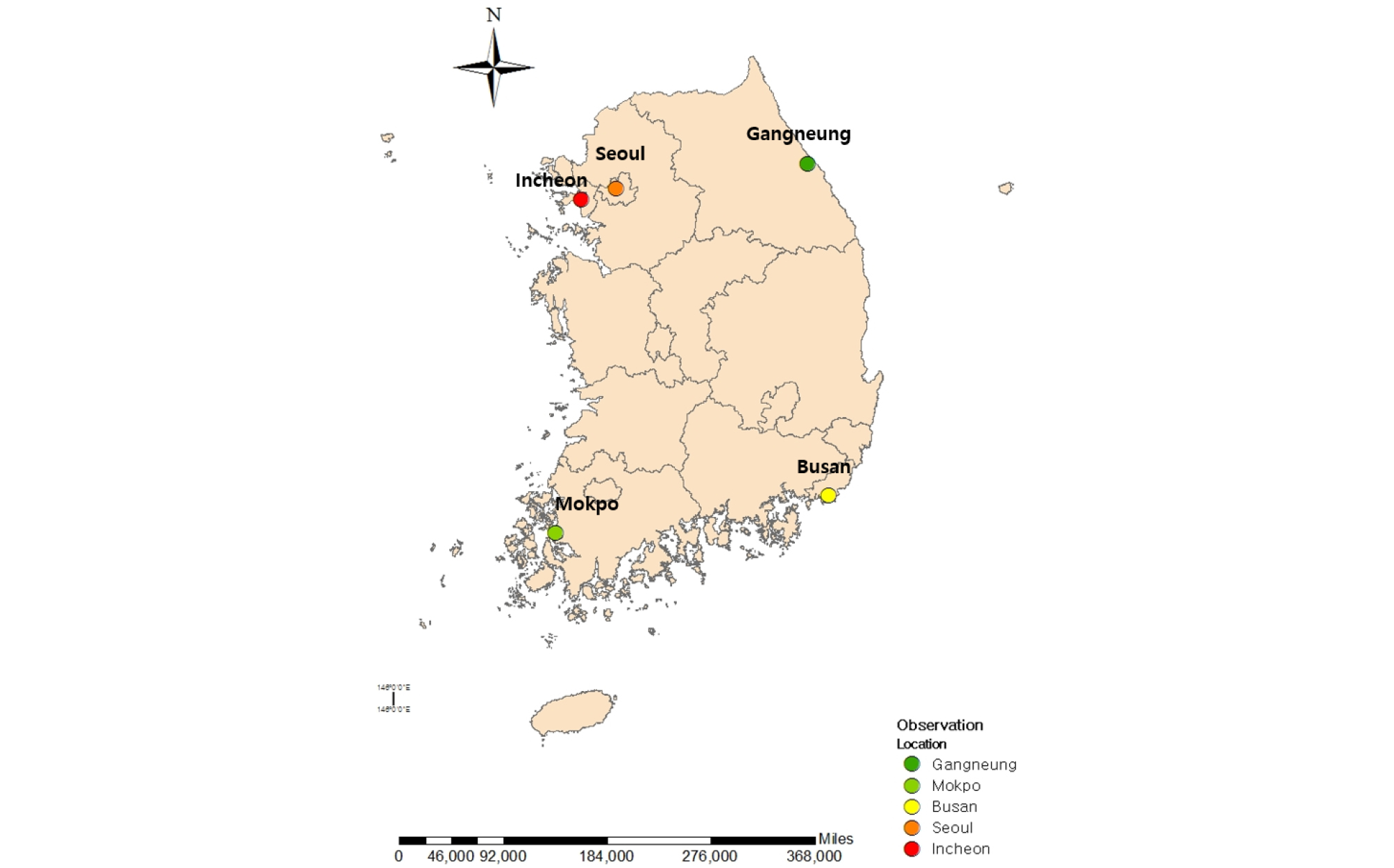
본 연구에서는 우리나라 관측소 중 5개 지점을 선정하였으며, 위치는 Fig. 1과 같다. 선정된 5개의 관측소(서울, 인천, 부산, 강릉, 목포)는 북위 33°에서 43°에 위치하며, 동경 124°에서 131°에 위치한다. 5개 관측소는 과거기간(1970-2005)의 강수량이 충분히 확보되어 있고, 내륙과 해안 지역에 골고루 위치하여 4계절에 따른 강수의 계절성도 잘 나타난다.
2.3 전지구모형
GCM은 대기, 해양, 빙하 및 지표면의 물리적 과정을 나타내며, 온실가스 농도 증가에 따른 기후의 변화 및 미래 기후 예측을 분석하는데 유용한 모형이다. GCM은 3차원의 격자로 구성되어 있는 모형으로서 격자간의 간격은 100-300 km (위도0.94°~경도2.81°)로 구성되어 있다. 본 연구에서 사용된 GCM은 현재 많이 사용되고 있는 CMIP5를 근거로 작성된 AR5를 기준으로 생성되었으며, 다양한 기후요소를 포함하고 있다. 본 연구에서 사용된 GCM은 Table 1과 같이 다양한 연구에서 우리나라에 적용된 바 있는 CESM1-BGC, CCSM4, CNRM-CM5, CSIRO-Mk3.6.0, BCC-CSM1.1, GFDL-ESM2G, MPI-ESM-LR, HadGEM2-AO, INM-CM4로 총 9개이다(Cho et al., 2018; Lee and Kim, 2010; Song and Chung, 2019).
Table 1. Basic information of GCMs used in this study
2.4 분위사상법
분위사상법은 대표적으로 많이 사용되고 있는 편이보정방법 중 하나이며, 다양한 형태로 사용되고 있다. Quantile delta mapping이 개발되어 강수의 극값에 대한 장기추세를 고려하여 기후 모형 편이보정에 반영한 연구(Eum and Cannon, 2017)와 spatial disaggregation with quantile delta mapping (SDQDM) 방법도 개발되어 이를 가뭄분석에 활용한 연구도 있다(Sung et al., 2018). 또한 Cho et al. (2018)은 simple quantile mapping (SQM)과 SDQDM 방법으로 상세화를 수행하였으며, 편이보정 이전의 GCM에 대하여 강수 및 기온의 시․공간적 단위의 재현성 평가를 통해 22개 GCM을 선정하였다. GCM은 격자 형태의 자료로 구성되어 있으므로 실제 관측되는 지점과 비교하였을 때 강수량 및 수문학적 요소들에서 차이가 발생한다. 분위사상법은 GCM의 모의값과 관측값의 차이를 보정하기 위해 대표적으로 사용되는 방법이며, 차이를 보정하는데 있어서 효과가 큰 방법이다(Dosiom and Paruolo, 2011; Gudmundsson et al., 2012). 분위사상법은 대표적으로 모수변환법(Parametric transformation), 비모수변환법(Non-parametric transformation), 분포기반변환법(Distribution derived transformation)으로 구분된다. 분위사상법은 GCM 모의값의 분포를 관측값의 분포와 동일하게 하기 위해 분위함수를 산정해야하며, 산정식은 (1)과 같다.
| $$P_o=h(P_m)$$ | (1) |
여기서 Po는 관측된 강수량 값, Pm은 GCM의 모의된 강수량 값, 그리고 h는 변환함수를 나타낸다. 이를 토대로 관측된 강수량은 누적분포함수의 역함수로 산정되며 Eq. (2)와 같다.
| $$P_o=F_o^{-1}(F_m(P_m))$$ | (2) |
여기서 Fm은 Pm의 누적분포함수이고, 은 Po의 누적분포함수의 역함수이다.
2.4.1 모수변환법
모수변환법은 가장 많이 사용되는 분위사상법 중 하나로 선형(Linear), 규모(Scale), 지수점근변환함수(exponential asymptotic transfer function) 방법이 사용된다(Piani et al., 2010). 지수점근변환함수는 Eq. (3)과 같으며, 선형은 Eq. (4), 규모는 Eq. (5)와 같다.
| $$P_o=(a+b\times P_m)\times(1-\exp(-\frac{P_m}\tau))$$ | (3) |
| $$P_o=a+b\times P_m$$ | (4) |
| $$P_o=b\times P_m$$ | (5) |
여기서 a는 가산보정계수, b는 곱셈보정계수, (a+b+Pm)는 점근선을 산정하기 위한 공식, 그리고 는 점근선에 접근하는 벡터를 결정하는 값이다. 본 연구에서는 모수변환법 중 선형, 규모, 지수점근변환함수을 사용하였다.
2.4.2 비모수변환법
비모수변환법은 대표적으로 경험적 추정법(Empirical quantiles), 로버스트 회귀분석(Robust regression), 스플라인 평활방법(Smoothing spline)이 사용된다. 경험적 추정법은 GCM의 모의값과 관측값의 경험적 누적분포함수를 일치시켜 변환하는 방법이며, 로버스트 회귀분석은 Q-Q Plot에서 관측값에 모의값을 대응시켜 지역선형최소자승 회귀분석식을 이용하여 일치시키는 방법 중 하나이고, 선형 방법과 Tricub 방법을 사용하여 산정한다. 스플라인 평활방법은 Q-Q Plot에서 스플라인 평활함수를 사용하여 추정하는 방법이다(Boe et al., 2007). 본 연구에서는 비모수변환법에서 로버스트 선형, 로버스트 tricub, 스플라인 평활함수 방법을 사용하였다.
2.4.3 분포기반 변환법
분포기반 변환법은 Eq. (2)에 포함되는 변환함수를 분포함수로 적용하는 방법이다. 분포기반 변환법은 현재 관측소의 실측값과 GCM의 모의값을 보정하는데 사용된다. 적절한 함수를 개발하여 적용할 수 있으며, 다양한 함수들을 재조합하여 적용할 수도 있다. 강수 분포 모의에 적합한 Bernoulli- Gamma와 강수량 극치 분석에 적합한 Bernoulli-Weibull 및 Bernoulli-LogNormal 방법 등이 있다. 여기서 Bernoulli는 강수의 발생을 결정하는데 사용되며, Gamma, Weibull, Log Normal은 강수량을 분석하는데 사용된다. Gamma는 Shape과 Scale의 매개변수를 이용하여 강수량을 추정하며(Cannon, 2008), 확률 밀도 함수를 산정하는 방법은 Eq. (6)을 사용하였다.
| $$g(x)=\left\{\begin{array}{l}\pi\times\gamma(x)\;\mathrm{if}\;x\;>\;0\\1-\pi\;\;\;\;\;\;\mathrm{if}\;x\mathit\;\leq\;0\end{array}\right.$$ | (6) |
여기서 는 Gamma 분포의 확률밀도함수를 나타내며, 는 강수가 발생할 Bernoulli 확률이다. 누적분포함수를 산정하는 방법은 Eq. (7)과 같으며, 는 Gamma 분포의 누적분포함수를 나타낸다.
| $$G(x)=\left\{\begin{array}{l}1-\pi+\pi\times\;\Gamma(x)\;\;\;\mathrm{if}\;x\;>\;0\\1-\pi\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{if}\;x\mathit\;\leq\;0\end{array}\right.$$ | (7) |
누적분포의 역함수를 산정하는 방법은 Eq. (8)과 같으며, 는 Gamma 분포의 누적분포함수 역함수를 나타내며, p는 누가확률을 나타낸다.
| $$G^{-1}(p)=\left\{\begin{array}{l}\Gamma^{-1}(\frac{p-1+\pi}\pi)\;\;\;\mathrm{if}\;\pi\;>\;1-p\\0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{if}\;\pi\;\leq\;1-p\end{array}\right.$$ | (8) |
본 연구에서 분포기반 변환법은 Bernoulli-Gamma, Bernoulli-Weibull, Bernoulli-LogNormal 방법을 사용하였다. Table 2는 본 연구에서 사용된 편이보정방법을 나타낸 것이다.
Table 2. Bias correction methods used in this study
2.5 역거리가중치법
역거리가중치법은 미계측 지점의 주변 지점의 실측값을 사용하여 공간적으로 보간하는 방법이다. 역거리가중치법은 지리학의 Tobler 제1법칙에 근거하며, 거리가 가까운 지점의 값이 상대적으로 거리가 먼 지점의 값보다 관련성이 높다는 사실을 이용한다(Tobler, 1970). 미계측 된 지점의 강수량을 산정하기 위해서 Eq. (9)을 사용하고, Eq. (10)을 사용하여 가중치를 산정한다.
| $$P_i=\sum_{k=1}^N\frac{w_s(x)}{{\displaystyle\sum_{k=1}^N}w_s(x)}P_i(x_s)$$ | (9) |
여기서 는 미계측 지역의 강수량, 는 미계측 지역 주변 GCM 모형의 격자 강수량이며 격자는 2개 이상의 지점이 포함된다.
| $$w_s(x)=\frac1{D_{(x,x_s)}^c}$$ | (10) |
여기서 는 보간 가중치이며, 는 두 격자간의 거리이다. 가중치를 계산할 때 Shepard 방법을 사용하였다. Shepard 방법은 Eq. (10)에서 Dc의 지수 c의 범위가 0~1 사이의 값을 가지게 되면 전체적으로 데이터의 분포가 좁게 보간되고, 1보다 크면 데이터의 분포가 넓게 보간된다. 본 연구에는 역거리가중치법을 이용하여 격자 자료를 관측소 지점 자료로 보간하였다.
3. 결 과
3.1 전망기간의 편이보정결과
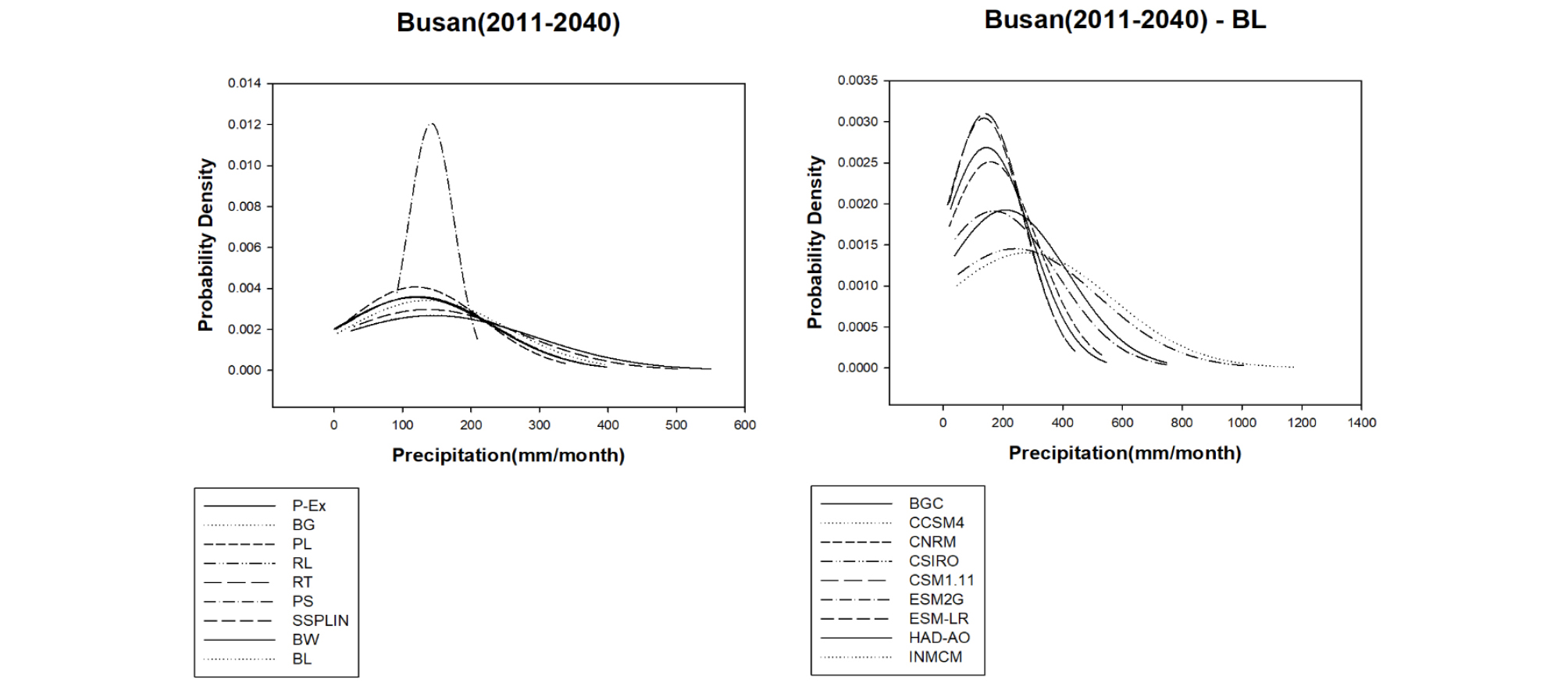
본 연구는 과거기간(1970-2005)에 대해 5개의 지점의 GCM에 9개(Bernoulli-Gamma (BG), Bernoulli-LogNormal (BL), Bernoulli-Weibull (BW), Robust Linear (RL), Robust Tricub (RT), 스플라인 평활함수(SSPLIN), 지수점근선변환함수방법(P-EAT), Linear (PL), Scale (PS))의 분위사상법을 적용한 결과를 토대로 3개의 전망 기간(2011-2040년, 2041-2070년, 2071-2100년)별로 월 강수량을 산정하였다. Fig. 2는 부산 지점의 2011-2040년에 대한 미래 월 강수량의 확률밀도함수를 산정하였으며, 편이보정방법별로 산정한 월 강수량과 BL에서 GCM별로 산정된 월 강수량을 각각 나타냈다. 편이보정방법과 GCM 모두 100 mm와 200 mm 사이의 월 강수량이 가장 많이 산정되었다. 편이보정방법에서 BG를 제외한 8개의 방법은 대체로 월 강수량의 분포가 넓게 산정되었으며, 월 강수량의 분포 차이가 크지 않았으나, 최대 강수량의 차이는 크게 산정되었다. 반면 GCM별 월 강수량의 분포 차이는 크게 산정되었으며, 최대 강수량의 차이도 크게 산정되었다.
3.2 불확실성 비교
본 연구는 과거기간(1970-2005)에 대해 5개 지점의 GCM에 9개의 분위사상법을 적용한 결과를 토대로 전망 기간에 구간별(2011-2040년, 2041-2070년, 2071-2100년)로 월 강수량 산정하였다. 산정된 월 강수량을 평균하여 GCM의 변동성을 기준으로 산정한 결과와 편이보정방법의 변동성을 기준으로 나누어 표준편차와 IQR을 산정하였다. 서울 지점의 2011년부터 2040년 구간에서 산정한 결과는 Table 3과 같다.
Table 3. Monthly average precipitation analysis of each criteria (2011-2040, Seoul)
서울의 전망기간 구간 중 2011년부터 2040년의 월 평균 강수량을 사용하여 표준편차와 IQR을 계산하였다. 편이보정의 기준과 GCM의 기준으로 나누어 각각 확인하였고, 기준별 표준편차와 IQR을 계산하였다. Table 3에서 GCM의 변동성을 기준으로 산정된 결과는 표의 행별로 평균, 표준편차, IQR를 계산한 결과이며, 편이보정방법의 변동성을 기준으로 산정된 결과는 표의 열별로 평균, 표준편차, IQR를 계산한 결과이다. 위의 방법을 토대로 5개의 지점에서 3개의 구간별로 기준별 평균, 표준편차, IQR를 산정한 결과는 Table 4와 같다.
Table 4. Monthly average precipitation analysis of each observatories
3.2.1 표준편차
2011년부터 2040년 구간에서 GCM을 기준으로 계산된 서울, 부산, 인천, 강릉, 목포 지점 순으로 표준편차를 분석한 결과는 13.4, 16.9, 11.0, 15.8, 7.5이며, 편이보정방법의 기준으로는 12.7, 23.5, 9.0, 23.3, 7.6으로 계산되었다. 2011년부터 2040년에서 서울과 인천 지점에서는 예측된 강수량이 GCM 별로 더 넓게 분포하였으나 다른 세 지점은 편이보정 방법으로 인해 차이가 더 크게 나타났다.
2041년부터 2070년 구간에서 GCM을 기준으로 계산된 5개의 지점의 표준편차 분석결과는 서울, 부산, 인천, 강릉, 목포 지점 순으로 15.4, 18.8, 12.2, 17.3, 10.9이며, 편이보정방법 기준으로는 13.4, 24.9, 9.8, 24.9, 8.7로 산정되었다. 서울과 인천 뿐만 아니라 목포까지 예측된 강수량이 GCM 별로 더 넓게 분포하였다. 전 구간과 비교하였을 때 서울과 인천에서는 GCM 기준의 결과와 편이보정방법 기준의 결과에 대한 차이가 증가하였고, 부산과 강릉에서는 차이가 감소하였으며, 전 구간과는 반대로 목포에서는 GCM 기준의 결과가 더 크게 산정되었다.
2071년부터 2100년 구간에서 5개의 지점을 GCM과 편이보정방법을 기준으로 계산된 결과는 서울, 부산, 인천, 강릉, 목포 지점 순으로 각각 21.9, 25.2, 18.7, 24.2, 12.2와 14.4, 27.1, 11.6, 26.7, 9.6으로 산정되었다. 서울, 인천, 목포 지점에서는 GCM 별 월강수량의 차이가 편이보정방법 별 차이보다 훨씬 컸으며, 부산과 강릉은 두 차이가 크게 감소하였다.
3.2.2 IQR
2011년부터 2040년 구간에서 GCM과 편이보정방법을 기준으로 서울, 부산 인천, 강릉, 목포 순으로 IQR을 계산한 결과는 각각 15.8, 18.1, 12.5, 13.4, 6.7과 18.5, 15.7, 10.7, 19.4, 8.1로 산정되었다. 2011년부터 2040년까지 IQR 분석결과로는 부산, 인천, 강릉에서는 GCM을 기준으로 산정된 IQR의 간격이 편이보정방법을 기준으로 산정된 간격보다 넓게 산정되었다.
2041년부터 2070년 구간에서 GCM을 기준으로 계산한 결과는 19.6, 20.5, 14.0, 21.2, 8.7이며, 편이보정방법을 기준으로 도출한 결과는 20.9, 15.7, 10.6, 14.8, 7.9로 산정되었다. 서울 지점을 제외한 4개의 지점에서는 GCM을 기준으로 산정된 결과가 IQR의 간격이 더 넓게 산정되었다. 서울 지점에서는 GCM과 편이보정방법의 차이가 전 구간과 비교하였을 때 GCM을 기준으로 감소하였으나, 4개의 지점에서는 두 기준의 차이가 증가하였다.
2071년부터 2100년 구간에서 GCM을 기준으로 계산한 결과는 서울, 부산, 인천, 강릉, 목포 지점 순으로 34.0, 26.6, 27.0, 38.2, 12.1이며, 편이보정방법의 결과는 9.0, 17.4, 10.9, 14.0, 7.9로 산정되었다. 2071년부터 2100년의 구간에서 분석결과로 5개의 지점 모두 GCM을 기준으로 산정된 간격이 더 넓어졌으며, 전체 구간 중 가장 큰 결과값을 도출하였다.
3.3 고찰
위의 결과를 정리하면 Tables 5 and 6과 같다. Table 5는 두 기준의 차이를 산정한 결과이며, 양수는 GCM을 기준으로 산정된 결과값이 큰 것을 나타내고 음수는 편이보정방법을 기준으로 산정된 결과값이 큰 것을 나타낸다. Table 6은 기준별 표준 편차 결과와 IQR의 간격이 크게 선정된 횟수를 나타냈다. 표준 편차에서 GCM을 기준으로 한 결과가 구간이 지날수록 선정횟수가 증가하며, IQR의 결과에서는 GCM을 기준으로 산정하였을 때 선정횟수가 2011년부터 2040년 구간을 제외한 모든 구간에서 높게 산정되었다. 서울, 부산, 인천, 강릉, 목포의 5개 지점에서 GCM과 편이보정방법별 불확실성 분석결과로 표준 편차에서는 두 기준 모두 2071년부터 2100년 구간의 값이 다른 구간보다 크게 산정되었으며, 강수량의 양 극값의 차이가 크게 산정되는 결과를 도출하였다. 서울, 인천, 목포에서는 GCM을 기준으로 산정한 월 강수량이 편이보정을 기준으로 산정한 월 강수량보다 넓게 산정하는 결과를 도출하였으며, 반대로 부산과 강릉에서는 편이보정방법을 기준으로 산정된 월 강수량이 더 넓게 산정되었다. 5개의 지점 중 서울, 인천, 목포에서는 GCM을 기준으로 산정된 결과가 평균을 중심으로 더 넓게 산정되었으며, 구간이 지날수록 편이보정방법을 기준으로 산정된 결과와의 차이가 커졌다. 부산과 강릉에서는 편이보정방법을 기준으로 산정된 결과가 평균을 중심으로 넓게 산정되었으나, 구간이 지날수록 GCM을 기준으로 산정된 결과와의 차이가 감소하였다.
Table 5. Results of differences in analytical metrics in Bias correction and GCMs
Table 6. Selected number of standard deviations and IQR in Bias correction and GCMs
| 2011-2040 | 2041-2070 | 2071-2100 | ||
| STDV | GCMs | 2 | 3 | 3 |
| Bias correction | 3 | 2 | 2 | |
| IQR | GCMs | 2 | 4 | 5 |
| Bias correction | 3 | 1 | 0 | |
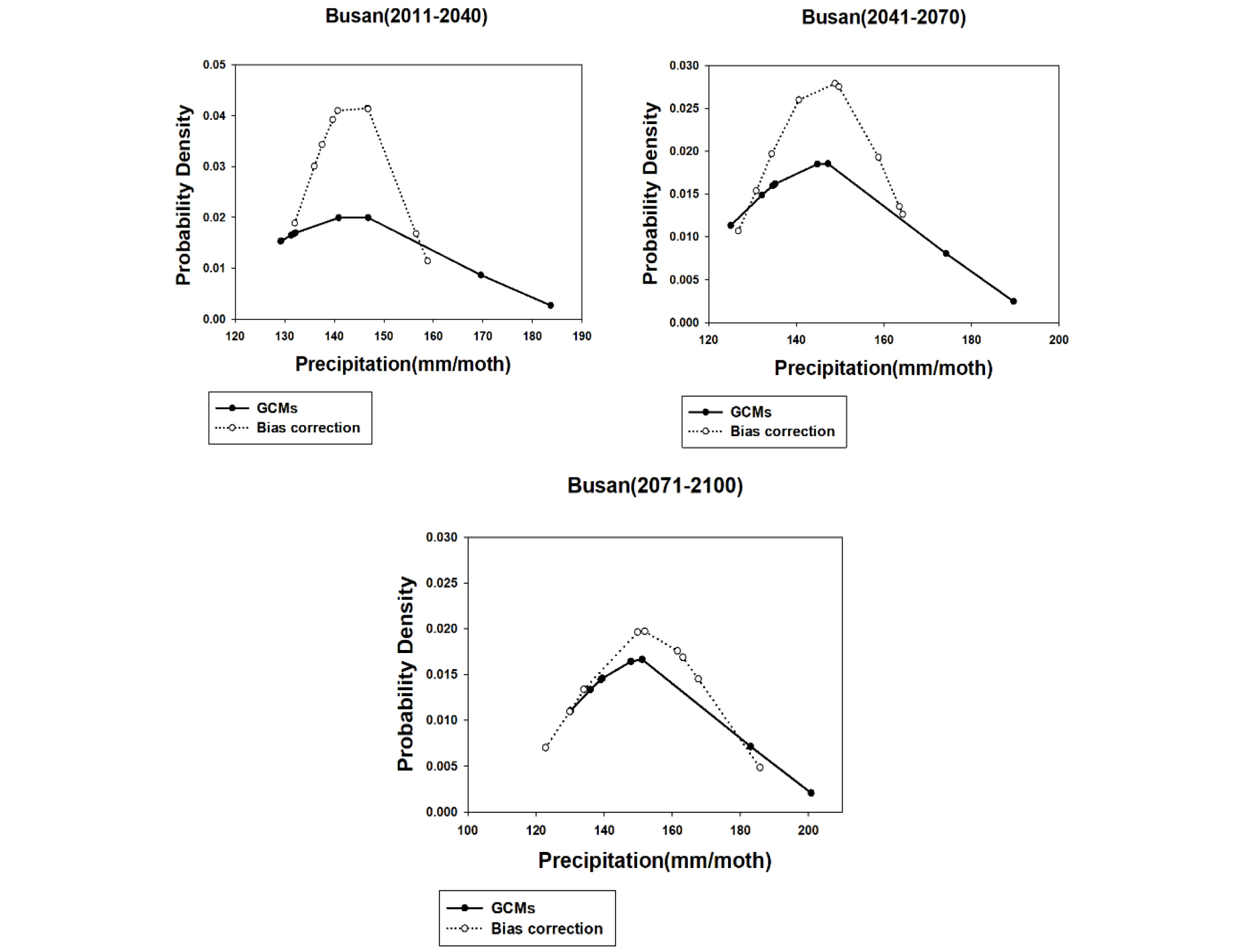
IQR의 분석결과로 2071년부터 2100년의 구간의 간격이 다른 구간의 간격과 비교하였을 때 가장 크게 산정되었으며, IQR의 사이에 포함되는 월 강수량을 다른 구간과 비교하였을 때 강수량의 폭이 넓게 산정되었다. 서울의 2011년부터 2040년, 2041년부터 2070년과 목포의 2011년부터 2040년의 결과를 제외하고 GCM을 기준으로 산정된 IQR이 더 넓게 산정되었으며, 구간이 지날수록 GCM을 기준으로 산정된 간격과 편이보정방법을 기준으로 산정된 간격과의 차이가 편이보정방법을 기준으로 감소하였으며, 최종적으로는 5개의 지점 모두 GCM을 기준으로 산정된 간격이 더 넓게 계산되었다. 위의 결과를 토대로 부산 지점의 GCM과 편이보정의 월 강수량을 평균한 결과를 확률밀도함수로 산정하였으며, 결과는 Fig. 3와 같다. 기간이 지날수록 편이보정을 기준으로 산정된 월 강수량의 분포가 점차 넓어지고 있으며, GCM을 기준으로 산정된 결과와 비교하였을 때 차이가 점차 줄어들었다.
4. 결 론
본 연구는 지점별 과거기간(1970-2005년)에 사용된 9개의 GCM과 9개의 편이보정방법을 기준으로 산정된 결과를 토대로 RCP4.5의 전망 기간(2011-2100년)을 3개(2011-2040년, 2041-2070년, 2071-2100년)의 구간으로 나누어 월 강수량을 산정하였다. 산정된 강수를 토대로 표준 편차와 IQR을 사용하여 기준별 변동성을 정량화하였고, 그 결과를 토대로 불확실성을 비교하였다.
표준 편차에서 부산과 강릉을 제외한 3개의 지점은 GCM을 기준으로 산정된 결과가 편이보정방법을 기준으로 산정된 결과보다 평균을 기준으로 더 넓게 산정되었으며, 인천과 강릉에서는 구간이 지날수록 GCM을 기준으로 산정된 결과와 편이보정방법을 기준으로 산정된 결과와의 차이가 감소하였다. IQR의 분석결과로 5개의 지점 모두 구간이 지날수록 GCM을 기준으로 산정된 간격이 넓게 산정되었다. 위의 결과를 토대로 5개의 지점에서는 구간이 지날수록 표준 편차가 GCM을 기준으로 점차 넓게 산정되었으며, 편이보정방법을 기준으로 산정된 결과가 넓은 지점은 GCM을 기준으로 산정된 결과와의 차이를 비교하였을 때 감소하였다. IQR의 분석결과로 5개의 지점 모두 기간이 지날수록 GCM을 기준으로 점차 크게 산정되었다. 기간별 선정 횟수로 표준 편차에서는 GCM을 기준으로 산정하였을 때 선정된 횟수가 편이보정방법을 기준으로 하였을 때 보다 많이 선정되었다. IQR의 결과에서는 GCM을 기준으로 산정하였을 때 선정 횟수가 많았으며 구간이 지날수록 GCM을 기준으로 산정된 결과가 더 많이 선정되었다. 위의 결과를 토대로 과거기간의 편이보정방법과 GCM 선정 방법에 따라 전망기간의 강수 형태도 다르게 산정될 수 있다는 결과를 도출하였으며, 과거기간의 편이보정방법과 GCM 선정 방법의 중요성을 확인할 수 있었다. 지점별 분석결과는 다르게 나타났으나, 구간이 지날수록 GCM을 기준의 결과가 점차 크게 산정되었다.
본 연구에서는 RCP4.5만을 사용한 결과로서 다양한 RCP 시나리오를 추가하여 연구를 수행하여야 하며, 지점을 보다 확대하면 보다 일반화된 결과를 제시할 수 있을 것으로 기대된다.