1. 서 론
2. 모형의 개발
2.1 CTM-2D
2.2 하천 내 유해화학물질의 거동 특성
2.3 흡․탈착 관련 수학적 모형 및 매개변수 추정
2.4 휘발․생화학적 반응 관련 수학적 모형 및 매개변수 추정
2.5 모형의 구조
3. 모형의 검증
4. 모형의 적용
4.1 대상 지역 및 데이터
4.2 유의 반응항 판별을 위한 민감도 분석
4.3 유의 반응항을 고려한 수치 모의
5. 결 론
1. 서 론
근년에 우리나라에서 일어나는 하천 내 유해화학물질 유입사고 발생건수는 증가하는 추세를 보이고 있다. 대표적인 사고로 1991년 구미 근교에서 일어난 페놀 원액이 유출되어 낙동강에 오염사고가 발생하였으며, 1994년 달성 근교의 유기용재(톨루엔, 밴젠) 유출사고, 2008년에는 김천 근교에서 페놀 유출사고가, 달성 근교에서 기름유출사고가 일어났으며, 최근 2014, 2017년에는 낙동강과 오십천에서 황산 유출사고 등이 일어났다. 특히 국내 취수량의 90 %는 하천 및 댐저수지의 지표수에서 취수하기 때문에 하천내 수질오염사고는 더욱 직접적인 영향을 미친다. 따라서, 하천 수질오염사고에 대한 적절한 대응책을 수립할 필요가 있다. 대응책은 사고의 유형 및 하천의 규모에 따라 달라지며, 일반적으로 소하천에서 사고가 일어난 경우 화학처리 및 임시저류시설과 같은 물리․화학적 초동 조치를 통해 대응하고 있다(NIER, 2012). 하지만, 대하천에서 일어나는 사고의 경우 이러한 직접적인 방법으로는 해결할 수 없으며, 오염 물질의 시공간적 분포를 예상하여 체계적이고 다각적인 대책을 마련할 필요가 있다.
하천수질사고 대응을 위하여 국내외의 많은 나라들은 수질오염 사고대응체계를 구축하여 운영하고 있다. 국외 대응체계로는 ICPR (라인강 보호위원회)의 RAM (Griffioen, 1989)이 있으며, 미국 환경보호국의 ICWater (Samuels et al., 2005)이 있다. 또한 국내의 대응체계로는 국립환경과학원 (NIER)의 WARMS (Mun et al., 2012)와 지류지천사고대응시스템(NIER, 2012)이 있다. 하지만 국내의 사고대응체계는 자체적으로 개발된 수질모델이 아닌 해외의 수질모형을 차용하고 있기 때문에 오염물질의 입력변수 확보에 제한이 있다고 평가된 바 있다(Ministry of Environment, 2015). 특히 WARMS의 경우 3차원 모형인 EFDC (Environmental Fluid Dynamics Code)라는 수리모의, 퇴적물 오염 및 부영양화 모의를 포함하는 다기능 지표수 모형(Tetra Tech, 2007)을 채택하였으나, 등방성 분산 계수를 반영하여 다지 하천이 만연한 한국 하천에 적합하지 않으며, 모형의 검보정이 미흡한 상태에서 사용되고 있는 실정이다.
유해화학물질 거동해석에 관한 2차원 수질모형 개발연구는 다수 진행 된 바 있다. 수치해석법에 따라 유한요소법 기반의 모형(Jia et al., 2013; Hayter et al., 1999)과 유한차분법 기반의 모형(Wool, 2017)으로 구분할 수 있다. 미시시피 대학에서 개발한 CCHE2D(Jia et al., 2013)는 유한요소법을 기반으로 비정상적인 난류 자유 표면 흐름과 유해화학물질 수송, 수질, 홍수, 하구 및 연안해석을 할 수 있도록 개발되었으며, WASP8 (Wool, 2017)은 자연 현상과 환경재해에 따른 수질 변화를 해석하고 예측하는 모형이 개발된 바 있다. 국내에서는 2차원 오염물질 거동 모형인 CTM-2D (Lee and Seo, 2007)가 개발되어 다양한 분야에 적용, 검증한 바 있으나(Lee and Seo, 2010; Seo et al., 2016; Park and Song, 2018; Park and Seo, 2018; Kim et al., 2018), 아직 유해화학물질의 거동 특성을 고려한 모형은 개발된 바 없다.
유해화학물질의 거동 특성을 고려한 모형은 흡․탈착, 휘발, 생화학적 반응 등 다양한 반응메커니즘을 반영하므로 복잡한 방정식의 해석이 요구되어 상당한 계산 소요시간을 필요로 한다. 하지만 신속한 대응이 요구되는 실제 사고 시에는 수질모형의 계산 소요시간을 줄이는 것이 중요하다. 따라서 신속한 모의를 필요로 할 시 각 물질의 반응특성에 따라 주요반응만 고려하여 계산소요시간을 단축할 필요가 있다. 기존 시스템은 매일 자동 업데이트되는 수리모의 결과를 바탕으로 사고발생시 미리 구축된 DB에서 자료를 취득하여 오염 물질의 시공간 분포를 예측할 수 있도록 운영되고 있으나, 오염물질 특성에 따라 유의하지 않은 반응항을 계산하는 데 추가적인 시간이 소요될 수 있다. 위의 사항들을 고려하면, 유해화학물질의 특성을 고려한 독성물질오염물질 모형을 국내 자체적으로 개발할 필요가 있다고 할 수 있다.
본 연구에서는 하천에 유출된 유해화학물질의 거동을 분석하기 위한 수심 평균 2차원 하천수질모형을 개발하고, 모형의 계산속도를 최소화하기 위해 유의반응항 판별을 이용한 효율적 모의수행 기법을 제시하였다. 유해화학물질의 거동을 지배하는 방정식과 해석 방법을 개발하고, 개발된 모형의 계산 결과를 해석해와 비교함으로써 모형을 검증하였다. 나아가서 실제 하천 지역에 개발된 모형을 통해 모의를 수행하고, 효율적인 수질모의 수행을 위한 유의반응항 판별 기법을 수립하였다.
2. 모형의 개발
2.1 CTM-2D
본 연구에서 개발한 유해화학물질 거동해석모형은 오염물질거동해석 모형인 CTM-2D (Lee and Seo, 2007)를 기반으로 하였으며, 반응메커니즘을 추가하여 모형개발을 완료하였다. CTM-2D는 하천수질 해석모형으로서, 비압축성 유체에서 물질의 3차원 이송․확산 방정식을 수심 적분한 2차원 이송-분산 방정식을 지배방정식으로 사용하는 2차원 유한요소모형이다(Lee and Seo, 2010). 구조적/비구조적 격자로 이뤄진 격자에서 유한요소법(FEM, Finite Element Method)를 기반으로 Streamline-Upwind Petrov-Galerkin (SU/PG) 기법(Brooks and Hughes, 1982)에 근거하여 가중 잔차법을 이용해 수치해를 구한다.
CTM-2D는 대하천의 오염물질의 거동해석을 위해 많은 연구들에서 사용되었다. Lee and Seo (2007, 2010)는 CTM-2D를 이용해 한강변 하수처리장에서 유출된 BOD의 2차원적인 거동에 조류가 미치는 영향을 분석하였으며, Seo et al. (2016)과 Park and Song (2018)은 섬강과 홍천강과 같은 만곡하천에서 보존성물질(로다민WT)의 2차원 혼합거동에 대해 분석하였다. 또한 Kim et al. (2018)은 수온과 하천흐름이 조류의 공간분포에 미치는 영향에 대해 낙동강에서 연구를 수행한 바 있다. 하지만 기존의 국내 모형에서는 유해화학물질의 반응 특성을 고려한 2차원 모형이 개발된 바 없으므로 본 연구에서는 유해화학물질의 반응 특성을 반영하여 CTM-2D의 독성물질 모듈을 개발하였다.
2.2 하천 내 유해화학물질의 거동 특성
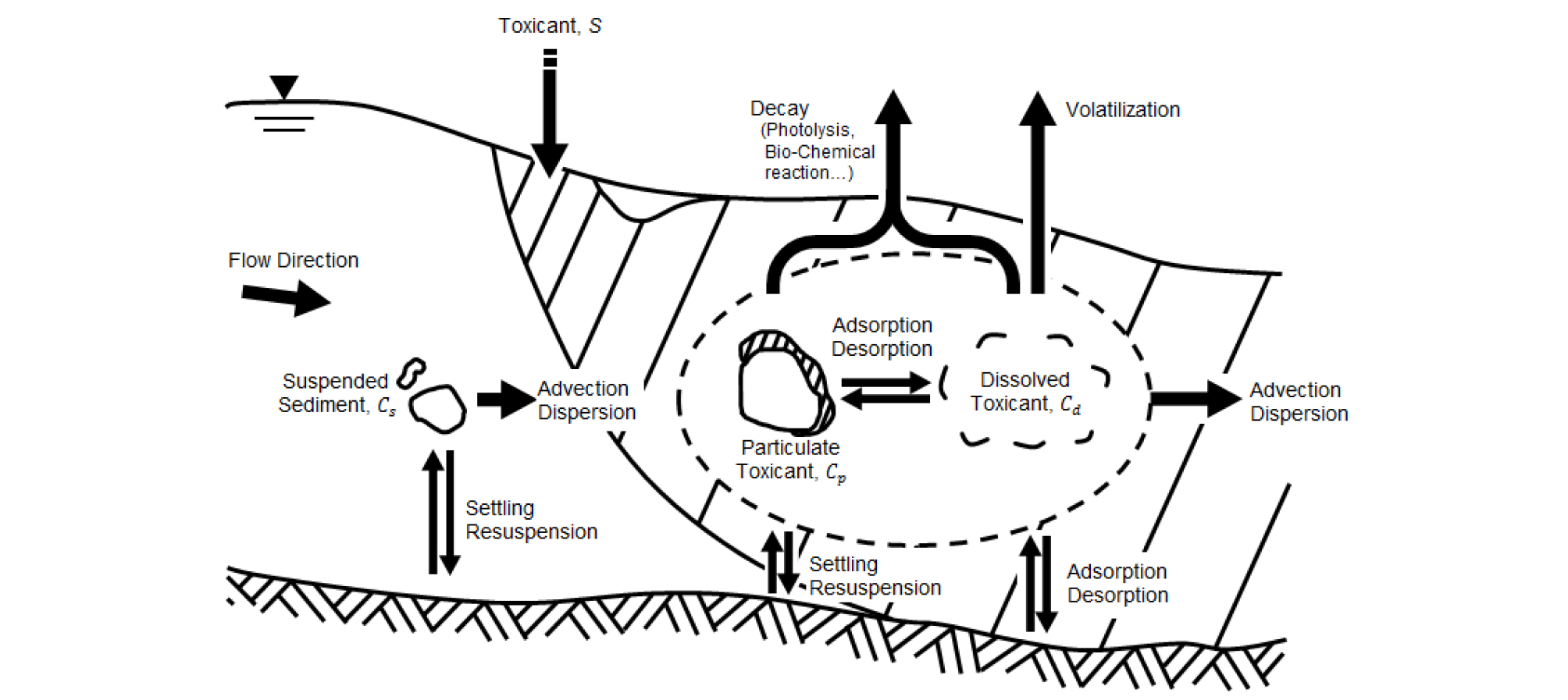
본 연구에서는 하천에 유입된 유해화학물질의 거동 특성을 반영한 2차원 오염물질 거동해석 모형을 개발하였다. 하천에 유입된 유해화학물질은 Fig. 1에 도시한 바와 같이 복잡한 물리적 상호 작용, 생화학적 반응 과정과 동시에 이송․확산을 하며 이동한다. 유입된 유해화학물질은 물에 용해된 형태와 부유사 및 하상에 흡착된 미립자 형태로 존재한다. 용존 형태의 화학물질과 부유사에 흡착된 화학물질은 이송․확산에 의해 지배되며, 하상에 흡착된 물질은 소류사의 이동이 지배적인 메카니즘으로 작용한다. 따라서 수체에 유입된 유해화학물질은 Fig. 1에 도시한 바와 같이 3개의 상 간에 흡․탈착, 휘발 그리고 생화학적반응 과정을 통해 물질교환이 일어나게 된다(Thomann et al., 1987). 이에 따라 본 연구에서는 CTM-2D의 지배방정식인 수심평균 이송․확산 방정식을 기반으로 용존농도 및 부유사 농도의 거동을 재현하고, 각 상 간의 흡․탈착, 휘발과정으로 인한 물질교환에 관한 수학적 모형을 채택하여 유해화학물질의 거동 해석모형을 개발하였다.
여기서 C 는 수심평균 농도; t는 시간; u, v는 종방향 및 횡방향 수심평균 유속, DL, DT는 종방향 분산계수 및 횡방향 분산계수, S는 반응항이다.
2.3 흡․탈착 관련 수학적 모형 및 매개변수 추정
흡․탈착은 두 상 사이의 계면에 축적된 물질의 이동과정을 일컫는데, 하천에 유입된 화학물질의 경우 이송․확산과 함께 발생한다. 흡․탈착으로 인한 물질교환의 경우 단시간에 이루어지는 것으로 보는 이론도 있으나, 하천에서의 오염물질의 이동속도 및 흡․탈착 속도를 고려하여 시간에 따른 농도의 변화를 자세히 분석할 필요가 있다(Kan et al., 1994; Lick, 2008). 따라서 하천에서 흡․탈착 과정을 고려하기 위해서는 시간에 따른 농도의 변화를 분석하게 된다. 흡․탈착 과정은 확산반응과정으로 가정하여 이를 직접 계산하는 확산모형(Diffusion Model)과 계산의 효율성을 위해 간단한 근사해로 재현하는 물질교환모형(Mass Transfer Model)이 있다. 일반적으로 수질모형에서는 물질교환 모형을 사용하고 있으며, 본 연구에서도 다음과 같은 물질교환식을 적용하였다.
| $$\frac{\partial C_p}{\partial t}=-k_s(C_p-K_pC_d)$$ | (2) |
여기서 Cp, Cd는 각 각 입자 내 평균농도 및 용존농도(kg/L)이며, ks는 물질교환속도(1/day)이며, Kp는 물-토양 분배계수 (L/kg)이다. 흡․탈착으로 인한 물질교환속도의 경우, 대상물질과 흐름조건에 따라 달라지므로 실험 결과를 관측하여 사용하는 것이 일반적이지만 선행 연구자들은 물-토양 분배계수를 통해 추정하는 식을 제시하였다. 본 연구에서는 Karickhoff and Morris (1985)가 소수성 물질에 대한 흡․탈착률과 토양-물 분배계수의 관계로 제시한 다음과 같은 식을 이용하였다.
| $$k_s=(0.03K_d)\;^{-1}$$ | (3) |
여기서 ks는 토양-물 사이의 흡․탈착율로 시간당 변화율[1/h]이며, Kd의 단위는 l/kg이며, 이 식의 상관계수(r)는 0.87이다. 또한 다음과 같은 Brusseau and Rao (1989)이 제시한 식도 같이 적용하였다.
| $$k_s=0.301-0.668\log K_d$$ | (4) |
본 연구에서는 Eqs. (3) and (4)를 선택적으로 사용할 수 있도록 하였으며, 이를 식 Eq. (2)에 대입하면 흡․탈착 매개변수는 토양-물 분배계수로 한정된다. 하지만 하천에 임의의 물질이 유입되었을 때는 해당물질의 토양-물 분배계수를 알 수 없어 추정해야하며, 기존 연구자들은 아래의 식과 같이 옥탄올-물 분배계수를 확장하여 토양-물 분배 계수를 추정하였다(Karickhoff, 1979; Karickhoff, 1984).
| $$K_d=f_{oc}K_{oc}$$ | (5) |
| $$K_{oc}=\beta\times(K_{ow})\;^\alpha$$ | (6) |
여기서 foc는 토양의 유기 탄소의 비율이고, Koc는 대상 물질의 유기탄소-물 분배 계수이고, α, β는 실험에 따른 회귀 계수이다.
Table 1과 같이 각 연구의 회귀계수는 물질의 특성이나 옥탄올-물 분배계수의 범위에 따라 달라져 모의대상물질이 어느 범위에 속하는지 고려하여 적용할 필요가 있다. 2000년대에 들어서서는 신약재나 농약재 등과 같은 특정 분야에 쓰이는 물질 별 분배계수를 연구하거나, 중성자와 이온의 물-옥탄올 분배계수를 통한 토양-물 분배계수를 추정하는 등, 토양-물 분배계수에 관련한 다양한 연구가 이루어지고 있다(Scheytt et al., 2005; Franco and Trapp, 2008; Yamamoto et al., 2009; Kozerski et al., 2014). 하지만, 친수성 물질을 포함한 추정식의 경우 생화학적 반응과 같이 물과 토양 사이에서의 교환 요인으로 작용할 수 있으므로 소수성(hydrophobic) 물질의 분배계수를 추정 시 오차가 발생할 수 있다. 본 연구의 유해화학물질 유입사고대응을 위한 수질모형의 경우, 흡․탈착 메커니즘이 소수성 물질에 한하여 적용이 될 것이기 때문에 물과 토양 사이에서의 물질교환만을 실험한 연구인 Karickhoff(1981)식을 적용하였으며, 이 식의 α와 β의 값은 각각 0.99, 0.45×10-3이다.
Table 1. Regression coefficient between soil-water and organic carbon water partitioning coefficient
| Authors | No. of materials | log Kow | β×103 | α | r |
| Kenaga and Goring (1980) | 45 | -1.7 ~ 6.6 | 24.00 | 0.54 | 0.93 |
| Rao and Davidson (1980) | 15 | -0.5 ~ 5.6 | 0.66 | 1.03 | 0.95 |
| Karickhoff (1981) | 6 | 1.0 ~ 6.5 | 0.45 | 0.99 | 0.99 |
| Schwarzenbach and Westall (1981) | 12 | 2.6 ~ 4.7 | 3.10 | 0.72 | 0.97 |
| Chiou et al. (1983) | 12 | 2.1 ~ 5.6 | 0.30 | 0.90 | 0.99 |
| Mingelgrin and Gerstl (1983) | 7 | 3.1 ~ 6.2 | 1.10 | 0.87 | 0.85 |
| Karickhoff (1983) | 10 | 2.1 ~ 6.6 | 0.63 | 1.00 | 1.00 |
| Mingelgrin and Gerstl (1983) | 7 | 3.1 ~ 6.2 | 1.10 | 0.87 | 0.85 |
| Curtis et al. (1986) | 22 | 1.4 ~ 6.6 | 0.59 | 0.92 | 0.94 |
| Pussemier et al. (1990) | 11 | 2.1 ~ 5.2 | 0.29 | 1.01 | 0.96 |
| Gao et al. (1996) | 119 | -3.0 ~ 9.7 | 5.94 | 0.75 | 0.91 |
| Girvin and Scott (1997) | 3 | 4.7 ~ 7.1 | 0.11 | 1.07 | 0.98 |
2.4 휘발․생화학적 반응 관련 수학적 모형 및 매개변수 추정
휘발 과정과 생화학 반응과정은 일반적으로 선형적인 물질 교환식으로 표현된다. 이에 따라 휘발 및 생화학적 반응의 경우 수질모형에서 하나의 메커니즘으로 간주되어 통합적인 감쇠계수를 사용하는 경우가 있다. 하지만 일부 유해화학물질은 하천으로 배출되었을 때 휘발이 오염물질의 거동의 지배적 요인인 경우가 있어 분리하여 해석할 필요가 있다고 평가된 바 있다(Rathbun and Tai, 1981). 따라서 본 연구에서는 두 현상을 별도로 모델링하였으며, 각 반응항은 다음과 같다.
| $$\frac{\partial C}{\partial t}=\lambda(C_{eq}-C)$$ | (7) |
| $$\frac{\partial C}{\partial t}=k_v(C_{eq}-C)$$ | (8) |
여기서 , kv는 순서대로 생화학 반응과 휘발에 의한 감쇠 계수이다. 일반적으로 주요 물질들의 생화학 반응 계수는 실험을 통해 산정된다. 반면 휘발계수는 하천 수심 및 유속와 같은 수리 특성에 따라서 달라질 수 있어 물질의 고유 특성으로 규정하기가 어렵다. 많은 연구자들은 실험실 실험을 통한 임의의 휘발성 화학물질의 휘발계수와 재폭기 계수와의 관계를 통해 자연에서의 재폭기 계수와 임의의 휘발성 화학물질의 휘발계수의 관계를 추정할 수 있음을 보였다. Tchobanoglous and Schroeder (1985)는 재폭기 계수를 물질의 고유특성인 산소의 수계확산계수와 수리특성인 유속, 그리고 수심을 통해 다음과 같이 제시하였다.
| $$k_r=294(D_{aq,O_2}u)\;^{1/2}/H^{3/2}$$ | (9) |
여기서 kr은 재폭기 계수(1/day); 는 산소의 수계 확산계수(m2/day); H는 하천의 수심(m)이다. 특히 휘발성이 강한 화학물질(액체막 저항이 강한 물질)의 경우 그 비율은 다음과 같이 추정할 수 있다(Dobbins, 1964).
| $$(k_{v,c}/k_{v,o_2})=(D_{aq,c}/D_{aq,o_2})\;^n$$ | (10) |
여기서 kv,c, Daq,c는 임의의 물질의 휘발계수 및 수계확산계수를 의미한다. n 의 값은 0.5 ~ 1 사이로 혼합조건에 따라 달라지는 값이며, 1에 가까울수록 난류가 강한흐름을 의미한다. 자연하천에서는 0.5 ~ 0.65 사이의 값으로 추정되었으며(Skelland, 1974; Smith et al., 1980; Ince and Inel, 1989), 본 연구에서는 0.6(Smith et al., 1980) 값을 사용하였다. 유입된 물질이 자연에 거의 존재하지 않는 물질이라고 가정하여 Ceq를 0 으로 가정하고 Eq. (5)와 Eq. (6)을 Eq. (4)에 대입하면 다음과 같이 정리된다.
| $$\frac{\partial C}{\partial t}=-k_vC$$ | (11) |
| $$k_v=294\frac{({D_{aq,O}}_2u)\;^{0.5}}{H^{1.5}}\left(\frac{D_{aq,c}}{D_{aq,o_2}}\right)^{0.6}$$ | (12) |
2.5 모형의 구조
정리한 식을 통합한 결과 본 연구에서 개발된 모형의 지배방정식은 아래와 같이 정리된다. Eq. (1)에서 반응항 S의 내용이 추가되어 각 방정식의 우변으로 정리되었다.
| $$\frac{\partial C_{pb}}{\partial t}=k_s(\frac{\delta_m}HK_dC_dC_{sb}-C_{pb})+\alpha_e(C_p-C_{p,eq})$$ | (15) |
여기서 는 각 각 용존농도, 부유사흡착농도, 부유사농도, 공극률을 포함한 하상의 밀도 그리고 하상흡착농도이며, 는 용존농도와 부유사흡착농도간의 교환 항, 는 용존농도와 하상흡착농도의 교환 항, 은 부유사의 부유/침강에 따른 부유사흡착농도와 하상흡착농도 교환 항으로, 부유사 거동해석모델인 STM-2D (Seo et al., 2009)에 따라 는 Ws/H이 쓰였다. 또한, Ws는 침강속도, 은 혼합층의 두께로 유사의 침전 재부유 혹은 용존물질의 하상 흡․탈착이 일어나는 층의 두께이다.
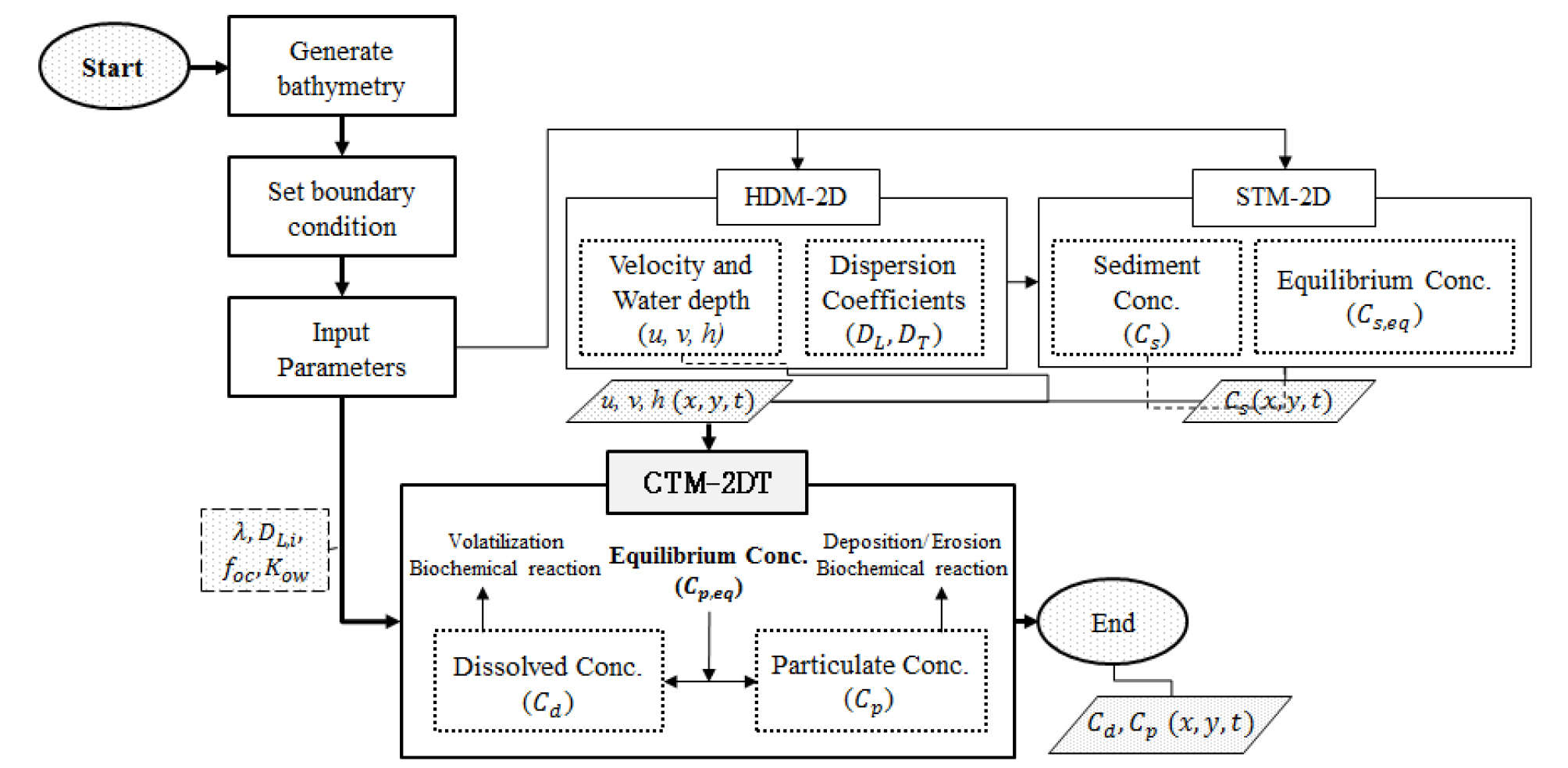
개발된 모형으로 모의를 수행하기 위해서, 우선적으로 유동해석모형과 부유사거동 해석모형을 통해 수질모형의 입력자료를 구축해야 한다. 유속과 수심을 모의하기 위해 유동해석 모형인 HDM-2D (Seo and Song, 2012)를 이용하였으며, 부유사 농도의 시공간 분포를 모의하기 위해 부유사 거동해석모델인 STM-2D (Seo et al., 2009)를 이용하여 부유사거동 모의를 수행하였다. Fig. 2는 각 모델 간의 연계도로, 세 모형 간의 변수 입출력 관계를 표현하였다.
3. 모형의 검증
개발된 모형의 반응항을 검증하기 위해 몇 가지 조건과 가정으로 해석해가 존재하는 모의 구역을 구성하였다. 토양-물 관련 항을 검증하기 위해서 유속이 0, 수심의 시공간적 변화가 없다고 가정한 정체된 수체 내에서 주입된 용존 농도의 거동을 모의하였으며, 휘발 항을 검증하기 위해 수심 및 유속이 일정한 가상 직사각수로에서 연속 선 주입 모의를 수행하였으며 각 조건에 대한 해석해와 비교하였다.
부유사에 흡착된 농도와 용존 농도 간의 물질 교환모형을 검증하기 위해 직사각형 수로 안에 유속이 없는 조건에서 검증을 진행하였다. 타 반응들은 일어나지 않고 부유사 흡․탈착만이 유일하게 일어난다고 가정했을 때 지배방정식을 아래와 같이 단순화 시킬 수 있었다. 단순화된 식을 t에 대해 라플라스 변환을 취하고, 해석해를 구하면 아래와 같다.
| $$C_p=-AC_{d0}\frac{e^{t(A-B)}}{A-B}-\frac A{B-A}$$ | (16) |
| $$C_d=AC_{d0}\frac{e^{t(A-B)}}{A-B}+\frac B{B-A}$$ | (17) |
| $$A=-k_sK_dC_{sb},\;\;\;B=k_s$$ | (18) |
하상에 흡착된 농도와 용존 농도 간의 물질 교환모형을 검증하기 위해서 부유사 흡탈착 항을 검증할 때와 같은 조건을 사용하였다. 직사각형 수로에서 유속이 없는 조건에서, 부유사의 농도가 0 ppm이고, 타 반응들은 일어나지 않고 하상과의 흡․탈착만이 유일하게 일어난다고 가정하였다. 단순화된 식의 해석해를 구하면 Eqs. (16) ~ (17)과 같은 식에 Eq. (18) 대신 아래와 같은 식으로 정리된다.
| $$A=-\frac{\delta_m}Hk_sK_dC_{sb},\;\;\;B=k_s$$ | (19) |
여기서 Kd를 추정하기 위해 Kow는 옥탄올-물 분배계수로 앞서 소개한 Karickhoff (1981)이 제안한 추정식을 사용하였으며, 은 Karim and Kennedy (1982)가 제안한 바와 같이 수심의 0.1 ~ 0.2배 수준으로 설정하였다.
휘발 모형을 검증하기 위해, 수심 및 유속이 일정한 가상 직사각수로에서의 연속 선 주입으로 가정하고, 문제를 단순화하기 위해 분산계수의 시공간적 변화가 없다고 가정하였다. 이 경우 수심 및 유속이 일정하여 전체 수로 내에 단일한 휘발계수가 계산된다. 따라서 유속 및 수심 그리고 수중확산계수에 따른 단일 값을 Eq. (12)를 이용해 해석해를 구할 수 있으며, 그 식은 다음과 같다.
Table 2에 각 반응항의 검증을 위한 조건을 정리하였다. 수치모형의 적용영역은 100 m × 2 m 크기 수로에 1차원 모의를 위하여 정사각형 모양 격자로 구성하여 요소 50개, 절점 102개로 구성하였으며, 지면 경사를 0 m/m로 설정하고 검증조건을 반영하여 정상등류를 구현하였다. 앞서 정리된 부유사 및 하상 흡․탈착항의 해석해는 시간에 따른 한 점의 농도의 변화이기 때문에 모의구역 한 절점의 시간에 따른 농도 값을 수치해로 사용하였다. 또한 휘발항의 해석해는 시간에 따른 1차원 공간의 농도분포이므로 수치해의 흐름방향 거리에 따른 농도를 해석해와 비교하여 검증을 완료하였다. 수치해와 해석해간의 오차를 분석하기 위해서 각 절점 별로 두 값의 차를 해석해로 나누어 산정하였으며, 식은 다음과 같다.
Table 2. Cases for validation of the reaction terms
| $$Error=\sum_1^N\left[\frac{\left|C_a-C_n\right|}{C_a}\right]/N\times100(\%)$$ | (21) |
여기서 N은 수치해로 나타낸 농도시간 곡선 혹은 농도거리 곡선의 데이터의 개수이며; Ca, Cn는 순서대로 해석해와 수치해를 의미한다.
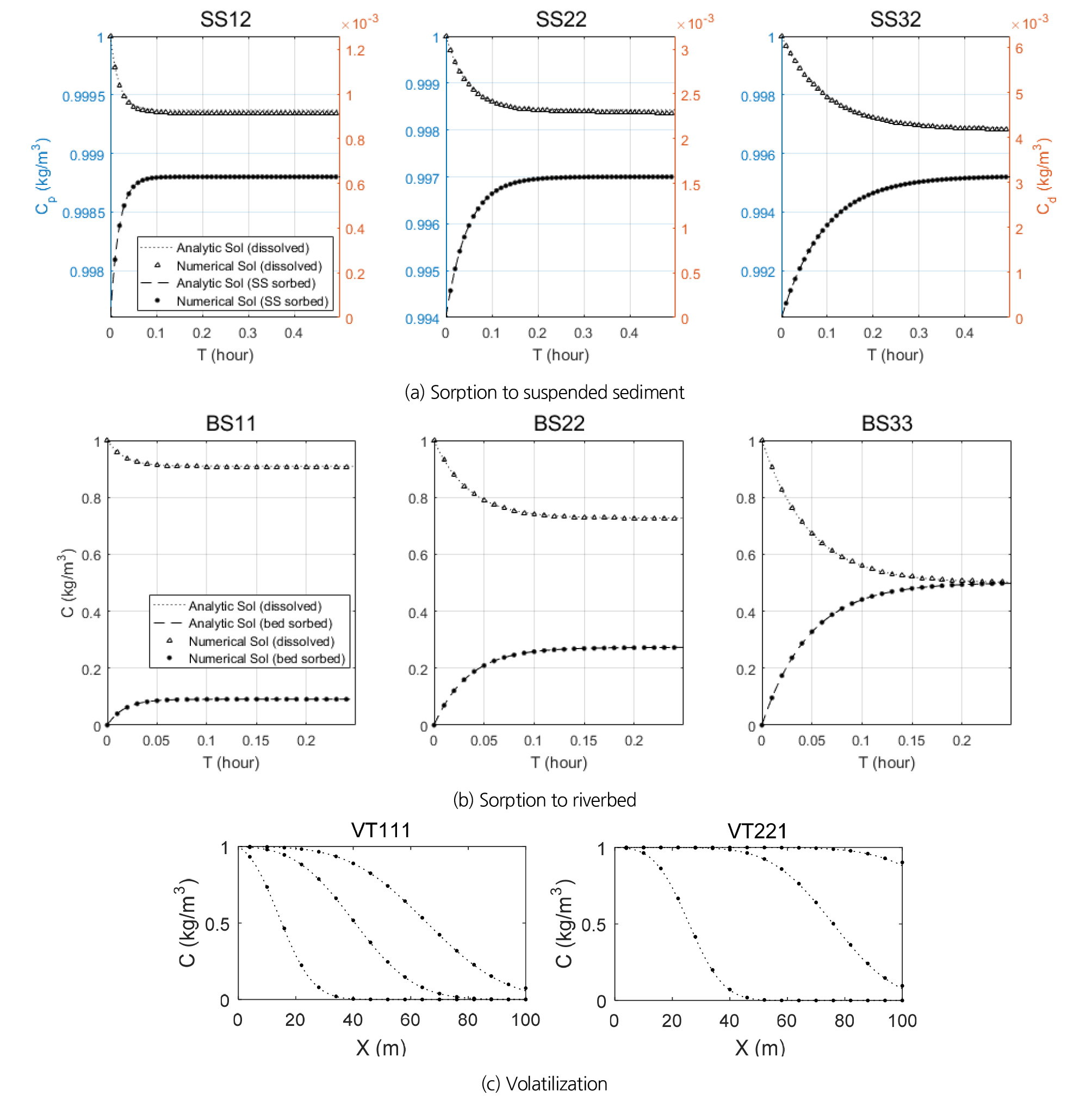
각 반응항별로 수치해와 해석해의 비교 결과를 Fig. 3에 도시하였다. 수치해와 해석해 간 오차를 계산한 결과, 부유사 흡착항의 경우 평균 약 0.003% 오차를 보였으며, 하상 흡착항의 경우 평균 약 0.04%의 오차를, 휘발항의 경우 평균 0.05%의 오차를 보여 수치모형의 우수성을 검증하였다.
4. 모형의 적용
4.1 대상 지역 및 데이터
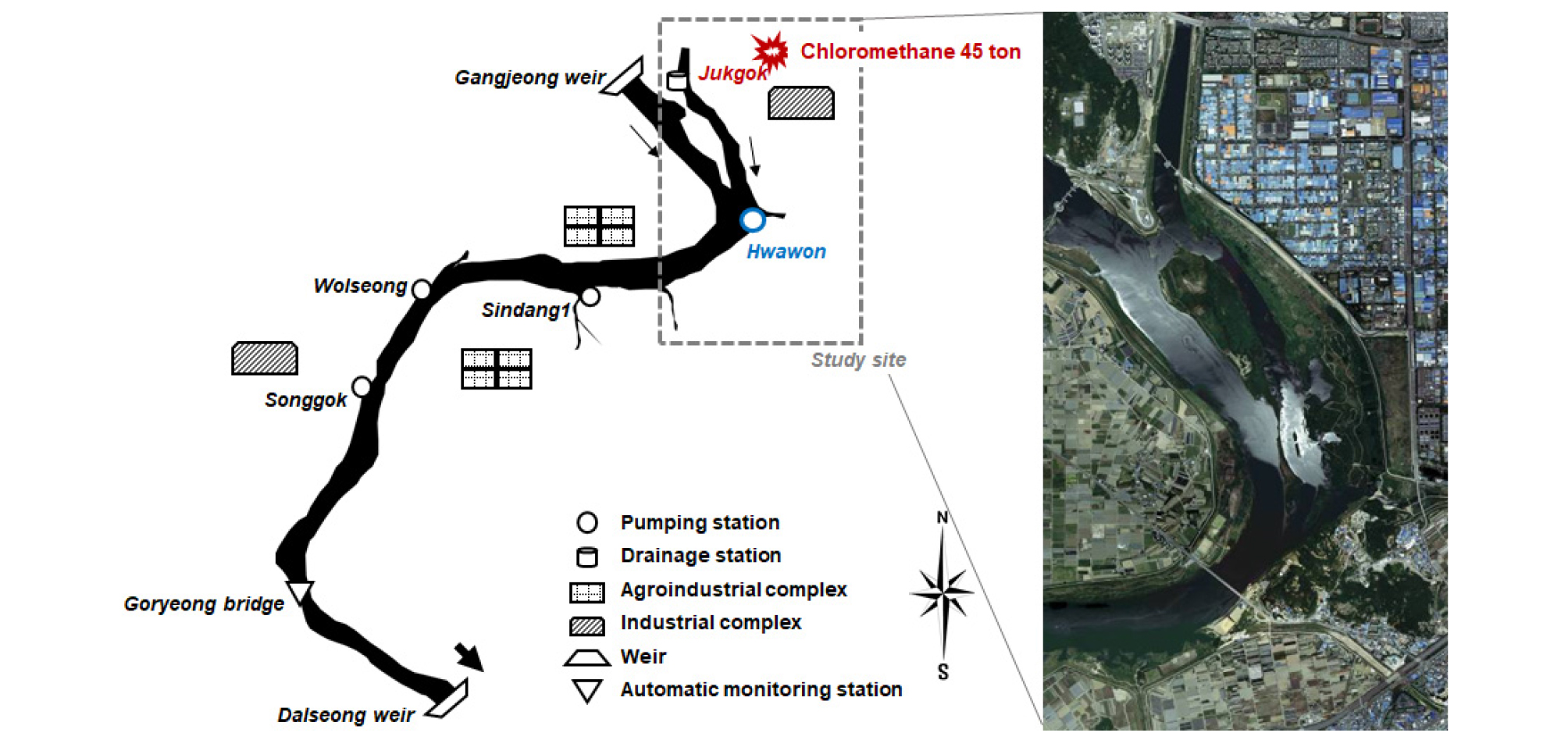
낙동강은 한국 남동부 지역의 용수 공급원으로 쓰이는 주요 하천 중 하나로서 길이는 525 km, 배수 면적은 23,817 km² 이며, 하천폭과 수심의 비가 52.2로 천수(shallow water)에 해당하는 하천이다(van Prooijen and Uijttewaal, 2005). 따라서 본 연구에서 개발한 수심 평균 2차원 모형은 대상하천에서 오염물질의 공간 변동성을 분석하는데 효과적인 모형으로 판단된다. 본 연구의 대상 구간은 Fig. 4에 도시한 바와 같이 상류 쪽에는 성서 산업단지가 밀집되어 있고, 중․하류 쪽에는 농업단지가 위치하고 있어 산업 중간재의 운반 중 차량 전복사고나 오염 폐수유출의 가능성이 큰 지역이다. 또한 대상구간의 상하류에 있는 강정보와 달성보에 의해 유량이 통제되고 있으며, 수심은 관리수위 이하로 운영되고 있어서 오염물질이 유입될 시 잔류 시간이 길어져 피해가 커질 수 있을 것으로 판단된다. 따라서 대상구간의 주요지점에서의 오염물질 체류시간을 예측하고 적절한 취용수 대책을 마련할 수 있는 사고대응시스템이 구축될 필요가 있다.
본 연구에서는 낙동강 강정고령보의 방류량 및 금호강 강창교의 유량 데이터를 사용하여 상류 경계조건을 설정하고, 달성보의 상류 수위를 이용해 하류단 경계조건을 설정하였다. 하천 표고자료는 2015년에 RTK 및 ADCP를 이용한 측량을 통해 구축된 DEM자료를 기반으로 하여 약 30 × 30 m 해상도 자료를 사용하였으며, 수치모형의 계산격자는 18,819개로 구성하였다. 또한 하상재료의 중간 입경은 Lyu et al. (2017)의 입도분석 결과인 0.8 mm를 사용하였으며, 부유사 입경은 상류 수질관측소에서 측정된 0.042 mm을 사용하였고, 하상재료의 유기탄소비율은 Four Major River Survey Committee (2016)가 달성보 구간에서 측정한 하상토의 완전연소 가능량 값을 사용하였다.
4.2 유의 반응항 판별을 위한 민감도 분석
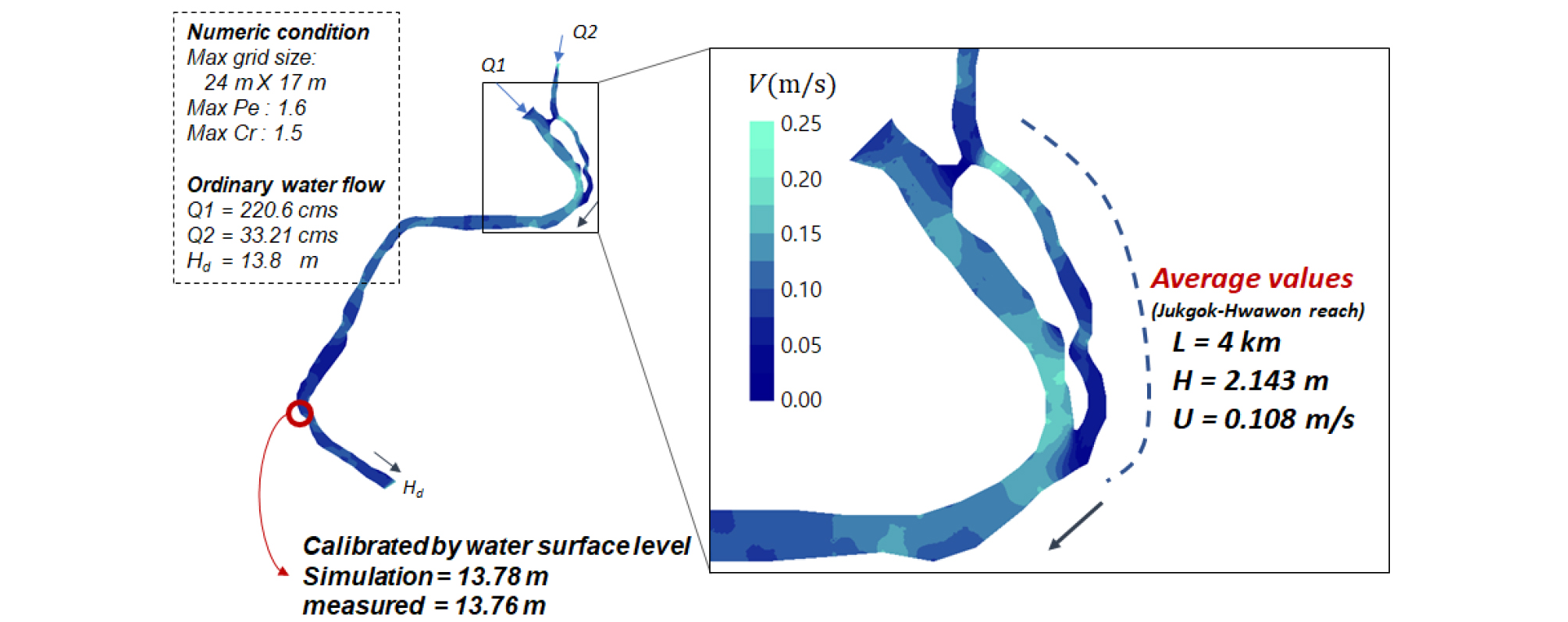
본 연구에서는 대상구간에서 2차원 수질모형의 효율적인 모의를 위한 반응항 중 유의항 판별을 위해 민감도분석을 하였으며, 그 과정은 다음과 같다. 첫째로, 대상구간의 유속 및 수심자료를 얻기 위해 2차원 흐름모형을 이용하여 수리해석을 수행하였다. 국립환경과학원 사고대응시스템(WARMS)에서는 수질사고에 대비해 수리모형을 매일 업데이트하고 있어, 이 과정은 실제 상황에서는 이미 이루어져 있는 단계이다. 본 연구에서는 HDM-2D로 수리모의를 수행하여 모의 결과인 유속 및 수심을 CTM-2D의 입력자료로 사용하였다. 흐름모형의 상․하류 경계조건으로는 국가수자원관리 종합정보시스템(WAMIS)에서 2018년 5월 9일에 관측된 강정고령보 및 달성보의 운영 방류량 및 상류수위를 이용하였다. 해당 모의시간 내 유량 및 수위 조건이 큰 변동이 없어 정상 흐름 모의를 하였다. 또한 적용지역의 하류에 위치한 구미대교의 수위자료로 보정을 위해 Manning 조도계수와 Smagorinsky 상수를 각각 0.023과 0.3의 보정값을 사용하였으며, Fig. 5는 보정된 수리모형의 결과와 평균수리조건을 보여준다.
둘째로, 오염물질 거동 모의 결과가 입력 매개변수 변화에 따라 정해진 기준 값 이상의 변화가 일어날 때, 입력된 매개변수 값을 해당 반응항의 유의성을 판단할 수 있는 임계값으로 채택하였다. 민감도분석 대상 매개변수는 옥탄올-물 분배계수(kow), 수계확산계수(Daq) 그리고 생화학적 반응계수()로서, 흡탈착, 휘발, 그리고 생화학반응을 대변하는 물성치를 선정하였다. 또한 수질모형의 모의 결과 중 주요지점에서의 체류시간(주요지점에서 계산 농도값이 기준 이상으로 검출되는 기간)과 첨두농도의 값이 10% 변하는 값을 임계값으로 선정하였다. 체류시간 및 첨두농도 기준 중 하나라도 만족하면 유의 반응으로 판별하도록 산정된 임계값 중 작은 값을 최종 임계값으로 선정하였다.
본 연구의 민감도 분석에서 실제 지형을 이용해 민감도 분석을 수행할 시 많은 계산시간이 소요됨으로, 사고발생 지점과 사고를 대비해야하는 주요지점 사이 구간의 유속 및 수심 평균치를 이용해 가상 직사각수로를 구성하여 민감도 분석을 수행하였다. 주요지점을 화원양수장으로 선정하고 유로연장이 4 km인 1차원 가상 직사각 수로를 구축한 뒤, 수리모의로부터 얻어진 평균수리조건인 유속 0.108 m/s, 수심 2.141 m를 적용하여 분석을 수행하였다. 옥탄올-물 분배계수, 수계확산계수 그리고 생화학적 반응계수 중 각 하나의 변수 값을 유의하지 않은 값으로부터 증가시키며 첨두농도 및 체류시간의 변화를 분석하였다.
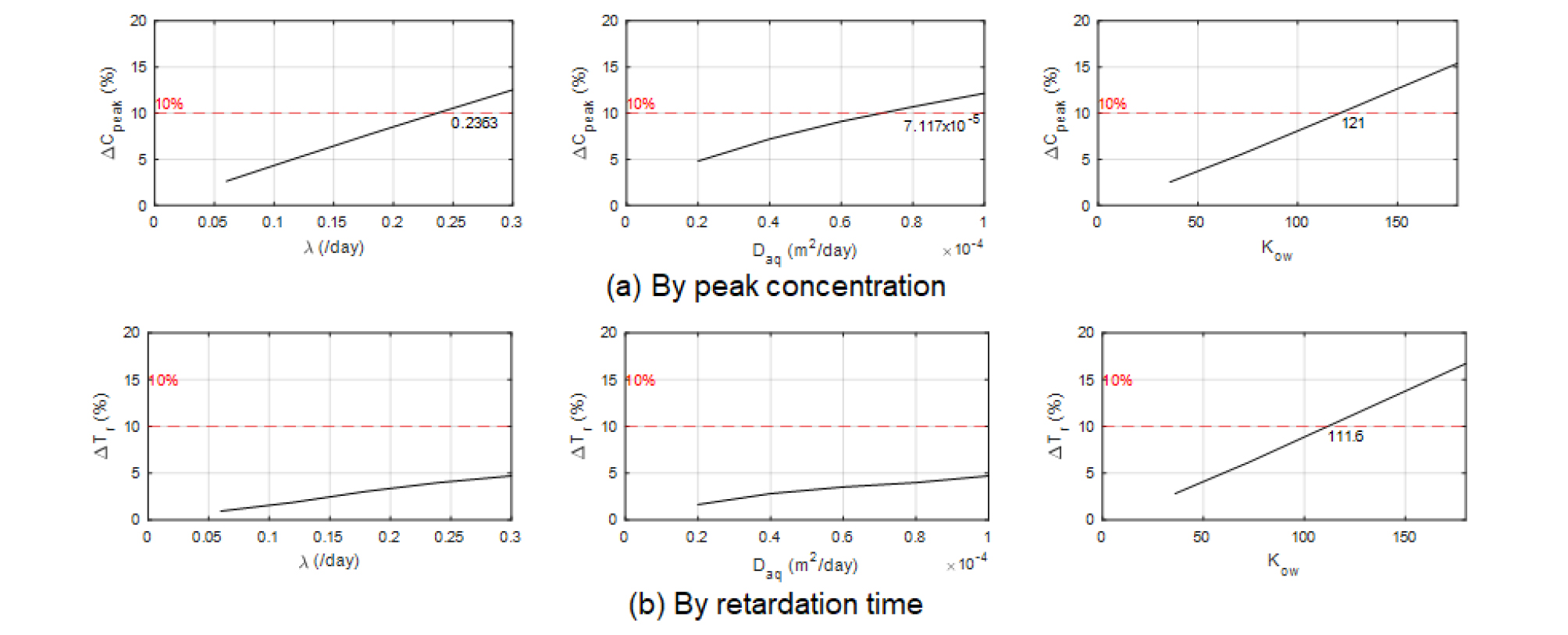
민감도 분석 결과를 Fig. 6에 도시하였다. 주요지점에서의 첨두농도는 생화학적 반응계수와 수계확산계수에 민감하고, 체류시간의 경우 물-옥탄올 분배계수에 민감한 결과를 보였다. 이는 휘발 및 생화학적 반응의 경우 감쇠반응의 일종으로 농도-시간 곡선의 형상이 크게 바뀌지 않은 상태에서 전체적인 농도의 값만 변화하기 때문에, 생화학적 반응계수 및 수계확산계수가 체류시간 보다는 첨두농도에 더욱 영향을 미치게 한 것을 알 수 있다. 또한 흡․탈착 과정의 경우 저장대와 유사한 효과를 나타내며 농도-시간 곡선에서 꼬리를 길게 늘어뜨리는 현상을 야기하므로 체류시간에 더욱 큰 영향을 미치는 것을 알 수 있다(Seo and Maxwell, 1992). 각 매개변수의 임계값의 경우, 체류시간과 첨두농도의 두 케이스 중 작은 값으로 선정하였으며, 생화학적 반응계수는 0.2363/day, 수계확산계수는 7.117⨯10-5 m2/day, 옥탄올-물 분배계수의 경우 111.5로 선정되었다.
4.3 유의 반응항을 고려한 수치 모의
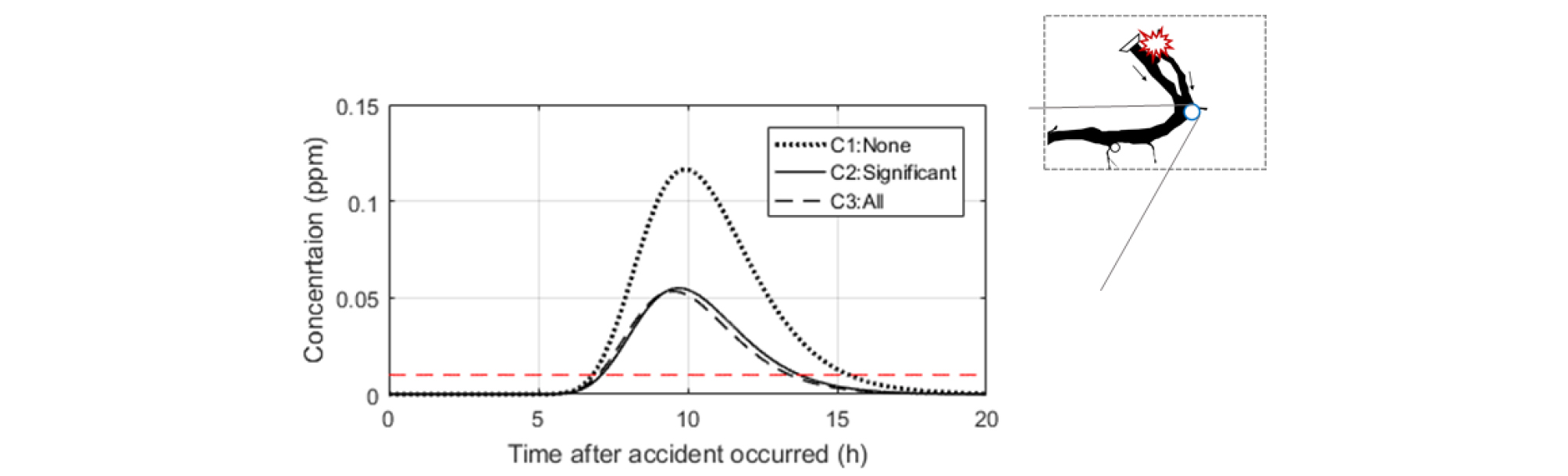
제시된 유의성 판별 알고리즘의 타당성을 평가하기 위해 휘발 및 생화학적 반응에 민감한 메탈린 염화물의 인자 특성(생화학적 반응계수 22.0/day, 수계확산계수 1.1⨯10-4 m2/day, 옥탄올-물 분배계수 8.13)을 반영하여 수행하였다. 이 경우에는 민감도 분석과는 달리 실제 지형을 이용해 수치 모의를 수행하였다. 수치모의는 3가지 조건에 대해 수행하였으며 각 케이스별 모의 조건 및 결과는 Table 3에 주어진 바와 같다. 여기서 C1은 모든 반응항을 고려하지 않은 모의이고, C2는 유의 반응항만 고려한 모의로 생화학, 휘발항만 고려하였으며, C3는 흡탈착까지 포함한 모든 반응항들을 반영한 모의이다.
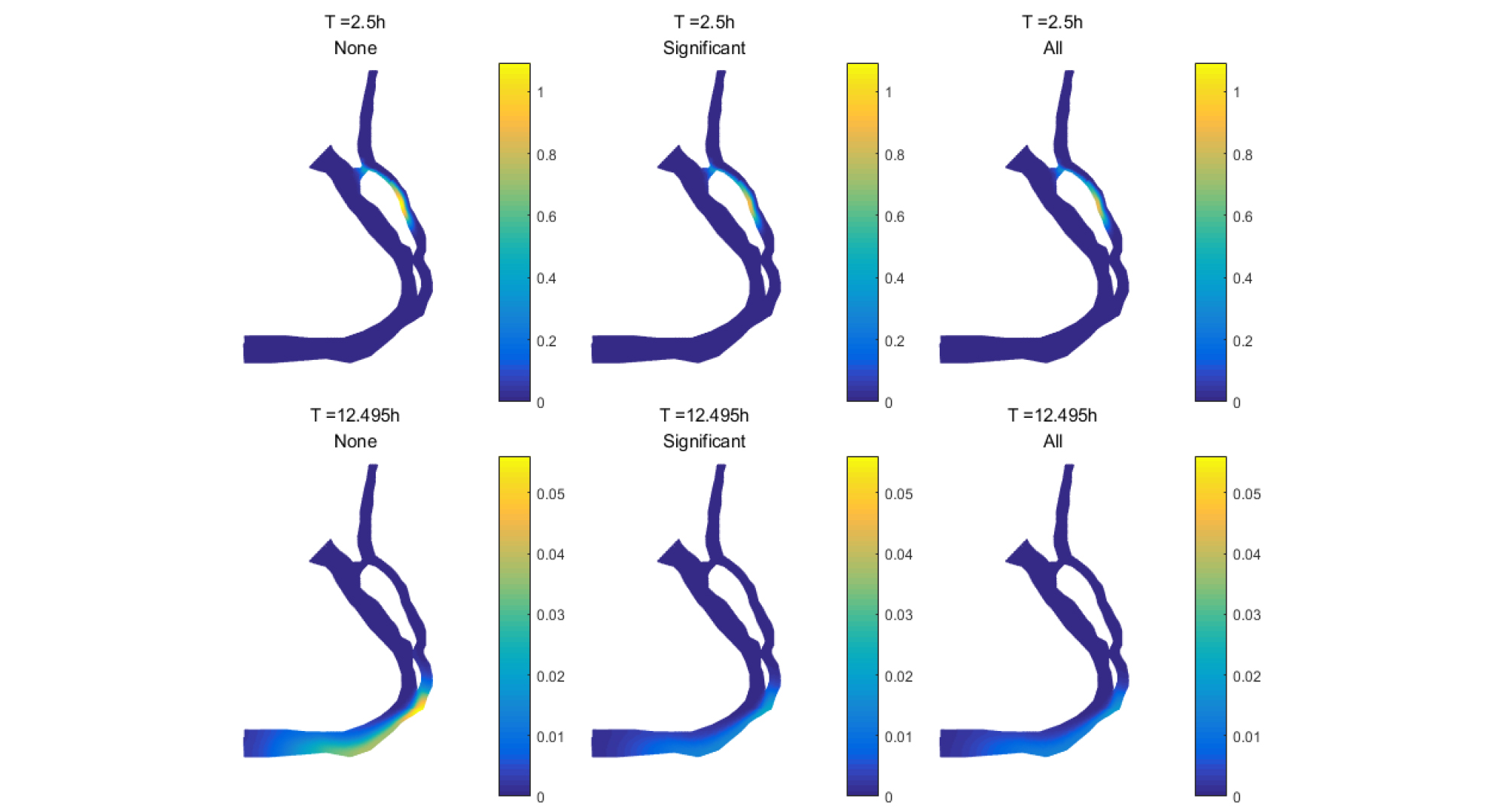
각 케이스의 모의결과는 Fig. 7과 같으며, 유의 반응항만을 고려한 결과와 모든 반응을 고려한 결과가 큰 차이가 없는 것을 알 수 있다. 3가지 조건을 자세히 비교하기 위해 화원양수장에서의 검출된 농도-시간 곡선을 Fig. 8에 도시하고, 각 케이스 결과를 Table 3에 수록하였다. Fig. 8의 농도-시간 곡선을 확인한 결과, 모든 조건의 모의는 사고 발생 후 약 6시간 이후에 화원양수장에 농도가 검출되었으며, 유해화학물질의 도달시간에는 반응항의 영향이 미미함을 확인할 수 있었다. 그러나 체류시간의 경우, 반응항을 전혀 반영하지 않은 결과와 유의한 반응항을 반영한 결과는 약 2시간 정도의 차이로 약 33 % 변화를 보였다. 또한 첨두농도의 경우에는 약 100 %의 변화를 보였다. 유의한 메커니즘만 반영한 결과와 유의하지 않은 메커니즘까지 모두 반영한 결과는 체류시간 및 첨두농도에서 3% 미만의 미미한 차이를 보였다. 그러나 계산시간의 경우, 모든 반응을 포함한 모의가 유의한 반응만을 포함한 모의보다 약 5배의 시간이 더 걸림을 알 수 있다. 유의한 반응만 고려되는 경우 흡탈착 반응항이 생략되어 Eq. (15)를 비롯한 하상흡착 부분이 간소화되기 때문이다. 이는 신속한 모의가 필요한 사고대응 상황에서는 유의한 반응항만을 고려하여 모의하는 경우에 모의시간을 획기적으로 단축시킬 수 있음을 명확하게 보여 주는 결과로 판단된다.
Table 3. Comparison of simulation cases
5. 결 론
본 연구에서는 하천에 유입된 유해화학물질의 혼합거동을 분석하기 위하여 수심 평균 2차원 하천수질모형을 개발하고, 모형의 계산속도를 최소화하기 위해 유의 반응항 판별 방법과 이에 기반한 효율적 모의수행 기법을 제시하였다. 수심 평균 2차원 하천수질모형인 CTM-2D에 흡․탈착, 휘발, 생화학적 반응을 재현할 수 있는 반응항들을 추가하였으며 개발된 모형을 해석해와 비교하여 검증하였다. 나아가서 실제 하천에 적용하여 유해화학물질의 특성을 고려한 효율적 모의수행방법을 제시하였다.
본 연구의 결론을 정리하면 다음과 같다.
1) 하천에 유입된 유해화학물질의 거동을 분석하기 위한 흡탈착, 휘발, 생화학적 반응이 추가된 2차원 하천수질모형을 가상수로에서 적용하여 해석해와 비교한 결과, 각 반응항 모두 0.1 % 미만의 오차를 보여 모형의 타당성이 입증되었다.
2) 낙동강-금호강 합류부 하류구간에 수질오염사고 가상시나리오를 구성하여 개발된 모형을 적용하였다. 구성한 조건 내에서 반응항들의 매개변수 민감도 분석을 수행하여 유의성 판단을 위한 임계값을 산출하였다. 모의 결과 중 체류시간과 첨두농도를 기반으로 선정한 주요 매개변수의 임계값은 생화학적 반응계수는 0.2363/day, 수계확산계수는 7.117⨯105 m2/day, 옥탄올-물 분배계수의 경우 111.5이다.
3) 유의 반응항 판별을 통한 효율적 수질모의 수행함으로써 실제 사고상황에 적용 가능성을 보였다. 낙동강 대상구간에 유입된 메탈린 염화물의 인자 특성을 반영하여 유의 반응항만 고려한 모의와 유의하지 않은 메커니즘까지 모두 반영한 모의 결과를 비교한 결과, 첨두농도 및 체류시간에서 약 5 % 정도의 변화를 보였으나, 계산시간의 경우 유의하지 않은 메커니즘을 모두 반영한 모의가 약 5배의 시간을 소요함을 보여주었다. 이러한 결과는 신속한 모의가 필요한 사고대응 상황에서 유의한 반응만을 고려하여 모의할 시 계산시간을 대폭 단축시킬 수 있음을 보여 주는 결과이다.