Preview
Research Article

Journal of Korea Water Resources Association. 30 September 2020. 701-715
https://doi.org/10.3741/JKWRA.2020.53.9.701

Evaluation of improvement effect on the spatial-temporal correction of several reference evapotranspiration methods

기준증발산량 산정방법들의 시공간적 보정에 대한 개선효과 평가
Chul-Gyum Kima*
,
Jeongwoo Leeb
,
Jeong Eun Leec
,
Hyeonjun Kimd
김 철겸a*
,
이 정우b
,
이 정은c
,
김 현준d
aResearch Fellow, Department of Land, Water and Environment Research, Korea Institute of Civil Engineering and Building Technology
bResearch Fellow, Department of Land, Water and Environment Research, Korea Institute of Civil Engineering and Building Technology
cSenior Researcher, Department of Land, Water and Environment Research, Korea Institute of Civil Engineering and Building Technology
dSenior Research Fellow, Department of Land, Water and Environment Research, Korea Institute of Civil Engineering and Building Technology
a한국건설기술연구원 국토보전연구본부 연구위원
b한국건설기술연구원 국토보전연구본부 연구위원
c한국건설기술연구원 국토보전연구본부 수석연구원
d한국건설기술연구원 국토보전연구본부 선임연구위원
* Corresponding Author
License (open-access):

©It is identical to the Creative Commons Attribution Non-commercial License (http://creativecommons.org/licenses.by-nc/3-0/)

ABSTRACT

This study compared several reference evapotranspiration estimated using eight methods such as FAO-56 Penman-Monteith (FAO PM), Hamon, Hansen, Hargreaves-Samani, Jensen-Haise, Makkink, Priestley-Taylor, and Thornthwaite. In addition, by analyzing the monthly deviations of the results by the FAO PM and the remaining seven methods, monthly optimized correction coefficients were derived and the improvement effect was evaluated. These methods were applied to 73 automated synoptic observation system (ASOS) stations of the Korea Meteorological Administration, where the climatological data are available at least 20 years. As a result of evaluating the reference evapotranspiration by applying the default coefficients of each method, a large fluctuation happened depending on the method, and the Hansen method was relatively similar to FAO PM. However, the Hamon and Jensen-Haise methods showed more large values than other methods in summer, and the deviation from FAO PM method was also large significantly. When comparing based on the region, the comparison with FAO PM method provided that the reference evapotranspiration estimated by other methods was overestimated in most regions except for eastern coastal areas. Based on the deviation from the FAO PM method, the monthly correction coefficients were derived for each station. The monthly deviation average that ranged from -46 mm to +88 mm before correction was improved to -11 mm to +1 mm after correction, and the annual average deviation was also significantly reduced by correction from -393 mm to +354 mm (before correction) to -33 mm to +9 mm (after correction). In particular, Hamon, Hargreaves-Samani, and Thornthwaite methods using only temperature data also produced results that were not significantly different from FAO PM after correction. It can be also useful for forecasting long-term reference evapotranspiration using temperature data in climate change scenarios or predicting evapotranspiration using monthly or seasonal temperature forecasted values.

Keywords
Reference evapotranspiration
FAO-56 Penman-Monteith
ASOS
Correction coefficient

본 연구에서는 FAO-56 Penman-Monteith (FAO PM)를 비롯하여 Hamon, Hansen, Hargreaves-Samani, Jensen-Haise, Makkink, Priestley-Taylor, Thornthwaite 등 총 8가지 기준증발산량 산정방법을 이용하여 전국 기상청 ASOS 지점을 대상으로 각 방법에 따른 기준증발산량을 산정하여 비교하였다. 또한 가장 신뢰성이 높은 것으로 알려진 FAO PM값을 기준으로 나머지 7가지 방법에 의한 월별 편차를 분석하여 지점별 월별 보정계수를 도출하고, 보정에 따른 개선효과를 평가하였다. 먼저 각 방법의 기본계수를 적용하여 기준증발산량을 산정한 결과, 방법에 따라 큰 편차를 나타내었으며 Hansen 방법이 상대적으로 FAO PM과 유사한 것으로 나타났다. 반면, Hamon과 Jensen-Haise 방법은 여름철을 중심으로 타 방법대비 매우 큰 값을 보였으며, FAO PM과의 편차도 크게 나타났다. 지역별로는 동해안 일부지역을 제외하고 대부분의 지역에서 FAO PM과 비교하여 기준증발산량을 과다하게 산정하는 것으로 분석되었다. FAO PM 결과와의 편차를 기반으로 지점별 월별 최적화된 보정계수를 도출하고 기준증발산량을 다시 비교한 결과, 지점에 따라 보정 전에 -46 mm∼+88 mm의 범위를 보였던 월 평균값은 보정 후 -11 mm∼+1 mm로 나타났으며, 연 평균값도 -393 mm∼+354 mm (보정 전)에서 -33 mm∼+9 mm (보정 후)로 보정을 통하여 편차가 크게 감소되었다. 또한, 기온자료만을 이용하는 Hamon, Hargreave-Samani, Thornthwaite 방법들도 보정을 통하여 FAO PM과 큰 차이없는 결과를 도출하였다. 특히 기온기반의 방법들은 기후변화 시나리오 중 상대적으로 불확실성이 낮은 기온자료만을 이용하여 미래의 장기간의 기준증발산량을 전망하거나, 월 또는 계절예측 기온정보를 이용하여 수개월간의 기준증발산량을 예측하는 경우에 유용하게 활용될 수 있을 것이다.

키워드
기준증발산량
FAO-56 Penman-Monteith
기상청 ASOS
보정계수

MAIN

  • 1. 서 론

  • 2. 연구방법

  •   2.1 대상지역 및 자료

  •   2.2 기준증발산량 산정방법

  •   2.3 기준증발산량 보정계수 도출방법

  • 3. 연구결과

  •   3.1 보정 전 기준증발산량 비교

  •   3.2 기준증발산량 보정계수 도출

  •   3.3 보정 후 기준증발산량 비교

  • 4. 요약 및 결론

1. 서 론

증발산량은 수문학적으로는 강수량으로부터 지표 유출량과 지하수 함양량을 추정하는 등 전체 물수지를 해석하는데 있어서 매우 중요하며, 농업적 측면에서는 작물의 용수 수요량을 결정하는 중요한 인자이다. 그러나 증발산량의 직접적인 계측이 쉽지 않기 때문에 물수지 방법에 의한 간접적인 추정이나 경험적이고 물리적인 수식을 이용한 이론적인 해석을 통해 산정하고 있다(Moon, 2018; Grismer et al., 2002). 이론적인 방법에 의해 증발산량을 산정하는 과정은 일반적으로 증발산에 관련된 기상인자들을 활용하여 에너지수지 및 공기동력학적인 방법으로 기준작물에 대한 기준증발산량을 추정하고, 여기에 다시 작물계수와 스트레스 계수(실제 수분조건 및 식생조건 고려) 등을 이용하여 실제증발산량으로 계산하고 있다.

Moon et al. (2013)과 Grismer et al. (2002)에서 언급된 것처럼 기준증발산량 산정을 위해 50가지 이상의 이론적인 방법들이 제안되고 있으며, 많은 연구자들에 의해 다양한 방법들이 상호 비교 연구되어 왔다. 하지만, 국내의 경우는 Choi et al. (2010)이 서울지점의 기상자료를 이용하여 15개의 산정방법에 의한 결과를 비교한 사례 외에는 몇 가지 대표적인 방법들에 대한 비교 연구(Kim and Chung, 1999; Rim, 2008; Rim et al., 2009; Park et al., 2017; Yoon and Choi, 2018)가 있었을 뿐, 많은 방법들에 대한 비교를 수행하지는 않았다. 반면 다양한 방법들이 개발되었던 국외의 경우에는 지역별, 기후특성별, 이론적 접근방법별 등으로 구분하여 많은 연구가 수행되었다. 그 중에서 10가지 이상의 방법들을 적용한 사례를 들면 다음과 같다. Irmak et al. (2003)은 미국 플로리다의 습한 기후지역에 대해 21가지의 산정방법에 대한 적용성을 비교한 바 있으며, Xystrakis and Matzarakis (2011)는 그리스 남부 Crete 섬지역에 일사량기반 6가지와 기온기반 7가지 등 총 13가지 방법에 의한 기준증발산량을 평가한 바 있다. 또한, Rácz et al. (2013)은 헝가리의 Debrecen Airport 관측지점에 대해 10가지 방법을 적용하였으며, Heydari et al. (2014)는 이란의 북부지역에 38가지 방법, Samaras et al. (2014)는 그리스 중부 지중해성 기후지역에 18가지 방법, Djaman et al. (2015)은 세네갈의 Senegal River Valley 지역에 16가지 방법, Neto et al. (2015)은 브라질의 Lete Lagoas 지역에 10가지 방법, Tomar (2015)는 인도의 Tarai 지역에 20가지 방법, Valipour (2015a)는 이란의 31개 지방에 일사량기반의 22개 방법, Valipour (2015b)는 동일한 31개 지방에 기온기반의 11개의 방법, Seiller and Anctil (2016)은 캐나다와 독일의 자연유역에 대해 24가지 방법, Peng et al. (2017)은 중국의 552개 지점에 대해 10가지 방법, Yeh (2017)은 대만의 서부지역에 대해 10가지 방법, Antonopoulos and Antonopoulos (2018)은 그리스 북부지역에 13가지 방법을 대상으로 각 방법들의 적용성을 비교 분석하였다.

상기 연구들은 공통적으로 접시증발량이나 FAO-56 Penman-Monteith (Allen et al., 1998) (이하 FAO PM)에 의한 값을 기준으로 각 방법들의 적용성을 제시하고 있다. 특히, FAO PM 방법은 증발산에 영향을 주는 다양한 기후인자들(태양복사량, 풍속, 수증기압, 기온, 상대습도 등)을 이용한 물리적 이론으로 구성되어 있어 보정없이 광범위하게 사용할 수 있는 가장 신뢰성이 높은 방법으로 인정되고 있다(Droogers and Allen, 2002; Shahidian et al., 2012; Abd El-Wahed and Abd El-Mageed, 2014; Heydari et al., 2014; Metcalfe et al., 2019). 그러나, 이 방법을 이용하기 위해서는 많은 기상인자들을 요구하고 있어 관측 기상자료가 부족하거나 자료의 신뢰성이 미흡한 경우에는 적용에 한계가 있다. 따라서, 대안으로 상기 연구들에서 적용한 것과 같이 제한된 자료만으로 기준증발산량을 산정할 수 있는 일사량기반 방법들(e.g., Abtew, Hansen, Jensen-Haise, Makkink, Priestley-Taylor, Turc)이나 기온기반의 방법들(e.g., Blaney-Criddle, Hamon, Hargreaves, McGuinness-Bordne, Romanenko, Thornthwaite)이 많이 활용되고 있으며, 지역에 따라서는 증발접시계수를 이용한 경험적 수식들도 많이 적용되고 있다. 그 중에서도 기온기반의 방법들은 관측정확도가 높은 기온자료만을 활용하기 때문에 많은 지역에서 적용성이 검토되고 있다.

기존 개발된 많은 방법들에도 불구하고 여전히 많은 방법들이 검토되고 있고, 새로운 방법들이 추가적으로 개발되는 이유는 기존의 방법들 중에서 최선의 방법을 결정하기가 쉽지 않기 때문이다. 대부분 특정 기후조건에서 개발된 경우가 많기 때문에 기후조건이 다른 지역에 적용할 경우 산정된 결과의 안정적인 신뢰성을 확보하기 어려우며, 동일한 기후조건이어도 지역에 따라 전혀 다른 모의성능을 나타내기 때문에 우선은 대상지역의 장기간의 자료를 기반으로 한 보정이 선행되어야한다(Xystrakis and Matzarakis, 2011). 각 방법의 수식을 보정하거나 결과의 정확성을 평가하기 위해서는 라이시미터 관측값을 이용하는 것이 가장 좋은 방법이나(Irmak et al., 2003; Samaras et al., 2014), 일부 지역을 제외하고는 다양한 조건을 고려한 장기간의 관측자료를 확보하기가 현실적으로 어렵다. 따라서, FAO PM 방법이 이에 대한 대안으로 제시된 후로는 이 값을 기준으로 각 방법들의 계수를 보정하는 연구가 많이 수행되어 왔다(Lee and Park, 2008; Lee et al., 2008; Droogers and Allen, 2002; Xu and Singh, 2002; Fooladmand and Haghighat, 2007; Ahmadi and Fooladmand, 2008; Cristea et al., 2013; Abd El-Washed and Abd El-Mageed, 2014; Valipour, 2015a, 2015b; Almorox and Grieser, 2016; Peng et al., 2017; Tegos et al., 2017; Gurski et al., 2018; Chang et al., 2019).

국내에서도 기준증발산량 산정을 위해 다양한 방법들이 적용되어 왔으며, 증발접시 증발량을 기준으로 한 각 방법들의 비교(Rim, 2008; Rim et al., 2009; Choi et al., 2010; Sur et al., 2012), FAO PM 결과와의 비교(Lee and Park, 2008; Lee et al., 2008; Moon et al., 2013; Kim et al., 2017; Yoon and Choi, 2018) 등의 연구가 수행되어 왔다. 그러나, 일부 연구(Lee and Park, 2008; Lee et al., 2008; Moon et al., 2013)에 의해 Hargreaves 공식의 계수를 보정하여 사용한 것 외에는 다른 방법들의 보정에 대한 연구는 거의 없었다. 상대적으로 국외 타 지역들보다 관측자료의 품질이나 증발산과 관련된 가용 기상자료가 충분하다보니 최근에는 FAO PM이 거의 표준화된 방법으로 활용되고 있다. 그러나 여전히 가용자료가 충분하지 않은 지역 또는 기간에 대해 적용하거나 관측자료의 품질 문제가 우려되는 경우에는 FAO PM 방법의 적용이 제한될 수밖에 없다.

본 연구에서는 FAO PM 방법을 비롯하여 국내외 대표적으로 많이 활용되고 있는 몇 가지 방법들을 대상으로, 국내에서 비교적 신뢰성이 높은 기상청 관측자료를 활용하여 각 방법에 의한 산정결과를 비교하는 한편, FAO PM 방법을 기준으로 각 대안방법들에 대해 지역별 월별로 편차를 분석하여 최적의 보정계수를 도출함으로써 국내 전 지역을 대상으로 대안방법들의 시공간적 적용성을 평가하고자 한다.

2. 연구방법

2.1 대상지역 및 자료

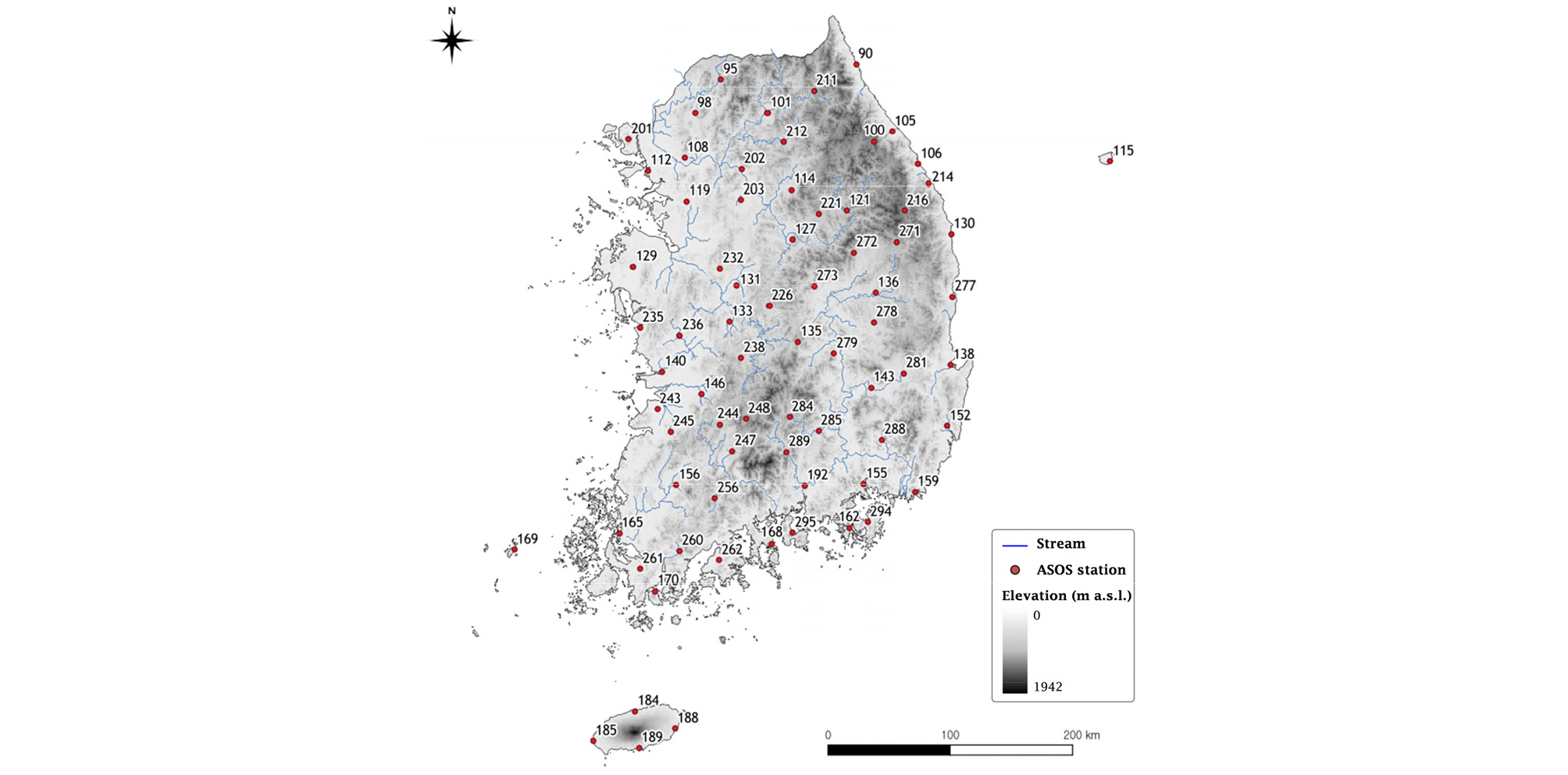
본 연구에서는 기상청 종관기상관측(Automated Synoptic Observation System; ASOS) 지점에 대해 1960년 1월부터 2019년 12월까지의 일 기상자료(최고/최저기온, 일조시간, 상대습도, 풍속)를 수집하였으며, 최소 20년 이상의 가용자료를 보유한 73개 ASOS 지점의 자료를 이용하여 기준증발산량 산정에 활용하였다. Fig. 1은 분석에 사용된 73개 ASOS 지점의 위치를 나타낸 것으로 숫자는 각 지점의 코드를 의미한다. Table 1은 분석에 사용된 각 지점의 지리적 위치 및 해발고도를 정리한 것이다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F1.jpg
Fig. 1.

Location of ASOS stations used in this study

Table 1.

Geographical locations and elevations of the ASOS stations used in this study

Site Station name Latitude (°N) Longitude (°E) Elevation (m a.s.l.) Site Station name Latitude (°N) Longitude (°E) Elevation (m a.s.l.)
90 Sokcho 38.25 128.56 18.06 192 Jinju 35.16 128.04 30.21
95 Cheorwon 38.15 127.30 155.48 201 Ganghwa 37.71 126.45 47.84
98 Dongducheon 37.90 127.06 115.62 202 Yangpyeong 37.49 127.49 47.26
100 Daegwallyeong 37.68 128.72 772.57 203 Icheon 37.26 127.48 80.09
101 Chuncheon 37.90 127.74 76.47 211 Inje 38.06 128.17 200.16
105 Gangneung 37.75 128.89 26.04 212 Hongcheon 37.68 127.88 139.95
106 Donghae 37.51 129.12 39.91 214 Samcheok 37.37 129.22 3.90
108 Seoul 37.57 126.97 85.67 216 Taebaek 37.17 128.99 712.82
112 Incheon 37.48 126.62 68.99 221 Jecheon 37.16 128.19 259.80
114 Wonju 37.34 127.95 148.60 226 Boeun 36.49 127.73 174.99
115 Ulleungdo 37.48 130.90 222.40 232 Cheonan 36.76 127.29 81.50
119 Suwon 37.27 126.99 34.84 235 Boryeong 36.33 126.56 9.98
121 Yeongwol 37.18 128.46 240.60 236 Buyeo 36.27 126.92 11.79
127 Chungju 36.97 127.95 116.30 238 Geumsan 36.10 127.48 170.34
129 Seosan 36.78 126.49 25.86 243 Buan 35.73 126.72 11.96
130 Uljin 36.99 129.41 50.00 244 Imsil 35.61 127.29 247.04
131 Cheongju 36.64 127.44 58.70 245 Jeongeup 35.56 126.84 69.84
133 Daejeon 36.37 127.37 68.90 247 Namwon 35.42 127.40 132.50
135 Chupungryeong 36.22 127.99 243.70 248 Jangsu 35.66 127.52 406.49
136 Andong 36.57 128.71 140.10 256 Juam 35.08 127.24 74.63
138 Pohang 36.03 129.38 3.94 260 Jangheung 34.69 126.92 45.02
140 Gunsan 36.01 126.76 23.20 261 Haenam 34.55 126.57 16.36
143 Daegu 35.88 128.65 53.50 262 Goheung 34.62 127.28 51.91
146 Jeonju 35.84 127.12 61.40 271 Bonghwa 36.94 128.91 324.30
152 Ulsan 35.58 129.33 82.00 272 Yeongju 36.87 128.52 210.79
155 Changwon 35.17 128.57 37.60 273 Mungyeong 36.63 128.15 170.61
156 Gwangju 35.17 126.89 72.38 277 Yeongdeok 36.53 129.41 40.61
159 Busan 35.10 129.03 69.56 278 Uiseong 36.36 128.69 81.81
162 Tongyeong 34.85 128.44 32.30 279 Gumi 36.13 128.32 48.88
165 Mokpo 34.82 126.70 38.00 281 Yeongcheon 35.98 128.95 93.80
168 Yeosu 34.74 127.74 64.64 284 Geochang 35.67 127.91 225.95
169 Heuksando 34.69 125.45 76.49 285 Hapcheon 35.57 128.17 32.00
170 Wando 34.40 126.70 35.24 288 Milyang 35.49 128.74 11.21
184 Jeju 33.51 126.53 20.45 289 Sancheong 35.41 127.88 138.07
185 Gosan 33.29 126.16 71.47 294 Geoje 34.89 128.60 45.40
188 Seongsan 33.39 126.88 20.34 295 Namhae 34.82 127.93 45.71
189 Seoguipo 33.25 126.57 49.03

2.2 기준증발산량 산정방법

본 연구에서는 일 단위로 기준증발산량을 산정할 수 있는 방법 중에서 대표적으로 많이 활용되고 있는 FAO-56 Penman-Monteith 방법(Allen et al., 1998)을 비롯하여 Hamon (Hamon, 1960, 1963), Hansen (Hansen, 1984), Hargreaves-Samani (Hargreaves and Samani, 1982, 1985), Jensen-Haise (Jensen and Haise, 1963), Makkink (Makkink, 1957), Priestley-Taylor (Priestley and Taylor, 1972), Thornthwaite (Thornthwaite, 1948; Pereira and Pruitt, 2004) 등 8가지 방법을 선정하였다. 선정된 방법들은 각 관측소별로 수집된 5가지 기상요소(최고/최저기온, 일조시간, 상대습도, 풍속)를 기준으로, 최고/최저기온만을 이용한 방법(Hamon, Hargreaves-Samani, Thornthwaite), 최고/최저기온과 일조시간을 이용한 방법(Hansen, Jensen-Haise, Makkink), 최고/최저기온, 일조시간, 상대습도를 이용한 방법(Priestley-Taylor), 그리고 5가지 기상요소를 모두 이용한 방법(FAO PM) 등으로 구분할 수 있다.

각 방법에 따른 기준증발산량 산정식은 Table 2와 같다.

Table 2에 제시된 식에 사용되는 주요 변수들의 값은 Allen et al. (1998)을 참고하여 다음과 같이 산정하였다.

$$R_n=R_{ns}-R_{nl}$$ (1)

여기서, Rn : 순복사에너지(MJ/m2/day), Rns : 지표면으로 입사하는 순태양복사에너지(MJ/m2/day), Rnl : 지표면으로부터 반사되는 순지구복사에너지(MJ/m2/day)이다.

Rns는 다음 식과 같이 지표면으로 입사하는 태양복사에너지(Rs)와 지표면 반사도인 알베도(α)를 이용하여 산정하였으며, 이때 Rs의 경우에는 Allen et al. (1998)에서 제시된 Angstrom 공식을 이용하여 일조시간(n)을 이용하여 변환하였다.

$$R_{ns}=\left(1-\alpha\right)\;R_s$$ (2)

$$R_s=\left(a_s+b_s\frac nN\right)\;R_a$$ (3)

여기서, α: 알베도(잔디 기준작물에 대해 0.23), Rs : 지표면으로 입사하는 태양복사에너지(MJ/m2/day), as & bs : 회귀상수(각각 0.25와 0.50 값이 추천됨), n : 실제 일조시간(hour), N : 최대가능일조시간(hour), Ra : 외기복사에너지(MJ/m2/day)이다.

Eq. (1)에서 Rnl은 아래와 같이 계산하였다.

$$\begin{array}{l}R_{nl}=\sigma\left[\frac{T_{\max,\;\mathrm K}^4+T_{\min,\;\mathrm K}^4}2\right]\;\left(0.34-0.14\sqrt{e_a}\right)\\\;\;\;\;\;\;\;\;\;\times\left(1.35\frac{R_s}{R_{so}}-0.35\right)\end{array}$$ (4)

여기서, σ: 스테판-볼츠만 상수(4.903×10－9 MJ/K4/m2/day), Tmax,K : 최대절대온도(K=℃+273.16), Tmin,K : 최소절대온도(K=℃+273.16), ea : 실제수증기압(kPa), Rso : 청명한(n = N) 날의 태양복사에너지(MJ/m2/day)이다.

Eq. (4)에서 ea와 Rso는 다음 Eqs. (5) ~ (6)에서와 같이 상대습도(RH)와 관측소 해발고도(z)를 이용하여 산정하였다.

$$e_a=\frac{RH}{100}\times e_s$$ (5)
$$R_{so}=\left(0.75+2\times10^{-5}z\right)R_a$$ (6)

여기서, es는 포화수증기압(kPa), z: 관측소 해발고도(m)이다.

증발산량 산정방법들에 적용된 계수들의 경우, Hamon 방법의 보정계수 kham는 기존 연구들(Lu et al., 2005; Lang et al., 2017)에서 제시되었던 1.2를 적용하였으며, Priestley-Taylor 방법의 보정계수 αpt는 Priestley and Taylor (1972)에서 평균값으로 제시된 1.26을 적용하였다. Hansen, Hargreaves-Samani, Jensen-Haise, Makkink 등 나머지 방법들의 계수들에 대해서도 Table 2에 제시한 것처럼 각각의 문헌에서 제시하는 기본값을 적용하였다.

Table 2에 제시된 Thornthwaite 식은 Pereire and Pruitt (2004)에 의해 제안된 수정식으로, Thornthwaite (1948)에 의해 처음 제안되었던 월 단위 기준증발산량을 일 단위로 변경하기 위하여 수정계수(C)를 사용하고 있다. Chang et al. (2019)의 연구에서도 이 수정식을 사용하여 일 기준증발산량을 산정한 바 있다. 먼저 본 연구에서는 지점별 월별 평균기온 자료를 이용하여 Chang et al. (2019)과 같이 Thornthwaite 방법에서 사용되는 a와 I값을 산출하였다.

$$I=\sum_{n=1}^{12}\left(0.2\;T_n\right)^{1.514}$$ (7)
$$\begin{array}{l}a=6.75\times10^{-7}I^3-7.71\times10^{-5}I^2+1.7912\times10^{-2}I+0.49239\end{array}$$ (8)

여기서, Tn은 월별 평균기온(℃)이다.

상기의 조건을 적용하여 Table 2에 제시된 각 방법별 산정식을 기반으로 지점별 일별 기준증발산량을 산정하였으며, 월 및 연 단위로 취합하여 각 산정방법에 의한 결과를 비교하였다.

Table 2.

Methods for estimating reference evapotranspiration used in this study

Method and literature Equation Required weather
parameters
FAO-56 Penman-Monteith
(Allen et al., 1998) 		ETo=0.408∆Rn-G+γ900T+273u2es-ea∆+γ1+0.34u2Tmax, Tmin, n, RH, u
Priestley-Taylor
(Priestley and Taylor, 1972) 		ETo=αpt×∆∆+γ×Rn-GλTmax, Tmin, n, RH
Hansen
(Hansen, 1984) 		ETo=0.7∆∆+γRsλTmax, Tmin, n
Jense-Haise
(Jensen and Haise, 1963) 		ETo=0.025×T+3RsλTmax, Tmin, n
Makkink
(Makkink, 1957) 		ETo=0.61∆∆+γRsλ-0.12Tmax, Tmin, n
Hamon
(Hamon, 1960, 1963) 		ETo=kham×0.165×216.7×N×esT+273.3Tmax, Tmin
Hargreaves-Samani
(Hargreaves and Samani, 1982, 1985) 		ETo=0.0023×Ra×Tmax-Tmin0.5×T+17.8λTmax, Tmin
Thornthwaite
(Thornthwaite, 1948; Pereira and Pruitt, 2004) 		ETo=C-415.85+32.24Tef-0.43Tef2,Tef>26℃16C10Tef/Ia,0℃<Tef≤26℃0,Tef≤0℃Tmax, Tmin

where, Tmax : maximum temperature (℃), Tmin : maximum temperature (℃), n : actual daylight hours (hr), RH : relative humidity (%), u : wind speed (m/s), ETo : reference evapotranspiration (mm/day), ∆ : slope of vapour pressure curve (kPa/℃), Rn : net radiation at the crop surface (MJ/m2/day), G : soil heat flux density (≒0 for day to ten days period) (MJ/m2/day), γ : psychrometric constant (kPa/℃), T : mean temperature (℃), u2 : wind speed at 2 m height (m/s), es : saturation vapour pressure (kPa), ea : actual vapour pressure (kPa), αpt : calibration constant of Priestley-Taylor method, λ : latent heat of vaporization (2.45 MJ/kg), Rs : total solar radiation (MJ/m2/day), kham : calibration coefficient of Hamon method, N : maximum possible daylight hours (hr), Ra : extraterrestrial solar radiation (MJ/m2/day), C : correction factor of Thornthwaite method (N/360), Tef : effective daily temperature (℃), I : thermal (or heat) index of Thornthwaite method, a : exponent of Thornthwaite method.

2.3 기준증발산량 보정계수 도출방법

서론에서 기술한 바와 같이, 국외의 경우 많은 연구자들에 의해 접시증발량이나 FAO PM 결과를 기준으로 다양한 모형들에 대한 보정계수를 산출하여 적용성을 검토하고, 월별로 변동형 계수를 적용하여 월별 및 계절별 변화를 함께 고려하고 있다(Fooladmand and Haghighat, 2007; Ahmadi and Fooladmand, 2008; Abd El-Wahed and abd El-Mageed, 2014; McCabe et al., 2015; Peng et al., 2017; Chang et al., 2019). 그러나 국내의 경우에는 Hargreaves 모형에 국한하여 지점별 전 기간에 대해 고정된 계수를 도출한 바 있다(Lee and Park, 2008; Lee et al., 2008; Moon et al., 2013).

본 연구에서는 시공간적 변화를 고려하기 위해 각 지점에 대해 월에 따라 변동형 보정계수를 도출하였다. 서론에서 언급한 것처럼 가장 신뢰성이 높은 것으로 알려진 FAO PM 방법에 의한 결과를 기준값으로 설정하고, 나머지 7가지 방법에 의한 결과를 기준값과 비교하여 각 방법에 대해 지점별 월별로 새로운 보정계수(Correction coefficient)를 산출하였다. 이 보정계수는 Table 2에 포함된 일부 방법들의 기존 보정계수(kham, αpt, C)와 별도로 FAO PM 월 증발산량과의 편차를 보정하기 위한 인자로서, 각 방법의 보정계수는 아래의 식과 같이 표현된다.

$$k_{X_i}=\frac{ETo_{PM_i}}{ETo_{X_i}}$$ (9)

여기서, kXi는 i월에 대한 X 방법의 보정계수, EToXi는 X 방법의 i월 기준증발산량 (mm/month), EToPMi는 FAO PM 방법에 의한 i월의 기준증발산량 (mm/month)이다.

즉, 보정계수가 1보다 크면 FAO PM 방법 대비 작게 산출된다는 의미이며, 1보다 작은 경우는 반대로 크게 산출된다는 것을 의미한다.

보정계수 산출을 위해 먼저 73개 지점에 대해 Table 2에서 제시된 각 방법별 산정식을 기반으로 일별 기준증발산량을 산정한 후 월 단위로 취합하였다. 그리고 월별 산정된 기준증발산량 자료에 대해 무작위로 보정과 검증자료로 구분하여 보정기간의 월 자료를 이용하여 보정계수를 산정한 후 나머지 자료를 이용하여 검증을 수행함으로써, 지점별 월별 100개의 보정계수를 선정하였으며, 선정된 100개의 보정계수를 평균하여 최적화된 보정계수를 도출하였다.

보정계수 선정과정에서의 적합성을 검증하기 위해 PBIAS (Percent bias), NSE (Nash-Sutcliff efficiency) (Nash and Sutcliffe, 1970), R2 (Coefficient of determination), 그리고 RMSE (Root mean square error)의 4가지 평가지수를 사용하였으며, 각각의 산정방법은 다음과 같다.

$$PBIAS=100\times\frac{{\displaystyle\sum_{i=1}^N}\left(S_i-O_i\right)}{{\displaystyle\sum_{i=1}^N}O_i}$$ (10)
$$NSE=1-\frac{{\displaystyle\sum_{i=1}^N}\left(S_i-O_i\right)^2}{{\displaystyle\sum_{i=1}^N}\left(O_i-\overline O\right)^2}$$ (11)
$$R^2=\left(\frac{\displaystyle\sum_{i=1}^N\left(O_i-\overline O\right)\;\left(S_i-\overline S\right)}{\displaystyle\sqrt{\sum_{i=1}^N\left(O_i-\overline O\right)^2}\;\sqrt{\sum_{i=1}^N\left(S_i-\overline S\right)^2}}\right)^2$$ (12)
$$RMSE=\sqrt{\frac1N\;\sum_{i=1}^N\left(S_i-O_i\right)^2}$$ (13)

여기서, O는 관측값(즉, FAO PM에 의한 산정값), S는 모형값(특정 방법에 의한 산정값), O와 S는 각각 관측값과 모형값의 평균이다.

3. 연구결과

3.1 보정 전 기준증발산량 비교

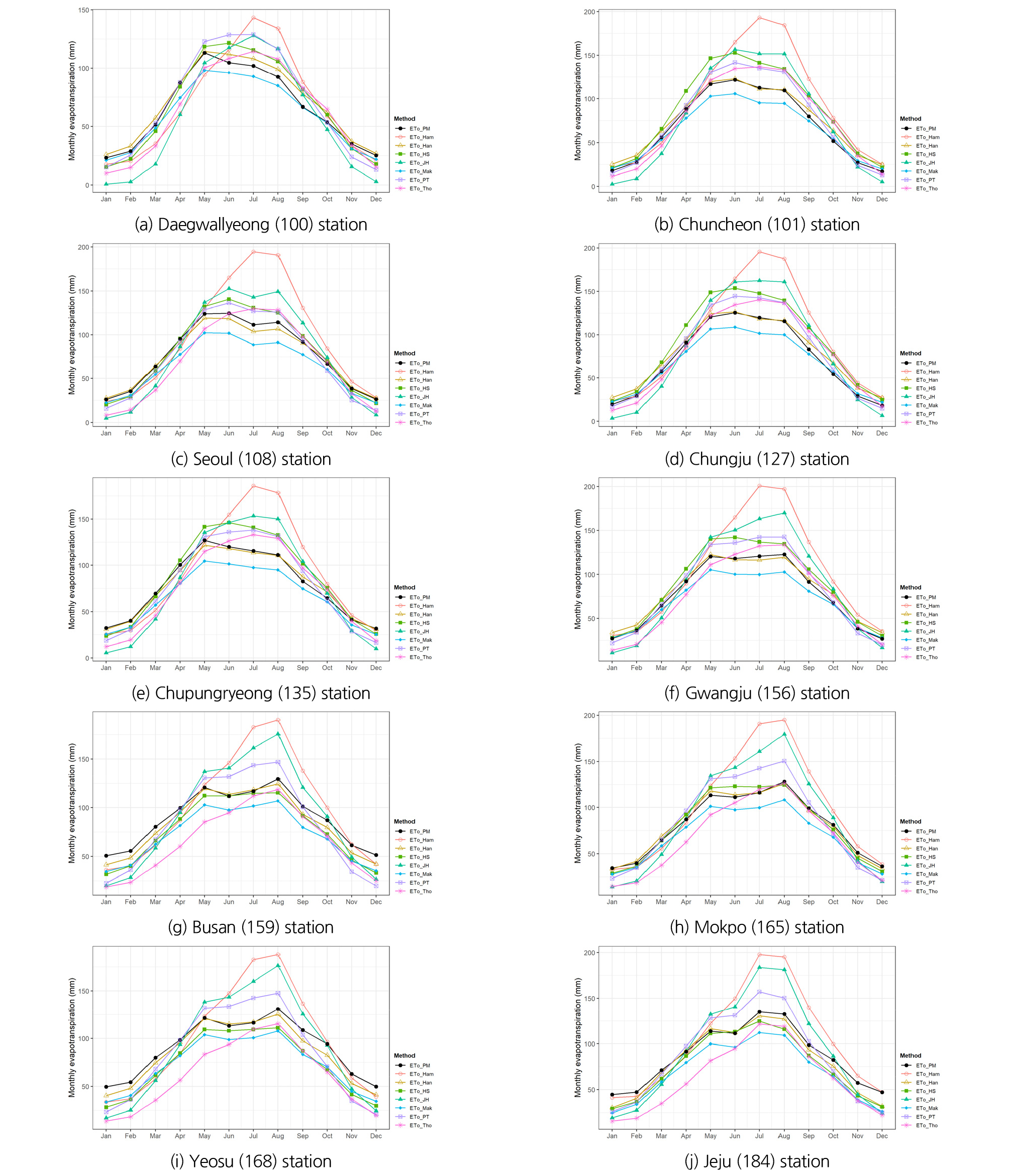
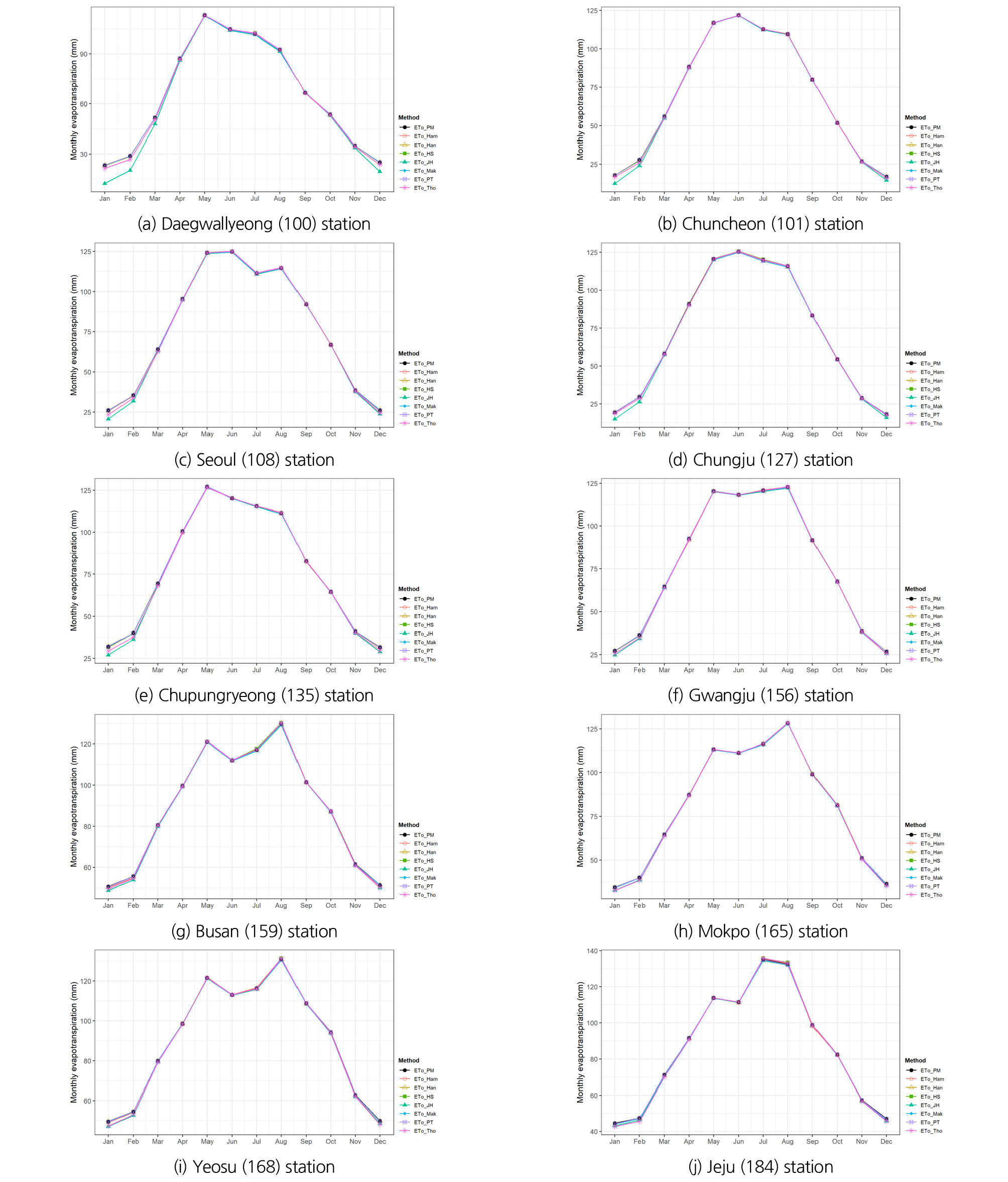
Fig. 2는 Table 2의 식을 적용하여 산정한 기준증발산량에 대해 월별 평균값을 산정한 것으로, 73개 ASOS 지점 중 대관령(100), 춘천(101), 서울(108), 충주(127), 추풍령(135), 광주(156), 부산(159), 목포(165), 여수(168), 제주(184) 등 주요 10개 지점에 대한 결과를 나타낸 것이다. 각 방법의 계수에 대해 기본값을 적용하여 산정한 결과로서, 대체로 여름철에 Hamon 방법과 Jensen-Haise 방법이 타 방법대비 큰 결과를 보이고 있는 반면, Makkink 방법은 가장 작은 증발산량을 보여주고 있다. 봄철과 겨울철의 경우에는 Thornthwaite와 Jensen-Haise 방법이 다른 방법들에 비해 작은 값을 나타내었다. 전반적으로 보았을 때에는 Hansen 방법이 FAO PM의 결과와 비슷한 경향을 보여주고 있다.

기존 Yeh (2017)의 연구에 의하면, 대만의 서부지역에 대해 FAO PM과 비교한 결과 모든 월에 대해 Jensen-Haise 방법은 과다 산정, Makkink과 Hamon 방법은 과소 산정하는 것으로 나타났다. 이때 Hamon 방법의 계수(kham)는 1.0을 적용한 것으로 본 연구에서 적용한 값(1.2)과 차이가 있다. 미국 North Carolina 산림지역에 대해 분석한 Rao et al. (2011)의 연구에서도 kham 값에 대해 1.0을 적용하였으나, 결과는 본 연구와 동일하게 여름철을 중심으로 Hamon 기준증발산량이 FAO PM보다 과다 산정되는 것으로 나타났다. Alkaeed et al. (2006)의 연구에서는 일본 Fukuoka 시의 서부지역을 대상으로 분석한 결과, FAO PM과 비교하여 Hamon 방법은 여름철에 상대적으로 크게 산정되고, Thornthwaite 방법은 봄철과 겨울철에 작게 산정되는 것으로 나타났다.

Fig. 2에서 나타난 결과에 대해 FAO PM 방법에 의한 월평균 기준증발산량을 기준으로 다른 7가지 방법들의 각 지점별 월별 편차를 분석해 보면, 대관령(100)은 -34 ~ +42 mm, 춘천(101)은 -19 ~ +80 mm, 서울(108)은 -28 ~ +83 mm, 충주(127)는 -19 ~ +76 mm, 추풍령(135)은 -27 ~ +70 mm, 광주(156)는 -21 ~ +80 mm, 부산(159)은 -40 ~ +66 mm, 목포(165)는 -27 ~ +75 mm, 여수(168)는 -44 ~ +66 mm, 제주(184)는 -36 ~ +63 mm로 나타났다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F2.jpg
Fig. 2.

Average monthly reference evapotranspiration before correction

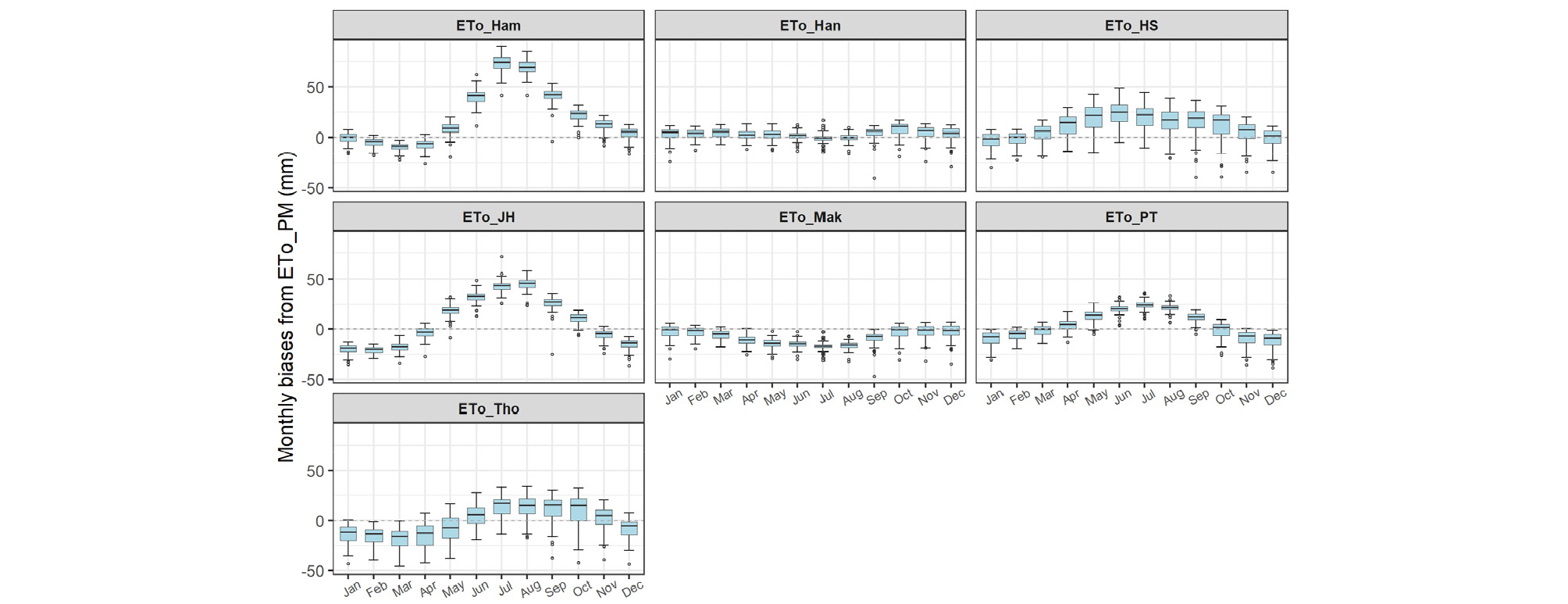
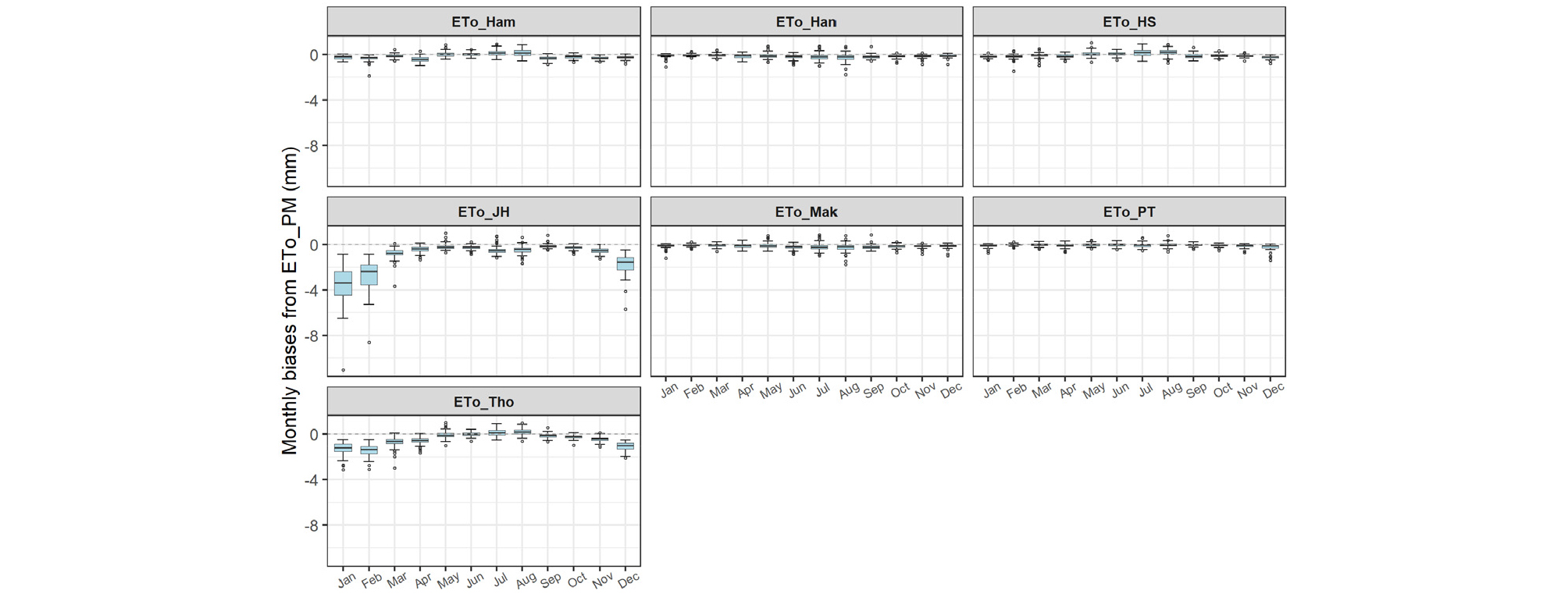
Fig. 3은 73개 지점에 대해 각 지점별 월별로 FAO PM 결과와의 편차를 박스플롯(Boxplot)으로 나타낸 것이다. 양의 값은 FAO PM 대비 크게 산정된 것을 의미하며, 음의 값은 반대로 작게 산정된 것을 의미한다.

Hansen 방법이 FAO PM 결과와 매월 거의 차이가 없는 것으로 나타난 반면, Hamon 방법과 Jensen-Haise 방법은 여름철을 중심으로 큰 차이를 나타내었다. 방법별로는 Hamon -26 ~ +88 mm, Hansen -29 ~ +17 mm, Hargreaves-Samani -39 ~ +45 mm, Jensen-Haise -36 ~ +56 mm, Makkink -35 ~ +7 mm, Priestley-Taylor -39 ~ +36 mm, Thornthwaite -46 ~ +32 mm로 나타났다. 따라서 보정을 하지 않고 기존 방법들을 사용할 경우 지점에 따라 월에 따라 매우 큰 편차를 유발할 수 있다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F3.jpg
Fig. 3.

Difference value between FAO PM method and others for monthly reference evapotranspiration before correction

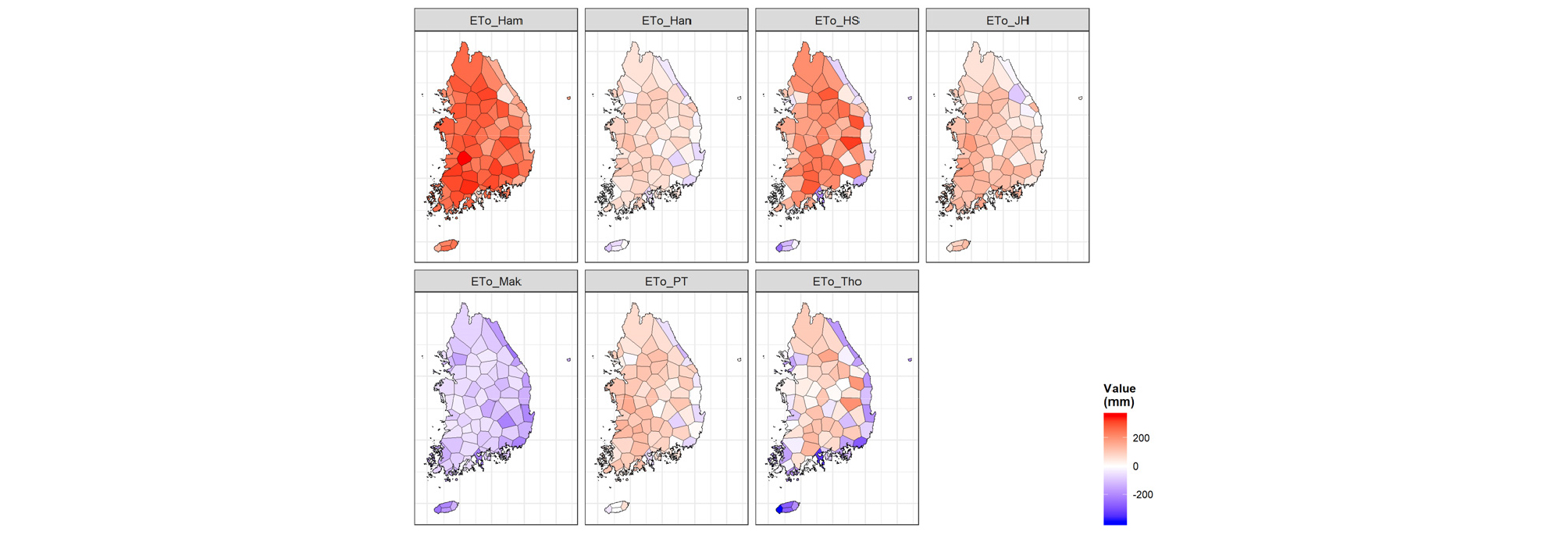
Fig. 4는 73개 ASOS 지점에 대한 티센망(Thiessen network)을 구성하여 연평균 기준증발산량에 대한 FAO PM 방법과 다른 방법들의 차이를 비교한 것으로, Hamon 방법은 모든 지역에서 과다하게 산정되는 반면, Makkink 방법은 과소하게 산정되는 것으로 나타났으며, Hansen, Hargreaves-Samani, Jensen-Haise, Priestley-Taylor, Thornthwaite 방법은 대체로 동해안 지역은 과소하게 나머지 지역에서는 과다하게 산정하는 것으로 나타났다.

지점에 따른 지역별 차이는 연간 -393 ~ +354 mm로 매우 큰 것으로 분석되었으며, 방법별로는 Hamon +44 ~ +354 mm, Hansen -98 ~ +119 mm, Hargreaves-Samani -245 ~ +321 mm, Jensen-Haise -92 ~ +181 mm, Makkink -237 ~ -29 mm, Priestley-Taylor -120 ~ +152 mm, Thornthwaite -393 ~ +201 mm로 나타났다.

서론에서 기술한 기준증발산량을 비교하는 많은 연구들에 의하면 각 방법에 적용되는 계수값 및 지역별 기후특성에 따라 상이한 결과가 나타나기 때문에 각 방법별 산정결과에 대해 원인을 규명하기는 쉽지 않다. 다만, Figs. 2 ~ 4에 나타난 것과 같이 산정방법에 따라 FAO PM과 큰 편차가 나타날 수도 있으므로, 지역의 기후특성을 반영한 충분한 보정이 필요하다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F4.jpg
Fig. 4.

Difference value between FAO PM method and others for annual reference evapotranspiration before correction

3.2 기준증발산량 보정계수 도출

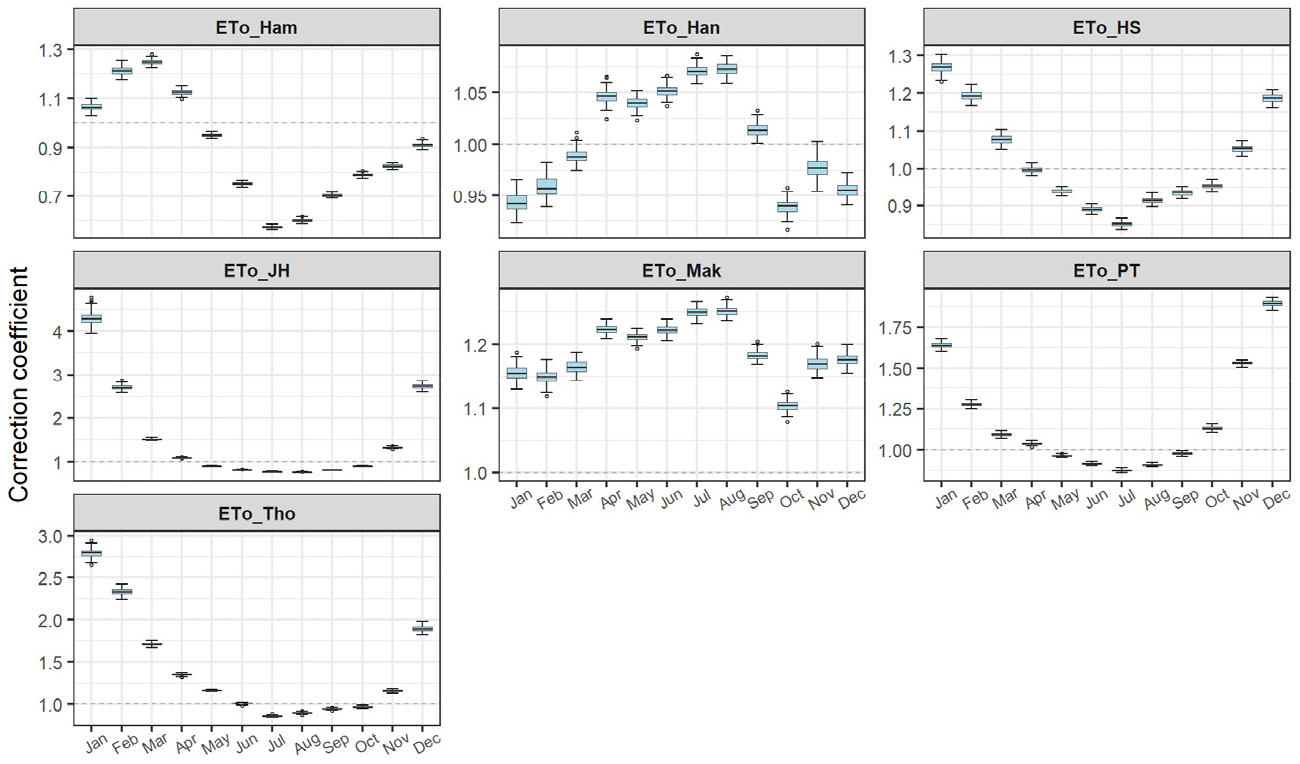
연구방법에서 기술한 것처럼 각 산정방법의 계수를 보정하는 대신에, 월별 산정된 FAO PM 결과를 기준으로 각 방법들에 의한 월별 기준증발산량과의 편차를 분석하여 월별 보정계수를 도출하였다. Fig. 5는 무작위 검증과정에서 도출된 총 100개의 보정계수를 박스플롯(Boxplot)으로 나타낸 것으로 서울(108) 지점의 결과이다. 산정방법별로 월별로 매우 상이한 값을 나타내고 있으며, 대체로 여름철보다는 증발산량 값이 상대적으로 작은 봄철과 겨울철에 보정계수의 불확실성이 크게 나타나고 있다. 이는 FAO PM 값을 기준으로 산정하는 보정계수가 봄철과 겨울철에는 증발산량 값의 작은 차이에도 더 크게 영향을 받기 때문이다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F5.jpg
Fig. 5.

Range of monthly correction coefficients of each method derived for Seoul (108) station

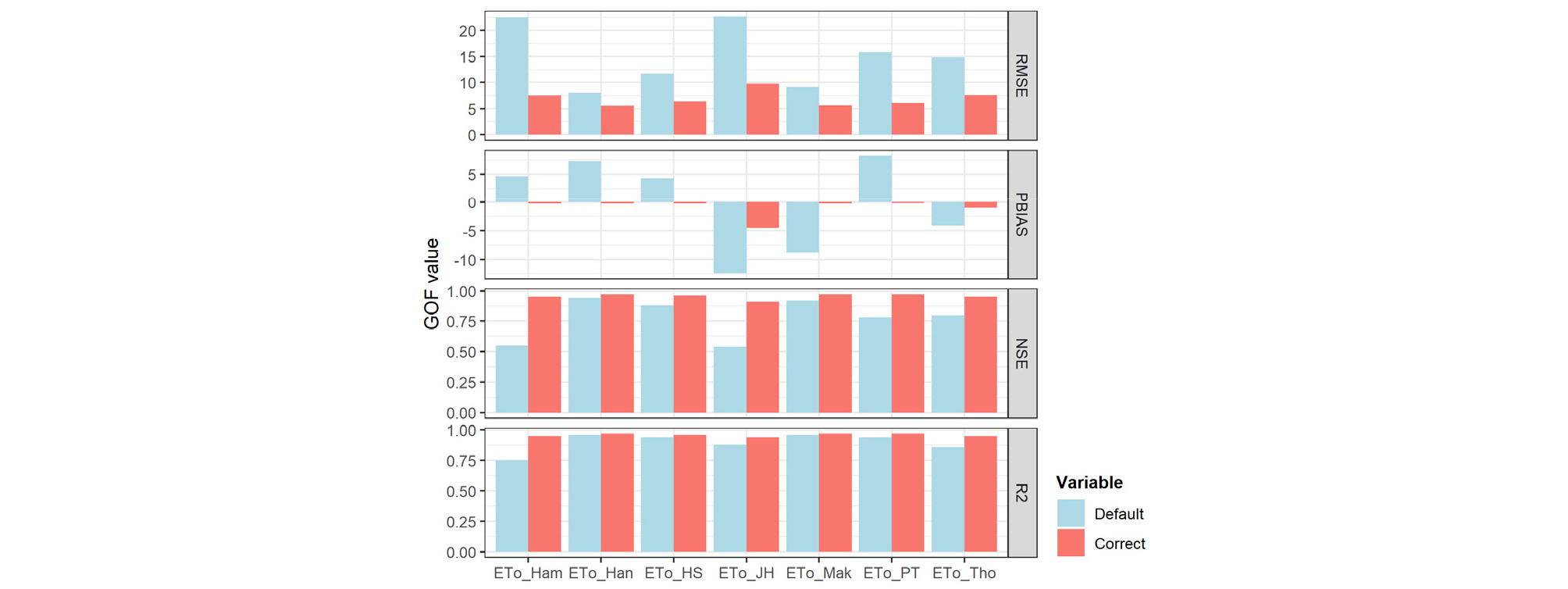
Fig. 6은 서울(108) 지점의 보정 전·후의 월 기준증발산량에 대한 적합도 분석 결과를 각 산정방법에 대해 나타낸 것으로, RMSE, PBIAS, NSE, R2 모두 보정을 통해 개선된 결과를 보이고 있으며, 특히 보정 전 FAO PM과 큰 편차를 보였던 Hamon, Jensen-Haise 방법의 개선효과가 크게 나타난 것을 알 수 있다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F6.jpg
Fig. 6.

Goodness of fit test results for monthly reference evapotranspiration before and after correction at Seoul (108) station

상기와 같은 방법으로 검증을 통하여 73개 대상지점에 대해 지점별 월별 보정계수의 범위를 도출하였으며, Fig. 5의 박스플롯상의 월별 평균값을 각 지점에 대한 최종 보정계수로 선정하였다. Table 3은 Fig. 2에서 제시한 10개 지점에 대해 월별 보정계수를 정리한 것이다. 대관령(100) 지점에서 Jensen-Haise 방법의 1월, 2월, 12월 보정계수가 상대적으로 매우 큰 값을 보였는데, 이는 즉 FAO PM 대비 해당월의 기준증발산량이 매우 작게 산정되고 있음을 의미한다. 춘천(101), 서울(108), 충주(127), 추풍령(135) 지점에서도 1월의 Jensen-Haise 보정계수가 4이상으로 분석되었다.

3.3 보정 후 기준증발산량 비교

Fig. 7은 Table 3에 제시된 월별 보정계수를 적용하여 산정한 각 방법의 기준증발산량과 FAO PM 기준증발산량을 비교한 것이다. 보정하기 전의 결과인 Fig. 2와 비교했을 때, 거의 모든 지점에서 보정된 값이 FAO PM 결과와 유사하게 나타나고 있음을 알 수 있다. 다만, 앞선 Table 3에서 나타난 것처럼 특정 월의 보정계수가 매우 크게 나타났던 대관령(100), 춘천(101), 서울(108), 충주(127), 추풍령(135) 지점에서 1월의 Jensen-Haise 결과가 여전히 타 방법에 비해 차이가 큰 것으로 나타났다. 그럼에도 보정 전과 비교해서는 그 편차가 크게 줄어든 것을 확인할 수 있으며, 분석한 73개 모든 지점에서 모든 월에 대해 보정된 기준증발산량이 FAO PM 결과와 비슷한 것으로 나타났다. 특히 기온자료만을 활용하는 가장 간단한 방법인 Hamon, Hargreave-Samani, Thornthwaite 방법 모두 보정된 결과가 FAO PM 결과와 비슷한 것으로 나타나, 가용자료가 부족한 지역에서의 활용성이 높을 것으로 기대된다. 반면, Jensen-Haise 방법을 적용하는 경우에는 지점에 따라 겨울철에 다소 편차가 크게 발생할 우려가 있으므로 주의가 필요하다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F7.jpg
Fig. 7.

Average monthly reference evapotranspiration after correction

Table 3.

Monthly correction coefficient according to the methods at 10 stations

Site Method Monthly correction coefficient
JAN FEB MAR APR MAY JUN JUL AUG SEP OCT NOV DEC
100 ETo_Ham 1.32 1.41 1.46 1.42 1.20 0.90 0.71 0.69 0.76 0.91 1.03 1.19
ETo_Han 0.90 0.87 0.90 1.00 0.99 0.93 0.94 0.93 0.86 0.86 0.94 0.94
ETo_HS 1.50 1.28 1.13 1.04 0.95 0.86 0.89 0.87 0.82 0.89 1.13 1.39
ETo_JH 17.02 7.33 2.71 1.43 1.08 0.88 0.79 0.78 0.87 1.12 2.17 6.89
ETo_Mak 1.10 1.05 1.07 1.17 1.15 1.08 1.10 1.08 1.01 1.01 1.13 1.15
ETo_PT 1.54 1.13 0.97 0.99 0.92 0.82 0.79 0.79 0.81 1.01 1.47 1.90
ETo_Tho 2.12 1.80 1.52 1.26 1.13 0.96 0.90 0.86 0.80 0.83 1.02 1.54
101 ETo_Ham 0.81 1.00 1.12 1.05 0.90 0.74 0.58 0.59 0.65 0.66 0.64 0.67
ETo_Han 0.70 0.78 0.88 0.97 0.98 0.99 1.01 0.99 0.91 0.81 0.76 0.68
ETo_HS 0.84 0.86 0.85 0.81 0.80 0.80 0.80 0.82 0.77 0.70 0.72 0.77
ETo_JH 4.75 2.72 1.47 1.04 0.86 0.78 0.74 0.72 0.75 0.83 1.20 2.73
ETo_Mak 0.86 0.94 1.04 1.13 1.13 1.15 1.18 1.16 1.06 0.96 0.92 0.84
ETo_PT 1.19 1.04 0.97 0.95 0.90 0.86 0.83 0.84 0.86 0.92 1.12 1.30
ETo_Tho 1.45 1.31 1.19 1.02 0.96 0.90 0.82 0.82 0.80 0.70 0.76 1.13
108 ETo_Ham 1.07 1.21 1.25 1.13 0.95 0.75 0.57 0.60 0.70 0.79 0.83 0.91
ETo_Han 0.94 0.96 0.99 1.05 1.04 1.05 1.07 1.07 1.01 0.94 0.98 0.96
ETo_HS 1.27 1.19 1.08 1.00 0.94 0.89 0.85 0.91 0.94 0.95 1.05 1.19
ETo_JH 4.30 2.71 1.52 1.09 0.90 0.82 0.78 0.76 0.81 0.90 1.33 2.73
ETo_Mak 1.16 1.15 1.17 1.22 1.21 1.22 1.25 1.25 1.18 1.10 1.17 1.18
ETo_PT 1.64 1.28 1.09 1.04 0.96 0.92 0.88 0.91 0.98 1.13 1.53 1.89
ETo_Tho 2.80 2.34 1.71 1.35 1.16 1.01 0.86 0.89 0.94 0.97 1.16 1.90
127 ETo_Ham 0.82 1.02 1.13 1.06 0.93 0.76 0.61 0.62 0.66 0.67 0.65 0.66
ETo_Han 0.70 0.79 0.88 0.95 0.97 0.99 1.01 0.99 0.91 0.80 0.75 0.67
ETo_HS 0.84 0.87 0.85 0.82 0.81 0.82 0.81 0.83 0.77 0.70 0.69 0.73
ETo_JH 4.22 2.55 1.43 1.03 0.86 0.78 0.73 0.71 0.75 0.82 1.15 2.37
ETo_Mak 0.86 0.95 1.04 1.12 1.13 1.15 1.17 1.15 1.06 0.95 0.91 0.82
ETo_PT 1.14 1.02 0.97 0.94 0.90 0.87 0.84 0.84 0.86 0.91 1.09 1.21
ETo_Tho 1.45 1.37 1.20 1.04 0.99 0.93 0.85 0.85 0.80 0.71 0.72 1.01
135 ETo_Ham 1.25 1.35 1.34 1.20 1.01 0.78 0.62 0.63 0.69 0.81 0.88 1.07
ETo_Han 1.04 1.02 1.03 1.07 1.04 1.02 1.02 1.00 0.95 0.91 0.97 1.03
ETo_HS 1.34 1.20 1.04 0.95 0.90 0.82 0.82 0.84 0.81 0.85 0.98 1.22
ETo_JH 4.95 2.98 1.64 1.15 0.94 0.82 0.75 0.74 0.79 0.92 1.38 2.92
ETo_Mak 1.26 1.21 1.22 1.25 1.21 1.18 1.18 1.17 1.11 1.07 1.15 1.25
ETo_PT 1.71 1.32 1.14 1.06 0.97 0.88 0.84 0.85 0.88 1.04 1.43 1.91
ETo_Tho 2.39 1.94 1.49 1.23 1.10 0.95 0.87 0.86 0.85 0.87 1.02 1.62
159 ETo_Ham 1.39 1.37 1.31 1.14 0.98 0.76 0.64 0.69 0.73 0.87 0.98 1.21
ETo_Han 1.22 1.15 1.09 1.04 1.01 0.98 0.99 1.04 1.09 1.09 1.14 1.22
ETo_HS 1.60 1.38 1.22 1.13 1.08 1.00 1.02 1.13 1.10 1.20 1.33 1.55
ETo_JH 2.45 1.89 1.36 1.04 0.88 0.79 0.72 0.74 0.84 0.95 1.24 1.88
ETo_Mak 1.46 1.36 1.28 1.22 1.18 1.15 1.15 1.21 1.27 1.28 1.35 1.46
ETo_PT 2.24 1.54 1.19 1.02 0.92 0.85 0.82 0.88 1.01 1.26 1.79 2.57
ETo_Tho 2.63 2.31 1.97 1.65 1.42 1.18 1.05 1.10 1.12 1.23 1.41 2.00
156 ETo_Ham 0.89 1.04 1.12 1.02 0.90 0.72 0.60 0.62 0.67 0.73 0.71 0.75
ETo_Han 0.81 0.85 0.91 0.96 0.98 1.01 1.04 1.02 0.97 0.87 0.83 0.79
ETo_HS 0.97 0.95 0.91 0.87 0.86 0.83 0.88 0.91 0.87 0.85 0.84 0.88
ETo_JH 2.24 1.80 1.26 0.98 0.84 0.78 0.74 0.72 0.76 0.81 0.99 1.52
ETo_Mak 0.97 1.01 1.07 1.12 1.14 1.18 1.21 1.19 1.13 1.02 0.98 0.95
ETo_PT 1.23 1.07 0.98 0.94 0.90 0.87 0.85 0.86 0.90 0.99 1.17 1.33
ETo_Tho 1.82 1.66 1.40 1.19 1.08 0.96 0.91 0.92 0.91 0.89 0.93 1.25
165 ETo_Ham 1.04 1.12 1.16 1.04 0.92 0.72 0.61 0.66 0.71 0.84 0.88 0.94
ETo_Han 1.01 0.95 0.93 0.95 0.96 0.98 1.00 1.02 1.02 1.02 1.06 1.07
ETo_HS 1.20 1.08 1.00 0.94 0.93 0.90 0.95 1.03 1.00 1.07 1.13 1.18
ETo_JH 2.30 1.85 1.30 0.99 0.84 0.77 0.72 0.71 0.79 0.91 1.19 1.77
ETo_Mak 1.22 1.13 1.10 1.10 1.11 1.14 1.17 1.18 1.19 1.19 1.26 1.29
ETo_PT 1.46 1.14 0.98 0.90 0.86 0.83 0.82 0.85 0.94 1.14 1.46 1.68
ETo_Tho 2.20 2.04 1.70 1.39 1.23 1.06 0.97 1.02 1.03 1.12 1.24 1.64
168 ETo_Ham 1.45 1.46 1.38 1.16 0.99 0.77 0.64 0.70 0.79 0.98 1.06 1.25
ETo_Han 1.22 1.13 1.07 1.03 1.00 0.98 0.99 1.04 1.11 1.14 1.18 1.20
ETo_HS 1.74 1.49 1.29 1.17 1.11 1.05 1.06 1.18 1.25 1.40 1.51 1.66
ETo_JH 2.71 2.07 1.41 1.05 0.88 0.79 0.72 0.74 0.86 1.01 1.31 1.97
ETo_Mak 1.47 1.34 1.26 1.20 1.17 1.14 1.15 1.21 1.30 1.33 1.39 1.44
ETo_PT 2.11 1.50 1.17 1.00 0.92 0.85 0.82 0.89 1.05 1.33 1.80 2.36
ETo_Tho 3.36 2.86 2.22 1.74 1.45 1.21 1.06 1.14 1.25 1.45 1.69 2.41
184 ETo_Ham 1.07 1.10 1.14 1.04 0.93 0.74 0.69 0.68 0.70 0.82 0.87 0.99
ETo_Han 1.45 1.16 1.03 0.98 0.98 0.99 1.03 1.04 1.05 1.09 1.22 1.45
ETo_HS 1.52 1.28 1.15 1.05 1.02 0.98 1.09 1.15 1.13 1.24 1.32 1.49
ETo_JH 2.21 1.69 1.27 0.99 0.86 0.79 0.73 0.73 0.81 0.95 1.27 1.87
ETo_Mak 1.77 1.39 1.21 1.15 1.14 1.15 1.20 1.21 1.23 1.28 1.46 1.76
ETo_PT 1.70 1.29 1.06 0.94 0.89 0.85 0.86 0.88 0.96 1.18 1.53 1.88
ETo_Tho 2.68 2.38 2.01 1.61 1.40 1.18 1.12 1.12 1.15 1.32 1.49 2.05

Fig. 8은 73개 지점에 대해 보정 후의 월평균 기준증발산량 편차를 Fig. 3과 같은 방법으로 비교한 것이다. Jensen-Haise 방법의 일부 월(1, 2, 12월)을 제외하고는 대부분의 지점에서 보정된 월평균 기준증발산량과 FAO PM 결과와의 편차가 ±3 mm 이내로 분석되었다. 방법별로는 Hamon -2 ~ +1 mm, Hansen -2 ~ +1 mm, Hargreaves-Samani -1 ~ +1 mm, Jensen-Haise -11 ~ +1 mm, Makkink -2 ~ +1 mm, Priestley-Taylor -1 ~ +1 mm, Thornthwaite -3 ~ +1 mm로 나타났다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F8.jpg
Fig. 8.

Difference value between FAO PM method and others for monthly reference evapotranspiration after correction

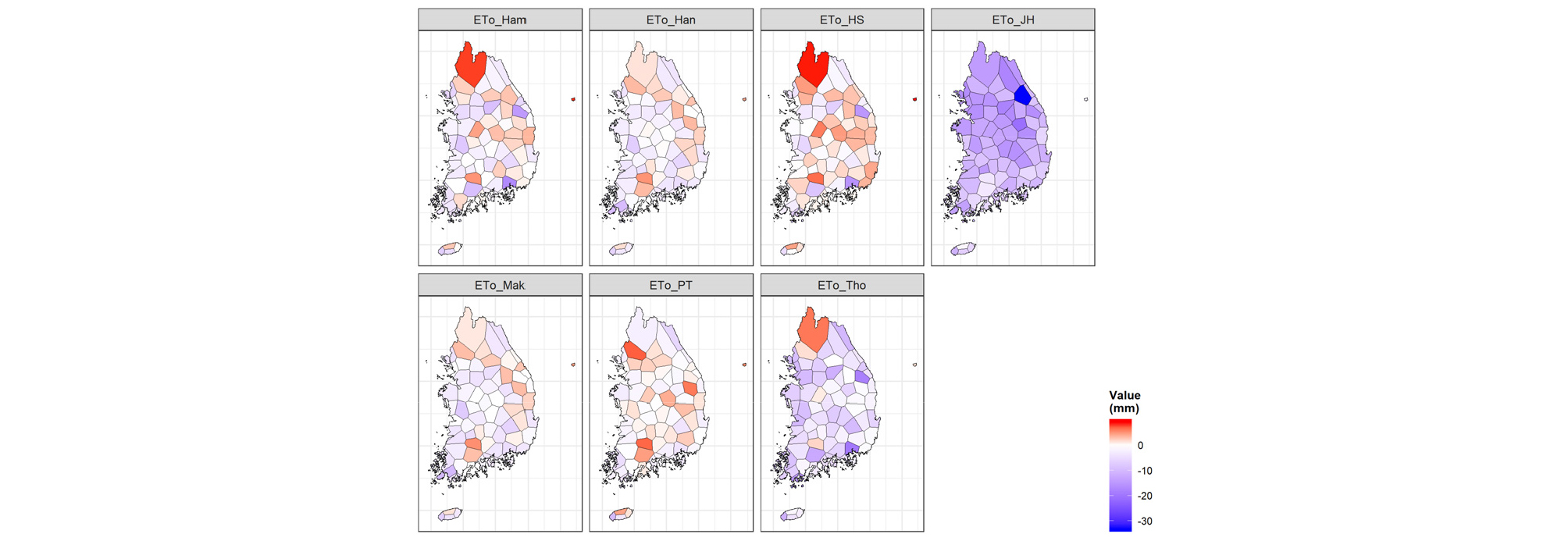
Fig. 9는 Fig. 4와 같이 ASOS 지점에 대한 티센망(Thiessen network)을 구성하여 보정 후의 연평균 기준증발산량에 대해 FAO PM 방법과의 편차를 비교한 결과이다. 보정 후에는 지역별 편차가 현저하게 감소하여 산정방법에 따라 연간 -33 ~ +9 mm의 편차(보정 전에는 -393 ~ +354 mm)를 나타내었다. 방법별로는 Hamon -17 ~ +9 mm, Hansen -9 ~ +5 mm, Hargreaves-Samani -16 ~ +9 mm, Jensen-Haise -33 ~ -1 mm, Makkink -10 ~ +5 mm, Priestley-Taylor -10 ~ +7 mm, Thornthwaite -19 ~ +6 mm로 분석되었다. 즉, 가용한 기상자료의 부족으로 FAO PM 방법을 적용하기 어려운 경우에도 나머지 대안방법들과 본 연구에서 도출된 보정계수를 활용하여 충분히 FAO PM과 유사한 결과를 도출할 수 있음을 의미한다.

http://static.apub.kr/journalsite/sites/kwra/2020-053-09/N0200530907/images/kwra_53_09_07_F9.jpg
Fig. 9.

Difference value between FAO PM method and others for annual reference evapotranspiration after correction

4. 요약 및 결론

본 연구에서는 FAO PM 방법을 비롯하여 Hamon, Hansen, Hargreaves-Samani, Jensen-Haise, Makkink, Priestley-Taylor, Thornthwaite 등 일 단위 기준증발산량 산정방법 8가지를 활용하여 전국 기상청 ASOS 지점을 대상으로 각 방법에 따른 월 및 연 단위 기준증발산량을 상호 비교하였다. 결측자료를 제외하고 20년 이상의 가용자료를 보유하고 있는 73개 지점의 일 기상자료(최고기온, 최저기온, 상대습도, 풍속, 일조시간)를 이용하여 각 방법별 일 단위의 기준증발산량을 산정하고, 월 및 연 단위로 값을 비교하였다.

각 방법의 계수에 대해 기본값을 적용한 상태에서 기준증발산량을 산정한 결과, 산정방법에 따라 큰 차이를 보였다. FAO PM 결과와 비교했을 때 월 평균값은 방법에 따라 -46 mm에서 +88 mm까지의 큰 차이를 보였으며, Hansen (편차 -29 mm ~ +17 mm)을 제외한 나머지 방법들의 편차가 크게 나타났다. 특히, Hamon 방법과 Jensen-Haise 방법은 여름철을 중심으로 FAO PM 대비 매우 크게 산정되는 것으로 나타났다. 연 평균값도 지점에 따라 -393 mm ~ +354 mm로 매우 큰 편차를 보였으며, Makkin 방법은 거의 모든 지역에서 과소 산정되는 반면, Hamon 방법은 과다하게 산정하는 것으로 나타났다. 나머지 Hansen, Hargreaves-Samani, Jensen-Haise, Priestley-Taylor, Thornthwaite 방법들도 동해안 일부 해안지역을 제외한 대부분의 지역에서 FAO PM과 비교하여 과다하게 산정하는 경향을 보였다.

각 산정방법들에 의한 편차를 최소화하고, 가용 기상요소가 부족하거나 결측으로 인해 FAO PM 방법을 적용하기 어려운 조건에서 나머지 방법들의 활용성을 높이기 위해 FAO PM 결과를 기준으로 월별 변동형 보정계수를 도출하였다. 보정계수 산출을 위해 각 지점별 과거의 가용자료에 대해 총 100회의 무작위 보정과 검증을 통하여 100개의 보정계수를 산출하고, 이를 평균하여 지점별 월별 보정계수를 결정하였다.

선정된 보정계수를 활용하여 다시 FAO PM과의 월 평균값에 대한 편차를 분석한 결과, Jensen-Haise 방법에서 겨울철(1, 2, 12월)에 타 방법에 비해 편차가 크게 나타났으나, 보정 전과 비교하여 확연히 개선되었음을 확인할 수 있었으며, 나머지 방법들의 편차는 ±3 mm 이내로 매우 양호한 것으로 나타났다. 연 평균값 또한 -33 mm ~ +9 mm로 보정 전에 비해 크게 개선되었으며 방법들 간의 편차도 매우 작은 것으로 나타났다. 특히, 기온자료만을 이용하는 Hamon, Hargreaves-Samani, Thornthwaite 방법들 또한 보정을 통해 FAO PM과 유사한 결과를 얻을 수 있었다.

이상과 같이 본 연구에서는 FAO PM 대비 간소화된 기상자료를 이용하여 기준증발산량을 추정할 수 있는 7가지 대안방법들의 적용성을 분석하였다. 보정이 되지 않은 상태에서는 산정방법에 따라 큰 편차가 발생하였으나, 보정을 통하여 각 방법들간의 편차 및 FAO PM과의 편차를 최소화할 수 있음을 확인하였다. 본 연구에서 분석한 73개 지점의 경우 충분한 기상자료가 확보되어 있어 FAO PM을 적용하는 것이 합리적일 수 있다. 그러나, Droogers and Allen (2002)이 언급한 것처럼, 기준증발산량 산정과정에서 습도, 풍속, 일사량 등으로부터 발생하는 불확실성이 기온에 의한 불확실성보다 5 ~ 25배 정도인 것을 감안할 때, 일부 기상요소가 결측되거나 품질문제가 우려되는 기간에 대해 적용할 경우에는 기온자료만을 이용하는 대안방법들이 유용하게 활용될 수 있을 것이다. 또한, 불확실성이 더욱 높을 것으로 우려되는 미래 기후변화 시나리오를 이용하여 미래 장기간의 기준증발산량을 전망하거나, 비교적 정확도가 높은 월 또는 계절 단위의 장기 기온예측정보를 활용하여 수개월간의 기준증발산량을 전망하는 경우에도 보정된 기온기반의 방법들(Hamon, Hargreaves-Samani, Thornthwaite)이 유용하게 활용될 수 있을 것이다.

Acknowledgements

본 연구는 한국건설기술연구원 주요사업 “가뭄대응 중소하천 물부족 위험도 평가 및 물 확보 기술 개발” 과제의 연구비 지원에 의해 수행되었습니다.

References

1
Abd El-Wahed, M.H., and Abd El-Mageed, T.A. (2014). "Estimating reference evapotranspiration using modified Blaney-Criddle equation in arid region." Bothalia Journal, Vol. 44, No. 7, pp. 183-195.
2
Ahmadi, S.H., and Fooladmand, H.R. (2008). "Spatially distributed monthly reference evapotranspiration derived from the calibration of Thornthwaite equation: A case study, South of Iran." Irrigation Science, Vol. 26, pp. 303-312.
10.1007/s00271-007-0094-8
3
Alkaeed, O., Flores, C., Jinno, K., and Tsutsumi, A. (2006). "Comparison of several reference evapotranspiration methods for Itoshima peninsula area, Fukuoka, Japan." Memoirs of the Faculty of Engineering, Kyushu Univ., Vol. 66, No. 1, pp. 1-14.
4
Allen, R.G., Pereira, L.S., Raes, D., and Smith, M. (1998). Crop evapotranspiration-guidelines for computing crop water requirements. FAO Irrigation and Drainage, Rome, Italy, pp. 23-56.
5
Almorox, J., and Grieser, J. (2016). "Calibration of the Hargreaves-Samani method for the calculation of reference evapotranspiration in different Köppen climate classes." Hydrology Research, Vol. 42, No. 2, pp. 521-531.
10.2166/nh.2015.091
6
Antonopoulos, V.Z., and Antonopoulos, A.V. (2018). "Evaluation of different methods to estimate monthly reference evapotranspiration in a Mediterranean area." Water Utility Journal, Vol. 18, pp. 61-77.
7
Chang, X., Wang, S., Gao, Z., Luo, Y., and Chen, H. (2019). "Forecast of daily reference evapotranspiration using a modified daily Thornthwaite equation and temperature forecasts." Irrigation and Drainage, Vol. 68, pp. 297-317.
10.1002/ird.2309
8
Choi, W., Choi, M. Oh, H., and Park, J. (2010). "Estimation on trends of reference evapotranspiration of weather station using reference evapotranspiration calculator software." Journal of the Korean Society of Civil Engineers, KSCE, Vol. 30, No. 2B, pp. 219-231.
9
Cristea, N.C., Kampf, S.K., and Burges, S.J. (2013). "Revised coefficients for Priestley-Taylor and Makkink-Hansen equations for estimating daily reference evapotranspiration." Journal of Hydrologic Engineering, ASCE, Vol. 18, No. 10, pp. 1289-1300.
10.1061/(ASCE)HE.1943-5584.0000679
10
Djaman, K., Balde, A.B., Sow, A., Muller, B., Irmak, S., N'Diaye, M. K., Manneh, B., Moukoumbi, Y.D., Futakuchi, K., and Saito, K. (2015). "Evaluation of sixteen reference evapotranspiration methods under sahelian conditions in the Senegal River valley." Journal of Hydrology: Regional Studies, Vol. 3, pp. 139-159.
10.1016/j.ejrh.2015.02.002
11
Droogers, P., and Allen, R.G. (2002). "Estimating reference evapotranspiration under inaccurate data conditions." Irrigation and Drainage Systems, Vol. 16, pp. 33-45.
10.1023/A:1015508322413
12
Fooladmand, H.R., and Haghighat, M. (2007). "Spatial and temporal calibration of Hargreaves equation for calculating monthly ETo based on Penman-Monteith method." Irrigation and Drainage, Vol. 56, pp. 439-449.
10.1002/ird.305
13
Grismer, M.E., Orang, M., Snyder, R., and Matyac, R. (2002). "Pan evaporation to reference evapotranspiration conversion methods." Journal of Irrigation and Drainage Engineering, ASCE, Vol. 128, No. 3, pp. 180-184.
10.1061/(ASCE)0733-9437(2002)128:3(180)
14
Gurski, B.C., Jerszurki, D., and Souza, J.L.M. (2018). "Alternative methods of reference evapotranspiration for Brazilian climate types." Revista Brasileira de Meteorologia, Vol. 33, No. 3, pp. 567-578.
10.1590/0102-7786333015
15
Hamon, W.R. (1960). Estimating potential evapotranspiration. Master thesis, Massachusetts Institute of Technology, Cambridge, M.A., U.S.
16
Hamon, W.R. (1963). "Computation of direct runoff amounts from storm rainfall." International Association of Scientific Hydrology, Vol. 63, pp. 52-62.
17
Hansen, S. (1984). "Estimation of potential and actual evapotranspiration." Nordic Hydrology, Vol. 15, pp. 205-212.
10.2166/nh.1984.0017
18
Hargreaves, G.H., and Samani, Z.A. (1982). "Estimating potential evapotranspiration." Journal of Irrigation and Drainage Division, American Society of Civil Engineers, ASCE, Vol. 108, pp. 223-230.
19
Hargreaves, G.H., and Samani, Z.A. (1985). "Reference crop evapotranspiration from temperature." American Society of Agricultural Engineers, Vol. 1, pp. 96-99.
10.13031/2013.26773
20
Heydari, M.M., Aghamajidi, R., Beygipoor, G., and Heydari, M. (2014). "Comparison and evaluation of 38 equations for estimating reference evapotranspiration in an arid region." Fresenius Environmental Bulletin, Vol. 23, No. 8a, pp. 1985-1996.
21
Irmak, S., Allen, R.G., and Whitty, E.B. (2003). "Daily grass and alfalfa-reference evapotranspiration estimates and alfalfa-to-grass evapotranspiration ratios in Florida." Journal of Irrigation and Drainage Engineering, ASCE, Vol. 129, No. 5, pp. 360-370.
10.1061/(ASCE)0733-9437(2003)129:5(360)
22
Jensen, M.E., and Haise, H.R. (1963). "Estimating evapotranspiration from solar radiation." Journal of the Irrigation and Drainage Division, ASCE, Vol. 89, pp. 15-41.
23
Kim, H., and Chung, S. (1999). "Estimation and comparison of reference crop evapotranspiration at the selected stationos in Korea." KCID Journal, KCID, Vol. 6, No. 2, pp. 37-46.
24
Kim, S.J., Kim, M., Lim, C.-H., Lee, W.-K., and Kim, B.-J. (2017). "Applicability analysis of FAO56 Penman-Monteith methodology for estimating potential evapotranspiration in Andong Dam watershed using limited meteorological data." Journal of Climate Change Research, Vol. 8, No. 2, pp. 125-143.
10.15531/ksccr.2017.8.2.125
25
Lang, D., Zheng, J., Shi, Jiaqi, Liao, F., Ma, X., Wang, W., Chen, X., and Zhang, M. (2017). "A comparative study of potential evapotranspiration estimation by eight methods with FAO Penman-Monteith method in southwestern China." Water, Vol. 9, No. 10, p.734, doi:10.3390/w9100734.
10.3390/w9100734
26
Lee, K.-H., and Park, J.-H. (2008). "Calibration of the Hargreaves equation for the reference evapotranspiration estimation on a nation-wide scale." Journal of the Korean Society of Civil Engineers, KSCE, Vol. 28, No. 6B, pp. 675-681.
27
Lee, K.-H., Cho, H.-Y., and Oh, N.-S. (2008). "Calibration and validation of the Hargreaves equation for the reference evapotranspiration estimation in Gyeonggi bay watershed." Journal of Korea Water Resources Association, KWRA, Vol. 41, No. 4, pp. 413-422.
10.3741/JKWRA.2008.41.4.413
28
Lu, J., Sun, G., McNulty, S.G., and Amatya, D.M. (2005). "A comparison of six potential evapotranspiration methods for regional use in the southwestern United States." Journal of the American Water Resources Association, AWRA, Vol. 41, pp. 621-633.
10.1111/j.1752-1688.2005.tb03759.x
29
Makkink, G.F. (1957). "Testing the Penman formula by means of lysimeters." Journal of the Institution of Water Engineers, Vol. 11, No. 3, pp. 277-288.
30
McCabe, G.J., Hay, L.E., Bock, A., Markstrom, S.L., and Atkinson, R.D. (2015). "Inter-annual and spatial variability of Hamon potential evapotranspiration model coefficients." Journal of Hydrology, Vol. 521, pp. 389-394.
10.1016/j.jhydrol.2014.12.006
31
Metcalfe, R.A., Petzold, H., Luce, J.J., and Buttle, J.M. (2019). "Evaluating seasonal and regional calibration of temperature-based methods for estimating potential evaporation in Ontario." Canadian Water Resources Journal, Vol. 44, No. 1, pp. 2-21.
10.1080/07011784.2018.1493399
32
Moon, J.W. (2018). "Analysis of reference evapotranspiration change in Korea by climate change impact." Journal of the Korean Society of Hazard Mitigation, KOSHAM, Vol. 19, No. 7, pp. 71-81.
10.9798/KOSHAM.2018.18.7.71
33
Moon, J.W., Jung, C.G., and Lee, D.R. (2013). "Parameter regionalization of Hargreaves equation based on climatological characteristics in Korea." Journal of Korea Water Resources Association, KWRA, Vol. 46, No. 9, pp. 933-946.
10.3741/JKWRA.2013.46.9.933
34
Nash, J.E., and Sutcliffe, J.V. (1970) "River flow forecasting through conceptual model. part 1-A discussion of principles." Journal of Hydrology, Vol. 10, pp. 282-290.
10.1016/0022-1694(70)90255-6
35
Neto, A.J.S., Júnior, J.C.F., Andrade, C.L.T., Lopes, D.C., and Nascimento, P.T. (2015). "Reference evapotranspiration estimates based on minimum meteorological variable requirements of historical weather data." Chilean Journal of Agricultural Research, Vol. 75, No. 3, pp. 366-374.
10.4067/S0718-58392015000400014
36
Park, J., Cho, J., Lee, E.-J., and Jung, I. (2017). "Evaluation of reference evapotranspiration in South Korea according to CMIP5 GCMs and estimation methods." Journal of the Korean Society of Rural Planning, KSRP, Vol. 23, No. 4, pp. 153-168.
37
Peng, L., Li, Y., and Feng, H. (2017). "The best alternative for estimating reference crop evapotranspiration in different sub-regions of mainland China." Scientific Reports, Vol. 7, No. 1 p. 5458, doi:10.1038/s41598-017-05660-y.
10.1038/s41598-017-05660-y28710418PMC5511263
38
Pereira, A.R., and Pruitt, W.O. (2004), "Adaptation of the thornthwaite scheme for estimating daily reference evapotranspiration." Agricultural Water Management, Vol. 66, pp. 251-257.
10.1016/j.agwat.2003.11.003
39
Priestley, C.H.B., and Taylor, R.J. (1972). "On the assessment of surface heat flux and evaporation using large-scale parameters." Monthly Weather Review, Vol. 100, No. 2, pp. 81-92.
10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2
40
Rácz, C., Nagy, J., and Dobos, A.C. (2013). "Comparison of several methods for calculation of reference evapotranspiration." Acta Silvatica et Lignaria Hungarica, Vol. 9, No. 1, dio: 10.2478/aslh-2013-0001.
10.2478/aslh-2013-0001
41
Rao, L.Y., Sun, G., Ford, C.R., and Vose, J.M. (2011). "Modeling potential evapotranspiration of two forested watersheds in the southern Appalachians." Transactions of the ASABE, Vol. 54, No. 6, pp. 2067-2078.
10.13031/2013.40666
42
Rim, C.-S. (2008). "Trends of annual and monthly FAO Penman-Monteith reference evapotranspiration." Journal of the Korean Society of Civil Engineers, KSCE, Vol. 28, No. 1B, pp. 65-77.
43
Rim, C.-S., Yoon, S.E., Song, J.I. (2009). "Evaluation of equations for estimating pan evaporation considering regional characteristics." Journal of the Korean Society of Civil Engineers, KSCE, Vol. 29, No. 1B, pp. 47-62.
44
Samaras, D., Rief, A., and Theodoropoulos, K. (2014). "Evaluation of radiation-based reference evapotranspiration models under difference mediterranean climates in central Greece." Water Resources Management, Vol. 28, pp. 207-225.
10.1007/s11269-013-0480-3
45
Seiller, G., and Anctil, F. (2016). "How do potential evapotranspiration formulas influence hydrological projections?" Hydrological Sciences Journal, Vol. 61, No. 12, pp. 2249-2266.
10.1080/02626667.2015.1100302
46
Shahidian, S., Serralheiro, R., Serrano, J., Teixeira, J., Haie, N., and Santos, F. (2012). "Hargreaves and other reduced-set methods for calculating evapotranspiration." Evapotranspiration-Remote Sensing and Modeling, Edited by Irmak, A., InTech, Rijeka, Croatia, pp. 59-79.
10.5772/18059
47
Sur, C., Lee, J., Park, J., and Choi, M. (2012), "Spatial estimation of Priestley-Taylor based potential evapotranspiration using MODIS imageries: The Nak-dong river basin." Korean Journal of Remote Sensing, Vol. 28, No. 5, pp. 521-529.
10.7780/kjrs.2012.28.5.5
48
Tegos, A., Malamos, N., Efstratiadis, A. Tsoukalas, I., Karanasios, A., and Koutsoyiannis, D. (2017). "Parametric modelling of potential evapotranspiration: A global survey." Water, Vol. 9, No. 10, p.795, doi:10.3390/w9100795.
10.3390/w9100795
49
Thornthwaite, C.W. (1948). "An approach toward a rational classification of climate." Geographical Review, Vol. 38, No. 1, pp. 55-94.
10.2307/210739
50
Tomar, A.S. (2015). "Compararive performance of reference evapotranspiration equations at sub-humid Rarai region of Uttarakhand, India." International Journal of Agricultural Research, Vol. 10, No. 2, pp. 65-73.
10.3923/ijar.2015.65.73
51
Valipour, M. (2015a). "Evaluation of radiation methods to study potential evapotranspiration of 31 provinces." Meteorological and Atmospheric Physics, Vol. 127, pp. 289-303.
10.1007/s00703-014-0351-3
52
Valipour, M. (2015b). "Temperature analysis of reference evapotranspiration models." Meteorological Applications, Vol. 22, pp. 385-394.
10.1002/met.1465
53
Xu, C.-Y., and Singh, V.P. (2002). "Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland." Water Resources Management, Vol. 16, pp. 197-219.
10.1023/A:1020282515975
54
Xystrakis, F., and Matzarakis, A. (2011). "Evaluation of 13 empirical reference potential evapotranspiration equations on the island of Crete in southern Greece." Journal of Irrigation and Drainage Engineering, ASCE, Vol. 137, No. 4, pp. 211-222.
10.1061/(ASCE)IR.1943-4774.0000283
55
Yeh, H.-F. (2017). "Comparison of evapotranspiration methods under limited data." Current Perspective to Predict Actual Evapotranspiration, Edited by Bucur, D., InTech, Rijeka, Croatia, pp. 1-23.
10.5772/intechopen.68495
56
Yoon, P.R., and Choi, J.-Y. (2018). "Assessment of reference evapotranspiration equations for missing and estimated weather data." Journal of the Korean Society of Agricultural Engineers, KSAE, Vol. 60, No. 3, pp. 15-25.
페이지 상단으로 이동하기