1. 서 론
2. 댐 운영에서의 ESP 활용에 관한 간단한 가상 예제
3. 국내 댐 사례를 활용한 ESP 효과 분석
3.1 분석 과정 개요
3.2 대상 댐의 선정
3.3 최적 방류량 결정 모형 및 적용 결과
3.4 모의 운영 및 적용 결과
4. 결론 및 향후 연구
1. 서 론
자연재해 완화와 수자원 관리 등에 대한 수문예측의 중요성은 이미 1975년 World Meteorological Organization (WMO)에 의해 연구자들에게 인식되어왔다(WMO, 1975). 이에 따라 미국 서부에서 하천 유량의 불확실성을 고려하여 중장기 물 공급 전망을 위해 제안된 방법론이 Extended Streamflow Prediction (Day, 1985)이고, 이후 National Weather Service (NWS)가 이 방법론을 Ensemble Streamflow Prediction (ESP)의 이름으로 공식 도입함으로써 그 개념이 정립되었다(RTI, 1997; Connelly et al., 1999). ESP란 강우-유출 모형에 미래에 일어날 가능성이 있는 모든 강우 시나리오를 입력하여 그 결과물로 다수의 유량 시나리오를 발생시키고 이를 통계 분석하여 확률로서 예측을 하는 기법이다(Day, 1985). ESP는 발생할 수 있는 유량 시나리오들(즉, 앙상블)의 가능성 범위를 생성하여 예측 불확실성을 정량화 할 수 있고, 연구의 목적에 따라 입력값 앙상블의 유연한 선택이 가능하여 Long-term과 Short-term prediction에 모두 적용될 수 있다는 장점이 있다. 또한, 확정론적 강우-유출 모형을 통해 유역의 초기 조건을 반영할 수 있다는 점이 통계기법에만 의존하는 유량 예측 모형과의 차별점이다.
국내에서는 21세기 들어서야 ESP 연구가 시작되었다. Kim et al. (2001)은 건설교통부와 한국건설기술연구원에서 매월 초 발간하였던 ‘물공급전망’을 개선하기 위해 ESP 도입을 제안하였고, 공주 지점에 적용하여 ESP의 우수성을 입증하였다. 이후 K-water에서 한강, 낙동강, 섬진강 유역에 ESP를 적용한 결과 유효한 방법임을 확인하였다(K-water, 2004). 현재 국가가뭄정보분석센터에서는 가뭄 모니터링 및 예측 기술 고도화를 위해 베이지안 ESP를 사용하여 전국 35개 댐유역의 가뭄분석을 실시하고 있으며, 모형의 실무적용을 위해 GUI 기반의 사용자 편의환경 개선 작업이 진행중이다(NDIC, 2018; 2021). 또한 한강홍수통제소에서도 Kim et al. (2001) 이후 ESP를 실무 활용에 검토하여 현재는 ‘수자원 현황 및 전망’(https://hrfco.go.kr/web/river/periodical_2.do)이라는 이름으로 확률예보를 실시하고 있으며 정확도 향상을 위해 꾸준한 연구를 진행 중이다(Han River FCO, 2009; 2022).
수자원 시스템의 운영에 있어 ESP의 효과를 증명한 연구는 수문 예측 분야보다는 적지만 지난 25년 동안 꾸준히 제기되어 왔다. Faber and Stedinger (2001)은 ESP를 수자원 관리에 적용하기 위해 ESP 시계열을 동적계획법 순환식에 직접적으로 사용하는 방법을 제안하고 이를 미국 윌리엄스 포크 지역에 적용하였다. 그리고 Eum (2007)은 여기에서 더 나아가 기존의 후진방법 계산을 전진방법으로 바꾸는 방법을 고안하여 한강, 낙동강, 섬진강 유역에 적용하고 용수부족량이 저감되었음을 보였다. 최근에는 Ramaswamy and Saleh (2020)가 HEC-HMS 모형을 이용하여 ESP를 생성하고 이를 사용하여 극단적인 강우 상황에서 실시간 저수지 운영을 고려 하였고, He et al. (2022)은 long short-term memory (LSTM) 모형으로 ESP를 생성하고 중국 한징유역에 적용하여 추가적인 전력 향상에 기여하였다. 이처럼 LSTM은 수문학적 비선형 관계 고려가 가능하고 장기 기억이 가능하여 수문학적 예측 분야에 많이 사용되고 있다.
수문예측 현업에서 이러한 ESP 채택의 커다란 성과에도 불구하고 댐과 하천 운영 등 수자원 관리의 현장에서는 아직도 단일 시나리오에 의존하는 것이 대다수 국가에서의 현실이고 우리나라도 예외는 아니다. 즉, 다수의 시나리오를 가진 유량 앙상블이 실시간으로 제공되고 있음에도 불구하고 댐 운영시에는 시나리오들의 평균값이나 중앙값이라는 단일 시나리오로 다시 계산하여 방류량에 결정에 활용하고 있는 현실에 머물러 있다(실무자 인터뷰 결과). 어렵게 수십, 수백 개의 시나리오를 생성해 놓고 정작 의사결정시에는 시나리오들에 담겨 있는 다양하고 귀중한 정보를 제대로 활용하지 못하고 있는 것이다. 홍수와 같이 급박한 상황에서 여러 개의 시나리오를 고려한다는 것은 현실적으로 어려운 일임에 분명하기에, 현업에서 앙상블 활용의 효과를 증명하는 것은 도전적 과제임에 분명하다. 본 연구에서는 댐 방류량 결정을 중심으로 ESP를 활용하는 것이 효과가 있음을 밝히고자 한다. 특히, 댐 운영자들의 이해를 돕기 위해 간단한 가상 예제로부터 시작하여 실제 댐 운영으로 확대해 나가면서 ESP 활용의 효과를 증명해 보이고자 하였다.
본 연구의 2장에서는 댐 운영에 관한 간단한 가상 예제를 통해 ESP를 활용한 경우와 그렇지 않은 경우에 있어 효과가 다름을 우선 소개하였다. 3장에서는 댐의 최적방류량을 계산할 때 ESP를 접목하는 방법론 하나를 제시하고 이를 실제 다목적댐에 적용하여 ESP 효과를 정량적으로 분석해보았다. 마지막으로 4장에 결론으로 마무리하고 향후연구를 기술하였다.
2. 댐 운영에서의 ESP 활용에 관한 간단한 가상 예제
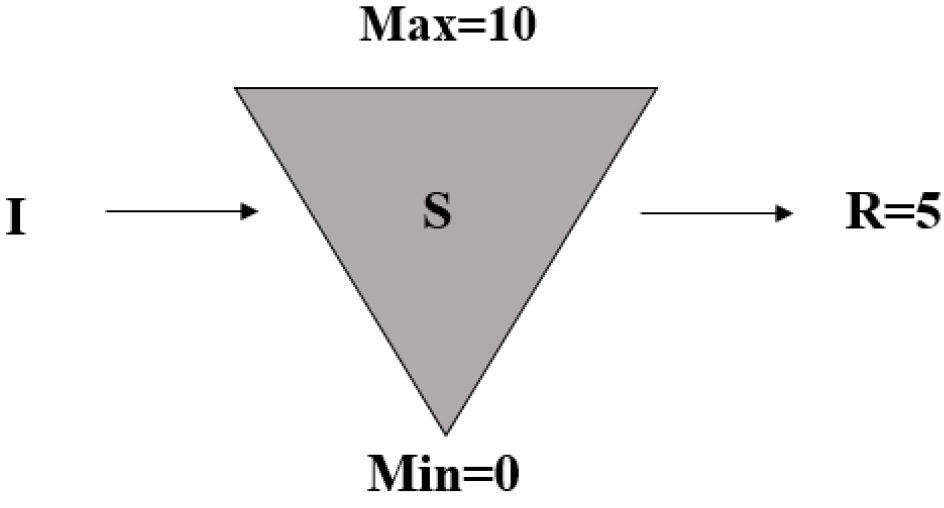
여기에 아주 간단한 저수지가 하나 있다(Fig. 1). 이 저수지의 최대저수량은 10이고, 최소저수량은 0이다. 그리고 매 시점마다 들어오는 유입량의 평균은 7이며, 운영기간 동안 일정하게 5만큼의 물을 공급하고자 한다. 초기저수량 10부터 시작하여 3번째 시점까지 요구방류량 5를 성공적으로 공급하면서 운영을 하는 것이 유일한 운영 목표라 가정한다.
Fig. 2(a)과 같이 이 가상의 댐에 매 시점마다 평균은 7로 동일하지만 표준편차는 각각 1과 2.5를 가진 두가지 정규분포의 예측 유입량이 들어온다고 가정한다. 예측 유입량 확률밀도함수의 표준편차가 1인 유입량을 Type W (즉, well-forecasted), 2.5인 유입량을 Type P (즉, poorly-forecasted)라고 부르기로 하는데(Eqs. (1) and (2)), 불편(unbiased)예측(즉, 예측의 평균이 참값과 일치하는 예측)의 경우 예측의 편차가 클수록 정확도가 낮기 때문이다. 한편 이 댐은 저수량이 2보다 낮아지면 미래 물공급에 차질이 생겨 피해가 발생하는데, 저수량 x에 대한 피해함수 c(x)는 Eq. (3)과 같이 시그모이드 함수를 따른다(Fig. 2(b)).
댐 운영에서 매우 드문 시나리오를 가정해 보자. 즉 0.01의 확률을 가지는 유입량이 3번에 걸쳐 연속적으로 발생하는 경우인데 Type W와 Type P 모두 이 시나리오가 발생할 확률은 10-6(=0.013)이다. 정규분포 확률밀도함수에 의하면 0.01의 확률을 갖는 Type W와 Type P 값이 각각 4.6737과 1.1841이므로, 물공급을 수행하면서 3번의 운영 후 최종 저수량은 Fig. 3에서와 같이 각각 9.0211 및 –1.4477가 된다.
이 예제에서의 결론은 예측의 평균이 같더라도 표준편차가 다르면 피해가 달라진다는 것이다. 거꾸로 해석하자면, 두 개의 케이스에서 피해가 다르기 때문에 댐 운영을 다르게 하여야 한다는 점이며, 특히 Type P로 예측된 상황에서는 물공급량을 보수적으로 줄여야 한다는 경고를 의미한다. 그러나, 만일(현업에서 통상적으로 하는 것처럼) 예측 앙상블이 이루는 분포를 무시하고 이들의 평균을 취하여 운영을 하다면 Type P에서도 Type W처럼 오판을 하여 피해로 이어질 것이다. 물론 이 가상의 예제는 발생하기 매우 드문 시나리오(예: 발생확률 0.01의 극한 가뭄)를 가정하였지만, ESP 예측 분포가 주는 경고만은 현업에서 의미있게 고려해야함은 분명하다.
3. 국내 댐 사례를 활용한 ESP 효과 분석
3.1 분석 과정 개요
앞서 제시한 가상 예제를 실제 댐을 예제로 적용해 보았는데, 몇 가지 가정을 전제로 시작하였다. 우선 두 가지 유형의 ESP를 생각해 보았는데, 두 예측유형 모두 편향되지 않은 예측(unbiased forecasting)으로 예측의 평균은 참값으로 동일한 반면 예측의 표준편차는 적고 큰 두가지로 가정하여 각각 유형W (Well forecasted ESP)와 유형P (Poorly forecasted ESP)라 명명하였다. 즉, 월 유입량 분포를 대수정규분포로 가정한 후 표준편차는 유형W인 경우 , 유형P의 경우 으로 설정하였다. 이는 극단적인 상황에서 두가지 예측 유입량에 따른 최적방류량의 거동을 확인하기 위해서이다.
최적화 문제 설정에서 가장 중요한 것은 최소화나 최대화 할 목적함수를 설정하는 것이다. 우리는 다목적댐의 용수공급 개선을 가장 시급한 문제로 삼았으므로 용수부족량을 Eq. (4)과 같이 방류요구량보다 부족한 방류량의 총량으로 설정하였다. 그리고 이를 최소화하는 모형을 구축하여 계산을 수행하였다.
여기서, 는 t시점 초의 저수량(), 시간 t 동안의 유입량()과 방류량()을 독립변수로 하는 목적함수를 의미하며, 와 는 각각 시간 t 동안의 요구방류량과 방류량이다. 제약조건에는 저수지 연속방정식(Eq. (5))과 최소() 및 최대()저수량(Eq. (6))이 포함된다.
본 목적함수와 제약조건으로 아래에 설명할 동적계획법으로 최적화를 진행하여 두가지 예측유형W, P 각각에 대해 최적방류량을 도출하였고, 그 차이점을 비교하였다. 또한 각 최적방류량로 모의 운영을 진행하여 운영 평가지표로 최적방류량의 성능을 평가함으로써 ESP 활용의 효용성을 정량화 하였다. 뒤에 설명하겠지만 본 연구에서는 Sampling Stochastic Dynamic Programming/Hist (SSDP/Hist)라는 동적계획법모형으로 과거 유입량(즉, Hist)에 대한 최적화를 수행하였고, Sampling Stochastic Dynamic Programming/ESP (SSDP/ESP)라는 모형으로 예측 유입량(즉, ESP)에 대한 최적화를 진행하였다.
3.2 대상 댐의 선정
예측의 효용성은 일반적으로 댐의 저수량이나 유역면적 등 댐의 특성에 따라 크고 작아질 것이다. 본 연구에서는 댐의 특성을 하나의 지표로 정량화하기 위해 Capacity Inflow Ratio (CIR)를 사용하였다. 이 지표는 과거 연구에서도 활용된 사례가 있는데, Karamouz and Houck (1987)는 CIR이 0.5에서 1사이의 댐을 “Large”, 1이상의 댐을 “Very Large”라고 분류한 바 있다. 본 연구에서는 전국의 모든 다목적댐을 CIR로 정렬(Table 1, Fig. 4)한 후, Large Dam과 Very Large Dam 중에서 같은 한강유역이면서 총 저수용량이 비슷하고 자료길이가 동일한 소양강댐과 충주댐을 연구의 대상지로 삼았다.
Table 1.
Capacity Inflow Ratio (CIR) of multi-purpose dams in Korea
연구대상지로 결정한 한강유역은 수도 서울을 관통하는 대한민국 중부의 최대하천인 한강과 북한강을 중심으로 연결되어 있다. 전체 유역면적은 25,953.6 km2(북한 포함 시 35,770.41 km2)이다. 유로연장은 494.44 km, 유역 평균폭은 75.5 km인 남한 제1의 하천으로 국토면적의 약 23 %를 차지하고 있다. 동일한 유역의 다목적댐인 소양강댐과 충주댐은 유사한 유입량 패턴과 총 저수용량을 보유하고 있다. 본 연구에서는 이러한 유역의 공통점을 가진 두 댐에서 총 유입량과 방류요구량에 따른 결과를 확인하였다.
소양강댐은 유역면적 2703 km2, 연간용수공급용량 1,213 MCM (million cubic meter)인 한강유역의 다목적댐으로 = 693.574 MCM이고 = 2478.906 MCM이다. 최적방류량 도출을 위해 SSDP/Hist모형에 사용된 1996년부터 2019년까지의 유입량 연평균은 2135.143 MCM, 모의 운영 위해 SSDP/ESP에 사용된 2020년부터 2022년까지의 유입량 연평균은 2522.661 MCM으로, 2020년 이후 20% 정도 증가 추세를 보이고 있었다.
충주댐은 유역면적 6,648 km2, 연간용수공급용량 3,380 MCM인 한강유역의 다목적댐으로 소양강댐보다 유역면적과 연간용수공급용량이 크며, = 454.027 MCM이고 = 2251.672 MCM이다. SSDP/Hist에 사용된 1996년부터 2019년까지의 유입량 연평균은 4898.079 MCM, SSDP/ESP에 사용된 2020년부터 2022년까지의 유입량 연평균은 4949.233 MCM으로 소양강댐과는 달리 큰 변화가 없었다.
Fig. 5에는 SSDP/Hist에 사용된 유입량 시계열을 box-plot으로, SSDP/ESP에 사용된 유입량 시계열을 꺾은 선 그래프로 나타내었다. 2020년과 2022년의 홍수기에 이전 과거 유입량보다 큰 유입량이 발생하였는데, 이는 2020년 태풍 BAVI, MAYSAK, HAISHEN이, 2022년 9월에는 HINNAMNOR가 북상하면서 한강유역에 영향을 미쳤기 때문이다.
3.3 최적 방류량 결정 모형 및 적용 결과
본 연구에서는 댐 방류량 최적화를 위해 동적계획법을 선택하였는데, 유입량과 유입량 예측에 존재하는 불확실성을 효과적으로 반영할 수 있기 때문이다. 특히 표본 추계학적 동적계획법(SSDP)은 유입량 시나리오를 분포로 전환한 후 이산화 하여야 하는 번거러움을 거칠 필요 없이 시나리오는 그대로 반영할 수 있다는 장점이 있다(Kelman et al., 1990). 여기서는 SSDP의 기초가 되는 모형들인 DDP와 SSDP를 우선 서술하면서 SSDP로 확장하여 설명하겠다.
Deterministic Dynamic Programming (DDP)는 Eq. (7)과 같이 동적계획법의 회귀방정식에 불확실성을 고려하지 않고 미래 유입량 를 정확하게 알 수 있다고 가정한 확정론적 모형이다. 에는 통상 과거 자료의 평균유입량이나 실적유입량 시계열이 사용되는데, 전자의 경우는 가장 초보적인 방류량을 제공하는 반면 후자의 경우는 가장 이상적인 방류량을 제공한다. 그러므로 DDP는 불확실성을 고려한 모형들의 성능이 위치할 구간을 설정해주는 역할을 한다.
여기서, 는 t시점의 잔여최적편익함수(cost-to-go function)이며 이를 갱신해나가면서 최적해를 찾는 정책반복법(policy iteration)을 통해 최적의 방류량을 도출한다.
반면 추계학적 동적계획법인 Stochastic Dynamic Programming (SDP)에는 유입량의 불확실성을 고려하기 위해 회귀방정식에 Eq. (8)와 같이 확률 개념이 도입되어야 한다. 전통적인 SDP에서는 유입량 를 분포로 변환하고 분포를 이산화 하여 각 이산값과 해당 확률을 곱함으로써 계산이 진행된다.
여기서, 는 유입량의 불확실성을 고려하기 위해 도입된 의 발생 확률로, 이를 각 에 곱하고 가중평균하여 최적의 방류량을 도출한다.
SSDP는 SDP의 순환식에 유량 시계열을 직접 적용하여 유입량의 불확실성을 표현하는 동시에 자료에 존재하는 시공간적 상관관계와 유량자료의 연속성을 반영하는 일종의 비모수적 접근방식이다(Eum et al., 2006). 따라서 SDP의 회귀방정식에서 대신 유입 시나리오 를 대입하면 Eq. (9)가 된다. Fig. 6은 ESP 예측 시계열을 첫번째부터 I번째까지 시간에 따라 도식화한것이다. 이때 는 이 중 i 번째 유입량 시계열의 t 시점의 값이다. Eq. (9)를 통해 각 유입량 시계열별 값을 산정한 후 Eq. (10)를 통해 최적방류량을 도출한다.
SSDP는 회귀방정식에서 볼 수 있듯이 현재 시점의 를 구하기 위해서 의 값이 필요하다. 그렇기에 전체 운영기간 동안의 유입량 시계열을 먼저 예측한 후, 후진방향으로 계산하면서 최적방류량과 을 계산해 나간다. 하지만 계산시점에 전체 운영기간의 유입량 시계열 예측을 필요로 하는 후진방향 계산은 한달을 초과하는 경우 그 정확도가 현저하게 떨어지는 단점이 있다. Eum et al. (2006)은 이를 개선하고자 먼저 과거 유입량으로 SSDP/Hist을 계산하고 얻은 를 SSDP/ESP의 최적방류량 계산시에 사용하여 전진방향으로 문제를 풀어 갈 수 있는 방법을 제안하였다. 즉, Fig. 7과 같이 SSDP/Hist에서 계산한 값들을 Eq. (11) 두번째 항의 로 대체한다. 그리고 다음 계산에서도 의 값을 SSDP/ESP의 로 사용하면서 최적방류량을 도출해나간다. SSDP/Hist의 유입량 시계열을 j라하고 SSDP/ESP의 유입량 시계열을 i라 할 때 시나리오의 확률은 Eq. (11)의 첫 항은 가 되지만 두번째 항은 이 된다.
Eum et al. (2006)은 의 계산에 있어서 모든 유입량 시계열에 동일한 확률을 부여하였지만 이상치에 가까운 사상마저 동일한 확률을 부여할 경우 최적해가 그 사상에 극단적으로 영향을 받는다는 단점이 발견되었다. 특히 기후변화로 인해 대부분의 댐 유역에서 극한 가뭄과 홍수라는 이상치가 최근 종종 발생하고 있었기에 개선이 필요하게 되었다. 그러므로 본 연구에서는 각 댐의 연유입량을 대수정규분포에 적합한 후 최빈값보다 적으면 비초과확률, 크면 초과확률을 각 시계열의 확률 로 부여하는 개념을 도입하였다. Fig. 8은 각각 소양강댐과 충주댐의 과거 유입량 24개년을 대수정규분포에 적합한 후 도시화한 확률밀도함수이며, 진한 회색부분 영역은 최빈값보다 작은 유입량 부분이고 연한 회색부분 영역은 최빈값보다 큰 유입량을 나타낸다.
본 연구에서는 유입량 자료를 3년씩 9개의 세트로 나누고 앞의 8개 세트로 SSDP/Hist를 수행한 후 마지막 세트로 SSDP/ESP을 진행하였다. 단일 세트를 1년씩 나눌 경우 해를 넘겨 여러 달 지속되는 물 부족을 탐지하기 어렵지만, 단일 세트를 수 년 이상 길게 가져갈 경우 초기저수량의 영향을 확인하기 어렵기 때문에 단일 세트를 3년으로 설정하였다. SSDP/ESP 계산은 두가지 종류의 유입량 자료를 필요로 하는데, 첫번째로 계산에 사용되는 과거 유입량과, 에 사용되는 예측 유입량이다. 여기서 과거 유입량은 세트1~8이며 값은 SSDP/Hist를 통해 계산된다. 그리고 예측 유입량은 세트9를 평균으로 하는 분포로 유형W와 P로 나누어진다. 즉, SSDP/ESP 유형W와 P 모두 SSDP/Hist에서 를 가져와 계산하지만, 예측 유입량의 표준편차만 다르게 한 것이다. 또한 앞서 언급한 바와 같이 평가지표의 상한선을 확인하고자 DDP를 사용하여 실적 유입량을 완벽한 예측으로 가정한 상태에서 최적방류량을 산출하였는데 이를 DDP/PERF라 명명하였다.
산출한 최적방류량을 모의 운영에 적용할 때 이 보다 작다면 방류를 하지 않고 보다 크다면 초과되는 양만큼 여수로로 빠져나가게하였다. 그리고 초기저수량의 영향을 확인하기 위해 과거 실적수위의 최대, 평균, 최소값을 사용하여 초기저수량으로 사용하였다. 이 값들은 소양강댐 1월초의 경우 각각 2159.658 MCM, 1616.219 MCM, 1086.166 MCM이었고, 충주댐 1월초의 경우 각각 2153.748 MCM, 1538.924 MCM, 892.698 MCM이었다.
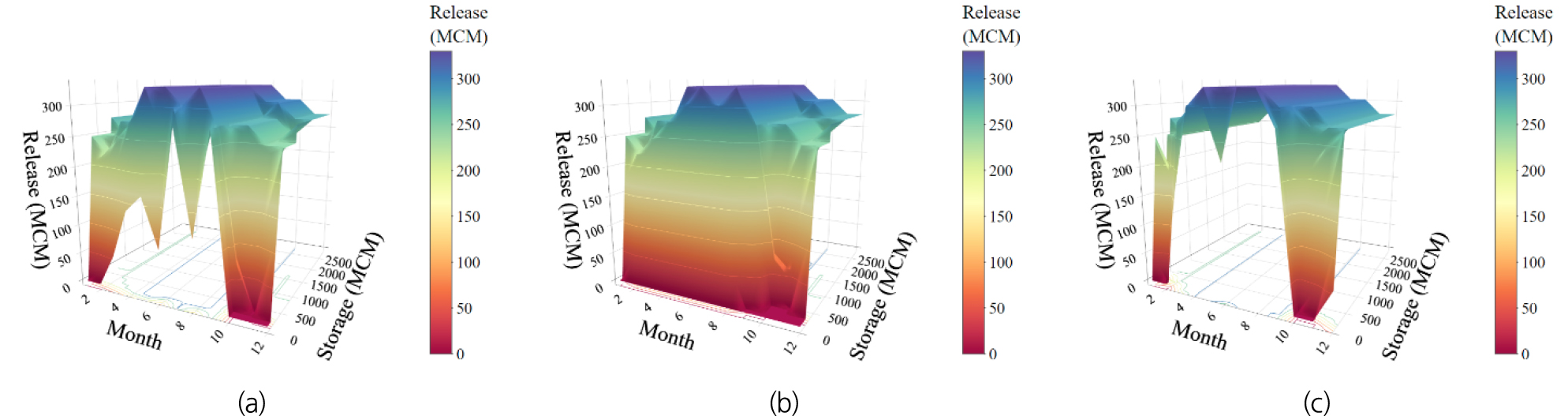
도출된 최적방류량은 유형W, P에 따라 다른 양상을 보였다. 소양강댐과 충주댐 모두 유형W의 경우에는 2020년, 2021년 그리고 2022년 모두 현재 저수량이 적어도 물을 방류하는 공격적인 방류를 하는 것으로 도출되었다. 반면 유형P에서는 최대한 물을 방류하지 않는 보수적인 최적방류량이 도출되었다. Figs. 9 and 10은 소양강댐과 충주댐의 최적방류량을 가장 차이가 뚜렷했던 세트9의 2020년과 2021년에 대해 3차원 그래프로 나타낸 것이다. 그래프의 x축은 월, y축은 현재 시점에서의 저수량, z축은 최적방류량을 빨간색부터 파란색까지 시각화하여 그래프 우측 컬러바로 표시하고 있다. 그 결과, 최적방류량의 차이는 저수량이 낮을때 두드러지게 나타났다. 즉, 그래프에서 방류량이 빨간색 부분까지 내려올수록 저수량이 낮을 때 방류를 하지않는 보수적인 정책을 보였고, 방류량이 파란색 부분까지 올라갈수록 저수량이 낮을 때도 방류를 진행하는 공격적인 방류 정책을 보였다. Fig. 9(a)는 소양강댐의 예측 유형W에 해당하는 최적방류량으로, 유형P인 Fig. 9(b)보다 공격적인 방류를 나타내고 있다. 그리고 Fig. 9(c)는 완벽한 예측을 가정한 최적방류량으로, 예측 유형 중 가장 공격적인 방류를 나타내고 있으며 유형W와 유사한 형태를 보였다. 이를 통해 최적방류량 결정에 있어 예측의 정확도가 매우 중요함을 확인할 수 있었다. 충주댐 또한 Fig. 10(a)의 유형W가 Fig. 10(b)의 유형P보다 공격적인 방류를, 그리고 Fig. 10(c) 완벽한 예측의 경우도 유형W와 유사하게 많은 양의 물을 방류함을 확인할 수 있었다.
이러한 차이는 사용된 ESP 예측 유입량에 기인한 것이다. 즉, 유형W의 ESP는 편향되지 않은(unbiased) 상태에서 적은 표준편차로 인하여 참값이 나올 확률이 유형P보다 크기 때문에 공격적인 결정이 가능한 것이다. 그리고 최적방류량 산출에 적용한 세트9의 유입량은 풍족한 편이었기 때문에 이는 유형W에서 요구량만큼 방류하도록 산출되었다. 가장 높은 성능이 예상되는 DDP/PERF에서는 가장 공격적인 최적방류량이 산출되었다. 이는 완벽한 예측을 가정하였을 때 모의 운영을 진행한 세트9의 유입량에 따라 필요만큼 충분한 물을 방류할 수 있었던 것이 원인으로 작용하였다.
유형W의 공격적인 방류와 유형P의 보수적인 방류는 만연한 불확실성하의 댐 방류 의사결정에 아이디어를 준다. 시나리오 W와 P의 유입량 분포의 표준편차가 상이하다는 원인이 최적방류량에서 공격적인 방류와 보수적인 방류라는 결과를 나타냈다. 이는 평균만으로 댐 운영을 한다면 이러한 변화를 반영하지 못한다는 것을 의미한다. 또한 표준편차가 적은 유입량(유형W)이 발생할 때 더욱 안정적으로 요구방류량에 맞추어 방류할 수 있음을 보였다.
3.4 모의 운영 및 적용 결과
앞서 언급한 바와 같이 각 댐의 각 예측유형(W, P)마다 8개 유입량 세트 하나 하나에 대하여 산출된 최적방류량을 2020년 1월부터 2022년 12월까지의 실적방류량으로 모의 운영하였다. 운영 결과의 평가는 절대적 지표와 상대적 지표로 나누어 정량화 할 수 있는데, Tables 2~4에 열거한 1, 2 열이 전자에 속하고 3, 4, 5열이 후자에 속한다. 상대적 지표는 댐의 요구방류량이라는 기준에 대한 만족도를 횟수(총 기간 중 몇 번 만족시켰는가?), 지속기간(총 기간 중 평균적으로 몇 개월 만족시켰는가?), 만족량(요구량에 비해 부족량이 평균적으로 얼마나 적었는가?)의 개념으로 정량화 하였는데, 일관성을 위해서 상대적 지표 세 개 모두 클수록 성능이 우수하며 최대 100%를 갖도록 설계하였다.
Table 2.
Summary of simulation results for the minimum initial storage of Dam CJ
| Type | Total Penalty (MCM) | Total Releases (MCM) | Frequency (%) | Duration (%) | Magnitude (%) |
| W | 667.086 | 9,900.0 | 77.8 | 13.9 | 93.4 |
| P | 673.129 | 9,872.5 | 75.0 | 16.4 | 93.3 |
| PERF | 649.020 | 10,065.0 | 94.4 | 44.4 | 93.6 |
Table 3.
Summary of simulation results for the average initial storage of Dam CJ
| Type | Total Penalty (MCM) | Total Releases (MCM) | Frequency (%) | Duration (%) | Magnitude (%) |
| W | 342.576 | 10,230.0 | 80.6 | 18.3 | 96.6 |
| P | 348.619 | 10,202.5 | 75.0 | 23.1 | 96.6 |
| PERF | 324.510 | 10,395.0 | 97.2 | 94.4 | 96.8 |
Table 4.
Summary of simulation results for the maximum initial storage of Dam CJ
| Type | Total Penalty (MCM) | Total Releases (MCM) | Frequency (%) | Duration (%) | Magnitude (%) |
| W | 336.533 | 10,257.5 | 83.3 | 19.2 | 96.7 |
| P | 348.619 | 10,202.5 | 77.8 | 23.1 | 96.6 |
| PERF | 324.510 | 10,395.0 | 97.2 | 94.4 | 96.8 |
우선 댐별로 비교해 보면 모든 지표에서 소양강댐은 거의 차이가 없었던 반면 충주댐은 예측유형별로 차이를 보이고 있었기 때문에 본 논문에서는 충주댐의 결과만 제시하였다. 이는 소양강댐의 경우 CIR이 커서 유입량에 비해 상당히 여유 있는 저수량을 가지고 있으며 모의 운영에 사용된 유입량도 평년보다 풍부했기 때문이다. 설사 Fig. 11처럼 최적방류량에서 두 유형이 극명한 차이를 보인다 하더라도 대부분 저수위가 낮을 때의 최적방류량 차이이기 때문에 모의 운영에서는 그런 수위까지 내려가지 않아서 일 것이다.
충주댐의 경우 두 예측유형별 모의 운영 결과를 비교해 보면 유형P보다 유형W가 총 패널티는 감소하고 총 방류량은 증가하였다. 이는 절대적 지표에서는 보다 낮은 불확실성 하에서 용수공급이 원활히 이루어질 수 있었다는 것을 보인다. 그리고 상대적 지표에서 횟수는 유형W이 유형P보다 2.8~5.6%의 향상을 보였고 이는 약 31~61일 동안 용수공급을 더 할 수 있었음을 의미한다. 그리고 만족량 또한 유형W이 유형P보다 양호한 결과를 보였지만 지속기간의 관점으로는 유형P가 양호함을 보였다. 이는 유형P의 보수적인 최적방류량이 횟수와 만족량에서는 불리하게 작용하였지만, 최대한 많은 물을 저장하고 있는 효과를 가져와 실패가 발생하였어도 저장되어 있는 저수량으로 인해 금방 회복하여 지속기간의 관점에서는 다소 유리하게 작용하였기 때문으로 사료된다. 완벽한 예측을 가정한 DDP/PERF와 유형W/P간의 차이는 횟수에서 약 20% 차이가 났고 지속기간에서는 약 20~60%의 차이를 보였다. 하지만 만족량에서는 차이가 많이 나지 않았는데, 이는 시스템 성공의 횟수와 지속기간과 달리 유량이 풍부했던 2019년부터 2020년의 유입량이 용수부족량 규모에서는 큰 차이를 불러오지 않았기 때문이다. 결과적으로 평가지표간에서는 Trade-off된 결과를 보였지만 총 패널티, 횟수 그리고 만족량에서 예측 유입량 분포의 표준편차가 작은 유형W가 전반적으로 성공적인 최적방류량을 도출할 수 있었다. 다음으로 초기수위에 대한 영향을 보면 초기저수량이 클수록 절대적 평가지표와 상대적 평가지표 모두에서 양호한 결과를 보였다. 이는 본 연구에서 고려한 용수공급이 초기저수량이 클수록 유리했기 때문이다.
Sung et al. (2022)는 대한민국의 다목적댐의 용수공급능력을 평가하는 통합지표를 개발하였는데, 이때 충분한 저류용량을 가진 소양강댐은 다목적댐 중 기간신뢰도 100%, 통합보조지표 2등급으로 가장 안정적으로 용수공급이 가능한 댐인 것으로 드러났고 충주댐의 경우는 본 연구의 결과와 동일한 이유로 기간신뢰도 93%, 통합보조지표 4등급으로 소양강댐의 뒤를 이었다. 본 연구에서도 소양강댐과 충주댐은 동일한 유역에 비슷한 총 저수용량을 가지고 있지만 CIR과 요구방류량에 의해 모의 운영 결과 차이가 나타난 것으로 사료된다. CIR은 연간유입량 대비 총 저수용량이기 때문에 CIR이 큰 소양강댐은 앞선 선행연구와 같이 유입량이나 요구방류량에 비하여 저수용량이 충분하여 유입량의 불확실성에 크게 좌지우지되지 않았다. 반면 충주댐의 경우 CIR이 소양강댐보다 작아 상대적으로 불확실성에 더욱 민감하게 반응하였으며, 이는 이수기 운영에 있어 예측의 정확도가 매우 중요함을 시사한다.
4. 결론 및 향후 연구
본 논문은 우선 가상 예제를 통하여 댐 운영자들에게 ESP의 효용성을 쉽게 설명하고자 하였다. 즉, 평균이 동일하다고 하여도 ESP 예측이 제시하는 범위가 다르면 댐 운영에 발생하는 비용이 상이하기 때문에 ESP 시나리오들을 그대로 사용함이 중요함을 강조하였다.
다음으로 본 논문은 가상 예제의 아이디어를 실제 댐 사례에 확장하였는데, 동일한 한강유역에 있지만 유입량 대비 보유 저수량 지표가 2배 이상 차이가 나는 소양강댐과 충주댐을 대상으로 하였다. 표본추계학적 동적계획법으로 최적방류량을 산출한 결과 소양강댐과 충주댐 모두 상대적으로 정확한 예측유형W에서 공격적인 방류를 하도록 산정되었고 상대적으로 정확하지 않은 예측유형P에서 보수적인 방류를 하게끔 산정되었다. 하지만 도출된 최적방류량으로 진행한 모의 운영에서는 소양강댐은 두 예측유형 간 평가 지표에서 거의 차이가 나타나지 않은 반면 충주댐에서는 예측유형W에서 평가지표가 전반적으로 양호하게 나타났다. 이는 CIR이 작고 요구방류량이 많은 댐일수록 이수기 운영에 있어 ESP의 예측 정확도가 중요하다는 점을 시사한다.
마지막으로, 위와 같은 의미있는 결과에도 불구하고 본 연구의 결론을 일반화 시키기 위해서 더 많은 예제에 대한 분석 연구가 수행되길 제안한다. 우선, 9개 유입량 세트 중 하나만 모의 운영에 사용하였는데, 교차검증(cross validation) 기법으로 모의 운영 결과를 더 늘려야만 상대적으로 유입량이 풍부했던 2020년부터 2022년 기간에만 의존했던 모의 운영 결과로부터 탈피할 수 있을 것이다. 또한 본 연구의 범용성을 확장하기 위해, 1) 서로 상충되는 목적함수와 제약조건 등에 대해서, 2) 편향(biased) 예측된 ESP 등 다양한 예측 정확도 지표에 대해서, 그리고 3) 여러 CIR 값에 해당하는 댐에 대해서, ESP 효용성을 살펴보는 연구로 이어지길 기대한다.