1. 서 론
2. 자료 및 방법
2.1 연구대상 지역 및 자료
2.2 정규화된 표준편차
2.3 교차상관계수를 이용한 지하수위 변동성 분석
3. 결과 및 고찰
3.1 원시자료를 이용한 직접적인 교차상관성 분석
3.2 정규화된 표준편차를 이용한 지하수위 변동성 분석
3.3 강우관측소들의 강수량이 지하수위에 미치는 영향 비교분석
4. 결 론
1. 서 론
지하수는 지표수와 더불어 유용가능한 중요한 수자원이며 특히 섬 지역의 경우 대부분 용수를 지하수에 의존하고 있기 때문에 지하수에 대한 연구는 중요하다. 제주도의 경우 지하수는 전체 수자원 이용량의 81%를 차지하는(JSSGP, 2018) 매우 중요한 수자원이기 때문에 지속적이고 안정적인 지하수 이용을 위해 지하수 취수가 지하수위에 미치는 영향에 대한 연구는 특히 중요하다. 지하수위의 변동성은 지하수 취수에 의한 영향뿐만 아니라 하천수위변화 및 기후변화와 계절적인 강수량의 변동성 등으로부터 또한 영향을 받는다(Todd and Larry, 2004; Yoon et al., 2016). 제주도의 경우 한국의 다우지역에 속하지만 투수성이 높은 지하지질 특성으로 인해 대부분의 하천은 건천으로서(Kim et al., 2014; Song et al., 2015) 하천수위가 지하수위에 미치는 영향은 거의 없으므로, 제주도 지하수자원의 적절한 관리를 위한 정보제공을 위해 강수량과 지하수 취수가 지하수위에 미치는 영향분석이 필요하다.
강수량 또는 지하수 취수가 지하수위 변동에 미치는 영향에 대해 다양한 연구가 수행되었는데, 먼저 강수량이 지하수위에 미치는 영향분석에 대한 대부분의 연구들은 두 변수간의 상관성이 낮다고 보고하였다. Lee and Koo (2000)는 평창강 및 보청천 대표유역에 대해 일단위 강우량과 지하수위의 상관성분석 결과 교차상관계수는 각각 0.406과 0.247로 상관성이 낮다고 보고하였고, Moon and Woo (2001)은 광주와 같이 비포화대의 두께가 얇아 지하수위가 강수로부터 직접적인 영향을 받는 경우를 제외하면 강수와 지하수위의 교차상관계수는 낮다(충주와 진주의 봄철 교차상관계수는 최대 0.172)고 보고하였다. Lee and Lee (2002)은 강원도 원주의 단열암반 대수층의 경우 강우와 지하수위의 교차상관계수는 최대 0.23로서 상관성이 낮다고 보고하였으며, Kim and Yum (2007)은 국가지하수관측망 112개소에 대해 군집분석을 통해 강우와 첨두지하수위 반응시간 간의 교차상관계수를 계산한 결과 0.393의 낮은 상관성을 보고하였다. Choi et al. (2011)은 제주도의 113개 지하수 관정 중 대부분(104개 관정)의 강수-지하수위 교차상관계수는 0.25 미만으로 계산됨으로써 상관성이 낮다고 보고하였으며, Park et al. (2011)도 또한 제주도 강수-지하수위 교차상관계수가 평균 0.47로 상관성이 낮다고 보고하였다. Song et al. (2013)은 제주도 동부지역의 강수량-지하수위 간의 교차상관계수를 평균 0.36으로 보고함으로써 두 변수 간의 상관성이 뚜렷하지 않았으며, Yoon et al. (2015)은 경북 고령군 낙동강 수변 충적층에 대한 강우-지하수위 간의 교차상관계수가 0.20~0.21로서 낮은 상관계수를 갖는다고 보고하였다.
비교적 명확한 강수량-지하수위 간의 상관성을 도출한 연구로서, Jang et al. (2015)은 경기도 안성시의 논농사 지역에 대해 시간 단위 강수량 및 지하수위 자료를 이용하여 강수량과 지하수위의 상관성을 분석한 결과 24시간 지체시 0.22~0.85(평균 0.59) 범위의 교차상관계수를 갖는다고 보고하였다. 하지만 이 지역은 지하수위가 최대 지하 2.5 m 이내로 얕게 형성되어 있어 강우에 의한 지하수위의 반응이 빠르게 나타나는 것으로 판단되며, 제주도의 경우는 두꺼운 비포화대층으로 인해(Kim et al., 2015) 강수량과 지하수위의 상관성은 이 경우와 다르다. 예외적인 연구로서, Yang and Kim (2011)은 강수와 지하수위의 상관성을 명확하게 분석하기 위해 이동평균법을 도입하였으며 제주도 위미 지점에 대해 일강우의 이동평균값과 지하수위 간의 교차상관계수 계산한 결과 0.71의 높은 상관계수를 도출하였다. 하지만 지하수 취수량과 지하수위 간의 상관성은 분석하지 않았다.
강수량과 지하수 취수량이 지하수위에 미치는 영향을 분석한 연구로서, Jeon et al. (2018)은 부산광역시 동래온천의 월별 강수량, 온천수위, 온천수 이용량 자료를 이용하여 분석한 결과 월별 온천수위는 월별 강수량과 상관성이 낮으나 온천수 이용량과는 비슷한 변동양상을 갖는다고 보고하였다. 하지만 온천수위와 온천수 이용량 간의 교차상관계수는 –0.410~0.535로서 그 상관성이 뚜렷하지 않았다.
본 연구의 목적은 제주도내 표선유역 중산간지역의 강수량과 지하수 취수가 지하수위에 미치는 영향의 명확한 비교분석에 있다. 강수량과 지하수 취수가 지하수위에 미치는 영향을 명확하게 비교분석하기 위해 본 연구에서는 각 변수의 원시시계열자료를 직접적으로 사용하여 비교분석하는 방법 대신 정규화된 표준편차(Shin et al., 2015)에 의해 변환된 시계열자료와 교차상관계수를 이용하여 강수량-지하수위 및 지하수취수량-지하수위 간의 상관성을 비교분석하였다. 이 방법의 기본 개념은 각 변수 시계열 자료의 연도별 변동성의 상관성 분석에 있다. 즉, 각 변수의 변동성을 연도별로 산정하고 변수들의 연 시계열 변동 추세가 변수 간에 일치하는지를 정량적으로 산정하고 비교하는데 있다. 그리고 복수의 강우관측소 강수량이 지하수위에 미치는 상대적인 영향 또한 비교분석하여 지하수의 흐름방향을 간접적으로 추정하였다.
2. 자료 및 방법
2.1 연구대상 지역 및 자료
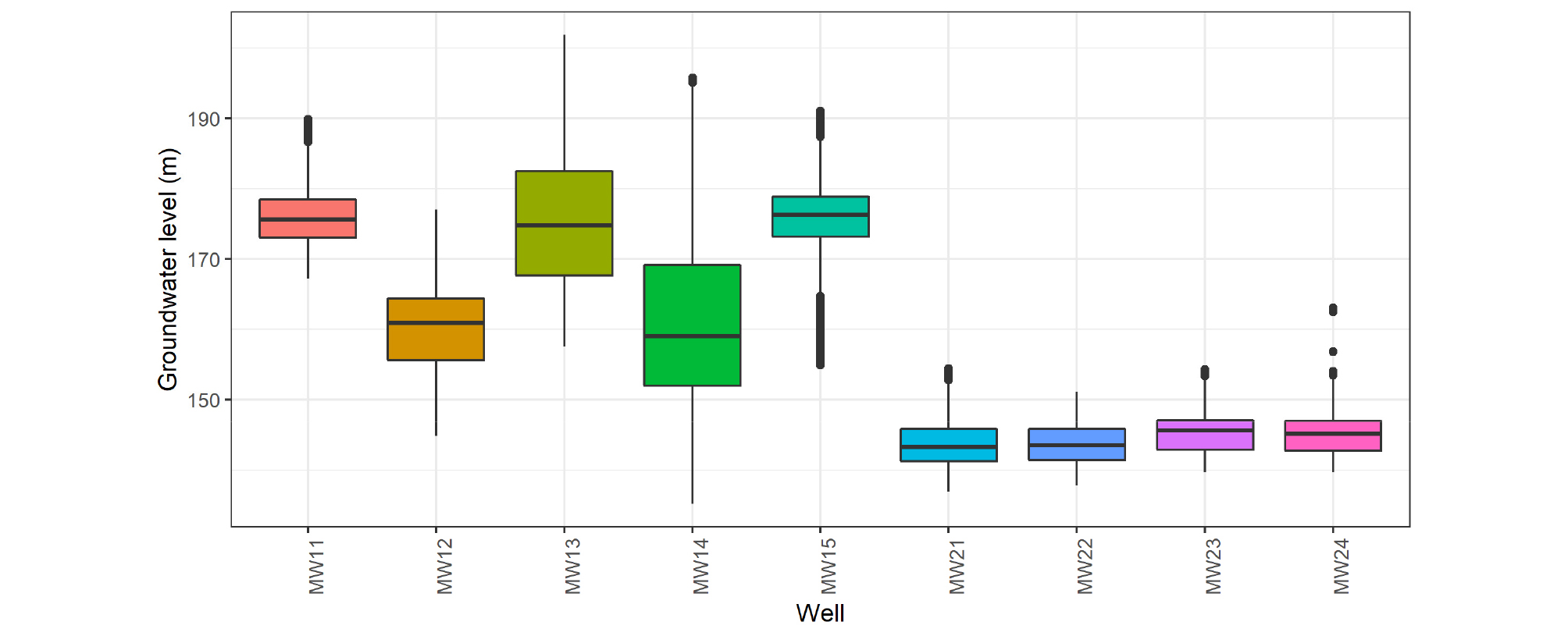
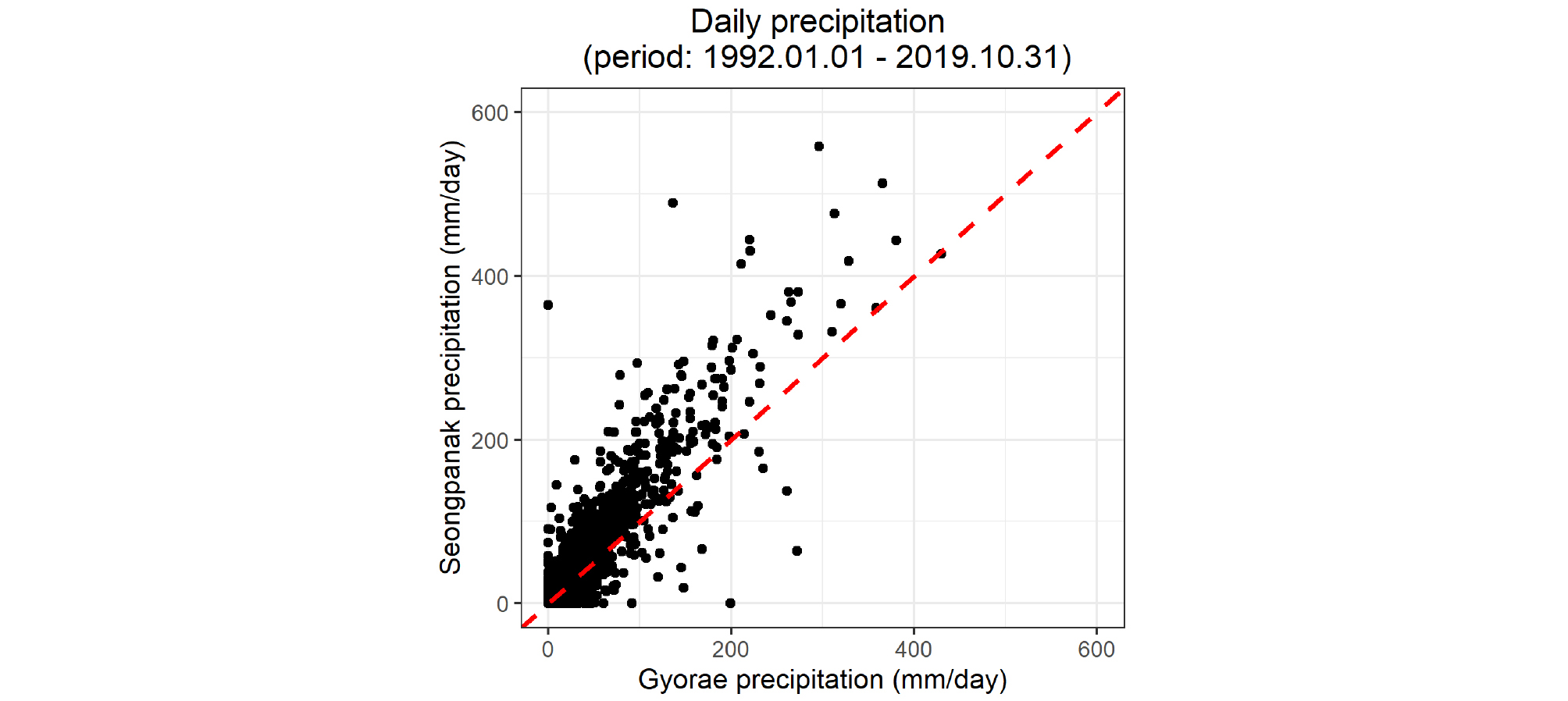
연구대상지역은 제주도 남동쪽 표선유역의 중산간에 위치한 9개 지하수위 관측정 지점이며, 일단위 관측정 지하수위 자료, 인근의 2개 강우관측소(성판악, 교래) 일단위 강수량자료 및 2개 지하수 취수정 일단위 취수량 자료를 사용하였다(Table 1). 성판악 강우관측소는 자동기상관측소(Automatic Weather Station)로서 기상청에서 운영중에 있으며(http://www.weather.go.kr/), 교래 강우관측소는 제주도 재난안전대책본부(http://bangjae.jeju119.go.kr/)에서 운영중에 있다. 강우관측소의 자료는 상기 웹사이트에서 다운받아 사용할 수 있으나 제주특별자치도개발공사에서 관측 및 관리하는 지하수위 및 취수량 자료는 공개적으로 제공되지 않는 자료이다. 대상지점의 지하수위 관측정, 강우관측소, 취수정의 위치는 Fig. 1과 같이 모식도로 나타내었으며 관측정 지하수위의 변동성은 Fig. 2와 같이 도시하였다. Fig. 2에서 보면 관측11호정(MW11)부터 관측15호정(MW15)의 지하수위 변동폭은 관정마다 큰 차이가 있으며 이 차이는 관정별 복잡한 지하지질의 차이가 기인한 것으로 판단된다. 반면 관측21호정(MW21)부터 관측24호정(MW24)의 지하수위 변동폭은 비슷한 것을 확인할 수 있다. 성판악과 교래 강우관측소의 일단위 강수량을 비교한 결과는 Fig. 3과 같으며 성판악 강우관측소의 강수량이 교래 강우관측소의 강수량보다 큰 것을 확인할 수 있다. 성판악 강우관측소(El. 763 m, Fig. 1)는 교래 강우관측소(El. 400 m, Fig. 1)보다 고지대에 위치해 있으며, 따라서 산지효과로 인해 성판악 강우관측소의 강수량이 더 큰 것으로 판단된다.
Table 1. Period of rainfall station, pumping well and monitoring well data
2.2 정규화된 표준편차
강수량과 취수량이 관측정들의 지하수위 변동에 미치는 영향을 분석하기 위해 정규화된 표준편차(normalized standard deviation)(Shin et al., 2015)와 교차상관계수를 이용하여 상관성분석을 수행하였다. 먼저, 정규화된 표준편차는 Eq. (1)과 같으며 정규화된 표준편차를 이용하여 지하수위와 강수량 등 각 변수들의 변동 정도를 정량적으로 계산할 수 있다(Shin et al., 2015).
| $$Nor.St.Dev=\frac\sigma{\mathit\triangle p}$$ | (1) |
여기에서, 는 각 변수(지하수위, 강수량, 지하수취수량) 일단위 자료의 연도별 표준편차이며 는 각 변수에 대해 전체기간의 일단위 최대값과 최소값의 차이이다. 따라서 정규화된 표준편차는 각 변수들에 대해 일단위 관측자료 전체기간의 최대변동폭이라는 동일한 기준 대비 연도별 변동성을 나타낸다. Table 2은 관측11호정(MW11) 지하수위, 성판악 강수량, 취수1호정(PW1) 지하수 취수량에 대해 일단위 자료의 연도별 정규화된 표준편차를 일례로 나타낸 것이다.
Table 2. Normalized standard deviation of groundwater level, precipitation, and pumping rate by year
2.3 교차상관계수를 이용한 지하수위 변동성 분석
각 변수들의 정규화된 표준편차 연도별 시계열값들과 교차상관계수를 이용하여 각 변수간의 상관성을 분석하였다. 교차상관계수는 독립된 두 개의 변수들의 상관관계를 나타내는 계수로서 –1.0~+1.0의 범위를 갖으며 0은 상관성이 없음을 나타내고 상관성이 높을수록 교차상관계수가 0값으로부터 멀어지게 된다(Mendenhall and Sincich, 2007). 이 정규화된 표준편차와 교차상관계수를 이용한 상관성분석은 각 변수의 변동특성을 변수 간에 비교분석 하는 것으로서, 강수의 지하수위 도달시간 지체특성과 비균질한 지하지질구조로 인한 복잡한 지하수 유동특성 등을 간접적으로 포함하고 있다.
예를 들면, Table 2에서 관측11호정(MW11) 지하수위의 정규화된 표준편차 연도별 시계열자료와 성판악 강수량의 정규화된 표준편차 연도별 시계열자료에 대해 교차상관계수를 계산하고, 같은 방법으로 관측11호정 지하수위의 정규화된 표준편차 연도별 시계열자료와 취수1호정(PW1) 취수량의 정규화된 표준편차 연도별 시계열자료에 대해 교차상관계수를 계산한다. 만약 관측11호정 지하수위의 정규화된 표준편차가 연도에 따라 증가하여 변동성이 증가하는 추세이며 성판악 강수량의 변동성 또한 증가하는 추세이지만 취수1호정 지하수 취수량의 정규화된 표준편차가 감소하여 변동성이 감소하는 추세라면 관측11호정 지하수위는 성판악 강수량과 양의 교차상관계수를 가지지만 취수1호정 지하수 취수량과는 음의 교차상관계수를 가지게 된다. 이것은 지하수위는 강수량과 관련성이 높지만 취수량과는 관련성이 낮음을 의미한다. 따라서 본 연구에서는 교차상관계수가 큰 양의 값을 가질수록 상관성이 커짐을 의미하며 큰 음의 교차상관계수를 가질수록 상관성이 작아짐을 의미한다.
본 연구에서는 Table 1의 2개의 강우관측소, 9개의 지하수위 관측정과 2개 지하수 취수정의 자료를 사용하여 연도별로 정규화된 표준편차를 계산하고, 지하수위-강수량 및 지하수위-지하수취수량 간의 교차상관계수를 계산하여 강수량과 지하수 취수량이 관측정 지하수위의 변동에 미치는 영향을 분석하였다. 또한 2개 강우관측소 강수량이 관측정 지하수위에 미치는 상대적인 영향을 비교분석 하였다.
3. 결과 및 고찰
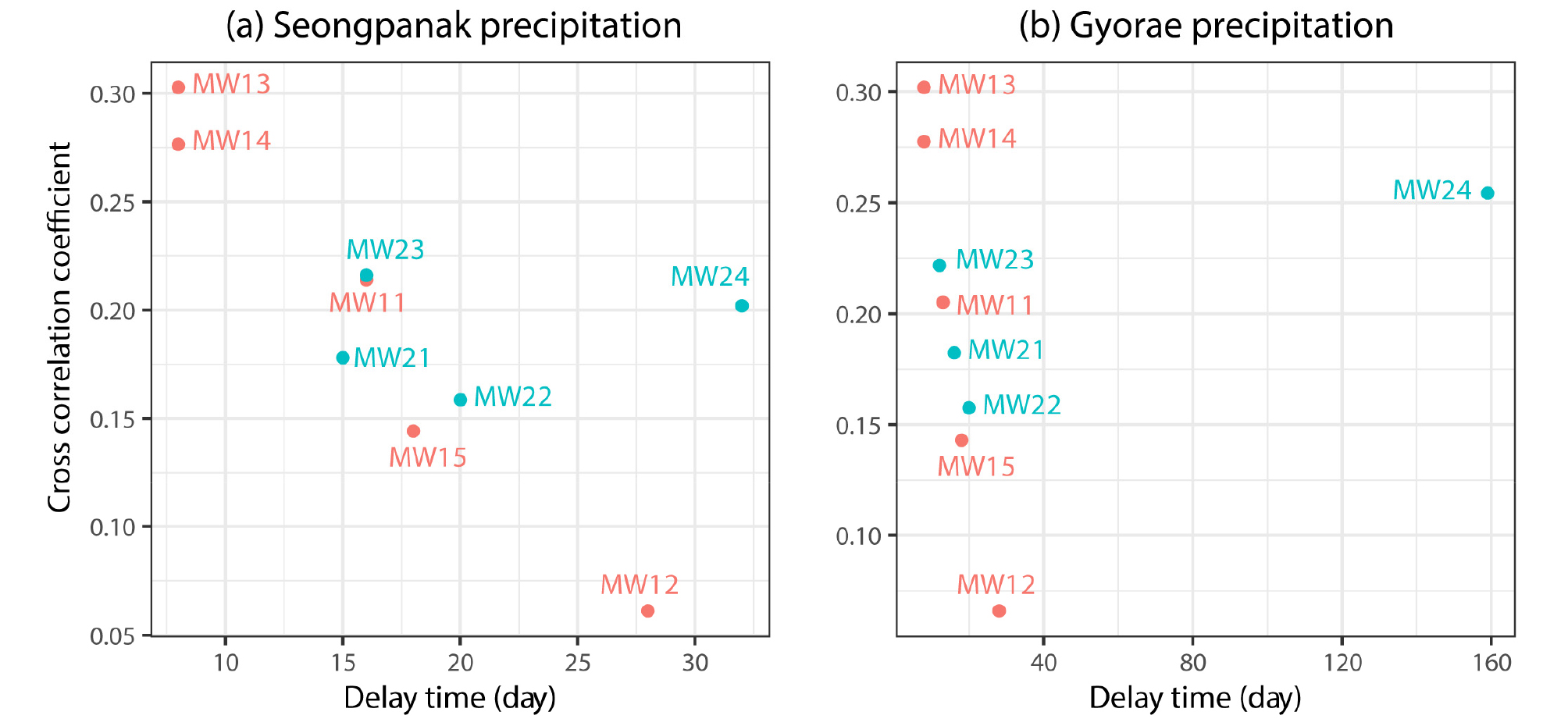
3.1 원시자료를 이용한 직접적인 교차상관성 분석
정규화된 표준편차를 이용한 분석에 앞서 일단위 원시자료를 이용한 직접적인 교차상관성 분석을 수행하였다. Fig. 4에서 보여주는 바와 같이 성판악과 교래 강수량자료에 대한 관측정 지하수위의 교차상관계수는 최대 0.3 정도로서 상관성이 낮다. 이러한 강수량과 지하수위의 낮은 상관성은 기존의 다양한 연구에서 보고되었으며(Lee and Koo, 2000; Moon and Woo, 2001; Lee and Lee, 2002; Kim and Yum, 2007; Choi et al., 2011; Park et al., 2011; Song et al., 2013; Yoon et al., 2015; Jeon et al., 2018), 특히 제주도 중산간지역의 경우 두꺼운 비포화대 층에 의한 강수의 지하수위 도달시간 지체와(Kim et al., 2015) 여러 화산활동에 의해 지층형성이 제각기 달라(Jo et al., 2014) 복잡한 지하지질구조 특성으로 인한 비포화대 내 지하수 유동의 복잡성으로 인해 강수량과 지하수위의 직접적인 상관성 분석은 더욱 어려운 것으로 판단된다. 취수정의 지하수 취수량과 지하수위간의 교차상관계수 산정 및 취수영향분석은 더욱 어려운데 그 이유는 비 강수 기간 동안의 자연적인 지하수위 하강이 취수에 의한 지하수위 하강과 중첩되어 각각의 영향을 분리하기 어렵기 때문이다. 따라서 본 연구에서는 대안적인 방법으로서 정규화된 표준편차에 의해 변환된 시계열자료와 교차상관계수를 사용하여 3.2절과 같이 강수량-지하수위 및 지하수취수량-지하수위 간의 상관성을 분석하였다.
3.2 정규화된 표준편차를 이용한 지하수위 변동성 분석
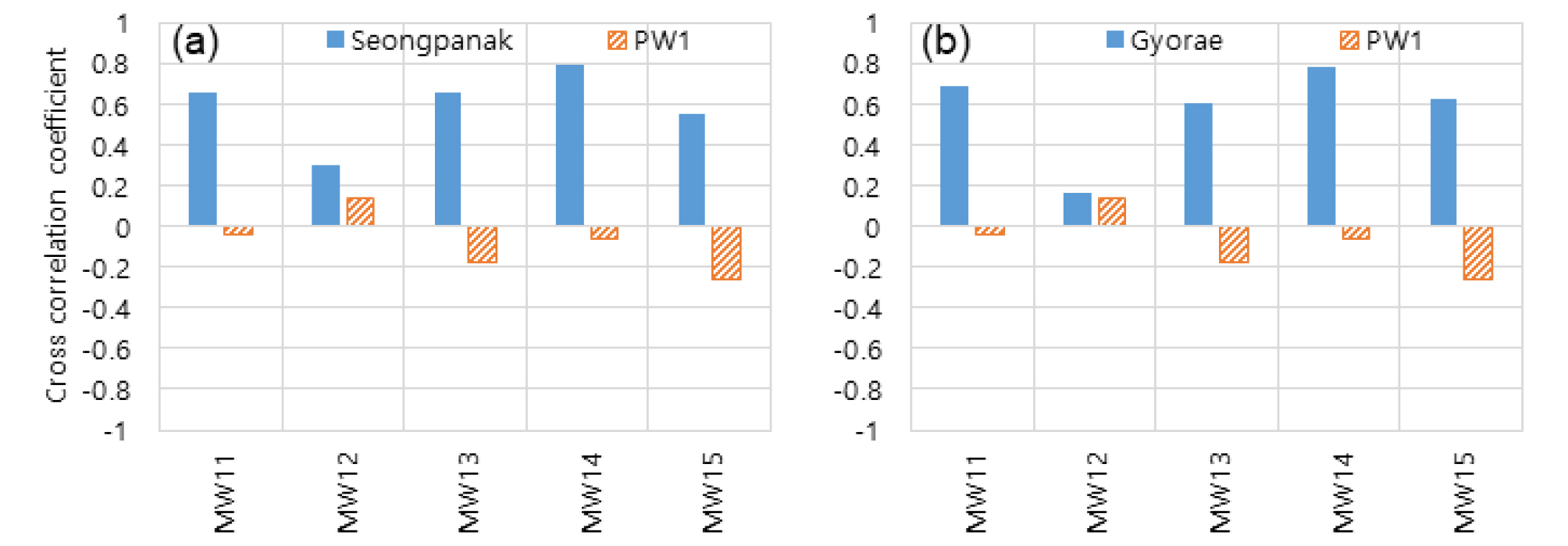
강수량, 지하수 취수량 및 관측정 지하수위에 대한 정규화된 표준편차 연도별 시계열값들을 이용하여 강수량-지하수위 및 지하수취수량-지하수위 간의 교차상관계수를 계산한 결과는 Figs. 5 and 6과 같다. Figs. 5 and 6에서 보는 바와 같이 관측정들의 지하수위와 강수량 간의 상관성은 Fig. 4에서 보여준 상관성보다 더욱 명확해진 것을 확인할 수 있다.
취수1호정의 경우(Fig. 5) 관측정 MW11, MW13, MW14들의 지하수위 변동성은 성판악 강수량의 변동성과 0.6이상의 교차상관계수를 갖고(Fig. 5(a)), 관측정 MW11, MW13, MW14, MW15들의 지하수위 변동성은 교래 강수량의 변동성과 0.6이상의 교차상관계수를 갖음으로써(Fig. 5(b)) 지하수위는 강수량과 밀접한 관계가 있음을 보여주고 있다. 특히, 관측정 MW14는 성판악과 교래 강우관측소의 강수량과 약 0.8의 교차상관계수를 갖음으로써 강수량과 매우 높은 상관관계를 갖음을 확인할 수 있다. 지하수 취수량의 경우 전술한 바와 같이 취수1호정 지하수 취수량이 증가하여 지하수 취수량의 변동성이 증가할 때 관측정 지하수위의 변동성이 증가한다면 지하수 취수량의 변동성과 지하수위의 변동성은 양의 상관관계를 가져야 한다. 하지만 취수1호정 지하수 취수량의 변동성은 약한 양의 교차상관성을 가지는 관측정 MW12를 제외한 모든 관측정의 지하수위 변동성과 약한 음의 교차상관계수를 가짐으로써 지하수위는 지하수 취수량의 영향을 거의 받지 않는 것으로 분석되었다. 또한 관측정 MW12는 지하수 취수량보다 성판악과 교래 강우관측소의 강수량과 상대적으로 높은 상관관계를 가짐을 알 수 있으며 지하수 취수량과의 교차상관계수는 비록 양의 상관계수를 갖지만 이 값 또한 0.2 이하로써 약한 상관성을 보여주고 있다. 본 연구에서 사용한 정규화된 표준편차를 활용한 분석방법은 강수량이 지하수위에 미치는 영향뿐만 아니라 취수량이 지하수위에 미치는 영향을 정량적으로 비교분석할 수 있다. 하지만 이 방법은 연도별 정규화된 표준편차 자료를 사용하기 때문에 원시 시계열자료의 기간이 충분히 길어야 신뢰할 수 있는 결과를 도출할 수 있다.
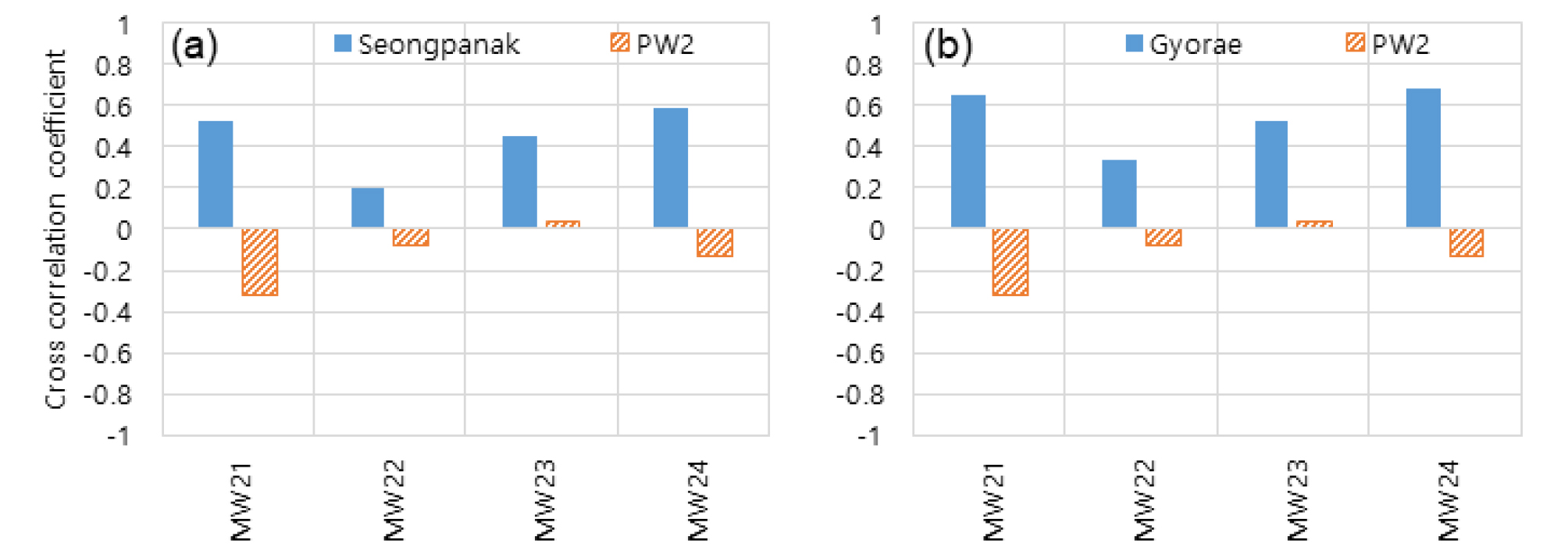
취수2호정의 경우(Fig. 6) 또한 관측정들의 지하수위 변동성은 지하수 취수량의 변동성보다 성판악과 교래 강우관측소의 강수량의 변동성과 상대적으로 높은 교차상관계수를 갖았으며 이것은 관측정들의 지하수위는 강수량과 상관관계가 있음을 의미한다. 관측정 MW24는 성판악 강우관측소 강수량과 약 0.6의 교차상관계수를 갖았으며(Fig. 6(a)), 관측정 MW21 및 MW24는 교래 강우관측소 강수량과 0.6 이상의 교차상관계수를 갖았다(Fig. 6(b)). 하지만 지하수 취수량의 변동성은 관측정들의 지하수위 변동성과 대부분 음의 교차상관계수를 가졌으며 이것은 전술한 바와 같이 지하수위는 지하수 취수량의 영향을 거의 받지 않는 것을 의미한다. 따라서 취수2호정 주변의 관측정 지하수위 또한 취수량보다 강수량과 밀접한 관계가 있는 것으로 분석되었다.
3.3 강우관측소들의 강수량이 지하수위에 미치는 영향 비교분석
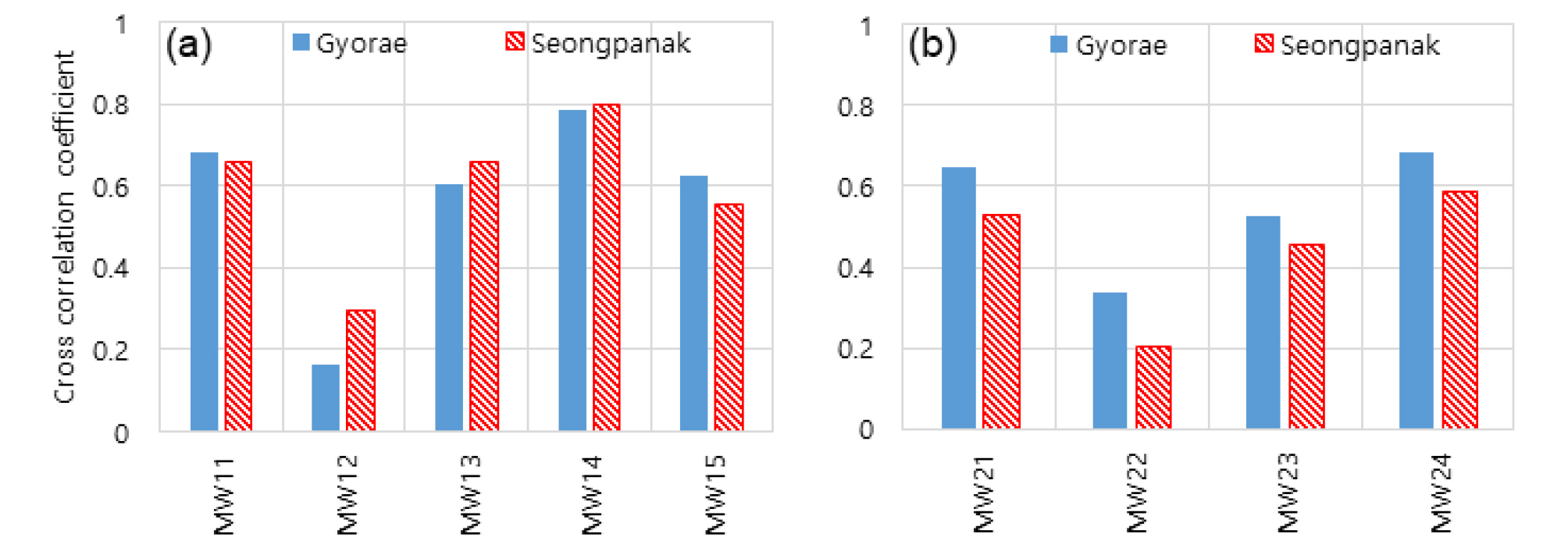
2개 강우관측소 강수량이 관측정 지하수위에 미치는 영향을 비교한 결과는 Fig. 7과 같다. Fig. 7에서 보는 바와 같이 관측정 MW12, MW13, MW14를 제외한 모든 관측정의 지하수위는 성판악 강우관측소 보다 교래 강우관측소의 강수량과 높은 교차상관계수를 가지는 것으로 나타났다. 이것은 대부분의 관측정 지하수위는 교래 강우관측소의 강수량으로부터 더 많은 영향을 받고 있음을 의미하며 따라서 교래 강우관측소 지점에서 침투된 강수가 성판악 강우관측소 쪽으로 흐르고 있을 가능성을 간접적으로 추정할 수 있다. 실제로 Fig. 1에서 교래 강우관측소 쪽에 보다 가까운 관측정 MW11~MW15의 평균 지하수위가 해발 약 169.8 m 였고 성판악 강우관측소 쪽에 보다 가까운 관측정 MW21~MW24의 평균 지하수위가 해발 약 144.3m 임을 고려하면(Fig. 2) 이 지하수 흐름방향의 추정은 가능할 것으로 판단된다
흥미로운 점은 Figs. 1 and 3에서 보여주는 바와 같이 성판악 강우관측소(El. 763 m)가 교래 강우관측소(El. 400 m)보다 고지대에 위치하고 있고 강수량 또한 성판악 강우관측소가 교래 강우관측소보다 많아 지표로 침투된 강수는 성판악 강우관측소에서 교래 강우관측소 방향으로 흐를 것으로 추측할 수 있으며, Song et al. (2015)에 의하면 표선유역의 지하수는 성판악 강우관측소에서 교래 강우관측소 방향으로 흐른다고 보고하였으나 본 연구결과에서는 그와 반대의 결과를 나타내고 있다는 점이다. 제주도 중산간지역의 지하지질은 매우 복잡하여 공간적 가변성을 가지므로 지역적으로 지하수 흐름방향은 다를 수 있으며 본 연구결과는 간접적인 추정이기 때문에 이 결과를 바탕으로 이 지역의 지하수 흐름방향을 단정 지을 수는 없다. 따라서 정확한 지하수 흐름방향의 분석은 향후 이 지역에 대한 정밀한 지하지질분석과 이를 기반으로 한 지하수 수치모델링에 의한 지하수 유동분석 후에 가능할 것으로 판단된다.
4. 결 론
본 연구에서는 제주도 남동쪽 표선유역 중산간에 위치한 지하수위 관측정 지하수위 자료, 인근 강우관측소의 강수량자료 및 지하수 취수정의 취수량 자료를 이용하여 강수량 및 지하수 취수량이 관측정 지하수위의 변동성에 미치는 영향을 분석하였다. 먼저 일단위 원시 시계열자료를 이용하여 강수량-관측정지하수위의 교차상관계수를 산정한 결과 최대 0.3의 낮은 교차상관계수를 가졌다. 본 연구에서 제시한 정규화된 표준편차를 이용하여 강수량-관측정지하수위의 교차상관계수를 산정한 결과 최대 0.8의 개선된 교차상관계수를 얻음으로써 더욱 명확한 상관성을 확인할 수 있었다. 또한 강수량의 변동성과 관측정 지하수위의 변동성은 대부분 양의 교차상관계수를 가짐에 비해 취수량의 변동성과 관측정 지하수위의 변동성은 대부분 음의 교차상관계수를 가짐으로써 본 연구 대상지역의 관측정 지하수위는 취수량의 영향은 거의 받지 않고 강수량의 영향을 크게 받음을 확인하였다. 마지막으로 성판악과 교래 강우관측소가 관측정 지하수위에 미치는 상대적인 영향을 비교분석한 결과 교래 강우관측소의 강수량이 관측정들의 지하수위에 더 영향을 미치는 것으로 분석되었다. 따라서 교래 강우관측소에서 침투된 강수는 성판악 강우관측소 방향으로 흐를 가능성이 있는 것으로 간접적으로 추정되며, 관측정들의 평균 지하수위(교래 강우관측소 쪽에 보다 가까운 관측정들의 평균 지하수위는 해발 약 169.8 m, 성판악 강우관측소 쪽에 보다 가까운 관측정들의 평균 지하수위는 해발 144.3 m)를 고려하면 이러한 추정은 가능할 것으로 판단된다. 하지만 제주도 중산간 지역의 지하지질구조는 화산암 지하지질구조 특성으로 인해 매우 복잡하기 때문에 정확한 지하수 흐름방향의 결정은 이 지역의 정밀한 지하지질분석과 이를 바탕으로 한 지하수 수치모델링에 의한 지하수 유동분석 후에 가능할 것으로 판단된다. 본 연구에서 사용한 정규화된 표준편차와 교차상관계수를 활용한 지하수위 변동분석 방법은 향후 다른 지역의 강수량과 지하수 취수량이 지하수위 변동성에 미치는 영향분석에 간편하게 활용될 수 있을 것으로 판단된다. 예를 들면, 제주도 및 내륙지역 전역에 강수량 및 지하수 취수량이 지하수위에 미치는 영향을 본 연구방법을 활용하여 계산하고 그 결과를 지도에 공간적으로 도시하여 지하수취수 가능지역 및 취약지역을 구분함으로써 지하수의 안정적 취수지역 설정에 활용할 수 있다. 본 논문의 3.1절에서는 일단위 원시시계열자료를 사용하여 강수량과 지하수위간의 직접적인 교차상관분석을 수행하였으나 월단위 및 연단위 시계열자료를 사용하면 개선된 상관성을 도출할 가능성이 있으며 이 연구는 향후 추진할 계획이다.