1. 서 론
토석류는 물, 흙, 자갈 등의 혼합물로서 발생 시 치명적인 인명 및 재산 피해를 발생시키나, 주로 산지에서 발생하기 때문에 국내에서는 홍수 및 태풍과 같은 재해에 비해 중요도가 낮게 취급되어 왔다. 하지만 이상기후로 인해 여름철에 집중호우의 빈도와 강도가 높아지고 있으며, 이로 인한 토석류의 발생 빈도 및 피해도 늘어나고 있다(KIGAM, 2006). 우리나라와 같이 국토의 약 64%가 산지로 이루어져 있는 경우 산림지역에서 발생하는 토석류는 도심지역에 큰 영향을 미칠 수 있다. 그 예로 태풍 ‘루사’, ‘매미’, ‘메기’, ‘미탁’ 등으로 인한 다수의 도심지역 토석류 피해 사례가 있다(Kim et al., 2011; Jun et al., 2013; Jang et al., 2020). 특히 도심지역에 직접적으로 타격을 입힌 2011년 서울 우면산 일대에서 발생한 일련의 산사태는 많은 인명피해와 재산피해를 야기했으며, 2019년 부산 사하구 야산에서도 산사태로 인해 다수의 인명피해가 발생하였다. 토석류를 대비하기 위한 방법으로는 사방댐 건설과 같은 구조적 방법과 재난경보 발령 등의 비구조적 방법이 있으며, 이러한 구조적・비구조적 대비를 위해서는 수치해석 모형을 통한 시나리오 기반 모의가 필수적이다.
과거 20여 년간 다수의 토석류 모형들이 개발됐다(O’Brien et al., 1993; Beguería et al., 2009; Pastor et al., 2009; Mergili et al., 2012). 대부분의 토석류 모형들은 유하단면을 직사각형으로 가정한 1차원 모형(Pratson et al., 2001; Shrestha et al., 2008; D’Aniello et al., 2015) 이거나, 지형의 형상을 반영하여 수직방향의 유속을 적분한 2차원 모형(Hsu et al., 2010; Hussin et al., 2012; Kim et al., 2013)이다. 국내에서는 Kim et al. (2013), Kang and Kim (2015), Lim and Kim (2019), Choi (2018) 그리고 Oh and Jun (2019)이 상용모형인 FLO-2D를 이용하여 토석류 거동을 분석했으나 이들 모형은 토석류의 연행작용을 고려할 수 없다는 한계가 있다. 토석류 유동 과정에서 나타나는 침식과 연행작용은 토석류의 유동을 분석함에 있어서 매우 중요한 역할을 수행한다. 연행작용은 토석류의 크기와 강도를 결정할 수 있으며(Hussin et al., 2012), 연행된 물질은 초기 토양 수분의 10~50배를 축적하기도 한다(Remaître et al., 2005). 따라서 토석류의 유동을 현실에 가깝게 구현하기 위한 연행작용 모형(Takahashi and Nakagawa, 1991; McDougall and Hungr, 2005; Sovilla et al., 2006; Medina et al., 2008; Frank et al., 2015)들이 개발되어져 왔고, 국내에서는 Jeong et al. (2018)이 UDS (Urban Debris flow Simulator)에 Takahashi and Nakagawa (1991)의 연행방정식을 도입하여 토석류 실험을 모의하고 분석했으며, Lee et al. (2016)은 대변형 3차원 유한요소해석모형인 ABAQUS에 연행식을 도입하여 3차원 토석류 모형을 구축했다.
An et al. (2019)은 상황에 따라 격자를 유동적으로 구성할 수 있는 쿼드트리 격자기반의 Deb2D를 개발하여 우면산 산사태에 적용하였다. Deb2D는 연행작용 및 건물의 영향 고려가 가능하며, GUI를 제공하고 있어 사용자가 손쉽게 사용할 수 있다는 장점이 있다. 하지만 An et al. (2019)은 2011년 우면산 산사태 유역 중 래미안 아파트 유역에 대해서만 적용되어 타 유역에 대한 추가적인 검증이 필요하며, 연행효과 및 매개변수에 대한 분석이 미비하였다. 이에 본 연구에서는 Deb2D 모형을 활용하여 2011년 우면산 산사태 지역 중 2개 유역(래미안 아파트, 신동아 아파트)을 대상으로 매개변수에 따른 연행효과, 피해 범위, 토석류 유하량, 피해 높이 등을 종합적으로 비교・분석하였다.
2. 방법 및 적용
2.1 Deb2D의 지배방정식 및 이산화
Deb2D 모형은 토석류의 유동을 모의분석하기 위해 2차원 천수방정식(shallow-water equation) 형태의 지배방정식을 사용하였으며, 연속식 및 운동량 보존방정식은 다음과 같다.
| $$\frac{\partial\overrightarrow q}{\partial t}+\frac{\partial\overrightarrow f}{\partial x}+\frac{\partial\overrightarrow g}{\partial y}=\overrightarrow s$$ | (1) |
여기서 t는 시간, x와 y는 직교 좌표, , , 그리고 는 고정된 x-y좌표에서의 유동을 나타내는 벡터, h는 토석류의 깊이, u와 v는 x-y방향에서 깊이에 따른 평균 속도, g는 중력 가속도, Qe는 연행율(Qe> 0) 또는 퇴적율(Qe< 0), Sgx와 Sgy는 각각 x-y방향에서의 중력가속도이다. Sfx와 Sfy는 각각 x-y방향의 토석류 유동을 나타내는 항으로 바닥마찰력과 난류마찰력을 포함한다. Deb2D에서는 토석류의 유동모형으로 Voellmy 모형, Bingham 모형, Coulomb 모형을 선택할 수 있으며 본 연구에서는 매개변수의 개수가 비교적 적고, 널리 사용되어 (Hürlimann and Graf, 2003; Rickenmann et al., 2006; Pirulli and Sorbino, 2008; Hungr and McDougall, 2009; Klaus et al., 2015) 적용성이 높은 Voellmy 모형을 적용하였다.
| $$\begin{array}{l}S_{fx}=\frac{\left|u\right|}u\left(\mu gh+\frac{g(u^2+v^2)}\xi\right),\\S_{fy}=\frac{\left|v\right|}v\left(\mu gh+\frac{g(u^2+v^2)}\xi\right)\end{array}$$ | (3) |
여기서 는 Coulomb 마찰 계수, 는 난류 마찰 계수이다. 연행속도를 결정하는 연행률(entrainment rate) Qe는 다음과 같이 주어진다(Sovilla et al., 2006).
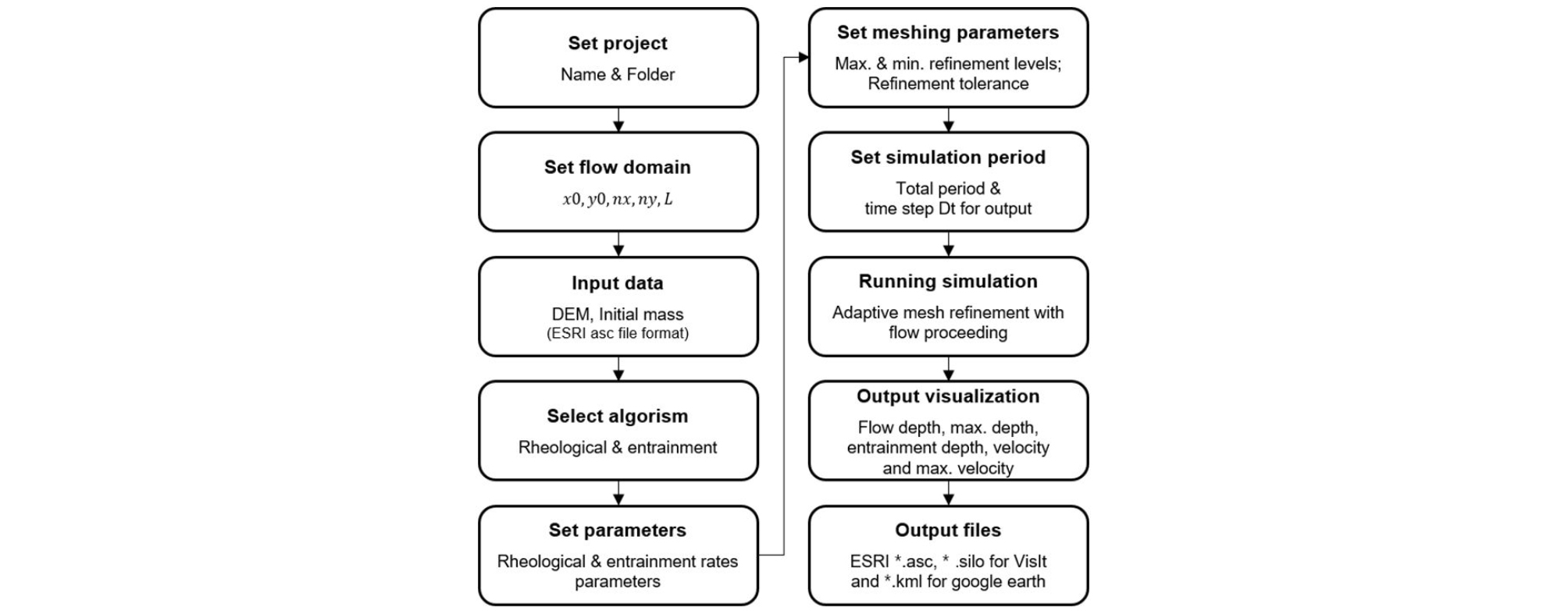
여기서 는 (x, y)좌표에 따른 최대 침식 깊이이며, 모의분석 시 공간분포의 형태로 주어진다. K는 무차원 유동 계수로 침식 속도를 결정한다. 본 연구에서는 back-analysis를 통하여 복수의 K값을 선정하고 이 값들이 토석류 흐름에 미치는 영향 즉, 민감도 분석을 수행하였다. 상세한 이산화 항들의 정의와 계산방법은 An et al. (2019)과 An et al. (2012)를 참고하기 바란다. Deb2D 모형의 적용 절차는 Fig. 1과 같다.
2.2 대상지역
본 연구에서는 Fig. 2 (a)와 같이, 우면산 북측에 위치한 래미안 아파트 유역(이하 래미안 유역)과 신동아 아파트 유역(이하 신동아 유역)을 대상으로 Deb2D를 적용하고 분석하였다. 대상 지역인 래미안 유역과 신동아 유역의 산사태 전・후 LiDAR DEM과 우면산 산사태 원인조사 추가 및 보완조사(Seoul City, 2014)(이하 보고서)를 통하여 최대 침식 깊이를 5 m로 설정하였고, 해당 유역의 하류부인 도심지역에 위치한 건물의 공간적 형태는 수치지형도를 활용하여 반영하였다. 각 유역의 산사태 발생부는 보고서와 산사태 발생 전・후 LiDAR DEM의 변화를 이용하여 초기 발생 지점은 Fig. 2 (b)과 같이 도출하였으며, 초기 발생량은 래미안 유역에선 354 m3, 신동아 유역에선 347 m3로 측정되었다. 보고서와 현장 조사에 따르면 래미안 아파트는 3층(약 10 m), 신동아 아파트는 2층(약 8 m)까지 산사태의 직접적인 피해가 발생한 것으로 보고되었다. 주행 중이던 자동차 블랙박스와 주변 CCTV 자료로 분석된 토석류의 최대 속도는 각각 약 28 m/s, 18.6 m/s로 확인되었으며, 이는 과거 다른 지역에서 분석된 토석류와 비교하여 매우 빠른 속도이다. 이러한 빠른 유동은 많은 강우로 인해 토석류의 체적농도가 적어져 유동성이 커졌기 때문으로 추정되고 있다(Son et al., 2012; Kim et al., 2013; Park et al., 2013; Lee et al., 2019). 현장 자료가 풍부한 래미안 유역을 대상으로 여러 매개변수 조합 결과의 정확도를 추정하고 매개변수를 보정하였다. 정확도 추정에 사용한 지표는 다음과 같다.
| $$acc.j=\left|\;1-\frac{\left|Obs.j-Sim.j\right|}{Obs.j}\;\right|$$ | (5a) |
| $$Acc={\textstyle\sum_{}^{}}\frac{acc.j\times w_j}{w_j}$$ | (5b) |
여기서 , , 그리고 는 각 비교 항목에서의 정확도, 관측값, 예측값 그리고 가중치 지표이며, Acc는 매개변수 조합의 종합적인 정확도를 의미한다. 또한 산정된 매개변수 값을 신동아 유역에 동일하게 적용하여 해당 매개변수의 범용성을 확인하였으며 신동아 유역에 대하여 적용한 매개변수 조합의 결과와 래미안 유역에 적용한 결과를 비교하여 매개변수 조합에 따른 토석류 모의의 특성을 분석하였다.
3. Deb2D 모의분석
본 연구에서는 Deb2D를 사용하여 토석류 유동에 대한 두 매개변수(, )와 토석류 연행작용에 대한 하나의 매개변수(K)를 Table 1과 같이 14가지 경우로 조합(p1 ~ p14)하고, 매개변수 변화에 따른 모의결과와 실측값을 Eqs. (5a) and (5b)에서 제시한 정확도 지표를 활용하여 비교분석하였다. 정확도 비교 항목은 1) 피해 지역의 범위, 2) 총 퇴적량, 3) 아파트 주변에서 관측된 토석류의 최대 높이, 4) 도로 인근에서 관측된 토석류의 첨두속도로 하였다. 각 항목에 대한 가중치는 계측값의 신뢰도 및 중요도를 종합적으로 판단하여 설정하였다(Table 2).
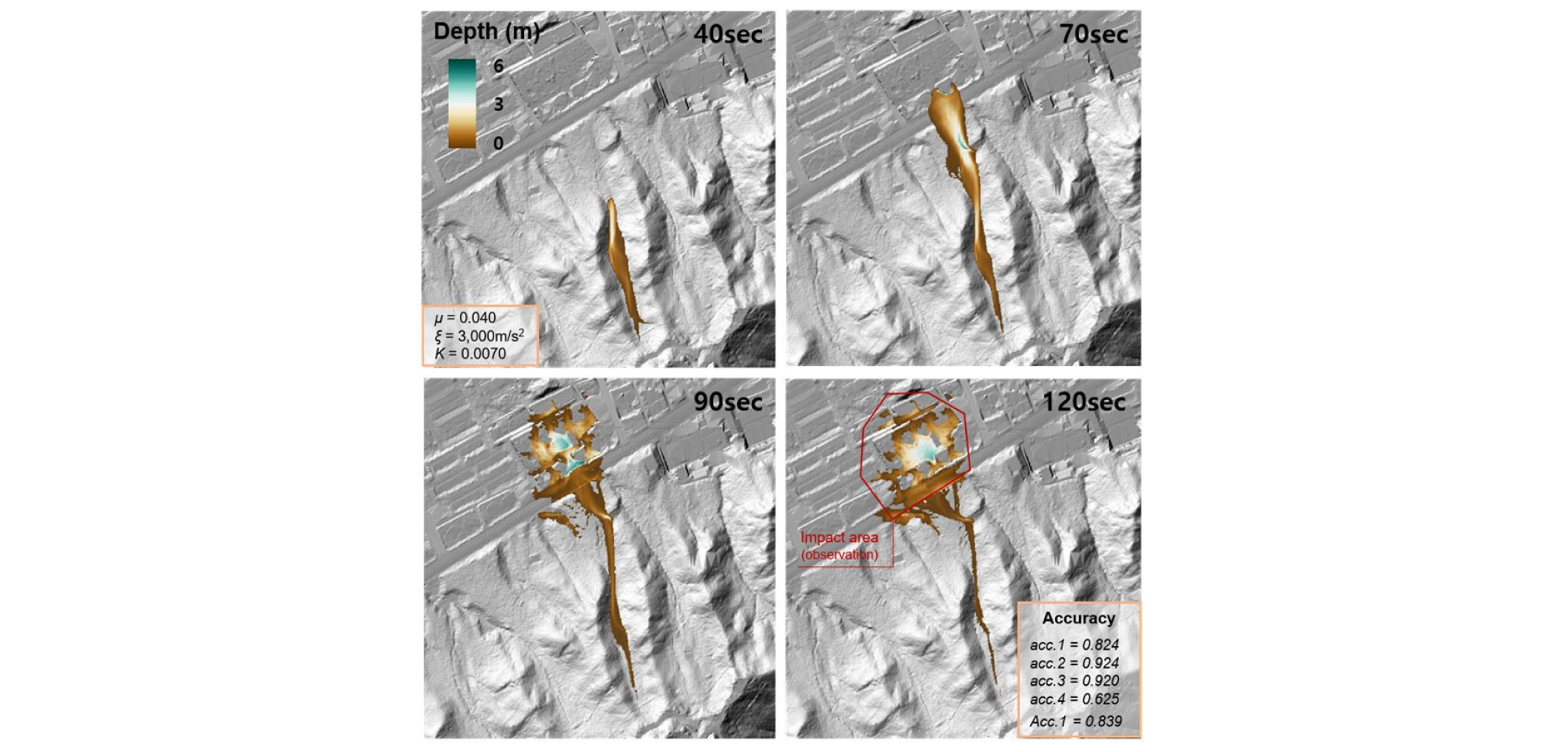
Deb2D를 래미안 유역에 적용한 결과를 Tables 1 and 2에 정리하였으며 Table1은 매개변수 조합에 대한 모의결과 데이터, Table 2는 정확도 지표 분석결과이다. 종합적으로 p10 ( = 0.04, = 3000 m/s2, K = 0.007)조합이 정확도 분석 결과 0.839로 가장 높은 것으로 나타났으며, 다음으로 p8 ( = 0.04, = 1000 m/s2, K = 0.007)조합의 정확도가 0.727순으로 높은 것으로 나타났다. 가장 우수한 예측 조합인 p10의 시간에 따른 토석류 유동 계산결과를 Fig. 3에 도시하였다. p10의 경우 예상 피해 범위는 0.824의 정확도를 나타내었으며, 퇴적량은 45,750 m3로 계산되어 0.924의 정확도를 나타내었다. 래미안 아파트 주변에 퇴적된 토석류의 최대 높이는 10.8 m로 계산되어 현장 조사 결과인 아파트 3층 높이(10 m로 환산)와 비교하여 0.92의 정확도를 나타내었다. 하지만 아파트 인근 도로 블랙박스 등을 통하여 관측된 토석류의 첨두속도는 약 28 m/s인 것과 비교하여 계산결과는 17.5 m/s로 다소 낮은 정확도 0.625로 분석되었다. p10뿐만 아니라 타 13종류의 매개변수 조합 적용 시에도 이처럼 빠른 첨두속도의 재현은 어려운 것으로 나타났으며, 이는 전술하였듯이 토석류 발생 시 많은 강우로 인한 효과를 Deb2D가 충분히 재현하지 못하고 있기 때문인 것으로 판단된다.
Table 1.
Observed and simulated debris flow in Raemian apartment basin with different parameters estimated at Raemian apartments
Table 2.
Estimation of accuracy for the back-analysis of the Raemian apartment basin using the sets of model parameters of Table 1
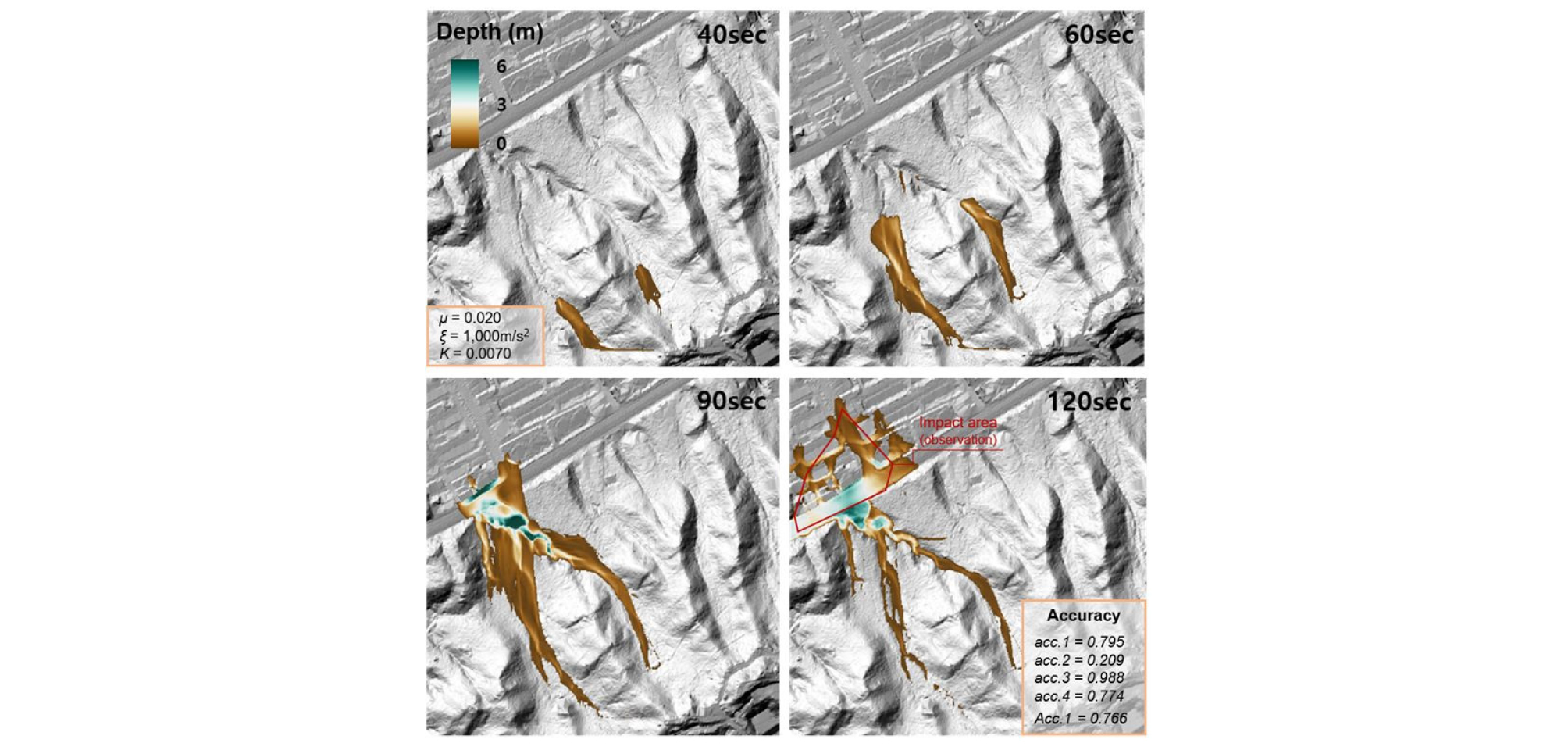
Deb2D를 신동아 유역에 적용한 결과를 Tables 3 and 4에 정리하였으며 Table3은 매개변수 조합에 대한 모의결과 데이터, Table 4는 정확도 지표 분석결과이다. 신동아 유역의 모의결과는 래미안 유역의 모의결과에 비하여 훨씬 매개변수의 변동에 민감하게 반응한 것을 확인할 수 있다. 특히 몇몇 조합(p1, p5, p6, p7, p11, p12, p13)들은 피해지역에 토석류가 도달하지 못하고 산지지역에 토석류가 정체되어 매우 낮은 정확도를 나타내었다. 종합적으로 p4 ( = 0.02, = 1000 m/s2, K = 0.007)조합의 정확도가 0.766, p10 ( = 0.04, = 3000 m/s2, K = 0.007)조합의 정확도가 0.664순으로 높은 것으로 나타나, 래미안 유역을 대상으로 산정한 매개변수 조합과는 다소 다른 것으로 분석되었다. 가장 우수한 예측 조합인 p4의 시간에 따른 토석류 유동 계산결과를 Fig. 4에 도시하였다. 신동아 유역의 경우, 래미안 유역에서 첨두속도를 재현하기 어려웠던 것과 달리 발생한 총 퇴적량을 재현하기 어려운 것으로 나타났다. p4의 경우 발생한 총 퇴적량은 98,298 m3로 계산되어, 관측값인 44,500 m3에 비하여 크게 산정 된 것으로 나타났다. p3 및 p9의 경우 발생한 퇴적량은 관측값과 유사하게 계산되었으나, 피해범위가 매우 작게 산정 된 것을 알 수 있다. 본 연구에서는 자료의 신뢰도 및 중요도를 고려하여 피해범위의 공간적 예측이 퇴적량에 비해 중요하다고 판단하여 가중치를 부여하였으나, 가중치의 변화에 따라 종합적인 정확도가 크게 달라질 수도 있음을 신동아 유역의 모의에서 확인할 수 있다.
Table 3.
Observed and simulated debris flow in SindongA apartment basin with different parameters estimated at SindongA apartments
Table 4.
Estimation of accuracy for the back-analysis of the SindongA apartment basin using the sets of model parameters of Table 3
매개변수의 조합에 따른 침식 양상의 변화를 알아보고자 6개의 매개변수 조합(p4, p6, p7, p8, p12, p10)을 선정하여 Figs. 5 and 6에 도시하였다. 는 토석류의 점성효과를 나타내는 매개변수로 값이 증가할수록 토석류 내부유동으로 인한 에너지가 크게 소산되어 흐름이 느려지게 된다. Figs. 5 and 6에서 값이 증가할수록(p4→p8→p12) 전반적으로 침식깊이 및 범위가 작아지는 것으로 나타났다. 는 토석류 유동의 난류마찰계수로 값이 작을수록 난류로 인한 에너지 소산이 커져 흐름의 유속이 느려지는 효과가 있다. 값이 증가할수록(p6→p8→p10) 중・상류지역에서 관측된 침식 깊이와 깊게 침식된 범위가 커지는 것으로 분석되었다. K는 침식율을 나타내는 매개변수로써 침식깊이에 가장 결정적인 영향을 미치는 매개변수이다. Figs. 5 and 6에서 확인할 수 있듯이 매개변수의 차이에 따라 침식깊이에 큰 영향을 미치며, 결과적으로 침식량 및 토석류 피해범위에도 큰 영향을 미친다. K값이 작을수록 상류지역의 전반적인 침식 깊이는 얕아지고 하류지역의 침식과정에 영향을 주어 침식된 너비가 완화되는 결과를 나타내었다.
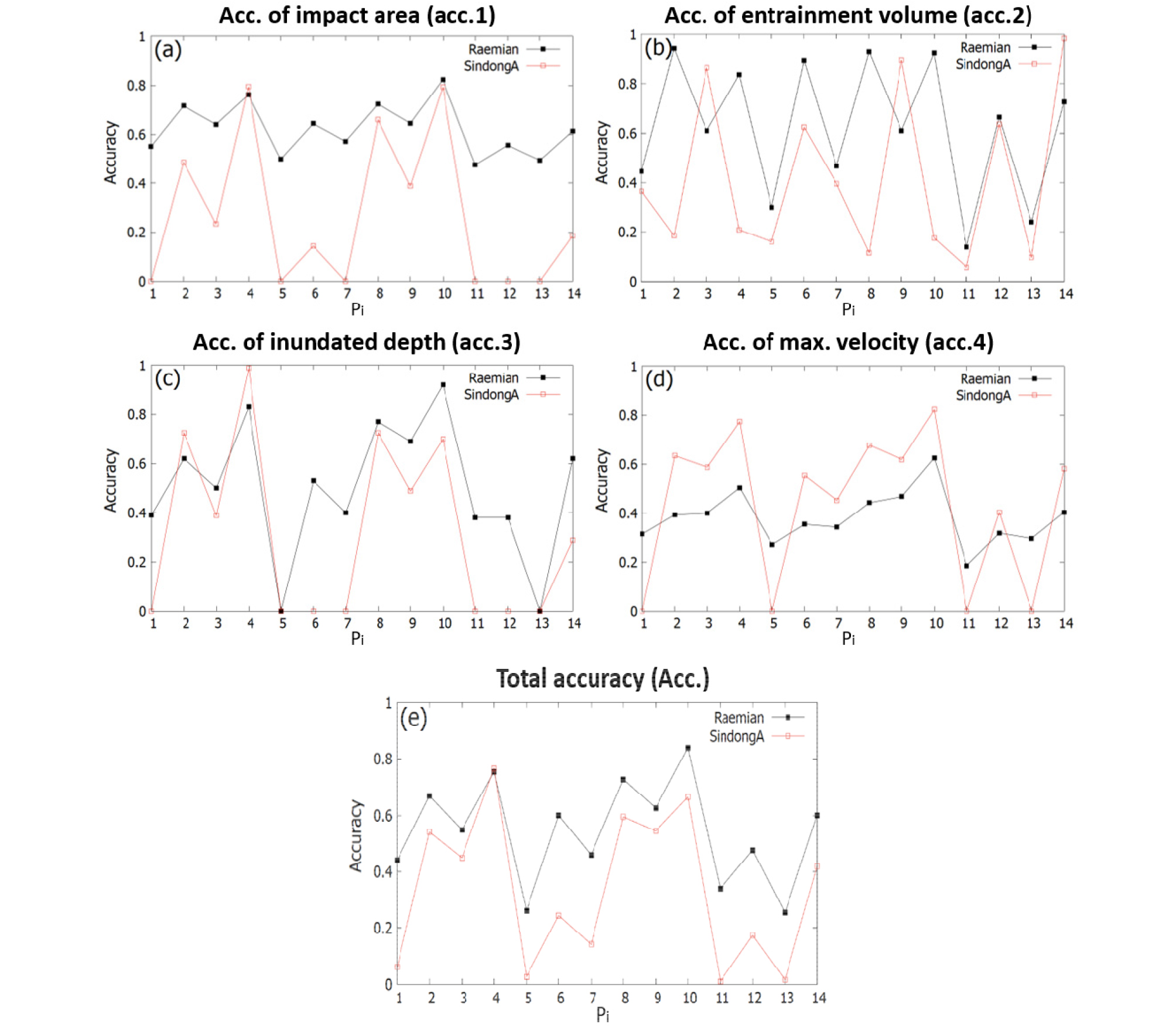
래미안 유역과 신동아 유역의 매개변수 조합에 따른 정확도 지표를 Fig. 7과 같이 그래프로 재정리하였으며, 매개변수와 각 항목들 사이의 의존도를 파악할 수 있었으며 래미안 유역과 신동아 유역의 전반적인 민감도를 확인・비교할 수 있었다. 첫 번째, 피해 지역 범위(acc.1)는 p4, p8그리고 p10에서 두 유역 모두 양호하며 비슷한 정확도를 기록했으며 세 조합 모두 K = 0.0070인 공통점을 보였다. 두 번째, 총 퇴적량(acc.2)의 경우 서로 상이한 정확도를 보여 분석에 어려움이 있었다. 세 번째, 아파트 주변의 토석류의 최대 높이(acc.3)는 피해 지역(acc.1)과 동일한 양상을 보여 p4, p8그리고 p10에서 양호한 결과를 나타냈다. 네 번째, 토석류의 최대 속도(acc.4)는 두 유역에서 비슷한 양상을 보였으며 양호한 정확도를 나타낸 매개변수 조합은 p10으로 나타났으며 비교적 값이 높을 때 양호한 정확도를 보였다. 마지막으로 종합 정확도 그래프에서 매개변수 조합 p4는 두 유역 모두 양호한 결과를 보임과 동시에 유사한 정확도를 나타냈다. 반면 비교적 값이 크고, 값이 작은 p5, p6, p11 그리고 p12에선 낮은 정확도를 나타냈다. 두 유역은 각 매개변수 조합에 따라 비슷한 정확도 양상을 보였으나 신동아 유역의 경우 래미안 유역보다 매개변수 변화에 따른 모형의 결과변화가 민감한 것으로 분석된다. 특히, 토석류의 최대 높이(acc.3)와 토석류의 최대 속도(acc.4)에서 변화에 큰 폭을 확인할 수 있었다. 보고서에 따르면 두 유역은 비슷한 지질 특성을 가지고 있으나 토립자가 지닌 불확실성과 각 유역 유하부가 가진 특징(길이, 사면 경사 등)으로 인해 모형의 매개변수 적용성에 대한 차이가 발생한 것으로 보인다.
4. 결 론
본 연구에서는 2011년 7월 우면산에서 발생한 토석류를 대상으로 연행작용을 고려한 토석류 모의의 매개변수를 분석하고자 하였다. 토석류 모형은 Deb2D를 이용하였으며, 토석류의 유동 과정에서 발생하는 침식 및 피해 지역에 대해 LiDAR DEM을 활용하여 현장의 지형 자료를 구축하였다. 현장의 블랙박스와 CCTV 등의 영상 자료, 현장 조사 자료 등에 근거하여 토석류 피해지역, 총 발생 침식량, 유동속도, 토석류 깊이에 대하여 정확도를 분석하였으며 그 결과를 요약하면 다음과 같다.
1) 래미안 및 신동아 유역에 대한 Deb2D의 적용성을 검토한 결과, 전반적으로 높은 정확성을 보였다. 다수의 매개변수 조합에 대하여 두 유역은 유사한 결과가 나타났으나 래미안 유역에 비하여 신동아 유역에 적용 시 매개변수 변화에 민감하게 반응하였다.
2) 공통적으로 두 개의 유역에서 분석된 토석류의 유동 속도는 현장 자료에 비해 과소평가되어 계산되었다. 많은 강우로 인해 발생한 토석류는 체적 농도가 적어 유동성이 매우 커지지만 이러한 특성을 Deb2D로 재현하기에는 한계가 있었던 것으로 판단된다.
3) 매개변수의 변화에 따른 침식양상을 정량적으로 분석하였다. 값이 증가할수록 침식깊이 및 범위가 작아지며, 값이 증가할수록 중・상류지역에서 관측된 침식 깊이와 깊게 침식된 범위가 커지고, K값이 작을수록 상류지역의 전반적인 침식 깊이는 얕아지고 하류지역의 침식과정에 영향을 주어 침식된 너비가 감소되는 것으로 분석되었다.
본 연구와 같은 수치해석 모형을 통한 과거 토석류 사건의 구현 및 분석은 산사태 및 토석류 발생 위험지역에 적용되어 피해규모와 범위를 예측하는데 도움을 수 있을 것으로 기대된다. 본 연구에서는 우면산에서 발생한 토석류만을 대상으로 분석을 진행하여 도출된 유동 및 침식 모형의 매개변수는 한정적일 수 있다. 따라서 향후 연구에서는 국내 환경에 적합한 토석류 해석을 위해 다양한 지역에서의 적용을 추가적으로 검토하고 있다. 또한 토석류의 유동과 피해 규모 및 범위 예측은 초기 발생량과 발생부에 큰 영향을 받으나, 초기 발생부에 대한 정보 및 자료의 구축은 매우 제한적이며 연행작용에 대한 자료구축도 매우 제한적이다. 본 연구에서는 이러한 제약을 극복하기 위하여 산사태 발생 전후의 LiDAR자료를 활용하였으며, 향후 산사태 발생 전후에 계측된 LiDAR자료의 활용성 및 범용성에 대한 연구가 추가적으로 필요할 것이다.