1. 서 론
2. 수치모형 적용성 검토
2.1 대상 지역
2.2 외력산정
2.3 수치모형
3. 수치모의 결과 및 분석
3.1 모델의 검증
3.2 급경사지에서의 토석류 범람
3.3 사방댐의 기능 평가
3.4 사방댐 설치 위치에 따른 영향평가
4. 결 론
1. 서 론
우리나라에서의 토석류 피해는 주로 산지 지역에서 발생하며 직·간접적인 피해가 다른 자연재해에 비해 피해가 적어 비교적 재해의 위험 리스크가 과소평가 되는 경향이 있다. 하지만 2011년 우면산 토석류 재해를 시점으로 토석류가 우리나라 지역사회의 안전을 위협하고 있는 재해로써 재평가되어 다양한 연구와 피해 저감을 위한 여러 대책이 수립되고 있다. 최근 발생한 2019년 10월 태풍 “미탁”이 한반도를 강타하여 부산 사상구에서는 밤사이 내린 집중호우에 의해 지반이 약해져 갑작스러운 토사 붕괴로 인해 토석류(Fig. 1)가 발생하였고 인명피해(4명) 및 재산 피해가 발생하였다. 재해복구를 위해서는 약 125억 원 이상이 필요한 것으로 조사되었다. 복구비용에 많은 예산이 투입되는 것은 불가피한 상황이지만 장기적인 시각으로 비추어 볼 때 사전에 피해를 저감 시키는 방재 시스템 개발, 예측 기술의 개발 및 사방시설의 도입 등의 기술을 도입하면 실제 발생한 직접적인 피해를 보다 적은 비용으로 효율적으로 피해 저감이 가능할 것이다.
우리나라는 국토의 63.7%가 산지로, 인구밀도가 높아 산지의 개발에 따른 주택과 각종 사회기반시설이 산지부에 입지하게 됨에 따라 산지 토사 재해에 취약하며 사방시설이 도입됨에 따라 해안지역에서는 하천으로부터 공급되는 토사량의 감소에 따라 연안 표시이동의 불균형으로 연안 침식이 가속화되고 있다(Kim et al., 2019). 이처럼 사방시설은 산지 지역만이 아닌 하천, 연안 지역을 포함한 유사계 전체의 토사량을 관리할 수 있는 대책을 마련해야 할 것이다.
행정안전부에서는 2009년 급경사지 재해예방에 관한 법률을 제정하고 현재까지 지속해서 관리하고 있으며 전국의 산사태 취약지역 24,075개소(KFS, 2017)로, 산지의 타 용도 전용과 불법 산림 훼손도 증가하고 있어 산사태 취약지역의 증가가 불가피하다. 여기에 세계적으로 급변하는 기후변화의 영향으로 돌발적으로 발생하는 국지성 집중호우의 출현 빈도나 그 강도가 증가하고 있어 특히 도시 생활권 주변의 급경사지에서 대규모 토석류의 발생 가능성이 커 지역사회의 안전을 위협하고 있다.
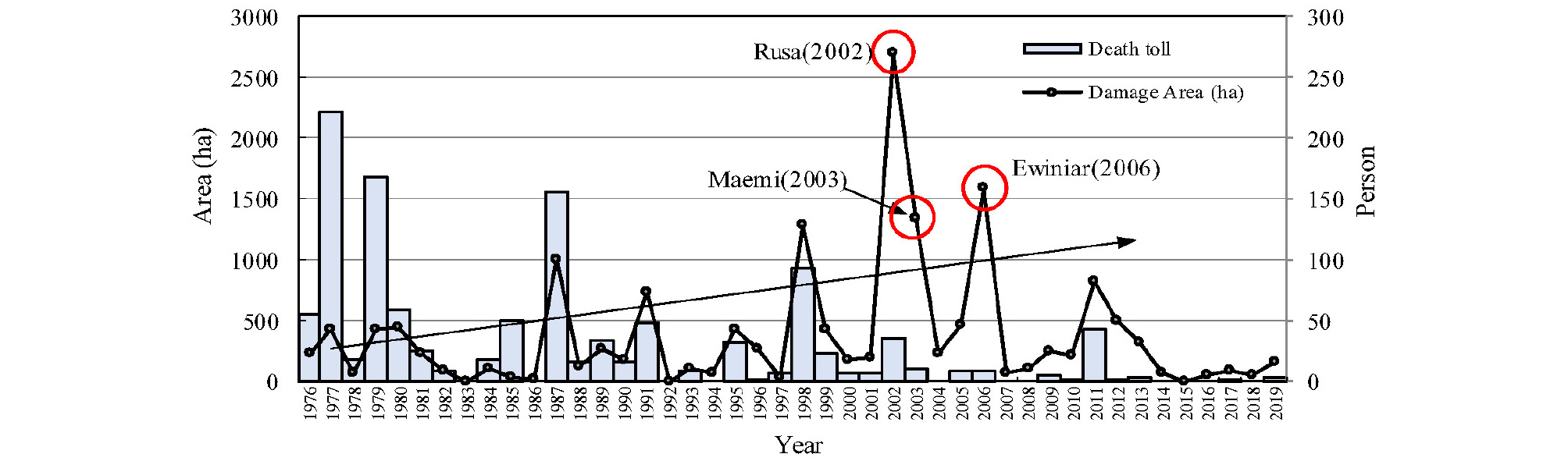
우리나라의 사방대책은 2011년 우면산 재해 이후 본격적으로 실시되었다. 또한, 2010년 이후 우리나라에 태풍이 동반한 극심한 강우의 출현이 적어 토사 재해 또한 감소하는 추세(Fig. 2)를 나타내고 있다. 하지만 세계적으로 발생하고 있는 재해 특성상 단 한 번의 최대급 강우가 발생한다면 매우 심각한 토사 재해가 발생하여 복구 및 회복이 힘든 지역사회의 붕괴를 초래하는 사례들이 보고(중국 광둥성 산사태 2015년)되고 있다. 또한, 1976년 이후 우리나라의 연평균 산사태 발생면적은 692 ha로 나타났으며 최근에는 국지성 호우, 태풍 등과 같은 기후변화로 인한 기상이변으로 연간 산사태 발생면적이 231 ha (1980년대) → 350 ha (1990년대) → 713 ha (2000년대)로 매우 증가하였다. 인명피해는 연평균 58명으로 도심지역의 산사태로 인한 대규모 인명피해가 발생하고 있다. 이처럼 우리나라도 토사 재해에 안전한 나라가 아닌 위험 위험이 큰 나라로서 국민적 관심과 대책이 요구된다.
국·내외적으로 토석류에 관한 연구가 활발히 진행되고 있다. 토석류 범람 특성에 관한 연구로는 Kim et al. (2013)은 FLO-2D 모형을 이용하여 모델의 성능과 토석류의 유동 매개변수를 분석하였지만 FLO-2D 모형이 침식물질과 우수의 연행작용을 고려할 수 없는 고유의 한계점을 지적하였다. Kim et al. (2015)는 연행작용이 고려 가능한 독자적인 토석류 모델을 개발하였으며 최대급 강우 발생에 따른 토석류 영향평가를 하였다. 사방댐과 관련된 연구로서 Honda and Egashira (1997) 및 Takahashi et al. (2001a)는 가장 일반적인 불 투과형 사방댐에 관한 연구를 수행하였고 특히 Takahashi et al. (2001b)은 사방댐의 높이와 상류로부터 공급되는 토사의 높이와의 관계를 이용하여 불 투과형 사방댐의 효과를 계산하는 방법을 제안하였다. 이 방법은 1차원 모델을 이용한 불 투과형 사방댐에 대해 Nakagawa et al. (2001), Satofuka and Mizuyama (2005) 등의 연구에서 토석류 피해 감소 효과에 대한 평가를 시행하였다. Choi et al. (2015)의 연구에서는 slit 댐을 이용하여 사방댐 배치에 따른 토석류의 흐름에 대한 실험을 실시하여 사방댐 사이의 간격과 배치 각도가 토석류를 포착시키는 기능에 대한 검토를 수행하였다. 이처럼 토석류는 흐름의 특성이 매우 복잡하여 메커니즘 분석에 있어 수리모형 실험에 의한 의존도가 높다. 사방댐을 월류하면서 발생하는 에너지의 소산 등을 평가하기 위해서는 3차원적인 평가가 요구되나 아직 토석류의 3차원적인 평가는 연구 초기 단계며 주변의 지형적 특성을 반영할 수 있는 독자적인 2차원 모델에 의한 연구가 활발히 진행 중이다.
본 연구에서는 우리나라 급경사지로 지정된 지역을 대상으로 방재성능목표에 따른 토사 유출량을 산정하고 그에 따른 토석류 영향평가와 피해 저감에 탁월한 사방댐의 기능 평가를 목적으로 한다. 사방댐 평가를 위해 개발한 2차원 토석류 모델의 신뢰성 확보를 위해 수리모형실험과의 비교 검증 결과 잘 일치하는 것으로 나타났다. 또한, 급경사지 주변의 지역적 특징과 토석류가 유하하면서 발생하는 침식·퇴적 작용을 평가하기 위해 평면 2차원 토석류 모델을 구축하여 직접 피해지역에 도달하는 토석류의 흐름 특성을 분석하였다. 피해 저감을 위해 설치한 사방댐의 제원(높이) 및 설치장소에 따라 토석류가 하류로 전달되는 흐름 특성을 분석하였고 특히 사방댐 설치장소가 토석류의 흐름이 발생하는 약 20° 이상의 지역에서는 사방댐의 기능이 현저히 떨어지는 것을 확인하였다.
2. 수치모형 적용성 검토
본 연구에서는 경상남도 김해시에서 지정한 산사태 위험지구 70개소 중 인명피해 리스크가 지역을 선정하였으며 외력 산정으로 김해시에서 지정한 방재성능목표 강우(2017년)에 의해 발생 가능한 토석류를 발달시켜 하류 지역에서의 범람 영향평가 및 피해 저감을 위한 사방시설을 도입하여 그 시설의 기능을 평가하였다.
2.1 대상 지역
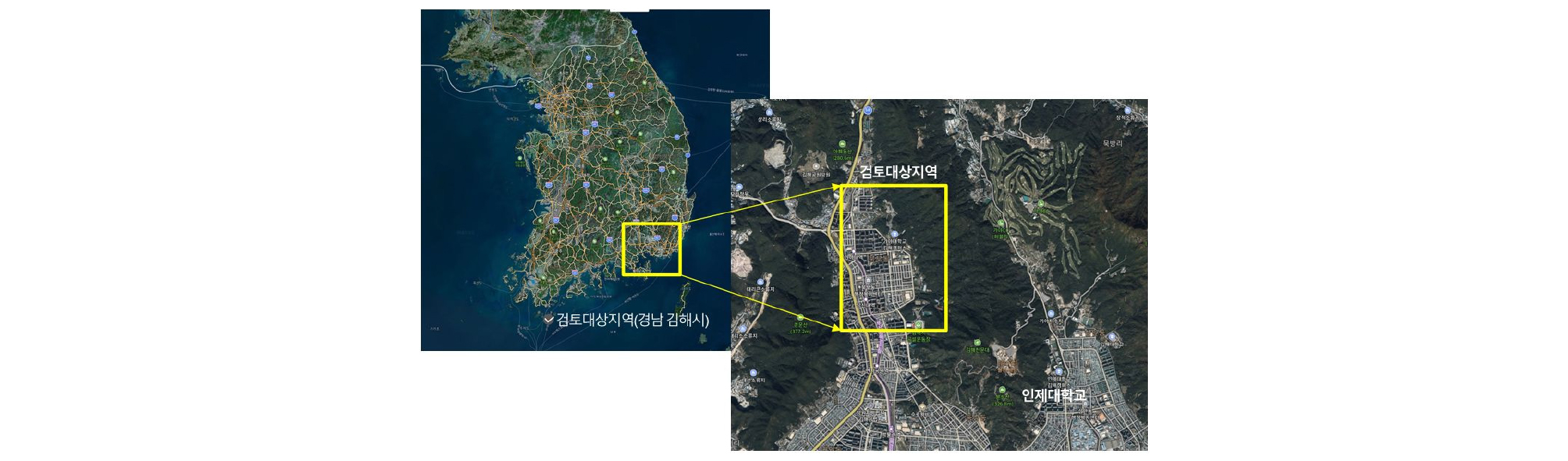
산림청에서는 산사태 위험지도를 제작 및 산사태 정보시스템과 연동하여 국민에게 방재 정보를 제공하고 있다. 이 지도는 산사태가 발생하는 원인 중 비교적 기인력이 큰 인자인 임상(숲모양), 경급(나무지름크기), 사면경사, 사면방위, 사면길이, 사면곡률, 모암, 토심, 지형습윤지수 9개를 선정하여 제작하였다. 산사태 예측정보의 제공과정은 기상청 강우자료(동네예보)분석 → 권역별 산사태 토양함수지수(예측기준)분석 → 읍·면·동 단위로 예측정보 등을 제공하고 있다. 경상남도 김해시에 지정된 산사태 위험지구 약 70개소 중 본 연구에서는 위험지구 인근에 주민이 밀집하여 피해가 클 것으로 예상되는 지역을 선정(Fig. 3)하여 토석류의 영향평가를 수행하였다.
2.2 외력산정
김해시는 자연재해대책법에 따라 방재성능목표를 설정하여 Table 1과 같이 공고(2017)하였다. 금회 산정한 방재성능목표와 강우자료를 분석하여 확률강우량(Kim, 2020)을 재산정하였으며, 이 결과를 이용하여 외력을 산정하였다. 그 결과 방재성능목표 강우량이 기존의 강우량보다 크게 산정되어(약 30년 빈도) 본 연구에서 산정한 확률강우량을 채택하였다. 검토대상 지역에서 발생 가능한 토사량을 산정하기 위해 빈도별 강우량을 산정하였다. 우선 대상 지역에서 가장 가까운 부산 관측소의 58개년(1961년∼2018년) 강우 자료를 이용하며 호우 상황을 조사한 결과, 하루 최대 강수량은 1991년 8월 23일에 발생한 439.0 mm가 최대치이고, 1시간 최대우량은 2008년 8월 13일에 발생한 106.0 mm, 10분 최대강수량은 1981년 9월 24일에 발생한 40.0 mm로 조사되었다. 또한, 빈도별 강우량을 산정하여 발생 가능 토사량을 산정하였다.
Table 1.
Disaster prevention performance target for rainfall
| Rainfall | Duration of rainfall (mm) | |||
| 1hr | 2hr | 3hr | ||
| Disaster prevention performance target | Gimhae (2017) | 95.0 | 130.0 | 155.0 |
| In this study | 30yr | 97.2 | 138.8 | 166.2 |
검토대상영역에서 발생 가능한 유출 토사량(Eq. 1)을 일본 국토기술 정책 종합 연구소(NILIM, 2016)에서 제시한 아래의 식에 의해 산정하였다.
| $$Q_{sp}=0.01{\textstyle\sum_{}}Q_p$$ | (1) |
| $$Q_p=\frac{P_v\bullet C_\ast}{C_d}$$ | (2) |
| $$P_v=\frac{10^3R_TA}{1-\lambda}\left(\frac{C_d}{1-C_d}\right)\;f_r$$ | (3) |
| $$R_T=\left[\frac{r_{24}}{24}\right]^{1.21}\bullet\;\left[\frac{24f^2}{{\displaystyle\frac C{60}}A^{0.22}}\right]^{0.606}$$ | (4) |
| $$f_r=0.05\left(\log A-2.0\right)^2+0.05$$ | (5) |
| $$C_d=\frac{\rho\tan\theta}{\left(\sigma-\rho\right)\;\left(\tan\phi-\tan\theta\right)}$$ | (6) |
여기서 Qsp는 토석류 피크유량, Qp는 유출량, Pv는 유출토사량(m), RT는 유효강우강도(mm/hr), A는 유역면적(km2), 는 공극율, Cd는 유동중 토석류의 용적 토사농도(토석류 발생지역에서의 토석류 농도로 산정), fr는 유출 보정율, C* (= 0.65)는 토석류 최대 용적 토사농도 그리고 본 검토에서는 김해시 방재성능목표 강우량은 30년 빈도와 유사하게 산정되어 토석류 피크 유량을 산정을 위해 30년 빈도의 24시간 누적강우량(335.7 mm)에 따른 토석류 영향평가를 실시하였다. 그 결과 유출 가능 토사량은 약 55,949 m3으로 산정되었으며 이를 이용하여 토석류 피크 유량(Qsp)을 산정하였다.
2.3 수치모형
급경사지에서의 2차원적인 토석류 해석과 불투과성 사방댐의 평가를 위해 Kim et al. (2015)의 모델을 이용하며 모델의 검증을 위해 Shrestha (2009)의 수리모형실험의 결과와 비교하여 모델의 신뢰성(Kim, 2020)을 평가하였다. 모델의 구성은 다음과 같다.
2.3.1 수치모형의 개요
기초방정식으로서 토사와 물이 혼연일체가 된 흐름으로 데카르트 좌표계에서의 토석류의 기초방정식은 x, y방향의 운동량 방정식(7), (8)와 전 체적에 대한 연속방정식(9), 조립자(10) 및 세립자(11)에 관한 연속방정식은 다음과 같다.
| $$\frac{\partial h}{\partial t}+\frac{\partial M}{\partial x}+\frac{\partial N}{\partial y}=i_b$$ | (9) |
| $$\frac{\partial z_b}{\partial t}+i_b=0$$ | (12) |
여기서 M = uh, N = vh : x, y방향의 유량 플럭스, u, v는 평균유속, h는 수위, 는 운동량 보정계수( = 1.25), g는 중력가속도, 는 입자와 물이 혼합된 밀도(≃토석류의 겉보기 밀도), 는 입자의 밀도, 는 물의 밀도, 는 x, y방향의 저면전단응력, ib는 퇴적(ib < 0), 침식(ib ≥ 0)속도, CL, CF는 토석류 속의 총 입자성분의 조립자 및 세립자 성분의 체적 농도, C*L, C*F는 각각 바닥면 퇴적층 안의 조립자 및 세립자 농도, C*DL은 입자가 흐름으로부터 분리해서 퇴적하는 경우의 퇴적층 안의 농도이다. zb는 침식 또는 퇴적 깊이로서 Eq. (12)을 이용한다.
2.3.2 사방댐의 평가
사방댐의 상류에서의 토석류 농도(퇴적)는 사방댐의 설치로 인해 평형 상태의 토석류 농도 보다 높아지며 항복 응력을 초과한 후 토석류 흐름이 중단 즉 퇴적(증착)이 발생한다. 이러한 토석류의 구조물에 의한 퇴적 메커니즘은 저면 전단 응력에서의 항복 응력을 포함한 유동 혼합물의 운동량 방정식에서 고려할 수 있다.
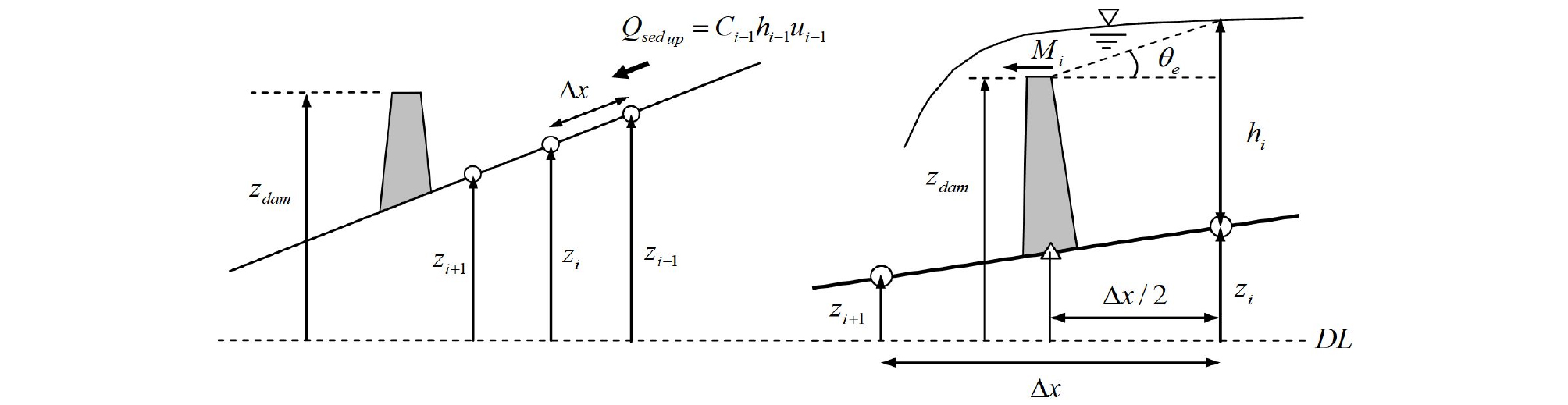
Takahashi et al. (1992) 및 Egashira et al. (2001) 이전의 연구에서는 증착 속도 모델은 유속에 비례하고 사방댐의 상류 퇴적은 계산될 수 없으며, 유속이 0이 되면 댐의 상류 퇴적도 너무 작아지는 문제점이 발생하였다. 하지만 사방댐의 상류에서 토사의 유동 증착은 매우 빠르게 증착되는 현상이 발생하며 이것은 증착 속도 방정식으로 계산될 수 없다. 따라서 사방댐의 상류에 대한 새로운 퇴적속도 방정식이 필요하다. 본 모델에서는 staggered gird을 이용하고 있으며 사방댐을 정의하는 위치는 수심과 하상고를 계산하는 스칼라량 지점이 아닌 유량 및 유속을 계산하는 벡터량의 평가점을 이용한다(Fig. 4). 사방댐을 통과하는 유출량을 계산하기 위해 아래의 식을 이용한다.
| $$Q_{sed_{up}}=C_{i-1}h_{i-1}u_{i-1}$$ | (13) |
| $$i_{dep}\propto\left(\tau_{\ast e}-\tau_{\ast y}\right)$$ | (14) |
| $$i_{dep}=K_{dep}\left(\tau_{\ast e}-\tau_{\ast y}\right)\frac{C_{i-1}h_{i-1}u_{i-1}}{C_\ast\mathit\triangle x}$$ | (15) |
| $$\tau_{\ast e}=\frac{\rho_Tghsin\theta}{\left(\sigma-\rho\right)gd_m}$$ | (16) |
| $$\tau_{\ast y}=\frac{Cghcos\theta\tan\phi}{gd_m}$$ | (17) |
여기서 e : restitution of sediment particles, kd : 0.0828, kf : 0.16
Takahashi et al. (2001a)는 불투과형 사방댐의 영향을 고려하는 방법을 제안했다. 사방댐으로부터 유출되는 유량을 산출할 때 댐의 천단수심() 의 위치는 Eq. 18에 의해 계산되며 유출유량과 흐름의 표면 기울기는 아래의 식으로 계산한다.
| $$\theta_e=\tan^{-1}\left\{\frac{\left[h_i+z_i-z_{dam}\right]}{\mathit\triangle x/2}\right\}$$ | (19) |
| $$\theta^{'_e}=\tan^{-1}\left\{\frac{\left[z_i-z_{dam}\right]}{\mathit\triangle x/2}\right\}$$ | (20) |
2.3.3 수치모형의 개요
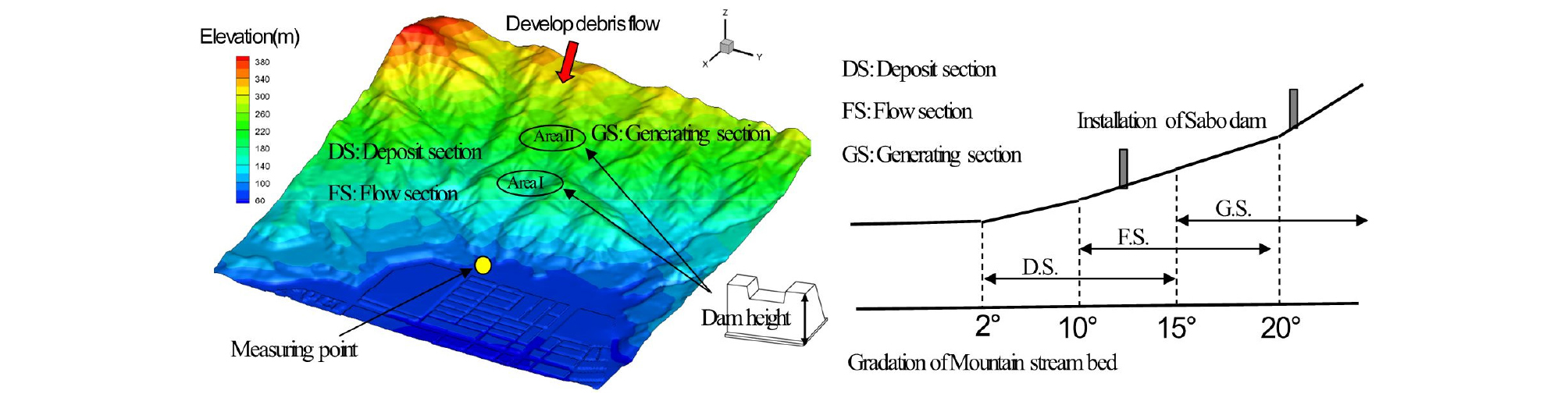
토석류 범람해석을 실시하기 위한 주요한 물성치를 Table 2에 나타내었다. 일반적인 토석류의 이동형태를 하상 경사에 따른 분류(Osanai et al., 2010)를 Fig. 5와 같이 구분하였다. 본 연구에서는 흐름이 발생하는 구간 특성에 따라 토석류의 흐름이 발생 및 퇴적되는 10∼20° (D.S and F.S) 및 토석류가 발달하는 20° (G.S) 이상의 지역에 불투과성 사방댐을 설치하여 설치장소에 따른 저감 특성을 파악하며 사방댐의 제원(높이)에 따라 에너지 저감효과에 대한 검토를 수행하였다. 각각의 실험조건에 대해 Table 3에 나타내었으며 검토대상지의 지형조건 및 토석류의 범람 특성을 파악하기 위해 선상지에 도달하는 지점을 Fig. 5에 나타내었다.
Table 2.
Parameters for numerical simulation
3. 수치모의 결과 및 분석
급경사지에서의 토석류 범람 해석을 통해 직접 피해지역에서의 범람 특성과 피해 저감 시설인 불투과성 사방댐을 이용한 영향평가를 하였다. 또한, 사방댐의 설치장소 및 사방댐의 제원에 따라 하류 지역으로 전파하는 토석류의 에너지 감소 효과에 대해 검토하였다. 본 연구에서 얻어진 주요한 결과는 다음과 같다.
3.1 모델의 검증
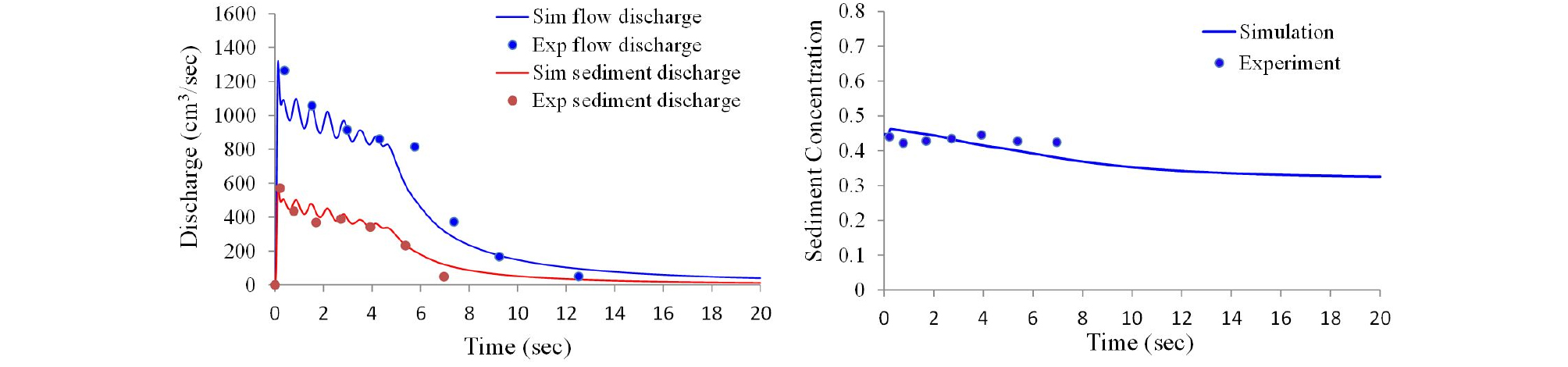
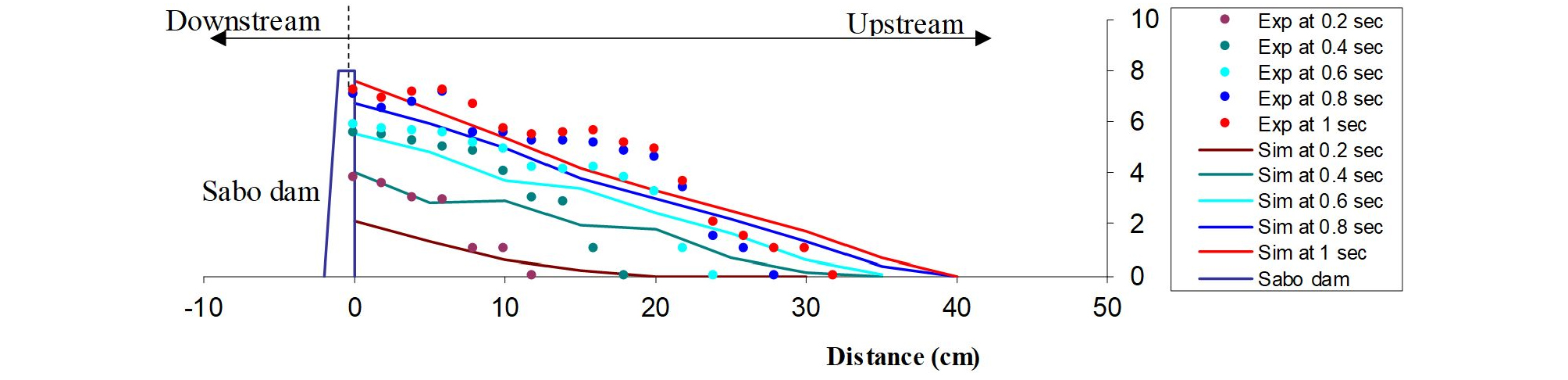
개발한 모델의 검증을 위해 Kim et al. (2013)의 수리모형실험 결과를 이용하여 모델의 검증을 실시하였다. 토석류의 총유출토사량, 토사 유출량 및 토사농도와의 결과를 Fig. 6에 나타내었으며 수리모형실험과 잘 일치하는 것으로 나타났다. 또한, 사방댐 설치에 따른 모델의 검증을 위해 Shrestha (2009)의 수리모형실험의 결과를 이용하여 모델의 검증결과의 비료를 Fig. 7에 나타내었으며 시간 경과에 따른 사방댐 전면부에서의 퇴적 양상을 잘 재현하고 있다. 위의 결과로부터 토석류의 흐름을 잘 재현하고 있는 것으로 판단된다.
3.2 급경사지에서의 토석류 범람
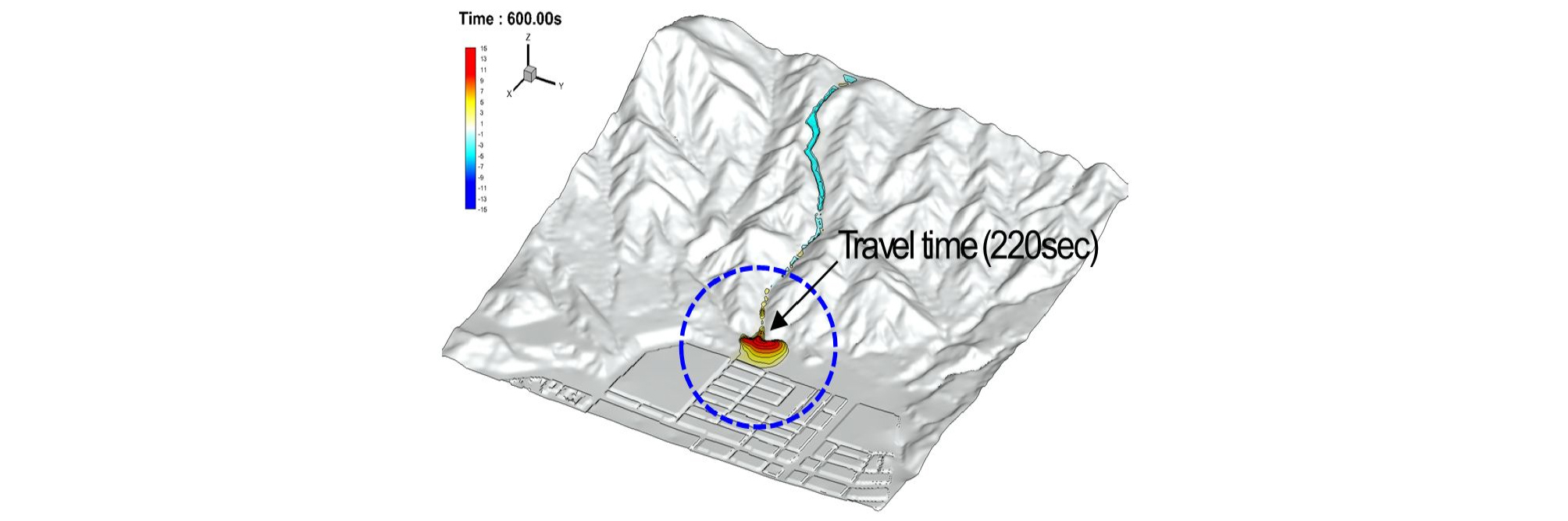
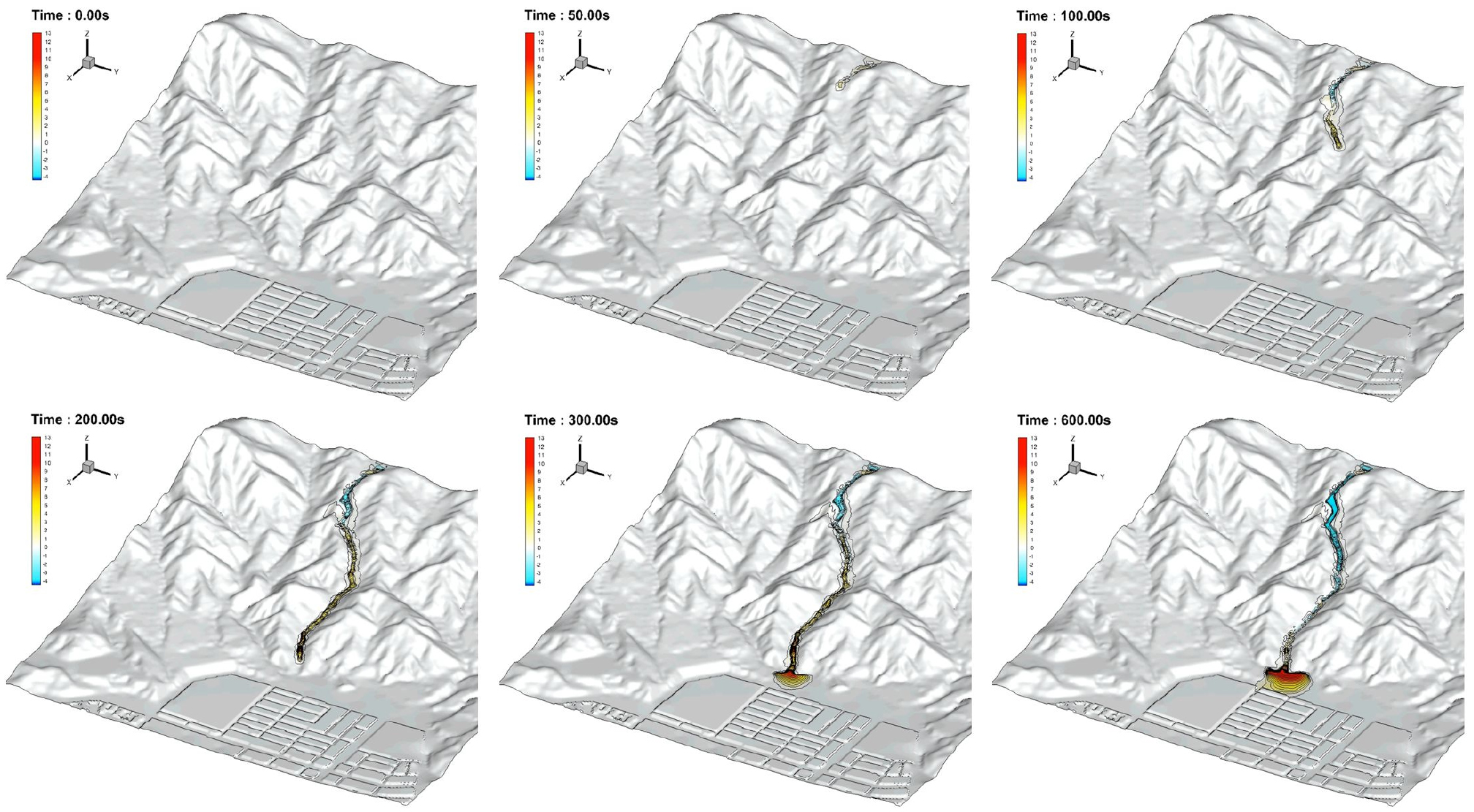
김해시 방재성능목표에 따른 발생 가능한 토사량에 의한 영향평가(Case A)를 실시하였다. 직접 피해지역인 Measuring point (선상지)에서 토석류의 도달시간은 토석류가 발달해 약 220s가 지나면 토석류가 유출되어 범람이 시작되는 것으로 나타났다(Fig. 8). 이 결과로부터 토석류의 전파속도는 매우 빠르며 대피경보가 발동되더라도 대피할 수 있는 시간적 여유가 없는 것으로 나타났다. 또한, 산지 상류부에서 토석류가 발달하여 범람지역에서 확산하는 시간적 경과에 따른 토석류의 범람 형태를 Fig. 9에 나타내었다. 토석류의 흐름이 하류 지역으로 전파되면서 주변의 지형적 특성에 따라 침식 및 퇴적이 반복적으로 발달하여 토석류가 하류 지역으로 유하하는 흐름 현상이 잘 재현되고 있다.
3.3 사방댐의 기능 평가
사방댐의 설치에 따른 토석류 에너지 저감효과를 평가하기 위해 사방댐의 높이를 4 m, 8 m의 조건으로 하상 경사 14.6° (D.S and F.S)의 지역(Area I)에 사방댐을 설치하였다. 사방댐의 설치는 하상 경사는 약 14.6°로 댐의 상류 지역에 유하하는 토사를 저장할 수 있는 장소를 채택하였다. 각각의 실험조건에 따른 직접 피해지역인 하류 지역에서의 영향평가를 도달시간 및 하류 지역에서의 정의한 x, y방향의 확산 정도로 사방댐 설치에 대한 영향평가를 정량적으로 실시하였다.
사방댐의 제원에 따른 하류지역으로 유출되는 토석류의 에너지 평가를 위해 선상지에서의 유출 토사의 도착시간을 조사하였다. 토사 유출은 사방댐의 높이 4 m (Case B)의 경우, 약 330 sec, 8 m (Case C)의 경우에는 400 sec에 발생하였고 토사 유출 이후 토사가 완전히 정지된 상태를 Fig. 10에 나타내었다. 이 결과로부터 사방댐의 높이가 증가함에 따라 약 20%의 저감율을 나타내었다.
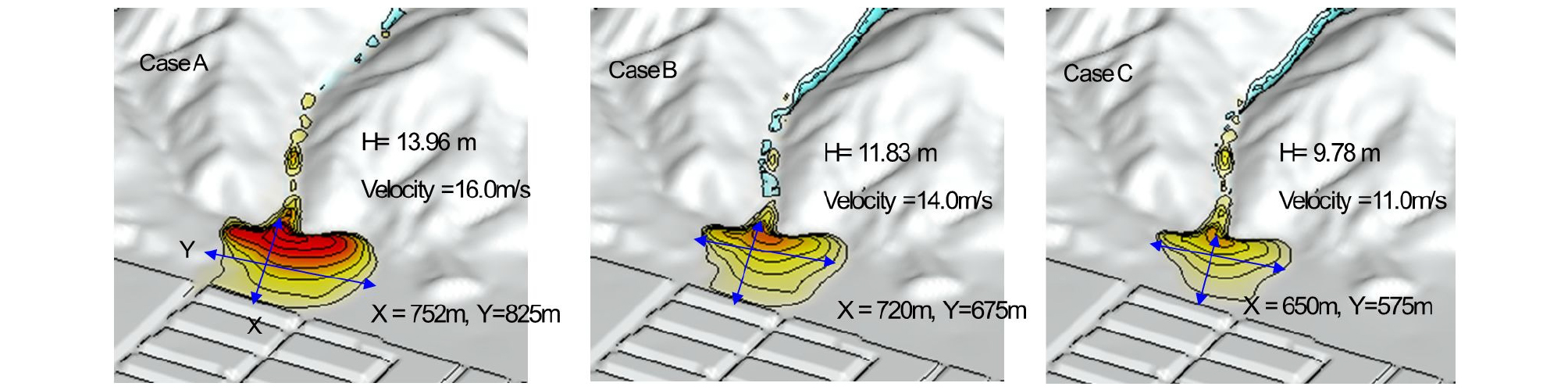
사방댐 설치에 따른 토석류가 하류 지역에서의 범람 형태를 비교한 결과를 Fig. 11에 나타내었다. 이 결과에서와 같이 사방댐(댐 높이 : h = 4.0 m)이 설치함에 따라 유하하는 토석류의 에너지를 감소시켜 하류 지역에서 범람이 축소되는 경향이 나타났으며, 사방댐이 없는 경우 하류 지역에서 최대 13.96 m (Case A)의 퇴적이 발생하였고 사방댐의 설치에 따라 11.83 m (dam height = 4.0 m) 및 9.78 m (dam height = 8.0 m)의 퇴적 높이가 발생하였다. 또한, 유출하는 토석류의 유속은 사방댐의 설치에 따라 각각 16% (Case B), 30% (Case C)의 저감되는 것으로 유체력이 감소하는 것으로 나타났다. 범람 형태는 사방댐의 설치와 댐이 높이가 증가함에 따라 하류 지역에서의 범람이 축소되는 경향으로 사방댐 설치에 따른 에너지 저감률을 Table 4에 나타내었다.
Table 4.
Downstream flooding patterns after the installation of the Sabo dam
3.4 사방댐 설치 위치에 따른 영향평가
사방댐의 설치장소를 토석류가 발달하는 지역(G.S)인 Area II(23.0°)에 설치하여 토석류의 저감효과를 검토하였다. 각각의 실험조건인 Case D 및 Case E에 따른 주요한 결과는 다음과 같다.
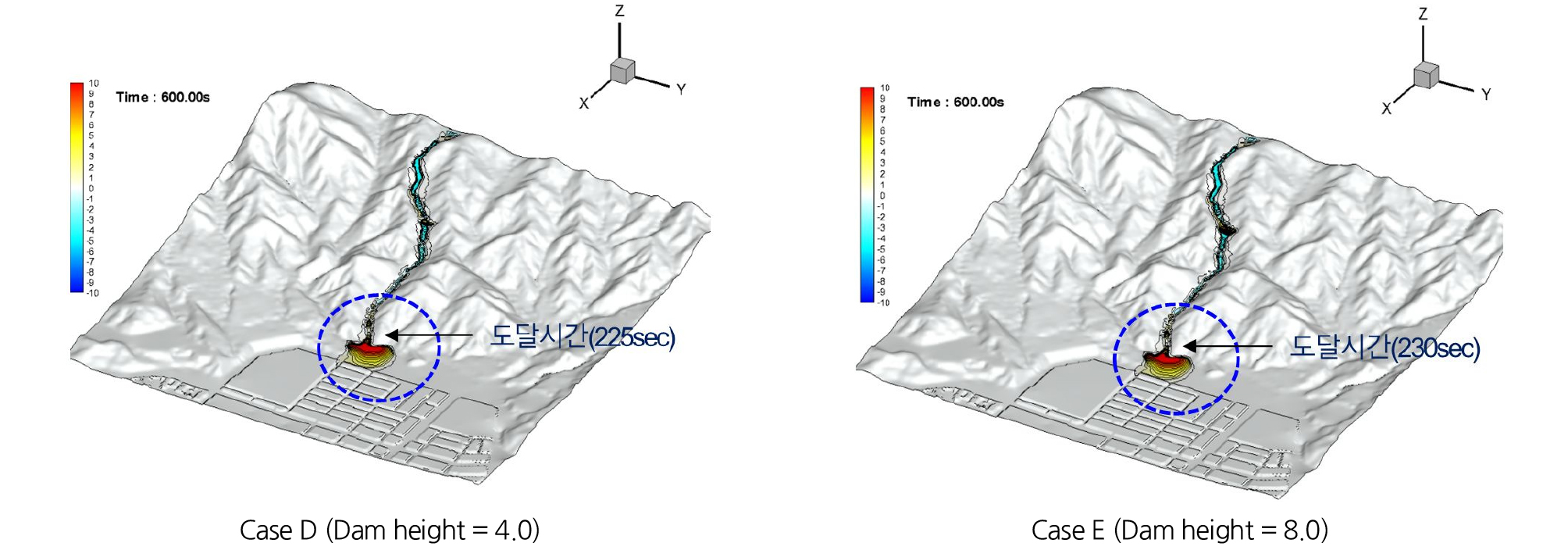
사방댐 설치에 따른 토석류가 하류 지역에 도달시간을 비교한 결과를 Fig. 12에 나타내었다. 이 결과와 같이 사방댐(댐 높이 : h = 4.0, 8.0 m)이 설치됨에 따라 유하하는 토석류의 지체시간은 댐 높이 4 m에 대해서는 약 5 sec, 8 m의 경우에는 약 10 sec 정도로 지체되는 것으로 나타났으며 선상지에서의 범람 형태도 사방댐의 없는 경우 Case A의 경우와 매우 유사한 범람 형태를 나타내고 있다. 이 결과로부터 사방댐의 설치장소가 토석류가 발달하는 지역(G.S)인 약 20° 이상의 하상 경사를 가진 지역에 사방댐을 설치할 경우는 토석류 에너지 저감효과는 미비한 것으로 나타났다.
4. 결 론
검토한 사방댐의 형태에 따른 저감효과를 평가하기 위해 실제 경상남도 김해시의 급경사지 지역으로 산정된 지역에 사방댐 설치하여 그에 따른 영향평가를 수행하였다. 본 연구의 주요한 결과는 다음과 같다.
검토대상 지역에서 발생 가능한 토사량을 산정하기 위해 부산 관측소의 58개년(1961년∼2018년) 강우 자료를 이용하며 빈도별 강우량을 산정하여 발생 가능 토사량을 산정하였다.
사방댐이 설치되지 않는 경우인 Case A를 기준으로 사방댐의 설치장소(하상 경사) 및 사방댐의 제원(댐 높이)에 따른 영향평가를 비교 분석하였다. 우선 사방댐이 없는 경우에는 하류 지역 즉 직접 범람 피해지역까지 토석류가 도달하는 시간은 약 220 sec가 소요되었으며 도달 속도는 16.0 m/sec로 조사되었다.
사방댐의 설치조건이 하상 경사가 14.6°와 사방댐의 높이 4 m (Case B), 8 m (Case C)의 경우에서는 사방댐이 설치됨에 따라 유하하는 토석류의 에너지가 감소하였고 범람지역에서의 확산 범위도 감소하는 경향이 나타났다. 하지만 하상 경사가 23.0°의 지역(G.S)에 사방댐이 설치된 경우인 Case D, E의 경우에서는 사방댐의 높이가 증가하였지만 하류 지역에 도달하는 토석류의 에너지 감소는 미비하며 범람 형태도 사방댐 설치 전인 Case A와 유사한 범람 형태를 나타내었다. 이 결과로부터 사방댐의 설치장소에 따라 유하하는 토석류의 에너지를 효과적으로 저감할 수 있으나 토석류가 발달하여 이동하는 구간에서의 사방댐 설치는 보다 정확한 지형조건을 이용하여 면밀한 검토가 필요한 것으로 판단된다.
본 연구에서는 급경사지에서의 토석류 에너지 저감을 위해 가장 일반적으로 사용되는 불투과성 사방댐에 대한 평가를 2차원 토석류 해석을 실시하였다. 향후 본 모델을 이용하여 더욱 다양한 사방구조물 형태의 저감 효과를 검토하고, 사방구조물의 설계조건인 외력 산정을 위한 충격력 검토와 토사 해저드맵 구축을 위한 연구를 진행할 것이다.