1. 서 론
2. 자료 및 방법론
2.1 대상자료
2.2 Bayesian logistic 회귀분석
3. 결 과
3.1 확률적 Inundation Mapping 및 평가
3.2 최적 모형의 선정
3.3 Population at Risk 산정
4. 결론 및 고찰
1. 서 론
도시지역은 지난 수십 년간 기후변화와 하천 인근 지역의 무분별한 개발로 인해 홍수와 침수피해가 가중되고 있으며, 사회경제적으로 다양한 문제를 발생시킨다. 도시화로 인한 불투수 포장 면적 증가로 자연적인 물순환 왜곡으로 빗물의 토양 침투량 감소와 지표면 유출량 증가가 도시홍수의 근본적 원인으로 지적되고 있다(Pouraghniaei, 2002; White and Greer, 2006). 홍수가 발생하기 쉬운 지역에 대해서는 재해 대비를 위한 장기적 계획이 고려되어야 하며 각별한 주의가 요구된다. 우리나라의 홍수방어대책은 댐, 제방 같은 홍수방어시설을 구축하는 구조물적 대책과 홍수 예·경보, 재해정보지도 등 비구조물적 대책이 있다. 구조물적 방재대책은 사업 추진에 많은 시간과 비용으로 인한 한계가 있으므로 적절한 구조물적 방재대책을 위해서는 먼저 비구조물적 방재대책을 통한 사전계획 및 모의가 필요하다(Lee et al., 2014). 이러한 측면에서 도시지역의 다양한 지표면 공간특성을 고려한 침수 발생 가능 지역 예측의 필요성은 더욱 높다고 할 수 있다(Song et al., 2014).
현재 국내·외에서는 도시지역의 침수문제를 개선하기 위해 다양한 연구들이 진행되고 있다. 홍수위험 연구에는 여러 수문모형이 사용되고 있다. 즉, 물리적 모형(physical model), 개념적 모형(conceptual model), 자료 기반 모형(data-driven model) 등이 있다(Devia et al., 2015). 자료 기반 모형 중 통계적 모형(statistical model)은 종속변수와 이를 설명하는 독립변수의 회귀분석과 상관관계 분석으로 가중치를 구하여 그 영향을 파악하고 입력과 출력의 함수적 관계의 도출이 가능하다(Lee et al., 2012). 다중통계분석 중 다중 로지스틱 회귀분석(multiple logistic regression, MLR) 방법은 홍수 발생과 여러 개의 지형적 홍수영향요인 간의 관계를 수학적으로 설명하여(Giovannettone et al., 2018; Park et al., 2017; Pradhan and Lee, 2010; Tehrany et al., 2014) 기존의 결정론적으로 표현되었던 홍수위험지도를 확률적 값으로 제시하는 것이 가능하다.
본 연구는 다음과 같은 과정으로 진행하였다. GIS 프로그램을 이용하여 고도, 경사 유출곡선지수, 하천까지 거리 등의 홍수영향요인과 100년 빈도 홍수위험지도의 공간정보를 GIS 정보로부터 구축하여 공간해상도 150 m×150 m의 Vector Grid로 변환하였다. 공간정보는 각 Vector Grid 필드 내에 수치화되어 저장되며 이를 행렬자료 형태로 추출하여 공학적 수치해석 및 프로그래밍을 수행하는 소프트웨어인 Matlab을 활용하여 전반적인 계산 과정을 구현하였다. 먼저, Logistic 회귀분석을 수행하여 여러 지형적 홍수영향요인(독립변수, X)과 100년 빈도 홍수위험지도(종속변수, Y)의 관계를 설명하는 회귀식을 구하여 모든 격자에 대해 침수확률을 구하였다. 추정 결과는 다시 GIS 프로그램을 통해 지도에 표출하여 100년 빈도 강우에 대한 확률론적 침수지도를 제시하였다.
하천관리를 위한 의사결정을 위해서는 침수 예상지역 내에서도 어느 지역의 홍수위험이 더 큰지 파악하는 것이 필요하므로 본 연구에서는 위험도 개념을 통해 상대적 우선순위를 도출하는 방법을 제시하는 데에 목적을 두었다. 수리·수문모형(수치모형)을 통해 제작된 홍수위험지도에 홍수와 관련된 지형학적 요소를 고려하여 통계적 기법을 개발하였으며, 제내지 일부지역으로 국한되어 작성된 빈도별 홍수위험지도를 활용하여 주변지역까지 확률적인 홍수위험지도로 확장하여 평가할 수 있는 절차를 개발하였다. 이처럼 홍수위험이 확률로 표현이 되면 추후 취약성 분석을 통해 산정된 피해액과 홍수위험확률을 곱하여 위험도를 구할 수 있고 그에 따른 보완, 방재대책 필요 여부 결정에 도움을 줄 수 있다.
본 논문의 구성은 다음과 같다. 1장에서는 논문의 목적 및 기존 연구사례에 대해서 서술하였다. 2장에서는 대상자료에 대해서 요약하여 제시하였으며, 본 연구에서 사용된 방법론에 대해서 수록하였다. 3장에서는 해석결과 및 토의를 제시하였으며, 마지막으로 4장에서 연구 결론 및 향후 연구 방향을 제시하였다.
2. 자료 및 방법론
2.1 대상자료
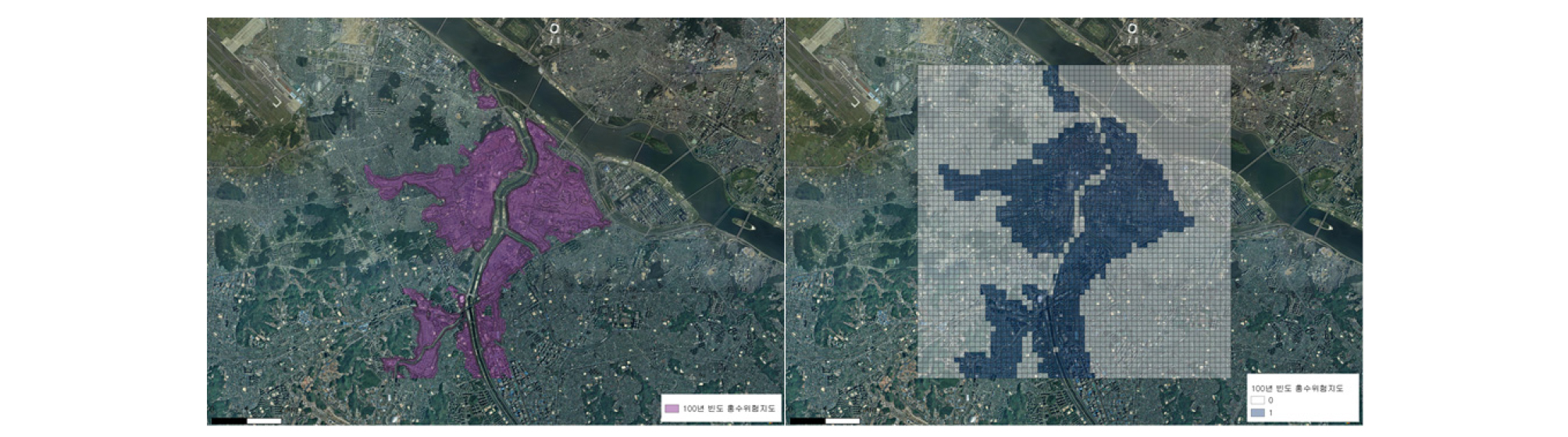
본 연구에서 통계적 모형으로 침수지역을 모의하기 위해서는 침수실적 자료가 필요하지만, 실제 100년 빈도 이상의 큰 강우에 의한 대규모 침수 발생 실적이 부족하여 100년 빈도 홍수위험지도를 침수실적자료로 가정하여 연구를 진행하였다. 따라서 연구를 위한 대상 지역으로는 홍수위험지도가 존재하는 국가하천 중 ○○천을 선정하였다. ○○천 유역내 토지이용은 1980년대 이후 도시화가 급속도로 진행되어 불투수층이 50% 이상을 차지하며(Rehabilitation of the Hydrologic Cycle in the Anyancheon Watershed Research Center, 2007) 이러한 도시화는 궁극적으로 홍수에 취약하게 만들어 피해를 가중시키는 요인으로 작용한다. 홍수에 취약하다고 판단되는 ○○천 하류의 홍수 위험지역을 포함하기 위한 9 km×9 km 범위를 선정하고 침수여부 및 지형적 홍수영향요인 값들이 격자 형태로 공간적으로 잘 표현될 수 있도록 적절 해상도의 격자로 나누었다. 본 연구에서 홍수 위험지역이라 함은 100년 빈도 홍수위험지도에서 침수지역으로 지정된 범위를 의미한다. 국가홍수위험지도는 100년 빈도 강우에 대하여 제방 월류, 파제에 의한 외수범람을 가정으로 홍수범람해석을 통해 제작되었다(Choi et al., 2014; MOIS, 2017; MOLIT, 2008; MOLIT et al., 2008). Logistic 회귀분석에서 종속변수 Y값은 이항 범주형(binary categorical) 자료이어야 하며 침수 발생 여부를 입력하기 위하여 3600개 격자에서 침수가 발생한 격자는 1, 침수가 발생하지 않은 격자는 0으로 변환하여 모형에 입력되도록 하였다(Fig. 1).
침수지역을 설명하기 위한 홍수영향요인으로는 지형적, 수문학적 영향을 고려하여 고도(elevation), 경사(slope), 유출곡선지수(curve number, CN), 하천까지 거리(distance to river)로 결정하였다. 이 자료들은 수치표고모형(digital elevation model, DEM), 토지피복도, 정밀토양도, 하천망도 자료들을 지리정보시스템(GIS) 프로그램을 사용하여 분석하여 구하였다. 지형의 표고 값이 수치로 저장된 격자방식 DEM으로부터 고도와 경사 vector 격자를 구축하였다. 강우시에 빗물이 지하로 침투되지 않고 유출되는 특성을 고려하기 위한 표면 유출 특성은 NCRS (Natural Resources Conservation Service)에서 개발된 유출곡선지수를 활용하였다. 유출곡선지수를 산정하기 위해 중분류 토지피복도와 세부정밀토양도를 이용하였다. 토지피복도, 토양도의 토지피복유형과 토양유형을 수문학적 토양군으로 재분류 후 이를 지정한 지역의 boundary 격자를 중첩시켜 각 면적마다 토지피복과 토양유형을 indexing하고 각 격자 면적마다 평균 유출곡선지수를 구하였다. 선행토양함수조건(AMC)은 홍수 시 충분히 많은 강우 후에 토양이 포화되어 침투율이 작고 유출률이 큰 상태를 가정하여 AMC-Ⅲ조건을 적용하였다. 외수 범람에 의한 침수는 하천으로부터 떨어진 거리에 의한 영향이 크므로 이를 구하기 위해 국가하천 및 지방하천의 하천망도를 이용하였다. 각 격자마다 가장 가까운 하천 수계까지의 최단 거리를 산정하였다.
홍수위험지도와 지형적 홍수영향요인들은 Logistic 회귀모형에 입력되기 위하여 Fig. 2와 같이 9 km×9 km 범위의 연구 대상 지역에 대해 3600개의 150 m×150 m 격자로 변환되었다. 이렇게 산정된 각 홍수영향요인은 값의 범위의 차이가 서로 크기 때문에 Logistic 회귀모형에 침수 예상지역을 모델링 할 독립변수로 입력되려면 값의 범위를 정규화하는 것이 매개변수 도출 면에서 더 좋은 결과를 얻을 수 있고 각 홍수영향요인의 영향을 파악하는 데 용이하다.
2.2 Bayesian logistic 회귀분석
다중선형회귀 분석은 종속변수 Y와 여러 독립변수 X간의 관계를 선형으로 가정하고 이를 가장 잘 표현할 수 있는 회귀계수를 자료로부터 추정하는 모형이다. 이 회귀계수들은 모델의 예측값과 실제값의 차이, 즉 오차 제곱의 합(error sum of squares)을 최소로 하는 값들이다. 일반적인 선형회귀에서는 종속변수 Y값은 연속형(continuous)이며 그 자체로 의미를 지니는 변수이지만 Y가 범주형(categorical) 변수일 때는 이 선형회귀를 그대로 적용할 수 없으므로 Logistic 회귀분석이 제안되었다. Logistic 회귀분석에서는 -∞ ~ +∞의 범위를 갖는 연속형 독립변수에 따른 종속변수의 관계를 0과 1 사이의 확률로 제시하며 각 독립변수가 종속변수에 미치는 영향의 정도를 정량적으로 분석할 수 있다. Logistic 회귀분석은 홍수영향요인과 빈도별 홍수위험지도로부터 관심 지역 전체에 대해 침수위험도를 확률로 제시하는 공식을 개발하기 위해 사용되었다.
Logistic 회귀분석에서 확률 p는 독립변수 X에 의존하며 종속변수 Y는 베르누이 분포를 따르는 베르누이 확률변수(Bernoulli random variable)라고 가정한다. 베르누이 확률변수는 베르누이 시행(Bernoulli trial)의 결과에 따라 0(실패) 또는 1(성공)의 두 가지 결과만을 가지는 이산형 확률변수를 말한다.
| $$p(Y\vert X,p)=Bernoulli(Y\vert p(X))$$ | (1) |
베르누이 시행에서 1이 나올 확률(p(y = 1|x))과 0이 나올 확률(1-p(y = 1|x))의 비를 Odds 함수라고 하며 이를 로그변환 하면 Eq. (2)의 좌변과 같은 Logit 함수가 된다. Eq. (2)의 우변은 설명변수가 n개인 다중선형회귀의 일반식과 같다.
| $$\ln\;\left(\frac p{1-p}\right)=Y=\beta_0+\beta_1X_1+\beta_2X_2+\dots+\beta_nX_n$$ | (2) |
위 식은 홍수위험지도의 침수 여부를 홍수영향요인을 사용하여 설명하기 위한 회귀모형이다. 격자로 변환된 홍수위험지도 상의 모든 셀은 침수 여부에 따라 0(침수되지 않음)과 1(침수)로 변환된 후 종속변수 Y로 입력된다. 동일 위치에 해당하는 여러 홍수영향요인의 값들은 독립변수 X에 입력되어 회귀식의 회귀계수인 을 추정하며 이 회귀계수는 독립변수들(홍수영향요인)이 홍수 발생에 미치는 영향의 정도를 나타내는 가중치가 된다.
모든 홍수영향요인 X에 대해 매개변수가 결정되면 Eq. (2)의 역함수인 Logistic 함수를 이용하여 계산한 p는 0과 1 사이 값을 가지는 확률로 계산된다.
| $$p=\frac1{1+e^{-Y}}=\frac1{1+e^{-(\beta_0+\beta_1X_1+\dots+\beta_nX_n)}}$$ | (3) |
Logistic 회귀분석에서 각 계수()들은 불확실성을 가지는 확률분포로 추정하기 위해 베이지안 추론을 이용하였다. 베이지안 추론을 적용하는 데 있어서 자료의 우도함수와 각 매개변수의 사전분포를 가정하고 베이즈 정리를 이용하여 매개변수의 사후분포를 유도하는 과정이 필요하다. 우도함수는 성공확률이 주어질 때, i번째 대상의 우도가 이항분포를 따름을 의미하며 그 식은 다음과 같다.
| $$Likelihood_i=p(x_i)\;^{y_i}(1-p(x_i))\;^{(1-y_i)}$$ | (4) |
p(xi)는 독립변수 벡터 xi를 가진 i번째 대상의 확률을, yi = 1 or 0는 i번째 대상의 사건 유무를 의미한다. 독립변수들이 서로 독립이라고 가정하면 n개 자료의 우도함수는 다음과 같다.
매개변수의 사전분포는 경우에 따라 매개변수의 가능값에 대해 알면 정보적(informative) 사전분포, 매개변수의 범위를 가늠할 수 없거나 자료 자체에서 추론하는 특성을 보고 싶으면 무정보적(non-informative) 사전분포를 선택할 수 있다. 본 연구에서는 3600개의 자료를 이용하여 상대적으로 적은 개수의 매개변수를 추정한다는 측면에서 자료의 우도가 주도적인 역할을 할 수 있도록 무정보적 사전분포로 가정하였다.
| $$\beta_j\;\sim\;Normal(\mu_j,\;\sigma_j^2)$$ | (6) |
무정보적 조건에서 가장 일반적으로 쓰이는 는 0이고, 은 충분히 큰 범위를 갖기 위해 10이나 100이 선정되므로 본 연구에서는 을 택하였다. 사후분포는 모든 매개변수에 대한 사전분포와 전체 우도함수의 곱을 통해 유도된다.
위 식의 앞부분은 매개변수에 대한 사전분포로 정규분포 확률밀도함수이다. 위 식에서 모든 매개변수에 대해 복잡한 다중 적분을 직접적으로 수행하는 것이 불가능하므로 베이지안 분석 방법인 깁스 표본법(Gibbs sampling)으로 각 매개변수의 사후분포를 추정하였다.
3. 결 과
3.1 확률적 Inundation Mapping 및 평가
먼저 100년 빈도 홍수위험지도에 대하여 Logistic 회귀분석을 수행하였다. 아래 Logistic 회귀모형에 입력된 변수들은 모두 3600개 격자에서 열 vector로 변환되었으며, 모형을 학습시키기 위해 종속변수 Y에는 100년 빈도 홍수위험지도, 독립변수 X1 … X4에는 고도, 경사, 유출곡선지수, 하천까지 거리의 변수들이 입력되었다.
| $$\ln\;\left(\frac p{1-p}\right)=Y=\beta_0+\beta_{ELEV}X_1+\beta_{SLOP}X_2+\beta_{CN}X_3+\beta_{DIST}X_4$$ | (8) |
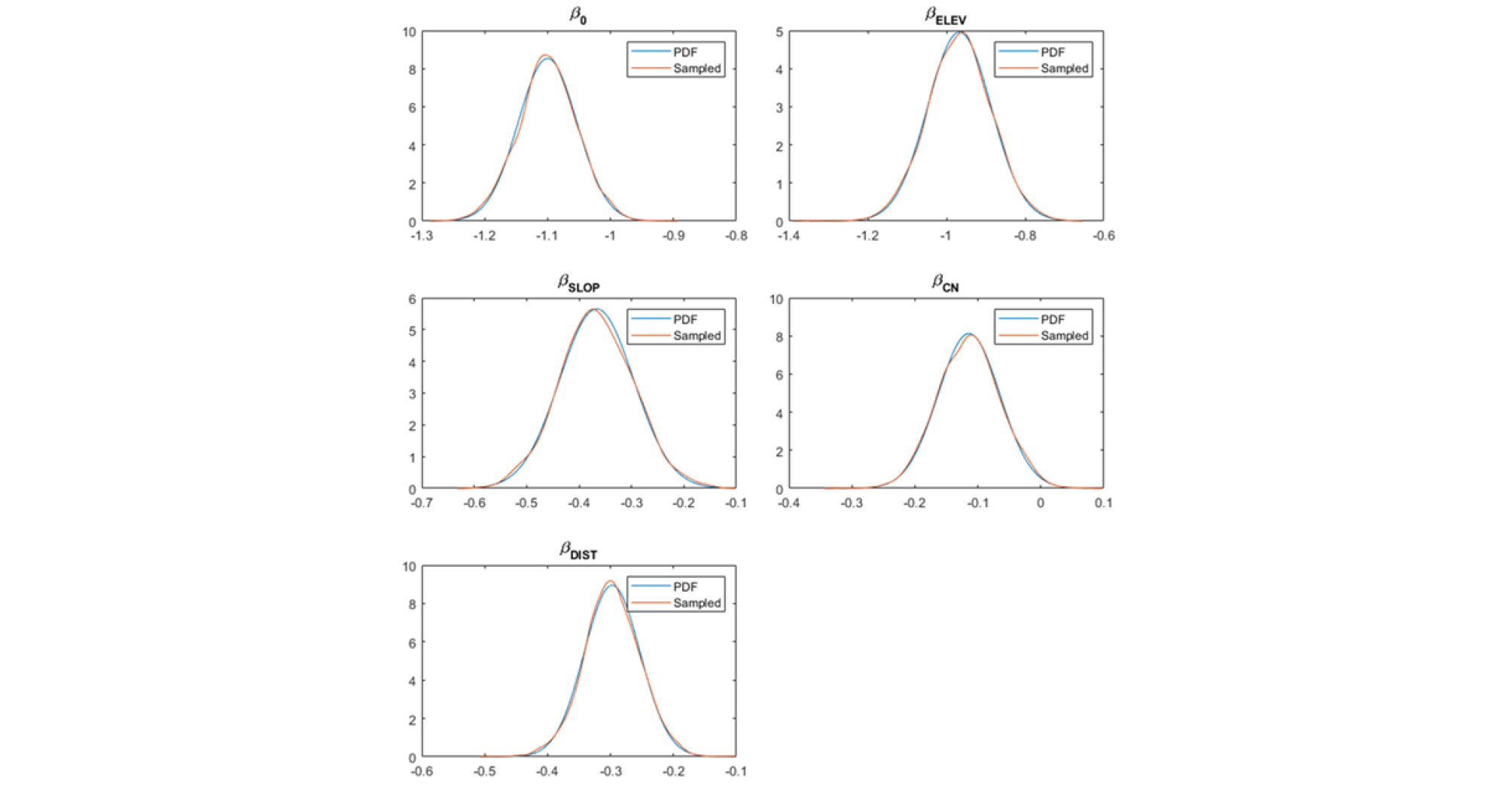
위 모형을 통해 추정된 회귀계수는 다음과 같으며 는 절편(intercept)이고 나머지 계수들은 홍수영향요인이 침수에 미치는 영향을 의미한다. 각 홍수영향요인이나 침수에 미치는 영향은 의 순서로 나타났다. 회귀계수 를 추정하는 과정에서는 Bayesian Logistic 회귀분석을 적용하였다. 베이지안 추론 깁스 표본법으로 추정된 매개변수는 확률분포로 주어지며 불확실성을 내포한다(Fig. 3). 추정된 회귀계수의 통계치는 Table 1과 같다.
Table 1. Statistics of the logistic regression coefficients of the probabilistic inundation map
| Regression Coefficient | Mean | Standard Deviation |
| -1.1001 | 0.0468 | |
| -0.9670 | 0.0805 | |
| -0.3665 | 0.0706 | |
| -0.1142 | 0.0491 | |
| -0.2974 | 0.0446 |
도출된 회귀계수 와 지역의 지형적 특성인 독립변수 X1 …X4를 다음 식에 입력하여 역으로 계산하면 p는 홍수위험지도 전체 면적에 대해 각 격자에서 홍수가 발생할 확률이 된다. 모든 격자에 대하여 계산하면 최종적으로 확률적 침수지도가 만들어진다.
| $$p=\frac1{1+e^{-Y}}=\frac1{1+e^{-(\beta_0+\beta_{ELEV}X_1+\beta_{SLOP}X_2+\beta_{CN}X_3+\beta_{DIST}X_4)}}$$ | (9) |
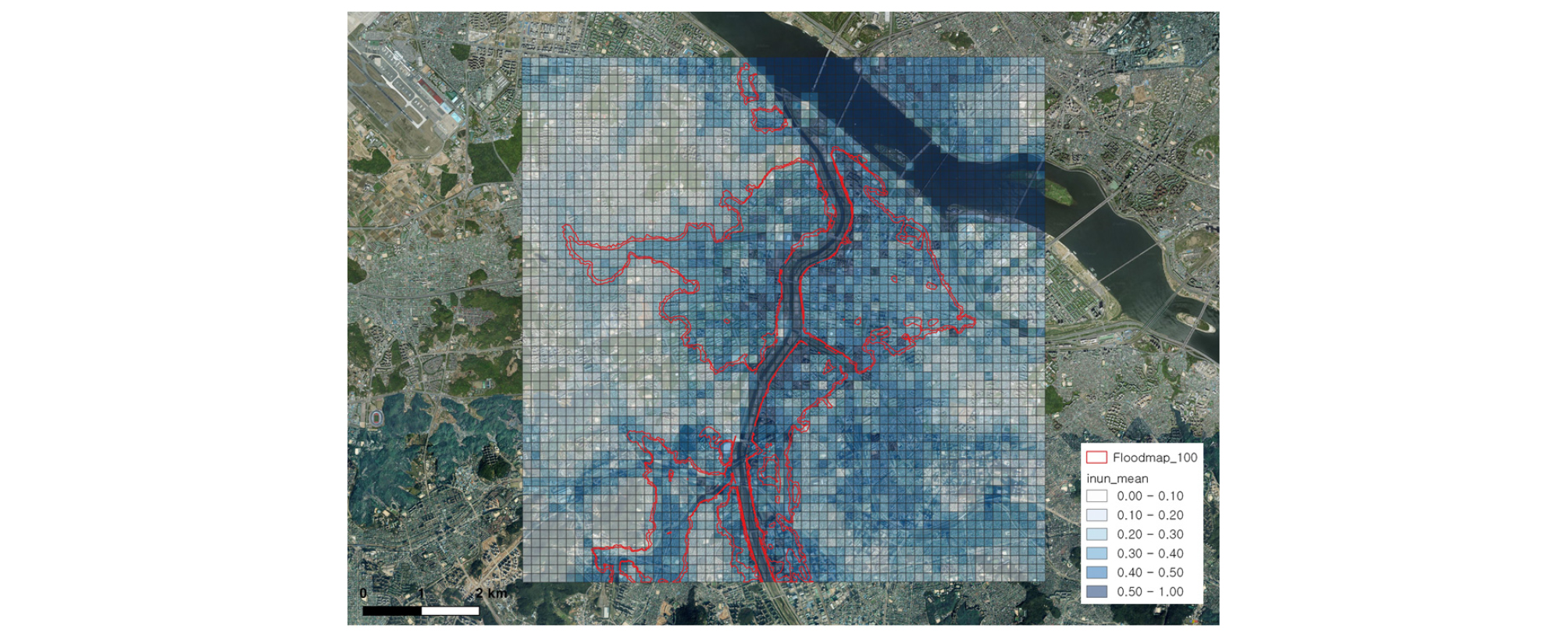
Fig. 4에는 Logistic 회귀모형을 통한 100년 빈도 확률적 침수지도를 도시하였다. 홍수위험지도와 비교하였을 때 침수지역으로 분류된 지역이 상대적으로 침수확률이 크게 추정되는 것을 확인할 수 있으며, 전반적으로 실제 홍수위험지도 침수지역 형태와 대략적으로 일치하는 것을 확인할 수 있었다. 단, 우측하단 지역 격자들에서 붉은 선으로 표시된 홍수위험지도 내 지역에 상응하는 침수확률이 나타나는 것을 볼 수 있는데, 이는 홍수영향요인과 침수여부의 관계로서 추정된 회귀계수와 해당 지역 고유의 지형적 특성이 반응한 결과이다. 특히, 침수에 크게 반응하는 고도 및 하천까지 거리 변수들이 해당 지역에서 홍수위험지도 내 침수확률이 높은 지역의 변수들과 유사한 값을 보였다. 즉, 이 지역은 홍수위험지도가 구축되어있지 않지만 지형적 요인으로 보았을 때 충분히 침수위험을 갖는 지역이라는 것을 설명한다.
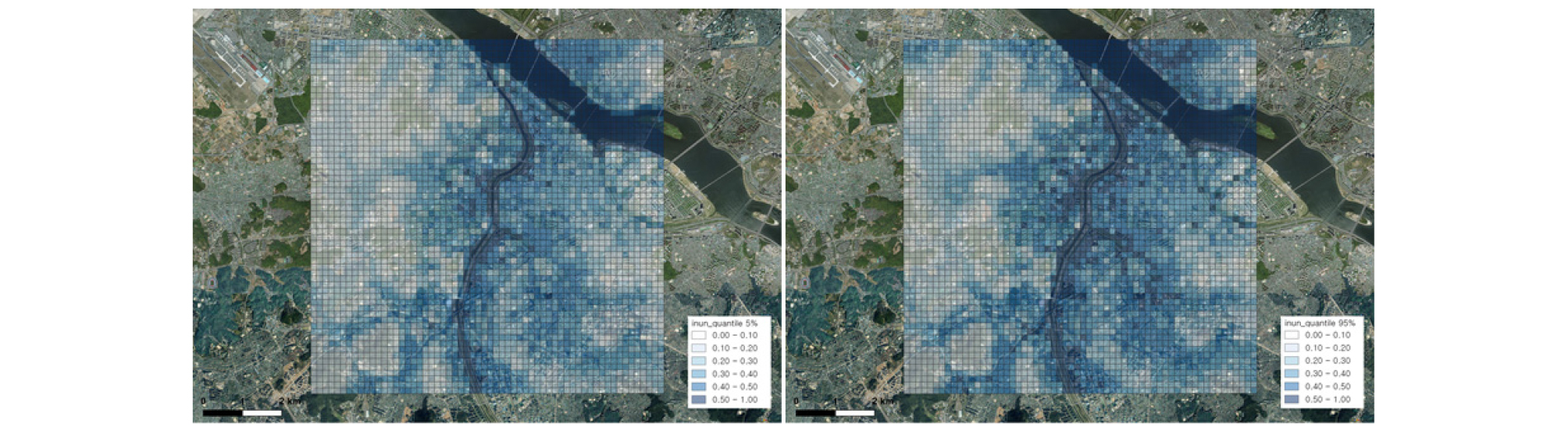
침수확률은 Bayesian 추론으로 추정된 회귀계수의 불확실성을 포함하여 계산되었기 때문에 각각의 격자 내에서 불확실성을 표현하는 확률분포 형태의 값을 가진다. Fig. 4는 추정된 침수확률의 50% 분위(quantile) 값이며, Fig. 5는 침수확률 지도의 5%와 95% 분위 값으로 불확실성 구간을 나타내며 오차 발생 가능성 구간이다. 불확실성 범위는 전 지역에 걸쳐 평균값에 거의 근접해있으므로 이는 모형의 불확실성이 적어 신뢰 가능한 수준인 것으로 확인되었다.
3.2 최적 모형의 선정
최적 모형은 설명변수의 종속변수에 대한 설명력과 설명변수의 경제성이라는 모형에 대한 penalty의 역할을 하는 두 개념을 기준으로 선택하게 된다. 이러한 관점에서, Spiegelhalter et al. (2002)는 DIC (deviance information criterion)를 제시하였다. DIC는 계층적 모형에 대한 AIC (Akaike information criterion)와 BIC (Bayesian information criterion)기준을 일반화한 형태이다. 특히, 모형의 사후분포가 MCMC (Markov chain Monte Carlo)방법을 통해 얻어지는 Bayesian 모형에서 적합한 모형을 선택함에 있어 특히 유용하게 사용된다. DIC는 편차(deviance) 의 평균값 와 필요 설명변수의 개수를 의미하는 를 결합한 것이다.
| $$DIC=p_D+\overline D$$ | (10) |
DIC는 AIC와 BIC처럼 작은 값을 가질수록 더 적절한 모형을 의미하는데, 적절한 모수의 개수를 의미하는 pD가 커지면 모형의 적합도를 의미하는 는 작아진다. 따라서 매개변수의 증가에 따른 우도의 개선정도를 종합적으로 평가할 수 있다. DIC의 장점은 MCMC 방법으로 생성된 표본으로부터 쉽게 계산될 수 있다는 점이다. 본 연구에서는 독립변수인 홍수영향요인의 모든 조합의 경우의 수에 대해 최적을 모형을 선정하기 위해 DIC 값을 검토하였고 그중 최소 DIC 값을 가지는 모형을 가장 적합한 모형으로 선택하였다.
Table 2의 독립변수 간 상관관계에서 ELEV와 SLOP의 상관계수가 상대적으로 크게 나타나는 것으로 확인되며 두 변수를 모두 입력하는 것이 모형의 적합도를 더 향상시키는 것으로 확인된다. 일반적으로 회귀분석에서 상관성이 크거나 거의 같은 자료들을 독립변수로 고려하면 공분산성으로 인해 모형의 적합도가 향상되지 않는다. 독립변수의 조합에 따른 모형의 회귀계수 변화는 Table 3에 기입하였으며 각 모형의 DIC 값을 구하여 Table 4에서 비교하였다. 최종적으로 독립변수 4개를 모두 입력하였을 때 DIC 값이 상당한 크기로 감소한 것으로 보아 각각의 독립변수(홍수영향요인)들 자체에서 종속변수(침수여부)에 대한 설명력을 갖는다는 것을 확인할 수 있었으며 본 연구에서는 4개 독립변수를 모두 사용한 모형을 채택하였다.
Table 2. Correlation between independent variables
| Independent variables | ELEV | SLOP | CN | DIST |
| ELEV | 1 | - | - | - |
| SLOP | 0.6444 | 1 | - | - |
| CN | -0.5495 | -0.5427 | 1 | - |
| DIST | 0.2377 | 0.1809 | -0.1851 | 1 |
Table 3. Comparison of regression coefficients for the combination of independent variables
Table 4. Comparison of DIC for the combination of independent variables
3.3 Population at Risk 산정
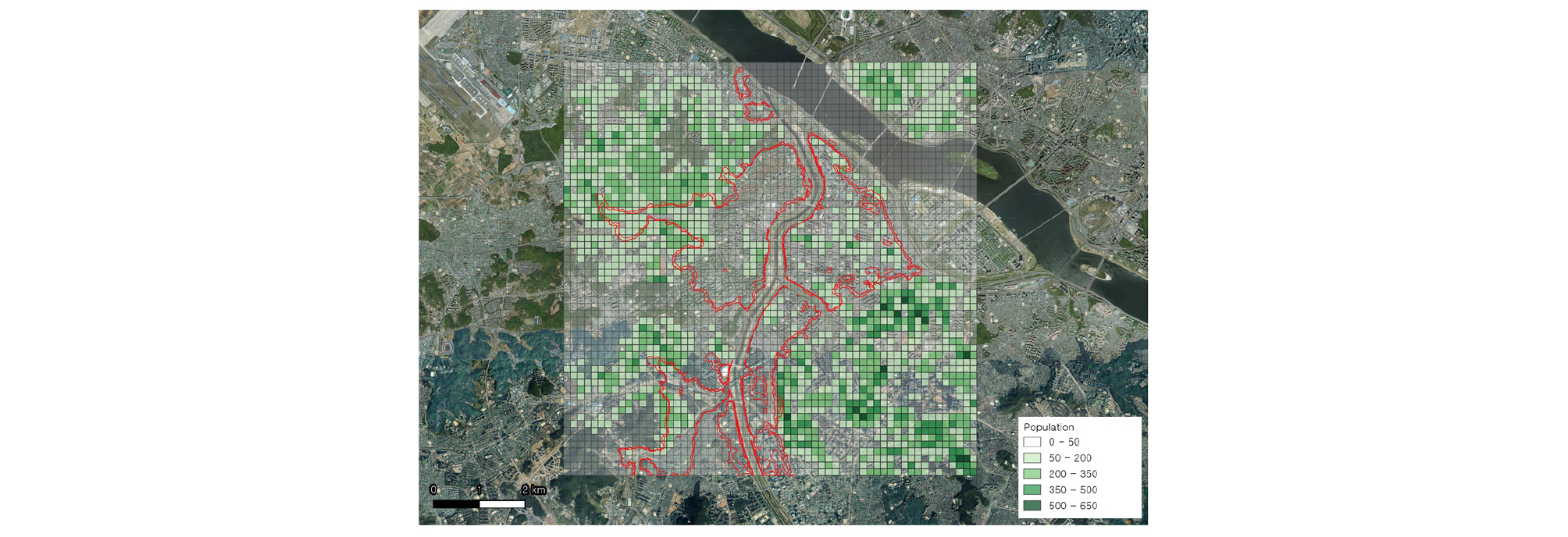
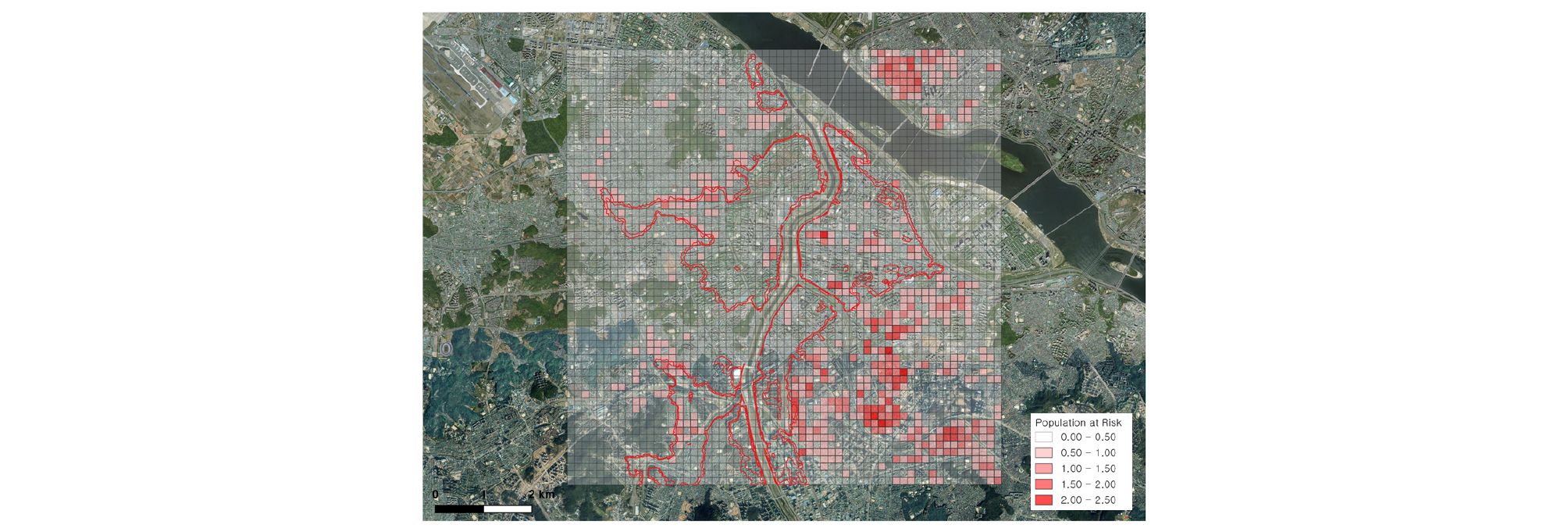
위험도는 침수 발생확률에 거주인구를 곱한 값인 위험노출인구(population at risk, PAR)로 정의될 수 있다. 이를 위하여 Fig. 6과 같이 건물종별 연면적별 주택 거주인구를 파악하기 위해 침수확률지도와 같이 3600개 격자별로 구축하였다. 최종적으로 거주인구 지도와 침수확률지도의 중첩으로, 100년 빈도 강우 발생 시 외수 범람에 의한 침수위험에 노출된 인구를 공간적으로 산정하였다(Fig. 7). 이는 강우 발생 시의 격자별 침수확률과 인구가 곱해진 값으로 다음과 같은 식에 의해 계산되었다.
| $$PAR\;=\;p_{rainfall}\times p_{inundation}\times Population$$ | (11) |
여기에서 prainfall은 100년 빈도 강우 발생확률인 1/100이며, 침수확률 pinundation은 Fig. 4의 침수확률, 인구 Population은 Fig. 6의 거주인구이다. 결과적으로, 어떤 지역(격자)에서 비교적 침수확률이 낮더라도 거주인구가 많으면 PAR은 증가하게 되고, 따라서 위험도가 더 크다는 의미를 갖는다. 이처럼 침수위험이 공간적으로 확률로서 표현이 되면 인구 및 주요기반시설 등의 밀집도에 따라 가중치를 두어 공간적으로 위험도 평가가 가능하다.
4. 결론 및 고찰
본 연구는 결정론적(deterministic) 방법으로 진행되던 홍수위험도 평가의 단점을 보완하기 위한 방법으로 제안되었으며, 홍수와 관련된 다양한 위험요소들을 고려하여 확률론적(probabilistic) 방법에 근거한 해석 방법을 제안하였다. 기존의 수치모형을 활용한 결정론적 해석결과인 홍수위험지도를 바탕으로 지형정보와 확률·통계학적 방법을 연계한 해석 방법을 개발하였다.
본 연구의 기반이 되는 Logistic 회귀모형은 홍수에 의한 침수와 홍수영향요인 간 관계를 설명하기 위해 고려되었으며, 확률정보와 위험지역내 거주인구와 연계된 위험도의 형태의 홍수위험지도 제시가 가능하였다. 또한, 홍수위험지도와 비교하였을 때 실제 홍수위험지도 침수지역에서 상대적으로 큰 침수확률로 모의 되는 것을 확인하였다. 침수확률의 공간적 분포를 통해 침수 예상지역 내에서도 홍수위험이 상대적으로 큰 지역을 효과적으로 파악할 수 있었으며, 피해액, 인명피해, 복구시간 등과 관련된 피해양상을 위험도 관점에서 제시함으로써 피해저감을 위한 투자우선순위 평가 및 홍수위험지구 간의 실질적인 위험도 평가가 가능하다고 판단된다.
사실 홍수 발생 여부를 나타내는 종속변수 Y의 입력자료에는 실제 침수흔적도가 필요하다. 다양한 홍수사상으로 인한 침수지도를 활용하여 분석해야 하지만 아직 우리나라에서 구축된 홍수실적 자료는 부족하다. 특히 100년 이상의 홍수사상에 대한 침수흔적도는 존재하지 않아 이를 활용하기에는 현실적으로 어려움이 있다. 이를 대체하기 위해 100년 빈도 홍수위험지도를 사용하였다. 홍수위험지도는 수치모형을 통해 제방 월류 또는 파제를 가정한 가상의 침수범위이다. 홍수위험지도는 여러 가정요소를 포함하고 있지만 모델링과정에서 다양한 수리수문학적 요소가 고려되었다는 점과 이를 불확실성이 포함된 확률론적 위험지도로 확장하는 것도 홍수위험도 관리측면에서 의미가 있으며 활용성도 클 것으로 판단된다.
Logistic 회귀모형을 통한 침수지역 모의 과정에서 수리수문학적 요소인 강우, 유량, 유속 등은 모형에서 직접적으로 고려되지 않았지만, 홍수시나리오와 수치모형을 통해 제작된 홍수위험지도를 입력자료로 사용하였기 때문에 그 영향이 간접적으로 반영되었다고 볼 수 있다. 또한, 지형자료를 통계적 근거로 사용했기 때문에 홍수위험지도와 비교했을 때 유사할 뿐 아니라 홍수위험지도에서는 나타내지 못한 지역의 피해액 또는 인명피해등과 연계한 홍수위험도를 제시하는 것이 가능하였다. 다만, 홍수위험지도에서 지정한 침수범위는 파제로 인한 외수 범람에 의한 극단적인 침수 상황을 모의한 것으로, 100년 빈도 강우가 발생했을 때의 제방이 파괴될 확률은 고려하지 못했다는 한계점과 장기간에 걸친 여러 빈도에 대한 침수범위 자료확보의 어려움이 존재한다. 홍수위험지도와 지형정보를 사용하여 모형을 학습시켰기 때문에 빈도별 침수정보와 지형정보만 제공된다면 지역에 관계없이 홍수위험도 추정이 가능하지만 침수흔적도의 자료확보가 난해하므로 수리학적 모형을 통해 내수침수 및 외수범람 등의 시뮬레이션을 통한 다양한 조건에서의 신뢰성 있는 침수범위 자료의 확보가 필요하다. 본 연구에서 한 개의 대상지역에 시험적으로 적용한 결과를 보여주었으며 지역별로 지형적 특성이 모두 다르므로 향후 다양한 지형적, 환경적 특성을 가진 넓은 구역에 대한 분석으로 어느 지역에도 적용 가능한 일반적 모형이 개발된다면 확률적 홍수위험지도의 도출이 가능할 것으로 생각된다.
기존의 결정론적 방법에서는 홍수위험지도를 침수심과 침수면적으로 나타내므로 홍수위험지도에서 지정한 침수면적 외의 지역에 대한 정보는 제공하지 못하였으나 본 연구에서 사용한 방법으로 홍수위험지도를 설정한 구역 전체에 대해 확률적 표현이 가능하였다. 즉, 제공되고 있는 침수 예상지역으로 지정되지 않은 지역이더라도 침수될 가능성은 내포하고 있음을 지형, 토지이용 등 홍수영향요인이라는 합리적 근거로서 평가가 가능하였다. 유역에 한정되지 않은 분석이 가능하고, 자료 구축의 용이성과 방법론의 간편성, 그리고 결과의 정확성 등을 고려하였을 때 해석결과의 활용성이 높을 것으로 판단된다.