1. 서 론
2. 연구 방법
2.1 입자 군집 최적화 기법
2.2 빗물이용시설의 모의 운영 모형
2.3 최적화 알고리즘의 구성
2.4 대상 지역
3. 연구 내용
3.1 최적화 기법을 이용한 빗물이용시설의 저류 용량 결정 방법
3.2 최적화 기법을 이용한 빗물이용시설의 저류 용량 결정 방법의 안정성 및 효율성 검증
3.3 개발 프로그램의 정확성 검증
3.4 특정한 보장률에 대한 분석 결과
4. 결 론
1. 서 론
대체 수자원으로서 빗물의 이용은 기존의 용수 공급을 보조할 수 있을 뿐만 아니라 빗물이용을 통한 관리비 및 수도세 저감, 교육적 효과, 쾌적한 주거공간의 창출 등을 기대할 수 있다(Choi et al., 2011b). 이와 관련하여 우리나라에서는 물의 재이용 촉진과 물 자원의 효율적 활용 등을 목적으로 ‘물의 재이용 촉진 및 지원에 관한 법률’ 제8조 제1항과 ‘물의 재이용 촉진 및 지원에 관한 법률 시행령’ 제10조 및 ‘물의 재이용 촉진 및 지원에 관한 법률 시행규칙’ 제4조에 따라 특정한 규모 이상의 공동주택, 학교, 골프장 등의 시설에 대하여 빗물이용시설을 설치하도록 규정하고 있다(Kang et al., 2015). 또한, 서울, 대전, 대구, 광주 등의 지방자치단체에서는 빗물이용시설 확대를 위해 공동 및 단독주택, 근린생활시설, 유치원, 어린이집 등 다양한 시설에 대하여 빗물저금통 설치 지원 사업을 시행하고 있다.
빗물이용시설의 설치를 법・제도적으로 의무화하고, 사회적으로 지원함에 따라 국내의 빗물이용시설의 설치 사례는 해마다 증가하고 있다. 실제로, Lee and Han (2019)에 의하면, 2010년의 빗물이용시설은 전국에 337개였던 것이, 2012년에 670개, 2013년 968개, 2014년 1,369개로 매년 40% 이상의 증가율을 보였다. 이러한 추세는 빗물이용시설의 계획과 설계에 대한 수요가 매년 증가함을 의미한다. 하지만 빗물이용시설의 저류 용량은 강수량, 지붕 면적, 용수 수요량 등의 지역적 영향을 크게 받으므로 표준화하여 계획되기 어렵다(Campisano and Modica, 2012). 따라서 빗물이용시설을 효과적이고, 효율적으로 계획할 수 있는 도구가 요구된다.
빗물이용시설 설치에 있어서 가장 중요하게 고려되어야 할 부분은 빗물이용시설의 저류 용량 산정에 관한 것이다(Park and Kwak, 2007). 그리고 이러한 빗물이용시설의 저류 용량 산정에는 복잡성과 정교함의 정도에 따라 다양한 방법들이 활용될 수 있다(Islam et al., 2014). 대표적인 방법들로서, 빠른 분석이 가능하여 사전 설계 단계에서 사용될 수 있는 도식적(graphical) 또는 질량 곡선(mass curve) 방법(Handia et al., 2003; Quadros, 2010; Santos and Pinto, 2013; Matos et al., 2013)과 유입량 및 잠재적 방류량 등과 저류 용량의 관계를 결정하는 통계적 방법(Lee et al., 2000; Guo and Baetz, 2007; Su et al., 2009; Raimondi and Becciu 2014)이 있다. 가장 많은 연구자들이 수행한 물 수지(water balance) 기반의 모의(simulation) 방법에 관한 연구들에서는 다양한 기법들이 활용되었다(Fewkes and Butler, 2000; Panigrahi, 2001; Villarreal and Dixon, 2005; Ghisi and Ferreira, 2007; Ghisi et al., 2007; Imteaz et al., 2011; Campisano and Modica, 2012; Santos and Pinto, 2013; Islam et al., 2014). 한편, 국내에서는 Han et al. (2004)이 빗물 이용률, 상수도 대체율, 사이클 수, 빗물 사용일수와 같은 빗물 운전인자의 선택도표를 활용한 빗물이용시설의 용량 결정에 관한 연구를 수행하였다. Choi et al. (2011a)은 신뢰도 평가 모형인 SARET (storage and reliability estimation tool)을 이용하여 빗물이용시설의 신뢰도 평가에 활용하였다. 또한, Kang et al. (2015)은 상용 프로그램인 SWMM의 LID (low impact development) 기능을 이용하여 강우-유출 분석과 빗물이용시설의 설계에 관한 동시 해석 방법과 이에 따른 홍수 저감 및 비점오염 저감의 분석 사례를 제시하였다.
상기의 연구들은 공통적으로 빗물이용시설의 적정 규모를 산정하기 위해 모의 방법 또는 통계적인 방법에 의한 반복적인 계산을 포함하고 있다. 실제로 빗물이용시설의 용량을 계획하는 실무에서는 다양한 저류 용량에 대하여 공급 보장률, 우수 이용률 등을 분석하기 위해 반복적으로 모의 운영을 수행하는 시행착오법(trial and error method)이 사용된다. 이러한 시행착오법은 많은 양의 자료에 대한 반복 계산을 요구하므로 분석에 많은 시간이 소요되고, 계산 상의 오류가 발생될 수도 있다.
본 연구에서는 최적화 기법을 통해 목표 공급량을 만족하는 최소의 저류 용량을 결정할 수 있는 빗물이용시설의 저류 용량 결정 프로그램을 개발하였다. 해당 프로그램의 개발 언어는 Python이고, 최적화 기법에는 입자 군집 최적화(particle swarm optimization; PSO) 알고리즘이 사용되었다. 본 연구에서는 개발된 프로그램을 인천 청라지구에 설치된 빗물이용시설의 설계자료에 적용하여 분석의 적절성을 평가하였다.
2. 연구 방법
2.1 입자 군집 최적화 기법
새 무리의 이동에 관한 사회적 행동 양식을 기반으로 한 입자 군집 최적화 알고리즘은 각 객체 간의 위치 및 최적해 정보를 공유하면서 전역 최적해(global optimum)를 찾아가는 휴리스틱(heuristic) 기법에 해당된다(Eberhart and Kennedy, 1995). 입자 군집 최적화 알고리즘은 군집을 기반으로 최적화를 수행한다는 점에서 대표적인 진화론적 탐색 기법 중 하나인 유전 알고리즘(genetic algorithm; GA)과 공통점이 있다. 하지만 유전 알고리즘이 교차, 돌연변이 연산자를 이용하여 각 객체가 가지고 있는 위치 정보를 교환하면서 전역해를 탐색하는 반면, 입자 군집 최적화 알고리즘은 이웃 객체들 중 최적해로 판단되는 객체의 위치 정보를 기반으로 기존 해에서 다른 해로 이동하면서 전역해를 탐색한다(Han, 2016).
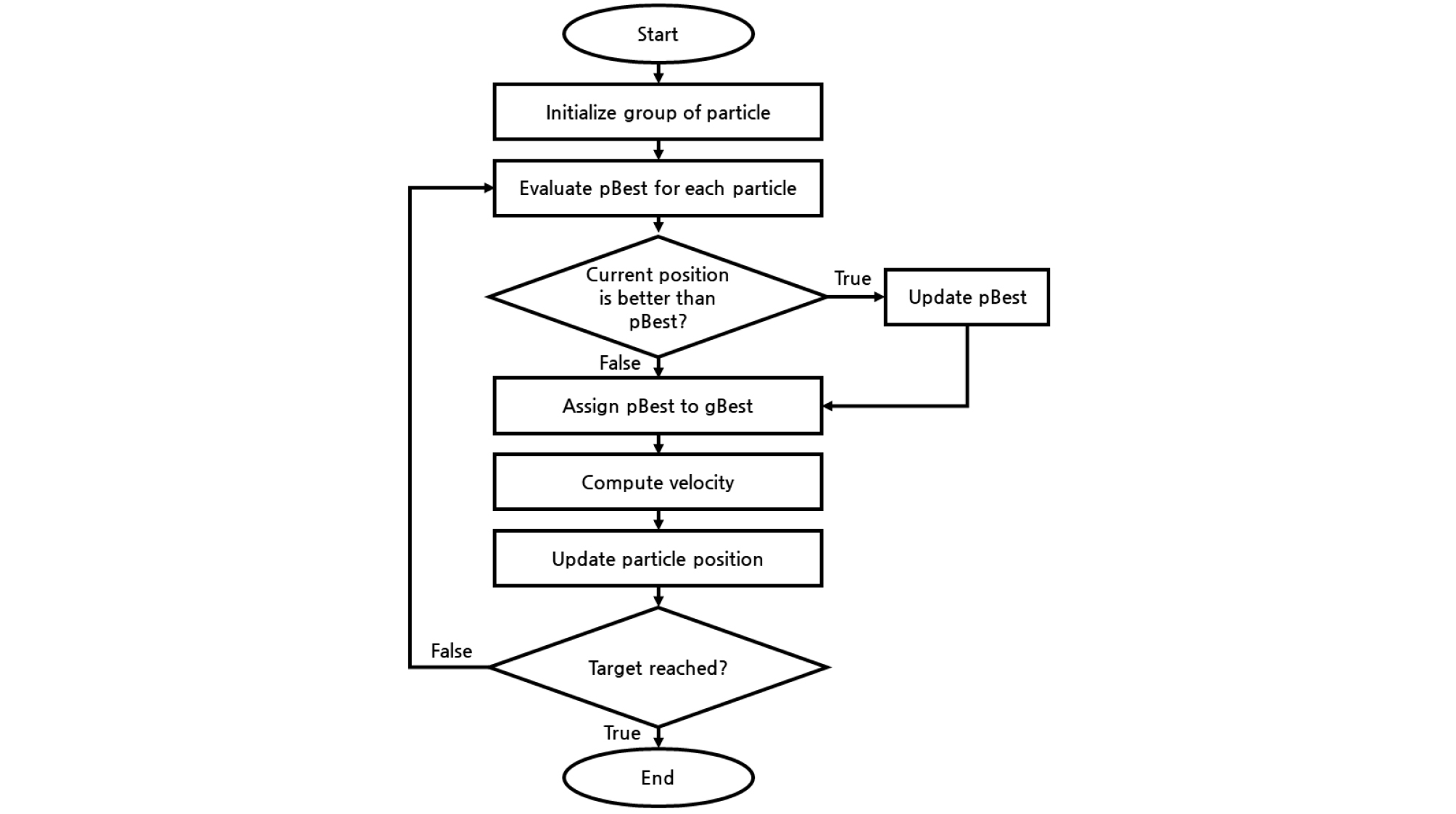
입자 군집 최적화 알고리즘은 각 군집 내 입자의 위치와 속도를 결정하는 4개의 단계를 통해 전역해를 탐색한다. 첫 번째, 각각의 군집 내 입자들에 대한 현재의 위치 정보를 분석한다. 즉, 현재 상태에 대하여 각각의 군집 내에서 최적의 위치를 가지는 입자를 pBest로 설정하여 현재의 위치가 이전 위치보다 좋으면 입자 위치가 갱신되고, 그렇지 않으면 유지된다. 두 번째, 각각의 군집 내 pBest 값을 비교하여 전체 군집에 대한 최적의 위치인 gBest를 평가한다. 세 번째, pBest와 gBest의 정보를 이용하여 속도를 갱신한다. 새로운 속도에 관한 계산식은 Eq. (1)과 같다.
| $$v_{i,t+1}=v_{i,t}\;+\;\alpha\varepsilon_1\left[pBest_{i,t}-x_{i,t}\right]\;+\;\beta\varepsilon_2\left[gBest_t-x_{i,t}\right]$$ | (1) |
여기서, i는 입자의 번호이고, t는 반복 계산의 횟수이다. 과 는 0에서 1 사이의 난수(random variable)이고, 와 는 상수이다. 네 번째, Eq. (2)를 이용하여 입자의 위치를 갱신한다.
| $$x_{i,t+1}\;=\;x_{i,t}\;+\;v_{i,t+1}$$ | (2) |
상기에서 기술된 네 가지의 단계는 최적해 탐색의 수렴 기준을 만족시킬 때까지 반복된다. Fig. 1은 입자 군집 최적화 알고리즘의 전역해 탐색 과정을 흐름도로 나타낸 것이다(Le et al., 2019).
2.2 빗물이용시설의 모의 운영 모형
본 연구에서는 빗물이용시설의 저류 용량 결정을 위해 목표 공급량과 보장률(reliability)의 개념(Eq. (5))을 사용한다. 즉, 본 연구의 목적은 목표한 보장률을 공급할 수 있는 빗물이용시설의 최소 규모(저류 용량)를 결정하는 것이다. 보장률은 장기간의 모의 운영에 의해 계산될 수 있으므로 빗물이용시설에 대한 모의 운영 모형이 필요하다.
본 연구에서는 빗물이용시설의 모의 운영 모형 구성을 위해 저수지 질량 보존식(reservoir mass balance equation)을 이용하였다. 그리고 공급량(yield)과 방류량(release)의 결정은 가용수량, 저류 용량, 목표 공급량 등을 고려하여 결정하였다. Table 1은 빗물이용시설의 모의 운영 모형에 사용된 수식들을 나타낸 표이다. Table 1에서 기호의 하첨자로 사용된 t는 모의 운영의 시간 간격을 나타내는데, 금회 연구에서는 일(日) 단위로 구성하였다. St, It, Yt, Rt는 각각 t 기간에 대한 빗물이용시설의 저류량(storage), 유입량(inflow), 공급량(yield), 방류량(release)이다. Tt는 기간 t의 목표 공급량(target draft)이고, C는 빗물이용시설의 저류 용량(capacity)이다.
Table 1.
Equations of simulation model for rainwater harvesting
| Classification | Simulation model | Remark | |
| Condition | Equation | ||
| Mass balance equation | - | ||
| Yield determination | |||
| Release determination | |||
2.3 최적화 알고리즘의 구성
목표 보장률에 대한 최소의 저류 용량을 결정하기 위한 최적화 기법으로 입자 군집 최적화 알고리즘을 이용하였다. 입자 군집 최적화 알고리즘은 다양한 언어(language)로 구성되어 있는데, 본 연구에서는 오픈 소스(open source)로 제공되고 있는 Python의 pyswarm을 이용하였다. 참고로 pyswarm은 입자 군집 최적화 알고리즘에 제약조건식을 고려할 수 있어 다양한 최적화 문제에 적용될 수 있는 장점이 있다.
목표 보장률에 대한 최소의 저류 용량을 결정하기 위해 구성한 최적화 기법의 목적함수는 빗물이용시설의 저류 용량을 최소화하는 것으로서 Eq. (3)과 같다. 제약조건은 설정된 목표 보장률을 만족시킬 수 있도록 탐색된 저류 용량에 의해 계산된 보장률이 목표 보장률 이상이 되도록 Eq. (4)와 같이 설정하였다. Eq. (5)는 탐색된 저류 용량에 의한 보장률을 산정하기 위한 수식으로서, 전체 기간 중 목표한 용수 공급이 수행된 비율을 나타낸다(KICT, 2004).
| $$\mathrm{Minimize}\;\;\;\;\;\;\;\;C$$ | (3) |
| $$R_{Sim}\;-\;R_{Tar}\;\geq\;0$$ | (4) |
| $$R_{Sim}\;=\;1-\frac{{\displaystyle\sum_{t=1}^N}L_t}N$$ | (5) |
여기서, RSim은 모의된 보장률이고, RTar은 목표 보장률이다. Lt는 기간 t에서 저류량이 ‘0’일 경우 ‘1’, 아니면 ‘0’의 논리변수(logical variable)이며, N은 총 모의 기간이다.
2.4 대상 지역
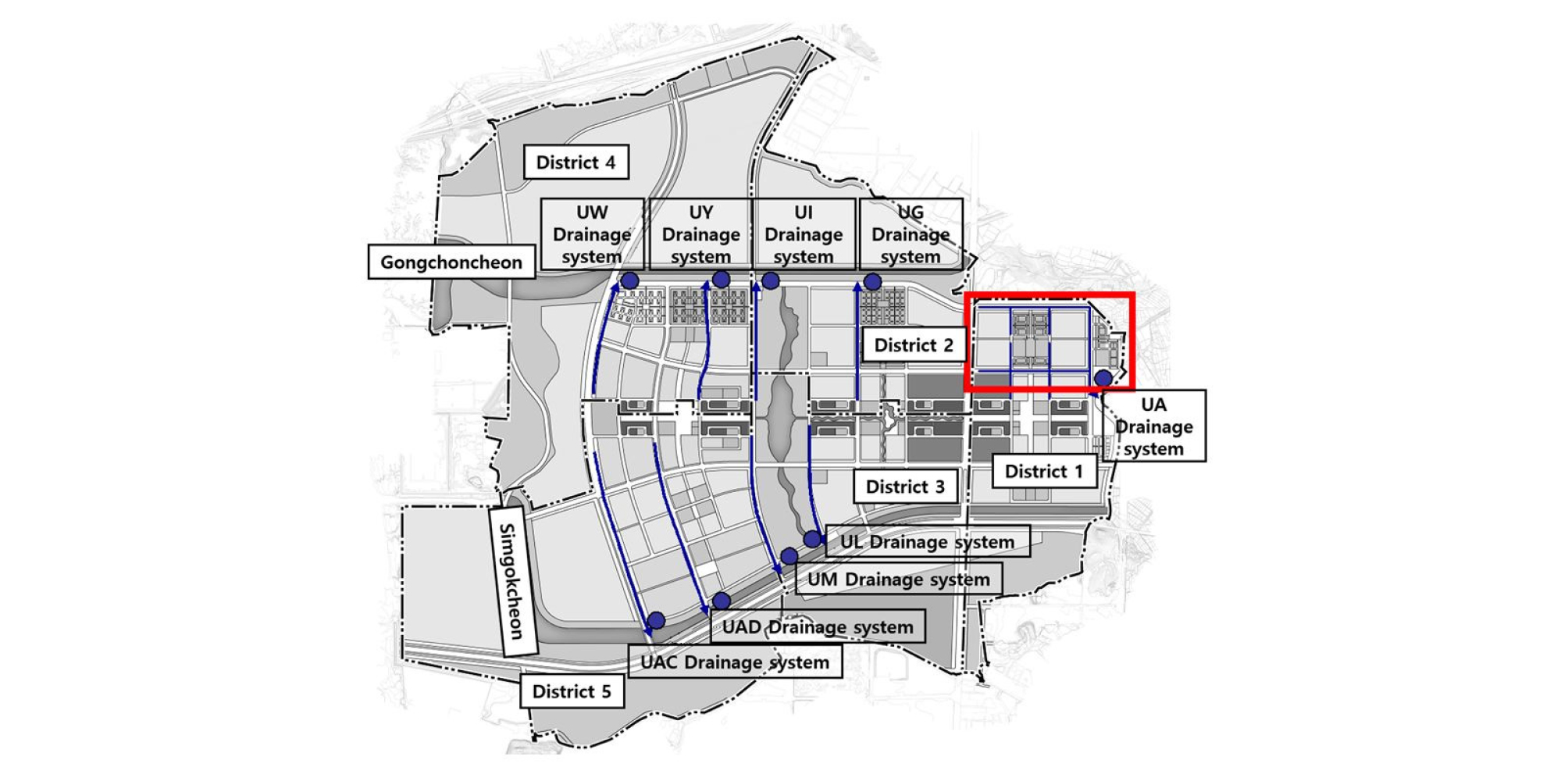
개발된 물이용시설의 저류 용량 결정 프로그램의 적절성을 검토하고자 기존 설계자료와 비교 검토하였다. 빗물이용시설에 대한 기존 설계 사례로서 한국토지공사(KLC)에서 2007년에 계획한 인천 청라지구의 일부 지역을 대상으로 하였다. 인천 청라지구는 물순환 시스템 시범도시로 지정되어 빗물이용시설 등을 포함한 다양한 물순환 시설이 도입된 지역이다(KLC, 2007).
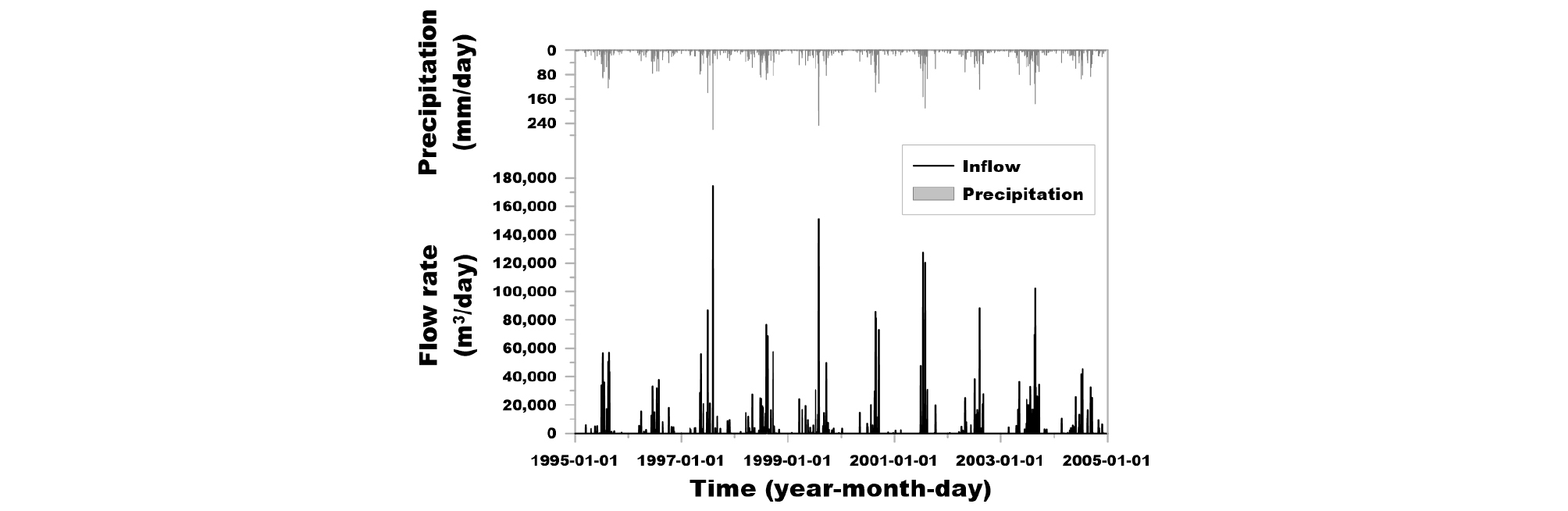
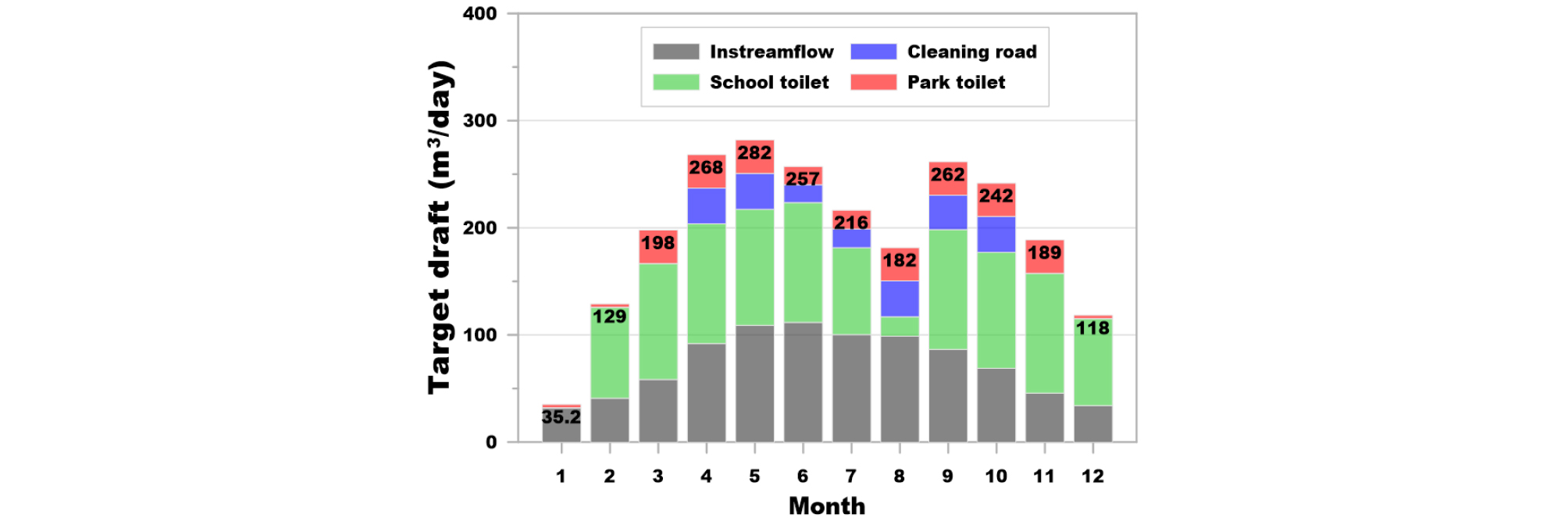
KLC (2007)에서는 인천기상대의 과거 10년(1995 ~ 2004년)간 기상관측 자료를 이용하여 인천 청라지구의 빗물이용시설에 대한 설치 위치와 용량 결정에 관하여 분석하였다. 기존 설계 자료와 최적화 기법으로 도출된 결과를 비교 검토하기 위한 대상 지역은 인천 청라지구의 1공구에 계획된 빗물이용시설이다(Fig. 2). KLC (2007)에 기술되어 있는 인천 청라지구 1공구에 위치한 빗물이용시설의 집수 면적은 73.92 ha이다. Fig. 3은 1995년부터 2004년까지 인천기상대의 일 단위 강우량 시계열과 인천 청라지구 1공구에 계획된 빗물이용시설의 유입량을 나타내는데, 이는 빗물이용시설 설계 당시에 SWMM5를 이용하여 유역 유출 모의된 결과이다. Fig. 4는 해당 빗물이용시설을 이용한 목표 공급량으로서 빗물 사용의 목적은 호소수 유지, 학교 및 공원의 화장실 세정, 도로 노면 청소이다. 빗물 사용의 목적별 목표 공급량은 KLC (2007)에서 인천 청라지구 1공구에 대하여 계획한 양이다. 본 논문에서는 용수 목적별 목표 공급량의 산정 방법을 약술하였으며, 자세한 산정 방법은 KLC (2007)에 기술되어 있다. 학교와 공원의 경우에는 시설별 사용 인구 수와 1인당 사용량을 바탕으로 산정되었고, 호소수 유지용수는 호소수의 면적과 인천 기상청의 증발산량을 이용하여 산정되었다. 노면 청소 수량은 도로 청소 연장과 청소수 원단위, 청소시기를 고려하여 산정하였다. 본 연구에서는 Figs. 3 and 4에 제시된 빗물이용시설의 일 단위의 유입량과 목표 공급량을 이용하여 최적화 기법을 이용한 저류 용량 분석에 활용하였다.
3. 연구 내용
3.1 최적화 기법을 이용한 빗물이용시설의 저류 용량 결정 방법
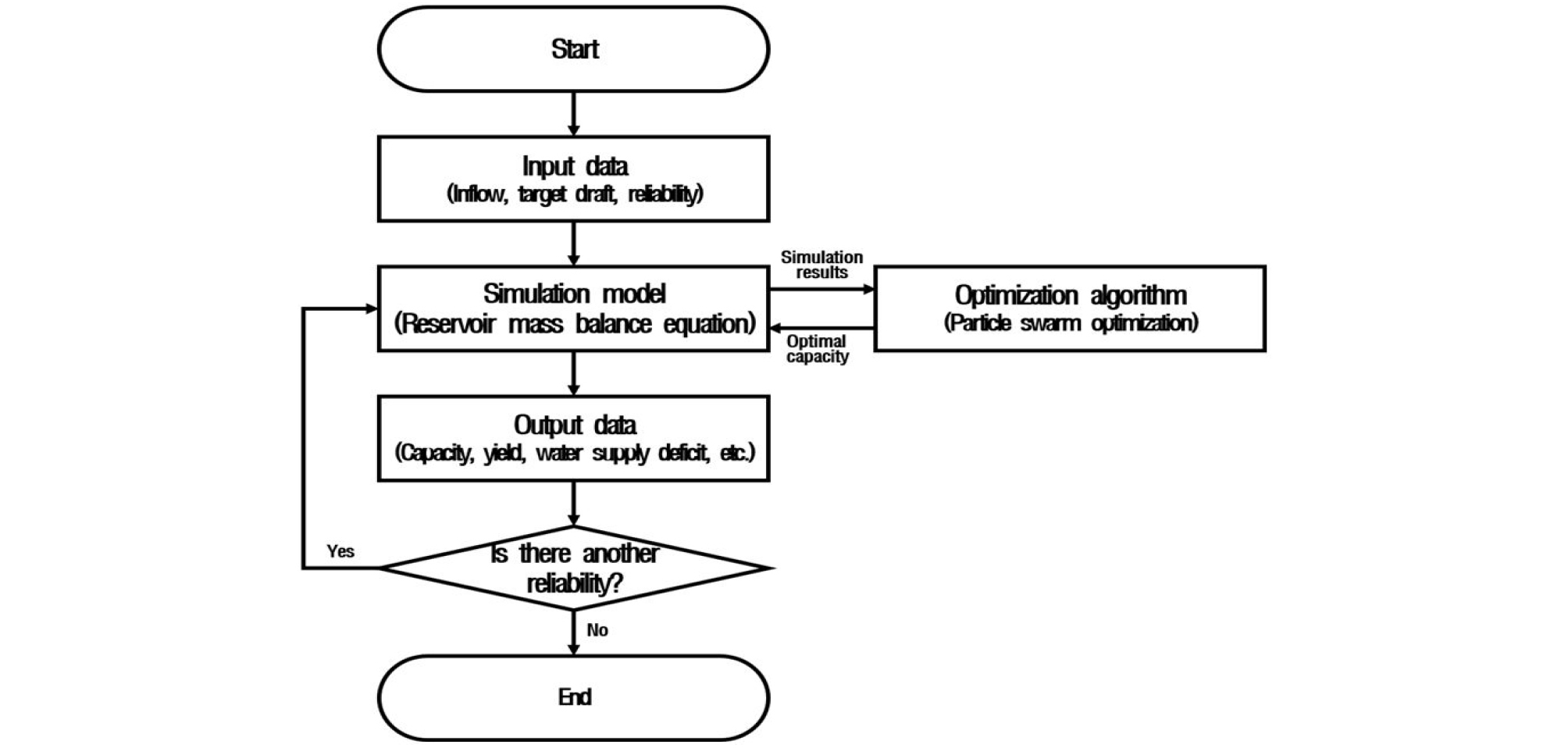
본 연구에서는 2.2절에서 제시한 빗물이용시설의 모의 운영 모형과 2.3절에서 제시한 최적화 알고리즘인 pyswarm을 python 언어를 통해 연계하였다. Fig. 5는 Phyhon을 이용하여 구현한 빗물이용시설의 저류 용량 결정 절차에 관한 모식도를 나타낸다.
최적화 기법을 이용한 빗물이용시설의 저류 용량 결정시 입력자료는 빗물이용시설로 유입되는 유입량 시계열, 목표 공급량 시계열, 목표 보장률이다. 이때 목표 보장률은 분석의 효율을 높이기 위해 여러 개가 동시에 고려될 수 있도록 하였다. 그리고 입력된 유입량 시계열과 목표 공급량 시계열에 따라 다수의 저류 용량 조건에 대하여 모의 운영되고, 최적화 알고리즘에 의해 목표 보장률을 만족하는 최소의 저류 용량을 결정한다. 최종적으로 결정된 저류 용량에 해당하는 저류량 시계열, 용수 공급 시계열, 용수 부족 시계열 등을 출력한 후 종료된다. 단, 다수의 목표 보장률이 입력된 경우에는 각각의 목표 보장률을 만족하는 저류 용량을 탐색하고, 관련된 출력자료를 생성한다.
3.2 최적화 기법을 이용한 빗물이용시설의 저류 용량 결정 방법의 안정성 및 효율성 검증
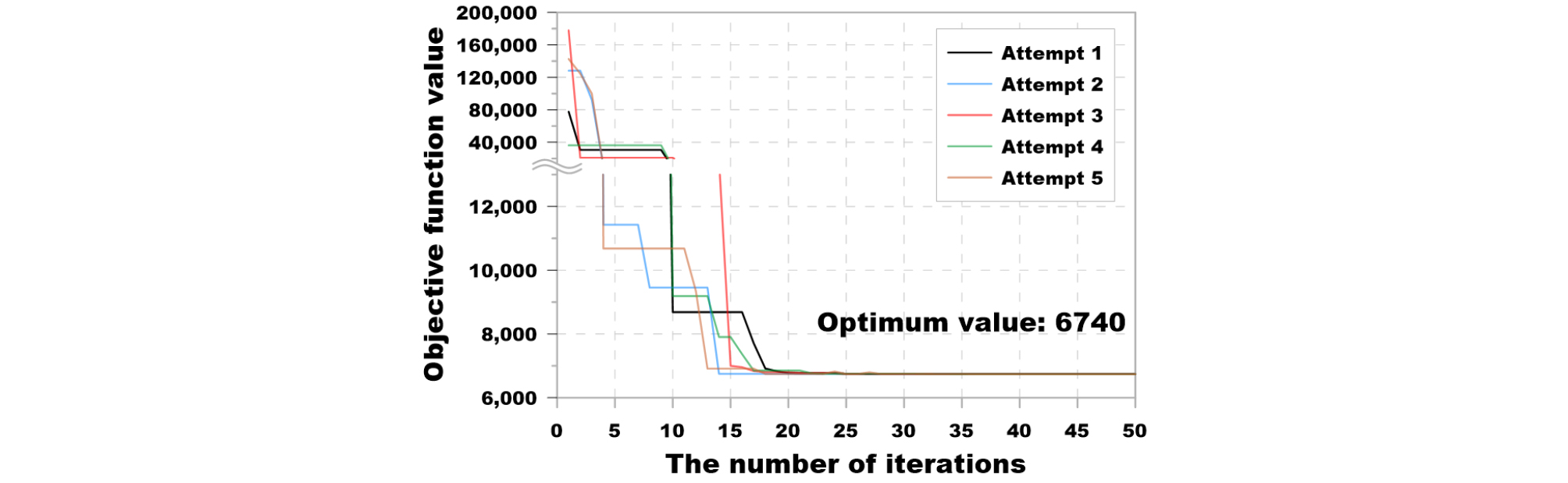
입자 군집 최적화 알고리즘은 전역 최적화 기법으로서 초기 조건의 설정에 관계없이 전역 최적해를 탐색할 수 있다. 하지만 적절한 초기 조건과 매개변수가 설정되지 못하면, 목적함수의 수렴에 많은 시간이 소요될 수 있다. 이에 최적화 알고리즘의 계산 효율을 높이기 위해 pyswarm의 매개변수를 추정하였다. Table 2는 pyswarm에서 제공하는 매개변수별 기본값(default value)과 금회 연구에서 계산 효율을 높이기 위해 결정한 매개변수를 나타낸다. Table 2에서 결정변수(decision variable)인 저류 용량의 상한은 연간 목표 공급량의 총합으로 설정하였으며, Alpha, Beta, Omega는 초기값을 사용하였다. 입자 개수와 반복 계산 횟수의 조합은 여러 차례의 최적화 결과가 소수점 단위 수준에서 유사한 결과로 수렴하는 조합 중 계산 시간이 가장 적게 소요되는 조합을 시행착오법으로 결정하였다. 입자 군집 최적화 알고리즘은 입자 개수보다는 반복 계산 횟수가 줄어듦에 따라 전역해 인근의 가능해(지역해)로 수렴하거나 최적해 탬색 이전에 계산이 종료되는 가능성이 큰 것으로 판단되었다.
Table 2에서 결정한 매개변수 조합의 적절성을 검토하기 위해 특정한 조건에서 목적함수의 수렴 정도를 분석하였다. Fig. 6은 인천 청라지구의 1공구에 계획된 빗물이용시설에 대하여 목표 보장률을 65.9%로 설정하여 5차례에 걸쳐 저류 용량을 분석한 결과이다. 참고로 pyswarm은 초기의 입자 위치를 난수로 발생시키기 때문에 분석할 때마다 분석 초기의 목적함수가 달라진다. Fig. 6에서 5차례 분석에 대한 초기의 입자 위치가 서로 상이하기 때문에 모든 분석 시작 시점의 목적함수 값이 상이하다. 하지만 약 20회가 지난 시점부터 유사한 값으로 수렴하고, 최종(50회)적으로 완전히 동일한 값(6,740 m3)이 나타나는 것으로 분석되었다. 또한, 상기의 분석 조건(10년간의 유입량 시계열)에서 각각의 계산에 소요된 시간은 10초 이내로서, 매우 빠르게 분석되어 분석 효율이 높은 것으로 판단되었다.
Table 2.
Estimation for parameters of pyswarm
3.3 개발 프로그램의 정확성 검증
KLC (2007)에서는 임의로 선정한 수많은 저류 용량을 고려하여 구성된 시나리오에 대하여 반복적으로 계산한 후, 공급 보장률과 우수이용률 분석을 통해 적절한 대안을 결정하였다. 따라서 KLC (2007)에서는 저류 용량이 입력자료이고, 보장률이 출력자료이다. 반면에 본 연구에서 개발한 빗물이용시설의 저류 용량 결정 프로그램의 입력자료는 보장률이고, 저류 용량은 출력자료이다. 본 연구에서는 KLC (2007)의 결과와 비교하기 위해 설계 당시의 저류 용량에 따른 분석 결과인 보장률을 입력자료로 설정하여 저류 용량을 분석하였고, 분석된 저류 용량이 KLC (2007)에서 가정된 저류 용량과 일치하는지 검토하였다.
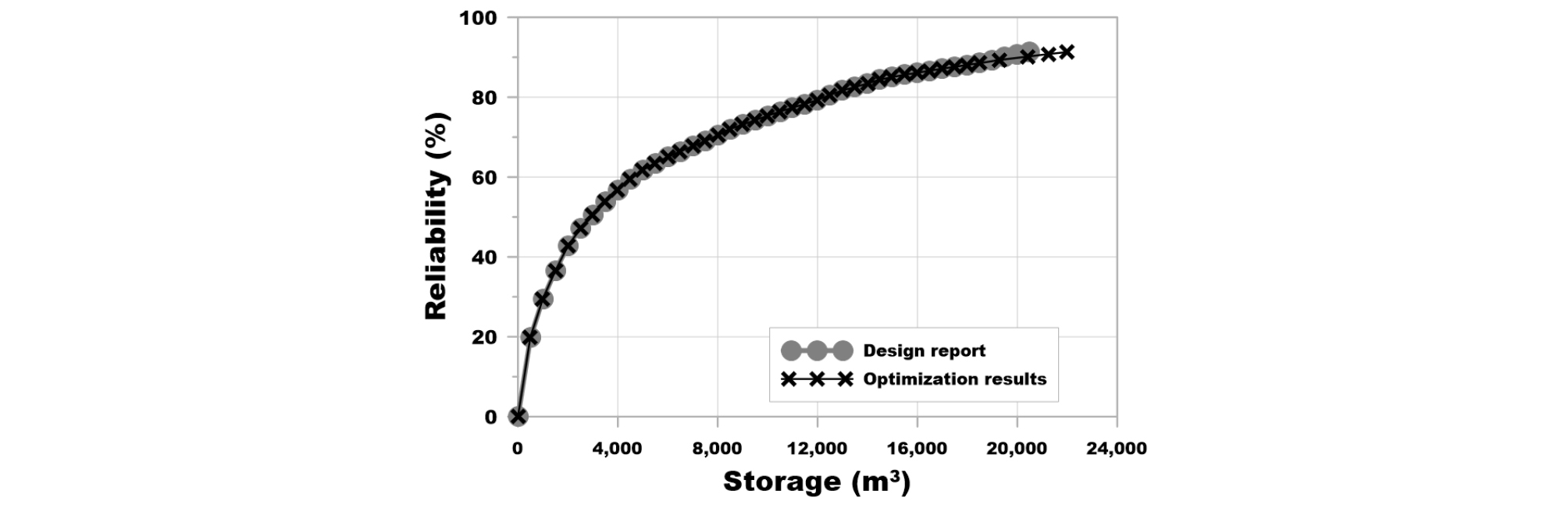
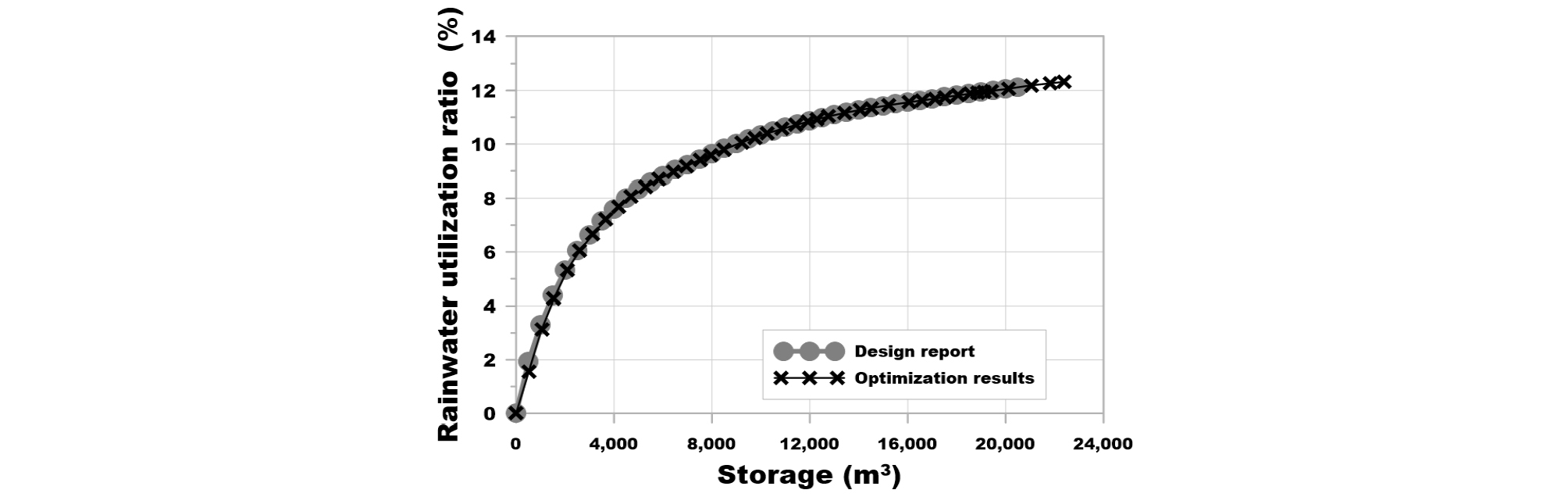
Figs. 7 and 8은 각각 KLC (2007)과 금회 연구에서 분석한 저류 용량에 따른 보장률과 우수이용률의 변화를 나타낸 그림이다. 우수이용률은 빗물이용시설의 총 유입량에 대한 총 용수 공급량의 비율을 나타내는 지표로서 산정 방법은 Eq. 6과 같다. Fig. 7에 제시된 40가지의 보장률별 저류 용량을 비교한 결과 약 0.6%의 차이만 발생되었다. Tabel 3에는 Fig. 7에 나타낸 결과 중 일부를 수치로 나타낸 것이다.
| $$RUR\;=\;\frac{{\displaystyle\sum_{t=1}^N}Y_t}{{\displaystyle\sum_{t=1}^N}I_t}$$ | (6) |
Figs. 7 and 8을 통해 금회 개발된 최적화 기법 기반의 저류 용량 산정 프로그램이 반복 계산을 통한 설계 결과와 매우 유사한 것을 확인할 수 있다. 즉, 금회 개발된 빗물이용시설의 저류 용량 산정 프로그램이 입력한 보장률에 대하여 저류 용량을 적절히 탐색하였다. 참고로 금회 개발된 최적화 기법 기반의 저류 용량 산정 프로그램은 다수의 보장률 조건에 대한 저류 용량 계산이 수 분 내에 일괄 계산되므로 KLC (2007)에서 제시한 보장률보다 많은 조건에 대하여 분석하였다.
3.4 특정한 보장률에 대한 분석 결과
KLC (2007)에서는 인천 청라지구의 1공구에 대하여 목표 공급량 대비 65.9%의 공급 보장률을 가지는 빗물이용시설을 계획하였다. 3.2절에서 기술한 바와 같이 65.9%의 보장률을 고려한 빗물이용시설의 저류 용량은 개발된 프로그램에 의해 6,740 m3으로 결정되었다. 본 절에서는 해당 빗물이용시설에 의한 분석 결과를 제시하였다.
Table 3.
Comparison between optimization results and design report
| Design report (KLC, 2007) | Optimization results | ||||
| Input | Output | Input | Output | ||
| Storage (m3) | Reliability (%) | Rainwater utilization ratio (%) | Reliability (%) | Storage (m3) | Rainwater utilization ratio (%) |
| 500 | 19.8 | 1.93 | 19.8 | 493 | 1.55 |
| 1,000 | 29.5 | 3.31 | 29.5 | 994 | 3.14 |
| 3,000 | 42.8 | 6.62 | 42.8 | 2,991 | 6.64 |
| 5,000 | 61.8 | 8.32 | 61.8 | 4,993 | 8.41 |
| 10,000 | 75.3 | 10.4 | 75.3 | 9,981 | 10.4 |
| 15,000 | 85.0 | 11.4 | 85.0 | 14,959 | 11.4 |
| 20,000 | 90.8 | 12.1 | 90.8 | 20,420 | 12.1 |
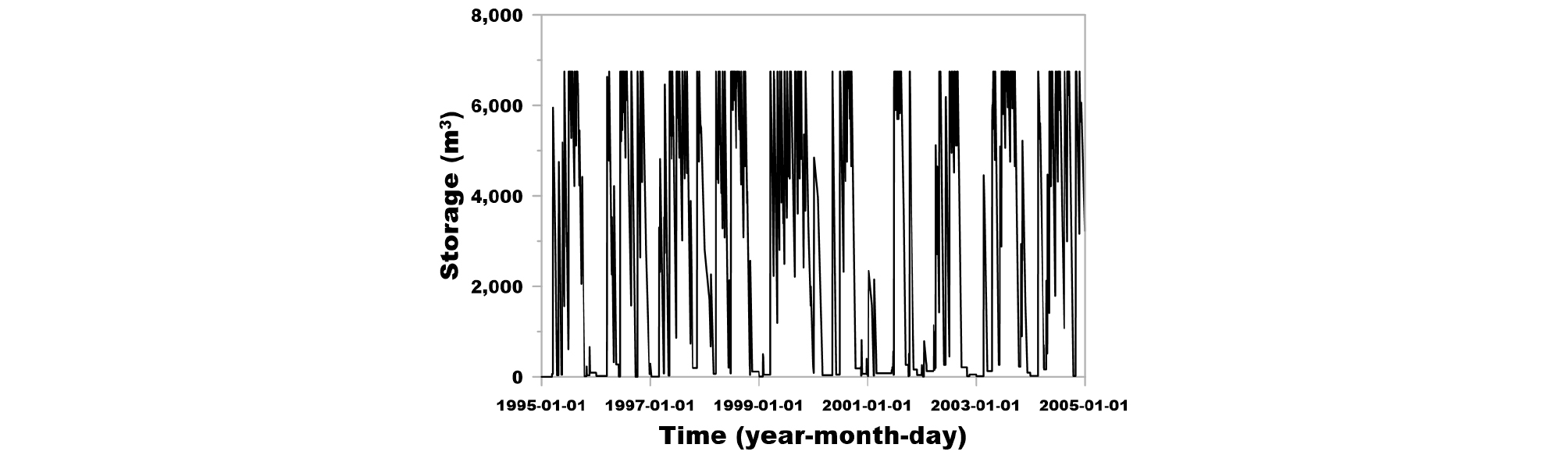
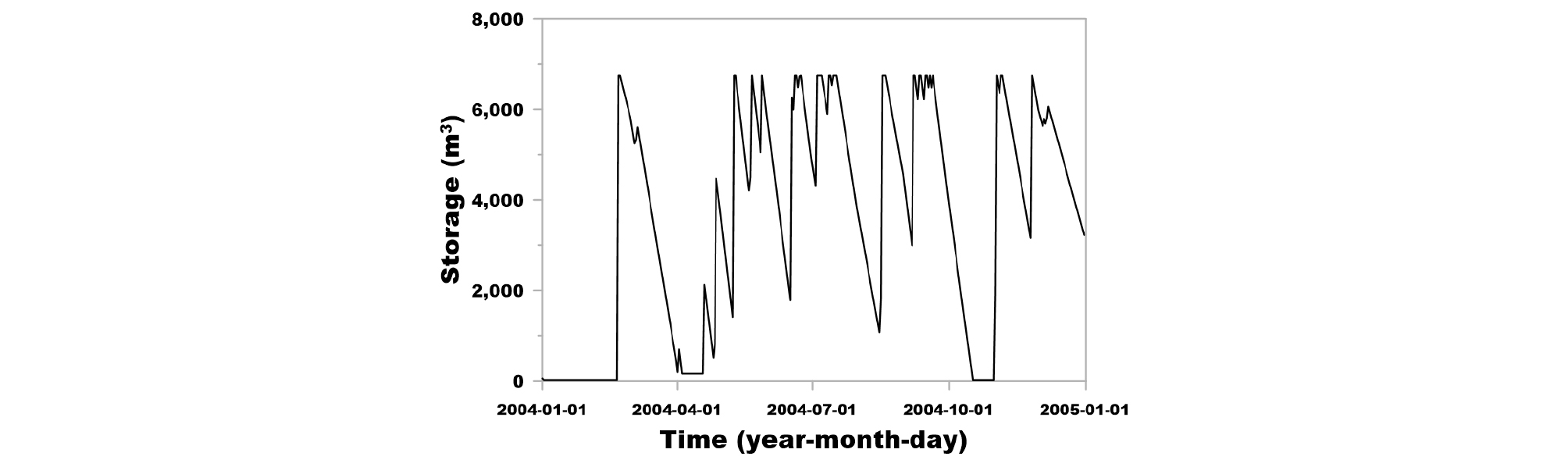
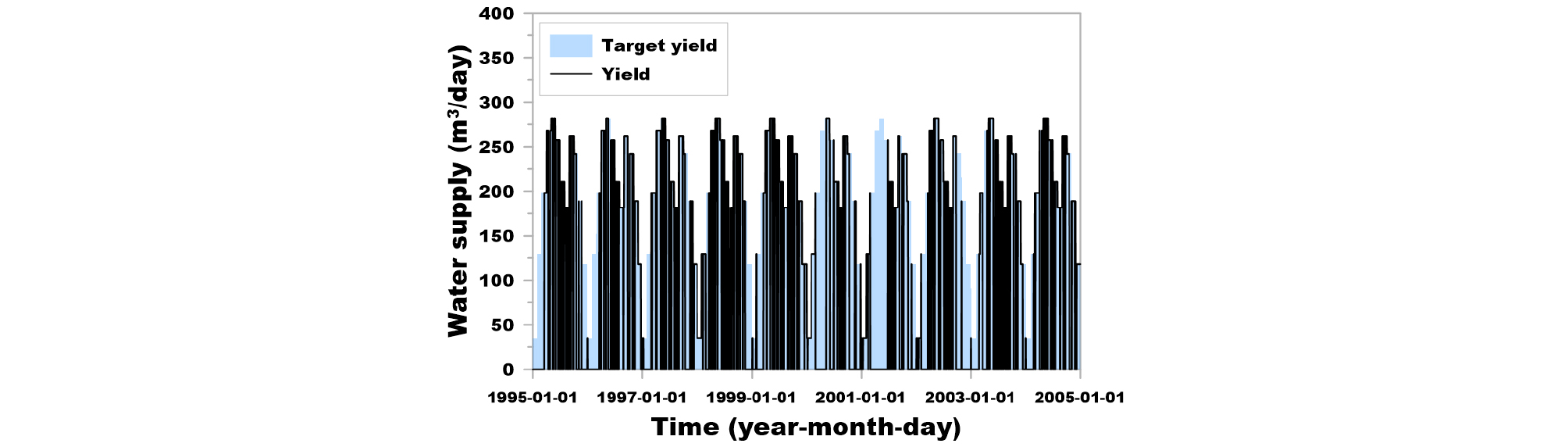
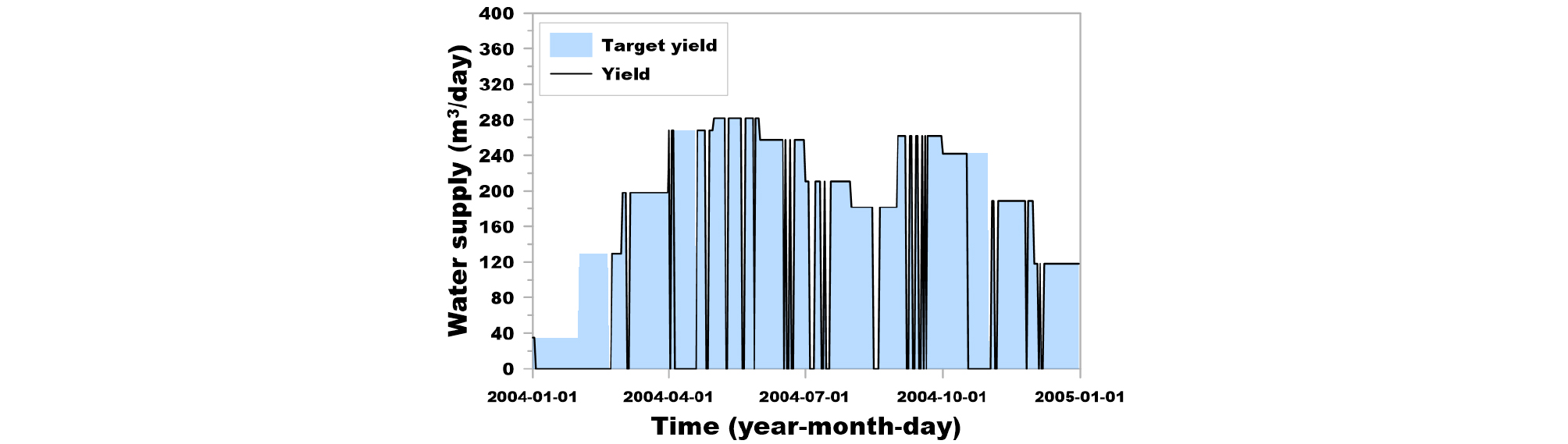
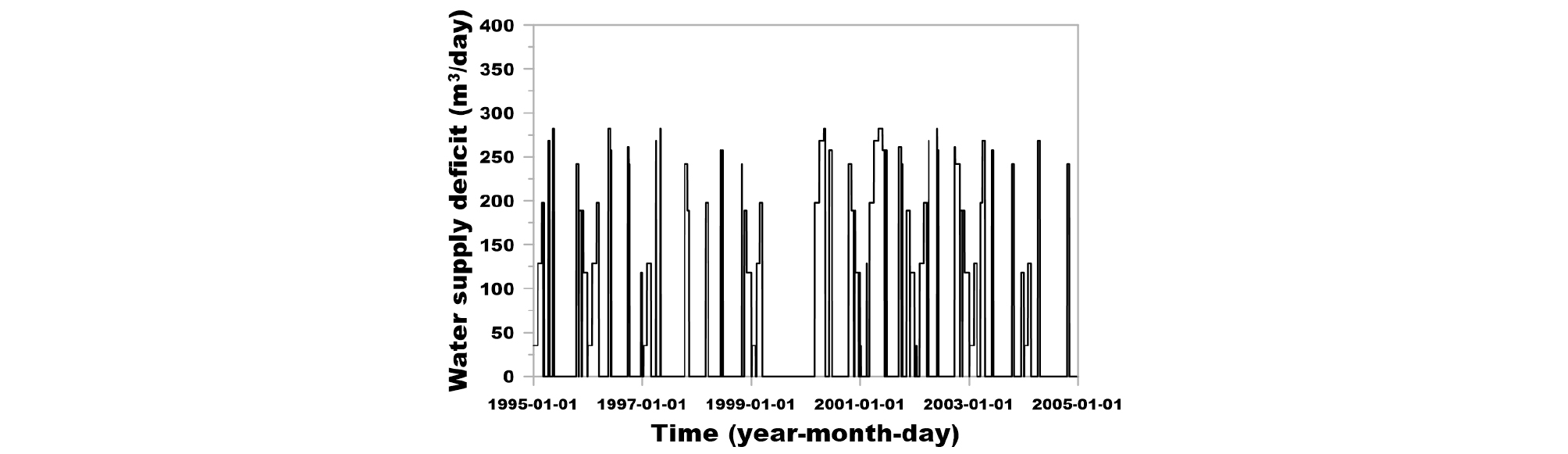
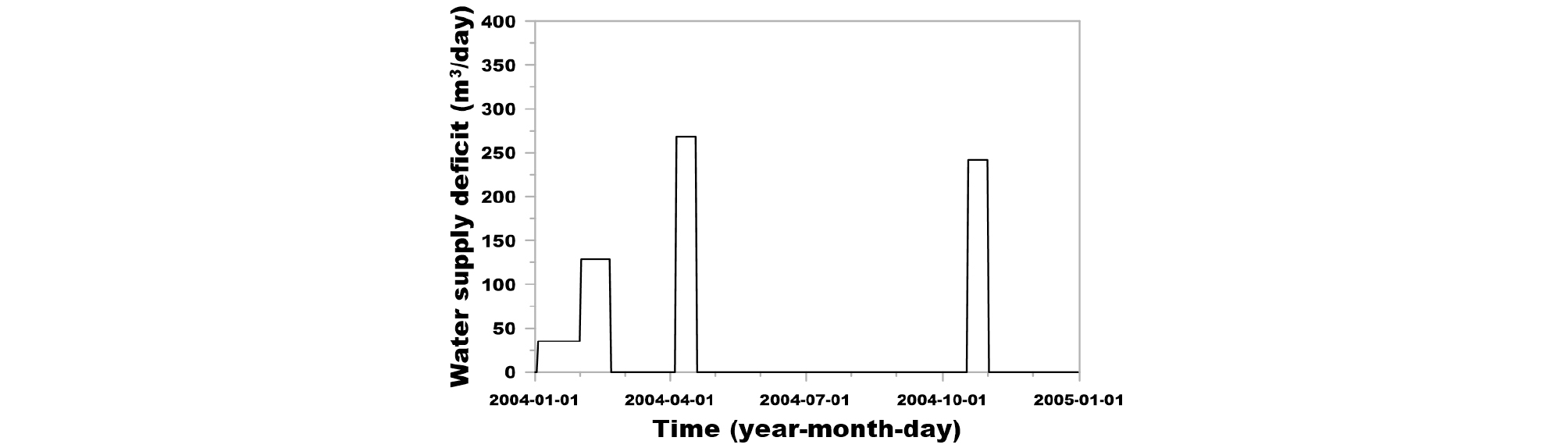
Fig. 9는 결정된 빗물이용시설에 대하여 1995 ~ 2004년 기간의 저류 용량 변화를 나타낸 그림이고, Fig. 10은 이를 2004년에 대해서만 나타낸 그림이다. 유사하게 Figs. 11 and 12는 빗물이용시설을 통한 용수 공급을 1995년부터 2004년까지 도시한 그림과 2004년에 대해서만 도시한 그림이다. 또한, Figs. 13 and 14는 각각 빗물이용시설을 통한 용수 공급 부족량을 1995 ~ 2004년의 기간과 2004년에 대하여 나타낸 그림이다.
KLC (2007)에서는 강우 시 빗물이용시설에 오염물이 유입되는 것으로 인한 오염물 공급을 차단하는 것으로 가정하여 강우 시에는 목표 공급량을 ‘0’으로 설정하였다. 본 연구에서는 해당 설계 방법과 동일한 조건을 고려하였는데, 이에 따라, Figs. 11 and 12에서 목표 공급량이 ‘0’이 되는 시기가 발생하는 것을 볼 수 있고, Figs. 13 and 14에서 해당 시기의 용수 공급 부족량이 ‘0’으로 분석되었다.
Table 4는 1995년부터 2004년까지 1년 단위로 공급 보장률 및 우수이용률을 산정한 결과를 나타낸 표이다. Table 4를 보면, 연중 빗물이용시설로 유입되는 총 물의 양과 보장률이 비례관계에 있지 않음을 확인할 수 있다. 이는 홍수기에 집중된 우리나라의 강우 특성에 기인한 것으로서, 갈수기에도 비교적 많은 강우량이 포함된 기간이 공급 보장률이 크다. 그 예로, 2004년은 앞서 제시한 10년 중 3번째로 유입량이 적었으나, 공급 보장률은 3번째로 크다.
Table 4.
Annual analysis results for yield, reliability, and rainwater utilization ratio
4. 결 론
일반적으로 빗물이용시설의 저류 용량을 계획하는 경우, 임의의 여러 저류 용량을 가정하여 저수지 질량 보존식 기반의 모의 운영을 통해 반복적으로 분석한다. 그리고 각각의 저류 용량에 대한 공급 보장률과 우수이용률 등을 검토하여 적절한 규모를 결정한다. 이러한 분석 방법은 매우 다양한 분석 시나리오를 구성하여 수행되어야 하므로 많은 시간과 노력이 요구된다.
이와 같은 분석 방법을 개선하기 위해 본 연구에서는 최적화 기법을 이용하여 임의의 공급 보장률에 해당하는 빗물이용시설의 저류 용량을 짧은 시간에 직접적으로 결정할 수 있는 프로그램을 개발하였다. 해당 저류 용량 산정 프로그램의 개발 언어는 Python이고, 저수지 질량 보존식 기반의 모의 운영 모형과 Python의 입자 군집 최적화 알고리즘인 pyswarm을 연계하여 구성되었다.
본 연구에서는 개발한 빗물이용시설의 저류 용량 산정 프로그램을 인천 청라지구 1공구에 설치된 빗물이용시설에 적용하여 적절성을 검토하였다. 우선, 최적화 알고리즘의 적절한 매개변수 추정을 통해 계산 시간의 효율을 높였고, 분석의 안정성을 확인하였다. 그리고 설계 당시와 금회 분석한 빗물이용시설의 저류 용량에 따른 공급 보장률을 비교하여 분석의 정확성을 검증하였다.
개발된 최적화 기법을 이용한 빗물이용시설의 저류 용량 산정 프로그램은 단일 목표 보장률에 대하여 10초 이내에 최적의 값을 결정할 수 있다. 또한, 다양한 목표 보장률에 대하여 일괄적인 계산이 가능하다. 따라서 금회 개발된 프로그램은 증가하는 빗물이용시설의 설계 수요에 효과적으로 대응할 수 있고, 빗물이용시설의 저류 용량 산정에 관한 기술력 제고에 기여할 수 있을 것으로 판단된다.