1. 서 론
2. 문헌 연구
2.1 지반운동예측식(GMPE)
2.2 국내 대상 지반운동예측식(GMPE) 연구 분석
2.3 국내 지진 데이터 수집 (PGV, PGA)
3. 국내 적합한 GMPE 결정 결과
3.1 PGV 예측 적합 GMPE
3.2 PGA 예측 적합 GMPE
4. 결 론
1. 서 론
전 세계적으로 대규모 지진의 발생 횟수가 점차 증대됨에 따라 세계 각국에서는 지진에 의한 사회기반시설물의 내진성능평가와 관련한 연구가 활발히 이루어지고 있다. 국내의 경우 규모 3.0 이상 중규모 지진이 과거보다 빈번히 발생하고 있으며, 2016년과 2017년에는 경주 및 포항에서 규모 5.0 이상의 대규모 지진이 발생된바 있다. 이와 관련하여 국내에서도 사회기반시설물에 대한 지진 위험도 평가의 중요성이 부각되고 있다. 여러 사회기반시설물 중 상수도시스템은 타 기반 시설물에 비해 그 규모가 방대하고 더욱이 지반아래에 매설되어 있어 손상범위를 예측하기 어렵고, 2차적인 피해(용수 공급 불가)까지 고려한다면 그 중요성은 타 기반시설물과 비교해 매우 크다.
상수도 시스템 내진성능평가는 크게 ‘예비평가’와 ‘상세평가’ 두 단계로 수행된다. 상수도 시스템을 구성하는 시설물은 타 기반시설물에 비해 매우 다양하고, 매설된 관로까지 고려한다면 그 공간적 범위가 매우 넓다. 그러므로, 모든 상수도 시스템 구성요소에 대하여 상세하게 지진에 대한 구조적 신뢰성 해석을 하기에는 한계가 있다. 따라서, 상세평가를 수행하기 전 문헌자료 및 현장조사를 기반으로 예비평가가 진행된다. 다음으로 상세평가가 진행되며 예비평가 결과와 내진성능 평가수준(기능수행수준/붕괴방지수준)에 따라 기존 상수도 시설 구성부재의 내진성능을 평가하게 된다. 기본적으로 펌프장과 배수지 같은 건축구조물의 경우 독립적인 구조적 내진성능평가가 가능하나 상수도시스템의 내진평가 대상을 상수도관로까지 포함할 경우, 같은 규모의 지진이 한 지점에서 발생하더라도 개별 상수도관로 별 파손확률은 모두 달라지므로 물공급 흐름의 특성이 고려된 관로의 공간적 파손확률의 검토가 반드시 필요하다. 결국, 공간적 파괴확률 결과와 상수도 시설물 내진성능평가 결과의 신뢰성을 높이기 위해서는 정확하고 합리적인 지반운동 모의가 필수적이다. 이러한 지반운동 모의는 지반운동예측식(Ground Motion Prediction Equation, GMPE)을 이용하여 수행된다. GMPE는 지진 발생에 의해 상수도 네트워크가 존재하는 공간적 위치에서의 지반운동을 정의하며, 지중에 매설된 시설물(예, 관로)의 파괴가능성을 산정하기 위해 활용된다. 각 지역에 적합한 GMPE의 제안을 위해 다양한 GMPE가 개발된 바 있다(Noh and Lee (1995), Junn et al. (2002), Cho and Park (2003), Yun et al. (2007), Emolo et al. (2015)). 그러나 현재까지 우리나라에서 발생한 지진의 규모의 다양성과 그 횟수는 상대적으로 적고 드물어 대부분의 연구가 특정 지진 이력만을 활용하였다. 따라서 최근 발생한 국내 지진 실정에 맞는 GMPE를 선정하여 국내 상수도 시설물 내진성능평가의 신뢰성을 제고할 필요가 있다.
본 연구에서는 과거부터 현재까지의 국내 계측 지진 데이터를 종합적으로 활용하여 상수도시설물의 지진에 의한 내진성능 평가에 적합한 GMPE를 선정하고자 하였다. 이를 위해 기존 국내외에서 활용된 바 있는 6개 GMPE의 형태와 특성을 검토하고, 각 제안식에 적합한 적정 매개변수를 추정하였다. 또한 국내 실제 지진계측자료를 분석에 활용하여 6개 중 국내 지진 모의에 가장 적합한 GMPE를 선정하여 제시하였다. 본 연구를 통해 결정된 적정 GMPE는 상수도관망의 수리학적 내진성능 평가에 직접적인 입력자료로 활용될 수 있다.
2. 문헌 연구
2.1 지반운동예측식(GMPE)
상수도시스템의 지진 취약성 평가 결과에 대한 신뢰성을 높이기 위해서는 정확한 지반운동 모의가 선행되어야한다. 일반적으로 GMPE는 상수도 네트워크가 매설된 공간적인 위치에서의 지진발생에 의한 지반운동을 정의한다. GMPE는 독립변수(지진 규모, 진원거리, 단층 및 지반 조건 등)와 종속변수(PGV-Peak Ground Velocity 또는 PGA-Peak Ground Acceleration과 같은 지반운동 등)을 고려하게 된다. GMPE와 관련하여 다양한 연구들이 진행되었으며 문헌 및 대상 지역마다 고려하는 조건에 따라 상이한 형태의 식으로 표현 될 수 있다. GMPE와 관련한 식은 대표적으로 아래 Eq. (1)과 같은 형태로 표현된다.
| $$\log(y)=c_0+c_1M+c_2R$$ | (1) |
여기서, y는 최대지반가속도 PGA (cm/sec2) 혹은 최대지반속도 PGV (cm/sec)를, c0-c2는 지반 조건 및 단층 등에 의한 독립변수에 따라 정의되는 계수, M은 지진 규모, R은 지진 거리(km)를 의미한다.
2.2 국내 대상 지반운동예측식(GMPE) 연구 분석
본 연구에서는 국내 적합한 GMPE를 선정하기 위해 국내 데이터를 활용한 문헌을 분석하였다. 분석 결과 국내 데이터를 활용하여 GMPE식을 도출한 연구는 총 6개로 구분할 수 있으며, Table 1과 같다. Table 1에 제시된 6개의 GMPE 중 1 ~ 4번 식의 경우 우리나라의 동남부 지역의 지진자료를 중점적으로 활용하여 만들어진 식이며, 5번식은 가상의 지진자료를, 6번 식은 200개 이상의 국내에 계측된 자료를 사용하여 제시된 GMPE이다. 기본적으로 활용된 자료의 수와 범위를 고려하면, 동남부의 지진특성을 명확히 표현하기에는 1 ~ 4번의 식이 6번 식에 비해 활용된 지진자료의 수가 상대적으로 적고 제한적이라 판단된다. 본 연구에서는 각 GMPE를 실제 발생한 국내 지진계측자료에 적용하여 상수도 네트워크 지진 모의 적합성을 평가하고, 최종적으로 국내에 전반적으로 적합한 GMPE를 산정하고자 하였다.
Table 1.
Representative GMPE
| Num | Study | Scale | Distance | Min M | Max M | Min R (km) | Max R (km) | Data |
| 1 | Noh and Lee (1995) | Moment scale | Epicenter | 1.4 | 3.7 | 10 | 165 |
Seven earthquake data of 1991 in the southeastern region of Korea |
| 2 | Park et al. (2001) | Moment scale | Hypocenter | 4.3 | 4.3 | 46.2 | 226.4 |
The earthquake data of June 26, 1997 and the earthquake off the coast of Ulsan on January 18, 1998 |
| 3 | Junn et al. (2002) | Moment scale | Hypocenter | 2.1 | 4.2 | 25 | 320 |
23 earthquake data from 1999 to 2000 in the southern regions of Korea |
| 4 | Cho and Park (2003) | Moment scale | Hypocenter | 3.2 | 3.9 | 10 | 120 |
Three data from earthquakes in Gyeongju in 1999 |
| 5 | Yun et al. (2007) | Moment scale | Fault rupture | 4.5 | 7.5 | 1 | 400 | Virtual earthquake data |
| 6 | Emolo et al. (2015) | Richter scale | Epicenter | 2 | 4.9 | 1.4 | 600 |
222 earthquake data across the korea from 2007 to 2012 |
6개의 우리나라 지진 데이터 기반 GMPE식을 분석한 결과 Noh and Lee (1995), Park et al. (2001) (이후 1번, 2번)에 의해 제안된 GMPE는 기본형태가 동일한 것으로 나타났으며 형태는 Eq. (2)와 같다.
| $$\log(y)=c_0+c_1R+\ln R$$ | (2) |
여기서, y는 PGV 또는 PGA를, R은 지진 거리를 의미한다. 1번 문헌의 경우 진앙거리를, 2번 문헌의 경우 진원거리를 사용하였다는 차이점이 있다. c0와 c1은 지반 조건 및 단층 등에 의한 독립변수에 따라 정의되는 계수(지진 및 지반의 성질 계수)를 의미한다. 해당 계수는 데이터를 기반으로 Eq. (2)를 회귀 분석하여 결정하게 되며, 관련 식은 아래 Eq. (3)과 같다.
| $$c_k=\xi_0^i+\xi_1^i\left(M_w-6\right)+\xi_2^i\left(M_w-6\right)^2+\xi_3^i\left(M_w-6\right)^3$$ | (3) |
ck는 0 혹은 1, Mw는 모멘트 규모, 마지막으로 ξ는 회귀 분석 계수를 의미한다. 두 문헌 모두 우리나라 동남부에 적용 가능하도록 계수를 제안하였다. 그러나, 동일한 지진 데이터를 활용하지 않아 산정된 계수는 상이한 결과가 도출된 것으로 나타났다. 해당 문헌에서 Eq. (3)에 의해 산정된 회귀 분석 계수는 Table 2와 같다. 1번 문헌은 PGV 산정을 위해 필요한 계수를 제공하지 않아 본 연구에서는 확보한 지진 데이터를 기반으로 가장 낮은 오차를 보인 자연 주파수(natural frequency) 0.5의 값을 PGV 산정에 활용하였다.
Junn et al. (2002)와 Cho and Park (2003)(이후 3번, 4번) 두 문헌에서 제안된 지반운동예측식은 기본형태가 서로 동일하며 1번 문헌과 유사하나, ln [min (R, 100)]와 ln [max (R, 100)] 항들을 추가하여 거리에 따른 감쇠 효과를 추가해준 차이가 있다. c2는 c0, c1와 마찬가지로 지진과 지반의 성질에 따른 계수를 의미하며 지진 데이터를 이용한 회귀분석을 통해 결정된다. 이들 계수를 구하는 식은 Eq. (3)과 동일하나, 1번 과 2번 문헌에서는 Eq. (3)의 k값을 0과 1만을 고려하였다. 반면에 3번과 4번 문헌에서는 k값을 0, 1, 2 까지 고려하였다는 차이점이 있다. 또한 3번과 4번 문헌에서는 Eq. (3)에 모멘트규모를 추가적으로 고려하였으며 두 문헌 모두 우리나라 동남부에 적용 가능한 계수를 제안하였으나 이 역시 활용된 지진 데이터가 달라 산정된 회귀분석계수가 상이하였다. 문헌별로 결정된 회귀 분석 계수는 Table 2와 같다.
Table 2.
GMPE regression coefficient for references (1~4)
| Num | Study | Dependent variable (D.V.) | Coefficient | ξ0 | ξ1 | ξ2 | ξ3 |
| 1 | Noh and Lee (1995) | PGA | c0 | 3.219E+00 | 3.350E-01 | -2.829E-02 | 6.357E-03 |
| c1 | -3.619E-03 | 1.128E-03 | -1.623E-04 | -3.507E-05 | |||
| PGV | c0 | 2.103E+00 | 7.389E-01 | -1.948E-01 | 3.446E-02 | ||
| c1 | -3.476E-04 | -1.714E-04 | -8.488E-05 | 1.210E-04 | |||
| 2 | Park et al. (2001) | PGA | c0 | 3.391E+00 | 3.601E-01 | -3.621E-02 | -6.385E-03 |
| c1 | -3.660E-03 | 1.267E-03 | -9.000E-05 | -2.667E-05 | |||
| PGV | c0 | 2.158E+00 | 5.974E-01 | -3.084E-02 | 7.930E-03 | ||
| c1 | -1.931E-03 | 1.1104E-03 | -1.489E-04 | -2.299E-05 | |||
| 3 | Junn et al. (2002) | PGA | c0 | 0.112E+02 | 0.511E+00 | -0.385E-01 | 0.292E-01 |
| c1 | -0.244E-02 | 0.140E-03 | -0.163E-04 | 0.599E-04 | |||
| c2 | -0.321E+00 | 0.105E+00 | -0.966E-02 | -0.650E-02 | |||
| PGV | c0 | 0.739E+01 | 0.106E+01 | -0.170E-01 | 0.253E-01 | ||
| c1 | -0.126E-02 | 0.312E-03 | 0.411E-05 | 0.292E-04 | |||
| c2 | -0.116E+00 | 0.927E-01 | -0.167E-01 | -0.407E-02 | |||
| 4 | Cho and Park (2003) | PGA | c0 | 0.107E+02 | 0.591E+00 | -0.562E-01 | 0.214E-01 |
| c1 | -0.238E-02 | 0.208E-03 | -0.205E-04 | 0.419E-04 | |||
| c2 | -0.244E+00 | 0.950E-01 | -0.880E-02 | -0.330E-02 | |||
| PGV | c0 | 0.751E+01 | 0.112E+01 | -0.462E-01 | 0.265E-01 | ||
| c1 | -1.300E-02 | 0.322E-03 | -0.103E-04 | 0.255E-04 | |||
| c2 | -0.115E+00 | 0.900E-01 | -0.131E-01 | -0.340E-02 |
앞서 제시한 문헌들에서 제시된 GMPE와는 달리 Yun et al. (2007)(이후 5번)은 다른 형태의 식을 제안하였다. P1부터 P8은 모두 회귀 분석 계수를, R₀는 교차 거리(cross-over distance)를 의미한다. 5번 문헌에서는 교차거리를 50 km로 가정하여 사용하였으며 지진 규모는 모멘트규모를, 지진 거리는 진원거리를 사용하였지만, 지진 데이터를 기반으로 진원거리를 사용하지 않았으며 파열거리를 진원거리로 환산하는 방법을 적용하여 관측된 파열거리 기반으로 진원거리를 산정하여 고려하였다. 그러나 지진 데이터에서 파열거리를 구하기가 어려워, 본 연구에서는 파열거리가 진앙거리와 동일하다고 가정하고 적용하였다. 회귀 분석 계수 산정 결과는 Table 3과 같다.
Table 3.
GMPE regression coefficient for reference (5)
| D.V. | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
| PGA | 3.05E+01 | -1.65E+00 | -6.50E+00 | 4.74E-01 | 5.29E+00 | -6.50E-02 | -1.10E+00 | 6.30E-02 |
| PGV | 3.07E+01 | -1.45E+00 | -6.38E+00 | 5.33E-01 | 5.38E+00 | -6.20E-02 | -1.25E+00 | 1.45E-01 |
Emolo et al. (2015)(이후 6번) 연구에서도 마찬가지로 다른 형태의 GMPE를 제안하였으며, 해당 문헌에서 제안한 GMPE는 Eq. (4)와 같다.
| $$\log(y)=a+bM+c\log\sqrt{R_{epi}^2+h^2}+dR_{epi}+es$$ | (4) |
여기에서 a, b, c, d, e는 회귀 분석 결과로 산정된 계수이며, 관측소 별로 부여하는 보정계수 s는 –1, 0, 1의 값이 활용된다. h의 경우는 관측소 주변 10 km 이내에 발생할 수 있는 현실적이지 못한 결과를 방지하기 위해 추가한 계수이다. 각 계수들은 고정값으로 부여되지 않고 평균 및 표준편차를 활용하여 제시하였으며, 해당 계수들은 Table 4와 같이 정리될 수 있다. 6번 문헌에서는 다른 연구들과 달리 지진 규모의 경우 리히터규모를 활용하고 지진거리는 진앙거리를 사용하였다.
Table 4.
GMPE regression coefficient for reference (6)
| D.V. | a | b | c | h | d | e |
| PGA | -5.75 ± 0.13 | 0.89 ± 0.03 | -0.66 ± 0.06 | 4.5 ± 3.0 | -0.0019 ± 0.0002 | 0.289 ± 0.005 |
| PGV | -3.07 ± 0.14 | 0.73 ± 0.03 | -0.76 ± 0.06 | 1.7 ± 2.3 | -0.0029 ± 0.0002 | 0.326 ± 0.006 |
해당 연구들의 GMPE는 모두 지반 조건, 지진 발생 원인(Source type) 등은 고려하지 않았다. 또한 6번 문헌의 연구를 제외한 다른 연구들은 한정된 지진 데이터(최대 23건)만 가지고 한 반면, 6번 문헌의 경우 2007년 3월부터 2012년 3월까지 총 222개 지진 데이터를 사용하였다. 지진 규모 단위는 일반적으로 리히터규모가 가장 보편적으로 알려져 있으나(기상청 자료 등), 국내 적용된 연구들 대부분이 GMPE에 모멘트규모를 사용하고 있다. 대부분의 연구에서 지진 규모 2에서 5 사이의 지진 데이터를 수집하여 GMPE를 검증하였고, 임의로 생성한 데이터를 통해 규모 4에서 7사이 지진의 지반운동 예측을 모의하였다. 지진 거리는 진원거리와 진앙거리가 대부분이지만, 5번 문헌에서는 특이하게 파열거리를 사용하였다. 다만, 앞서 언급한 것과 같이 파열거리에 대한 데이터는 구하기 어려워 본 연구에서는 파열거리는 진앙거리와 같다고 가정하였다.
Table 1의 데이터 요약을 토대로 6번 문헌에서 제시된 지반운동예측식이 다양한 데이터를 사용함으로써 비교적 정확한 예측이 될 수 있을 것으로 예상되었다. 1번부터 4번까지의 문헌의 경우 활용한 지진 데이터의 수가 적은 반면, 국내 남부 혹은 남동부 지역 데이터로 회귀 분석 계수를 산정하여 해당 지역 지진에 좀 더 특화된 지반운동예측식이 될 것으로 판단된다.
2.3 국내 지진 데이터 수집 (PGV, PGA)
상수관로의 경우 수평적으로 매설되어 있는 구성요소로 PGV에 의한 영향이 PGA 보다 크다. 따라서, 본 연구에서는 국내 발생한 이력이 있는 지진 중 PGV 데이터를 확보할 수 있는 자료를 기반으로 분석하고자 하였다. 2016 ~ 2019년까지 총 10건의 지진 데이터를 수집할 수 있었으며, 지진 규모는 3.9부터 5.8, 진앙거리는 11 km ~ 582 km 이다. 확보한 10건의 지진 별 PGV 데이터와 진앙거리의 정보는 Table 5와 같다.
Table 5.
Summary of domestic earthquake PGV data
관로 이외에 배수/양수시설, 펌프, 탱크 와 같은 수직적인 구성요소들은 PGV보다 PGA의 영향을 많이 받는다. 이러한 구성요소들의 파손/파괴 모의는 본 연구의 대상인 관로를 벗어나지만, 본 연구에서 선정한 GMPE가 타 구성요소들을 포함한 상수도 시설물의 전반적인 측면에서 적합한가를 판단하기 위해 국내 지진 PGA 데이터를 수집하고 해당 데이터를 적용한 적합성 평가를 수행하였다. PGA의 경우 2016 ~ 2019년까지 총 16건의 지진 자료를 수집하였다. 지진 규모는 3 ~ 5.8, 진앙거리는 10 km ~ 502 km 이다. 그 외 각 지진 별 PGA 데이터와 진앙거리의 정보는 Table 6과 같다.
Table 6.
Summary of domestic earthquake PGA data
3. 국내 적합한 GMPE 결정 결과
3.1 PGV 예측 적합 GMPE
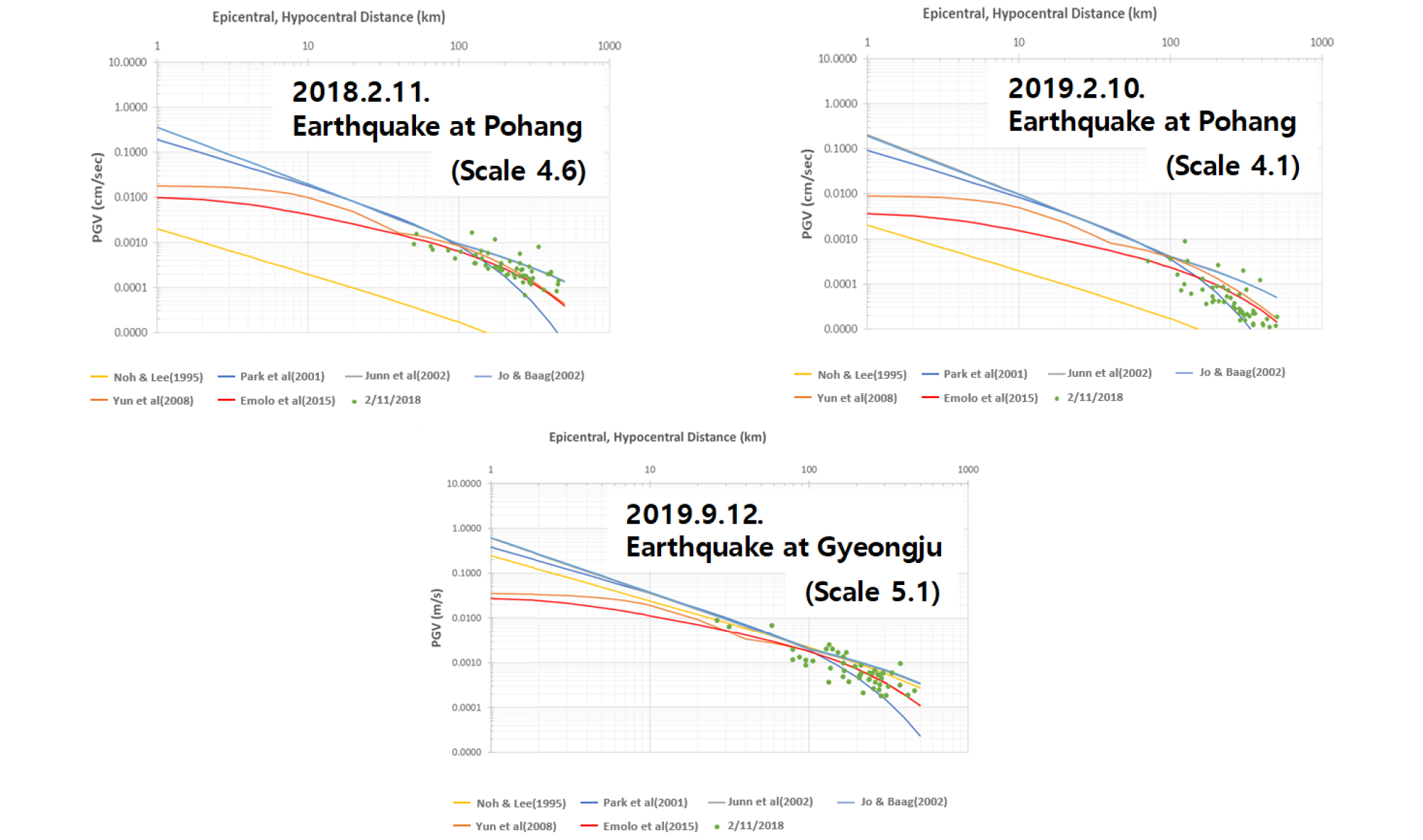
PGV에 적합한 GMPE를 선정하기 위해 2016년부터 2019년까지 발생한 10개의 지진데이터를 적용하였으며 이들 결과 중 뚜렷한 양상을 보이는 2018년 2월 11일 (Table 5의 7번 지진), 2019년 2월 10일 (Table 5의 8번 지진), 2019년 7월 21일 (Table 5의 10번 지진)의 지진 데이터 적용 결과를 분석하였다. 해당 세 지진 데이터에 각 GMPE를 적용하여 예측한 PGV 결과는 Fig. 1과 같다.
Fig. 1를 보면, Yun et al. (2007)와 Emolo et al. (2015)의 경우 관측 값을 관통하는 것을 확인 할 수 있다. Yun et al. (2007)의 GMPE 적용 결과의 경우, 지진거리 40 km 근방에서 변곡점이 생기는 것은 방법론에서 언급한 바와 같이 모의 시 R₀를 40 km로 가정했기 때문이다. 해당 적용 결과를 활용하여 국내 적용에 적합한 GMPE 여부를 보다 정확히 판단하기 위해 RMSE와 SAE를 활용해 두 오차 값으로 정량적 수치 비교를 하였으며, 해당 결과는 각 Table 7 (RMSE), Table 8 (SAE)와 같다.
Table 7.
GMPE conformity results using PGV data of 10 earthquake (RMSE)
| No. | Noh and Lee (1995) | Park et al. (2001) | Junn et al. (2002) | Cho and Park (2003) | Yun et al. (2007) | Emolo et al. (2015) | Min. error formula |
| 1 | 0.0007181 | 0.0007190 | 0.0006672 | 0.0006675 | 0.0006764 | 0.0006757 | Junn et al. (2002) |
| 2 | 0.0018606 | 0.0008283 | 0.0008227 | 0.0007499 | 0.0008741 | 0.0008804 | Cho and Park (2003) |
| 3 | 0.0046081 | 0.0025042 | 0.0024356 | 0.0019528 | 0.0015699 | 0.0022400 | Yun et al. (2007) |
| 4 | 0.0009863 | 0.0002879 | 0.0003349 | 0.0003311 | 0.0004929 | 0.0006487 | Park et al. (2001) |
| 5 | 0.0028069 | 0.0011679 | 0.0010155 | 0.0009526 | 0.0013270 | 0.0010769 | Cho and Park (2003) |
| 6 | 0.0004661 | 0.0002772 | 0.0002492 | 0.0002501 | 0.0002282 | 0.0002664 | Yun et al. (2007) |
| 7 | 0.0005143 | 0.0005267 | 0.0005074 | 0.0004865 | 0.0002928 | 0.0002552 | Emolo et al. (2015) |
| 8 | 0.0001461 | 0.0001398 | 0.0001606 | 0.0001644 | 0.0001272 | 0.0001040 | Emolo et al. (2015) |
| 9 | 0.0005292 | 0.0004396 | 0.0004467 | 0.0004466 | 0.0004412 | 0.0004591 | Park et al. (2001) |
| 10 | 0.0001805 | 0.0003504 | 0.0003648 | 0.0003969 | 0.0002697 | 0.0001065 | Emolo et al. (2015) |
Table 8.
GMPE conformity results using PGV data of 10 earthquake (SAE)
| No. | Noh and Lee (1995) | Park et al. (2001) | Junn et al. (2002) | Cho and Park (2003) | Yun et al. (2007) | Emolo et al. (2015) | Min. error formula |
| 1 | 0.0167086 | 0.0168841 | 0.0141577 | 0.0141609 | 0.0149771 | 0.0143575 | Junn et al. (2002) |
| 2 | 0.0519831 | 0.0282718 | 0.0315471 | 0.0280735 | 0.0250080 | 0.0252245 | Yun et al. (2007) |
| 3 | 0.1585453 | 0.0708294 | 0.0810441 | 0.0663331 | 0.0456805 | 0.0733781 | Yun et al. (2007) |
| 4 | 0.0200660 | 0.0080280 | 0.0128488 | 0.0124806 | 0.0102091 | 0.0096019 | Park et al. (2001) |
| 5 | 0.1185162 | 0.0539176 | 0.0425334 | 0.0363684 | 0.0416352 | 0.0378914 | Cho and Park (2003) |
| 6 | 0.0185442 | 0.0107819 | 0.0097715 | 0.0097936 | 0.0081676 | 0.0085354 | Yun et al. (2007) |
| 7 | 0.0253554 | 0.0202719 | 0.0220871 | 0.0209977 | 0.0125647 | 0.0099422 | Emolo et al. (2015) |
| 8 | 0.0060352 | 0.0051022 | 0.0093187 | 0.0095469 | 0.0062772 | 0.0042122 | Emolo et al. (2015) |
| 9 | 0.0163384 | 0.0117590 | 0.0193487 | 0.0193300 | 0.0143118 | 0.0128553 | Park et al. (2001) |
| 10 | 0.0095001 | 0.0130700 | 0.0164091 | 0.0176562 | 0.0124401 | 0.0056415 | Emolo et al. (2015) |
Tables 7 and 8에서 확인할 수 있듯이, Yun et al. (2007)과 Emolo et al. (2015)의 GMPE가 최소오차인 경우가 절반을 차지했다. RMSE 기준으로 적합한 GMPE의 횟수를 검토하면, Yun et al. (2007) 2번 Emolo et al. (2015)가 3번 도출됐으며, SAE 기준으로 Yun et al. (2007) 3번 Emolo et al. (2015)가 3번 도출되었다. 특히, Yun et al. (2007)이 최소 오차를 보이는 경우에도 Emolo et al. (2015)의 오차가 유사한 값을 나타냄을 알 수 있다. 이러한 양상은 2번과 6번 지진의 SAE 결과에서 확인할 수 있었다.
전반적으로 RMSE와 SAE 기준의 Emolo et al. (2015)의 GMPE가 다른 GMPE에 비해 오차가 적게 산정되는 경향이 있는 것으로 파악되었다. 이에 따라 PGV 예측에는 Emolo et al. (2015)의 GMPE가 가장 정확도가 높을 것으로 판단된다.
3.2 PGA 예측 적합 GMPE
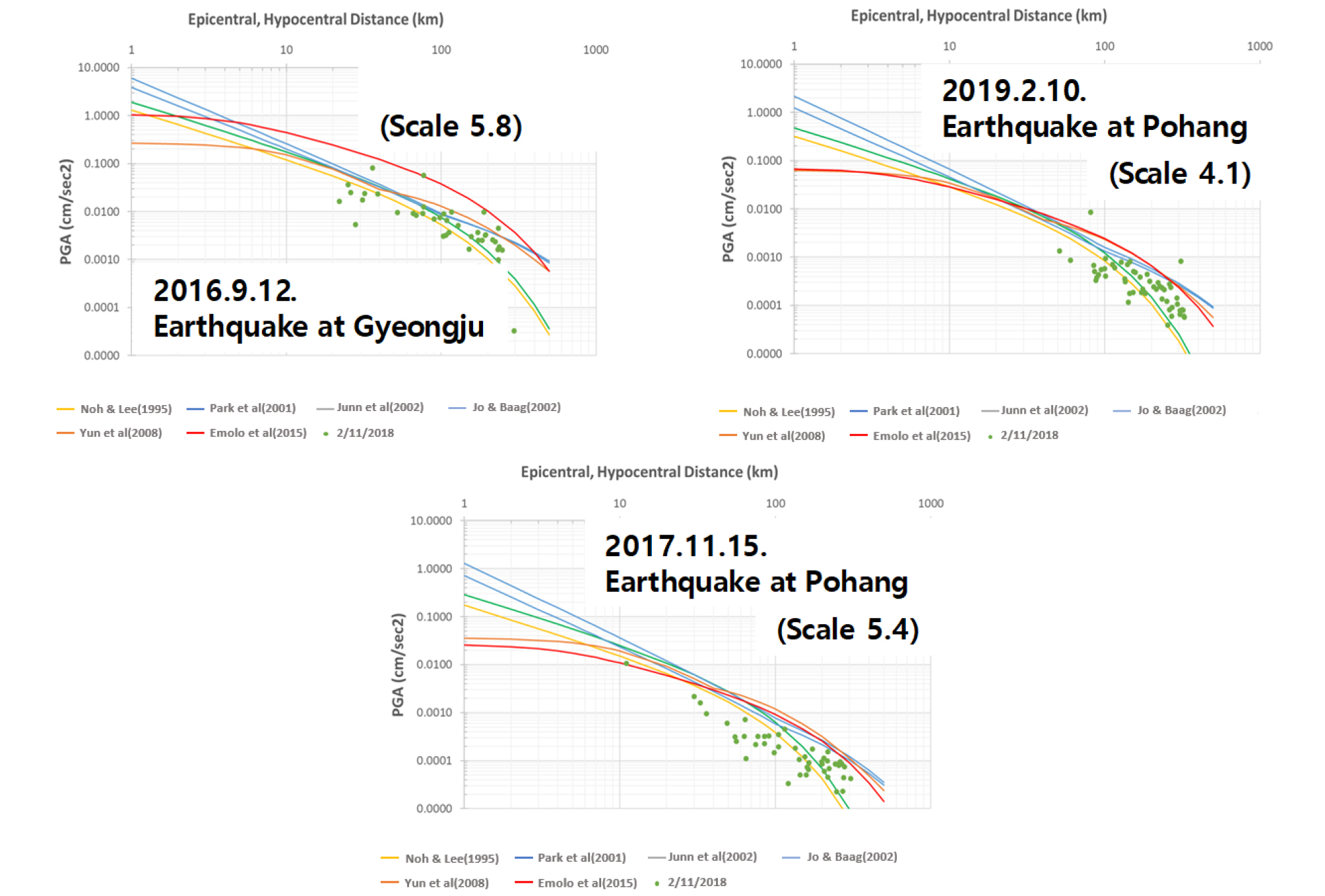
PGA에 적합한 GMPE를 선정하기 위해 2016 ~ 2019년까지 발생된 16개 지진자료를 적용하였으며, 해당 결과 중 2016년 9월 12일 (Table 7에서 1번 지진), 2017년 11월 15일 (Table 7에서 5번 지진), 2019년 2월 10일 (Table 7에서 16번 지진)의 지진 데이터 적용 결과를 분석하였다. 해당 세 지진 데이터에 각 GMPE를 적용하여 예측한 PGA 결과는 Fig. 2와 같다.
Fig. 2를 보면, Noh and Lee (1995)와 Park et al. (2001)의 경우 타 GMPE 보다 정확하게 관측 값을 관통하는 것을 확인 할 수 있다. 앞선 분석과 마찬가지로 그래프만으로는 정성적으로 판단하기 어려우므로 RMSE와 SAE를 활용한 두 오차 값으로 정량적 수치 비교를 하였으며, 해당 결과는 각 Table 9 (RMSE), Table 10 (SAE)에 제시되어 있다.
Table 9.
GMPE conformity results using PGA data of 16 earthquake (RMSE)
| No. | Noh and Lee (1995) | Park et al. (2001) | Junn et al. (2002) | Cho and Park (2003) | Yun et al. (2007) | Emolo et al. (2015) | Min. error formula |
| 1 | 0.00012 | 0.00012 | 0.00013 | 0.00012 | 0.00013 | 0.00012 | Emolo et al. (2015) |
| 2 | 0.00010 | 0.00024 | 0.00026 | 0.00016 | 0.00042 | 0.00025 | Noh and Lee (1995) |
| 3 | 0.00018 | 0.00018 | 0.00017 | 0.00017 | 0.00017 | 0.00017 | Emolo et al. (2015) |
| 4 | 0.00101 | 0.00163 | 0.00187 | 0.00111 | 0.00178 | 0.00108 | Noh and Lee (1995) |
| 5 | 0.00068 | 0.00130 | 0.00144 | 0.00084 | 0.00139 | 0.00111 | Noh and Lee (1995) |
| 6 | 0.00087 | 0.00154 | 0.00172 | 0.00099 | 0.00163 | 0.00102 | Noh and Lee (1995) |
| 7 | 0.00067 | 0.00121 | 0.00135 | 0.00079 | 0.00128 | 0.00105 | Noh and Lee (1995) |
| 8 | 0.00069 | 0.00131 | 0.00166 | 0.00077 | 0.00156 | 0.00091 | Noh and Lee (1995) |
| 9 | 0.00082 | 0.00141 | 0.00166 | 0.00096 | 0.00157 | 0.00121 | Noh and Lee (1995) |
| 10 | 0.00292 | 0.00294 | 0.00291 | 0.00291 | 0.00292 | 0.00291 | Cho and Park (2003) |
| 11 | 0.00041 | 0.00094 | 0.00090 | 0.00045 | 0.00091 | 0.00056 | Noh and Lee (1995) |
| 12 | 0.00170 | 0.00178 | 0.00183 | 0.00169 | 0.00184 | 0.00168 | Emolo et al. (2015) |
| 13 | 0.00265 | 0.00357 | 0.00524 | 0.00333 | 0.00445 | 0.00748 | Noh and Lee (1995) |
| 14 | 0.00108 | 0.00115 | 0.00125 | 0.00114 | 0.00142 | 0.00152 | Noh and Lee (1995) |
| 15 | 0.01323 | 0.01237 | 0.01025 | 0.01199 | 0.01122 | 0.02040 | Junn et al. (2002) |
| 16 | 0.01341 | 0.01554 | 0.01775 | 0.01542 | 0.01626 | 0.06710 | Noh and Lee (1995) |
Table 10.
GMPE conformity results using PGA data of 16 earthquake (SAE)
| No. | Noh and Lee (1995) | Park et al. (2001) | Junn et al. (2002) | Cho and Park (2003) | Yun et al. (2007) | Emolo et al. (2015) | Min. error formula |
| 1 | 0.00255 | 0.00244 | 0.00491 | 0.00422 | 0.00410 | 0.00323 | Park et al. (2001) |
| 2 | 0.00342 | 0.00761 | 0.01072 | 0.00659 | 0.01728 | 0.01012 | Noh and Lee (1995) |
| 3 | 0.00207 | 0.00199 | 0.00426 | 0.00367 | 0.00413 | 0.00333 | Park et al. (2001) |
| 4 | 0.02251 | 0.03781 | 0.04450 | 0.02839 | 0.05122 | 0.03558 | Noh and Lee (1995) |
| 5 | 0.01926 | 0.03662 | 0.04468 | 0.02735 | 0.05079 | 0.03945 | Noh and Lee (1995) |
| 6 | 0.02177 | 0.03809 | 0.04381 | 0.02714 | 0.04953 | 0.03413 | Noh and Lee (1995) |
| 7 | 0.02005 | 0.03423 | 0.04098 | 0.02471 | 0.04524 | 0.03614 | Noh and Lee (1995) |
| 8 | 0.01896 | 0.03521 | 0.04395 | 0.02534 | 0.04973 | 0.03258 | Noh and Lee (1995) |
| 9 | 0.02280 | 0.03844 | 0.04796 | 0.03037 | 0.05314 | 0.04127 | Noh and Lee (1995) |
| 10 | 0.02778 | 0.03322 | 0.03267 | 0.02885 | 0.03729 | 0.03105 | Noh and Lee (1995) |
| 11 | 0.00845 | 0.01918 | 0.01964 | 0.01076 | 0.02288 | 0.01455 | Noh and Lee (1995) |
| 12 | 0.03298 | 0.04134 | 0.04454 | 0.03649 | 0.04956 | 0.03870 | Noh and Lee (1995) |
| 13 | 0.08340 | 0.10772 | 0.15102 | 0.10880 | 0.15241 | 0.25320 | Noh and Lee (1995) |
| 14 | 0.02138 | 0.02680 | 0.03912 | 0.03165 | 0.05096 | 0.05379 | Noh and Lee (1995) |
| 15 | 0.22636 | 0.24449 | 0.23818 | 0.22729 | 0.25743 | 0.68732 | Noh and Lee (1995) |
| 16 | 0.29295 | 0.38175 | 0.46357 | 0.40032 | 0.46964 | 1.93439 | Noh and Lee (1995) |
Tables 9 and 10에서 확인할 수 있듯이, PGA 예측 시 Noh and Lee (1995)의 GMPE가 대부분의 지진 데이터에서 최소오차를 나타냄을 확인했다. 총 16개의 지진 데이터 중 RMSE 기준, 11개의 지진에서, SAE 기준 14개의 지진 데이터에서 Noh and Lee (1995)에 의해 제안된 GMPE가 적합함을 알 수 있다. 따라서 PGA의 경우 Noh and Lee (1995)의 GMPE가 가장 적합성이 높은 것으로 판단된다.
결국, 상수도시스템의 시설물 중 땅속에 매설된 관로와 지중에 설치된 건축물의 경우 적합 GMPE가 서로 다를수 있음을 확인하였으며, 상수도시스템의 특성을 명확히 보여주는 관로의 공간적파손확률을 검토하기 위해서는, PGV 예측의 정확도가 높았던 Emolo et al. (2015)의 GMPE를 최종적으로 국내 적용하기 가장 적합한 식으로 결정할 필요가 있음을 확인하였다. Table 11은 Emolo et al. (2015) 식의 PGA 및 PGV 계수를 나타낸다.
Table 11.
Emolo et al. (2015) GMPE's regression coefficient
| a | b | c | h | d | e | |
| PGA | -7.16 | 0.96 | -0.8 | 4.6 | 0.0013 | 0.261 |
| PGV | -5.75 | 0.89 | -0.66 | 4.5 | -0.0019 | 0.289 |
4. 결 론
본 연구에서는 우리나라에서 발생한 지진 계측자료를 기반으로 상수도시스템의 내진성능 평가에 필수적인 GMPE를 적절히 선정하고자 하였다. 이를 위하여 기존 연구에서 제시 및 활용된 바 있는 다수 GMPE의 특성을 우선적으로 분석하여 대표적인 6개 식을 선정하였다. 6개 식의 상대적 적합성을 평가하기 위하여, 국내에서 발생된 10개 이상의 과거 지진 계측자료 (PGV, PGA)를 대상으로 예측을 실시하여 오차분석을 통한 적합한 GMPE를 결정하였다. 적용 결과 Emolo et al. (2015)의 GMPE가 수평구조물인 상수관로에 대해서는 PGV 예측의 정도가 가장 적합한 것으로 나타났으며 배수지, 펌프가 설치될 수 있는 수직 건축 구조물의 경우에 대해서는 Noh and Lee (1995)의 GMPE가 가장 적절한 것으로 나타나, 구조물의 설치 환경이 지진파 감쇠에 직접적인 영향을 미칠 수 있음을 확인하였다. 독립적인 수직건축구조물의 경우 기존 타 건축구조물과 같이 지진에 의한 구조적 성능유지여부가 중요하나, 상수관로의 경우 여러 관로구조물의 연결에 의한 물 공급이 이루어지므로 공간적인 파손확률의 정확도 높은 예측이 요구되며, 이와 같은 공간적 파손확률을 활용한 물공급 가능여부 등이 수리학적으로 분석되어야 한다. 따라서 국내 상수도 관로 시스템의 내진성능평가에 있어 본 연구에서 적합하다고 제시된 GMPE를 활용한다면 보다 합리적이고 정확도 높은 평가가 이루어질 수 있을 것으로 기대된다. 향후, 지속적인 지진계측자료의 축적을 통한 국내에 적합한 새로운 형태의 GMPE 산정 역시 필요한 과제라 판단된다. 본 연구를 통해 결정된 적정 GMPE는 상수도관망의 수리학적 내진성능 평가에 직접적으로 활용 가능하다. 즉, 파손확률 모형과의 연계를 통한 지진시 관로 파손률의 정량화가 가능하며, 파손 및 누수에 의한 단수지역 파악 등과 같은 피해범위 산정시 보다 객관적이며 합리적인 결과 도출이 가능하다. 최종적으로 이와 같은 내진성능 정량화 결과는 지진재해가 발생하였을 경우 그 피해를 최소화할 수 있는 최적 복구방안 마련과 선제적 관망 내진 설계의 기준 자료로 활용될 수 있다.