1. 서 론
2. 자료 및 연구방법
2.1 LSTM
2.2 대상유역 선정
2.3 입력자료 구축
3. 모형 적용 및 분석
3.1 학습변수에 따른 모형성능 분석
3.2 입력변수에 따른 결과 분석
4. 결론 및 고찰
1. 서 론
우리나라의 경우 연 강수량의 약 70%가 홍수기(6∼9월)에 집중되어 있어 홍수피해와 갈수기의 가뭄 피해 또한 증가하고 있으며, 이로 인한 수자원 관리의 어려움이 심화되고 있는 실정이다(Kim and Yang, 2004). 현재 국내에는 물 관련 재해 대응 및 수자원 관리를 위하여 21개의 다목적댐과 14개의 용수댐 등 총 18,000여개의 댐이 운영되고 있으며(Choi et al., 2016; Kang et al., 2010), 저수된 물을 매시간 유입량과 저수량을 고려하여 적절한 방류량을 결정하는 것이 댐 운영의 핵심이다(Kwon and Shim, 1997). 따라서 댐 운영을 위한 선결과제는 정확한 유입량 산정이며, 만약 미래의 댐 유입량을 정확히 예측할 수 있다면 효율적인 댐 운영을 통해 수자원 관리의 어려움을 줄일 수 있다(Eom and Jung, 2019).
기존에는 수위나 유량을 예측하기 위해 주로 개념적 또는 물리적 모형이 사용되어 왔으나 이러한 모형은 기후, 지질, 지형 등 수문과정의 다양하고 복잡한 변수를 모두 고려하기가 어려우며, 매개변수 결정을 위해 많은 자료가 필요하다. 또한 이러한 불확실성으로 인해 계산과정을 거치는 동안 다양한 오차가 반복 누적되는 단점이 있다(Jung et al., 2018).
그러나 최근 데이터 예측분야에서 관심이 높아지고 있는 인공신경망(Artificial Neural Network, ANN)모형은 개념적·물리적 특성과 상관없이 입·출력 자료의 상관관계를 반복 학습하여 정확도 높은 예측을 수행하기 때문에 하천 수위 예측이나 댐 유입량 예측 등 다양한 수문분야에 활용되고 있다(Park et al., 2018). 인공신경망은 인간이나 동물의 생물학적인 뇌의 신경세포(Neuron)를 수학적으로 모델링하여 기계가 스스로 학습할 수 있도록 만든 것이며, 과거에는 학습에 필요한 방대한 자료를 처리할 수 있는 능력이 부족하여 많이 활용되지 않았으나, 최근 빅데이터 처리 기술이 발전함에 따라 다시 주목받게 되었다. 이처럼 빅데이터와 인공신경망을 함께 결합시킨 알고리즘을 딥러닝(Deep Learning)이라고 하며, 다양한 분야에서 활용되고 있다. 딥러닝 알고리즘 중 하나인 LSTM (Long Short-Term Memory)모형은 시계열 자료에 특화된 RNN (Recurrent Neural Network)모형의 긴 시간 의존성 문제를 해결하기 위하여 개발된 알고리즘이며, 구글(Google)에서 개발한 대규모 수치해석 함수인 텐서플로우(TensorFlow)와 결합하여 사용되고 있다.
Jeong et al. (2003)은 강우-유출 모형의 불확실성을 해결하기 위하여 앙상블 신경망 모형을 이용하여 대청댐의 유입량을 예측하였으며, Tank모형의 결과와 비교하여 신경망 모형의 정확도를 검증하였다. 국내 연구로 Kim (2010)은 대청댐 유역을 대상으로 시계열 자료 예측 알고리즘인 ARIMA모형을 이용하여 실시간 유입량 예측을 분석 및 평가하였으며, Bae et al. (2010)은 소양강댐의 과거 유입량 자료와 일기예보 자료를 퍼지추론(Nero-fuzzy) 알고리즘 기법에 적용시켜 댐의 월 유입량을 예측하였다. Jung et al. (2018)은 금강의 수위를 다중회귀분석모형으로 예측한 결과, RMSE가 0.159∼0.231값으로 나타났으나 LSTM모형의 예측 결과, RMSE가 0.012∼0.017로 인공신경망 모형의 예측결과가 더 우수하다는 것을 보였다. 국외의 연구로 Wang et al. (2009)은 중국 양쯔강을 대상으로 자기회귀모형 TAR과 인공신경망을 이용한 웨이블릿 네트워크모델 WNM을 활용하여댐의 유입을 예측하고 비교하였다. 국외 연구로 Tran and Song (2017)은 텍사스 트리니티강의 침수 수위를 예측하기 위해 표준 RNN, RNN-BPTT, LSTM의 세 가지 모형을 이용하였으며, 그 중 LSTM모형의 성능이 가장 우수한 것을 보였다.
본 연구는 LSTM모형을 구축하여 금강 상류에 위치한 용담다목적댐의 유입량을 예측하고 실측값과 비교하여 모형의 학습 변수별 정확도를 평가하였으며, 단일 및 다중 입력 자료에 따른 예측결과를 월별로 분석하여 한정된 수자원을 효율적으로 활용하기 위한 댐 운영 기초 자료로서의 적용성을 판단하였다.
2. 자료 및 연구방법
2.1 LSTM
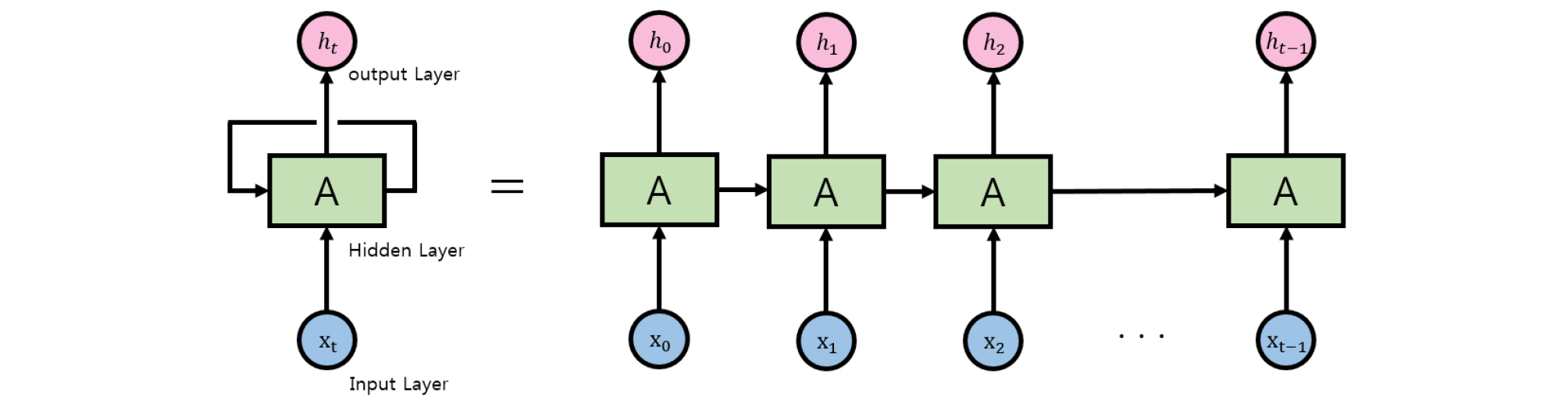
RNN (Recurrent Neural Network)은 시계열 데이터처리에 적합한 알고리즘으로 알려져 있으며, Fig. 1과 같이 스스로 반복학습을 통해 이전 단계에서 얻은 정보를 지속적으로 사용한다. 그러나 얻고자 하는 정보의 시간 격차가 증가함에 따라 학습의 어려움이 발생하며, 이러한 ‘긴 기간 의존성(Long-Term Dependencies)’을 해결하기 위해 Hochreiter (1991)와 Schmidhuber (1997)가 만든 알고리즘이 LSTM (Long Short-Term Memory Network)이다.
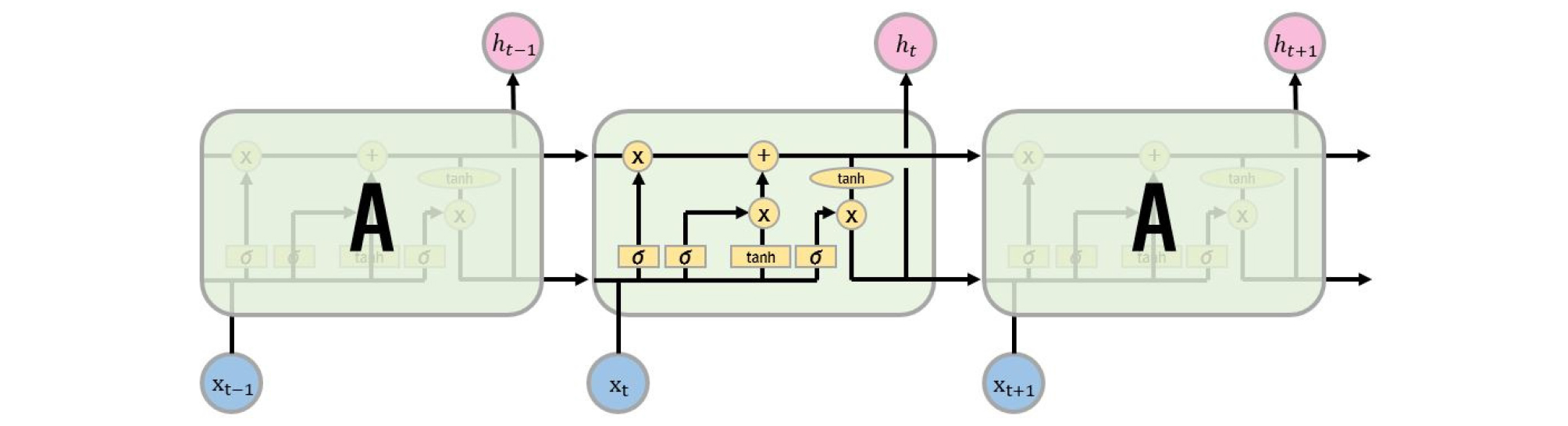
LSTM은 Fig. 2와 같이 하나의 셀(Cell)안에 여러 개의 게이트(Gate)가 존재하며 체인형태를 이룬다. 게이트는 셀을 제어 및 보호하고 망각(Forget Gate Layer), 입력(Input Gate Layer), 출력(Output Gate Layer) 게이트로 나눌 수 있다.
먼저 망각게이트(ft)에서는 정보를 제거할지 유지할지 결정하며 Eq. (1)으로 나타낼 수 있다.
| $$f_t=\sigma(W_f\bullet\lbrack h_{t-1},\;x_t\rbrack+b_f)$$ | (1) |
여기서, : 활성화함수, Wf : 게이트 가중치, ht-1 : 전 단계 출력값, : 새로운 값, bf : 편향값
그 다음 입력게이트(it)에서는 새로운 정보 중 저장할 정보를 결정하며, tanh (Hyperbolic Tangent) 함수를 통해 새로운 셀의 상태를 만든다.
| $${\widetilde C}_t=\tanh\;(W_c\bullet\lbrack h_{t-1\cdot}x_t\rbrack+b_c)$$ | (2) |
| $$i_t=\sigma\;(W_i\bullet\lbrack h_{t-1},x_t\rbrack+b_i)$$ | (3) |
| $$C_t=f_t\;\bullet\;C_{t-1}+i_t\;\bullet\;{\widetilde C}_t$$ | (4) |
여기서, : 활성화함수를 통해 만들어진 새로운 셀 상태, Wc : 셀 상태 가중치, bc : 편향값, Ct : 셀 상태
마지막으로 출력게이트(ot)는 셀에 저장된 정보 중 출력할 값을 결정한다.
| $$o_t=\sigma(W_o\bullet\;\lbrack h_{t-1},\;x_t\rbrack+b_o)$$ | (5) |
| $$h_t=o_t\;\bullet\;\tanh(C_t)$$ | (6) |
여기서, ht는 새로운 출력값이다.
2.2 대상유역 선정
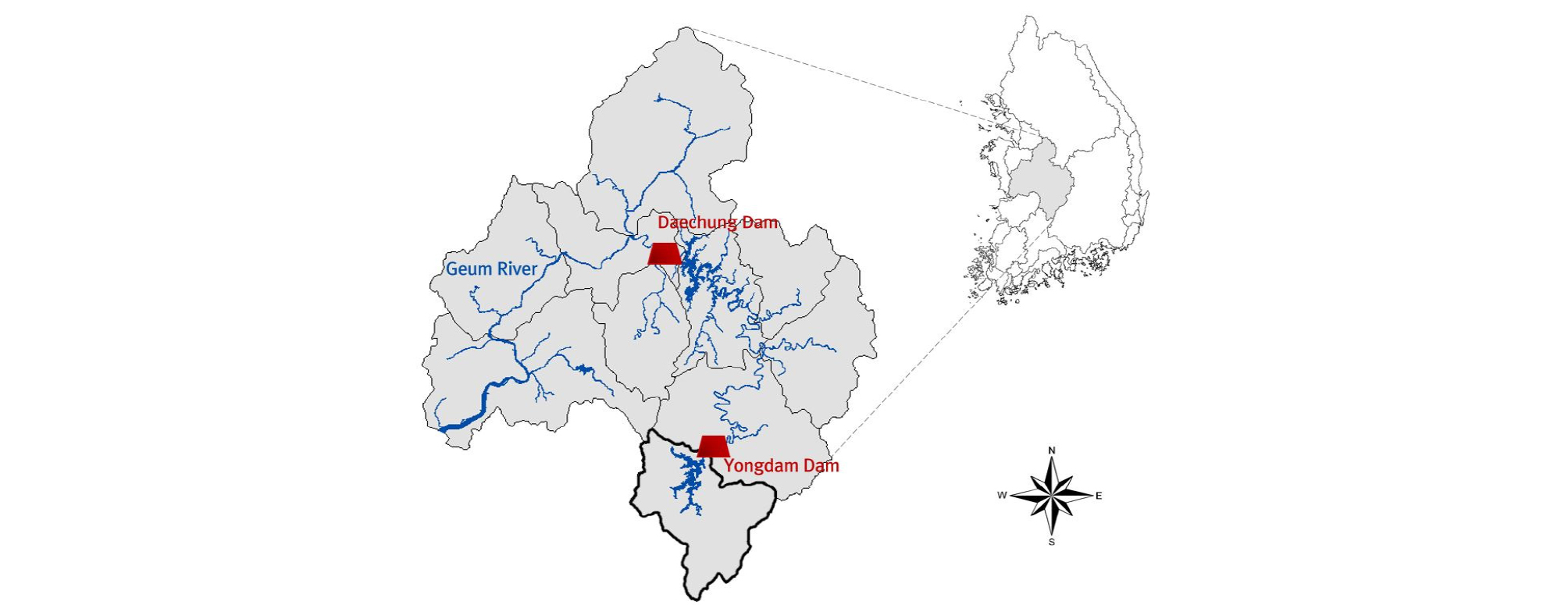
금강 유역에는 총 9개의 댐이 운영되고 있으며, 그 중 다목적댐으로는 대청댐과 용담댐이 있다. 과거 유입량 자료만을 활용하여 미래의 유입량을 예측하기 위해서는 상류댐에 의한 인위적 영향이 적어야 한다고 판단되어 금강 최상류에 위치한 용담 다목적댐을 대상유역으로 선정하였다. 용담댐은 전라북도 진안군에 위치하고 있으며, 금강 본류 외의 주요 유입하천으로는 정자천, 진안천, 구량천, 주자천이 있다. 댐의 높이는 70 m, 댐 길이는 498 m, 총 길이는 38.5 km, 최대수심은 70 m, 저수면적은 37.2 km², 최대 저수용량은 815×10⁶m³으로 국내에서 5번째로 큰 규모를 가진다. 용담댐 유역은 무주군, 진안군, 장수군을 포함한 충청남도, 전라북도, 경상남도에 걸쳐있으며, 유역면적은 930 km²으로 금강유역 면적의 약 9.45%에 해당하며, 용담댐 유역의 면적구성은 79.9%가 산림지대이며, 62.09%가 얕은 토심을 이루고 있다(Fig. 3). 기상적인 특성으로 연평균강우량 1,230 mm, 연평균기온11.6℃이며, 연평균 유입되는 유입량은 32억2천만m³이다.
2.3 입력자료 구축
신경망 모형의 입력 및 검증 자료는 국가수자원관리종합정보시스템(WAMIS)에서 제공하는 용담댐의 2006년부터 2018년까지의 시간당 유입량 자료를 사용하였다. 용담댐의 시간당 유입량은 유입하천의 개수가 많고 복잡하여 직접 측정이 어렵기 때문에 수위-유량 관계 곡선을 통해 산정하며, 이 과정에서 이상치(Outlier)가 발생한다. 이상치는 모형의 예측 성능을 저하시키고 결과가 왜곡될 수 있기 때문에 보정이 필요하며, 이를 판단하고 보정하기 위하여 용담댐 유역의 시간당 강수량을 산정하였다.
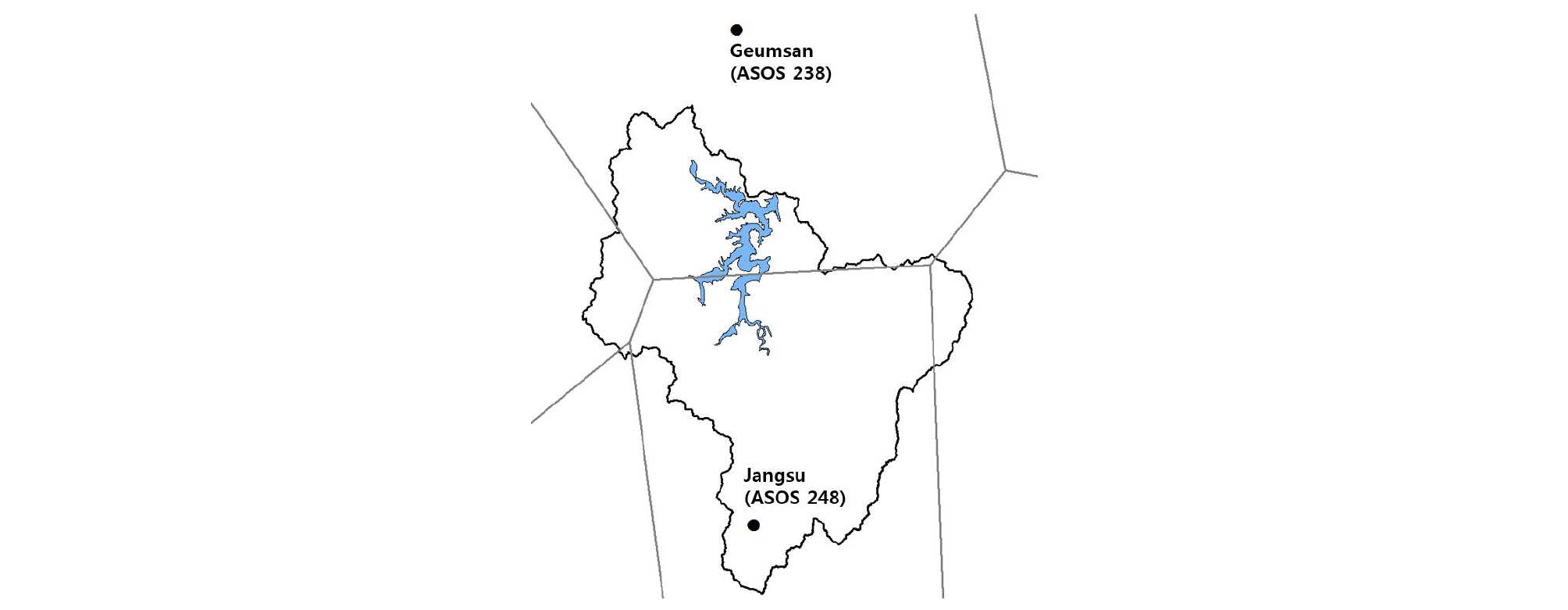
종관기상관측(ASOS) 지점인 장수(248번)와 금산(238번)의 강수량 자료를 활용하여 용담댐 유역의 2006년부터 2018년까지의 시간당 강수량을 산정하였으며, 두 관측소의 위치는 Fig. 4와 같다. 본 연구에서는 산정된 용담댐유역의 시간당 강수량과 유입량을 비교한 결과, 강우가 발생하지 않았음에도 불구하고 높은 유입량이 발생하는 경우를 이상치로 판단하였으며, 그 값을 전후 한 시간 유입량 자료의 평균치로 보정하였다.
신경망 모형이 넓은 범주의 자료를 학습할 때에는 함수값이 발산하여 예측의 성능을 저하시키기 때문에 몇 가지 방법에 의하여 활용하기 좋은 정보로 가공하여야 한다. 이러한 과정을 전처리(Pre-processing)이라 하며, 대표적인 전처리 방법으로는 정규화(Normalization)와 표준화(Standardization)가 있다. 용담댐의 시간당 유입량자료는 이상치를 제거한 후에도 최소값 0.1 ㎥/s부터 최대값 3,373.2 ㎥/s까지 넓은 범주를 가지고 있어 반드시 전 처리 과정을 거쳐야 한다. 따라서 본 연구에서는 정규화 작업을 통하여 모든 입력 자료를 0부터 1사이의 값으로 변환하였으며, 정규화 함수의 식은 Eq. (7)와 같다.
| $$Y_i=\frac{X_i-X_\min}{X_\max-X_\min}$$ | (7) |
여기서, Yi : 정규화된 변수값, Xi : 실제 변수값, Xmin : 변수의 최소값, Xmax : 변수의 최대값
3. 모형 적용 및 분석
3.1 학습변수에 따른 모형성능 분석
본 연구에서는 모형이 2006년 1월 1일부터 2015년 2월 5일까지의 자료를 학습하여 2015년 2월 5일부터 2018년 12월 31일까지의 유입량을 예측하도록 하였다. 훈련 구간에서 이루어지는 학습의 방식은 다양한 변수(Train Parameter)에 따라 달라지며, 학습 방식은 모형의 예측 성능과도 직결된다. 따라서 본 절에서는 4가지 변수에 따른 모형의 정확도를 판단하여 가장 적합한 모형을 선정하였다. 모형의 정확도를 판단하기 위한 지표로써 평균제곱근오차(RMSE, Root Mean Square Error), 평균절대오차(MAE, Mean Absolute Error), 용적오차(VE, Volume Error)를 사용하였으며, 산정식은 Eqs. (8)~(10)와 같다. 세 가지 오차 모두 그 값이 0에 가까울수록 높은 정확도를 나타낸다.
| $$\mathrm{RMSE}\;=\sqrt{\frac{{\displaystyle\sum_{i=1}^N}{(y-\widehat y)}^2}N}$$ | (8) |
| $$\mathrm{MAE}=\frac{{\displaystyle\sum_{i=1}^N}\left|y-\widehat y\right|}N$$ | (9) |
| $$\mathrm{VE}=\frac{{\displaystyle\sum_{i=1}^N}y-{\displaystyle\sum_{i=1}^N}\widehat y}{{\displaystyle\sum_{i=1}^N}y}\times100(\%)$$ | (10) |
여기서, : 예측값, : 실제값, N : 데이터의 개수
시퀀스 길이(Sequence Length)는 모형이 한 시점의 데이터를 학습하는데 몇 시간 자료를 이용할지 결정한다. 모형이 자료의 복잡성을 학습하는데 있어 은닉층의 크기(Hidden Dim)가 클수록 유리하지만, 오히려 과적합(Overfitting)이 발생할 수 있기 때문에 적절한 크기를 설정하는 것은 매우 중요하다. 학습계수(Learning Rate)가 큰 값을 갖게 되면 빠른 학습이 가능하지만 최소값을 구하기 전에 발산(Overshooting)할 수 있으며, 반대로 너무 작은 값을 갖게 되면 최소값을 찾는 학습시간이 길어진다는 문제점이 있다. 전체 자료를 한 번에 학습하는 것은 속도 저하와 메모리의 한계 등의 문제가 발생하기 때문에 학습의 반복횟수(Iteration)에 따라 나누어 진행하여야 한다. 다양한 변수 조건에 따른 모형의 성능을 비교하기 위하여 4가지 학습 변수인 Sequence Length, Hidden Dimension, Learning Rate와 Iteration의 값을 변화시켜 조합함으로써 총 16개 모형을 구축하여 실시하였고 그 결과는 Table 1과 같다. 16가지 모형의 RMSE는 0.004∼0.0197사이의 값으로 산정되었으며, 특히 8번과 11번 모형의 RMSE는 0.0006(0.06%)과 0.0004(0.04%)로 가장 낮은 오차율을 보였다. MAE 값은 6.85∼9.56으로 10번과 11번 모형이 가장 낮게 산정되었다. VE는 14번 모형을 제외하고는 0.1∼3.57사이의 값으로 산정되었으며, 6번과 8번이 가장 작은 값을 갖는다. 대체적으로 Learning Rate와 Iteration의 값은 작을수록, Sequence Length와 Hidden Dim의 값은 클수록 모형의 성능은 향상하는 것으로 볼 수 있으나, 이것이 절대적인 기준은 되지 않는다는 것을 알 수 있다.
Table 1. Model performance results according iteration
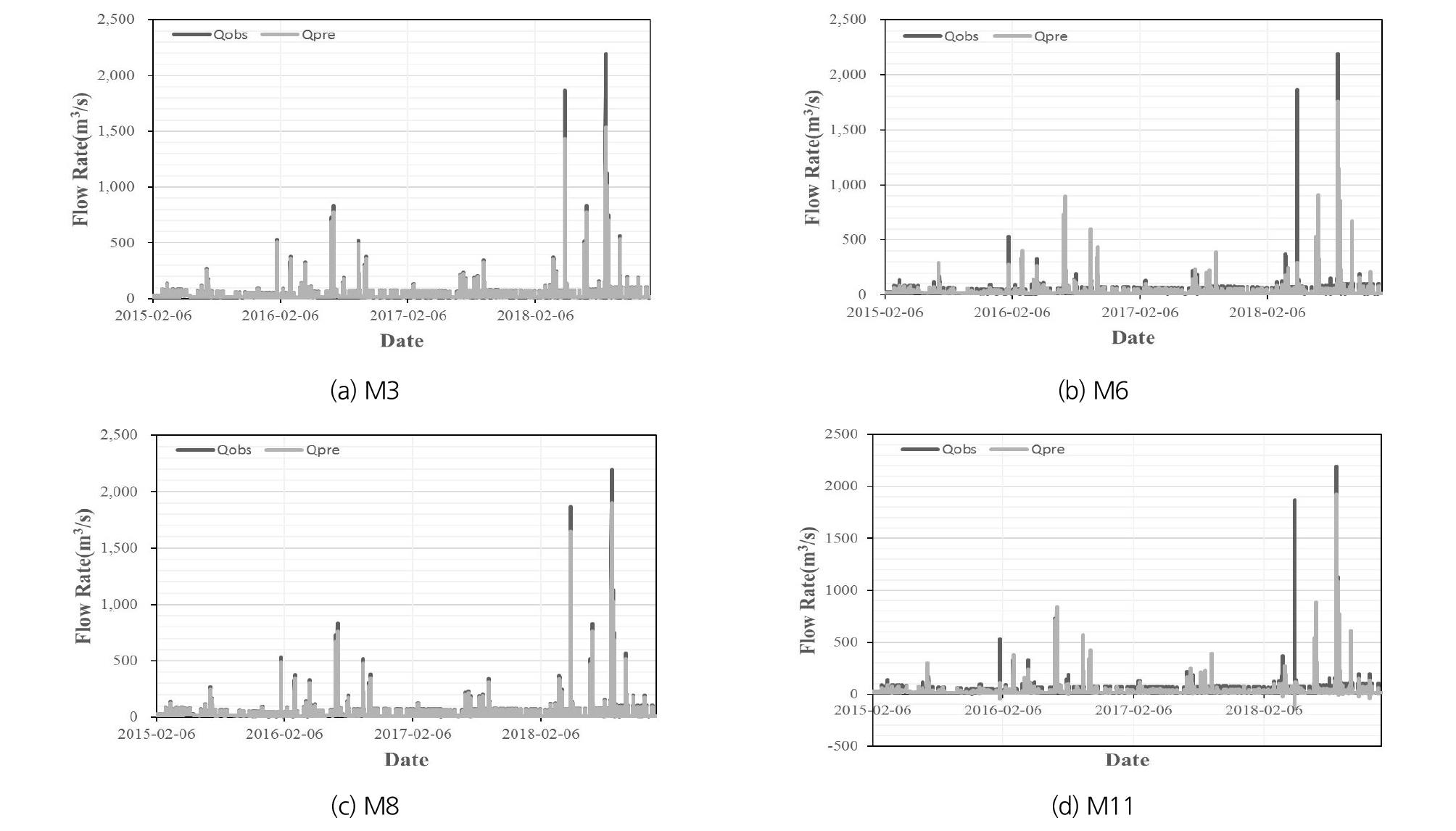
세 가지 오차를 기준으로 가장 성능이 좋은 모형은 M3, M6, M8, M11 으로 볼 수 있으며 그 결과는 Table 2, Fig. 5와 같다. 네 가지 모형의 예측 유입량은 실제 관측 유입량과 비교하였을 때 최소·최대 유입량은 차이를 보이지만, 예측 기간의 평균 유입량과 총 유입량은 실측값과 비슷하게 나타났다. 그 중 모형 M8의 예측유입량이 관측유입량에 가장 가깝게 산정된 것으로 보아, 최종적으로 Sequence Length가 3, Hidden Dim이 20, Learning Rate가 0.0001, Iteration이 5000일 때 성능이 가장 좋은 것으로 판단된다.
Table 2. Boundary value of observed and predicted inflow
3.2 입력변수에 따른 결과 분석
일최대유입량(Daily Maximum Inflow)은 수공구조물의 설계와 운영에 있어 중요한 지표가 된다. 그러나 Table 2에서 LSTM모형의 과거 유입량 자료만을 이용한 예측 최대유량은 모두 실제유량보다 과소 추정되는 것을 알 수 있다. 이러한 문제점은 학습 자료로 더 많은 유입량 자료를 이용하여 해결할 수 있으나, 용담댐과 같이 과거 유입량 자료의 개수가 적을 경우 새로운 입력 자료를 활용하여야 한다. 따라서 본 절에서는 용담댐 유역의 시간당 강수량 자료를 새로운 입력자료(Input Data)로 사용하여 분석을 실시하였으며, 분석에 사용되는 학습변수는 모형 M8과 동일하게 하였다.
3.2.1 유입량 비교분석
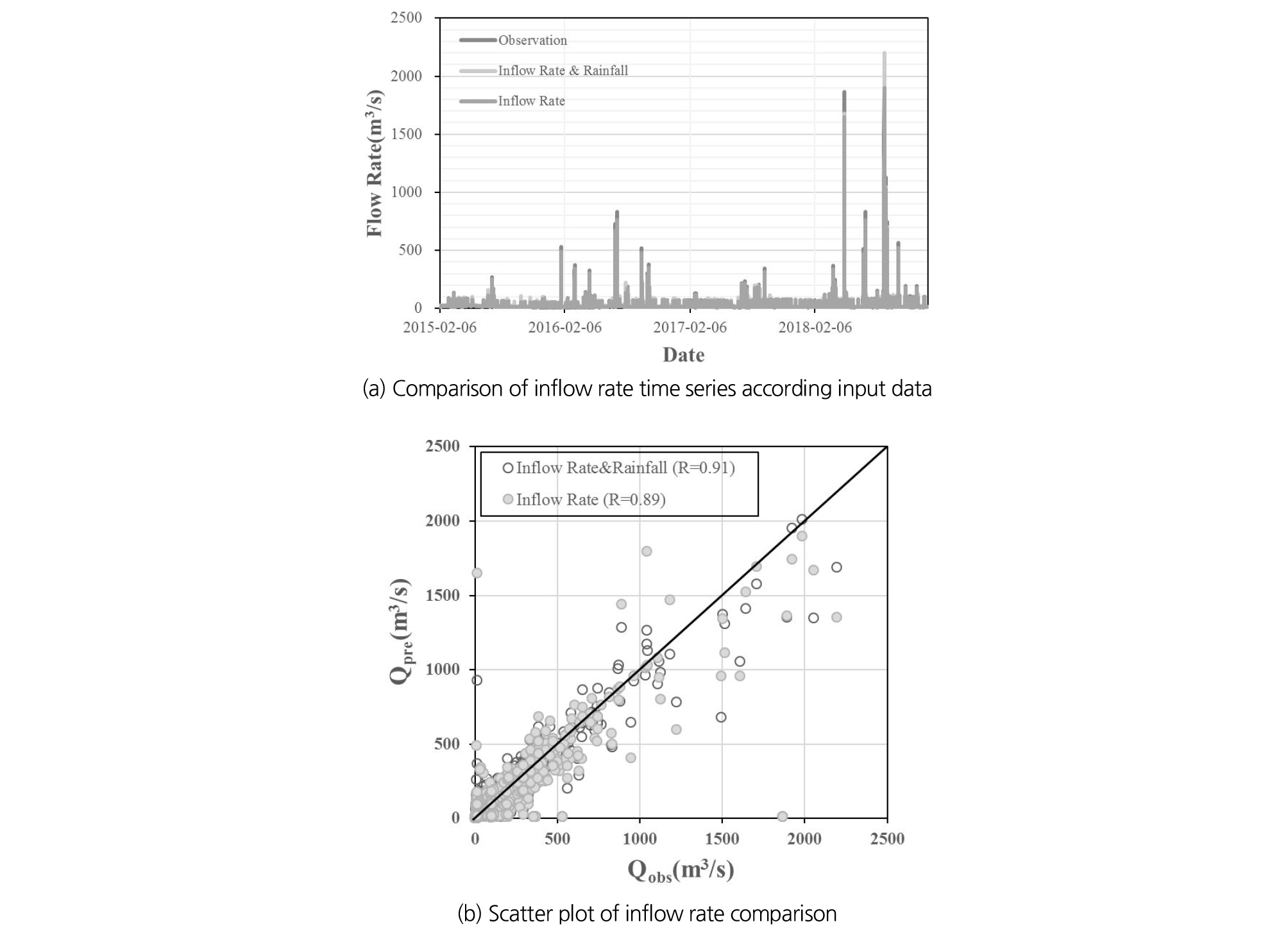
Fig. 6(a)는 유입량 자료만 이용한 모형과 강수량 자료를 추가로 이용한 모형의 예측 유입량을 실제 유입량과 함께 예측 기간에 대한 시계열 자료로 나타낸 것이다. Fig. 6(b)에서 유입량 자료만을 이용한 경우 상관계수가 0.89, 강수량 자료를 추가한 경우 0.91로 기간 전체의 예측 정확도는 상승한 것을 알 수 있다. 예측 기간의 최소유입량, 최대유입량, 평균유입량, 총 유입량을 실제 유입량과 비교하였을 때(Table 3) 강수량 자료까지 이용한 경우가 유입량 자료만 이용한 경우보다 최대유입량이 1,871.50 ㎥/s에서 2,037.79 ㎥/s까지 166.29 ㎥/s만큼 증가하였고, 평균유입량은 0.06 ㎥/s 증가하였다. 그러나 최소유입량까지 증가추세를 보이며, 실제 유입량의 최소치보다 1.27 ㎥/s만큼 높아졌다. 따라서 강수량 자료를 이용한 경우 예측유입량은 전체적으로 증가하나, 여전히 최대유량은 관측값보다 각각 155.11 ㎥/s 작게 산출된다는 것을 알 수 있다.
Table 3. Model performance results according input data-inflow
| Classify | Inflow (m3/s) | ||||
| Min | Max | Avg | Total Vol. | ||
| Observation | 0.10 | 2,192.90 | 23.78 | 812,997.30 | |
| Input Data | Inflow Rate | 0.34 | 1,871.50 | 23.76 | 812,179.12 |
| Inflow Rate & Rainfall | 1.37 | 2,037.79 | 23.82 | 814,142.20 | |
3.2.2 오차 비교분석
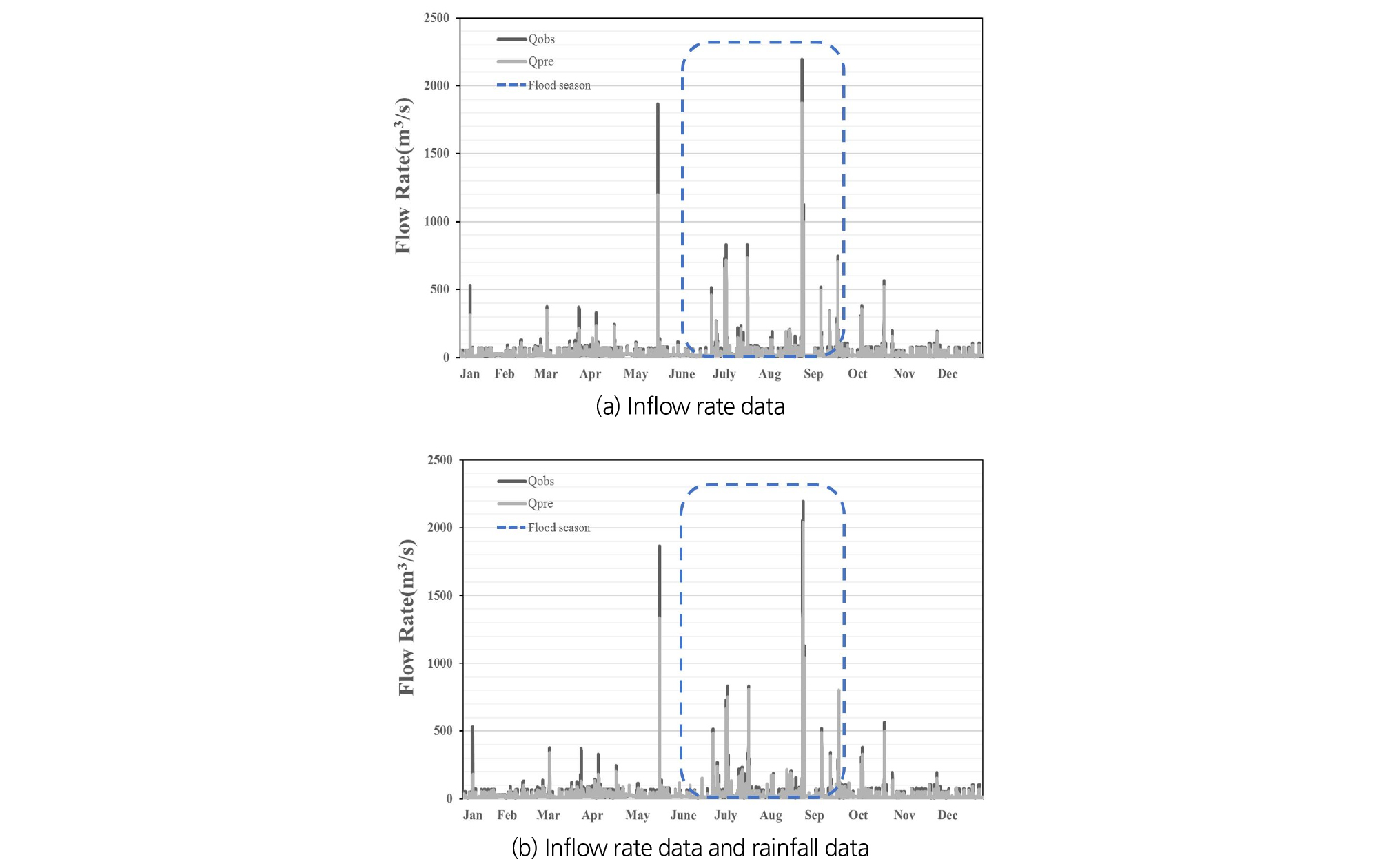
다음은 입력 자료에 따른 오차를 비교하기 위해 예측 결과의 RMSE, MAE, VE를 산정하였으며, 그 결과는 Table 4와 같다. 유입량 자료와 강수량 자료를 함께 사용하여 예측을 수행한 결과, 유입량 자료만 이용했을 때보다 MAE와 VE는 낮아졌으나, RMSE는 오히려 더 높아진 것을 알 수 있었다. Fig. 7은 월별 예측 유입량을 비교한 결과이다.
Table 4. Model performance results according input data-error
| Input Data | Error | ||
| RMSE | MAE | VE | |
| Inflow Rate | 0.0006 | 7.01 | 0.10 |
| Inflow Rate & Rainfall | 0.0054 | 7.00 | -0.01 |
강수량 자료를 함께 이용한 경우(Fig. 7(b)), 강수량이 많은 홍수기(6∼9월)에는 예측유량과 관측유량의 차가 유입량 자료만 이용했을 때(Fig. 7(a))보다 작게 나타나지만, 강수량이 적은 이수기에는 오히려 강수량 자료를 이용하지 않은 경우보다 과소 추정된 것을 알 수 있었다. 이로 인해 강수량 자료를 이용한 모형의 MAE와 VE는 더 낮지만, RMSE는 더 크게 산정된 이유를 알 수 있었다. 결론적으로, 홍수기의 최대유입량을 예측하고자 할 때에는 강수량 자료를 함께 사용하는 것이 더 좋을 것으로 판단되며, 홍수기를 제외한 이수기에는 강수량 자료를 사용하지 않는 것이 더 정확한 것으로 판단된다.
4. 결론 및 고찰
본 연구에서는 금강 유역에 위치한 용담 다목적댐을 대상으로 시계열 자료 예측에 큰 강점을 갖는 LSTM모형을 이용하여 댐 유입량 예측 분석을 실시하였다. 분석 자료로는 WAMIS에서 제공하는 용담댐의 2006년부터 2018년까지의 시간당 유입량 자료를 사용하였으며, 역대 최대 유입량과 강수량자료를 바탕으로 이상치를 제거하였다. 또한 신경망 모형의 입력 자료로 활용하기 위한 전처리 과정으로 모든 자료를 0에서 1까지의 값으로 정규화 하였다. LSTM모형은 파이썬 언어를 활용하여 구축하였으며, 전체 데이터를 훈련데이터와 예측데이터로 나누어 예측을 실시하였다.
LSTM모형은 여러 가지 변수를 조정하여 학습방식을 설정할 수 있는데, 이에 따른 예측의 정확도가 달라지기 때문에 최적의 학습변수를 찾는 것이 중요하다. 본 연구에서는 Sequence Length, Hidden Dim, Learning Rate, Iteration의 변화에 따른 예측분석을 실시하였으며, 총 16개 모형의 분석 결과, 모든 모형의 RMSE는 0.004∼0.0197, MAE는 6.85∼9.56, VE는 0.1∼3.57사이의 값으로 산정되어 매우 높은 정확도의 예측을 수행한다는 것을 알 수 있다. 그 중 Sequence Length=3, Hidden Dim=20, Learning Rate=0.0001, Iteration=50000의 값을 갖는 모형의 RMSE가 0.0006, MAE가 7.01, VE가 0.1으로 예측 성능이 가장 우수한 것으로 판단되었다. 그러나 모형의 성능이 높아짐에 따라 분석시간 또한 증가하기 때문에 대용량 데이터 분석 시 분석시간 또한 고려해야 할 것으로 생각되며, 실제 실무에서 활용하기 위해서는 사용자의 판단으로 적절한 학습변수를 설정하는 것이 중요할 것으로 생각된다.
또한 예측 유입량을 실제 유입량과 비교하였을 때 평균 유입량과 총 유입량의 차이가 적게 나타나기 때문에 계절규모의 댐 운영에 효율적인 예측 시스템으로 활용가능 할 것으로 보여진다. 그러나 예측 유입량의 최소 및 최대 유입량은 모형의 성능에 관계없이 실제 유입량과 차이를 보이는데, 최대 유입량은 홍수기 댐 운영에 있어 중요한 지표가 될 수 있기 때문에 이러한 문제점을 해결하고자 강수량 자료를 추가 입력 자료로 활용하였다. 강수량 자료를 과거 유입량 자료와 함께 입력하여 예측한 결과 실제 첨두유량에 가까워졌으나, 전체적으로 값이 상승하여 오히려 최저 유량과의 차이가 커지는 문제점이 발생하였다. 따라서 홍수기 유량을 예측할 때에는 강수량 자료도 함께 사용하는 것이 좋다고 판단되나, 홍수기를 제외한 이수기에는 강수량 자료를 이용하지 않는 것이 더 적합하다고 판단된다. 따라서 용담댐과 같이 과거 유입량 자료가 부족한 경우, 유입량에 관련된 다양한 인자들을 모형의 추가 입력 자료로 사용한다면 실제 댐 운영에 사용가능한 신뢰도 높은 예측 유입량을 산정할 수 있을 것이라 기대된다.