1. 서 론
2. 기본이론
2.1 기계학습 알고리즘
2.2 예측 정확도 평가
3. 모형구축
3.1 대상 유역 현황
3.2 입력자료
3.3 학습 파라메터
4. 모의결과 및 분석
4.1 예측 결과
4.2 홍수예측모형의 예측 정확도 분석
5. 결 론
1. 서 론
최근 전세계적인 기후변화의 영향으로 강우가 집중되고 강우강도가 강해지면서 홍수피해의 규모를 증가시키고 있다. 기존에는 관측되지 않았던 규모의 강우가 내리는가 하면 기록적으로 장기간 동안 장마가 지속되기도 한다. 특히, 이러한 피해들은 아세안 국가들에 집중되고 있으며, 최근 해수면상승, 태풍 및 집중호우로 인해 침수가 빈번히 발생하는 등 아세안 국가 국민들 중 최소 2,000만 명이 영향을 받고 있다.
인도네시아는 최근 20년 간 급속한 경제성장과 도시화 과정에서 인구와 산업의 과도한 도시집중으로 인해 자카르타와 반둥을 포함하는 광역 수도권 지역은 홍수발생으로 인한 피해 위험에 직면해 있다. 특히, 찌따룸강 상류 유역에 위치한 반둥 지역은 지형학적으로 분지 형태를 가지고 있어서 홍수에 매우 취약한 실정이다. 이에 인도네시아 공공사업주택부(Ministry of Public Works and Housing, MPWH)는 구조적인 홍수관리대책 시행과 더불어 한국국제협력단(KOCIA)의 무상원조사업(ODA)을 통해 2017년에 찌따룸강 상류(Upper Citarum River) 유역에 대하여 홍수예경보시스템을 구축하여 운영 중에 있다. 그럼에도 불구하고, 찌따룸강 상류(Upper Citarum River) 지역은 홍수발생시 인명 및 재산피해의 위험에 여전히 노출되어 있어 신속하고 정확한 홍수예경보의 실시를 통해 피해를 경감시키는 노력이 지속적으로 필요한 실정이다.
인공지능을 활용한 홍수예측 연구는 국내외에 아주 활발하게 진행되고 있다. Fang et al. (2021)은 홍수민감도를 예측하기 위해 LSTM 기법을 활용하여 홍수취약성 지도를 작성하여 의사결정지원모델을 제안하였다. Le et al. (2019)은 일별 유출량과 강우량을 입력데이터로 하여 LSTM으로 하천의 유량을 예측하는 모델을 제시하였다. Tran and Song (2017)은 텍사스 트리니티강의 침수 수위를 예측하기 위해 표준 순환신경망(Recurrent Neural Network, RNN), RNN-BPTT, LSTM의 세 가지 모형으로 예측하였고, 가장 우수한 성능의 모형을 제시하였다. 국내에서는 Kim et al. (2023)은 홍수예경보시스템 운영을 지원하기 위해 필리핀 동비사야스(Eastern Visayas)의 CarayCaray 유역의 홍수예측을 위하여 심층신경망(DNN)과 LSTM을 적용한 바 있으며, Kim et al. (2022)은 도달시간이 짧은 소하천의 홍수위예측을 위하여 심층신경망(DNN)과 장단기 메모리(LSTM) 모형을 이용하여 왕숙천의 남양주시(진관교) 지점에 대해 홍수위 예측력을 평가하였다. Kim et al. (2021)이 LSTM을 적용하여 설마천의 전적비교 관측소의 홍수위를 예측하는 모형을 개발하였으며, Jung et al. (2021)은 장단기 메모리(LSTM) 기반의 딥러닝 기법을 적용하여 섬진강 수계 구례 지점의 하천 수위를 선행예측하고 기존의 서포트벡터머신(SVM) 모형과 다층퍼셉트론(MLP) 모형을 적용한 결과와 비교분석하여 적용성을 평가하였다. Lee et al. (2021)은 심층신경망(DNN)과 LSTM을 기반으로 한 딥러닝 모형을 활용하여 태화강 유역의 울산시(태화교) 지점의 수위를 예측하여 기존 물리적 모형에 의한 예측결과와 비교 평가하였다. Park and Kim (2020)은 LSTM으로 2개의 상류지점 수위를 이용하여 수위를 예측하는 하드웨어 및 소프트웨어를 개발하여 검증하였다. Yoo et al. (2019)은 시간적 매개변수(Time delay = 2시간)를 고려한 NARX 신경망 모형을 사용하여 한강대교의 수위를 예측하였으며 적합성 판단을 위하여 인공신경망(ANN) 모형과 순환신경망(RNN) 모형의 결과를 비교하는 연구를 수행하였다. 또한 Jung et al. (2018)은 감조하천의 수위예측을 위하여 한강 잠수교를 대상으로 LSTM을 적용하여 시퀀스길이에 따른 정확도를 검토하였다.
본 연구에서는 시계열 예측에 주로 사용되는 LSTM을 활용하여 동일지점의 수위와 강우자료를 활용하여 수위를 예측하는 모형을 개발하였으며, 소유역의 산지하천에 대한 최적선행예보시간을 제안하였다.
2. 기본이론
본 연구에서는 기존의 홍수예경보시스템에서 활용하고 있는 물리적 기반 홍수예측모형을 보완하여 신속한 경보가 가능한 인공지능 기반의 홍수예측모형을 개발하였다. 또한, 다양한 방법으로 예측의 정확도를 분석하여 인공지능 기반의 홍수예측 모형의 적용성을 검토하였다.
2.1 기계학습 알고리즘
본 연구에서는 기존의 관측값을 학습하여 선행예보시간별로 홍수위를 예측하는 모형을 구축하였다. 관측값은 10분 단위 시계열 자료의 형태를 가지고 있어 시계열 기계학습에 적합한 기법을 적용하는 것이 필요하다. 시계열 자료의 기계학습을 위하여 최근에는 초기의 RNN을 개선한 LSTM (Long Short-Term Memory)이 적용되고 있다. LSTM은 RNN의 단점인 시점이 길어질수록 과거의 정보가 뒤로 충분히 전달되지 못하는 장기의존성(Long-Term Dependencies) 문제를 해결한 모형으로 RNN에서 발생하는 오차경사의 기울기 소실 및 최적화 오류를 해결하고 입력 자료에 대한 정보를 더욱 장기적으로 기억하기 위해 은닉층에 셀 상태(cell state) 구조를 추가한 모형이다(Jung et al., 2018). RNN이 은닉층 내에 1개의 하이퍼탄센트(tanh) 층(layer)을 두고 있는 것에 반해 4개의 layer가 특별한 방식으로 정보를 주고받도록 되어 있다(Olah, 2015)(Fig. 1). 따라서, 본 연구에서는 LSTM을 활용하여 홍수예측 모형을 구축하였다.
LSTM에서는 입력게이트(input gate), 망각게이트(forget gate), 출력게이트(output gate)가 있어 전 단계의 정보 중에서 버릴 것과 업데이트 할 것을 결정하여 다음 단계로 전달한다. 먼저 망각게이트는 어떤 정보를 버릴 것인가에 대한 계산을 하며, 이전 단계의 과 현재 단계의 를 시그모이드 함수(sigmoid function)에 적용하여 0과 1사이의 값을 산정한다. 이 값은 현재 상태와 곱해지게 되며, 이 과정에서 정보를 사용할지 제거할지를 선택한다. 다음으로 입력게이트라 불리는 시그모이드 함수가 업데이트할 데이터를 결정한다. 하이퍼탄젠트(tanh) 함수를 통해 새로운 후보 값들의 벡터를 만들게 되고, 값과 조합하여 셀 상태에 더한다. 이런 과정을 통해 과거 상태의 값을 업데이트해서 새로운 상태의 값을 만든다. 마지막으로 출력게이트를 통해 최종적인 결과가 도출되며, 셀 상태의 도출되는 부분을 결정하는 단계가 된다.
본 연구에서는 LSTM 모형의 셀의 units 변수로 ‘hidden_dim’과 ‘hidden_layer_unit’를 파라미터로 LSTM 레이어 구성 부분을 설정하고, ‘gate’ 정보의 경우 기본적인 LSTM 메카니즘에 따라 레이어를 설정하였다. 본 연구의 LSTM 모형은 3개의 은닉층(hidden layer)을 가지고 있으며 각각의 층(layer)간 ‘hidden state’ 값을 전달하기 위해 ‘return_sequences=True’로 설정하여 모든 ‘hidden state’ 값이 반환되도록 설정하였다. 또한 ‘return_states’의 설정을 통해 ‘cell state’의 반환을 설정하게 되는데 기본값은 ‘False’로 하여 마지막 시간 단계에 대한 표현만 필요할 경우에 사용된다. 이는 입력과 동일한 차원의 출력이나 전체 시계열에 대한 결과를 도출하지 않고 특정 기간의 시계열 예측을 도출하기 때문에 기본값으로 설정하였다. 그리고, 예측결과의 과적합 방지를 위해 입력게이트에서 각 층(layer)에 ‘Drop-out rate’를 설정하였다.
2.2 예측 정확도 평가
LSTM 기반 홍수위 예측 모형의 성능을 평가하기 위하여 6개의 지표를 적용하였다. 홍수위 예측에 대한 전반적인 평가를 위하여 통계변량인 Nash-Sutcliffe 효율성 계수(NSE; Nash-Sutcliffe model efficiency coefficient), 결정계수(R2; Coefficient of determination) 및 평균 제곱근 오차(Root Mean Squared Error, RMSE)를 사용하였다(Krause et al., 2005). 또한, 홍수예측 특성상 첨두수위 예측 정확도도 중요한 요소이므로 첨두수위 예측에 대한 정확도를 평가하기 위하여 첨두오차(Error of peak value, EPeak)를 적용하였으며, 오차의 분석을 위하여 최대오차(Maximun error, Emax)와 평균 절대 백분율 오차(Mean Absolute Percentage Error, MAPE)를 적용하여 오차를 정량화하였다. 각 지표별 산정식과 범위는 Table 1에 나타냈다.
Table 1.
Fit Indicators and equations for validating prediction accuracy
NSE는 모형의 예측능력을 평가하는 통계적 지표로 -∞~1의 범위에서 나타나며, NSE가 1에 가까울수록 예측값이 관측값의 경향을 잘 반영하는 것으로 판단할 수 있고, NSE가 음의 값이면 예측값보다 관측값을 평균한 값이 더 예측 성능이 좋다는 것을 나타낸다.
R2는 모형의 예측값과 관측값 사이의 상관관계를 나타내는 지표로 0~1의 범위에서 나타나며, R2가 0이면 예측값과 관측값 사이에 상관관계가 없고, 1이면 예측값이 모든 관측값에 정확히 부합한다고 판단할 수 있다. R2는 예측값과 관측값의 경향이 유사하지 않아도 서로 선형관계를 이루는 조건에서 1에 근접한 값을 나타나는 특성이 있으나, NSE는 이러한 한계는 없다.
RMSE (Root Mean Squared Error)는 예측값과 관측값이 얼마나 일치하는지를 나타낸다. 예측값과 관측값이 정확하게 일치할 때 RMSE는 0이며, 일치하는 정도가 감소할수록 RMSE값이 커지게 된다. 첨두오차는 첨두에서 발생하는 예측값과 관측값의 오차를 나타내며, 0에 가까워질수록 예측된 첨두수위의 정확도가 높다고 판단할 수 지표이다.
최대오차(Maximum error)는 예측값과 관측값간에 최대로 발생하는 오차의 절대값을 나타내고, 평균 절대 백분율 오차(Mean Abosolute Percentage Error, MAPE)는 예측값과 관측값의 차이를 관측값으로 나누어 백분율로 표시한 지표로서 2개의 지표는 0에 가까워질수록 예측정확도가 높아지는 것을 의미한다.
3. 모형구축
본 연구에서는 찌따룸강 상류 유역의 수문관측자료를 수집하여 LSTM 기반의 예측모형 개발을 위한 입력자료를 구성하였다. 대상 유역에서 자료의 결측이나 이상치 등을 검토하여 수문자료가 양호한 수위관측소 2개소 및 강우관측소 4개소를 선정하였다. 이어 선정된 관측소의 강우 및 수위 자료를 활용하여 학습, 검증, 시험 자료로 분류하여 구축하였으며, LSTM 알고리즘을 바탕으로 모형을 개발하였다.
3.1 대상 유역 현황
인도네시아 서부 자바(West Java)에 위치한 찌따룸(Citarum)강 유역의 홍수예경보시스템은 2017년 찌따룸강 상류(Upper Citarum River)를 대상으로 시스템이 구축되어 현재 찌따룸강 유역관리청(BBWS Citarum)에서 운영 관리 중에 있다. KOICA (2017)에 따르면, 찌따룸강 상류의 유역면적은 1,825 km2이고 해발표고 625~2,600 m 사이에 위치하고 있으며, 큰 규모의 오목한 분지 형상으로서 홍수발생시 침수에 취약한 특성을 가지고 있다. 찌따룸강 상류 구간의 본류 36 km 구간내 하상표고의 차이는 약 11.62 m로 하상경사는 0.000323로 알려져 있다.
찌따룸강 상류 유역에는 강우관측소 13개소, 수위관측소 8개소가 설치되어 있고(Fig. 2), 관측자료는 매 10분 간격으로 찌따룸강 유역관리청에 있는 서버로 송신되어 수집되고 있다.
3.2 입력자료
본 연구에서는 찌따룸강 상류 수위관측소중에서 홍수피해 정도가 심하면서 하류에 위치한 Dayeuh Kolot 지점을 목표수위관측소로 선정했다. 이는 상류에 위치한 강우관측소 및 수위관측소 등의 참조관측소를 최대한 많이 확보하여 참조관측소 선택조건에 따른 LSTM 모형의 예측정확도를 검토하기 위해서이다. 앞서 서술한 바와 같이 찌따룸강 상류 관측소는 10분 단위의 강우와 수위 관측 자료의 확보가 가능하다. 2016년 7월 1일부터 2023년 5월 31일까지의 강우 및 수위자료를 수집하였으며, 강우 및 수위자료를 검토하여 결측기간과 홍수예측시 학습효과가 없는 8시간 이상 지속되는 무강우 기간은 입력자료에서 제외하여 학습자료를 구축함으로써 학습의 효율성을 높이고자 하였다.
전처리후의 강우 및 수위자료는 Fig. 3에 나타냈다. 2017년 1월~2020년 2월 자료는 학습자료(training data)로 활용되며, 이 중 후반부 20%는 검증(validation)에 활용되고 모델에서 자동으로 추출된다. 2020년 2월~2021년 1월 자료는 시험(test)에 활용된다. 각각의 기간 및 자료의 수는 Table 2에 나타냈다.
Table 2.
Period of flood and simulation conditions for original and preprocessed data
| Classification | Original data | Preprocessed data |
| Period of flood | 2016-07-01 00:00~2023-06-15 14:40 | 2017-01-11 15:00~2021-01-02 14:10 |
| Number of data | 336,919 | 81,594 |
Dayeuh Kolot 수위관측소를 목표관측소로 하고, 상류의 강우 및 수위관측소를 참조관측소로 하여 선행예보시간(현재시점 기준으로 0.5, 1, 2, 3, 4, 5, 6시간 후)에 따른 수위예측이 가능하도록 LSTM 모형 개발을 위한 입력자료를 구축하였다. 학습자료에 해당하는 X는 현재시점의 강우와 수위자료이며, 예측값에 해당하는 Y는 0.5, 1, 2, 3, 4, 5, 6시간 후의 수위로 설정하였다. 선행예보시간 별로 학습을 개별로 진행하나 입력자료는 한번에 구축하였다. 또한, 본 연구에서는 수문자료의 수집률이 상대적으로 안정하지 않은 동남아시아 국가들의 특성을 고려하여 참조관측소를 최소화하여 예측할 수 있는 조건을 검토하기 위하여 관측자료를 가진 관측소를 활용하여 참조관측소 학습조건(training case)을 분류하여 입력자료를 구성하였으며, 입력자료의 구조는 Table 3에 나타냈다. 학습조건 1(case 1)은 가용한 수문관측소 6개를 전부 활용하여 학습자료를 구축한 조건이며, 학습조건 2(case 2)는 상류의 수위관측소인 Majalaya 관측소만 참조관측소로 활용한 조건이다. 학습조건 3부터 6까지는 강우관측소 1개씩만을 참조관측소로 활용하는 조건이며, 학습조건 7과 8은 각각 목표관측소인 Dayeuh Kolot 수위관측소로부터 가까운 거리에 있는 2개의 강우관측소(Dayeuh Kolot, Sapan)의 조합과 먼거리에 있는 2개의 강우관측소(Paseh-Cipaku, Kertasari)의 조합이다.
Table 3.
Structure of input dataset for 8 cases
3.3 학습 파라메터
인공지능을 활용하는 모형의 구축에는 학습을 위한 파라메터를 선정하는 것이 무엇보다 중요하다. 파라메터의 설정을 통해 학습의 효율성과 정확성이 결정되며, 적절한 형태의 학습에 맞는 파라메터를 설정하는 것이 필요하다. 본 연구에서 적용하는 LSTM의 경우 ‘Activation function’으로 비선형 함수인 ‘ReLU’를 적용하였다. ‘Optimizer’로는 ‘Adam Optimizer’, ‘Loss Function’은 ‘Mean squared error’로 설정하였다. 딥러닝 인공신경망 구조를 갖도록 ‘Hidden layer’는 총 3개 층으로 구성하였고, 적용하고자 하는 찌따룸강의 도달시간은 3시간 이내이므로 강우 발생이 수위변화에 충분히 반영되도록 ‘Sequence length’는 18로 설정하여 입력자료가 직전 3시간의 자료를 참조할 수 있도록 하였다. 기타 모형에 사용된 학습 파라메터는 Table 4에 나타냈다.
4. 모의결과 및 분석
4.1 예측 결과
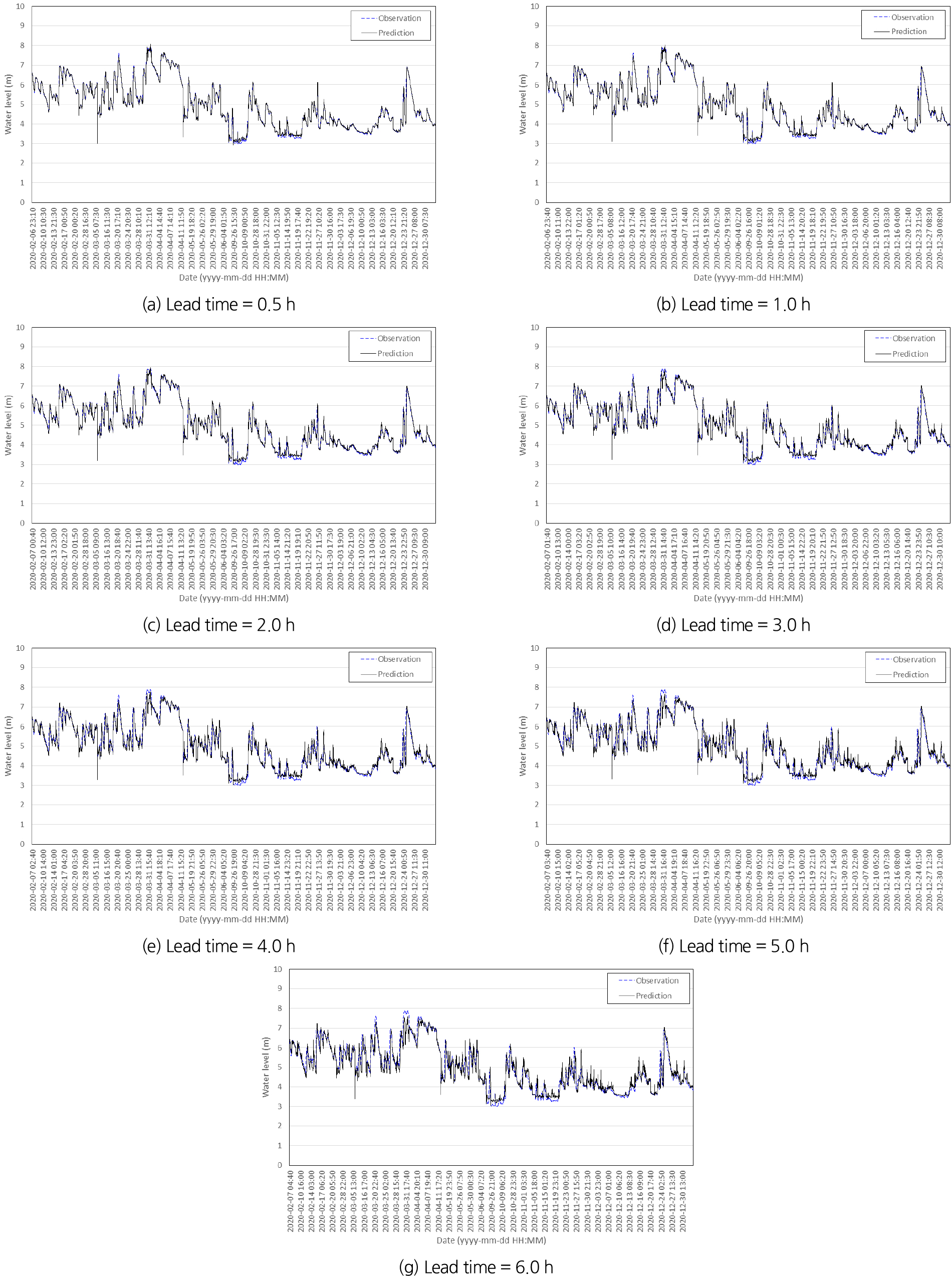
학습이 완료된 모형에 대해 시험(test) 모의를 수행하여 예측의 정확도를 분석하였다. 시험에 사용된 자료는 2020년 2월~2021년 1월 기간 동안에 각 관측소별로 81,594개이다. 8개의 학습조건(case)별로 선행예보시간 0.5, 1, 2, 3, 4, 5, 6시간에 대해서 예측모의를 수행하였으며, Fig. 4는 대표적으로 학습조건 1(case 1)에서의 관측치와 예측치의 결과를 도시한 것이다. 학습조건 1에 대한 예측결과를 보면 전체적으로는 예측결과가 관측결과의 경향을 잘 표현하고 있으나, 선행예보시간이 길어질수록 정확도가 낮아지는 것을 볼 수 있다.
4.2 홍수예측모형의 예측 정확도 분석
각 학습조건 별, 선행예보시간 별 예측결과를 바탕으로 예측정확도 분석을 수행하였다. 먼저 모형적합도 분석을 위해 NSE와 R2값을 산정했고, 오차 분석으로는 RMSE, 최대오차, 첨두오차, MAPE를 산정하였다. 각각의 산정결과는 Table 5에 나타냈다.
Table 5.
Analysis of prediction results for each lead time and case
Moriasi et al. (2015)은 수문모형의 적합도를 판정하는 기준으로 NSE와 R2에 대해서 제시하였다(Table 6). NSE의 경우 0.8이상인 경우 최고 등급인 “very good” 등급, R2의 경우 0.85이상 일 때 최고 등급인 “very good” 등급으로 판단한다. 본 연구의 예측결과는 모든 선행예보시간에 대해서 NSE는 0.89 이상으로 나타났고, R2도 모든 선행예보시간에 대해서 0.89 이상으로 나타나 NSE와 R2 값 모두 “very good” 등급의 높은 적합도를 나타냈다(Figs. 5 and 6).
Table 6.
Grading criteria of model fit indicators (Moriasi et al., 2015)
| Grade | Very good | Good | Satisfactory | Not satisfactory |
| NSE | NSE ≥ 0.80 | 0.80 > NSE ≥ 0.70 | 0.70 > NSE ≥ 0.50 | 0.50 > NSE |
| ≥ 0.85 | 0.85 > ≥ 0.75 | 0.75 > ≥ 0.60 | 0.60 > |
8개의 학습조건(case)별 예측정확도를 검토한 결과, 선행예보시간 3시간까지는 모든 학습조건의 NSE 값이 0.95 이상이고, 각 학습조건간의 예측정확도도 거의 차이가 없는 것으로 나타났다. 선행예보시간 4시간 이후에는 전체적으로 NSE 값이 0.95 이하로 떨어지면서 각 학습조건간의 정확도도 차이가 발생하기 시작하고, 선행예보시간이 증가함에 따라 학습조건별 상대오차도 증가하였다. 이러한 경향은 R2 값에서도 유사한 경향을 나타내고 있다. 따라서, NSE나 R2 값을 근거로 선행예보시간 3시간까지는 어느 정도 신뢰성있는 예측값을 제공할 수 있을 것으로 판단된다.
학습조건별 예측정확도는 참조관측소로서 수위관측소인 Majalaya 관측소가 포함된 학습조건 1(case 1)과 학습조건2(case 2)의 NSE 값은 각각 0.8962~0.9947 및 0.8988~0.9948로 나타났다. 이 값은 강우관측소만을 참조관측소로 활용한 학습조건 3~8까지의 NSE값 범위인 0.8991~0.9965보다 낮게 나타난 결과이며, 본 연구사례의 경우에는 강우관측소만으로 참조관측소를 구성하는 경우에 예측정확도가 더 나은 결과를 제공하는 것을 알 수 있다. 이와 같은 결과는 Majalaya 수위관측소의 자료 품질에 기인한 것으로 추정할 수 있으나, 참조관측소의 자료특성과 관측소간 정확도에 영향을 주는 특성에 대한 추가적인 연구가 필요한 것으로 판단된다.
홍수예측에서 시계열의 정확도와 함께 중요한 요소는 첨두수위의 예측정확도이다. 첨두수위오차(Error of Peak Water Level)는 예측첨두수위와 관측첨두수위의 차이로 나타냈으며, 음수값인 경우, 관측첨두수위보다 낮게 예측되었다는 것을 나타낸다. Fig. 7에 나타낸 바와 같이 모든 선행예보시간에서 관측첨두수위보다 대부분 낮게 예측된 것을 알 수 있으며, 선행예보시간과 상관없이 오차의 범위도 유사하게 나타났다. 첨두수위가 관측값보다 전체적으로 낮게 예측되는 원인은 학습기간의 첨두수위가 시험(test) 기간의 첨두수위보다 낮아서 과소 산정될 수 있거나, 강우 및 수위자료의 품질 등 복합적인 원인에 의해서 발생할 수 있으며 이에 대한 추가적인 자료 확보를 통해 규명할 필요가 있다.
5. 결 론
본 연구에서는 찌따룸강 상류 유역의 수문관측자료를 바탕으로 인공지능 기반의 예측모형 개발을 위한 입력자료를 구성하였다. 대상 유역에서 자료의 결측이나 이상치 등을 검토하여 수문자료가 양호한 수위관측소 2개소 및 강우관측소 4개소를 선정하였다. 이어 선정된 관측소의 강우 및 수위 자료를 활용하여 학습, 검증, 시험 자료를 분류하여 구축하였으며, LSTM 알고리즘을 바탕으로 모형을 개발하였다.
본 연구에서는 찌따룸강 상류 수위관측소중에서 홍수피해 정도가 심하면서 하류에 위치한 Dayeuh Kolot 지점을 목표수위관측소로 선정했다. 이는 상류에 위치한 강우관측소 및 수위관측소 등의 참조관측소를 최대한 많이 확보하여 참조관측소 선택조건에 따른 LSTM 모형의 예측정확도를 검토하였다. 이를 위하여 2016년 7월 1일부터 2023년 5월 31일까지의 10분 단위 강우 및 수위자료를 수집하였으며, 강우 및 수위자료를 검토하여 결측기간과 홍수예측시 학습효과가 없는 8시간 이상 지속되는 무강우 기간은 입력자료에서 제외하여 학습자료를 구축하였다. 선행예보시간(0.5, 1, 2, 3, 4, 5, 6시간)에 따른 수위예측이 가능하도록 LSTM 모형 개발을 위한 입력자료를 구축하였다.
또한, 본 연구에서는 수문자료의 수집률이 상대적으로 안정하지 않은 동남아시아 국가들의 특성을 고려하여 참조관측소를 최소화하여 예측할 수 있는 조건을 검토하기 위하여 관측자료를 가진 관측소를 활용하여 참조관측소 학습조건(training case)을 8개로 분류하여 입력자료를 구성하였다. 학습조건 1(case 1)은 가용한 수문관측소 6개를 전부 활용하여 학습자료를 구축한 조건이며, 학습조건 2(case 2)는 상류의 수위관측소인 Majalaya 관측소만 참조관측소로 활용한 조건이다. 학습조건 3부터 6까지는 강우관측소 1개씩만을 참조관측소로 활용하는 조건이며, 학습조건 7과 8은 각각 목표관측소인 Dayeuh Kolot 수위관측소로부터 가까운 거리에 있는 2개의 강우관측소(Dayeuh Kolot, Sapan)의 조합과 먼거리에 있는 2개의 강우관측소(Paseh-Cipaku, Kertasari)의 조합한 것이다.
학습이 완료된 모형에 대해 시험 모의를 수행하여 예측의 정확도를 분석하였다. 8개의 학습조건에 대해 예측모의를 수행한 결과, 전체적으로는 예측결과가 관측결과의 경향을 표현하고 있으나, 예보선행시간이 길어질수록 정확도가 낮아지는 것으로 나타났다. 8개의 학습조건별 예측정확도를 검토한 결과, 선행예보시간 3시간까지는 모든 학습조건의 NSE 값이 0.95 이상이고, 각 학습조건간의 예측정확도도 거의 차이가 없는 것으로 나타났다. 선행예보시간 4시간 이후에는 전체적으로 NSE 값이 0.95 이하로 떨어지면서 각 학습조건간의 정확도도 차이가 발생하기 시작하고, 선행예보시간이 증가함에 따라 학습조건별 상대오차도 증가하였다. 이러한 경향은 R2 값에서도 유사한 경향을 나타내고 있다. 따라서, NSE나 R2 값을 근거로 선행예보시간 3시간까지는 어느 정도 신뢰성있는 예측값을 제공할 수 있을 것으로 판단된다.
학습조건별 예측정확도는 참조관측소로서 수위관측소가 포함된 학습조건 1(case 1)과 학습조건 2(case 2)의 NSE 값이 강우관측소만을 참조관측소로 활용한 학습조건 3~8까지의 NSE값보다 낮게 나타났으며, 본 연구사례의 경우에는 강우관측소만으로 참조관측소를 구성하는 경우에 예측정확도가 더 나은 결과를 제공하는 것을 알 수 있었다.
본 연구에서는 수문관측 인프라가 제한적이고, 높은 품질의 수문자료 확보가 제한적인 조건에서 신속하고 효율적인 홍수예측값을 제공하는 방안으로 LSTM을 이용한 홍수예측모형을 구축하여 적용성을 검토하였다. 홍수도달시간이 짧고, 유역이나 하도에 대한 정보가 부족하여 물리 기반 모형을 적용하기 어려운 조건에서 인공신경망 기반 홍수예측모형이 유용한 예측결과를 제공할 수 있다는 점을 확인하였다. 그럼에도 불구하고 본 연구에서 개발한 모형의 활용성을 검증하기 위하여 물리 기반 모형 등의 결과와 비교검토하는 연구가 수행될 필요가 있으며, 인공신경망을 기반으로 하는 홍수예측모형과 물리 기반 모형이 상호 보완적으로 홍수예측정보를 제공할 수 있도록 연계 운영에 대한 추가적인 연구가 필요할 것으로 판단된다.