1. 서 론
2. TELEMAC-2D 모형의 적용성 검토
2.1 모형의 특징
2.2 계산격자의 수렴성
3. 분류각 변화에 의한 흐름특성 수치실험
3.1 본류에 대한 분류의 유량변화
3.2 흐름분리구역의 특성
3.3 유속분포의 특성
4. 분류각과 유량변화에 대한 흐름특성 수치실험
4.1 본류에 대한 분류의 유량 변화
4.2 흐름분리구역 특성
5. 결 론
1. 서 론
하천은 일반적으로 직선구간(straight), 사행구간(meander), 그리고 합류(confluence)와 분류(bifurcation)가 연속적으로 연결되어 있다. 하천에서 분류부는 충적 선상지, 망상하천, 하천 저수로, 델타에서 흔히 볼 수 있다. 하지만 개수로 분류부에서는 분류흐름의 불안정성, 분류되는 두 하도로 홍수배제 유량배분, 분류부 주변 토사퇴적 등 다양한 문제가 발생하기 때문에(Schielen et al., 2008), 하천을 계획하거나 관리하기 위해서는 그 수리학적 특성을 이해하는 것이 공학적으로 중요하다. 특히, 망상하천에서는 년 단위 혹은 이보다 짧은 시간 단위로 사주와 저수로의 이동, 분류와 합류로 인하여 분류부의 생성과 소멸이 반복적으로 발생하며, 그 변동 특성이 매우 복잡하므로, 지형학적 변화 과정을 이해하는 것은 많은 한계가 있다(Kleinhans et al., 2013).
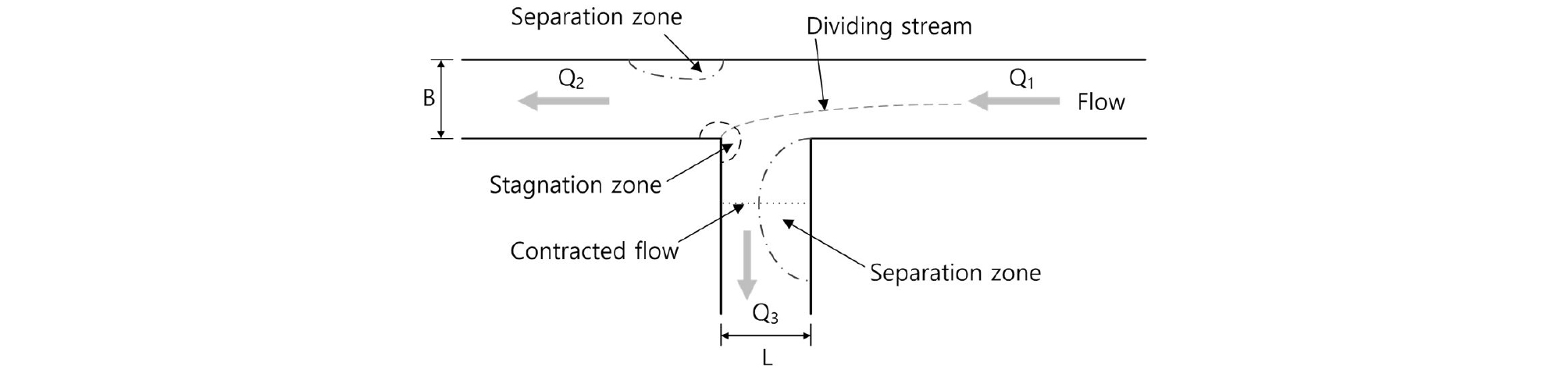
Fig. 1처럼 복잡한 분류부 흐름 구조는 하천 취수(water intake) 지점, 아라뱃길과 같은 주운수로, 관개수로와 같은 용수의 공급망(water supply network), 홍수배제를 위한 배수체계(drainage system) 등에서도 나타난다. 직선수로에서 흐름의 유선은 대부분 흐름방향에 평행하지만, 분류각을 가진 취수로 또는 배수로가 직선수로의 한 측벽에 설치될 때 흐름의 유선은 분류수로 쪽으로 방향이 바뀌며 분류수로 입구의 한쪽 측벽에서 흐름분리구역이 발생한다. 이러한 분류부 주변 수리학적 흐름특성을 이해하는 것은 취수와 배수시설의 위치선정, 분류수로 입구 토사퇴적 저감 등 수공구조물의 계획과 관리를 위해 매우 중요하다.
최근 국내에서는 기후변화에 대비하기 위해 기존 수자원 활용의 고도화와 수원 시설물의 연계를 강화하는 수자원정책을 추진하고 있으며(MOLIT, 2016), 빈번한 가뭄 발생으로 수자원의 시공간적 불균형을 해소하기 위해 기존 수원이나 개수로형 용수 공급망에 양수펌프장이나 개수로형 분류수로를 연결하여 분류부를 신설하는 사례가 점차 증가하고 있다 . 그러나 분류부 흐름에 대한 물리모형과 수치모형을 이용한 분석은 대부분 90° 분류각에 국한되어 분류각 변화가 흐름에 미치는 영향에 대한 연구가 매우 부족한 실정이다.
분류각 변화에 대한 물리적 실험연구는 Bulle (1926)가 최초로 시행한 이후 Rao and Sridharan (1967), Keshavarzi and Habibi (2005), Pirestani et al. (2011), Alomari and Khaleel (2012) 등이 연구하였다. 하지만 물리모형 실험은 대부분 취수시설물의 최적 취수구 각도 선정을 위한 분류각도별 최대 분류유량비(Q3/Q1) 분석과 분류유량비 실험공식 산출에 국한되었으며, 실험마다 최대 분류유량비 발생 분류각도가 상이하고 흐름분리구역과 유속분포 등 수리학적 흐름특성 변화에 대한 연구는 부족하다. Shettar and Murthy (1996)와 Afrouz et al. (2015)은 분류각 변화에 의한 흐름분리구역의 변화에 대해 수치모의 결과를 제시했지만 정량적 분석결과는 제시하지 못하였다.
최근 국내에서 Jung et al. (2016)은 2차원 수치모형을 이용하여 90° 개수로 분류부에서 분류수로 폭과 분류유량비 변화에 따른 흐름분리구역의 규모, 유속분포 등 흐름특성을 분석하였고, Jung et al. (2019)은 2차원 수치실험을 통해 90° 분류부 분류유량비 계산식의 비교분석, 분류유량비 변화에 따른 분류부 흐름특성 변화를 분석하였다. 그러나 국내에서도 대부분 90° 분류각에 대한 수치실험 연구만이 이루어져 분류각 변화에 따른 흐름특성 변화에 대한 추가 연구가 필요하다.
따라서 본 연구에서는 분류흐름에 대하여 선행 연구자들의 실내실험 결과를 이용하여 2차원 수치모형의 적용성 검토와 수치실험을 통한 분류각과 유량변화에 의한 분류부 주변 유속분포, 흐름분리구역의 규모와 분류유량비 변화에 대해 분석하고 그 특성을 파악하였다.
2. TELEMAC-2D 모형의 적용성 검토
2.1 모형의 특징
2차원 수치모형은 90° 분류수로 상류흐름(subcritical flow)에서 실내실험과 3차원 수치모형과 비교하더라도 분류유량비(Q3/Q1)와 분류부 수면형(water surface profiles)을 양호하게 모의할 수 있으며(El Kadi Abderrezzak and Paquier, 2009), 90° 분류수로 천이흐름, 상류흐름, 사류흐름에서 분류유량 계산오차는 0.66 ~ 2.52% 정도의 양호한 모의가 가능하다(Ghostine et al., 2013). 하지만 De Heer and Mosselman (2004)은 30° 개수로 분류부 실내실험 결과에 대해 정렬격자를 사용한 수치모의에서 실험결과보다 와(eddy)의 크기가 주수로에서는 크고 분류수로에서는 작게 모의되었다. 이것은 정렬격자를 이용한 수치모의를 위해 분류수로 시점부 상류 부분을 곡선형으로 격자를 구성한 것과 정렬격자망에서 분류각이 작아질수록 격자의 직교성과 grid smoothness로 인한 편차로 이산화공식에서 절단오차의 증가가 주요 원인으로 분석되었다.
따라서 본 연구에서는 비정렬 삼각격자를 적용하며 Eqs. (1) ~ (3)과 같이 비보존형 2차원 천수방정식을 SUPG 유한요소법으로 계산하고, k-Ɛ Model을 적용한 난류응력 계산과 모멘트 확산응력을 고려할 수 있는 TELEMAC-2D 모형을 이용하였다. TELEMAC-2D 모형은 프랑스 연구기관인 EDF에서 개발 및 배포 중인 오픈소스(open source) 모형으로서 상류(subcritical flow)와 사류흐름(supercritical flow)을 모두 모의할 수 있고, 격자수에 대해 자유롭고 멀티코어 CPU를 이용한 병렬처리(parallel processing)로 계산시간 단축이 가능한 특징이 있다.
| $$\frac{\partial h}{\partial t}+u\bullet\overrightarrow{\nabla\;}(h)+hdiv\;\left(\overrightarrow u\right)\;=\;S_h$$ | (1) |
| $$\frac{\partial u}{\partial t}+\overrightarrow{u\;}\bullet\overrightarrow{\nabla\;}(u)=-g\frac{\partial Z}{\partial x}+S_x+\frac1hdiv\;\left(h\nu_t\overrightarrow{\nabla\;}u\right)$$ | (2) |
| $$\frac{\partial v}{\partial t}+\overrightarrow{u\;}\bullet\overrightarrow{\nabla\;}(v)=-g\frac{\partial Z}{\partial y}+S_y+\frac1hdiv\;\left(h\nu_t\overrightarrow{\nabla\;}v\right)$$ | (3) |
여기서, h는 수심, t는 시간, u와 v는 x, y 방향으로 수심 평균된 유속, g는 중력가속도, 는 와점성계수, Z는 자유수면 수위, Sh, Sx, Sy는 유체의 생성 또는 소멸항이다.
TELEMAC-2D는 난류 계산을 위해 Constant Viscosity, Elder Model, Smagorinski Model, k-Ɛ Model을 적용할 수 있다. Constant viscosity는 난류점성을 전체 해석영역에 대해 일정한 값을 부여하고, Elder Model은 주흐름의 종․횡방향 난류점성을 각각 일정한 값을 부여함에 따라 재순환 영역의 형태와 정도에 영향을 미친다. 즉 낮은 점성계수는 오직 작은 와만이 소산되는 경향이 있는 반면 높은 값을 적용했을 때에는 큰 재순환영역이 소산되는 경향이 있으므로 적용 시 주의가 요구된다. Smagorinski Model은 분산을 고려하지 못하며 큰 와를 가지는 해양영역(maritime domains)에 일반적으로 적용한다. k-Ɛ Model은 난류점성에너지 k (turbulent kinetic energy)와 난류소산에너지 Ɛ (turbulent dissipation)의 이송을 모의하여 모형에서 직접 결정하도록 하며 넓은 수치해석 영역에 적용 된다(EDF-R&D, 2014). 따라서 본 연구에서는 난류를 고려한 분류부 수치모의의 정확성을 위해 k-Ɛ Model을 적용하였다.
2.2 계산격자의 수렴성
CFD 수치모의는 공학적 시스템의 설계, 조사 및 운영분야에 적용할 경우 엄격한 검증과정이 요구되며(AIAA, 1998), 검증과정은 일반적으로 수치 해가 특정 수준의 정확도에 도달했는지 확인하고, 지배방정식이 올바르게 계산되어 수치적으로 신뢰할 수 있는지 확인하는 형식을 취한다. 따라서 수치모형의 검증을 위해 격자 독립성(grid independence) 또는 격자 수렴성(grid convergence)에 대한 입증이 필요하며, 이를 위해 격자 해상도에 대한 모의결과를 제시해야한다(Hardy et al., 2003).
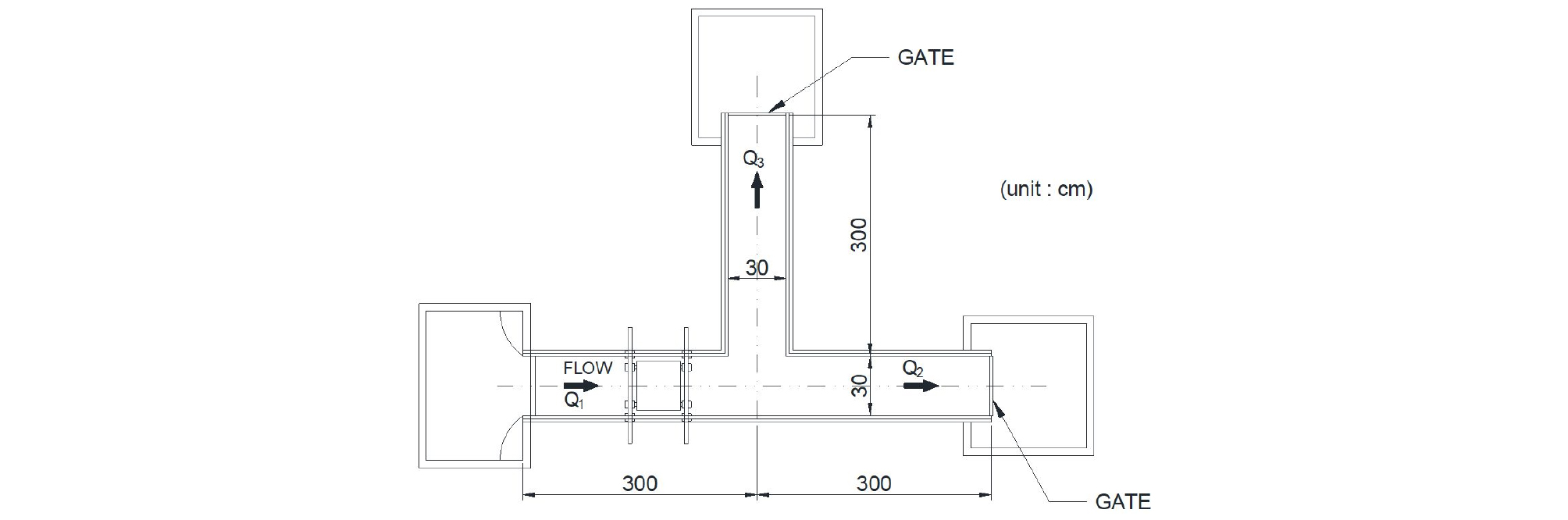
본 연구에서는 분류각 변화 수치모의 실험을 위해 적용한 Shettar and Murthy (1996)의 실내실험수로는 Fig. 2와 같이 폭이 0.3 m로 전구간이 동일하며, 수로바닥은 시멘트로 매끄럽게 수평으로 마감되었고, 상류유입 흐름의 유량(Q1)과 프루우드 수(F1)는 각각 0.00567 m3/s, 0.54이다. 실내실험에서 분류수로로 분류되는 분류유량비(Q3/Q1)는 0.52이며, 이는 실험수로 말단에 설치된 수문을 이용하여 주수로와 분류수로 하류단 수심을 달리하며 조절한 결과이다. 본 연구에서 수치모의를 위한 하류단 경계조건은 Table 1과 같이 선행연구 결과를 참고하여 분류유량비를 만족하는 동시에 수심과 유속분포 실험결과와 최소오차를 나타내는 경계조건을 결정하였으며, 수로바닥 조도계수는 0.012, 측벽 조도계수는 0.013을 적용하였다.
Table 1.
Downstream boundary conditions for numerical simulation
| Channel | 2D simulation | 3D simulation | ||
| Lai (2010) | Jung et al. (2019) | This study | Lai and Wu (2019) | |
| Main | 5.55 cm | 5.47 cm | 5.47 cm | 5.55 cm |
| Branch | 4.65 cm | 4.65 cm | 4.65 cm | 4.65 cm |
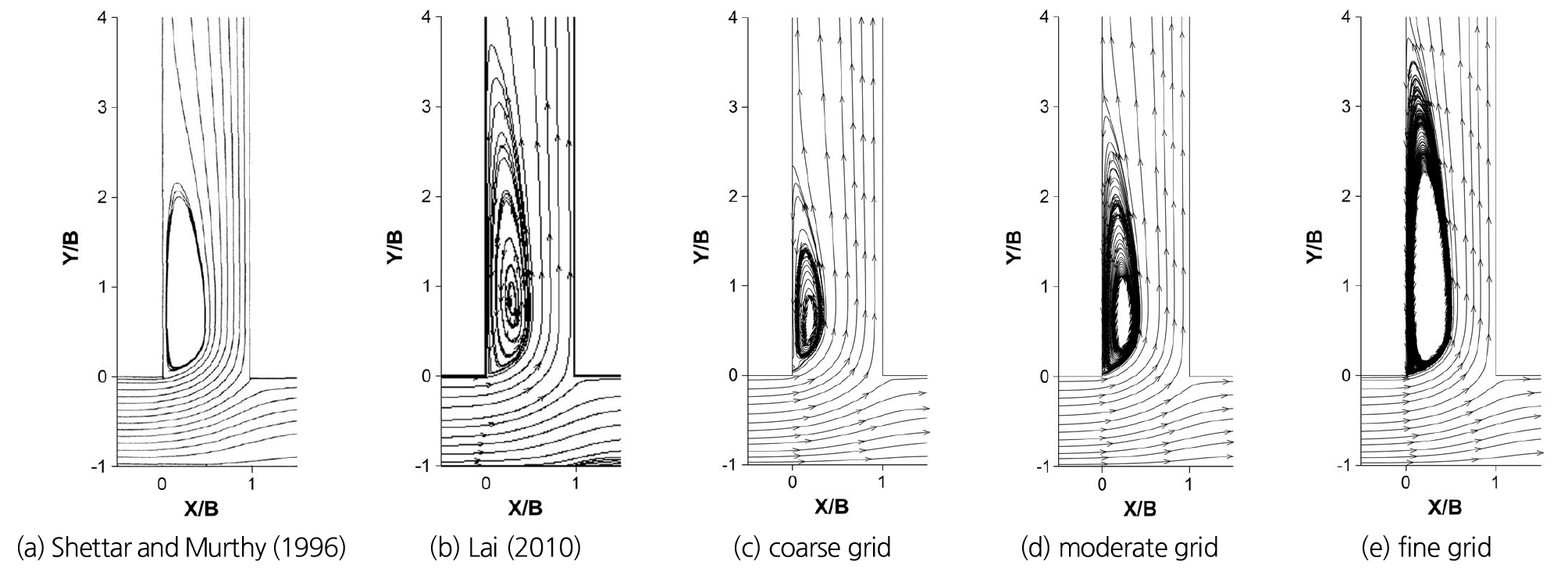
본 연구에서도 격자의 수렴성을 분석하기 위해 해석영역을 960개의 성긴 격자(coarse grid), 9,768개의 중간 격자(moderate grid), 17,818개의 조밀한 격자(fine grid)를 구성하여 격자해상도별 모의결과를 비교 분석하였다.
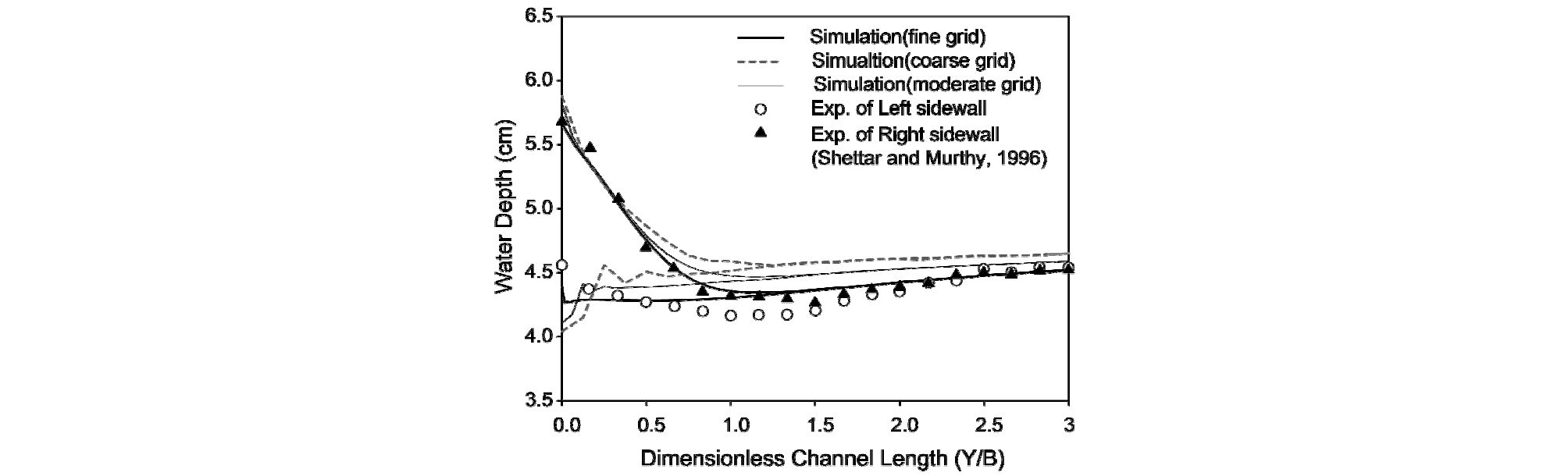
분류유량비(Q3/Q1)는 성긴 격자, 중간 격자, 조밀한 격자 각각 0.523, 0.514, 0.523으로 계산오차는 실내실험 결과와 –0.5 ~ 1.2%에 불과하지만, 분류수로에서 종방향 수심분포와 수심평균 유속분포는 큰 차이를 나타낸다. Fig. 3과 같이 격자해상도가 낮을수록 분류수로 입구인 Y/B = 0 ~ 0.5구간에서 수면형이 급변하며 Y/B = 0 ~ 2.5구간에서의 수위 저하와 회복현상과 같은 수면형 계산오차의 증가와 수치모의의 안정성에 영향을 미치게 된다. 또한 격자해상도가 낮을수록 수심을 과대 산정함에 따라 분류수로 우측벽면으로 흐름가중과 유속증가 현상에 대한 모의능력이 저하되며(Fig. 4), Table 2와 같이 수심평균 유속분포 계산오차가 증가하고, Shettar and Murthy (1996)도 2차원 수치모의 연구에서 분류부 주변 조밀한 격자구성의 필요성을 제기하였다.
Table 2.
Comparison of RMSE values of depth-averaged velocity in branch channel
| Cross section | RMSE (m/s) | ||
| Coarse grid | Moderate grid | Fine grid | |
| Y/B = 0.65 | 0.109 | 0.084 | 0.067 |
| Y/B = 1.65 | 0.122 | 0.106 | 0.090 |
| Y/B = 2.65 | 0.072 | 0.063 | 0.054 |
| Mean | 0.103 | 0.085 | 0.071 |
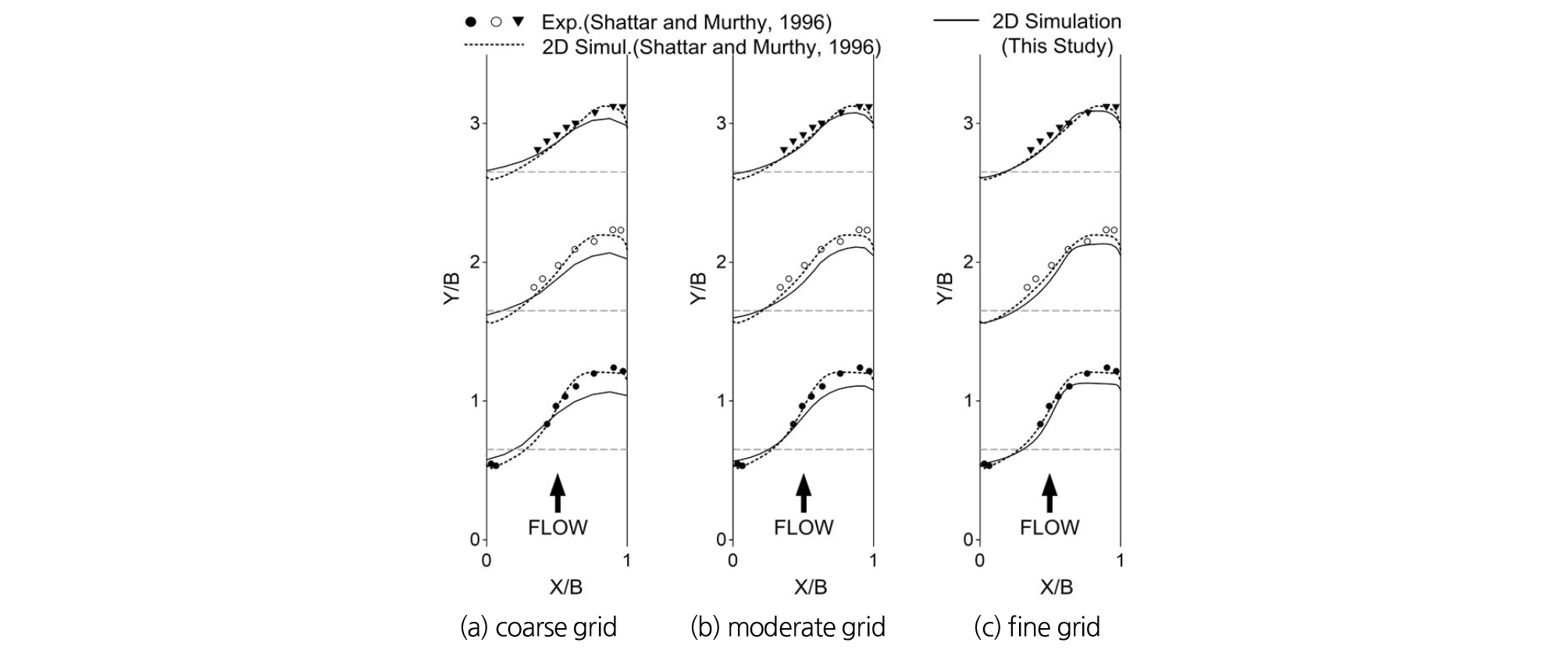
Fig. 5와 같이 동일한 실내실험에 대해 Shettar and Murthy (1996), Lai (2010)의 2차원 수치모의 결과와 격자 해상도별 분류수로 흐름분리구역 모의결과를 비교하였다. 조밀한 격자 모의결과와 위 두 선행 연구들은 흐름분리구역의 최대 폭이 분류수로 폭(B) 대비 약 0.5B로 거의 동일하게 계산되었고, 흐름분리구역의 길이는 Lai (2010) 모의결과처럼 약 3.8B로 유사하게 계산되었다. 하지만 성긴 격자와 중간 격자는 흐름분리구역 폭이 각각 0.33B, 0.44B로 좁고 길이도 각각 2.3B, 3.1B로 과소 모의하였다.
이러한 원인은 주수로 흐름으로부터 분류되어 분류수로로 유입되는 분류부 흐름은 만곡이 발생하고, 분류수로 입구 주변에서부터 발생하는 흐름분리구역(separation zone)과 이차류(secondary flow)에 의해 분류수로 내 흐름이 우측벽면 부근으로 가중되므로 (Jung et al., 2016; 2019) 흐름분리구역의 규모가 과소 모의되면 상대적으로 유효 유수단면 폭은 증가하여 우측 벽면 주변 흐름가중과 최대유속까지 과소 모의되는 문제점이 나타난다.
따라서 분류부 흐름은 수리학적으로 복잡한 흐름구조를 가진 불안정성 때문에 수치모의 분석에 있어서 격자의 수렴성에 대한 검토가 중요하며, 본 연구에서는 분류부 흐름 실내실험 결과에 대하여 분류유량비 조건을 만족하며 수심과 유속분포 오차가 최소인 조밀한 격자가 격자의 수렴성을 확보한 것으로 판단되므로 이 격자를 이용하여 수치실험을 수행하였다.
3. 분류각 변화에 의한 흐름특성 수치실험
본 연구에서는 분류각 변화가 분류부 흐름특성에 미치는 영향을 분석하기 위해 상류유입 흐름의 유량(Q1)은 0.00567 m3/s, 하류단 경계조건은 주수로와 분류수로 수심을 각각 5.47 cm와 4.65 cm, 수로바닥 조도계수는 0.012, 측벽 조도계수는 0.013로 Shettar and Murthy (1996)의 실내실험에 대한 경계조건을 동일하게 적용하였다. 수치모의 실험을 위해 45° ~ 90°까지 15° 간격으로 분류각만을 변화시키며 4 개의 격자를 구성하였으며, 격자 해상도에 따른 흐름계산 오차의 최소화를 위해 분류수로의 조밀한 격자 해상도를 유지시켰다.
3.1 본류에 대한 분류의 유량변화
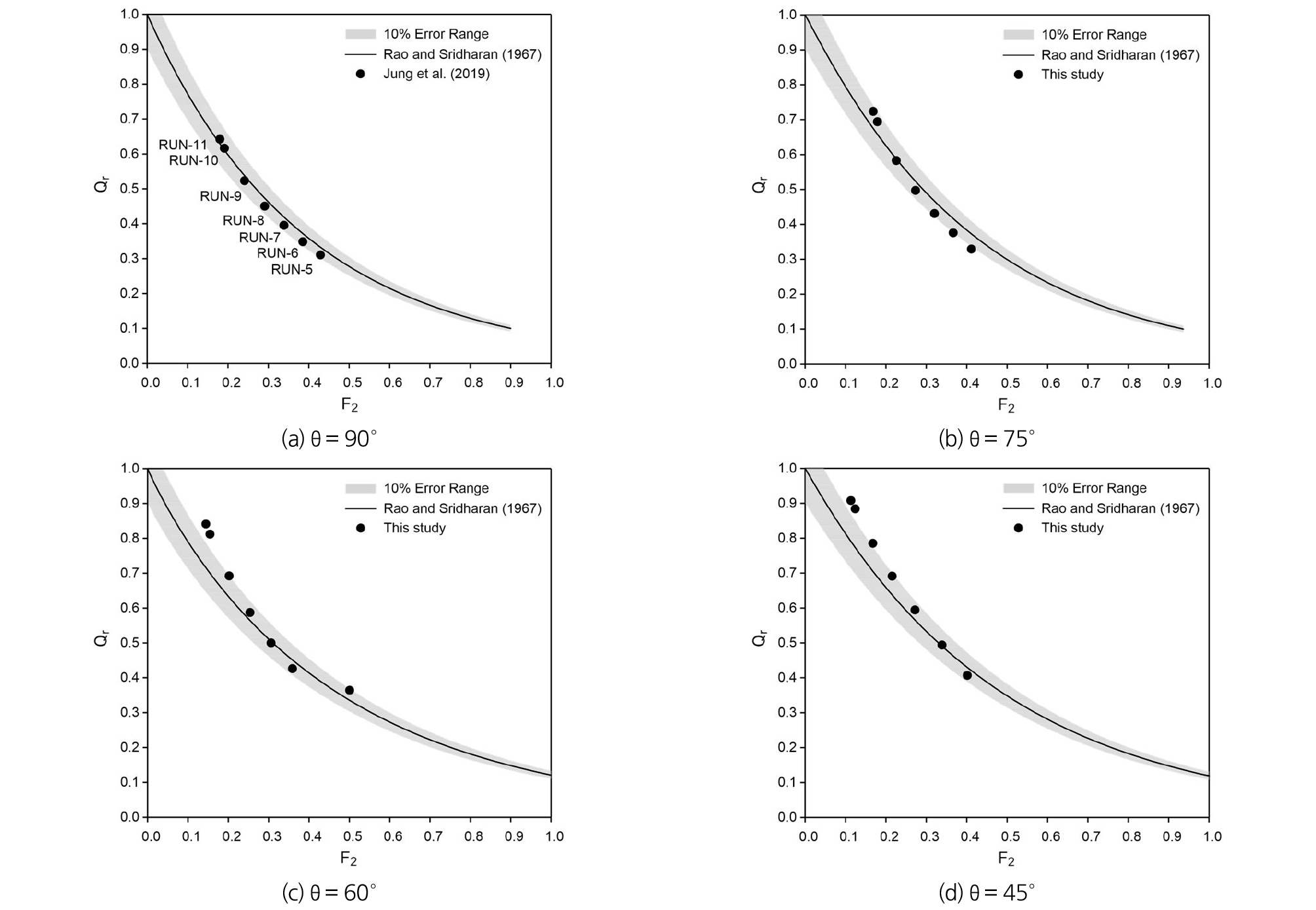
동일한 경계조건에서 분류각만 변경된 경우, 분류각이 변경되더라도 분류부 상류 유입흐름 프루우드 수(F1)는 0.52로 일정하게 유지되지만, 분류각이 90°에서 45°로 감소 시 Table 3과 같이 분류유량비(Q3/Q1)는 0.523에서 0.785로 약 50.1% 상승하였다. 이 모의결과는 Rao and Sridharan (1967)가 다양한 경계조건에 대한 587회의 실내실험을 통해 분류유량비 0.7 이하의 흐름에 대해 제안한 분류각도별 분류유량비(Qr) 회귀식과 10% 이내 오차로 매우 양호한 모의결과를 나타냈다.
이러한 현상은 분류부 상류 유입흐름에서 분류되어 분류수로로 유입되는 흐름은 만곡부와 유사한 흐름특성을 가지게 되며(Neary and Odgaard, 1993), 본 연구와 같이 분류각이 90°에서 45°로 감소하면 90° 만곡 흐름에서 135° 완만곡 흐름으로 변화한 것처럼 급격한 흐름방향의 전환과 에너지손실이 감소하기 때문이다. 따라서 분류각이 감소하면 분류수로로 유입되는 흐름의 곡률반경은 증가하고 분류부에서 상대적인 에너지 소산이 감소하며 주수로와 분류수의 하류방향으로 흐르는 흐름의 관성력과 하류단 경계조건에 의한 압력경사의 영향으로 분류수로에 유입되는 분류유량이 증가하게 된다.
Table 3.
The result of simulation for diversion flow discharge ratio
| Case | Q3 / Q1 | |||
| Simulation | Rao and Sridharan (1967) | Relative error (%) | ||
| RUN-1 | 90° | 0.523 | 0.538 | 2.8 |
| RUN-2 | 75° | 0.582 | 0.588 | 0.9 |
| RUN-3 | 60° | 0.692 | 0.631 | -8.8 |
| RUN-4 | 45° | 0.785 | 0.705 | -10.1 |
3.2 흐름분리구역의 특성
90° 분류부에서 흐름분리구역은 주수로의 하류방향으로 높은 모멘트를 가진 흐름이 분류수로로 유입되기 때문에 발생하고(Neary and Odgaard, 1993), 흐름분리구역의 위치와 크기는 분류유량비에 따라 달라지며, 분류유량비가 증가하면 분류수로에서 발생하는 흐름분리구역의 길이와 폭은 감소한다(Jung et al., 2019; Hsu et al., 2002; Kasthuri and Pundarikanthan, 1987). 수치모의를 통해 계산된 유속성분의 분포에 따라 작성된 유선을 통해 흐름분리구역의 크기와 위치를 밝히는 데 사용할 수 있으며(Keshavarzi and Habibi, 2005), 종방향 흐름분리구역의 규모는 유속과 유선분포, 종방향 프루우드 수의 분포를 통해 산출할 수 있다(Jung et al., 2019).
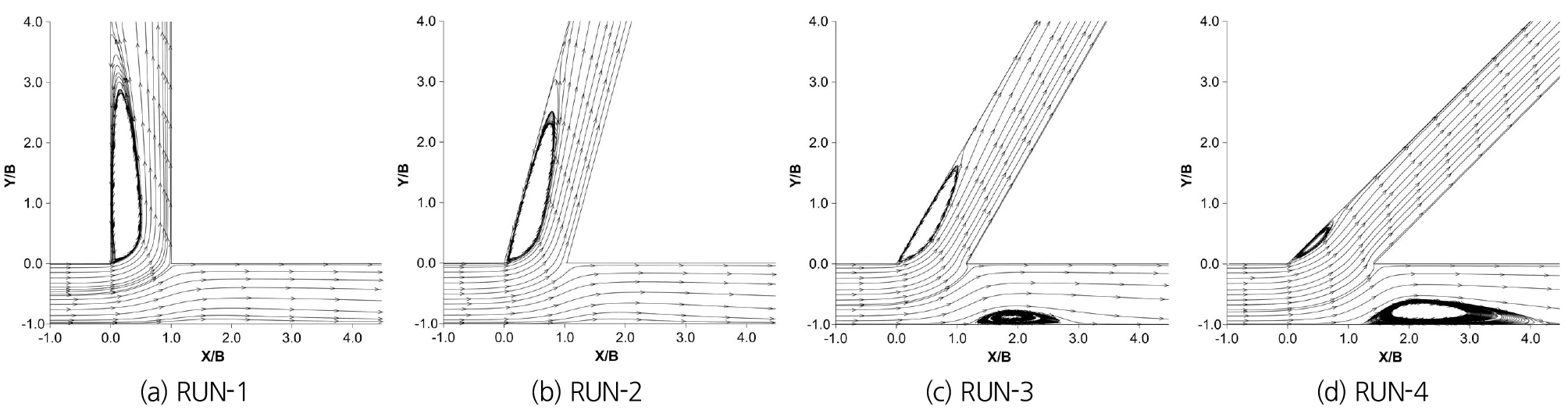
본 연구에서는 동일한 경계조건에서 15° 간격의 분류각 변화에 따른 흐름분리구역의 위치와 규모 변화에 대한 분석을 수행하였다. Fig. 6과 같이 분류각이 감소하면 분류수로로 유입되는 유량이 증가함에 따라 흐름분리구역의 길이와 폭이 감소하고, 주수로에서는 분류부 직하류 우측벽에서 발생하는 흐름분리구역의 규모가 증가하며 유선의 급격한 굴절이 발생하게 된다.
90° 분류부에서 주수로의 흐름분리구역은 분류부 직하류의 주수로에서 분류수로가 있는 반대편 측벽 주변에서 발생하고, 분류유량비가 0.7을 초과할 때부터 발생한다(Jung et al., 2019, 2016; Hsu et al., 2002; Rao and Sridharan, 1967). Fig. 6(c)와 같이 분류각이 60°로 감소함에 따라 분류유량비가 약 0.7인 흐름조건이 형성되면서 주수로 직하류부에 흐름분리구역이 발생하는 유사성을 나타냈다. 이것은 분류각이 분류유량비와 함께 주수로와 분류수로에서 흐름분리구역의 발생조건 및 규모와 관련된 중요한 요소임을 의미한다.
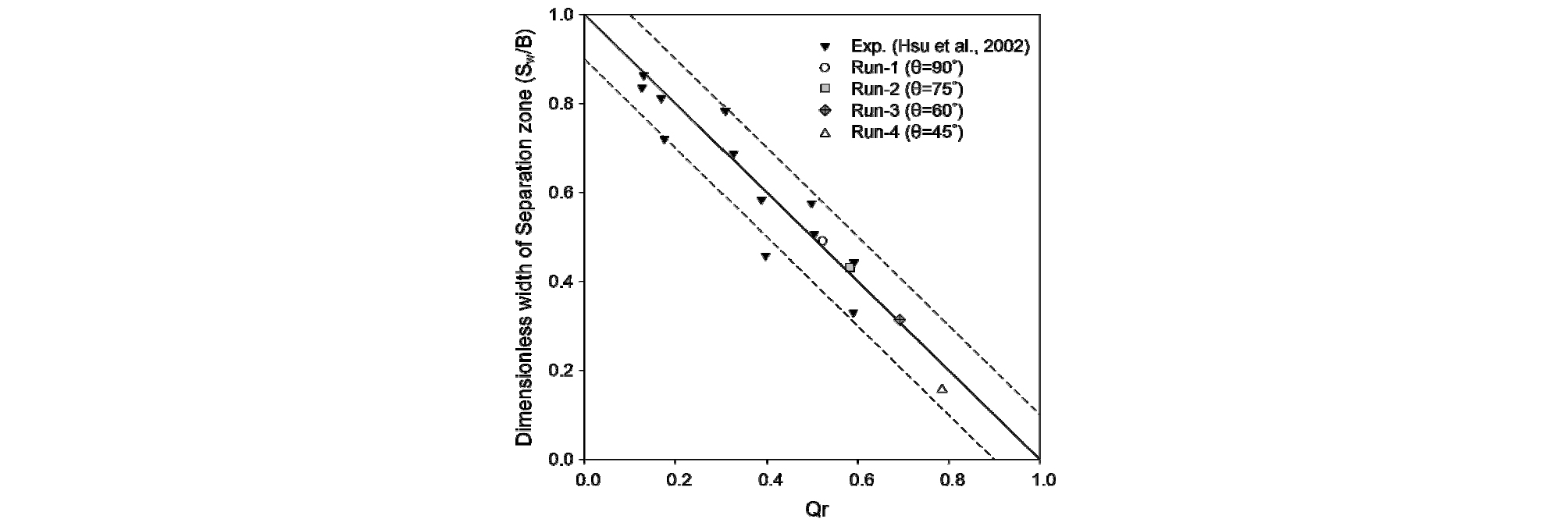
Hsu et al. (2002)은 Fig. 7과 같이 90° 분류수로에 대한 실내실험을 통해 F1 = 0.33 ~ 0.70 범위이고 분류유량비가 0.7 이하의 흐름에서 분류수로에 발생하는 흐름분리구역의 최대 폭(SW)은 분류유량비에 따라 선형적으로 변화한다는 연구결과를 제시하였다. 90° 모의결과인 RUN-1은 Hsu et al. (2002)의 연구결과와 일치하였으며, 분류각이 감소하여 분류유량비가 0.7 미만이지만 주수로에 흐름분리구역이 발생한 RUN-3도 분류수로에서의 최대 흐름분리구역의 폭 변화는 그 선형성을 유지하였다. 분류유량비가 약 0.8에 근접하고 분류수로 내 흐름분리구역 규모보다 주수로의 흐름분리구역 규모가 더 큰 RUN-4에서는 오차가 증가하게 된다.
3.3 유속분포의 특성
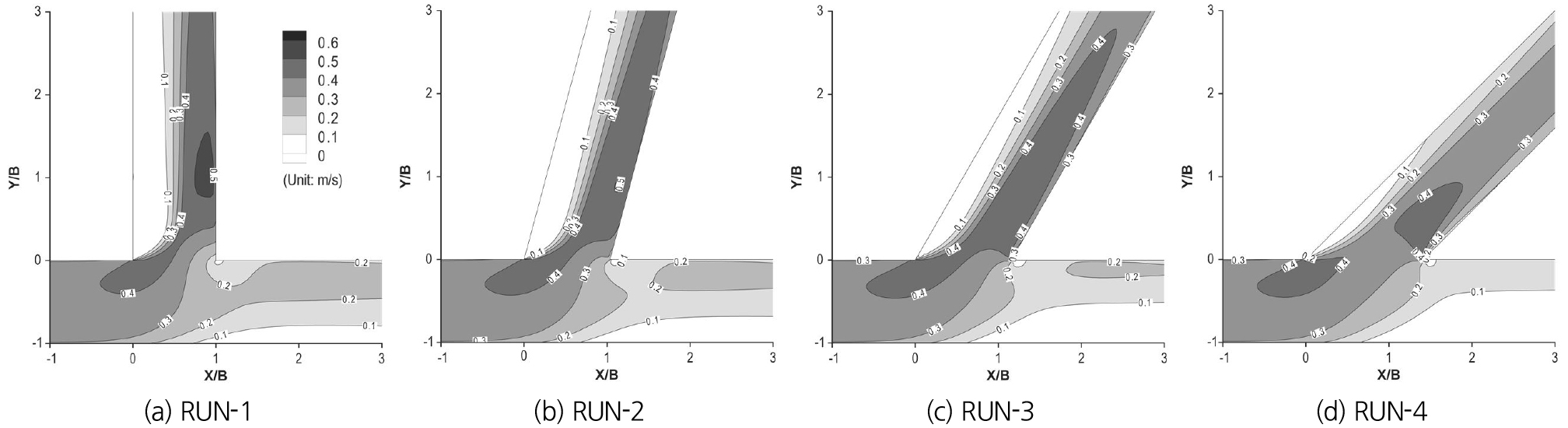
동일한 경계조건에서 분류각이 감소하면 Fig. 8과 같이 분류부 상류 X/B = -1 ~ 0 구간에서 0.4 m/s 이상의 상대적인 고유속 분포구역이 상류방향으로 확대되며 X/B = 0.8부터 주수로 하류방향으로 0.1 m/s 이하의 저유속 분포구역이 확대된다. 분류수로에서는 분류각이 90°일 때 최대 0.5 m/s 이상의 고유속 영역이 분류수로 우안에 발생하고 0.1 m/s 이하의 저유속영역이 흐름분리구역 주변에서 넓게 분포하게 된다. 하지만 분류각이 감소함에 따라 분류수로로 유입되는 유량이 증가하고 0.1 m/s 이하의 저유속 영역, 0.4 m/s 이상의 고유속영역과 최대유속도 감소한다. 또한 Fig. 8(a)와 같이 분류각이 90°일 때 X/B = 1.0지점의 분류수로 입구 주변에서 0.2 m/s 이하의 흐름정체구역 형성을 확인할 수 있지만, Fig. 8(b) ~ (d)와 같이 분류각이 감소함에 따라 0.1 m/s 이하 소규모 흐름정체구역만 형성된다.
이러한 현상은 분류각이 감소함에 따라 주흐름에서 분리되어 분류수로로 유입되는 흐름의 곡률반경과 유량이 증가하고 흐름분리구역의 규모는 감소하여 유효 유수단면 폭은 확대되며 분류수로 우측벽 주변으로 흐름가중이 감소하고, 주수로에서는 주수로 하류방향 유량 감소로 인해 흐름정체구역 반대 측벽에서 흐름분리구역이 형성됨에 따라 유효 유수단면 폭 감소와 함께 좌측벽면 주변으로 흐름이 가중되기 때문이다.
4. 분류각과 유량변화에 대한 흐름특성 수치실험
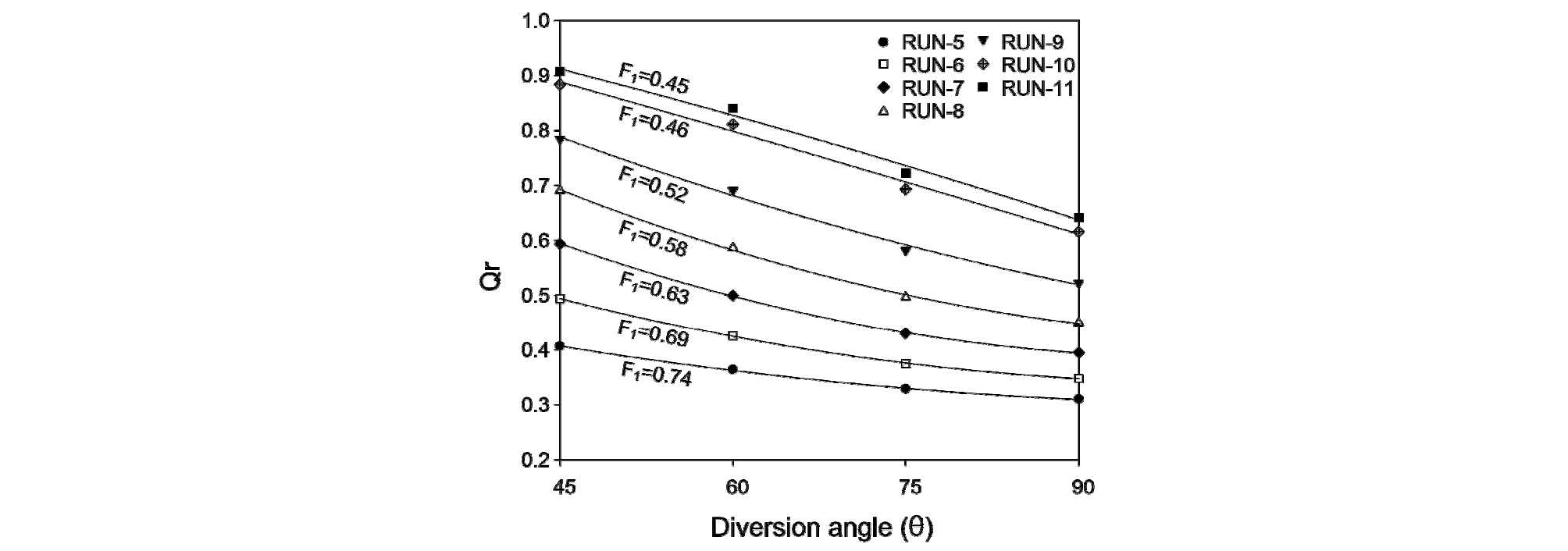
Shettar and Murthy (1996)의 90° 분류흐름 실내실험 결과를 이용하여 다양한 분류흐름 형성조건을 검증하고 수치실험을 수행한 Jung et al. (2019)의 흐름조건을 이용하여 분류각과 분류유량비 변화에 따른 흐름특성 분석 연구를 수행하였다(Table 4). 주수로와 분류수로 하류단 수심은 각각 5.47 cm와 4.65 cm로 동일하게 적용하였고 상류 유입유량만 변화시키며 7개의 상류 유입흐름의 프루우드 수(F1)와 관성력 변화에 따른 분류유량비(Qr)가 다른 흐름조건에 대해 45° ~ 90°까지 15° 간격으로 분류각을 변화시키며 수치실험을 수행하였다.
Table 4.
Hydraulic conditions for numerical experiments
| CASE | Q1 (ℓ/s) | Qr (Q3 / Q1) | F1 |
| RUN-5 | 7.94 | 0.310 | 0.74 |
| RUN-6 | 7.37 | 0.348 | 0.69 |
| RUN-7 | 6.80 | 0.395 | 0.63 |
| RUN-8 | 6.24 | 0.450 | 0.58 |
| RUN-9 | 5.67 | 0.523 | 0.52 |
| RUN-10 | 5.10 | 0.616 | 0.46 |
| RUN-11 | 4.97 | 0.642 | 0.45 |
4.1 본류에 대한 분류의 유량 변화
분류부 상류 유입흐름의 프루우드 수(F1)와 분류각을 변화시키며 수치실험을 수행한 결과 Fig. 9와 같이 모든 흐름에서 분류각 변화에 따른 분류유량비 변화율은 비선형적으로 변화하며 프루우드 수(F1)에 따라 그 변화율도 다르게 나타난다. 분류각이 90°에서 45°로 감소함에 따라 F1이 가장 큰 RUN-5가 31.1%로 최소 분류유량비 증가율을 나타냈으며, 분류유량비 0.7 이하인 RUN-8까지 분류유량비 증가율은 53.5%로 증가하며, 분류유량비가 0.7을 초과하면서 분류유량비 증가율은 다시 RUN-11 41.4%까지 감소하게 된다.
본 수치실험 결과를 Fig. 10과 같이 Rao and Sridharan (1967)이 실내실험을 통해 분류각도별 분류유량비 분포에 대한 회귀식과 비교한 결과 분류유량비 0.7 이하에서는 회귀식의 10% 분류유량비 오차범위 내에 분포하는 것을 확인할 수 있으며, 분류유량비가 0.7을 초과할 경우 분류수로 뿐만 아니라 주수로에서도 흐름분리구역의 발생으로 오차가 증가한다. Rao and Sridharan (1967)도 동일한 원인으로 인해 해당 회귀식 적용범위를 분류유량비 0.7 이하로 제한하였다. 따라서 실내실험을 통한 회귀식과 수치실험 결과는 주수로와 분류수로 폭이 동일하고 상류 유입흐름의 프루우드 수(F1)가 0.45 ~ 0.74 범위의 상류흐름(subcritical flow)에서 다양한 각도의 개수로 분류유량비를 계산하는데 최소한의 가이드라인으로 적용할 수 있을 것으로 판단된다.
4.2 흐름분리구역 특성
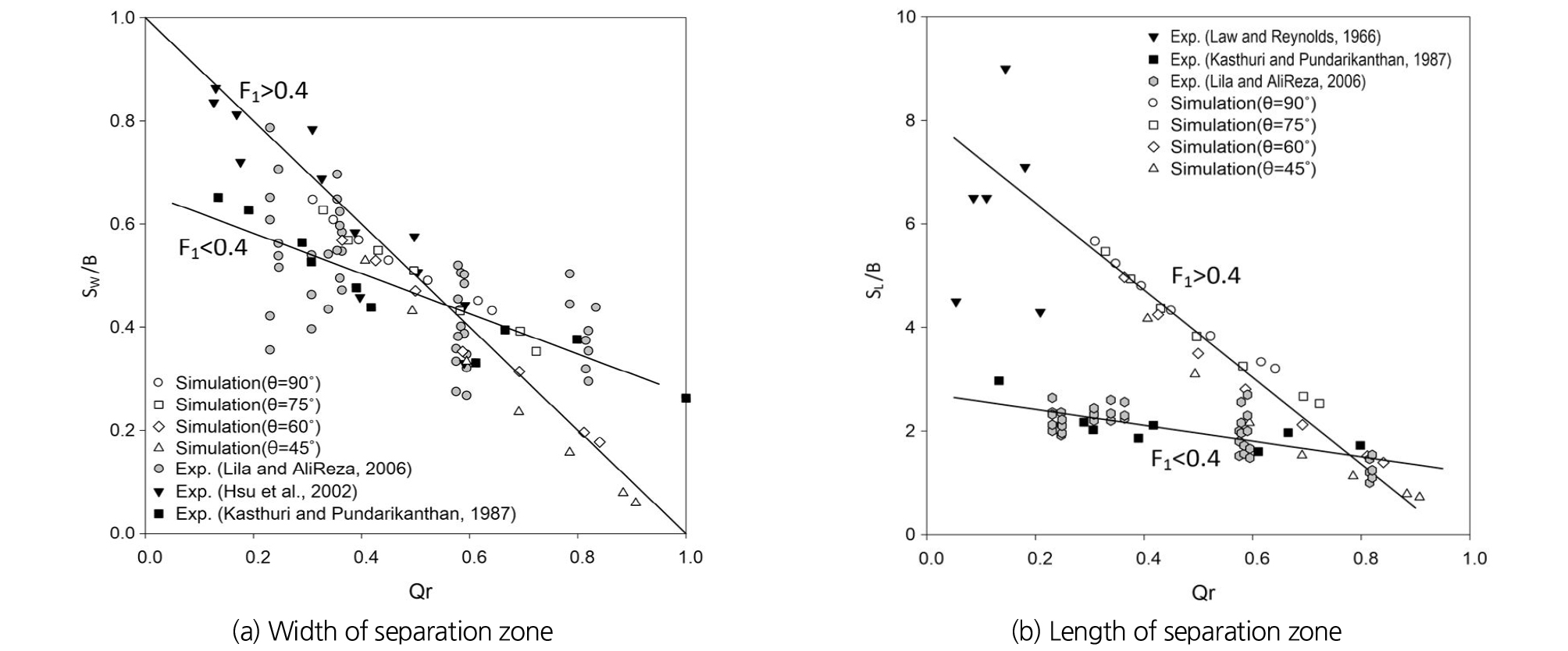
본 수치실험에 따른 흐름분리구역 변화에 대한 결과를 비교분석하기 위해 Table 5와 같이 선행 실내실험연구 결과를 이용하였다. Law and Reynolds (1966), Kasthuri and Pundarikanthan (1987), Hsu et al. (2002)은 90° 분류각에서 흐름분리구역에 대한 실내실험 연구를 수행하였고, Lila and AliReza (2006)는 45°, 56°, 67°, 79°, 90° 5개 각도에서 흐름분리구역의 폭과 길이에 대해 연구하였다. 위 실내실험 연구에서는 실내 실험수로 하류단에 설치된 수문(gate)이나 보(weir)를 이용하여 하류단 수위를 변화시키며 분류유량비를 조절하였고, 고정된 경계조건에서 상류 유입유량(Q1)이나 분류각만 변화시키며 실내실험을 수행하였다. 따라서 본 수치모의 실험 조건과 같이 주수로보다 분류수로 하류단 수위가 낮은 경계조건에서 분류부 상류 유입유량과 분류각이 감소할수록 흐름의 관성력보다 횡방향력이 분류흐름에 더 큰 영향을 미치게 되며, 주수로에서는 주수로 하류 방향으로 흐르는 유량이 감소하여 흐름분리구역이 발생하고 규모도 점차 증가하게 되며, 분류수로에서는 분류유량비가 증가함에 따라 흐름분리구역의 규모는 점차 감소하게 된다. 하지만 흐름분리구역에 대한 실내실험 연구는 연구자들마다 실험목적과 조건이 상이하고, 흐름분리구역 길이(SL)와 폭(SW)에 대한 경계구분의 어려움, 관측장비의 설치간격, 연구 당시 관측장비의 기술적 한계와 관측오차, 후속 연구부족 등으로 실무적으로 적용 가능한 연구가 아직 부족한 실정이다. 따라서 본 연구에서는 수치모의 실험결과와 실내실험 결과를 이용하여 흐름분리구역에 대한 회귀분석을 수행하였다.
Table 5.
Hydraulic conditions for experiments
| Experiments | F1 |
| Law and Reynolds (1966) | 0.67 ~ 0.76 |
| Kasthuri and Pundarikanthan (1987) | 0.10 ~ 0.40 |
| Hsu et al. (2002) | 0.33 ~ 0.70 |
| Lila and AliReza (2006) | 0.03 ~ 0.12 |
Fig. 11과 같이 회귀분석한 결과 분류각과 분류부 상류 유입유량의 변화에 따른 분류유량비가 변화하는 경우 분류수로에서 발생하는 흐름분리구역의 규모는 선형적으로 변화하지만 분류부 상류 유입흐름의 프루우드 수(F1)에 따라 그 변화율은 달라진다. Fig. 11과 Table 6과 같이 F1 > 0.4인 경우 F1 < 0.4인 흐름보다 무차원화된 흐름분리구역의 폭(SW / B) 변화율은 약 2.56배 높으며, 무차원 흐름분리구역 길이(SL / B) 변화율은 약 5.5배 높게 나타난다. 이러한 현상은 분류각이 감소할수록 분류수로로 유입되는 흐름의 곡률반경은 증가하고, 분류수로 하류단 방향 압력경사의 영향에 관성력이 점차 가중되어 분류수로 내 주흐름은 분류수로 우측벽면에서 수로 중앙으로 점차 이동하게 되며 결국 흐름분리구역은 감소하게 되며, 분류부 상류 유입흐름의 프루우드 수가 0.4 이하로 관성력이 작은 흐름은 분류각이 감소함에 따라 분류수로 하류단 방향으로 가중되는 관성력의 규모가 작기 때문에 흐름분리구역 규모의 변화율도 작게 나타나게 된다. 하지만 본 연구는 주수로와 분류수로 폭 비율, 조도계수, 수로바닥 경사 등에 따라 달라지므로 향후 추가 연구가 필요하다.
5. 결 론
본 연구에서는 2차원 수치모형을 이용하여 개수로 분류부에서 하류단 경계조건의 변화 없이 분류각과 분류유량비 변화에 따른 유속분포, 흐름분리구역의 크기, 분류각과 유량비 변화의 상관관계 등 흐름특성을 파악하였다.
1) 분류부 흐름해석에서 격자해상도가 낮으면 분류수로 입구에서 수치해석 오류가 증가하고, 분류수로 내 수면저하 현상과 수심평균 유속분포 계산오차가 증가하며, 흐름분리구역 규모를 과소 산정하는 문제가 발생하므로 분류부 주변 수공설계와 수치모의 시에는 격자 수렴성 분석을 통해 오차를 최소화해야 한다.
2) 상 ․ 하류단 경계조건 변화 없는 조건에서 분류각이 90°에서 45°까지 감소하면 주흐름에서 분리되어 분류수로로 유입되는 흐름의 곡률반경이 증가하고 급격한 흐름방향의 전환에 의한 에너지손실은 감소하며, 주수로와 분류수로 하류방향으로 흐르는 흐름의 관성력과 하류단 경계조건에 의한 압력경사의 영향으로 분류수로에 유입되는 분류유량비가 0.523에서 0.785로 약 1.5배 증가하며, 분류각이 감소하여 분류유량비가 0.7 미만이지만 주수로에 흐름분리구역이 발생하더라도 분류수로의 최대 흐름분리구역 폭 변화는 그 선형성을 유지하였다. 하지만 분류유량비가 0.7을 초과하면 분류수로보다 주수로에 발생되는 흐름분리구역 규모가 더 커지면서 분류수로 흐름분리구역의 폭 변화는 선형성을 유지하지 못한다.
3) 분류부 상류 유입흐름의 프루우드 수가 F1 = 0.45 ~ 0.74인 흐름에서 분류각을 90°에서 45°로 15° 간격으로 감소할 때마다 분류유량비는 각각 6 ~ 10%, 17 ~ 30%, 32 ~ 54%로 비선형적으로 증가하며, F1가 최대 0.74인 흐름에서 분류유량비 증가율이 31.1%로 최소값을 나타내고 F1 = 0.58 일 때 분류유량비가 0.7 이하이면서 최대 분류유량비 증가율 53.5%을 나타내며, F1이 0.58보다 감소할수록 분류유량비가 0.7을 초과하면서 그 증가율도 함께 감소하게 된다.
4) 분류부 상류 유입흐름의 프루우드 수(F1)가 0.4 이하로 관성력이 작은 흐름은 분류각이 감소함에 따라 분류수로 하류단 방향으로 가중되는 관성력의 규모가 작기 때문에, F1 > 0.4인 경우 F1 < 0.4인 흐름보다 무차원화된 흐름분리구역의 폭(SW / B) 변화율은 약 2.56배 높으며 무차원 흐름분리구역 길이(SL / B) 변화율은 약 5.5배 높게 나타난다.