1. 서 론
2. 본 론
2.1 기존 단일사상 강우-유출 모형 매개변수 최적화
2.2 단일사상 강우-유출 모형 매개변수 결정방법 개선
3. 적용 및 고찰
3.1 대상유역의 단일사상 강우-유출 자료 및 적합도 검정
3.2 분석결과
4. 결론 및 토의
1. 서 론
하천기본계획, 수자원관리계획 및 설계 등은 기본적으로 강우빈도해석, 유역특성인자 산정, 홍수량 산정 등의 일련의 절차에 의해서 진행되며, 국내에서는 홍수량 산정 표준지침(ME, 2018)을 따르고 있다. 각 과정을 살펴보면 지점빈도해석 또는 지역빈도해석을 통한 확률강우량 산정 방법은 국내외에서 다양한 기법이 개발되어 국내에 적용되고 있으며(Kwon et al., 2013; Kim et al., 2014), 유역특성인자(도달시간, 저류상수 등) 산정 역시 최근 표준지침에서 국내 실정에 맞는 공식이 개발됐지만 기존에는 국외에서 개발된 공식을 활용하였다. 이렇게 산정된 유역특성인자는 주변의 유량관측소 지점을 대상으로 매개변수의 검정(calibration) 및 검증(verification) 과정을 거쳐 최적의 매개변수를 결정하고 있다.
그러나 표준지침과 설계홍수량 산정요령(MLIT, 2012)을 살펴보면 유역특성인자 매개변수의 검정 및 검증 시 명확한 방법이 정해지지 않아 실무자의 혼동을 야기할 위험성이 존재한다. 즉, 확률강우량 산정의 경우 최적의 확률분포 선정, 매개변수 산정방법 등은 다양하고 통계적 기법이 개발되었으며, 실무에서도 적절하게 사용하고 있다. 반면 유역특성인자를 고려한 매개변수의 추정의 경우 유역의 지형적·지리적 특성 등으로 인한 관계 규명이 어려워 일반적으로 경험적인 방법과 더불어 개인의 주관적인 판단을 통한 산정이 주로 이루어지고 있다. 기본적으로 매개변수 추정을 위해서는 경험공식을 통해 초기값을 산정하고 이를 최적화(optimization) 과정이 필수적으로 요구된다. 즉, 다양한 최적화 방법이 모형내에서 제공되고 있으며, 관측된 유출수문곡선을 잘 재현할 수 있도록 특정 목적함수(object function)가 최소 또는 최대화될 때 까지 체계적으로 변화한다(HEC, 1990). 우리나라의 설계홍수량 산정 시 대부분 Clark 단위유량도를 활용하고 있으며, 이때 도달시간(Tc)과 저류상수(K)가 매개변수 최적화를 통해 추정될 수 있다.
순간단위도(instantaneous unit hydrograph, IUH)는 Clark (1945)에 의해 처음 소개되었다. IUH는 유효강우량에 의해 전체 유역에 균일하게 적용이 되며, 유역별 유출수문곡선이 산정되며, 도달시간과 저류상수 매개변수가 필요하다. 국외에서는 많은 연구자들이 도달시간에 대한 다양한 정의가 이루어졌다. a) 유효강수량이 종료되는 시간부터 총 유출수문곡선의 변곡점까지의 시간, b) 유효강수량의 중심으로부터 직접유출 수문곡선의 중심이 되는 시간, c) 최대 강우강도로부터 첨두유량 발생까지의 시간, d) 유효강수량의 중심으로부터 직접유출의 첨두가 발생하는 시간, e) 유효강수량 중심으로부터 총 유출의 첨두가 발생하는 시간, f) 유출 발생 시간부터 유출의 첨두가 발생하는 시간, g) 강우가 유역 최원점에서 시작하여 유역출구까지 도달하는 시간, h) 유효강수량이 종료되는 시점부터 직접유출이 종료되는 시간으로 정의되고 있다(Kirpich, 1940; Bell and Kar, 1969; NRCS, 1972; McCuen et al., 1984; Garg, 2001; Grimaldi et al., 2013a,b; Seyam and Othman, 2014; Liu et al., 2015; Disley et al., 2015; Ayalew et al., 2015; Petroselli and Grimaldi, 2015; Nardi et al., 2015; Gazendam et al., 2016; Perdikaris, et al., 2018). 국내에서도 일반적으로 g) 유역 최원점에 강우가 떨어져 유역출구까지 도달하는 시간을 도달시간으로 사용되고 있으며, 본 연구에서도 해당 정의를 인용하였다. 도달시간의 경우 측정된 유속 자료를 기반으로 산정 되지만 특정 유역을 제외하고는 계측된 유량자료가 부족하여 간접적으로 추정되고 있다. 이러한 이유로 미계측 유역에서는 도달시간 추정을 위해 유역의 물리적 특성에 대한 도달시간 관련 공식이 개발되었으며, 특히 1920년대 이후 다양한 규모와 지형적 특성을 포함한 경험 공식들을 개발한 바 있다(Williams, 1922; Kirpich, 1940; Chow, 1962; Kennedy and Watt, 1967; Watt and Chow, 1985; NRCS, 1986; Haktanir and Sezen, 1990). 이때 NRCS (National Resources Conservation Service) 방법을 제외하고, 일반적으로 유역면적, 유로 연장, 유역 경사, 유역 형상 매개변수 등을 이용하여 산정된다.
일반적으로 HEC-1 및 HEC-HMS와 같은 단일 강우-유출 모형에 적용되는 최적화 방법은 크게 두 가지 문제점이 존재한다. 첫 번째는 기존 최적화 기법의 경우 첨두홍수량의 형상 및 크기 등을 효과적으로 재현하는 것에 초점이 맞춰져 있어, 최적화 후 홍수량과 유역특성인자간의 반응 관계가 규명되지 못하고 있다. 즉, 홍수량이 증가함에 따라 도달시간 및 저류상수는 줄어드는 특성을 고려하지 못하는 점이 있다. 이러한 문제점은 특히 댐 설계 및 재평가 시 산정되는 가능최대홍수량(probability maximum flood, PMF) 산정에 있어 두드러진다. 즉, PMF는 유역반응에 기반을 두어 홍수량이 가장 큰 상태를 가정하게 되며, 이때 과거 홍수량자료를 기준으로 유역반응이 가장 빠른 매개변수를 활용하게 된다. 그러나 일반적인 최적화 방법의 경우 이러한 경향성을 파악하는데 어려움이 있다. 두 번째는 추정된 매개변수의 결정 방법에 대한 문제점이 있다. 실무에서는 다수의 단일사상 강우-유출 자료가 존재하는 경우 매개변수를 개별적으로 추정하고 이를 평균하여 유역 대표 매개변수로 활용하고 있다. 이러한 경우 개별 강우-유출 자료만이 매개변수 추정에 활용되므로 표본오차(sampling error)로 인한 매개변수의 불확실성 증가와 더불어 추정된 매개변수의 신뢰성이 결여되는 문제점이 있다. 이러한 점에서 본 연구의 목적은 단일 강우-유출 모형의 최적화 시 나타나는 문제점을 개선하는 것이다. 이를 위하여 Clark 합성단위도법을 기반으로 다수의 강우-유출 자료를 동시에 활용하여 매개변수를 추정할 수 있는 기법을 제안하고자 한다. 본 논문의 구성은 다음과 같다. 1장에서는 논문의 배경 및 목적에 대하여 언급하였으며, 2장에서는 기존 단일사상 강우-유출 모형 매개변수 최적화의 문제점 및 본 연구에서 개발된 방법론에 대해 기술하였다. 3장에서는 연구대상 유역에 적용한 결과를 기술하였으며, 마지막으로 결론 및 토의를 4장에 수록하였다.
2. 본 론
2.1 기존 단일사상 강우-유출 모형 매개변수 최적화
일반적으로 국내에서는 강우-유출 자료가 풍부한 계측유역에서 호우 사상들에 대한 홍수수문곡선과 단위도의 매개변수를 조정하여 첨두홍수량의 크기와 수문곡선 형상 등이 유사하도록 검정 및 검증 과정을 거쳐 매개변수를 결정하고 있다(설계홍수량 산정요령, 홍수량 산정 표준지침). 강우-유출 자료는 우리나라 주요 계측지점에서 지속적으로 강우-유출 자료를 확보하고 있으며, 자연유출량 관점에서 자료의 축적이 이루어지고 있다. 그러나 홍수량 산정 표준지침(ME, 2018) 및 설계홍수량 산정요령(MLIT, 2012)에서 제시된 매개변수 결정의 경우 최적화 방안이 제시되지 않고 있으며, 엔지니어의 주관적 판단이 개입될 수 있는 등 산정된 결과의 신뢰성이 확보되지 못하는 단점이 존재한다. 일반적으로 수행되고 있는 매개변수 최적화 방법은 다음과 같다.
1) 수계별 홍수통제소 및 국가수자원관리종합정보시스템(WAMIS) 등에서 분석대상 유역의 강우-유출 사상을 수집한다. 특히 유역내 태풍·집중호우가 발생했던 비교적 규모가 크거나 피해가 발생했던 강우-유출 사상을 포함한다.
2) 일반적으로 Clark 단위도법의 매개변수는 경험적인 방법을 사용하거나, HEC-1 또는 HEC-HMS에 내장되어 있는 최적화 방법을 통해 강우-유출 사상별로 검정을 수행한다.
3) 강우-유출 사상별로 최적화된 매개변수는 산정된 결과의 평균 또는 사용자의 주관적 판단에 의하여 채택되며, 이후 특별한 홍수사상이 발생하지 않는 한 채택된 매개변수를 지속적으로 사용하고 있다. 그러나 강우-유출 사상별 홍수수문곡선의 형상 및 첨두유량 재현에 최적화 목적이 국한되어 있고, 사상별로 제한된 정보만이 이용된다는 측면에서 불리한 측면이 있다.
강우-유출 사상별 검정 및 검증을 통해 산정된 매개변수는 실제 활용되기 위해 통계적 절차를 수반하여야 한다. 그러나 국내외 많은 연구에서는 단일사상 강우-유출 매개변수 산정 보다는 장기유출에 초점이 맞춰져있어 단일사상에 대한 연구는 상대적으로 미진하였다. 이러한 점에서 본 연구에서는 앞서 제시된 문제점을 극복하고, 기존 Clark 합성단위도법과 계층적 Bayesian 모형을 도입하여 최적의 매개변수 산정이 가능한 모형을 개발하였다. 더불어 산정된 결과는 홍수량에 따라 유역특성인자의 반응 관계 규명이 가능하였으며, 본 연구에서 도입하여 제안하고자 하는 모형의 연구내용을 요약하면 다음과 같다.
2.2 단일사상 강우-유출 모형 매개변수 결정방법 개선
2.2.1 Clark 합성단위도법
본 연구에서는 Clark 합성단위도법을 기반으로 유역특성인자를 산정하였다. 먼저 단위도는 특정 시간동안 균일한 강도로 유역 전반에 걸쳐 균등하게 내리는 단위 유효우량으로 인해 발생하는 직접유출수문곡선으로 정의된다. 우리나라에서는 일반적으로 합성단위도 방법인 Snyder, SCS, Nakayasu, Clark 방법 등을 주로 사용하고 있으며, 우리나라에서는 주로 Clark 방법을 채택하여 활용되고 있다.
Clark 방법의 기본 개념은 유역은 선형수로(linear channel)와 유역출구에 위치한 선형저수지(linear reservoir)로 구성되어 있다고 가정한다. 분석대상유역의 시간-면적곡선을 작성하고 순간단위유효우량으로 인한 유역출구에서의 직접유출수문곡선인 순간단위도(instantaneous unit hydrology)를 산정하는 방법이다. 이때 유량으로 환산하려면 분석대상 유역면적을 곱하여 환산한다. 일반적으로 Clark 방법은 유출의 전이효과(translation) 뿐만 아니라 유역의 저류효과(attenuation)도 고려하여 실제 유출의 물리적 특성을 잘 나타낸다고 알려져 있다. 먼저 시간-면적곡선 작성을 위해 도달시간(Tc)를 산정하는 것이 필요하며, 본 연구에서는 미국 육군공병단에서 제공하고 있는 Eqs. (1)~(3)을 통해 시간면적 곡선을 산정하였다(Clark, 1945).
| $$T_i=\frac{t_i}{t_c}$$ | (1) |
| $$TA_i=1.414T_i^{1.5}\;\;\;\;\;\;\;\;\;\;\;\;(0\leq T_i<0.5)$$ | (2) |
| $$1-TA_i=1.414\;\left(1-T_i\right)^{1.5}\;\;\;\;\;\;\;\;\;\;\;\;(0.5\leq T_i<1.0)$$ | (3) |
여기서, Ti는 총 도달시간에 대한 i시간구간의 비, tc는 도달시간(hr), TAi는 시간-면적 곡선의 누계값을 의미한다. 순간단위도 산정을 위해 추정되는 선형추적계수는 Eq. (4)와 같이 계산한다.
| $$C=\frac{2\triangle t}{2K+\triangle t}$$ | (4) |
이때, C는 선형추적계수, K는 저류상수(hr), △t는 시간구간을 의미한다. 마지막으로 산정된 시간-면적곡선과 선형추적계수를 기반으로 순간단위도 및 합성단위도를 Eqs. (5) and (6)과 같이 계산하게 된다.
| $$IUH_i={\overline{CTA}}_i\;+\;(1-C)\;IUH_{i-1}$$ | (5) |
| $$UH_i=\frac12\left(IUH_i+IUH_{i-1}\right)$$ | (6) |
IUHi는 순간단위도의 종거, C는 선형추적계수, 는 시간구간 i에서의 평균 시간면적 종거(= 0.5 (TAi + TAi-1))를 의미한다.
2.2.2 Bayesian 기반 Clark 합성단위도법 매개변수 추정
기존 HEC-1 및 HEC-HMS 모형에서 제공하는 최적화 방법(Ford et al., 1980)은 매개변수 최적화 시 매개변수의 추정이 효과적이지 못하고 특히, 물리적인 범위 내에서 수렴되지 못하는 경우가 자주 발생한다(Kwon et al., 2012). 더불어 최적화 수행시 RMSE (Root mean square error), PEP (Percentage errors in peak discharge) 등에 초점이 맞춰져 있어 단일사상 강우-유출별 홍수량 자료와 유역특성인자간의 관계가 규명되지 못하는 단점이 존재한다. 이러한 점에서 본 연구에서는 앞서 언급한 기본적인 Clark 합성단위도법 개념을 준수하여 모형을 구축하였으며, 확률통계학적 관점에서 매개변수가 추정될 수 있도록 Bayesian 기법을 도입하여 연구를 진행하였다.
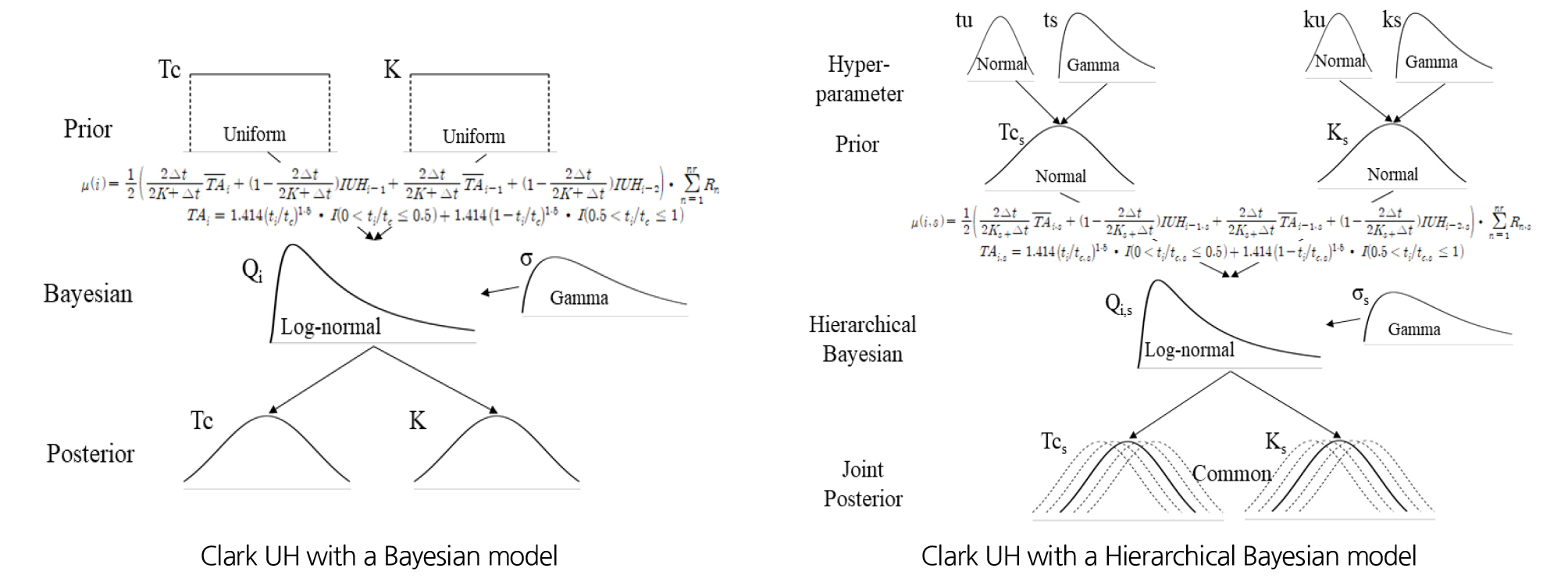
본 연구에서는 단일 강우-유출 모형의 매개변수 추정 시 2가지 방법론을 제시하였다. 첫째, 개별 강우-유출 사상을 대상으로 매개변수를 추정하는 방법으로 기존 최적화 방식과 같지만 Bayesian 기법을 이용하여 매개변수의 사후분포를 추정하게 된다. 둘째, 개별 강우-유출 사상만이 사용되는 첫 번째 방법과는 다르게 다수의 강우-유출 사상이 동시에 매개변수 추정에 사용되며, 계층적 Bayesian 기법 개념을 활용하여 개별적인 강우-유출 특성을 고려하면서 전체 강우-유출 관계의 특성 또한 평가가 이루어질 수 있는 방법이라 할 수 있다. 즉, 강우빈도 분석에서 이루어지는 지역빈도해석과 유사한 개념으로 개별사상 단위에서 이루어지는 매개변수의 추정을 Hyper-parameter를 통해 수렴(shrinkage)할 수 있도록 하여 매개변수의 추정 시 불확실성을 줄이는 방법이라 할 수 있다. 이에 대한 모식도는 Fig. 1과 같다. 이러한 과정을 통해 다수의 자료를 동시에 활용할 수 있는 장점이 있으며, 기존 방법에 비하여 매개변수 추정 시 추정되는 매개변수간의 유사성이 확보되는 장점이 있다.
소양강댐 유역내 유역특성인자(Tc, K)의 매개변수는 단일사상 강우-유출별 모형의 경우 균등(uniform) 분포로 가정(Eq. (7))하였으며, 계층적 Bayesian 모형의 경우 매개변수의 사전분포를 정규(normal)분포로 가정하였으며, Hyper-parameter는 정규(normal)분포 및 감마(gamma)분포로 가정(Eq. (13))하였다. 개별 강우-유출 사상을 이용한 모형과 다수의 강우-유출 사상을 이용한 우도함수는 다음 Eqs. (7) and (13)과 같이 정의할 수 있다.
| $$Q_i\;\sim\;LN(\mu(i),\;\sigma)$$ | (7) |
| $$t_c\;\sim\;dunif(1,20)$$ | (10) |
| $$K\;\sim\;dunif(1,20)$$ | (11) |
| $$\sigma\;\sim\;dgamma(0.1,0.1)$$ | (12) |
| $$Q_{i,s}\;\sim\;LN(\mu(i,s),\sigma_s)$$ | (13) |
| $$t_{c,s}\;\sim\;dnorm(tu,ts)$$ | (16) |
| $$K_s\;\sim\;dnorm(ku,ks)$$ | (17) |
| $$tu\;\sim\;dnorm(2,1)$$ | (18) |
| $$ts\;\sim\;dgamma(1,1)$$ | (19) |
| $$ku\;\sim\;dnorm(2,1)$$ | (20) |
| $$ks\;\sim\;dgamma(1,1)$$ | (21) |
| $$\sigma_S\;\sim\;dgamma(0.1,0.1)$$ | (22) |
Eqs. (7) and (13)의 우도(likelihood) 함수와 사전분포를 이용하여 각 모형별 매개변수들의 결합사후분포(joint posterior distribution)를 추정할 수 있다. 모든 매개변수에 대한 적분을 통해 직접적으로 추정하는 것은 불가능 하여 MCMC 방법 중 깁스표본법을 이용하여 추정하였다. 최종적으로 가장 적합한 모형을 채택하기 위해 BIC (Bayesian information criterion) (Schwarz, 1978)를 이용하여 모형별로 비교하였다. BIC 값은 모형 선택의 기준으로 잘 알려져 있으며 다음 Eq. (23)과 같이 계산될 수 있다.
| $$BIC=\ln\;(n)k-2\ln\;(\widehat L)$$ | (23) |
여기서 는 우도이며 Eqs. (7) and (13)으로 부터 계산되며, n는 관측자료의 개수, k는 추정되는 매개변수의 개수를 의미한다. BIC 값을 산정하여 비교하였을 때 작은 값이 적합도가 높은 것으로 판단할 수 있다.
3. 적용 및 고찰
3.1 대상유역의 단일사상 강우-유출 자료 및 적합도 검정
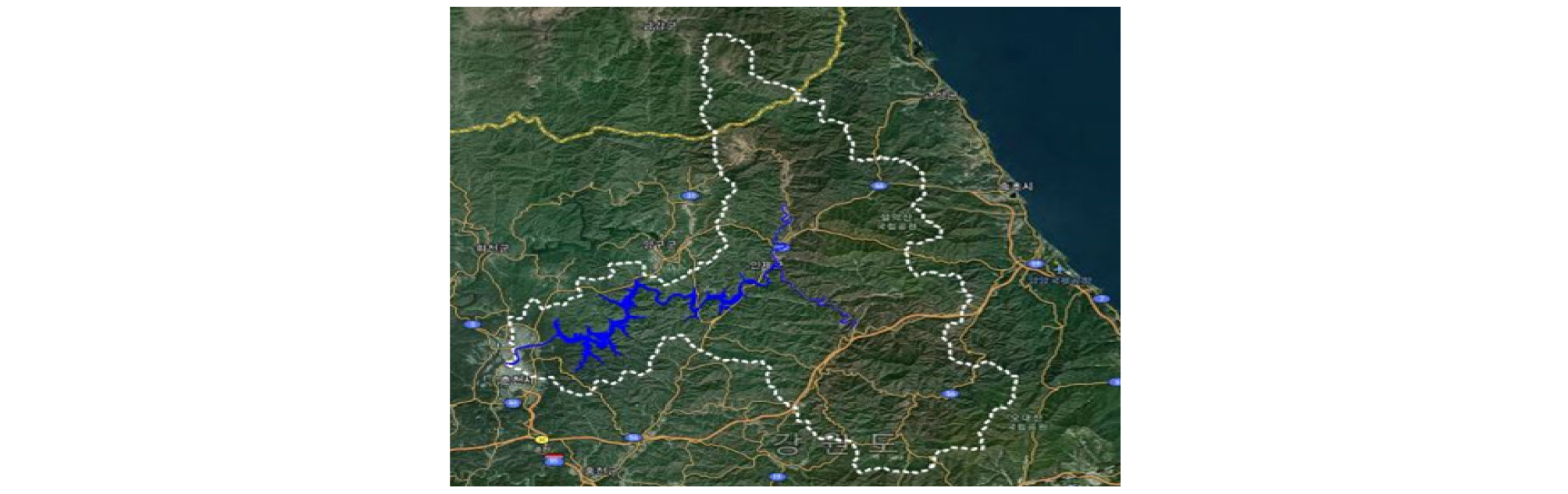
본 연구에서는강우-유량 정보가 존재하는 소양강댐 유역을 하나의 단일유역으로 가정하여 매개변수의 최적화를 수행하였다. 최적화 관점에서 소유역별로 강우-유출 자료가 없는 경우 소유역을 분할하여 매개변수를 추정하는 것은 큰 의미를 찾기 어렵다. 이러한 점에서 본 연구에서는 소양강댐 상류 유역을 단일 유역으로 가정하였으며(Fig. 2), 일반현황은 Table 1과 같다.
Table 1. Basin characteristics of Soyanggang dam basin
| Basin Name | Area (km2) | Flow Length (km) | A/L | A/L2 |
| Soyanggang dam | 2,703 | 164.24 | 16.98 | 0.10 |
소양강댐의 유역특성인자 산정을 위해 단일사상 강우-유출 자료 1990년, 2002년 등 분석 대상댐 유역의 주요 홍수사상을 중심으로 총 9개 사상을 채택하였으며, 각 사상별 자료 현황은 Table 2와 같다.
Table 2. The basic statistics of each single rainfall-runoff events used in this study
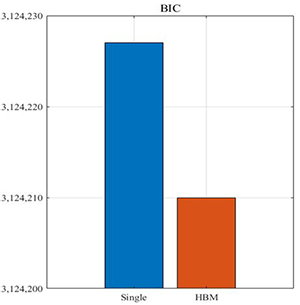
본 연구에서는 앞서 언급하였듯이 각 모형별 적합성 검정을 위해 BIC 기준을 활용하였으며, 그 결과를 제시하여 비교하였다. Table 3을 보면 각 단일사상 강우-유출 사상별로 개별적으로 최적화를 수행한 경우의 BIC 값과 계층적 Bayesian 모형으로 BIC를 산정하여 비교한 결과 계층적 Bayesian 모형을 통한 통합 최적화 모형의 BIC가 상대적으로 작은 것을 확인 할 수 있다. 최종적으로 BIC 값이 작은 계층적 Bayesian 모형을 채택하여 결과를 도출하였다.
Table 3. Comparison of bayesian information criterion (BIC) between the proposed models
3.2 분석결과
단일사상 강우-유출 모형의 정확성은 추정되는 매개변수에 의존하게 된다. 그러나 국내에서 일반적으로 적용되고 있는 최적화 방법의 경우 명확하게 정립이 안 되어 있으며, 유출수문곡선의 형상과 크기를 재현하는 것에만 초점이 맞춰져있어 산정된 매개변수를 실무에서 사용하기란 무리가 있다. 더불어 산정된 단일사상 강우-유출별로 매개변수 산정이 이루어지므로 추정된 매개변수 간 상관성이 없을 뿐만 아니라 신뢰성이 다소 결여되었다. 이러한 점에서 본 연구에서는 앞서 언급하였듯이 Clark 합성단위도법을 기본 모형으로 활용하였으며, 추정되는 매개변수는 계층적 Bayesian 기법을 도입하여 분석하였다.
먼저 기존 실무에서 사용되고 있는 HEC-1 모형을 활용하여 단일사상 강우-유출별 매개변수 최적화를 수행하였다. 앞서 언급하였듯이 HEC-1 모형에서는 각각 소유역에 대하여 관측된 유출수문곡선을 가장 잘 재현하도록 단위유량도 등을 활용하여 최적화가 제공되고 있다. HEC-1 매뉴얼에서는 목적함수 STDER의 값을 최소화하기 위해 아래 Eqs. (24) and (25) 기반으로 최적화가 이루어지며, 저유량보다 첨두유량의 정확한 재현에 초점을 두고 있다.
| $$STDER=\sqrt{\sum_{i=1}^n\left(QOBS_i-QCOMP_i\right)^2\;\times\;WT_i/m}$$ | (24) |
| $$WT_i=\left(QOBS_i+QAVE\right)/\left(2\times QAVE\right)$$ | (25) |
여기서 QCOMPi는 i시간의 계산된 유출수문곡선의 종거, QOBSi는 관측 유출수문곡선의 종거, n은 수문곡선의 종거수, WTi는 평균유량을 초과하는 유량에 대해 오차를 가중시키는 가중치이다. QAVE는 평균관측유량이다. 이렇듯 HEC-1 모형을 활용하여 본 연구에서 채택된 9개의 단일사상 강우-유출 자료를 최적화한 결과는 Table 3에 제시하였다. 산정결과 도달시간의 경우 본 연구에서 제안한 모델 결과와 그림은 비슷한 양상을 보이지만, 저류상수의 경우 이상치로 고려될 만큼 통계적으로 유의하지 않은 결과가 도출되었다. 이러한 결과는 매개변수가 수렴하지 못하고 발산하는 결과라 사료되며, K/ (Tc + K) 범위 역시 0.9를 상회하는 이상치를 나타내고 있다.
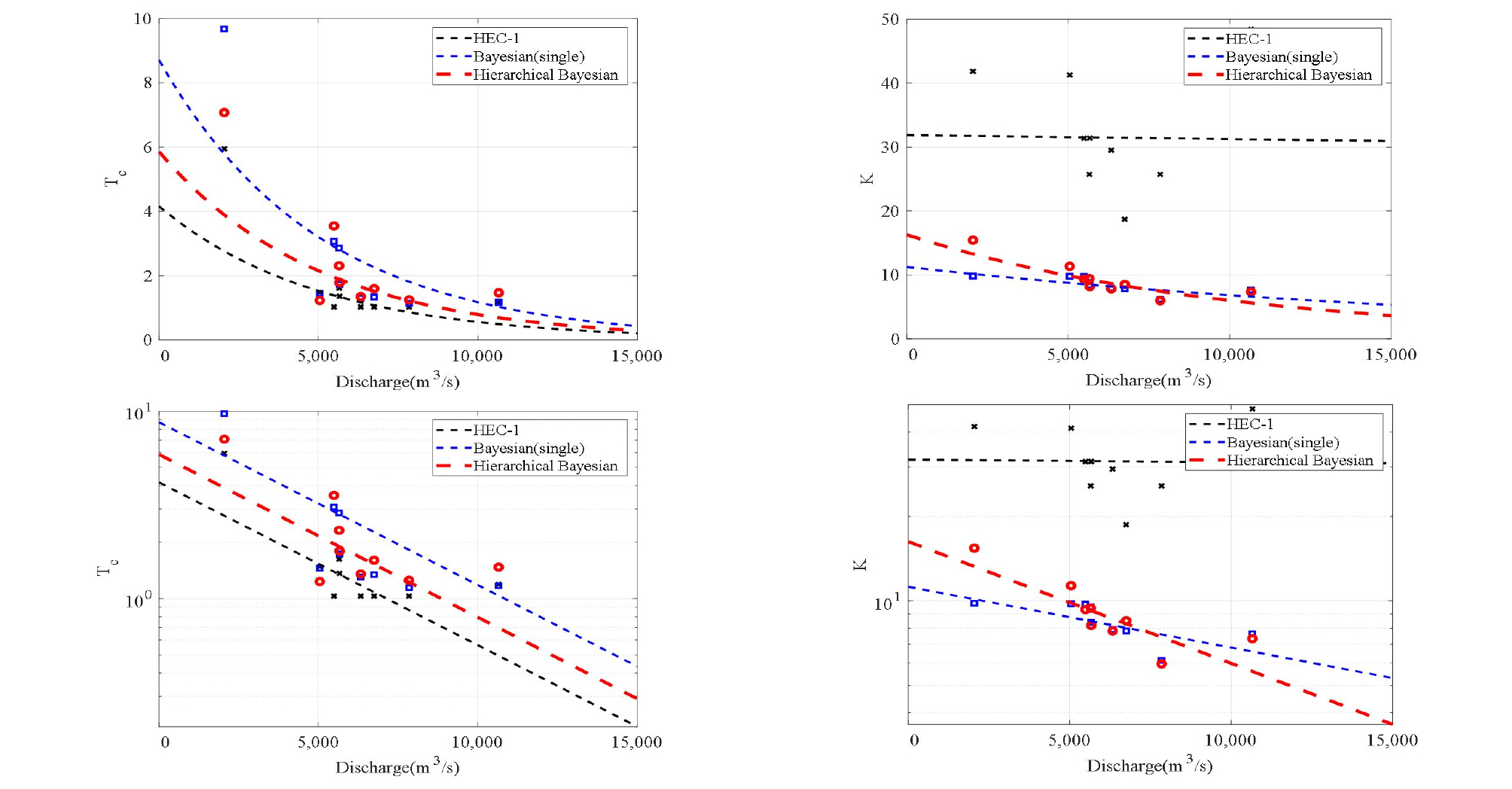
이러한 점에서 본 연구에서는 기존 HEC-1 모형 내 최적화 방법의 단점을 개선하고자 새로운 매개변수 최적화 모형을 개발하였으며, 이를 기반으로 산정된 결과는 Table 4에 제시하였다. Fig. 3을 살펴보면 단일사상 강우-유출별 첨두홍수량(x축)과 최적화된 매개변수(y축)를 도시한 결과, 기존 HEC-1 모형의 경우 저류상수 산정 결과는 통계적으로 이상치라 간주되며 명확한 관계가 나타나지 않는 것을 볼 수 있다. 반면, 본 연구에서 제안한 모형의 경우 첨두홍수량이 증가할수록 도달시간과 저류상수가 감소하고 있다. 즉, 도달시간의 경우 약 1시간, 저류상수의 경우 약 6시간에서 수렴하는 것을 확인 할 수 있다. 이러한 결과의 장점은 기존 PMF 산정 시 효과적으로 활용될 수 있을 것으로 판단된다. 즉, 기존 최적화기법을 활용하는 경우 최대홍수량을 발생시키는 유역특성인자(도달시간 및 저류시간)의 수렴여부를 규명하기 어려웠으며, 추정된 매개변수의 신뢰성을 확보할 수 없는 단점이 존재하였다. 본 연구에서 제안된 모형은 실무자의 주관적 개입을 최소화 할 수 있고, 기존에 수행되었던 방법과 비교하였을 때 보다 신뢰성 있는 결과를 제시할 수 있을 것으로 판단된다.
Table 4. The estimated basin characteristics (Tc, K ) and comparison between HEC-1 model, Clark UH with bayesian model and Clark UH with hierarchical bayesian model
추가로 국외(HEC, 1990; Kilduff et al., 2014)에서는 도달시간과 저류상수간 관계의 일반적인 범위를 K/ (Tc + K) = 0.3 ~ 0.9으로 제시하고 있으며, 본 연구에서도 이를 도입하여 매개변수 산정 결과를 검토하였다. 산정된 결과를 살펴보면 본 연구에서 제안한 모형은 0.3~0.9범위 내에 위치하는 것을 확인 할 수 있지만, HEC-1 모형의 경우 그 비율이 모두 0.9를 초과하고 있는 것을 확인 할 수 있으며, 이러한 결과는 매개변수가 수렴하지 못하고 발산하는 문제가 그대로 반영된 결과이다.
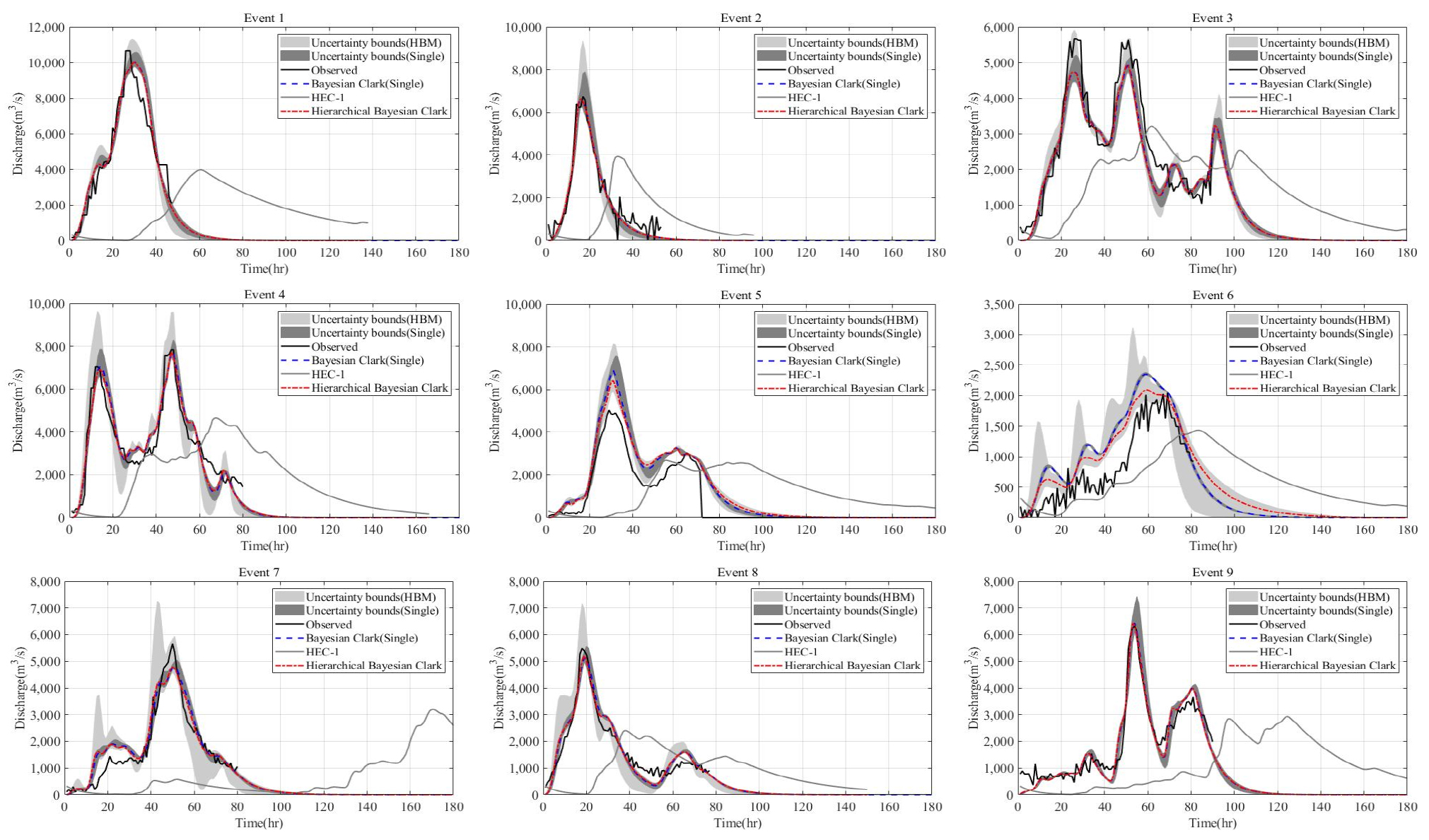
본 연구에서 개발한 모형을 통해 도출된 유출수문곡선과 관측된 유출수문곡선을 도시화한 결과는 Fig. 4와 같으며, 그 결과 매우 일치된 결과를 보여주고 있는 것을 확인 할 수 있다(Table 5). 더불어 기존 HEC-1에서 제공되고 있는 매개변수 최적화 방법에 비해 다양한 통계적 적합성 지표(goodness-of-fit)들을 비교해 본 결과 상당히 개선되었음을 확인 할 수 있었다. 본 연구에서 활용된 통계적 평가 수단은 상관계수(correlation coefficient, CC), 편의(bias), 평균제곱오차(RMSE), 일치계수(Index of agreement, IoA), Nash-Sutcliffe 계수를 사용하였다(Eqs. (26)~(31)).
Table 5. A comparison with different statistical goodness-of-fit measures between observed and simulated discharge (Bayesian and hierarchical bayesian model)
| $$CC=\frac{{\displaystyle\sum_{t=1}^n}(q_o(t)-\overline{q_o})\;(q_s(t)-\overline{q_s})}{n-1}$$ | (26) |
| $$Bias=\frac1n\sum_{t=1}^n(q_o(t)-q_s(t))$$ | (27) |
| $$RMSE=\sqrt{\frac1n\sum_{t=1}^n\left(q_o(t)-q_s(t)\right)^2}$$ | (28) |
| $$IoA=\frac{{\displaystyle\sum_{t=1}^n}\left(q_o(t)-q_s(t)\right)^2}{{\displaystyle\sum_{t=1}^n}\left(\vert q_s(t)-\overline{q_o}\vert+\vert q_o(t)-\overline{q_o}\vert\right)^2}$$ | (29) |
| $$NS=\frac{F_o^2-F^2}{F_o^2}$$ | (30) |
| $$F^2=\sum_{t=1}^n\left[q_o(t)-q_s(t)\right]_t^2,\;\;F_o^2=\sum_{t=1}^n\left[q_o(t)-\overline{q_o}\right]_t^2\;$$ | (31) |
4. 결론 및 토의
현재 우리나라에서 수행되고 있는 강우-유출 사상의 매개변수 최적화 또는 최적의 매개변수 결정시 HEC-1 또는 HEC-HMS 모형 등을 활용하고 있지만, 매개변수의 발산, 검증된 모형의 부재, 부정확한 매개변수 추정 방법 등으로 산정된 결과의 신뢰성이 결여되고 있다. 뿐만 아니라 강우-유출 자료가 계측된 유역을 소유역으로 분할하여 최적화가 이루어지기 때문에 도달시간의 역전, 하도저류상수의 최적화 처리기법 등의 통계적 기법의 부재로 매개변수 산정시 상당한 불확실성을 내포하고 있다. 더불어 한정된 자료를 활용하여 각각의 단일사상 강우-유출 자료를 통해 이루어지는 매개변수 최적화 방법은 물리적인 유역특성을 반영한 매개변수 추정이 어렵다. 이러한 점에서 본 연구에서는 기존 Clark 합성단위도법을 기반으로 계층적 Bayesian 모형과 결합하여 유역특성인자(도달시간, 저류상수)를 추정할 수 있는 모형을 개발 및 평가하였으며, 도출된 결론은 다음과 같다.
1) 기존에는 유역특성인자(도달시간, 저류상수)를 CAD, GIS 등의 프로그램으로 산정한 후, HEC-1 또는 HEC-HMS 등의 모형을 활용하여 매개변수 최적화가 수행되었다. 그러나 최적화 수행시 발산되는 문제점이 존재하였으며, 소유역 분할로 인해 도달시간 등 역전 현상으로 인해 추정된 매개변수의 신뢰성을 확보하지 못하는 단점이 존재하였다. 이러한 점에서 본 연구에서 개발된 모형의 경우 매개변수가 발산 없이 안정된 추정이 가능한 것을 확인하였다.
2) 일반적으로 최적화 분석 시 개별 강우-유출 사상을 중심으로 분석하고, 이를 평균하여 분석대상 유역의 최적매개변수로 채택하는 경우가 일반적이다. 그러나, 개별 사상 분석의 경우 홍수량에 따른 유역특성인자 매개변수의 반응 정도를 추정할 수 없을 뿐만 아니라, 채택된 매개변수 역시 채택된 강우-유출 사상을 효과적으로 재현하지 못하는 단점이 존재하고 있다. 이러한 점에서 본 연구에서 제안한 모형의 경우 기존 Clark 모형에 계층적 Bayesian 기법을 도입하여 홍수량 크기에 따른 매개변수들의 관계를 보다 명확하게 확인할 수 있었으며 모의된 유량의 경우에도 기존 HEC-1 모형을 통한 홍수량보다 개선된 결과를 얻을 수 있었다.
단일사상 강우-유출 모델링은 분석대상 유역의 최적 매개변수 결정을 위해 기초적인 과정이라 할 수 있으며, 보다 정확한 통계적 기법의 개발은 댐 위험도 분석, 기후변화에 따른 홍수량 변동성 분석 등 다양한 분야에서 활용이 가능할 것으로 판단된다. 나아가 댐의 PMF 산정시 국내에서는 PMF를 발생시키는 유역특성인자의 수렴정도를 엔지니어의 주관적인 요소가 개입되어 결과의 신뢰성이 담보되지 못하고 있다 할 수 있다. 이러한 점에서 본 연구에서 제안한 모형의 경우 홍수량에 따른 유역특성인자 반응이 효과적으로 파악되며, 주관적 요소를 배제한 통계적 기법의 적용으로 실무에서 보다 신뢰성 있는 결과를 도출 할 수 있을 것으로 기대된다. 향후 연구에서는 유역특성인자 산정시 기후변화 요소를 고려하여 산정이 가능한 공식을 개발할 예정이다.