1. 서 론
2. 우리나라 수자원의 무유출량 현황과 모의
2.1 우리나라 수자원의 무유출량 현황
2.2 적용지역과 사용자료
3. 방법론
3.1 수문 모델링(Hydrological modeling)
3.2 정확성 판단
3.3 심화된(intensified) 간헐하천 유역의 유출량 모의
4. 결 과
4.1 관측값을 통한 모형의 적합성 평가 및 비교
4.2 심화된 간헐하천 유역에서의 두 모형의 비교
5. 결 론
1. 서 론
우리나라의 국토 대부분은 산지로 이루어져 있어 빠른 유출이 발생하며 한해의(intra-annual) 강수가 여름철(7월, 8월, 9월)에 집중해서 발생한다. 이러한 지형적 기후적인 특성의 영향으로 겨울철과 봄철이 되면 자연적으로 발생하는 하천의 유출량이 적어지게 된다(Lee, 2008). 이 시기에 적어지는 유출량 가운데 종종 무유출량(zero-flow)이 발생하곤 하는데 이러한 무유출량이 종종 혹은 자주 발생하는 유역을 간헐하천 유역(Ephemeral catchment)이라고 부른다(Tooth, 2000). 간헐하천 유역은 우리나라뿐만 아니라 세계적으로 절반 이상의 많은 유역이 이 분류에 속한다(Skoulikidis et al., 2017). 제한적인 수자원이 주어지는 이러한 간헐하천 유역에서 신뢰성 있고 정확한 유출량의 예측과 수문 모델링은 수문학적 의사결정(decision making)에 있어 중요하게 된다(Vogel, 2017). 하지만 이 유역에 대한 수문 모델링은 상당한 어려움을 갖고 있다. 우선, 현재 사용되고 있는 수문 모형들은 유출량 생성과정(streamflow-generation process)에서 나타나는 한계점(threshold)을 기반으로 한 유출 과정을 표현하지 못한다(Pilgrim et al., 1988; Ye et al., 1997). 또한, 확률적 수문 모델링에서 자주 사용되는 우도 함수(likelihood function)와 그에 따른 유출 예측값은 시계열 유출 자료의 생성에 있어서 무유출의 표현에 적합하지 않다. 본 연구에서는 간헐하천 유역의 특성을 고려하는 확률적 격자형 수문 모형을 구축하고자 한다.
수문 모형에 대하여 모수(parameters), 모형의 구조(structure), 그리고 에러 모형(error model) 등을 기반으로 다양한 불확실성이 존재한다(Ahn and Kim, 2019). 이 중에 특히 적합한 에러 모형의 사용은 불확실성을 기반으로 한 통합적인 유출량 예측에 중요한 역할을 한다(Renard et al., 2011). 이 에러 모형은 일반적으로 모형의 예측과 관측치의 차이에 대한 통계적인 설명으로 만드는데 가우시안 모형(Gaussian predictive model)이 가장 기본적인 에러 모형의 형태이다. 근 10년간 에러 모형의 발전에 있어서 이분산성(heteroscedasticity)과 지속성(persistence)을 설명하기 위한 연구들이 많이 진행되었다(e.g., Ahn and Kim, 2019; Evin et al., 2014; Schoups and Vrugt, 2010). 이러한 유연한 방식의 모수화를 기반으로 한 연구들은 수문 모형의 에러 모형의 특성을 표현하는데 상당히 공헌하였다. 하지만 수문 모형의 적용과 에러 모형의 사용에 있어서 무유출량에 대한 고려는 상대적으로 적은 주목을 받아왔다(McInerney et al., 2019). 이에 기인하여 기존의 제시되는 에러 모형의 대부분은 0의 값의 낮은 한계값(lower bound of zero) 을 인식하지 못하고 또한 0의 값에서 상당히 높게 발생하는 이산적인(discrete)유출량의 분포를 표현하지 못한다.
본 연구에서는 무유출량의 에러 모형을 기반으로 한 수문모형을 구축하고 이에 대한 결과(performance)를 살펴보고자 한다. 본 연구에서 사용한 에러 모형은 최근에 McInerney et al. (2019)에서 제안된 Censoring 방식을 기본으로 하고 있다(Section 3.1.2 에 자세히 묘사되어 있음). 격자형 모형을 고려하기 위해서 대표적인 강우-유출 모형 중 하나인 Sacramento Soil Moisture Accounting Model (SAC-SMA) 모형을 사용하였으며 라우팅 모형의 결합을 통하여 격자형 강우-유출 모형을 구축하였다. 이 강우-유출 모형에 검열된 오류 모형(censoring error model)을 결합하였으며 무유출량을 고려하지 않은 강우-유출 모형과의 비교를 위해 기존의 전통적인 가우시안 오류 모형을 추가적으로 구축하였다. 이러한 모형의 구축과 평가에 앞서서 우리나라의 최근 수문 모형을 추가로 살펴봄으로써 무유출량에 대한 고려의 필요성을 살펴보고자 한다.
2. 우리나라 수자원의 무유출량 현황과 모의
2.1 우리나라 수자원의 무유출량 현황
본 연구에서는 우리나라의 무유출량 현황을 살펴보고 또한 주요 유역의 수문 모의에 사용된 모형을 조사하기 위해 연구한 과거 논문을 우선 살펴보았다(Table 1). 조사된 논문은 총 50개로 Journal of Korea Water Resource Association (JKWRA), Journal of the Korean Association of Geographic Information Studies (KAGIS), 그리고 Journal of the Korean Society of Civil Engineers (KSCE)를 기반으로 각각 64%, 10%, 8%를 포함하고 있다. 이 연구 동향에 대한 조사에 있어서 최신 자료를 기반으로 조사하기 위해서 비교적 최근 기간인 2010~2019년까지의 기간을 기준으로 자료를 조사하였다. Table 1는 사용된 수문 모형(hydrological model), 적용 유역(catchment), 최적화 방법(optimization objective)을 기반으로 정리하였다.
Table 1.
List of the studies applying hydrologic models over the Korean peninsula
| No. | Reference | Hydrological model | Catchment | Optimization objective |
| 1 | Jung et al. (2010) | KIMSTORM | Chungju | DTP, EQP, NSE, VCI |
| 2 | Kim et al. (2010) | S-RAT | Jungnang, Naelin river | NPE, NSE, PTE, RRMSE |
| 3 | Lee et al. (2010) | SWMM-GE, TANK_O, TANK_GS | Gapcheon |
AIC, BIC, NSE,PBIAS, PEE, ROV, RRMSE, |
| 4 | Shon et al. (2010) | SWAT | Nakdong river | RPE, RE, MAD, RMSE, R2 |
| 5 | Jung et al. (2011) | SWAT | Saemangeum | NSE, R2 |
| 6 | Bae et al. (2011) | PRMS, SLURP, SWAT | Yongdam and 8 basins including | NSE, R2, RMSE, VE |
| 7 | Bae and Lee (2011) | SCS-CN | Nakdong river | NSE, REV, REQ, RMSE |
| 8 | Kang et al. (2011) | SWAT | Nakdong river | NSE, R2 |
| 9 | Kim and Kim (2011) | SWAT, SWMM | Joman river, HaeBan | NSE, R2 |
| 10 | Lee and Seo (2011) | SWAT | Yongdam, Daecheong | NSE, R2, RMSE |
| 11 | Park et al. (2011) | SWAT | Yongdam, Daecheong | QER, VER |
| 12 | Choi et al. (2012) | NRCS | 3 basins including Andong | NSE, R2, RMSE |
| 13 | Jang and Ahn (2012) | SWAT | Nakdong river | ASCE, NSE, R2 |
| 14 | Joh et al. (2012) | SWAT | Chungju | NSE, R2 |
| 15 | Kim and Kim (2012) | SWAT, TANK | Chungju, Soyang | MAE, NSE, RB, RMSE |
| 16 | Kim et al. (2012) | SWAT-MODFLOW | Sindun river | NSE, R2 |
| 17 | Lee et al. (2012a) | SWAT | Namgang | NSE, R2, RMSE |
| 18 | Ryu et al. (2012) | SWAT | Mandae stream | NSE, R2 |
| 19 | Shin et al. (2012) | RHESSYS | Seolma river | NSE, R2 |
| 20 | Ahn et al. (2013) | SWAT | Seolma river | NSE, R2 |
| 21 | Choi et al. (2013) | RHESSYS | Naeseong | NSE, R2, RE, RMSE |
| 22 | Choi (2013) | SWAT | Seom river | NSE, R2 |
| 23 | Jeong et al. (2013) | SWAT | Chungju, The regulation | NSE, R2, RMSE |
| 24 | Kang et al. (2013) | TANK | 8 basins including Yongdam | R2, RE, RMSE |
| 25 | Kim et al. (2013) | FEH-REFH | Namcheon | NSE, R2, RMSE |
| 26 | Lee et al. (2013) | DHVPM | Chungju | NSE, REP, RMSE |
| 27 | Jung et al. (2014) | GRM | Gam, Naeseong river | R2 |
| 28 | Kim et al. (2014) | SWAT-K | Paldang | MAE, NSE, R2, RMSE |
| 29 | Kim et al. (2014) | SWAT | Chungju, Soyang | NSE, R2, RMSE |
| 30 | Kim et al. (2014) | SWAT | Yongdam | NSE, R2, RMSE |
| 31 | Park et al. (2014) | TFN | Chungju | RACF |
| 32 | Ahn et al. (2015) | SWAT | Anseong river | NSE, R2, RMSE |
| 33 | Ahn et al. (2015) | KIMSTORM | Nam river | NSE, R2, VCI |
| 34 | Choo et al. (2015) | SWAT | Miryang | R2 |
| 35 | Jang et al. (2015) | SWAT | Imha | NSE, RMSE |
| 36 | Jung et al. (2015) | SWAT | Yongdam | NSE, R2 |
| 37 | Kim et al. (2015) | SWAT-K | Oedo river | R2 |
| 38 | Lee et al. (2015) | SWAT-MODFLOW | Anseong river | R2 |
| 39 | Won et al. (2015) | SWAT | 11 rivers including Han river | NSE, R2 |
| 40 | Lee et al. (2016) | SWAT | Chungju | NSE, R2 |
| 41 | Jang and Kim (2017) | SWAT | Haean | NSE, R2, RMSE |
| 42 | Lee et al. (2017) | VIC | Soyang | NSE, R2, REV, RMSE |
| 43 | Moon et al. (2018) | ANFIS | Chungju, Soyang | NRMSE, R2 |
| 44 | Kim et al. (2018) | SWAT | Boryeong | NSE, R2, RMSE |
| 45 | Lee et al. (2018) | SWAT | Yongdam, Daecheong | NSE, PBIAS, R2, RMSE |
| 46 | Lee et al. (2018) | SFM, SSARR, TANK, VFLOTM | Jungnang river | MAE, MAPE, RMSE |
| 47 | Ghafouri-Azar and Bae (2018) | PRMS | 5 basins including Yongdam | NSE, RMSE |
| 48 | Shin et al. (2018) | SWAT | 4 basins including Yongdam | NSE, R2 |
| 49 | Kim et al. (2019) | ABCD, K-DRUM, PRMS, TANK | 6 basins including Andong | R2, RE |
| 50 | Lee et al. (2019) | SWAT | 4 basins including Andong | NSE, PBIAS, R2, RMSE |
우선 사용된 모형을 살펴보면 대표적인 준분포형 모형(semi-distributed model)중에 하나인 Soil & Water Assessment Tool (SWAT) 모형을 가장 많이 사용하였으며 그 외에 TANK 모형, PRMS 모형 등을 사용하였다. SWAT 모형은 다양한 주제로 폭넓게 사용되었는데 그 중 주로 미래 기후 변화가 유역에 주는 영향을 평가하였다(Ahn et al., 2013; Jang and Kim, 2017; Lee et al., 2018). 또한 SWAT 모형은 변형된 모형도 많이 제시되었다(Ahn et al., 2013; Kim et al., 2014). 최근에는 자료에 대한 접근과 컴퓨터 성능의 향상으로 분포형 모형이 많이 사용된 것도 알 수 있다(Lee et al., 2017; Lee et al., 2018).
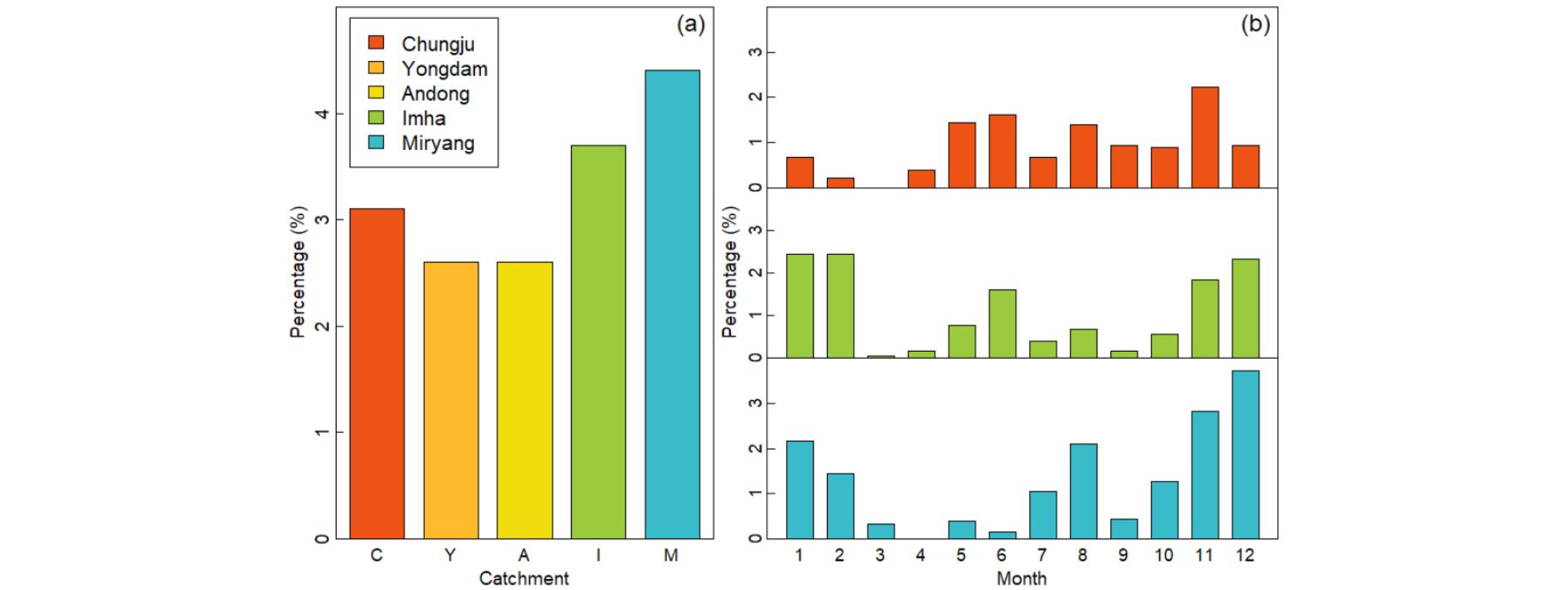
살펴본 논문 중에서 가장 많이 사용한 유역은 충주댐 유역이었다. 두 번째로 많이 사용한 유역은 용담댐과 안동댐 유역이었으며 임하댐과 밀양댐 유역이 다음으로 적용되었다. 이들 유역에 무유출량의 유무를 조사하기 위해서 국가 수자원 관리 종합 정보 시스템(Water Management Information System, WAMIS)에서 유출량 자료를 수집하여 무유출량에 대한 비율을 조사하였다. 사용된 기간은 2001~2018년까지 총 18년간 일별 자료를 사용하였다(Fig. 1). Fig. 1(a)는 주요 유역에 대한 총 일수 대비 무유출량에 대한 비율을 나타낸 것이다. 또한 Fig. 1(b)는 Fig. 1(a)에서 높은 비율의 무유출량을 보이는 3 유역을 뽑아 월별로 무유출량의 비율을 나타내었다. Fig. 1(a)에서 무유출이 발생하는 연별 비율은 용담 유역과 안동 유역으로 2.6% 였으며 밀양 유역이 가장 높은 비율인 4.4% 를 갖는 것으로 나타났다. 월별로 무유출량의 비율을 살펴보면 무유출량은 저수기 기간인 겨울철(11월, 12월, 1월, 2월)에 상대적으로 많이 나타나는 것을 알 수 있으며 가장 적게 나타나는 기간인(3월, 4월, 7월, 9월)에 비해 최대 18배 더 많이 나타나는 것을 알 수 있었다. 여기서 특이하게도 홍수기 기간인 여름철에도 유역에서 월 최대 2.1% 이상의 무유출량의 비율이 나타나는데 이 현상에 대한 원인에 대해서는 좀 더 연구가 필요로 해 보인다. 종합적으로 우리는 우리나라에서 주된 수문 유역들이 0의 유출량을 고려해야 하는 간헐하천 유역인 것을 알 수 있다.
과거 진행된 연구들의 수문 모델링에 사용되는 최적화 방법(optimization)은 대부분 NSE (Nash-Sutcliffe Efficiency)나 RMSE (Root Mean Square Error)을 최대 혹은 최소화하는 방법을 사용하였다. 이는 최적화의 방법론에서 기대 유출량에 대한 분산의 동질성을 기반으로 하고 있으며 무유출량에 대한 고려는 되지 않고 있음을 알 수 있다. 이는 수문 모델링에 있어서 아직까지 그 필요성에도 불구하고 무유출량에 대한 고려는 되지 않고 있음을 알 수 있었다. 따라서 본 연구에서는 무유출량의 고려가 수문모델링에서 어떠한 역할을 하는지 살펴보고자 한다.
2.2 적용지역과 사용자료
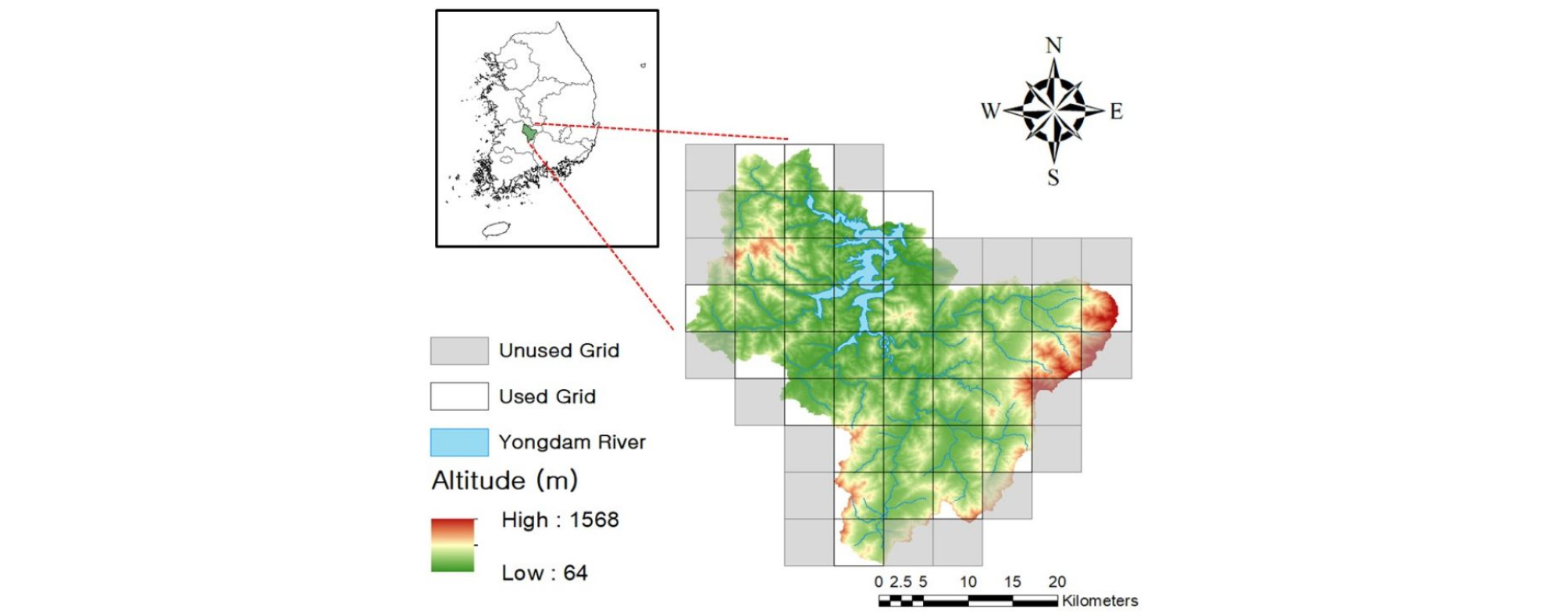
본 연구에서는 간헐하천 유역이면서 최근 연구에 자주 사용된 용담댐 유역을 대상유역으로 지정하였다(Fig. 2). 대상유역으로 지정된 용담댐 유역은 금강의 상류에 위치하며 유역 면적은 930 km2이고 저수면적은 36.2 km2을 갖는다. 유역의 연평균 강우량은 1,259.7 mm 이고 2004~2018 년까지 총 15년도 유역 연평균 유입량 20.57 m3/s이다. 전체 분석 기간은 용담댐 유출량 자료가 시작되는 2001년부터 2018년도까지 일 단위로 사용하였고 유역의 그리드를 표현하기 위해서 5.5 km × 5.5 km의 해상도를 기반으로 총 38개의 격자 망으로 구성하였으며 Fig. 2의 회색으로 표시된 부분은 모의에서 제외하였다.
격자형 수문 모형의 구축을 위해 기상 자료와 routing 모형에서 사용하는 지형 자료를 각각 그리드 격자에 맞게 변환하였다. 기상 자료는 Korean Meteorological Administration (KMA)가 운영하는 ASOS (Automated Surface Observing System)기반의 60개의 관측소에서 2001년부터 2018년까지 총 18년의 관측 자료를 수집하였으며 수집한 자료를 그리드 격자에 맞추기 위하여 ordinary kriging 방법(Cressie, 1988)으로 재배열하였다. 또한, 본 연구에서 사용한 수문 모형은 지형 자료의 각 그리드 격자에 해당하는 유출 방향이 필요하다. 따라서 각 그리드의 유출 방향을 얻기 위해 국가수자원관리종합정보시스템(WAMIS)의 공간 해상도 30 m × 30 m이고 수치지형도가 1:5000인 DEM (Digital Elevation Model)자료를 활용하였으며 DEM자료의 고도 차를 이용하여 유출 방향 라스터(flow direction raster)를 8방위로 구축하였다.
3. 방법론
무유출량을 고려한 확률적 수문 모형의 구축과 기존의 확률적 수문 모형 방법에 대한 비교를 위한 방법론은 크게 세 가지 부분으로 구성되어 있다. 첫 번째는 본 연구에서 이용한 수문 모델링의 소개이며 두 번째는 모형의 평가방법에 대한 소개이다. 마지막으로 좀 더 심화된(intensified) 간헐하천 유역의 유출량 모의 및 정확성 평가방법론으로 구성된다.
3.1 수문 모델링(Hydrological modeling)
시간 t에서의 관측된 유출량을 qt이라 할 때 수문학적 모형은 h로 사용한 데이터와 매개변수의 벡터는 C와 로 나타낼 수 있다. 여기서 는 에러 성분을 의미한다.
| $$q_t=h(\mathrm C\vert\Omega)+\varepsilon_t$$ | (1) |
시간 t에서 확률적인 유출량의 예측은 입력 불확실성, 모델 매개변수의 불확실성, 예측 에러의 불확실성을 포함하는 예측 불확실성을 표현하기 위해서 확률밀도함수/확률질량함수(pdf)로 표현할 수 있다. 확률적인 유출량의 예측은 밑에서 설명하고자 한다. 또한, 랜덤변수인 를 그것의 변수값인 와 구분을 두고자 한다.
3.1.1 분포형 수문모형(Distributed Hydrologic Model)
본 연구에서는 개념적 집중형 모형 Sacramento Soil Moisture Accounting (SAC-SMA) (Burnash et al., 1973)과 하천 라우팅 모형을 결합하여 만든 분포형 모형인 SAC-SMA 모형을 이용하여 강우-유출 과정을 묘사하였다. 분포형 SAC-SMA 모형은 토양 수분을 계산하고 직접 유출과 증발산 그리고 flow routing의 총 19개의 매개변수를 사용하여 유출 과정으로 구성되어 있다(Table 2). SAC-SMA 모형은 강수량 및 최대, 최소 온도의 시계열 자료를 입력 자료로 사용되며 일단위로 유출을 모의하였다.
SAC-SMA 모형은 유출량 모의에서 많이 사용되어 왔다(e.g., Huang et al., 2016; Lee et al., 2012b; Samuel et al., 2014; Zhang et al., 2012). SAC-SMA 모형은 지표면 유출 구역과 지표 아래에 2개의 토양 저장소인 상부 토양층(Upper Zone, UZ)과 하부 토양층(Lower Zone, LZ)을 기반으로 전체 유입량을 예측한다. 상부 토양층에서 토양 수분 상태는 자유수(UZFWM)와 수분 장력(UZTWM) 상태로 이루어져 있으며 하부토양층에서 기본적인 자유수(LZTPM)와 보조적인 자유수(LZTSM), 그리고 수분 장력(LZTWM)이 토양 수분 상태로 이루어져 있다. 위에 5개의 수분 상태 외에도 수분 장력은 불투수 영역(ADIMP) 에서 빠른 유출(fast runoffs)과 느린 유출(slow runoffs)을 생성한다. 빠른 유출 영역에서는 지표면 유출 및 불 투수 영역에서 유출되는 직접 유출이 일어나며 느린 유출 영역에서는 중간 유출과 기본 기저 유출 및 보조 기저 유출이 일어나며 이를 모두 포함하면 총 하천의 유입량이 된다(Koren et al., 2004). 그리고 상부 토양층이 포화상태가 되면 ADIMP에서 직접 유출이 생성되고 영구 불 투수 영역(PCTIM)에서는 지표면 유출이 생성된다. 위 과정에서 원래 특정된 16개의 매개변수를 사용하여 구현되지만 본 연구에서는 과거의 다른 연구(e.g., Chu et al. (2010))에서 진행했었던 것처럼 13개의 매개변수(Table 2)를 활용하였으며 제외된 3개의 매개변수(SIDE, RIVA, RSERV)는 Peck (1976)에서 제시한 값을 참조하여 기본값으로 설정하였다.
Table 2.
The parameters of the SAC-SMA and lohamnn routing model parameters
입력변수로 사용되는 일 최대/최소온도는 Hargreaves 공식(Hargreaves and Samani, 1982)을 기반으로 일별 잠재증발산량을 계산하였다. 여기서 Allen et al. (1998)에서 제안한 열 복사에너지를 추정하였다. 매개변수 PETBS를 사용하여 추가적인 잠재증발산량에 대한 보정 계수로 사용하였다.
그리드 내에서 라우팅 과정으로 시간(t)에서 유출량(q)은 단위유량도(IUH; Nash, 1957)를 사용하여 묘사하였다. 여기서 유역은(SH)로 구현되며 각각은 저장 계수(SC) 를 기반으로 저수량과 배출량 사이에 선형적인 관계로 정의하였다. 순간단위도는 gamma distribution (Wi et al., 2015)으로 Eq. (2)와 같이 수학적으로 표현된다.
| $$q_t=\frac{\Omega^{SC}}{\Gamma(SH)}\left(t\cdot\Omega^{SC}\right)^{\Omega^{SH}-1}\exp\left(-\Omega^{SC}\cdot t\right)$$ | (2) |
여기서 는 감마 함수를 나타낸다.
그리드 사이의 유출량의 이동은 Saint-Venant 방정식의 확산파 근사법(diffusive wave approximation) (Lohmann et al., 1998)과 유출 방향 라스터를 통해 얻은 여행 경로(travel path)로 계산하였다. Saint-Venant 방정식은 Eq. (3)와 같다.
| $$\frac{\partial Q}{\partial t}+\Omega^{VELO}\frac{\partial Q}{\partial x}-\Omega^{DIFF}\frac{\partial^2Q}{\partial^2t^2}=0$$ | (3) |
여기서 VELO와 DIFF는 매개변수로 각각 파의 속도와 확산성의 매개변수를 의미한다.
3.1.2 확률기반 에러모형(Probabilistic Error Model)
무유출량을 고려하기 위해 에러 성분()을 최근에 연구된 (McInerney et al., 2019)에서 제안한 검열된 오류 모형으로 모형화하였다. 이 오류 모형은 특정값(본연구에서는 0의 값) 이상만 갖도록 하며 left-censored (LC)된 Gaussian (NLC)에 의해 0의 유출의 발생이 가능하도록 하한값을 설정하였다.
| $$\varepsilon_t\sim N_{LC}\left(0,\;\sigma^{LC^2},\;\varepsilon_t^{LC}\right)$$ | (4) |
| $$\varepsilon_t^{LC}=z\left(0\vert\Omega^z\right)-z\left(Q_t\vert\Omega^z\right)$$ | (5) |
여기서 는 분산 매개변수이고 는 비정규성을 개선하고 예측 불확실성을 이분산성 특징으로 변환한 함수를 나타낸다. 그리고 MLC모형의 비교를 위해 평균이 0이고 일정한 분산()을 가지는 기존의 정규화된 오류 모형(MNE)을 개발하였다. MNE모형은 간헐하천 유역에서 수문학적 모델링으로서 사용되어왔다(Ahn and Kim, 2019). 그리고 각각의 모형(MLC and MNE)의 우도 함수(likelihood)는 관측된 유출량인 qt에 대해 계산할 수 있다.
| $$L^{M_\neq}={\textstyle\prod_{t=1}^T}\;z'\left(q_t\vert\Omega^z\right)f_{LC}\left(z\left(q_t\vert\Omega^z\right)\vert z'\left(q_t\vert\Omega^z\right),\;\sigma^{NE^2}\right)$$ | (7) |
여기서 tq = 0는 관측 데이터의 유출량이 0이 되었을 때를 나타낸다.
3.2 정확성 판단
두 모형(MLC and MNE)을 비교하여 정확성을 평가하기 위하여 각각 2001~2008년을 동일한 기간으로 보정을 시행하였고 그 이후 2009~2018년을 검정 기간으로 적용하여 모형의 적합성을 평가하였다. 이를 위하여 simulated annealing optimization (Bélisle, 1992)을 사용하여 두 모형의 매개변수(Table 2)를 독립적으로 보정하였으며 매개변수의 불확실성을 고려하기 위해서 각각의 모형을 20회씩 독립적으로 최적화를 실시하였다. 분포형 모형의 구현이기 때문에 병렬 컴퓨터 프로세스를 방식을 사용하였다.
우선 두 모형의 전체적인 정확도를 평가하기 위해서(Nash and Sutcliffe, 1970)에서 제안한 NSE (Nash-Sutcliffe Efficiency)와 (Gupta et al., 2009)에서 제안한 KGE (Kling-Gupta Efficiency), 그리고 (Legates and McCabe Jr, 1999)에서 제안한 mNSE (Modified Nash-Sutcliffe efficiency)를 사용하여 최적화한 예측값의 정확성을 비교하였다. NSE는 모형 효율성 계수로 수문 모형의 성능을 비교하고 KGE는 상관계수(r), 변동성(), 관측값과 예측값의 평균 비율()을 사용하여 모형의 관측된 시계열과 모의 결과의 시계열을 비교한다. 그리고 mNSE는 NSE를 수정한 모형 평가 방법으로 NSE가 예측값에 높은 유출량이 포함되어 있을 경우 이를 과장하여 모형의 성능을 비교하는 부분을 수정하여 예측값의 낮은 유출량이나 무유출량을 더 정확하게 평가 할 수 있다.(Criss and Winston, 2008). 따라서 두 모형의 모의 성능 평가를 위해 기존에 사용된 NSE와 KGE, 그리고 mNSE를 사용하여 두 모형을 비교하였다.
| $$\mathrm{NSE}=1-\frac{\sum_{i=1\;}^N\left|S_{\mathit i}\mathit-O_{\mathit i}\right|^2}{\sum_{i=1\;}^N\left|O_{\mathit i}\mathit-\mu_{\mathrm o}\right|^2}$$ | (8) |
| $$\mathrm{KGE}=1-\sqrt{{(r-1)}^2+{(\alpha-1)}^2+{(\beta-1)}^2}$$ | (9) |
| $$\mathrm{mNSE}=1-\frac{\sum_{i=1\;}^N\left|S_i\mathit-O_i\right|}{\sum_{i=1\;}^N\left|O_i\mathit-\mu_{\mathrm o}\right|}$$ | (10) |
여기서 S와 O는 각각 예측 값과 관측 값을 나타낸다.
3.3 심화된(intensified) 간헐하천 유역의 유출량 모의
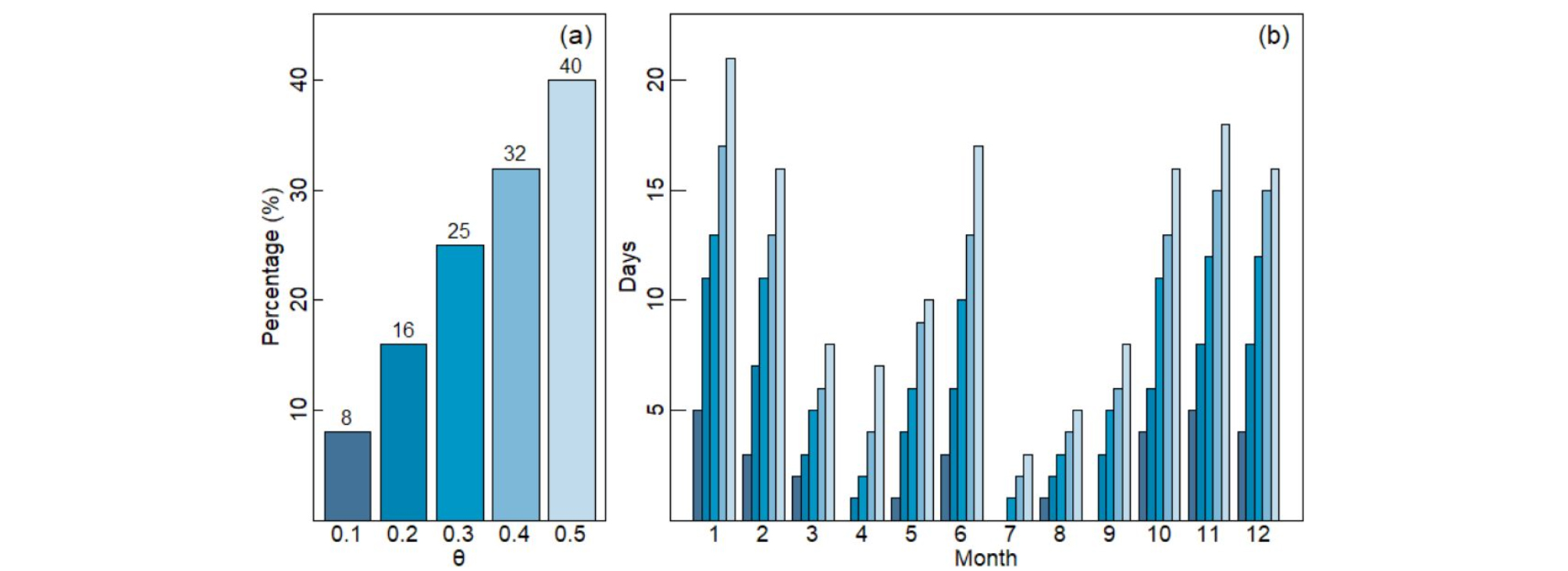
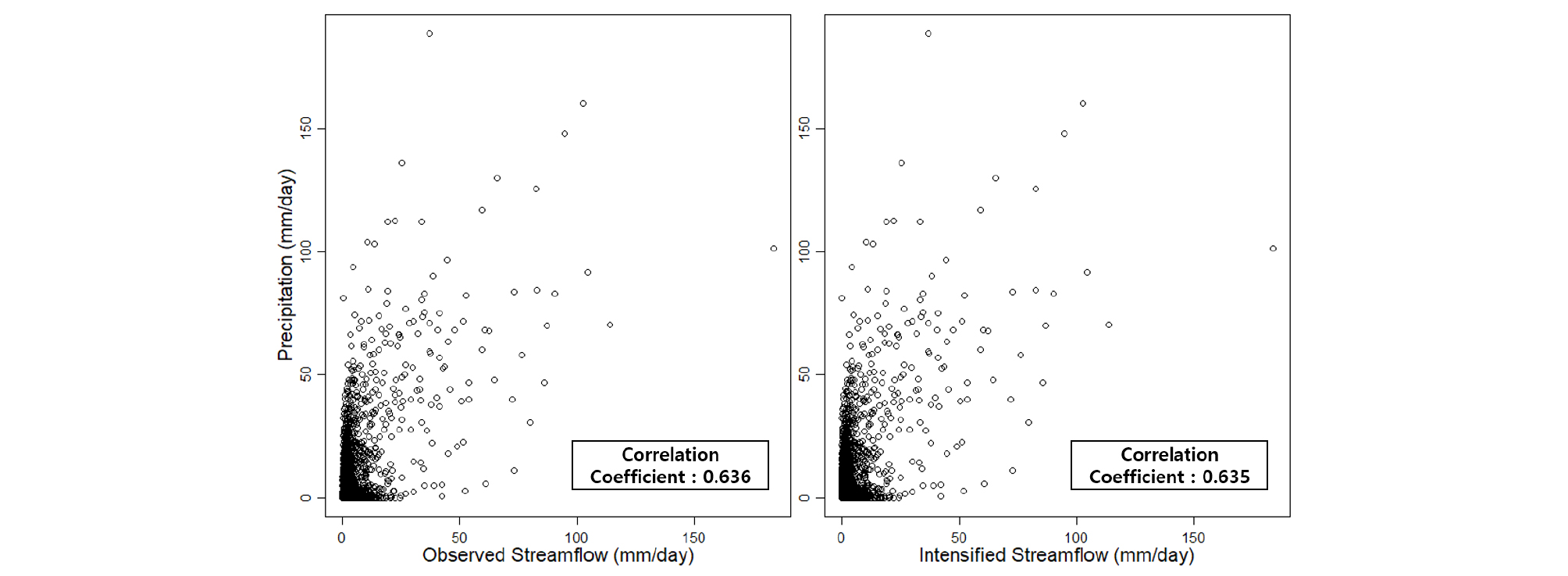
본 연구에서는 간헐하천 유역의 특성에 따른 두 모형의 정확성을 확인하기 위해서 관측된 유출량을 변화시켜서 무유출량의 비율을 증가시키는 방법으로 새로운 유출량을 모의하였다. 강우와 유출의 비선형적인 관계를 유지하면서 무유출량의 비율을 증가시키기 위해서 관측된 유출량에서 특정값()을 줄이는 방법을 사용하였으며 Fig. 3은 각각의 다르게 정의된 (0.1부터 0.5까지 0.1씩 증가)에 따른 무유출량의 변화를 나타낸 것이다. Fig. 3(a)에서 막대선 위에 표시된 숫자는 각각에 얻어진 무유출량의 비율을 의미하는데 이는 이 0.1 증가할 때마다 약 8%의 무유출량 발생 빈도가 선형적으로 증가한다는 것을 알 수 있다. Fig. 3(b)는 증가에 따른 월별 무유출량 증가를 나타낸다. 여름철인 7월의 무유출량은 증가에 큰 영향을 받지 않지만 초여름철인 6월의 무유출량은 겨울철(11월, 12월, 1월)과 비슷한 비율의 무유출량을 갖는 것을 알 수 있다. 높은 을 사용하면 현실의 관측값에 대한 왜곡이 심하게 발생하므로 본 연구에서는 비교적 여름철인 7월과 8월에 무유출량이 발생되지 않고 6월의 무유출량이 크게 증가하지 않는 0.2의 을 사용하여 심화된 간헐하천 유역으로 적용하기로 하였다. 그리고 0.2의 을 사용하였을 경우 왜곡되는 정도를 비교하여 나타내기 위해서 산점도 그래프를 추가하였다(Fig. 4). Fig. 4(a)는 강수량과 기존의 관측값, Fig. 4(b)는 강수량과 수정된 관측값의 상관관계를 나타낸다. 두 그래프의 상관계수의 차이가 크지 않고 나타나는 다른 큰 차이가 없으므로 유출량에 0.2의 차를 적용시켰으며 그리드로 구축된 실제 강우량 그리고 최저/최고 온도를 사용하여 두 모형을 새롭게 검보정을 실시하였다. 이 유역의 모델링에 있어서도 앞 3.1절에서 설명한 방식과 동일하게 적용하였으며 각각의 모형을 앞선 모델링과 마찬가지로 독립적으로 20회씩 최적화를 시켰다.
4. 결 과
4.1 관측값을 통한 모형의 적합성 평가 및 비교
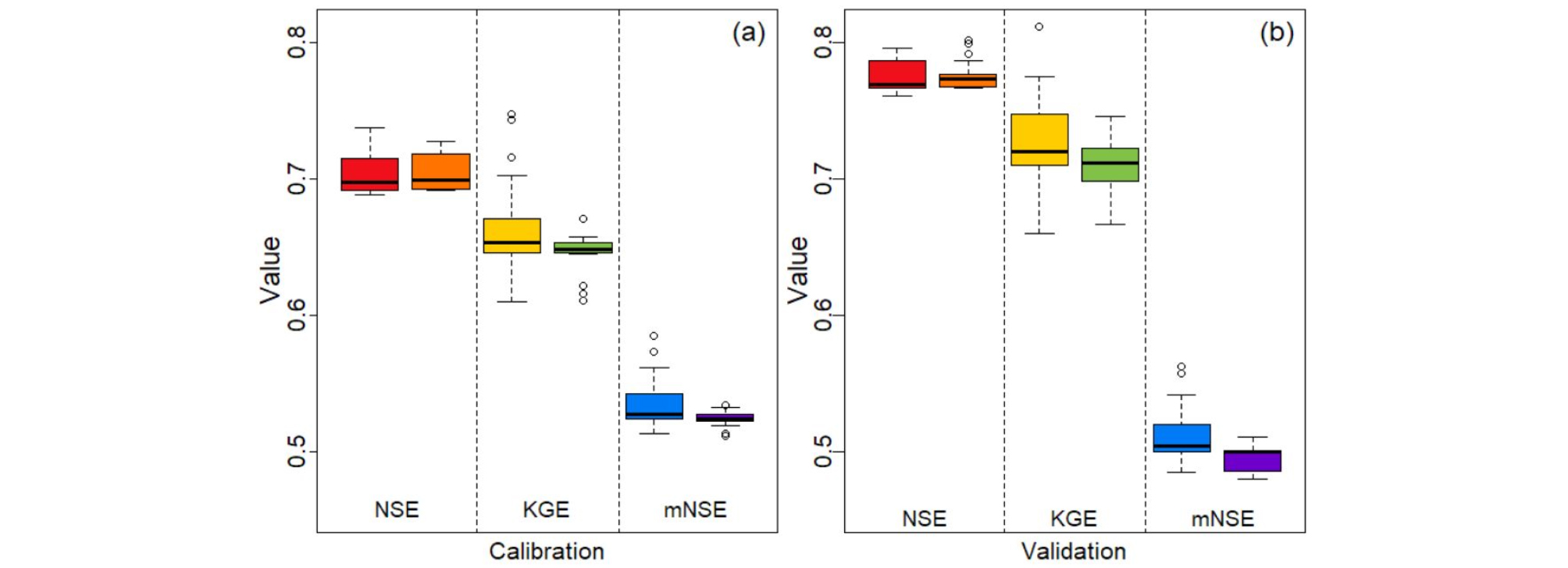
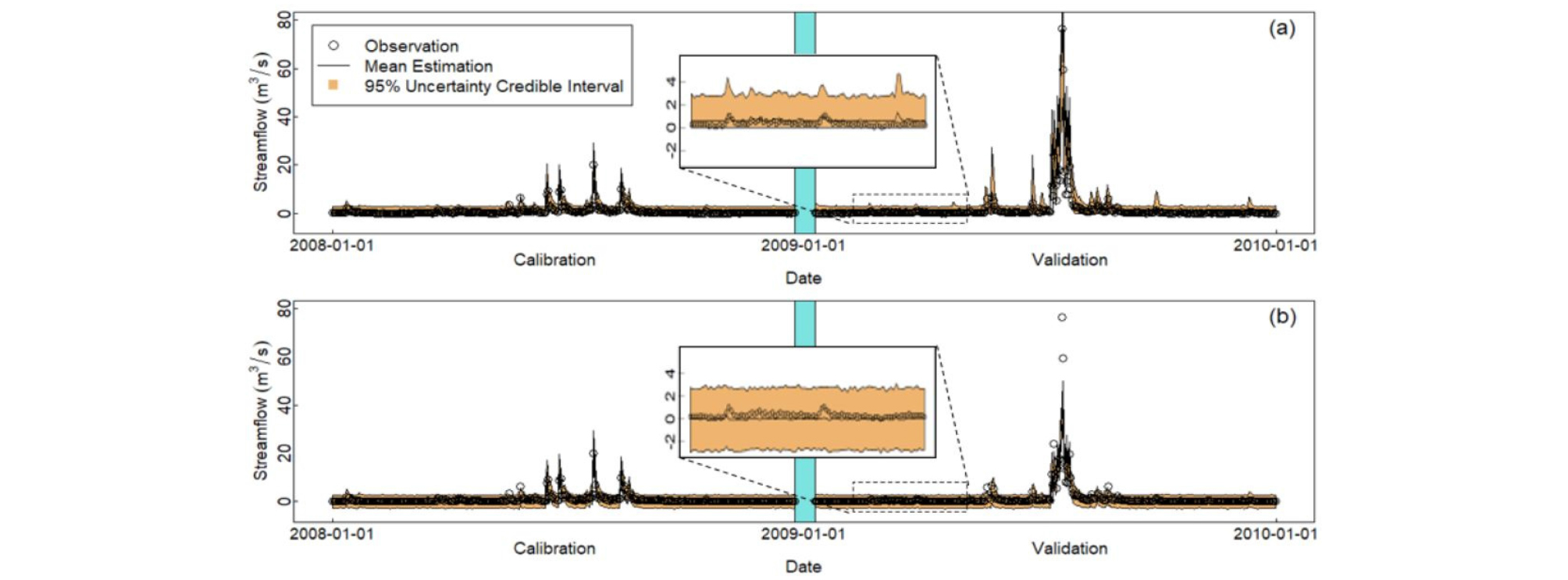
Fig. 5는 관측된 유출량 값으로 두 모형의 최적화를 실시한 20개 결과값을 NSE, KGE, mNSE의 metrics을 사용하여 Boxplot으로 나타내었다. 또한 Figs. 5(a) and 5(b)는 20개의 얻어진 파라메터 셋을 기반으로 랜덤으로 선택하여1000개의 유출량을 구축하였으며 구축된 유출량 시나리오에 대한 95%의 신뢰 구간을 결정하였는데 그 신뢰 구간의 표시를 위하여 2008년 1월 1일부터 2008년 12월 31일까지의 보정 기간을 표시하였다. 또한 2009년 1월 1일부터 2009년 12월 31일까지의 검정 기간을 사용하여 그 예시를 나타내었다.
Fig. 5를 우선 살펴보면 두 모형의 보정(calibration)기간에 대한 평균 NSE, KGE, mNSE는 MLC모형이 0.70, 0.66, 0.54이며 MNE모형이 0.70, 0.64, 0.52의 결과를 보였다. 또한 검정(validation)기간에 대한 정확도의 평균은 MLC모형이 0.78, 0.73, 0.51을 MNE모형이 0.78, 0.71, 0.50을 가진다. 여기서 사용한 보정 기간과 검정 기간은 3.2절에서 설명했듯이 2001~2008년과 2009~2018년으로 각각 총 8년과 10년을 사용하였다. 얼핏 보면 두 모형의 검보정 결과가 상당히 신뢰할 만한 수준이고 유사한 결과를 보이지만 그 안에서 유의미한 차이가 존재한다. 우선, 보정 결과에 대한 분포 형태가 다르다(Fig. 5(a)). 두 모형의 NSE는 정확성에 대한 분포의 차이가 거의 없지만 KGE, mNSE의 경우 MLC모형이 정확도에 대한 분포가 상대적으로 넓게 퍼져있어 MNE모형이 좀 더 안정적인 결과를 나타낸다고 이야기할 수 있다. 이는 MNE모형이 좀 더 신뢰할 만한 결과를 모의한다고 할 수 있지만 보정에 대한 정확도보다 중요한 검정 기간에 대한 결과를 살펴보면 또 다른 결과를 추론할 수 있다. 특히 MNE모형의 결과가 KGE와 mNSE에서 MLC모형보다 낮아진 결과를 보여준다. 두개의 metrics (KGE와 mNSE)에서 중앙값이 MLC모형이 더 좋은 결과를 보임과 동시에 전체적인 분포에서도 MLC모형이 더 좋은 결과를 보여준다. 이러한 MLC모형의 결과는 일별 자료들을 합하여 얻어지는 월별 유출량의 계산에 있어서도 유의미한 차이를 만들어 내었다(제시되지 않음).
Fig. 6를 살펴보면 우선 95%의 신뢰구간에서 관측값이 포함 되는 비율은 두 모형(MLC, MNE)이 각각 전체 보정기간에서 94.9%, 93.9%을 포함한다. 검정기간에서는 각각 92.1% 와 95.6%를 포함한다. 비록 검정기간에 대한 신뢰구간에 포함되는 비율은 MNE모형이 더 높은 값을 보이지만 이는 상대적으로 넓게 예측된 예측간격(interval)에 대한 과적합(overfitting)에 대한 결과로 보여진다. 이를 확인하기 위하여 본 연구에서는 검정 기간에 대한 신뢰구간의 표준편차를 확인하였고 두 모형(MLC, MNE)에 대한 결과는 1.45과 1.52으로 상대적으로 넓어진 것을 확인할 수 있다. 또한 Fig. 6에서 확인되는 것 같이 MNE모형의 신뢰 구간이 0 이하의 음수값이 포함되어 예측의 결과에 현실성이 떨어지는 것을 알 수 있다.
요약을 하면 두 모형 다 상당한 결과를 보여주며 우리나라에서 간헐하천 유역에 대한 수문모델링으로 사용가능하다고 논할 수 있지만 무유출량을 고려한 MLC모형이 조금 더 정확한 NSE, KGE, mNSE결과를 보여주는 것을 확인 할 수 있다. 본 연구에서 사용된 유역인 용담댐 유역은 평균적으로 1년에서 9.5일(2.6%)정도의 낮은 무유출 비율을 보였는데 미래에 용담댐 유역의 무유출 비율이 증가할 시 수문 모델링에서 어떠한 결과에 보일 지를 확인하기 위하여 관측값을 수정한 심화된 간헐하천 유역을 추가로 모의하였다.
4.2 심화된 간헐하천 유역에서의 두 모형의 비교
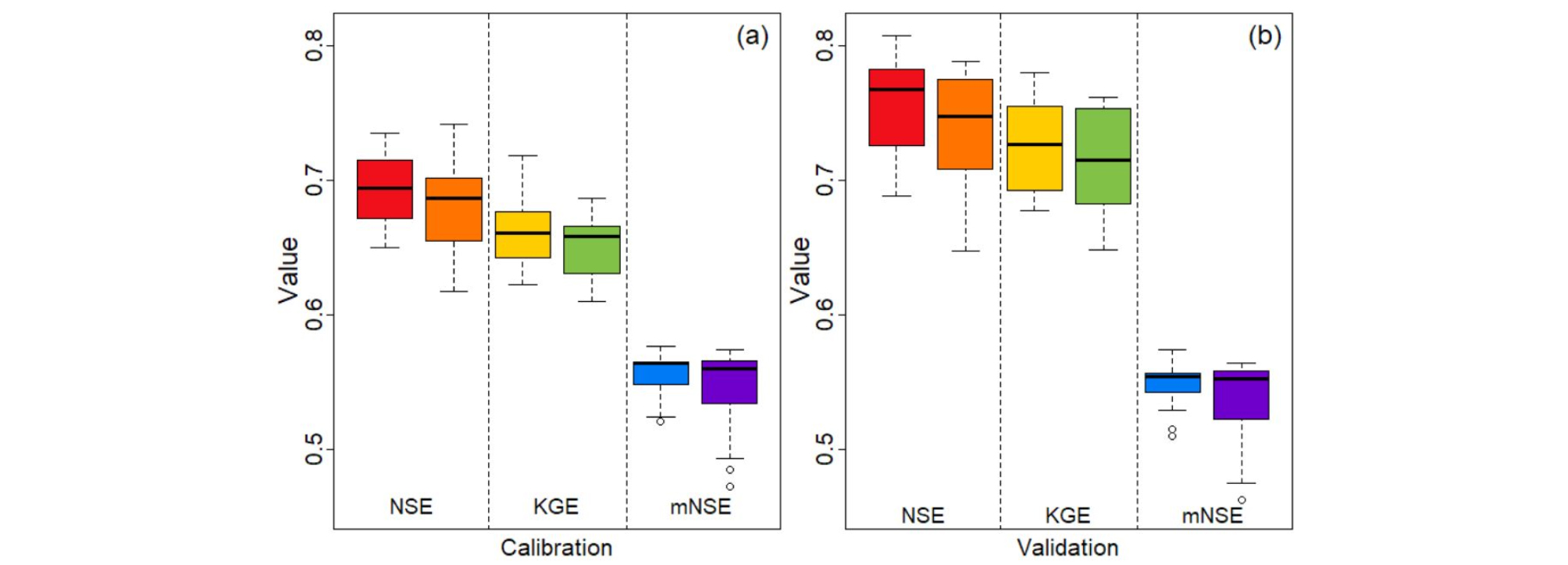
심화된 간헐하천 유역의 모의를 위하여 본 연구에서는 를 0.2 로 설정하였고 이는 평균적으로 연간 58일의 무유출 빈도를 나타낸다. Fig. 7은 심화된 간헐하천 유역의 수정된 관측값을 통해 최적화를 실시한 20개의 결과값을 NSE, KGE, mNSE 의 metrics을 사용하여 Boxplot으로 나타내었다. 수정된 관측값을 사용하여 4.1에서 구축한 방법과 동일하게 95%의 신뢰 구간 사용하였으며 Fig. 6와 큰 차이를 보이지 않아서 사용하지 않고 검보정 결과 제시하였다.
Fig. 7을 살펴보면 두 모형의 보정 기간에 대한 평균 NSE, KGE, mNSE는 MLC모형이 0.69, 0.66, 0.56이며 MNE모형이 0.68, 0.65, 0.55의 결과를 보였다. 또한 검정 기간에 대한 정확도의 평균은 MLC모형이 0.75, 0.72, 0.55를 MNE모형이 0.74, 0.71, 0.54을 가진다. 두 모형의 검보정 결과가 실제 용담댐 유역에 대한 모델링과 유사한 결과를 보이지만 자세히 살펴보면 그 보다 더 유의미한 차이를 보인다. 우선, 보정의 결과(Fig. 7(a))를 확인하면 MLC모형의 중앙값이 전체적으로 MNE모형보다 더 좋은 결과를 나타내고 있다. 또한 3개의 지수에 대한 결과에 있어서 분포의 범위가 작아져서 MLC모형의 신뢰성이 높은 것을 확인할 수 있다. 그리고 보다 중요한 검정 기간에 결과를 살펴보면(Fig. 7(b)) MLC모형의 결과가 모든 metrics (NSE, KGE, mNSE)에서 MNE모형보다 높은 결과를 보여준다. 또한, MNE모형의 정확도에 대한 분포가 상대적으로 넓게 분포하여 그 적합성이 떨어지는 것을 확인할 수 있다.
요약하면 두 모형 다 무유출 비율이 증가한 경우에 있어서도 여전히 상당히 신뢰할 만한 결과를 보여주지만 4.1절에서 비교하였을 때보다 무유출량을 고려한 MLC모형이 정확한 NSE, KGE, mNSE 결과를 보여주는 것을 확인 할 수 있었다.
5. 결 론
본 연구는 무유출이 발생하는 간헐하천 유역을 대상으로 무유출량을 고려하는 MLC모형과 무유출량을 고려하지 않은 MNE모형을 비교하여 유역의 무유출 고려에 대한 필요성을 알아보고자 하였다. 이에 대한 논의는 아직 우리나라 유역에 대해서 아무 논의가 없었던 것으로 판단된다.
이를 확인하기 위해서 본 연구에서는 우선 50개 이상의 과거 수문 모델링에 관한 논문들을 조사하였고 그 안에서 연간 9.5일(2.6%)정도의 무유출량이 발생하는 용담댐 유역을 시범 유역으로 선정하였다. SAC-SMA 모형을 이용한 격자형 수문 모형을 구축하였으며 두개의 서로 다른 에러 모형을 사용하여 두개의 독립적인 모형(MLC와 MNE)을 구축하였다. 또한 구축한 두 모형을 기존의 관측값과 미래에 용담댐 유역의 무유출 비율이 증가하였을 때를 가정하여 수정한 심화된 간헐하천 유역을 사용하여 수문 모형의 결과를 비교하였다.
무유출량을 고려한 MLC모형이 조금 더 정확한 결과를 보여주는 것을 확인 할 수 있었으며 MNE모형의 경우 신뢰 구간이 0 이하의 음수값이 포함되어 MLC모형이 조금 더 현실성 있는 신뢰구간을 형성하는 것을 확인하였다. 이는 두 모형의 결과가 무유출의 빈도가 상대적으로 적은 용담댐 유역에서 유의미한 차이를 가지고 있으므로 이보다 더 높은 무유출의 빈도를 가지고 있는 국내의 다른 유역들에서 무유출량을 고려하는 수문 모형을 구축한다면 더욱 분명한 차이를 야기한다고 판단할 수 있다. 이러한 예상은 무유출의 빈도를 높게 수정한 심화된 간헐하천 유역에서 두 모형을 모의하여 비교하였을 경우에 두 모형의 NSE, KGE, mNSE결과가 기존의 관측값을 사용하였을 경우보다 차이가 나타나는 것을 확인하여 추론할 수 있었다. 결과적으로 본 연구에서 구축한 모형의 결과는 무유출의 빈도 증가에 따라 무유출량을 고려하는 MLC모형의 효율이 높아진 것을 확인할 수 있었으며 두 모형의 결과가 무유출량 정도에 영향을 받는 것을 알 수 있었다.
본 연구의 제약조건으로 적용된 유역이 댐을 기반으로 한 유역으로 이에 따른 불확실성이 존재한다. 특히 Fig. 1(b)에서 알 수 있듯이 여름철에 많은 강수가 발생함에도 불구하고 무유출량 발생하는데 이러한 무유출량은 댐의 수위 변화에 따라 산정되는 유입량을 추정하는 방식에서의 오류로 인하여 발생하였을 가능성이 존재한다. 이러한 오류는 저수위의 측정에 있어서 바람과 같은 다른 변수들에 영향을 받을 수 있기 때문에 더욱 더 불확실 할 가능성이 존재한다. 하지만 이러한 제약조건 속에서도 MLC모형이 MNE모형 보다 높은 신뢰도를 보여주는 것을 확인하였으며 이는 우리나라의 수문모형에서 무유출량의 고려가 여전히 유용하다는 것을 의미한다.
요약하면 본 연구를 통하여 국내 유역에서도 무유출을 가지는 유역을 확인할 수 있었으며 수문 모델링에서 무유출량을 고려하는 연구를 통해 기존의 연구에서 가지고 있는 문제점과 제약을 벗어나 유출량 예측을 보다 현실적으로 가능함을 확인하였다. 이러한 신뢰도 높은 수문 모델링의 가능성과 함께 보다 정교한 수자원 계획 및 관리를 기대 할 수 있을 것이라 판단된다.