1. 서 론
2. 대상자료 및 분석방법
2.1 대상유역
2.2 가뭄과 연관된 강우특성 인자 및 군집분석
3. 방법론
3.1 표준강수지수
3.2 가뭄심도-지속기간-빈도 곡선
3.3 비정상성 빈도해석
4. 결 과
4.1 표준가뭄지수를 활용한 가뭄 발생 특성 분석
4.2 순위도출을 활용한 GCMs 선정
4.3 비정상성 빈도분석을 통한 SDF 곡선 산정
5. 결 론
1. 서 론
기상학적인 가뭄은 강수량의 공급 요인이 기대치보다 적은 경우에 발생될 수 있는 자연재해이며, 기후변화는 유역의 기상상태 변화와 밀접한 연관성을 가지고 있다(Janga Reddy and Ganguli, 2013). 1900년대 이후로 전지구 평균 온실가스 농도 및 온도는 2100년까지 빠른 증가로 인해 극한 수문사상의 발생 특성 변화가 제시되고 있다(IPCC, 2013; Ashrit et al., 2005). 국내의 경우도 기후변화에 따른 월별 또는 계절별 극한 수문사상 특성의 변동에 따른 가뭄발생 위험이 증가 될 수 있다. 따라서 기후변화와 연관된 장래의 발생 가능한 가뭄 규모와 가뭄 특성을 파악하고, 이에 따른 안정적인 수자원 공급 정책 등의 선제적 대응책 마련의 필요성이 제기되고 있다.
인위적 요인을 배제하는 경우 자연 상태의 물 공급 측면에서는 지역의 기상학적 가뭄을 평가하는 것이 기후변화를 고려한 가뭄 영향 평가에 보다 직접적일 수 있으며, 이러한 경우 적절한 장래 기후변화 시나리오에 따른 예측 강우 선택이 의미를 가질 수 있다. 온실가스 대표경로(Representative Concentration Pathways, RCP)는 기후변화와 기상변수 간의 관계를 고려하여 기상변수들의 전망결과를 제시하는 것으로 농도변화와 관련한 4개 시나리오로 구분되며, 이들 중에서 RCP 8.5는 가장 극단적인 온실가스 배출 시나리오이다. Yoon and Joe (2015)은 9개 GCMs에 다른 근 미래의 극치 강수 및 빈도분석 연구를 위해 RCP 8.5 시나리오를 적용한 바 있으며, Lee et al. (2016a)은 2045년을 기준의 RCP 8.5 자료를 이용한 미래 PMPs 산출에 활용한 바 있다.
RCP 8.5 와 같은 이례적인 시나리오에 나타난 극한 수문사상을 분석하는 경우에 적절한 확률분포형 선택이 매우 중요해진다. 이를 위해 극치 이론(Extreme Value Theory)은 분포형 꼬리 부분의 사상 발생을 위기 상황으로 인식 및 가치변화 분석을 하는 것으로 GEV (Generalized Extreme Value) 분포는 극치 이론과 맥락을 같이 할 수 있는 것으로 알려져 있다(Katz, 2013; Leadbetter et al., 1983; Gumbel, 1958).
한편으로는 기후변화 시나리오를 기반으로 다양한 전지구기후모형(General Circulation Model, GCM)이 제시 및 미래 수문특성과 관련한 연구에 적용되고 있다. Dubrovský, et al. (2014)은 16개 GCM 앙상블에 따른 미래 기후 변동성 평가를 수행한 바 있다. 다만 다양한 해상도에 따라 다양하게 제시되는 GCM을 활용은 다른 측면으로는 미래의 불확실성 범위의 확대 문제와 연결될 수 있으며, 분석 목적에 맞는 변수 설정 및 순위도출 등에 따른 모델 선택이 필요하다(Jeong et al., 2018; Hong et al., 2018). McMahon et al. (2015)은 23개 GCM별 기온 및 강우와 관측 자료의 비교를 통해 GCM별 모의 능력을 평가 한 바 있다.
RCP 8.5에 따른 여러 GCM 모델들은 미래 기후 극치를 평가하기 위한 입력 자료로서 활용성을 갖는다. 따라서 기후 극치의 발생 빈도를 분석하기 위해 사용될 수 있지만 가뭄 특성상 특정한 가뭄 극치 사상의 발생을 빈도만으로 평가하는 것은 어려움이 있다.
따라서 극치 가뭄에 대한 특정을 분석하기 위해서는 세 가지 변수가 이용 될 수 있으며, 빈도 외에 심도나 지속기간과 연관을 통해 정량화가 함께 이루어질 수 있다(Lee et al., 2016b). SDF 곡선은 대표적인 정량화를 위한 대표적인 방법 중 하나이다(Dalezios et al., 2000; Kim et al., 2014).
Lee et al. (2015)은 관측자료 기반의 매개변수적 빈도해석 절차를 통해 한반도 5대강 유역의 SDF 곡선을 구축 한 바 있다. 다만 기후변화에 따른 예측 수문자료는 비정상 계열을 따를 수 있으며, 이에 따라 빈도해석 절차에 대한 개선이 요구될 수 있다. Park et al. (2015)은 비모수적 통계기법인 Kernel Smoothing Density Function 기법을 적용한 빈도해석 및 SDF 곡선의 작성을 수행한 바 있다.
비정상성 가정은 기후변화에 따른 수문 사상의 매개변수 변동을 의미하며, 기후변화의 경우 일반적으로는 온실가스 농도 등의 추세를 고려한 선형추세를 반영할 수 있다(Milly et al., 2008; Katz, 2013; Jung et al., 2019).
비정상성 빈도분석 절차 내에서 베이지안 추론은 관측과 예측 공간 사이에 존재하는 미지분포의 매개변수 연결을 통해 불확실성 식별을 위한 것이다. 매개변수의 불확실성을 고려한 재현수준의 사후분포 간격을 산정하고, 샘플링 접근으로 수렴성을 가지며, 이를 통해 복잡한 사후분포 산정에 용이한 것으로 알려져 있다(Gelman et al., 2003; Gelman and Shirley, 2011).
대표적인 샘플링 기법으로 MCMC (Markov Chain Monte Carlo)가 있으며, 다양한 범위의 통계적 모델링을 제공하는 마르코프 체인을 사용하여 샘플의 추출 및 샘플의 평균을 통해 기댓값에 대한 근사를 수행한다(Lee and Zhang, 2002). Lee et al., (2010)은 경향성을 고려한 확률강우량과 불확실성 구간 추정에 MCMC 기법을 적용한 바 있다. 다만 상대적으로 복잡성이 크거나 다중 최적화 등에 한계를 보일 수 있다(Sherri et al., 2017).
이러한 문제를 극복하기 위해 유전자 알고리즘을 차용한 DE (Differential Evolution)와 MCMC를 결합하여 DE-MC (Differential Evolution Markov Chain) 기법이 제안되었다(Vrugt et al., 2009).
본 연구에서는 기상청에서 보유하고 있는 장기 시계열 자료를 토대로 12개 지점을 선정하여 해당 지점 관측자료 및 RCP 8.5 기후변화 시나리오 기반 10개 GCM 일단위 강우량 자료를 수집하였다. 관측 자료를 토대로 기후변화 영향에 따른 강우발생일수 및 총강우량의 추세변동과 지역적 위치에 따른 가뭄의 공간적 특성 차이를 검토하고자 하였다. 공간적 특성 파악을 위한 군집분석은 두 인자의 추세 증감 및 16방위에 따른 그룹화를 통해 8개의 Zone으로 그룹화 하였다. 또한 시간적 특성 파악에는 관측기반(S0) 64년(1954~2017년), 근 미래(S1) 41년(2018~2058년), 먼 미래(S2) 41년(2059~2099년)으로 구분하여 가뭄 심도별 및 지속기간별에 대한 분석을 수행하였다.
가뭄평가에는 기상학적 가뭄지수인 표준강수지수(Standardized Precipitation Index, SPI)를 사용하였고, 입력 자료에는 관측 및 GCM별 예측을 결합한 단일 시계열 자료의 지속기간별(1, 3, 6, 9, 12 개월) 입력 자료를 구축하였으며, 예측 자료의 불확실성을 줄이고 개연성 있는 모델의 선택을 위해 강수 및 가뭄지수 인자를 이용한 순위도출을 적용하였다.
기후변화를 고려한 비정상성 빈도해석을 위해서는 SPI 지수를 입력인자로 베이지안 기반의 샘플링 기법인 DE-MC를 적용하였고, 12개 지점별 미래 SDF (Severity-Duraion-Frequency) 곡선 및 지속기간별 및 재현기간별 가뭄심도를 산정하였다. 산정된 결과는 군집분석 결과를 토대로 비교 검토를 수행하였다.
2. 대상자료 및 분석방법
2.1 대상유역
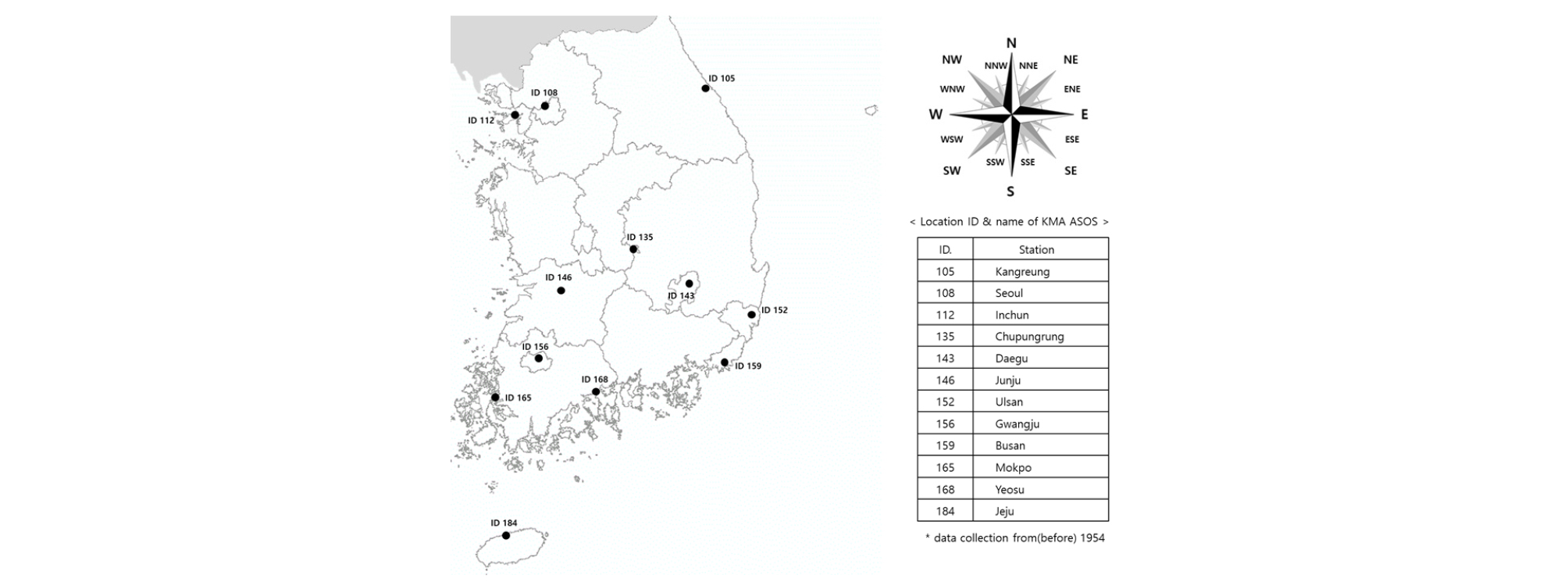
본 연구에서는 남한지역을 대상으로 하여 기후변화 시나리오와 결합한 기상학적 가뭄지수 산정 및 비정상성 빈도분석을 수행하고자 하였다. 기상학적 가뭄지수 산정을 위한 주요인자는 강우자료이며, 자료 수집은 기상청 종관기상관측시스템(Automated Synoptic Observing System, ASOS)을 통해서 획득하였다.
기상청 강우 관측지점은 Fig. 1에서와 같이 여러 관측지점으로 이루어져 있으나 관측 시작 시점에는 차이를 보인다. 따라서 여러 지점들 중에서 1954년을 포함한 비교적 장기 강우관측 자료를 보유하고 있는 Fig. 1의 12개 지점을 선정하였다.
또한 미래 가뭄특성 분석을 위한 10개의 GCM은 Table 1로 제시하였으며, G1~G10으로 구분하였다(Jeong et al., 2018; Yoon et al., 2017). CIMIP5 GCM으로부터 생산되는 자료의 경우 Model Output Statistics (MOS) 기법 중 Bias Correction Spatial Disaggregation (BCSD)와 기후시나리오 내 장기추세를 반영하기 위한 Quantile Delta Mapping (QDM) 방법을 결합한 BCSD with quantile delta mapping (SDQDM)을 통해 공간적 상세화를 수행한 자료를 활용하였다(Eum and Cannon, 2017). 자료기간은 관측기반(S0)은 1954~2017년까지 64개년 기간 자료를 수집하였으며, 예측치는 근 미래(S1) 2018~2058년, 먼 미래(S2) 2059~2099년 기간 자료를 적용하였으며, 일 강우자료를 대상으로 하였다.
Table 1. Selected GCMs (Yoon et al., 2017)
2.2 가뭄과 연관된 강우특성 인자 및 군집분석
유역에서의 강우 발생은 자연 상태에서 제공되는 가용수자원의 공급을 의미하며, 총강수량 부족 또는 강우발생일수 감소경향은 가뭄 발생 가능성을 증대 시킬 수 있다. 따라서 기후변화 영향에 따른 유역 수문 변동특성 탐지를 위해 강우발생일수(Rainy Days, RD)와 총강수량(Total Rainfall, TR)에 대한 월별 및 분기별 합산을 하였고, 결과에 대한 연도별 추세 변화를 검토하고 이에 따른 그룹화를 수행하였다.
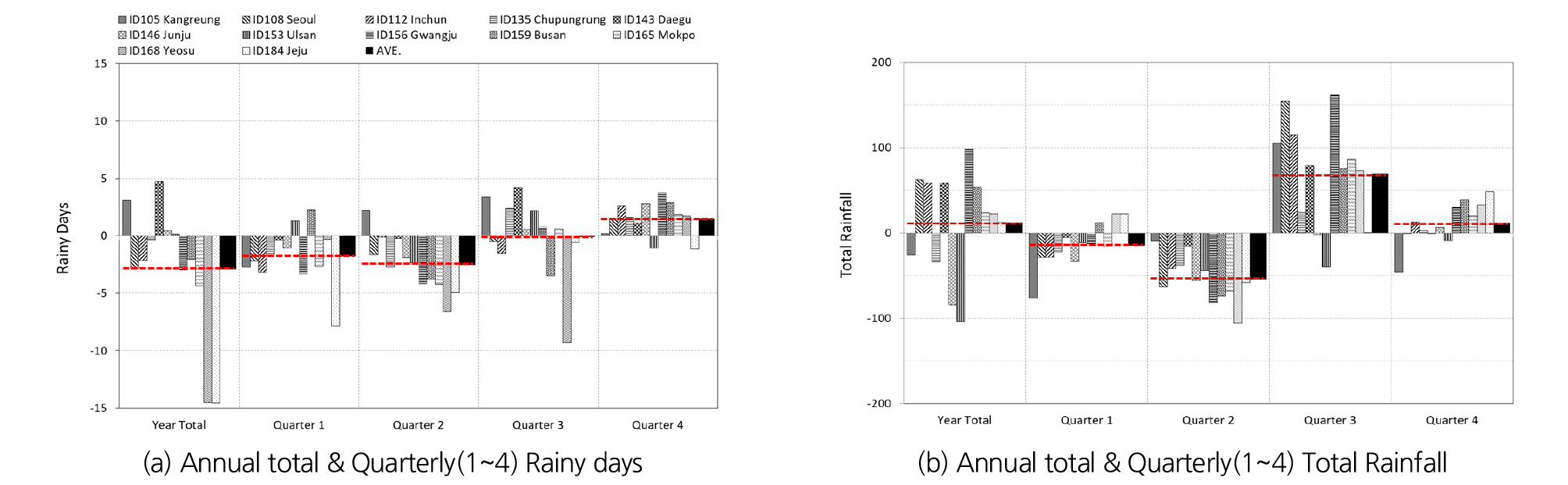
시간 단위는 연 단위와 분기별 1분기(1~3월), 2분기(4~6월), 3분기(7~9월), 4분기(10~12월)로 구분하였고 결과는 Fig. 2로 나타내었다. 계절별 구분도 고려될 수 있으나 기후변화에 따른 계절 구분기준 변화 및 계절별 지역적 발생 시점의 차이를 고려하여 동일 기간의 분기로 구분하였다.
추세변화량은 선형 추세를 의미하며, 기울기 및 절편을 산정하고, 함수 값의 기준을 동일 시작점인 0으로 하여 함수 값 초기와 종기 값 차이에 따른 경향성 증감을 나타내었다.
Fig. 2(a)의 연도별 강우발생일수는 남부지역으로 갈수록 감소 추세이고, 제주와 여수는 가장 큰 폭의 감소가 나타났다. 또한, 1분기 부산과 울산, 2분기 강릉을 제외한 대부분 지역에서 감소를 보였으며, 3, 4분기에는 증가 추세로 나타났다.
Fig. 2(b)의 분기별 총강우량은 강릉, 광주, 전주, 울산에서 감소를 보였다. 또한, 1, 2분기는 대부분 감소, 3분기는 대체적인 증가를 보였다.
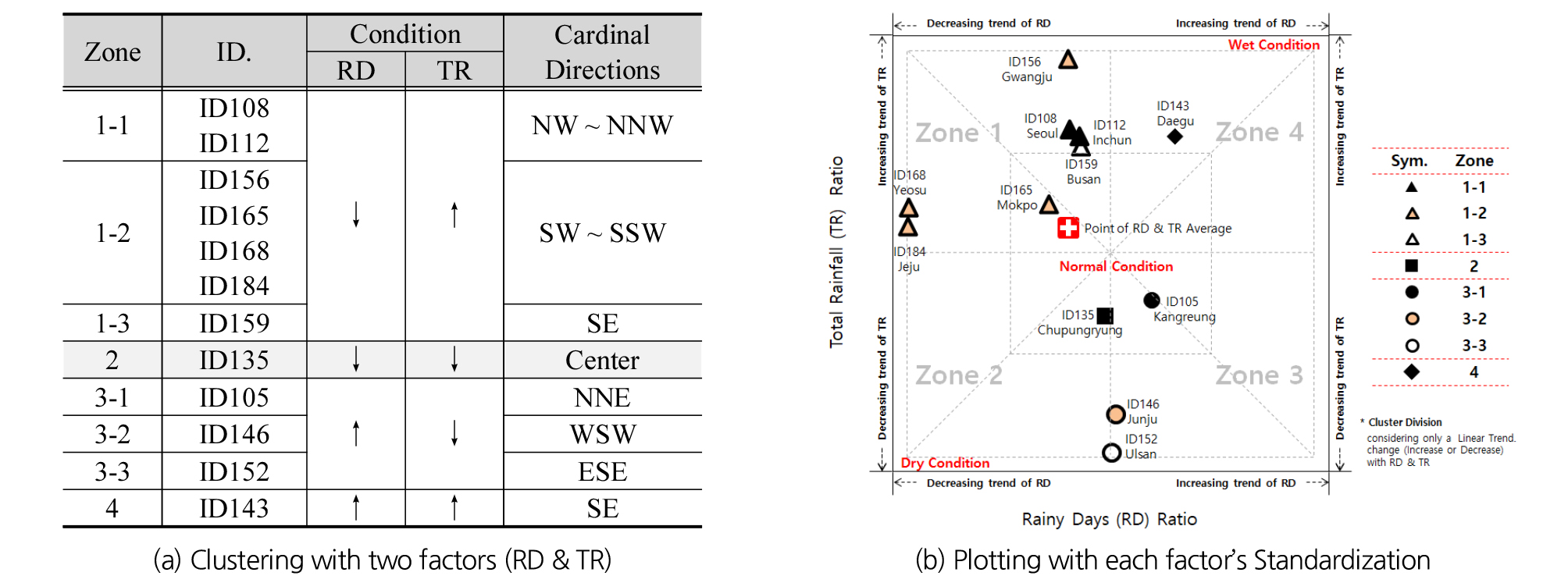
두 인자의 추세 증감에 대한 고려 및 추풍령(ID135)을 중심으로 16방위로 구분하여 Fig. 3(a)와 같이 12개 관측 지점에 대한 그룹화를 수행하였다. 또한, 인자별 표준화를 통해 Fig. 3(b)로 제시하였으며, 중심부일수록 정상상태, 우측 상향은 습윤, 좌측 하향은 건조 상태를 나타내도록 하였다.
RD (강우발생일수) 감소, TR (총강우량) 증가로 분류되는 Zone 1은 Fig. 3의 좌측 상향에 위치하며, 7개 지점이 포함되었다. Zone 1-1인 서울 및 인천과 1-3인 부산은 지리적인 차이에도 불구하고 Fig. 3에서는 두 인자에 따른 특성의 유사성이 높았으며, 1-2는 바다에 인접한 제주, 여수와 목포와 내륙인 광주가 포함되었다.
RD 감소, TR 감소로 분류되는 Zone 2는 추풍령만이 포함되었다. 특성상 가뭄에 가장 취약한 구조이지만 RD의 변화는 적고 TR만 다소 감소가 됨에 따라 정상상태인 중심부 부근에서 위치하였다.
RD 증가, TR 감소로 분류되는 Zone 3에는 세 개 관측소가 포함되며, 추풍령을 중심으로 북북동(NNE) 방향에는 3-1인 강릉, 서남서(WSW) 방향은 3-2인 전주, 동남동(ESE) 방향으로는 3-3인 울산이 포함되었다. Fig. 3에서와 같이 세 지역 모두 RD의 추세 변동이 적은 반면에 TR의 추세 변화가 나타났으며, 강릉은 상대적으로 중심 부근에 가까이 위치하였고, 전주와 울산은 TR의 추세 감소 폭이 다른 지점들에 비해 큰 것으로 나타났다.
RD 증가, TR 증가로 분류되는 Zone 4의 경우에는 대구 관측지점이 선택되었다. 강우 발생일수의 감소 폭이 큰 제주와 여수를 제외하면 전체적으로 총 강우량의 지역적 편차가 강우 발생일수보다 큰 것으로 분석되었다.
3. 방법론
3.1 표준강수지수
표준강수지수(Standardized Precipitation Index, SPI)는 기상학적 가뭄지수 평가를 위한 방법으로 통계적 절차에 따른 강수의 과함과 부족에 대한 정량적 해석기법이다(McKee et al., 1995).
가뭄의 평가는 장시간에 걸쳐 발생을 고려한 이동평균(Moving Average, MA)이 고려됨에 따라 지속기간 1, 3, 6, 9, 12개월을 적용하였다. 또한 통계적 절차에 따른 가뭄지수 산정을 위한 분포형은 다음 Eq. (1)과 같이 기상청 수문기상 정보시스템의 Gamma 분포형을 적용하였다.
| $$F_s(x)=\frac1{\alpha^\beta\Gamma(\beta)}x^{\beta-1}e^-\frac x\alpha$$ | (1) |
여기서, Fs는 분포형 누가확률분포, (>0)는 크기 매개변수, (>0)는 모양 매개변수이다.
산정된 기상학적 가뭄지수 결과를 가뭄 심도 구분 기준에 따라 분류하면 -1.0~-1.5는 보통가뭄(Moderately Drought), -1.5~-2.0은 심한가뭄(Severely Drought), -2.0 이하는 극한가뭄(Extreme Drought)으로 구분될 수 있다(McKee et al., 1995).
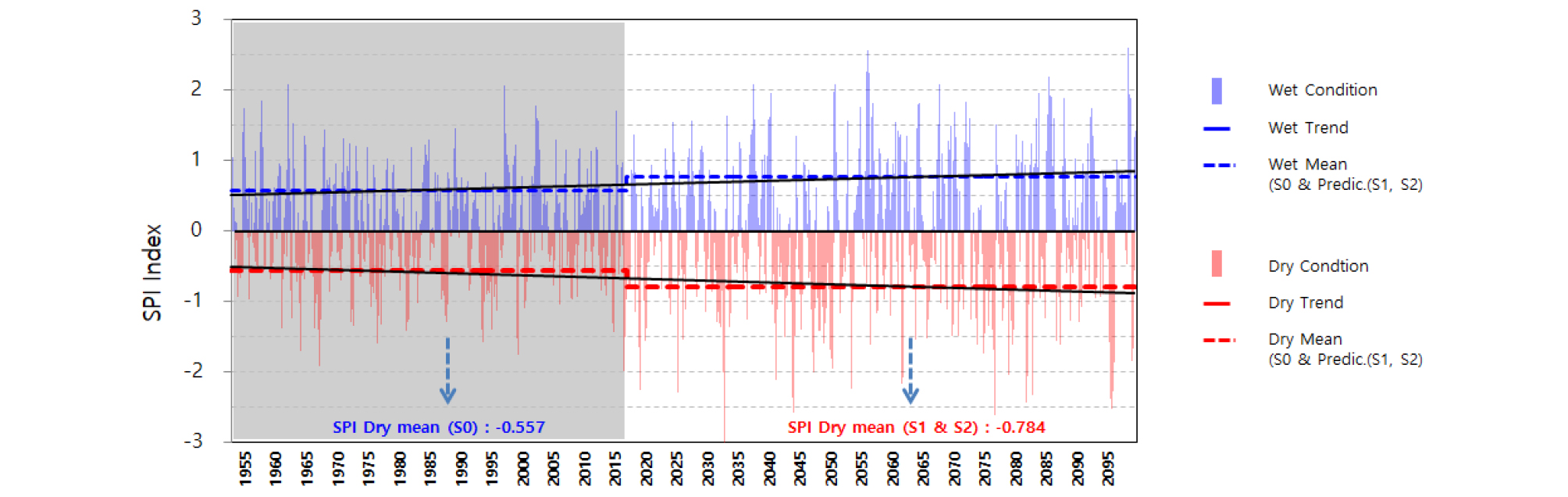
Fig. 4는 IPSL-CM5A-LR 모델의 12개 지점별 SPI 6 산정결과에 대한 관측 및 예측자료의 단일 시계열 자료 구성을 이용한 SPI 지수의 시계열 지수를 도시한 것이다. 또한 관측 및 예측치 평균의 변화 및 선형 추세를 함께 나타내었다.
관측치는 평균 –0.557, 예측치는 –0.784로 미래 수문환경에서 건조 상태가 심화되는 결과를 보였고, 추세에 있어서도 미래로 갈수록 습윤(Wet)은 상승되는 반면에 건조(Dry)는 하강됨에 따라 극치기후의 변동폭이 커질 수 있는 것으로 나타났다.
3.2 가뭄심도-지속기간-빈도 곡선
SDF(Severity-Duration-Frequency) 곡선은 미래 극한 수문환경에서 발생 가능한 극한 가뭄을 가뭄심도, 지속기간 및 빈도의 세 인자를 이용하여 정량적으로 나타내기 위한 방법으로 지속기간별로 산정된 SPI를 나누어 연 최대치 가뭄심도를 구성하고, 이를 토대로 빈도분석을 수행한다. 빈도해석을 통해 산정된 결과는 최종적으로 지속기간 및 재현기간에 따라 SDF 곡선의 작성이 이루어진다.
또한 일반적인 빈도해석 절차는 통계적 과정을 통해 적합도 검정 및 최적 확률분포형을 선정 등이 이루어진다(Park et al., 2015). 다만 이러한 절차는 기후변화와 같은 비정상성 문제를 다루는데 있어서는 어려움이 있음에 따라 본 연구에서는 비정상성 빈도분석 기법을 적용하였다.
3.3 비정상성 빈도해석
3.3.1 극단치 분포
극한가뭄 분석을 위한 분포형의 선정은 샘플링 결과가 Gumbel, Frechet, Weibull 분포 중에 하나를 따르는 극단값 이론과 맥락을 같이 할 수 있는 GEV를 선택하였다(Katz, 2013; Leadbetter et al., 1983; Gumbel, 1958). 다음 Eq. (2)는 GEV 누적 분포 함수를 나타내었다(Coles, 2001).
| $$\Psi(x)=\exp\left\{-\left(1+\xi\mathit\;\mathit{(\frac{x\mathrm-\mu}\sigma)}\right)^\frac{-1}\xi\right\},\;\left(1+\xi\mathit\;\mathit{(\frac{x\mathrm-\mu}\sigma)}\right)>0$$ | (2) |
여기서, 는 위치매개변수, 는 축척매개변수, 는 형상매개변수를 의미한다. 특히, 는 분포의 꼬리 거동을 지배한다. →0은 Gumbel, <0, Weibull, >0은 Frcheche 분포로 구분된다.
한편으로 매개변수의 시간흐름에 따른 고정/변동성을 고려할 필요가 있으며, 정상성은 시간불변성, 비정상성은 변동성을 의미한다(Renard et al., 2013; Meehl and Arblaster, 2003). 다음 Eq. (3)은 매개변수가 시간 흐름에 따른 선형적인 거동을 나타내었다.
| $$f(\theta)=\theta_1t+\theta_0$$ | (3) |
여기서, 이고, t는 시간이다.
3.3.2 베이즈 정리
베이즈 정리(Bayes Theorem)는 사후확률의 추론을 위한 통계학적 접근 흐름으로 기존 가설에 자료를 반영하여 새로운 것을 만드는 아이디어이며, 몬테카를로 기법 등을 적용해 사후확률 추론을 이룰 수 있다.
다음 Eq. (4)는 관측치 사이의 독립성을 가정한 GEV 분포의 매개변수 추정을 위한 베이즈 정리를 나타내었다(Renard et al., 2013; Coles, 2001).
| $$p(\beta\vert\overrightarrow y,x)\propto(\overrightarrow y\vert\beta,x)\;p(\beta\vert x)$$ | (4) |
여기서, 는 GEV 분포의 매개변수, 는 자료, 는 사전분포(Prior distribution), 는 우도 함수(Likelihood function), 는 사후분포(Posterior Distribution)를 의미한다.
베이지안 추론은 사전확률분포 함수와 가능도(Likelihood)를 이용하여 사후분포 함수를 추정하는 것으로 모수를 고정된 것이 아닌 확률적 규칙의 지배를 받는 변수로 취급한다.
다음의 Eq. (5)는 비정상성을 가정한 베이지안 추론식을 나타내었다.
여기서, x(t)는 비정상성을 가정한 모든 공변량 값의 집합이고, 와 는 각각 비정상성 및 정상성에 따른 매개변수이다.
3.3.3 마르코프 연쇄 몬테 카를로 방법
통계적인 개념의 샘플링은 임의의 확률분포로부터 표본을 추출하는 작업을 의미하는 것으로 주어진 상태의 복잡성 있는 분포형에 적절한 샘플링이 요구되며, 몬테카를로는 알려진 샘플링 기법이다.
한편으로는 확률과정은 ‘시간의 진행과정에서 어떤 상태의 확률적 변화 과정’으로 정의되며, 확률분포를 따르는 확률변수의 이산적인 시간 구간마다 값의 생성을 의미한다.
마르코프 연쇄(Markov Chain)는 이산확률과정(Discrete-time Stochastic Process)을 의미하며, 현재 가 바로 이전 상태에서만 영향을 받는 확률과정으로 이전 단계에 종속적인 마르코프 성질을 가지며, 마르코프 연쇄는 Eq. (6)을 만족하는 경우이다.
| $$p(x_t\vert x_0,x_1,\dots,x_{t-1})=p(x_t\vert x_{t-1})$$ | (6) |
제시된 몬테카를로와 마르코프 체인의 두 가지 수학적인 특성을 기반으로 하는 것이 MCMC (Markov Chain Monte Carlo) 샘플링 기법이며, 매개변수 추정은 베이지안 추론에 따른 가설이 갱신되는 것을 기반으로 한다.
3.3.4 차분진화 마르코프 연쇄
DE (Differential evolution)는 베이지안에 따른 조건부적 샘플링을 의미하는 것으로 교차(Crossover), 변이(Mutation)가 적용되는 측면에서 유전자 알고리즘과 유사성이 있다. 다음 Eq. (7)은 DE의 i번째 구성원 xi에 대한 식이다(Storn and Price, 1997).
| $${\mathbf x}_{\mathbf p}={\mathbf x}_{\mathrm R0}+\gamma({\mathbf x}_{\mathrm R1}-{\mathbf x}_{\mathbf R\mathbf2})$$ | (7) |
여기서 는 모집단 로부터 무작위 선택된다. DE를 베이지안 추론 기반의 마르코프 연쇄와 연계를 세밀한 균형이 필요하다(Waagepetersen and Sorensen, 2001; Gelman et al., 2003). Eq. (7)은 다음 Eq. (8)로 대체되어진다.
| $${\mathbf x}_{\mathrm p}={\mathbf x}_{\mathrm i}+\gamma({\mathbf x}_{\mathrm R1}-{\mathbf x}_{\mathrm R2})+\varepsilon$$ | (8) |
여기서, 는 생성되는 벡터이며, 는 연쇄의 i번째이고, 와 는 연쇄 내에서 랜덤하게 선택되는 것들이다(). 또한 은 가우시안 분포의 오차로 생성되는 벡터의 퇴화(Degeneracy)를 해소한다. DE에서 확률적인 수용 규칙은 , 이며, 이러한 알고리즘에 따른 일련과정 및 그 결과가 DE-MC로 정의될 수 있다.
4. 결 과
4.1 표준가뭄지수를 활용한 가뭄 발생 특성 분석
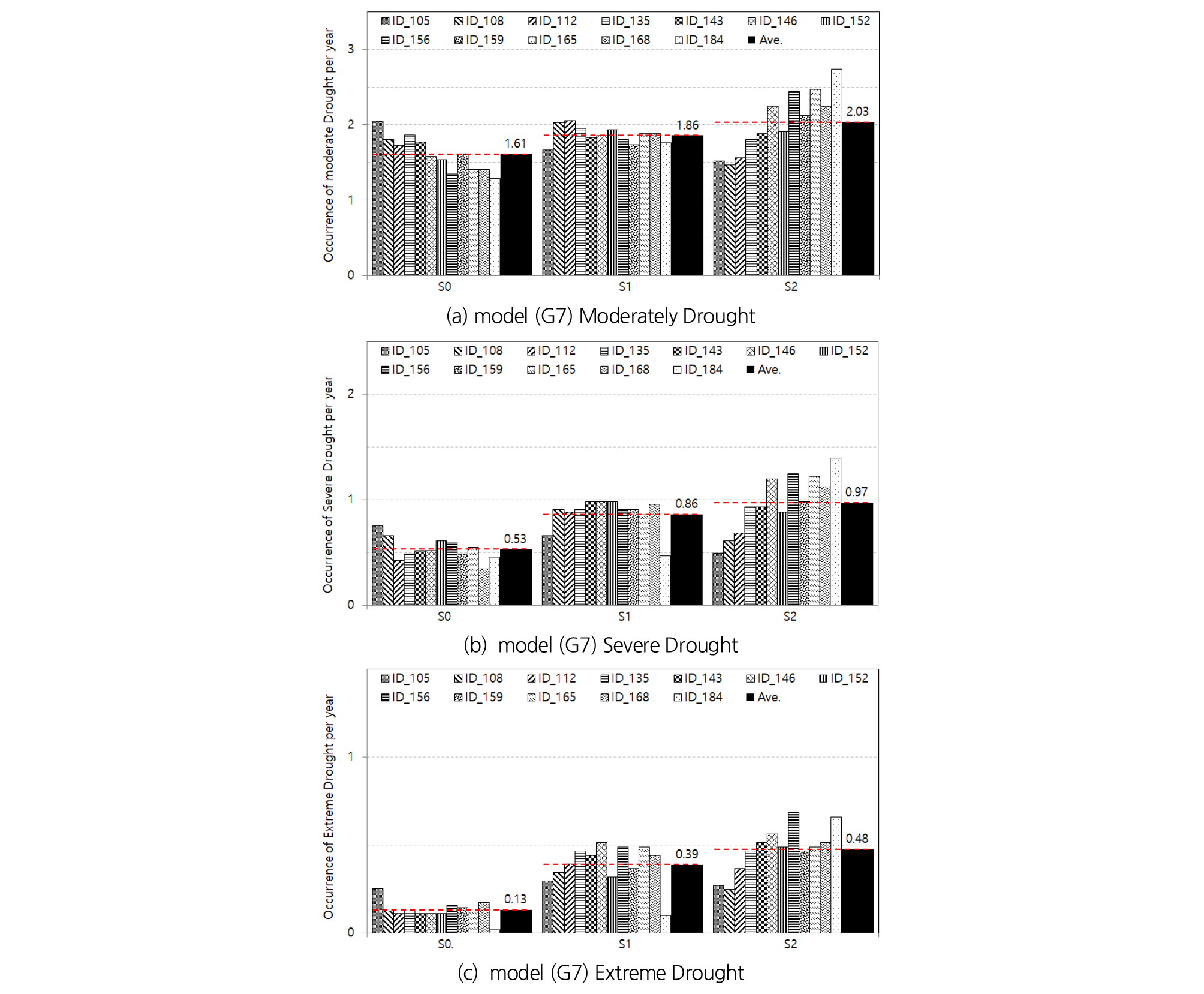
Fig. 5는 IPSL-CM5A-LR 모델의 SPI 6에 대한 12개 지점 각각의 가뭄심도별 및 기간별 구분에 따른 연 평균 발생횟수를 도시하여 나타낸 것으로 Figs. 5(a)~5(c)는 각각 보통가뭄, 심한가뭄, 극한가뭄이며, 기간별 구분은 관측기간(S0), 근 미래(S1), 먼 미래(S2)로 나타내었다.
Fig. 5(a)인 기간별 S0, S1, S2에 대한 보통가뭄의 연평균 발생횟수는 각각 1.61, 1.86, 2.03회로 먼 미래로 갈수록 증가를 보였고, S0에서는 남부 지방으로 갈수록 가뭄 발생이 감소를 보인 반면에 S1은 평균과 유사하며, S2는 남부 지방으로 갈수록 가뭄 발생이 증가를 보였다.
Fig. 5(b)도 기간별 S0, S1, S2에 대한 심한 가뭄의 연평균 발생횟수는 각각 0.53, 0.86, 0.97회로 먼 미래로 갈수록 증가를 보였고, S0에서는 남부 지방으로 갈수록 평균에 비해 다소 감소를 보인 반면에 S1는 제주와 강릉에서 큰 폭의 감소를 보였으며, S2는 남부 지방으로 갈수록 가뭄 발생이 증가로 나타났다.
Fig. 5(c)인 기간별 S0, S1, S2에 대한 심한 가뭄의 연평균 발생횟수도 각각 0.13, 0.39, 0.48회로 먼 미래로 갈수록 증가를 보였고, S0에서는 강릉이 0.25회로 평균보다 2배 큰 발생을 보인 반면에 제주는 0.02회로 나타났으며, S1과 S2에서는 북부 지방으로 갈수록 감소를 보였다.
다음 Table 3은 10개 GCM 모델들의 가뭄 심도별 12개 관측지점을 평균한 것으로 S0와 S1 간의 증감 및 S0, S2와 S1, S2 간의 증감을 나타내었다. 여기서 평균 발생 횟수(freq.)는 기간별 총 발생횟수(Num.)를 각각의 자료 기간으로 나눈 것이다. 분석결과 G1, G4, G5, G9 모델들에서는 미래로 갈수록 가뭄 발생이 감소하였고, 반면에 G7, G10은 모두 증가로 나타났으며, G2, G3, G6, G8에서는 S1에서 가장 큰 가뭄 발생을 보였다.
Table 3. Comparison of drought occurrences by each GCM and drought class for 3 different periods (S0, S1, S2)
또한, Table 4는 IPSL-CM5A-LR 모델의 SPI 6에 대한 12개 지점별 및 심도별 미래 예측 가뭄 발생횟수의 총합을 나타내었다. 산정결과 12개 지점에 대한 평균 심도별 발생횟수는 보통가뭄, 심한가뭄, 극한가뭄별로 각각 159.6, 75.2, 3.0회이고, 총합은 231.0회로 나타났으며, 이에 따른 12개 지점별 대소를 산정하고 음영으로 구분하여 나타내었다.
Table 4. Comparing occurrence by each drought class for 12 stations with IPSL-CM5A-LR
Zone 1-1, 3-1 및 3-3에 해당하는 강릉, 서울, 인천 및 울산에서는 심도별 가뭄 발생횟수가 평균에 비해 적은 발생을 보였다. 또한 1-3에 해당하는 부산은 심한 가뭄의 경우를 제외하고는 평균에 비해 적게 나타났다. 이와 달리 추풍령을 기준으로 서남 지역에 분포되어 있는 Zone 3-2인 전주와 1-2에 해당하는 4개 지역 중에서 광주, 목포, 여수 등 3개 지역이 심도별 가뭄 발생이 평균 이상을 보이는 것으로 나타났으며, 1-2에 속하는 제주는 극한 및 심한 가뭄은 평균보다 작은 발생을 보였으나 보통가뭄이 전 관측소에서 가장 큰 발생을 보였다.
이외에 Zone 3은 극한가뭄, Zone 4는 심한가뭄 및 극한가뭄에서 평균보다 상회하였고, 심한가뭄과 극한가뭄 각각은 전주가 89회, 광주가 48회로 가장 큰 발생을 보였다.
4.2 순위도출을 활용한 GCMs 선정
다양한 GCM의 제공은 장래 수문특성을 분석하는데 충분한 활용가치를 가질 수 있는 반면에 정보가 많을수록 선택에 대한 어려움이 있으며, 샘플링을 적용하는 경우에는 효율성 문제가 발생 할 수 있다.
따라서 순위 도출에 따른 적정성 있는 모델의 선택 기준을 제시하고자 하였으며, 결과는 Table 5와 같다. 순위 도출에 적용된 인자는 가뭄 관련 기상인자(총강우량, 가뭄발생일수)와 가뭄지수와 관련한 심도별 발생횟수 및 지속기간 관련 인자를 적용하였다.
Table 5. Rankings of 10 GCMs for precipitation & SPI characteristic based on RCP 8.5
기상인자를 적용한 순위도출을 산정한 결과 TR은 G6, RD는 G7 모델이 선택되었으며, 결과의 평균에 따라 G6, G7, G8 모델이 선택되었다.
또한 극한 가뭄상태를 나타낼 수 있는 기상학적 가뭄지수의 가뭄 심도 및 가뭄 지속기간의 적용을 통해 G2, G6, G7, G8 모델들이 선택되었다.
마지막으로 기간별 S0, S1, S2에 따른 가뭄 증감을 나타내는 Table 6의 결과를 Fig. 5와 같이 도시적으로 나타내어 패턴 변화를 ◯, △, X로 구분하였으며, 그 결과 ◯에 해당하는 G7, G8, G10과 △를 나타내는 G2, G3, G6 모델들이 선택되었다.
순위 도출 평균 및 기간별 증감의 확인과정을 통해서 G6, G7, G8 모델들을 최종 선택하였다.
Table 6. SDF relationship for 12 stations-return periods (50yr, 100yr) and duration (6, 9, 12 months) with SDF mean of G6, G7, G8
4.3 비정상성 빈도분석을 통한 SDF 곡선 산정
Fig. 6은 전체 비정상성 빈도분석에 따른 SDF 산정절차를 나타내었다. DE-MC에 따른 샘플링을 적용한 비정상성 빈도분석은 단계 3에 해당하며, 샘플링은 수렴성을 고려하여 1회당 3,000번에 대한 반복 수행이 이루어졌다.
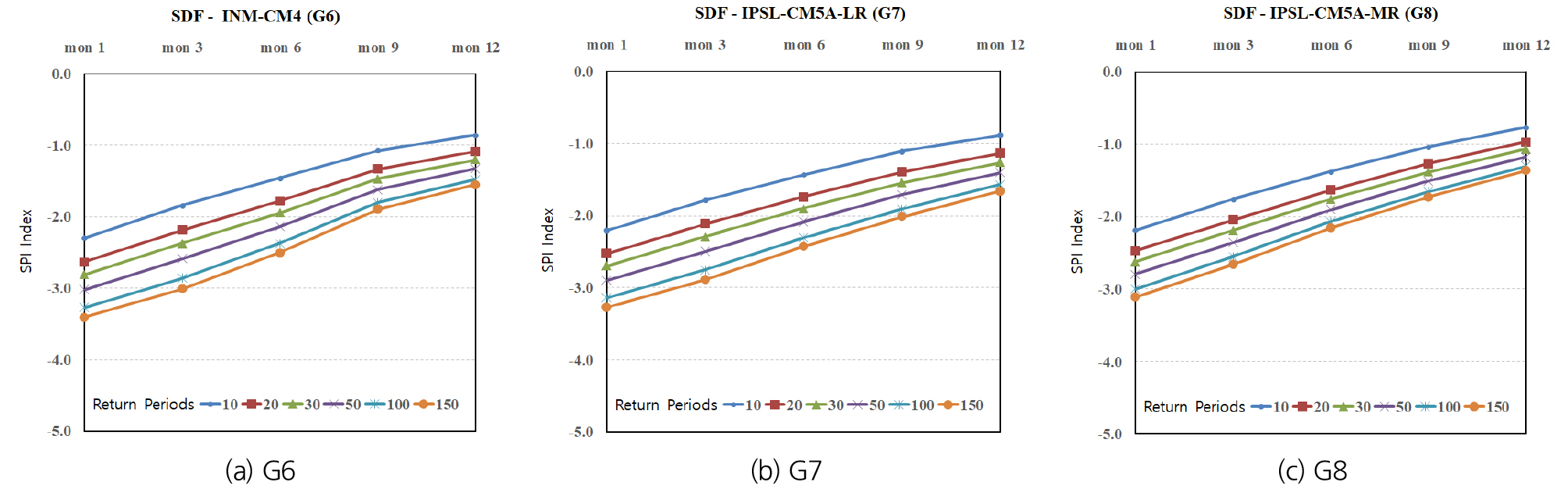
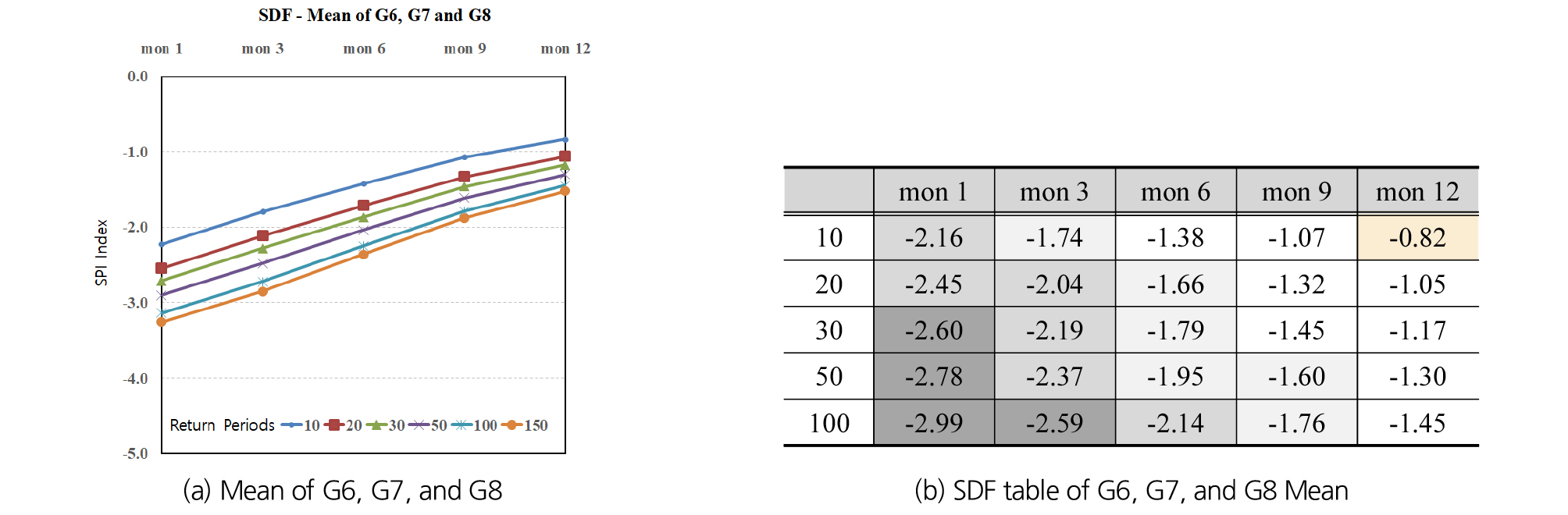
비정상성 빈도분석을 통해 12개 지역별 SDF 곡선을 산정하였으며, Figs. 7(a)~7(c)는 선택된 3개 모델별 12개 지역의 평균 SDF이다. 또한, 세 가지 모델의 평균 SDF를 도시한 것이 Fig. 8(a)이며, 정량화된 SDF 값으로 지속시간별 및 재현기간별에 따른 가뭄 심도로 나타낸 것이 Fig. 8(b)이다.
Fig. 8(b)의 SDF 추정 결과 재현기간 10년, 지속기간 12개월의 –0.82를 제외하고는 보통가뭄 이상의 발생 가능성이 제시되었다.
지속기간 6개월의 경우 심한가뭄은 20년, 50년 빈도에서 발생을 보였고, 100년 빈도에서는 극한가뭄의 발생 가능성이 제시되었다. 지속기간 9개월에서도 50년 및 100년 빈도에서 심한가뭄 발생 가능성을 보였으며, 지속기간 12개월에서는 보통가뭄이 20년 빈도 이상에서 발생을 제시하였다.
Table 6은 관측소별 SDF 산정결과 및 Fig. 8(b)의 평균 SDF와의 편차를 대소로 구분하고, 편차의 음의 값을 가질수록 가뭄 심도가 평균보다 큰 경우로 하여 음영으로 구분하였다. 또한 재현기간 50, 100년 빈도에 해당하는 가뭄의 장기 피해 가능성 검토를 위해 지속기간은 6, 9, 12개월을 적용하였다.
산정결과 전체평균과 지역별 SDF와의 차이가 –0.11~0.14로 지역별 편차는 크지 않지만 지역적 위치에 따른 가뭄특성의 차이가 나타났다.
Zone의 구분기준에 따라 추풍령을 기준으로 북쪽에 위치하는 Zone 1-1, 3-1에서는 바다에 인접한 인천과 강릉에서 평균보다는 적은 위험을 보이는 반면에 내륙인 서울은 높게 나타났다.
추풍령 포함 및 추풍령 기준 남서쪽에 위치하는 Zone 1-2, 2, 3-2의 경우에는 제주를 제외한 전주, 광주, 여수, 목포, 추풍령 모두 평균보다 위험이 높게 나타났다.
추풍령 기준 남동쪽에 위치하는 1-3, 3-3 및 4의 경우에는 대구는 평균보다 높은 위험을 보인 반면에 울산 및 부산은 평균보다 가뭄 위험이 적게 나타났다.
결과적으로는 내륙 및 바다 인접으로 구분하는 경우 서울, 추풍령, 대구, 전주, 광주 등 내륙의 5개 지역 모두 가뭄 위험이 평균에 비해 높게 나타난 반면에 여수와 목포를 제외한 바다 인접 지역에서는 평균보다 가뭄 위험이 적게 나타났다.
5. 결 론
본 연구는 기후변화에 영향으로 인하여 가뭄과 관련한 수문특성이 변동되고 있으며, 인간활동과 관련한 인위적인 요인이 변화되지 않는다면 가뭄 규모 및 그 피해는 장래에 더욱 확산이 될 것으로 전망되고 있음에 따라 장래의 가장 극한 상황에 따른 가뭄 평가 및 정량화를 수행하고자 하였다. 이를 위해서 RCP 8.5 시나리오 기반의 GCMs를 이용한 가뭄전망 특성 분석 및 기상학적 가뭄지수를 산정하였고, 비정상성 빈도분석에 따른 주요 지점별 SDF 곡선을 작성하였다. 주요 지점에는 기상청 산하에서 관리되는 1954년 이전부터 비교적 장기 강우 관측자료를 보유한 12개 지점을 선정하였다.
미래는 근본적으로 불확실성을 가지고 있어 예측자료의 선택도 쉽지 않다. 이에 따라 기후변화의 원인적 측면과 관측된 여러 기상 및 수문 관련 자료들의 기후역학적 관계 분석 등을 통해 시나리오별 다양한 예측이 이루어지고 있음에 따라 극한 수문 환경에 따른 가뭄 분석을 위해 RCP 8.5의 선택은 타당성을 가질 수 있다. 다만 GCM 선택은 별개의 문제이며, 여러 GCM을 이용한 분석결과를 분위 추정 및 앙상블로 나타낼 수 있지만 이런 경우 불확실성의 폭은 증가하고, 시나리오 간의 경계가 모호해질 수 있으며, GCM 앙상블에 따른 결과는 평균에 가까운 과소추정이 될 수 있다.
따라서 불확실성 범위를 감소 및 적정성 있는 모델 선택을 위해 순위 도출에 따른 GCM 선택 기준을 제시하고자 하였으며, 가뭄 관련한 강우 발생일수, 총강수량 및 가뭄지수의 심도별 가뭄 발생횟수와 지속기간 등을 고려하였고, 선택된 모델을 대상으로 기간별 현재(S0)와 미래(S1, S2)로 구분 및 가뭄 심도별 발생횟수 변동 추이 등에 대한 검토를 함께 수행하였다. 결과적으로 선택된 3개 GCM은 관측된 수문특성과 유사한 추세를 보였으며, 가뭄에 해당하는 건조는 음의 방향, 습윤은 양의 방향으로 추세가 확대됨에 따라 미래로 갈수록 변동 폭이 커지는 양상으로 나타났다. 또한, 기간별 S0, S1, S2에 따른 가뭄 심도별 추이에서는 보통가뭄, 심한 가뭄 및 극한가뭄 각각이 점차적 증가를 확인하였다.
강우는 유역의 자연적인 가용수자원의 역할을 함에 따라 강우의 발생일수가 감소하거나 총 강우량이 감소가 되는 경우 가뭄 발생확률이 높아진다. 한반도는 전 지구 기후 역학적인 측면에서는 매우 협소하지만 이러한 두 인자의 발생 특성은 지역별로 차이가 나타날 수 있음을 고려하여 두 인자의 연도별 추세 증감 및 공간적 위치 특성에 따라 그룹화를 수행하였다. 전체평균 및 12개 지점 중에서 7개 지점이 연도별 강우 발생일수는 감소 및 총 강우량은 증가 감소 양상으로 나타났다. 그룹화한 결과 두 인자의 추세 증감에 따라 4개 Zone으로 구분하였고, Zone 1과 3은 공간적인 위치 특성에 따라 각각 3개의 하부 그룹으로 하여 8개로 구분되었다. 이는 추후에 전체 기상 관측소로 확대 적용될 수 있을 것이다. 총 강우량의 증가는 월별 및 분기별 발생 특성에 따라 건기에는 감소, 우기에는 증가 양상으로 나타났다.
RCP 8.5는 비정상성을 전제하고 있음에 따라 SDF의 산정을 위해 DE-MC 샘플링 기법에 따른 비정상성 빈도분석을 적용하였고, 지점별 SDF 곡선을 작성하였으며, 이를 평균과의 편차와 비교하였다. 산정결과 극한가뭄은 6개월(100년 빈도), 심한가뭄은 6개월(50년 빈도), 9개월(50, 100년 빈도), 보통가뭄은 12개월(50, 100년 빈도)에 발생 위험을 보였다. 평균과 지역별 편차는 –0.11~0.14로 나타남에 따라 상대적인 편차가 크지 않은 것으로 판단되었다. 이는 여러 모델의 평균 과정에서 수렴성 문제가 나타날 수 있으며, 다른 측면으로는 한반도의 공간적 범위가 크지 않음에 따라 미래에는 한반도 전역이 가뭄에 취약할 수 있음을 의미하는 것으로 판단할 수 있다.
SDF 결과를 Zone에 따라 구분하는 경우 추풍령을 기준으로 북쪽에 위치하는 Zone 1-1, 3-1에서는 서울을 제외한 인천과 강릉이 평균보다 적은 위험으로 나타났으며, 남서쪽에 위치하는 Zone 1-2와 3-2에서는 제주를 제외하고 내륙과 바다에 인접한 모든 지역에서 평균 이상의 가뭄 위험이 증가로 나타났다. 이러한 결과는 관측치에서 보인 두 인자의 증감 패턴 및 예측 가뭄특성과 상당히 일치되는 특성으로 나타났다.
한편으로는 SDF의 결과에서 다른 두 결과와 달리 내륙 및 바다 인접성에 따른 특성 차이로 나타났다. 내륙에 위치하는 5개 지점에서는 모두가 SDF의 평균 이상으로 나타나는 반면에 바다에 인접하는 경우는 추풍령을 기준으로 남서쪽에 위치하고 있는 여수, 목포만 평균보다 큰 값으로 나타났고, 나머지 지역에서는 평균 이하로 분석되었다.
본 연구결과는 공간특성을 고려한 미래 가뭄특성 파악 및 가뭄 위험성 정량화 수행 결과로 지역별 가뭄 발생 대비를 위한 지속적인 물관리 정책의 마련을 위해 충분한 활용성을 가질 것으로 판단되었다.