1. 서 론
2. 연구방법
2.1 몬순특성을 고려한 GCM 모의성능 평가요소 선정
2.2 GCM 모의성능 비교 및 평가체계
3. 대상지역 및 자료수집
4. 결과 및 분석
4.1 기후변수별 GCM의 과거 재현성 비교
4.2 GCM의 과거 기후모의 성능평가 및 적정 GCM 선정
4.3 선정된 GCM의 과거 기후모의 성능 검증
4.4 선정된 GCM의 월평균 기후모의 성능평가
5. 결 론
1. 서 론
기후변화에 따른 수자원의 영향은 관측자료 또는 기후변화 시나리오 자료를 기반으로 평가될 수 있다. 관측자료 기반의 평가방법은 화석, 퇴적암 등 고기후자료 혹은 장기간의 관측자료로부터 도출된 수문기상인자의 변동성이나 경향성을 바탕으로 미래 수자원의 변동성을 전망하는 방법이다. 이 방법은 과거자료의 특성이 미래에도 유지된다는 가정 하에 수자원 변동성을 전망하기 때문에 관측 값의 오차가 전망결과에도 그대로 전이된다는 단점이 있다. 이러한 이유로 일반적으로는 전구기후모델(Global Climate Model, GCM)로부터 산출된 기후시나리오 하에서 수자원을 전망하는 방법이 활용된다(Bae et al., 2008; Bae et al., 2011; Bae et al., 2015). GCM은 지구시스템 모의과정 내 물리적 및 역학적 모수화, 공간해상도 등의 차이로 인해 구조적 불확실성(structural uncertainty)을 내포하며, GCM에 따라 기후모의성능 및 전망결과가 서로 다르게 나타난다. 통상, 과거 관측모의성능이 좋지 않은 GCM은 전망결과에서도 불확실성이 크며 이러한 불확실성을 최소화하기 위해서 분석지역에 적합한 GCM을 선정하거나 다중 GCM을 사용하는 방안이 활용된다. 다중 GCM의 활용은 특정 GCM을 선택함에 있어 발생하는 불확실성을 고려할 수 있는 최선의 방법으로, 수자원 분야에서는 여러 GCM 정보를 단순평균하거나 가중치를 부여하여 통계적으로 통합하는 다중모델앙상블(Multi-Model Ensemble, MME) 기법을 주로 활용하고 있다(Jung et al., 2012; Lee and Bae, 2015; Kim et al., 2020b). 이 때, MME 전망결과의 신뢰도를 확보하기 위해서는 과거 관측기후를 상대적으로 잘 모의하는 GCM을 선별하는 것이 중요하다(Taylor et al., 2012; Thanh and Bae, 2013; Lutz et al., 2016).
일반적으로 GCM의 모의성능 우위는 다중 GCM의 과거 기후재현성 평가결과를 서로 비교함으로써 판별된다(Kim et al., 2020a). 최근 연구들은 모의성능이 좋지 않은 GCM은 제외하거나 해당 결과에 낮은 가중치를 적용하는 반면, 상대적으로 모의성능이 우수한 GCM을 우선적으로 활용하는 추세이다(Tebaldi and Sanso, 2009; Sexton et al., 2012; Tegegne et al., 2019). Intergovernmental Panel on Climate Change (IPCC)는 GCM 선정 시 최소 2개 이상의 GCM을 사용하되, 관심분야의 기후특성을 잘 재현하는 GCM이 포함되어야 한다는 가이드라인을 제시하고 있다(IPCC, 2013). 공통적으로는 GCM의 모의성능을 기준으로 적정 GCM을 선택적으로 활용해야 함을 시사하고 있으며, 이를 위해서는 전망결과가 합리적이면서도 연구목적에 부합하는 GCM 선정기법의 적용이 요구된다.
그러나, GCM의 모의성능은 대상지역, 평가에 활용되는 기후변수, 평가기간, 평가지표 및 방법에 따라 다르게 평가될 수 있기 때문에 전 세계적으로 다양한 방법론이 존재한다. 이 중, 기후변수는 연구목적이나 대상지역의 기후특성에 따라 적용여부가 결정되므로 GCM의 모의성능을 평가함에 있어 가장 민감한 요소 중 하나이다. 대체로 수자원 분석을 목적으로 하는 경우에는 수문순환 및 강우-유출해석에 민감한 지표의 기온 및 강수량 변수가 활용되며(Immerzeel et al., 2013; Sorg et al., 2014; Warszawski et al., 2014), 해당 변수의 기후값(climatology) 혹은 극치값에 대한 평가가 수행된다(Cannon, 2015; Lutz et al., 2016; Wang et al., 2018). 이처럼 GCM 선정 시 평가결과에 민감한 영향을 미치는 변수만을 활용하는 방법은 적용이 간단하다는 장점이 있지만, 특정변수만으로 기후시스템 전반을 평가하는 데에는 한계가 있다. 이에 따라 GCM 선정 시 다양한 기후특성을 고려해야한다는 필요성이 제시되고 있으며(Cannon, 2015; Lutz et al., 2016; Wang et al., 2018), 적용 대상지역의 기후특성과 밀접한 기후요소와 영향범위를 고려하여 GCM을 선정하는 연구들이 수행되고 있다(Sperber et al., 2013; McSweeney et al., 2015). Sperber et al. (2013)은 인도 몬순 특성을 고려하고자 엘리뇨 지표와 강수량을 선정하였으며, 이에 대한 GCM의 모의성능을 평가하였다. McSeeney et al. (2015)는 지역별 계절기후를 구성하는 주요 기후특성을 고려하여 GCM을 선정하였다. 동남아시아에 대해서는 연평균 강수량, 기온 및 850 hpa 바람장을 GCM 성능평가 요소로 고려하였고, 유럽지역의 경우에는 연평균 강수량, 기온 및 원격상관지수를 활용하였다. 한편, 국내에서 Hwang et al. (2018)은 동아시아 해안지역 및 한반도 지역의 강우특성을 평가하기 위해 강우량 통계치, 강우 사상패턴과 극한 사상지표를 선정하고, 이를 활용하여 29개 GCM의 강우 재현성을 정량적으로 평가하였다. Jung et al. (2018)은 한반도 지역에 대한 강수 및 기온인자의 계절별 평균, 경년변동성, 극한기후지수 재현성과 동아시아 지역을 대상으로 한 몬순의 공간분포 재현성을 평가하였고, TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) 기법을 적용하여 통합된 평가결과를 기준으로 대표 GCM을 선정하였다. 다수의 선행연구들은 강수 및 기온변수 기반의 GCM 선정기법이 주를 이루고 있어 다양한 기후변수를 활용한 GCM 선정기법 개발이 요구된다. 따라서, 본 연구에서는 몬순기후 특성을 고려하는 다중 기후요소를 활용하여 기후재현성이 우수한 GCM을 선정하는 기법을 개발하고 그 적용성을 평가하고자 한다.
2. 연구방법
2.1 몬순특성을 고려한 GCM 모의성능 평가요소 선정
아시아 지역은 몬순의 영향을 받는 지역으로 계절 및 지역에 따라 기후가 변화하기 때문에 기후특성을 규정하기가 어렵다. 일반적으로 기후재현성 평가에 활용되는 강수량 변수는수자원 영향평가 결과에 지배적인 영향을 미치는 요소 중 하나이지만, 장마 등 강수량의 변화는 대기대순환에 의해 발생하므로 연관된 변수를 고려하면 보다 합리적인 평가가 가능하다. 따라서, 본 연구에서는 GCM 선정 시 수자원 영향평가에 민감한 변수인 강수량, 지표기온 뿐만 아니라 아시아 지역의 몬순 기후특성과 유관한 기후변수를 고려하였다. 이를 위해 몬순특성과 이와 유관한 기후변수를 검토하였으며, 각 변수에 대한 GCM의 기후재현성을 평가하였다. 지표기온, 강수량 외 대기순환 및 이상기상 현상의 지표로 활용되는 12개 변수(강수량(pr), 최고 지표온도(tmax), 최저 지표온도(tmin), 상향 장파복사량(rlut), 해면기압(psl), 해수면온도(tos), 대기온도(ta), 지상 2 m 지표온도(tas), 지오포텐셜 고도(zg), 비습도(hus), 동서풍(ua), 자오선 풍속(va))를 선정하였으며, 각 변수는 Table 1에 제시하였다. Table 1에서 ‘**’가 표시된 변수는 3차원 기상장으로 8개의 지오포텐셜 고도(1000, 850, 700, 500, 250, 100, 50 및 10 hpa)에 따라 자료가 존재하며, 이 중에서 지상의 등압선 분포와 유사하여 기상예보에 주로 활용되는 850 hpa 고도 값을 활용하였다. 각 기후변수를 선정한 근거는 다음과 같다. 12개의 기후변수 중 강수량 및 지표면에서의 온도는 유출해석 시 입력자료로 유출모의 결과와 직결되며, 이 외에 지표면 자료 및 대기지표 변수는 기후현상의 변화를 간접적으로 확인할 수 있는 지표에 해당한다(Nyunt et al., 2012). 장파복사량은 이산화탄소나 메탄, 수증기 등이 지표면에 도달한 뒤 태양광을 흡수하고 나서 대기층을 뚫고 우주로 방출되는 단위면적당 복사량이다. 이는 지구에 입사하는 태양복사에너지와 함께 에너지수지를 결정하는 요소 중 하나로 값의 시공간적인 변화는 기후변화와 기상현상의 변동을 파악하는 척도이다. 기압 차이는 날씨변화 및 이상기상 현상을 예상하는 중요한 요소로, 고도의 영향이 고려된 해면기압을 선정하였다. 해수면 온도는 해양과 대기의 연결고리 역할을 하며 대기와 열, 수증기, 운동량 등을 교환한다. 해수면 온도증가는 열에너지 축적을 의미하며, 해빙현상의 가속화, 대기 중 수증기량을 증가시켜 기상이변을 초래한다. 또한, 엘리뇨, 라니냐 발생여부에 대한 판단기준으로 활용된다. 동서풍 및 자오선 풍속은 대기순환 요소 중 하나로 기후, 날씨변화 및 해류형성, 제트기류 생성에 영향을 준다.
Table 1.
The 12 climate variables used for GCM evaluation in Asian monsoon region
2.2 GCM 모의성능 비교 및 평가체계
GCM의 성능은 과거기간에 대한 GCM 산출물이 관측기후 특성을 얼마나 잘 재현하는지에 따라 평가된다. 이 때, GCM은 특정시점에 대한 관측값과의 비교가 불가능하므로 대체로 20년 이상의 장기 관측자료가 활용된다. 본 연구에서는 30년(1976 ~ 2005년)의 자료기간 중 아시아 지역의 수자원 특성에 많은 영향을 주는 여름 몬순기간(6 ~ 9월)을 평가기간으로 선정하였다. 이에 대한 각 GCM의 과거 기후재현성을 관측자료와 비교하여 통계적으로 평가하고 점수체계를 활용하여 순위를 산정하였다. 몬순기후의 지역적인 영향범위를 고려하기 위해 평가 대상지역의 공간적인 범위를 아시아 몬순 도메인으로 선정하였으며, 대상지역에 대한 설명은 3장에 기술하였다. GCM의 기후모의 성능평가는 공간규모에서 수행되며, GCM으로부터 산출된 기후장이 과거 관측 기후장의 공간적인 패턴을 반영하는지 평가하였다. 평가를 위해 각 기후요소에 대해 개별 GCM과 관측자료로부터 평가기간에 대한 기후평년값을 산정하고 이를 동일한 공간장에 대해 비교하였다.
일반적으로 다중 GCM 간의 성능차이를 비교하기 위한 평가방법으로는 Taylor diagram이 주로 활용된다. Taylor diagram은 관측자료와 모의자료와의 통계치로부터 두 자료 간의 상관성, 오차, 변동성을 지표화하고, 이를 그래프 위의 한 점으로 도식화하는 방법이다(Taylor, 2001). 이 방법은 단일 기후변수를 활용하거나 GCM 간의 모의성능 차이가 큰 경우에 GCM 간의 모의성능을 한눈에 비교할 수 있다는 장점이 있지만, 다중 기후변수를 활용하여 모의성능을 평가하거나 GCM 간의 모의성능 차이가 모호한 경우는 이 도표만으로 GCM을 선정하기가 어렵다. 본 연구에서는 통계적 지표를 활용하여 GCM의 모의성능을 정량화하고, GCM 간 성능비교를 위해 모의성능 평가 매트릭스를 도입하였다. 공간적인 재현성 평가를 위한 통계적 지표로 GCM 모의값과 관측값(또는 재분석자료) 사이의 공간상관계수(Pattern Correlation Coefficient, PCC) 및 정규화된 평균제곱근 오차(Root Mean Square Error, RMSE)를 선정하였으며, 몬순기간에 해당하는 월 평균값을 기준으로 평가를 수행하였다. PCC는 개별 GCM과 관측값의 공간적인 분포가 얼마나 일치하는지를 측정할 수 있으며, RMSE는 정량적인 측면에서 두 자료의 정확도를 평가하는 척도로 개별 GCM과 관측값 사이의 양적오차를 의미한다.
12개의 기상변수에 대한 통계지표를 산정하기 위해 GCM 및 관측자료로부터 여름몬순기간(6 ~ 9월)에 해당하는 월별 평균 기후값을 산정한다. 관측 및 각 GCM의 월별 평균 기후값을 Eqs. (1) ~ (4)에 적용하여 월별(k월) 평균 GCMi와 관측값 간의 PCC (Ri,k) 및 RMSE (Ei,k')를 산정한다.
| $$R_{i,k}=\frac{{\displaystyle\frac1N}{\displaystyle\sum_{n=1}^N}\left(f_{i,k,n}-\overline{f_{i,k}}\right)\left(r_{o,k,n}-\overline{r_{o,k}}\right)}{\sigma_{fi,k}\;\sigma_{ro,k}}$$ | (1) |
| $$\sigma_{fi,k}^2=\frac1N\sum_{n=1}^N\left(f_{i,k,n}-\overline{f_{i,k}}\right)^2$$ | (2) |
| $$\sigma_{ro,k}^2=\frac1N\sum_{n=1}^N\left(r_{o,k,n}-\overline{r_{o,k}}\right)^2$$ | (3) |
| $$E_{i,k}'=\left[\frac1N\sum_{n=1}^N\left[\left(f_{i,k,n}-\overline{f_{i,k}}\right)-\left(r_{o,k,n}-\overline{r_{o,k}}\right)\right]^2\right]^{1/2}$$ | (4) |
여기서, 은 k월 GCMi의 표준편차, 은 k월 관측값의 표준편차, i(i=1,…, M)는 GCM 종류, N은 평가영역 내 전체 지점 수, n (n=1,…, N)은 각 지점, k (k=6, 7, 8, 9)는 몬순기간 월, fi,k,n는 k월 지점 n에서의 GCMi 값, ro,k,n은 k월 지점 n에서의 관측값을 의미한다. 는 k월의 전체지점에 대한 GCMi의 평균값, 는 관측값의 평균값이다.
이후, Eqs. (5) and (6)과 같이 각 GCMi의 월별(6 ~ 9월) 통계치를 기하평균하여 몬순기간 평균 PCC (Ri)와 RMSE (Ei')를 산정한다. Table 2는 강수량 변수에 대한 GCM 모의성능 평가결과이다. GCM 모의성능 비교 시 기준값을 산정하기 위해 아래 Eqs. (7) and (8)과 같이 전체모델의 통계치를 평균한 앙상블평균값(RMME, E'MME)을 산정한다.
| $$R_i=\frac1L\sum_{k=6}^9R_{i,k}$$ | (5) |
| $$E_i'=\frac1L\sum_{k=6}^9E_{i,k}'$$ | (6) |
| $$R_{MME}=\frac1M(\sum_{i=1}^MR_i)$$ | (7) |
| $$E'_{MME}=\frac1M(\sum_{i=1}^ME'_i)$$ | (8) |
Table 2.
Evaluation matrix of GCM simulations for individual climate variable
| Scorei | Ri ≥ RMME | Ri ≺ RMME |
| E'i ≤ E'MME | +1 | 0 |
| E'i ≻ E'MME | 0 | -1 |
여기서, L (L = 4)은 전체 평가 개월 수, M은 전체 GCM의 개수이다.
모의성능 평가결과를 정량화하기 위해 Table 2와 같이 평가 매트릭스를 구성하였다. GCM의 모의성능은 기후변수의 앙상블평균 PCC (RMME) 및 RMSE (E'MME)와 비교하여 점수를 부여하였다. 이 때, MME는 다중 GCM의 모의결과의 불확실성을 최소화하는 값으로 GCM 결과의 상대적 우위를 판단할 수 있는 객관적인 기준값이다(Kim et al., 2020b). Table 2를 기준으로 산정한 개별 GCMi의 변수별 점수(Scorei)를 전체 기후특성변수(j)에 대해 확장하면, 변수 j에 대한 GCMi의 모의성능평가 점수는 Scorei,j로 표현된다. 이를 Eq. (9)로부터 각 변수에 대한 점수를 평균하여 전체 변수에 대한 GCMi의 최종 모의성능 평가점수(Scorei,)를 산정한다.
| $$Score_{i,total}=\sum_{j=1}^PScore_{i,j}$$ | (9) |
여기서, j (j=1,…, P)는 각 기후변수, P (P = 12)는 전체 기후변수의 개수이다.
이후, 최종점수가 높은 순으로 GCM의 모의성능 평가순위를 결정한다. 최종순위를 기준으로 하되, 수자원 영향평가 시 가장 중요한 요소인 강수량 변수의 모의성능을 고려하여 최종 GCM을 선정한다. GCM의 선정순위는 목표성능에 따라 달라질 수 있으나, 본 연구에서는 MME 보다 우수한 GCM을 선정하고자 전체 순위의 상위 1/3에 해당하는 33%를 기준으로 설정하였다. 최종점수를 기준으로 상위 33% 이내의 순위에 해당하는 GCM 중 강수량 모의성능이 낮은 GCM (강수량 평가점수: “-1”)은 제외한 나머지를 최종 GCM으로 선정한다.
3. 대상지역 및 자료수집
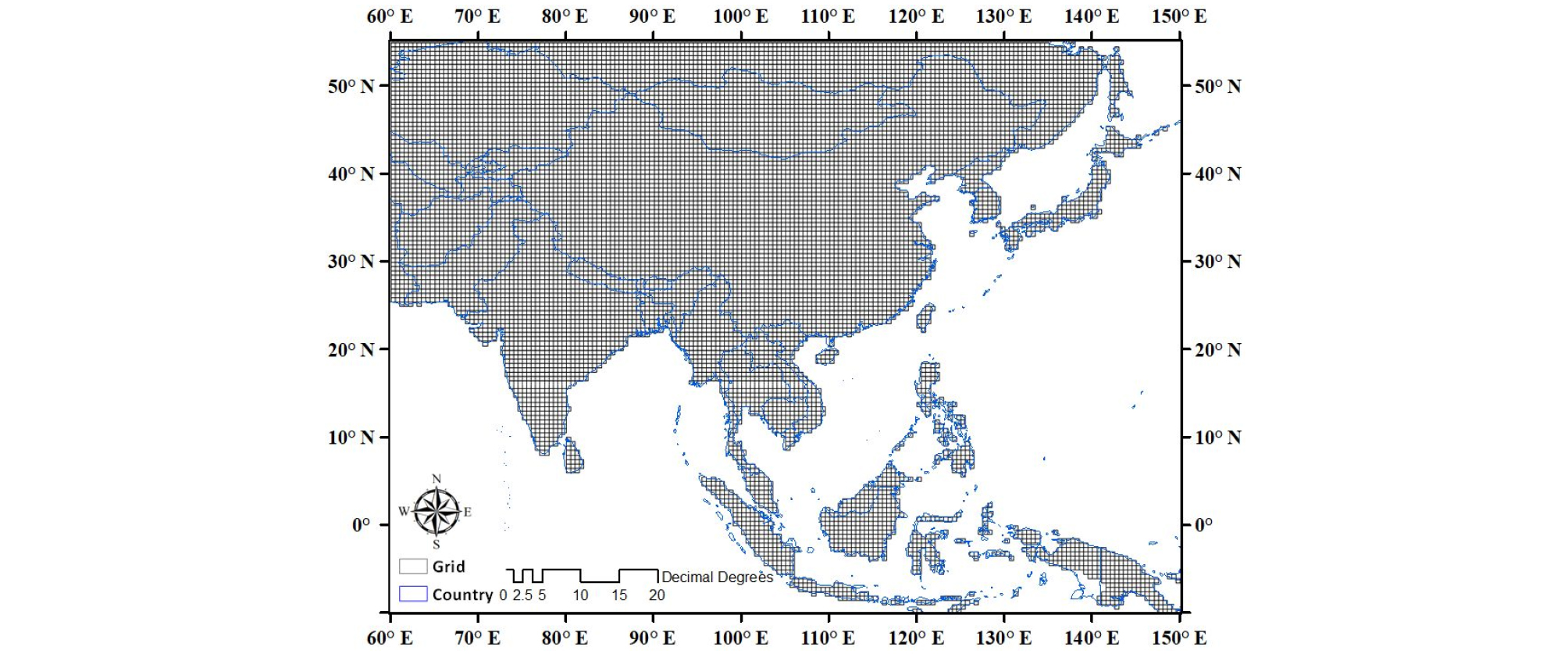
아시아 몬순지역의 기후특성을 잘 반영하는 GCM을 선정하기 위한 대상지역은 Fig. 1과 같다. 아시아 몬순지역의 공간적 범위는 위도 9.75° S ~ 54.75° N, 경도 60.25° E ~ 149.75° E의 범위에 해당한다. 이 지역은 열대, 온대, 한대 및 극 기후대 특성이 모두 나타나는 지역으로 다양한 기후가 혼재되어 있다. 또한, 동아시아 및 서남아시아 지역은 동아시아 및 인도몬순의 영향으로 여름철에 연 강수량이 집중되는 지역으로 강수량의 계절적 변동성이 큰 지역이다. 관측 및 GCM 정보는 자료에 따라 공간해상도가 상이하기 때문에 대상지역을 0.5° × 0.5° (약 50 km)의 동일한 격자체계로 구성하였다. 각 자료는 수문분야에서 활용도가 높은 이중선형보간법(Bilinear interpolation method)을 통해 공간해상도 및 격자체계를 통일하여 활용하였다(Singh and Fiorentino, 1996).
GCM의 과거 기후모의 성능평가를 위해서는 장기간의 관측자료가 요구된다. 보다 현실적인 기후변화 시나리오를 산출하기 위해 자료의 활용성이 기 검증된 격자 관측자료를 우선적으로 수집하였고, 관측자료가 부재한 기후변수에 대해서는 재분석자료를 수집하여 활용하였다. 평가에 활용되는 12개 변수 중 3개 변수(강수량, 최고기온, 최저기온)는 관측자료가 가용하였다. 강수량 자료는 신뢰성 있는 유출모의를 수행하는데 필수자료로 자료의 해상도와 자료의 보유기간(1948 ~ 2006년)을 고려하여 APHRODITE (Asian Precipitation-Highly-Resolved Observational Data Integration Towards Evaluation of water resources) 강수량 자료를 선정하였다(Yatagai et al., 2012). 최고기온과 최저기온 자료는 University of Washington에서 가공한 격자자료를 활용하였다(Adam and Lettenmaier, 2003; Adam et al., 2006). 나머지 8개 변수에 대한 관측자료는 NOAA에서 생산한 OLR-AVHRR (Outgoing Longwave Radiation-Advanced Very High Resolution Radiometer)자료와 ECMWF (Cethe European Centre for Medium-Range Weather Forecasts)에서 생산한 CERA-20C (the Coupled ECMWF Re-Analysis system-20C) 재분석자료를 활용하였다. 장파복사량에 대한 활용성은 Liebmann and Smith (1996)와 Schreck et al. (2018)에서 제시된 바 있다. CERA-20C 재분석자료는 대기, 해양, 지표 및 빙하 등의 정보를 포함하여 과거기후를 기반으로 생산된 격자자료로, Laloyaux et al. (2018)에서 그 활용성이 입증된 바 있다. 수집된 변수는 2차원 및 3차원 자료이며, 각 변수별 수집자료에 대한 정보는 Table 3에 제시하였다.
Table 3.
Description of observed datasets
본 연구에서는 CMIP5 (Coupled Model Intercomparison Project phase 5) GCM 중 historical 및 RCP 시나리오(RCP 4.5 및 RCP 8.5)에 대한 자료가 모두 가용한 GCM을 우선적으로 검토하였다. 현재 PCDMI (Program for Climate Model Diagnosis and Intercomparison)에서 제공되고 있는 GCM 중에서 일 단위 자료가 가용한 GCM은 44개이며, GCM의 모의성능 평가에 활용되는 12개 기후변수에 대한 정보가 모두 존재하는 19개 GCM을 수집하였다. Table 4는 선정된 19개 GCM (19 GCMs) 정보를 제시한 것이며, 표에 제시된 공간해상도는 모델에서 제공하는 지표면 자료에 해당하는 격자수이다.
Table 4.
Description of 19 GCMs
4. 결과 및 분석
4.1 기후변수별 GCM의 과거 재현성 비교
12개 기후변수에 대한 19 GCMs의 과거(1976 ~ 2005년) 몬순기후 재현성을 평가하였다. 통상 GCM은 지역규모에서 활용하기 위해 상세화(downscalling)되며, 이 과정에서 관측자료에 의해 편이보정된다. 그러므로, GCM의 객관적인 성능평가를 위해서는 상세화 이전 원자료의 모의성능을 평가하는 것이 바람직하다. 본 연구에서는 GCM 원자료로부터 공간적인 기후정보를 추출하였으며, 이를 관측 기후정보와 비교하여 통계적 평가를 수행하였다.
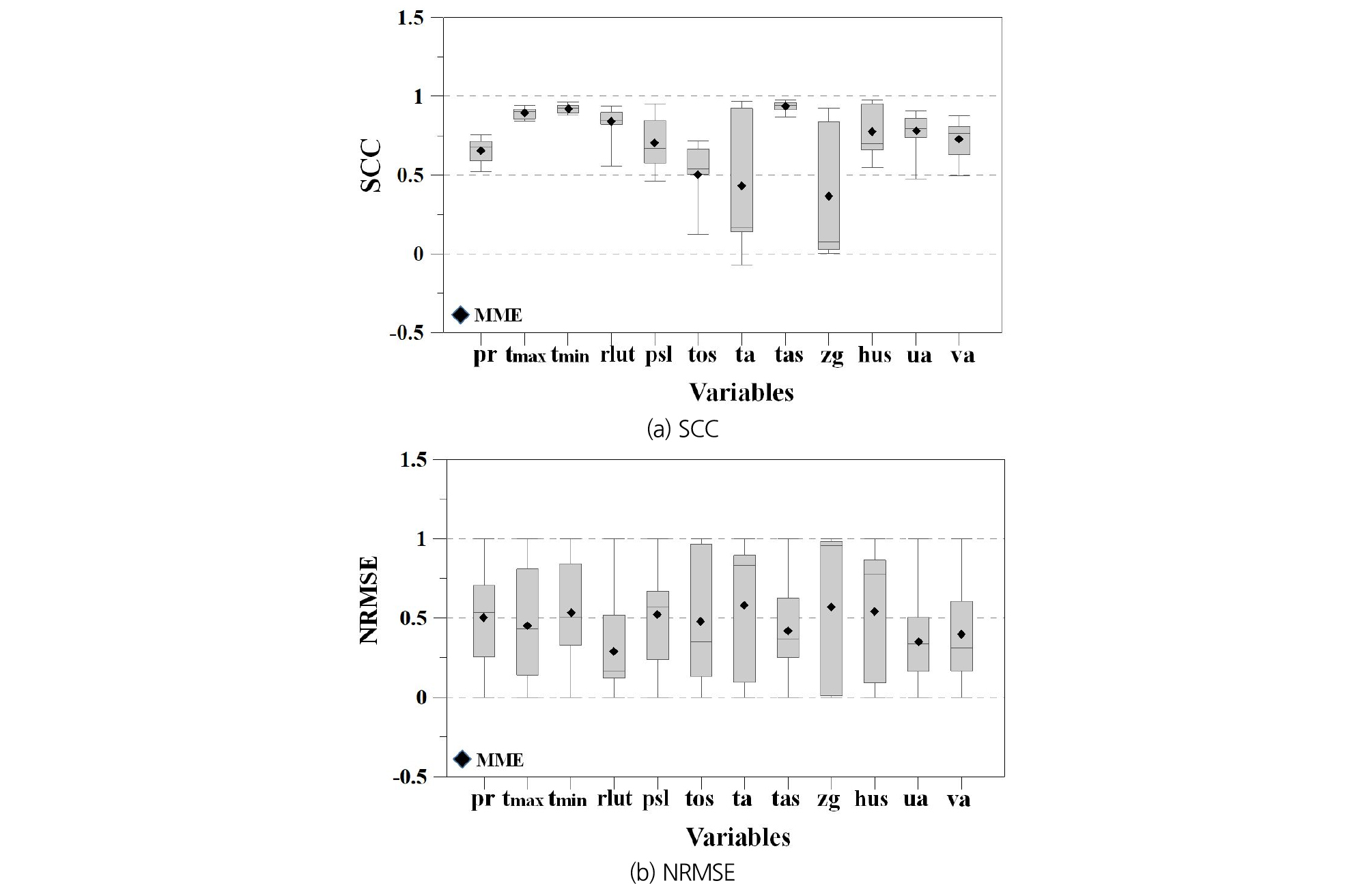
Fig. 2는 기후변수별 19 GCMs 모의자료와 관측자료 간의 SCC와 RMSE 값의 범위를 Box-whisker로 나타낸 것이다. 기후변수 간의 상호비교를 위해 RMSE의 단위는 0 ~ 1의 범위로 표준화하였으며, NRMSE로 표기하였다. 각 Box-whisker는 몬순기간(6 ~ 9월)에 대한 월별 SCC와 NRMSE의 범위로 각 기후변수에 대한 GCM의 모의오차를 의미한다. 대체로 19 GCMs의 과거 지표기온(tmax, tmin, tas)에 대한 SCC는 0.84 이상으로 매우 높았으며, 관측자료의 공간적인 기후패턴을 잘 모의하는 것으로 나타났다. 강수량(pr), 장파복사량(rlut), 비습도(hus)에 대한 SCC는 0.5 이상으로 전반적으로 관측값의 공간적 패턴을 잘 반영하였다. 나머지 대기온도(ta)와 지오포텐셜 고도(zg) 등 3차원 기상변수에 대한 SCC는 상대적으로 낮았으며, 모의값이 넓게 분포하였다. 이는 해당 변수에 대한 GCM 모의값이 관측값의 공간적 패턴을 잘 반영하지 못하며, GCM 간의 모의성능 편차도 큰 것을 의미한다. 한편, GCM의 모의성능이 좋지 못한 기후변수들은 대체로 NRMSE의 산정결과도 우수하지 못한 것으로 분석되었다. 해수면온도(tos), 대기온도(ta), 지위고도(zg)는 NRMSE에서 MME의 모의성능도 0.5 이상으로 나타났으며, GCM 간의 편차도 크게 나타나 전반적으로 관측값과의 오차가 크게 발생하였다. 반면, 수자원 영향평가 시 기존 GCM 평가에 주로 활용되는 지표기온, 강수량 변수의 모의성능은 상대적으로 우수하였으며, GCM 모의성능 간의 편차도 작은 것으로 확인되었다.
4.2 GCM의 과거 기후모의 성능평가 및 적정 GCM 선정
Table 5는 각 기후변수에 대한 19 GCMs의 정량적 평가지표(SCC, RMSE)를 MME와 비교하고, 점수화하여 나타낸 것이다. GCM의 개별 변수에 대한 평가점수는 전술한 GCM 모의 성능평가 매트릭스를 기반으로 산정되었으며, 이를 합산하여 최종평가 점수를 산정하였다. 평가결과, GCM의 모의성능은 각 기후변수의 종류에 따라 상이하게 나타났다. 이는 기후모형 성능평가 시 활용되는 기후변수에 따라 평가결과 및 GCM 선정결과가 달라질 수 있음을 의미한다. 강수량(pr), 지표온도(tmax, tmin, tas) 등 강우-유출해석에 사용되는 수문해석 변수에 비해 대기에서 관측된 3차원 기후변수들(ta, zg, hus, ua 등)은 대체로 성능평가 점수가 낮은 것으로 확인되었다.
Table 5.
Results of the GCM evaluation based on the skill scores
Table 6은 19 GCMs의 평가순위와 최종 GCM 선정결과를 나타낸 것이다. 최종점수가 높은 순서로 19 GCMs의 개별순위를 산정하고, 선정기준을 만족하는 GCM 중 강수량 모의성능이 좋지 않은 CMCC-CM을 제외한 5개 GCM을 아시아 몬순특성을 고려한 적정 GCM으로 최종선정하였다. 5개 GCM (이하, 5 GCMs)은 순위 순서대로 NorESM1-M (NorM), bcc-csm1-1-m (Bccm), CNRM-CM5 (CNC5), CMCC-CMS (CMCS), CanESM2 (Can2)이다. 선정된 5 GCMs 중 4 GCMs (NorM, Bccm, CNC5, Cans2; CMCS는 미적용)은 동남아시아 지역에 대한 여름몬순 재현성이 우수하다고 제시된 바 있으며(McSweeney et al., 2015), Bccm을 제외한 4 GCMs (NorM, CNC5, CMCS, Cans2)은 동아시아 및 국내 영역에 대한 기후에 적합한 대표 GCM으로 선정된 바 있다(Jung et al., 2018). Bccm의 경우, Jung et al. (2018)과 평가결과가 상이하였으나 이는 기후 재현성 평가 시 적용 조건(기후변수, 공간적 범위)의 차이에서 기인한 것으로 판단된다. 이외에도 5 GCMs은 아시아 몬순지역 기후변화 연구에 다수 활용된 바 있어 제시된 GCM 선정기법 및 5 GCMs의 적용성을 확인하였다(Guo et al., 2016; Chen et al., 2017; Liu et al., 2018; Wang et al., 2019).
Table 6.
Results of GCM selection considering the rank and precipitation score
| No. | GCM (Abb.) | Total score | Rank | pr score | Selection | References |
| 1 | ACC0 | 2 out of 11 | 8 | 1 | X | |
| 2 | ACC3 | -2 out of 11 | 13 | -1 | X | |
| 3 | Bcc1 | -1 out of 11 | 12 | -1 | X | |
| 4 | Bccm | 9 out of 11 | 2 | 1 | O | Wu et al. (2014) |
| 5 | BNUM | 3 out of 11 | 7 | 1 | X | |
| 6 | Can2 | 6 out of 11 | 5 | 1 | O | Yang and Saenko (2012) |
| 7 | CMCM | 6 out of 11 | 6 | -1 | X | |
| 8 | CMCS | 8 out of 11 | 4 | 1 | O | Davini et al. (2014) |
| 9 | CNC5 | 9 out of 11 | 3 | 1 | O | Voldoire et al. (2013) |
| 10 | GFD3 | 2 out of 11 | 9 | 1 | X | |
| 11 | GFDG | -2 out of 11 | 14 | 0 | X | |
| 12 | HadC | 0 out of 11 | 11 | 1 | X | |
| 13 | IPAL | -5 out of 11 | 16 | -1 | X | |
| 14 | IPAM | -3 out of 11 | 15 | -1 | X | |
| 15 | IPBL | -10 out of 11 | 19 | -1 | X | |
| 16 | MIRE | -8 out of 11 | 18 | -1 | X | |
| 17 | MIRC | -7 out of 11 | 17 | -1 | X | |
| 18 | MRI3 | 1 out of 11 | 10 | -1 | X | |
| 19 | NorM | 10 out of 11 | 1 | 0 | O | Bentsen et al. (2013) |
4.3 선정된 GCM의 과거 기후모의 성능 검증
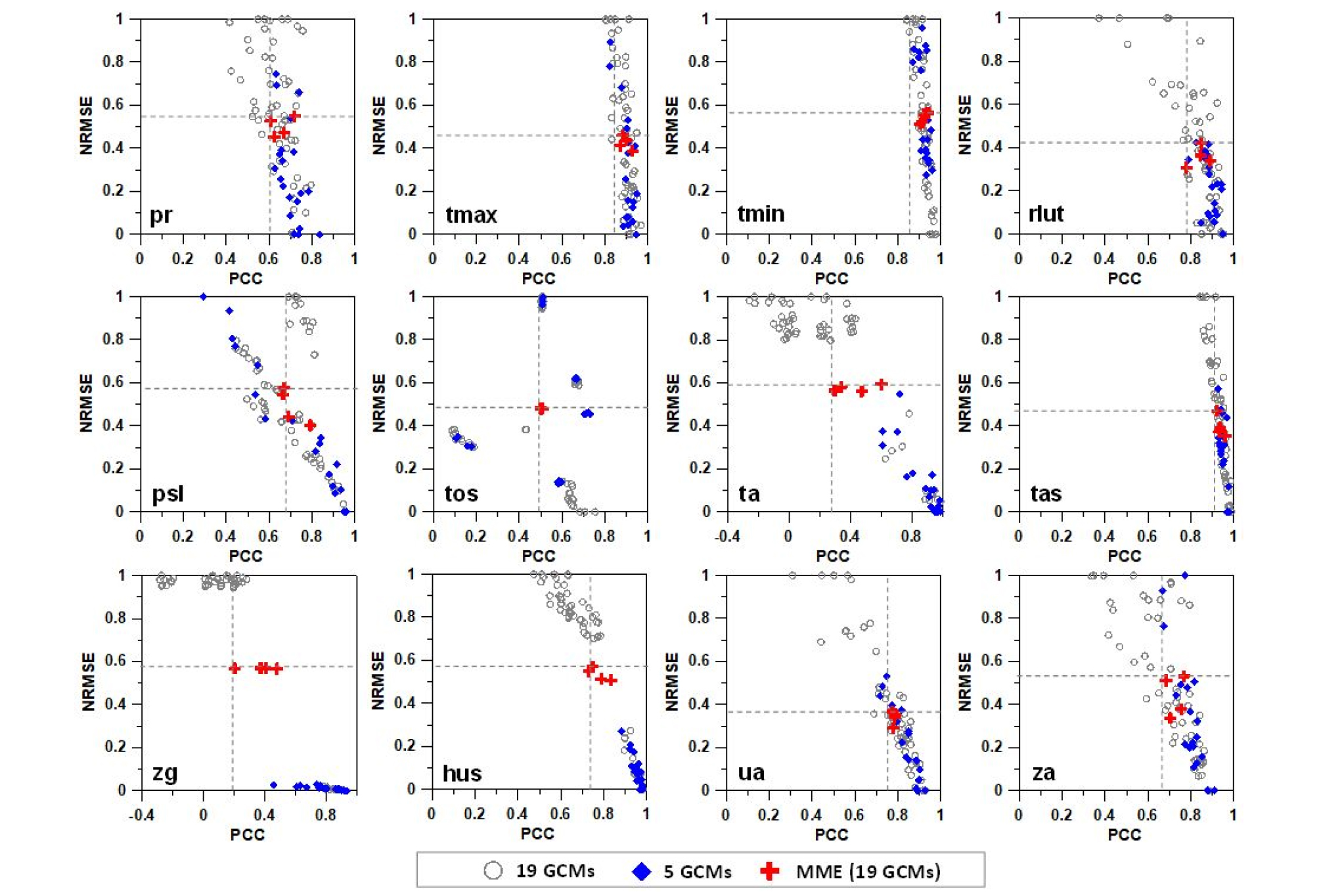
선정된 5 GCMs은 전반적인 몬순기후 특성을 고려하는 12개 기후변수 재현성을 기반으로 선정된 것이므로 개별 기후변수의 특성을 잘 고려하는지 평가할 필요가 있다. 5 GCMs과 전체 19 GCMs 및 MME (19 GCMs)의 월별(6 ~ 9월) 모의성능을 비교하여 GCM 선정방법과 선정결과에 대한 적정성을 평가하였다. Fig. 3은 12개 기후특성에 대한 개별 19 GCMs, 선정된 5 GCMs 및 19 GCMs으로부터 산정된 MME (이하, MME (19GCMs))의 평가지표(SCC, NRMSE) 값을 함께 도시한 것이다. 평가결과, 월별 및 기후변수별로 편차는 있지만 MME는 전반적으로 각 기후변수에 대한 평균 이상의 모의성능을 나타내었다. 평가대상 월에 대한 MME의 최소 SCC와 최대 RMSE 값을 기준값으로 설정하였으며, Fig. 3에 회색 점선으로 나타내었다. 여기서, 회색 점선을 기준으로 한 사분면 위치에 따라 2사분면에 위치한 값은 SCC와 NRMSE가 MME에 비해 모의성능이 우수하지 못함을 의미하며, 4사분면에 위치한 값은 상대적으로 MME에 비해 성능이 우수함을 의미한다. 나머지 1사분면 및 3사분면에 위치한 값은 둘 중 하나의 조건만 만족함을 의미한다. 선정된 5 GCMs은 해면기압(psl) 변수를 제외한 나머지 11개 변수에서 모두 4사분면 혹은 1, 3사분면에 위치하였다. 즉, 선정된 5 GCMs은 상대적으로 MME와 비슷하거나 우수한 성능을 나타내었으며, 아시아 몬순지역에 대한 기후재현성이 전반적으로 우수함을 확인하였다.
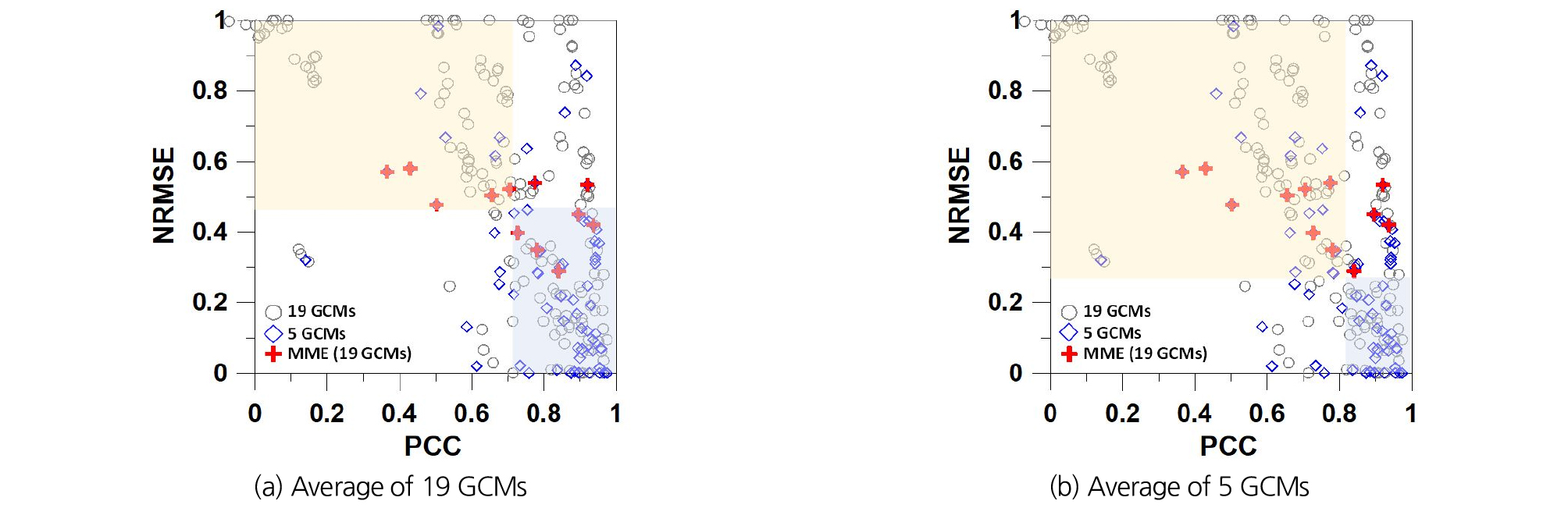
Fig. 4는 개별 19 GCMs과 선정된 5 GCMs, MME (19 GCMs)의 12개 변수에 대한 대푯값(SCC, NRMSE) 분포를 도시한 것으로, 변수별 대푯값은 과거 몬순기간(6 ~ 9월)의 통계치를 평균하여 산정하였다. 기후변수별로 편차는 있지만 MME는 전반적으로 각 기후변수에 대하여 평균이상의 모의성능을 나타내었으며, 5 GCMs은 아시아 몬순지역에 대한 과거 기후재현성이 전반적으로 우수한 것으로 나타났다. Fig. 4(a)는 MME (19 GCMs)의 12개 기후변수에 대한 평균 SCC와 NRMSE의 범위를 활용하여 두 지표가 모두 우수한 영역(4사분면; 파란색 음영)과 모두 우수하지 않은 영역(2사분면; 노란색 음영)을 표시한 것이며, Fig. 4(b)는 MME (5 GCMs)에 대한 동일한 평가결과이다. 12개 기후변수에 대한 MME (19 GCMs)의 SCC와 NRMSE의 평균은 0.71, 0.47이고, 5 GCMs는 각각 0.82, 0.27로 분석되었다. 5 GCMs은 MME에 비해 전반적으로 기후모의 성능이 우수한 것으로 나타났다.
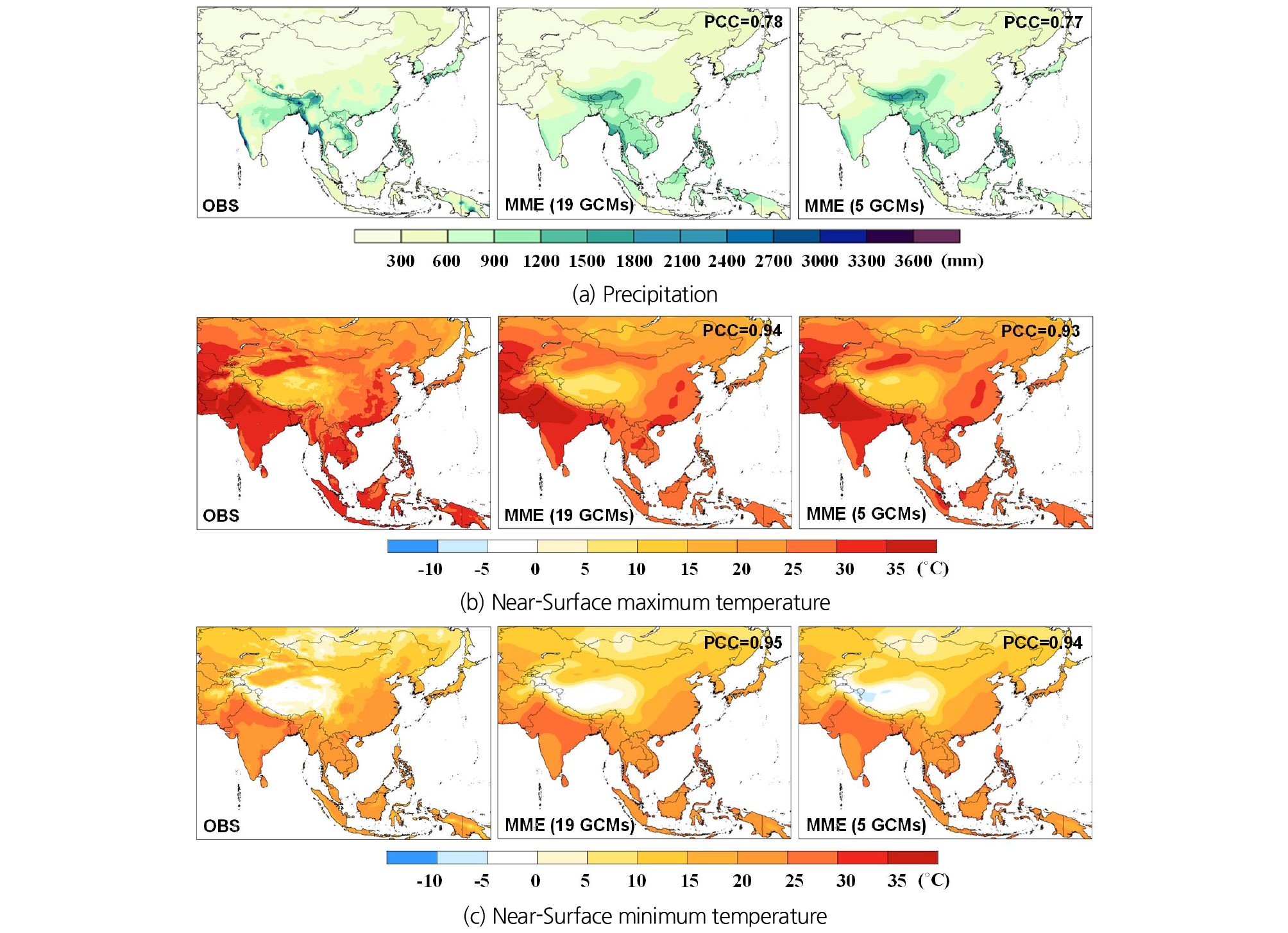
Fig. 5는 강수량, 최고 및 최저기온 변수에 대한 과거(1976 ~ 2005년) 몬순기간(6 ~ 9월)의 평균값에 대한 공간분포도이다. MME (19 GCMs)와 선정된 5 GCMs으로부터 산정된 MME (이하, MME (5 GCMs)) 모두 과거 관측기후의 공간분포를 잘 반영하였다. MME (5 GCMs)와 관측자료와의 PCC는 강수량의 경우 0.77, 최고기온(최저기온)의 경우 0.94(0.95)로 나타나 관측값의 공간적인 기후패턴을 잘 모의하였다. MME (19 GCMs)과 MME (5 GCMs)의 PCC 차는 0.01로 두 자료 간의 차이는 미미하였다.
4.4 선정된 GCM의 월평균 기후모의 성능평가
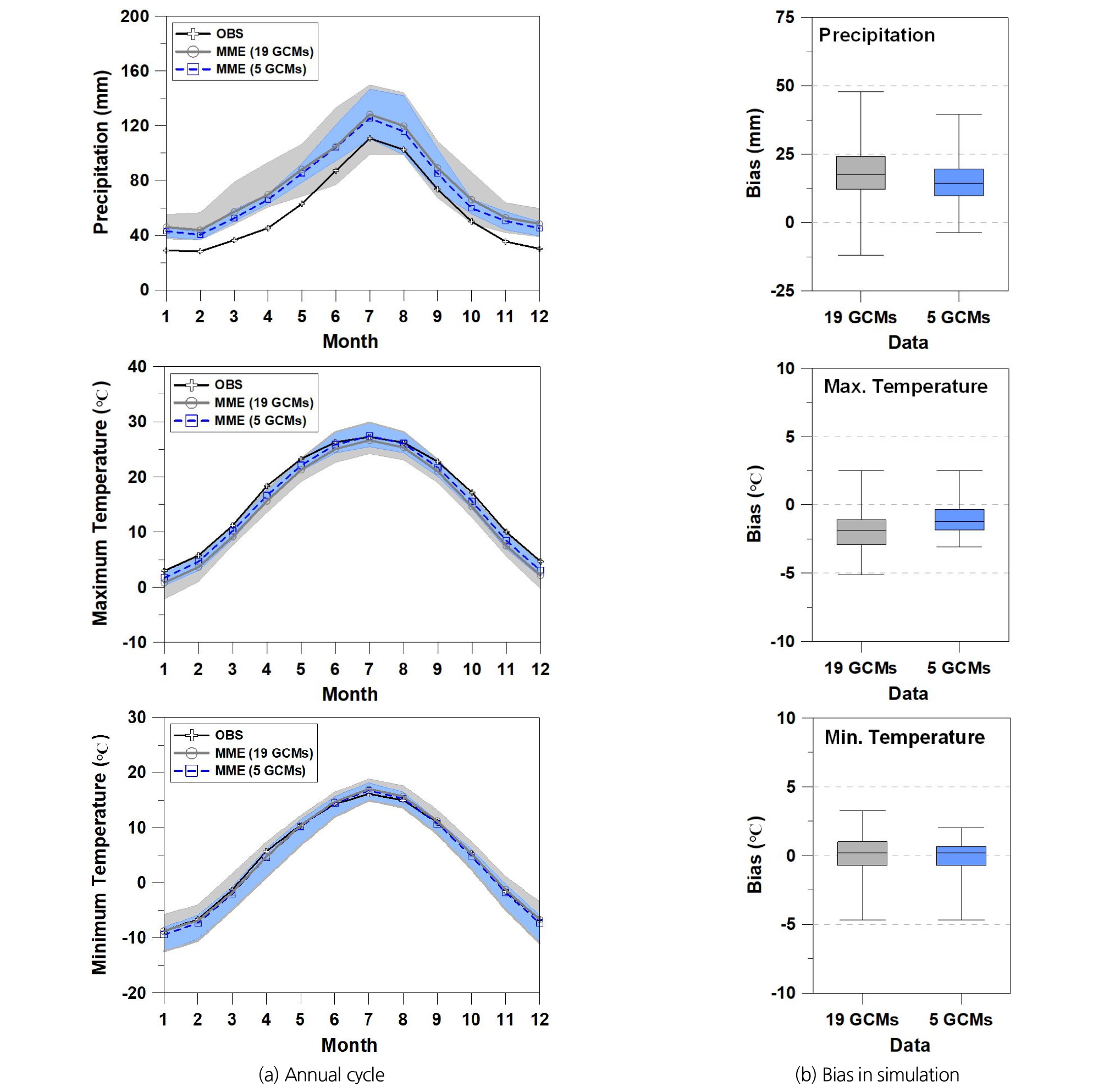
Fig. 6(a)은 관측값(OBS), 19 GCMs 및 5 GCMs으로부터 산정된 아시아 몬순지역의 과거(1976 ~ 2005년) 월 평균 기후값을 나타낸 것이다. 이 때, 평가에 활용된 GCM (19 GCMs 또는 5 GCMs)의 범위와 MME를 함께 도시하였다. MME (19 GCMs)와 MME (5 GCMs)의 패턴은 서로 유사하였으며, 대체로 관측값의 월별 패턴을 잘 반영하였다. 상대적으로 MME (19 GCMs) 대비 MME (5 GCMs)가 관측값에 더욱 유사하였다. 강수량 대비 최고기온 및 최저기온에 대한 MME (5 GCMs)의 모의성능이 우수하였으며, 모의값 간의 불확실성도 낮았다. Fig. 6(b)는 각 월에 대해 개별 GCM과 관측값 간의 편차를 산정한 후, 19 GCMs 및 5 GCMs이 갖는 편차 범위를 각각의 Box-whisker로 나타낸 것이다. 모든 변수에서 5 GCMs의 편차가 19 GCMs에 비해 밀집되어 있어, 관측값과 더 유사한 것으로 나타났다. 선정된 GCMs은 19 GCMs을 적용하는 경우에 비해 최고 및 최저기온, 강수량 모의결과의 불확실성을 저감할 수 있을 것으로 판단된다.
5. 결 론
본 연구에서는 아시아 몬순지역을 대상으로 아시아 몬순특성을 고려하는 GCM 선정방법을 개발하고, 이를 적용하여 적정 GCM을 선정하였다. 이를 위해 기후변화 수자원 영향평가에 활용되는 강수량, 지표기온 이외에 몬순특성과 연관된 다양한 기후변수를 선정하여 각 변수에 대한 19개 GCM의 모의성능을 평가하고, 이를 점수화하여 최종 5개 GCM을 선정하였다. 선정된 GCM의 모의성능을 검증하여 금회 제시한 GCM 선정방법의 적정성을 평가하였으며, 다음과 같은 결론을 도출하였다.
1) 12개 기후변수에 대한 GCM의 모의성능은 매우 상이하게 나타났으며, 상대적으로 기온변수에 대한 GCM의 모의성능이 가장 우수하였다. GCM은 기온에 비해 강수량 자료의 공간적인 기후패턴을 잘 모의하지 못하는 것으로 나타났다. 또한, GCM의 모의성능은 2차원 지표관측 변수보다는 3차원 대기관측 변수에서 낮게 나타났으며, 모의결과 간의 편차도 큰 것으로 확인되었다. 즉, 모의성능 평가에 활용하는 기후요소에 따라 GCM 선정결과가 달라질 수 있으며, 개별 기후변수는 독립적으로 모의되는 것이 아니므로 GCM 모의성능 평가 시 다양한 기후변수를 활용할 필요가 있음을 확인하였다.
2) GCM의 과거 기후재현성과 강수량 모의성능을 고려하여 5 GCMs (NorESM1-M, bcc-csm1-1-m, CNRM-CM5, CMCC-CMS, CanESM2)을 적정 GCM으로 선정하였다. 19 GCMs으로부터 산정된 MME는 전반적으로 평균적인 기후모의 성능을 나타내었고, 선정된 GCM은 몬순기간에 대한 12개 관측 기후변수특성을 잘 모의하였다. 19 GCMs MME와 관측값 간의 SCC, NRMSE는 12개 기후변수 평균 0.71, 0.47로 나타나 전반적으로 기후특성을 잘 모의하였다. 한편, 5 GCMs과 관측값 간의 SCC, NRMSE는 12개 기후변수 평균 0.82, 0.27로 나타나 MME에 비해 기후모의 성능이 더욱 우수하였다.
3) MME (5 GCMs)와 MME (19 GCMs) 모두 과거 관측 강수량 및 기온특성을 잘 모의하였으며, 두 자료의 몬순 기후재현성(강수량, 최고기온 및 최저기온)은 대체로 유사한 것으로 확인되었다. 그러나, 산출된 기후자료의 불확실성은 5 GCMs이 19 GCMs에 비해 낮게 나타났다. 또한, 관측자료와의 편차도 5 GCMs이 19 GCM에 비해 더 작게 나타나 적용된 GCM 선정방법이 적절한 것으로 판단된다.
본 연구는 아시아 지역의 기후특성을 고려한 GCM 선정기법을 개발하고, 이를 활용하여 적정 GCM을 선정하였다는 측면에서 연구의 가치가 있다고 판단된다. 다양한 기후변수에 대한 GCM의 재현성 평가결과는 적정 GCM의 판단기준을 설정하는데 기초정보로 활용될 수 있다. 다만, 본 연구에서는 몬순과 관련된 12개 기후변수 모의성능 평가결과에 동일한 가중치를 부여하여 최종 GCM을 선정하였다는 측면에서 한계가 있다. 향후, 기후변수의 중요도를 합리적으로 고려하기 위해서는 TOPSIS 등 적정 가중치 산정기법을 적용할 필요가 있다. 본 연구결과에서 제시한 바와 같이 GCM의 과거 재현성은 기후변수의 종류와 공간적 범위에 따라 평가결과가 달라질 수 있다. 따라서, GCM 선정 시 불확실성을 최소화하기 위해서는 적용 대상지역의 기후특성 및 기후시나리오의 활용목적을 고려한 모의성능 평가와 더불어 종합적인 판단이 필요할 것이다.