1. 서 론
2. 인공신경망과 순환신경망 기법
3. LSTM을 이용한 지하수위 예측 모델 개발
3.1 대상지역 및 관측자료 처리
3.2 LSTM 모델 설계
3.3 모델의 검증
4. 모델의 적용
4.1 지하수위 예측기법 적용
5. 결 론
1. 서 론
지하수 유동은 수리지질학적 특성과 시스템 경계 조건에 의해 결정되는 동시에 수문기상학적 요소 및 인위적 양수와 같은 요소까지 포함되며 각종 비선형성과 공간적 변동성으로 인해 시스템적인 예측이 현실적으로 어려운 것으로 평가된다(Sahoo et al., 2017). 실제로 기후변화의 영향을 고려한 지하수의 장기적인 가용성을 예측하는 것은 지표수보다 더 복잡하다(Alley et al., 2002). 주된 과제는 한 시스템 구성 요소의 변경 사항이 다른 시스템 구성 요소에 어떤 영향을 미치는지를 예측할 수 있어야 한다는 것이다. 이러한 예측을 위해서는 기후 인자, 지표수 수문, 농업용수 사용 간의 관계를 정량화 함으로써 그에 따른 지하수 반응을 살펴보는 것이 필요하다(Sahoo et al., 2017). 따라서 지하수위의 예측을 위해서는 물리적인 모델링 외에 비선형 상호 의존성에 기반한 머신 러닝(Maching learnig) 방법이 동원되고 있다(Sahoo and Jha, 2013; Behzad et al., 2010; Yoon et al., 2011). 수문학에서의 머신 러닝 기법은 다양하게 적용되어 왔으며 물리적 수치모델의 수준에 육박하거나 훨씬 더 정확한 성능을 달성할 수 있음을 입증한 바 있다(Coppola et al., 2003; Parkin et al., 2007; Nikolos et al., 2008; Chu and Chang, 2009; Sung et al., 2017).
최근 인공신경망(Artificial neural network)에 기반한 딥러닝(Deep learning) 기술이 컴퓨터 비전, 음성신호 인식 및 예측 분야에 적용되어 기존의 머신러닝 기법에 의한 결과보다 향상된 성과를 보이고 있다. 특히 순환신경망(Recurrent neural network)의 하나인 LSTM (Long short term memory) 기법은 자료의 장기의존성 문제를 해결하여 지하수위 변동과 같이 연속적인 형식의 자료를 학습하고 예측 하는데 탁월한 성능을 가지고 있다(Zhang et al., 2018). Jung et al. (2018)은 LSTM을 이용하여 감조하천의 수위를 매우 높은 정확도(NSE 0.99)로 예측하였다. Tran and Song (2017)은 LSTM 모델을 이용하여 하천수위자료를 기반으로 침수수위를 예측하였으며 예측정확도는 일반적인 순환신경망보다 높은 것으로 나타나 시계열 예측에 대한 LSTM 모델의 적합성을 보여주었다.
인공신경망을 이용한 예측 모델의 구축은 일반적으로 1) 입출력 텐서로 구성된 데이터준비, 2) 입출력을 정의하는 층으로 구성된 모델 설계, 3) 손실함수, 네트워크 최적화 등을 이용한 모델 학습, 4) 검증 데이터를 이용한 모델 검증의 4단계로 구성된다. 본 연구에서는 제주도 한경면 지역에 설치된 11개 지하수위 관측정의 관측자료를 대상으로 LSTM에 기반한 예측 모델을 개발 및 적용하고자 한다. 최근까지 Python 언어에 기반한 많은 딥러닝 프레임워크가 개발되어 왔고 그중 TensorFlow가 각광받고 있으며 여러 배포자들을 통해 배포되고 있다. 본 연구에서는 Anaconda사를 통해 배포되는 TensorFlow의 성능이 뛰어남이 입증된 바 있어(Helmus, 2018), 이를 backend로 도입하였으며 이를 이용하기 위한 frontend로 Keras (Chollet, 2017)를 도입하였다. 또한, 모델의 학습속도를 향상시키고자 NVIDIA CUDA 아키텍처(NVIDIA, 2016)를 도입하였다. 개발된 예측모형을 제주도 한경면에 위치한 11개 지하수 관측소 관측자료에 적용하고 변동성 예측 결과의 분석을 통해 LSTM 모델의 적정성을 평가하였다.
2. 인공신경망과 순환신경망 기법
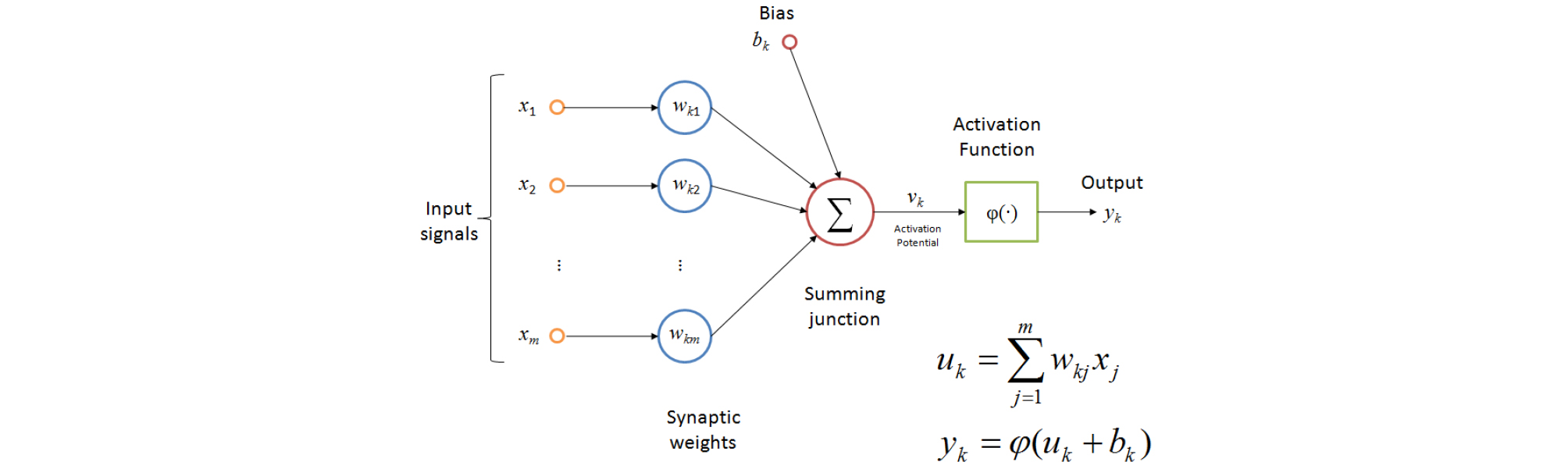
인공신경망은 사람의 신경계에 존재하는 신호 전달체인 뉴런을 인공적으로 모사하여 입력자료에 오차가 일부 존재하고 비선형적인 문제를 빠르게 해결하는 방법이다. Fig. 1은 수식으로 표현된 인공뉴런이다. 입력 x는 연결가중치 w를 가지며 이 가중치와 입력의 곱의 총합인 uk와 Bias bk의 합인 Vk가 활성화 함수 φ를 만족하면 뉴런은 활성화 되어 출력값을 내놓는다. 이러한 뉴런들의 집합을 층의 형태로 만들고 입력층, 은닉층, 출력층으로 구성하여 인공신경망을 구축할 수 있으며 특히 입력층과 출력층 사이에서 신호를 전달하는 은닉층이 하나 이상 존재하는 신경망을 다층신경망 이라 한다.
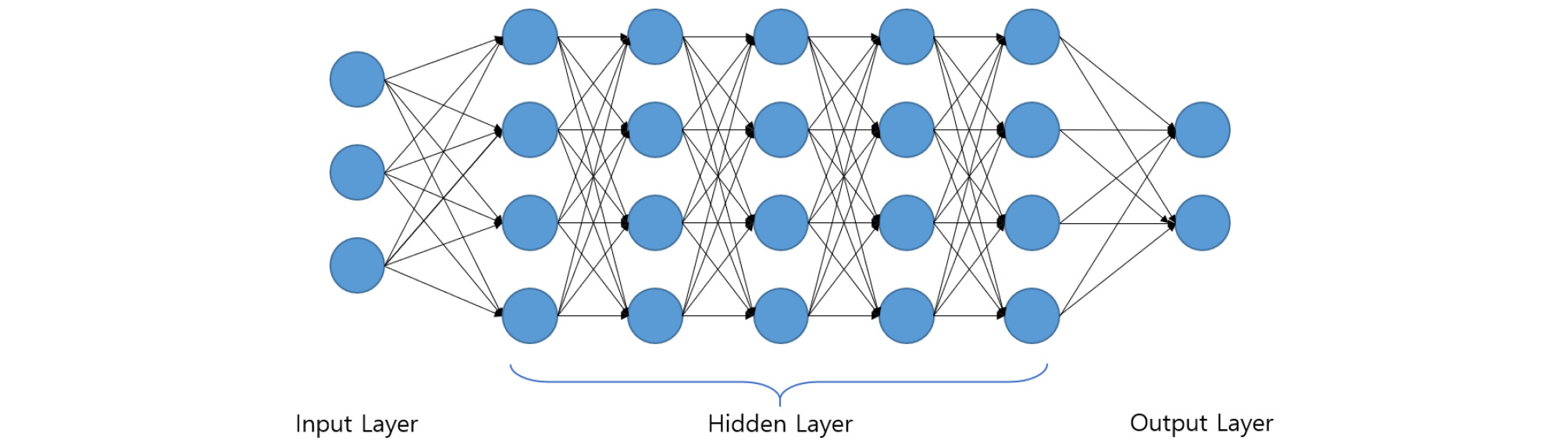
다층퍼셉트론(Multi layer perceptron, MLP)은 기존의 인공신경망에서 비선형문제를 해결하기 위한 계층구조이며 2000년 이후 하드웨어의 발달로 연산속도가 향상되고 MLP의 문제를 해결하기 위한 알고리즘이 발표되기 시작하며 인공신경망은 새로운 전환기를 맞이하게 되었다. 최근 활발히 연구되는 딥러닝은 인공지능의 한 표현이며 머신러닝의 범주 안에서 특별한 인공신경망의 하나로 간단하게 정의될 수 있다. 딥러닝의 딥은 데이터로부터 모델을 만들 때 다수의 은닉층을 사용하여 심도가 깊은 신경망을 구성했다는 것을 의미한다(Fig. 2).딥러닝 모델은 학습을 위해 수십에서 수백개의 연속된 층을 가지고 있으며 이들을 모두 학습자료를 이용해 자동으로 학습시킨다(Brownlee, 2018; Chollet, 2017)
순환신경망(Recurrent neural network)은 인공신경망 알고리즘의 일종으로 스스로를 반복하면서 이전 단계에서 얻은 정보가 지속되도록 한다. Fig. 3은 RNN의 기본구조와 연속 구조로 왼쪽 그림에서 신경망 A는 입력 Xt를 받아 ht를 출력으로 내보내며 신경망 A를 둘러싼 반복구조는 다음 단계에서 이전 단계의 정보를 받는다는 것을 보여준다. 오른쪽 그림은 연속적인 리스트의 형태로 이는 시퀀스 형식의 자료를 다루기에 최적화된 구조를 가진 신경망인 것을 알 수 있다. 실제로 RNN은 음성인식, 언어모델, 번역 등의 연속적이 자료를 다루는 분야에서 두각을 나타내고 있다. 그러나 RNN은 자료의 처음과 끝이 너무 먼 경우 지난 정보를 계속 이어가는데 문제가 발생한다.
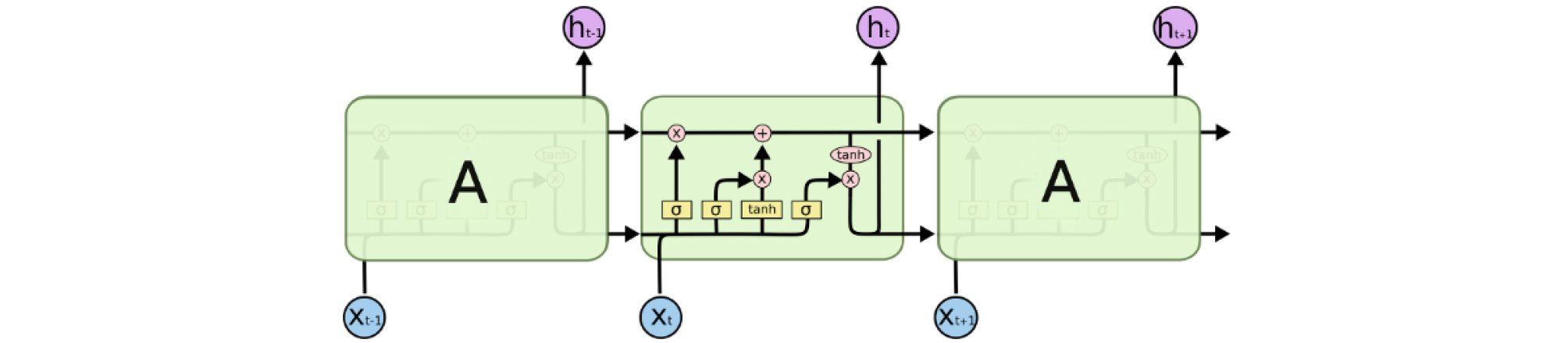
이러한 장기의존성에 의한 문제를 해결하기 위해 특별한 RNN의 하나인 LSTM이 제시되었고 연속적인 자료에서 나타나는 문제를 잘 해결했다(Hochreiter and Schmidhuber, 1997). LSTM도 RNN처럼 연속된 체인과 같은 구조를 가지고 있으나 하나의 모듈에 4개의 층이 서로 정보를 주고 받도록 고안되어 있다(Fig. 4).
LSTM의 핵심은 셀상태(cell state)를 통해 정보를 보존할지 모두 버릴지 결정하고 보존한다면 어떤 것을 저장할지 결정하는데 있다. 저장된 정보에 의해 현재의 정보를 업데이트 한 후 역시 셀상태에 따라 활성함수에 의해 출력을 결정한다.
3. LSTM을 이용한 지하수위 예측 모델 개발
3.1 대상지역 및 관측자료 처리
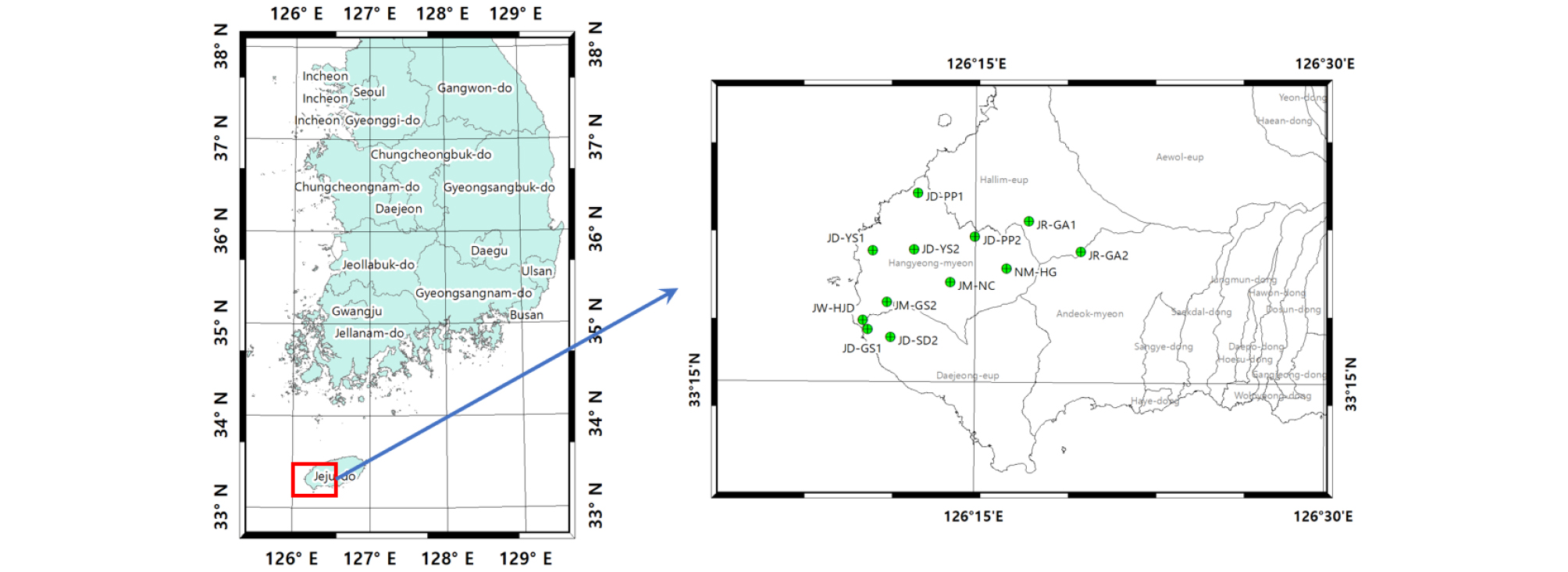
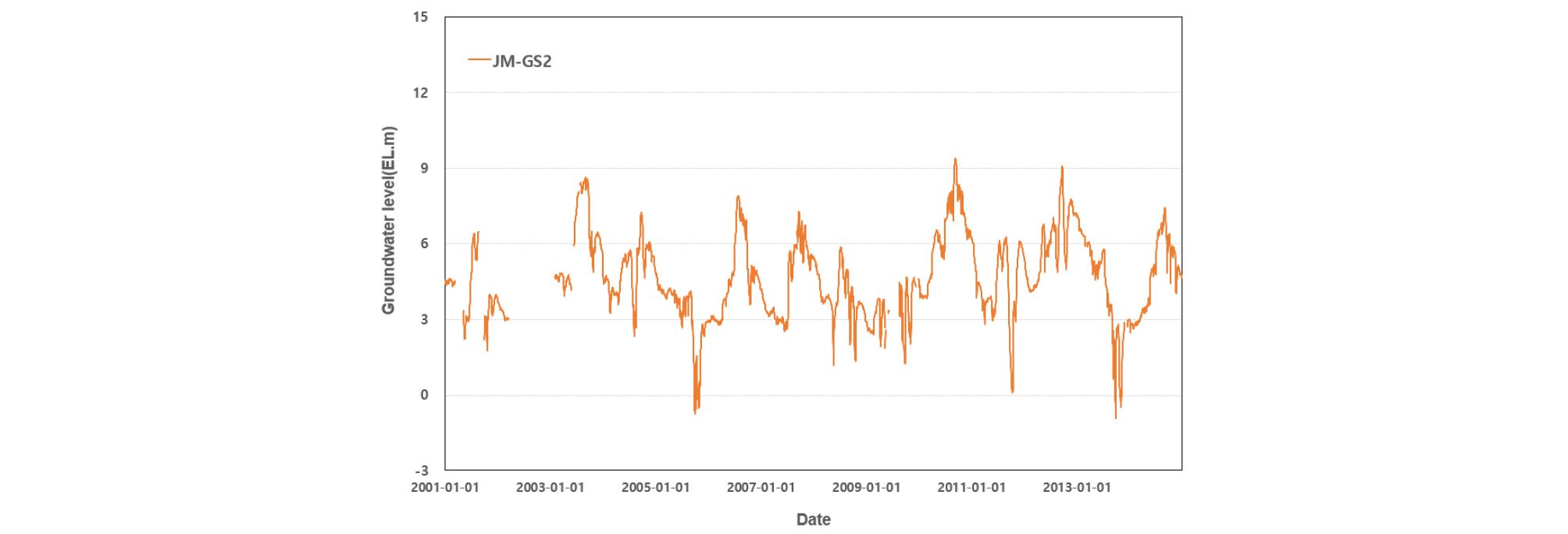
제주도 지하수위는 일반적으로 조석 영향에 의한 자기상관성이 높고 또한 강수의 영향이 잘 반영되는 것으로 알려져 있다(Song et al., 2013). 이러한 특성을 고려한 입출력 텐서를 구성하기 위해 각 지하수 관측정의 수위변동 관측자료와 같은 기간의 강수량 자료를 추가 입력자료로 선택하였다. 조석자료는 주기가 약 12시간으로 지하수위 자료와 시간간격이 일치하지 않고 지하수위 자료에 영향이 거의 나타나지 않아 추가하지 않았다. 지하수위 자료에서 분석 및 예측을 위해 수집된 지하수위 관측자료는 제주도 서부의 한경면에 위치한 다수의 관정(Fig. 5)에서 관측된 지하수위로 각 관측정별로 위치에 따라 서로 다른 관측개시일로부터 2014년 12월 31일까지의 일단위 수위변화를 관측한 시계열 자료이다. 신경망을 이용한 시계열 예측에서 입력자료의 품질은 예측결과의 품질에 직접적인 영향을 미친다. LSTM도 신경망의 일종이므로 잡음이 많고 정규화되지 않은 학습자료를 이용하여 학습시키면 예측 결과의 품질이 낮아진다. 따라서 LSTM 모델을 수행하기 전 입출력자료에 대한 적절한 전처리 기법의 적용은 필수적이다. 예를 들어 Fig. 6은 지하수 관측정 중 고산2(JM-GS2)의 지하수 관측자료를 도시한 것으로 2001년부터 2014년까지 일단위로 지하수위가 관측되었으나, 첫 3년동안(2001-2003년)은 결측이 많이 발생한 것으로 나타나며 그 이후에서 간헐적으로 수일간 결측이 나타난다. 이러한 결측구간에 대해 취할 수 있는 대응방안은 전통적으로 규칙에 의해 모두 버리거나, 일정한 값으로 채우거나(예를들면 평균, 중간값), 보간 또는 k-nearest neighbors (kNN)등을 이용하여 근사하는 방법이 있다.
본 연구에서는 결측구간이 짧고 제한적으로 나타나므로 개발 효율성을 고려하여 비교적 간단한 선형보간법을 결측처리전략으로 선택하였으며 다음 수식과 같이 정의된다(Davis, 2002).
| $$y'=\frac{(y_2-y_1)(x'-x_1)}{x_2-x_1}+y_1$$ | (1) |
여기서 y1과 y2는 관측값이며 x1과 x2는 관측시점이고 은 에서 보간된 값이다. 2002년에서 2003년 사이에 10일 이상의 장기결측이 발생한 구간에 대해서는 선형보간 등을 통한 결측처리를 하더라도 자료자체에 왜곡이 존재하게 되므로 예측결과의 품질을 보장할 수 없다. 그러므로 이러한 장기결측은 해당구간을 그대로 삭제하여 입력자료에서 제외하였다.
결측처리가 적용된 자료셋을 이용하여 지도학습(supervised learning)용 입력 텐서를 구성하였다. 지하수위는 선행지하수위 및 강수량과 밀접한 관계를 가지므로 일단위 예측의 경우 전일의 지하수위와 강수 조건에 따라 당일의 지하수위를 예측한다. Table 1은 이러한 전략에 따라 구성된 지도학습자료의 구성을 보여준다. 여기서 GWL (t-1)과 PRCP (t-1)는 각각 시간 t-1일 때 지하수위 및 강수량 이며 GWL (t)는 시간 t일 때 관측된 지하수위이다. 시계열 예측에서는 일반적으로 선행시간(Lead time)이 증가 할수록 예측정확도가 감소하는 것으로 알려져 있다(Jung et al., 2018; Yoon et al., 2014). 본 연구에서는 모든 모델에 하나의 선행시간(1일)만 고려하여 모델을 구축하고 예측을 수행하였다.
Table 1. Input dataset for supervised learning
| Day | GWL (t-1) | PPCP (t-1) | GWL (t) |
| 1 | 0.4480 | 0.0 | 0.4453 |
| 2 | 0.4453 | 0.0 | 0.4373 |
| 3 | 0.4373 | 0.0 | 0.4346 |
| 4 | 0.4346 | 0.0 | 0.4373 |
| 5 | 0.4373 | 0.0 | 0.4373 |
| ⦙ | ⦙ | ⦙ | ⦙ |
결측처리가 적용되고 학습에 적절한 텐서로 자료가 구성되었다 하더라도 자료의 값이 네트워크 가중치보다 크거나 균일하지 않은 상태로 LSTM 모델에 적용하는 것은 네트워크의 수렴을 방해하므로 이를 해결하기 위해서는 정규화(normalization) 과정을 통해 변환하여야 한다(Chollet, 2017). 본 연구에서는 Min-Max scaling 기법을 이용하여 변환하였다. Min-Max scaling은 자료의 분포가 0 ~ 1사이에 위치하도록 변환하는 것으로 다음 Eq. (2)로 정의된다.
| $$x'=\frac{x-\min(x)}{\max(x)-\min(x)}$$ | (2) |
여기서 x는 실측값이고 x’은 정규화된 값이다. 이 과정을 거친 후 자료는 비로소 신경망에 주입될 준비를 마치게 된다.
3.2 LSTM 모델 설계
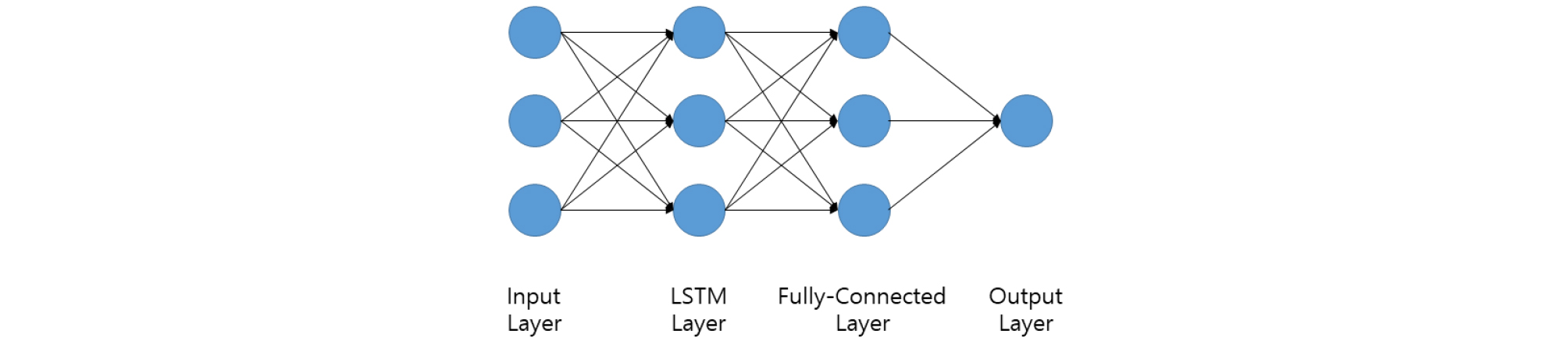
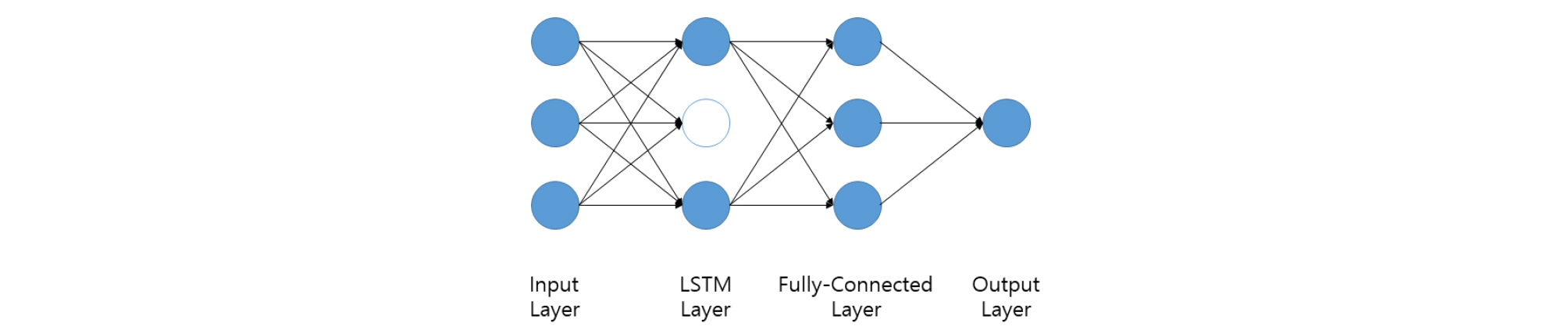
제주도 지하수위 변화를 예측하기 위해 전형적인 LSTM 모델을 설계하였다. 고안된 LSTM 모델은 입력층 다음에 LSTM층이 존재하고 그다음 모든 뉴런들이 다음 층과 완전히 연결된 완전연결층(fully-connected)과 연결되어 최종적으로 출력층을 통해 예측결과가 나온다(Fig. 7). 입력층에 주입되는 자료는 학습을 위한 자료와 학습 종료 후 모델의 성능을 평가하기 위한 검증자료로 구분하여 모델에 적용하였다.
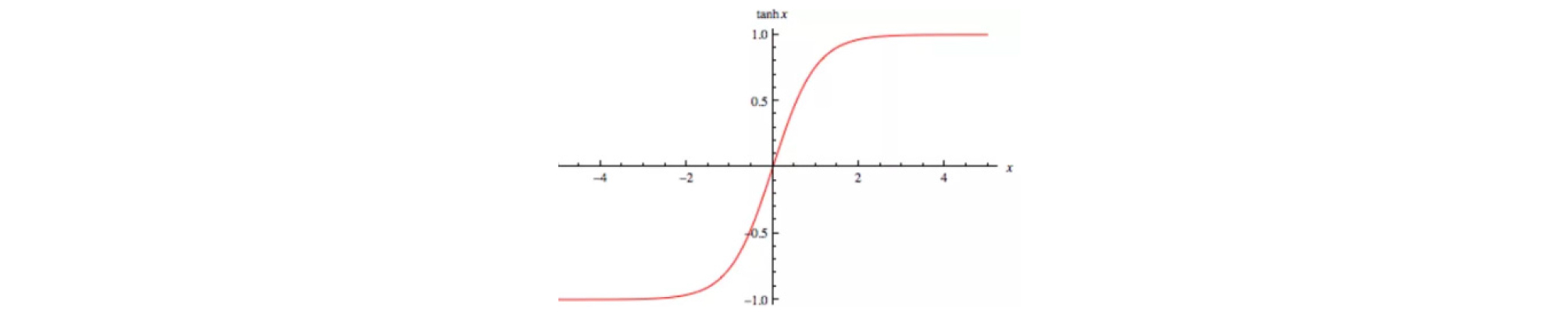
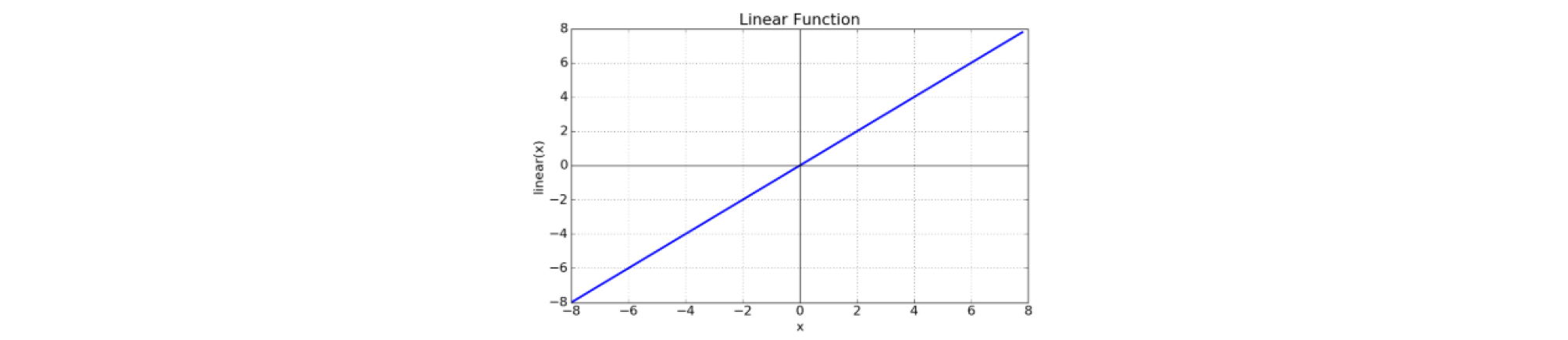
LSTM 층의 활성함수(Activation function)는 hyperbolic tangent (Fig. 8)로 구성하였으며 완전연결층의 활성함수는 linear function (Fig. 9)으로 설정하였다.
네트워크의 갱신을 위한 손실함수는 평균절대오차(Mean absolute error)로 선정하였으며 최적화는 Adam optimizer를 이용하였다. 손실함수의 최소화하는 방향으로 가중치를 결정하는 여러 방법 중에 Adam optimizer는 시계열 예측을 다루는 LSTM 에서 흔히 선택되는 기법이다(Kingma and Ba, 2015). LSTM층과 완전연결층 사이에 과대적합(Overfitting)을 방지하기 위해 Dropout을 적용하였다. Dropout이 적용되는 층은 학습을 하는 동안 무작위로 해당 층의 출력이 발생되지 않아 네트워크의 연속성이 단절되어 일부 뉴런들의 부적합한 연결을 방지하게 되어 과대적합을 감소시킨다(Srivastava et al., 2014). Fig. 10은 Dropout이 적용된 LSTM 모델을 나타낸다.
3.3 모델의 검증
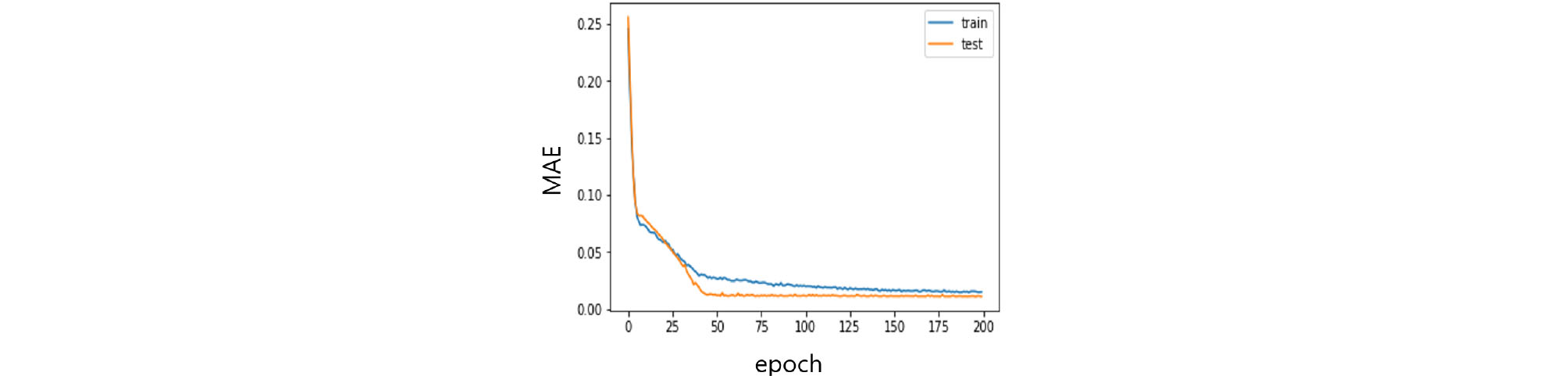
학습이 완료된 모델에 검증용 입력자료를 주입하여 모델의 검증을 수행하였다. 학습용 자료를 이용하여 학습을 한번 마치는 것을 epoch라 하는데 학습율에 따라 epoch를 반복하여 학습시킬 수 있다. 본 모델의 개발에서는 200회를 기본 반복횟수로 하고 학습상태에 따라 조정하였다. 반복횟수는 정해진 값이 아니며 입력자료의 특성 및 모델의 구성에 따라 목표 성능에 도달하기까지 달라진다. 본 연구에서는 각 관측소 모델별 학습률 곡선(Fig. 11)을 참조하여 기본 반복횟수를 결정하였다. Figs. 11 and 12는 실제 개발된 코드를 수행하여 나타난 결과이다. Fig. 11을 이용하여 학습시 에러와 검증시 에러값을 보고 학습이 충분히 되었는지 판단하고 실제 검증자료를 이용하여 예측을 실시한 후 Root mean square error (RMSE)와 Coefficient of determination (R2)에 의한 모형 적합도를 평가하였다(Fig. 12). 만일 적합도가 낮게 나타나면 반복횟수 및 변수의 조정을 통해 모델의 디자인을 재설정하여 최적 모델이 선정되도록 하였다.
4. 모델의 적용
4.1 지하수위 예측기법 적용
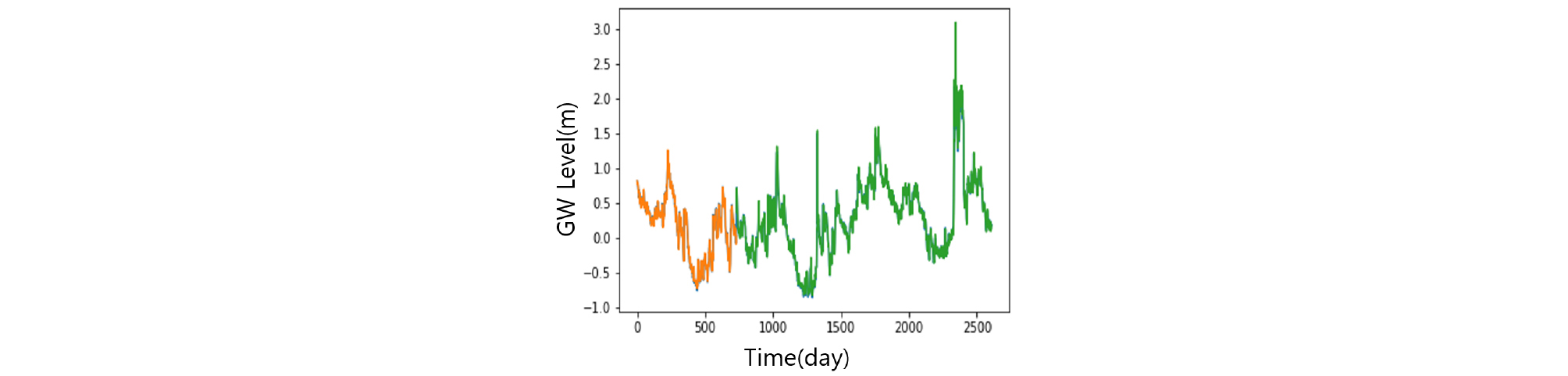
제주도 한경면의 고산1, 고산2, 판포2, 신도2, 용수1, 용수2, 낙천, 금악1, 금악2, 한장동, 한경 관측정(Fig. 5)자료에 대해 LSTM 모델을 적용하여 지하수위를 예측하고 실측수위와 비교하였다. 각 관측소별로 자료수가 달라 학습에 사용한 자료와 검증에 사용한 자료의 수를 다르게 적용하였다. 기본적으로 4계절 1주기가 반영되는 처음 365일간의 자료를 학습에 사용하고 나머지를 검증에 사용하였으며 자료의 양이 많거나 학습결과가 좋지 않는 경우에는 학습자료의 수를 늘려 모델의 성능을 향상시키고자 하였다. Table 2는 각 관측정별로 모델에 사용된 자료의 개요이다. 초기 학습결과에 따라 모델을 구성하는 여러 파라미터를 변경하여 모델을 최적화하게 되는데 이 파라미터 들을 특별히 하이퍼 파라미터(Hyper parameter)라고 부르며 이들의 조합에 따라 모델의 성능이 좌우된다. 하이퍼 파라미터의 최적값을 찾기위한 조정 방법은 과학적인 접근보다 사용자의 경험에 의존하는 기술적 요소가 더 많이 적용된다(Brownlee, 2018). 이는 하이퍼 파라미터의 수가 많고 그 적용범위가 매우 넓고 복잡함에 기인한 것이며 최근 유전자알고리즘(Genetic algorithm), 담금질기법(Simulated annealing)등의 최적화 기법과 조합하여 이를 해결하려는 시도가 이루어지고 있다. 본 연구에서 사용한 하이퍼 파라미터들 대부분은 모든 모델에서 같은 값들을 사용했으며 학습반복횟수와 배치사이즈 및 자료의 크기만을 조정하여 최적모델 값을 결정하였다(Table 3).
Table 2. Number of data for the training and testing
Table 3. Applied hyper parameters
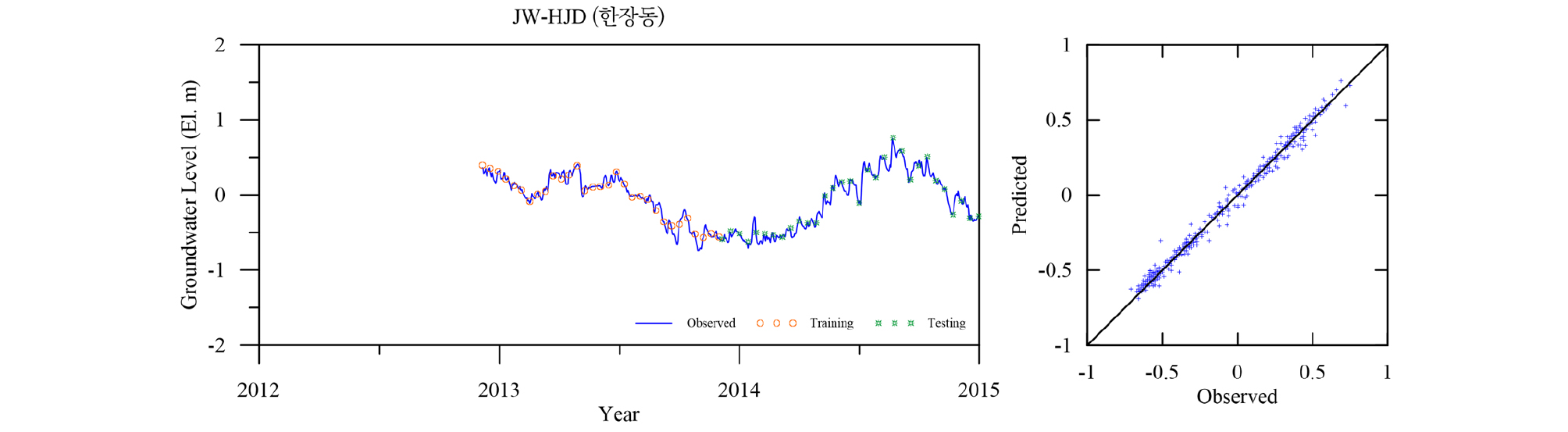
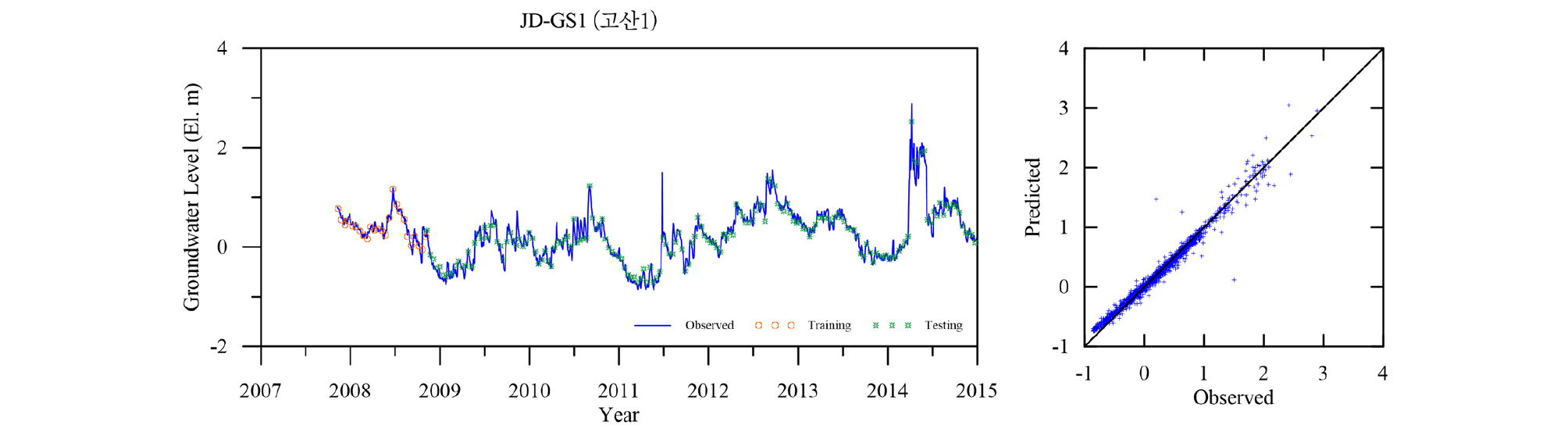
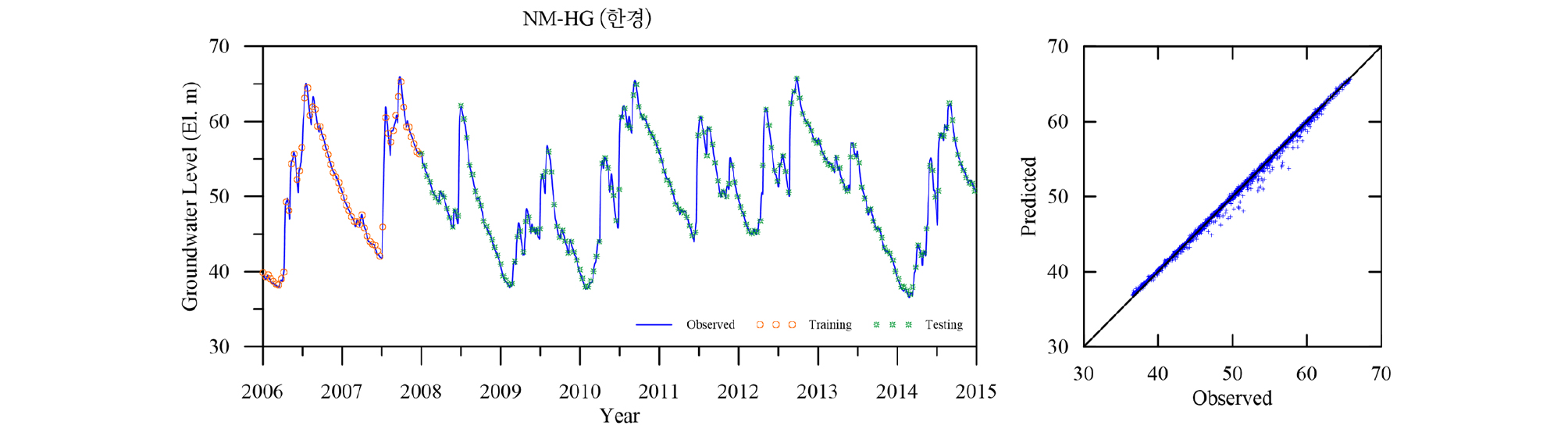
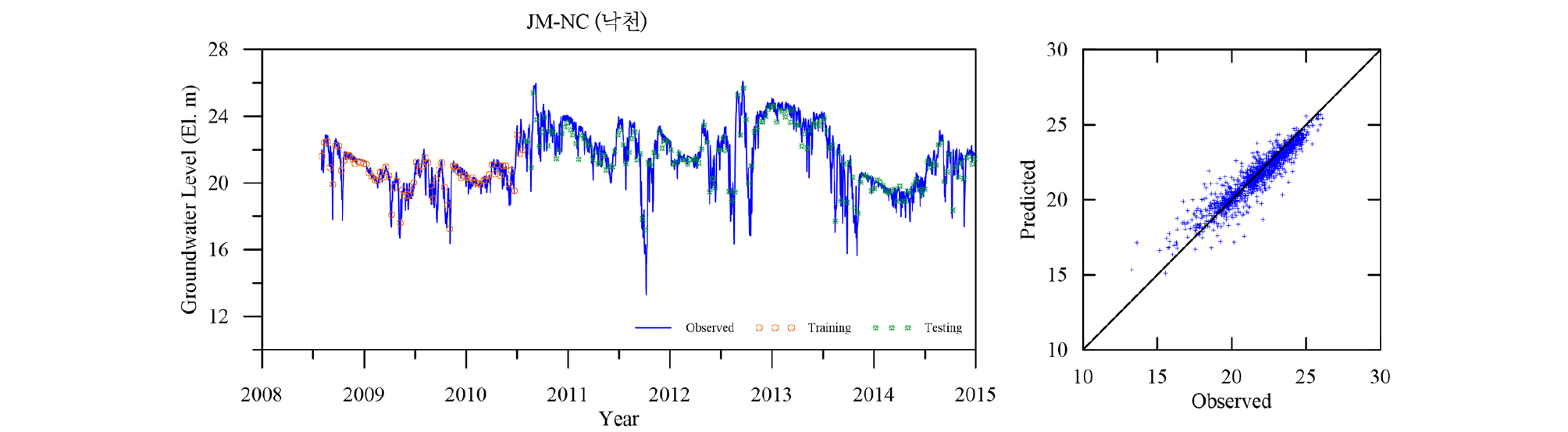
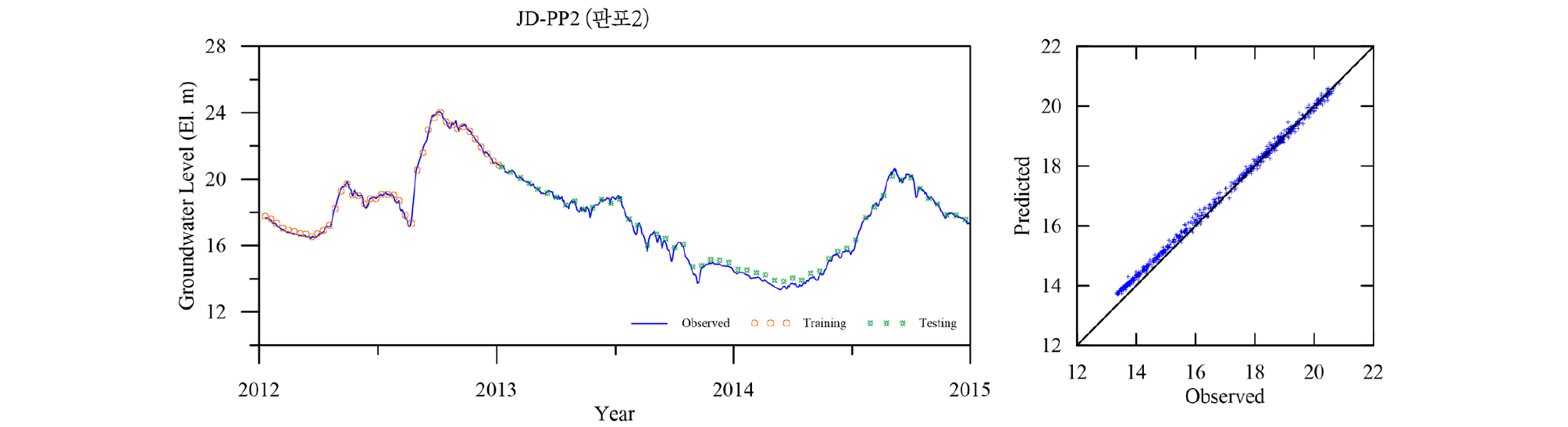
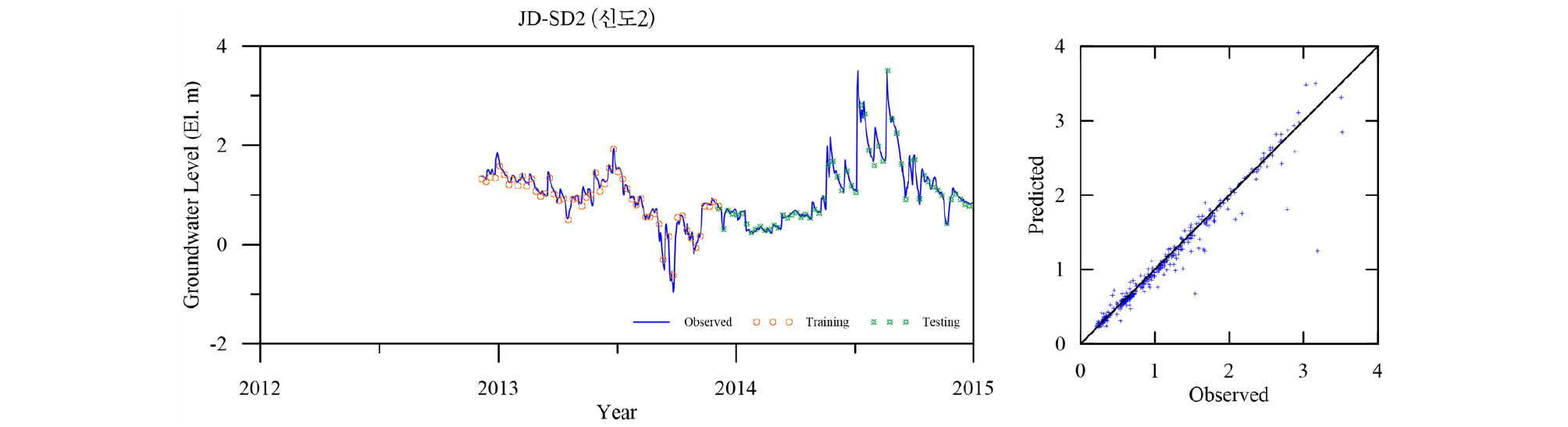
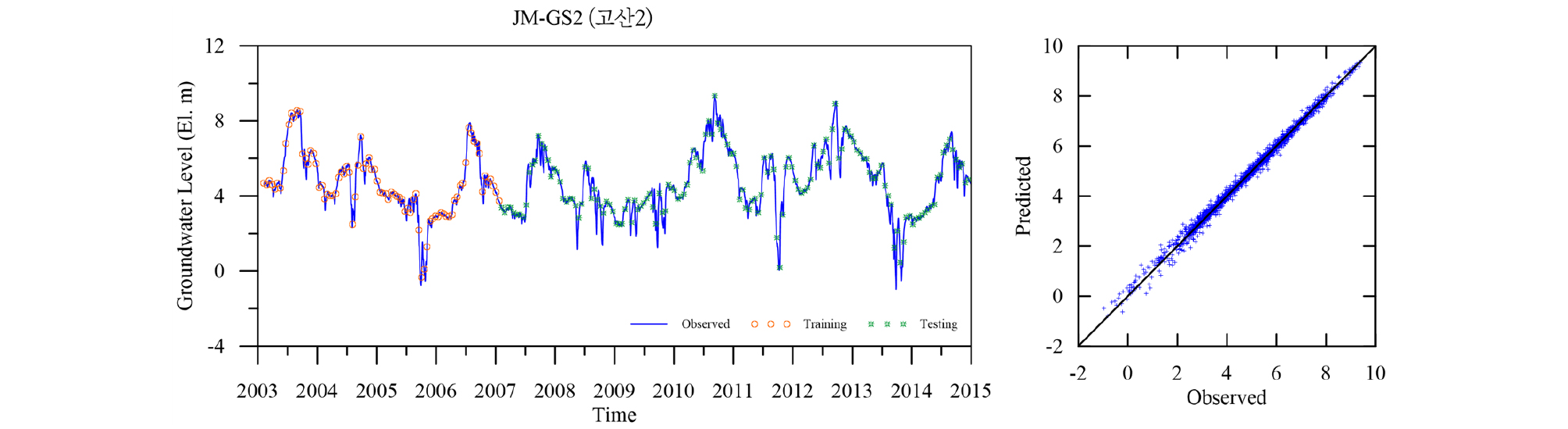
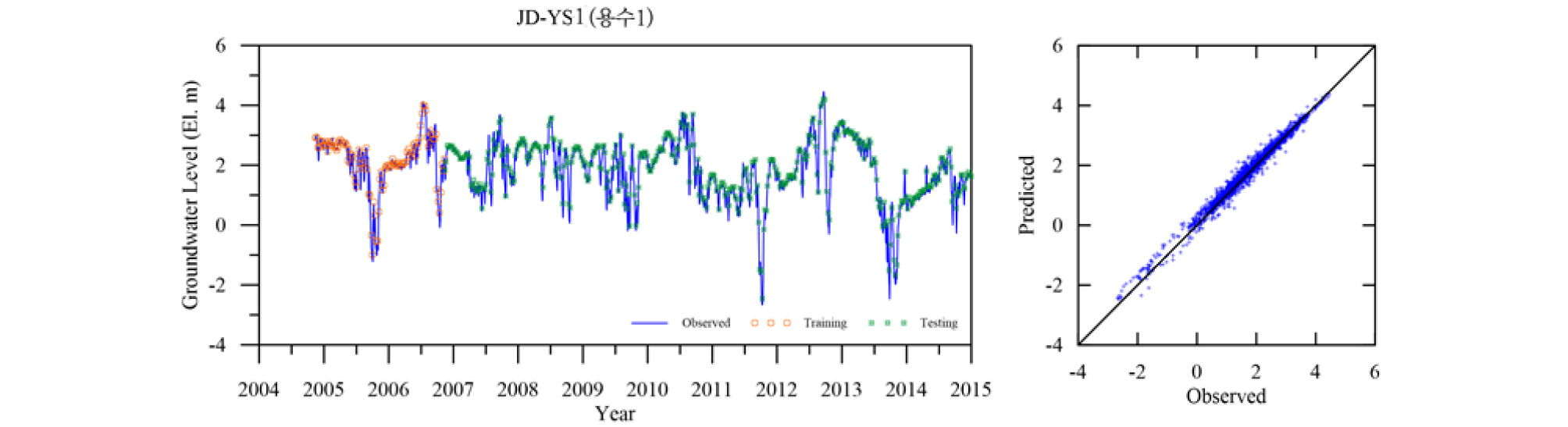
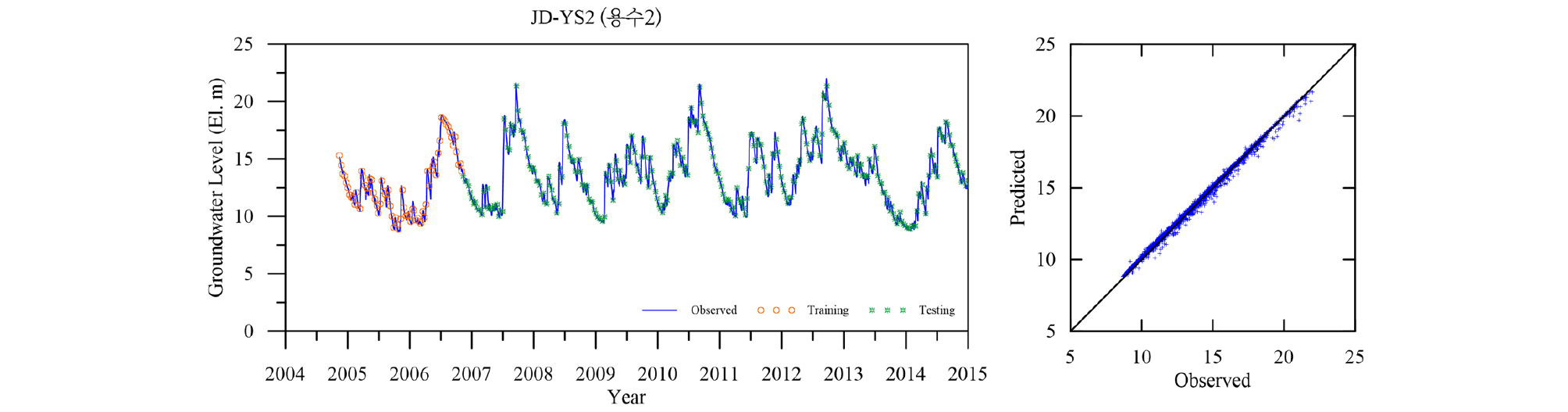
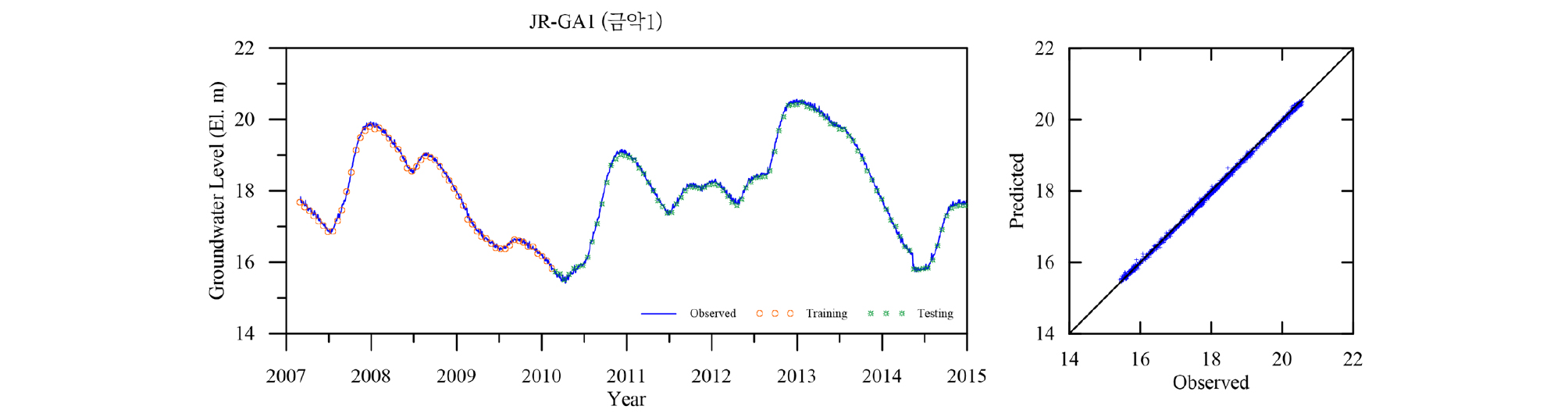
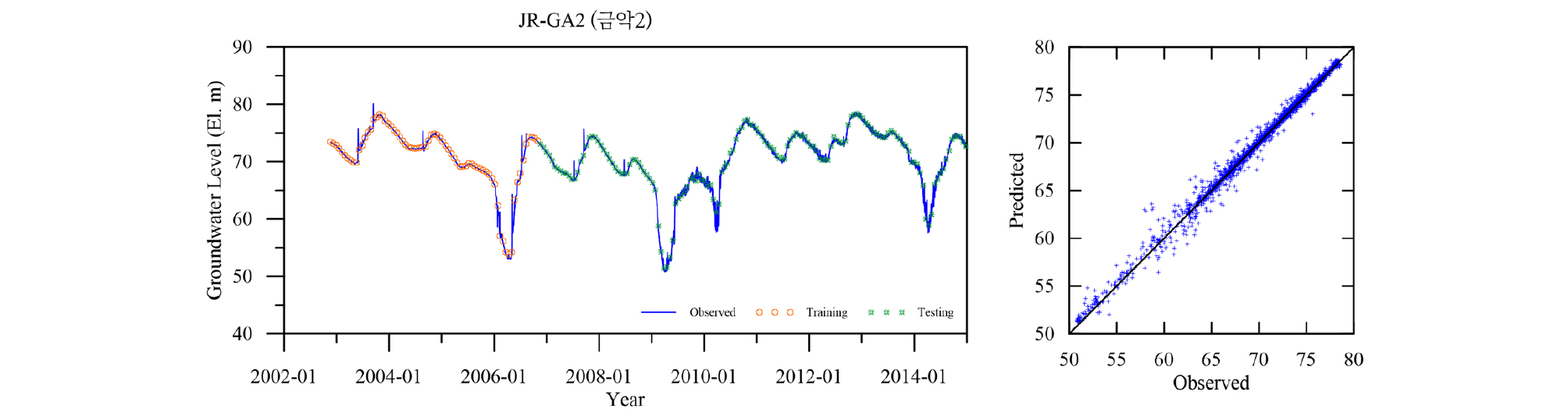
Table 4에 각 관측소의 학습 및 검증 결과를 요약하였다. 모든 관측소의 모델 검증결과인 결정계수 R2가 평균 0.98로 매우 좋은 결과를 나타낸다. 이는 LSTM 모델이 시퀀스형 자료의 학습 및 예측에 뛰어난 성능을 보이는 RNN 중에서도 자료의 순서가 중시되는 시계열 자료의 분석에 특히 적합한 모델임에 기인한 것으로(Zhang et al., 2018) 입력자료의 품질이 확보되고 적절한 수준의 최적화가 이루어지면 일정 수준의 이상의 예측능력을 보이는 것으로 판단된다. 대부분의 관측소 예측결과가 결정계수 0.95 이상을 보이는데 반해 낙천 관측소의 예측결과는 0.89로 다소 낮은 것으로 나타났는데 이는 지하수위에 영향을 주는 요소가 선행지하수위와 강수 외에 다른 요소(양수 등)가 존재하는 것으로 추정되며, 이를 모델 구성에 추가하면 모델의 성능을 향상 시킬 수 있을 것으로 판단된다. Figs. 13~23은 각 관측소별로 적용된 LSTM 모델의 실측 및 예측 지하수위에 대한 결과를 나타내고 있다.
Table 4. Results of test for stations
5. 결 론
본 연구는 제주도 한경지역의 지하수위 관측자료에 LSTM 모델을 이용하여 지하수위를 예측하는 기법의 개발에 관한 연구로 그 결과를 요약하면 다음과 같다.
1) 지하수위 관측자료는 결측치에 대한 전처리가 반드시 필요하며 보간 등의 결측처리 방법에 의해 적절히 처리된 자료의 사용은 높은 품질의 결과를 얻을 수 있다.
2) LSTM 모델을 적용한 한경지역 지하수위 예측모델을 개발하였으며 최적의 결과를 도출하기 위한 네트워크의 하이퍼 파라미터를 제시하였다. 대부분의 관측소에서 LSTM 모델이 잘 적용되었으며 예측정확도는 결정계수 R2가 평균 0.98로 매우 높게 나타났다.
3) 하이퍼 파라미터 추정과 관련하여 일부 관측소에 상대적으로 낮은 적합도가 나타나는 경우는 지하수위의 변화에 상관성이 높은 제3의 자료를 추가할 경우 개선될 수 있을 것으로 판단된다.
4) 최소 1년간의 관측자료를 기준 학습자료로 제시하였으며, LSTM 모델은 제한된 학습자료에도 충분히 높은 예측 성능을 보이는 것으로 나타나 향후 다른 자료에 확대 적용 시 활용성이 높을 것으로 예상된다.