1. 서 론
2. 이론적 배경
2.1 Latin Hypercube Sampling (LHS)
2.2 Sequential Uncertainty Fitting version 2 (SUFI-2)
3. 연구 대상 및 방법
3.1 내성천 유역 SWAT 모형의 구축
3.2 모의 실행 및 반복 횟수에 따른 불확실성 분석
4. 연구 결과
4.1 모의 수행 결과
4.2 최적 매개변수 값
4.3 모의 결과의 불확실성
4.4 모의 방법 추가 시의 검토 결과
5. 결 론
1. 서 론
SWAT (Soil and Water Assessment Tool)은 토양, 토지이용 및 토지관리 상태의 변화에 따른 유역의 유출량, 유사량 및 영양물질의 영향을 예측하기 위한 모형으로(Anorld et al., 1993), 수문 예측 및 물수지 분석에 널리 활용되고 있다. SWAT 모형을 활용한 분석에 있어 가장 큰 쟁점 중 하나는 불확실성(uncertainty)으로, 수문모의 과정의 다양한 매개변수를 고려하여 최적화해야함으로 모형 보정(calibration) 과정에 복잡성(complexity) 증가와 많은 시간이 소요된다. 이와 더불어 입력자료, 모형의 구조, 매개변수의 불확실성은 모형의 보정을 어렵게 만드는 요인으로 작용한다(Petersen et al., 2003; Arnold et al., 2010).
모형의 신뢰도와 예측의 정확성을 높이고 모의 결과의 불확실성을 정량화하기 위한 검·보정 알고리즘 및 불확실성 분석 방안은 그간 많은 연구가 수행되어 왔다. 일반적으로 사용되는 매개변수 보정의 기법은 MCMC (Markov Chain Monte Carlo, Vrugt et al., 2008), GLUE (Generalized Likelihood Uncertainty Estimation, Beven and Binley, 1992), ParaSol (Parameter Solution, Van Griensven and Meixner, 2007) 및 SUFI-2 (Sequential Uncertainty Fitting, Abbaspour et al., 2004) 등이 있으며, 이들은 SWAT-CUP 프로그램을 활용하여 SWAT 모형과 간편하게 연계하여 적용할 수 있다.
그 중 SUFI-2는 목적함수를 이용하여 매개변수를 최적화하는 전역 탐색 알고리즘(global search algorithm)을 활용한다. 매개변수 검·보정은 각각의 매개변수가 아닌 하나의 조합으로 연결되어 수행된다. 매개변수는 모의 수행이 반복될수록 사용자가 지정한 초기 범위에서 점차 좁은 범위로 불확실성을 좁혀가며 일정한 값으로 수렴된다. SUFI-2는 수행 과정이 복잡하지만 SWAT-CUP의 다른 알고리즘보다 계산 시간이 적게 소요된다는 장점이 있다(Sellami et al., 2013).
SWAT-CUP의 SUFI-2를 이용한 자동보정 과정에서 불확실성 요인으로 작용할 수 있는 사항은 (1) 매개변수의 선택, (2) 보정 기법, (3) 목적함수, (4) 매개변수의 초기 범위, (5) 모의(simulation)의 실행(run) 및 반복(iteration) 횟수, (6) 위치, 개수 등 보정 자료의 선택으로 구분할 수 있다(Abbaspour et al., 2018). 이들은 SWAT 모형 구조 및 입력 자료에 내재된 불확실성이며, 그 전이 과정을 정확하게 파악하여 나타내는 것이 거의 불가능하다. 따라서 본 연구는 SWAT 매개변수 보정 과정에 있어 사용자의 설정에 따라 발생할 수 있는 불확실성에 대해 평가하고자 수행되었다.
선행연구에서는 목적함수의 선택에 따른 불확실성에 대한 분석을 수행하였으며, 선택된 목적함수에 따라 산정된 유량의 모의 값과 관측 값 사이의 수문학적 유사성을 평가하고 최종적으로 극치 값 모의에 적합한 최적의 목적함수를 SSQR 및 MNS로 제시한 바 있다(Yu et al., 2020). 한편, 본 연구에서는 MNS 목적함수를 이용하여 SWAT 모형의 보정을 수행하였으며, 모의 실행 및 반복 횟수에 따른 불확실성을 파악하고 SWAT-CUP 이용한 효율적인 보정 방안 제시를 주요 목적으로 하였다.
2. 이론적 배경
2.1 Latin Hypercube Sampling (LHS)
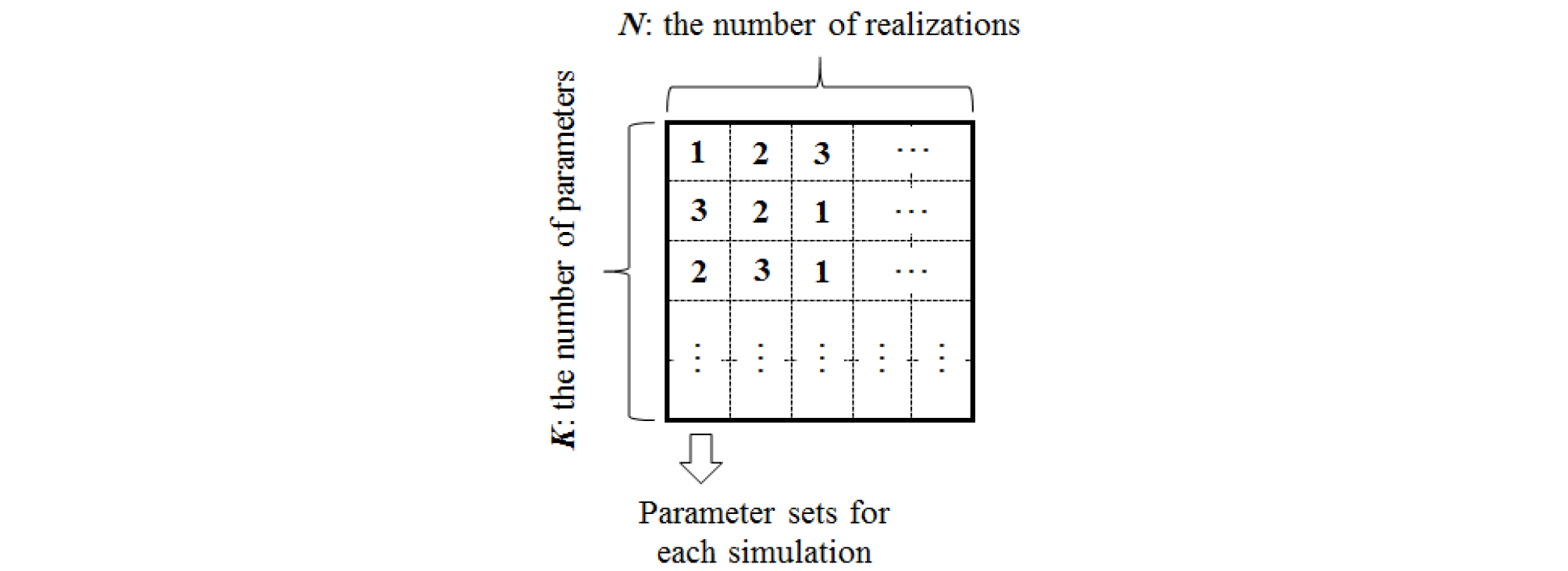
LHS는 다차원 분포에서 추출하는 표본의 수를 효과적으로 줄이기 위해 사용되는 통계적 기법으로, 계층적 방식의 Monte Carlo 표본추출 방식이다(McKay et al., 1979). 확률밀도함수 f (x)를 갖는 K개 변수 x = [x1, x2, …, xK]T에서 표본추출 수행 시, 각 변수의 범위는 겹치지 않는 N개의 동일한 간격으로 나눠진다. N개의 x1은 무작위 순서로 N개의 x2와 쌍을 이루고, N개의 (x1, x2)는 또다시 x3와 조합되는 방식으로, K개의 변수가 NK개의 셀(cell)을 갖는 큐브(cube)를 형성하게 된다. 전체 큐브에서 설계행렬(design matrix)에 의해 사용자가 설정한 개수의 표본이 선택되며, 표본공간(sampling space) V는 Eq. (1)과 같이 결정된다.
| $$V_{ij}=F^{-1}\left(\frac{P_{ij}-R_{ij}}n\right)$$ | (1) |
여기서, N × K 행렬 P는 각 열 k는 1, …, N의 난수 순열을 포함하며, N × K 행렬 R은 균등분포(uniform distribution) U(0,1)으로부터 생성된 난수로 이루어져 있다. F-1은 정의된 누적분포함수의 역함수를 의미하며, SUFI-2에서는 매개변수의 타당한 범위에 따라 각 간격에 해당하는 값이 발생할 확률이 모두 동일한 균등분포를 적용한다.
2.2 Sequential Uncertainty Fitting version 2 (SUFI-2)
SWAT-CUP에서 제공하는 최적화 기법 중 하나인 SUFI-2는 Hypercube의 다변량 균일 분포에 의해 매개변수의 불확실성을 정량화하여 나타낼 수 있는 방법이다. SUFI-2를 이용한 매개변수 보정 과정은 다음과 같다(Abbaspour et al., 2007).
1) 선택된 매개변수 집합()의 보정을 위한 목적함수 g를 결정한다.
2) 각 매개변수에 대하여 물리적으로 타당한 범위를 결정한다().
3) LHS 방법을 통해 2에서 정의된 매개변수 모집단에서 표본추출을 수행하여, n개의 각 시행마다 서로 다른 값을 갖는 매개변수 조합을 결정한다(Fig. 1).
4) 각 시행(예, n=500)마다 관측 값에 가장 잘 부합하는 매개변수 조합을 결정하기 위해 목적함수를 계산한다. 또한 Eq. (2)에 나타낸 것과 같이 민감도 행렬 Jij와 공분산 행렬 C를 산정하여, 각 시행에 따른 목적함수의 변화량을 측정한다.
| $$J_{ij}=\frac{\bigtriangleup g_i}{\bigtriangleup b_j}\;\;i=1,\;\cdots,\;C_2^n,\;\;j=1,\;\cdots,\;m$$ | (2a) |
| $$C=\sigma_g^2\left(J^TJ\right)^{-1}$$ | (2b) |
여기서, 는 초기 매개변수에 대하여 각 시행마다 산정되는 목적함수의 변화량, 는 j번째 매개변수의 변화량, 은 민감도 행렬에서 행의 개수, m은 총 매개변수의 개수, 는 목적함수의 분산을 나타낸다.
5) Eq. (3)에 나타낸 것과 같이 공분산 행렬 C를 이용하여 각 매개변수에 대한 95% 신뢰구간을 산정한다. 여기서 는 j번째 매개변수의 최적 값, 는 자유도(n-m)이다.
| $$b_{j,lower}=b_j^\ast-t_{\nu,0.025}\;\sqrt{C_{jj}}$$ | (3a) |
| $$b_{j,upper}=b_j^\ast+t_{\nu,0.025}\;\sqrt{C_{jj}}$$ | (3b) |
6) 최종적으로 매개변수의 범위는 Eq. (4)와 같이 갱신되며, 새로운 매개변수 bj에 의해 산정된 목적함수에 따라 다음 시행을 위한 최적의 매개변수 값이 결정된다.
| $$b'_{j,min}=b_{j,lower}-max\left[\frac{(b_{j,lower}-b_{j,min})}2,\frac{(b_{j,max}-b_{j,upper})}2\right]$$ | (4a) |
| $$b'_{j,max}=b_{j,upper}+max\left[\frac{(b_{j,lower}-b_{j,min})}2,\frac{(b_{j,max}-b_{j,upper})}2\right]$$ | (4b) |
3. 연구 대상 및 방법
3.1 내성천 유역 SWAT 모형의 구축
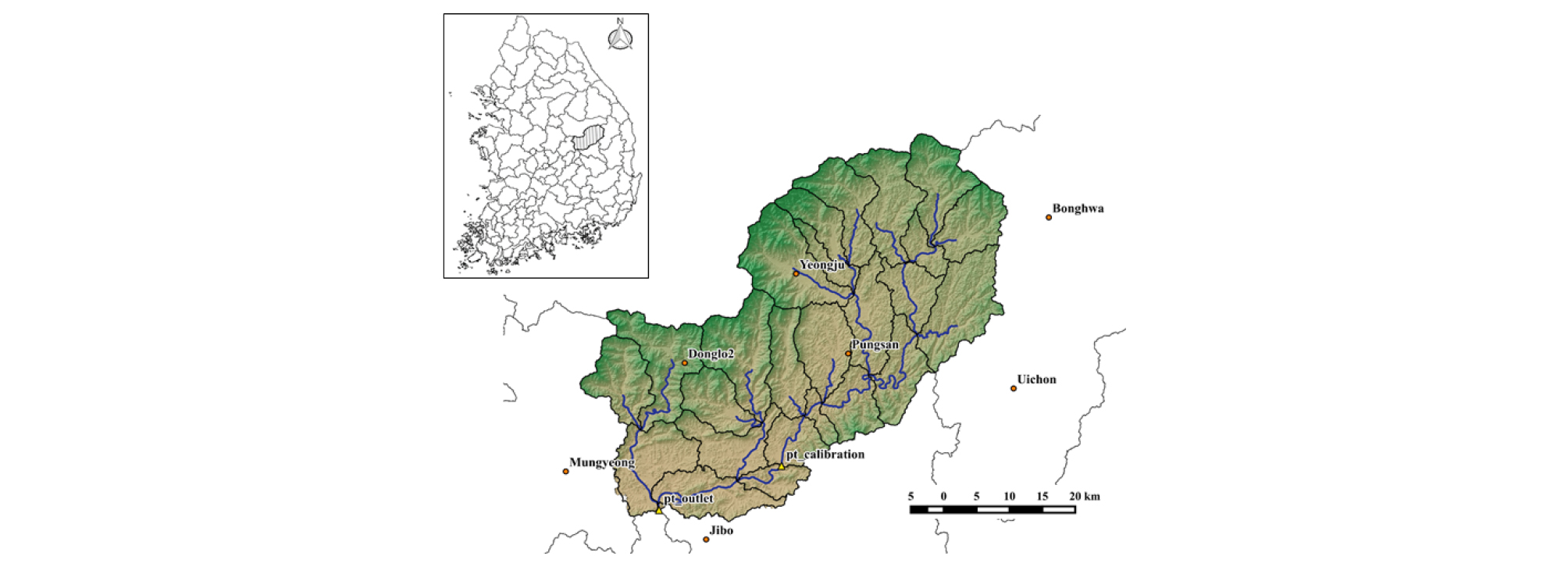
본 연구는 선행연구(Yu et al., 2020)와 동일하게 내성천 유역을 대상으로 구축된 SWAT 모형을 이용하여 수행되었다. 내성천 유역은 총 26개 소유역으로 분할되었으며, 최종 유출구, 관측소 위치 및 검·보정 지점은 Fig. 2에 나타낸 것과 같다. 모의기간은 초기 2년의 warm-up 기간을 포함하여 30년(1989.01.01.~2018.12.31.)이며, 보정기간은 실측 유량자료가 있는 9개년(2007.01.01.~ 2015.12.31.)을 대상으로 시행되었다. 보정의 대상이 되는 매개변수 또한 선행연구에서 선별한 주요 유출 모의과정에 관련된 23개 변수가 동일하게 적용되었다.
3.2 모의 실행 및 반복 횟수에 따른 불확실성 분석
3.2.1 목적 함수
선행연구에서 목적함수의 선정 또한 보정 결과에 영향을 미치는 것을 확인하였다(Yu et al., 2020). 일반적으로 결정계수(coefficient of determination, R2)와 모형효율(Nash-Sutcliffe Efficiency, NS)가 목적함수로 적용된다. 그러나 NS는 분산의 제곱(p=2)을 사용하여 극치 값이 지나치게 과소 또는 과대 산정되는 경향이 존재하여, 본 연구에서는 p값을 1로 조정해 극치 값에 대한 평가 효율을 높이기 위해 도입된 Eq. (5)의 MNS (Modified NS)를 목적함수로 적용하였다. 한편, 보정이 완료된 매개변수를 적용한 모형의 성능평가를 위한 지표로는 Eqs. (6)~(8)에 나타낸 R2, NS, 그리고 PBIAS (Percent Bias)를 이용하였으며, 이들은 모의 결과의 서로 다른 수문 특성에 따라 모의 성능을 평가한다.
| $$MNS=1-\frac{{\displaystyle\sum_i}\left|Q_m-Q_s\right|_i^p}{{\displaystyle\sum_i}\left|Q_{m,i}-{\overline Q}_m\right|_i^p}$$ | (5) |
| $$NS=1-\frac{{\displaystyle\sum_i}{(Q_m-Q_s)}_i^2}{{\displaystyle\sum_i}{(Q_{m,i}-{\overline Q}_m)}^2}$$ | (7) |
| $$PBIAS=100\times\frac{{\displaystyle\sum_i}{(Q_m-Q_s)}_i}{\displaystyle\sum_iQ_{m,i}}$$ | (8) |
여기서, 및 는 각각 관측값 및 모의값을 나타내며, 과 는 관측값과 모의값의 평균을 의미한다. 또한 MNS 산정 시 p=1으로 적용되었다.
3.2.2 모의 실행 및 반복 횟수 설정
SWAT-CUP을 이용하여 보정된 최종 매개변수의 값은 사용자가 입력하는 매개변수 및 그 값의 범위와 모의 실행 및 반복 횟수 등에 따라 크게 좌우된다. 만약 모의 횟수를 500번으로 설정하였다고 가정하면 사용자가 정의한 각각의 매개변수의 범위는 500개의 동일 구간으로 나눠진다. 예를 들어, 매개변수 xk의 범위를 0~1으로 지정하였다면, 0.002(1/500)의 등간격으로 총 500개의 값이 생성된다. 따라서 23개 매개변수의 가능한 조합은 50023개이며, 그 중 500개의 조합이 LHS 알고리즘에 따라 무작위로 선택되어 가장 관측 값에 잘 부합하는 모의결과를 산출하는 조합이 최적 매개변수로 선정된다.
기존 연구에서 주로 500-1500번의 모의 수행을 권장하고 있지만(Schuol and Abbaspour, 2006; Yang et al., 2008; Andersson et al., 2009), 적정 모의 횟수에 관한 기준은 제시된 바 없다. 본 연구에서는 최소화된 계산 소요시간으로 모의 성능을 극대화할 수 있는 매개변수 보정 방안을 결정하기 위해 250, 500 및 1,000번의 모의 실행 횟수에 대하여 각각 동일한 방법으로 15회 반복 수행하였다. 즉, 어떠한 실행 횟수에서 더 효율적으로 목적함수의 최적 값을 산정할 수 있으며, 이와 더불어 어떤 최종의 매개변수 값이 산정되는지를 결과를 비교를 통해 검토하였다.
3.2.3 불확실성 분석
SUFI-2에서는 모의 결과의 불확실성을 95 PPU (95% prediction uncertainty band)를 통해 정량화하여 나타낸다. Eq. (2)를 이용하여 산정된 95% 예측 구간을 포함하는 매개변수를 이용하여 95 PPU가 계산되며, 이를 바탕으로 p-factor와 r-factor가 정의된다. p-factor는 95 PPU에 관측 값이 포함되는 비율을 나타내는 지표로, p-factor가 1일 때 관측 값이 95% 예측구간에 100% 포함됨을 의미한다. 반면 r-factor는 95 PPU의 평균 폭(band width)을 나타내며, 값이 0에 가까울수록 보정 결과가 관측 값과 잘 부합하는 것이다(Eq. (9)).
| $$r-factor=\frac{{\displaystyle\frac1n}{\displaystyle\sum_{t_i}^n}\left(y_{t_i,\;97.5\%}^M-y_{t_i,\;2.5\%}^M\right)}{\sigma_{obs}}$$ | (9) |
여기서, 와 는 각각 95 PPU의 상한 값과 하한 값을 의미하며, 는 관측 값의 표준편차를 나타낸다.
4. 연구 결과
4.1 모의 수행 결과
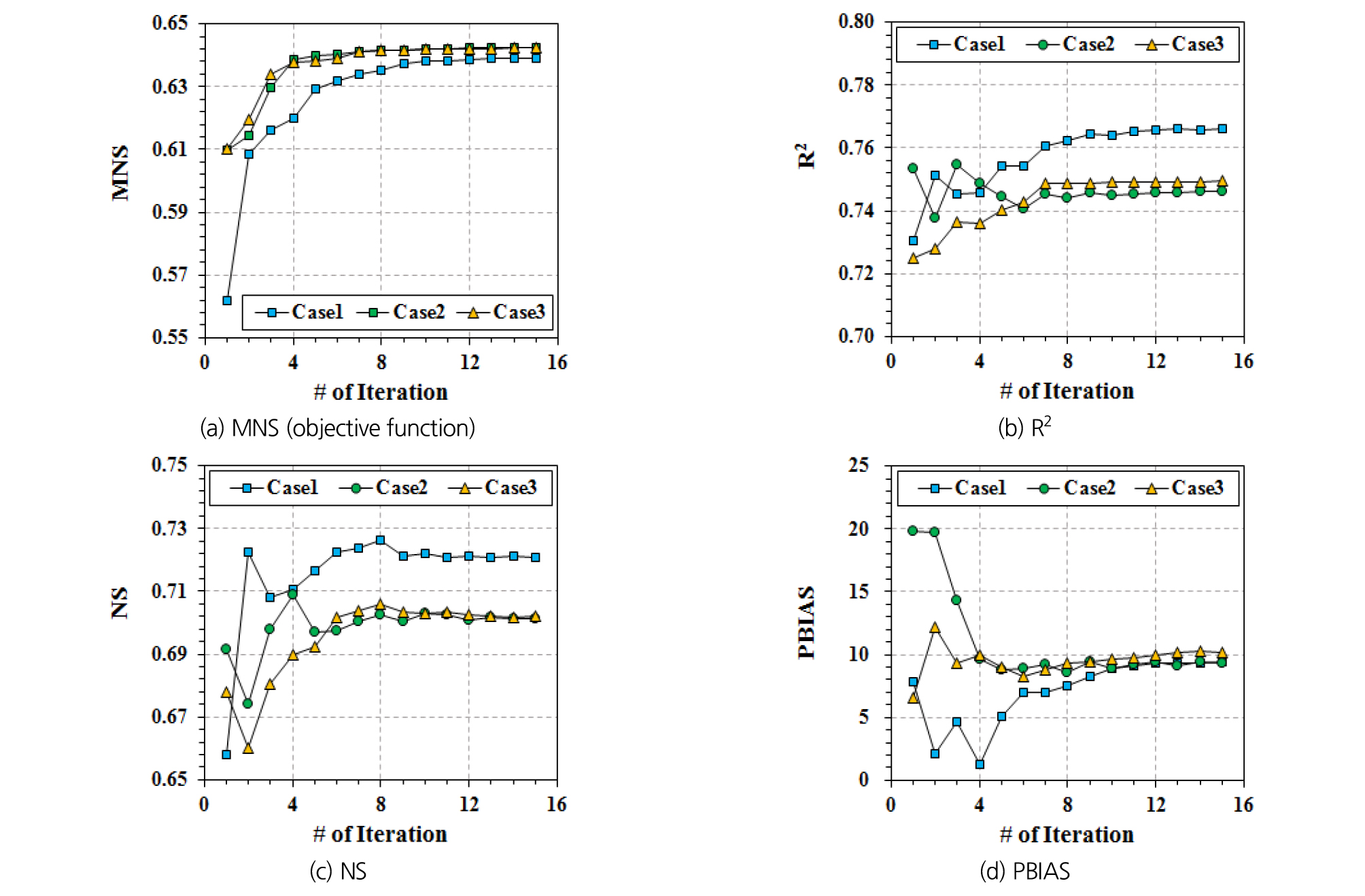
Fig. 3은 앞서 설정한 각 모의의 실행 및 반복에 따른 모형의 성능 평가 지표를 도시한 것이다. 여기서 Case1~3은 모의 실행 횟수(250, 500 및 1,000번)를 기준으로 구분되었다. MNS, R2 및 NS는 1에 가까울수록. PBIAS는 절댓값이 0에 가까울수록 관측 값과 모의 값이 잘 일치함을 나타낸다. MNS를 기준으로 살펴보면(Fig. 3(a)), Case2와 Case3는 초기 1~4회 반복 모의 이후부터는 큰 차이를 보이지 않았으며, 특히 8번째 반복 이후부터는 Case1~3의 모의 실행 횟수에 상관없이 목적함수 값이 유사하게 산정(MNS 0.64)되는 것으로 나타났다.
반면, R2, NS 및 PBIAS의 산정 결과는 MNS와 다른 양상을 보였는데, R2, NS의 경우 초기의 모의에서 Case2의 모의 성능이 가장 좋은 것으로 평가되지만 그 이후의 반복 수행에서는 Case1의 모의 결과가 더 우수한 것으로 나타났다. 또한, PBIAS는 첫 번째 모의 수행에서 Case2가 가장 좋은 결과를 나타내지만 이후 Case1의 편차가 가장 적으며 4번째 반복에서 최적 값을 나타내었다. 한편, Case2와 Case3는 8번째 반복 수행 이후부터는 모든 지표에서 큰 차이를 나타내지 않았다. 이와 같은 결과는 본 연구에서 선정한 목적함수 MNS의 모의 특성에 기인한 것으로, MNS는 극치 값에 대하여 다른 평가지표 함수보다 더 민감하게 반응하기 때문이다(Yu et al., 2020).
이러한 분석 결과를 통해 모의 실행 횟수가 적어더라도 여러 번 반복하여 수행하면 같은 수준의 모의 결과를 얻을 수 있다는 것을 확인하였다. 그러나 매개변수 최적화에 소요되는 시간의 관점에서 계산 과정의 효율을 비교하면, 모의 실행 횟수가 클수록 적은 반복으로 검·보정을 수행할 수 있으므로 보다 효율적 방법으로 평가할 수 있다.
4.2 최적 매개변수 값
SUFI-2 알고리즘에서 매개변수의 범위는 물리적으로 타당한 범위 내에서 결정되며, 각기 설정한 실행 횟수의 모의가 반복되면서 점차 범위가 좁혀진다. 따라서 모의의 반복을 거듭할수록 매개변수는 하나의 값으로 수렴하게 된다. 그러나 SWAT-CUP을 이용한 자동보정 수행 시 각 매개변수 값의 허용 범위를 넘어서는 결과가 제시되기도 한다. 따라서 사용자는 반드시 매 시행마다 매개변수 범위를 확인할 필요가 있다. 본 연구에서는 보정 결과가 국부 최적 값(local optimum)으로 고착되는 것을 최대한 방지하기 위해, 물리적 상하한 범위를 벗어나는 값은 Table 1에 제시된 초기범위로 각각 재설정하여 매개변수 보정을 수행하였다.
Table 1. The best fitted parameter values estimated from the 8th iteration
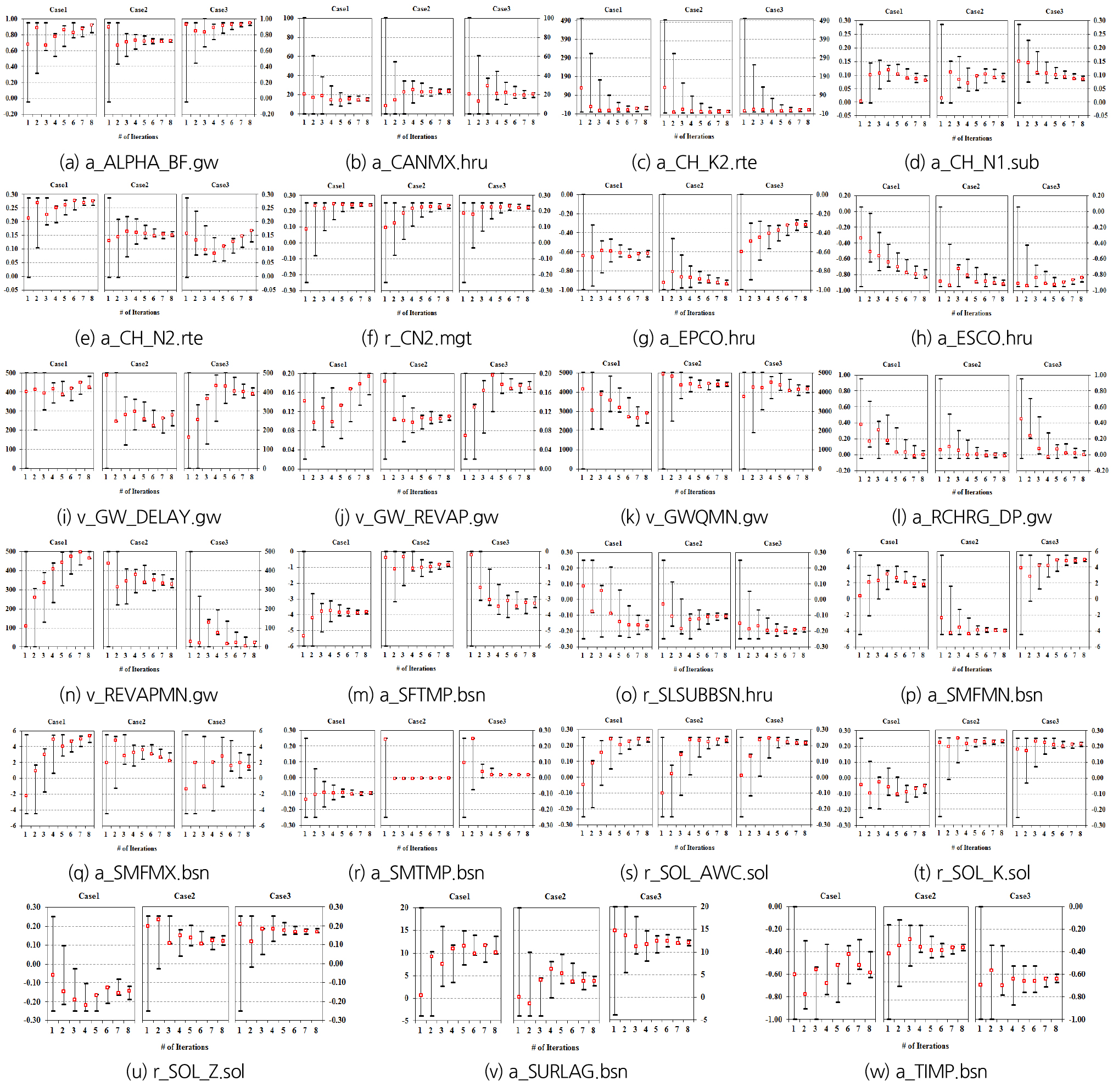
Fig. 4는 모의 실행 및 반복 횟수에 따라 매개변수 보정 결과가 달라지는 것을 보여준다. 그림에서 총 23개의 매개변수 중 단 6개(CH_K2, CANMX, CH_N1, CN2, RCHRG_DP, SOL_AWC)만 모의 실행 횟수에 상관없이 최종 결과 값이 유사한 수준으로 산정되었으며, 그 외의 경우 각기 다른 모의 실행 횟수인 Case1~3의 경우에서 각각 상이한 값으로 수렴되었다. 결정론적 모형(deterministic model)에서는 단일한 매개변수 조합이 하나의 모형을 구성한다. 그러나 그 반대, 즉 매개변수의 최적화 과정에서 동일한 모의 결과를 산출하는 수천 개의 매개변수 조합이 존재하는 경우는 동일한 자료를 이용하여 모형을 구축하더라도 보정 방법에 따라 최종 매개변수의 값이 달라질 수 있다. 따라서 상기 결과는 SWAT 모형의 비고유성(non-uniqueness)을 보여준다.
4.3 모의 결과의 불확실성
모의 결과에서 동일한 수준의 모의 성능을 갖는 것으로 평가되더라도 매개변수의 불확실성에 따라 모의 결과의 신뢰성이 크게 좌우되기 때문에, 최종 보정된 모형을 결정하기 전에 불확실성 검토 또한 고려해야 한다. SWAT의 모의결과에서 p-factor와 r-factor는 이러한 불확실성을 나타낼 수 있는 지표이다. 매개변수의 범위가 넓으면 관측 값이 95 PPU에 포함될 확률이 높으므로, p-factor가 1에 가까운 값을 갖게 된다. 일반적으로 유출량 모의에 대하여 p-factor가 0.70~0.75 사이의 값이면 적합하다고 판단한다. 반면 r-factor는 95 PPU의 평균 폭과 관련되어 있으므로, 0에 가까울수록 불확실성 구간이 좁다.
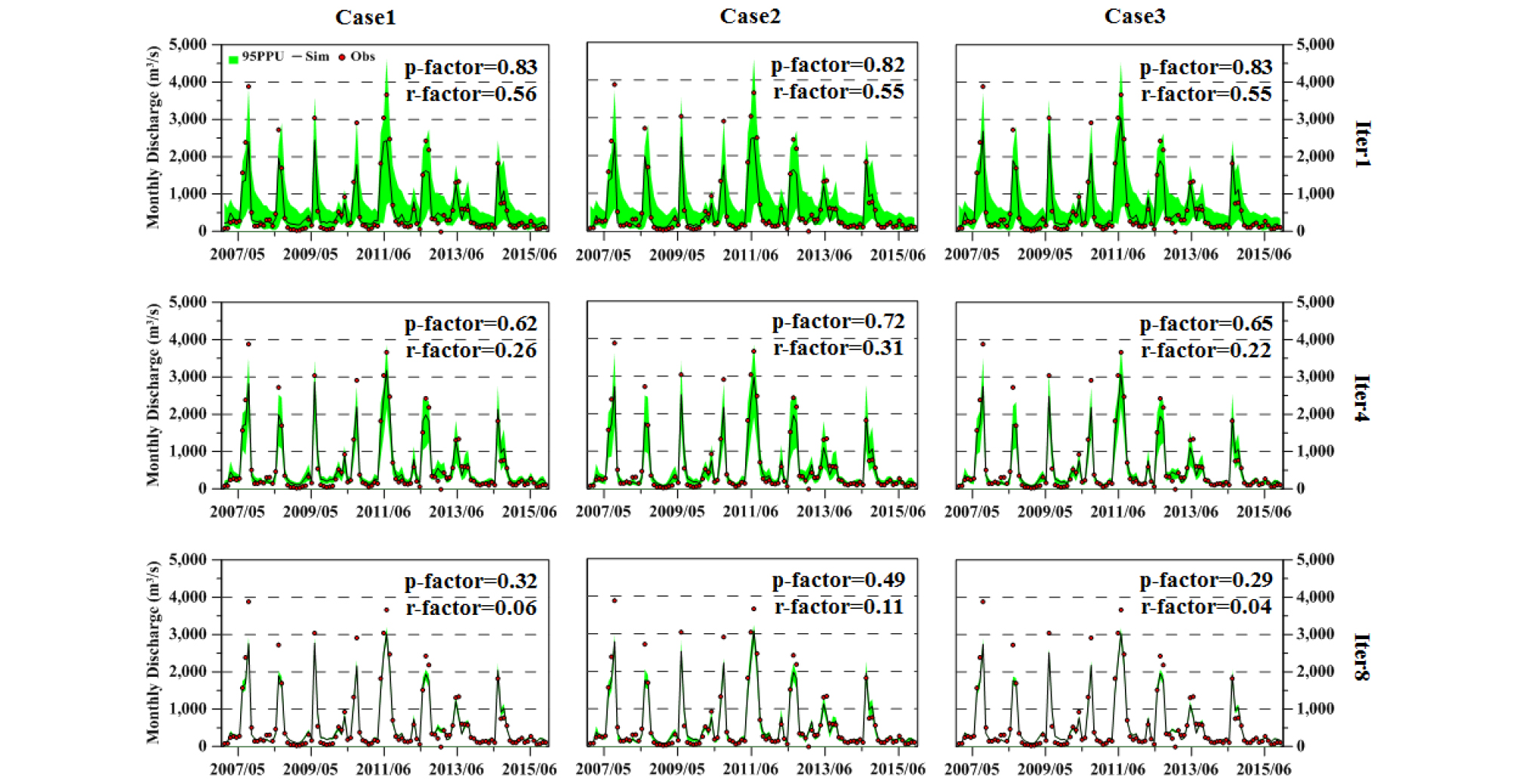
Fig. 5는 모의 실행 및 반복 횟수별로 각각 보정된 모형의 월 단위 유출량 모의 결과를 도시한 것으로, 왼쪽에서 오른쪽으로 갈수록 모의 실행 횟수가 증가하고 위에서 아래로 갈수록 그 반복 횟수가 증가한다. 한편, 앞서 Fig. 3(a)에서 살펴보았듯이 Case2 및 Case3은 4번째 반복에서, Case1은 8번째 시행에서 MNS 값이 0.64에 도달하여 최종적으로는 같은 수준의 모의 성능을 갖는 것으로 평가되었다. 그러나 Fig. 5의 p-factor와 r-factor를 이용한 불확실성 평가는 서로 다른 양상을 나타내었다.
Fig. 5에서 볼 수 있듯이 각각 설정한 실행 횟수의 모의를 많이 반복할수록 매개변수가 점차 하나의 값으로 수렴하기 때문에 95 PPU의 폭이 좁아지면서 r-factor가 감소한다. 그러나 모의 성능은 4번째 반복 이후 크게 달라지지 않으므로 그만큼 95 PPU에 포함되는 관측 값의 수가 감소하여 p-factor 또한 감소한다. 이러한 분석 결과는 모의 수행의 반복 횟수가 늘어날수록 매개변수가 점차 하나의 값으로 수렴하게 되므로 불확실성은 감소하지만, 모의 성능은 그에 비해 크게 나아지지 않는다는 것을 시사한다.
4.4 모의 방법 추가 시의 검토 결과
SWAT 매개변수는 모형의 불확실성을 나타내는 분포이다. 즉, 매개변수는 모형의 구조, 입력자료 및 검·보정 과정의 불확실성을 그대로 보여주는 일종의 지표로 간주할 수 있다(Abbaspour et al., 2018). 따라서 본 연구에서는 앞서 보정 방법에 따른 모형의 불확실성을 분석하기 위해 같은 조건 하에서 구축된 SWAT 모형에 대해 SUFI-2 알고리즘의 모의 실행 및 반복 횟수를 변화하여 매개변수의 최적 값을 비교하였다. 그 결과 1,000번 모의 실행의 경우(Case3)에서 초기 1~3번 반복의 목적함수 값이 상대적으로 좋은 결과를 나타낸 반면, 반복이 거듭될수록 모의 실행 횟수에 상관없이 목적함수 값이 Case1~3에서 유사하게 산정되는 것을 알 수 있었다.
이에 본 절에서는 Case1~3의 결과와 더불어 첫 번째 시행에서 1,000번 모의 수행 후, 500번 모의를 반복하는 것으로 설정한 Case4를 추가하여 분석을 수행하였다. Table 2는 그 Case2~4의 비교 검토결과를 나타낸 것으로, Case2와 Case3의 모의 결과가 유사하게 평가되는 것과 같이 Case4의 모의 결과 또한 큰 차이를 나타내지 않았다. 초기 반복(iteration 1~3)에서는 약간의 격차가 존재하지만 4번째 이후부터는 모의 성능을 나타내는 지표를 통해서는 Case2~4 모두 눈에 띄는 차이를 나타내지 않는다.
Table 2. The calibration results for the number of simulation run and iteration
한편, Table 1은 8번째 반복 모의 수행된 결과로 산정된 최종 매개변수 값을 나타낸다. 매개변수는 Fig. 4에서 볼 수 있듯이 설정된 실행 횟수의 모의를 반복할수록 변화의 폭이 좁아지며 하나의 값으로 점차 수렴한다. 그러나 몇몇 매개변수를 제외하고, 그 모의 실행 횟수에 따른 매개변수의 최종 수렴 값은 상이하게 나타났다. 하지만, Table 1에서 Case2와 Case3의 매개변수 값을 비교하면 총 23개 중 17개 변수가 유사하게 산정되는 것을 확인할 수 있었다.
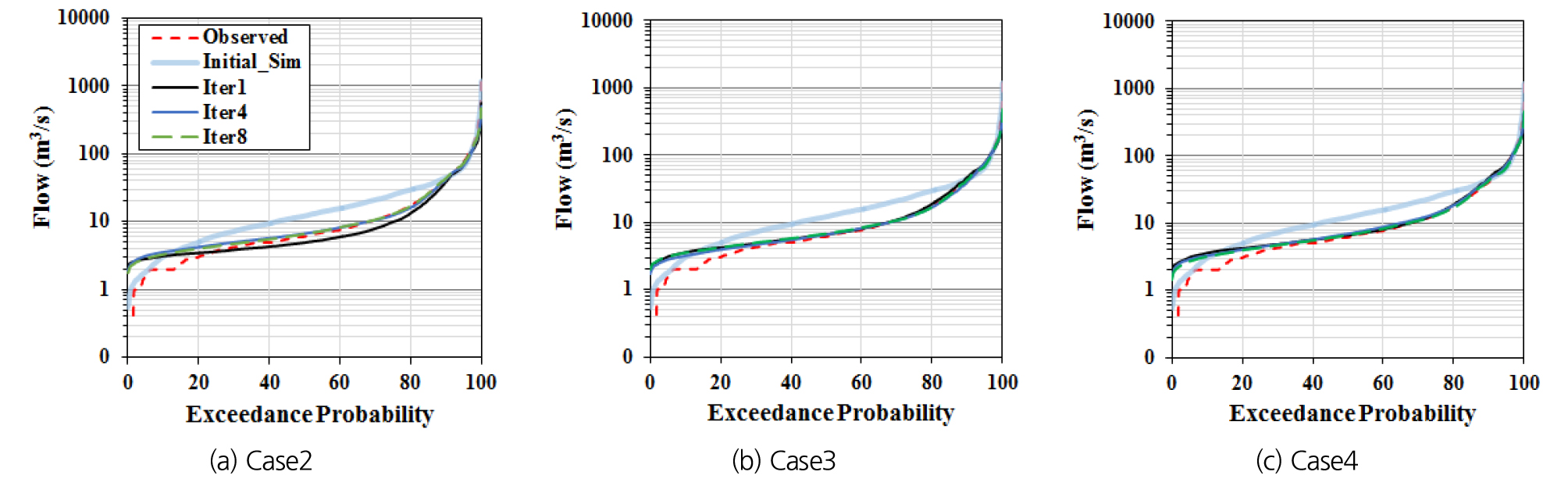
이와 더불어 Fig. 6에 나타낸 FDC (Flow Duration Curve)는 Table 1의 최적 매개변수 값을 적용하여 산정된 유출량 모의 결과를 보여준다. 여기서 Case2의 경우 첫 번째(Iter1)와 이후 반복(Iter4와 8)의 모의 결과가 다소 차이가 존재하는 것으로 나타났다. 그러나 Case3과 Case4의 모의 결과는 처음 Iter1 이후의 수문특성 차이가 미미한 수준이다. 이와 같은 결과들은 모의의 반복을 통하여 산정된 최종 매개변수 값은 초기 실행 횟수와 그에 따른 매개변수 산정 값에 큰 영향을 받는다는 점을 시사한다.
5. 결 론
본 연구에서는 SWAT-CUP 프로그램을 이용한 SWAT 모형 매개변수 검·보정 수행 시의 불확실성을 파악하고 효율적인 보정 방안을 제시하기 위해 SUFI-2 알고리즘 적용, 그 모의 실행 및 반복 횟수를 다르게 하여 분석을 진행하였으며, 그 결과 다음과 같은 결론을 도출하였다.
1) SUFI-2 알고리즘은 LHS 기법을 이용하여 표본 추출을 수행하고, 사용자가 선택한 매개변수에 대하여 최적의 조합을 찾아내는 효율적인 전역 탐색 방법이다. 그러나 가능한 모든 조합을 평가하는 것이 아니며, 탐색 공간(search space)이 넓고 모형의 구조가 복잡한 경우에는 최적 매개변수를 찾는 데에 오랜 시간이 소요된다는 단점이 있다. 또한 모의 실행 횟수에 따라 국부 최적 값으로 결과가 고착될 가능성이 있으며, 모의 실행 횟수를 크게 설정할수록 반드시 보정 효율이 높아지는 것은 아니다. 본 연구에서 모의 실행 횟수를 250, 500, 1,000번으로 설정하여(Case1~3) 모의를 반복 수행한 결과 4번째 반복 이후 Case2와 Case3의 목적함수가 같은 값에 도달했으며, 8번째 반복 이후부터는 Case1의 목적함수도 유사한 값에 도달하는 것을 확인하였다.
2) 모형의 매개변수는 모의의 반복을 거듭할수록 불확실성 구간이 좁혀지며 하나의 값으로 수렴하게 된다. 그러나 모의의 실행 횟수에 따라 그 최종 결과 값은 상이하게 나타난다. Case1~3과 더불어 Case4(초기 1,000번 모의 실행, 이후 500번 모의 실행을 반복)를 추가하여 8번 반복 이후의 최적 매개변수 값을 비교한 결과, Case3과 Case4의 매개변수 값이 유사하게 수렴되는 것을 확인하였다. 이와 같은 결과를 통해 모형의 최종 보정 결과는 매개변수 값 산정을 위한 초기 모의 실행 횟수에 매우 의존적인 것으로 판단된다.
3) 모의의 반복을 거듭할수록 목적함수에 의해 평가되는 모형의 성능이 향상되는 것으로 나타나기 때문에 큰 횟수의 모의 실행을 많이 반복해야 좋은 보정 결과를 얻을 수 있는 것으로 보일 수 있다. 그러나 초기 설정한 횟수의 모의 실행에 따라 매개변수의 값이 변화하는 것과 달리 이의 반복 실행을 통한 최종 SWAT 모의 결과는 크게 달라지지 않았다. 따라서 1,000번 이상의 큰 모의 실행 횟수를 설정하여 초기 1-2회 정도 반복 모의하는 것이 효율적이며, 초기 이후부터는 그 모의 실행 횟수를 감소시켜 500번 모의를 반복 수행하여도 충분하다.
이와 같은 분석 결과를 종합하면 Case4의 방법이 가장 효율적인 SWAT-CUP을 이용한 SWAT 모형 검·보정 방안으로 판단된다. 그러나 본 연구는 하나의 중권역을 대상으로 수행되었기 때문에 일반화하는 것은 타당하지 않을 수 있다. 또한 많은 선행 연구에서 효율적 매개변수 보정을 위해 다지점(multi-site) 및 다변수(multi-variable)를 고려한 사항을 권장하므로, 추가적인 방안을 고려해야할 필요가 있다.