Analysis of solute transport in rivers using a stochastic storage model

Byunguk Kim; Il Won Seo; Siyoon Kwon; Sung Hyun Jung; Se Hun Yun

doi:10.3741/JKWRA.2021.54.5.335

Preview

Research Article

Journal of Korea Water Resources Association. 31 May 2021. 335-345
https://doi.org/10.3741/JKWRA.2021.54.5.335

Analysis of solute transport in rivers using a stochastic storage model

확률론적 저장대모형을 이용한 하천에서의 물질혼합거동 해석

Byunguk Kim^a

Il Won Seo^b^*

Siyoon Kwon^c

Sung Hyun Jung^d

Se Hun Yun^e

김 병욱^a

서 일원^b^*

권 시윤^c

정 성현^d

윤 세훈^e

^aM.S. Course, Department of Civil and Environmental Engineering, Seoul National University, Seoul, Korea

^bProfessor, Department of Civil and Environmental Engineering, Seoul National University, Seoul, Korea

^cPh.D Course, Department of Civil and Environmental Engineering, Seoul National University, Seoul, Korea

^dPh.D Researcher, Department of Civil and Environmental Engineering, Seoul National University, Seoul, Korea

^ePh.D Course, Department of Civil and Environmental Engineering, Seoul National University, Seoul, Korea

^a서울대학교 건설환경공학부 석사과정

^b서울대학교 건설환경공학부 교수

^c서울대학교 건설환경공학부 박사과정

^d서울대학교 건설환경공학부 박사후 연구원

^e서울대학교 건설환경공학부 박사과정

^{*Corresponding Author}

ABSTRACT

The one-dimensional solute transport models have been developed for recent decades to predict behavior and fate of solutes in rivers. Transient storage model (TSM) is the most popular model because of its simple conceptualization to consider the complexity of natural rivers. However, the TSM is highly dependent on its parameters which cannot be directly measured. In addition, the TSM interprets the late-time behavior of concentration curves in the shape of an exponential function, which has been evaluated as not suitable for actual solute behavior in natural rivers. In this study, we suggested a stochastic approach to the solute transport analysis. We delineated the model development and model application to a natural river, and compared the results of the proposed model to those of the TSM. To validate the proposed model, a tracer test was carried out in the 4.85 km reach of Gam Creek, one of the first-order tributaries of Nakdong River, South Korea. As a result of comparing the power-law slope of the tail of breakthrough curves, the simulation results from the stochastic storage model yielded the average error rate of 0.24, which is more accurate than the 14.03 and 1.87 from advection-dispersion model and TSM, respectively. This study demonstrated the appropriateness of the power-law residence time distribution to the hyporheic zone of the Gam Creek.

Keywords

Solute transport analysis

Tracer test

Breakthrough curve tail

Stochastic storage model

Residence time distribution

Power-law distribution

하천에서의 용존물질의 혼합거동을 신속하게 예측하기 해석하기 위하여 1차원 추적모형이 개발되어 왔다. 그 중 저장대모형(Transient Storage Model, TSM)은 자연하천의 복잡하고 불규칙한 수리·지형적인 특성을 단순하게 반영할 수 있다는 장점때문에 가장 많이 사용되는 1차원 추적모형이다. 하지만 TSM의 정확도는 본류대 및 저장대의 면적, 물질교환계수 등 모형의 매개변수에 의존하며 이들은 직접적으로 측정될 수 없다는 단점이 있다. 또한 TSM은 농도곡선의 꼬리에 나타나는 저장대특성의 형태를 지수함수형태로 반영하는데 이는 실제 추적자실험을 통해 관측되는 꼬리는 형태와 다르다는 평가가 제기되고 있다. 이에 따라 본 연구에서는 1차원 확률론적 저장대모형에 대한 수치모형을 개발하여 자연하천에 적용하고 그 결과를 TSM의 모의결과와 비교하였다. 상기의 모형을 검증하기 위하여 낙동강의 1차 지류 중 하나인 감천의 4.85 km의 구간에서 추적자 실험을 실시하였다. 본 추적자 실험을 통해 측정한 농도곡선과 본 연구에서 제시된 확률론적 저장대모형의 모의 곡선의 꼬리부 멱함수 기울기를 비교해본 결과, 오차율은 평균 0.24으로 나타났는데, 이는 1차원 이송-분산 모형과 TSM로부터의 오차율인 14.03과 1.87에 비해 보다 정확한 값이다. 본 연구 결과, 감천에서의 저장대 특성을 나타내는 하상의 체류시간분포는 지수함수분포보다는 멱함수 분포에 가까운 것으로 밝혀졌다.

키워드

오염물질 혼합 해석

추적자 실험

농도곡선꼬리

확률론적 저장대모형

하상 체류시간

멱함수 분포

MAIN

1. 서 론
2. 연구 방법
2.1 지배방정식 설계
2.2 저장대에서의 체류시간분포
2.3 저장대에서의 체류확률분포
2.4 확률론적 저장대모형 수치모델링
3. 추적자 실험
4. 모의 결과 및 분석
4.1 모형 매개변수 산정 및 적용
4.2 모의결과 분석
4.3 모형 매개변수 분석
5. 결 론

1. 서 론

최근 산업 발전이 급속하게 진행됨에 따라 화학원료의 사용량도 급격히 증가하고 있으며, 화학원료의 취급, 유통 과정에서 화재, 폭발, 운반사고가 발생하여, 각종 유해화학물질이 하천으로 유입되는 사고가 빈번하게 발생하고 있다. 따라서, 이러한 사고가 발생되었을 때, 신속한 대응을 위한 수질 사고 대응 시스템 구축이 요구되고 있고, 이를 위해서 하천에 유입된 화학물질의 이동 및 혼합 거동을 신속하고 정확하게 예측하기 위한 추적모형의 필요성이 대두되고 있다(Fischer et al., 1979; Seo et al., 2016; Kim et al., 2019; Noh et al., 2021).

지류 및 지천 등 중·소규모 하천에 유입된 화학물질의 이동 및 혼합거동을 해석하기 위해서, 국내에서는 국립환경과학원이 채택한 1차원 이송-분산 모형(Advection-Dispersion Equation, ADE)이 사용되고 있는데, 이 모형은 하천에서 오염물질이 평균유속에 의하여 이송되고 난류 및 전단류에 의하여 분산되는 혼합거동을 해석할 수 있는 기본적인 모형이다(Fischer et al., 1979). 하지만, 실제 하천에 유입된 물질의 거동을 살펴보면 여울 및 웅덩이, 식생, 수공 구조물, 하상재료 등의 저장대에 의해 오염물질의 일부가 저장 또는 지체되는 현상이 강하게 발생되며, 오염물질 일부의 이동이 지체됨에 따라 오염운의 형태가 긴 꼬리를 가지는 것으로 관측된다. 더불어, 오염물질의 일부의 이동이 지체되면, 시간에 대한 농도변화 곡선도 왜곡되어 긴 꼬리를 가진 형태가 되는데, 이와 같은 왜곡이 발생되면 기존의 1차원 이송-분산 모형으로는 정확한 예측이 불가능하다.

실제 하천의 혼합 거동 해석을 위해 지난 수십년동안 하천의 저장대의 영향을 고려한 모형이 활발하게 연구되고 있다(Hays et al., 1967; Valentine and Wood, 1977; Bencala and Walters, 1983; Seo and Maxwell, 1992; Kim and Seo, 2020; Kwon et al., 2021). 저장대모형(Transient Storage Model, TSM)은 기존의 ADE 모형에 하천내에 존재하는 저장대의 영향을 추가한 개념적인 모형으로서 가장 많이 사용되는 모형이다. 이 모형에서는 하천 단면을 흐름이 존재하는 본류대영역과 흐름이 정체되어 있는 저장대영역으로 구분하고 두 영역 사이의 선형적인 물질교환이 발생하는 것으로 모델화하여 저장대 효과를 고려하였다(Bencala and Walters, 1983). TSM에서는 복잡한 자연하천의 저장대특성을 저장대영역의 크기와 단일물질교환계수로 묘사하고 있으며 이에 따라 TSM의 정확도는 이 매개변수들에 크게 의존하고 있다(Bencala et al., 2011). 하지만 이러한 TSM의 매개변수는 직접적으로 측정하기 어렵기 때문에 불확도가 매우 큰 것으로 보고되고 있다(Choi et al., 2020). 또한 TSM에서 모의한 농도곡선(Breakthrough Curves, BTCs)의 꼬리부에서 추적자 실험에서의 취득한 농도곡선의 꼬리 분포와 차이를 보인다는 문제점이 제기되어 왔다(Haggerty et al., 2000; Worman et al., 2002; Meerschaert et al., 2008).

TSM의 단점을 해결하기 위하여 2000년대에 들어와서는 다양한 개념적인 모형이 제시되고 있다. Deng et al. (2004, 2006)은 기존의 ADE의 분산항을 F차 미분의 형태로 표현한 Fractional Advection-Dispersion Equation (FADE)를 제시하여 실제현상과 유사한 F값을 찾고 이를 수치적으로 모델링하였고, Boano et al. (2007b)은 Continuous Time Random Walk (CTRW)모형을 제시하여 하천에서 임의의 시간에 물질이 이동한 거리를 확률론적으로 모델링하였다. 이후 여러 연구자들이 Solute Transport In River (STIR)모형을 제안하였는데, 이 모형은 주흐름영역에 존재하는 저장대효과와 하상에 의한 저장대효과를 분리하여 해석하여 두개 이상의 저장대영역을 고려한 모형이다(Marion and Zaramella, 2005a; Marion et al., 2008; Bottacin-Busolin et al., 2011; Zaramella et al., 2016; Bottacin-Busolin et al., 2020). 하지만 이 모형의 경우 고려된 저장대영역의 개수가 증가함에 따라 모형의 정확도는 향상되지만, 동시에 매개변수의 수도 증가하여 이에 따른 불확도가 커지는 단점이 있다.

본 연구에서는 STIR모형의 체류시간분포(Residence Time Distribution, RTD)를 이용한 확률론적 저장대 모델링 프레임워크를 구축하였다. 기존의 ADE모형에 체류시간분포로 설계한 전달함수(Transfer function)을 합성곱(Convolution)으로 연산하여 저장대 효과를 포함하는 수치모형을 개발하였다. 개발된 수치모형의 검증을 위해 낙동강의 1차 지류인 감천에서 Rhodamine WT를 이용한 추적자 실험을 실시하였다. 검증 과정에서 ADE와 TSM을 동시에 적용하여 그 결과를 비교하였으며, 특히 기존의 TSM의 한계라고 제시되어 왔던 농도곡선의 꼬리에서의 농도감소의 형태를 정량적으로 비교하여 본 연구에서 개발한 확률론적 저장대모형의 우수성을 검증하였다.

2. 연구 방법

2.1 지배방정식 설계

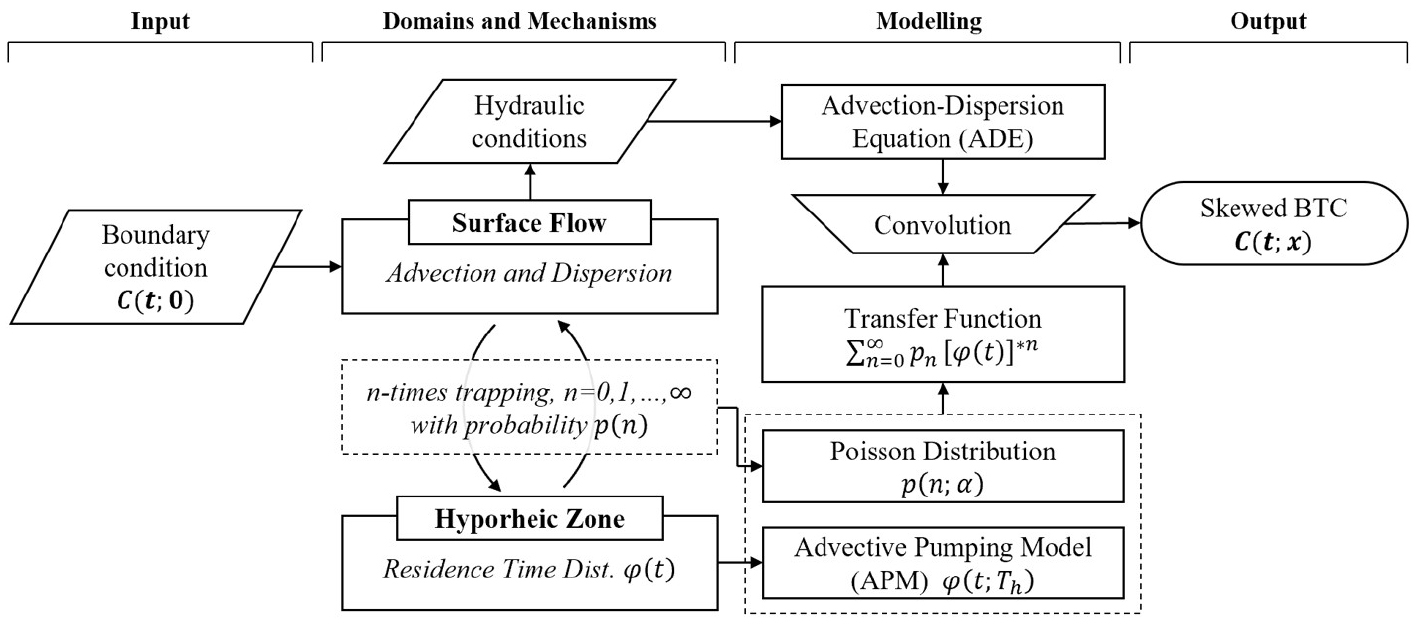
본 연구에서는 Marion and Zaramella (2005a)와 Marion et al. (2008)에서 제시한 체류시간분포를 이용한 일반적 모델링 프레임워크를 적용하여 Fig. 1과 같이 확률론적으로 하천에서 물질 혼합을 해석하였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-05/N0200540505/images/kwra_54_05_05_F1.jpg

Fig. 1.

Schematic diagram of the stochastic trapping mechanism in a river

본 모형에서는 하나의 입자가 하천흐름을 따라 거리 x만큼 이동하는데 걸리는 시간(T)을 무작위 변수로 보며, 이에 대한 확률밀도함수를 r (t ; x)로 표현한다. r (t ; x)는 기본적으로 하천의 유속에 의한 이송과 난류 및 전단류에 의한 분산 및 전단류에 의한 영향을 받으며, 입자가 저장대 영역에 갇히는 경우 그 저장대에서의 체류시간 T_r만큼 전체 T가 지체된다. 다시 말해, T_r은 저장대 영역에서 입자의 체류시간이며 입자가 거리 x를 이동하는데 상기의 갇힘 사건이 n번 발생할 경우 전체 저장대 영역에서의 체류시간 $T_{r | n} = n T_{r}$ 이다. 이러한 저장대에서의 체류시간 T_r의 확률밀도함수를 $φ_{r} (t)$ 라고 하였을 때, n번의 갇힘이 발생한 경우의 체류시간분포 $φ_{r | n} (t)$ 는 각각의 사건을 독립사건으로 보아 n ‒ 1번의 $φ_{r} (t)$ 의 합성곱 연산을 이용하여 다음과 같이 계산할 수 있다.

(1)

φ_{r | n} (t) = φ_{r} (t) \overset{n - 1 t i m e s}{\overset{⏞}{* \dots *}} φ_{r} (t) = {[φ_{r} (t)]}^{* n}

여기서, 기호 *는 시간에 대한 합성곱 연산이며 아래와 같이 정의된다.

(2)

φ_{r} (t) * φ_{r} (t) ≜ \int_{0}^{t} φ_{r} (τ) φ_{r} [t - τ] d τ

여기서, $τ$ 는 가변수이며 만약 n = 0이라면 $φ_{r | 0} (t)$ 는 디랙 델타 함수(Dirac delta function)의 형태로 나타난다. 입자가 대상 모의구간 내에서 저장대 영역에 갇히는 횟수 n 또한 이산적인 무작위 변수(n = 0, 1, 2, ...)이다.

하천에서의 물질 혼합 거동에서 분산보다 이송이 지배적일 경우, 입자가 n번 갇힐 확률은 물질이 모의구간에서 머문 전체시간에 대한 함수로 표현할 수 있으며 조건부확률의 분포 p(n)를 따른다. 따라서 전체 저장대영역에서의 체류시간분포는 다음과 같다.

(3)

r_{r} (t; x) = \sum_{n = 0}^{\infty} p (n) φ_{r | n} (t; x)

만약 주흐름영역에서 저장대 영역이 존재하지 않아 저장대효과가 발생하지 않는다면, 물질의 혼합거동은 유속에 의한 이송과 난류 및 전단류에 의한 분산에 지배적으로 영향을 받는다(Taylor, 1954; Elder, 1959; Fischer, 1968, Baek et al., 2019; Shin et al., 2020). 따라서, 이러한 조건에서 주흐름영역에서의 체류시간분포 r_w (r ; x)는 ADE 모형으로부터 얻을 수 있다.

(4)

\frac{\partial r_{w} (t; x)}{\partial t} + U \frac{\partial r_{w} (t; x)}{\partial x} = K \frac{\partial^{2} r_{w} (t; x)}{\partial x^{2}}

여기서, U (m/sec)는 구간 평균 유속, K (m²/sec)는 종분산계수이다. 결과적으로, 거리 x인 모의구간에서 저장대특성을 고려한 전체 체류시간분포 r (t ; x)는 r_w (t ; x)와 r_r (t ; x)의 합성곱으로 연산되어 다음과 같이 표현된다.

(5)

r (t; x) = \int_{0}^{t} r_{w} (τ; x) r_{r} (τ - t; x) d τ

상류단에서의 주입조건이 펄스주입인 경우, Eq. (4)의 편미분방정식의 해석해를 이용하여 본 확률론적 저장대 모형의 지배방정식의 해석해를 다음과 같이 표현할 수 있다.

(6)

r (t; x) = \int_{0}^{t} [\frac{x}{\sqrt{4 π K τ^{3}}} e x p \{- \frac{{(x - U τ)}^{2}}{4 K τ}\}] [\sum_{n = 0}^{\infty} p (n) φ_{r | n} (t - τ; x)] d τ

본 모형에서는 Fig. 2의 모형 프레임워크 흐름도와 같이 기존의 저장대를 고려하지 않은 ADE의 모의결과에 저장대의 특성을 반영한 전달함수를 적용하여 저장대 영향을 받은 왜곡된 농도곡선을 출력할 수 있다. 그리고 본 모형의 전달함수는 하천에서 입자가 저장대에 갇히는 횟수의 확률분포와 저장대에서의 체류시간분포의 연산으로 구할 수 있다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-05/N0200540505/images/kwra_54_05_05_F2.jpg

Fig. 2.

Modelling framework for the stochastic storage model

상기의 체류시간분포는 단위농도의 물질이 유입되었을 때, 하천에서 체류시간의 확률밀도함수이며 아래의 식을 통해 농도분포로 변환될 수 있다.

(7)

C (t; x) = r (t; x) \times \frac{M}{Q (t)}

여기서 C (g m^‒3)는 본류대에서의 물질의 농도, M (g)은 유입된 물질의 전체 질량, 그리고 Q (m³sec^‒1)는 유량이다.

2.2 저장대에서의 체류시간분포

본 연구에서 제시된 체류시간분포를 이용하는 모델링 프레임워크의 가장 큰 장점 중 하나는 저장대의 영향을 반영하는 체류시간분포의 형태를 유연하게 적용할 수 있다는 점이다. 하천에 흐르는 입자의 체류시간분포의 형태에 대해서 다양하게 연구되어 왔는데, Worman et al. (2002)의 연구에서는 디랙 델타 함수(Dirac delta distribution), 균등분포(Uniform distribution), 지수분포(Exponential distribution), 그리고 로그정규분포(Lognormal distribution)을 비교하여 로그정규분포의 적합성을 검증하였으며, Haggerty et al. (2000, 2002)과 Meerschaerte et al. (2008)에서는 멱함수 분포(Power-law distribution)의 타당성을 주장하였다.

모형화하고자 하는 저장대에서의 체류시간을 직접적으로 측정하기 어렵기 때문에 본 연구에서는 체류시간분포에 Marion and Zaramella (2005a)와 Marion et al. (2008)의 연구에서 채택되어 사용된 이송펌프모형(Advective Pumping Model, APM)을 적용하였다(Elliott, 1991; Elliott and Brooks, 1997). APM은 다양한 저장대의 형태 중 사구형태의 하상 구조에서 하상면에서 생기는 흐름박리현상으로 수두경사가 야기되고, 이로 인해 발생하는 본류대와 하상대(hyporheic zone)간의 물질 교환을 해석한 물리 기반 모형이다(Boano et al., 2007a). 본 모형에서는 하상에서의 수두경사를 삼각함수로 가정하거나 하상의 사구모양을 삼각형으로 가정하며 이러한 복잡한 물질교환기작을 단순화시켜 해석하지만, 유속이나 사구의 크기 등의 다양한 수리학적, 지형학적 인자를 고려한 해석을 위해 유용하게 활용될 수 있다. 특히, 본 연구와 같은 하천에서의 물질혼합모형에서 저장대를 해석하기 위한 도구로 활용되고 있다.(Worman et al., 2002; Marion et al., 2003; Zaramella et al., 2003; Marion and Zaramella, 2005b).

Elliott and Brooks (1997)의 음함수 형태의 체류시간에 대한 누적밀도함수에 대하여 Marion and Zaramella (2005a)은 정해와 근사한 해석해를 아래와 같이 제시하였다.

(8)

φ_{r} (t) = \frac{π / T_{h}}{10.66 \frac{T_{h}}{t} + {(\frac{t}{T_{h}} + 2)}^{2}}

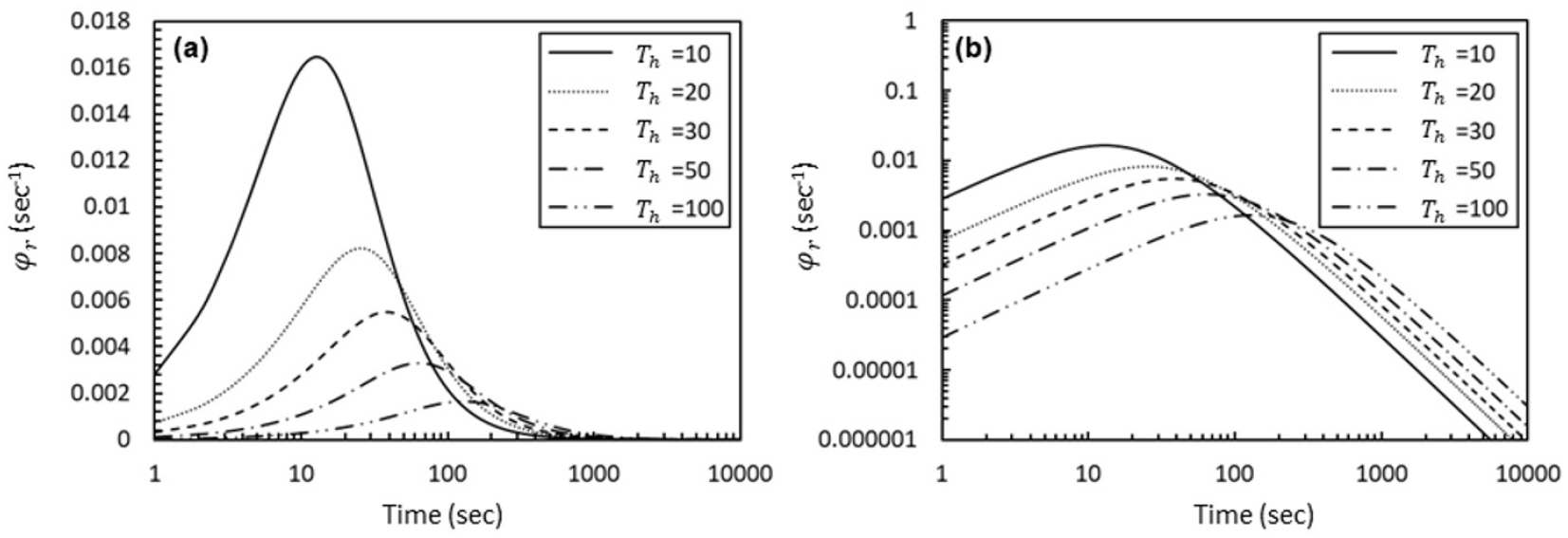
여기서, T_h (s^‒1)는 상기의 정의된 하상의 저장대영역에서의 체류시간분포를 결정하기 위한 매개변수이다. Eq. (8)의 분포의 형태는 t가 증가함에 따라 Eq. (9)과 같이 멱함수 분포(Power-law distribution)를 따르게 된다.

(9)

\lim_{t \to \infty} φ_{r} (t) \approx π T_{h} t^{- 2}

Fig. 3에서 나타내는 것과 같이, Eq. (8)을 따르는 체류시간분포의 경우 매개변수 T_h에 따라서 저장대영역에 갇힌 입자가 빨리 빠져나오는지 천천히 빠져나오는지가 결정된다. 또한 Fig. 3의 그래프는 확률밀도함수이기 때문에 T_h와 무관하게 곡선 아래 면적의 합이 1에 근사하며, 즉 T_h가 증가하여 그래프의 첨두가 낮아짐과 동시에 꼬리는 두꺼워진다. 이는 전체 모형의 모의 결과 농도 그래프의 꼬리형태에 직접적으로 영향을 주기 때문에 모의 대상 하천의 저장대 특성을 대표할 수 있는 적절한 매개변수 T_h의 결정이 모의 결과의 정확도를 결정한다. 따라서 대상 하천의 저장대 특성을 정확하게 반영하기 위해서는 적절한 체류시간분포의 매개변수를 결정하여야 한다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-05/N0200540505/images/kwra_54_05_05_F3.jpg

Fig. 3.

Distribution of $φ_{r}$ according to varying parameter $T_{h}$ (a) semi-log plot (b) log-log plot

2.3 저장대에서의 체류확률분포

본 연구에서는 모의구간 내에서 저장대 영역이 균일(Uniform)하게 분포되어 있다는 가정 하에서 다음과 같이 체류횟수에 대한 확률밀도함수(Trapping probability distribution)를 설계하였다. 하천에 흐르는 입자가 저장대 영역에 갇히는 사건은 베르누이 과정(Bernoulli process)에 해당되며 그 입자가 이전에 갇혔던 과거 경험(history)에 영향을 받지 않기 때문에 매 체류사건은 독립적이라고 할 수 있다(Marion et al., 2008). 이에 따라 시간적 혹은 공간적으로 정의된 구간 내에서 본 사건이 발생할 확률은 푸아송 분포(Poisson distribution)을 따르도록 설계하였다. $α_{h} T_{c}$ 를 매개변수로 하는 푸아송 분포의 식은 다음과 같다.

(10)

p (n; α_{h}, T_{c}) = \frac{{(α_{h} T_{c})}^{n} e^{- α_{h} T_{c}}}{n!}

여기서, $α_{h}$ (sec^‒1)는 단위 시간당 체류확률, T_c (sec)는 특성 시간이며 입자가 모의구간 내에서 머무는 시간을 나타내는 매개변수로서 T_c = x/U로 정의하였다. 매개변수 $α_{h} T_{c}$ 는 푸아송 분포의 특성에 따라 체류사건횟수의 평균과 분산을 나타내며 이 값이 커질수록 하천을 따라 흐르는 입자가 저장대영역에 갇히는 횟수가 많아지는 것을 의미한다. 하천 규모에 따라 $α_{h}$ 의 값은 10^-5부터 10^-2의 정도에서 추정된다(Marion and Zaramella, 2005a; Marion et al., 2008b; Bottacin-Busolin et al., 2011; Zaramella et al., 2016; Bottacin-Busolin et al., 2020).

2.4 확률론적 저장대모형 수치모델링

Eq. (6)의 지배방정식 해석해는 계산시간이 빠르며 결정론적인 계산으로 오차가 발생할 우려가 적은 장점이 있지만, 상류단의 주입농도의 조건이 제한적이라는 단점을 가지고 있다. 본 연구에서는 추적자 실험을 통하여 측정된 농도곡선을 경계조건으로 입력하고자 확률론적 저장대모형을 유한차분법(Finite Difference Method, FDM)과 Crank-Nicolson 방법을 이용한 수치해석을 통하여 모델링하였다. Eq. (4)의 ADE 모형 편미분방적식에 대하여 유한차분법을 적용하여 공간적으로 이산화하였으며, 모의구간을 동일간격의 유한한 불연속적인 지점으로 설정하고 이웃하는 지점간의 변화율을 이용하여 편미분방정식을 행렬방정식으로 전환시켰다. 유한차분법은 2차원 이상의 영역에서 적용하기에는 다방향의 변화율을 정의하기가 어렵고 물리적으로 보존법칙을 만족하지 못할 우려가 있다는 단점이 있지만, 본 연구와 같은 1차원 모형에는 적용이 용이하고 편미분방정식에서 1차 연립방정식으로의 변환이 직접적이라는 장점이 있다. 이러한 ADE의 수치모형의 모의 결과에 Eq. (3)의 전달함수를 합성곱으로 연산하여 저장대에 영향을 받은 왜곡된 BTC를 출력하는 방식으로 계산이 진행되며, 본 연구에서는 이러한 계산과정을 Python 프로그램 언어로 코드화하였다.

3. 추적자 실험

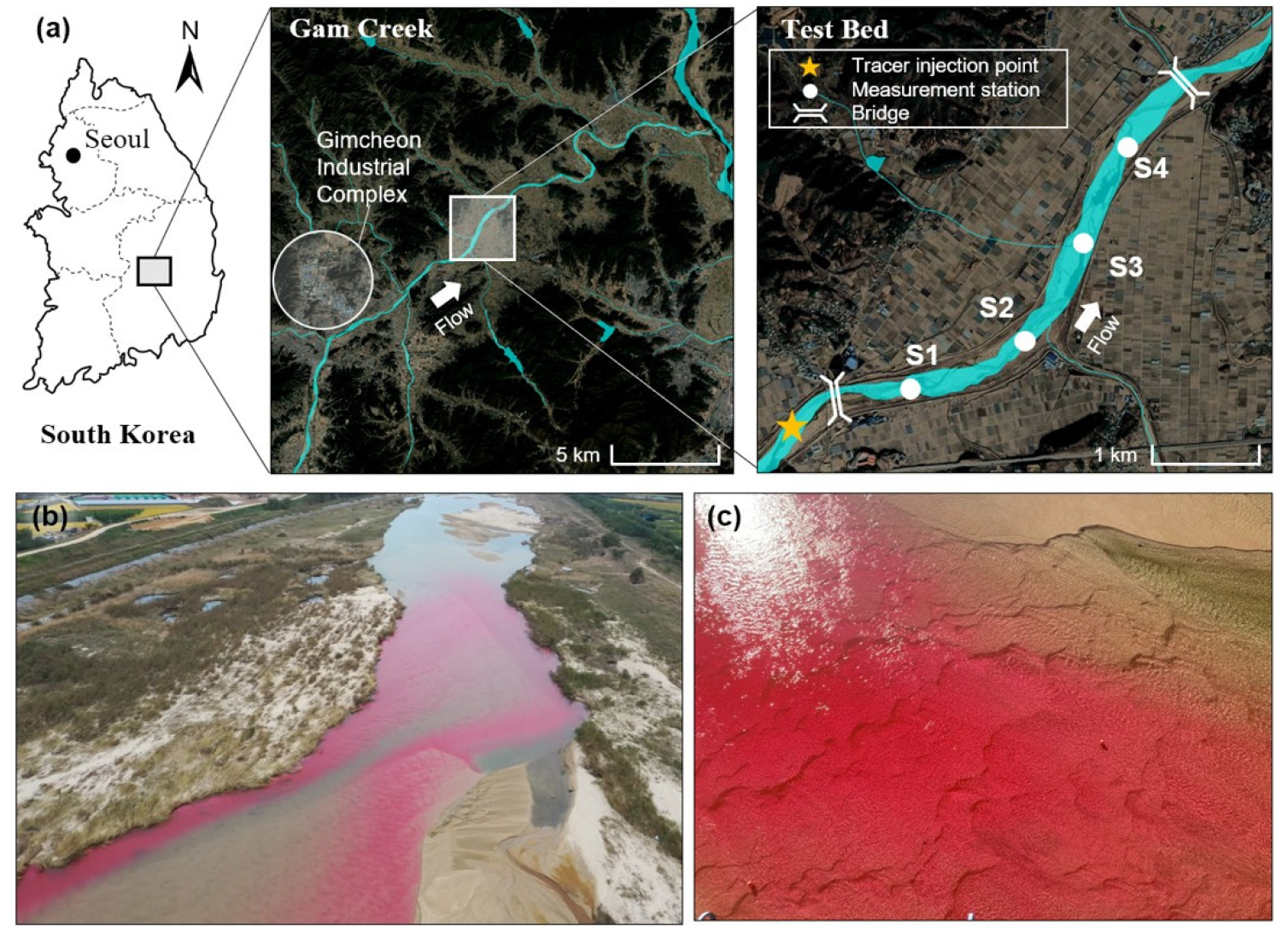
모형 검증을 위한 추적자 실험은 Fig. 4(a)와 같이 경상북도 김천시와 구미시에 걸쳐 위치한 낙동강 제1지류인 감천에서 수행하였다. 감천은 주변에 많은 농경지, 산업 단지, 그리고 주거지역이 복합적으로 분포하여 있는 하천으로 유해화학물질 유출 사고 시 잠재적으로 매우 피해가 큰 지역이다. 또한, 감천은 대표적인 모래하천으로 Fig. 4(b)와 같이 복잡한 다지 구간(Braided flow)이 다수 존재하며 Fig. 4(c)와 같이 전체 구간에 걸쳐 하상에 사구(dune)가 형성되어 있다. 이러한 감천의 지형학적 특성은 흐름 정체영역을 형성하게 되고 오염물질의 저장대 효과를 상승시키기에 본 모형의 저장대효과에 대한 모의기능을 검증하기에 적합한 하천으로 판단된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-05/N0200540505/images/kwra_54_05_05_F4.jpg

Fig. 4.

(a) Site map of the test bed in Gam Creek, South Korea (b) Tracer behavior affected by storage effect in shallow area (c) Streambed shape of Gam Creek where dunes are formed

감천 추적자 실험은 2019년 10월에 진행되었으며, 총 4.85 km 구간을 Table 1과 같이 3개의 리치로 소구간으로 분할하여 실험을 진행하였다(Kim et al., 2021). 실험 당시 유량은 12.82 ~ 12.91 m³/s로 풍수기에 해당하며 평균 유속도 약 0.6 m/s로 높게 측정되었다. 실험에 사용된 추적자는 Rhodamine WT 형광물질이며, YSI-600OMS 형광 측정 센서를 이용하여 농도를 측정하였다. YSI-600OMS의 오차 범위는 측정치의 ±5% 또는 1 ppb이며 이러한 오차 범위를 고려하여 2,000 ppb 농도의 Rhodamine WT 용액 총 20 L를 주입하였다. 센서 보정은 0 ~ 200 ppb 농도범위에 대한 표준 보정 용액을 사용하여 수행하였고 단면 평균 농도를 얻기 위해 모든 측정 단면에 대해 3 ~ 4개의 센서를 균일 한 횡방향 거리로 설치하였다. 이후 각 측선의 모든 센서에서 농도 데이터를 평균하여 단면 평균 농도를 취득하였다. 수리량 계측을 위해 음향 도플러 유속계(Sontek Flowtracker)을 사용하여 유속장 및 수심을 측정하였다. 측선 위치 및 하상 경사 등 지형 측량은 RTK-GPS (Sokkia GRX 1)을 사용하였다. 계측된 수리량은 Table 1과 같이 각 소구간에 대한 평균값으로 계산되었으며, 이는 모형의 매개변수를 결정하기 위하여 사용되었다.

Table 1.

Surveyed average hydraulic data in each sub-reach

	notation, unit	RC0 (I.P.-S1)	RC1 (S1-S2)	RC2 (S2-S3)	RC3 (S3-S4)
Flowrate	Q, m³s^-1	11.94	12.82	12.91	12.84
Sub-reach length	RL, m	820	1,200	830	2,000
Mean depth	H, m	0.392	0.361	0.358	0.431
Mean width	W, m	57.5	57.4	58.9	53
Mean velocity	U, m s^-1	0.569	0.668	0.665	0.681
Channel Slope	S	0.000825
Sinuosity	S_n	1.05	1.07	1.03	1.08

또한, 1차원 모형에서는 횡방향, 연직방향으로 물질이 완전히 혼합되었다고 가정하기 때문에 단면평균농도값을 측정하기에 앞서 완전혼합거리를 확보해야 한다. Kilpatrick and Wilson (1989)은 다중주입의 경우에서 횡방향, 연직방향 완전혼합을 위해 요구되는 거리는 아래의 식으로 제시하였다.

(11)

L_{0} = 0.1 {(\frac{1}{n})}^{2} \frac{U W^{2}}{E_{z}}

여기서, L₀ (m)는 요구거리, n은 주입지점의 개수, E_z는 횡방향 혼합계수이며 E_z / (HU^*) = 0.15로부터 계산될 수 있다. 본 추적자 실험에서는 9점 주입을 하였으며, Table 1에 기재되어 있는 주입지점(I.P.)에서 첫번째 측선(S1)까지의 구간(RC0)에서의 구간평균수리량을 Eq. (11)에 입력하여 계산한 결과는 701 m이며, RC0의 구간길이를 820 m로 설정하여 완전혼합거리를 확보하였다.

4. 모의 결과 및 분석

4.1 모형 매개변수 산정 및 적용

본 연구에서 구축한 확률론적 저장대모형을 감천에 적용하여 계산된 농도분포를 추적자 실험으로부터 얻어진 실측 농도곡선과 비교하여 모형의 정확도를 검증하였다. 나아가서, 같은 조건에서 ADE와 TSM을 이용한 모의 결과와도 비교하였다. 특히 기존 TSM의 한계점 중 하나로 제시된 농도곡선 꼬리부에서의 모의 오차에 대해 중점적으로 분석하였다. TSM의 경우, 지배방정식은 Eq. (12)과 같이 ADE 모형에 저장대 영역과 이에 따른 두개의 부가적인 저장대 매개변수( $α$ , A_S)를 추가한 식이며, 이 부가적인 저장대 매개변수에 0을 대입하게 되면 기존의 ADE모형과 동일한 형태를 갖는다.

(12a)

\frac{\partial C}{\partial t} = - \frac{Q}{A_{F}} \frac{\partial C}{\partial x} + \frac{1}{A_{F}} \frac{\partial}{\partial x} (A_{F} K_{F} \frac{\partial C}{\partial x}) + α (C_{S} - C)

(12b)

\frac{\partial C_{s}}{\partial t} = α \frac{A_{F}}{A_{S}} (C - C_{S})

여기서, C_s (g m^‒3)는 저장대에서의 농도값, A_F와 A_S (m²sec^‒1)는 본류대와 저장대의 단면적, K_F (m²/sec)는 본류대에서의 종분산계수, $α$ (sec^‒1)는 본류대와 저장대 사이의 물질교환계수이다. 저장대 농도에 대한 지배방정식인 Eq. (12b)의 해석해(Seo and Maxwell, 1992)로부터 TSM은 C_s를 시간에 대한 지수함수형태로 나타나고 있음을 알 수 있다.

1단계에서는 Eq. (4)를 사용하여 저장대 영향이 고려되지 않은 체류시간분포을 모의하였으며, 본 과정에서 매개변수로서 유속과 분산계수를 입력하였다. 유속의 경우 추적자 실험에서 측정한 자료를 적용하였다. 하천 흐름방향 분산특성은 전단력으로 인한 유속의 분포에 의하여 발생한다(Rutherford, 1994). 이를 근거로 Marion et al. (2008)은 Fischer (1975)가 제시한 종분산계수의 준경험식을 적용하였으며 이에 대한 정확도를 검증하였다. 하지만 Fischer (1975)의 식은 하폭이 넓은 흐름에서 종분산계수를 과도하게 산정되는 경향을 보인다. 하폭 3.1 m의 비교적 좁은 하천에서 모형을 적용한 Marion et al. (2008)의 연구와 달리 본 연구 대상 구간의 평균 하폭은 56.43 m이며, 이에 따라 하폭이 무한히 넓은 경사면에서의 종분산계수 산정식인 Elder (1959)의 식을 적용하였다(Fischer et al., 1979).

(13)

K = 5.93 H U *

여기서, $U^{*} = \sqrt{g R_{H} S}$ 는 등류수심에서의 전단유속이며 동수반경 R_H 그리고 평균하상경사 S로부터 계산된다. 상기의 식은 지형이 불규칙한 자연 하천의 경우 저장대효과를 고려하지 못한다는 단점이 있다. 그럼에도 불구하고, 분산계수를 일반적으로 사용가능한 수심, 하상경사 등의 흐름특성으로부터 분산계수를 산정 할 수 있다는 이점이 있으며, ADE모의와 저장대효과의 적용을 분리하여 진행하는 본 모형에 적합하다. 본 연구에서는 상기의 식에서 계산된 종분산계수 값을 조정하지 않고 그대로 사용하였다.

2단계에서는 확률론적 저장대모형의 매개변수 $α_{h}$ 와 $T_{h}$ 를 산정하였는데, 모의 결과를 추적자 실험 농도 측정 데이터와 비교하여 최소의 오차를 발생시키는 최적의 매개변수를 찾는 방식을 이용하였다. 오차는 평균 제곱 오차(Mean Squared Error, MSE)를 사용하였으며 이는 다음과 같이 정의된다.

(14)

M S E = \frac{1}{N_{o b s}} \sum_{j = 1}^{N_{o b s}} {(C_{o b s}^{j} - C_{s i m}^{j})}^{2}

여기서, ${C_{o b s}}^{j}$ 는 j번째 시점(time step)에서 측정된 농도값, $C_{s i m}^{j}$ 는 j번째 시점(time step)에서 모의된 농도값, N_obs은 측정데이터 수이다. 최적의 매개변수를 찾기 위하여 quasi-Newton 방법을 사용하여 최솟값을 찾는 SLSQP (Sequential Least Squares Programming)을 활용하였다(Kraft, 1988).

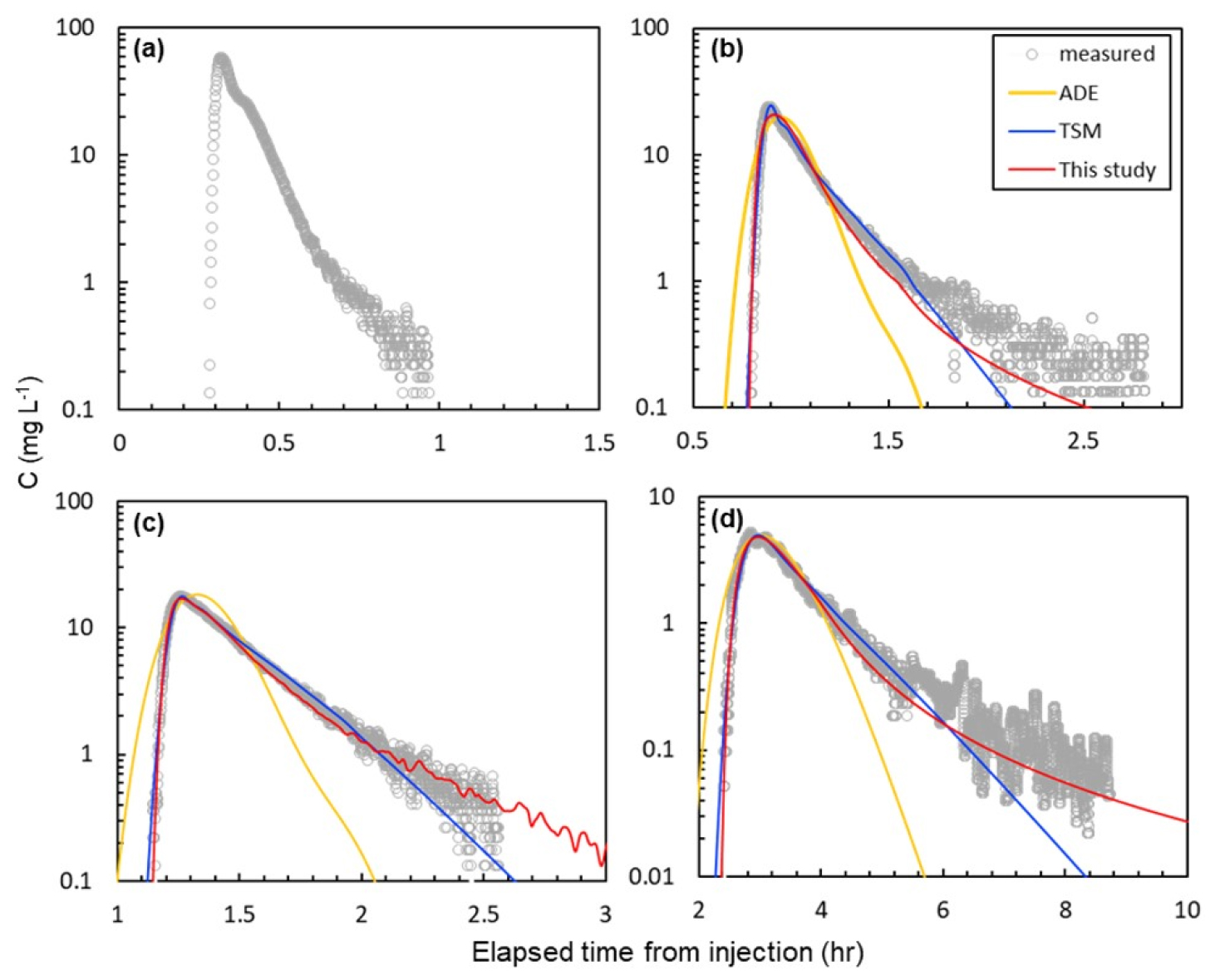
3단계에서는 상기의 방법으로 추정한 매개변수를 이용하여 감천 추적자 실험과 동일한 조건하에서 모의를 수행하여 체류시간분포 모의결과값을 농도분포로 변환 후 추적자 실험의 농도 측정 결과와 비교하여 모형을 검증하였다. 또한 동일한 조건에서 Eq. (12)의 ADE와 TSM을 이용한 모의 결과와도 비교하였다. ADE와 TSM의 매개변수는 Noh et al. (2019)에서 제시한 최적화기법을 적용하여 매개변수를 추정하였으며 그 결과는 Table 2에 명시되어 있다. 모의 시 각 소구간의 상류 경계조건으로 측정된 농도데이터의 횡방향 평균값을 주입하였으며, Fig. 5에 S2, S3, 그리고 S4에서의 모의결과들과 횡방향평균 농도측정값을 비교하였다.

Table 2.

Estimated parameters required by each model

model	parameter	notation, unit	RC1 (S1-S2)	RC2 (S2-S3)	RC3 (S3-S4)
ADE	1D LDC¹⁾	D_L, m² s^-1	9.42	4.51	23.4
ADE	Flow zone area	A_F, m²	22.7	20.7	43.0
TSM	TSM LDC	D_L, m² s^-1	0.57	0.59	4.89
	Flow zone area	A_F, m²	20.9	19.6	35.5
	Storage zone area	A_S, m²	4.75	3.07	12.0
	Exchange coefficient	$α$ , 10^-4 s^-1	3.76	2.92	1.54
CDE with APM	Elder's LDC	D_L, m² s^-1	0.12	0.11	0.15
	RTD time scale	T_h, s	5.88	19.3	17.5
	Probability per unit time	$α_{h}$ , 10^-3 s^-1	3.76	0.82	2.90

1) Longitudinal dispersion coefficient

4.2 모의결과 분석

수치 모의시 경계조건으로는 농도 측정 데이터를 주입하였으며, Fig. 5에 S2, S3, 그리고 S4에서의 모의결과들과 측정치를 비교하였다. 모의 결과 농도 곡선을 보면, 모든 측선에서 본 연구에서 제안하는 확률론적 저장대모형의 모의 결과가 다른 모형의 결과에 비해 실측 농도곡선의 꼬리부에서 농도감소추세를 보다 근접하게 따르는 것으로 보인다. 확률론적 저장대모형의 경우, S3(Fig. 5(c))에서 농도곡선의 하강부에서 해의 변동특성을 보이는 데 이는 실측 농도곡선의 꼬리부에서의 변동성을 반영한 결과로 판단된다. TSM의 경우에도 선행연구 결과와는 달리 꼬리부에서 어느 정도 측정데이터를 따라가는 것으로 보이는 데, 이는 디랙 델타 함수 형태의 농도곡선을 경계조건으로 주입한 선행연구와 다르게 본 연구에서는 이미 왜도와 꼬리를 갖고 있는 측정농도곡선을 입력조건으로 사용하였기 때문이다. 하지만 TSM이 갖고 있는 지수함수형태의 체류시간분포의 구조적 부정확성 때문에 본 연구에서 개발한 확률론적 저장대모형의 모의 결과보다는 실제 측정 결과와 차이를 보이고 있는 것으로 나타났다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-05/N0200540505/images/kwra_54_05_05_F5.jpg

Fig. 5.

BTCs measured from tracer test and simulated from each one-dimensional solute transport model (a) measured BTC at S1 applied as boundary condition (b) BTC comparison at S2 (c) BTC comparison at S3 (d) BTC comparison at S4

전체 곡선의 정확도를 평가한 결과, S1, S2, S3에서의 확률론적 저장대모형으로부터의 모의결과의 결정계수(R²)는 각각 0.977, 0.998, 0.989이며, TSM으로부터의 모의결과의 결정계수는 각각 0.995, 0.995, 0.974이다. S2와 S3에서는 본 연구의 모형의 정확도가 높았지만, S1에서는 TSM의 정확도가 더 높았다. 이는 4개의 매개변수를 농도곡선에 최적화하여 모의결과를 산출하는 TSM과 달리, 본 모형은 2개의 저장대 매개변수만을 최적화하기 때문에 일부 구간에 TSM보다 낮은 정확도를 보인 것으로 판단된다.

하지만 꼬리부에서의 정확도를 비교하였을 때 이와 다른 결과를 보였다. 꼬리부에서의 예측정확도를 정량적으로 분석하기 위하여, 최고농도 이후 감소하는 부분에서 최고농도의 20% 이하의 해당하는 부분을 꼬리부로 설정하고 이에 대한 멱함수 기울기를 계산하여 모형별로 비교하여 Table 3에 수록하였다. 이 표에서 APM을 적용한 확률론적 저장대모형이 다른 두 모형에 비해 보다 측정치에 근접한 값을 보이고 있음을 알 수 있다. 본 모형에서 전체 측선에서의 오차율의 평균값을 계산해보면 0.195로 14.03 그리고 1.866의 값을 보인 ADE와 TSM에 비해 월등히 낮은 오차율을 보이고 있음을 알 수 있다. 즉, 멱함수 분포의 형태를 갖는 APM으로부터 얻은 체류시간분포가 기존의 모형에 비해 보다 실제현상과 가까운 결과를 산출하는 것으로 밝혀졌다.

Table 3.

Comparison of the power-law slope of the tail of BTCs at each section

	S2	S3	S4	Averaged error rate
Tracer test	3.789	6.298	3.811	-
ADE	92.39	103.4	16.35	14.03
TSM	16.11	17.46	6.001	1.866
This study	3.332	5.140	4.885	0.195

4.3 모형 매개변수 분석

감천에서의 상기의 3가지 모형에서 추정된 종분산계수를 비교해보면, Table 2와 같이 ADE와 TSM의 종분산계수는 전체 구간 평균값이 각각 12.44 m²/s, 2.02 m²/s 이다. ADE모형에서는 저장대혼합과정을 별도로 모형화하지 않기 때문에 난류 및 전단류뿐만 아니라, 하천의 불규칙성으로 인한 저장대의 영향도 분산계수에 포함되어 있어 TSM보다 높게 추정되었다. TSM에서는 저장대와 관련된 두개의 매개변수가 저장대의 영향을 별도로 반영하고 있기 때문에 분산계수가 ADE 모형에서의 추정값보다 낮은 값을 보인다. 본 연구에서 개발한 확률론적 저장대모형에서는 물리적 이론을 기반하고 있는 Elder (1959)의 식으로 계산된 종분산계수를 이용하고 있는데, 감천 전체 구간 평균값은 0.139 m²/s으로 TSM에서 사용한 값보다 더 작은 값이다. 이를 적용한 본 연구의 모형의 모의결과가 TSM의 모의결과보다 농도곡선의 꼬리부에서 더 높은 정확도를 보인 것은 분산항과 저장대의 영향을 분리하여 해석하는 확률론적 저장대모형의 구조적 우수성에 기인하는 것으로 판단된다. TSM의 경우 전술한 바와 같이 전체 농도곡선에 대한 모의 정확도는 우수하지만, 전단류에 의한 분산과 저장대의 영향을 제대로 구분하여 반영하지 못하며, 단순화된 저장대 모델링으로 인해 농도곡선의 꼬리부에서 확률론적 저장대모형보다 낮은 정확도를 보이는 것으로 판단된다.

TSM과 확률론적 저장대모형의 경우, 두 모형의 구조적 차이가 있기는 하지만 저장대에서의 혼합과정을 나타내는 TSM의 A_S, $α$ 와 비교하여, 확률론적 저장대모형의 $α_{h}$ 와 $T_{h}$ 의 물리적 의미를 살펴보면 다음과 같다. $α_{h}$ 는 하천에서 입자가 저장대에 갇히는 횟수의 정도의 매개변수로서 A_S와 같이 모의구간에서의 저장대 영역에 관련된다고 할 수 있다. $T_{h}$ 의 경우 입자가 저장대 영역에서 얼마나 오래 머무는지에 대한 매개변수이며 이는 물질교환속도를 나타내는 TSM의 $α$ 와 의미가 유사하다. 하지만 이러한 두 모형의 매개변수의 물리적 의미의 연관성을 파악하기 위해서는 많은 양의 모의 데이터를 필요로 하며 이와 동시에 하천의 수리인자와의 관계에 대한 분석도 병행되어야 하기 때문에, 실제 하천에서의 제한된 실험자료를 활용하기에는 한계가 있다.

5. 결 론

본 연구에서는 자연하천에서 오염물질 혼합거동 해석을 위해 기존에 널리 사용되어왔던 1차원 저장대모형인 TSM의 한계점을 극복하고자, 하천에서 저장대의 영향을 확률론적으로 접근한 모형을 제시하였다. 본 연구에서는 STIR 모형의 모델링 프레임워크를 이용한 수치모형을 개발하여 다양한 체류시간분포의 형태를 적용할 수 있도록 하였다.

감천의 하상특성을 고려하여 사구의 하상형태로부터 발생하는 저장대 효과를 고려한 확률론적 저장대모형을 적용한 결과, ADE, TSM을 이용한 모의 결과보다 실측 농도곡선의 꼬리부의 감소특성을 정확하게 모의하는 것으로 나타났다. 본 모형에 의한 농도곡선 꼬리부에서의 멱함수 기울기에 대한 오차율 평균값은 0.24로서 14.03 및 1.87의 값을 보인 ADE와 TSM에 비해 월등히 낮게 나타나는 것으로 밝혀졌다. 이에 따라 사구가 형성되어 있는 모래하천인 감천의 저장대 특성에 의한 체류시간분포는 지수함수 분포의 형태보다는 멱함수 분포의 형태에 가까운 것으로 판단된다.

본 연구에서 개발한 확률론적 저장대모형은 모형화 과정에서 공간적으로 분포되어 있는 저장대 영역은 하천의 흐름방향에 따라 균일하다고 가정하고 균일한 매개변수를 적용하였다. 또한, 모의구간 전체에서 하상재료와 같은 저장특성은 균질성을 가져야 하며 이에 따라 입자가 저장대 영역에 갇혔을 때 그 체류시간분포는 매 갇힘사건마다 동일하다고 가정하였다. 하지만 실제 하천은 공간적으로 이질적이며 상기의 가정으로부터 불확도가 발생할 수 있다. 뿐만 아니라, 본 연구에서 적용하였던 최적화 기법은 오차를 최소화하는 매개변수를 평가하는 가장 단순한 기법을 사용하였는데, 복잡한 하천의 저장 특성을 대표하는 이러한 매개변수를 추정하는 과정은 non-convex 함수의 형태를 갖는 경우가 많으며, 상기의 기본적인 최적화 기법으로는 초기추정값(Initial guess)에 크게 의존하기도 하며 국부최적값(Local optimum)에 빠질 우려가 있다. 이에 따른 매개변수의 불확도를 최소화하기 위하여 보다 고차원적인 최적화기법을 적용할 필요가 있다.

Acknowledgements

본 연구는 과학기술정보통신부 및 국토교통부 “공공혁신조달 연계 무인이동체 및 SW플랫폼 개발 사업”(20DPIW-C153746-02)의 연구비 지원에 의하여 연구되었습니다. 본 연구는 서울대학교 공학연구원과 건설환경종합연구소의 지원 하에 이루어졌습니다.

References

Baek, D., Seo, I. W., Kim, J.S., and Nelson, J.M. (2019). "UAV-based measurements of spatio-temporal concentration distributions of fluorescent tracers in open channel flows." Advances in Water Resources, Vol. 127, pp. 76-88. 10.1016/j.advwatres.2019.03.007

Bencala, K.E., and Walters, R.A. (1983). "Simulation of solute transport in a mountain pool-and-riffle stream: A transient storage zone model." Water Resources Research, Vol. 19, pp. 718-724. 10.1029/WR019i003p00718

Bencala, K.E., Gooseff, M.N., and Kimball, B.A. (2011). "Rethinking hyporheic flow and transient storage to advance understanding of stream‐catchment connections." Water Resources Research, Vol. 47, No. 3, pp. 1-9. 10.1029/2010WR010066

Boano, F., Packman, A. I., Cortis, A., Revelli, R., and Ridolfi, L. (2007a). "A continuous time random walk approach to the stream transport of solutes." Water Resources Research, Vol. 43, No. 10, pp. 1-12. 10.1029/2007WR006062

Boano, F., Revelli, R., and Ridolfi, L. (2007b). "Bedform-induced hyporheic exchange with unsteady flows." Advances in Water Resources, Vol. 30, No. 1, pp. 148-156. 10.1016/j.advwatres.2006.03.004

Bottacin-Busolin, A., Dallan, E., and Marion, A. (2020) "STIR-RST: A software tool for reactive smart tracer studies." Environmental Modelling & Software, Vol. 135, 104894. 10.1016/j.envsoft.2020.104894

Bottacin-Busolin, A., Marion, A., Musner, T., Tregnaghi, M., and Zaramella, M. (2011). "Evidence of distinct contaminant transport patterns in rivers using tracer tests and a multiple domain retention model." Advances in Water Resources, Vol. 34, No. 6, pp. 737-746. 10.1016/j.advwatres.2011.03.005

Choi, S.Y., Seo, I.W., and Kim, Y.O. (2020). "Parameter uncertainty estimation of transient storage model using Bayesian inference with formal likelihood based on breakthrough curve segmentation." Environmental Modelling & Software, Vol. 123, 104558. 10.1016/j.envsoft.2019.104558

Deng, Z., Bengtsson, L., and Singh, V.P. (2006). "Parameter estimation for fractional dispersion model for rivers." Environmental Fluid Mechanics, Vol. 6, No. 5, pp. 451-475. 10.1007/s10652-006-9004-5

Deng, Z.Q., Singh, V.P., and Bengtsson, L. (2004). "Numerical solution of fractional advection-dispersion equation." Journal of Hydraulic Engineering, Vol. 130, No. 5, pp. 422-431. 10.1061/(ASCE)0733-9429(2004)130:5(422)

Elder, J. (1959). "The dispersion of marked fluid in turbulent shear flow." Journal of Fluid Mechanics, Vol. 5, No. 4, pp. 544-560. 10.1017/S0022112059000374

Elliott, A.H. (1991). Transfer of solutes into and out of streambeds. Ph. D. dissertation, California Institute of Technology, Pasadena, CA, U.S.

Elliott, A.H., and Brooks, N.H. (1997). "Transfer of nonsorbing solutes to a streambed with bed forms: Theory." Water Resources Research, Vol. 33, No. 1, pp. 123-136. 10.1029/96WR02784

Fischer, H.B. (1968). "Dispersion in Natural Streams." Journal of the Sanitary Engineering Division, ASCE, Vol. 95, pp. 927-943. 10.1061/JSEDAI.0000900

Fischer, H.B. (1975). "Simple method for predicting dispersion in streams." Journal of the Environmental Engineering Division, ASCE, Vol. 101, No. 3, pp. 453-455. 10.1061/JEEGAV.0000360

Fischer, H.B., List, E.J., Koh, R.C.Y., Imberger, J., and Brooks, N.H. (1979). "Mixing in inland and coastal waters." Academic Press, Vol. 4, pp. 2758-2771.

Haggerty, R., McKenna, S.A., and Meigs, L.C. (2000). "On the late‐time behavior of tracer test breakthrough curves." Water Resources Research, Vol. 36, No. 12, pp. 3467-3479. 10.1029/2000WR900214

Haggerty, R., Wondzell, S.M., and Johnson, M.A. (2002). "Power‐law residence time distribution in the hyporheic zone of a 2nd‐order mountain stream." Geophysical Research Letters, Vol. 29, No. 13, pp. 18-1-18-4. 10.1029/2002GL014743

Hays J.R., Krenkel P.A., and Schnelle K.B. (1967). Mass transport mechanisms in open-channel flow. Technical Report, No. 8, Vanderbilt University, Nashville, TN.

Kilpatrick, F.A., and Wilson, J.F. (1989). "Measurement of time of travel in streams by dye tracing." US Government Printing Office, Vol. 3, pp. 1-27.

Kim, B., and Seo, I.W. (2020). "Development of one-dimensional river storage model for mixing analysis of hazardous chemicals in rivers." Proceedings of the Korea Water Resources Association Conference. KWRA, pp. 148-148.

Kim, B., Seo, I.W., Kwon, S., Jung, S.H., and Choi, Y. (2021). "Modelling One-dimensional reactive transport of toxic contaminants in natural rivers." Environmental Modelling & Software, Vol. 137, 104971. 10.1016/j.envsoft.2021.104971

Kim, J.S., Baek, D., Seo, I.W., and Shin, J. (2019). "Retrieving shallow stream bathymetry from UAV-assisted RGB imagery using a geospatial regression method." Geomorphology, Vol. 341, pp. 102-114. 10.1016/j.geomorph.2019.05.016

Kraft, D. (1988). A software package for sequential quadratic programming. DFVLR, German.

Kwon, S., Noh, H., Seo, I. W., Jung, S.H., and Baek, D. (2021). "Identification framework of contaminant spill in rivers using machine learning with breakthrough curve analysis." International Journal of Environmental Research and Public Health, Vol. 18, No. 3, 1023. 10.3390/ijerph1803102333498931PMC7908193

Marion, A., and Zaramella, M. (2005a). "A residence time model for stream-subsurface exchange of contaminants." Acta Geophysica Polonica, Vol. 53, No. 4, 527.

Marion, A., and Zaramella, M. (2005b). "Diffusive behavior of bedform-induced hyporheic exchange in rivers." Journal of Environmental Engineering, Vol. 131, No. 9, pp. 1260-1266. 10.1061/(ASCE)0733-9372(2005)131:9(1260)

Marion, A., Zaramella, M., and Bottacin‐Busolin, A. (2008). "Solute transport in rivers with multiple storage zones: The STIR model." Water Resources Research, Vol. 44, No. 10, pp. 1-10. 10.1029/2008WR007037

Marion, A., Zaramella, M., and Packman, A.I. (2003). "Parameter estimation of the transient storage model for stream-subsurface exchange." Journal of Environmental Engineering, Vol. 129, No. 5, pp. 456-463. 10.1061/(ASCE)0733-9372(2003)129:5(456)

Meerschaert, M.M., Zhang, Y., and Baeumer, B. (2008). "Tempered anomalous diffusion in heterogeneous systems." Geophysical Research Letters, Vol. 35, No. 17, pp. 1-5. 10.1029/2008GL034899

Noh, H., Baek, D., and Seo, I.W. (2019). "Analysis of the applicability of parameter estimation methods for a transient storage model." Journal of Korea Water Resources Association, Vol. 52, pp. 681-695.

Noh, H., Kwon, S., Seo, I.W., Baek, D., and Jung, S.H. (2021). "Multi-gene genetic programming regression model for prediction of transient storage model parameters in natural rivers." Water, Vol. 13, No. 1, 76. 10.3390/w13010076

Rutherford, J.C. (1994). River mixing. John Wiley and Son Limited, Hoboken, NJ, U.S.

Seo, I.W., and Maxwell, W.H.C. (1992). "Modeling low-flow mixing through pools and riffles." Journal of Hydraulic Engineering, Vol. 118, No. 10, pp. 1406-1423. 10.1061/(ASCE)0733-9429(1992)118:10(1406)

Seo, I.W., Kim, J.S., and Jung, S.H. (2016). "Numerical simulation of two-dimensional pollutant mixing in rivers using RAMS." Procedia Engineering, Vol. 154, pp. 544-549. 10.1016/j.proeng.2016.07.550

Shin, J., Seo, I.W., and Baek, D. (2020). "Longitudinal and transverse dispersion coefficients of 2D contaminant transport model for mixing analysis in open channels." Journal of Hydrology, Vol. 583, 124302. 10.1016/j.jhydrol.2019.124302

Taylor, G.I. (1954). "The dispersion of matter in turbulent flow through a pipe." Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, Vol. 223, No. 1155, pp. 446-468. 10.1098/rspa.1954.0130

Valentine, E.M., and Wood, I.R. (1977). "Longitudinal dispersion with dead zones." Journal of the Hydraulics Division, Vol. 103, No. 9, pp. 975-990. 10.1061/JYCEAJ.0004845

Worman, A., Packman, A.I., Johansson, H., and Jonsson, K. (2002). "Effect of flow-induced exchange in hyporheic zones on longitudinal transport of solutes in streams and rivers." Water Resources Research, Vol. 38, No. 1, pp. 2-1-2-15. 10.1029/2001WR000769

Zaramella, M., Marion, A., Lewandowski, J., and Nützmann, G. (2016). "Assessment of transient storage exchange and advection-dispersion mechanisms from concentration signatures along breakthrough curves." Journal of Hydrology, Vol. 538, pp. 794-801. 10.1016/j.jhydrol.2016.05.004

Zaramella, M., Packman, A.I., and Marion, A. (2003). "Application of the transient storage model to analyze advective hyporheic exchange with deep and shallow sediment beds." Water Resources Research, Vol. 39, No. 7, pp. 1-12. 10.1029/2002WR001344

Journal of Korea Water Resources AssociationISSN:2799-8746(Print) 2799-8754(Online)한국수자원학회

Preview

Analysis of solute transport in rivers using a stochastic storage model

ABSTRACT

MAIN

Fig. 1.

Schematic diagram of the stochastic trapping mechanism in a river

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 2.

Modelling framework for the stochastic storage model

(7)

(8)

(9)

Fig. 3.

Distribution of φr according to varying parameter Th (a) semi-log plot (b) log-log plot

(10)

Fig. 4.

(a) Site map of the test bed in Gam Creek, South Korea (b) Tracer behavior affected by storage effect in shallow area (c) Streambed shape of Gam Creek where dunes are formed

Table 1.

Surveyed average hydraulic data in each sub-reach

(11)

(12a)

(12b)

(13)

(14)

Table 2.

Estimated parameters required by each model

Fig. 5.

BTCs measured from tracer test and simulated from each one-dimensional solute transport model (a) measured BTC at S1 applied as boundary condition (b) BTC comparison at S2 (c) BTC comparison at S3 (d) BTC comparison at S4

Table 3.

Comparison of the power-law slope of the tail of BTCs at each section

Acknowledgements

References

Distribution of $φ_{r}$ according to varying parameter $T_{h}$ (a) semi-log plot (b) log-log plot