1. 서 론
2. 연구방법
2.1 불확실성을 고려한 Bayesian 추론 기반의 홍수량 빈도해석
3. 분석자료
3.1 수문조사를 통한 실측유량 자료
4. 연구결과
4.1 불확실성을 고려한 매개변수 추론 및 홍수량 빈도해석
5. 결 론
1. 서 론
최근 전 세계적으로 기후변화 영향에 의한 강수 현상의 변동성 증대와 맞물려 국지성 집중호우의 발생빈도와 강도가 증가하고 있다. 이러한 기상현상에 의해 수반되는 돌발홍수와 같은 자연재해는 사회기반시설의 훼손에 따른 경제적 손실 및 인명피해와 직결된다. 우리나라는 2000년대 이후 태풍 루사(2002년 8월), 매미(2003년 9월), 차바(2016년 10월) 등과 같은 대형 태풍의 내습과 2020년 이례적인 장기간의 장마로 인해 기록적인 폭우가 발생하였으며 2020년의 강우량 및 강우일수를 동시에 고려한 이변량 빈도분석 결과 800년 빈도 이상으로 분석되었다(Kim et al., 2020). 이와 같은 자연재해의 선제적 대응 차원에서, 과거에 축적된 자료를 통해 자연현상을 규명하고 현실적인 측면에서의 수문해석의 필요성이 증대되고 있다(Singh et al., 2005).
다양한 수문자료 중 강수현상으로 기인되는 유량은 인간이 수자원을 활용하기 위하여 정량적으로 파악해야만 하는 수문자료로 하천관리, 수자원 관리 및 수자원 배분 등과 같은 분야에서 객관적인 기준으로 평가되어야 한다. 그러나 유량자료는 강수자료에 비해 관측자료의 연한이 상대적으로 짧으며, 댐 상류부 유역에 있는 주요 지점을 제외한 대부분 지점은 자연유량 자료의 취득이 어려워 수공구조물 설계과정에서 실측유량 홍수량 빈도해석 결과보다는 장기간의 강수량 자료로 산정된 설계강우량을 이용하여 강우-유출 관계에 따라 특정 빈도에 해당하는 설계홍수량을 사용하는 것이 일반적이다(Ahn et al., 2014).
수자원 계획 및 설계에 활용되는 홍수량 산정기법은 홍수량 빈도해석 방법과 강우-유출 모형에 의한 방법으로 구분된다. 홍수량 빈도해석 방법은 홍수량 자료를 직접 빈도해석 하여 확률 홍수량을 산정하며 이론적으로 가장 정확한 홍수량 산정기법으로 평가된다(ME, 2019). 하지만, 현재 시점에서 우리나라의 실측유량 자료연한은 강우량에 비하여 절대적으로 제한적이며 다수의 연구와 실무에서 강우-유출 모형, 기왕 홍수자료, 홍수흔적 및 경험적 공식 등을 검토하여 홍수량을 산정하였다(Chebana and Ourada, 2008; Alcantara and Ahn, 2021).
최근 한국수자원조사기술원(前 유량조사사업단)이 출범한 이후 수문조사 성과로 다수의 홍수 사상 자료가 지속적으로 축적되고 있으며 최근 품질관리를 통한 수위-유량관계곡선의 신뢰도를 확보하여 양질의 실측유량 자료를 생산하고 있다. 국내외에서 수행된 실측유량에 대한 빈도해석 연구사례를 살펴보면 Yoon et al. (2005)은 실측 홍수량 자료의 지역빈도 분석결과와 지표홍수량, 유역특성인자 사이의 상관성 분석을 통해 지류하천 유역에 대한 확률홍수량을 산정하였으며, Kim and Lee (2009)는 장기유출모형을 활용해 모의된 유량과 첨두유량 사이의 상관관계에 따른 빈도홍수량 변화 특성을 파악하여 한강유역의 다목적댐이 빈도홍수량 변화에 미치는 영향을 정량적으로 분석하였다. Machado et al. (2015)는 스페인 중부지역에 위치한 타구스 강의 400년 이상 관측된 기왕 유량자료에 대하여 정상성 및 비정상성 홍수빈도해석 방법으로 접근하여 최근 10년 동안 기후변동성에 의해 유량의 특성이 변화했음을 확인하였다. Engeland et al. (2018)은 노르웨이의 4개 유역에서 실측된 유량자료를 활용하여 Bayesian 방법과 연계한 홍수빈도해석을 통해 과거에 발생했던 홍수를 정량적으로 평가하였으며, 관측연한이 짧은 홍수자료에 대해 불확실성 구간을 제시함으로써 설계홍수량의 신뢰성을 확보할 방법을 제안하였다.
본 연구는 수문조사로 확보한 실측유량을 빈도해석 기법에 적용하는 것으로 기존 연구와 차별성을 가지고 있다. 즉, 10년 이상의 실측유량 자료의 가용지점이 증가하는 추세에서 실측유량의 직접유량 빈도해석 결과와 확률강우량과 강우-유출모형을 활용한 홍수량 해석 결과를 검토하였다. 세부적으로 실측유량을 활용한 홍수량 빈도해석 기법을 평가하기 위한 본 연구의 구성은 다음과 같다. 1장에서는 연구의 배경 및 목적을 요약하여 서술하였으며, 2장에서는 Bayesian 추론기법을 적용하여 불확실성을 고려한 홍수량 빈도해석 기법을 서술하였다. 3장에서는 연구에 활용된 실측유량 자료를 설명하였으며, 4장에서는 실측유량 자료를 사용한 홍수량 빈도해석 결과를 평가하였다. 최종적으로 5장에서는 본 연구의 결론 및 활용방안을 서술하였다.
2. 연구방법
2.1 불확실성을 고려한 Bayesian 추론 기반의 홍수량 빈도해석
한정된 수자원을 효율적으로 이용하고 홍수 및 가뭄 등과 같은 풍수해에 효율적으로 대응하기 위해서는 하천의 유량을 파악하는 것이 필수이다. 특히, 유량자료는 수자원의 효율적인 계획과 관리, 수공구조물 설계, 홍수예보 업무 등 이수, 치수, 수생태계 및 수질관리를 위한 가장 기본적이면서 중요한 자료이다. 홍수량 분석은 수문해석의 결과물로 수공구조물 설계 및 하천관리를 위한 기초적인 자료로 사용된다. 따라서 신뢰성 있는 수문해석은 수자원 관리계획의 성패를 좌우한다. 수문자료 빈도해석에 활용되는 확률분포형은 매개변수의 개수와 형태가 서로 다른 특징을 가지고 있으며 동일한 확률분포형을 선정하더라도 매개변수 추정 방법에 해석결과의 차이가 발생한다.
본 연구에서는 홍수량 또는 강수량 등의 극치 빈도해석 시에 일반적으로 가장 많이 사용되는 분포인 일반 극치 분포(generalized extreme value distribution, GEV)의 변형 형태이며 ‘한국 확률강우량도 개선 및 보완 연구’(MLT, 2011)에서 모든 관측소에 대하여 최적 확률분포형으로 채택한 Gumbel 분포를 적용하여 홍수량 빈도해석을 수행하였다(Kwon et al., 2008a; Lee et al., 2010; Solomon and Prince, 2013; Kang et al., 2015; Bhagat, 2017).
Fisher-Tippett Type-I분포로도 알려진 Gumbel 분포는 상대적으로 자료연한이 짧은 수문자료의 빈도해석에 널리 사용되고 있으며 Gumbel 분포의 확률밀도함수(Probability density function, PDF)와 누적분포함수(Cumulative distribution function, CDF)는 Eqs. (1a)~(1b)로 표시할 수 있다.
여기서 는 축척 매개변수로(Scale parameter) > 0이고 는 위치 매개변수(Location parameter)이며 는 의 범위를 가진다.
누적분포함수(F)가 주어진 조건에서 어떤 크기의 수문사상이 발생할 확률을 의미하는 초과확률(Exceedance probability)을 이용하여 재현기간에 따른 확률홍수량()은 Eq. (2)로 산정된다.
불확실성을 고려한 수문해석을 위하여 사전분포와 사후분포의 개념을 도입한 Bayesian 기법을 활용한 빈도해석 연구가 다수 진행되었다(Smith et al., 2015; Kim et al., 2018; Shin et al., 2020; Uranchimeg et al., 2020). Bayesian 기법은 다양한 분야에서 통계분석에 활용되고 있으며 빅 데이터의 활용이 증가함에 따라 유용한 통계적 도구로 활용되고 있다(Na and Yoo, 2021). Bayes’ 정리는 매개변수 와 확률변수 y의 결합확률분포는 사전분포(Prior distribution)와 우도(Likelihood)의 곱으로 추론되는 개념으로, 사후분포(Posterior distribution)는 사전분포와 우도의 곱에 비례하여 우도와 사후분포가 연속적으로 갱신되면서 불확실성을 정량적으로 해석할 수 있다는 장점이 있다(Kwon et al., 2008b). 즉 Eqs. (3a)~(3c)과 같이 확률분포형의 매개변수는 확률분포를 가지게 된다.
사전분포를 통한 매개변수 추정을 위한 Bayes’ 정리로 사후분포는 Eq. (4)와 같이 정리된다.
여기서, Y는 벡터형 자료로서 수문자료를 의미하며 는 확률분포형의 매개변수를 의미한다. 즉, 우변의 분모 는 주변분포(Marginal distribution)이고 우변의 분모 는 발생할 가능성을 고려한 우도함수를 나타내는 것으로 Eq. (5)와 같다.
수문자료를 특정 확률분포형에 적합하여 분석하기 위해서는 수문자료로부터 확률분포의 특성을 대표하는 매개변수를 추정하는 것이 필수적이다. 이를 위해서 본 연구에서는 MCMC (Markov Chain Monte Carlo) 기법을 활용하였다. MCMC 기법은 단변량(Univarate) 및 다변량(Multivariate) 등으로 가정된 확률밀도함수의 구조가 복잡하여 결합 확률(joint probability)을 정확히 고려하기 어려운 경우에 적용하는 방법으로 서로 독립인 형태의 변량 대신에 Markov Chain을 따르는 변량을 연속적으로 추출하여 사용하게 된다(Belkhiri and Kim, 2021). Markov Chain을 통해서 초기에 추출된 변량들은 연속적인 모의 과정으로 충분한 시간이 흐르게 되면 가정한 확률분포에 수렴하게 된다. 본 연구에서는 Bayesian MCMC 방법 중 깁스 표본법(Gibbs sampling)을 활용하여 매개변수를 추정하였다.
불확실성을 고려한 Bayesian 기법 홍수량 빈도해석 결과의 비교를 위해서 극치 빈도해석에 있어 널리 활용되고 있는 최우도법(Maximum likelihood method, ML)으로 산정된 매개변수를 활용하였다. 최우도법은 매개변수 추정이 편리하여 매개변수 추정시 효율성을 비교하는 기준으로 사용되며 매개변수 추정시 표본자료들의 발생할 결합확률 또는 확률분포 매개변수의 함수로 정의되는 우도함수를 결정하고, 이 우도함수(Likelihood function)를 최대화하는 매개변수를 최적 값으로 고려한다. 하지만 이상치가 있는 경우에 왜곡성을 재현하지 못하는 단점이 있다(Shin et al., 2014).
일반적으로 우도함수의 직접적 도출은 편리성의 사유로 대수 우도함수(Logarithmic likelihood function)를 주로 사용한다. 예를 들어, 표본자료가 길이 인 구간으로 나누어져 있으며, 수문자료()가 독립이고 표본이 균등분포로 주어져 있다고 가정하면, 에 대한 확률밀도의 값은 으로 정리된다. 즉, 수문자료는 서로 독립적이므로 수문자료가 발생할 결합 확률과 관측자료의 결합 확률이 최대화되는 것은 우도함수를 최대화하는 것과 같으며, i개의 매개변수()를 가지는 우도함수와 대수우도 함수의 형태는 Eqs. (6a)~(6c)과 같다.
3. 분석자료
3.1 수문조사를 통한 실측유량 자료
국내외적으로 수문조사는 국가의 물 관리 및 자연재해 예방, 지역 간 물 분쟁, 효율적인 용수공급, 수질관리 및 하천주변 지역의 친수환경 조성 및 홍수량 산정 등과 같이 하도구간에 존재하는 각종 수공구조물 설계의 기초자료를 확보하기 위하여 수행된다. 수문조사는 유량, 유사량, 증발산량 및 토양수분량 조사로 구분되며 수문조사의 가장 큰 비중을 차지하는 유량조사는 하천단면을 여러 개의 측선으로 구분하고 각 측선의 단면적과 유속을 측정하여 단면의 전체유량을 산정한 이후에 동시간의 하천 수위와의 관계로 정립되는 수위-유량관계곡선식을 이용하는 방법과 유속 또는 유량을 직접 측정할 수 있는 시설을 설치하여 실시간으로 유속 또는 유량을 측정하는 자동유량측정 방법 등이 있다.
체계적인 수문조사를 수행하여 일관성 있는 수문정보를 제공하기 위하여 한국수자원조사기술원(Korea institute of hydrological survey, KIHS)에서 수행하는 수문조사 중 유량조사는 4대강 홍수통제소 관할 수위관측소 지점을 대상으로 수행된다. 측정된 자료의 체계화된 품질관리 과정을 통하여 신뢰도 높은 수위-유량 관계곡선식을 개발하여 실측유량 자료를 생산하고 있으며 홍수예보지점 및 바다의 조석이나 하구의 배수영향을 받는 지점은 무인으로 유량을 취득할 수 있는 자동유량측정시설을 구축하여 실시간으로 유량자료를 취득한다(Fig. 1).
Table 1은 한국수자원조사기술원(前 유량조사사업단) 출범 이래 2007년부터 현재까지 15년간 수행한 연도별 유량측정 지점 수이다. 본 연구에서 활용한 실측유량 자료는 총 559개의 수위관측소 중 접근이 불가하거나 지형학적 제약조건으로 측정이 불가한 지점은 제외하였으며, 2007년부터 현재까지 수문조사가 수행된 지점의 유량자료는 수문조사 보고서에 수록된 자료를 활용하였다.
Table 1.
Current status of streamflow measurement stations performed by KIHS
| Year | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
| Site | 99 | 107 | 120 | 158 | 142 | 171 | 193 | 200 | 206 | 208 | 212 | 211 | 216 | 216 | 258 |
Table 2는 수위관측소별로 확보 가능한 유량자료 연한을 구분한 결과이며, 10년 이상의 장기적이고 연속적인 유량자료를 확보할 수 있는 지점은 108개소로(42.2%) 파악되었다. 권역별로는 낙동강 권역이 29%로 가장 높은 조사율을 확인하였으며 섬진강 유역이 8%로 가장 낮은 조사율로 확인되었다. 본 연구에서는 10년 이상의 연속자료 확보가 가능한 주요 지점 중 6개 지점을 대상으로 홍수량 빈도해석을 수행하였다. 권역별로는 한강 유역의 영월군(영월대교), 서울시(중랑교), 연천군(사랑교) 및 낙동강 유역의 함안군(계내리) 지점, 금강 유역의 청주시(흥덕교) 지점, 섬진강 유역의 구례군(구례교) 지점의 유량자료를 사용하였다.
Table 2.
Current status of data duration at streamflow stations each river basin (accrued)
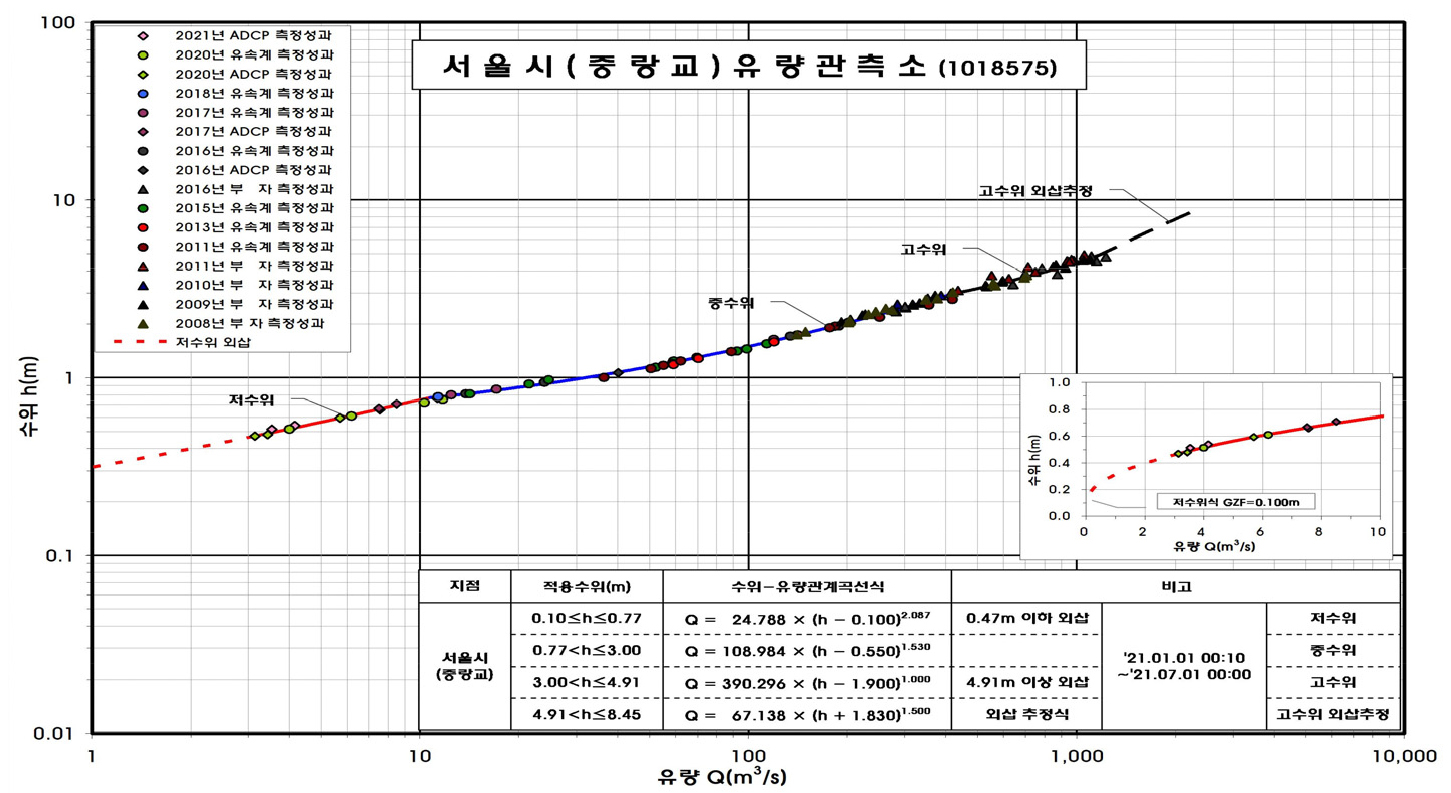
인명과 재산에 대한 피해가 예상될 때 하천구역과 배후지역에 하천수위 상승 예측을 통해 범람위험 가능성을 사전에 제공하고 대응시간 확보 및 피해 최소화를 위한 목적으로 홍수주의보와 홍수경보를 발령하는 홍수예보를 수행하고 있다. 홍수주의보는 계획홍수량의 50%를 초과하는 유량이 흐를 때의 수위와 최근 5년의 평균 저수위로부터 계획홍수위까지 60%에 해당하는 수위 도달시 발령되며 홍수경보는 계획홍수량 70%에 해당하는 유량이 흐를 때의 수위와 최근 5년의 평균 저수위로부터 계획홍수위까지 80%에 해당하는 수위 도달시 발령된다. Table 3은 분석지점의 위치정보 및 수위-유량관계곡선식(Fig. 2)을 적용하여 산정한 홍수주의보 유량과 홍수경보 유량을 나타낸다.
Table 3.
Station information and control flood by rating curve (unit : m3/s)
4. 연구결과
4.1 불확실성을 고려한 매개변수 추론 및 홍수량 빈도해석
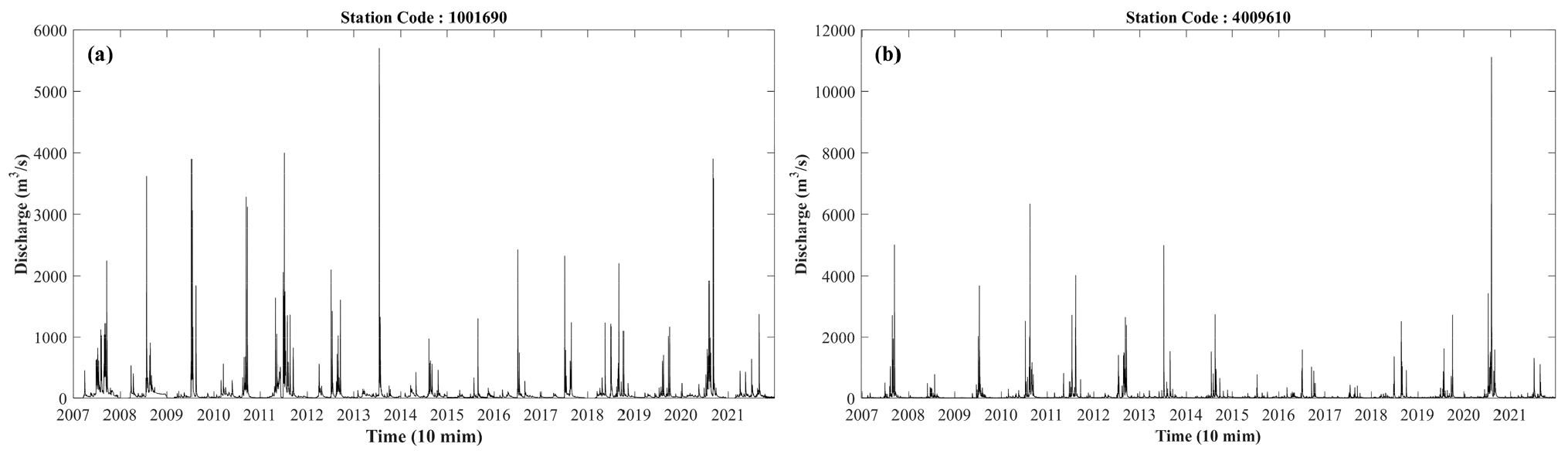
수문자료를 분류하는 개념에서 극치 수문자료는 일정기간(1년) 동안의 자료로 고려되고, 연 최대치(Annual maximum)와 비매년 최대치(Non-annual maximum)로 구분할 수 있다. Fig. 3은 구례군(구례교) 지점과 영월군(영월대교) 지점의 10분 단위 유량자료의 시계열을 도시한 결과이다.
관측 수문자료가 가용한 경우 실제 관측된 자료를 활용하여 빈도해석을 수행하는 것이 가장 적절한 방법으로 알려져 있다(Stedinger et al., 1993). 그러나 유량자료는 공인된 계측자료를 활용해야 할 뿐만 아니라, 강수량 자료에 비하여 상대적으로 누적된 자료의 연한이 짧아 빈도해석 시 불확실성이 크게 발생한다는 단점이 있다(Chae et al., 2018). 본 연구에서는 활용한 유량자료의 자료연한은 15년으로 연 최대치 계열을 추출하는 경우 신뢰성 있는 빈도해석을 위한 조건에 제약성이 있어 확보된 각 지점별 홍수사상의 유량자료를 활용하여 빈도해석을 수행하였다.
앞서 언급하였듯이, 본 연구에서는 홍수량 빈도해석에 활용되는 유량자료에 대한 최적 확률분포형으로 Gumbel 분포를 가정하였으며, Gumbel 분포 확률지(Probability plot)를 활용하여 비교함과 동시에 경험적 누적분포함수(Empirical distribution function)를 도시하여 유량자료에 대한 확률분포형의 적합성 여부를 검토하였다. 적합도 검정 분석결과는 선정된 모든 지점의 유량자료에 대한 확률분포형이 Gumbel 분포 확률지와 계단 형태로 나타나는 경험적 누적분포에 근접하여 유량자료에 대한 확률분포로 Gumbel 분포의 선정이 적합하였음을 확인하였으며 대표 지점으로 연천군(사랑교) 결과를 Fig. 4에 도시하였다.
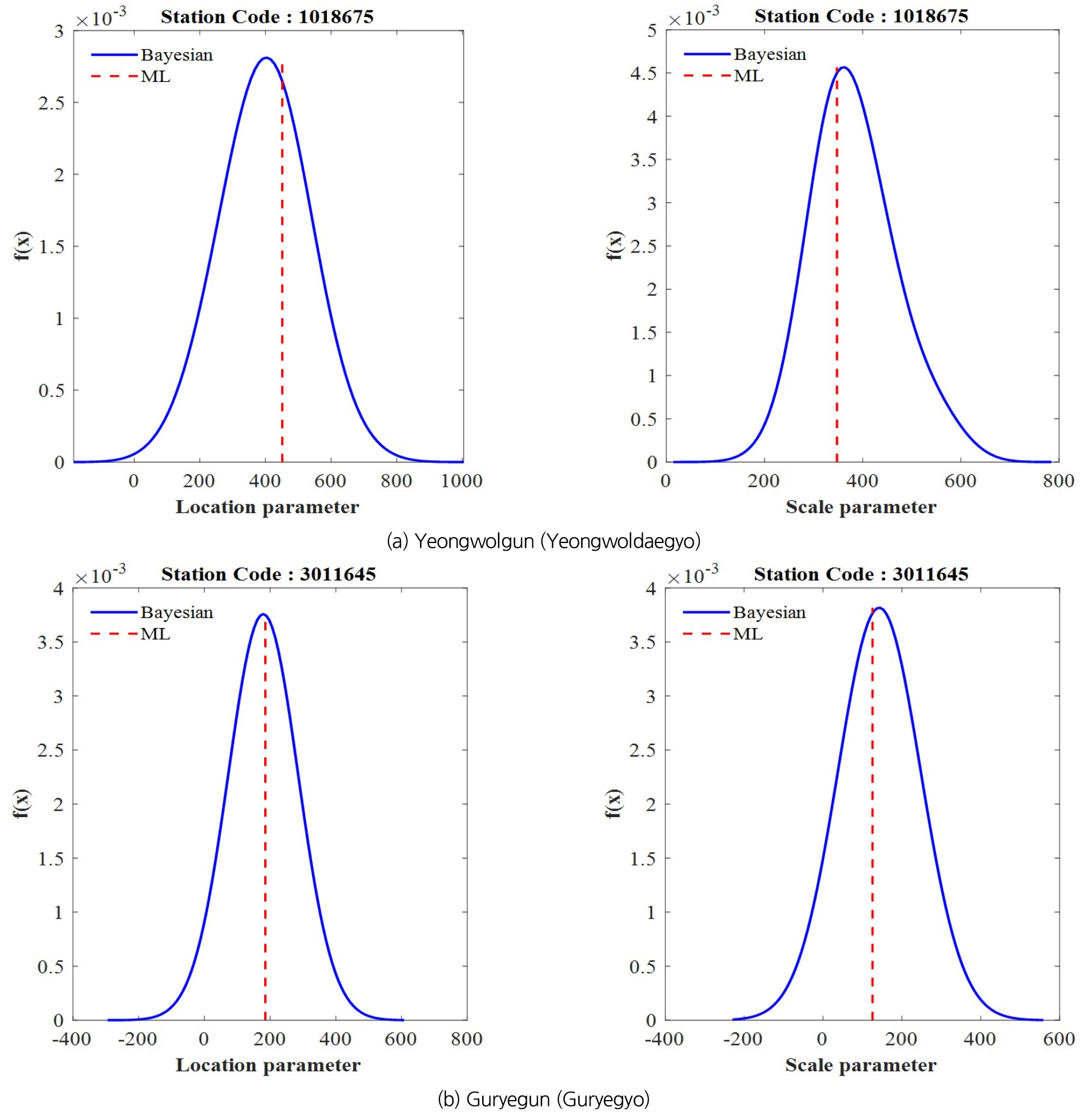
Fig. 5는 Bayesian 기법을 통하여 도출된 매개변수 분포를 도시한 결과이다. 여기서, 파란색 실선은 Bayesian 기법으로 도출된 매개변수의 사후분포를 의미하며, 붉은색 점선은 최우도법을 적용하여 산정된 매개변수이다. 결과적으로, 최우도법에 의해 산정된 매개변수가 Bayesian 기법을 통해 추론된 매개변수 사후분포 확률밀도함수의 중앙값 근처에 적절하게 포함하고 있는 것을 확인하였으며, Table 4에 정리된 매개변수의 중앙값(Median)과 비교를 통해 Bayesian 기법을 통해 도출된 매개변수가 적절하게 도출되었음을 확인할 수 있다.
Table 4.
Station information and control flood by rating curve (unit : m3/s)
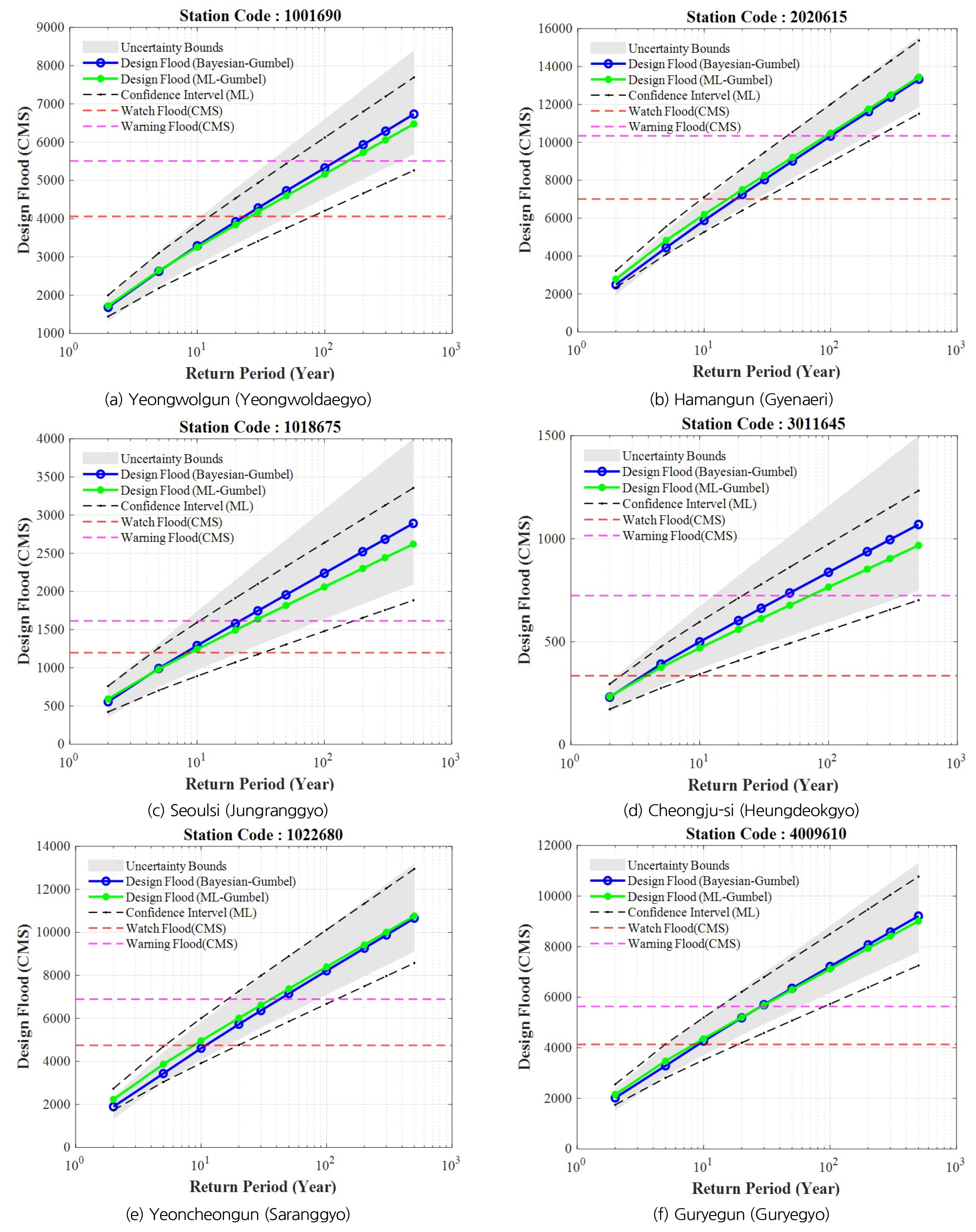
Tables 5~7은 Bayesian 기법과 최우도법으로 추정한 매개변수에 의한 빈도별 홍수량 산정 결과이며, Fig. 6은 빈도별 홍수량을 도시한 결과이다. Bayesian 기법으로 산정된 빈도별 홍수량을 홍수예보의 관점에서 홍수주의보 및 홍수경보를 발령하는 유량과 비교하였을 때, 홍수주의보를 발령하는 상태의 유량은 분석지점에서 약 5~20년 빈도에 구간에, 홍수경보를 발령하는 상태의 유량의 경우 분석지점에서 약 30~100년 빈도의 구간에 포함되고 있는 것을 확인하였다. 유역의 특성을 반영하여 기존의 홍수주의보 및 홍수경보에 해당하는 유량은 영월군(영월대교)와 함안군(계내리) 지점과 같이 계획홍수량이 상대적으로 큰 경우 고빈도의 범위에 포함되고 있으며 상대적으로 계획홍수량이 작은 청주시(흥덕교) 지점은 저빈도의 범위에 포함되고 있다.
Table 5.
Parameter estimation result using Bayesian model and ML
Table 6.
The estimated design flood according to Bayesian-based return periods (unit : m3/s)
Table 7.
The estimated design flood according to ML-based return periods (unit : m3/s)
매개변수 불확실성 구간이 좌우대칭의 형태는 나타내는 것은 오차의 분포형을 정규분포로 가정한 사유로 판단되며, 최우도법을 통해 추정한 6개 지점의 빈도별 홍수량에 대한 신뢰구간과 Bayesian 기법을 통해 산정된 매개변수의 불확실성 구간이 매개변수에 의해 다소 차이가 발생하였으나, 유사한 거동 특성을 보이는 것을 확인하였다. 즉, Bayesian 기법으로 유량자료를 직접빈도 해석하여 산정된 재현기간별 홍수량을 홍수예보 과정에서 사용되는 홍수주의보 및 홍수경보를 발령하는 유량과 비교한 결과는 정량적으로 유의미한 결과가 도출되었음을 의미한다. 이러한 결과에 기반하여, 향후 체계적이고 지속적인 수문조사를 통하여 유량자료를 확보한다면 기상자료에 의존하는 수문분석과 비교하여 현실성 있는 홍수분석이 가능할 것으로 판단된다.
5. 결 론
기후변화가 점차 가시화됨에 따라 수자원은 국가 재산의 중요한 자원으로 부각되고 있다. 2020년 총 109건의 홍수특보(주의보 78건, 경보 31건)가 발령되었다. 이와 같이, 지구 온난화 현상으로 거의 매년 막대한 홍수 등 수많은 재산과 인명피해가 나타나고 있어 효율적인 하천관리와 홍수예·경보를 위해 정확한 홍수량 산정의 중요성이 제기되고 있다. 수자원의 효율적인 관리를 목적으로 홍수피해를 저감하고 환경친화적인 수자원의 역할을 제대로 자리매김하기 위하여 무엇보다 필요한 사항은 신뢰성 있는 유량자료의 확보를 통해 실측자료에 기반한 홍수량 빈도해석을 수행하는 것이다. 본 연구에서는 공인된 실측유량 자료를 활용하여 홍수량 빈도해석을 수행하였으며 다음과 같이 결과를 정리하였다.
첫째, 하천 유량의 활용성을 높이기 위해서는 실시간 자료와 장기간 축적된 연속 유량자료가 필요하다. 미국, 유럽 및 일본 등은 지속적으로 재정투자를 하여 최소 30년~100년 이상의 유량자료를 확보하여 국가 수자원의 계획수립 및 재해방지 목적으로 장기간의 수문자료를 활용하고 있지만, 우리나라는 30년 이상의 연속된 유량자료를 확보한 지점이 극소수인 실정이다. 기후변동성에 따른 집중호우, 태풍, 가뭄 및 홍수 등의 풍수해가 우리의 일상생활에 직면하고 있는 상황에서 극한 수문사상으로 유발되는 도시홍수 및 지류하천의 홍수피해 등의 대응을 위하여 안정적이고 지속적인 수문조사가 수행되어야 할 것으로 판단된다.
둘째, 유량측정의 궁극적인 목적은 정확하고 신뢰성 있는 유량자료를 확보함으로써 이수 및 치수 사업, 국가 수자원 계획 등에 기초자료로써 활용되는 것이다. 이론적으로 홍수량 빈도해석에 가장 적합한 실측유량을 기반으로 최우도법과 Bayesian 기법을 활용하여 빈도해석을 수행한 결과, 자료의 길이가 비교적 길지 않음에도 불구하고 산정된 확률홍수량은 기존의 강우-유출 모형을 적용하여 산정된 확률홍수량과 유사한 결과가 도출되었다. 홍수예보에 사용되는 수위를 수위-유량 관계 곡선식을 대입하여 산정한 유량과 비교 한 결과 홍수주의보와 홍수경보에 해당하는 유량의 적절성을 확인하였다.
셋째, 빈도해석을 수행하는 과정에서 최적의 매개변수를 산정하기 위하여 도입한 Bayesian 기법은 강우량 자료와 비교해 상대적으로 자료의 수가 부족한 실측 유량자료를 직접적으로 적용하는 한계성을 효과적으로 개선하였으며, 사후분포를 통한 불확실성을 정량화하였다. 최우도법을 통해 산정된 확률홍수량에 대한 신뢰구간과 Bayesian 기법을 통해 추정된 불확실성 구간을 함께 도시하여 비교하였을 때 다소 차이가 발생하였으나, 이는 홍수량 빈도해석시 자료가 부족할 경우 과대추정 될 수 있음을 의미하며 지속해서 실측유량 자료가 축적된다면 충분히 신뢰성 있는 결과가 도출될 수 있음을 의미하는 것으로 해석할 수 있다.
기후변동성으로 인하여 극한홍수 발생에 대한 불확실성이 점차 증가하고 있는 시점에서, 실측 유량자료를 활용한 본 연구의 결과는 기존 빈도해석 방법에서 벗어나 새로운 기법의 도입을 통해 제한적인 자료를 활용한다는 점과 함께 매개변수의 불확실성을 정량화하는 점에서 차별성을 갖는다 할 수 있다. 즉, 실측 유량자료를 통해 확률홍수량을 산정하는데 있어 상대적으로 연구가 미진했던 불확실성의 신뢰성을 제고하는데 목적이 있으며, 향후 실측 수문자료가 충분히 축적된다면 수자원 및 하천의 효율적인 관리를 위한 목적으로 다양하게 활용이 가능할 것으로 판단된다.