Estimation of evaporation from water surface in Yongdam Dam using the empirical evaporation equaion

Minwoo Park; Joo-Heon Lee; Yong-kyu Lim; Hyun-Han Kwon

doi:10.3741/JKWRA.2024.57.2.139

Preview

Research Article

Journal of Korea Water Resources Association. 29 February 2024. 139-150
https://doi.org/10.3741/JKWRA.2024.57.2.139

Estimation of evaporation from water surface in Yongdam Dam using the empirical evaporation equaion

경험적 증발량 공식을 적용한 용담댐 시험유역의 수면증발량 추정

Minwoo Park^a

Joo-Heon Lee^b

Yong-kyu Lim^c

Hyun-Han Kwon^d^*

박 민우^a

이 주헌^b

임 용규^c

권 현한^d^*

^aMaster Course, Department of Civil and Environmental Engineering, Sejong University, Seoul, Korea

^bProfessor, Department of Civil Engineering, Joongbu University, Goyang, Korea

^cWater Resources Management Research & Planning Department., General Manager of Water Supply and Demand Analysis Team, K-water, Daejeon, Korea

^dProfessor, Department of Civil & Environmental Engineering, Sejong University, Seoul, Korea

^a세종대학교 건설환경공학과 석사과정

^b중부대학교 토목공학과 교수

^c한국수자원공사 물관리기획처 물수요공급분석부 부장

^d세종대학교 건설환경공학과 교수

^{*Corresponding Author}

ABSTRACT

This study introduced a method of estimating water surface evaporation using the physical-based Penman combination equation (PCE) and the Penman wind function (PWF). A set of regression parameters in the PCE and PWF models were optimized by using the observed evaporation data for the period 2016-2017 in the Yongdam Dam watershed, and their effectiveness was explored. The estimated evaporation over the Deokyu Mountain flux tower demonstrated that the PWF method appears to have more improved results in terms of correlation, but both methods showed overestimation. Further, the PWF method was applied to the observed hydro-meteorological data on the surface of Yongdam Lake. The PWF method outperformed the PCE in the estimation of water surface evaporation in terms of goodness-of-fit measure and visual evaluation. Future studies will focus on a regionalization process which can be effective in estimating water surface evaporation for the ungauged area by linking hydrometeorological characteristics and regression parameters.

Keywords

Water resources management

Evaporation

Latent heat flux

PCE

Wind functiom

Uncertainty

본 연구에서는 물리 기반 증발량 경험식인 Penman 혼합식(Penman combination equation, PCE)과 경험적인 바람 함수(Penman wind function, PWF)를 이용한 저수지 증발량 추정 방법을 제시하였다. 용담댐 시험유역에서 2016-2018년 기간의 실측 증발량 자료를 이용하여 두 가지 경험식에 매개변수를 추정하고 적용성을 검토하였다. 용담댐 시험유역 중 덕유산 플럭스 타워에서 PWF와 PCE에 대해 증발량을 평가한 결과, PWF 방법이 상관성 측면에서 더욱 개선된 결과를 보여주었지만, 두 가지 방법 모두 과대 추정 현상을 나타내었다. 용담호 수면 위에서 관측된 기상자료를 활용하여 PWF 방법을 통한 증발량을 평가하였으며, 관측 수면증발량과 통계적 지표 및 시각적 평가에서 우수한 성능을 확인하였다. 향후 본 연구를 통해 산정된 매개변수를 이용하여 저수지 수면 증발량을 간접적으로 추정할 수 있을 것으로 판단되나, 정확한 저수지 수면증발량 추정을 위해서는 타 댐들에 수면 증발량을 종합적으로 연계한 지역화 연구도 필요할 것으로 판단된다.

키워드

수자원 관리

증발량

잠열 플럭스

PCE

바람 함수

불확실성

MAIN

1. 서 론
2. 연구방법
2.1 Dalton 법칙 기반의 바람 함수(PWF)
2.2 Penman Combination Equation (PCE)
2.3 PCE와 PWF 적용방안
3. 연구결과
3.1 대상유역
3.2 분석결과
4. 결 론

1. 서 론

최근 기후변화로 인한 기후변동성 증가로 인해 수문학적 순환(hydrological cycle) 측면에서 변동성도 증가하고 있으며, 이로 인해 수자원 관리 측면에서도 불확실성이 확대되고 있다. 증발은 가용 수자원을 평가하는 데 핵심적인 수문 변수로서, 수자원 관리 측면에서 증발량의 정량적인 평가는 매우 중요하다. 특히 기후변화에 따른 온도 증가로 인해 야기되는 증발량 증가는 수자원 확보 측면에서 더욱 중요해지고 있다. 증발로 인한 수자원 손실은 사회경제적으로 영향을 미치게 되며 우리나라와 같이 생공용수 수원으로 댐 용수를 대부분 활용하는 경우 수자원 안정적 확보 측면에서 더욱 중요성이 크다. 국내외 연구를 살펴보면 증발로 인한 수자원 손실로 인해 용수확보에 어려움이 발생한 사례(Pérez et al., 2020)가 있었으며, 200만 인구의 도시에서 사용되는 물의 27%에 해당하는 수자원이 증발로 인해 손실(Alvarez et al., 2008)된 사례도 보고되고 있다. 이밖에 튀르키예의 호수와 댐에서 발생하는 연간 증발량을 분석한 결과, 증발량이 생활용수와 산업용수의 사용량보다 더 높게 나타났으며(Gökbulak and Özhan, 2006), 호주의 일부 지역에서는 저수지에 저장된 물의 40%가 증발로 인해 수자원 손실이 발생한 사례도 보고되고 있다. 장기간에 걸친 증발량의 변화는 지표 및 대기 간의 수문 반응을 변화시키고 농작물의 경작에도 영향을 미치며, 해안지방에서는 하천 유입량 등의 변화로 생태계의 변화를 가져올 수 있다(Lee et al., 2007). 따라서, 증발을 이해하고 모니터링하는 것은 효과적인 수자원 관리뿐 아니라 관개계획, 생태계 측면에서도 매우 중요하다.

증발은 액체 상태의 물이 증기로 변화하여 대기 중으로 유입되는 과정으로, 하천에서 발생하는 증발량의 정량화는 효율적인 하천관리에 유용하다. 그러나 우리나라의 수자원 계획 시 하천 및 저수지 증발 손실이 충분히 고려되고 있지 않다. 이는 현실적으로 증발에 의한 수자원 손실을 정확히 평가하는 것이 어려운 것도 하나에 사유로 고려될 수 있다. 즉, 하천 및 저수지 증발의 정량화에 대한 어려움은 주로 직접 측정과 관련된 복잡성에 기인한다. 우리나라는 물순환 분석이 유역에 집중되어 있어 증발량을 추정하기 위해 활용되는 수문 기상자료가 부족한 실정이며, 증발 접시를 활용한 직접적인 관측 방법은 매우 제한적이다. 증발을 측정하기 위해 활용하는 증발 접시는 큰 호수의 증발현상이나 지표면과 대기의 상호 작용으로 인해 일어나는 증발 등을 추정할 수 있는 토대를 제공하기 때문에 수자원 분야나 농업 분야에 유용하게 활용되고 있다. 그러나 직접 관측은 다양한 물리적 및 기후적 환경 조건에서 저수지, 하천, 육지에 대한 고유한 증발량을 구분하여 나타낼 수 없고, 시간과 자원 소모가 큰 증발 팬을 활용한 관측 방법 특성상 시험유역과 같은 특정 장소에서의 연구목적에 한정되어 사용하는 것이 일반적이다. 특히 작은 하천의 경우, 하천의 증발 표면적이 작아 모니터링하는데 어려움이 있으며 에디 공분산과 같은 미기상학적 측정 방법의 적용 또한 쉽지 않다(Guenther et al., 2012; Szeitz and Moore, 2020).

앞서 언급하였듯이 미기상학적 방법을 포함한 방법들은 현장 관측을 원칙으로 진행되어, 실제 관측이 쉽지 않다. 반면 기상인자를 통한 증발량 추정 방법은 기상인자만 구축되어 있다면 다른 추정 방법과 비교하여 용이하게 증발량을 추정할 수 있다(Kim et al., 2021). 즉, 증발량은 증발 현상을 지배하는 주요 인자들의 물리적 관계를 설정하는 경험적 방정식을 통해 추정할 수 있다. 증발 현상은 공기와 수증기의 혼합체가 포화상태에 도달할 때까지 계속되며 증기압에 영향을 미치는 인자가 곧 증발 현상을 지배하는 인자들이며 물과 공기의 온도, 바람, 상대습도, 대기압, 수질 및 수표면의 성질과 형상 등이 이에 속한다(Yoon, 2007). 증발량을 산정하는 방법에는 물 수지 방법, 에너지 수지 방법, 공기 동역학적 방법, 에너지 수지 방법과 공기 동역학적 방법을 혼합 적용하는 방법 등이 있으며, 증발에 관여하는 물 공급에 제약이 없다는 가정 아래 기상자료와 태양방사 에너지 등의 자료를 이용하여 증발량을 산정한다(Yoon, 2007).

본 연구에서는 저수지 증발량을 정량적으로 추정할 수 있는 증발량 경험식을 유도하는 데 목적이 있으며, 용담댐 유역을 대상으로 접근방법에 대한 적합성을 평가하고자 한다. 수체에 증발과 관련된 열 플럭스인 잠열 플럭스는 수체의 열 손실 메커니즘의 중요한 인자로 인식되고 있다. 잠열은 증발 시 액체에서 증기로 또는 응축 시 증기에서 액체로 물의 상변화와 관련된 에너지 전달을 나타내며 온도와 밀접한 관계가 있다. 수체 표면의 수증기압은 수온에 따라 지수적으로 증가하며, 수온의 부정확성은 수면의 포화 수증기압에 부정확한 결과를 초래할 수 있다(Wang et al., 2019). 따라서, 수온은 증발량의 정확성에 영향을 미치게 된다. 다양한 규모의 수체에서 증발 플럭스를 측정하는 것과 시간 단위의 하천 온도 모델 도입을 통해 증발 플럭스의 추정을 개선하는 것은 수자원 관리 측면에서 매우 중요한 것으로 인식되고 있다(Maheu et al., 2014). 이러한 관점에서 수체 온도와 관련된 증발을 모델링하는 것은 저수지 내 증발량을 산정하는 것 뿐만 아니라 증발과 관련된 열 플럭스의 전달을 이해하는데 중요한 의미가 있다. 다양한 환경 조건에서 증발을 추정하기 위해 여러 가지 수학적 모델과 공식이 개발되었으며, 수체의 열역학과 관련된 연구에서는 일반적으로 Penman 혼합식(Penman Combination Equation, PCE)과 경험적인 바람 함수(Penman Wind Function, PWF)를 활용하여 잠열 플럭스를 추정하고, 이를 토대로 증발량을 산정한다(Moore and Leach, 2021). 그러나 두 방법 모두 관측된 저수지 증발량을 이용하여 지역적 상수들을 결정하는 과정이 필요하며, 이러한 매개변수 추정 과정 없이 사용되는 경우 증발량의 과대 또는 과소 추정되는 경우가 많아 활용하는 데 주의가 필요하다.

본 연구는 국외 선행연구에서 제시한 증발량 산정 경험식의 국내 저수지에 대한 적용성을 검토하는 데 목적이 있다. 이에 선행연구에서 제안된 증발량 산정방법인 PCE와 PWF을 적용하였으며, 용담댐 시험유역의 수문 기상자료를 활용하여 증발량을 추정하였다. 증발량 결과를 통해 각 식의 정확성을 비교함으로써 국내 저수지에 적용성을 평가하였다. 본 연구에서 제시하는 방법론에 대한 적용성 등을 종합적으로 살펴보기 위해서 용담댐 호내 증발량 뿐만 아니라, 내륙에서 관측중인 지표 증발량에 대해서도 평가를 실시하였다.

본 논문의 구성은 다음과 같다. 1장에서는 본 연구 내용의 전반적인 내용에 관해 서술하였으며, 2장에서는 선행연구에서 적용한 증발량 산정 경험식에 대해 자세하게 소개하여 국내 수문 기상자료를 활용한 적용방안에 대해 제시하였다. 3장에서는 각 경험식의 매개변수를 관측값에 대해 최적화 후 해당 유역에 대한 증발량을 평가하였으며, 4장에서는 결론 및 향후 연구 방향에 관해 서술하였다.

2. 연구방법

증발이란 열을 흡수함으로써 액체 상태에서 기체 상태로 상전이가 일어나는 과정이며, 온도, 증발 표면적, 습도, 풍속, 순 복사에너지 등에 따라 달라진다. 저수지에서 증발량 측정은 계절별 수위 및 유입량 변화 등 시공간적으로 변동성 및 운영상 어려움으로 직접 관측된 자료 취득은 어려우며, 일반적으로 경험식을 통해 증발량을 추정하고 있다. 본 절에서는 일반적으로 증발량을 추정할 때 사용되는 경험식과 기상변수를 소개하였으며, 저수지 증발식으로 공식화하는 방안을 제시하였다. 국내 수문 기상자료를 활용하여 기존 경험식을 통해 수면 증발량을 추정하였고, 관측자료를 기반으로 경험식의 매개변수를 검 보정하고, 이를 통해 추정된 수면증발량과 관측 수면증발량을 비교하였다.

2.1 Dalton 법칙 기반의 바람 함수(PWF)

증발을 산정하는 데 사용되는 경험식 중에는 난류 이송 공식으로 표현되는 공기역학의 기본 원리를 기반으로 증발을 추정하는 바람 함수(PWF)가 있다. PWF는 Dalton (1802) 법칙에 기반 한 경험식이며, 지역에 따른 경험적인 매개변수를 통해 비교적 용이하게 증발률 산정이 가능하다는 장점이 있다. Dalton 법칙에 기반한 바람 함수는 Eq. (1)과 같이 나타낸다. Eq. (1)은 수증기가 대기 중으로 증발할 때 공기와 결합하여 혼합물을 만들고, 이 혼합물에 작용하는 전체 압력은 증기압과 건조한 공기의 압력의 합과 같은 것을 표현한다. 이는 자유표면으로부터 물 분자의 이동이 증기압의 연직 방향 기울기에 정비례한다는 것을 의미한다.

(1)

E = (a + b \times u) (e_{0} - e_{a})

여기서, u는 풍속(wind speed, m/s)을 나타내며, a, b는 지표면과 공기에서 증기압과 풍속의 특정 조건에 따라 달라지는 경험적 계수를 나타내며, 증발률을 산정할 때는 이 계수들을 지역에 따라 보정한다. $e_{0}$ 는 표면의 증기압(kPa)을 나타내고, $e_{a}$ 는 주변 대기의 증기압(kPa)을 나타낸다. 개방된 수로의 흐름에서, 지하수의 움직임이 현저한 지역의 수로 바닥 근처를 제외하고 수온은 보통 그 깊이에 대해 전체적으로 균일해야 한다. 따라서 표면의 증기압 $e_{0}$ 은 일반적으로 주변 수온에서의 포화증기압으로 산정된다(Moore and Leach, 2021). 최종적으로 PWF는 Eq. (2)와 같이 표현한다.

(2)

E = (a + b \times u) (e_{s a t a t w a t e r} - e_{a})

여기서, $e_{s a t a t w a t e r}$ 은 수표면 위 수온에 대한 포화증기압(kPa)을 나타내며, Tetens (1930)공식을 기반으로 온도에 따른 포화증기압 공식에 따라 산정된다. 온도 $T$ 가 0℃보다 낮을 때 포화증기압 $e_{s a t a t w a t e r}$ 는 Eq. (3)과 같이 표현되며(Murray et al., 1966), 온도 $T$ 가 0℃보다 높을 때 포화증기압 $e_{s a t a t w a t e r}$ 는 Eq. (4)와 같이 표현한다(Monteith and Unsworth, 2013). 수표면 위 주변 대기의 증기압 $e_{a}$ 는 주변 대기의 포화증기압 $e_{s a t a t a i r}$ 의 상대습도 RH (relative humidity, %)로부터 산정되며, Eq. (5)와 같다.

(3)

e_{s a t a t a i r} = 0.6108 \times e^{\frac{21.88 T}{T + 265.5}}

(4)

e_{s a t a t a i r} = 0.6108 \times e^{\frac{17.27 T}{T + 237.3}}

(5)

e_{a i r} = e_{s a t a t a i r} \times R H

2.2 Penman Combination Equation (PCE)

공기 동역학적 방법과 에너지 수지 방법을 혼합한 혼합 적용 방법은 증발량을 추정하기 위해 수문 기상 분야에서 널리 사용되는 대표적인 경험식이다. Penman (1948)은 Eulerian 원리를 이용하여 에너지 수지 모델을 구축하여 증발식 Penman Combination Equation (PCE)을 제안하였다. PCE는 지표면에서 발생하는 순 복사에너지 균형과 표면에너지의 결합을 통해 개발되었으며, 포화증기압과 수온의 관계를 고려한 선형 근사를 이용하여 바람 함수와 에너지 수지를 혼합하여 개발되었다. Eulerian 원리에 따른 에너지 평형식은 Eq. (6)과 같다.

(6)

\bar{d} ρ_{w} c_{p w} \frac{σ T_{w}}{σ t} = R_{n} + Q_{h} - L E + Q_{b} - \bar{d} ρ_{w} c_{p w} v \frac{σ T_{w}}{σ x}

여기서, $\bar{d}$ 는 평균 수심(m), $ρ_{w}$ 는 물의 밀도(kg/m³), $c_{p w}$ 는 물의 비열(J/kg/°C), $T_{w}$ 는 수온(°C), $t$ 는 시간(s), $R_{n}$ 은 순 복사량(net radiation, W/m²), $Q_{h}$ 는 현열 플럭스(sensible heat flux, W/m²), $L$ 은 증발 잠열(latent heat of vaporization, J/kg), $E$ 는 증발률(kg/m²/s), $Q_{b}$ 는 바닥 열 플럭스(the bed heat flux, W/m²), $v$ 는 평균 유속(m/s), $x$ 는 수로 중 위치(m)를 나타낸다. Eq. (6)에서 수온의 변화로 인한 축열의 변동(the rate of heat storage change associated with the water column)을 𝜙로 정의할 수 있으며, Eq. (7)과 같이 나타낼 수 있다.

(7)

ϕ = \bar{d} ρ_{w} c_{p w} [\frac{σ T_{w}}{σ t} + v \frac{σ T_{w}}{σ x}] = Q_{h} + R_{n} + Q_{b} - L E

증발하는 표면이 포화상태라고 가정했을 때, 현열 플럭스 $Q_{h}$ 와 증발률 $E$ 는 공기동역학 방정식을 사용하여 수학적으로 표현할 수 있으며, Eqs. (8) and (9)와 같다.

(8)

Q_{h} = ρ_{a} c_{p a} \frac{(T_{a} - T_{0})}{r}

(9)

E = \frac{ρ_{a} ϵ}{p_{a}} \frac{e_{s} (T_{0}) - e_{s} (T_{a})}{r} + \frac{ρ_{a} ϵ}{p_{a}} \frac{e_{s} (T_{a}) - e_{a}}{r}

여기서, $ρ_{a}$ 는 공기의 밀도(kg/m³), $c_{p a}$ 는 공기의 비열(J/kg/°C), $T_{0}$ 와 $T_{a}$ 는 수표면과 대기의 온도(°C), $r$ 은 표면과 주변 대기 사이의 열 전달에 대한 저항(s/m), 𝜖는 물과 공기의 몰 질량비, $p_{a}$ 는 대기압(kPa), $e_{s}$ 와 $e_{a}$ 는 수표면과 대기의 증기압(kPa)을 나타낸다. Eq. (10)은 온도 $T_{0}$ 에서의 포화증기압 $e_{s} (T_{0})$ 을 나타내며 포화증기압 곡선의 도함수 $s$ 는 Eq. (11)을 통해 계산된다.

(10)

e_{s} (T_{0}) = e_{s} (T_{a}) + s (T_{0} - T_{a})

(11)

s = \frac{4098.171 ∙ 0.611 ∙ e^{\frac{17.27 T}{237.3 + T}}}{(237.37 + T)^{2}}

에너지 평형 방정식에서 얻은 Eq. (7)과 포화증기압 곡선에서 얻은 Eq. (10)을 공기역학 방정식에서 얻은 Eqs. (8) and (9)의 결합식에 대입하면, 증발률 $E$ 에 대한 결과식은 Eq. (12)로 나타낼 수 있다.

(12)

E = \frac{s}{s + γ} \frac{(R_{n} - ϕ + Q_{b})}{ρ_{w} L_{v}} + \frac{γ}{s + γ} \frac{ρ_{a} ϵ}{p_{a}} \frac{(e_{0} - e_{a})}{r}

여기서 $L_{v}$ 는 잠재 증기화열(Latent heat of vaporization, J/kg)을 나타내며, 𝛾는 습도계 상수(psychrometric constant, kPa/°C)를 나타내며, Eq. (13)과 같다.

(13)

γ = \frac{p_{a} c_{p a}}{ϵ L_{v}}

하천 흐름을 장기적인 관점으로 봤을 때 하천 바닥 열 플럭스 $Q_{b}$ 와 축열의 변동𝜙는 실질적으로 순 복사에너지 $R_{n}$ 에 비해 상당히 작다. 따라서 $Q_{b}$ 와 𝜙는 Eq. (12)에서 제외할 수 있고, 결과적으로 $R_{n} - ϕ + Q_{b} \approx R_{n}$ 로 나타낼 수 있다. Eq. (12)의 두 번째 항은 수증기의 이동에 대한 공기동역학적 표현으로써, 일반적으로 경험적 계수 $a, b$ 에 대한 바람 함수로 표현할 수 있다. 최종적으로 PCE는 Eq. (14)와 같이 나타낸다.

(14)

E = \frac{s}{s + γ} \frac{R_{n}}{ρ_{w} L_{v}} + \frac{γ}{s + γ} (a + b ∙ u) (e_{s a t a t a i r} - e_{a i r})

2.3 PCE와 PWF 적용방안

PCE와 PWF는 기상인자를 이용하여 증발을 산정할 수 있는 식으로 개발되었으므로 육지 및 저수지에 적용하기 위해서는 기상학적 자료가 필요하다. 그러나 앞서 언급하였듯이 국내 물순환 분석의 초점은 수면으로부터 직접 관측되는 기상정보를 얻기에는 어려움이 있다. 이에 본 연구에서는 다음과 같은 단계로 PCE와 PWF를 저수지의 수면 증발식으로 공식화하는 방안을 제시하였다. 먼저, 증발식의 다양한 기상인자가 구축된 육지기반의 기상 관측소를 선정한다. 이때, 대상 지점에서 모든 기상정보를 직접 측정하는 것이 가장 합리적이나, 정보 취득이 어려운 경우 목표 지점으로부터 1 km 내외에서 가까운 기상 관측소를 선택해야 한다. 증발식을 통해 하천 온도를 추정하는 선행연구들에 따르면 수면 위에서 직접 기상 정보를 취득하거나, 태양 복사 에너지와 같은 직접 관측이 어려운 경우 1 km 이상 떨어진 내륙 지점에서 수집된 기상 정보를 활용할 수 있다고 알려지고 있다. 둘째, PCE와 PWF를 대상 유역에 적용하고 증발량을 산정한다. 셋째, 각 추정치를 실제 관측치와 비교하여 우수한 결과를 도출하는 증발식을 선정한다. 넷째, 수면 위의 기상자료가 구축된 지점에 대해 선정한 증발식을 적용하여 수면증발량을 추정한다. 마지막으로, 증발량 추정치와 관측치의 상관성분석을 통해 증발식을 평가한다.

본 연구에서 활용된 PCE는 수온 자료가 필요하지 않지만, PWF는 수온 자료가 활용된다. 그러나 일반적으로 수표면에서의 수온은 대기 온도와 차이를 가지나 수온의 측정은 기온의 측정보다 번거로우므로 수표면 온도에서의 포화증기압 대신 대기 온도에서의 포화증기압을 사용하여 증발량을 산정한 연구 사례도 있다(Yoon, 2007). 따라서, 육지 기반에서 적용된 PWF 방법의 경우 수표면에 대한 포화증기압을 대기 온도에 대한 포화증기압으로 사용하였다. PWF의 기상인자들을 육지 기반 관측소에서 측정하여 증발량을 추정하는 경우 수면 위에서 측정된 기상자료와 상당히 다를 수 있기 때문에, 수면증발량에 대해 편향된 추정치를 제공할 수 있다. 단기적인 해결 방법은 현장 특성의 유사성에 기초하여 문헌에서 매개변수 범위를 선택하고, 불확실성 평가의 일부로 매개변수를 보정하는 것이다(Moore and Leach, 2021). 이러한 점에서 평균 제곱근 오차(RMSE)를 목적함수로 삼아 관측치에 대한 매개변수를 최적화한다. RMSE는 독립변수를 이용하여 종속변수를 추정하는 방법으로, 독립변수가 하나일 때는 단순선형회귀를 적용한다. 증발식의 경우 독립변수가 여러 개이므로 다중선형회귀 방법인 RMSE를 적용하여 오차를 최소화한다. RMSE의 형태는 Eq. (15)와 같이 나타낼 수 있다.

(15)

R M S E = \sqrt{\frac{1}{N} \sum_{i = 1}^{n} (E_{o b s} - E_{p r e d})^{2}}

여기서, $E_{o b s}$ 는 관측 증발량을 나타내며, $E_{p r e d}$ 는 본 연구에서 활용된 증발식을 통해 추정한 증발량에 해당한다.

3. 연구결과

본 연구에서는 PCE 및 PWF 증발식에 대한 적용성을 살펴보기 위하여 매개변수를 최적화하여 증발량을 추정하였다. 두 가지 증발량 산정 접근법에 대해 용담댐 시험유역의 플럭스 타워 육지 기반 기상자료와 용담댐 용담호에서 구축된 수문 자료를 활용하였다. 두 가지 접근방법을 통해 추정된 증발량은 각 대상 유역에서 관측된 증발량과 상관성 분석을 통해 비교하여 평가하였다.

3.1 대상유역

용담댐 시험유역에서는 1999년부터 다양한 수문 관측이 이루어지고 있으며 증발산량의 수문 기상자료 생산을 위한 관측소를 운영 중이다. 앞서 언급한 것처럼 본 연구 목적은 저수지 증발량 추정을 위한 PCE 및 PWF 증발량 추정식에 적용성을 살펴보기 위함이다. 그러나 저수지 호내 증발량 자료가 충분하게 활용이 어렵다는 측면에서 용담댐 시험유역 내 지면 증발량도 분석 대상으로 하였으며, 저수지 증발량 추정 시 검증을 위한 수단으로 활용하였다.

용담댐 유역 내 덕유산 플럭스 타워는 금강 수계 구량천의 상류부 덕곡제 유역 내(위도 35°50ʹ~ 35°53ʹN , 경도 127°42ʹ~ 127°44ʹE)에 위치하며, 용담댐 시험유역 내에서 증발산량을 관측하기 위해 2011년 한국수자원공사에서 설치 및 관리하고 있다. 플럭스 타워는 연직 풍속과 수증기 농도의 공분산으로 증발산량을 측정하는 에디 공분산법을 활용하며, 대기 온도, 순 복사량, 현열, 잠열, 지중열 등을 측정하고 연산하여 관측자료로 제공한다. 용담댐 시험유역의 에디 공분산 시스템은 플럭스 타워 24 m에 설치되어 있으며, 에디 공분산시스템 기기 목록은 Table 1과 같다. 플럭스 타워를 관측자료로 활용한 이유는 직접 생태계와 대기 사이의 연직 방향 플럭스를 정량화하여 측정하기 때문에, 기존의 증발산량 관측 방법보다 관측지점에 영향을 끼치지 않으며 비교적 넓은 지역에 대한 플럭스를 구할 수 있다는 장점이 있다.

Table 1.

Eddy-covariance system instrument list (K-water)

Instrument	Instrument model	Height (m)	Observation
3D wind direction anemometer	CSAT3	24	Wind direction, Wind speed
$C O_{2} / H_{2} O$ gas analyzer	EC155	24	$C O_{2}, H_{2} O$
Net radiation	CNR4	23	Net radiation
Weather sensor	WXT510	2, 19	Precipitaion
Soil temperature sensor	TCAV	-0.05	Soil temperature
Heat flux	HFP01	-0.05	Heat flux
Soil moisture	CS616	-0.1, 0.2, 0.4, 0.8	Soil moisture
Snow gauge	WDR-205	2, 16	Precipitation
Condensation sensor	237-L35	4, 9, 16	Dew point

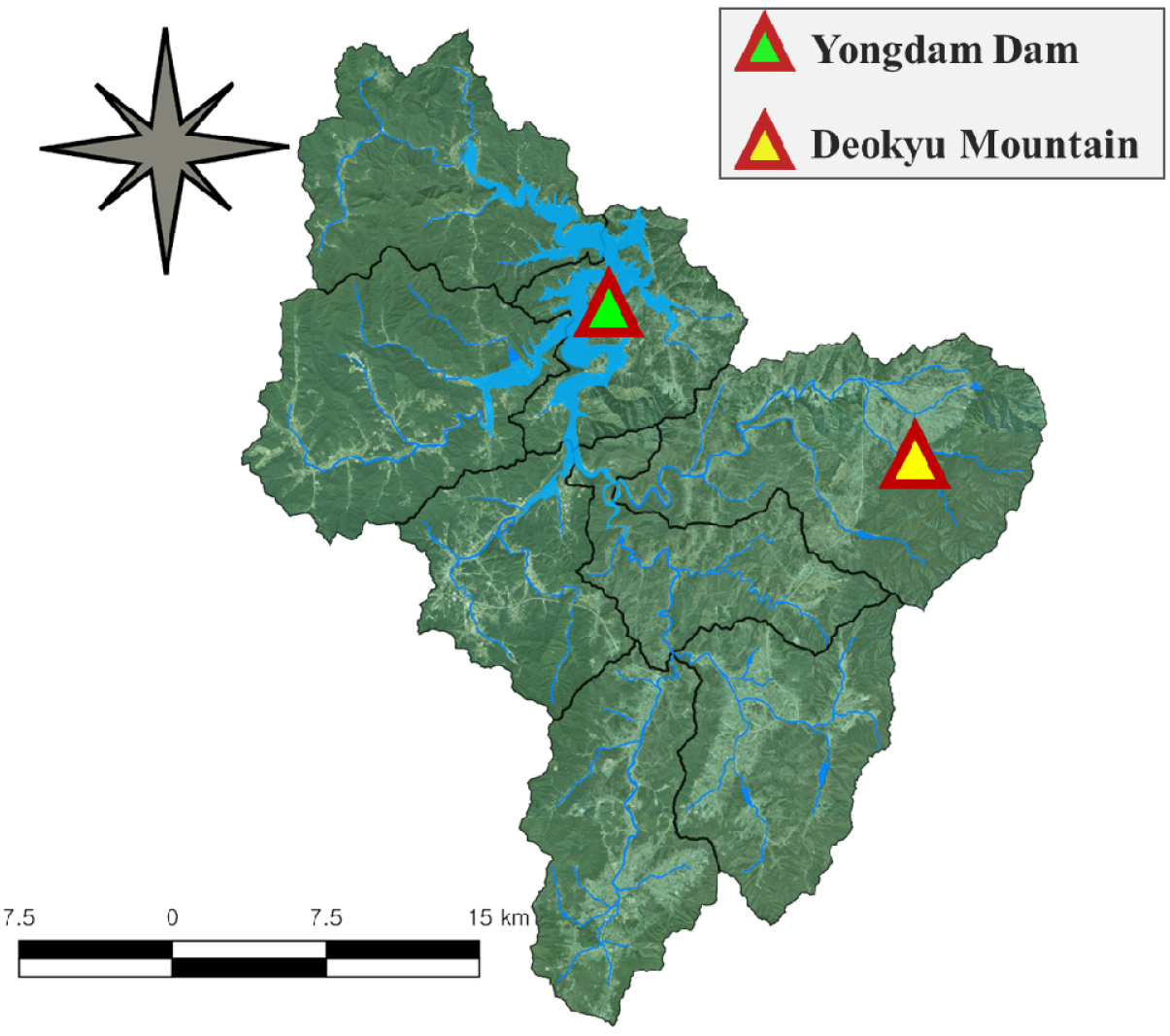
용담댐 저수지의 손실량 중 수표면 증발량을 추정하기 위해서 용담댐 시험유역 내 용담호 수면증발 관측자료를 활용하였다. 2013년부터 측정되고 있는 수면증발 관측지점은 전라북도 무주군 안성면 덕산리 금강 유역의 최상류(위도 36°00ʹ~35°35ʹN, 경도 127°20ʹ~127°45ʹE)에 위치하며, 용담댐 시험유역 내 용담호 수면 위에서 관측된다. 팬 내부 수심이 1 m인 대형 증발 팬을 고정하는 방식으로 설치하여 수위 자료와 실제 수면에서 관측된 수온, 풍속, 상대습도, 복사량만 아니라 증발량 관측자료를 포함한다. Fig. 1은 본 연구에서 활용한 용담댐 시험유역 내 위치한 2개의 증발산량 관측소를 도시한 결과를 나타낸다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F1.jpg

Fig. 1.

Yongdam watershed along with evapotranspiration station

3.2 분석결과

3.2.1 덕유산 플럭스 타워 증발량 추정

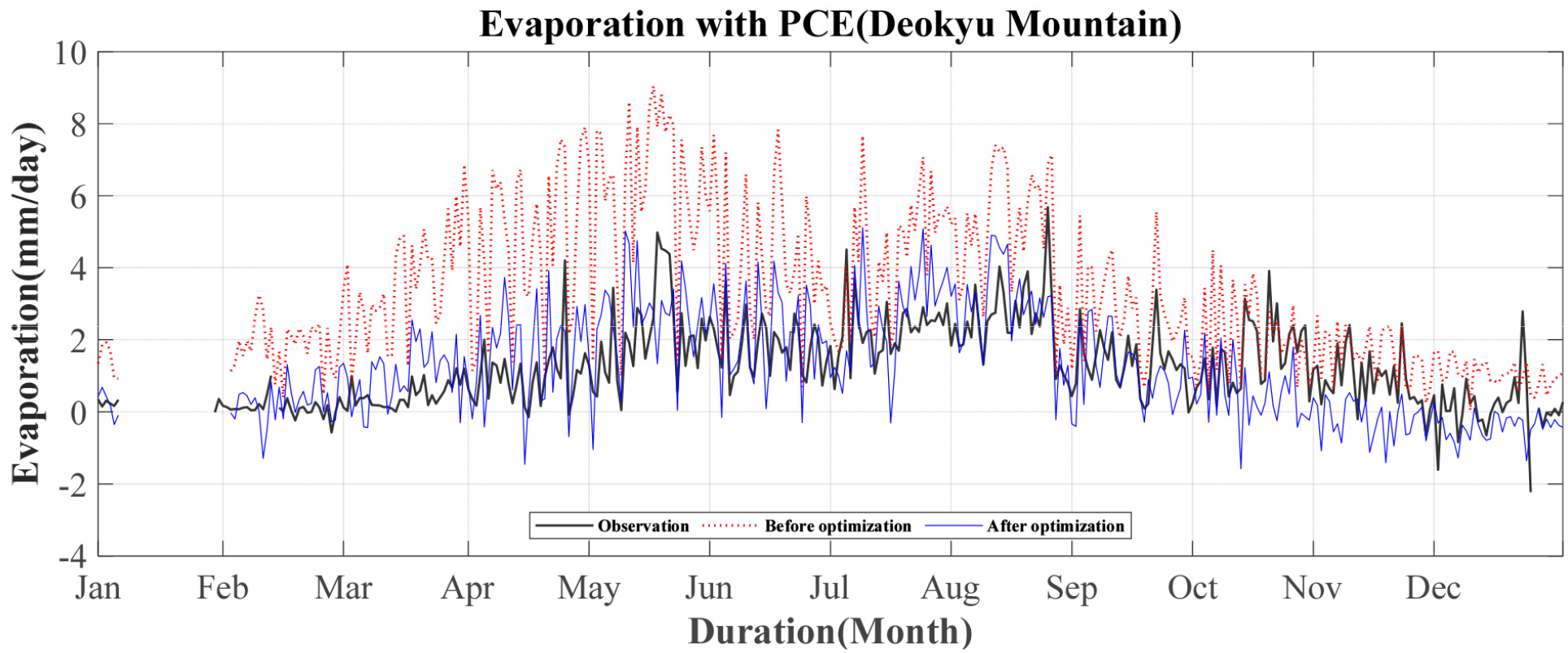
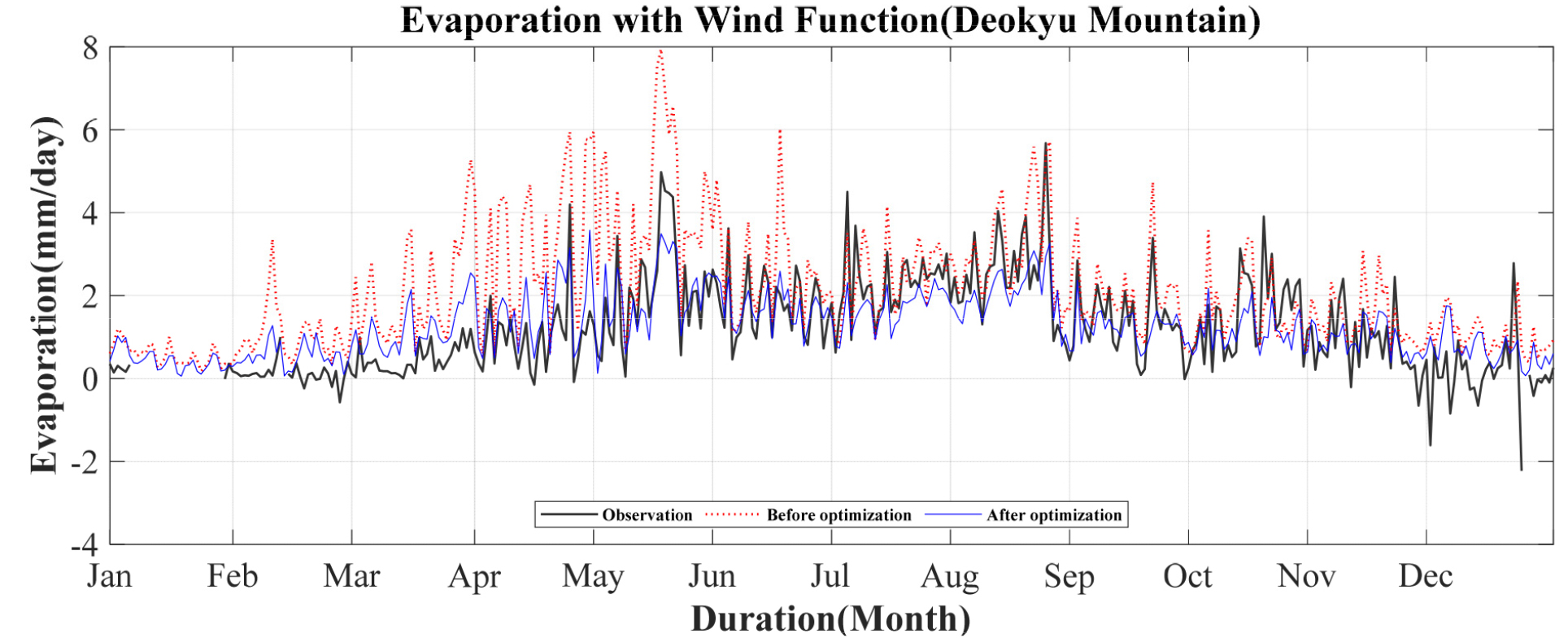
본 연구에서는 용담댐 시험유역 내 위치한 덕유산 플럭스 타워의 2016년 기상자료를 활용하여 PCE와 바람 함수를 통해 일일 증발량을 추정하였다. 증발의 관측값은 플럭스 타워로부터 관측된 기상자료를 활용하여 $E = Q_{e} / (L \times ρ_{w})$ 관계에 따라 산정된다. Penman이 제시한 경험적 매개변수를 적용하여서 일증발량을 추정한 결과를 Figs. 2 and 3에 도시하였다. PCE를 적용하여 증발량을 추정한 결과, 전체기간에서 관측값보다 과대 추정된 것을 확인할 수 있다. 수체에서 관측된 기상자료가 아닌 육지에서 관측된 자료를 기반으로 추정되었으므로 1월부터 6월까지의 오차가 상대적으로 크게 나타났다. PWF를 적용하여 증발량을 추정한 결과, 7월부터 12월 사이에서 비교적 관측값의 특징을 잘 반영한 것으로 보이지만 여전히 1월부터 6월까지의 오차가 크게 나타난 것을 확인할 수 있다. Fig. 4에 각 경험식에 따라 추정된 증발량을 관측된 증발량과 산점도를 통해 상관성을 도시하였다. PWF를 적용하여 추정된 증발량이 PCE를 적용하여 추정된 증발량보다 상관성이 비교적 높은 것을 시각적으로 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F2.jpg

Fig. 2.

Evaporation by PCE (Deokyu Mountain, 2016)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F3.jpg

Fig. 3.

Evaporation by PWF (Deokyu Mountain, 2016)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F4.jpg

Fig. 4.

Comparison of observed and estimated evaporation scatter plots. The left panel indicates evaporation estimated by PCE and the right panel indicates estimated by wind function

PCE와 PWF에 적용된 매개변수는 Penman이 제시한 경험적 매개변수를 적용하였으므로 용담댐 유역의 지형 및 기상학적 특성을 효과적으로 반영하는데 한계가 있다. 따라서, 관측 증발량 및 기상자료를 활용하여 매개변수 보정을 하였으며, 목적함수로 RMSE를 적용하여 관측 증발량에 대해 최적화를 실시하였다.

매개변수 최적화 결과, $a, b$ 는 PCE에서 각 각 -1.75×10^-8 m•s^-1•kPa^-1, -2.64×10^-8 kPa^-1이고, PWF에서는 4.44×10^-8m•s^-1•kPa^-1, -0.67×10^-8 kPa^-1으로 추정되었다. Figs. 5 and 6에 최적화된 매개변수를 적용하여 추정한 증발량을 도시하였다. Fig. 7에 각 경험식에 따라 추정된 증발량을 관측된 증발량과 산점도를 통해 상관성을 도시하였다. 매개변수를 최적화하기 전 추정된 증발량 결과와 비교하여 더 적합한 결과를 확인할 수 있다. PWF를 적용한 증발량의 경우 상대적으로 모형 적합 결과가 낮았던 1월부터 6월까지의 개선 정도가 두드러지게 나타내고 있으며, 관측된 증발량과 비교하여 전체적으로 유사한 거동을 확인할 수 있었다. 따라서 모형에 효율성 및 정확성 측면에서 PWF 방법이 저수지의 증발량을 추정하는 데 있어서 적합성이 있다고 판단되었다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F5.jpg

Fig. 5.

Evaporation by PCE after optimizing parameters (Deokyu Mountain, 2016)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F6.jpg

Fig. 6.

Evaporation by PWF after optimizing parameters (Deokyu Mountain, 2016)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F7.jpg

Fig. 7.

Comparison of scatter plosts between observed and estimated evaporation. The left panel indicates evaporation estimated by PCE and the right panel indicates estimated by PWF

3.2.2 용담댐 용담호 증발량 추정

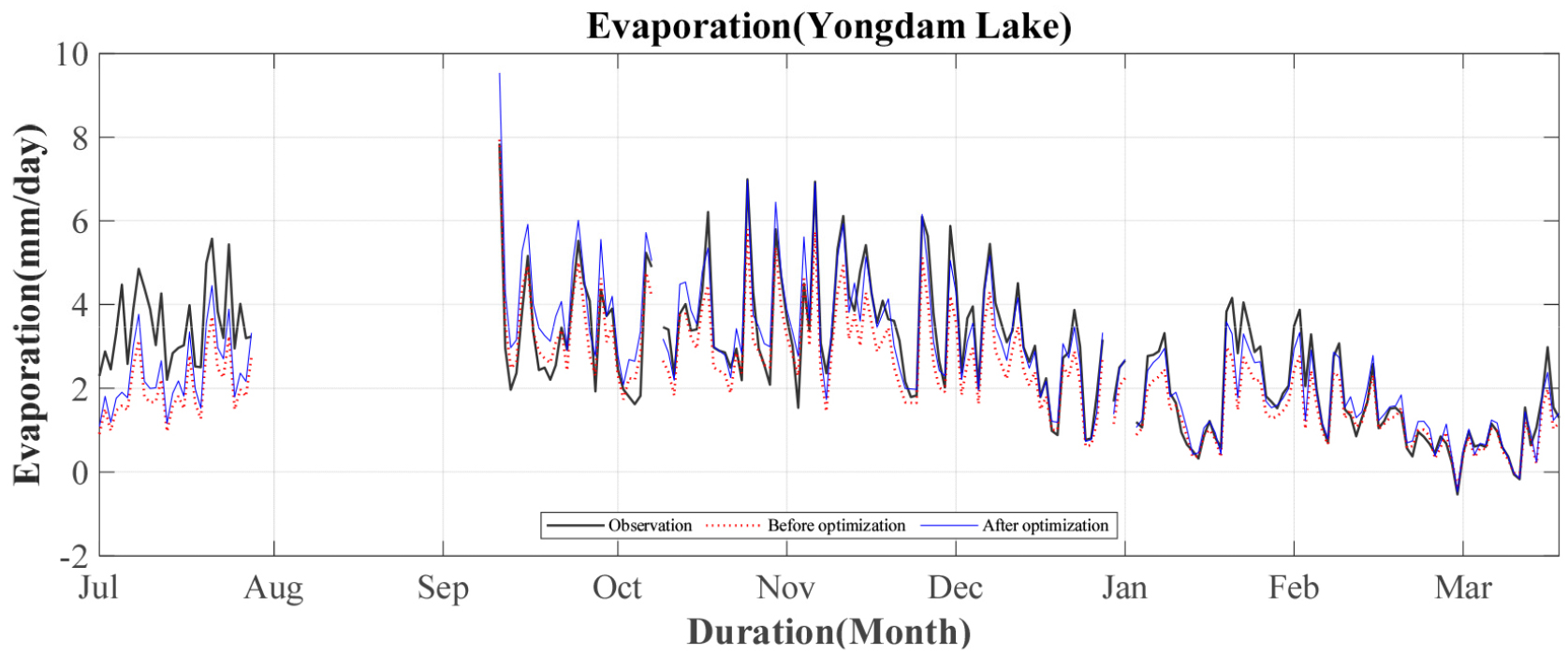
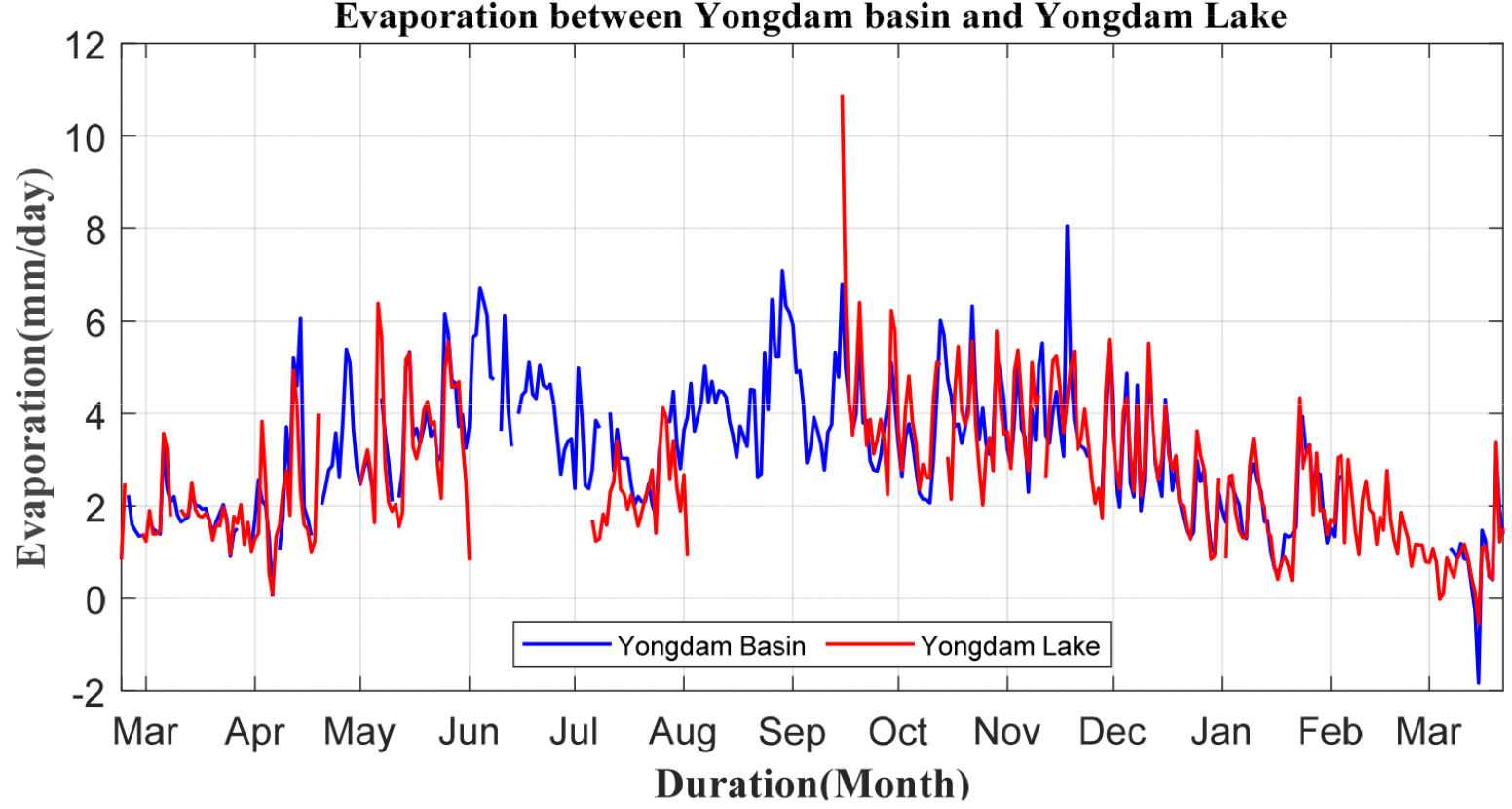
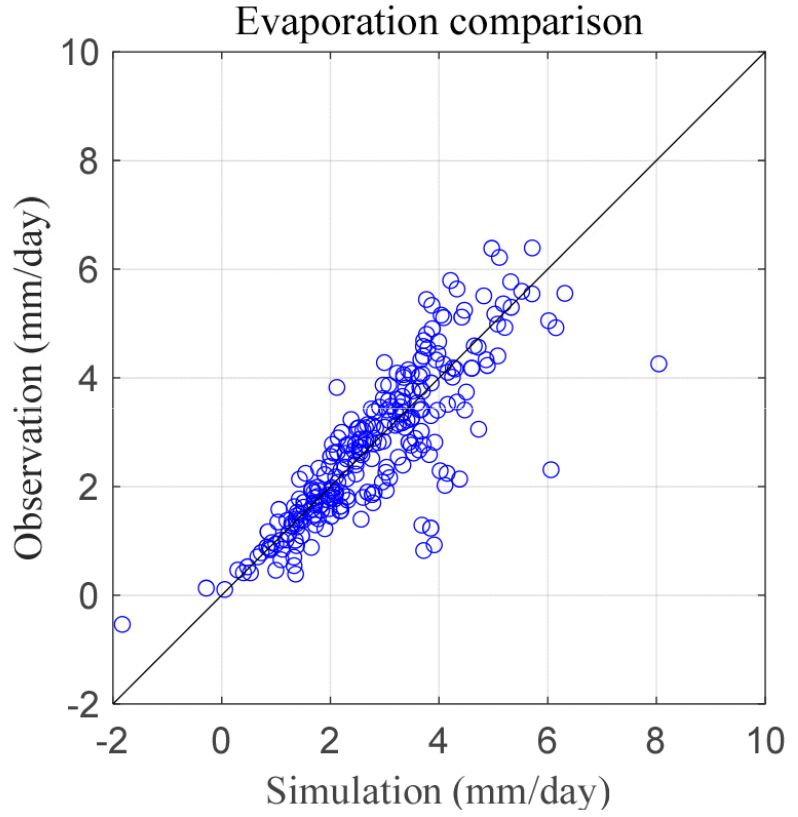
앞서 덕유산에서 분석한 결과를 통해 PWF 방법이 증발량 추정 측면에서 적용성이 더 우수하다는 것을 학인하였다. PWF의 매개변수를 덕유산 플럭스 타워에서 증발량을 추정한 방법과 마찬가지로 RMSE 방법을 통해 매개변수를 최적화하였으며, 추정된 매개변수 $a, b$ 는 각각 1.80×10^-8 m•s^-1•kPa^-1. 1.94×10^-8 kPa^-1와 같다. 용담호의 수면자료를 활용하여 오결측 구간을 제외하고 최적화된 매개변수를 PWF에 적용하여 증발량을 추정하였으며 Fig. 8에 도시하였다. 덕유산에서 추정된 증발량에 비해 실제 수면 위 관측자료에 적용한 증발량은 상대적으로 우수한 결과를 나타내었으며, Fig. 9에 산점도(scatter plot)를 통해서도 저수지 수면 증발량 추정 측면에서, PWF 방법의 적합성을 확인할 수 있었다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F8.jpg

Fig. 8.

Evaporation by PWF after optimizing parameters (Yongdam Lake, 2017-2018)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F9.jpg

Fig. 9.

Scatter plot of observed and estimated evaporations obtained from optimization process

본 연구에서는 상대적으로 자료 연한이 짧은 용담호 관측 수면 증발량 자료를 대상으로 연구를 진행하였다. 이러한 점에서 추정된 PWF 방법에 적용성 및 확장성을 평가하기 위하여, 용담호 수면에서 측정된 관측자료를 배제하고 장기간 수문 기상자료가 확보된 용담댐 유역의 자료를 PWF 방법에 적용하여 용담호 수면 증발량을 추정하고 이를 실제 관측증발량과 비교하였다. 즉, 교차검증 목적으로 용담댐 유역자료를 통해 간접적으로 용담호 내 증발량을 추정하기 위하여 유역 내 진안주천의 수문 기상자료를 입력자료로 사용하였다. 모의된 수면 증발량과 용담호 수면 증발량과의 비교 결과를 Figs. 10 and 11에 나타내었으며, 상관계수는 0.86으로 평가되었다. 따라서, 본 연구에서 도출된 매개변수의 적용성이 우수하다고 판단되며, 실험적으로 추정된 매개변수와 과거 수문자료를 이용하여 Hindcast 분석을 실시하였다. 즉, 과거 6년 동안(2016-2021년)에 용담호 수면증발량을 모의하여 Fig. 12에 추세선과 함께 도시하였다. 짧은 자료 기간으로 인해 통계적인 유의성은 부족하지만 용담호 증발량이 최근 감소 추세에 있다는 것을 확인할 수 있었다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F10.jpg

Fig. 10.

Comparison of evaporation rates (Yongdam Basin, 2017-2018)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F11.jpg

Fig. 11.

Scatter plot of observed and simulated evaporations

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057206/images/kwra_57_02_06_F12.jpg

Fig. 12.

Hindcasting approach to Yondam Lake evaporation using historical records and PWF method (Yongdam Lake, 2016-2021)

4. 결 론

본 연구에서는 저수지 증발량을 산정하는 경험식을 유역 내 수문 기상자료와 수면 위에서 직접 관측된 수문 기상자료를 활용하여 평가하였다. 용담댐 시험유역에서 2016-2018년 기간의 실측 증발량 자료를 이용하여 두 가지 경험식에 대한 적용성을 검토하였다. 물리 기반 증발량 경험식인 PCE 및 PWF 매개변수 최적화를 통해 저수지 수면 증발량 평가를 시도한 사례가 국내외에서 많지 않다는 측면에서 활용성 및 확장 가능성이 큰 연구라 판단되며, 본 연구 결과를 통해 도출된 결과를 요약하면 다음과 같다.

첫째, 본 연구에서는 저수지에서 증발량을 평가하기 위해 용담댐 시험유역의 두 개의 증발산량 관측소를 대상으로 하여 증발량을 산정하였다. 증발량 산정을 위해 용담댐 시험유역 덕유산 플럭스 타워의 육지 기반 기상자료와 용담호의 수면 위 기상자료를 활용하였다. 증발량을 산정하기 위한 경험식으로 Dalton 법칙을 기반으로 한 바람함수 PWF와 PCE 방법을 적용하였다.

둘째, 용담댐 시험유역 중 덕유산 플럭스 타워에서 PWF와 PCE에 대해 증발량을 평가한 결과, PWF 방법이 상관성 측면에서 더욱 개선된 결과를 보여주었지만, 두 가지 방법 모두 과대 추정 현상을 나타내었다. RMSE를 목적함수로 하여 매개변수를 최적화한 후 증발량을 추정한 결과, 증발량에 대한 과대 추정 경향이 현저하게 감소한 것을 확인할 수 있었다. 그러나, PCE를 통한 증발량은 여전히 특정 기간에서 과대 추정되는 문제점이 있었으며, PCE에 비해서 PWF 방법이 저수지 수면 증발량 산정식으로 적합성이 크다고 판단된다.

셋째, 용담호 수면 위에서 관측된 기상자료를 활용하여 PWF 방법을 통한 증발량을 평가하였다. PWF 방법을 통해 용담호에서 수면 증발량을 추정한 결과, 관측 수면증발량과 통계적 지표 및 시각적 평가에서 우수한 성능을 확인하였다. 또한, 본 연구에서 도출된 매개변수의 활용성 검증 차원에서 용담댐 유역 인근 수문 기상자료를 활용하여 용담호 수면증발량을 모의한 결과에서도 우수한 성능을 확인하였다. 이러한 결과는 특히 수면증발량 추정 시 결측 자료가 있는 경우 활용성이 크다고 판단된다.

향후 본 연구에서는 용담댐 주변에 이용 가능한 수문 기상자료를 이용하여 PWF 증발량 추정식에 매개변수를 최적화하여 제시하였으며, 특히, PCE 방법을 적용하기 위해 요구되는 기상자료 취득이 제한적인 지역에 대해서는 본 연구를 통해 산정된 매개변수를 이용하여 저수지 수면 증발량을 간접적으로 추정할 수 있을 것으로 판단된다. 다른 유역으로 모형 결과를 확대 적용하기 위해서는 타 댐들에 수면 증발량을 종합적으로 연계한 지역화 연구도 반드시 필요할 것으로 판단된다.

Acknowledgements

본 결과물은 환경부의 재원으로 수자원종합연구 및 한국환경산업기술원의 가뭄대응 물관리 혁신 기술개발사업의 지원을 받아 연구되었습니다(과제번호:2022003610003).

Conflicts of Interest

The authors declare no conflict of interest.

References

Alvarez, V.M., González-Real, M.M., Baille, A., Valero, J.M., and Elvira, B.G. (2008). "Regional assessment of evaporation from agricultural irrigation reservoirs in a semiarid climate." Agricultural Water Management, Vol. 95, No. 9, pp. 1056-1066. 10.1016/j.agwat.2008.04.003

Dalton, J. (1802). "Experimental essays on the constitution of mixed gases; on the force of steam or vapor from waters and other liquids, both in a Torricellian vacuum and in air; on evaporation; and on the expansion of gases by heat." Memoires of the Literary and Philosophical Society of Manchester, Vol. 2, pp. 535-602.

Gökbulak, F., and Özhan, S. (2006). Water loss through evaporation from water surfaces of lakes and reservoirs in Turkey. Official Publication of the European Water Association, Bonn, Germany.

Guenther, S.M., Moore, R.D., and Gomi, T. (2012). "Riparian microclimate and evaporation from a coastal headwater stream, and their response to partial-retention forest harvesting." Agricultural and Forest Meteorology, Vol. 164, pp. 1-9. 10.1016/j.agrformet.2012.05.003

Kim, H.J., Kim, K., and Kwon, H.H. (2021). "Development of a surrogate model based on temperature for estimation of evapotranspiration and its use for drought index applicability assessment." Journal of Korea Water Resources Association, KWRA, Vol. 54, No. 11, pp. 969-983. 10.3741/JKWRA.2021.54.11.969

Lee, K.H., Oh, N.S., and Jeong, S.T. (2007). "Analysis on the change in the pan evaporation rate in the Coastal zone." Journal of Korean Society of Coastal and Ocean Engineers, JKSCOE, Vol. 19, No. 3, pp. 244-252.

Maheu, A., Caissie, D., St‐Hilaire, A., and El‐Jabi, N. (2014). "River evaporation and corresponding heat fluxes in forested catchments." Hydrological Processes, Vol. 28, No. 23, pp. 5725-5738. 10.1002/hyp.10071

Monteith, J., and Unsworth, M. (2013). Principles of environmental physics: plants, animals, and the atmosphere. Academic Press, Amsterdam, Netherlands, pp. 13-22.

Moore, R.D., and Leach, J.A. (2021). "Predicting latent and sensible heat fluxes in stream temperature models: Current challenges and potential solutions." Water Resources Research, Vol. 57, No. 2, e2020WR028712. 10.1029/2020WR028712

Murray, F.W. (1966). On the computation of saturation vapor pressure. Rand Corporation, Santa Monica, CA, U.S. p. 9.

Penman, H.L. (1948). "Natural evaporation from open water, bare soil and grass." Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, Vol. 193, No. 1032, pp. 120-145. 10.1098/rspa.1948.003718865817

Pérez, A., Lagos, O., Lillo-Saavedra, M., Souto, C., Paredes, J., and Arumí, J.L. (2020). "Mountain lake evaporation: A comparative study between hourly estimations models and in situ measurements." Water, Vol. 12, No. 9, 2648. 10.3390/w12092648

Szeitz, A.J., and Moore, R.D. (2020). "Predicting evaporation from mountain streams." Hydrological Processes, Vol. 34, No. 22, pp. 4262-4279. 10.1002/hyp.13875

Tetens, O. (1930). "Uber einige meteorologische Begriffe." Zeitschrift für Geophysik, Vol. 6, pp. 297-309.

Wang, W., Xu, F., Liu, S., Wei, L., Feng, J., Wei, H., Dong, L., Wu, Y., and Kobayashi, T. (2019). "Estimating evaporation from irrigation canals in the midstream areas of the Heihe River Basin by a Double-Deck Surface Air Layer (DSAL) Model." Water, Vol. 11, No. 9, 1788. 10.3390/w11091788

Yoon, Y.N. (2007). Hydrology: Fundamentals and applications. Cheingmoongak, pp. 135-161.

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Estimation of evaporation from water surface in Yongdam Dam using the empirical evaporation equaion

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

Table 1.

Eddy-covariance system instrument list (K-water)

Fig. 1.

Yongdam watershed along with evapotranspiration station

Fig. 2.

Evaporation by PCE (Deokyu Mountain, 2016)

Fig. 3.

Evaporation by PWF (Deokyu Mountain, 2016)

Fig. 4.

Comparison of observed and estimated evaporation scatter plots. The left panel indicates evaporation estimated by PCE and the right panel indicates estimated by wind function

Fig. 5.

Evaporation by PCE after optimizing parameters (Deokyu Mountain, 2016)

Fig. 6.

Evaporation by PWF after optimizing parameters (Deokyu Mountain, 2016)

Fig. 7.

Comparison of scatter plosts between observed and estimated evaporation. The left panel indicates evaporation estimated by PCE and the right panel indicates estimated by PWF

Fig. 8.

Evaporation by PWF after optimizing parameters (Yongdam Lake, 2017-2018)

Fig. 9.

Scatter plot of observed and estimated evaporations obtained from optimization process

Fig. 10.

Comparison of evaporation rates (Yongdam Basin, 2017-2018)

Fig. 11.

Scatter plot of observed and simulated evaporations

Fig. 12.

Hindcasting approach to Yondam Lake evaporation using historical records and PWF method (Yongdam Lake, 2016-2021)

Acknowledgements

Conflicts of Interest

References