1. 서 론
보통 수일 이내의 단기 기상예측은 일기도 및 중규모 기후모형을 이용한 역학적 해석과 그리고 전문예보관의 분석 및 경험 등을 기반으로 이루어지고 있으며, 모델링과 컴퓨팅 기술의 발달로 인해 과거에 비해 예측능력이 높아지고 있는 추세이다. 반면 한 달에서 수개월 시간 규모에 해당하는 장기예측은 주로 통계모형과 기후모형에 의해 이루어지는데, 아직 충분한 수준의 예측성을 확보하지 못한 상태이며 최근 지속적으로 관심과 연구가 집중되고 있는 분야이다. 장기예측 대상은 매일매일의 날씨가 아닌 월평균 혹은 계절평균 기상요소로서 가뭄과 홍수, 폭염을 비롯한 기상이변으로 인한 재해를 대응하고 안정적인 수자원 확보와 관리는 물론 특히 농업생산성 확보를 위해 필수적인 정보이다. 우리나라 기상청에서도 역학적 모형인 전지구 기후모형의 결과를 이용하여 강수량과 기온에 대한 1 ~ 3개월 전망자료를 제공하고 있다. 그러나, 한반도의 지리적 특성상 갑작스런 폭우나 태풍 등의 발생, 과거에 비해 빈번해진 이상기후 현상 등으로 인해 정확한 예측이 쉽지 않은 상황이며, 제공되는 정보 또한 정성적 수준의 3분위 확률정보로 실무에 활용하기에는 제한적이다.
월 및 계절단위의 장기예측을 위한 방법은 크게 역학적 방법과 통계적 방법으로 구분할 수 있다(Doblas-Reyes et al., 2005; Schepen et al., 2012; Kim et al., 2018; Kim et al., 2020). 역학적 모형을 이용한 장기예측의 경우에는 예측모형의 특성상 초기조건의 불확실성과 적분시간에 따른 오차의 증가 등으로 예측기간이 길어질 경우 예측성이 저하되는 문제가 있다. 반면 통계적 모형은 역학적 방법에 비해 모형 구성이 간단하고 계산이 빠르며 예측기간의 제한이 상대적으로 덜하고 경우에 따라서는 높은 예측성을 보여주기도 한다. 하지만 통계적 특성상 지속적이고 안정적인 예측결과를 보장하기 어렵다는 단점이 있다. 그럼에도 통계적 모형은 구성이 비교적 간단하고 다양한 구성이 가능하다는 장점으로 인해 많은 연구자들에 의해 활용되고 있다. 일정 기간 이상 지속되는 대규모의 대기 변화나 순환 현상 등은 지구 대기순환시스템에 기여하여 다른 광범위한 지역의 계절적 기후에 영향을 주게 되는데, 이를 원격상관성이라 한다(Barnston and Livezey, 1987; Lim and Kim, 2013). 이러한 원격상관성을 기반으로 강수량과 기온을 중심으로 한 통계적 장기예측이 많이 시도되어 왔으며, 그 외에도 유출량, 적설량, 작물수확량, 해충발생 등의 예측에도 통계적 기법이 활용되었다(Kim et al., 2020). 국내에서도 2000년대 이후 계절예측 기술 개발이 활발하게 진행되어 회귀모형, 정준상관모형, 인공신경망모형 등을 이용한 연구들이 많이 수행되고 있다.
그간 많이 수행되어 온 통계적 예측과 관련해서는 Kim et al. (2020)이 언급한 것처럼 2가지 한계가 있다. 하나는 과거의 자료를 이용하여 보정과 검정을 통해 최적화된 예측모형을 도출하였기 때문에 과거와 다른 기후특성을 보이는 미래기간에 대해 예측성을 확보하기 어렵다는 것이며, 다른 하나는 활용되는 예측인자의 선행기간에 따라 예측선행기간에 제한을 받는다는 것이다. 이에 대한 해결책으로 Kim et al. (2020)은 예측시점 및 예측선행기간에 따라 탄력적으로 예측인자를 선별하여 예측모형을 구성하는 방법으로 한강권역의 강수량을 예측한 바 있다.
본 연구에서 예측하고자 하는 기온정보는 지역의 중장기적인 기후변화 및 생태환경의 변화를 판단하는 중요한 지표이다. 또한, 증발산량에 대한 간접적 추정을 통한 가용수자원의 평가, 수자원 계획 등과도 밀접한 관련을 가지고 있다. 북반구 지역의 기온 변화는 엘리뇨 남방진동(El Niño-Southern Oscillation, ENSO), 인도양 쌍극자(Indian Ocean Dipole), 북서태평양(western North Pacific) 몬순(monsoon) 등의 영향을 많이 받는 것으로 알려져 있으며(Lee et al., 2019), 특히 우리나라를 포함한 동아시아 지역의 겨울철 기온 및 겨울몬순(East Asia winter monsoon)의 경우에는 북극진동(Arctic Oscillation, AO)과 연관성이 높다고 알려져 있다(Jeong and Ho, 2005; Li et al., 2014; Park and Ahn, 2016; He et al., 2017; Woo et al., 2020). 기존 연구의 대부분은 기온에 대한 정량적인 값의 제시보다는 분석된 원격상관성을 통해 전지구적 대기순환 및 질량 변화가 광범위한 지역에 걸쳐 그리고 시간적인 지연을 통해 어떻게 영향을 주는지에 대한 역학적 관계를 규명함으로써 상관성이 높게 나타난 기후지수들을 이용한 통계적 예측모형의 활용 가능성을 제시하고 있다. 여전히 실질적인 예측값의 도출에는 한계가 있다고 볼 수 있다.
본 연구에서는 월 및 계절 단위의 장기 기온예측을 위해 Kim et al. (2020)과 같이 전지구 기후패턴과의 원격상관성을 기반으로 통계적 예측모형을 구성하여 한강권역에서의 미래기간(1 ~ 12개월 선행월)에 대한 평균기온의 예측 가능성을 평가하였다. 기후패턴들 간 또는 기후패턴과 평균기온 사이의 역학적 관계는 고려하지 않았으며, 예측시점에 따라 통계적으로 상관성이 높은 기후지수를 추출하여 예측모형의 예측인자로 활용하였다.
2. 연구방법
2.1 예측대상 및 예측인자
본 연구에서는 한강동해, 한강서해, 안성천 등을 모두 포함하는 한강권역 전체에 대한 월 평균기온을 예측대상으로 선정하였다. 예측인자로는 미국 해양대기청(National Oceanic and Atmospheric Administration, NOAA) 등에서 제공하고 있는 글로벌 기후지수 중 지속적으로 업데이트가 이루어지고 있는 39개 지수와 한강권역의 8가지 기상요소(강수량, 평균기온, 상대습도, 평균해면기압, 일조시간, 평균풍속, 평균운량, 소형증발량)에 대한 월 평균자료를 이용하였다. Kim et al. (2020)에서 적용된 예측인자와 비교하여 글로벌 기후지수는 동일하며, 한강권역 기상요소 중 평균수증기압과 평균현지기압 대신에 기온과 상관성이 상대적으로 높은 평균해면기압(AvgSLP), 평균풍속(WND), 평균운량(CLOUD), 소형증발량(SmallEV) 등을 예측인자에 추가하였다.
예측대상을 포함한 예측인자에 대해 1948 ~ 2020년의 월 자료를 활용하였으며, 1992 ~ 2020년의 월 평균기온을 대상으로 예측모형을 구성하고 예측성을 평가하였다.
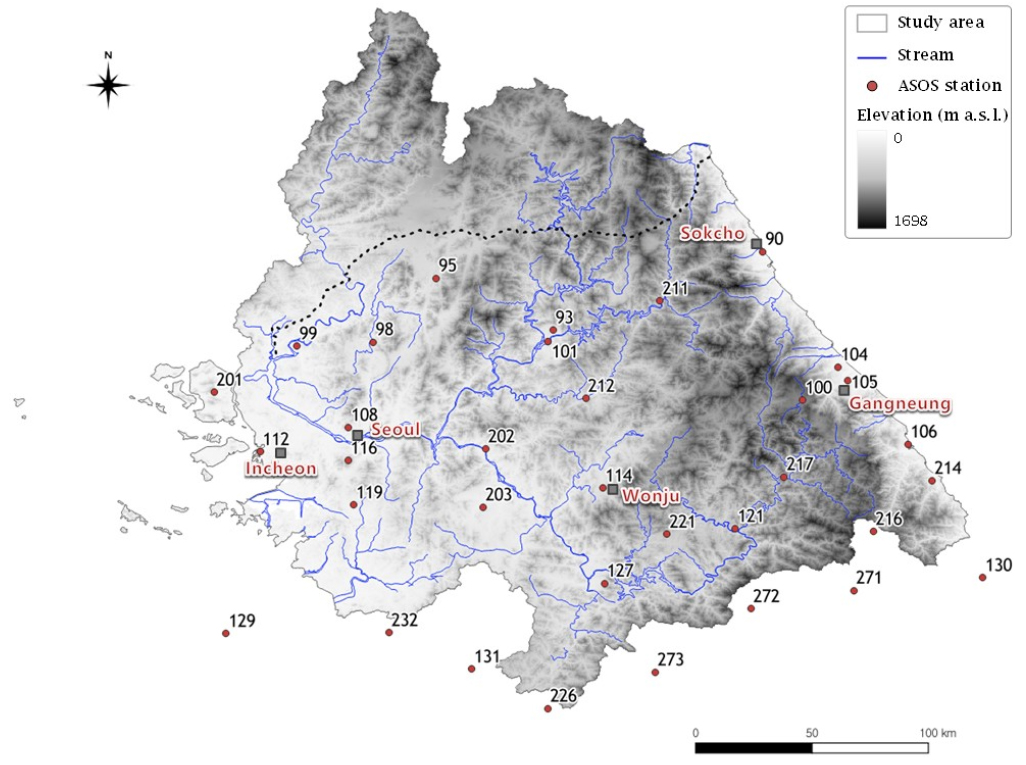
한강권역의 기상요소 값은 Fig. 1과 같이 기상청 종관기상관측(Automated Synoptic Observation System, ASOS) 34개 지점의 관측자료를 티센면적평균하였으며, 대상지역 및 각 지점에 대한 지리적 정보는 Kim et al. (2020)과 동일하다.
예측인자로 활용한 39개의 글로벌 기후지수와 8개의 한강권역 기상요소에 대해서는 Table 1에 정리하였다.
Table 1.
Predictors used in this study (Kim et al., 2020)
2.2 원격상관성 분석
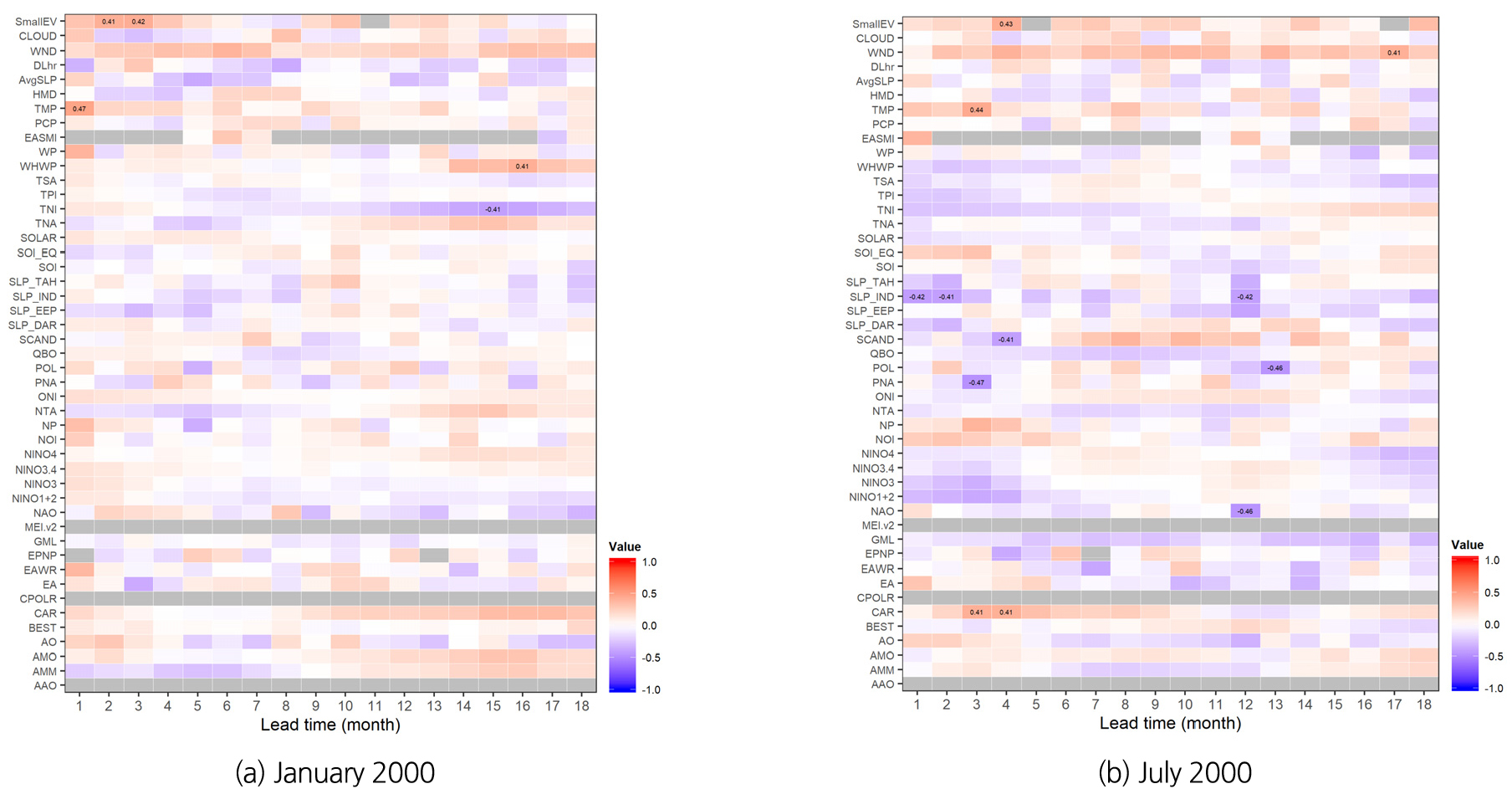
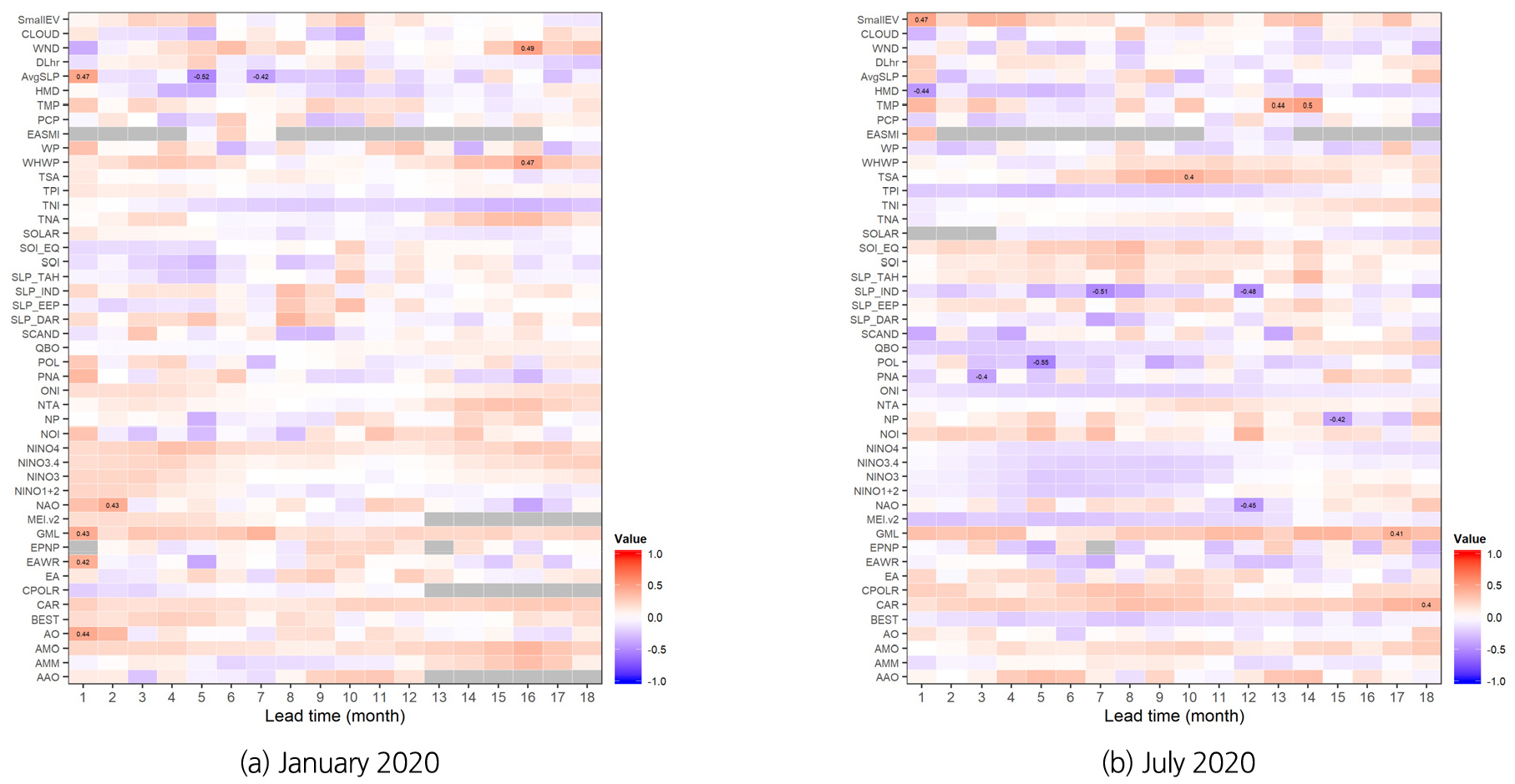
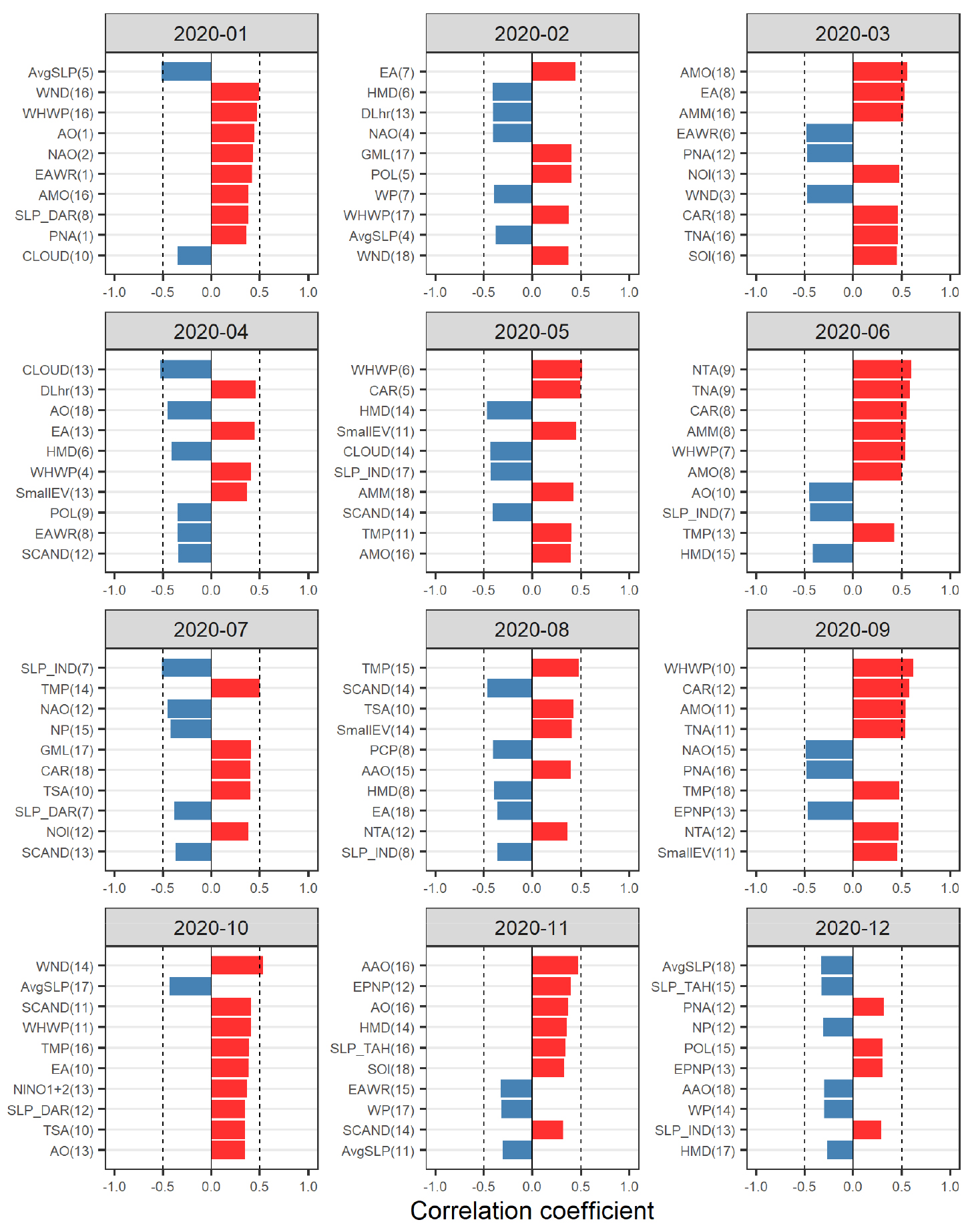
예측모형에 필요한 최적의 예측인자를 선정하기 위하여, 먼저 예측대상(월 평균기온)과 예측인자와의 상관성을 분석하였다. 예측대상월을 기준으로 과거 40년 자료에 대해 예측인자별로 1 ~ 18개월 선행자료와 예측대상과의 상관성을 분석하였다. 예를 들어, Fig. 2(a)는 2000년 1월 기온을 예측하기 위하여 과거 40년간(1960 ~ 1999년)의 1월 기온과 각 기후지수들의 선행 1개월에서 18개월 자료들과의 지연상관성을 나타낸 것이며, Fig. 2(b)는 2000년 7월을 기준으로 과거 40년간의 자료에 대해 예측대상과 예측인자와의 지연상관성을 분석한 결과이다. 붉은색과 푸른색은 각각 양의 상관성과 음의 상관성을 나타내며, 회색은 해당기간의 자료가 결측되어 상관성이 분석되지 못한 것을 의미한다. 상관성의 절대값이 0.4 이상인 경우에는 수치도 같이 표기하였다. 마찬가지로 Fig. 3은 각각 2020년 1월과 7월을 기준으로 한 과거자료의 지연상관성 분석결과이다.
Fig. 2(a)와 같이 2000년 1월을 기준으로 한 과거 40년간의 1월 기온자료와 각 예측인자들간의 상관성 분석 결과에서는 1개월 선행 TMP과의 상관도가 +0.47로서 가장 큰 것으로 나타났다. 이는 예측대상월인 2010년 1월을 기준으로 과거 40년간(1960 ~ 1999년)의 1월 기온과, 1개월 이전인 1959 ~ 1998년 12월의 TMP 자료가 상관성이 가장 높게 분석되었음을 의미한다. 다음으로 3개월 선행 SmallEV와의 상관도(+0.42), 15개월 선행 TNI와의 상관도(-0.41) 등이 높게 나타났다.
Fig. 2(b)의 2000년 7월을 기준으로 한 분석에서는 3개월 선행 PNA와의 상관도가 -0.47로 가장 높게 나타났으며, 뒤를 이어 12개월 선행 NAO -0.46, 13개월 선행 POL -0.46 등의 상관도가 높게 나타났다. Fig. 3(a)와 같이 2020년 1월을 기준으로 했을 때는 5개월 선행 AvgSLP -0.52, 16개월 선행 WND +0.49, 16개월 선행 WHWP +0.47 등의 상관성이 높게 나타났으며, Fig. 3(b)의 2020년 7월을 기준으로 했을 때는 5개월 선행 POL -0.55, 7개월 선행 SLP_IND -0.51, 14개월 선행 TMP +0.50 등의 상관성이 높은 것으로 분석되었다. 대체로 겨울철에는 양의 상관성이 높은 기후지수들이 많은 반면, 여름철에는 음의 상관성이 높은 기후지수들이 많이 나타났다. 반면에 Kim et al. (2020)이 수행했던 강수량과 기후지수들의 상관성 결과에서는 겨울철에 음의 상관성이 높고, 여름철에는 양의 상관성이 높은 것으로 분석되었다.
2.3 예측모형 구성
예측모형으로서는 비교적 구성이 간단한 통계적 기반의 다중회귀모형을 활용하였으며, 구성형태는 아래 Eq. (1)과 같이 Kim et al. (2020)에서 제시한 강수량 예측모형과 유사하다.
여기서, Y : 예측대상인 월 평균기온(℃), : 회귀계수, : 예측인자로서 상관성이 높은 기후지수, : 잔차항이다.
Figs. 2 and 3과 같이 각 예측대상월을 기준으로 해당 월에 대한 과거 40년간의 기온 자료와 각 기후지수의 선행(1 ~ 18개월) 자료에 대한 지연상관성 분석을 통해 상관성이 높은 10개의 기후지수를 도출하였다. 기존 강수량에 대해 예측모형을 구성하였던 Kim et al. (2020)의 연구에서는 회귀모형의 변수를 4개로 고정하고, 가능한 모든 조합의 회귀모형을 구성한 후, 40년간 자료에 대해 leave-one-out 교차검증을 통해 최적의 예측모형을 선별하였다. 반면, 본 연구에서는 과거 40년간의 자료 중에서 무작위로 20년간 자료를 추출하고 단계적 회귀분석(stepwise regression) 방법을 적용하여 회귀모형을 구성하였으며, 보정에 사용되지 않은 나머지 20년간 자료를 이용하여 회귀모형의 적합성을 검증하였다. 각 월별로 적합성이 검증된 1000개의 다중회귀모형을 도출할 때까지 무작위 보정과 검증과정을 반복하였다.
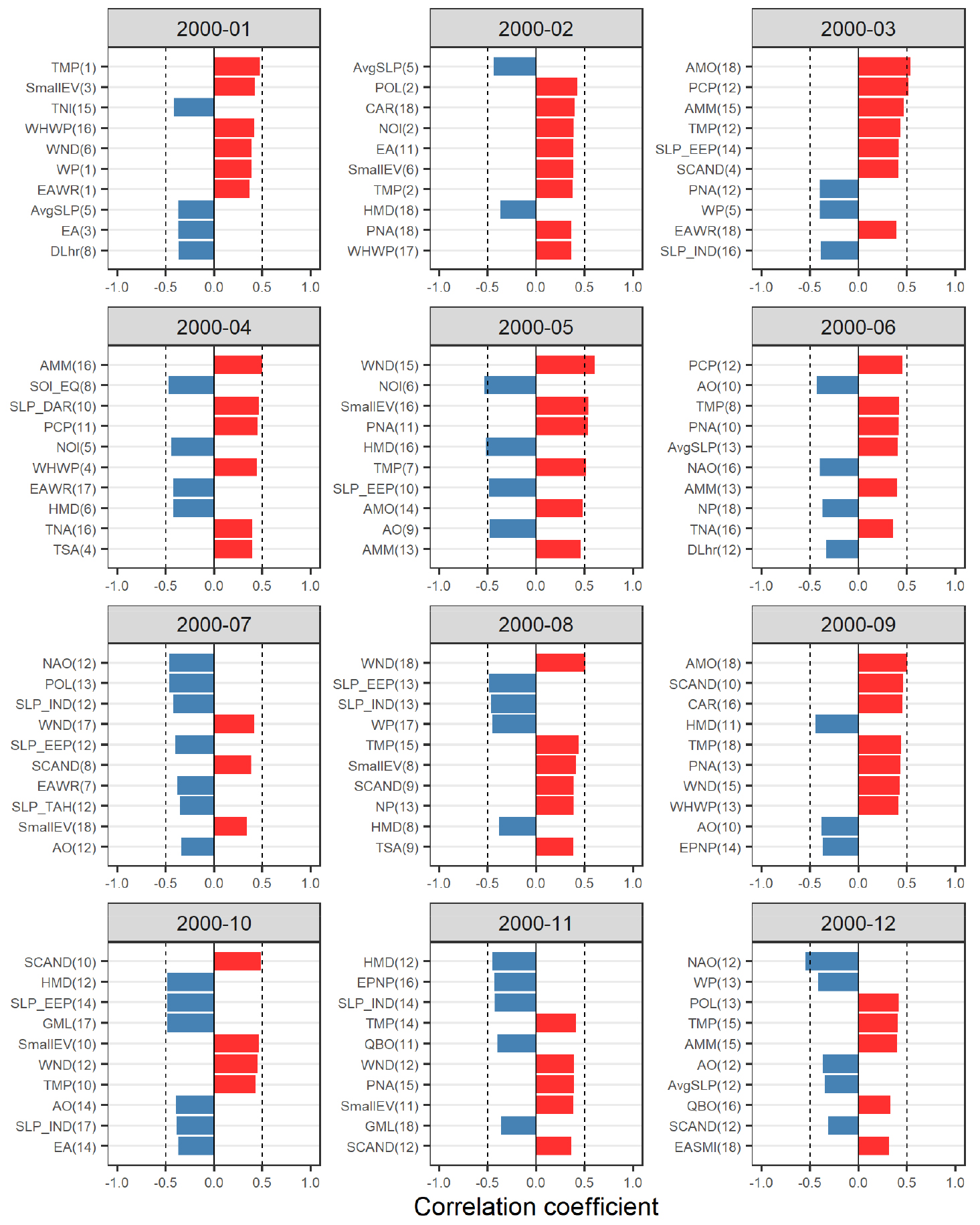
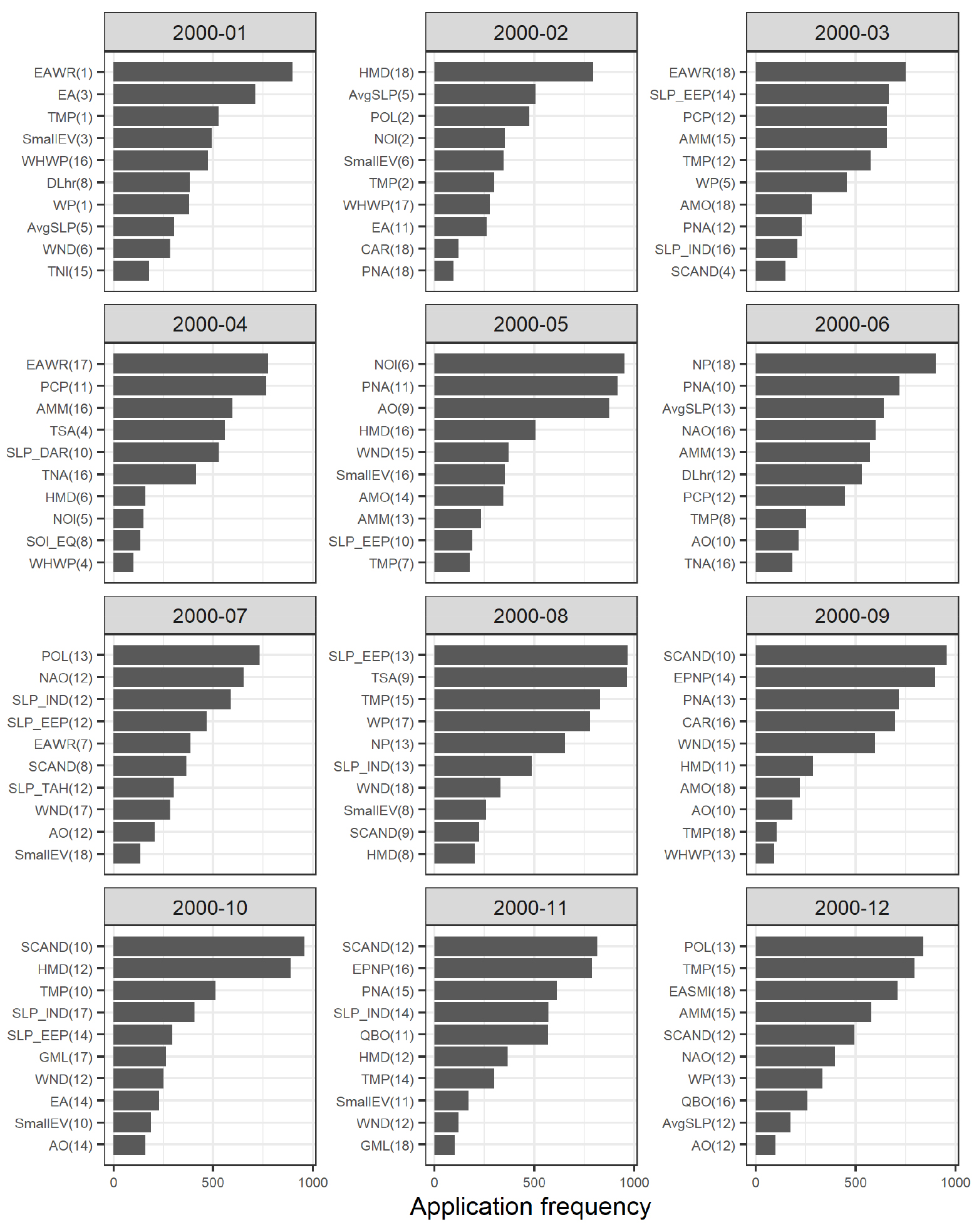
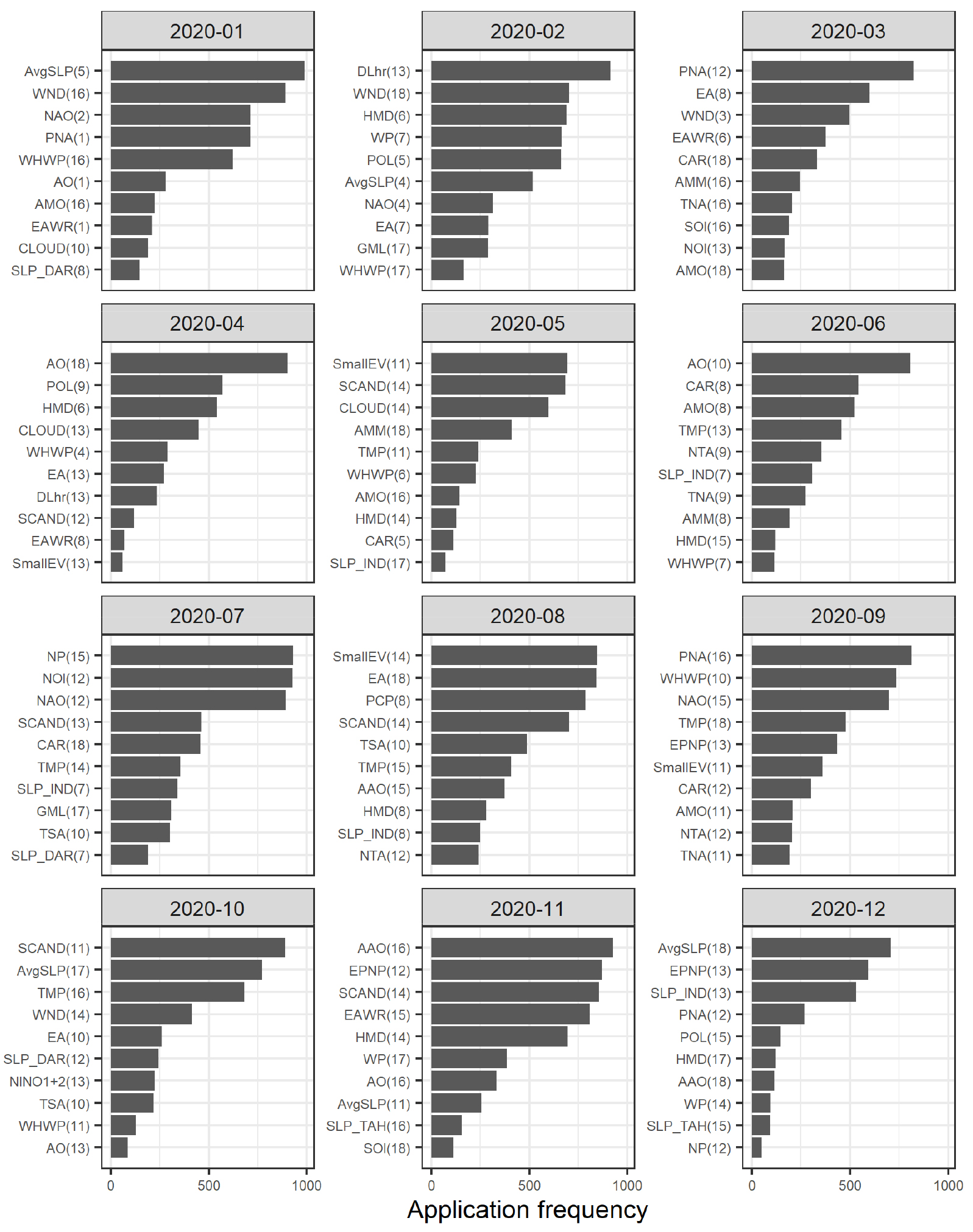
월별 예측모형을 선별하는 과정에서 예측시점을 기준으로 최소 1개월에서 최대 12개월까지의 선행예측을 위하여, 각 예측대상월에 따라 활용가능한 기후지수의 선행기간을 제한하였다. 예를 들어, Figs. 4 and 5는 각각 2000년과 2020년의 월별 예측모형들을 구성하기 위해 활용된 기후지수들을 나타낸 것으로, 괄호 안의 숫자는 지연상관성 분석에서 활용한 기온자료를 기준으로 한 기후지수자료의 선행개월 수(1 ~ 18)를 의미한다. 즉, Fig. 4의 첫 번째 2000년 1월에 대한 결과 중 TMP(1)은 2000년 1월 기온을 예측하기 위해 과거 40년간(1960 ~ 1999년)의 1월 기온자료와 상관성 분석을 한 결과, 1개월 이전인 1959 ~ 1998년의 12월에 대한 TMP 자료가 상관도가 가장 높았음을 의미한다.
Fig. 4의 2000년 7월의 경우, 예측모형의 예측인자 후보로 NAO(12), POL(13), SLP_IND(12) 등의 기후지수들이 선정되었다. 2000년 7월은 예측시점인 1999년 12월을 기준으로 선행기간 7개월에 해당되기 때문에 7개월 이상의 선행기간을 가진 기후지수 자료만 예측모형에 활용되었으며, 앞의 Fig. 2(b)에서 상관성이 높게 나타났던 PNA(3)는 제외되었다. 마찬가지로 Fig. 5의 2020년 7월에 대한 예측에서도 앞서 Fig. 3(b)에서 상관성이 가장 높게 나타난 POL(5) 자료는 제외되었다.
구성된 다수의 회귀모형에 대해서는 교차검증을 통하여 예측성이 높은 회귀모형들을 예측모형으로 선별하였으며, 선별된 회귀모형들을 이용하여 각 월별 기온 예측범위를 도출하고 관측치와 비교하여 예측성을 평가하였다.
3. 적용 결과
3.1 기후지수 활용빈도
상관성이 높은 10개의 기후지수를 조합하여 각 월별로 최적화된 예측모형을 도출하였으며, Figs. 6 and 7은 각각 2000년과 2020년의 월 예측모형에서 활용된 기후지수들의 현황을 나타낸 것이다. 예를 들어, Fig. 6에 나타난 것처럼 2000년 1월 예측모형에는 EAWR(1)이 가장 많이 활용되었는데, Fig. 4에서 분석된 것처럼 상관성이 높은 인자가 가장 많이 활용된 것은 아님을 알 수 있다. 그러나 2000년 7월 예측모형에는 상관성이 상대적으로 높게 나타난 NAO(12)와 POL(13) 자료가 실제 예측모형 구성에서도 많이 활용된 것으로 나타났다. 마찬가지로 Fig. 7에서와 같이 2020년 6월 예측모형에는 AO(10) 자료가 가장 많이 활용된 반면에 Fig. 5에서 분석된 상관성은 상대적으로 높지 않았으며, 2020년 11월 예측모형에서는 상관성이 높은 AAO(16)과 EPNP(12) 자료가 많이 활용된 것으로 나타났다. 이는 단계적 회귀분석과 무작위로 수행된 교차검증을 통해 적합도가 높은 다중회귀모형을 추출하는 과정에서 일부 설명력이 높은(상관도가 높은) 기후지수가 제외되는 경우도 있기 때문이다.
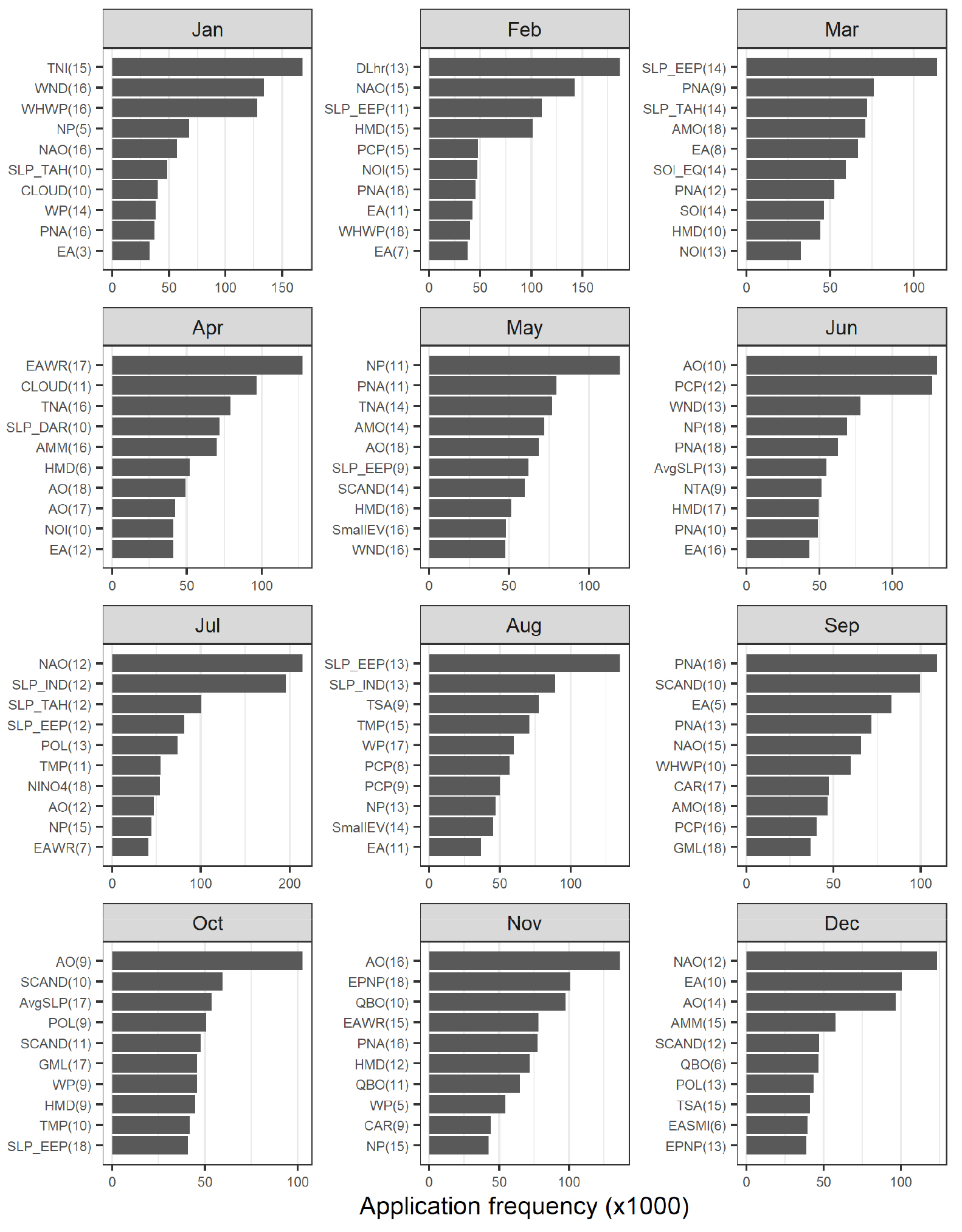
Fig. 8은 전 기간(1992년 1월 ~ 2020년 12월)에 대해 월별로 기후지수의 적용빈도를 분석한 것이다. 앞서 Figs. 4 ~ 7에 나타난 것처럼 통계적 분석의 특성상 예측대상월에 따라 기후지수들의 상관성이나 활용빈도가 다양하게 나타나지만, Fig. 8과 같이 비교적 장기간에 대한 분석결과로부터 계절별로 또는 월별로 대상지역(한강권역)에 대한 평균기온과의 상관성에 대한 경향을 파악할 수 있다. Fig. 8에서 겨울철(1월, 2월, 12월) 예측모형에는 TNI(15), DLhr(13), NAO(12) 등의 기후지수가 많이 활용된 반면에 여름철(6월, 7월, 8월) 예측모형에서는 AO(10), NAO(12), SLP_EEP(13) 등의 기후지수가 많이 활용된 것으로 나타났다. 즉, 겨울철에는 TNI, DLhr, NAO 등과 같은 기후지수가 한강권역의 평균기온과 통계적으로 연관성이 높음을 알 수 있으며, 여름철 기온은 AO, NAO, SLP_EEP 등의 기후지수와 연관성이 높다고 볼 수 있다.
기존의 연구들에 의하면, AO가 동아시아 지역의 겨울철 기온에 영향을 준다는 연구들이 많았다(Jeong and Ho, 2005; Lim and Kim, 2013; Li et al., 2014; Park and Ahn, 2016; He et al., 2017; Woo et al., 2020). 이 외에도 Lim and Kim (2013)은 AO를 포함하여 EAWR, WP, ENSO 등과 상관성이 높다고 제시한 바 있으며, Park and Ahn (2016)은 AO와 WP, Kim et al. (2017)은 EA와 WP, Yoo et al. (2018)은 EAWR, SCAND, PE (polar/Eurasian), Woo et al. (2020)은 AO와 ENSO 지수들을 이용하여 동아시아 겨울철 기온과의 상관성을 분석한 바 있다. 그러나 Lim and Kim (2013)에서도 언급된 것처럼, 분석기간에 따라 그리고 각 기후지수의 선행기간에 따라 상관성이 다르게 나타나기 때문에 본 연구에서는 예측대상월에 따라 탄력적으로 상관성이 높은 기후지수들을 활용하여 예측모형을 구성하였다.
3.2 월 기온 예측결과
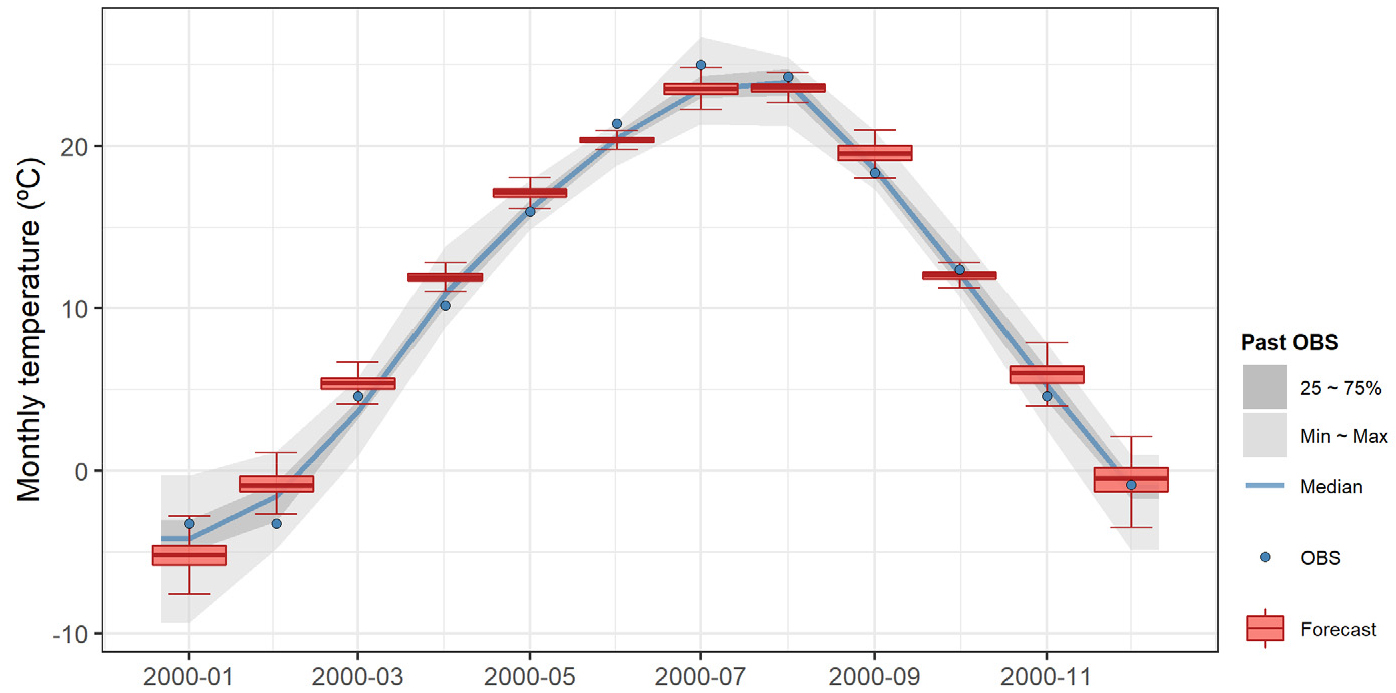
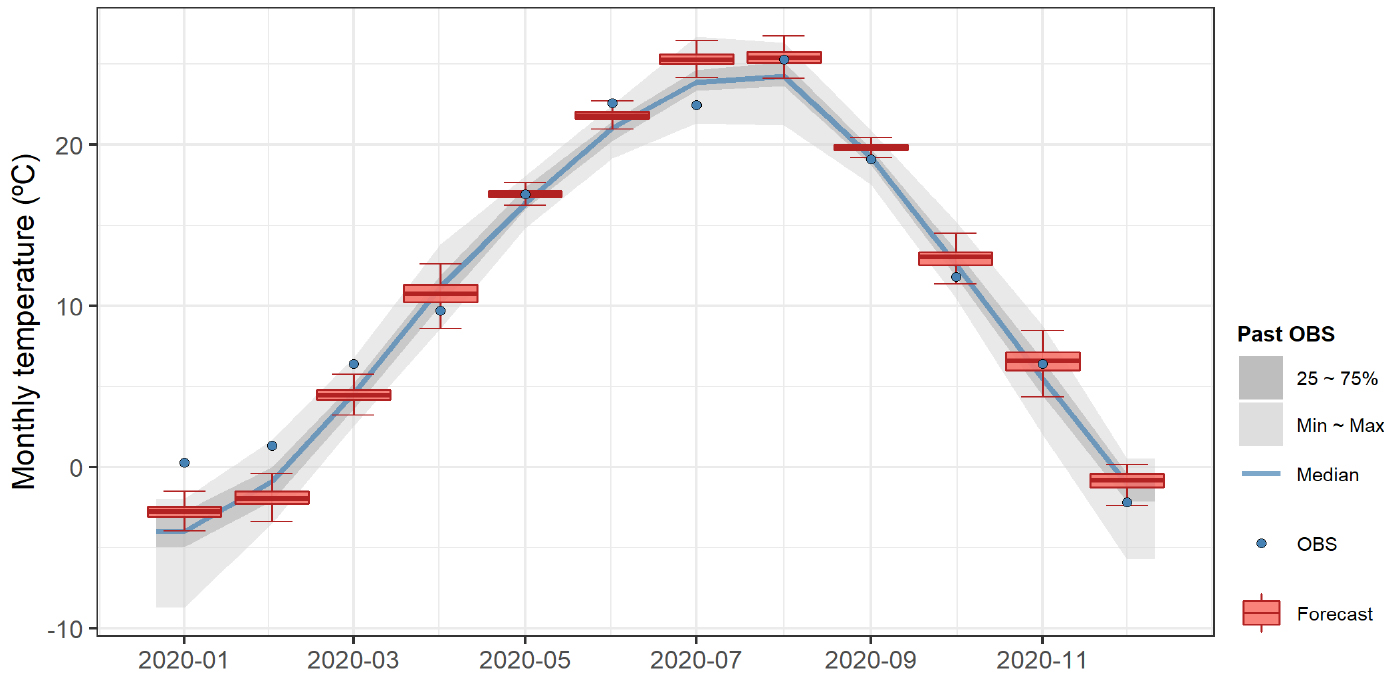
Figs. 9 and 10은 각각 1999년 12월과 2019년 12월에 예측한 2000년과 2020년에 대한 월 평균기온의 예측치와 과거의 관측치를 비교한 결과이다. 각 월별 붉은색 박스플롯은 대상월에 대한 예측범위를 나타낸 것이며, 회색음영과 푸른색 굵은 선은 동일한 월에 대한 과거 30년간의 관측치의 범위 및 중앙값(Median)을 나타낸 것이다. 푸른색 점은 각 월별 관측값을 의미한다. Fig. 9에서 2000년 1월 결과는 선행예측기간 1개월에 해당하며, 2000년 12월 결과는 선행예측기간이 12개월이다. 마찬가지로 Fig. 10도 예측시점인 2019년 12월을 기준으로 선행예측기간이 1 ~ 12개월에 해당하는 결과이다.
일부 예측범위가 관측치를 벗어나는 경우도 있으나, 대체로 관측치의 월별 값 및 변동성과 잘 부합하는 것으로 나타났다. 기온자료의 특성상 Kim et al. (2020)에서 분석한 강수량에 비해 불확실성이 낮아 예측이 용이한 특성이 있지만, 과거자료에서 나타난 것처럼 연도에 따라 매우 큰 차이가 나타나기도 한다. 반면 예측치의 범위는 이보다 좁은 범위를 가지면서도 Figs. 9 and 10에서 나타난 것처럼 예측치의 범위나 평균값, 중앙값 등이 관측치와 유사한 결과를 보이고 있다. 즉, 과거의 관측치를 사용하는 것보다는 본 연구에서 개발된 예측모형을 통해 신뢰성 있고 안정적인 월 평균기온의 예측이 가능하다고 할 수 있다.
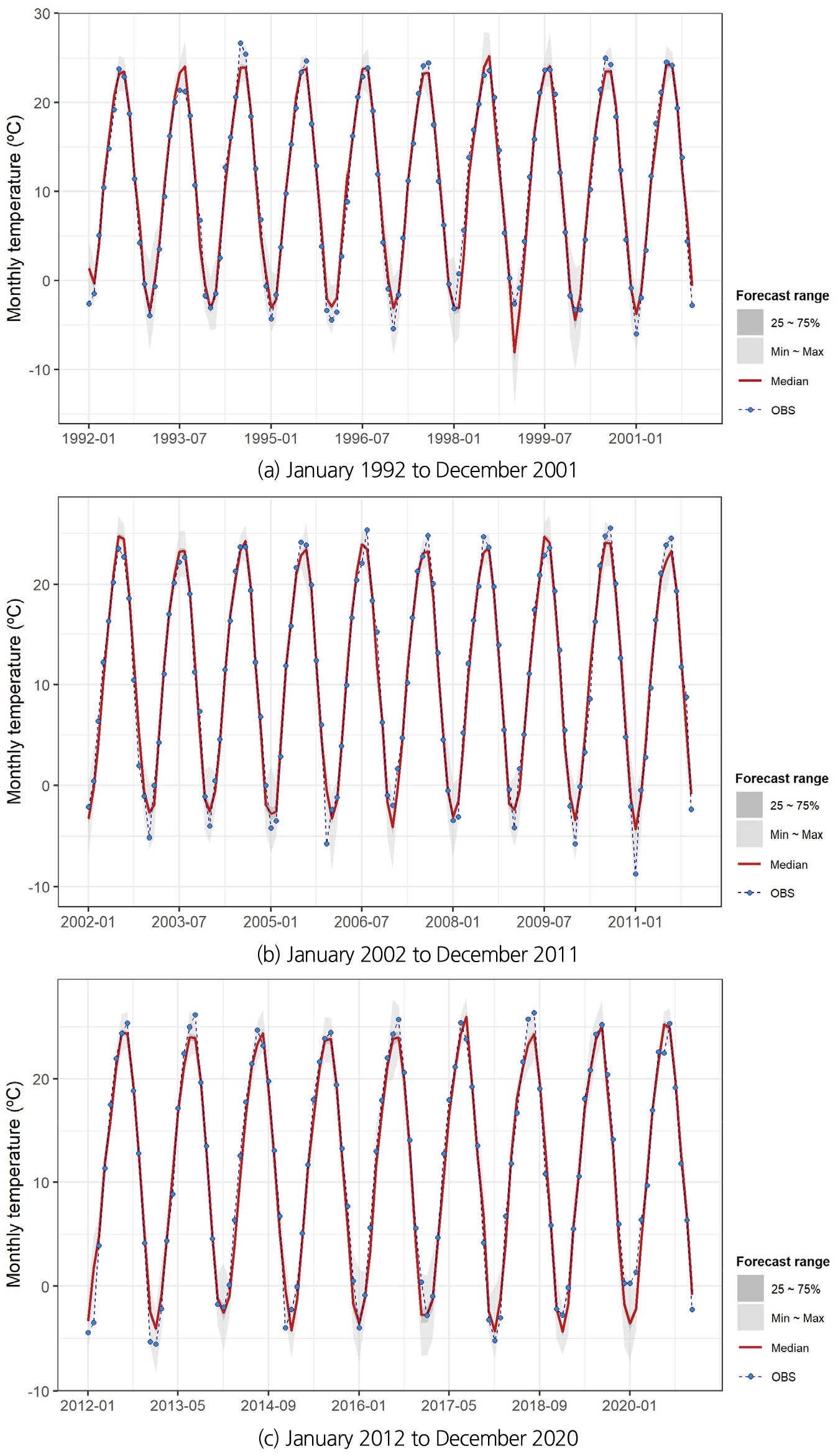
Fig. 11은 전체 분석기간(1992 ~ 2020년)에 대해 약 10년 단위로 구분하여 각 월별 예측치의 범위와 중앙값, 관측치를 함께 비교한 것이다. 대체로 예측치의 최대 ~ 최소 범위 안에 관측치가 포함되고 있으며, 예측치의 중앙값도 일부 겨울철과 여름철을 제외하고는 전 기간에 대해 관측치와 유사하게 나타나고 있다. 다만, 관측자료의 통계적 특성에 기반하여 구성된 모형의 특성상 2011년 1월과 같이 역대 최악의 한파가 있었던 경우나 평년대비 유난히 높은 기온을 기록했던 1994년, 2010년, 2013년, 2018년의 여름철에는 관측치와 다소 큰 차이를 나타내고 있다.
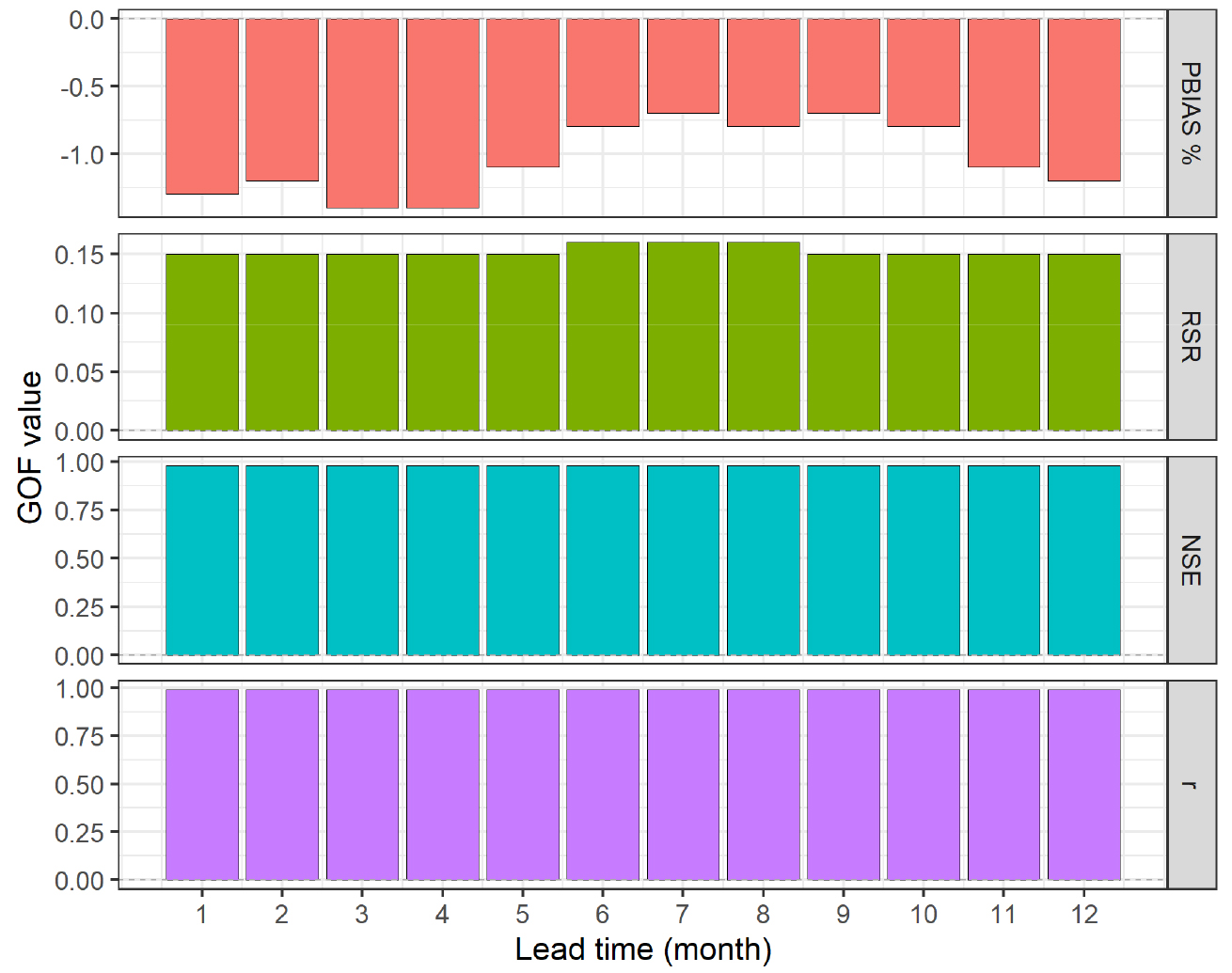
Fig. 12는 전체 분석기간에 대해 예측선행기간별 월 평균기온의 예측성을 나타낸 것이다. 각 월별 예측치의 평균값과 관측치를 대상으로 PBIAS (Percent bias), RSR (Ratio of RMSE to the standard deviation of the observations), NSE (Nash-Sutcliffe efficiency), r (Pearson correlation coefficient) 등의 대표적인 적합도(Goodness of fit, GOF) 평가지수를 분석하였다. PBIAS는 -1.4 ~ -0.7%, RSR은 0.15 ~ 0.16, NSE는 0.98, r은 0.99로 높은 적합성을 나타내었다.
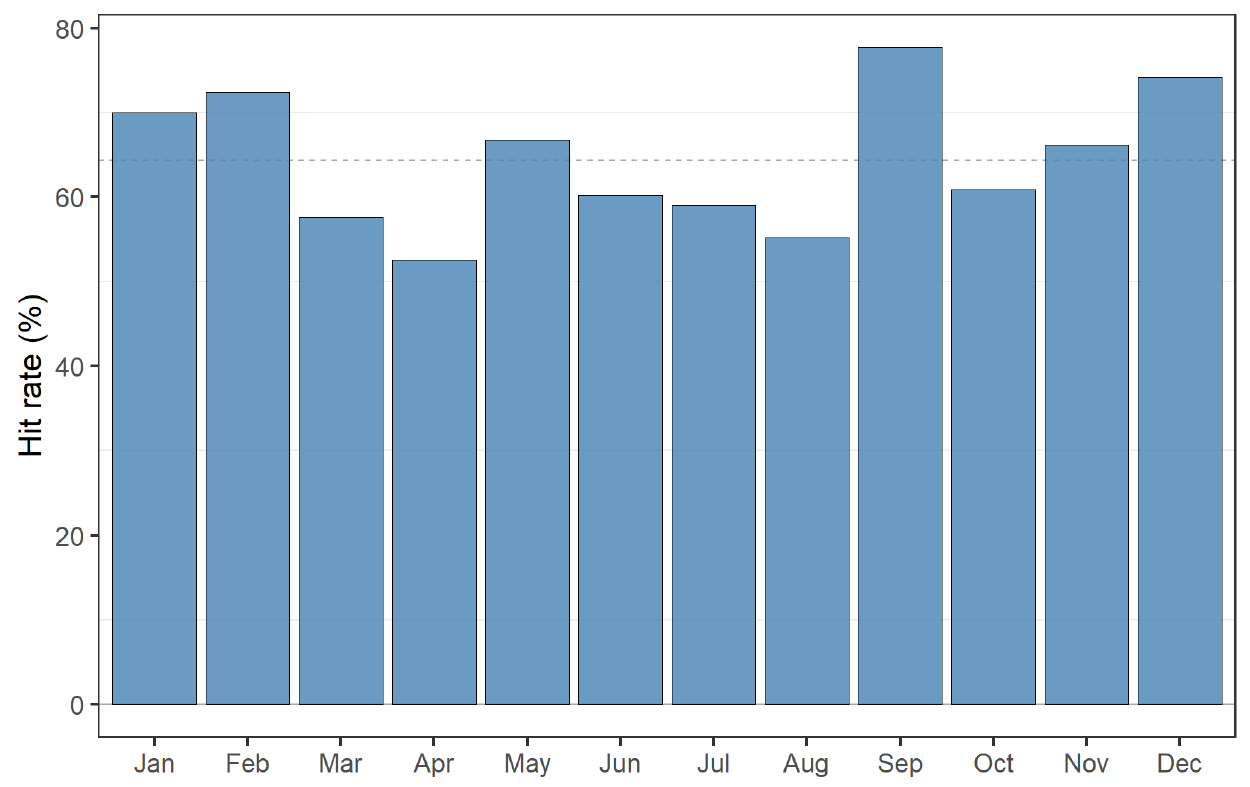
Fig. 13은 앞의 Fig. 11에서 제시한 예측치의 최소 ~ 최대범위(회색 음영) 안에 관측치(푸른색 점)가 포함될 확률을 산정하여 분석기간 전체에 대해 월별로 비교한 것이다. 월별로는 9월(77.8%), 12월(74.2%), 2월(72.4%), 1월(70.0%)의 예측성이 상대적으로 높은 반면, 4월(52.5%), 8월(55.2%), 3월(57.6%)의 예측성이 상대적으로 낮은 것으로 분석되었으며, 모든 월에 대한 평균은 약 64.4%로 나타났다.
4. 결 론
본 연구에서는 한강권역을 대상으로 글로벌 기후지수 및 대상권역 기상자료를 예측인자로 하는 다중회귀모형 기반의 월평균기온 예측모형을 구성하고 미래기간(1 ~ 12개월)에 대한 예측성을 평가하였다.
예측인자로서는 AAO, AMM, AMO 등을 비롯한 39종의 글로벌 기후지수와 8종의 한강권역 기상인자(강수량, 평균기온, 상대습도, 평균해면기압, 일조시간, 평균풍속, 평균운량, 소형증발량) 등 총 47종에 대한 월 자료를 활용하였다. 각 예측대상월을 기준으로 과거 40년간의 예측대상(한강권역 평균기온)과 각 예측인자에 대한 1 ~ 18개월 선행자료와의 지연상관성 분석을 통해 상관성이 높은 10개의 기후자료를 선정하였다. 선정된 기후자료에 대해 단계적 회귀분석(stepwise regression) 방법과 무작위 보정 및 검증을 통하여 월별로 적합도가 높은 1000개의 다중회귀모형을 도출하여 예측모형으로 활용하였다.
예측모형 및 예측결과의 활용성을 평가하기 위하여 1992년 1월부터 2020년 12월을 예측대상월로 선정하여 각 월별 도출된 예측값과 실제 관측값을 비교한 결과, 일부 겨울철과 여름철을 제외하고는 예측치의 범위 및 중앙값이 관측치와 잘 부합하는 것으로 분석되었다. 각 월별 예측치의 평균값과 관측치를 대상으로 분석한 적합도는 PBIAS는 -1.4 ~ -0.7%, RSR은 0.15 ~ 0.16, NSE는 0.98, r은 0.99로 비교적 높게 나타났다. 또한 각 월별 관측치가 예측범위에 포함될 확률은 평균 약 64.4%로 나타났으며, 9월, 12월, 2월, 1월의 예측성이 상대적으로 높은 반면, 4월, 8월, 3월의 예측성이 상대적으로 낮은 것으로 분석되었다. 그럼에도 과거자료에 기반한 통계적 모형의 특성상, 한파가 극심했던 2011년 1월이나 평년대비 높은 기온을 기록했던 1994년, 2010년, 2013년, 2018년 여름철 기온에 대한 예측결과는 타 기간에 비해 관측치와의 편차가 크게 나타났다.
본 연구에서 구축한 예측모형은 예측시점을 기준으로 미래 12개월에 대한 전망이 가능하며, 선행기간에 따라 상관도가 높은 기후지수를 선별하여 활용함으로써 기후변화 등에 따른 기후지수들의 변동성을 고려할 수 있고 예측월에 따라 탄력적으로 최적의 예측변수를 선정하여 예측모형을 도출할 수 있는 장점이 있다. 또한 현재 기상청에서 제공하는 1 ~ 3개월의 정성적 확률정보와 비교하여 1 ~ 12개월의 정량적 예측범위에 대한 도출을 통하여 보다 다양한 활용이 가능하다. 직접적으로는 최대 12개월에 대한 예측정보를 기반으로 계절적 폭염이나 한파에 대한 사전예측이 가능하며, 간접적으로는 정량적 예측정보를 이용한 추가적인 분석을 통해 기온과 상관도가 높은 증발산량에 대한 미래 전망이나 수문생태환경에 대한 변화를 전망하는 경우에도 유용하게 활용될 수 있을 것이다. 다만, Woo et al. (2020)의 연구에서와 같이 각 기후지수들간의 역학적 관계나 기후지수와 예측대상간의 역학적 관계에 대해서는 고려하지 않고, 순수하게 통계적 상관성에 기반하여 예측모형을 구성하였다. 따라서 통계적 모형의 한계로 인해 과거와 크게 다른 이상현상에 대해서는 예측성이 다소 떨어질 수 있는데, 이는 향후 보다 많은 자료가 구축되어 다양한 통계적 특성이 예측모형에 반영될 수 있다면 어느 정도 극복할 수 있을 것으로 기대한다.