1. 서 론
일반적으로 유역 전반에 내린 강우의 영향으로 수위가 상승하여 침수 피해가 발생하지만 최근 우리나라는 강수강도가 증가하고 일부 지역에 집중적으로 호우가 내리는 현상인 국지성 호우의 증가도 수위 상승 원인이 되어 하천 주변 인프라의 침수 위험성이 대두되고 있다. 실제로 2020년 8월에는 집중호우로 인해 전국의 인명피해는 42명, 시설물 피해는 2만 5,524건으로 집계되었다. 이와 같이 국지성 호우로 인한 인명 및 재산 피해를 감소시키기 위한 목적으로 신속한 예보의 필요성이 증대되고 있다.
현대에는 과학문명으로 인해 여러 매체를 통한 다량의 자료들이 신속하게 생산되고 있다. 이를 빅데이터(Big Data)라고 하는데 일정한 형태의 데이터 모델을 준수하는 정형자료와 데이터 모델이 없거나 개념이 정의되지 않은 비정형자료가 빅데이터에 포함되어있다. 과거에는 정형자료를 주로 입력자료(Input data)로 활용하였으나 최근에는 스마트폰의 보급과 카카오톡, 페이스북, 트위터와 같은 다양한 소셜미디어의 등장으로 비정형자료의 생성이 확대되어 입력자료로 활용되기 시작하였다. 정보통신정책연구원(KISDI)에 따르면, 비정형자료 형태 중 하나인 SNS (Social Network Services)의 지난 8년 동안 이용률은 꾸준히 증가하였고 2011년 대비 2018년도에는 약 31.4%의 상승세를 보였다. 또한 뉴스 기사의 감정 어휘 발생 빈도에 따른 주가변동성 현상 파악(Yu and Lee, 2018)과 비정형 농업기상자료를 활용한 농산물 도매가격 예측(Jang et al., 2017) 등의 비정형자료를 이용한 연구들이 증가하고 있는 만큼 비정형자료 활용에 대한 관심도가 높아지고 있는 추세이다. 따라서 본 연구에서는 파급력이 강해진 비정형자료를 이용하여 제외지에 해당하는 하천변 사회기반시설의 침수 대비를 위한 수위 예측 모형을 개발하고자 하였다.
일반적으로 수위 예측 모형은 물리적 기반의 수치모형과 데이터 기반의 기계학습 모형으로 분류된다. 과거의 하천 수위 예측은 주로 수치 모형을 통해 사용되었다. Han et al. (2000)은 홍수 추적 모형인 DAMBRK를 이용하여 실시간으로 하천에서 범람의 위험정도를 해석하였고 Bae and Lee (2011)은 낙동강 본류 유역에 홍수 예측이 가능한 강우-유출 모형을 개발하여 대유역에 관해 평가하였다. 그러나 강우-유출 모형의 현상은 비선형적이라 예측에 한계가 있었다. 또한 수문모형은 예보를 위한 선행시간 확보에 제한이 있고 검증되지 않은 시공간적인 불확실성으로 최종 예측결과에 영향을 미친다(Jung et al., 2018). 최근에는 신속하고 정확한 예측을 위한 데이터 기반의 홍수 예측 시스템에 대한 관심이 증가하고 많은 양의 데이터를 수집·처리할 수 있는 기술이 발전하였다. 컴퓨터가 데이터의 패턴을 학습하고 예측값을 도출할 수 있는 알고리즘(기계학습)에 대한 많은 연구들이 이에 해당한다. 기계학습은 수치모형과 비교하였을 때 수위 예측 시 소요되는 시간이 단축되어 침수 발생 후 대피가 이루어져야하는 최소한의 시간인 골든타임 안에 신속한 예보 및 경보가 가능해진다. 데이터 기반의 RNN (Recurrent Neural Network) 기법을 사용한 연구로 Tran et al. (2016)은 하천 유량, 강수량, 수위의 변수들을 가지고 예측 모델을 통해 생성된 30분 및 60분 후의 하천 수위를 결과로 제시하였다. 이전의 방법에 비해 RNN 기법은 시계열 데이터 처리에 특화되어 보다 정확한 하천 수위를 예측할 수 있으나, 가중치 소실(Vanishing gradients)의 문제로 인해 데이터가 구축되어 쌓이다보면 예기치 못한 오류가 발생할 수 있다는 단점이 존재한다. 그 외에도 Behzad et al. (2010)은 인공신경망 모델(Artificial Neural Networks model, ANN)을 이용하여 실시간으로 수위를 예측하였으나 높은 정확도를 보여주지 못하였다. 이러한 문제를 해결하기 위해 LSTM (Long Short-Term Memory) 기법이 등장했다. LSTM 기법은 기존 RNN 기법의 장기 의존성과 가중치 소실 문제를 해결하였다. 시계열 자료에 대한 정확도를 보장하고 있는 LSTM 기법은 태양광 발전량에 많은 영향을 미치는 일사량 예측(Kim et al., 2021), 조류인플루엔자(HPAI) 확산 경로 예측(Choi et al., 2020), COVID-19로 인한 사망자수 예측(Gautam, 2021) 등 다양한 분야에서 활발하게 연구가 진행 중이다. 수위 예측 분야에서 Jung et al. (2018)은 12개년의 자료로 3개년에 대한 수위 예측을 LSTM 기법으로 진행하였고 Liang et al. (2018)은 2003년부터 2012년까지의 일 데이터를 사용하여 중국의 둥팅 호수의 수위 변화를 연구하여 SVM (Support Vector Machine) 모형보다 LSTM 모델이 더 정확도가 높다는 것을 확인하였다. 유출량 모의 성능 분석 연구에서도 RNN 모델에 비해 LSTM 모델은 선행 시간이 길어져도 정확성이 더 유지되는 것으로 파악되었다(Kim et al., 2019). 이러한 데이터 기반의 연구는 주로 수위, 강수량 등의 수문자료를 입력자료로 활용하여 예측 결과값으로 도출하였다.
그러나 최근에는 계측 센서 없이 홍수 지역을 찾기 위해 트위터 자료를 이용하거나(Asmai et al., 2019) 재난 발생에 대한 트윗을 실시간으로 감지할 수 있는 GeoBurst 프로그램을 개발하는(Zhang et al., 2016) 등 실시간으로 활용이 가능하고 시·공간의 정보를 얻을 수 있다는 점에서 SNS를 통한 홍수발생예측의 가능성이 확대되고 있다(Lee and Hwang, 2019). 따라서 본 연구에서는 현재 수위 예측 모형에서 많이 활용되고 있는 수문자료와 같은 정형자료의 활용뿐 아니라, 비정형자료를 함께 사용하였다. 정형자료와 함께 비정형자료를 사용한 상호 보완형의 자료와 정형자료만을 사용한 자료를 기계학습에 적용하여 도출된 결과가 수위 예측 정확도에 미치는 영향을 비교 및 분석하였다.
2. 본 론
2.1 연구방법
2.1.1 LSTM 기법
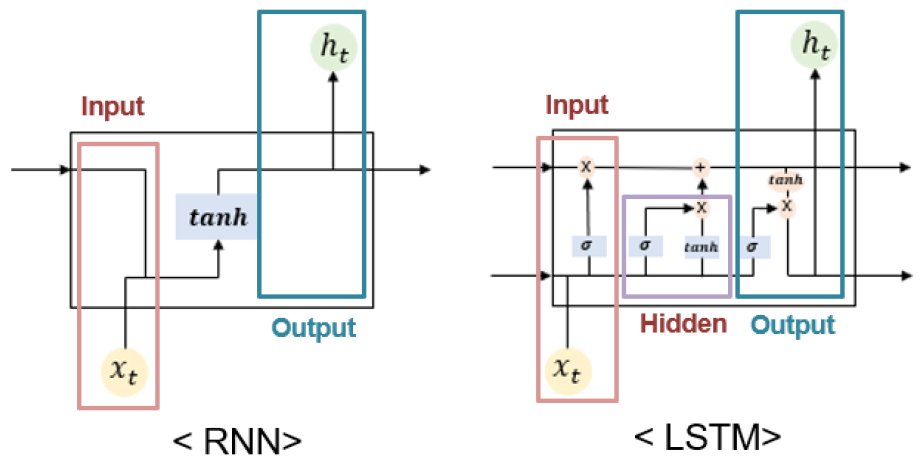
LSTM (Long Short-Term Memory) 기법은 Hochreiter and Schmidhuber (1997)이 제안한 기법으로 RNN 기법에서 발생하는 가중치 소실 문제를 해결하여 시계열 자료 처리에 특화되어 있는 것으로 알려져 있다(Tran et al., 2017). LSTM 기법의 구조는 Fig. 1과 같으며 입력 게이트(Input gate), 출력 게이트(Output gate), 망각 게이트(Forget gate)로 이루어졌고 이러한 여러 게이트가 연결되어있는 셀(Cell)로 구성이 되어있다. 관련 식은 Eqs. (1)~(6)과 같다.
여기서 ft는 망각 게이트, 는 활성화 함수, Wf는 망각 게이트의 가중치, ht는 새로운 출력 값, xt는 현재의 입력, bf는 기울기를 나타낸다. 다음 단계인 입력 게이트(it)는 입력할 값을 결정하고 새로운 셀 상태를 업데이트한다.
여기서 는 활성화 함수에 의해 생성된 새로운 셀 상태, Wc, Wi는 셀의 가중치, bi, bc는 기울기를 나타낸다. 마지막 단계인 출력 게이트(ot)는 무엇을 출력할지 결정하는 것이다.
여기서, Wo는 출력게이트의 가중치, bo는 기울기를 나타낸다.
2.1.2 텍스트 마이닝(Text mining)
텍스트 마이닝(Text mining)이란 비정형화된 텍스트 자료나 이산형 자료의 집합으로부터 지식을 발견하는 과정이고 본 연구에서는 데이터 분석을 위한 통계 및 그래픽스를 지원하는 무료 소프트웨어 환경인 R studio에서 수행하였다. 텍스트 자료에는 논문, 기사, 이메일과 같은 실생활에서 만들어지는 문서 형태의 자료나 SNS에서 만들어지는 디지털 형태의 문서 또는 웹로그 데이터와 같은 문서 형태의 비정형 자료가 존재한다. 이를 시각화하기 위한 방법으로는 워드클라우드(Wordcloud), 워드트리(Wordtree), 사회 연결망 분석(Social network analysis)이 있다. 텍스트 마이닝의 절차로는 텍스트 자료의 수집, 전처리과정(형태소 분석, 어간 추출, 품사 할당), 자료변환(용어-문서 행렬), 자료 분석(워드클라우드, 워드 나무, 사회 연결망 분석, 토픽 모델링) 순으로 진행된다. 전처리 과정에서는 숫자나 기호가 있는 문장에서 부수적인 역할을 하는 것을 여과하고 주요한 역할을 하는 어간을 추출한다. 또한 부사적인 의미를 가진 단어를 불용어(Stop words)처리를 하는데 이 과정은 비정형자료를 분석이 가능한 정형화된 형태로 변환하는 것이다. 본 연구에서는 텍스트 데이터를 시각화하기 위해 하나의 텍스트에 출현하는 단어를 빈도별로 표출한 그래프인 워드 클라우드를 사용하였다. 또한 다루는 데이터의 언어가 한글이므로 KoNLP (Korean Natural Language Processing)라는 한글 텍스트 마이닝 패키지를 설치하여 R studio에서 사용 가능한 형태로 구현하였다.
2.2 연구대상지 선정
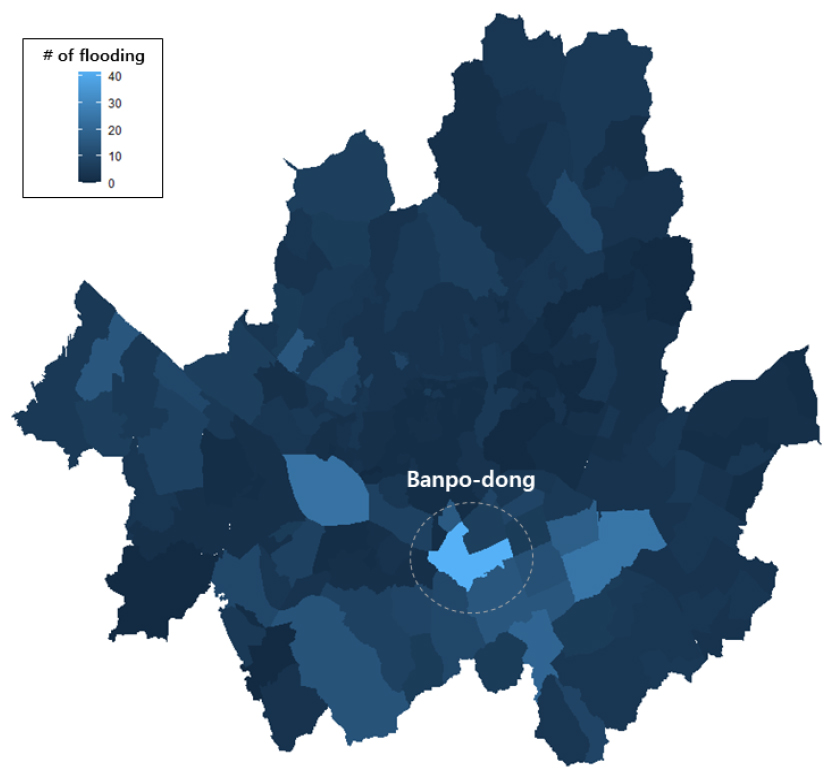
본 연구에서는 2009년~2020년의 총 12년간 네이버(Naver) 뉴스 기사를 바탕으로 서울에서 실제 침수가 일어난 장소를 이벤트 중심으로 수집을 한 후 Fig. 2와 같이 나타내었다. 그 결과, 반포동이 가장 많이 침수가 일어난 지역으로 나왔으며 특히 잠수교(24건), 국립중앙도서관(5건), 반포한강공원(15건)으로 가장 많이 언급된 잠수교를 본 연구의 연구대상지로 선정하였다. 잠수교의 수위 예측을 통하여 제외지이자 친수공간인 반포한강공원의 침수 영향도 파악할 수 있다.
2.3 데이터 구축
2.3.1 정형자료
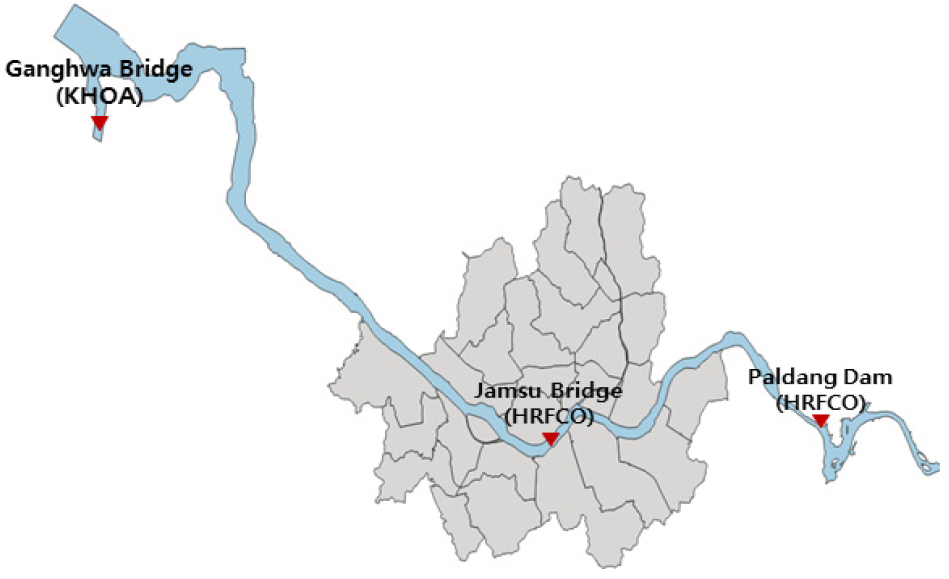
입력자료 중 정형자료는 잠수교 수위, 강화대교 조위, 팔당댐 방류량의 10분 단위 시계열 자료이다. 수위와 방류량은 한강홍수통제소, 조위는 국립해양조사원에서 수집하였으며 2009년부터 2019년까지 잠수교의 수위를 분석한 결과 6, 7, 8월에 가장 높은 수위를 보였다. 고수위에서의 수위예측을 통해 침수 피해를 막고자 2015년~2020년 6, 7, 8월을 연구기간으로 선정하였다. Table 1은 정형자료로 구축한 인자를 정리하였고 Fig. 3은 연구대상지의 위치를 나타내었다.
Table 1.
Structured input data
2.3.2 비정형자료
IBM (International Business Machines Corporation) 에 따르면 비정형자료는 빅데이터 중 70~80%를 차지하고 정형자료의 증가율에 비해 비정형자료의 증가율이 약 15배 정도가 더 많을 정도로 중요성이 대두되고 있다. SNS 중 광고성 문구가 적고 정보공유의 목적으로 주로 사용되는 개방형 채널인 트위터를 선정하였다. 기간은 2015년~2020년의 6, 7, 8월 중 실제로 침수가 일어났던 시간 직전까지, 장소는 서울시로 트위터 상에서 시·공간적 조건을 설정하였다. 이후 텍스트 마이닝 중 워드클라우드를 이용하여 수집된 트윗 중 장마기간에 많은 비중을 차지하는 단어인 ‘비(폭우)’, ‘장마’, ‘홍수’를 제외한 ‘나무’, ‘복구’, ‘차량’, ‘강풍’, ‘태풍’, ‘누수’, ‘상수도’를 도출하였고 최종적으로 사용한 검색어는 ‘비(폭우)’, ‘장마’, ‘홍수’, ‘나무’, ‘복구’, ‘차량’, ‘강풍’, ‘태풍’, ‘누수’, ‘상수도’이다(Fig. 4). 해당 단어를 검색하여 1분 단위로 도출되는 트윗의 개수를 수집하였고 자료의 순도와 내용의 중복성을 피하기 위해 리트윗(Retweet)은 제외하였다.
2.3.3 데이터 결합
비정형자료를 수위 예측 알고리즘 내 적용하기 위해서는 정형화된 형태로 변환하는 과정이 필수적이다(Ha and Ahn, 2019). 따라서 2.3.2와 같이 텍스트 마이닝을 통해 도출된 검색어로 1분 단위의 이벤트 중심 트윗을 수집하였다. 10분 단위의 정형자료와 이종결합을 하기 위해서 수집한 트윗을 10분 단위로 가공하였고 기간에 맞추어 정형자료와 결합하였다.
2.3.4 데이터 전처리
4가지 정형자료의 인자가 유의미한 지 여부를 판단하기 위해 t-test분석 및 P-value를 도출하였다. t-test는 두 개의 집단에서 평균의 차이를 통해 검증하는 가장 보편적인 통계 방법이고 3가지의 조건을 충족시켜야 한다. 첫 번째, 자료는 모두 동일 간격을 가진 연속형 수치여야 한다(identical interval and continuity). 두 번째, 두 집단은 서로 독립적이어야 하며(independence) 마지막으로 자료의 수치는 정규성을 가져야 한다(normality). 입력자료인 잠수교 수위, 강화대교 조위, 팔당댐 방류량, 트윗의 개수에 대하여 t-test 분석 및 P-value를 도출한 결과는 Table 2와 같다. 일반적으로 P-value 값이 0.05 이하면 유의미한 인자로 판단하여(Ruxton, 2006) 본 연구에서 사용한 4가지 정형자료의 인자(수위, 조위, 방류량, 트윗의 개수)는 P-value가 0.0 이하라 사용 가능하다고 판단되었다.
또한 수위를 포함한 나머지 입력자료(조위, 방류량, 트윗의 개수)별로 3시간 후의 잠수교 수위에 어떤 영향을 미치는 지 오차지표인 MAE (Mean Absolute Error), RMSE (Root Mean Square Error), IOA (Index Of Agreement), R2 (Coefficient of determination)를 통하여 정확도를 비교해보았다. 관련 식은 Eqs. (7)~(10)과 같고 오차지표를 통해 도출된 값은 Table 3에 정리하였다.
Table 2.
Results of t-test
| Input Data | P-value | Usage status |
| Water surface elevation (EL.m) | ~0.0 | Available |
| Outflow (m3/s) | ||
| Tide Level (cm) | ||
| Tweets |
Table 3.
Degree of error by input data
| Input Data | MAE | RMSE | IOA | R2 |
| W* | 0.292 | 0.371 | 0.985 | 0.873 |
| W, O† | 0.301 | 0.402 | 0.986 | 0.802 |
| W, T※ | 0.231 | 0.330 | 0.989 | 0.930 |
| W, T, O | 0.228 | 0.271 | 0.994 | 0.950 |
여기서, N은 자료의 개수, Si는 모형의 예측값, 는 모형의 평균값, Oi는 관측값, 는 관측 평균값을 의미한다. 오차를 비교한 결과, 수위 예측을 위해 과거의 수위, 방류량, 조위 자료 모두 사용한 경우가 가장 정확도가 높다고 판단되어 최종 입력자료로 선정하였다.
2.4 수위예측 알고리즘 구축 및 침수 검증
본 연구에서는 수위 예측 모형의 실제 모의에 앞서 최적의 값을 도출하기 위해 전체 기간 중 가장 높은 수위를 갖는 2020년을 비교값으로 지정하여 학습기간과 비교하였다. 학습기간은 5가지의 경우로 분류하고 도출된 예측 수위 값을 오차지표(MAE, RMSE, IOA, R2)로 비교하여 기간을 조정하였다. 그 결과, 학습기간은 2015년~2019년, 실행기간은 2020년으로 선정하였다(Table 4).
또한 LSTM 기법 내에 있는 매개변수를 이용해 민감도 분석을 수행하였다. 설정한 매개변수는 반복횟수(Iteration), 시퀀스 길이(Sequence length), 학습률(Learning rate), 은닉층(Hidden layer)으로 총 4가지이며 Table 5는 민감도분석을 수행하는 경우를 정리하였다. 매개변수당 고정값(1, 1000, 5, 0.05)을 선정하였고 예측 값의 정확도를 평가하기 위한 평가지표로 RMSE, MAE, IOA, R2를 사용하였으며 예측자료는 3시간 후 잠수교 수위로 설정하였다.
Table 6은 민감도분석을 통해 도출된 최적값이다. 민감도분석을 통해 도출된 최적값은 시퀀스길이 1, 반복횟수 1000, 은닉층수 5, 학습률 0.05이며 매개변수 당 4가지 경우에서의 오차지표를 비교하여 선정하였으며 향후 수위예측 알고리즘 내에서도 사용하였다.
정형자료와 비정형자료를 사용한 예측값, 정형자료만을 사용한 예측값의 정확도를 오차지표로 비교하였다(Table 7).
Table 4.
Separation of learning / execution period
Table 5.
Test cases for sensitivity analysis
| Parameter | Setting Value | Evaluation |
| Sequence Length | 1*, 5, 10, 20 | RMSE, MAE, IOA, R2 Comparison |
| Iteration | 10, 100, 1000*, 10000 | |
| Hidden Layer | 1, 2, 5*, 10 | |
| Learning Rate | 0.005, 0.01, 0.05*, 0.1 |
Table 6.
Results of sensitivity analysis
Table 7.
Comparison of degree of error on data types
| MAE | RMSE | IOA | R2 | |
| SD* | 0.252 | 0.295 | 0.992 | 0.919 |
| SD+UD† | 0.225 | 0.269 | 0.994 | 0.937 |
비정형자료의 사용 유무에 따른 오차를 비교한 결과, 정형자료만 사용했을 경우의 오차가 더 높게 나왔다. 이는 비정형자료도 함께 사용하여 수위예측에 적용하였을 때 정확도가 더 높음을 알 수 있다.
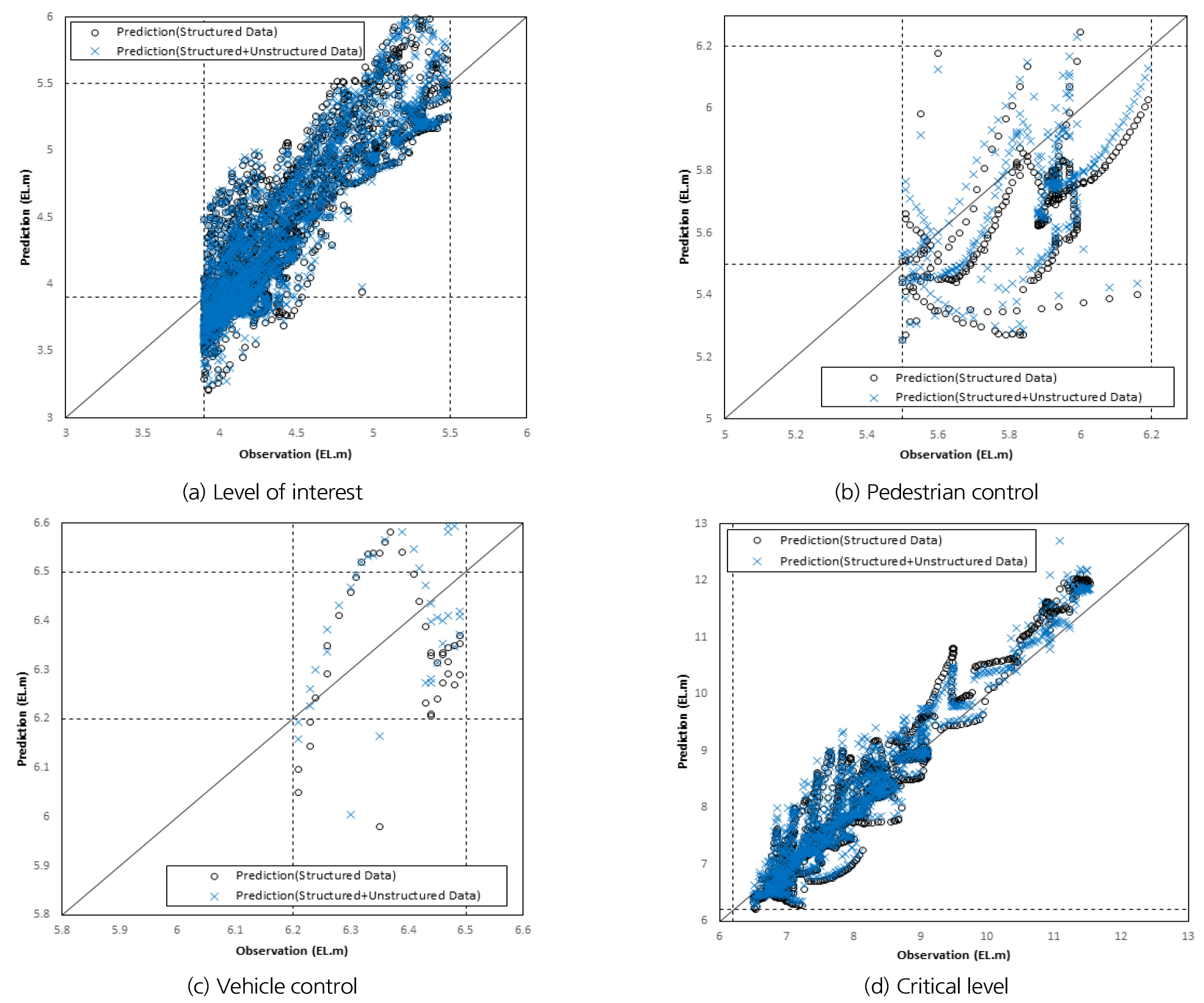
이를 세분화하여 분석하기 위해 잠수교의 수위 구간별로 나누어 비교해보았다(Figs. 5 and 6). 잠수교의 수위구간인 관심구간(EL. 3.9 m 이상), 보행자 통제구간(EL. 5.5 m 이상), 차량 통제구간(EL. 6.2 m 이상), 심각구간(EL. 6.5 m 이상)으로 분리하여 관측값과 예측값 사이의 오류율을 2가지 방법으로 비교해보았다.
우선, 관측값과 예측값(정형자료만 사용했을 경우, 정형자료와 비정형자료를 사용했을 경우)의 비교를 긍정오류율(Rfp)과 부정오류율(Rfn)로 나타내었다. 긍정오류율은 침수가 발생하지 않았으나 예측 모형이 침수가 발생한 것으로 판단하는 경우를 의미하고 부정오류율은 침수가 발생하였으나 예측모형이 침수가 발생하지 않은 것으로 판단하는 경우를 의미한다.
긍정오류율(Rfp)과 부정오류율(Rfn) 관련된 식은 Eqs. (11) and (12)과 같다.
여기서, FP는 예측값은 침수가 맞으나 실제 침수가 발생하지 않은 경우, TN은 예측값과 실제 모두 침수가 발생하지 않은 경우, TP는 예측값과 실제 모두 침수가 발생한 경우, FN은 예측값은 침수가 아니나 실제로 침수가 발생한 경우를 의미한다.
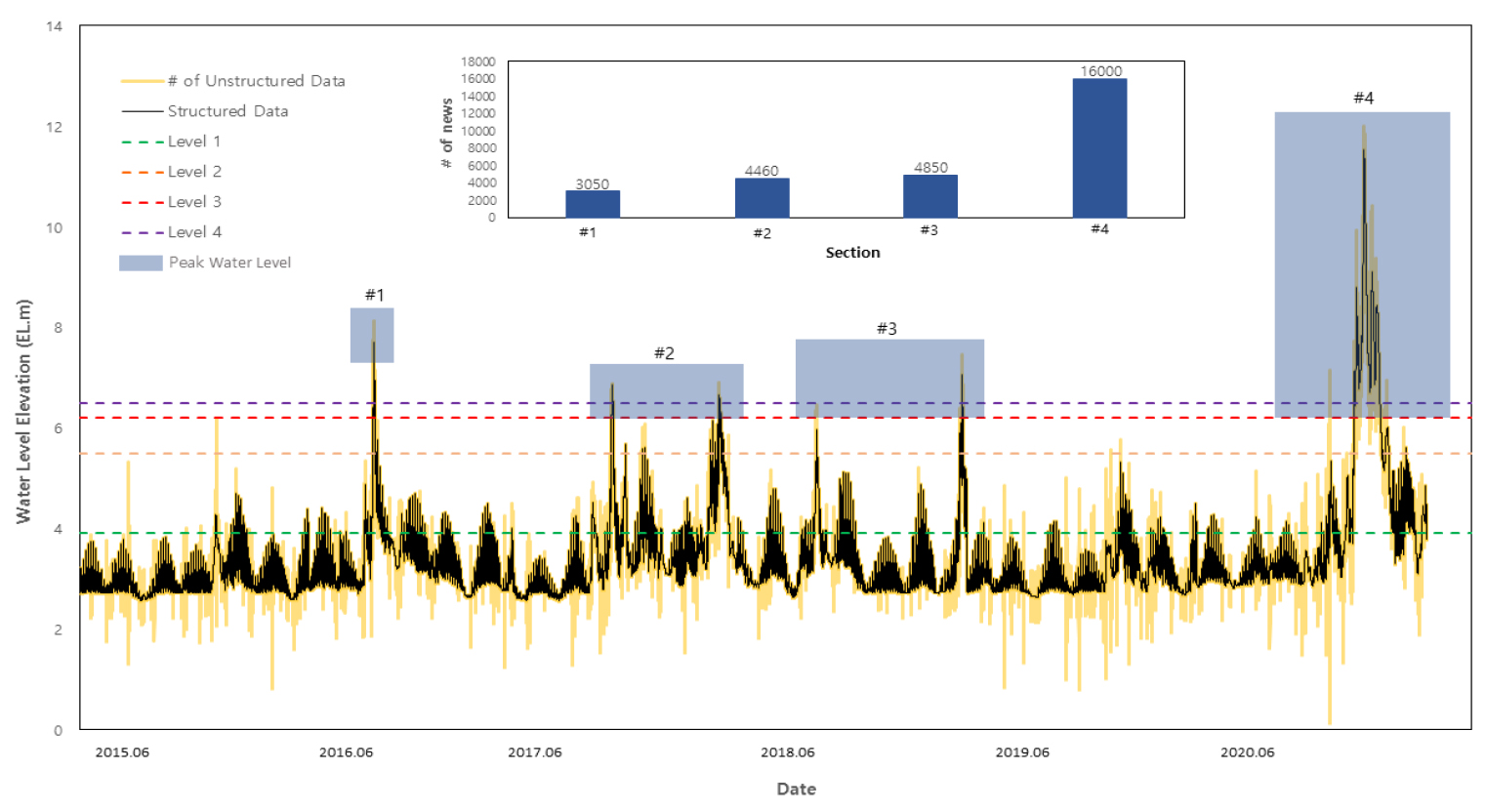
긍정오류율과 부정오류율을 비교해본 결과, 정형자료만을 사용한 경우 모든 구간에서의 긍정오류율이 비정형자료를 함께 사용한 경우보다 낮게 나왔다. 긍정오류율은 보수적인 예/경보로 인명피해를 감소시킬 수 있다는 점에서 중요하다. 한편 부정오류율은 위기 상황에서 예/경보를 하지 않아 인명 및 재산피해를 발생할 수 있다는 단점이 존재하는 데, Table 8을 통해 비정형자료를 함께 사용했을 때 긍정오류율이 더 높아 침수 대비에 유리함을 알 수 있다. 비정형자료의 유무가 어느 수위 기준까지 영향을 미치는 지 판단하기 위해서 수위 관측값과 비정형자료의 개수를 그래프에 포함하였다(Fig. 6). 동일 시간대 관측수위와 같이 표현된 노란색 밴드의 폭은 비정형자료의 개수를 의미한다. Level 1(관심구간)과 Level 2(보행자 통제구간)보다 Level 3(차량 통제구간)과 Level 4(심각구간)에서의 비정형자료의 개수가 2020년 8월을 제외하고 더 적다는 것을 알 수 있다. 실제로 Level 4(심각구간) 이상의 수위를 기록한 2016년, 2017년, 2018년, 2020년의 홍수와 관련된 인터넷 기사를 집계해보니 3050건, 4450건, 4850건, 16000건이었다.
이는 2020년 발생했던 폭우로 인해 홍수에 대한 사회적인 관심도가 그 전에 비해 더욱 증가하였음을 언론기사의 게재수로써 정량적인 판단을 할 수 있었고 2020년 8월에만 예외적으로 많은 수의 비정형자료가 수집된 이유를 설명할 수 있었다. 따라서 Table 8에서 관심구간(EL. 3.9 m 이상)~보행자 통제구간(EL. 5.5 m 이상)에서의 긍정오류율이 높게 나왔고 Fig. 6에서 해당 구간의 비정형자료의 개수가 많다는 것을 고려해보면 비정형자료가 수위 값 예측 시 효과적인 자료임을 도출할 수 있다.
한편, 예측 결과 중 정형자료 대비 비정형자료의 비율을 산정하여 분석하였다. 구간별 예측 결과(2020년 6, 7, 8월) 내에서 사용된 관측값(2015년~2019년 6, 7, 8월) 중 정형자료 대비 비정형자료 개수의 비율(Ratio)을 비교해본 결과, 전체적으로 5~18% 정도밖에 미치지 못 하였는데, 이는 낮은 비율의 비정형자료임에도 모델의 정확도에 영향을 미쳤다고 판단할 수 있었다(Table 9). 특히 관심구간(EL. 3.9 m 이상), 보행자 통제 구간(EL. 5.5 m 이상)에서의 비율이 5% 및 8%임에도 긍정오류율이 정형자료만을 사용했을 경우보다 비정형자료를 함께 사용했을 경우가 더 높게 나오는 것으로 보아 관심구간(EL. 3.9 m 이상)과 보행자 통제구간(EL. 5.5 m 이상)에서 정형자료에 비해 상대적으로 적은 양의 비정형자료가 상대적으로 예측결과에 큰 영향을 미쳤음을 판단할 수 있다. 따라서 비정형자료의 개수가 증가할 경우 관심구간(EL. 3.9 m 이상)~보행자 통제구간(EL. 5.5 m 이상)에서 더욱 높은 정확도 도출할 것이라 판단된다.
Table 8.
Rates of positive error and negative error
3. 결 론
2021년 7월, 독일에서는 홍수로 인한 최악의 인명피해가 발생하였고 우리나라에서도 이상기후 중 특히 호우와 태풍에서의 피해가 극심하여 많은 인명 및 재난 피해를 겪고 있는 상황이다. 따라서 이러한 돌발홍수와 같은 재난으로부터의 피해를 비구조적인 관점에서 대응하기 위하여 침수 예/경보를 위한 수위 예측 알고리즘을 개발하고자 하였다.
본 연구는 시계열자료에 특화되어 있는 기계학습 기법 중 LSTM 기법을 이용하였다. 기계학습 내 입력자료로 정형자료를 중심으로 사용하는 기존 연구와는 달리 본 연구에서는 비정형자료를 정형자료와 함께 활용하여 상호 보완형의 자료를 생성한 후, 정형자료만을 사용한 경우와 비교 및 분석하였다.
연구대상지는 서울의 잠수교로 선정하였고 연구기간은 2015년부터 2020년 6, 7, 8월, 입력자료는 잠수교의 수위, 강화대교 조위, 팔당댐 방류량, 서울시의 트윗의 개수로 지정하였다. 해당 기관에서의 입력자료를 수집한 후에는 t-test, 입력자료 간의 오차비교, 최적의 값을 도출하기 위해 학습기간과 실행기간을 각각 2015년~2019년, 2020년으로 설정하였고 민감도 분석을 수행하였다. 비정형자료의 포함 유무에 따라 예측수위 값의 정확도가 어떻게 변화하는지 비교한 결과, 비정형자료를 사용한 경우의 정확도가 정형자료만을 사용했을 때에 비해 관심구간(EL. 3.9 m 이상)을 제외한 나머지 구간에서 모두 높게 나왔다. 이를 침수 대비에 활용하기 위하여 구간별로 긍정 및 부정오류율을 나타낸 결과, 비정형자료를 사용한 경우의 긍정오류율이 정형자료만을 사용한 경우보다 더 높게 나와 활용도가 높을 것으로 예상되었다. 따라서 침수 예측에 있어서 정형자료와 함께 비정형자료를 이용한 상호 보완형의 자료가 더욱 효과적임을 알 수 있다.
특히 수위 구간을 세분화하여 분석하였을 때 관심구간(EL. 3.9 m 이상), 보행자 통제구간(EL. 5.5 m 이상)에서 차량 통제구간(EL. 6.2 m 이상), 심각구간(EL. 6.5 m 이상)에 비해 비정형자료 개수는 적음에도 불구하고 긍정오류율의 차이가 더 크므로 해당 구간에서 비정형자료의 영향이 좀 더 크다는 것을 파악할 수 있었다.
그러나, 비정형자료를 사용하는 데에 있어 한계점도 존재하였다. 첫째, 본 논문에서 비정형자료를 추가로 사용한 경우의 수위 예측 정확도가 다소 향상되었으나, 수집한 비정형자료의 개수가 정형자료의 개수에 비해 적은 비중을 차지하고 있어 향상 정도가 크지 않았다고 판단된다. 따라서 본 논문에서 사용된 텍스트데이터(트위터) 뿐만 아닌 이미지데이터, 영상데이터 등 자료의 양적인 부분에 있어 범위를 확대하여 보다 많은 자료를 구축할 필요성이 있다. 둘째, 비정형자료의 특성상 사건 발생 후에 자료가 생성되기 때문에 시간의 간격 차이가 존재할 수 있고 자료의 순도에 대해서도 문제가 제기될 수 있다는 점이다. 비정형자료는 익명의 사람들이 자료를 생성한다는 점에서 다양한 다량의 정보를 얻을 수 있다는 장점이 존재하지만 반대로 출처를 알 수 없는 정보도 존재하기 때문에 보다 고도화된 전처리과정이 필요하다. 이러한 한계점을 보완하여 차량 통제구간(EL. 6.2 m 이상)과 심각구간(EL. 6.5 m 이상)에서의 정확한 예측을 위하여 해당 연구대상지 지점에서의 차량 통행량 데이터, CCTV 영상자료 등을 활용하거나 동일 시간 간격으로 자료를 재가공할 수 있는 세밀한 데이터 전처리 과정을 거친다면 보다 정밀하고 정확도 높은 예측값 도출이 가능할 것이다. 향후 다양한 비정형자료의 신뢰도가 확보되어 실제 재난 예·경보에 활용되기를 기대한다.