1. 서 론
2. 연구지역 및 데이터
3. 방법론
3.1 시간 안정성 분석(TSA)
3.2 통계 분석(SSM)
3.3 랜덤 조합 방법(RCM)
4. 연구 결과 및 토의
4.1 토양수분의 시공간 변동성 분석
4.2 시간 안정성 분석
4.3 통계적 샘플링 개수 분석
4.4 랜덤 조합 샘플링 개수 분석
5. 결론 및 요약
1. 서 론
토양수분 함량은 일반적으로 토양 속 통기대(aeration zone)에 존재하는 물의 양으로 정의되며, 지표면 담수량의 작은 비율(~0.05%)을 차지하고 있지만 물순환 과정에서 중요한 역할을 담당하는 변수 중 하나이다(Seneviratne et al., 2010; Shiklomanov, 1998; Pachepsky et al., 2003). 토양수분 데이터는 농업(Hardie, 2020), 폭염, 홍수, 가뭄 등 자연재해 분석(Lorenz et al., 2010; Wasko and Nathan, 2019; Yao et al., 2023) 및 기후 모니터링(Seneviratne et al., 2010)의 기초자료로 유용하게 활용되고 있다. 한반도에서는 매년 7-9월에 발생하는 홍수로 인해 막대한 인명, 재산 피해가 발생하고 있으며, 홍수 피해가 빈번하게 발생하는 경사지 및 유역에서 토양수분의 분포는 홍수량에 영향을 미친다. 따라서 홍수 등 물 관련 자연 재난을 예방하고 이에 대응하기 위해서는 토양수분 함량의 정확한 측정이 요구된다.
현재 국내에서 보편적으로 사용되는 토양수분 계측 기법은 관측 범위에 따라, 건토중량법, 유전율식 관측 기기 등을 이용한 지점 관측 방법과 위성, 항공기 등에 탑재된 초분광 센서, 열적외선 센서, 마이크로파 센서 등을 이용한 광범위 관측 기법으로 나눌 수 있다(Lee et al., 2020). 전 지구 규모의 토양수분 관측 기술은 넓은 공간 범위의 토양수분 데이터를 획득할 수 있다는 장점이 있지만(Wanders et al., 2014), 데이터의 신뢰성을 확보하기 위해 관측 대상 지역 내에 밀도 높게 설치된 지점 관측 토양수분 데이터를 이용한 평가 및 보정이 필수적이다(Albergel et al., 2012). 최근 이러한 필요성에 따라 청미천 유역(Gwak et al., 2015), 설마천 유역(Jeong et al., 2018; Kim et al., 2019), 성균관대학교 자연과학캠퍼스 식물원(Kim et al., 2016), 홍천강 유역(Jeong et al., 2023) 등 국내 다양한 지역을 대상으로 지점 토양수분 관측망을 설치하였고 이를 토대로 활발한 연구가 수행되고 있다.
지점 토양수분 관측 데이터는 각 설치 지점마다 지형, 토성, 식생 등 요소의 영향을 받아 시공간적으로 상이하게 나타나기 때문에 인공위성 자료와 비교하기 위하여 소유역을 대표할 수 있는 지점 산정이 요구된다(Jacobs et al., 2004; Yu et al., 2018). 이에 Vachaud et al. (1985)는 시간 안정성 분석(Temporal Stability Analysis, TSA)을 정의하였고, 이는 최소한의 지점 측정으로 소유역의 시공간 평균값을 파악할 수 있다는 개념이다. Martínez-Fernández and Ceballos (2005), Jacobs et al. (2004)는 시간 안정성 기법의 타당성을 검증하였으며, 이 분석 기법은 수평 방향으로 공간 면적의 확장(Brocca et al., 2012), 연직 방향으로 다양한 토양 깊이(Choi and Jacobs, 2007)에서 모두 토양수분의 대표 지점을 선별할 수 있어 매우 유용하다.
그러나, 70% 이상이 산지로 이루어진 국내에서는 대표 지점만으로 높은 신뢰도 수준에서 대상 지역의 평균 토양수분 값을 나타내기에 부족한 실정이다. 이에 각 소유역에서 토양수분 평균 거동 특성을 반영할 수 있는 필요 지점 개수 분석이 요구된다. 대상 지역의 토양수분 변화를 적절히 반영할 수 있는 필요 지점 개수 산정에 기준을 제공하는 앞선 연구들에서는 주로 토양수분의 공간적 변동성에 초점을 맞춘 통계적 샘플링 방법(Statistical Sampling Method, SSM)과 토양수분의 시계열 변화에 초점을 맞춘 랜덤 조합 방법(Random Combination Method, RCM)을 중심으로 연구가 수행되고 있다(Wang et al., 2008; Singh et al., 2019). SSM은 각 관측 날짜에서의 공간 토양수분의 변동성 측정 지표로 활용하였고 ±2%, ±4% 오차 범위 내에서 필요 지점 개수를 산정하였다(Brocca et al., 2010). Brocca et al. (2012)은 RCM을 이용하여 평균 토양수분을 분석한 대표적인 연구로, 무작위로 추출한 토양수분 지점의 시계열 값을 회귀모델의 성능 지표로 정확도를 평가하였다.
높은 정확도의 토양수분 데이터를 생산하기 위해서는 지점 토양수분에 대한 분석이 선행되어야 한다. TSA, SSM, RCM은 각각 Temporal Stability of Index (TSI), 표준편차, Coefficient of Determination (R2)과 Root Mean Square Error (RMSE) 정확도 지표들을 이용하여 공간 대표성을 지니는 토양수분 관측 지점 및 최적의 지점 개수를 산정할 시 효과적이며, 복잡한 지형과 다양한 식생 환경에서도 적용이 가능하다. 특히, 비용 절감의 목적으로 공간 대표성을 지니는 토양수분 관측 지점을 선별하고 최적의 관측 지점 개수 산정을 위해 미국의 Walnut Creek 유역(Jacobs et al., 2004), 이탈리아의 Tiber 하천 유역(Brocca et al., 2012)에서는 TSA, SSM, RCM이 활용되었다.
국내의 경우 알맞은 토양수분 센서의 설치 위치와 다양한 소유역을 대상으로 토양수분의 평균적인 시공간 변화 특성을 나타낼 수 있는 적절한 센서의 개수 결정을 위한 기준이 지형의 복잡성으로 인해 모호하다. 본 연구에서는 2018년부터 2019년까지(11월-3월 제외) 청미천, 설마천 시범지역에서 지점 토양수분의 시공간 변동성을 살펴보고자 하였다. 두 시범지역에 설치된 TDR 센서의 토양수분 함량(토심 10 cm)을 기반으로 TSA를 통하여 시공간 변동성을 대표하는 최적의 지점을 확인하였다. 또한, SSM과 RCM을 활용하여 공간 평균 토양수분 및 시간 변동성을 효과적으로 나타낼 수 있는 지점 개수를 파악하고 신뢰성 있는 지점 토양수분 데이터 확보 방안을 도출하는 것을 목표로 한다.
2. 연구지역 및 데이터
본 연구의 대상 지역은 청미천과 설마천 유역 내에 설치된 TDR 토양수분 관측망이다. 청미천은 한강의 제1 지류로서 해당 유역은 약 동경 127° 17' 0''~ 127° 44' 15'', 북위 36° 57' 30''~37° 13' 30''에 위치하며, 유역면적은 약 559.60 km2, 유로 연장 60. 80 km이다. 청미천 유역 내 약 동경 127° 39' 43''~127° 39' 46'', 북위 37° 2' 24''~37° 2' 26''에는 TDR 토양수분 시험 관측소가 설치되었고 장비 설치 면적은 약 0.5 km2, 평균 고도 403 m, 평균 경사 약 16°로 충청북도 음성군의 수레의산 산지 사면에 위치하고 있다(Gwak et al., 2015). 청미천 유역은 사양토(sandy loam)가 대표적인 토성이고 식생 분포는 낙엽활엽수(Carpinus)와 참나무(Quercus)가 혼합되어 있는 특징을 가진다(Kim, 2012). 인근 음성군을 기준으로 연평균 기온과 강수량은 각각 11.9°C, 1208.3 mm이며 계절적 차이가 뚜렷하다. 청미천 관측소 내의 18개 TDR 지점들은 토양 내 유출 흐름에 따라 A (9개 지점), B (2개 지점), C (3개 지점), D (4개 지점) 라인으로 나누며(Gwak et al., 2015), 각 지점 관측소에 10 cm, 30 cm, 40 cm, 50 cm, 60 cm, 90 cm 토심별로 매설되어 2시간 간격으로 토양수분 데이터를 제공하고 있다.
설마천 시범 관측소는 임진강의 제1 지류인 설마천의 유역(약 동경 126° 53' 40''~126° 58' 10'', 북위 37° 54' 50''~37° 58' 10'') 내에 설치되어 있다. 설마천 유역은 유역면적 18.56 km2, 유로 연장 10.77 km, 평균 경사가 약 19°인 급경사 산지의 사행 하천에 속한다(Kim et al., 2018). 해당 유역은 사질 양토(loamy sand)가 주요 토성이고 작은 절리가 발달되어 소량의 강우 발생 시 하천의 수위에 큰 변화가 없고, 일정 강도 이상의 강수로 인해 파쇄대가 포화된 이후에는 하천의 수위가 급격히 증가하는 현상을 보인다(Kim et al., 2019). 해당 유역에서는 활엽수림과 혼효림이 우세하고 있으며 인근 파주시를 기준으로 근 5년(2018-2022년) 연평균 기온은 약 11.0°C, 연 평균 강수량은 약 1,286 mm로 여름철에 고온다습하다. 설마천 유역 내 설마리 범륜사 우측에 위치하여 있는 TDR 토양수분 시험 관측소(약 동경 126° 57' 4''~126° 57' 6'', 북위 37° 56' 13''~37° 56' 16'')에는 총 19개 지점들을 포함하며 유출 흐름을 기준으로 A (8개 지점), B (7개 지점), C (4개 지점) 3개 라인으로 나누어지며 각 지점에 10 cm, 20 cm, 30 cm, 40 cm, 50 cm, 60 cm 깊이로 탐침을 설치하여 2시간마다 토양수분을 측정하고 있다.
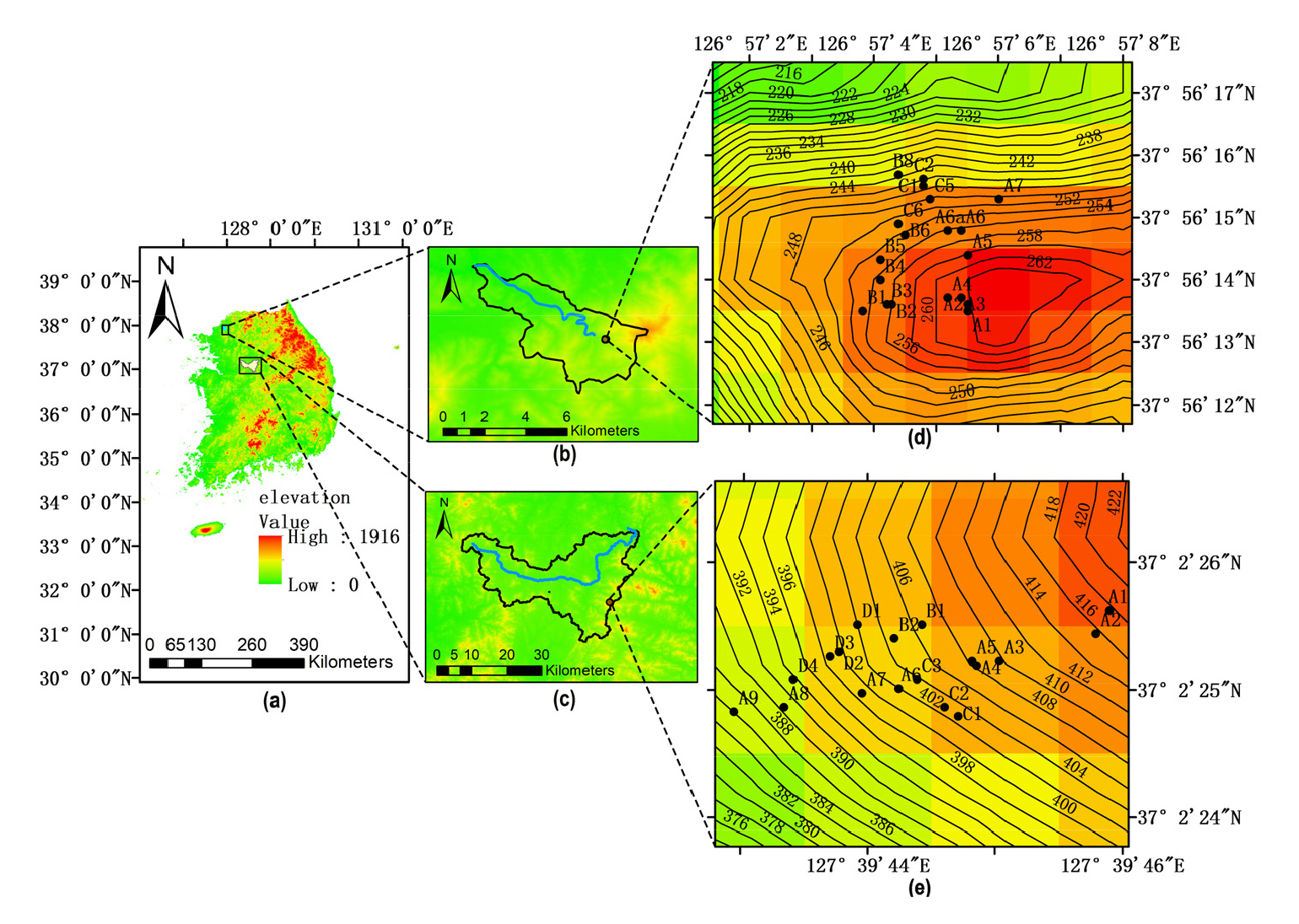
공간을 대표하는 토양수분 지점과 지점 개수를 추정하기 위해 사용된 장비는 Soil moisture Equipment 사의 MiniTRASE TDR이다. Soil moisture Equipment 사에 의하면 1.6 V의 피크 펄스 진폭으로 측정하여 ±2%의 측정 정확도(표준 waveguide 사용시)를 나타내며, Hur et al. (2009)의 코어 측정값과 비교한 연구에서는 MiniTRASE TDR 토양수분 측정 장비는 약 1.4%의 오차로 정밀도가 검증되었다. 또한, 청미천과 설마천 유역의 부피 밀도(bulk density)는 각각 1-1.5 g/m3과 0.92 g/m3로 교정이 필요하지 않음을 나타낸다(Kim, 2012; Jeong et al., 2024; Tomer et al., 1999; Quinones et al., 2003). 본 연구는 International Soil Moisture Network (ISMN)에서 제공하는 청미천과 설마천 유역 내에 설치된 각각 18개, 19개 TDR 토양수분 관측소 지점의 2018년 8월 21일부터 2019년 8월 20일까지 동절기를 제외한 토심 10 cm의 데이터를 활용하였으며, 2시간 간격의 데이터를 일 단위로 평균하였다. 토양수분 데이터의 측정 오류를 최소화하기 위해 ISMN의 품질 플래그를 사용하여 토양수분 절댓값 보정이 된 정상적이고 신뢰할 수 있는 데이터를 선별하여 사용하였다(Dorigo et al., 2013). 강우량 자료는 기상청에서 제공하는 청미천 시범지역은 음성군, 설마천 시범지역은 파주시의 일별 자료를 활용하였다. Digital Elevation Model (DEM)은 NASA의 Space Shuttle Endeavour 플랫폼에 탑재된 Shuttle Radar Topography Mission (SRTM)를 제공받아 ArcGIS를 사용하여 청미천과 설마천 유역의 등고선을 형성하였으며(Fig. 1), DEM 데이터에서 고도, 경사도, 경사 방향을 계산하여 사용하였다.
3. 방법론
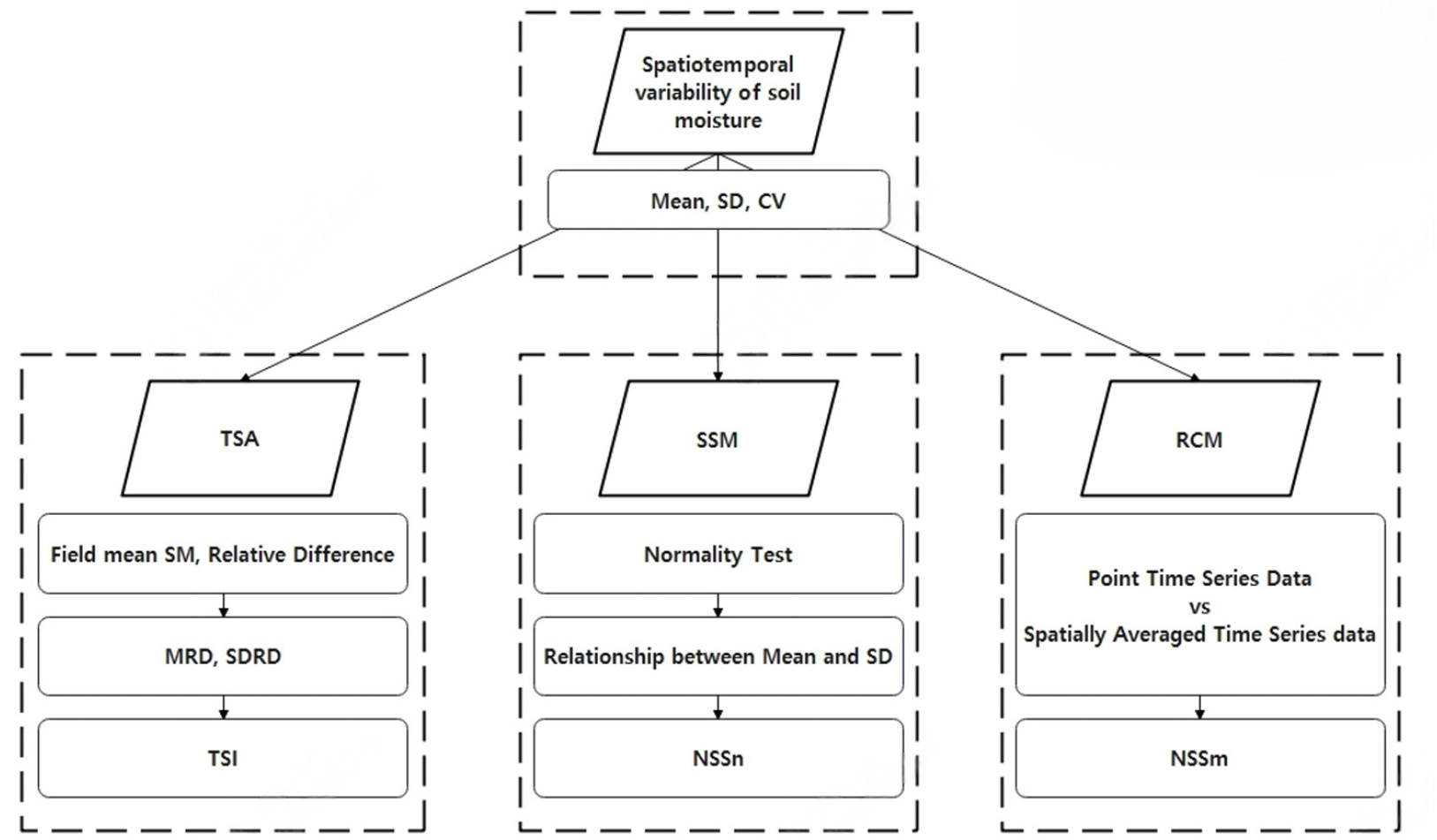
본 연구에서는 TSA, SSM과 RCM 분석 방법을 적용하여 청미천과 설마천 시범 지역의 토양수분 시공간 변동성을 분석하였으며 전체적인 방법론의 흐름도는 Fig. 2에 도시되었다.
3.1 시간 안정성 분석(TSA)
시간 안정성은 토양수분의 지점 위치와 시간 불변의 관계를 기반으로 정의되었으며, 시간이 지남에 따라 여러 지점 중 특정 위치에서 공간 평균값을 유지할 수 있다는 개념으로 대표 지점 선별에 도움을 주는 기법이다(Vachaud et al., 1985). 시간 안정성 분석의 첫 번째 단계는 특정 지점 i, 날짜 j에서의 토양수분량()과 각 표본 날짜에 대한 공간 평균 토양수분() 간의 상대적 차이()를 계산하는 것이다.
위 식에서 N은 지점 표본 개수를 의미한다. 두 번째 단계는 상대적 차이()를 기반으로 상대적 차이의 평균(Mean of the Relative Difference, MRD; )과 상대적 차이의 표준편차(Standard Deviation of the Relative Difference, SDRD; )를 계산한다.
위 식에서, M은 시간 표본 개수를 의미한다. MRD는 관측 지역 전체에 대한 특정 지점의 습윤/건조 정도를 나타내는 지표로, 양수 값은 습윤, 음수 값은 건조한 환경임을 의미한다. SDRD는 측정의 정밀도로 정의되며, 값이 클수록 평균 토양수분을 포착하는 데 있어서 변동성이 큼을 의미한다(Jacobs et al., 2004).
이후, 앞서 계산한 MRD와 SDRD를 기반으로 Jacobs et al. (2004)에 제안한 TSI를 사용하여 최적의 대표 지점을 식별하였다. TSI 값이 0에 가까울수록 시간 안정성이 높은 지점임을 의미한다.
3.2 통계 분석(SSM)
토양수분의 시공간 변동성을 파악하기 위해, 본 연구에서는 평균, 표준편차 및 변동계수를 사용하였다. 두 연구 지역 토양수분의 시계열 변화를 탐지하기 위해 계절 평균 토양수분 값을 사용하였으며, 공간적인 변동성을 분석하기 위해 표준편차와 변동계수를 활용하여 분석하였다.
연구 지역의 공간 평균 토양수분 추정에 필요한 최대 지점 개수()를 파악하기 위해 Gilbert (1987)에서 제안한 통계적 샘플링 방법(SSM)을 사용하였다. 통계적 샘플링 방법은 표본들이 서로 독립적이고 정규분포의 가정하에 계산된다(Wang et al., 2008; Brocca et al., 2010). Shapiro-Wilk 방법으로 토양수분의 전체적인 변동 패턴이 정규분포/로그 정규분포를 따르는지 평가하였으며, 이 테스트에서는 유의 수준이 0.05 이상 되어야 귀무가설(데이터가 정규분포/로그 정규분포를 따름)을 채택한다. 정규분포에 해당하는 날짜에 대해 토양수분의 평균값과 표준편차의 관계를 도출하여 다양한 공간 평균 토양수분 조건에서 각각 필요한 지점 개수를 산정하여 최종적으로 최대 지점 개수를 결정한다. 아래 식에서 은 신뢰 수준 에서의 t 분포 값, 는 표준편차, AE는 절대 오차를 의미한다. 이는 일정한 절대 오차와 표준편차 하에 처음에는 의 값을 사용하고 이후에는 을 이용하여 될 때까지 반복하여 계산한다.
일원 배치 분산 분석(One-way ANOVA)을 이용하여 지형 인자들(고도, 경사도, 경사 방향)이 각 지점의 시간 안정성 미친 영향을 평가하였다. 이후, 상관계수(pearson correlation coefficients)를 사용하여 각 지형 인자와 지점들의 시간 안정성 사이의 관계를 정량화하였다.
3.3 랜덤 조합 방법(RCM)
특정한 정확도 범위에서 관측망 평균 토양수분 값의 시계열 변화를 추정하는 데 필요한 최소 지점 개수()를 산정하기 위해, Brocca et al. (2012)에서는 부트스트랩 반복 샘플링을 기반으로 랜덤 조합 방법(RCM)을 제안하였다. 랜덤 조합 방법은 통계적 샘플링 방법과 달리 정규분포의 가정을 필요하지 않으며(Dane et al., 1986; Wang et al., 2008), 지점 토양수분 값의 시간적 변동성을 고려하여 지점 개수를 계산한다. 랜덤 조합 방법의 단계는 다음과 같이 구성된다(Brocca et al., 2012).
1) 총 A개 토양수분 관측 지점 중에서 랜덤으로 B개 지점의 시계열 데이터를 반복적으로 K번 선택한다(A > B, K = 1,000).
2) B개 지점의 값을 평균하여 K개의 토양수분 시계열 데이터를 획득한다.
3) R2과 RMSE를 사용하여 랜덤으로 추출한 K개의 데이터와 A개 관측 지점의 평균 시계열 값을 비교한다.
4) 산출한 K개의 R2과 RMSE 데이터를 평균하여 사용한다.
5) B값이 1부터 A-1 될 때까지 단계 1-4를 반복하여 계산한다.
여기서, 일반적으로 선택한 토양수분 지점 개수가 많을수록 지역 평균 시계열 데이터와의 일치도가 높으며(Brocca et al., 2010), R2 값이 0.95 이상, RMSE 값이 2% 이하의 기준에서 토양수분의 최소 지점 개수를 판단한다(Brocca et al., 2012).
4. 연구 결과 및 토의
4.1 토양수분의 시공간 변동성 분석
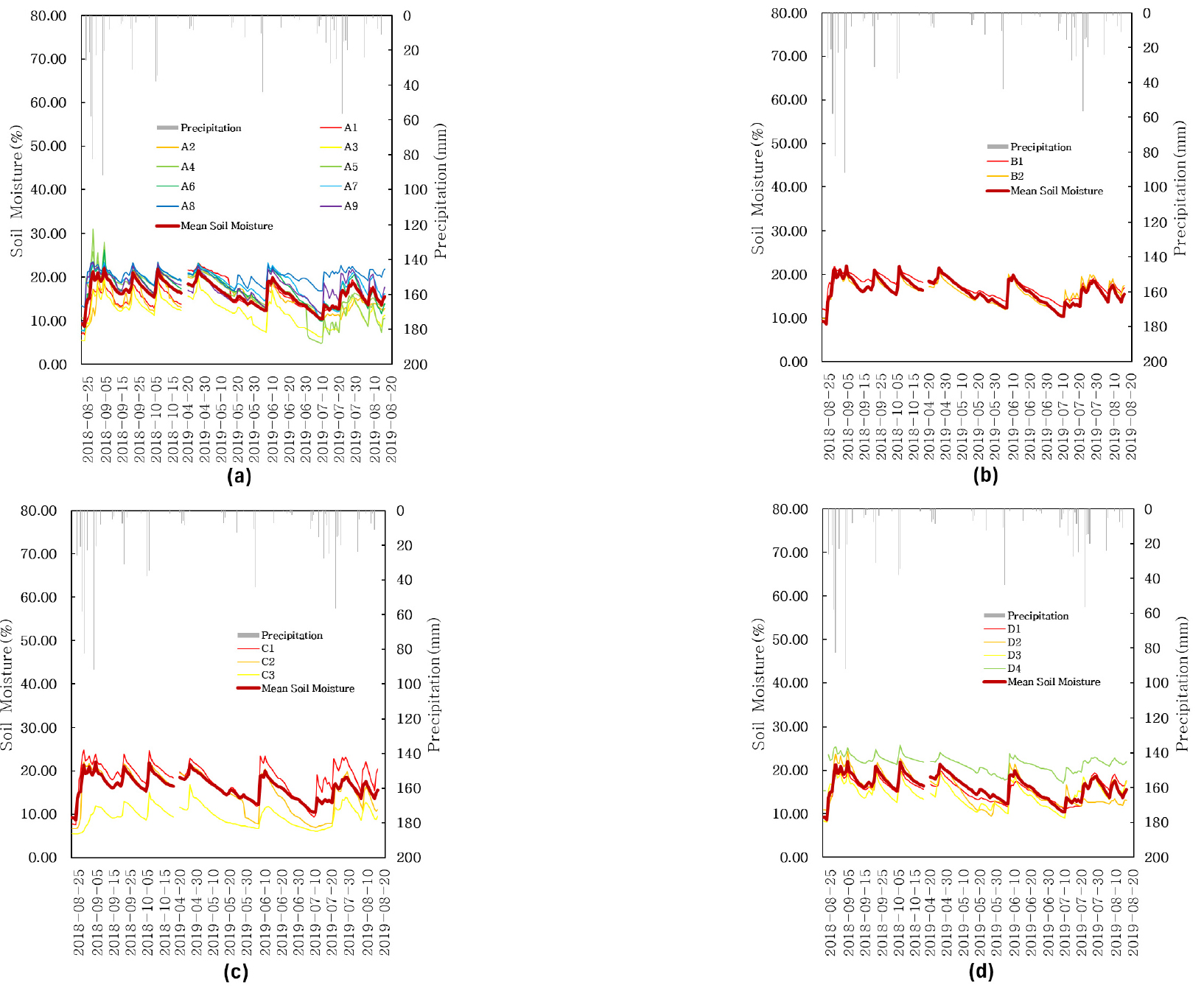
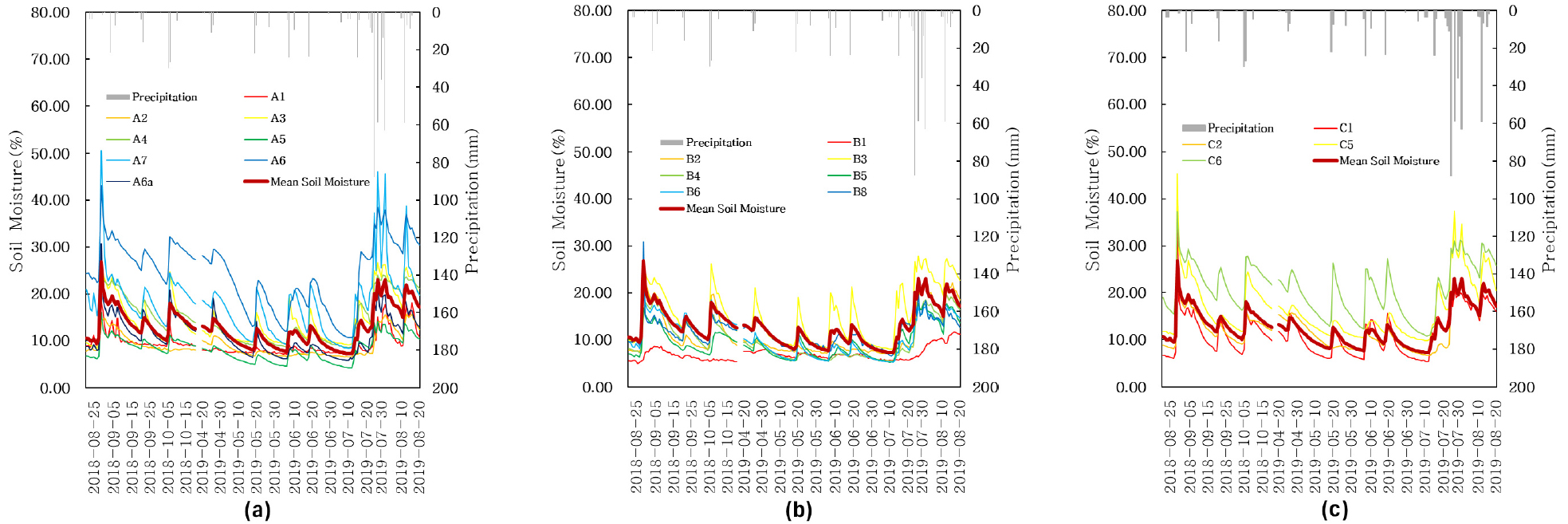
토양수분의 시공간 변동성을 파악하기 위해 2018년 8월 21일부터 2019년 8월 20일(동절기 제외)까지 청미천과 설마천 시범지역에서 각 단면선의 지점 토양수분 값과 강우량을 Figs. 3 and 4에서 확인할 수 있다. 봄(4월, 5월), 여름(6월, 7월, 8월), 가을(9월, 10월)로 나누어서 살펴보면, 두 시범지역 모두 가을철에 평균 토양수분 함량이 가장 높으며, 청미천이 설마천 시범지역보다 약 3.74% 높게 나타났다(Figs. 3 and 4). 이 현상은 청미천 시범지역에서 가을철에 강우 직후 토양수분 감소 시 기울기가 -0.025로 높게 나타나기 때문이며, Gwak et al. (2015)의 연구 결과와 유사하다. 설마천 시범지역에서는 가을철에 토양수분의 재충전(recharge) 현상이 발달하여 토양수분 값이 높은 것으로 판단된다(Kim, 2009). 두 연구 지역에서 각 단면선에 따른 계절별 평균 토양수분의 변동성을 분석하기 위해 봄, 여름, 가을 동안 각 단면선에서의 토양수분 평균값 차이를 Table 1에서 확인할 수 있다. 청미천 시범지역의 A에서는 계절별 평균 토양수분의 차이가 0.92-5.50%로 다른 단면선에 비해 뚜렷한 시간 변동성을 나타냈다. 특히 A5 지점에서는 가을철에 높은 평균 토양수분 값(18.48%)을 보이고 있으나 여름철에는 다른 지점들에 비해 낮은 값(12.98%)을 보여주었다. B에서는 토양수분의 계절적인 차이가 작고 각 계절의 평균 토양수분은 약 16% 좌우로 비교적 안정적이다. C에서는 C1과 C3 지점은 계절별 평균 토양수분 값이 비교적 안정적인 패턴을 보여주지만, C2 지점은 가을철과 여름철의 평균적 차이가 5.94%로 큰 변화를 확인할 수 있다. D에서는 D2를 제외한 지점에서는 계절별 차이가 비교적 작게 나타났다. 설마천 시범지역의 A에서는 계절별 평균 토양수분 차이의 범위는 1.15-6.60%로 시간 변동성이 다른 단면선에 비해 큰 것을 확인할 수 있다(Table 1). 그중 A6 은 전체 지점에서 가장 높은 토양수분 값을 보이고 있으며 계절별 차이도 가장 큰 것으로 나타났다. 반면 B에서는 B1 지점이 계절별 평균 토양수분 값이 가장 낮으며 계절적 차이(0.59%) 또한 가장 작은 것으로 확인되었다. C에서는 C1과 C2 지점에서 토양수분의 계절적 변화가 작으며, C5와 C6 지점의 계절별 평균 토양수분 차이가 비교적 큰 것으로 나타났다. 관측 기간 동안 청미천과 설마천 시범지역 내 각 지점의 시계열 토양수분 값은 다른 범위에서 계측되며, 평균 변동계수는 각각 0.20, 0.37로 큰 공간 변동성을 보이고 있다. 각 단면선으로 살펴보면, 청미천 시범지역에서는 C 라인 지점들의 공간 변동성이 가장 크고 B 라인 지점들에서 공간적 차이가 가장 적은 것으로 나타났다(Table 2). D 라인 지점들은 A 라인 지점들보다 표준편차와 변동계수의 수치가 높아 공간적 토양수분 값이 차이가 큼을 나타낸다. 설마천 시범지역은 A 라인과 C 라인에서는 공간 변동성이 크고 B 라인에서는 토양수분 값이 공간적으로 유사하다는 것을 확인할 수 있다(Table 2). Figs. 3 and 4의 청미천과 설마천 시범지역의 공간 평균 토양수분과 강수량의 시계열 변화는 전반적으로 유사한 경향을 보였으며, 강우 발생에 따른 상승 이후에 토양수분 함량은 점차 감소하는 것을 확인할 수 있다. 강우량, 지형, 토양층의 깊이, 토성의 차이로 인해 두 연구 지역의 토양수분이 변화하는 것으로 판단된다(Gwak et al., 2015; Lee et al., 2005). 따라서, 본 절의 결과는 청미천과 설마천 관측 지점의 토양수분 값은 시간상으로는 강우량과 민감하게 반응하고 공간적으로는 서로 상이한 변동 특성을 보이고 있으나, 공간 평균 토양수분은 강우량과 민감하게 반응하는 정상적인 패턴을 나타낸다.
Table 1.
Average differences in seasonal average soil moisture in transect lines of the CMC and SMC demonstration areas
| A line (%) | B line (%) | C line (%) | D line (%) | |
| CMC | 3.74 | 2.63 | 3.63 | 2.67 |
| SMC | 3.82 | 3.53 | 3.30 |
Table 2.
Spatial standard deviation and coefficient of variation in transect lines of the CMC and SMC demonstration areas
| A line | B line | C line | D line | |||||
| SD (%) | CV | SD (%) | CV | SD (%) | CV | SD (%) | CV | |
| CMC | 2.77 | 0.18 | 1.05 | 0.06 | 4.52 | 0.32 | 3.44 | 0.21 |
| SMC | 5.76 | 0.42 | 2.87 | 0.26 | 4.61 | 0.32 | ||
4.2 시간 안정성 분석
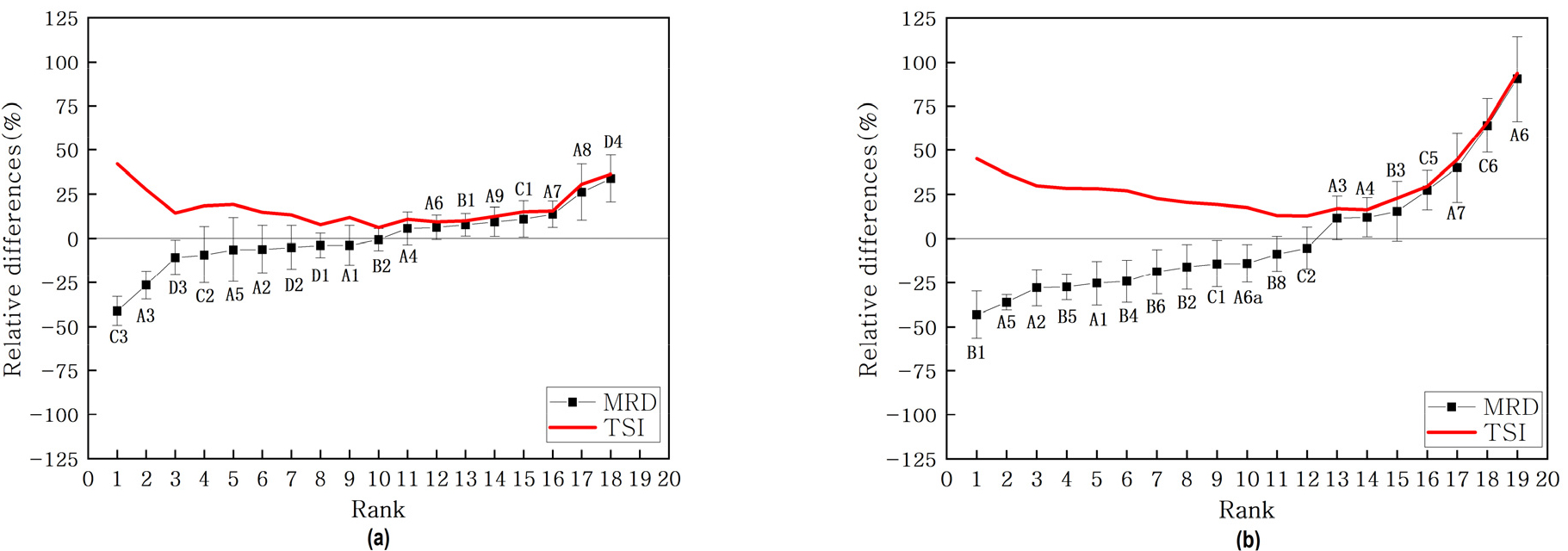
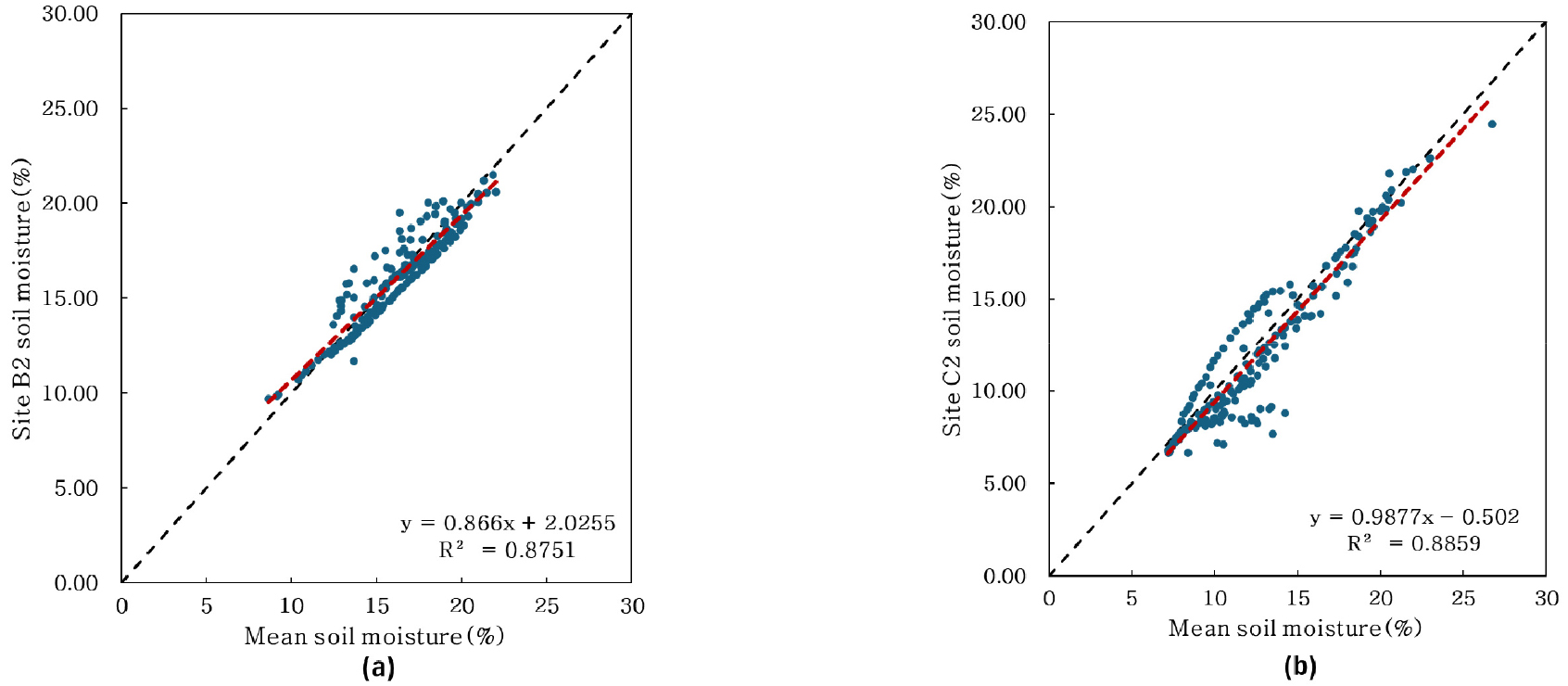
본 장에서는 청미천과 설마천 시범지역의 토양수분 관측망 중 공간 평균값을 대표할 수 있는 지점을 선별하고자 하였으며, Fig. 5는 두 시범지역을 대상으로 MRD, SDRD 및 TSI 분석 결과를 나타냈다. 공간 평균값을 기준으로 MRD는 두 시범지역에서 건조로부터 습윤한 지점 순서로 나열하였고 SDRD는 토양수분 값의 변동성, TSI는 시간상으로 가장 안정적인 지점을 나타낸다. MRD 분석은 오차 범위가 ±10% 이내에서 공간 평균을 나타내는 토양수분 지점은 청미천 11곳(건조 7곳, 습윤 4곳), 설마천 2곳(건조 2곳, 습윤 없음)으로 나타냄으로써 청미천 시범지역이 더 안정적인 경향을 나타내는 것으로 파악되었다. SDRD 분석에서는 청미천 시범지역의 토양수분 값은 6-18%, 설마천 시범지역은 4-24% 사이에서 변동하였으며, 설마천 시범지역의 상대적 차이의 변동 범위가 청미천 시범지역보다 더 큼을 판단할 수 있다. 이는 청미천 시범지역의 경사도가 설마천 시범지역과 비교하였을 때 완만하고, 따라서 완만한 경사의 청미천 시범지역의 지점들에서 공간 평균 토양수분 패턴과 유사한 경향을 나타냈다(Jacobs et al., 2004). TSI 분석에서는 두 시범지역 모두 공간 평균값보다 낮은 토양수분 지점(MRD < 0)인 B2(청미천 시범지역), C2(설마천 시범지역)에서 가장 대표성을 띠는 것을 확인할 수 있다. 대표 지점들의 신뢰도를 평가하기 위해, 결정계수(R2)를 적용하여 각 시범지역의 평균 토양수분과 대표 지점들의 시계열 토양수분 값을 비교한 결과를 Fig. 6에서 확인할 수 있다. B2 지점과 청미천 시범지역의 평균 토양수분 값 사이에는 R2이 약 0.88, C2 지점과 설마천 시범지역의 평균 토양수분 값 사이에는 R2이 약 0.89로 높은 정확도를 보여주었다. 청미천과 설마천 내의 시범지역에서는 모두 높은 정확도로 공간 평균 토양수분을 대표할 수 있는 지점을 산정할 수 있었으며, 토심 10 cm를 대상으로 시간 안정성을 산정할 시 대표 지점이 건조할 가능성이 높다고 판단 되고 이는 선행연구와도 일치한다(Jacobs et al., 2004; Choi and Jacobs, 2007; Penna et al., 2013).
앞선 연구에서는 지점별 토양수분과 공간 평균값의 상관관계는 건기에서 습윤기로 기상 상황이 변동될 때 크게 감소할 수 있으며(Brocca et al., 2012), 평탄한 지역은 구릉지보다 지점 토양수분과 공간 평균 토양수분 값의 상관성이 높은 것으로 분석되었다(Dari et al., 2019). 청미천과 설마천 시범지역을 대상으로 지형 인자(고도, 경사도, 경사 방향)가 MRD, SDRD, TSI, 지점 토양수분의 시계열 변화 패턴에 대한 One- way Anova 분석 결과를 Table 3에서 확인할 수 있다. 청미천 시범지역에서는 공간 대표성을 지니는 지점이 지형 인자와의 상관성이 낮은 것을 확인하였으며, 설마천 시범지역의 경우 지점 토양수분의 시계열 변화 패턴과 공간 평균 토양수분 간의 상관관계는 고도, 경사도에 따라 구분할 수 있음을 확인할 수 있다. 일반적으로 토양수분 함량은 고도와 반비례 관계를 나타내며, 높은 고도일수록 토양수분의 배수량이 많고 유입량이 적으며(Qiu et al., 2001), 또한 Jacobs et al. (2004)의 ‘경사도가 시간 안정성에 영향을 준다’라는 선행연구와 일치한다. 하지만 고도, 경사도가 지점별 시계열 토양수분 간의 pearson correlation coefficients 값은 각각 -0.09, 0.16으로 유의미한 결과라고 볼 수 없으며, 이는 연구 지역의 면적이 제한적이기 때문이라고 판단된다.
Table 3.
One-way anova for tests of difference in mean values by topography indices in the CMC and SMC demonstration areas
| MRD | SDRD | TSI | R between point and spatial average value | ||
| CMC | Elevation | 0.239 | 0.216 | 0.566 | 0.141 |
| Gradient | 0.218 | 0.249 | 0.320 | 0.211 | |
| SMC | Elevation | 0.279 | 0.670 | 0.586 | 0.001⁎ |
| Gradient | 0.787 | 0.779 | 0.397 | 0.001⁎ | |
| Aspect | 0.706 | 0.934 | 0.837 | 0.219 | |
4.3 통계적 샘플링 개수 분석
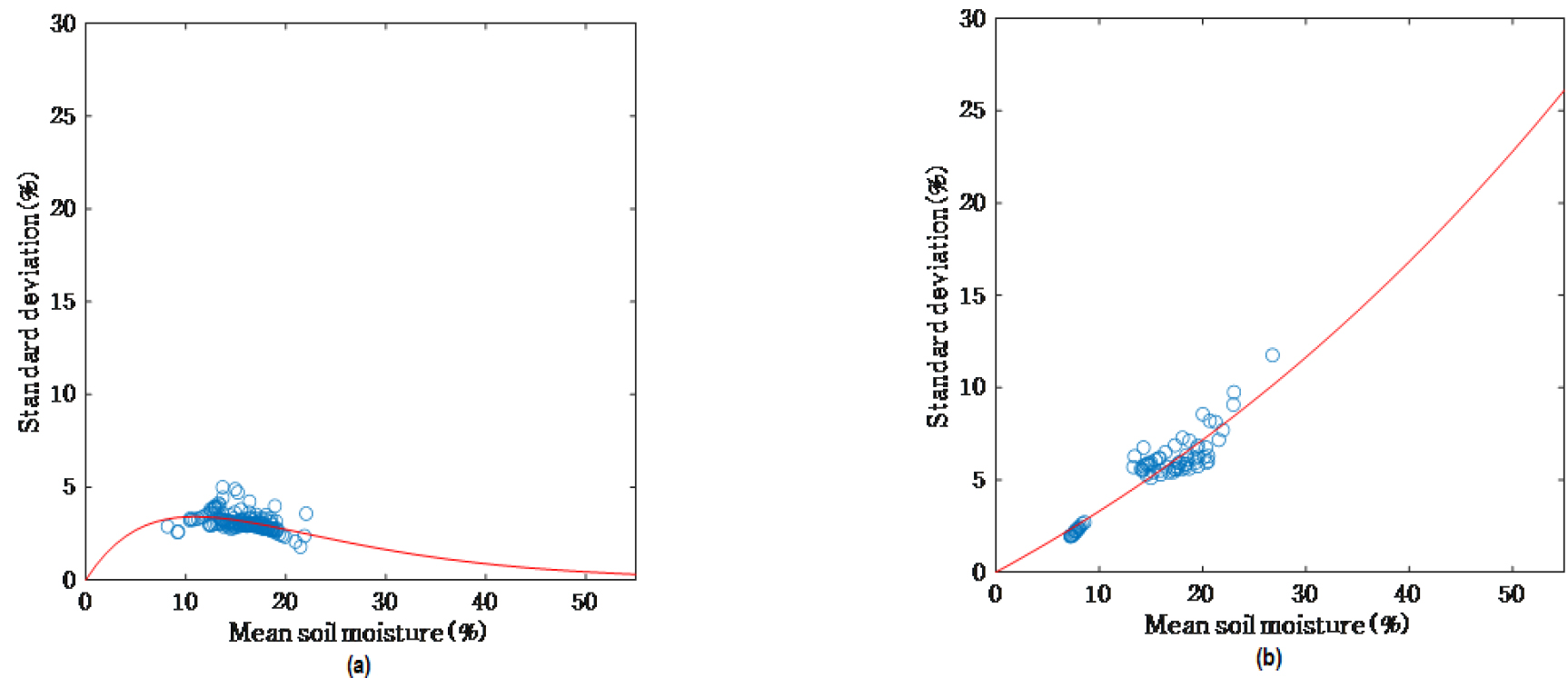
본 장에서는 높은 정확도의 공간 평균 토양수분 추정을 위해, SSM 방법으로 적절한 토양수분 지점 개수를 산정하고자 한다. 각 날짜의 토양수분 값에 대해 정규성 검정과 평균치와 표준편차의 관계를 우선 분석하였다(Brocca et al., 2010). 토양수분의 변동성을 나타냄에 있어서 상대적으로 평탄한 청미천 시범지역은 정규분포(88%), 경사도가 비교적 큰 설마천 시범지역은 로그 정규분포(97%)가 더 적절한 것으로 나타났다. 또한, 설마천 내 시범지역에서는 연구 기간 동안 각각 총 기간의 43% 토양수분 공간 패턴이 정규분포에 부합되었다. 정규분포에 부합되는 기간의 토양수분 값들을 기반으로 Fig. 7는 토양수분의 거동 범위(0-55%) 내에서 청미천과 설마천 시범지역의 공간 평균치()와 표준편차() 사이의 지수 관계를 나타냈다. 선행연구들의 토양수분 통계량 간의 경험적 7회귀 공식 (Bell et al., 1980; Jacobs et al., 2004; Brocca et al., 2012; Famiglietti et al., 2008)에 근거하여 청미천 시범지역의 계수 A와 B는 각각 0.850, 0.092이며, 설마천 시범지역은 0.305, -0.008로 나타났다. 평균 토양수분 0-55% 범위 내에서 청미천 시범지역의 경우 표준편차는 평균 토양수분이 커짐에 따라 증가하다가 감소하는 패턴을 보이고 있고(Owe et al., 1982; Famiglietti et al., 2008) 최대치는 평균 토양수분 함량이 약 10-20%에 나타난다. 이는 Choi and Jacobs (2007)의 토양수분 변동성이 중간 정도의 평균 수분 조건(15-25%)에서 가장 높은 결과와 유사하다. 반면, Fig. 7(b)의 설마천 시범지역에서는 평균 토양수분이 증가함에 따라 표준편차는 큰 폭으로 증가하는 것을 확인할 수 있으며, 이 결과는 Famiglietti et al. (1998)의 연구와 일치한다. 두 연구 지역의 서로 다른 결과는 지형, 토성, 식생 등 요소의 복합적인 영향을 받아 형성된 것으로 판단된다(Lee et al., 2005).
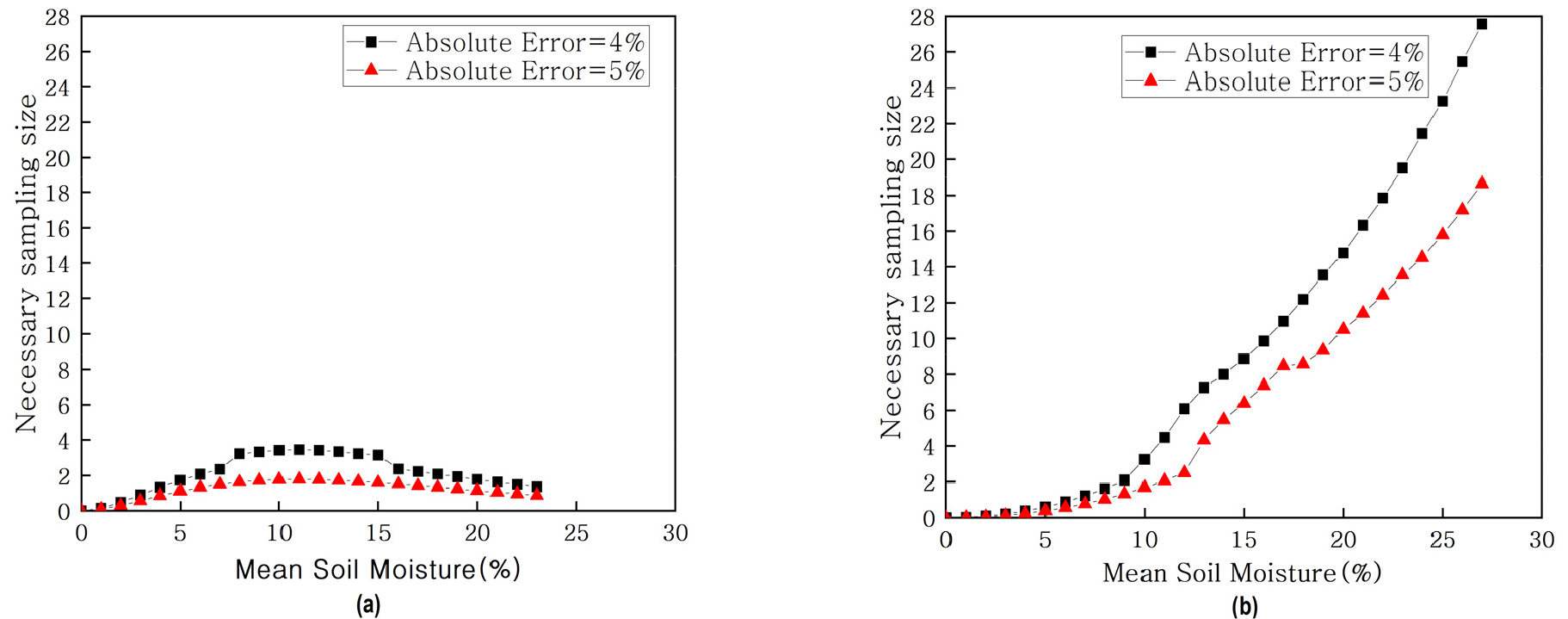
전 세계 토양수분 위성의 요구 사항을 살펴보면, Jackson et al. (1999)는 ±4% 이상, Walker and Houser (2004)는 ±5% 이상 정확도의 지점 토양수분 관측을 제안하였다. Fig. 8은 연구 기간 동안 청미천과 설마천 시범지역의 실제 공간 평균 토양수분의 범위(청미천 시범지역 최대 공간 평균 토양수분 22.03%, 설마천 시범지역 최대 공간 평균 토양수분 26.76%)를 고려하여 95% 신뢰 수준, ±4%, ±5% 오차범위를 기준으로 필요 지점 개수(NSS) 결과를 나타냈다. 오차범위가 감소함에 따라 공간 평균 토양수분을 포착하는 데 필요 지점 개수는 증가하는 경향이 있다(Wang et al., 2008). 특히, 설마천 시범지역은 토양수분 표준편차가 크기 때문에 ±5% 오차에서는 최대 19개 지점이 필요한 반면 ±4% 오차 범위 내에서는 큰 폭으로 증가하여 최대 28개의 지점 개수가 필요한 것으로 나타났다. 설마천 시범지역의 필요한 최대 지점 개수는 토양수분 평균치가 커짐에 따라 증가하며, 평균 토양수분 함량이 27%일 때 가장 많은 지점이 필요한 것을 확인할 수 있다. 청미천 시범지역의 경우 절대 오차가 ±4%, ±5%일 때 공간 평균 토양수분을 추정하는 데 필요한 최대 지점 개수는 각각 4개와 2개로 나타났다. 청미천 시범지역에서는 평균 토양수분 함량이 약 8-15% 사이에 최대 지점 개수가 필요하며, 필요 지점 개수는 동일함을 알 수 있다. 이러한 결과는 Jacobs et al. (2004)의 ‘다양한 지역의 평균 토양수분을 적절히 반영하려면 3-32개의 지점이 필요하다’라는 선행연구와 일치한다. 따라서, 본 절의 결과는 청미천과 설마천 내 소규모 지역에서 요구되는 최대 토양수분 지점 개수는 다르게 나타나며, 공간 토양수분 함량의 변동성이 클수록 지점 개수가 확대되어야 한다는 것을 확인할 수 있다.
4.4 랜덤 조합 샘플링 개수 분석
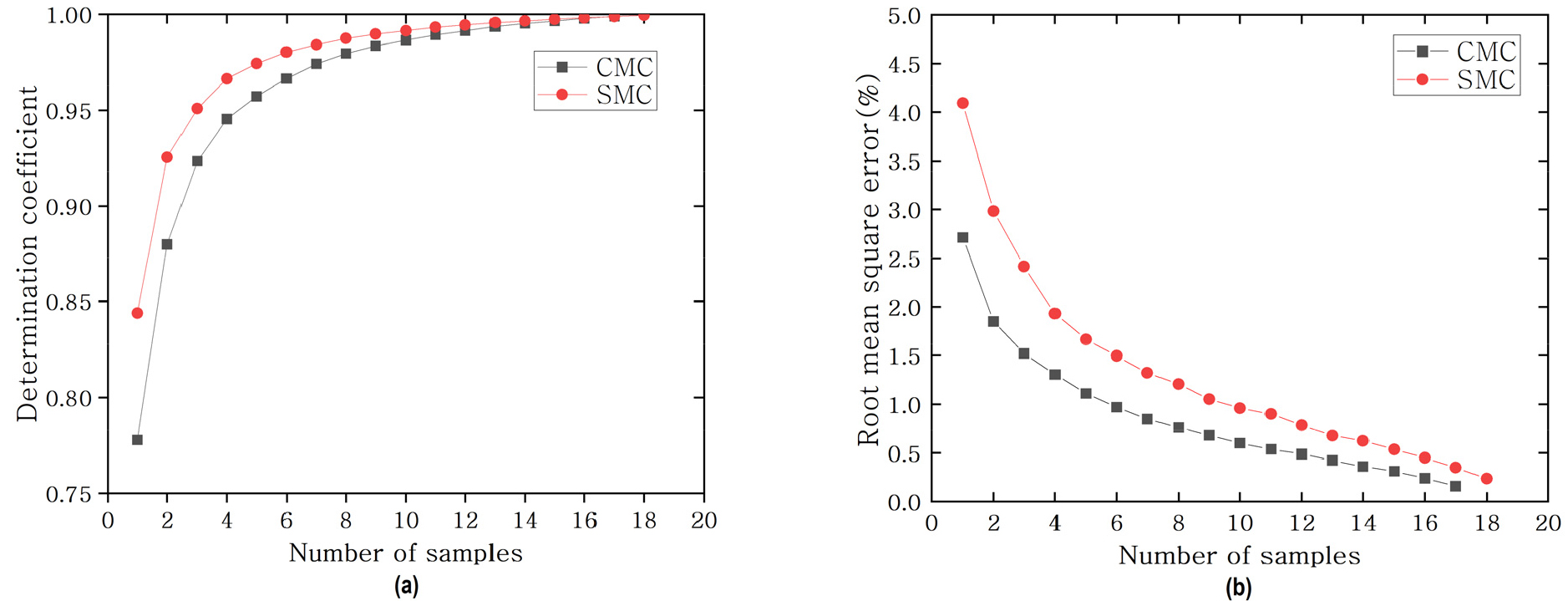
본 장에서는 공간 평균 토양수분의 시계열 변화를 추정하기 위해, R2과 RMSE를 사용하여 공간 평균치와 무작위로 선택한 지점들의 평균 시계열 토양수분 값 간의 관계를 분석한 결과를 Fig. 9에 나타냈다. 단일 지점을 무작위로 선택하면, 청미천 시범지역의 경우 평균 R2과 RMSE 값은 각각 0.78과 2.71%였으며 설마천 시범지역의 경우는 R2은 0.84, RMSE는 4.09%인 것으로 나타났다. 이는 앞선 4.2장에서 분석한 시간 안정성을 나타내는 지점보다 낮은 R2값을 보이고, 지점 토양수분에 대한 시간 안정성 사전 분석이 없을 경우에 무작위 지점으로 공간 평균 시계열 값을 추정한 정확도가 떨어지는 것을 보여준다.
정확도를 평가하는 지표(R2과 RMSE)와 토양수분 지점 개수 사이의 관계를 살펴보면, Fig. 8과 동일하게 두 시범지역에서 모두 토양수분 지점 개수가 많아짐에 따라 공간 평균 시계열 변화 추정의 정확도가 높아지는(R2 증가, RMSE 감소) 경향을 보인다(Fig. 9). 청미천과 설마천 시범지역 모두 최소 4개의 토양수분 지점이 있어야 2% 이하의 RMSE, 0.95 이상의 R2 정확도로 공간 평균 토양수분의 시계열 변화를 포착할 수 있음을 확인할 수 있다(Fig. 9). 동일한 지점 수에서는 청미천 시범지역이 설마천 시범지역보다 RMSE 값이 낮은 것을 확인할 수 있는데, 각 지점의 시계열 값과 공간 평균 토양수분 값의 차이가 작기 때문에 이러한 결과를 나타내었다(Figs. 3 and 4). 하지만 특이하게도 동일한 지점 수에서 설마천 시범지역과 비교하면 청미천 시범지역은 R2값은 낮게 나타났으며, 이것은 청미천 시범지역의 지점 간 토양수분 시계열 증감패턴이 지점별로 다른 양상을 나타냄으로써 공간 평균 토양수분과의 차이에서 형성된 것으로 판단된다(Figs. 3 and 4). 따라서 공간 평균 토양수분의 시계열 패턴과 시계열 토양수분 값은 TSA 분석으로 청미천과 설마천 시범지역 토양수분의 시공간 안정성을 해석하는 데 있어서 같이 고려해야 할 사항으로 판단된다.
5. 결론 및 요약
본 연구에서는 토양수분의 시공간 변동성을 나타내는 대표 지점과 지점 개수를 파악하기 위해 MRD와 SDRD를 기반으로 하는 시간 안정성(TSA) 분석, 통계적(SSM) 및 랜덤 조합 샘플링 개수 분석 방법(RCM)을 활용하였다. 연구 지역은 국내의 청미천과 설마천 유역 내에 있는 소규모 시범지역이며, 2018년 8월 21일부터 2019년 8월 20일(동절기 제외)까지 각 지점에서 TDR 방식으로 관측한 토심 10 cm의 토양수분 값을 사용하였다. 또한, 시간 안정성(TSA) 분석으로 두 연구 지역의 단일한 토양수분 대표 지점을 선별하고, 통계적 기법(SSM)과 랜던 조합 샘플링 방법(RCM)으로 일정한 정확도에서 공간 평균 토양수분을 효과적으로 나타낼 수 있는 최적 및 최소 토양수분 지점 개수를 분석하였다.
통계 분석을 기반으로 두 연구 지역에서 토양수분 시공간 변동성을 분석하였으며, 각 단면선 지점별 토양수분 값은 시공간 변화 패턴은 서로 다른 것을 확인할 수 있었다. 특히, 청미천과 설마천 내 시범지역은 모두 A라인에서 계절적 변동성이 가장 큰 것으로 나타났으며, 공간적 변동성은 각각 C라인(CMC 시범지역)과 A라인(SMC 시범지역)에서 가장 높은 것을 확인하였다.
여러 토양수분 지점에서 공간 평균 토양수분을 대표하는 최적의 토양수분 지점을 산정하는 TSA 분석에서는 청미천과 설마천 시범지역은 각각 B2 지점(R2=0.88), C2 지점(R2=0.89)에서 가장 대표성이 나타났다.
통계적 샘플링 방법으로 최대 토양수분 지점 개수를 분석한 결과는 절대 오차가 적어질수록 공간 평균 토양수분을 산정하는 데 필요한 최대 지점 개수는 많아지는 경향을 보였으며, 이는 Wang et al. (2008) 선행연구 결과와도 일치한다. 또한, 공간 변동성이 클수록 최대 토양수분 지점 개수가 더 많이 필요하다.
랜덤 조합 샘플링 분석 결과에서는 2% 이하의 RMSE, 0.95 이상의 R2 정확도에서 공간 평균 토양수분의 시계열 변화를 추정하려면 청미천과 설마천 시범지역 모두 최소 4개 이상의 지점이 필요한 것으로 나타났다. 반면, 통계적 샘플링 분석 결과에서는 청미천과 설마천 시범지역에서 ±5%의 절대 오차에서 최대 각각 2개와 19개, ±4%의 절대 오차에서 최대 4개와 28개의 토양수분 지점이 요구되는 것을 확인하였다. 이는 지점 토양수분의 시계열 패턴이 일치하고 각 지점과 공간 평균값의 토양수분 시계열 차이가 작을수록 필요한 토양수분의 최소 지점 개수는 적은 것을 확인할 수 있다.
이러한 결과를 바탕으로 복잡한 지형의 한반도에서 최적의 토양수분 표본 및 표본 개수를 산정할 수 있는 가이드 라인을 제시하였으며, 또한 다른 지형적 조건인 청미천과 설마천 내 시범지역의 토양수분을 비교하여 분석한 데 의의가 있다. 추후 한반도 전역에서 지점 토양수분의 최적화 네트워크를 구축하여 원격탐사 자료와 결합시킨다면, 보다 정확한 공간 토양수분량을 모의하여 수자원 관리 정책 수립에 기여할 수 있을 것으로 기대된다.