1. 서 론
2. 적용 모형
2.1 SWAT
2.2 TensorFlow - LSTM
3. 모형의 구축
3.1 메콩강 유역
3.2 SWAT 모형 구축
3.3 LSTM 모형 구축
4. 유출 모의결과 분석
5. 결 론
1. 서 론
메콩강은 동남아시아 6개국을 관통하는 국가공유 하천이며 하천길이는 약 4,350 km, 유역면적은 795,000 km2으로 세계에서 12번째로 길고, 10번째로 수량이 많은 강이다. 메콩강은 중국 칭하이 성에서 발원하여 중국 운남성과 미얀마, 태국, 라오스, 캄보디아, 베트남을 거쳐 남중국해로 흐르고 주변국에 대한 사회 ․ 경제적 영향력이 막대한 동남아시아의 주요 국가공유하천이다. 1995년 라오스, 태국, 캄보디아, 베트남은 메콩강의 자원을 효율적으로 관리하고 조화롭게 사용할 수 있도록 메콩강위원회(Mekong River Commission, MRC)를 설립하였으며, 1996년부터 중국과 미얀마가 MRC의 “협력 파트너”로 참여하고 있다.
최근 중국이 자국 서북부지역의 전력공급을 위한 수력발전 댐 건설 등 대규모 개발사업을 추진함에 따라 메콩강을 둘러싸고 중국과 주변국 5개국의 갈등이 커지고 있다. 중국은 이미 메콩강(중국명 ‘란창강’) 상류에 7개의 댐(최상류로부터 미아오웨이댐, 궁궈차오댐, 샤오완댐, 만완댐, 다차오산댐, 눠자두댐, 징훙댐)을 건설하여 운영하고 있으며, 21개의 댐을 추가로 건설할 계획을 발표했다. 하지만 이러한 유역개발사업은 기후변화와 함께 메콩강의 수리 ․ 수문 패턴의 변화를 초래하고 있으며, 그 불확실성은 보다 심화되고 있다. 실제로 2004년과 2006년에는 메콩강 유역에 대규모 홍수가 발생하였으며, 2010년과 2016년에는 극심한 가뭄이 발생하였다.
특히, 메콩강 최하류에 위치한 캄보디아와 베트남은 메콩강 수문환경 변화에 매우 민감하여 동남아시아 최대 담수호인 캄보디아 톤레삽 호수의 수량은 우기 시 메콩강 본류에서의 유입량에 의존하며, 이러한 톤레삽 호수의 수위변화는 캄보디아 GDP의 50% 이상을 차지하는 1차 산업(농업, 어업, 산림업 등)에 지대한 영향을 미치게 된다(Johnston and Kummu, 2012). 또한, 베트남의 삼각주(메콩델타)는 동남아시아 최대 곡창지대로서 메콩강 본류의 수위변화는 이 지역의 농업생산성 증감을 결정하는 중요한 자원이며 궁극적으로 베트남 국가경제에 미치는 영향이 막대하다고 할 수 있다(Baran and Myschowoda, 2009).
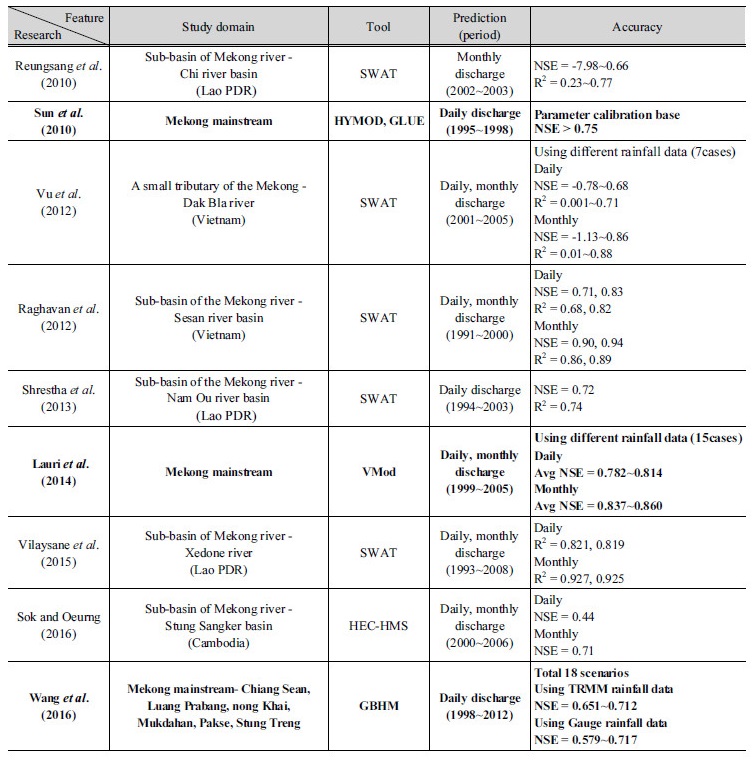
유역개발 및 기후변화 등과 관련하여 메콩강 유역의 유출해석을 위한 많은 연구들이 수행되었으며, 이에 관한 최신 연구는 Table 1과 같다. MRC에서는 메콩강 유역의 소유역(sub-basin) 또는 지류(tributary)의 수문해석을 위한 기본모형으로 SWAT (Soil and Water Assessment Tool)을 활용하고 있으며, 실제로 Table 1과 같이 강우-유출 해석과 관련된 많은 연구들이 SWAT 모형을 이용하여 수행되었으며, 국가별 대상유역에 따라 정확도 평가지수인 NSE (Nash-Sutcliffe Efficiency)가 -7.98~0.94로 불규칙하게 나타난 것으로 분석되었다. Table 1에서 메콩강 본류의 유출모의에 관한 연구는 굵은 글씨체로 표기된 바와 같이 HYMOD, VMod, GBHM 등 각기 다른 모형으로 적용된 바 있으며, 상기 SWAT 모형을 이용한 메콩강 지류 유출해석 결과와 달리 메콩강 본류 유출모의에 대한 모형의 정확도는 비교적 안정적으로 산정된 것으로 나타났으나 물리적(physics-based) 분포형 모형인 VMod와 GBHM 모형과 달리 유역을 몇 개의 저수지로 개념화한 비교적 간단한 개념적(conceptual) 수문모형인 HYMOD 모형 역시 우수한 결과를 제공하는 것으로 나타났다.
일반적으로 유출모의를 위해서는 (1) 모의 목적, (2) 가용 자료, (3) 컴퓨팅 자원(computing resources) 등을 근거로 수문모형을 선택하게 된다. 즉, Table 1의 모든 수문모형들은 메콩강 본류와 지류의 임의 지점을 대상으로 유출량 시계열 변화를 모의하는데 그 목적이 있으며, 개별 모형별로 요구하는 자료의 종류와 양이 다르다. 또한, 입력자료의 형태 및 매개변수의 종류에 따라 모의에 필요한 계산량 및 계산시간이 다르며, 물리적 분포형 수문모형이 개념적 집중형 수문모형 보다 가용 자료 및 컴퓨팅 자원이 월등히 많이 요구된다(Lee, 2008). 특히, Kokkonen and Jakeman (2001)은 단순히 하천 유출모의를 목적으로 할 경우, 단순한 모형도 복잡한 모형과 유사하게 우수한 모의결과를 제공하는 것을 확인한 바 있으며, EPA (2017)에서는 유출해석을 위해 실무적으로 전술한 세 가지 조건을 만족하는 적절한 모형을 선택하여 적용하는 것을 권고하고 있다.
이상의 개념적, 물리적 수문모형이외에도 인공신경망(artificial neural networks)을 이용하여 수리 ․ 수문 관련 물리적 지식을 배제하고 장기간 입 ․ 출력자료를 지도학습(supervised training)시킨 데이터 기반(data-driven)의 black-box 수문모형의 개발 및 적용에 관한 다양한 연구가 수행된 바 있다(Shreenivas and Shrikant, 2010; Hitogoto et al., 2016; Kim et al., 2018). 최근에는 장기간 양질의 수문자료의 수집이 가능해지고, 딥러닝 오픈소스 라이브러리가 공개됨에 따라 과거 시계열자료의 특성(feature)을 기억하고 학습에 반영할 수 있는 순환신경망(Recurrent Neural Networks, RNN)을 이용한 수문시계열 분석 및 예측 연구가 다시 각광받고 있다. Minns and Hall (1996)은 강우-유출 모의에 있어 인공신경망의 적용 가능성을 제시한 바 있으며, Tran and Song (2017) 및 Jung et al. (2018)은 Hochreiter and Schmidhuber (1997)가 제안한 LSTM (Long Short Term Memory) 기법을 수문 시계열 예측에 활용한 바 있으며, LSTM 기법은 전통적인 RNN 모형이 가지고 있는 장기의존성(long-term dependency) 문제를 해결함으로써 보다 정확한 수문 시계열 자료 예측이 가능함을 제시하였다.
본 연구에서는 캄보디아 톤레삽 호수 및 베트남 메콩델타 지역의 수리 ․ 수문 변동성 평가 등 메콩강 하류 유역의 수자원 관련 분석 시 기초자료(또는 입력자료)로 활용되는 메콩강 본류 주요 지점중 하나인 Kratie 수위국의 일유량 예측을 위한 유출해석 시스템을 구축하고 그 정확도를 검증하는 것을 목적으로 하고 있다. 유출해석을 위해 MRC의 기본 수문해석모형으로 사용되고 있는 SWAT과 Google에서 제공하는 딥러닝 오픈소스 라이브러리 TensorFlow의 LSTM을 이용하여 2003년부터 2007년까지의 메콩강 Kratie 수위국 지점에서의 유출모의를 수행하고, 유출모의 정확도 및 두 가지 방법론의 장 ․ 단점을 비교 ․ 분석한다. SWAT 모형의 경우, 지역상세데이터(local data) 획득이 불가능함에 따라 범용(globally-available) 입력자료(지형, 토지이용, 토양, 수문 등)를 이용하였으며, 2000~2002년 자료를 기반으로 자료 모형의 warming-up 및 매개변수 보정 후 2003~2007년 일유량 모의를 수행한다. LSTM을 이용한 유출모의의 경우, Kratie 지점을 기준으로 상류 10개 수위관측소의 두 기간(2000~2002, 2008~2014) 일수위 자료를 이용하여 심층신경망을 학습시키고, SWAT 모형과 마찬가지로 2003~2007년을 대상으로 Kratie 지점에 대한 일수위를 모의 후 수위-유량관계곡선식을 이용하여 일유량으로 환산한다. 2장에서는 유출해석을 위한 SWAT 모형과 LSTM 기법의 이론적 배경, 3장에서는 두 모형을 이용한 유출해석 시스템의 구축, 4장에서는 적용 및 분석결과를 제시하며, 마지막으로 5장에서는 연구결과의 요약 및 고찰에 대해 기술한다.
2. 적용 모형
2.1 SWAT
현재 MRC에서는 메콩강 수자원 이용 및 수재해 예방을 위해 의사결정시스템(decision support framework, DSF)을 구축하여 운영 중이며, DSF의 수문해석 Toolbox로 SWAT 모형을 이용하여 메콩강 하류 전지역(9개 주요 소유역으로 분할)에 대해 수문해석 시스템을 구축 ․ 운영하고 있다. 이에 대한 보다 자세한 사항은 MRC의 공식홈페이지(http://portal.mrc mekong.org/mrctoolbox)에서 확인할 수 있다.
SWAT 모형은 미국농무성 농업연구소(USDA-ARS)에서 개발된 준분포형 물리적 강우-유출모형으로 유역에서의 유출, 토지이용 변화 등에 따른 토사(sediment)의 이동 및 화학물질의 거동 예측 등이 가능하다. SWAT 모형은 GIS 소프트웨어인 ArcGIS와 연계하여 해석을 수행하며, GIS상에 입력된 지형 및 수계(river network) 자료를 이용하여 대상유역을 여러 개의 소유역으로 분할한 후 유역의 토지이용현황, 토양특성 등을 고려하여 동일한 특성을 나타내는 HRU (Hydrologic Response Unit)로 세분화 한다. SWAT 모형에서 수문해석은 Eq. (1)과 같은 물수지 방정식에 의해 산정된다.
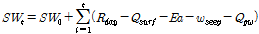 (1)
(1)
여기서,  는 최종 토양수분량(mm),
는 최종 토양수분량(mm),  는
는  일의 초기 토양수분량(mm),
일의 초기 토양수분량(mm), 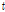 는 시간(일),
는 시간(일), 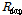 는
는 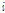 일의 강수량(mm),
일의 강수량(mm), 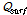 는
는 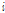 일의 지표유출량(mm),
일의 지표유출량(mm), 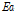 는
는 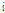 일의 증발산량(mm
일의 증발산량(mm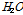 ),
), 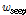 는
는 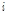 일의 토양층에서 투수층으로 투수되는 총량(mm),
일의 토양층에서 투수층으로 투수되는 총량(mm), 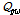 는
는 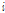 일의 하천으로의 회귀수량(mm)을 나타낸다. 유출량은 각각의 HRU에 대해 독립적으로 계산되며, 하도추적과정을 통해 유역 최종 출구지점에서의 유출량을 산정할 수 있다. 하도추적(river routing)은 Muskingum 또는 변동저류계수방법(variable storage coefficient method)에 의하여 계산된다.
일의 하천으로의 회귀수량(mm)을 나타낸다. 유출량은 각각의 HRU에 대해 독립적으로 계산되며, 하도추적과정을 통해 유역 최종 출구지점에서의 유출량을 산정할 수 있다. 하도추적(river routing)은 Muskingum 또는 변동저류계수방법(variable storage coefficient method)에 의하여 계산된다.
2.2 TensorFlow - LSTM
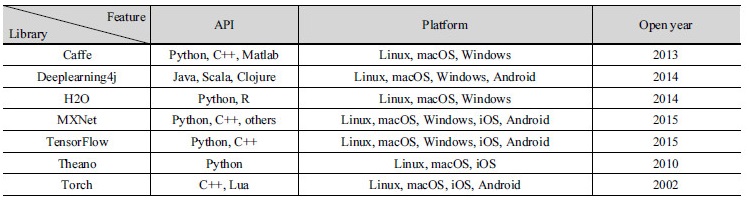
2010년 후반부터 딥러닝과 관련된 다양한 오픈소스 소프트웨어 라이브러리가 개발 ․ 공개면서 수리 ․ 수문분야 이외에도 원격탐사, 지형학, 지질학 등 다양한 분야에서 딥러닝 알고리즘이 활용되고 있다. Table 2는 대표적인 딥러닝 오픈소스 소프트웨어 라이브러리를 정리한 것이며, 본 연구에서는 Google에서 개발한 TensorFlow를 이용하여 메콩강 유출모의 심층신경망(deep neural network)을 구축하였다. TesnsorFlow는 대규모 기계학습을 위한 강력한 오픈소스 소프트웨어 라이브러리로서 동적 다차원 배열(tensor)의 데이터 흐름을 노드(node)와 엣지(edge)로 구분하여 표현한다. 노드는 수학적 연산, 데이터의 입 ․ 출력, 데이터의 읽기 ․ 저장 등의 작업을 수행하며, 엣지는 노드간의 데이터의 입출력 관계를 나타낸다. 즉, TensorFlow를 이용한 신경망 모형에서 노드는 신경망의 각 레이어(layer)에서 입 ․ 출력 활성화 함수(activation function) 설정 및 입 ․ 출력 정보 생성 등을 결정하며, 엣지는 레이어별 뉴런(neuron)을 연결하는 가중치(weight) 정보를 포함하게 된다. TensorFlow는 구축된 신경망 모형의 실행(running) 및 디버깅(debugging) 등을 시각화할 수 있도록 TensorBoard를 제공하고 있으며, 사용자는 TensorBoard를 이용하여 신경망의 연산흐름을 웹상의 그래프를 통해 확인할 수 있다.
LSTM은 순환신경망(recurrent neural network)의 특수한 예로서 연속된 관측값이 서로 연관성이 있을 때 주로 사용되며, 즉, 시간과 관계된 연속된 데이터의 분석에 유용하다. 순환신경망의 가장 큰 특징은 특정 시점에서의 상태(state)를 저장하고, 상태가 각 시점의 입력과 출력에 따라 변화한다는 점이다. 순환신경망은 여러 가지 변형된 형태가 있지만 기본적으로 특정 시점 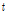 에서의 상태(
에서의 상태(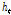 )는 바로 직전의 상태(
)는 바로 직전의 상태(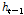 )와 현재의 입력(
)와 현재의 입력(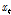 )에 따라 결정되며, 상태(
)에 따라 결정되며, 상태(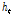 )에 따라 출력(
)에 따라 출력(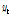 )가 결정되므로 데이터의 순차적인 의존성(sequential dependency)을 반영할 수 있다.
)가 결정되므로 데이터의 순차적인 의존성(sequential dependency)을 반영할 수 있다.
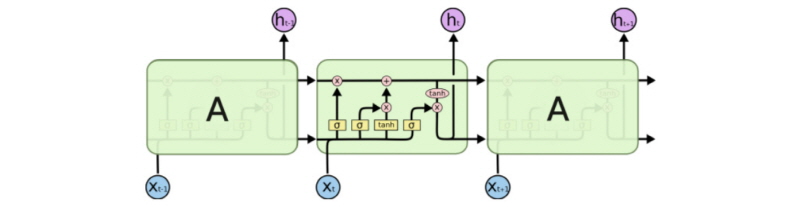
이러한 순환신경망은 이론적으로 신경망 학습 시 과거의 모든 연속된 데이터를 반영하여야 하나 실제로는 신경망의 출력층(output layer)으로 부터 멀리 떨어진 은닉층(hidden layer)은 손실함수(loss function)의 기울기 소실(gradient vanishing)로 인하여 가중치 업데이트가 거의 이뤄지지 않아 학습효과가 저하하는 문제가 발생할 수 있다. LSTM은 이러한 순환신경망의 단점을 보완하고자 고안되었으며, 가장 큰 특징은 가중치를 업데이트할 때, 이전 정보를 계속 기억할지 혹은 잊을지를 판단하는 Fig. 1과 같은 신경망 구조가 포함되어 있다는 점이다.
LSTM은 특정 시점의 상태(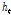 )를 업데이트하기 위해 셀(cell,
)를 업데이트하기 위해 셀(cell, 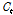 )이라는 개념을 도입하여 입력과 현재까지의 상태를 이용하여 내부에 가지고 있는 정보를 업데이트할 것인지 아닌지를 판단한다(Olah, 2015). 연속된 데이터가 어느 정도 정리가 되었을 경우, 지금까지의 상태 정보를 잊고 새로 입력된 데이터를 좀 더 활용하게 되며, 반대로 새로 입력된 데이터가 유용하지 않을 경우, 이전 단계까지의 상태를 좀 더 기억하고 업데이트를 조금만 수행하게 된다. 그리고 이러한 상태를 최종적으로 셀에 저장하게 된다. Fig. 1의 LSTM 연산절차를 수식화하면 다음과 같이 정리할 수 있다.
)이라는 개념을 도입하여 입력과 현재까지의 상태를 이용하여 내부에 가지고 있는 정보를 업데이트할 것인지 아닌지를 판단한다(Olah, 2015). 연속된 데이터가 어느 정도 정리가 되었을 경우, 지금까지의 상태 정보를 잊고 새로 입력된 데이터를 좀 더 활용하게 되며, 반대로 새로 입력된 데이터가 유용하지 않을 경우, 이전 단계까지의 상태를 좀 더 기억하고 업데이트를 조금만 수행하게 된다. 그리고 이러한 상태를 최종적으로 셀에 저장하게 된다. Fig. 1의 LSTM 연산절차를 수식화하면 다음과 같이 정리할 수 있다.
첫 번째, 망각게이트(forget gate, 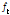 )는 셀에서 전 단계 상태(
)는 셀에서 전 단계 상태(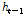 )와 새로운 입력(
)와 새로운 입력(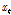 )을 받아들여 어떤 정보를 잊을지를 Eq. (2)에 의해 결정하게 된다.
)을 받아들여 어떤 정보를 잊을지를 Eq. (2)에 의해 결정하게 된다.
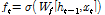 (2)
(2)
여기서, 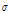 는 시그모이드 함수(sigmoid function),
는 시그모이드 함수(sigmoid function), 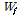 는 망각게이트의 가중치를 나타낸다.
는 망각게이트의 가중치를 나타낸다.
두 번째, 입력게이트(input gate, 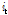 )에서는 Eq. (3)과 같이 어떤 정보를 셀에 저장할 것인지를 결정하게 되는데 이는 크게 다음과 같은 두 단계로 구분된다. 1) 시그모이드 함수를 이용해 무엇을 업데이트 할지 결정하고, 2) 하이퍼탄젠트(hypertangent, tanh) 함수를 이용해 새로운 셀 상태 업데이트 시 사용되는 후보 셀(
)에서는 Eq. (3)과 같이 어떤 정보를 셀에 저장할 것인지를 결정하게 되는데 이는 크게 다음과 같은 두 단계로 구분된다. 1) 시그모이드 함수를 이용해 무엇을 업데이트 할지 결정하고, 2) 하이퍼탄젠트(hypertangent, tanh) 함수를 이용해 새로운 셀 상태 업데이트 시 사용되는 후보 셀(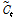 )을 생성하게 된다.
)을 생성하게 된다.
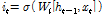 (3)
(3)
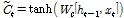 (4)
(4)
여기서, 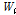 는 입력게이트의 가중치,
는 입력게이트의 가중치, 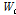 는 후보 셀의 가중치를 나타낸다.
는 후보 셀의 가중치를 나타낸다.
다음으로 과거의 셀 상태(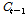 )와 후보 셀(
)와 후보 셀(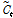 )을 Eq. (5)와 같이 조합하여 현재의 셀 상태(
)을 Eq. (5)와 같이 조합하여 현재의 셀 상태(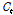 )를 업데이트하게 된다.
)를 업데이트하게 된다.
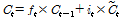 (5)
(5)
세 번째, 출력게이트(output gate, 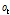 )는 Eq. (6)과 같이 시그모이드 함수를 이용해서 셀 상태의 어느 부분을 출력하고자 하는지 결정하고, 마지막으로 Eq. (7)과 같이 하이퍼탄젠트 함수를 이용하여 활성화된 셀 상태(
)는 Eq. (6)과 같이 시그모이드 함수를 이용해서 셀 상태의 어느 부분을 출력하고자 하는지 결정하고, 마지막으로 Eq. (7)과 같이 하이퍼탄젠트 함수를 이용하여 활성화된 셀 상태(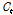 )와의 곱을 통해 특정 시점의 상태(
)와의 곱을 통해 특정 시점의 상태(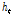 )를 업데이트하게 된다.
)를 업데이트하게 된다.
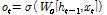 (6)
(6)
 (7)
(7)
여기서, 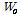 는 출력게이트의 가중치를 나타낸다.
는 출력게이트의 가중치를 나타낸다.
LSTM은 셀이라는 개념을 도입하여 전 상태와 현재 입력에 따라 현재 상태를 얼마나 기억할지, 얼마나 업데이트할지, 무엇을 업데이트할지를 선택적으로 결정하게 됨으로써 순환신경망보다 더 복잡하고, 시간적으로 더 멀리 떨어진 연관관계를 모델링할 수 있다(Tran and Song, 2017).
3. 모형의 구축
3.1 메콩강 유역
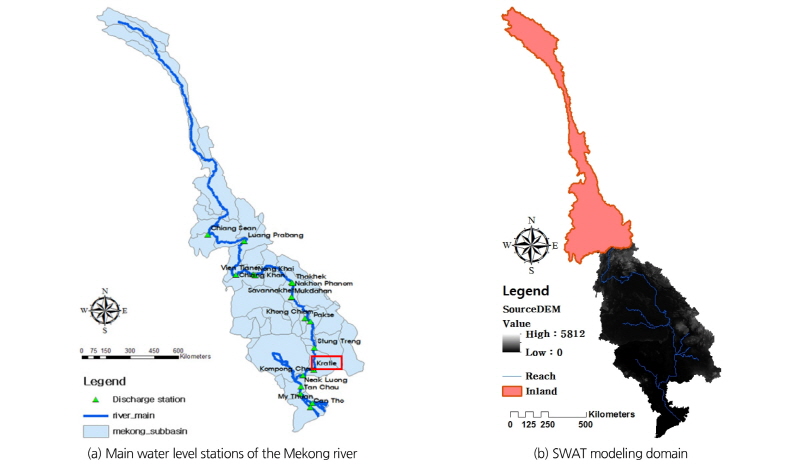
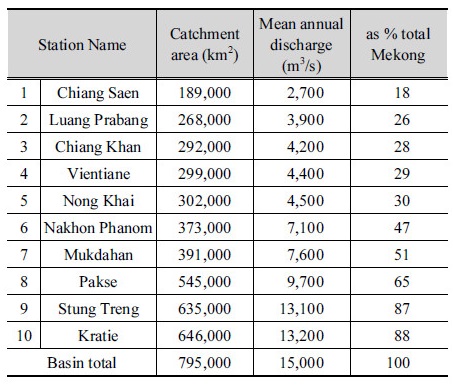
전술한 바와 같이 메콩강은 최상류 중국에서 발원해서 최하류 베트남 메콩델타를 관통하는 국가공유하천으로 유역면적이 남한의 약 10배(795,000 km2)에 달하며, 연평균 유량은 약 15,000 m3/s 이다. Table 3은 메콩강 공유국가별 유역면적, 유출량 기여도 정보를 나타내고 있다. Fig. 2는 메콩강 하류지역(중국에 위치한 상류를 제외)의 주요 수위국 지점의 위치를 보여주고 있으며, Table 4는 해당 수위국을 기준으로 한 유역면적과 유출량을 나타내고 있다. Fig. 2 and Table 4와 같이 본 연구에서 대상으로 하는 Kratie 지점에서의 연평균 유량은 메콩강 본류의 약 90%에 해당하고, 지리적으로도 캄보디아 톤레삽 호수와 베트남 메콩델타 지역의 최인접하여 해당지역의 수리 ․ 수문 해석을 위한 매우 중요한 지점이다(Kummu et al., 2014).
3.2 SWAT 모형 구축
SWAT 모형을 이용한 메콩강 본류 Kratie 지점에서의 강우-유출 모의를 위해서는 기초자료(수문기상, 지형, 토지이용, 토양 등)의 수집 및 가공이 필요하다. 본 연구에서는 Fig. 2(b)와 같이 기초자료 획득이 어려운 메콩캉 상류지역을 제외하고 Luang Prabang 지점으로부터 Kratie 지점까지의 유역에 대해서 기초자료를 획득하여 모형을 구축하였으며, 메콩강 상류의 유입량을 고려하기 위해 Luang Prabang 지점의 수위-유량관계곡선식을 모형의 상류 경계조건으로 적용하였다(Lee et al., 2018).
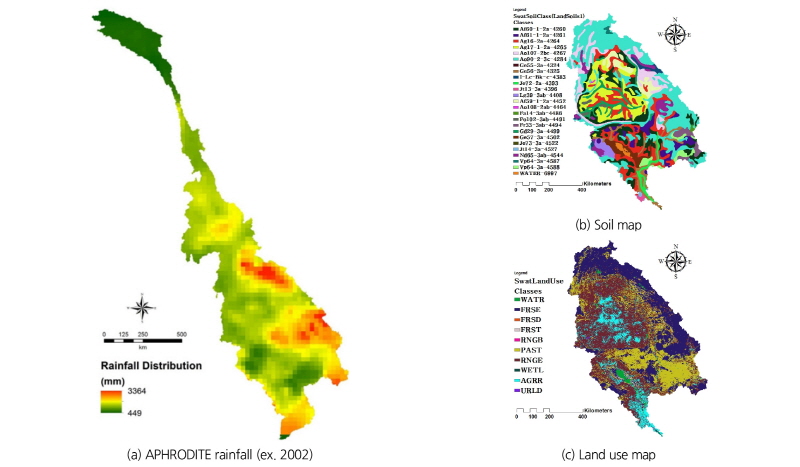
수치표고모형(DEM) 자료는 USGS에서 제공하는 Hydro-SHED (Hydrological data and maps based on SHuttle Elevation Derivatives at multiple Scales), 토지이용도는 GLCF (Global Land Cover Facility)에서 제공하는 MODIS LandCover, 토양도는 FAO (Food and Agriculture Organization of the United Nations)에서 제공하는 자료를 이용하였다. 이상의 자료들은 각기 다른 공간해상도(spatial resolution)를 가지고 있으며, 본 연구에서는 MODIS LandCover 자료의 최고 해상도에 해당하는 30 arc-second (약 1 km)를 기준으로 SWAT 모형의 입력자료를 리샘플링하였다. 강우의 경우, 아시아 지역의 지점강우자료를 이용하여 보정 후 격자기반의 강우장(rainfall field) 형태로 제공하는 APHRODITE (Asian Precipitation Highly Resolved Observational Data Integration Towards Evaluation of Water Resources)의 2000년부터 2007년까지의 일강우를 수집하여 30개 HRU에 대한 면적강수량으로 환산한 후 적용하였다. 또한 기타 기상자료인 상대습도, 풍속, 기온, 일사량의 자료는 메콩강 공유국가별 주요도시의 월평균 자료를 사용하였다. Fig. 3은 대상유역의 SWAT 모형 구축을 위한 기초자료 현황을 나타내고 있다.
또한, SWAT-CUP (Calibration and Uncertainty Program)의 SUFI-2 (Sequential Uncertainty Fitting-version 2) 알고리즘을 이용하여 4개(Nong Khai, Mukdahan, Khong Chaim, Kratie) 관측소의 관측유량을 이용하여, 모형의 매개변수를 보정하였다. 매개변수의 경우, Shrestha et al. (2013)에 의해 메콩강 유역 중 라오스의 Nam Ou 유역에 적용된 바 있는 11개의 매개변수를 선택하였으며, 최소 및 최대범위를 지정하여 2000번의 반복수행을 통해 최적 매개변수를 도출하였다.
3.3 LSTM 모형 구축
TensorFlow의 LSTM 모형의 학습 및 예측을 위해 가능한 장기간의 수위자료가 요구됨에 따라 본 연구에서는 비교적 자료의 양적, 질적 신뢰성이 확보되고, 모든 관측소가 해당기간의 자료를 확보하고 있는 2000년부터 2014년 8월까지의 일수위 자료를 획득하였다. 또한, Kratie 지점보다 상류에 위치한 Table 4의 9개 관측소 이외의 Mukdahan (태국) 관측소의 수위자료도 획득하여 총 10개 관측소의 일수위자료를 이용하여 LSTM 모형을 학습시키고, SWAT 모형과 동일하게 2003~2007년에 대해 Kratie 지점의 수위를 예측한 후, 수위-유량관계곡선식을 이용하여 유량으로 환산하였다. 유량 자료를 사용하지 않은 이유는 MRC에서는 Table 4의 몇몇 지점에 대해서는 유출량 정보를 직접 제공하지 않으며, 수위-유량관계곡선식 역시 많은 불확실성을 내포하고 있고 이는 신경망 학습 시 왜곡을 발생시킬 수 있기 때문에 본 연구에서는 LSTM 모형을 이용하여 Kratie 수위를 모의 후 이를 유량으로 환산하여 모의결과를 분석하였다.
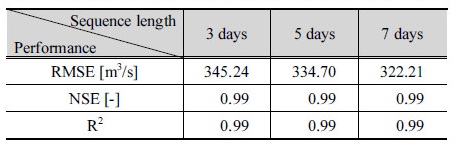
LSTM 모형의 매개변수의 경우, 민감도 분석을 통해 학습률(learning)은 0.01로 고정하였으며, 은닉층(hidden layer)은 22개, 신경망의 충분한 학습을 위하여 반복횟수(epoch)는 5000번으로 결정하였다. 마지막으로 메콩강 홍수파의 시간적 연속성을 고려하기 위해 시퀀스 길이(sequence length)를 3일, 5일, 7일로 변화시키며 모의결과의 변동성을 분석하였다. 예를 들어 시퀀스 길이가 3일일 경우, Kratie 지점기준 상류 10개 관측소의 현재 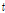 일의 수위를
일의 수위를 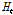 , 1일 전의 수위를
, 1일 전의 수위를 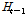 , 2일 전의 수위
, 2일 전의 수위 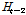 라 하면 10개 관측소의 연속된 3일 데이터 구조가 심층신경망 모형에 계속적으로 학습되고, 다음 날의 Kratie 수위인
라 하면 10개 관측소의 연속된 3일 데이터 구조가 심층신경망 모형에 계속적으로 학습되고, 다음 날의 Kratie 수위인 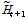 가 예측결과로 도출되게 된다. 심층신경망 모형은
가 예측결과로 도출되게 된다. 심층신경망 모형은 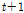 일에 해당하는 실제 Katie 수위와 예측수위인
일에 해당하는 실제 Katie 수위와 예측수위인 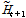 의 오차함수(error function)가 최소가 될 때 까지 역전파법(back propagation method)을 이용하여 신경망의 가중치를 업데이트하게 된다.
의 오차함수(error function)가 최소가 될 때 까지 역전파법(back propagation method)을 이용하여 신경망의 가중치를 업데이트하게 된다.
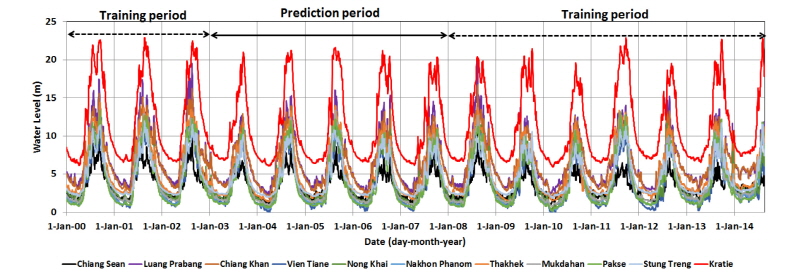
Fig. 4는 2000년부터 2104년까지 Table 4의 수위관측소별 일수위 시계열 자료를 나타내며, 점선 구간은 LSTM 모형의 9년 8개월의 학습기간(2000~2002년, 2008~2014년 8월), 실선 구간은 학습된 LSTM 모형의 예측기간(2003~2007년, 5개년)을 나타낸다. 본 연구의 목적은 메콩강 본류의 장기 유출량의 거동을 분석하는 것이기 때문에 학습구간을 홍수기와 갈수기로 구분하지 않고, 전 기간에 대한 연속적인 수위자료를 LSTM 모형에 적용하였다.
4. 유출 모의결과 분석
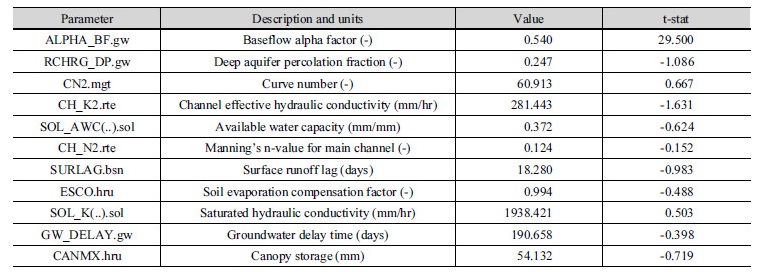
SWAT 모형의 경우, 2000년부터 2007년까지 모형 안정화 기간(2000~2002년)을 포함한 총 8년에 대한 강우-유출모의를 수행하였으며, SWAT-CUP을 통해 추정된 최적 매개변수는 Table 5와 같다. 여기서, t-stat값은 각 매개변수 값을 매개변수별 표준편차로 나눈 값으로 매개변수별 상대적인 민감도를 의미하며, 절댓값이 클수록 목적함수 값에 대한 민감도가 높음을 의미한다. 매개변수 추정결과, 기저유량감소계수인 ALPHA_BF의 t-stat값 범위가 29.5로 11개의 매개변수 중 다른 매개변수에 비해 가장 민감하게 반응하는 것으로 나타났다.
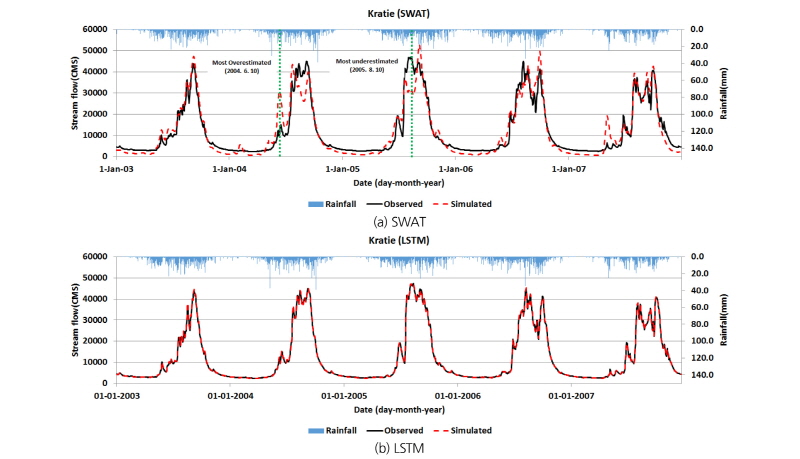
Table 5의 최적 매개변수를 적용한 SWAT 모형의 강우-유출 모의결과는 Fig. 7(a)와 같다. 모의결과의 정확도를 정량화하기 위해 RMSE (Root mean square error)와 NSE (Nash- Sutcliffe Efficiency), R2 (Coefficient of determination)를 산정하였으며, 개별 수식은 Eqs. (8)~(10)과 같다.
 (8)
(8)
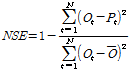 (9)
(9)
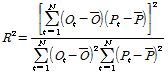 (10)
(10)
여기서, 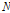 은 자료의 개수,
은 자료의 개수, 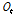 와
와 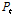 는 시간
는 시간 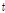 에서의 실측치와 모의치,
에서의 실측치와 모의치, 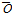 와
와 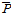 실측치와 모의치의 평균값을 나타낸다.
실측치와 모의치의 평균값을 나타낸다.
SWAT 모형의 정확도를 검토한 결과 RMSE는 3941.71 m3/s, NSE는 0.9, R2는0.91로 산정되어 Table 1의 타 연구결과와 비교하여도 비교적 우수하게 모의되었으며, Fig. 5(a)에서 나타난 바와 같이 모의기간 전반에 걸쳐 유출량 변동성이 비슷하게 모의된 것으로 나타났다. 다만, 홍수기 시 년도별 첨두값의 경우, 2003년과 2007년은 비교적 정확하게 모의된 반면, 2004~2006년은 첨두 발생일시와 첨두량이 불일치하는 것으로 분석되었다. 특히, 2004년 6월 10일은 모의기간 중 가장 과대모의(+20,685 m3/s)되었으며, 2005년 8월 10일은 가장 과소모의(-16,548 m3/s)된 것으로 나타났다.
LSTM 모형의 모의결과는 Table 6과 같이 시퀀스 길이의 조정에도 불구하고, 모든 결과에 대한 NSE 및 R2가 0.99 이상으로 매우 우수하게 산정되었으며, RMSE는 시퀀스 길이가 길어짐에 따라 약 10 m3/s씩 미세하게 감소, 평균적으로 약 330 m3/s의 오차가 발생하는 것으로 나타났다. Fig. 5(b)는 시퀀스 길이 7일에 대한 유출수문곡선으로 갈수기와 홍수기에 구분 없이 전 모의기간에 걸쳐 유출량이 매우 우수하게 모의되었다.
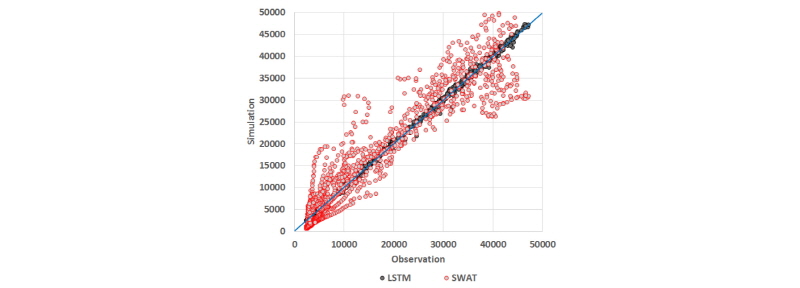
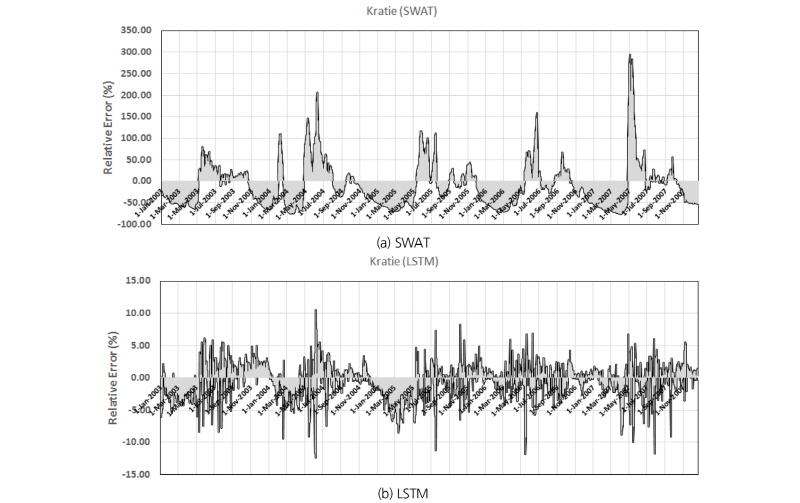
Fig. 6은 SWAT과 LSTM 모형의 유출량 산포도이며, LSTM 모형은 유량의 고저에 상관없이 매우 안정적으로 유출 모의결과를 제공하는 반면, SWAT 모형은 저유량과 고유량 부분에서 산포도가 매우 넓게 분포된 것을 확인할 수 있다. Fig. 7은 관측유량대비 오차(모의유량-관측유량)의 비인 상대오차율(%)을 나타내고 있으며, +는 과대모의, -는 과소모의를 의미한다. SWAT 모형은 모의기간에 대해 평균적으로 -11.2%의 상대오차율을 나타냈으며, 최대 294%, 최소 -76%의 범위로 매우 불규칙하게 분포된 반면, LSTM 모형은 평균적으로 -0.5%, 최대 10%, 최소 12%의 상대오차율을 나타내는 것으로 분석되었다.
5. 결 론
본 연구에서는 물리적 강우-유출 모형인 SWAT과 심층신경망 모형인 LSTM 모형을 이용하여 메콩강 본류 Kratie 지점 상류 대유역(646,000 km2)에 대한 유출모의를 수행하고, 그 결과를 비교 ․ 분석하였다. SWAT 모형의 구축을 위해 범용 입력자료(지형: HydroSHED, 토지이용: GLCF-MODIS, 토양: FAO-Soil map, 강우: APHRODITE 등)을 이용하였으며, warming-up 및 매개변수 보정 후 2003~2007년 일유량 모의를 수행하였다. LSTM을 이용한 유출모의의 경우, 딥러닝 오픈소스 라이브러리인 TensorFlow를 활용하여 Kratie 지점기준 메콩강 상류 10개 수위관측소의 두 기간(2000~2002, 2008~2014) 일수위 정보만을 이용하여 심층신경망을 학습하고, SWAT 모형과 마찬가지로 2003~2007년을 대상으로 Kratie지점에 대한 일수위 모의 후 수위-유량관계곡선식을 이용하여 유출량으로 환산하였다.
본 연구에서 구축한 SWAT 모형의 정확도를 정량적으로 평가한 결과는 RMSE: 3941.71 m3/s, NSE: 0.9, R2: 0.91로 유출량의 시간적 변동성을 기수행된 타 연구결과에 비해 우수한 것으로 분석되었으나, 일부 기간에 대해서는 모의결과가 과대산정되거나 과소산정되었다. 이에 반해 LSTM 모형은 NSE 및 R2가0.99로 매우 우수하게 산정되었으며, RMSE는 평균적으로 약 330 m3/s의 오차가 발생하는 것으로 나타났다. 또한 SWAT 모형은 저유량과 고유량 부분에서 정확도가 불규칙한 반면, LSTM 모형은 유량의 고저에 상관없이 매우 안정적으로 유출 모의결과를 제공하는 것으로 분석되었다.
비선형적인 자연계에서의 유출해석을 위해 이미 국내 ․ 외적으로 다양한 물리적 강우-유출 모형이 개발되었으며, 충분한 물리적 데이터와 매개변수 보정이 보장될 경우, 이러한 모형들은 강우-유출 시 ․ 공간적 수문변동성을 분석하는데 유용한 도구임은 이미 수많은 선행연구들에 의해 증명된 바 있다. 다만, 이러한 물리적 모형은 그 복잡성으로 인해 모형구조, 격자스케일, 매개변수 등에서 불확실성 문제가 발생할 수도 있으며, 자료구축 및 모의시간 등에서도 제약을 받기도 한다. 따라서 특정 지점에서의 시계열 분석이 목적일 경우, 종속변수에 영향을 미칠 수 있는 가용한 모든 독립변수를 데이터화하여 특정 시점의 시계열 예측에 있어 선행 정보를 기억하고, 이를 예측에 반영하는 LSTM 모형은 수문자료 시계열 예측에 있어 강우-유출 모형을 대체할 수 있으리라 판단된다.
특히, 본 연구에서 이용한 TensorFlow는 GPU 환경에서도 딥러닝을 구현할 수 있도록 라이브러리를 제공하므로 학습 및 모의에 걸리는 연산시간을 감축함으로써 향후 빅데이터 기반의 수문시계열 예측모형으로 확장이 가능하다. 특히, 메콩강과 같은 대유역에서 홍수예 ․ 경보 시스템 구축 시 예측 강우정보의 획득이 불가능하거나 저해상도의 예측강우정보를 이용할 수 밖에 없는 경우, 이러한 심층신경망 모형은 홍수예측을 위한 중요한 도구로서 활용이 가능할 것이다.