1. 서 론
2. 방법론 및 자료
2.1 방법론
2.2 자료
3. 미계측 유역의 유황곡선 추정을 위한 심층신경망 모형 개발 및 평가
3.1 DNN 모형 구축
3.2 DNN 모형 검증
4. 결 론
1. 서 론
최근 우리나라는 기후변화에 따라 집중호우로 인해 강우의 몰림 현상 등 다양하고 복합적인 재난이 나타나고 있다. 이런 여러 기상 현상 중에서 가뭄은 전 세계적으로 기후변화의 영향과 밀접한 관련성이 있다고 알려져 있고, 자연현상과 물에 대한 사용자 간의 갈등으로 인해 사회에 커다란 영향을 미친다. 이를 평가하기 위해 일반적으로 유황곡선을 통해 하천의 유량특성을 파악한다. 유황곡선의 산정을 위해서는 장기간의 일 유량 관측자료가 필요하지만 시간, 예산, 인력, 안전 등의 경제적인 문제로 인하여 모든 하천을 해마다 측정하기에는 어려움이 있다(Jeung, 2019). 이로 인하여 유량 자료의 기간이 짧거나 없는 미계측 유역의 경우 근처의 유량 관측소를 사용할 수 없을 때의 하천 유출 특성은 일반적으로 회귀방정식을 사용하여 예측하여 사용하거나 장기간의 일 유량 관측자료를 보유한 관측소의 자료를 이용하여 갈수량을 추정해야 하는 실정이다(Lim, 2020). 또한, 기존의 국내 미계측 유역의 갈수량 산정 방법인 비유량법이 실무에서 주로 사용됐으나 유역면적 비로 유황곡선을 산정하는 비유량법의 경우 유황곡선에 영향을 미치는 다양한 지형학적, 기상학적, 수문학적인 인자를 고려하지 못하므로 미계측 유역의 갈수량을 보다 정확히 추정하기 위해서는 해당 유역의 유역특성 인자가 고려되어야 한다(Lim, 2020).
미계측 유역의 유출량을 산정하기 위한 전통적인 방법으로 다양한 회귀분석이 있다. 회귀분석에 관하여 많은 선행연구가 이루어졌으며 연구 동향은 다음과 같다. Ryoo and Chong (2008)은 소양강, 충주, 횡성댐의 과거 호우 사상을 대상 유역으로 선정하여 유역의 수문 사상들을 독립변수로 한 회귀분석을 통하여 강우에 따른 예상 유출률을 산정하여 과거 홍수기 댐 유입률과 유역 수문 사상과의 관계를 분석하였다. Choi et al. (2012)는 중랑천 유역을 대상으로 입력자료의 자기상관분석을 통해 독립변수의 시간 규모를 결정한 후 최소자승법, 가중 최소자승법, 단계별 선택법의 각기 다른 회귀계수 산정 방법을 이용한 홍수예측 모형을 구축하고 중랑천 유역의 다양한 홍수 사상에 적용하여 평균제곱근오차, Nash-Suttcliffe 효율계수, 평균절대오차, 수정 결정계수를 이용하여 구축된 다중선형회귀 모형의 회귀계수 선정 방법에 따른 홍수예측 성능을 비교・검토하였다. Lee (2016)은 국내 16개의 댐 상류 유역을 대상으로 유황곡선을 산정하여 관측치와 비교・검토를 수행하였으며 관측자료의 길이가 짧거나 미계측 기간이 지속적으로 발생하는 유역의 갈수량을 산정한 후 관측치와 비교・분석하여 인위적인 유량의 조절이 발생 하는 댐 하류의 유황 변화를 평가하였다.
미계측 유역의 유출량을 산정하기 위한 최신기술은 머신러닝을 사용하는 것이다. 머신러닝은 최근 다양한 분야에서 수요가 증가하고 있다. 강우와 하천의 유출량은 비선형적인 현상이므로 일반적인 선형모형으로 예측하는 것에는 한계가 있다. 머신러닝은 비선형성 관계를 가진 빅데이터 기반의 자료를 분석하는데 적합하다. 최근 하천의 유량분야 연구 동향을 살펴 보면 하천의 수위를 예측한 사례들을 살펴보면 주로 시계열 모형(Time series model)과 인공신경망(artificial neural network, ANN)을 활용하여 하천 수위를 예측하였다(Tiwari and Chatterjee, 2010; Jun and Lee, 2013; Byeon et al., 2014; Castillo et al., 2018). 하천의 수위를 예측한 연구를 살펴보면, 수위를 예측하는데 있어 인공신경망을 하천 수위예측에도 적용시켜 Baseflow recession analysis와 같이 그 적용 가능성을 평가하고 Rezaeianzadeh et al. (2018)은 하천 수위 모델링을 통하여 미국 해안 Alabama 주 상류에 위치한 습지에 적용하였다(Rezaeianzadeh et al., 2015; 2018).
하천 유량 예측에 관한 기존 연구들을 살펴보면, 주로 통계적 모형을 사용하였고, 강우, 온도 등 기상학적 자료들만을 독립변수로 사용하였다. 그러나 하천의 유량의 경우 유역의 특성 즉, 하천 경사, 조도 계수 등이 많은 영향을 미친다. 또한, 다양한 통계모형을 적용하여 지역에 맞는 통계모형을 평가 및 비교하여 예측하였던 하천에서의 유량 예측 연구과는 달리 인공신경망만을 활용하여 다양한 통계모형들과 적용 가능성을 비교 및 평가하지 못하는 한계가 있었다(Kim et al., 2020). 이에 본 연구에서는 새로운 패러다임에 맞는 머신러닝 기법인 DNN 기법을 사용하여 하천의 유량을 예측하는 방법을 제시하고자 한다. DNN 기법은 ANN 기법의 단점인 학습 과정에서 최적 매개변수 값을 찾기 어렵고, 학습시간이 느린 단점을 보완한 방법이다. 따라서 본 연구에서는 머신러닝 기법인 DNN 기법을 통해 미계측 유역에 적용 가능한 유황곡선을 산정하고자 한다. 먼저, 하천의 유황곡선에 영향을 미치는 인자들을 수집하고 인자들 간의 상관 분석, 다중 공선성 분석을 통해 통계적으로 유의한 변수를 선정하여, DNN 모형을 구축 및 학습을 진행하였고 Test를 통해 구축된 DNN 모형의 신뢰도를 평가하였다.
2. 방법론 및 자료
2.1 방법론
2.1.1 개요
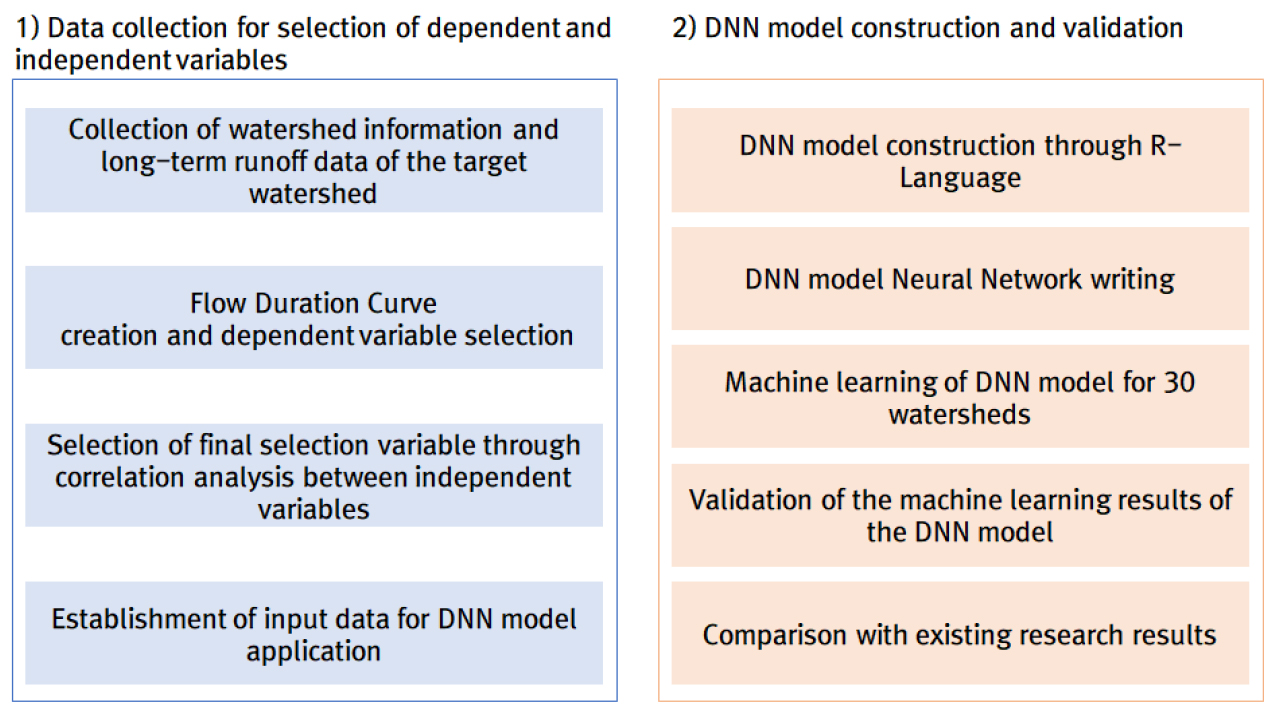
본 논문에서는 미계측 유역의 유황곡선 산정을 위한 회귀모형을 개발하기 위하여 전국의 중권역 40개 지점을 대상으로 국가수자원관리종합시스템(Water Resources Management Information System, WAMIS)에서 제공하는 장기유출 자료를 이용하여 종속변수인 유황 곡선을 산정하였으며 유황 곡선을 14개의 구간으로 나누어 종속변수로 설정하였다. 또한, 독립변수인 유역특성인자 18개와 기상특성인자 3개를 수집하여 상관 분석을 수행하여 독립변수를 선정하였으며 종속변수와 선정한 독립변수를 이용하여 DNN (Deep Neural Network) 머신러닝 기법을 기반으로 유황곡선 산정 모형을 개발하였다. Fig. 1은 본 논문의 연구흐름도이다.
2.1.2 유황곡선
하천의 유량은 강우량, 유역면적, 하천수계조직, 지형 등에 따라 달라질 수 있다. 강우량과 유역면적이 크면 유량도 크게 발생하며 특히 호우성의 연속강우량은 유량을 급격하게 증가시킨다. 유역의 지세가 험준하면 강수가 일시에 하천을 따라 집중되기 때문에 유량이 많고, 지질이 불투수성이거나 지표수의 유하를 방해하는 초목 등이 적을수록 조도계수가 작아지기 때문에 유량이 많다. 따라서 하천의 유량 변화는 강우에 대한 유역의 반응구조를 나타내게 된다(Yoon, 2007). 하천에서 시간에 따른 유량변동을 나타내는 방법에는 유량수문곡선과 유황곡선이 있다(Yoon, 2007). 유량수문곡선은 유량의 월 혹은 계절적인 변동보다 발생 수위 측면의 변동성에 관한 정보를 나타내고 있다(Park, 2003).
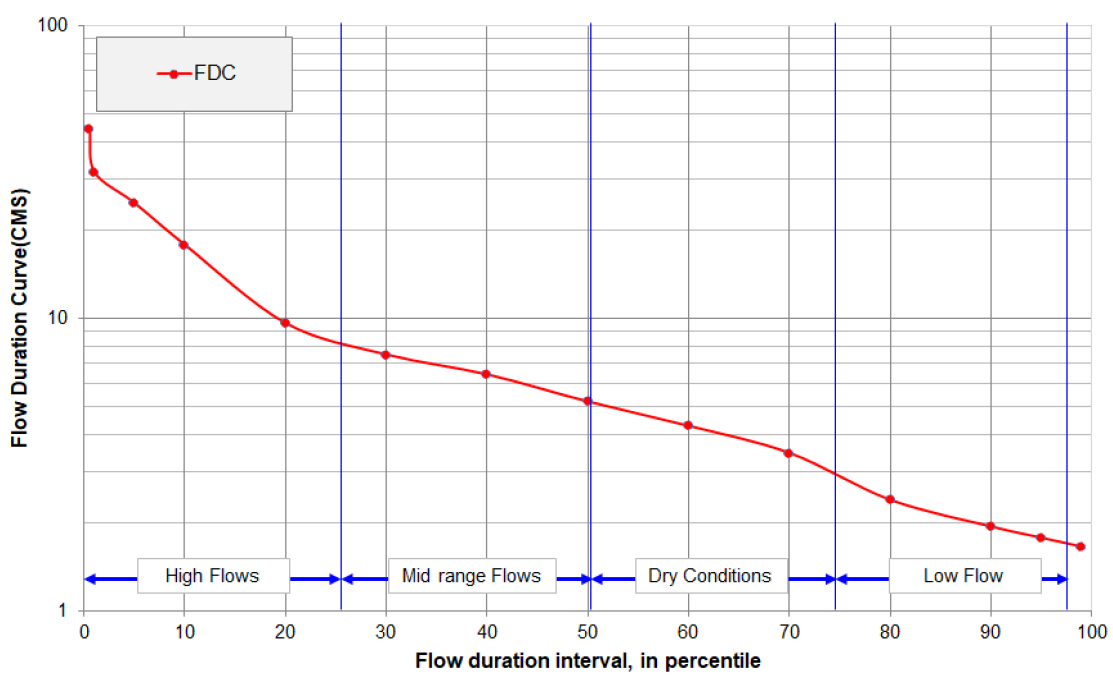
유황은 연평균유량과 전 자료 기간 유황으로 분석할 수 있다. 연평균유량은 1년 365일 각각에 대한 유량을 최대 유량부터 365위 까지 순위를 정하고 특정 지속일수 순위의 유량을 자료기간 년 수에 대한 평균을 취하여 얻어진다(Yoon, 2007). 전 기간유황은 보유하고 있는 전 기간의 유황을 큰 것부터 작은 순으로 순위를 정한 후 그 초과확률의 백분율로 나타낼 때 Q26%을 풍수량, Q50.7%을 평수량, Q75.3%을 저수량 그리고 Q97.3%을 갈수량으로 정의한다. 미국이나 유럽에서는 확률개념을 사용하여 유황을 산정하고 있다(Yoon, 2007). Fig. 2는 유황곡선의 구조를 나타낸 그림이다.
이렇게 산정된 유황곡선은 하천수계상의 어떤 지점에서의 하천유량의 규모와 변동성과 같은 하천특성을 평가하기 위한 수단으로 사용된다. 하지만 유황곡선을 산정하기 위해 30년 이상의 유량자료의 확보가 필수적이다. 하지만 국가하천 단위 이하의 하천의 경우 장기간의 유량자료가 없거나 중간 일정기간 결측된 관측소가 있어 하천별 유황곡선을 산정하기에 한계가 있다. 이에 본 논문에서는 국가수자원관리종합시스템에서 제공하고 있는 장기유출량 자료를 활용하여 미계측 유역(자료가 결측이거나, 유량측정을 할수 없는 유역)의 유황곡선을 머신러닝기법을 통해 추정하고자 한다.
2.1.3 심층신경망(Deep Neural Network, DNN)
다양한 종류의 심층 신경망 구조가 존재하지만, 대부분의 경우 대표적인 몇 가지 구조들에서 파생된 것이다. 그렇지만 여러 종류의 구조들의 성능을 동시에 비교하는 것이 항상 가능한 것은 아닌데, 그 이유는 특정 구조들의 경우 주어진 데이터 집합에 적합하도록 구현되지 않은 경우도 있기 때문이다(Matsumoto et al., 2016). 심층 신경망(Deep Neural Network, DNN)은 입력층(input layer)과 출력층(output layer) 사이에 여러 개의 은닉층(hidden layer)들로 이뤄진 인공신경망(Artificial Neural Network, ANN)이다. 심층 신경망은 일반적인 인공신경망과 마찬가지로 복잡한 비선형 관계(non-linear relationship)들을 모델링할 수 있다(Matsumoto et al., 2016). 예를 들어, 사물 식별 모델을 위한 심층 신경망 구조에서는 각 객체가 이미지 기본 요소들의 계층적 구성으로 표현될 수 있는데 이때, 추가 계층들은 점진적으로 모여진 하위 계층들의 특징들을 규합시킬 수 있다. 심층 신경망의 이러한 특징은, 비슷하게 수행된 인공신경망에 비해 더 적은 수의 유닛(unit, node)들 만으로도 복잡한 데이터를 모델링할 수 있게 해준다. 이전의 심층 신경망들은 보통 앞먹임 신경망으로 설계되어 왔지만, 최근의 연구들은 심층 학습 구조들을 순환 신경망(Recurrent Neural Network, RNN)에 성공적으로 적용했다. 일례로 언어 모델링(language modeling) 분야에 심층 신경망 구조를 적용한 사례 등이 있다. 합성곱 신경망(Convolutional Neural Network, CNN)의 경우에는 컴퓨터 비전(computer vision) 분야에서 잘 적용되었을 뿐만 아니라, 각각의 성공적인 적용 사례에 대한 문서화 또한 잘 되어 있다. 더욱 최근에는 합성곱 신경망이 자동 음성인식 서비스(Automatic Response Service, ARS)를 위한 음향 모델링(acoustic modeling) 분야에 적용되었으며, 기존의 모델들 보다 더욱 성공적으로 적용되었다는 평가를 받고 있다. 심층 신경망은 표준 오류역전파 알고리즘으로 학습될 수 있다. 이때, 가중치(weight)들은 아래의 Eq. (1)을 이용한 확률적 경사 하강법(stochastic gradient descent)을 통하여 갱신될 수 있다(Matsumoto et al., 2016).
여기서, η는 학습률(learning rate)을 의미하며, C는 비용함수(cost function)를 의미한다. 비용함수의 선택은 학습의 형태(지도 학습, 자율 학습 (기계 학습), 강화 학습 등)와 활성화함수(activation function)같은 요인들에 의해서 결정된다(Matsumoto et al., 2016). 예를 들면, 다중 클래스 분류 문제(multiclass classification problem)에 지도 학습을 수행할 때, 일반적으로 활성화함수와 비용함수는 각각 softmax 함수와 교차 엔트로피 함수(cross entropy function)로 결정된다. softmax 함수는 아래 Eq. (2)와 같이 정의 된다(Matsumoto et al., 2016).
이때, Pj는 클래스 확률(class probability)을 나타내며, Xj와 Xk는 각각 유닛 j로의 전체 입력(total input)과 유닛 k로의 전체 입력을 나타낸다. 교차 엔트로피는 Eq. (3)과 같이 정의되며, 이때 이때, dj는 출력 유닛 j에 대한 목표 확률(target probability)을 나타낸다(Matsumoto et al. 2016).
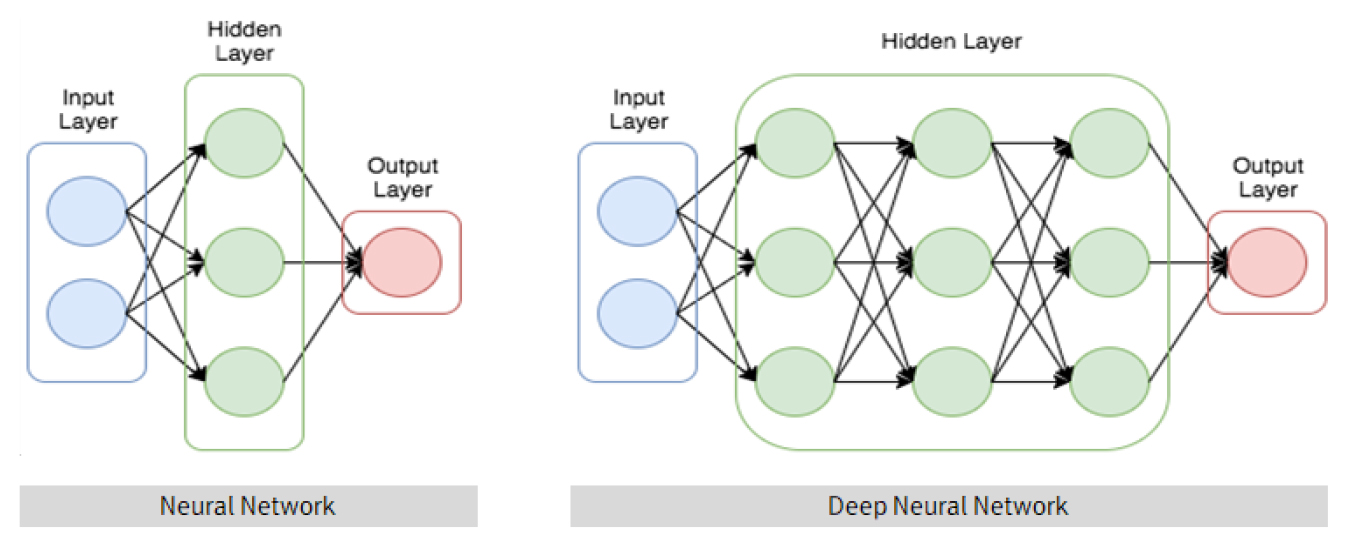
여기서 Pj는 해당 활성화함수를 적용한 이후의 j에 대한 확률 출력(probability output)이다. Fig. 3는 전통적인 Neural Network의 구조와 Deep Neural Network의 구조를 비교한 그림이다.
2.2 자료
2.2.1 대상유역 현황
본 논문의 대상유역 선정은 상류에 인위적인 유량조절이 발생하지 않으며 장기간의 연속적인 유량자료를 제공하고 있는 국가수자원종합관리시스템에서 40곳의 중권역 유역의 장기유출량 자료를 사용하였다.
한강 수계에 위치하고 있는 남한강 상류, 섬강, 달천, 소양강, 평창강, 충주댐, 홍천강과 한강 동해에 위치한 삼척오십천, 강릉남대천, 인북천, 양양남대천 등 11곳을 선정하였다. 낙동강 수계에 위치한 계측 유역은 남강댐, 내성천, 병성천, 안동댐과 낙동강 동해에 위치한 영덕오십천 등 13곳을 선정하였다. 금강 수계에 위치한 계측 유역은 무주남대천, 미호천, 보청천, 용담댐 등 8곳을 선정하였으며 섬진강 수계에 위치한 계측 유역은 섬진강댐, 보성강, 오수천, 요천 등 4곳을 선정하였다. 또한 영산강 수계에 위치한 계측 유역은 영산강 상류, 영암천, 지석천, 황룡강 등 4곳을 선정하였다. 남강댐 유역부터 영덕오십천 유역까지 30개 유역을 분석 유역으로 선정 하였으며 영동천 유역부터 황룡강 유역까지 10개의 유역을 검증 유역으로 선정하여 회귀모형의 검증을 수행하였다. 각 수계별로 선정된 대상 유역의 위치를 Fig. 4에 도시하였다.
2.2.2 종속변수 산정
본 논문에서는 유황곡선을 산정하기 위하여 40개 유역의 장기유출자료(1966년~2017년)을 이용하여 유황분석을 수행하였다. 분석 방법은 우리나라에서 보편적으로 사용되고 있는 지속일수에 대한 유황분석을 수행하였으며 분석 결과를 토대로 각 유역 별로 Q0.5, Q1, Q5, Q10, Q20, Q30, Q40, Q50, Q60, Q70, Q80, Q90, Q95, Q99를 추출하였다(Table 1).
Table 1.
Dependent variable calculation result
2.2.3 독립변수 선정
본 논문에서 사용한 유역특성인자는 국가수자원관리종합시스템에서 제공하고 있는 유역 면적, 유역 둘레, 유역평균경사, 유역평균표고, 원형비, 형상인자, 세장율 등 유역의 특성을 나타낼 수 있는 40개의 유역인자를 수집하였다. 또한 기상특성인자의 경우 기상자료개방포털에서 제공하는 연강수량, 연평균 기온을 적용하였으며 연증발산량을 적용하여 대상 유역의 기상학적 특성을 반영하였다. Table 2에 독립변수의 목록이며 Table 3은 유역별 21개 독립변수 값을 정리하였다.
Table 2.
Independent variable
2.2.4 최적 독립변수 선정을 위한 다중공선성 진단
회귀분석에서 다중공선성의 판단은 독립변수 간 상관관계가 높을 경우에 발생한다. 이 경우 입력 자료의 변화에 민감하게 반응하여 변동성이 높아져 회귀모형의 설명력이 떨어지게 된다. 회귀모형의 설명력을 확보하기 위한 방법으론 유역특성변수들 간의 다중공선성을 확인하여 또한 문제를 일으키는 변수를 제거하거나 능동형회귀분석(Ridge Regression), 주성분 분석(PCA) 또는 단계적 회귀분석(Stepwise Regression)이 있다. 본 연구에서는 단계적 회귀분석을 이용하여 공차한계 검토를 통해 다중공선성을 측정하여 머신러닝 모형 구축에 적절한 변수를 선택하였다.
Table 3의 다중공선성 진단 결과를 보면 유역평균경사(S), 형상계수(Rs), 원형지(Rc), CN, 연증발산량(ET), 연강수량(P)의 분산팽창계수(Variance Inflation Factors, VIF)가 0에서 10사이로 해당 변수를 선택하였을 시 다중공선성의 문제가 해소 될 수 있음을 확인할 수 있다. 이에 본 논문에서는 유역평균경사(S), 형상계수(Rs), 원형지(Rc), CN, 연증발산량(ET), 연강수량(P)의 변수를 머신러닝 모형 구축에 활용하고자 한다.
Table 3.
Multicollinearity diagnosis results
3. 미계측 유역의 유황곡선 추정을 위한 심층신경망 모형 개발 및 평가
3.1 DNN 모형 구축
본 논문에서는 미계측 유역의 유황곡선을 추정하기 위해 심층신경망(Deep Neural Network, DNN)을 사용하였다. 먼저 2절에서 모형에 적용 할 입력자료(종속변수, 유역특성변수)를 구축하였으며 유역특성변수의 다중공선성 진단을 통해 Table 4의 독립변수를 선정하였다.
Table 4.
Status of independent variables selected according to multicollinearity diagnosis
| No. | Independent variable | Symbol | No. | Independent variable | Symbol |
| 5 | Effective basin width | S | 15 | CN | CN |
| 7 | Shape factor | Rs | 19 | Annual evapotranspiration | ET |
| 8 | Circularity ratio | Rc | 20 | Annual precipitation | P |
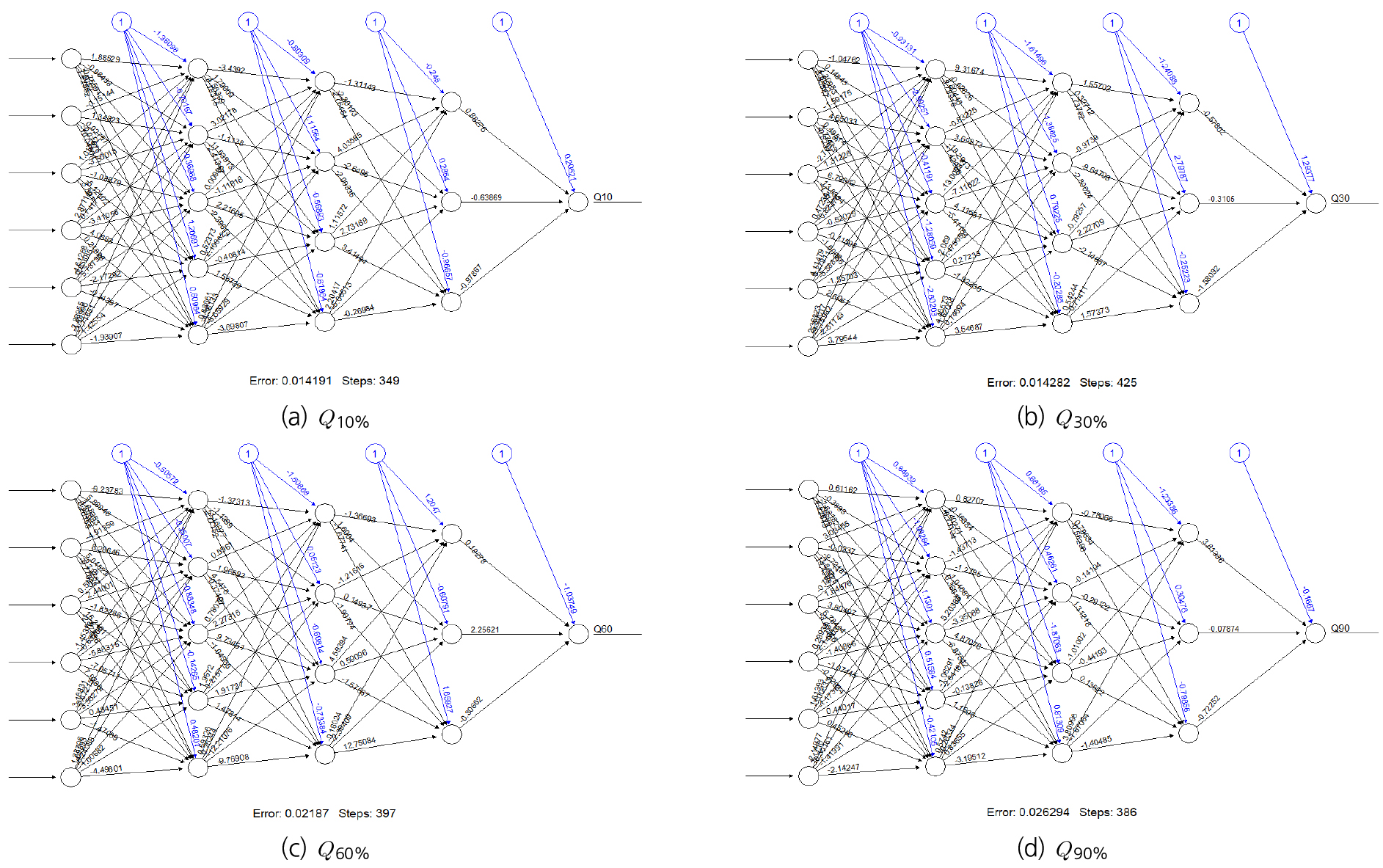
본 DNN 모형을 구축 후 학습데이터는 30개 유역 중 무작위하게 75%를 선택하였고, 나머지 25%의 데이터를 이용하여 테스트를 진행하였다. 먼저 75%의 데이터를 이용하여 종속변수 별 학습을 진행하였다. Table 6은 각 종속변수별 오차와 반복 학습 횟수를 기록하였고 Fig. 5는 Q10, Q30, Q60, Q90에 대해 DNN 모형의 구조도를 나타낸 그림이다. Table 5는 DNN 모형 학습 결과에 다른 오차와 학습 반복 횟수 현황이다.
Table 5.
Different errors in the training results of the DNN model and the number of training iterations
Table 6.
Test results for 10 watersheds
3.2 DNN 모형 검증
본 연구에서는 DNN 모형의 학습에 따른 정확도 검증을 위해 40개 유역의 자료 중 10개 유역을 대상으로 테스트를 진행하였다. 테스트 유역은 Table 1에서 Test 1~10 유역이다. 테스트는 총 2가지의 단계로 진행하였다. 첫째, 테스트 결과에 대한 Actual과 Predicted의 유황곡선을 작성하여 각 Predicted의 percentile이 Actual을 얼마나 잘 모사하는지 확인, 둘째 scatter plot을 통해 결과의 회귀선이 1:1선과 얼마나 잘 일치하는지, 또는 결정계수를 확인하였다.
Table 6은 10개 유역을 대상으로 진행한 테스트 결과 값이고, Fig. 6는 총 10개 유역의 결과 중 4개 유역을 무작위로 선정하여 작성한 유황곡선이다. Fig. 6에서 (a)는 평창강유역, (b)는 양양남대천유역, (c)는 위천역, (d)는 임하댐유역이며 Predicted가 Actual을 잘 모사하는 것을 볼 수 있다. Fig. 6(c)는 0~40까지의 percentile은 잘 모사하였지만 50 percentile 이후에는 평균 0.67 정도의 오차를 보이는 것을 확인하였다. 그 원인은 Table 5의 Q40와 Q60가 다른 변수에 비해 학습 횟수가 짧고 오차가 큰 상태로 모형 구축이 완료되어 다른 변수보다 신뢰도가 낮기 때문으로 판단된다. 하지만 DNN 모형의 전반적인 모의능력은 매우 양호하다고 판단된다.
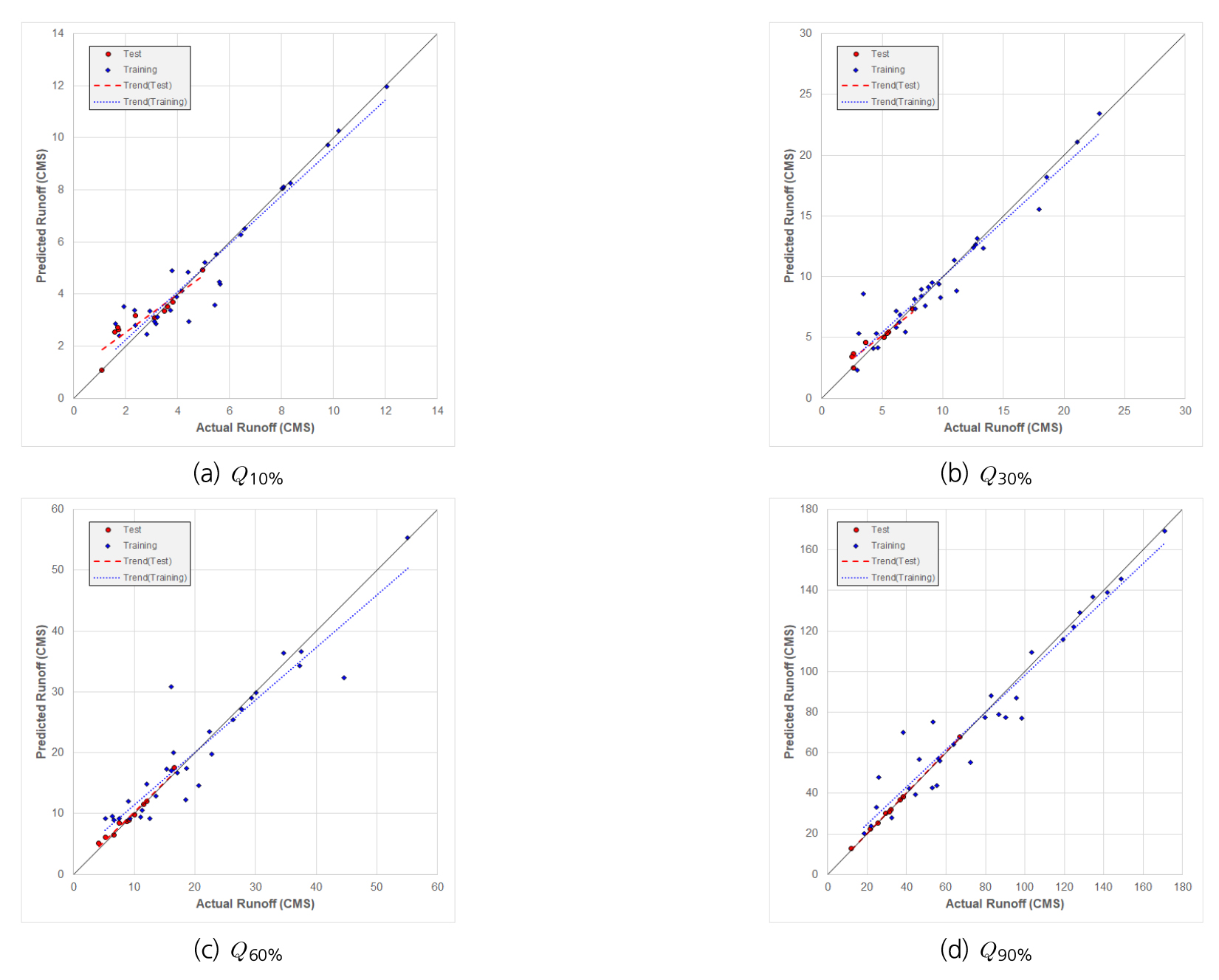
Fig. 7는 30개 Train에서 임의로 추출한 Soyang-river 유역의 Q10%, Q30%, Q60%, Q90%에 대한 Train 값과 Actual과 Predicted에 대한 Scatter Plot이다. 각 그림에서 푸른 점은 Train data, 붉은 점은 test data, 푸른 점선은 Train의 기울기, 붉은 점선은 Test 기울기 이다. 결과를 살펴보면 각 기울기 값이 검정 실선인 1:1선에 매우 근접하게 위치하는 것을 확인하였고, Table 7의 각 유역별 상관계수를 살펴보면 모두 0.9이상으로 높은 신뢰도를 가지는 것을 확인 할 수 있다.
Table 7.
Coefficient of determination in 10 watersheds
4. 결 론
본 연구에서는 미계측 유역의 유황곡선을 추정하기 위해 새로운 패러다임에 맞는 머신러닝 기법인 DNN기법을 사용하였다. DNN기법은 ANN기법의 단점인 학습과정에서 최적 매개변수값을 찾기 어렵고, 학습시간이 느린 단점을 보완한 방법이다. 따라서 본 연구에서는 머신러닝 기법인 DNN기법을 통해 미계측 유역에 적용 가능한 지역화 유황곡선을 산정하고자 하였다. 먼저, 하천의 유황곡선에 영향을 미치는 인자들을 수집하고 인자들간의 상관분석, 다중공선성 분석을 통해 통계적으로 유의한 변수를 선정하여, 머신러닝 모형에 입력자료를 구축하였다. DNN 모형을 이용하여 30개 유역을 대상으로 기계학습을 수행하였으며 10개의 검증 유역에 대해 검증하였다.
1) 본 논문에서는 미계측 유역의 유황곡선을 추정하기 위해 심층신경망(Deep Neural Network, DNN)을 사용하기 위해 입력자료(종속변수, 유역특성변수)를 구축하였으며 유역특성변수의 다중공선성 진단을 통해 독립변수를 선정하였다. 선정된 독립변수는 총 21개중 6개의 변수가 선택되었다. 선택된 변수는 유역평균경사, 형상계수, 원형비, CN, 연증발산량, 연강수량으로 모두 하천 유출량에 큰 영향을 주는 변수이다. 특히 연증발산량과 연강수량은 하천의 가용 수자원에 영향을 미치는 변수로 하천의 갈수량과 저수량에 큰 영향을 미칠 것으로 판단된다.
2) 본 연구에서는 DNN 모형을 구축하고 학습에 따른 정확도 검증을 위해 40개 유역의 자료중 10개 유역을 대상으로 테스트를 진행하였다. 본 DNN 모형을 구축 후 학습데이터는 30개 유역중 무작위하게 75%를 선택하였고, 나머지 25%의 데이터를 이용하여 테스트를 진행하였다. 먼저 75%의 데이터를 이용하여 종속변수 별 학습 및 테스트를 진행하였다. 테스트 결과에 대한 Actual과 Predicted의 유황곡선을 작성하여 각 Predicted의 percentile이 Actual을 잘 모사하는 것을 확인하였다. 또한 Scatter plot을 통해 결과의 회귀선의 상관계수가 모두 0.99 이상으로 높은 신뢰성을 가지는 것을 확인하였다.
본 연구에서는 미계측 유역의 하천 유량을 예측하기 위해 DNN 모형을 사용하였으며, DNN 모형의 적용성을 검토한 결과 높은 신뢰성을 가진다고 판단하였다. 이러한 연구 결과는 국토의 70%이상이 산지로 되어있어 하천의 유량의 파악이 힘든 우리나라에 뛰어난 적용성을 가진다고 할 수 있다. 특히 남한과 북한이 서로 공유하고 있는 임진강, 북한강 등의 경우 상류유역의 관측수문자료를 획득하기 어려운 지역에 대한 유출량 확보에 큰 도움이 될 것이라 판단된다. 또한 본 연구에서 구축한 DNN 모형의 입력자료 중 기상(연증발산량, 연강수량) 변수에 기후변화 시나리오를 적용한다면 미계측 유역의 미래 하천 수량 확보 연구에 큰 도움이 될 것이라 판단된다.