1. 서 론
2. 연구방법
2.1 침수 위험도 평가 방법
2.2 지하역사 모형 수치모의 및 검증
3. 침수흐름 해석 결과 및 대피 위험도 평가
3.1 침수 흐름 시뮬레이션 결과
3.2 침수 흐름 대피 시 사고 발생 유형 분포 비교
3.3 침수 흐름 대피 위험도 평가 방법 비교
4. 결 론
1. 서 론
기후변화와 도시개발의 영향으로 인해 도심지 내 홍수 피해가 증가하고 있다. 도심지 내 지하공간은 쇼핑몰, 지하철 등 유용한 공간으로 활용되고 있으나, 홍수 발생 시 우수 유입에 따른 인명피해가 심각히 우려되는 공간이 된다. 특히 지하역사의 경우 유동인구가 많은 시설이므로 인명피해를 막기 위해 침수 상황에 대한 철저한 대비가 필요하다. 기후변화로 인한 강우강도 증가 및 집중 강우의 발생은 도시침수 위험도를 증가시켰으며, 빈번한 지하역사 침수 사례로 이어지고 있다. 2022년 서울, 경기도 집중호우로 인해 안양천 유역에 위치한 개봉역, 금천구청역 등과 삼성역, 이수역 등 지하시설에서 침수 피해가 발생한 바 있으며, 2023년에도 금천구청역, 역곡역 등에서 침수피해 사례가 발생했다. 지하역사의 빈번한 침수피해 발생에 따라 지하역사로 유입된 우수의 침수흐름 특성 및 침수 위험도 분석에 대한 연구가 필요한 상황이다.
홍수 시 지하공간의 침수위험을 평가하기 위한 여러 연구들이 수행된 바 있다. 홍수로 인한 침수상황 특성 상 침수흐름에 대한 실시간 계측에 한계가 있기 때문에 많은 연구들이 2차원 침수흐름 해석결과에 기반한 침수 위험도 분석 연구를 수행했다. Ishigaki et al. (2010)은 2차원 시뮬레이션을 통해 지하역사로 이어진 계단에 우수가 유입될 때 안전한 대피 경로를 제안한 바 있다. Nakasaka and Ishigaki (2021)은 2차원 침수흐름 해석 시뮬레이션 결과로부터 대형 지하쇼핑몰의 보행 위험구간을 판별하였으며, 이 결과를 바탕으로 대피 안전 경로를 제시했다. Shin et al. (2021)은 다층 구조로 이뤄진 지하공간에서 침수흐름 해석을 위한 2차원 흐름해석 모형을 개발하였으며, 침수방지 시설의 설치효과에 대해 검증했다. 시뮬레이션 외에도 실규모 실험을 통해 침수공간 대피 위험도 평가 연구가 이뤄진 바 있다. Shao (2010)은 강우강도와 지하공간 침수심과의 관계를 해석해로 제시하여 지하공간 설계 기준을 제시했다. 이후 Joo and Kim (2015)은 다양한 침수상황을 가정한 대피 모의실험을 수행하였으며, 지하공간으로 이어지는 계단에 대한 대피 안전기준을 제시했다.
침수 흐름 발생 시 대피 위험구간을 판단하기 위해서는 적절한 위험도 평가 기준을 적용할 필요가 있다. 침수 위험도 평가 기준은 침수공간에 대한 대피 안전성을 판단하기 위해 필요하기 때문에 인체의 보행 안정성에 근거한 침수 위험도 평가 기준을 개발해왔다. Jonkman and Penning-Rowsell (2008)은 침수흐름에 대한 인체의 모멘트 안정성과 마찰 안정성에 대한 실험결과로부터 안전한 대피가 가능한 침수심 및 유속 범위를 제시한 바 있다. Xia et al. (2014)는 인체에 작용하는 외력을 분석하여 침수흐름에 의한 인체의 보행 안정성을 판단할 수 있는 한계유속 계산식을 제시했다. 인체 안정성을 고려한 평가 기준 외에도 침수흐름으로 인해 발생하는 유속과 침수심을 통해 침수 위험도를 평가할 수 있는 기준이 제시된 바 있다. DEFRA and EA (2006)에서는 침수심과 유속을 이용한 경험식을 통해 4단계의 침수 위험도 평가 기준을 제시했다. Kreibich et al. (2009)는 침수흐름이 갖는 외력 계산식을 제시하였으며 이를 이용한 3단계 침수 위험도 평가 기준을 제안했다. Ishigaki et al. (2010)은 침수흐름에 의해 발생하는 한계비력(specific force)을 제안하였으며, 안전한 대피가 가능한 한계비력 기준을 제시했다. 기존 연구에서 제시한 침수 위험도 평가 방법의 선택에 따라 침수 위험도 판단 결과에 차이가 발생할 수 있으므로 어떤 침수 위험도 평가 방법의 선택이 적절한지 판단할 필요가 있다. 또는 여러 침수 위험도 평가 방법을 함께 적용하여 침수 위험도에 대한 종합적 판단이 이뤄질 필요가 있다.
본 연구에서는 지하역사 침수 시 인명 대피 경로 설정에 필요한 5가지의 침수 위험도 평가 기법을 적용하고 평가 결과에 대해 비교했다. 이를 위해 단순 지하역사 형상에 대해 준 3차원 침수흐름 해석 시뮬레이션을 수행하였으며, 이를 통해 다음의 분석을 수행하였다. (1) 우수 유입 위치 및 유입 유량 변화에 따른 침수 흐름 분석; (2) 침수 위험도 평가 방법 별 지하역사 침수위험 판단 영역 분석 및 비교; (3) 침수 위험도 평가 방법에 기초한 침수 위험도 증가 요인 분석. 이러한 분석 결과로부터 다양한 침수 위험도 평가 방법에 따른 보행 위험구간 판단 영역의 차이를 비교했고, 5가지의 침수 위험도 평가 방법을 종합적으로 고려한 보행 위험 조건에 대해 제시했다. 이를 통해 지하철 역사에서 발생할 수 있는 우수유입지점 수, 우수유입량 변화가 보행 위험도에 미치는 영향을 분석했다.
2. 연구방법
2.1 침수 위험도 평가 방법
지하공간 침수 시 침수흐름에 의한 대피 안전도 평가를 위해 Ishigaki et al. (2010)은 단위 폭 당 한계비력(specific force, M0)을 대피 안전도 평가지표로서 제안했다. 한계비력은 동수압과 정수압의 합으로써 다음 식과 같이 계산한다.
여기서 U는 수심평균 유속, h는 침수심, g는 중력가속도이다. Ishigaki et al. (2010)은 안전한 대피가 가능한 한계비력 범위를 제안하였으며, 성인 남성의 경우 M0 < 0.125 m2, 노년층 남성인 경우 M0 < 0.1 m2, 노년층 여성의 경우 M0 < 0.08 m2 일 때 안전한 대피가 가능한 것으로 제안했다.
인체의 보행 안정성 측면에서 침수 위험도를 평가할 수 있다. 침수 흐름 속에서 인체에는 마찰력, 항력, 중력, 부력, 수직항력이 작용한다. 침수흐름에 의한 5가지 힘은 인체의 보행 안정성에 영향을 미치며, 마찰력에 의한 미끄러짐(sliding) 안정성과 모멘트에 따른 전도(toppling) 안정성을 고려한 침수 위험 분석방법으로 구분할 수 있다(Xia et al., 2014). 미끄러짐 사고는 침수흐름에 의해 발생하는 항력이 인체의 바닥 마찰력보다 큰 경우 발생하며, 전도 사고는 항력에 의한 모멘트가 체중에 의한 모멘트보다 큰 경우 발생한다(Jonkman and Penning-Rowsell, 2008). Xia et al. (2014)은 인체 모형을 이용한 실험을 통해 미끄러짐(sliding) 및 전도(toppling) 사고가 발생할 수 있는 한계 유속(Uc) 계산식을 개발했다. Eqs. (2) and (3)은 각각 미끄러짐과 전도 사고 발생 한계 유속 계산식이다.
여기서 hp와 mp는 각각 대상의 키와 몸무게이고, 𝜌는 물의 밀도이다. 한계유속 계산결과보다 침수흐름의 유속이 큰 경우 미끄러짐 또는 전도 사고가 발생할 우려가 있다.
침수 위험도에 대한 세부적 분류를 위해 많은 연구에서 침수흐름에 의한 운동량(momentum) 계산결과를 기준으로 세분화된 평가 기준을 제시한 바 있다. DEFRA and EA (2006)은 침수심과 유속을 통해 다음 식과 같은 침수 위험도(Flood Hazard Degree, FD) 계산식을 제시했다.
FD를 이용한 침수 위험도 평가 방법은 4단계로 분류되며, FD ≤ 0.75인 경우 “Low”, 0.75 < FD ≤ 1.25인 경우 “Moderate”, 1.25 < FD ≤ 2.0인 경우 “Significant”, 2.0 < FD인 경우 “Extreme”으로 분류한다. Kreibich et al. (2009)은 침수흐름 강도(Flood Intensity Factor, FIF)를 제안하여 침수 위험도를 분석했다.
FIF를 이용한 침수 위험도 평가 방법은 3단계로 분류되며, FIF ≤ 0.5인 경우 “Attention”, 0.5 < FIF ≤ 1.5인 경우 “Alert”, 1.5 < FIF인 경우 “Serious”로 판단한다.
2.2 지하역사 모형 수치모의 및 검증
본 연구에서는 준3차원 수리동역학모형 EFDC (Environmental Fluid Dynamics Code)를 이용하여 지하역사 내 침수흐름 시뮬레이션을 수행했다. EFDC의 동수역학모형은 Reynolds averaged Navier-Stokes equation (RANS)를 지배방정식으로 하며, 연직 방향의 운동량 방정식은 정수압을 가정하여 해석한다. EFDC는 난류폐쇄기법으로써 Smagorinsky 모형과 Mellor-Yamada 모형을 이용하며, 각각 수평 동점성계수와 연직 동점성계수를 산정한다(Hamrick, 1992). EFDC 모형은 연직방향 흐름 가속이 중요한 계단영역에 적용하는 것에 한계가 있으나, 침수흐름 전파 해석을 위한 마름/젖음 기능, 우수유출부에서 수위변동에 따른 유출량 계산이 가능한 수위-유량 곡선 경계조건 적용이 용이하여 본 연구의 침수흐름 해석 시뮬레이션에 활용하였다. 모형의 한계를 고려하여 본 연구에서는 계단을 통해 유입되는 우수흐름의 영향이 비교적 크지 않은 1개 층으로 구성된 지하역사 모형을 대상으로 침수흐름 시뮬레이션을 수행하였다.
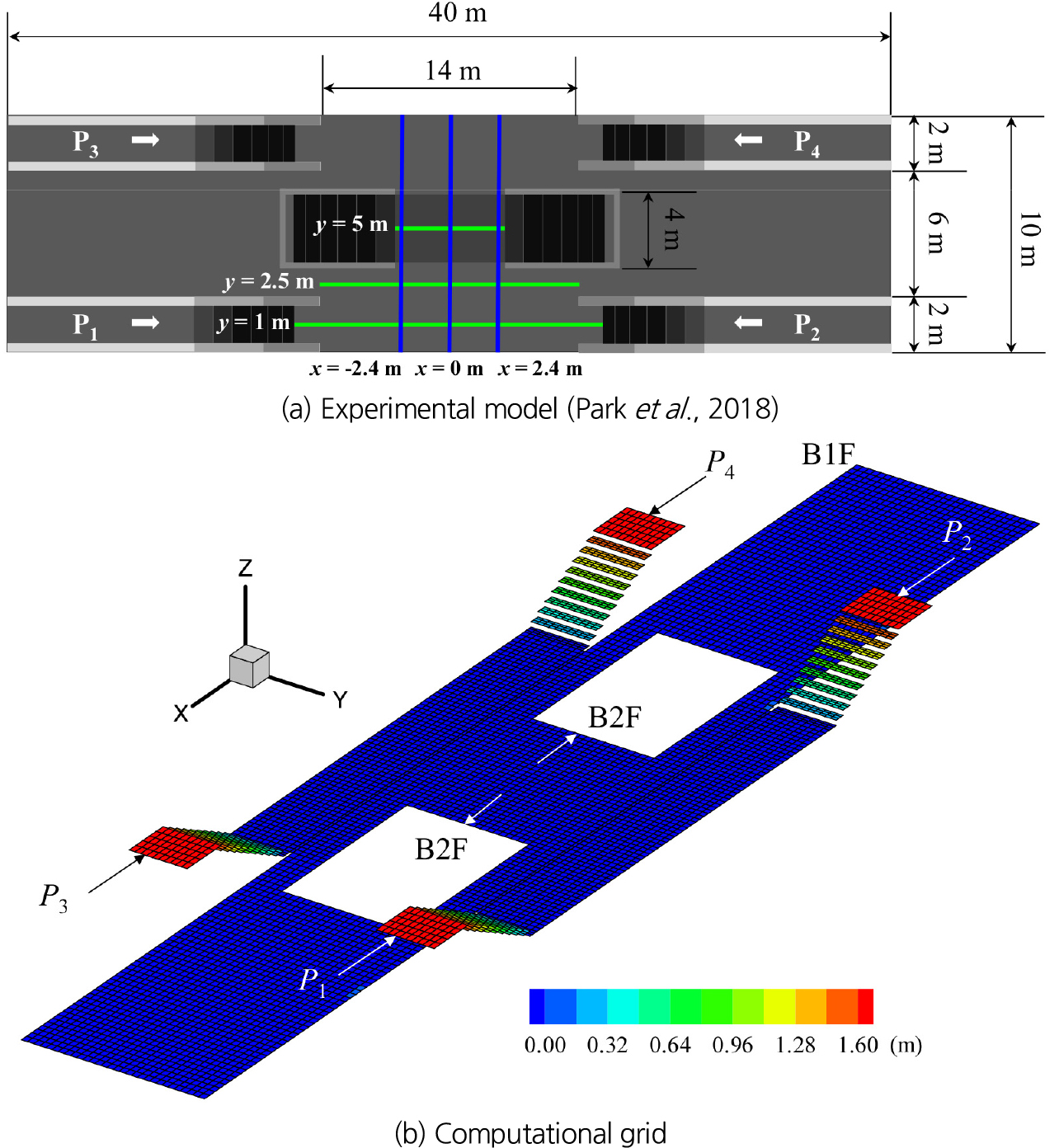
침수 취약성 분석을 위한 지하철 역사의 형상은 Park et al. (2018)에서 제시한 길이 40 m, 폭 10 m의 단순 지하철 형상을 이용했다(Fig. 1(a)). 수치모의 대상 영역은 지상과 연결된 지하1층(B1F)에 해당하는 구간이며, B1F로 향하는 계단 4개소, 지하2층(B2F)으로 연결되는 계단 2개소가 위치해있다. Park et al. (2018)은 1/20 축척의 실험모형을 제작하여 4개의 B1F 계단으로 3.78×10-4 m3/s의 유량이 유입되는 조건에 대해 실험을 수행하였으며, Fig. 1(a)의 y = 1 m, 2.5 m, 5 m 지점에서 digital point gauge (KENEK PH-340)를 이용하여 침수심을 측정했다. 실험에 사용된 유량은 80 mm/hr의 강우 발생 시 사당역으로 유입되는 유량 0.68 m3/s을 Froude 상사에 따라 변환한 유량이다. 수치모의 수행 및 검증을 위해서 실제 규모의 지하철 형상에 0.68 m3/s의 유량이 4개의 B1F 계단으로 유입되는 조건을 이용했다. 수치 모의를 위한 계산격자는 Fig. 1(b)와 같다. 수치모의를 위한 계산조건으로 time step은 Courant- Friedrichs-Lewy (CFL) condition을 만족시키기 위해 0.1 sec로 설정했고 수평 동점성계수 계산을 위한 Smagorinsky constant는 0.2를 적용했다.
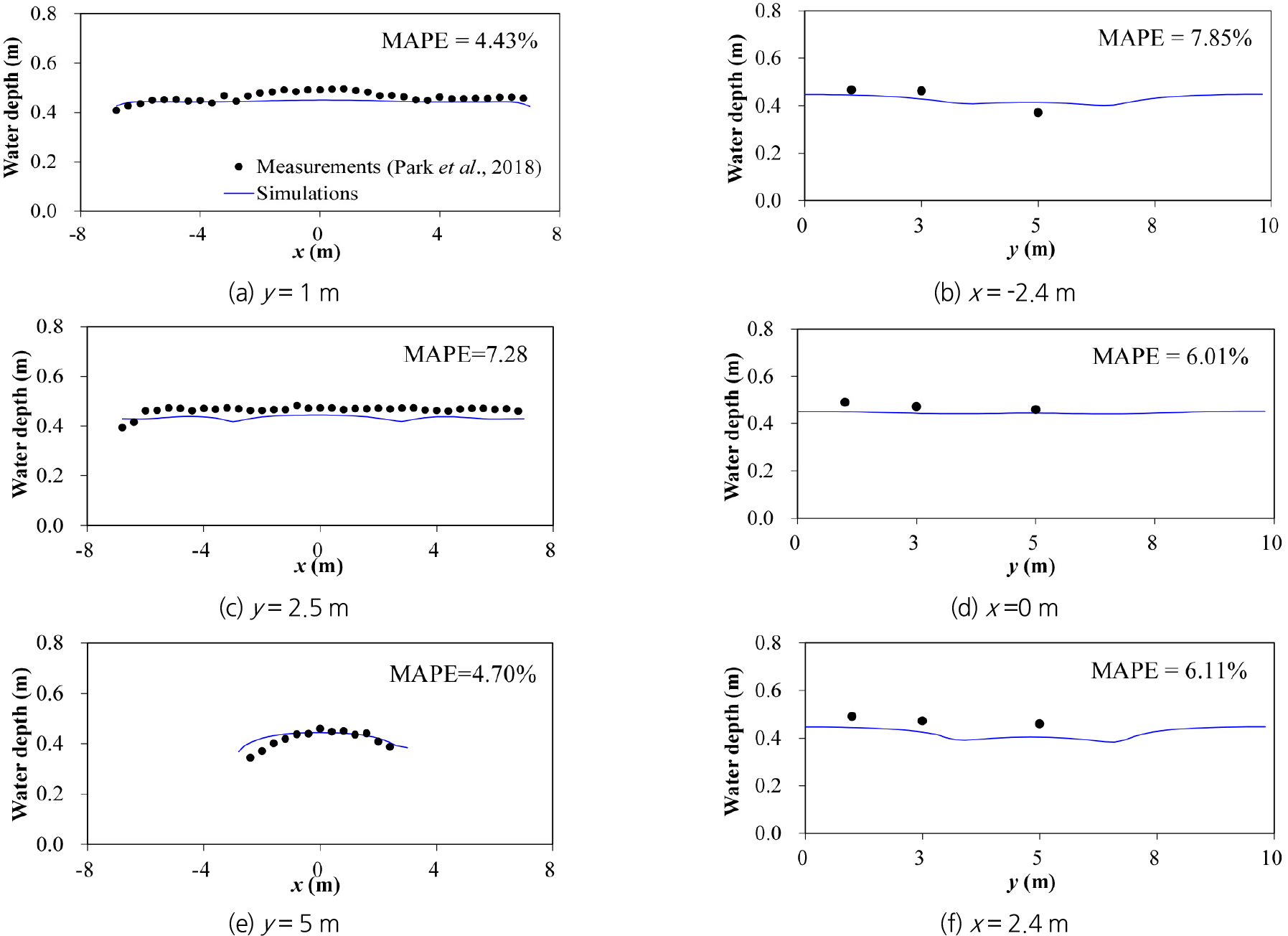
상술한 Park et al. (2018)의 실험과 동일한 조건의 시뮬레이션 결과로부터 침수심의 x축, y축 방향 변화를 비교했다. 침수심 비교를 위해 실험측정 결과를 길이축척(1/20)을 고려하여 실제 규모의 침수심으로 변환하여 비교했다. 침수심 비교 지점은 Fig. 1(a)에 나타낸 x축을 따른 3개 측선(y = 1 m, 2.5 m, 5 m)과 y축을 따른 3개 지점(x = -2.4 m, 0 m, 2.4 m)이다. Fig. 2는 준3차원 시뮬레이션을 위해 연직 방향 Layer 수는 10개로 설정하여 모의한 결과이다. y = 1 m 지점은 우수가 유입되는 계단에 해당하는 측선이고, y = 2.5 m 지점은 지하역사와 B2F로 향하는 계단 사이 복도에 위치한 측선, y = 5 m 지점은 B2F로 향하는 계단이 위치한 측선이다. 세 측선에서 침수심 시뮬레이션 결과가 모두 10% 미만의 오차를 나타냈으며, 평균오차(Mean Absolute Percentage Error, MAPE)는 5.47%로 나타났다. y축을 따르는 3개 측점에서 수심을 비교한 결과 평균오차가 6.66%로 계산되어 마찬가지로 10% 미만의 오차를 보였다. EFDC의 동수역학 모듈은 연직 방향의 운동량 방정식을 정수압을 가정하여 해석하기 때문에 정수압 흐름 가정이 성립하지 않는 계단에서의 자유낙하 흐름 재현에 한계가 있다. 하지만 침수 흐름 내 대피 취약성 분석을 위해 수심 평균 유속과 침수심을 활용하기 때문에 평균 10% 미만의 오차를 갖는 시뮬레이션 결과를 적용할 수 있을 것으로 판단된다. 특히 B1F 계단을 통해 발생하는 침수흐름에 대한 침수심 비교 결과(Fig. 2(a))에서 4.43%의 오차가 발생했으므로 계단 흐름 시뮬레이션 결과가 갖는 오차가 침수심 계산 결과에 큰 영향을 주지 않았음을 보여준다.
준 3차원 흐름해석을 위해 연직 Layer 수의 적절한 결정이 필요하다. Table 1은 연직 Layer 수의 변화에 따라 x축을 따른 3개 측선(y = 1 m, 2.5 m, 5 m)의 수심 모의 결과 오차를 비교한 결과이다. Layer 수가 5개에서 10개로 증가했을 때 오차의 감소폭이 크게 나타났으나, Layer 수가 10개 이상인 경우 4.40% ~5.47%로 나타나 오차 감소 폭이 크지 않았다. 과거 연구에서 EFDC를 이용한 준3차원 시뮬레이션을 위해 Layer의 수를 10개 이상으로 결정한 바 있으며(Liu and Garcia, 2008; Shin et al., 2021), Layer수의 증가에 따라 계산 시간이 증가하기 때문에 본 연구에서는 연직 Layer 수를 10개로 하여 시뮬레이션을 수행했다.
Table 1.
Mean absolute percentage errors (MAPE) with change of the number of vertical layers
| Sec. | Number of layers | |||
| 5 | 10 | 20 | 50 | |
| A | 6.63% | 4.43% | 3.35% | 5.39% |
| B | 9.67% | 7.28% | 4.55% | 3.01% |
| C | 4.63% | 4.70% | 5.30% | 6.84% |
| Average | 6.98% | 5.47% | 4.40% | 5.08% |
Fig. 2에 제시한 시뮬레이션 결과 검증 수치모의조건(∆t = 0.1 sec, Layer 수 = 10, Smagorinsky coefficient = 0.2)을 이용하여 지하역사 침수 상황에 대한 시뮬레이션을 수행하였으며, 우수 유입 지점과 유입유량(Q)에 따라 Table 2와 같은 수치모의 조건을 설정했다. 유입 유량은 지상 계단을 통해 유입되는 우수의 월류심을 0.3, 0.4, 0.5 m로 가정하여 다음 식과 같은 자유낙하 흐름을 가정한 위어 공식을 통해 결정했다(Nakasaka and Ishigaki, 2021).
여기서 Cd는 유량계수이고, H는 지상계단을 통해 유입되는 우수의 월류 수심이다. Eq. (6)의 계산을 위한 유량계수, Cd는 도로에서 지하공간으로 유입되는 우수의 유량을 계산하기 위해 Nakasaka and Ishigaki (2021)이 제시한 0.85를 이용했다. 시뮬레이션 조건 중 최대 월류심인 0.5 m는 성인 무릎높이에 해당한다(Seong et al., 2019). 유입된 우수는 B1F 복도를 통해 B2F 계단으로 유출되며, 유출지점의 경계조건은 Eq. (6)를 이용한 수위-유량 곡선을 통해 계산된 월류 유량으로 설정했다. 그리고 B1F로 향하는 4개의 계단에서 우수 유입 발생 가능 조건을 고려하여 각 유량 별 6개의 유입 조건을 결정했다.
Table 2.
Simulation conditions for subway station inundation
3. 침수흐름 해석 결과 및 대피 위험도 평가
3.1 침수 흐름 시뮬레이션 결과
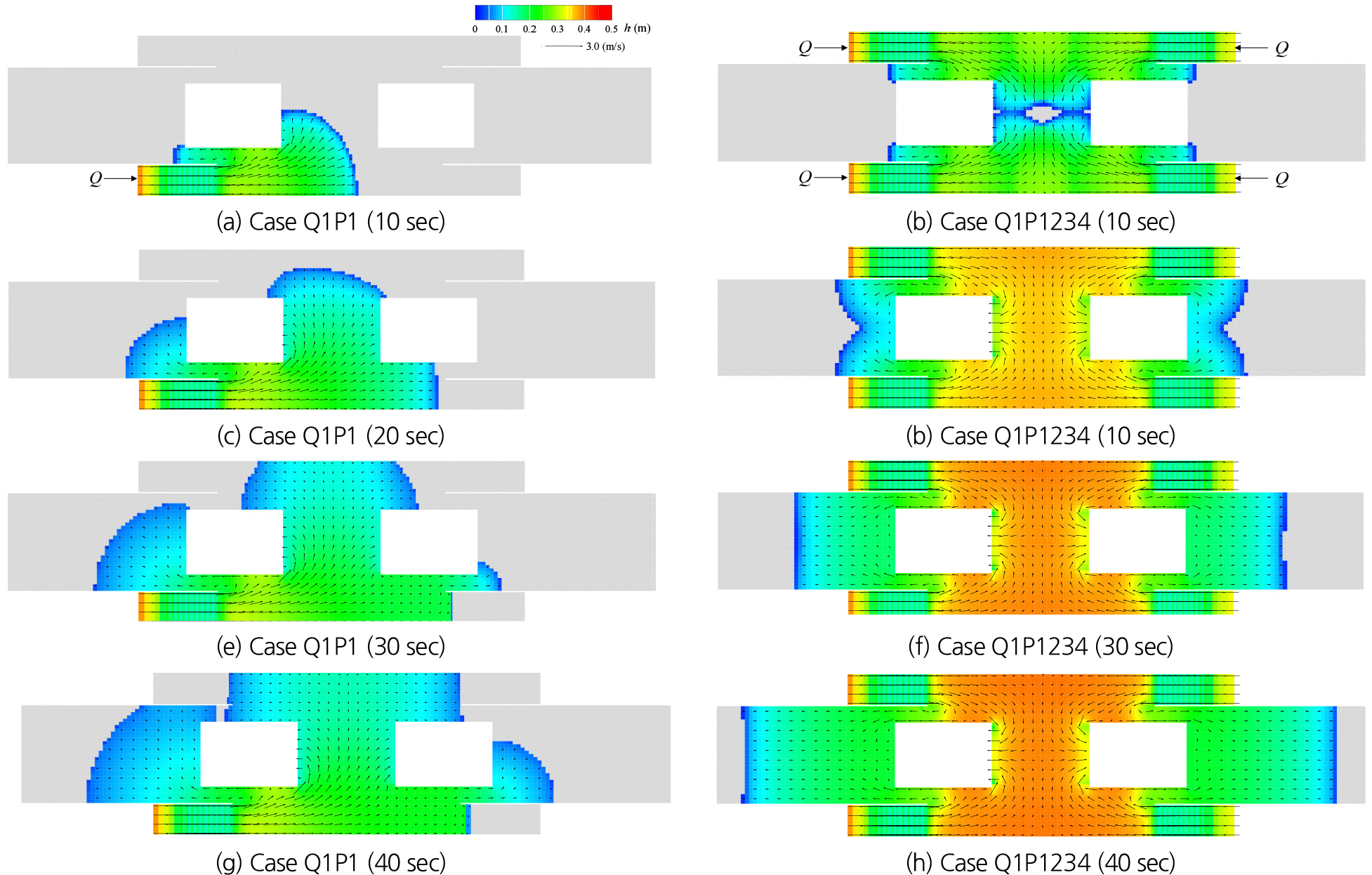
Fig. 3는 우수 유입 조건에 따른 침수 흐름의 시간변화를 보여주며, 침수심과 유속 벡터를 나타낸다. Case Q1P1은 P1 계단에서 0.3 m의 월류 수심으로 P1 입구를 통해 우수가 유입되는 Case이며, Case Q1P1234는 같은 유량으로 모든 계단에서 우수가 유입되는 상황을 모의한 결과이다. Case Q1P1에서는 우수 유입 10 sec 후 좌측 B2F 계단으로 우수가 유입되며, 20 sec 후에는 우측 B2F 계단으로도 우수 유입이 진행됐다. 40 sec 이후에는 중앙 통로가 모두 침수됐고, 우측보다 좌측 통로의 더 많은 영역이 침수됐다. Case Q1P1234의 경우에는 Case Q1P1보다 더 빠른 속도로 침수가 진행됐다. 우수 유입 10 sec 이후에 중앙 통로 대부분이 침수됐고 이후 지속적으로 침수심이 상승한 후 정상상태에 도달하는 결과를 나타냈다. 우수 유입 지점 수가 4개로 증가함에 따라 침수 흐름이 빠른 속도로 전파됨을 확인할 수 있으며 B2F가 위치한 중앙 통로를 중심으로 침수심이 빠르게 증가함을 확인할 수 있다. 또한 우수흐름의 선단에서 낮은 침수심을 나타내는 Case Q1P1과 달리 Case Q1P1234에서는 각 계단을 통해 유입된 우수 흐름이 서로 충돌하여 국부적으로 침수심이 상승하는 결과를 나타냈다.
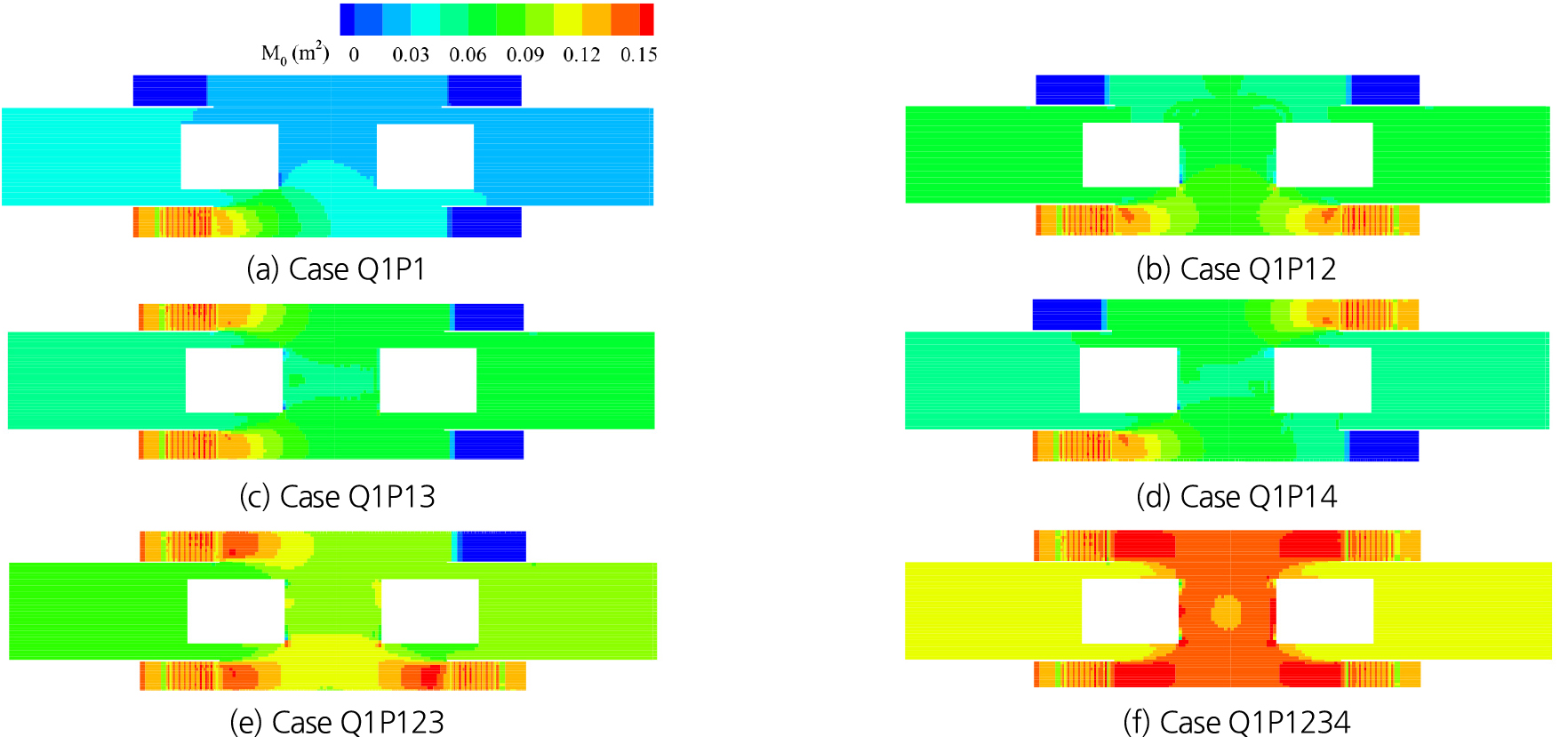
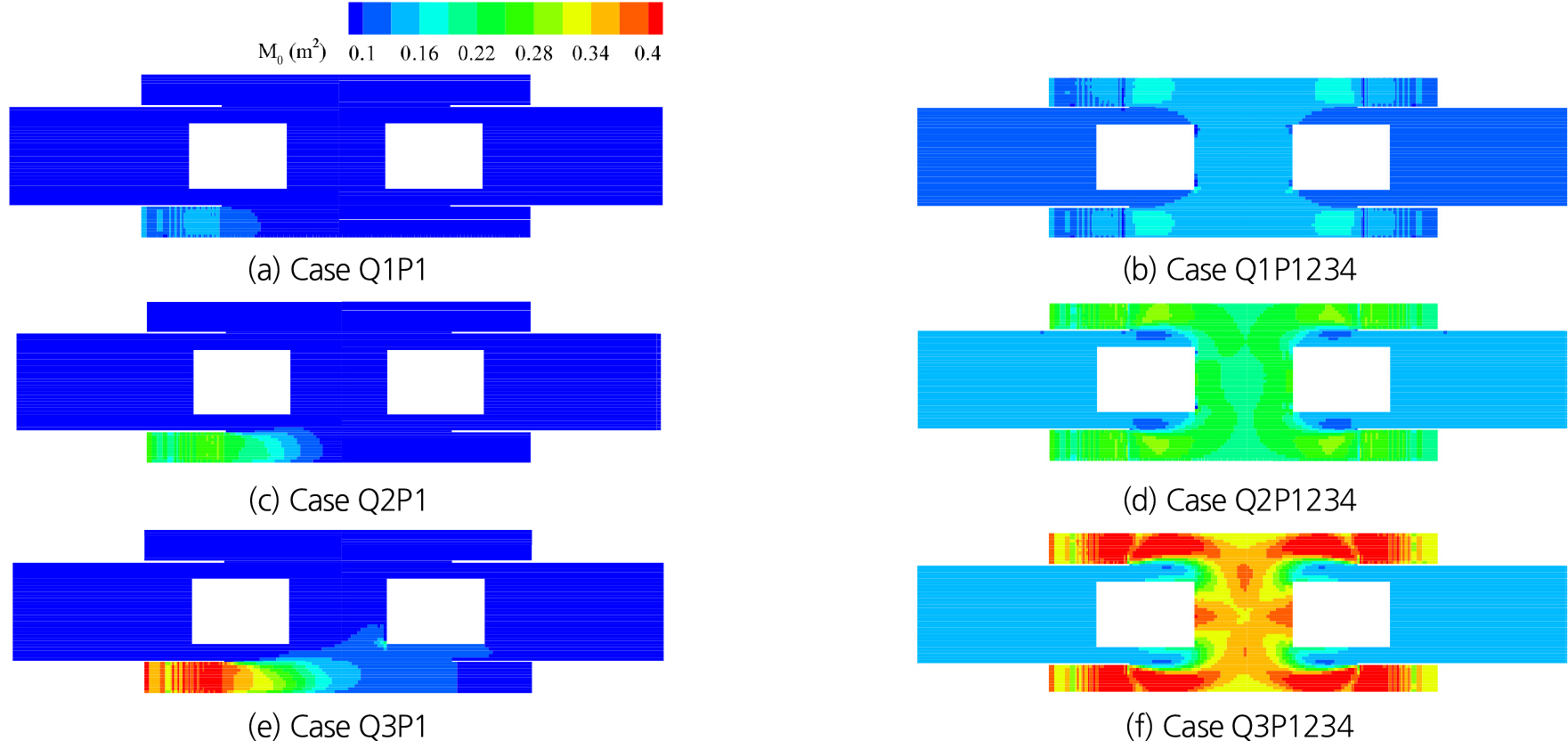
우수 유입 지점 수의 변화가 침수 흐름에 미치는 영향을 분석하기 위해 Q1 유량조건에서 우수유입 지점 변화에 따른 한계비력(M0, Eq. (1)) 분포의 변화를 비교했다. Fig. 4는 침수흐름이 정상상태(steady state)에 도달한 이후 침수심과 유속을 이용하여 M0를 계산한 결과이다. 모든 모의조건에 대해 침수계단과 연결된 복도에서 다른 영역에 비해 높은 한계비력이 나타냈다. 우수가 1개 계단으로만 유입되는 Case Q1P1의 경우 우수유입 지점 주변에서는 M0 > 0.07 m2로 높은 한계비력을 나타냈지만 대부분의 영역에서 M0 < 0.04 m2으로 상대적으로 낮은 한계비력이 나타났다. 우수가 2개 지점에서 유입되는 경우에는 대부분의 영역에서 M0 > 0.07 m2로 나타나, Case Q1P1 보다 한계비력이 더 상승된 결과를 나타냈다. 노년층 여성의 경우 M0 < 0.08 m2인 조건에서 안전한 대피가 가능하므로 (Nakasaka and Ishigaki, 2021) 우수 유입 지점이 2개 이상인 경우 노년층 여성의 대피에 어려움을 겪을 수 있음을 보여준다. Case Q1P1234에서는 중앙통로와 B1F 계단으로 이어지는 모든 영역에서 M0 > 0.125 m2로 나타나 모든 연령층에서 대피에 어려움을 겪을 가능성이 있는 것으로 나타났다.
Fig. 5는 유입 유량의 변화에 따른 한계비력의 분포를 비교한 결과이다. 우수 유입량이 증가함에 따라 한계비력이 증가하며, 1개 지점에서 우수가 유입할 때 보다 4개 지점에서 유입되는 경우 더 많은 영역에서 한계비력이 증가했다. P1에서만 우수가 유입되는 경우 모든 유량 조건에서 침수계단의 M0 > 0.08 m2으로 나타났다. 월류심 0.5 m에 해당하는 우수 유입 조건(Case Q3P1)에서는 침수계단을 지나 우측 복도 영역까지 M0 > 0.08 m2으로 나타나 노년층 여성의 대피 위험지역이 증가했다. Case Q3P1에서 최대 침수심은 0.52 m로 나타났으나, 우수가 4개 지점에서 유입되는 Case Q3P1234에서는 0.82 m까지 증가하여 성인 엉덩이 높이(0.85 m; Seong et al., 2019)까지 침수심이 상승했다. 이에 따라 Case Q3P1234에서는 대부분의 영역에서 M0 > 0.125 m2로 나타나 전 연령층에서 대피에 어려움을 겪을 것으로 예상된다.
3.2 침수 흐름 대피 시 사고 발생 유형 분포 비교
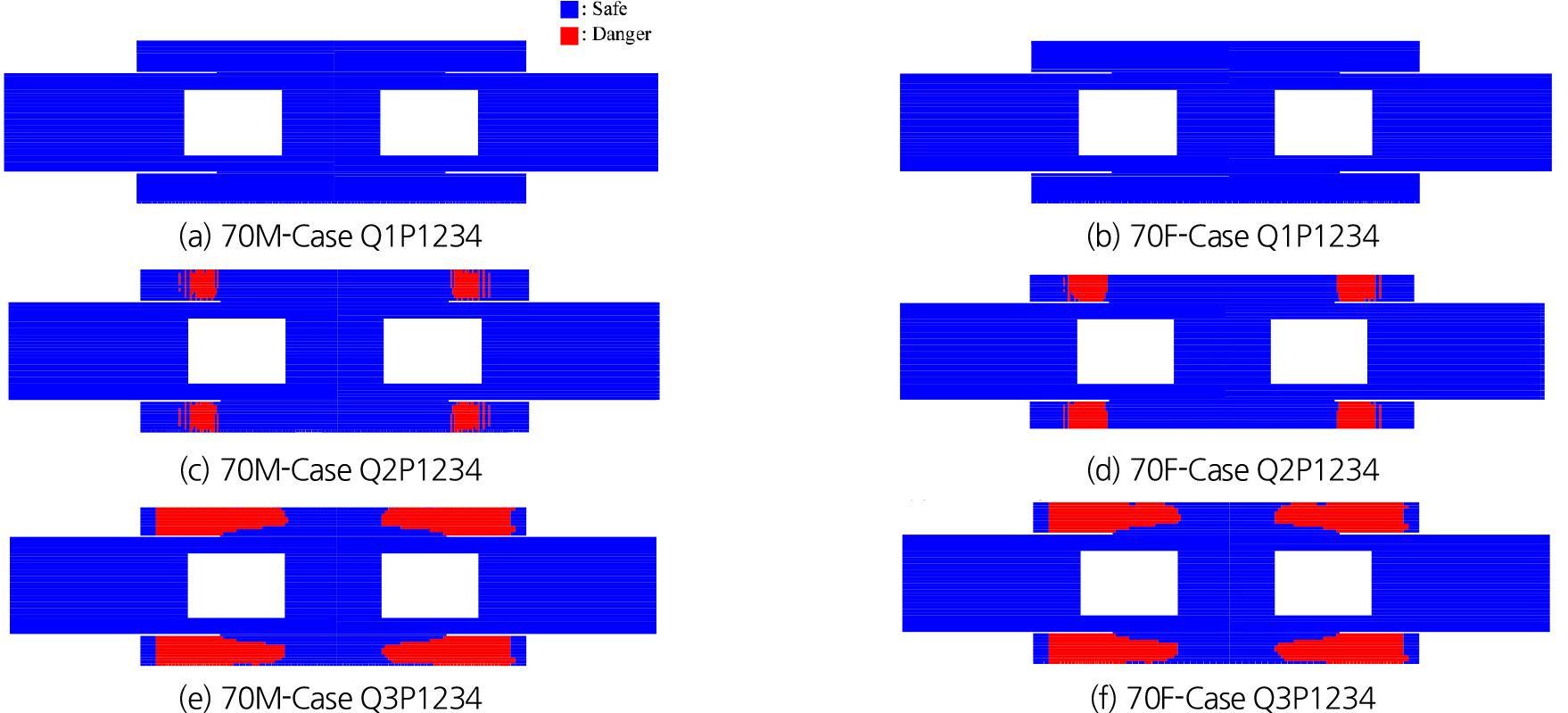
침수공간 대피 시 취약 연령대로 판단되는 70대 남성 및 여성의 표준체형을 적용하여 미끄러짐(sliding) (Eq. (2)) 및 전도(toppling) (Eq. (3)) 사고 발생 가능성이 있는 영역을 분석했다. 국민건강보험공단 통계자료(NHIS, 2019)로부터 70대 남성의 평균 키 165.5 cm, 몸무게 66.5 kg, 70대 여성 평균 키 152.3 cm, 몸무게 57.3 kg을 적용하여 미끄러짐 및 전도 사고 발생 우려가 있는 한계유속을 계산했다. 그리고 4개의 B1F 계단에서 모두 우수가 유입되는 상황에 대한 시뮬레이션 결과로부터 미끄러짐 및 전도 사고 발생 우려 영역을 구분했다. Fig. 6는 미끄러짐 사고 발생 가능 지점을 유입 유량 변화에 따라 비교한 결과이며, 70M은 70대 남성, 70F는 70대 여성을 의미한다. Q1 유량조건에 대해 70대 남성 및 여성 모두 미끄러짐 사고가 발생할 수 있는 유속이 나타나지 않았다. 따라서 Case Q1P1234와 같이 월류심이 30 cm인 우수 유입 상황에 대해 미끄러짐 사고 발생 가능성이 낮은 것으로 나타났다. Q2와 Q3 유량조건에서는 침수계단에서 미끄러짐 사고가 발생할 수 있는 것으로 나타났다. Q3 유량조건에서는 침수 계단을 포함하여 계단이 위치한 복도에서도 미끄러짐 사고가 발생할 수 있다는 것을 보여준다. 70대 남성의 미끄러짐 사고 발생 가능 영역이 70대 여성보다 다소 작게 계산되어 70대 여성이 남성보다 다소 미끄러짐 사고에 취약할 수 있음을 알 수 있다.
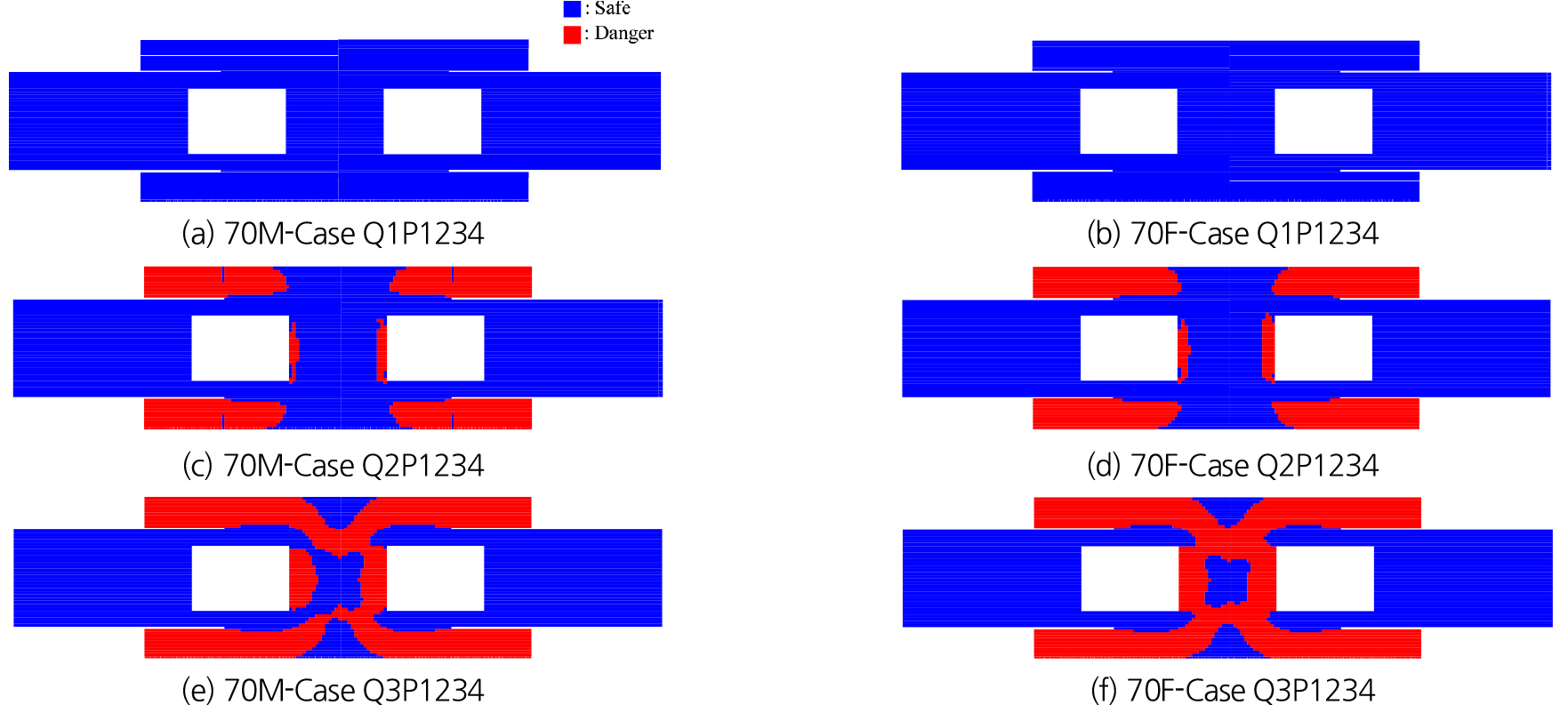
Fig. 7은 전도 사고 발생 가능 영역을 비교한 그림이다. Case Q1P1234의 경우 미끄러짐 사고와 마찬가지로 전도 사고 발생 가능성 또한 낮은 것으로 나타났다. Q2와 Q3 유량조건에서는 미끄러짐 사고보다 전도 사고 발생 가능 영역이 더 넓게 분포하고 있다. Q2 유량 조건에서는 B1F계단과 B2F계단의 근처에서 주로 전도 사고 발생 가능성이 높게 나타났다. Q3 유량 조건에서는 중앙 통로에서도 전도 사고 발생 우려가 있는 것으로 계산됐다. 전도 사고 발생 가능 영역 또한 70대 남성이 70대 여성보다 더 작게 계산되어 미끄러짐 사고와 전도 사고 모두 70대 여성이 취약한 것으로 나타났다.
한계비력은 한계유속을 이용한 대피 안전 구간 판단 방법에 비해 보수적 판단을 내릴 수 있다. 한계비력 기준으로는 Case Q1P1234에 대해 중앙통로와 침수계단에서 M0 > 0.125 m2으로 나타나 대피에 어려움이 발생할 것으로 판단할 수 있는 반면(Fig. 4(f)), 미끄러짐과 전도 사고 발생 기준으로는 대피에 안전한 것으로 판단할 수 있다. 또한 Q2와 Q3 유량조건에서도 한계비력을 이용한 판단 기준이 미끄러짐 및 전도 사고 발생 기준에 비해 더 넓은 영역을 대피 위험 지역으로 판단했다. 한계비력은 사고 발생 여부 외에도 침수 흐름에 대해 대피에 어려움을 겪을 수 있는 기준을 제시하여 더 넓은 지역을 대피 위험 구간으로 판단할 가능성이 있다. 반면, 미끄러짐 및 전도 사고 발생 한계 유속의 경우에는 침수 흐름이 인체에 작용하는 외력을 고려하여, 인체가 넘어질 수 있는 조건을 제시하기 때문에 더 극한의 상황을 판단하는 기준이라 할 수 있다.
3.3 침수 흐름 대피 위험도 평가 방법 비교
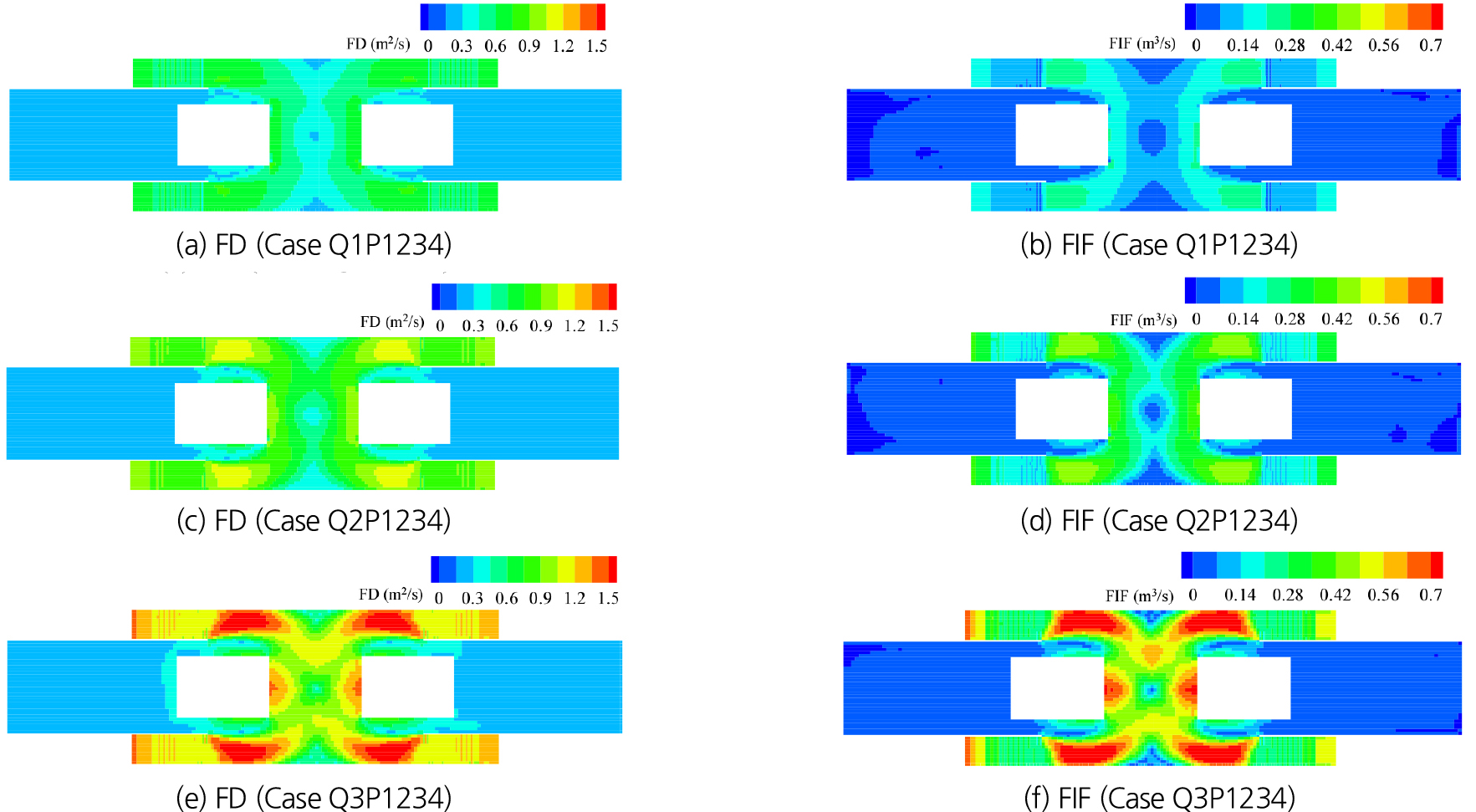
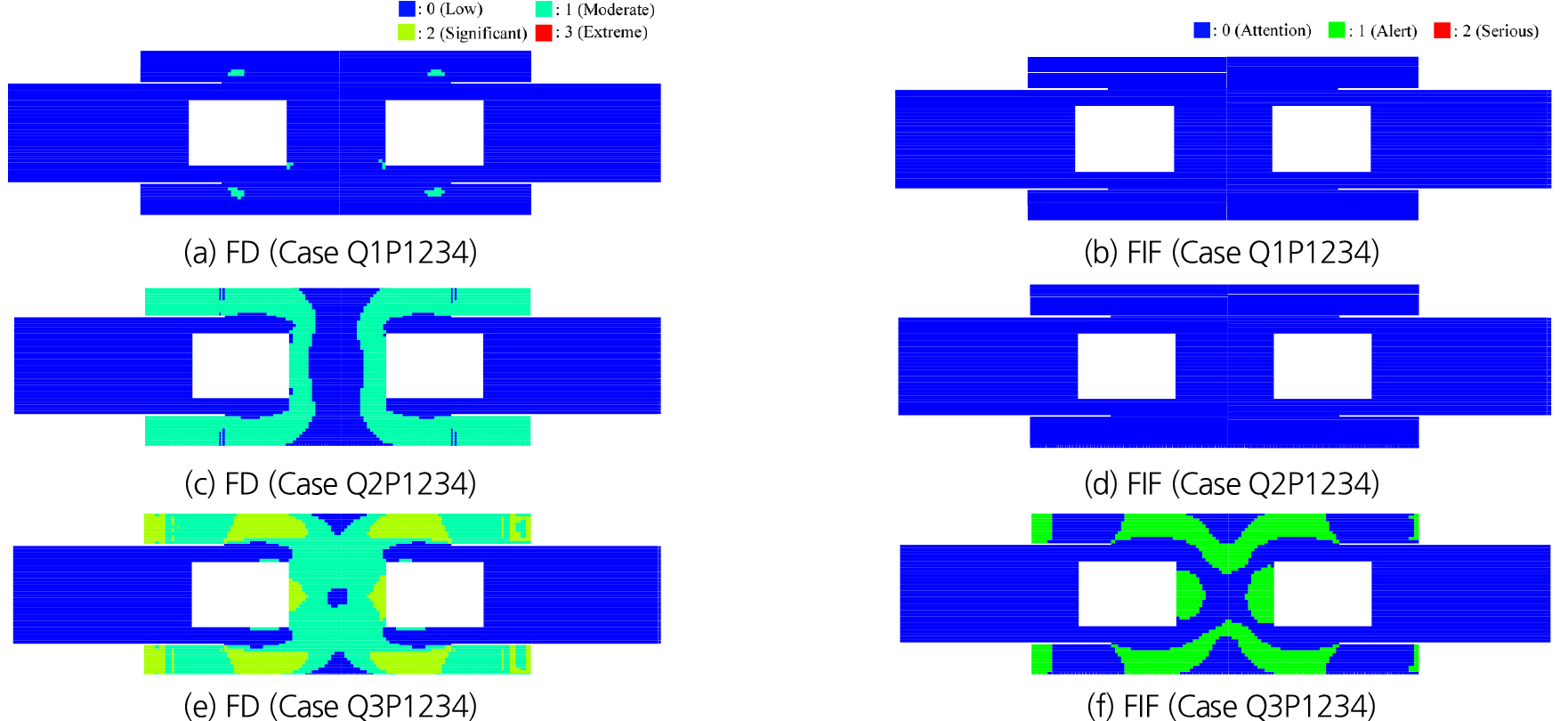
지하 공간 침수 위험도 평가 지표, FD (Eq. (4))와 FIF (Eq. (5))를 이용하여 모든 B1F 계단에서 침수가 발생하는 상황에 대한 침수 위험도를 분석했다. Fig. 8은 유량 변화에 따른 FD와 FIF 계산결과를 비교한 그림이다. 유량 증가에 따라 침수 위험도가 상승하는 결과가 나타났으며, 침수 계단 인접 복도와 중앙통로, B2F 계단 근처에서 높은 FD와 FIF 값이 나타났다. 특히 FD와 FIF 모두 침수계단 아래에서 가장 높은 값을 나타내어 주요 대피 경로에 해당하는 B1F 계단에서 가장 위험도가 크다는 결과를 보였다. 이는 한계비력과 전도 사고 발생 한계유속 계산결과와 유사한 결과를 도출하고 있음을 보여준다.
Fig. 9은 Fig. 8의 FD, FIF 계산결과로부터 위험도 평가 지표에 따라 모의영역의 대피 위험도를 나타낸 결과이다. FD의 경우 계산 결과에 따라 4단계(Low, Moderate, Significant, Extreme)로 위험도를 평가하고, FIF는 3단계(Attention, Alert, Serious)로 위험도를 평가한다. FD 평가 방법에 따르면 Q1 유량 조건에서는 흐름이 급변하는 B1F 계단 연결통로 구석에서 Moderate 정도의 위험도를 나타냈고, Q2, Q3로 유입 유량이 증가함에 따라 대피 위험 영역이 증가했다. 침수계단과 중앙통로를 중심으로 Moderate 수준의 위험도를 나타냈으나, Q3 유량조건에서는 B1F 계단 하부와 B2F 계단 입구 부근에서 Significant 수준의 위험도를 나타냈다. 반면, FIF 평가 방법에 따르면 월류 수심이 0.4 m 조건에 해당하는 Q2 유량까지는 대피 위험도가 거의 없는 것으로 나타났다. 그리고 Q3 유량 조건에서 Alert 수준의 대피 위험 영역이 나타났으며, FD 평가 방법과 유사하게 B1F 하부 계단, B2F 계단으로 이어지는 동선을 따라 대피 위험 영역이 발생했다.
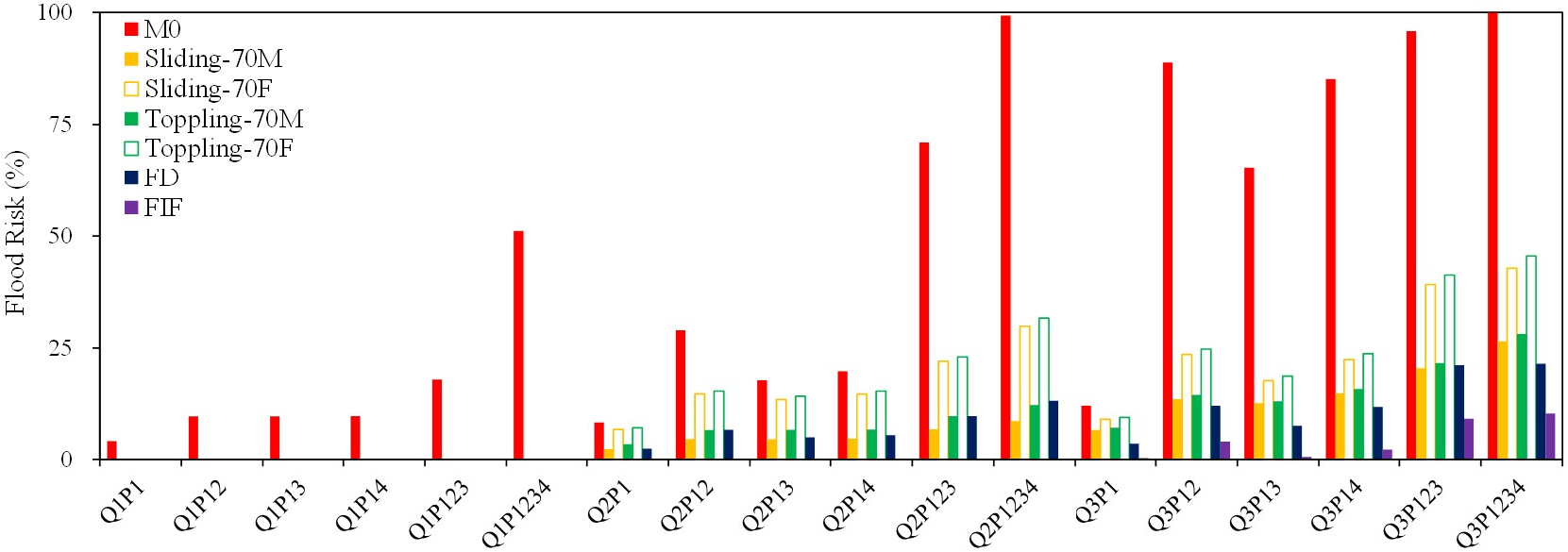
침수 위험도 평가 방법에 따라 대피 위험도 판별 결과에 차이가 있음을 확인할 수 있다. 따라서 각 침수 위험도 평가 방법에 따른 대피 위험도 비교를 위해 Fig. 10과 같이 정규화된 침수 위험도를 비교했다. 비교한 평가 방법은 한계비력, 미끄러짐 및 전도 사고 한계 유속, FD, FIF이며, 각 평가 방법에 대한 최대 위험도 대비 시뮬레이션 Case 별 침수 위험도의 비(%)를 계산하여 정규화된 값을 비교했다. 예를 들어 한계비력의 경우 M0 > 0.125 m2 발생 영역을 전체 영역으로 나눈 비를 계산했고, 미끄러짐 및 전도 사고 발생 한계유속을 초과하는 유속 발생 영역을 전체 영역으로 나눈 비를 보여준다. FD는 4단계 평가 구간을 0~3점으로 평가한 후 최대 위험도(모든 평가 영역에서 Extreme 발생 가정)로 나눈 비를 적용했고, 같은 방식으로 FIF는 3단계 평가 구간을 0~2점으로 평가한 후 최대 위험도(모든 평가 영역에서 Serious 발생 가정)로 나눈 비를 계산했다. 평가 방법 별로 비교했을 때 한계비력이 가장 많은 영역을 침수위험 구간으로 판단했다. 그리고 전도 사고 와 미끄러짐 사고, FD, FIF 평가방법 순으로 침수 위험 판단 영역이 감소했다. 또한 침수 위험도 비교 결과로부터 한계비력과 FIF가 다른 위험도 평가 지표와 비교하여 침수 위험 영역을 각각 과대, 과소산정하는 결과를 나타낼 수 있음을 보여준다.
Table 3는 18개 시뮬레이션 Case를 각 침수 위험 평가 방법에 따라 위험 영역이 큰 순으로 정렬한 결과이다. 각 평가 방법 별 위험도 순위에 따라 가장 높은 위험도를 갖는 Case를 17점, 가장 낮은 위험도를 갖는 Case를 0점으로 평가할 때, 7개의 평가 방법 별 점수를 종합하여 최종 침수 위험도 순위(Risk rank)를 결정했다. 그 결과 유입 유량이 큰 조건이 우수 유입 지점수가 많은 조건보다 대체로 높은 침수 위험도를 나타냈다. 하지만 4개 B1F 계단에서 우수가 유입되는 Case Q2P1234가 Case Q3P13과 Case Q3P1보다 높은 위험도를 나타났다. 우수 유입 지점이 2개인 경우 같은 방향으로 우수가 유입되는 Case Q3P13보다 우수 유입 방향이 서로 달라 침수 흐름이 충돌하게 되는 Case Q3P12, Case Q3P14가 더 높은 침수 위험도를 나타냈다. 따라서 지하역사 침수 상황 발생 시 우수 유입을 성인 무릎 높이 미만(0.5 m)으로 감소시킴과 동시에 침수 흐름이 서로 충돌하는 방향으로 발생하지 않도록 방수판 등 침수피해 저감 시설을 설치할 필요가 있다.
Table 3.
Evacuation risk rank according to the evaluation methods
4. 결 론
본 연구에서는 준3차원 침수흐름 시뮬레이션 결과를 이용하여 단순한 형태의 지하역사 내 침수흐름 및 침수 위험도를 분석했다. 시뮬레이션 결과로부터 우수유입량과 우수유입지점 수 변화에 따른 침수 위험도를 분석하고, 침수 위험도 평가 방법 간 차이를 비교했다. 모든 침수 위험도 평가 방법에서 침수계단과 계단 하부 복도에서 다른 영역에 비해 높은 침수 위험도가 나타나는 것으로 계산됐다. 하지만 침수 위험도 평가 방법에 따라 침수 위험 영역 판단 결과에서 차이를 나타냈다. 한계비력을 이용한 기준이 가장 넓은 영역을 침수 위험 영역으로 판단하였으며, 전도 사고, 미끄러짐 사고, FD, FIF 평가 방법 순으로 침수 위험 발생 영역이 감소하는 것으로 나타났다. 특히 한계비력과 FIF는 다른 침수 위험도 평가 방법과 비교하여 위험 판단 영역을 각각 과대, 과소 판단하는 것으로 나타났다.
침수 위험 영역은 우수유입 발생 지점 수 보다 우수유입량에 지배적 영향을 받는 것으로 나타났다. 우수유입 지점이 2개 이상일 때 우수유입량이 크면 우수유입 지점이 4개인 경우보다 더 많은 영역에서 침수위험 발생 구간이 발생할 수 있다. 또한 우수유입에 의한 침수흐름 진행 방향도 침수 위험 발생 영역 판단 결과에 영향을 미쳤다. 2개 지점에서 우수가 유입될 때 침수흐름이 동일한 방향으로 진행될 때 보다 반대방향으로 진행되어 서로 충돌하는 흐름이 발생될 때 침수 위험 구간 판단 영역이 더 커질 수 있음을 알 수 있었다. 이러한 분석 결과는 단순한 지하철 역사 모형에 기초한 결과로서 다층구조, 복잡한 구획들로 구성되어 있는 실제 지하철 역사에 적용하는 것에 한계가 있다. 하지만 본 연구 결과는 침수 위험도 평가 결과에 영향을 미치는 우수유입 조건과 다양한 평가 기준의 복합적 적용 필요성이 있음을 보여준다. 향후 연구에서는 실제 지하철 구조를 반영한 모의영역 내 침수흐름 발생 시 시민들의 대피 안전성을 분석하고자 한다. 본 연구에서 충분히 검토하지 못했던 실제 지하철 역사의 복잡한 내부 시설을 고려한 침수 위험도 분석 및 다양한 침수 위험도 평가 기준 별 시민들의 대피 안전성 평가 결과에 대해 비교하고자 한다.