1. 서 론

최근 전세계적인 기후위기로 인해 홍수 및 가뭄의 빈도와 규모가 증가하고 있으며 이에 따른 수재해 대응과 수자원 관리에 많은 어려움이 따른다(Thomas and Lopez, 2015; Cook et al., 2020; Tabari, 2020). 댐 운영은 이러한 수자원 관리의 중요한 요소이며 댐 유입량의 예측은 효율적이고 안전한 댐 운영과 관리의 필수적인 부분이다. 이러한 댐 운영을 위해서는 정확한 댐 유입량의 예측이 전제되어야 하지만 강우-유출 과정은 시·공간적 변동과 자료 간의 비선형성을 포함하고 있으며 자연계에 존재하는 모든 물리적 특성을 고려하기가 어렵다는 한계가 있다. 이는 정확한 유입량 예측을 어렵게 하는 요인이며 연 중 강수 집중 및 홍수 피해가 발생하는 홍수기(6~9월)의 선행시간 확보와 용수 확보가 필요한 이수기(10~5월)의 용수 조절 등 많은 부분에 영향을 미친다. 이러한 관점에서 댐 운영의 효율적이고 빠른 의사결정을 위해서는 보다 긴 시간의 신뢰도 높은 예측 정보를 확보하는 것이 필요하며 이를 위해서는 높은 정확도를 갖는 실시간 유입량 예측 기술이 수반되어야 한다.

일반적으로 댐 유입량의 예측은 강우-유출 관계를 고려하기 위해 물리적 모형, 통계적 모형 등 다양한 형태의 수문 모형이 활용되어 왔다(Devia et al., 2015; Mosavi et al., 2018; Sit et al., 2020). 기존에는 물리적 모델링을 기반으로 수문 시스템 내의 존재하는 여러 관계를 수학적으로 표현하고 기상 및 지형자료 등을 활용하여 유량을 예측하였다. 그러나 수많은 변수들 간의 복잡한 관계를 단순화하는 과정은 부정확성과 불확실성을 내재하고 있으며 계산 과정에서 이로 인한 오차의 누적이 발생함에 따라 예측 정확도는 감소하게 된다.

이러한 문제를 개선하기 위해 수문 분야에서는 최근 인공지능 기술을 활용한 연구가 수행되고 있다. 특히, 인공신경망(Artificial Neural Network)과 이를 기반으로 하는 딥러닝(Deep Learning)의 수문 활용에 관한 연구가 활발히 진행 중이다. 이러한 인공신경망은 수문자료에 존재하는 비선형성 등의 다양한 패턴을 찾고 이를 구현할 수 있는 기법으로 알려져 있다(Hsu et al., 1995; Yaseen et al., 2015; Kratzert et al., 2018). 비교적 적은 변수만으로도 모델링이 가능하고 실제 물리현상에 대한 복잡성을 요구하지 않으며 비선형성을 고려할 수 있다는 점을 근거로 수문분야에 대한 적용 사례는 증가하고 있다.

유량 예측에 관한 인공신경망의 수문분야 적용 연구는 1990년대부터 부각되어 현재에 이르고 있다(Kim, 2000). 국외에서는 Hsu et al. (1995)은 강우-유출 모델링에서 인공신경망이 물리적 과정을 설명하기 어려운 부분에 활용될 수 있음을 제시한 바 있다. Dawson and Wilby (1998)는 강우-유출에 대한 학습을 통해 인공신경망 모형이 유량 예측모델로써 활용될 수 있음을 제시하였다. Imrie et al. (2000)은 하천 유량 예측에 대하여 인공신경망 모형을 적용하고 성능을 개선하기 위한 방법을 제안하였다. Jain and Kumar (2007)는 시계열 분석 기법과 인공신경망을 결합한 모형을 활용하여 월단위 하천 유량 예측에 관한 연구를 수행하였으며, Toth and Brath (2007)는 학습에 필요한 충분한 자료가 확보된다면 인공신경망 모형이 실시간 유량 예측에서 활용성이 높음을 제시하였다. Chen et al. (2013)은 태풍기 홍수 예측에 대하여 인공신경망의 한 형태인 순환신경망(Recurrent Neural Network)의 적용성을 제시한 바 있다. Kumar et al. (2015)은 신경망 구조와 웨이블릿 분석 및 부트스트랩 기법을 활용한 저수지 유입량 예측 연구를 수행하였다. Fuente et al. (2019)은 수치예보모델과 연계한 인공신경망 및 장·단기 네트워크 모형이 단기 유량 예측에 활용될 수 있음을 제시하였다. 최근에는 인공신경망의 개선된 형태인 순환신경망, LSTM (Long-Short Term Memory) 등의 수문분야 적용 사례가 증가하고 있으며(Hu et al., 2018; Kratzert et al., 2018; Xiang et al., 2020; Kao et al., 2020), 물리적 모형과의 연계를 통한 예측 성능 개선에 관한 연구도 수행되고 있다(Noori and Kalin, 2016; Cui et al., 2021).

국내에서는 Kim (1993)이 인공신경망을 활용한 유출수문곡선을 모의하고 적용성을 제시한 바 있다. Sim and Kim (1998)은 인공신경망 모형을 기반으로 하는 저수지의 유입량 예측에 관한 연구를 수행하였다. Kim (2000)은 인공신경망 모형을 활용한 일 유출량 예측에 관한 연구를 수행하였으며 Kang and Park (2003)은 소유역에서의 일단위 장기유출해석에 관한 인공신경망 모형의 적용성을 검토한 바 있다. Jeong and Bae (2004)는 인공신경망 모형과 퍼지이론의 결합 형태인 ANFIS를 활용하여 기상예보정보를 활용한 월단위 댐 유입량 예측에 관한 연구를 수행한 바 있다. Park et al. (2018)은 일단위 댐 유입량 예측에 대한 순환신경망 모형을 적용 및 평가하였으며 Mok et al. (2020)은 시단위 댐 유입량 자료와 LSTM 모형을 활용하여 예측유입량의 월별 분석 및 평가를 수행하였다. Lee et al. (2020)은 HEC-HMS 및 HEC-5모형과 NARX 인공신경망 모형을 연계한 실시간 하천홍수 예측에 관한 연구를 수행한 바 있다. Kim et al. (2021)은 홍수량 예측에서 인공신경망 모형의 최적 활성화 함수의 선정에 관한 연구를 수행하였다.

이와 같이, 국내·외 연구에서 인공신경망을 활용한 유량 예측은 강우-유출 관계에 존재하는 비선형성을 고려하여 예측 정확도를 향상하는 데 주안점을 두고 있다. 더욱이 최근에는 순환신경망, LSTM 등 다양한 형태와 구조를 갖는 모형들이 유량 예측에 관한 연구에 적용되고 있다. 이들 모형은 인공신경망 모형을 기반으로 하므로 수문 분야에서 활용하기 위해서는 기본 구조에 대한 이해와 적용을 통해 특징 및 한계점에 대한 면밀한 검토가 선행되어야 한다. 실시간 유입량 예측의 경우, 인공신경망의 활용을 위해서는 예측 정보의 활용 범위와 강우-유출 특성을 고려하여 홍수기 및 이수기를 포함하는 장기간 자료의 학습이 요구되며 이에 대한 적용 및 평가가 필요하다. 기존 연구는 일단위 이상의 유량 예측과 사상 단위의 홍수 유량 예측에 대한 평가가 주로 진행되었으며, 장기간 시단위 자료를 활용한 인공신경망 모형 기반의 실시간 유량 예측에 관한 평가가 요구되는 실정이다.

본 연구에서는 국내 주요 댐 상류 유역을 대상으로 실시간 유입량 예측을 위한 인공신경망 모형을 적용하여 선행시간별 예측유입량의 평가와 이에 영향을 미치는 요인을 분석하고 이의 관계와 특징을 제시하고자 한다. 이를 통해 실시간 유입량 예측 모형으로써의 인공신경망 모형의 특징과 한계점을 규명하고자 한다.

2. 연구방법

각 대상유역에 대하여 장기간(15년)의 강수 및 댐 유입량 자료를 구축하여 모형 학습 및 적용을 위한 훈련, 검증, 평가기간으로 구분하였다. 강수는 지점별 관측자료로부터 티센면적가중법에 따른 유역평균강수량을 활용하였다. 연 평균유입량에 따라 풍수년(wet year), 평수년(normal year), 갈수년(dry year)으로 구분하고 훈련(training), 검증(validation), 평가(test) 데이터 세트에 동일한 비율로 구성되도록 하여 홍수기 및 이수기를 포함하는 장기간 수문시계열 자료의 다양한 관계와 특성이 모형 학습에 반영될 수 있도록 하였다. 각 대상유역별 학습한 모형을 통해 평가기간에 대한 선행 1, 3, 6시간의 예측유입량을 산정하였으며 홍수기 및 이수기에 대한 예측 성능을 평가하였다. 입력자료가 모형의 예측 성능에 미치는 영향을 확인하기 위해 각 입력자료의 과거길이(sequence length)에 따른 성능 변화를 평가하였다. 단기간 예측 수문곡선의 적합도를 확인하기 위해 평가기간 주요 사상별 관측 수문곡선과의 비교 및 평가를 수행하였다.

2.1 인공신경망

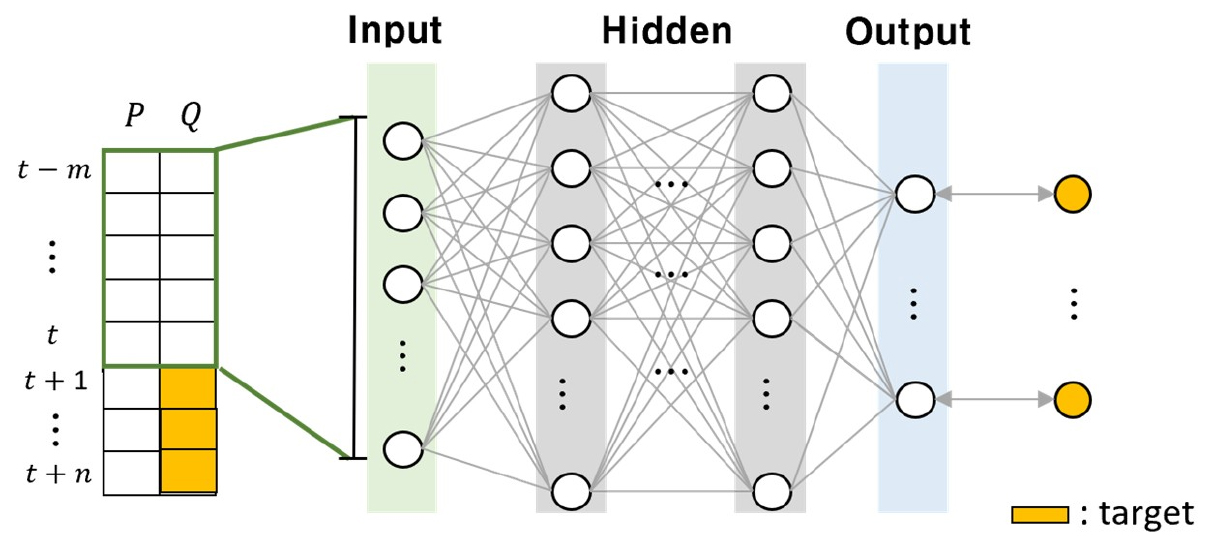
인공신경망 모형은 딥러닝의 여러 모형 중 기본 구조로써 시냅스의 결합으로 구성되는 노드(뉴런)으로 결합 세기를 변화시켜 문제를 해결하는 구조를 갖는다. 이러한 인공신경망 모형은 통계적 학습 이론(statistical learning theory)을 배경으로 하며 주어진 입력샘플(입력값 및 목표값)에 대한 패턴을 학습을 통해 찾아 주어진 입력에 대한 일반화된 최적의 출력을 얻는데 목적이 있다(Goodfellow et al., 2016). 모형은 Fig 1과 같이, 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)으로 구성되며 입력값에 가중치를 곱하고 편향을 더하는 선형 결합과 이를 활성화 함수(activation function)에 의해 비선형 변환하여 다음 층으로 전달 또는 출력하는 구조를 갖는다. 여기서, 모형의 입력값(input value)은 현재(t)부터 과거 m시간 단위의 강수(P) 및 유입량(Q) 자료를 활용하고 목표값(target value)은 미래 n시간에 대한 유입량을 활용할 수 있다.

Fig. 1.

Structure of artificial neural network

이러한 인공신경망 모형의 학습은 출력층에서 산정되는 출력값(output value)과 목표값 간의 오차에 대하여 이를 최소화하는 학습파라미터(가중치 및 편향)를 찾아 자료의 관계를 나타내는 것이다. 학습에 대한 계산 과정은 입력에 대한 모델의 출력과 목표 간의 손실을 계산하는 정방향 연산과 손실을 최소화하도록 학습파라미터를 업데이트하는 역방향 연산을 통해 최적의 학습파라미터를 찾을 때까지 반복 및 업데이트를 수행한다. 각 노드별 학습파라미터는 무작위 값으로 초기화하며 서로 다른 초기조건으로부터 학습 과정을 통해 자료 내에 존재하는 다수의 패턴들을 찾게 된다.

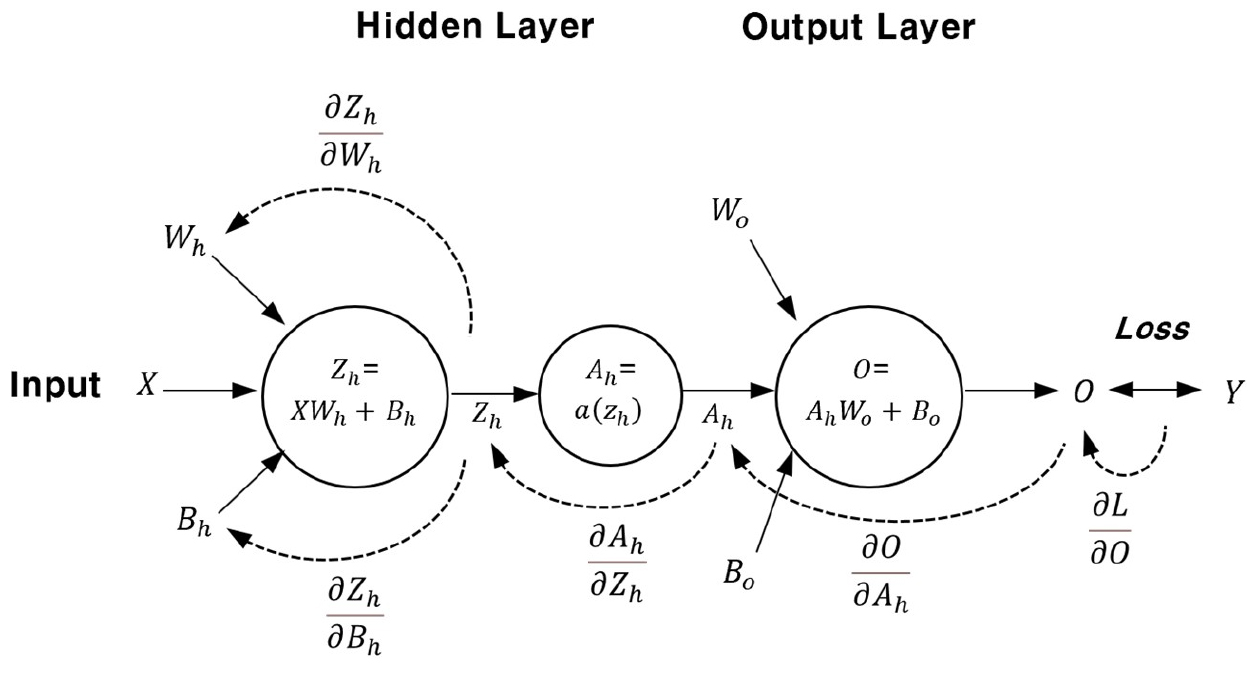
Fig. 2와 같이, 인공신경망에서의 순방향 연산은 입력층의 입력값에 대하여 은닉층에서의 선형결합 및 비선형변환과 은닉층 노드별 출력값에 대한 선형결합 및 출력의 계산과정을 거친다. Eqs. (1)~(3)은 각 층에 대한 순방향 연산의 계산과정을 나타낸다. a는 비선형 변환을 수행하는 활성화 함수이며 대표적으로 sigmoid 함수, tanh 함수, ReLU 함수 등이 있다(Chollet, 2017; Kim et al., 2021). 모형의 출력값과 목표값의 오차는 손실함수(loss function)를 통해 산정되며 모형의 손실은 각 입력샘플에 대한 평균 손실로써 계산된다. 여기서, 대문자는 행렬을 의미하며 X는 입력값, W는 가중치, B는 편향, A는 비선형변환값, O는 출력값, L은 손실함수값, Y는 목표값을 의미하고 아래첨자 h는 은닉층, o는 출력층, k는 입력자료의 k번째 입력샘플을 의미한다.

Fig. 2.

Forward and backward calculation in artificial neural network

역방향 연산에서는 계산된 평균 손실로부터 각 노드별 학습파라미터에 대한 업데이트를 수행한다. 업데이트는 Eq. (4)의 경사하강법에 의해 수행되며 업데이트의 정도를 나타내는 학습률(η)과 최적해에 도달하기 위한 방향인 편미분항(∂L∂W)을 이용하여 이전 학습파라미터에 대한 새로운 값을 찾게 된다. 예를 들어, 은닉층이 1개인 인공신경망에 대한 은닉층 가중치 업데이트에 대하여 은닉층 활성화함수가 tanh 함수인 경우의 편미분항은 Fig. 2의 역전파 과정과 미분의 연쇄법칙에 따라 다음의 Eq. (5)로 계산된다. 여기서 ⊗는 행렬의 원소별 곱셈(element-wise product)을 의미하며 위첨자 T는 행렬의 전치를 의미한다.

2.2 인공신경망 모형 기반 실시간 유입량 예측 모형

인공신경망 모형 기반의 유입량 예측은 과거 강수 및 유입량에 대한 정보와 예측 기간의 유입량에 대한 정보 간의 관계를 찾아 신뢰도 높은 예측 정보를 생산하는 데 있다. 국내 주요 홍수예보지점은 홍수 발생 가능성을 고려하여 선행 6시간을 확보할 수 있도록 하고 있다. 이러한 예측 선행시간에 따른 유입량 예측을 위해서는 입·출력자료의 구성이 중요하며 주어진 입력값에 대하여 목표값을 가장 잘 맞출 수 있는 최적의 모형을 구성하는 것이 중요하다. 실시간 예측을 위해서는 현재를 기준으로 과거 기간 정보로부터 미래 기간에 대한 정확도 높은 예측 정보를 확보하는 것이 필요하며, 모형은 입·출력자료를 어떻게 구성하느냐에 따라 예측의 개념이 달라 질 수 있으므로 이에 대한 판단과 분석이 요구된다.

인공신경망을 활용한 수문시계열의 실시간 예측은 전체 시계열 자료로부터 고정길이 단위로 나눈 입력샘플을 입력하여 매 시간스텝별 예측유입량을 산정하는 구조이다. 이러한 실시간 예측은 목표하는 예측 기간 정보에 따라 단일 단계 예측(single-step-ahead)과 다중 단계 예측(multi-step-ahead) 모형으로 구분되며 출력의 형태에 따라 단일 출력과 다중 출력으로 구분된다(Chang et al., 2007; Taieb et al., 2010). 단일 단계 예측은 특정 예측 시점별 유입량의 예측을 목표로 모형을 최적화하는 것을 의미하며, 현재 시점 이후부터 예측 시점 이전 사이의 값을 고려하지 않는다. 다중 단계 예측은 출력 형태에 따라 이전 스텝의 예측값을 다음 스텝 예측에 활용하고 이를 예측기간 끝까지 수행하는 반복법과 여러 시간스텝의 예측값을 한 번에 산정하는 직접법으로 구분된다. 다만, 인공신경망 모형은 입력변수의 시간 변화를 내부적으로 고려하지 않으므로 선행 1~6시간 유입량에 대한 다중 출력을 갖는 구조로써 직접법을 적용할 수 있다. 이 경우, 인공신경망 모형의 계산과정에 따라 각 선행시간별 손실의 평균값이 역전파 과정에 활용되므로 모형의 학습이 어려울 수 있다.

본 연구에서는 유입량 예측 구조에 따라 단일 단계 예측과 다중 단계 예측을 고려하여 구성하였다. 각 예측 모형은 과거 기간 강수 및 유입량 자료를 입력받아 예측유입량을 출력하는 형태로써, 단일 단계 예측은 선행 1, 3, 6시간의 예측유입량을 단일 출력하는 구조를 고려하고 다중 단계 예측은 선행 1~6시간의 유입량 전체를 다중 출력하는 구조를 고려하였다.

3. 대상유역 및 자료 구축

3.1 대상유역

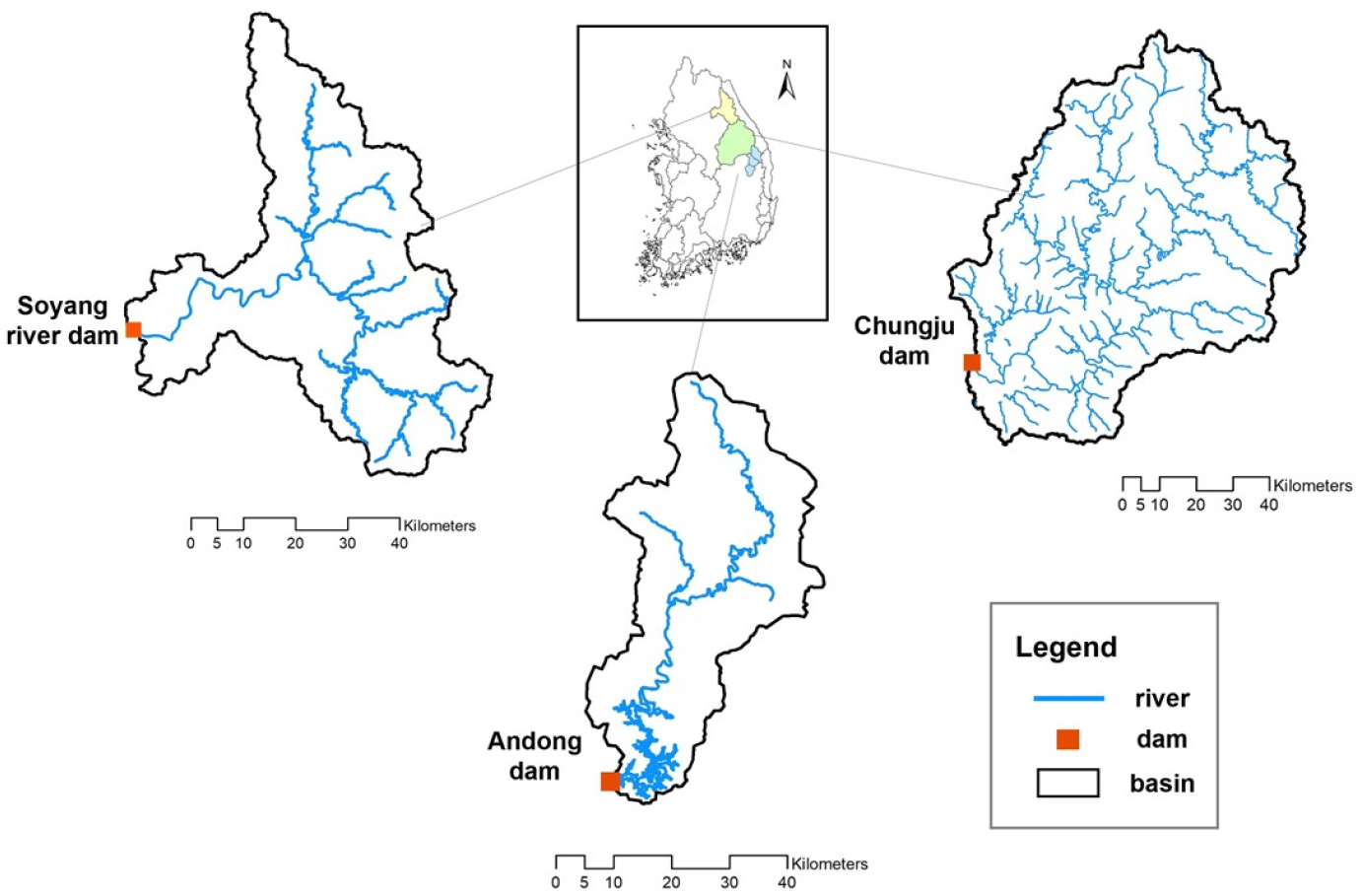
인공신경망 모형이 입·출력 자료간의 관계를 도출하고 일관적인 성능을 갖기 위해서는 장기간의 축적된 자료를 활용한 학습이 요구된다. 따라서 본 연구에서는 15년 이상의 시단위 수문시계열 자료를 갖추고 수공구조물의 인위적인 영향이 적은 댐 상류 유역을 대상유역으로 선정하였다. 모형의 적용성을 평가하기 위해 국내 유역 중 안동댐 유역(AD), 소양강댐 유역(SY), 충주댐 유역(CJ)을 선정하였다(Fig. 3). 이들 세 유역은 태백산맥을 발원지로 하며 안동댐 유역의 면적은 1580 km², 소양강댐 유역은 2700 km², 충주댐 유역은 6600 km²으로써 서로 다른 유역 면적과 특성을 갖는다.

Fig. 3.

Study area

3.2 자료수집 및 데이터세트 구성

본 연구에서 사용한 입력자료는 국가수자원관리종합정보시스템(WAMIS)에서 제공하는 각 유역별 관측소별 강수 자료와 댐 유입량 자료를 활용하였다. 활용한 자료의 전체 기간은 2006년부터 2020년까지 총 15년이고 자료의 시간 해상도는 1시간이다. 인공신경망 모형 적용 시 자료의 품질은 모형의 학습과 결과의 신뢰도에 영향을 미치므로 자료의 품질 향상을 위한 전처리 과정이 요구된다. 특히, 댐 유입량 자료는 관측 과정에서의 내·외부적인 요인에 의해 불규칙 변동과 음의 값 등 관측 오차를 포함하고 있다(Yoo et al., 2012; Eom and Jung, 2019). 이러한 점을 고려하여 본 연구에서는 자료의 품질 확보를 위해 매 시점별 관측값을 기준으로 이전 시간까지의 관측값의 변화와 강수 조건 등을 고려하여 급상승 및 급하강 등의 이상치와 결측치를 보정하였다. 강수는 지점별 관측자료로부터 티센면적 가중법에 따른 유역평균강수량을 활용하였다. 모형의 학습과 적용을 위해 각 강수 및 유입량은 연도별로 훈련(60%, 9년), 검증(20%, 3년), 평가(20%, 3년)세트로 구분하였다. 다만, 시간 순서에 따라 구분하는 경우, 가뭄의 영향이 컸던 2014~2017년이 검증세트로 구분될 수 있으며 모델 검증에 영향을 미칠 수 있을 것으로 판단하였다. 따라서 연 평균유입량에 따라 각 연도를 풍수년(Wet Year), 평수년(Normal Year), 갈수년(Dry Year)으로 구분하고 훈련, 검증, 평가 데이터세트에 동일한 비율로 구성되도록 하여 각 모델이 고유량 및 저유량에 대한 학습이 적절하게 이루어지도록 하였다. 또한 과거 자료는 학습에 사용하고 최근 자료는 검증 및 평가기간에 활용될 수 있도록 세트를 구성하였다. 강수와 유입량은 서로 다른 값의 범위를 가지므로 Eq. (6)의 최소-최대 표준화(min-Max scaling)를 적용하여 0~1사이의 값으로 변환하였다.

3.3 모형의 구성

인공신경망 모형은 학습파라미터 외에 모델러가 결정하는 하이퍼파라미터(hyperparameter)가 있으며 반복횟수, 은닉층 노드수, 은닉층 수, 손실함수, 학습률 등이 있다. 금회에는 모형의 일반적인 성능을 평가하기 위해 동일한 모형 구성 조건에 대하여 대상유역별 모형 학습 및 평가를 수행하였다.

최적화를 위한 손실함수로 평균제곱오차(Mean Sqaured Error, MSE)를 사용하였고, 학습파라미터의 업데이트를 위한 방법으로 경사하강법을 기반으로 하는 Adam Optimizer를 적용하였다. 학습률은 0.0001로 하였으며 다른 매개변수는 Kingma and Ba (2015)가 제시한 기본값을 사용하였다. 자료의 비선형 변환을 위한 활성화 함수로 tanh 함수를 사용하였다. 반복횟수는 최소 100번 이상, 최대 1000번 이하 중 과대적합이 발생하지 않는 범위 내에서 조기 종료(early stopping)되도록 하였다. 은닉층 수는 시행착오를 통해 2개 층으로 결정하였으며 은닉층 노드 수는 입력 변수의 크기와 과대적합을 고려하여 32로 설정하였다. 모델의 구성과 학습은 파이썬(python) 언어 기반의 딥러닝 지원 도구인 TensorFlow2를 사용하였다.

실시간 유입량 예측 모형의 성능을 평가하기 위해 R² (coefficient of determination), RMSE (Root Mean Sqaured Error), NSE (Nash-Shutcliffe Efficiency)를 적용하였다(Eqs. (7)~(9)).

여기서, Q 및 Q^는 관측 및 예측유입량, Q는 평균 유입량을 의미한다.

4. 결과 및 분석

4.1 예측 단계 구분에 따른 모델 성능 평가

예측 단계 구분에 따른 대상유역별 선행시간에 따른 예측유입량을 산정 및 평가하였다. 학습에 관여한 훈련 및 검증세트는 제외하고 평가세트를 대상으로 하였다. 모형의 조건은 3.3에서 제시한 바와 같으며, 과거길이 12시간에 대한 단일 단계 예측 및 다중 단계 예측에 대한 결과를 비교하였다. 단일 단계 예측은 각 선행기간(1, 3, 6시간)별 유입량을 목표값으로 하여 모델을 학습한 것이며 다중 단계 예측은 1~6시간 전체를 목표값으로 학습한 것이다.

Table 1은 각 예측 단계 방식에 따라 유역별 선행시간별 예측유입량에 대한 평가 결과이다. 평가 결과, 두 예측 성능은 선행 1시간 예측의 NSE가 최소 0.79, 3시간 예측이 0.70, 6시간 예측이 0.57 이상으로써 비교적 양호한 성능을 보이는 것으로 판단된다. 그러나 각 선행시간별 결과에 대한 두 방식에 성능은 큰 차이가 없는 것으로 확인되었다. 다만, 충주댐 유역은 선행 1시간에 예측에 대하여 단일 단계 예측의 RMSE 175.82, NSE 0.79이고 다중 단계 예측의 RMSE는 154.33, NSE 0.84로 나타나, 인공신경망 모형이 변수의 시간 변화를 내부적으로 고려하지는 않지만 예측기간의 정보가 많을수록 짧은 선행시간에 대한 예측 성능은 개선될 수 있는 것으로 판단된다. 다만, 긴 선행시간에 대한 예측일수록 성능이 낮아지기 때문에 모델 구성 시 긴 선행시간에 대한 관계를 반영할 수 있는 조건을 고려해야 할 것으로 판단된다.

4.2 선행시간별 관측 및 예측유입량 비교

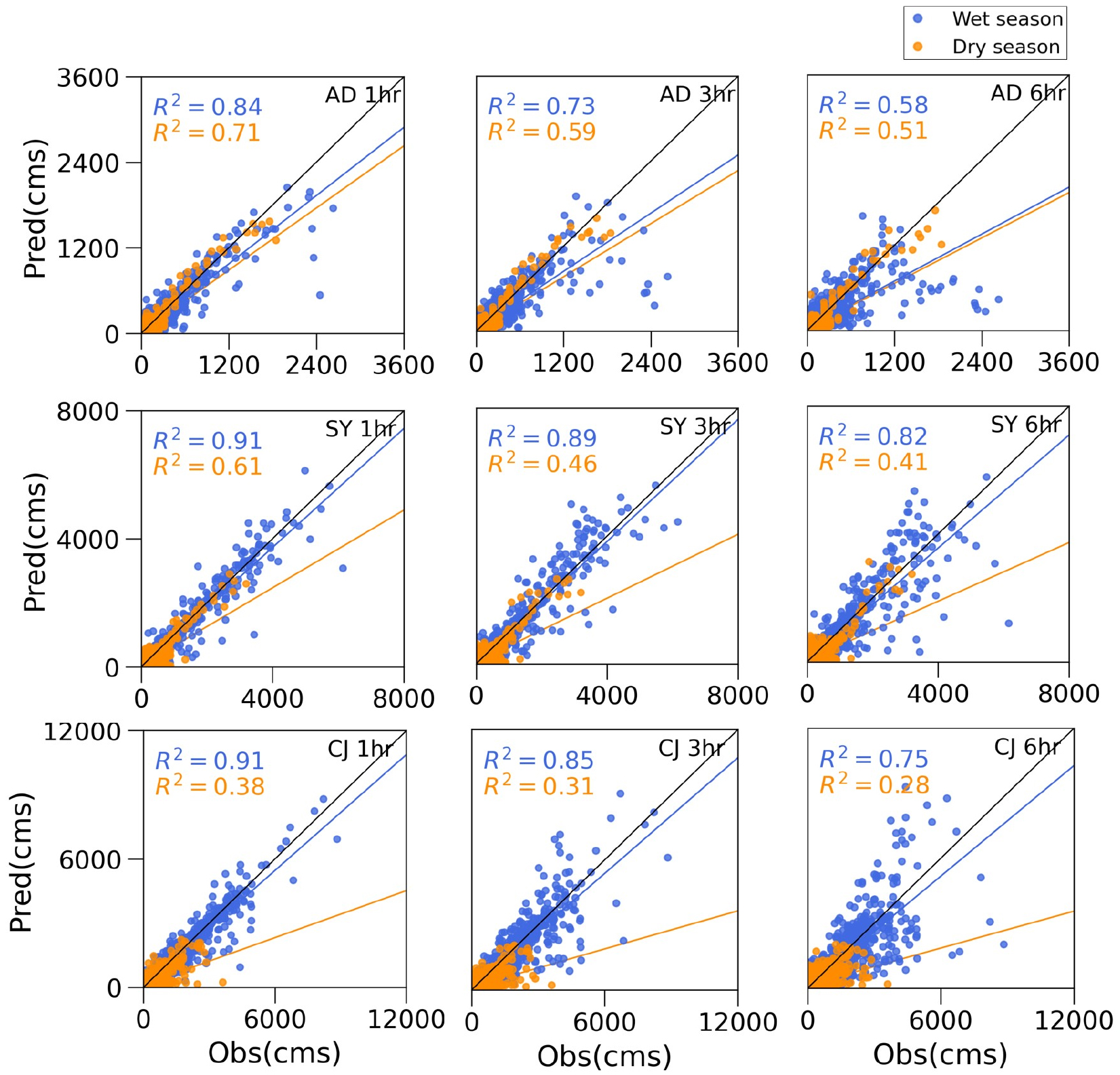
각 선행시간별 관측 및 예측유입량을 비교 및 평가하였다. Fig. 4는 홍수기 및 이수기에 대한 대상유역별 선행시간별 관측 및 예측유입량을 도시한 것이다. 평가 결과, 세 대상유역에서 대부분 예측유입량은 관측과 비교하여 과소 추정되는 것으로 나타났다. 선행 1시간 예측에 대하여 유역면적이 상대적으로 큰 소양강댐 및 충주댐 유역은 홍수기 예측에 대하여 높은 적합도를 보이는 반면, 이수기 예측에 대해서는 다소 낮은 적합도를 나타냈다. 안동댐 유역은 홍수기 및 이수기의 유입량 예측에 대한 R²가 각각 0.84, 0.71로 다른 유역에 비해 차이가 적으며, 소양강댐 유역은 각각 0.91, 0.61, 충주댐 유역은 각각 0.91, 0.38로써 이수기 유량에 대한 예측 정확도는 다소 낮고 홍수기 및 이수기의 성능 편차가 큰 것으로 나타났다. 유역면적이 클수록 홍수기와 이수기의 예측 성능의 편차는 큰 것으로 나타났으며 유역면적이 작을수록 상대적으로 홍수기의 성능이 낮고 이수기의 성능이 높은 반면, 유역면적이 클수록 홍수기의 성능이 높고 이수기의 성능이 낮은 경향을 보인다. 이는 인공신경망 모형이 전반적으로 강우-유출에 대한 입·출력 관계가 비교적 잘 나타나는 홍수기에 대해 적용성이 높다고 할 수 있으며 강수 및 유입량 외에 다른 특성들이 이수기 유입량 예측에 강한 영향을 주는 것으로 판단된다. 이수기 유출은 대부분 기저유출로 발생하므로 증발산, 풍속, 토양수분량, 습도 등 다양한 변수의 영향을 크게 받기 때문에 예측 성능의 개선을 위해서는 이러한 변수들을 고려해야 할 것으로 사료된다.

Fig. 4.

Comparison of observed and predicted inflow of wet and dry season

4.3 입력자료 과거길이에 따른 유입량 예측 성능 평가

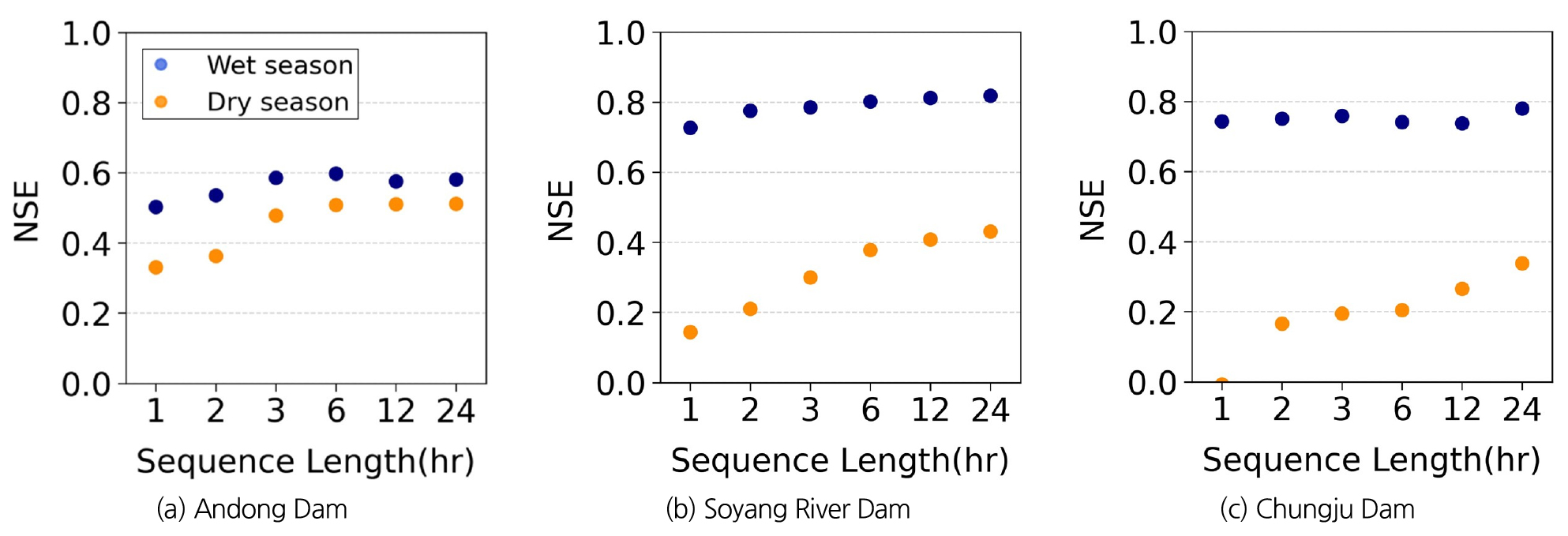
입력자료에 대한 과거길이가 유입량 예측에 미치는 영향에 대하여 대상유역별로 각각의 모형을 구성 및 평가하였다. 모형의 예측 성능을 확인하기 위해 평가세트에 대한 다중 단계 예측 모델의 결과 중 선행 6시간 예측 결과를 비교하였다. Fig. 5는 대상유역별 입력자료의 과거길이에 따른 예측 성능 변화를 도시한 것이다.

평가 결과, 전반적으로 과거길이가 길어질수록 예측 성능이 향상되는 것으로 나타났으며홍수기보다는 이수기의 성능 변화가 두드러지는 것을 확인하였다. 안동댐 유역(Fig. 5(a))의 과거길이에 따른 이수기 NSE는 0.33~0.51, 소양강댐 유역(Fig. 5(b))은 0.14~0.43, 충주댐 유역(Fig. 5(c))는 0.0~0.34의 범위를 나타내었으며, 긴 과거길이를 입력자료로 활용하는 예측 모형에 대해 이수기 예측 성능이 높은 것으로 나타났다. 이는 인공신경망 모형의 입력자료에서 과거길이가 수문자료 내에서 도달시간과 같은 물리적인 특성과 연관이 있는 것으로 판단된다. 이러한 과거길이에 따른 예측 성능의 변화는 장기간의 강우-유출 특성이 모형 학습 및 예측에 영향을 미친다고 판단할 수 있으며 예측 성능의 개선을 위해서는 4.2절에서 전술한 바와 같이 과거길이 외에 다양한 수문·기상 변수들이 필요함을 시사한다.

Fig. 5.

Results of prediction performance according to input sequence length

4.4 주요 홍수 사상별 관측 및 예측수문곡선의 비교

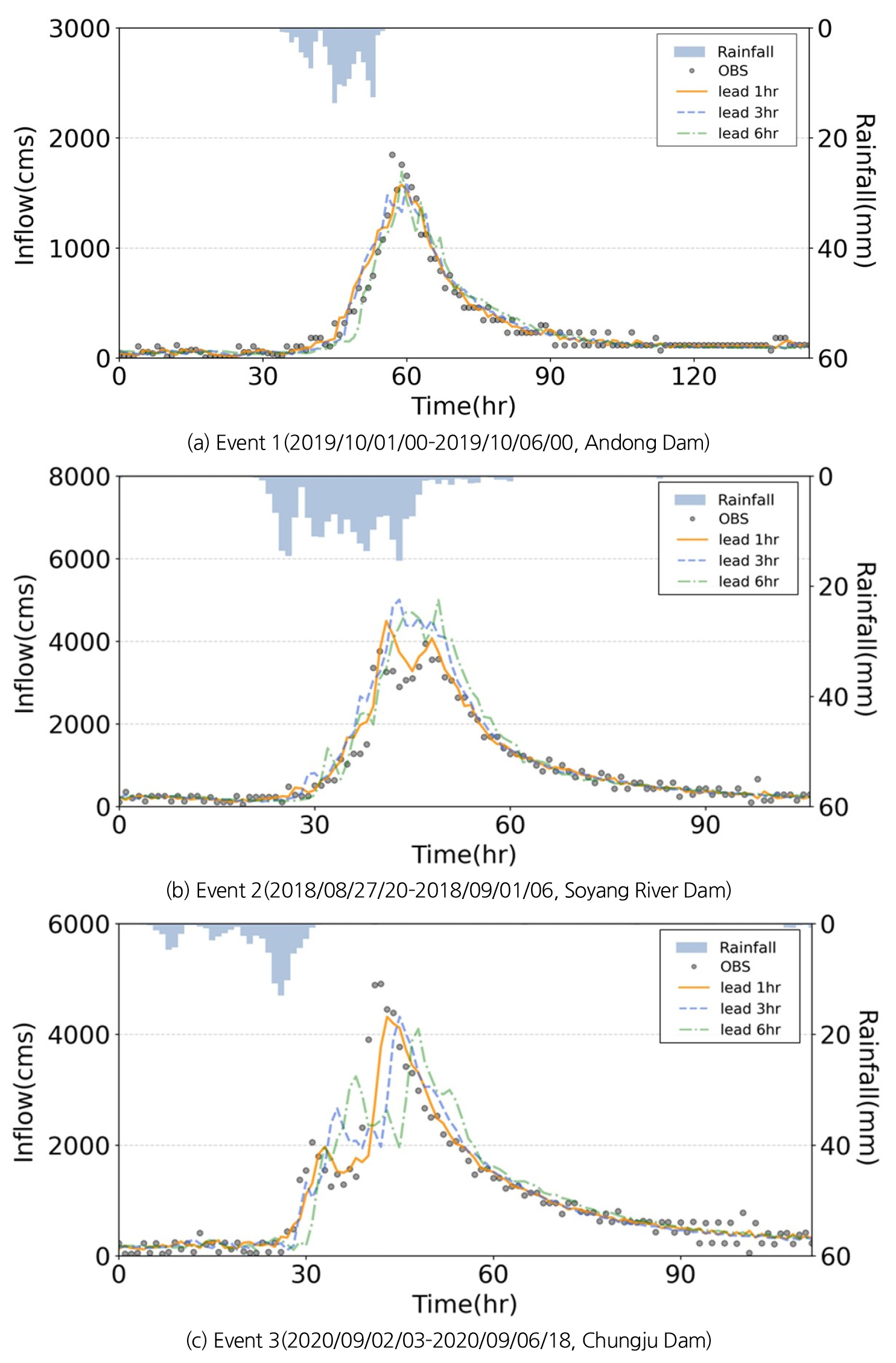
각 유역별 주요 홍수 사상을 선정하여 과거길이 12시간에 대한 다중 단계 예측 결과와 관측수문곡선을 비교 및 평가하였다. Fig. 6은 각 유역별 주요 홍수 사상에 대한 수문곡선을 나타낸 것이다.

Event 1(Fig. 6(a))의 경우, 선행시간별 예측수문곡선은 관측과 비교적 유사한 것으로 나타났으나, 첨두시간은 각 선행시간별로 2~3시간의 지연이 있고 첨두유량은 관측대비 -8~-14%의 차이를 보여 과소 추정되는 것으로 나타났다. Event 2(Fig. 6(b))의 경우, 선행 1시간 및 3시간의 첨두유량이 관측보다 4~6시간 앞서 나타났으나 선행시간별로 첨두시간이 지연되는 것으로 나타났으며 첨두유량은 관측 대비 최대 28%의 차이를 보여 전반적으로 과대 추정되는 것을 확인하였다. Event 3(Fig. 6(c))의 경우, 예측수문곡선이 관측과 비교하여 지연되고 첨두유량은 과소 추정하는 것으로 나타났다.

각 선행시간별 학습한 인공신경망 모형의 예측수문곡선은 관측과 비교하여 상승부 및 하강부를 포함한 전반적인 형태가 유사한 것으로 나타났으며 강수에 따른 유입량의 상승 및 하강에 대한 응답은 비교적 잘 모의하는 것으로 판단된다. 각 대상유역별 사상마다 차이는 있으나, 홍수 사상에 대하여 예측 선행시간이 길어질수록 첨두시간의 지연과 첨두유량의 과소 추정 경향을 나타났다. 이는 시단위 유입량의 노이즈와 강한 자기상관성이 유입량 예측에 대한 모형의 학습에 영향을 준 것으로 판단된다. 실시간 유입량 예측의 관점에서 홍수 사상의 첨두유량에 대한 예측 성능은 인공신경망 모형의 한계점으로 판단된다. 다만, 예측수문곡선의 개형이 관측과 비교적 유사한 점은 강우-유출에 대한 관계를 인공신경망 모형이 학습 가능한 것으로 이해할 수 있으며 이러한 한계점을 보완하면 실시간 유입량 예측 모형으로써 인공신경망 모형이 충분히 활용 가능한 것으로 판단된다.

Fig. 6.

Observed and predicted hydrographs for each events

5. 결 론

본 연구에서는 인공신경망 모형의 실시간 유입량 예측의 활용성을 평가하고자 국내 주요 댐 상류 유역을 대상으로 선행시간별 예측유입량을 산정 및 평가하였으며 예측에 미치는 요인에 대한 영향을 분석하고 이의 관계 및 특징을 제시하였다. 도출된 결과를 요약하면 다음과 같다.

1) 대상유역별로 각 선행시간별 단일 단계 예측과 선행 1~6시간에 대한 다중 단계 예측 결과는 NSE 0.57~0.79 이상으로써 비교적 양호한 성능을 나타내었다. 다만, 두 예측 단계에 대한 큰 차이는 없는 것으로 확인되었다. 선행 1시간 예측의 경우, 다중 단계 예측 단계의 결과가 더 좋은 경우도 있으며 이는 인공신경망 모형의 학습 시 예측 기간의 정보가 많을수록 모형의 단기간 예측 성능은 개선될 수 있는 것으로 판단된다.

2) 각 선행시간별 관측 및 예측유입량을 비교 및 평가하였으며 각 대상유역별 관측 대비 예측유입량은 다소 과소 추정되는 경향이 나타났다. 각 유역별로 홍수기의 R²는 0.8 이상으로 높은 적합도를 나타내나 이수기는 0.4 미만으로 낮은 적합도를 보인다. 유역면적이 클수록 홍수기와 이수기의 성능 편차는 큰 것으로 나타났으며, 유역면적이 상대적으로 큰 소양강댐 유역과 충주댐 유역은 이수기의 예측 성능이 낮은 것으로 나타났다. 강수 및 유입량 외의 다른 요인들이 유입량 예측에 강한 영향을 주는 것으로 판단할 수 있으며 예측 성능의 향상을 위해서는 유출 특성에 따라 이에 영향을 미치는 증발산, 풍속, 토양수분량, 습도 등의 다양한 변수들을 고려해야 할 것으로 판단된다.

3) 다중 단계 예측에서 선행 6시간 예측에 대해 입력자료의 과거길이에 따른 성능 변화는 홍수기보다 이수기에서 큰 차이를 보이며 과거길이가 증가할수록 이수기의 성능이 향상되는 것으로 나타났다. 이는 인공신경망 모형의 입력자료에서 과거길이가 수문자료 내에서 도달시간과 같은 물리적인 특성과 연관이 있는 것으로 판단된다. 이러한 과거길이에 따른 예측 성능의 변화는 장기간의 강우-유출 특성이 모형의 학습 및 예측에 영향을 미친다고 판단할 수 있으며, 예측 성능의 개선을 위해서는 과거길이 외의 수문·기상 변수들이 필요함을 시사한다.

4) 주요 홍수 사상에 대한 관측 및 선행시간별 예측 수문곡선을 비교 및 평가하였다. 선행시간이 길어질수록 정확도는 감소하지만 수문곡선의 형태는 유사한 것으로 나타났다. 다만, 선행시간에 따라 첨두시간이 지연되는 현상이 발생하며 일부 사상마다 차이는 있으나 첨두유량은 과소 추정되는 경향이 확인되었다. 이러한 결과는 인공신경망 모형이 실시간 유입량 예측 모형으로써 수문자료로부터 강우-유출에 대한 관계를 학습하여 활용할 수 있는 것으로 이해되나 홍수기 첨두유량에 대한 예측 정확도는 개선이 필요할 것으로 판단된다.

최근 딥러닝의 수문분야 적용에 대한 다양한 연구가 활발히 진행되고 있다. 본 연구에서 제시한 결과는 딥러닝 모형들의 기본 구조인 인공신경망 모형에 대하여 실시간 댐 유입량 예측에서 특징과 한계점을 규명한 것에 의의가 있다. 향후, 물리적 모형과의 연계와 다양한 수문·기상 변수에 따른 딥러닝 모형의 영향 평가를 통해 본 연구에서 제시한 이수기 예측 성능 및 홍수기 첨두유량 정확도를 개선하고자 한다. 아울러, 예측기간 정보에 대한 수치예보 자료의 활용을 통해 정확도 높은 유입량 예측과 긴 선행시간의 확보 등이 가능할 것으로 기대된다.