1. 서 론
2. 모형의 매개변수 검/보정
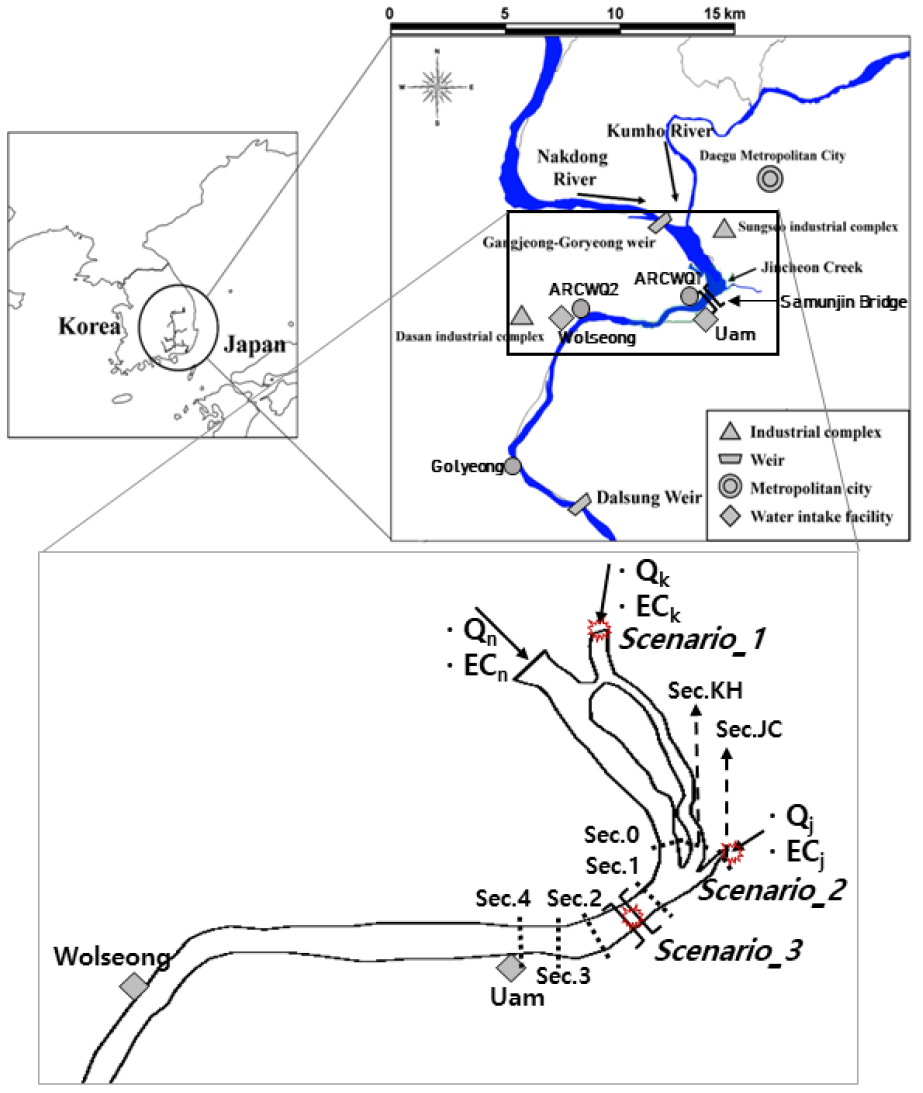
2.1 연구대상 구간
2.2 모형의 민감도 분석
2.3 모형의 검/보정
3. 수질사고 시나리오 기반 혼합 해석
3.1 Scenario_1(금호강에 페놀 유입)
3.2 Scenario_2(진천천에 페놀 유입)
3.3 Scenario_3(사문진교에서 페놀 유입)
4. 결 론
1. 서 론
평면 2차원 혼합 해석시 연안이나 호소의 경우 수평방향 분산(dispersion)이 균일하다고 볼 수 있지만, 종/횡의 비율이 세장(細長)한 하천의 경우 종/횡방향의 유속크기나 특성이 상이하여 이에 기인한 분산특성도 다를 수 밖에 없다(Fischer et al., 1979; Seo et al., 2003; Seo et al., 2006). 특히 농도가 서로 다른 지류와 본류가 만나는 합류부 일대는 복잡한 혼합특성이 발생하고, 적절한 종분산과 횡분산계수 값을 부여함으로써 이러한 혼합 특성을 정확히 구현할 필요성이 있다(Seo et al., 2008). 예를 들어 Fig. 1은 지류에서 오염물질이 유입되는 경우를 가정하여 본류와 만나는 합류부에서의 혼합특성을 개념적으로 도시한 것이다(Jung et al., 2019). 그림에서 보듯이 지류에서 연속적으로 주입되는 오염물은 초기에 3차원적 거동을 보이다 하류로 가면서 단면 전체에 균일하게 퍼지게 된다. 이후 지류가 본류에 합류하면서 오염물질이 본류 좌안에 치우쳐져 있다가 점차적으로 하폭방향으로 균일하게 퍼져나가게 된다. 즉 지류 내에서 완전 혼합된 오염물은 1차원적 해석으로 충분하지만, 이것이 본류로 유입된 직후에는 하폭방향으로 농도 차이가 명백히 발생하므로 2차원적 해석이 필요하다는 뜻이다. 특히 이 경우, 횡방향(하폭방향)의 혼합능력(mixing capacity)을 반영하는 횡분산계수의 적절한 결정이 해석 정확도를 높이는 핵심요소라 할 수 있다(Baek, 2018; Baek and Seo, 2016, 2017; Han et al., 2019).
오염물 혼합 현상을 2차원으로 해석하는 지배방정식인 수심 적분된 이송-분산 방정식을 기술하면 다음과 같다.
여기서 C는 오염물질의 수체 내 농도, u와 v는 종방향 및 횡방향의 유속, DL와 DT는 종방향 및 횡방향의 분산계수, k는 감쇠계수(decay coefficient)이다. 모두에서 지적했듯이 상기 방정식을 기반으로 수치모형을 구축할 때 종/횡방향의 분산특성이 크게 구별되지 않는 호소나 연안이 주 분석대상지면 종/횡분산계수를 구분하지 않는 경우도 많다. 준 3차원 모형인 EFDC (Environmental Fluid Dynamics Code)가 그 대표적이 예이다. 허나 본 연구의 목적이 하천 합류부에서 종분산과 횡분산의 기여도가 얼마나 다른지를 파악해야 하기에 종/횡분산계수가 분리되어 입력되는 대표적인 모형인 RAMS 내 CTM-2D (Seo et al., 2016)를 분석의 도구로 사용하였다.
본 연구의 대상영역으로 낙동강에 금호강과 진천천이 합류하는 강정고령보 하류에서 달성보 상류 구간을 선택하고, 종/횡분산계수 값의 차이에 따른 2차원적 혼합특성을 살펴보았다. 이를 위해 먼저 종/횡분산계수 각각이 혼합특성에 얼마나 민감한지 확인하고자 매개변수(분산계수)들의 민감도분석(sensitivity analysis)을 수행하였다. 이후 실측을 통해 취득한 전기전도도(Electronic Conductivity, EC)를 활용하여 종분산 및 횡분산계수를 각각 검/보정하였다. 다음으로 금호강 및 진천천 상류단에 유해물질이 유입되었을 경우를 가정하여 분산계수가 검/보정된 모형으로 하류 양수장(우암/월성 양수장)에 도달하는 유해물질의 농도를 예측해 보았다. 또한 분산계수가 검보정되지 않은 모형(종/횡분산계수를 동일한 값으로 부여)으로 유해물질의 양수장 도달 농도를 계산하여 두 결과를 비교하였다. 이를 기반으로 종/횡분산계수값의 비율에 따라 유해물질이 양수장에 도달하는 시간, 첨두농도 등의 특징이 어떻게 달라지는 분석해 보았다.
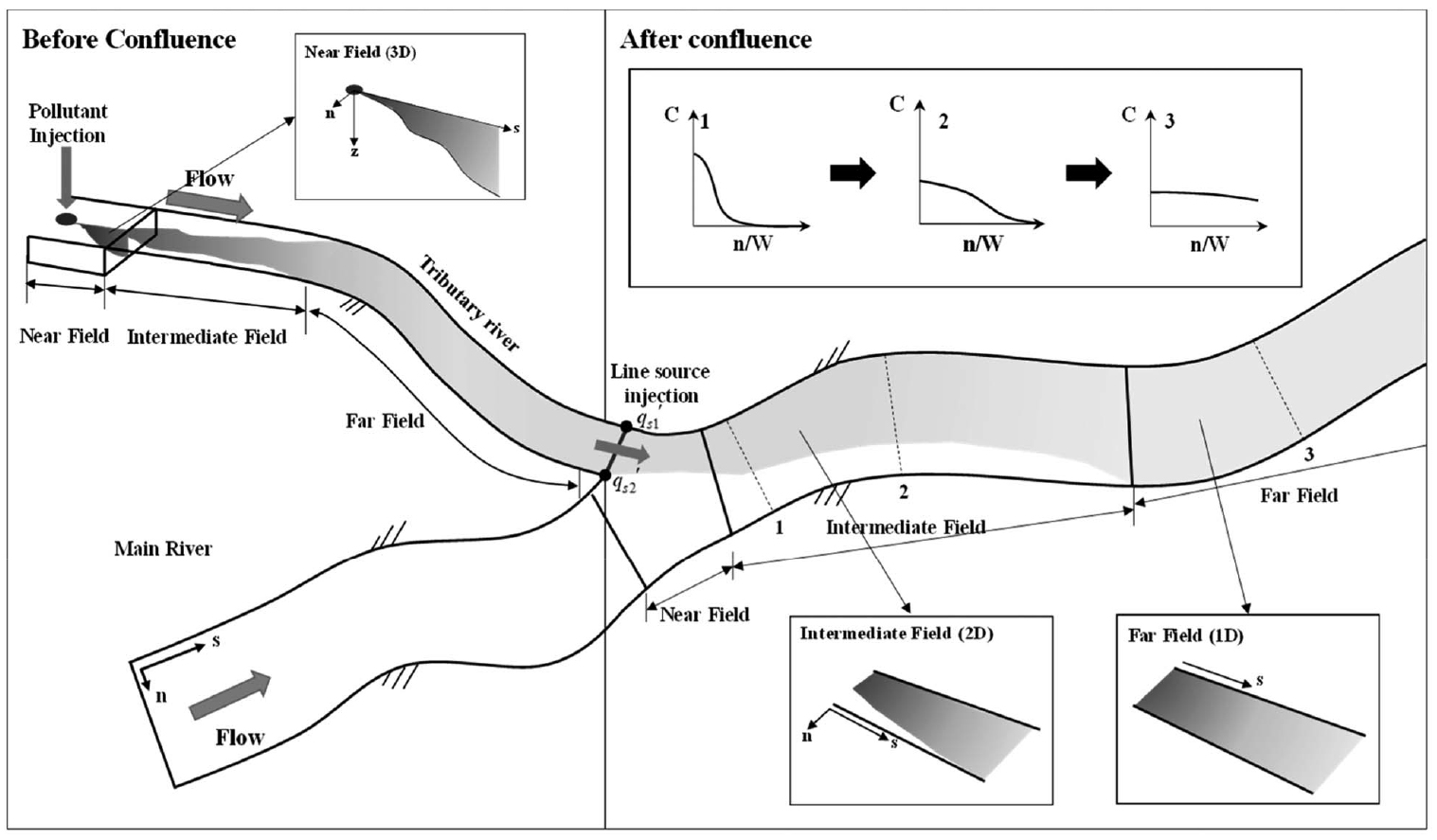
Fig. 1.
Mixing process at river confluence with continuous pollutant inputs from tributary (after Jung et al., 2019)
2. 모형의 매개변수 검/보정
2.1 연구대상 구간
평면 2차원 혼합 모형을 적용할 구간으로는 낙동강 강정-고령보에서 달성보 구간을 선택하였다. 이 구간은 Fig. 2에서 보는 바와 같이 강정고령보 직하류에 제 1 지류 금호강과 진천천이 좌안으로부터 낙동강 본류로 합류되며, 인근 대구광역시 공단과 성서산업단지로 인하여 수질오염사고 발생확률이 높은 구간이다. 즉 하수처리장의 오작동, 산업단지의 수질오염사고 등을 대비하여 합류부의 수질변화 및 오염수의 혼합거동을 분석하는 것이 필요한 구간이다.
연구대상구간에 2차원 혼합 모형을 적용하기 위해서는 매개변수인 종/횡분산계수의 검/보정이 필요하다. 해당구간에서 국립환경과학원(NIER, 2015)에 의해 관측된 전기전도도(EC) 자료를 모형의 검/보정에 활용하였다. 전기전도도란 물질 또는 용액에서 전하를 운반할 수 있는 정도를 의미하는 것으로 전기전도도를 통해 수중의 용존 염류의 농도를 측정할 수 있다. 즉 이 값의 변화를 통하여 하천에 유입된 특정 오염원의 농도를 간접적으로 알 수 있다(NIER, 2015).
전기전도도의 관측은 2014년 8월 27일(Case 1)과 같은 해 10월 23일(Case 2) 두 차례에 걸쳐 수행되었으며 실험구간의 길이는 대략 9.3 km이다. 해당 구간에서 관측된 평균 수질 및 수리량을 Table 1에 정리하였다. 낙동강 본류 총 8개 단면에서 단면별 EC 횡분포를 측정하였는데, Fig. 2에서 보듯이 금호강 합류 직전 지점인 Sec. 0에서부터 합류부 직하류인 Sec. 1을 포함하여 Sec. 4까지 측정하였다. 또한 지류(금호강과 진천천) 각각의 경계단면인 Sec.JC, Sec.KH에서도 수리량과 EC를 측정하였다.
Table 1.
Summary of field measurements
2.2 모형의 민감도 분석
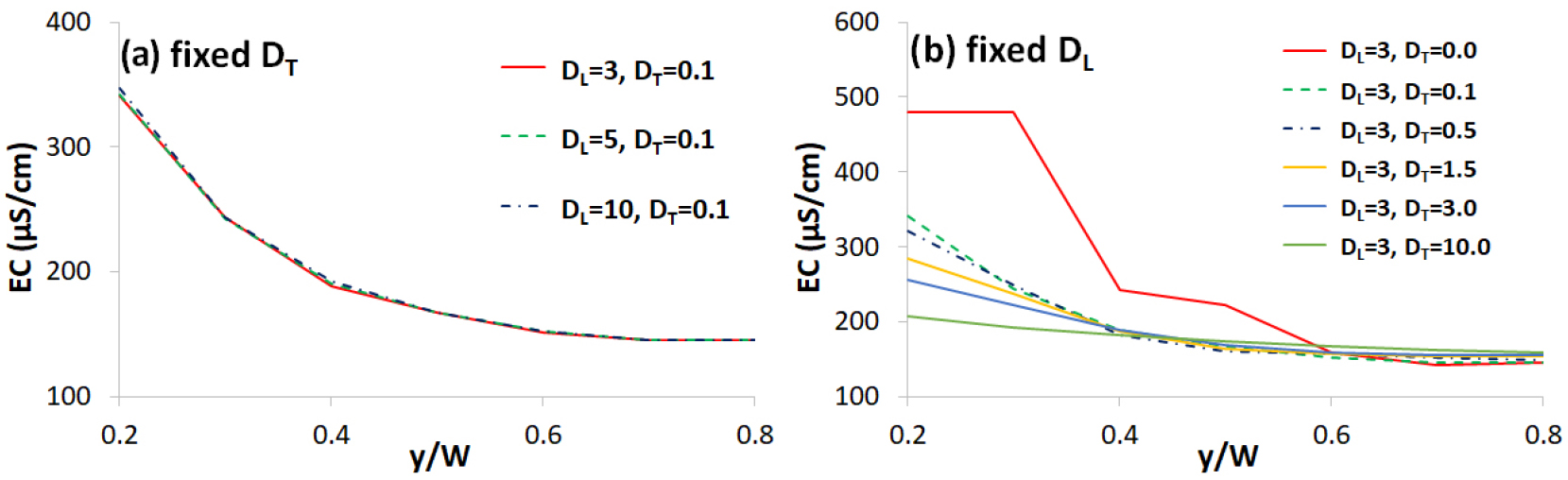
모형의 매개변수인 종분산 및 횡분산계수의 민감도 분석을 해당 구간에서 수행하였다. Case 1의 상황을 재현하여 수리량 및 수질을 모형의 경계조건으로 부여하였다. Table 1에서 보듯이 낙동강 본류의 유량이 금호강에 비해 약 5배, 진천천에 비해 약 100배 이상 크지만, 전기전도도(수질)는 금호강과 진천천이 낙동강에 비해 2 ~ 4 배 이상 크다(금호강은 대구시의 하수처리수, 진천천은 성서공업단지의 영향으로 사료됨). 따라서 합류 후 첫 번째 관측 단면인 Sec. 1에서는 좌안측이 우안측에 비해 상대적으로 큰 농도가 발생할 것이라 예상할 수 있다(고농도의 금호강이 좌안측에서 합류하므로). 이때 종분산 및 횡분산계수 값에 따라 Sec. 1에서의 횡방향 농도분포가 얼마나 변화하는지 민감도를 분석할 필요성이 있으며, 그 결과를 Fig. 3에 도시하였다. 이 그림에서 횡축은 무차원 횡방향 좌표로 좌안이 0, 우안이 1을 의미한다.
먼저 횡분산계수를 0.1 m2/s로 고정한 이후 종분산계수를 3 ~ 10 m2/s의 범위에서 변화시켰다(Fig. 3(a)). 종분산계수가 1 m2/s 미만인 경우 Peclet number가 커져 수치해가 발산하는 경우가 발생하였기 때문에 안정적인 수치해를 얻기 위해 상기와 같은 종분산계수 범위를 설정하였다. 횡분산계수를 0.1 m2/s로 고정한 이유는 자연하천에서 범용적으로 사용되는 Fischer et al. (1979)의 다음 식을 사용했기 때문이다.
여기서 H는 평균수심, U*는 마찰유속이다. Fig. 3(a)에서 보듯이 결과적으로 종분산계수는 농도의 횡방향 분포에 거의 영향을 미치지 못함을 확인할 수 있었다. 다음으로 종분산계수를 3 m2/s로 고정한 이후 횡분산계수를 0 ~ 10 m2/s로 변화시켰다. Fig. 3(b)에서 보듯이 횡분산계수가 0인 경우, 좌안측 고농도가 우안측으로 분산(dispersion)되지 못하여 좌안측에 고농도가 머물고 있음을 확인할 수 있다. 횡분산계수를 점차적으로 증가시키면 횡분산이 강화되어 좌안측 고농도가 우안측으로 분산되어 횡분포가 편평하게(flat) 변해감을 볼 수 있다. 즉 연구대상지와 같은 합류부 직하류 단면에서는 횡분산계수가 농도분포에 매우 민감하게 반응함을 확인할 수 있었고, 횡분산계수의 산정에 세심한 주의가 필요함을 환기시킨다.
2.3 모형의 검/보정
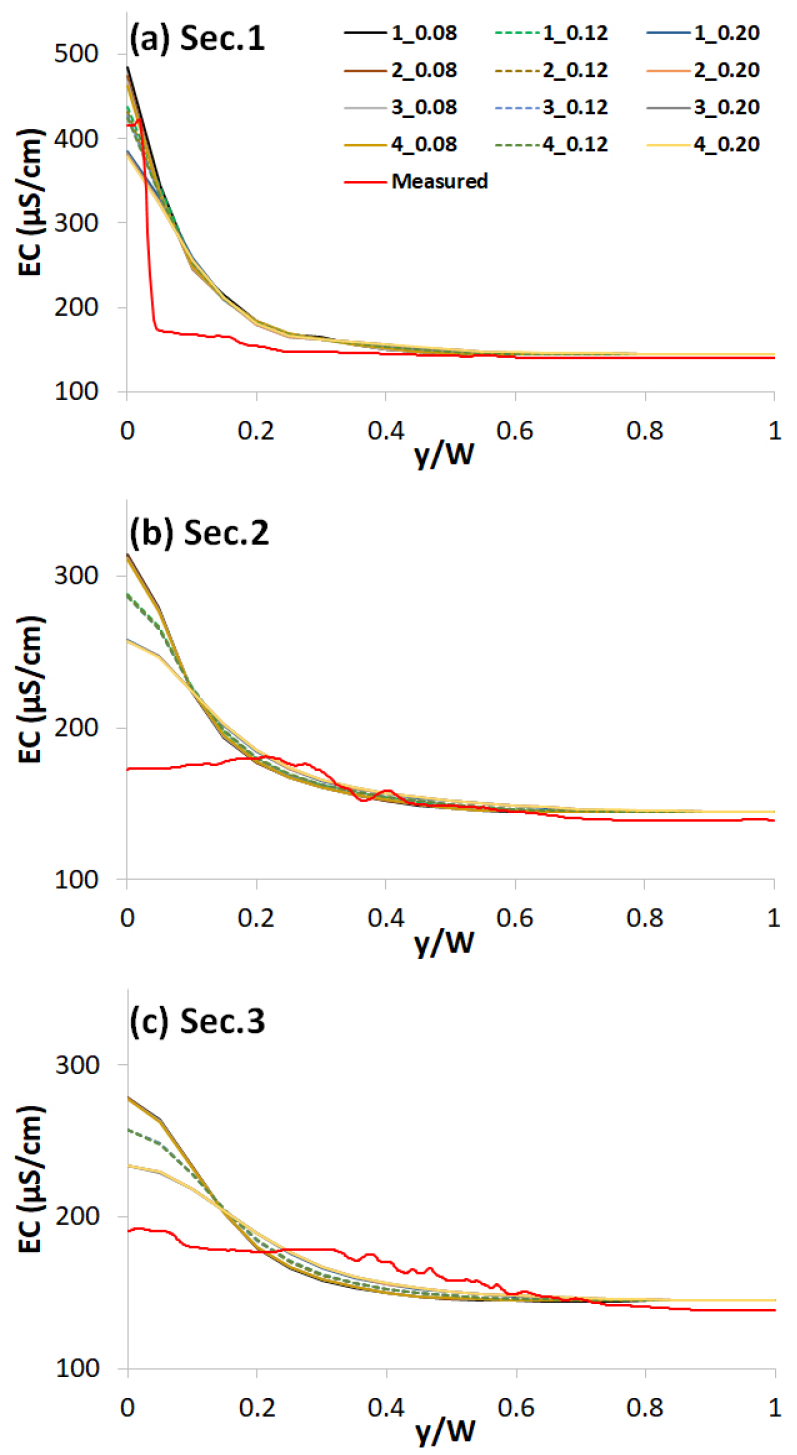
Table 1에서 요약한 EC 관측자료 중 Case 1을 기준으로 모형을 보정(calibration)하고, Case 2로 검증(validation)하였다. 종분산 및 횡분산계수는 시행착오법(trial and error)을 활용하여 보정하였다. 종분산계수는 1 m2/s에서 4 m2/s 까지 1 m2/s의 간격으로 총 4개와 횡분산계수는 0.08 m2/s에서 0.20 m2/s 까지 0.02 m2/s의 간격으로 총 7개를 조합하여 28가지 경우를 모의하였다. 그리고 Sec. 4 이후의 EC 분포는 횡방향으로 큰 차이가 없어 Sec. 1 ~ 3까지의 세 단면 자료만 보정에 활용하였다. 그 결과 분산계수에 따른 EC 관측값과 모의값을 Fig. (4)에 도시하였다. 그림에서 보듯이 관측 횡분포는 하류로 갈수록 급속하게 편평해지는 반면, 모형에 의한 계산치는 분산계수 변화에 상관없이 Sec. 2 ~ 3의 경우 좌안에서 고농도가 지속적으로 발생하는 불일치도 나타났다. 모형의 재현성 평가를 Table 2에 정리하였다. 여기서 결정계수(R2)는 정확도를, 편이백분율(Percent bias, PBIAS)은 관측치와 모형치간 오차를 대표하는 지표로서 다음과 같이 정의된다(Moriasi et al., 2007).
Table 2.
Evaluation of reproducibility on calibrated dispersion coefficients (DL /HU* = 24.35, DT /HU* = 0.97)
모형의 정확도와 오차의 최소치를 종합적으로 판단하여 종분산계수는 3 m2/s (무차원계수 DL/HU* = 24.35)으로, 횡분산계수는 0.12 m2/s (무차원계수 DT/HU* = 0.97)로 결정하였다. 두 분산계수 값간 차이는 약 25배였다. Rutherford (1994)에 의하면 사행이 심하지 않는 자연하천에서 무차원 횡분산계수는 0.3 ~ 0.9의 범위에 있다고 정리한 바 있는데, 보정된 횡분산계수는 합리적인 범위 내에 있다고 사료된다. 그리고 결정된 무차원 종분산계수는 전단류(shear flow)의 연직분포만을 고려한 Elder (1959)의 값(5.93)에 비해 크게 산정되었지만, 실제 자연하천에서 무차원 종분산계수를 관측한 과거 연구결과들과 비교하여 큰 차이를 보이지 않는다. 그 예로 Piasecki and Katopodes (1999)는 미국 Potomac강에서 2차원 혼합모형을 기반으로 무차원 종분산계수를 21.0 ~ 63.0의 범위로 제안한 바 있다. Baek and Seo (2010)는 추적기법(2D ST RP)을 활용하여 홍천강 만곡구간에서 무차원 종분산계수를 9.8 ~ 87.7로 산정하였으며, Seo et al. (2016)은 감천, 미호천, 청미천, 섬강 등지에서 무차원 값의 범위를 22.6 ~ 48.5으로 제안한 바 있다.
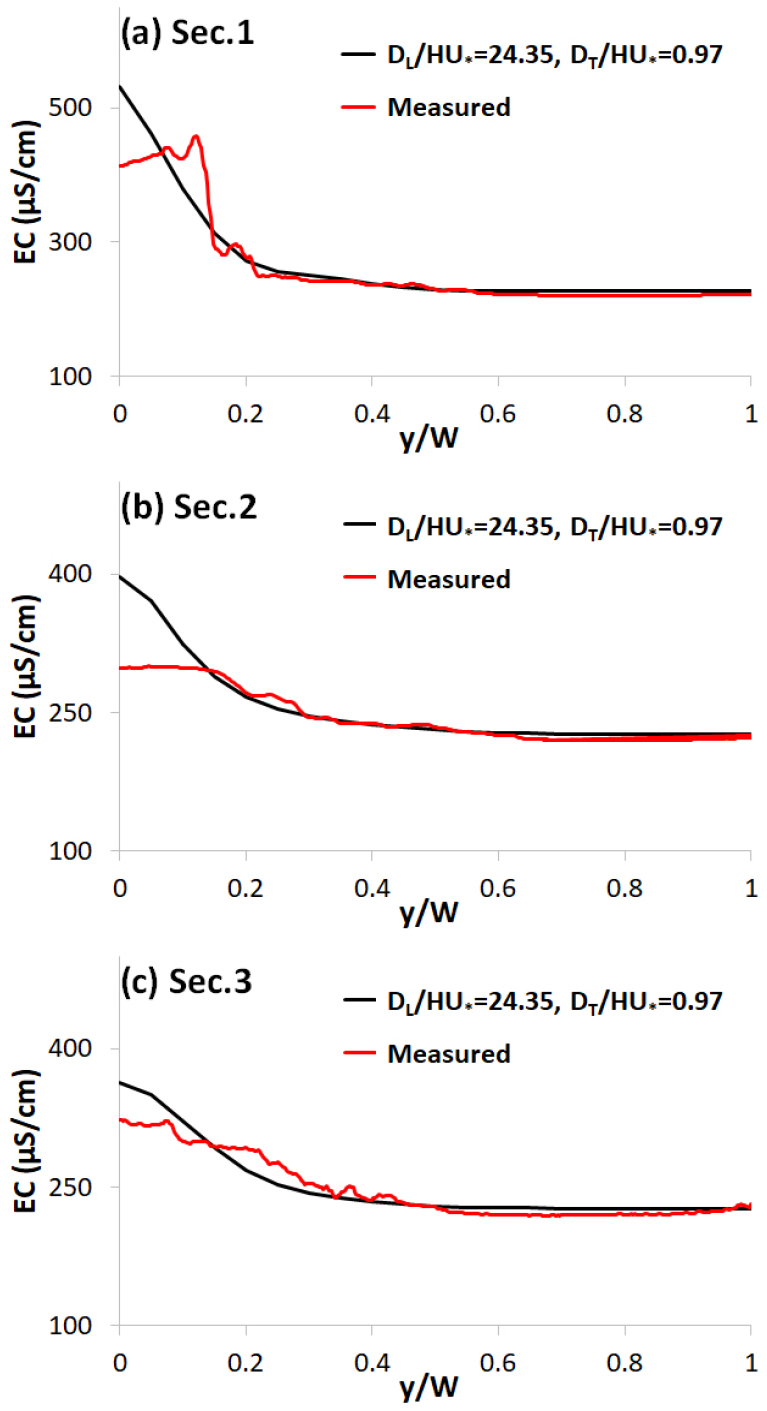
위와 같이 Case 1의 자료로 보정한 종/횡분산계수를 Case 2 자료로 검증해 보았다. 그 결과를 Fig. 5에 도시하였다. 그림에서 보는 바와 같이 모형의 계산치가 관측치를 비교적 잘 모사하고 있다. 또한 Table 2에 재현성 지표인 결정계수(R2)와 편이백분율(PBIAS)을 기록하였는데, Case 1 보다 나은 수치를 보였다.
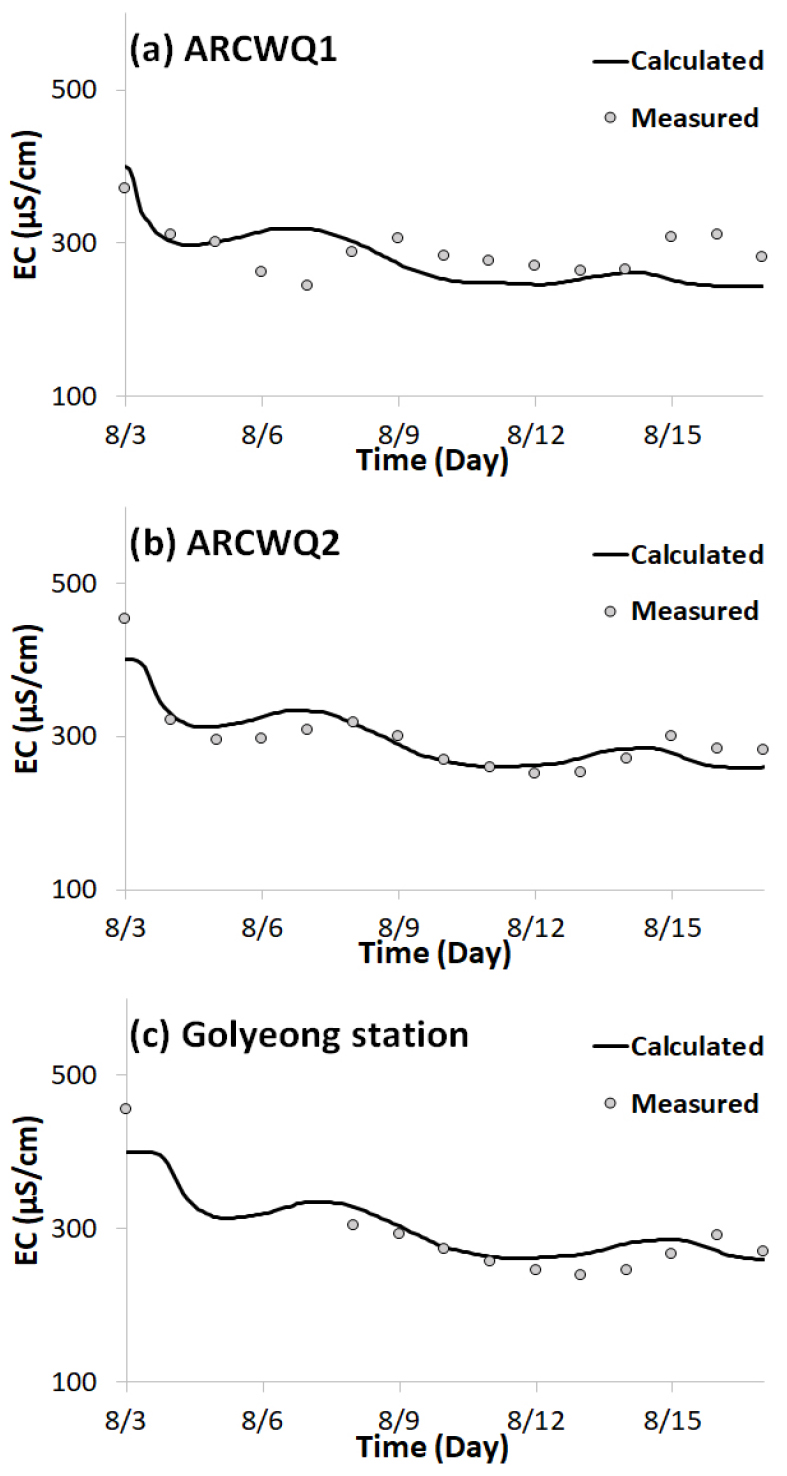
이상의 검/보정은 특정일에 흐름이 정상상태(steady state)라는 가정하에 수행된 것이다. 흐름이 부정류(unsteady flow)인 경우에도 결정된 종/횡분산계수가 사용하기 적절한지에 대해서는 검증해 볼 필요가 있다. 본 연구에서는 Fig. 2에 표기된 바와 같이 ARCROM (첨단기술 기반 하천 운영 및 관리 선진화 연구단)에서 설치한 자동 수질센서 ARCWQ1과 ARCWQ2, 그리고 물환경정보시스템에서 제공하는 고령관측소의 EC 값을 이용하여 종/횡분산계수를 검증하였다. 모의 기간은 2014년 8월 3일부터 동년 8월 17일까지 총 15일이며, 국가수자원관리종합시스템(WAMIS)에서 제공하는 해당 기간의 강정고령보와 강창교의 유량 및 달성보의 수위 자료를 수리모의를 위한 경계조건으로 할당하였다. 또한 물환경정보시스템에서 제공하는 다산관측소, 강창관측소, 성서관측소의 실시간 수질(EC) 측정값을 모형 경계 입력치로 할당하였다. 그 결과를 Fig. 6에 도시하였다. 이 그림에서 보는 바와 같이 정상상태에서 보정된 종/횡분산계수는 부정류 상황에서도 관측 농도를 잘 재현하였다. 또한 Table 2에 결정계수(R2)와 편이백분율(PBIAS) 값을 명기하였는데, PBIAS가 낮은 수치를 보여 관측치와 모형치간 차이가 근소함을 확인할 수 있었다.
3. 수질사고 시나리오 기반 혼합 해석
이상의 논의에서 관측농도자료를 바탕으로 모형의 매개변수인 종분산 및 횡분산계수를 검보정하였으며, 본 연구대상지에서는 두 값의 차이가 약 25배에 달하는 것을 확인하였다. 만약 해당 낙동강유역에서 수질오염사고가 발생하여 본 2차원 모형을 활용할 때, 검보정된 분산계수 대신 부적절한 값을 사용한다면 유해물질의 확산거동이 얼마나 달라지는지 확인할 필요성이 있다. 이를 위해 다음과 같은 시나리오를 상정하여 모형을 모의해 보았다. 금호강, 진천천, 사문진교 각각에서 유해물질이 사고로 유입되었다고 가정한 후, 하류에 있는 양수장들(좌안에 우암양수장, 우안에 월성양수장 위치함; Fig. 2 참조)에 도달하는 유해물질 농도를 계산하였다. 모의 기간은 2014년 8월 3일부터 동년 8월 17일까지 총 15일이며, 8월 4일 00시부터 02시까지 2시간 동안 유해물질이 5 ppm의 농도로 각 지점(금호강, 진천천, 사문진교)에 유입되었다고 가정한다. 유해물질은 페놀로 간주하였으며 휘발성 물질임을 감안하여 감쇠계수(decay rate)를 0.03/day로 설정하였다(Ahmadi et al., 2017). 분산계수에 따라 양수장에 도달하는 유해물질의 특성을 살펴보기 위해 먼저 검보정된 모형(무차원 종/횡분산계수를 각각 24.35와 0.97로 부여)으로 모의하였다. 그리고 검보정이 되지 않은 모형(무차원 종/횡분산계수가 24.35로 동일하게 부여)으로 모의하여 두 경우의 결과 차이를 분석하였다.
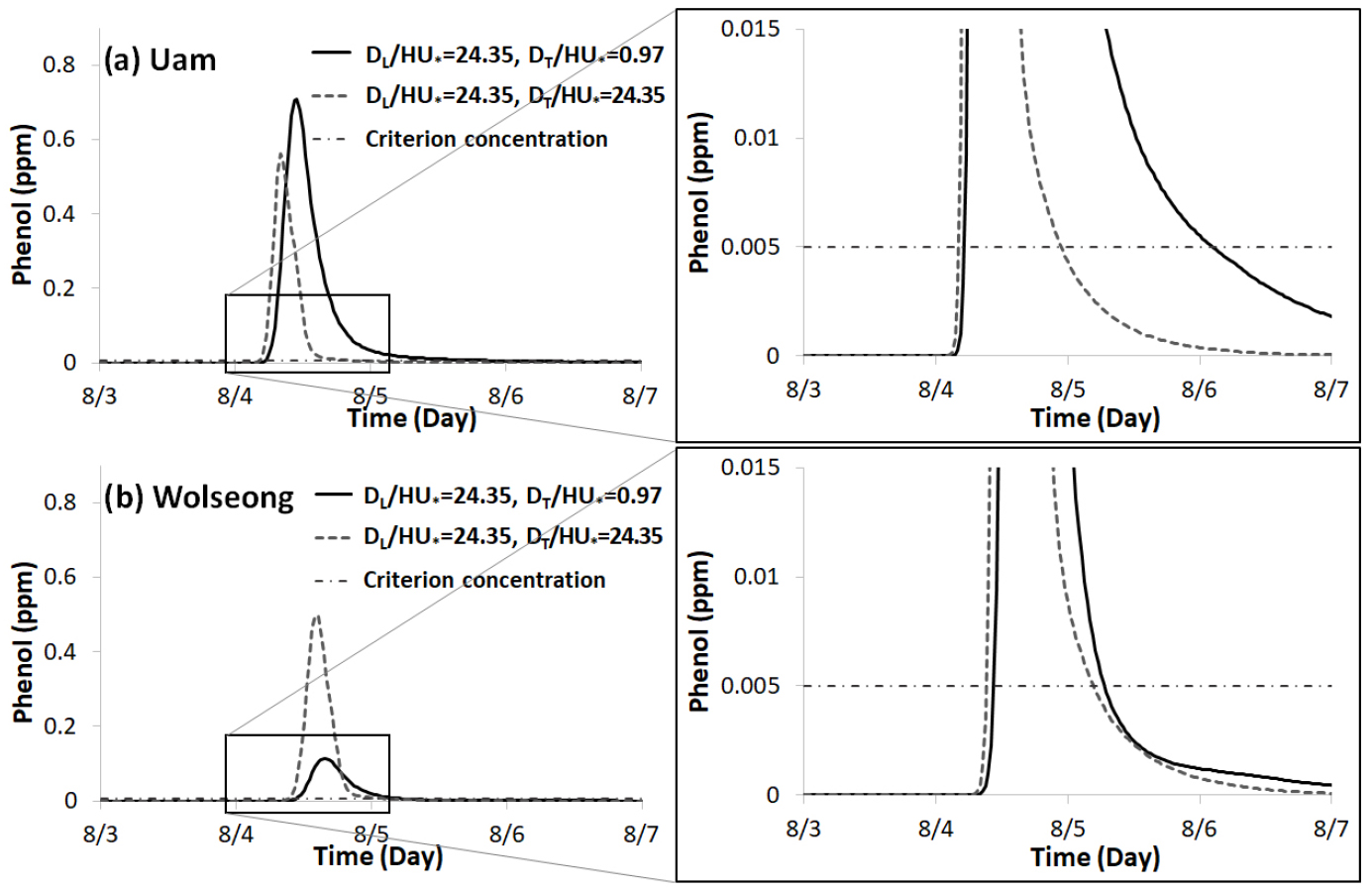
3.1 Scenario_1(금호강에 페놀 유입)
Fig. 2에서 보듯이 페놀이 유입된 금호강 사고 지점에서 우암양수장 까지 거리는 약 6 km, 월성양수장 까지는 약 10 km이다. 종/횡분산계수가 동일한 경우와 그렇지 않은 경우에 따라 모의된 우암양수장의 결과는 Fig. 7(a), 월성양수장의 결과는 Fig. 7(b)와 같다. 이 그림에서 확인할 수 있듯이 좌안측에 있는 우암양수장에서는 검보정된 모형의 결과가 종/횡분산계수가 동일한 경우에 비해 고농도가 발생하고, 지속시간도 길었다. 이는 좌안에서 합류하는 금호강에 고농도의 페놀이 존재하고 횡분산계수를 작은 값으로 부여하면 횡방향 분산(우안쪽으로 혼합되려는 기작)이 활발하지 않아 좌안측에 고농도가 유지됐기 때문으로 사료된다. 반면 조금 더 하류이면서 우안측에 있는 월성양수장을 보면 반대의 경향이 나타난다. 검보정된 모형의 결과가 종/횡분산계수가 동일한 경우에 비해 첨두치가 훨씬 낮게 발생하였다. 이는 상대적으로 횡분산이 활발하지 않아 우안측으로 유해물질이 많이 도달하지 못했음을 의미한다. Table 3에 양수장별 발생 첨두 농도, 도달시각 등을 정리하였다. 우암양수장의 경우 검보정된 모형의 결과가 그렇지 않은 모형의 결과보다 첨두농도가 크게 발생한 반면, 월성양수장에서는 반대의 경향이 나타나고 첨두치의 차이가 약 5배에 달하였다. 또한 페놀의 취수기준을 0.005 ppm으로 삼고(ME, 2020) 그 이상의 농도에서는 취수중단이 필요하다고 가정한 양수장별 기준농도 도달시각, 취수 중단 시간 등을 Table 3에 명기하였다. 페놀 유입으로 인한 취수중단시간을 보면 우암양수장에서는 검보정된 모형이 그렇지 않은 모형의 결과에 비해 약 2.2배 길었으며, 월성양수장에서는 큰 차이가 없었다. 분산계수의 적절한 할당은 사고 대응 의사결정에도 매우 중요한 역할을 할 수 있음을 시나리오 분석을 통해 확인할 수 있다.
Table 3.
Comparison of concentration characteristics at water intake facilities
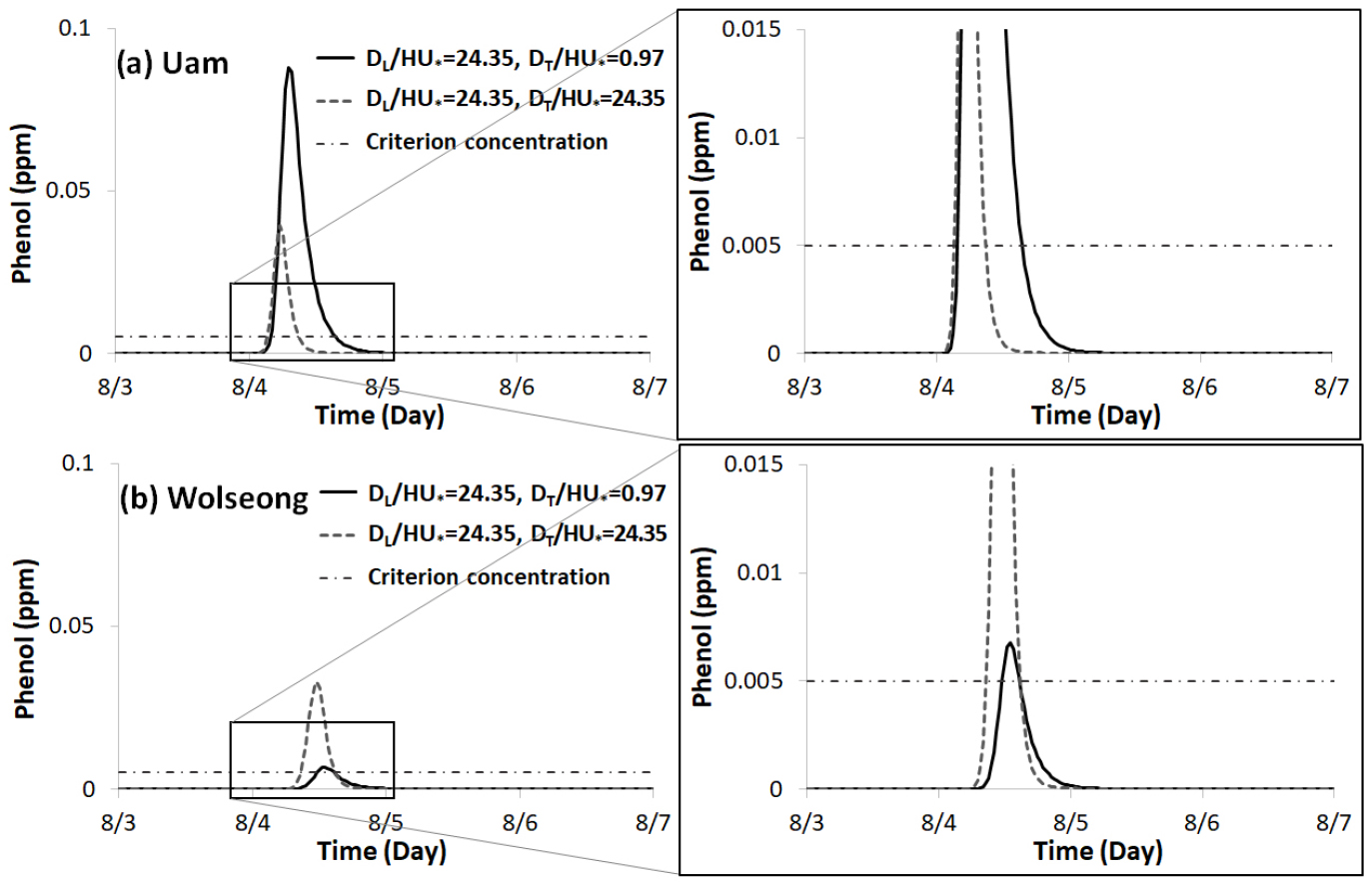
3.2 Scenario_2(진천천에 페놀 유입)
Fig. 2에서 보듯이 페놀이 유입된 진천천 사고 지점에서 우암양수장 까지 거리는 약 3 km, 월성양수장 까지는 약 7 km이다. 종/횡분산계수가 동일한 경우와 그렇지 않은 경우에 따라 모의된 우암양수장의 결과는 Fig. 8(a)에, 월성양수장의 결과는 Fig. 8(b)에 각각 도시하였다. 그리고 첨두농도, 도달시간, 기준농도 지속시간 등을 Table 3에 기재하였다. 이 그림과 표에서 보는바와 같이 Scenario 1(금호강에 페놀 유입)과 비교하여 첨두농도, 지속시간 등에서는 차이가 있었으나 전체적으로 농도곡선은 유사한 경향을 보여주고 있다. 이는 진천천이 금호강 직하류 좌안측에서 낙동강으로 합류하고 있으므로 유해물질의 혼합거동도 비슷할 수 밖에 없기 때문이다. 페놀 유입으로 인한 취수중단시간을 보면 우암양수장에서는 검보정된 모형이 그렇지 않은 모형의 결과에 비해 약 2배 길었으며, 월성양수장에서는 그와 반대로 종/횡분산계수가 동일한 모형의 결과가 2배 가까이 길어졌다.
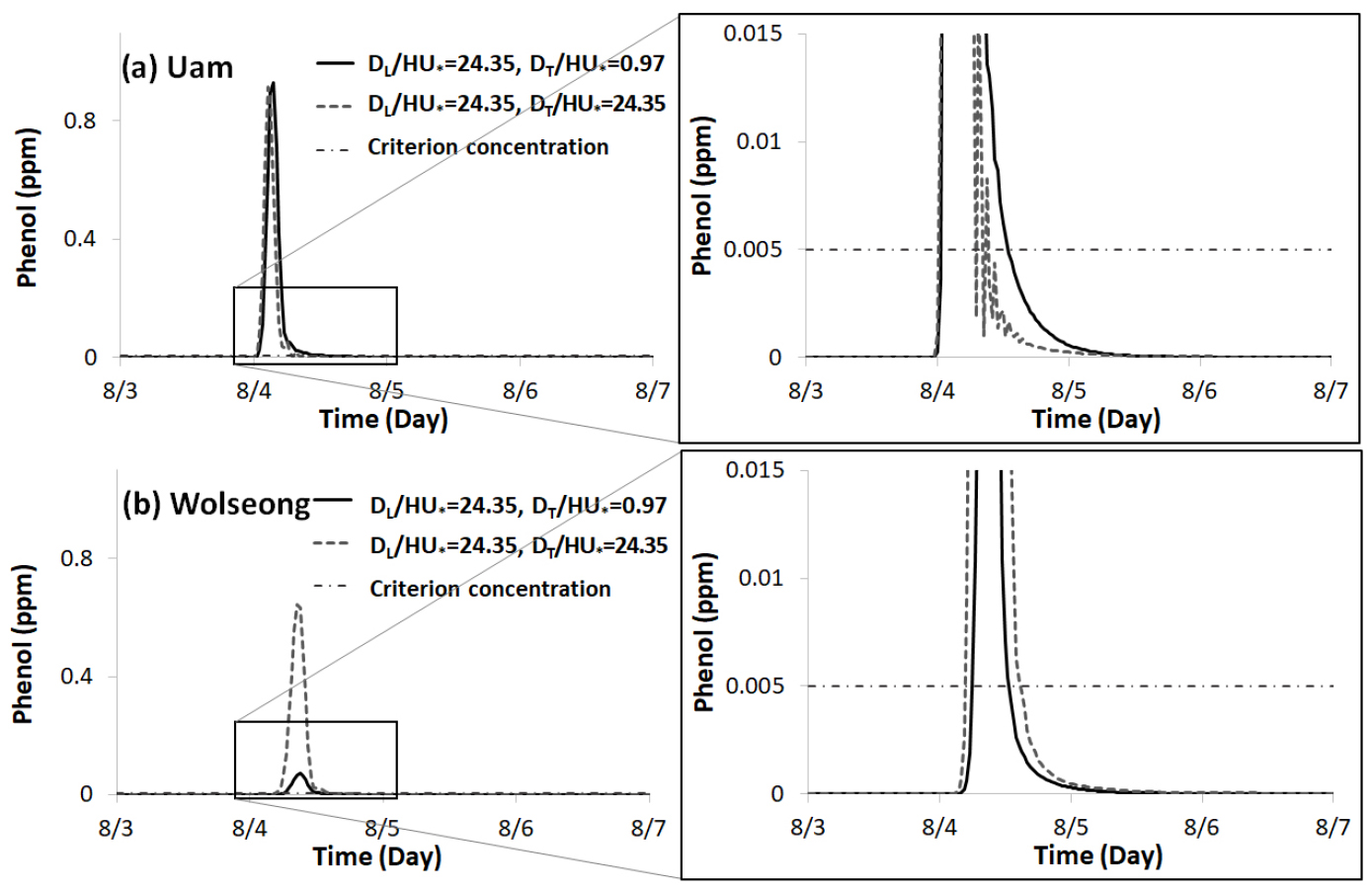
3.3 Scenario_3(사문진교에서 페놀 유입)
페놀을 실은 화물차가 사문진교를 지나다가 좌측 지점(y/W=0.2)에서 전복되어 낙동강에 유입되는 수질사고를 가정하는 것이 Scenario_3이다. 사문진교에서 우암양수장까지 거리는 약 2 km, 월성양수장까지는 약 6 km이다(Fig. 2). 종/횡분산계수가 동일한 경우와 그렇지 않은 경우에 따라 모의된 우암양수장의 결과는 Fig. 9(a)에, 월성양수장의 결과는 Fig. 9(b)에 각각 도시하였다. 첨두농도, 도달시간, 기준농도 지속시간 등을 Table 3에 또한 기재하였다. 이 그림과 표에서 보듯이 사문진교와 가까운 우암양수장에서는 분산계수의 영향이 크지 않아 농도곡선의 차이도 크지 않다. 반면 하류 월성양수장에서는 첨두농도, 지속시간 등에서 상당한 차이를 보였다. 분산계수에 따라 취수중단 시간이 우암양수장에서는 약 1.4배, 월성양수장에서는 약 0.7배의 차이가 발생하였다. 결과적으로 종/횡분산계수값의 비율에 따라 유해물질이 양수장에 도달하는 시간, 첨두농도 등의 특징이 매우 상이하게 나타났다. 이는 실제로 페놀이 유입된다면 양수장 등에서 적정시간 취수중단 등의 조치를 취해야 하는데, 해석모형의 분산계수가 의사결정에 큰 영향을 미칠 수 있음을 보여준 단적인 사례라 할 수 있겠다.
4. 결 론
하천에 유입된 유해물질의 거동을 평면 2차원적으로 평가할 때, 종방향 및 횡방향분산계수를 적절히 입력하는 것이 해석 정확도를 높이는데 필수적인 요소임에도 불구하고 다른 매개변수들에 비해 간과되는 경향이 많다. 특히 수질농도가 서로 다른 지류와 본류가 만나는 경우, 합류 이후 혼합거동은 분산계수에 의해 좌우된다고 할 수 있다. 이에 본 연구는 낙동강에 금호강과 진천천이 합류하는 구간을 연구대상지로 선택하고, 상류 특정지점에서 유해물질(페놀)이 유입되었다는 가정하에 분산계수가 검/보정된 모형(종/횡분산계수가 25배 차이)으로 하류 양수장에 도달하는 유해물질의 농도를 예측해 보았다. 결과의 비교검증을 위해 분산계수가 검보정되지 않은 모형(종/횡분산계수를 동일한 값으로 부여)으로 유해물질의 양수장 도달 농도 또한 계산해 보았다.
만일 펄스 형태의 페놀이 금호강이나 진천천 상류에 유입된다면 하류 낙동강 좌안측에 있는 우암양수장에서는 검보정된 모형의 결과가 종/횡분산계수가 동일한 경우에 비해 고농도가 발생하고, 지속시간도 길었다. 이는 좌안에서 합류하는 금호강이나 진천천에 고농도의 페놀이 존재하고 횡분산계수를 작은 값으로 부여하면 횡방향 분산이 활발하지 않아 좌안측에 고농도가 유지됐기 때문으로 해석된다. 반면 조금 더 하류이면서 우안측에 있는 월성양수장을 보면 반대의 경향이 나타난다. 검보정된 모형의 결과가 종/횡분산계수가 동일한 경우에 비해 첨두치가 훨씬 낮게 발생하였다. 이는 같은 원리로 횡분산이 활발하지 않아 우안측으로 유해물질이 많이 도달하지 못했음을 의미한다. 페놀을 실은 화물차가 사문진교를 지나다가 전복되어 낙동강에 유입되는 수질사고를 가정하면 사문진교와 가까운 우암양수장에서는 분산계수의 영향이 크지 않아 농도곡선의 차이도 크지 않았다. 반면 하류 월성양수장에서는 첨두농도, 지속시간 등에서 상당한 차이를 보였다.
실제로 페놀과 같은 유해물질이 유입된다면 취/양수장에서 취수기준 농도를 넘어가는 경우 취수중단 등의 조치를 취해야 하는데 본 연구에서 모의한 시나리오에서는 종/횡분산계수를 각각 어떤 값으로 부여하였느냐에 따라 2배 이상의 취수중단 시간 차이가 발생하였다. 이는 해석모형의 분산계수가 수질사고 대응 의사결정에 큰 영향을 미칠 수 있음을 보여준 좋은 사례라 할 수 있겠다. 앞으로 하천에 수질사고 예측/대응 시스템을 구축하는 경우, 계산엔진으로 활용되는 이송-분산 모형의 분산계수 결정에 유의해야 함을 다시금 환기시킨다. 그리고 본 연구의 대상지인 낙동강/금호강 합류점과 같은 국내 대표 합류구간들에서는 분산계수의 값을 추후 연구를 통해 미리 산정해 놓는 것이 효과적인 사고대응에 필요한 작업이라 사료된다.