1. 서 론
2. 피해도 분석 모형
2.1 개별 관로의 피해도 분석모형
2.2 단위관망의 피해도 분석
2.3 Monte Carlo Simulation
3. 실제 상수도관망 적용결과
3.1 내덕1동 상수도관망
3.2 개별 파이프의 누적피해도(Sy) 분석결과
3.3 단위관망의 누적피해도 분석결과
4. 결 론
1. 서 론
우리나라 상수도관망의 총연장은 22만 8천여 km이며 매년 증가하는 추세이다. 이 가운데 21년 이상 경과된 노후관은 79,461 km (34.8%)이며 교체가 시급한 실정이다(ME, 2022). 2019년에 발생한 인천의 적수 사고와 같은 상수도관망의 노후화 문제로 인한 관로 사고의 발생이 증가하고 있으며 최근 관로 사고 3건 중 1건은 노후화에 기인한 것으로 여겨지고 있다(K-water, 2015). 특히 상수도관은 관 외부로는 토양과 접촉하고 있으며, 내부로는 수돗물과 접촉하고 있어 토양 또는 물과 관련된 다양한 물리 화학적 인자에 의해 노후화가 진행된다. 관의 노후화는 부식에 원인 한 것으로 이는 관의 두께를 감소시키고 관 자체가 가지고 있는 강도가 저하되어 결국에는 상수도관이 파괴되어 사용할 수 없게 된다. 국외에서는 SOC 시설물의 고령화 추세에 따른 사고 발생 위험성 증가, 시설물 보수/보강에 막대한 예산 소요 예측으로 국민의 안전 확보를 위한 사고예방, 적시 개량을 위한 과학적인 진단기술 확보, 그리고 개량을 통한 시설물의 수명증가 등이 주요 이슈로 부각되고 있다. 따라서 효율적이고 합리적인 유지관리를 위해 사용연수에 따른 상수도관망의 상태파악 및 그에 따른 안전도 분석에 대한 연구가 필요하다.
Caleyo et al. (2002)는 노후화가 진행중인 파이프의 잔존수명을 예측할 수 있는 추계학적 방법을 제시하였다. 이 연구에서는 시간경과에 따라 일정한 부식 형태를 갖는 정상상태 부식모델을 적용하였다. 시간경과에 따른 부식으로 인한 파괴확률 산정을 위해 SORM (Second Order Reliability Method) 방법을 사용하여 해석하고 Monte Carlo Integration 방법을 한계상태 함수로 적용되었다. 하지만 확률변수들은 모두 lognormal 분포함수 또는 정규분포로 가정하여 사용하였다.
Kim et al. (2014), Kim et al. (2006)은 파이프의 부식과 노후화에 대한 연구를 진행하였지만 부식속도와 부식의 특성에 대한 연구만 진행되었으며, 상수도관의 피해도 분석 연구는 부족한 것으로 확인되었다.
Bae et al. (2008)은 상수도관의 내면 및 외면의 부식상태를 평가하였으며, 내면 및 외면의 부식속도와 매설연수의 관계를 통해 내면 및 외면 부식속도, 국내의 토양특성이 관 외면부식에 미치는 영향을 평가하여 관 외면의 노후상태를 예측할 수 있는 부식속도 모델을 제안하였다. 연구를 통해 토양의 부식 영향인자에 의해서 부식성이 좌우되는 것이 아닌 이들 인자를 포함한 다양한 인자들이 복합적으로 관 부식에 영향을 끼치는 것으로 판단했다.
Park (2011)은 상수관의 개량 우선순위를 결정하기 위해 평가되어야 하는 인자를 관의 파손이 전체관망에 미치는 영향과 개별관로의 특성으로 구분하였다. 또한 퍼지기법을 통해 상수도관의 개량우선순위를 결정할 수 있는 모형을 개발하였다. 하지만 제안한 방법론의 실제 관망에 대한 적용성은 검토해야할 것으로 판단된다.
Petersen and Melchers (2012)는 파이프 부식과 관의 노후화 특성을 파악하기 위한 연구를 진행하였다. 하지만 국내와 동일하게 하나의 파이프를 추적하여 부식깊이와 노후에 대한 특성을 분석하지 않고, 임의의 파이프를 통해 분석을 진행하였다. 그리고 파이프 내면부식과 외면부식을 하나의 부식으로 판단하고 분석하였기 때문에 데이터 자체의 편차가 큰 것으로 확인되었다.
Park and Kim (2017)은 상수도 기술진단 중 점수평가법을 통해 노후도를 평가하여 연구대상지역 상수관로의 잔존수명을 추정할 수 있는 모델을 개발하였다. 하지만 관로의 사고이력 및 토양의 물리화학적 성질 등을 고려하지 못하였다.
본 연구에서는 상수도관망의 사용연수에 따른 피해도를 정량적으로 산정하기 위해 추계학적 방법으로 피해도 산정모형을 개발하였다. 우선, 관내 압력과 사용연수에 따른 관두께 변화를 예측하였고 피해에 가장 큰 영양을 미치는 인자를 압력지수와 노후지수로 결정하여 상수도관망의 사용연수에 따른 피해도를 분석하였다. 관두께의 영향을 받는 노후지수는 MCS (Monte Carlo Simulation)을 이용해 확장된 데이터가 사용되었다. 이를 통해 실제 상수도관망의 피해도를 분석할 수 있었고, 시간에 따른 누적피해도를 산정할 수 있었다.
2. 피해도 분석 모형
2.1 개별 관로의 피해도 분석모형
본 연구에서는 상수도관망의 시간에 따른 피해도를 정량적으로 산정하기 위해 추계학적 해석방법을 사용하여 모형을 수립하였다. 우선 상수도관망 전체의 피해도를 분석하기 위한 개별관로의 피해도 평가식을 Eq. (1)과 같이 수립하였다.
여기서, 는 상수도관망의 단위관망(중블럭, 소블럭)별 피해율을 산정하기 위한 개별 파이프의 매설 경과년수에 따른 피해도이다. 식에 포함된 변수는 각각 , , , 이며 는 각 파이프의 매설 경과년수이고, 는 각 파이프의 초기관두께이다. 는 압력지수이며, 각 파이프의 정상류 상태의 압력 값과 최대수압설계기준 압력 값을 비교하여 결정하였으며, 아래 Eq. (2)와 같이 표현 가능하다.
여기서, 는 피해도 분석을 진행하기 위한 대상 파이프의 정수압 수두(m)이고 은 상수도 설계기준에 따른 최대 설계수압(수두 71 m)을 적용하였다. 은 노후지수로 아래 Eq. (3)과 같이 표현 가능하다.
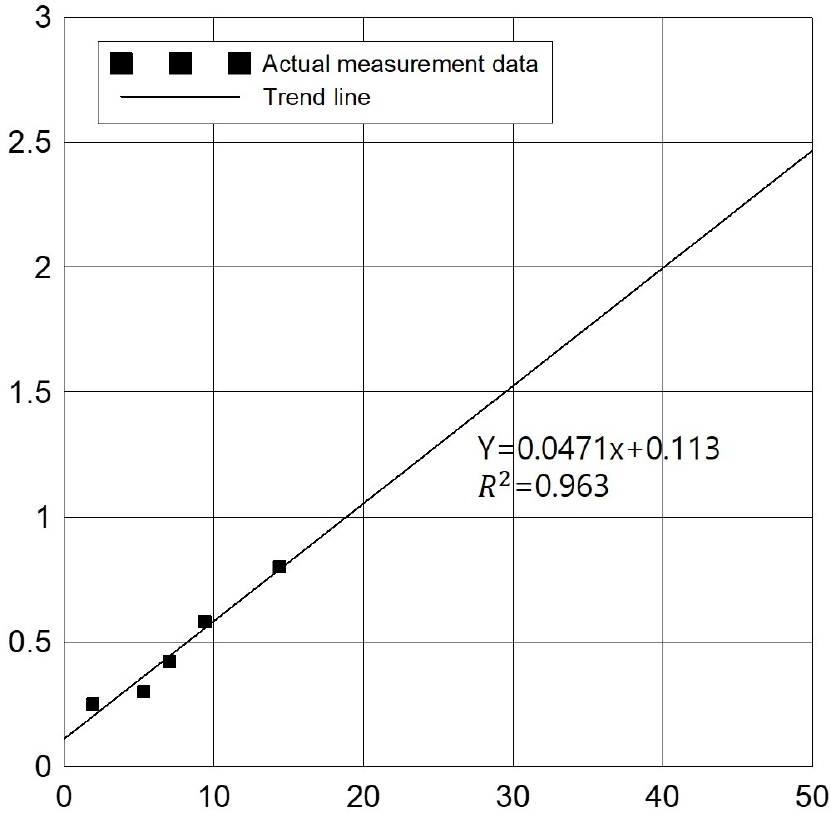
여기서, 는 대상 파이프의 초기 관두께(mm)이고, 은 잔존 관두께(Remaining Thickness)이다. 잔존관두께는 상수도관의 사용연수에 따른 부식깊이를 고려하여 해당관의 초기 관두께에 부식깊이를 빼주어 결정하였다. 시간에 따른 부식깊이의 변화는 Fig. 1과 같이 Romanoff (1957)의 실측데이터를 사용하여 결정하였다. 부식깊이 변화의 경우 국내외 많은 연구가 진행되었지만 선행연구의 경우 하나의 파이프를 추척하여 부식깊이를 분석하지 않고 여러 지역에 매설되어 있는 임의의 파이프를 통해 분석을 진행하였다. 또한, 파이프 내면부식과 외면부식을 하나의 부식으로 판단하여 분석을 진행하였으며, 직경이 비슷한 범위의 파이프를 하나의 그룹으로 묶어 연구를 진행하였다는 한계점이 존재한다. 따라서 본 연구에서는 부식 발생이 가능한 재질인 Steel pipe이고, 사용연수 증가에 따라 하나의 파이프를 추적하여 부식 깊이를 측정한 Romanoff (1957)의 실측데이터를 사용하여 노후지수를 산정하였다.
2.2 단위관망의 피해도 분석
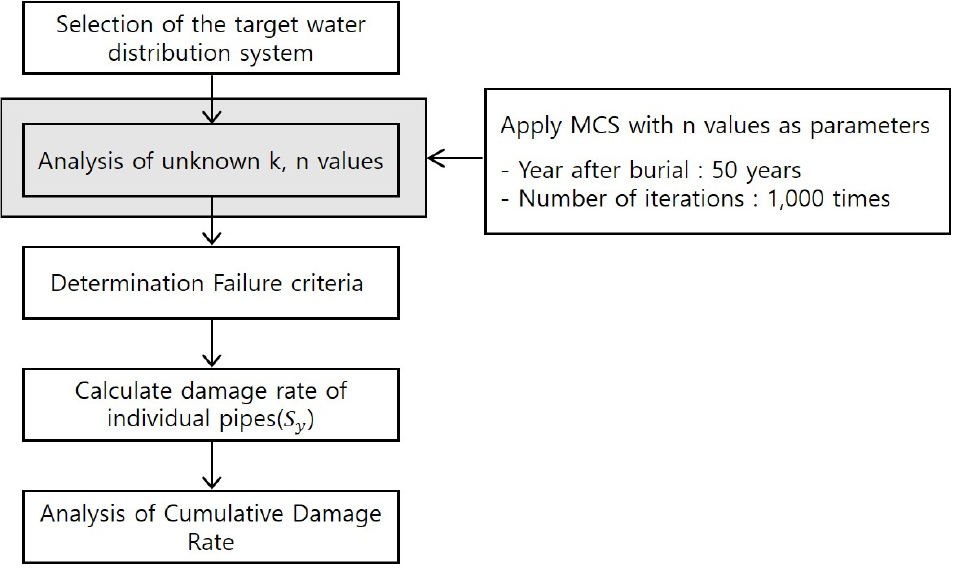
먼저 개별 상수도관의 매설경과년수에 따른 피해도()산정 후 단위관망(중블럭, 소블럭)별 상수도관망의 피해도를 분석하기 위한 모형을 수립하였다. 는 단일 상수도관에 대하여 하나의 피해도 값을 도출하며 이때 도출된 값이 정해진 수치 이상 나타날 경우 Failure 상태인 것으로 판단하여 불능 또는 파괴상태의 상수도관이고, 1이라고 표현하였다. 만약 피해도 값이 정해진 수치 이하로 나타날 경우 안정된 상수도관으로 판단하여 0으로 표현하였다(여기서 0은 제 기능을 하고 있는 상수도관을 의미한다). 본 연구에서는 임의로 0.2를 피해도 Failure 기준으로 정하였다. 이후, 단위관망에서 대상 상수도관을 선정한 후 각 상수도관의 피해도분석을 통해 단위관망의 매설경과년도에 따른 누적피해도(Cumulative damage rate)를 산정 할 수 있다. 아래 Eq. (4)는 단위관망의 누적피해도 산정식이며, 은 개별 상수도관의 분석결과 중 Failure 상태인 상수도관의 개수이고, 는 피해도 분석에 사용된 전체 상수도관의 개수이다. 본 연구에서는 Failure가 발생한 상수도관 개수인 를 전체 상수도관 개수인 으로 나누어주어 누적피해도를 산정하였다. Fig. 2는 MCS를 적용한 상수도관망의 누적피해도 평가의 순서도이다.
2.3 Monte Carlo Simulation
결정론적모형(deterministic model)은 변수 사이의 관계가 확실하여 방정식을 이용하여 모형을 만들고 수학적인 방법을 통해 변수에 대한 해를 찾아 예측치를 정확하게 결정할 수 있는 모형이다. 반면에 확률론적모형(probabilistic model)은 결과를 정확하게 예측할 수 없는 모형이기 때문에 확률모형의 모수(parameter)에 대해 여러 수치적인 방법(numerical method)을 반복적으로 시도하여 확률변수의 분포를 얻게 된다. 이러한 분포를 생성하기 위해 반복적으로 이용하는 수치를 일련의 난수(random number)로부터 얻기 위해 MCS (Monte Carlo Simulation)를 이용하게 된다(Stephenson and Holbert, 2003). MCS는 모의실험의 형태로 불확실한 상황에서 의사결정을 하기 위한 확률적분포를 무작위로 생성하는 방법이다. MCS 연구는 두 가지 유형의 사양을 다르게 지정할 수 있으며 첫 번째는 조작요인(manipulated factors)인 모집단의 사양(population specification)이고 두 번째는 몬테카를로 변수(Monte Carlo Variable)이다. 몬테카를로 변수는 표본의 사례와 반복횟수(replication)를 나타낸다.
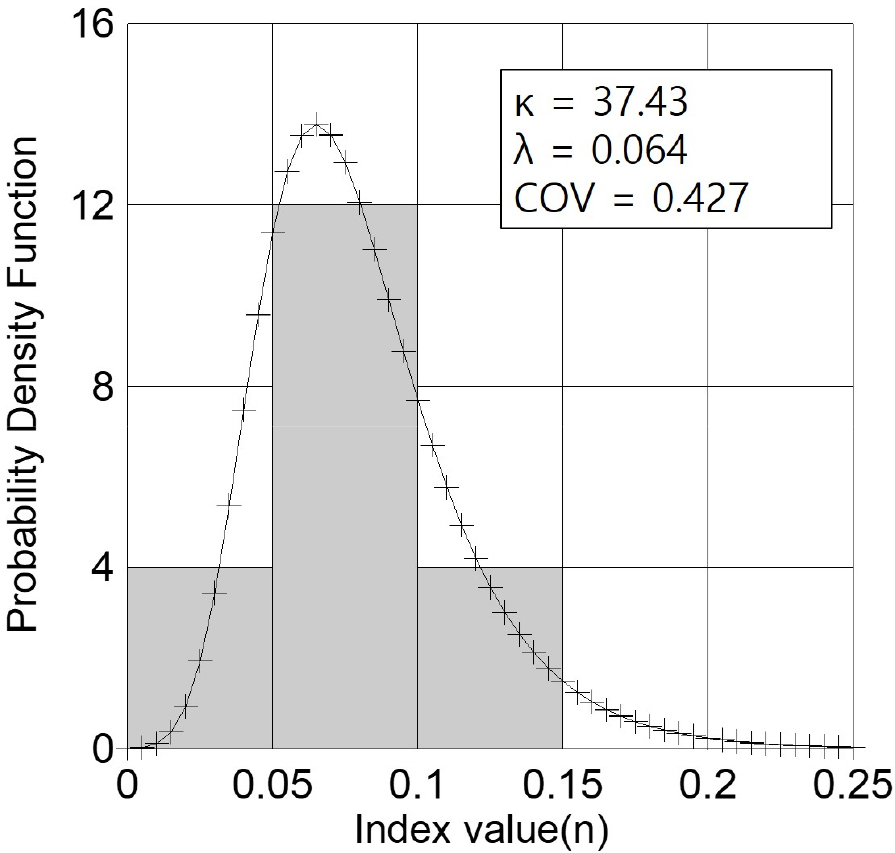
본 연구에서는 사용연수 증가에 따른 대상 상수도관망의 누적피해도 분석을 위해 MCS를 사용하였다. Romanoff (1957)의 매설경과년수 증가와 이에 따른 부식에 의한 관두께 변화 실측치를 사용하여 산정된 노후지수(aging index, )를 모수로 사용하여 랜덤하게 난수를 발생시켜 개별상수도관의 매설 경과년도에 따른 노후도 값을 확장하여 피해도를 분석하였다. 난수를 발생시킨 노후지수의 확률밀도함수는 Fig. 3과 같이 검벨분포로 확인되었다. 아래 Eq. (5)는 노후지수의 검벨분포 함수이고 통계적 특성 분석결과 Table 1과 같이 평균은 0.08, 축척계수(κ)는 37.43, 형상계수(λ)는 0.064, COV (Coefficient of variation)는 0.427로 나타났다. 통계적 특성결과를 사용하여 MCS를 통해 매설경과년도 50년, 반복횟수 1,000회를 적용하여 개별관로에 대한 피해도 분석을 진행하였다.
Table 1.
Analysis result of statistical characteristics of aging index ()
| Mean | Standard deviation | Coefficient of variation | κ | λ |
| 0.0803 | 0.0343 | 0.427 | 37.43 | 0.064 |
개별 파이프의 누적피해도 분석을 위해 압력지수 값을 결정하였다. 값은 해당 파이프의 정수압(m)과 설계기준 최대수압(m)를 통해 산정하였다. 대상 파이프는 관 직경 200 mm이상 관 길이 100 m이상을 기준으로 적용하였으며 이에 해당되는 파이프 14개를 대상으로 분석하였다. 그 결과 대상 파이프의 값은 Table 2와 같이 나타났다.
3. 실제 상수도관망 적용결과
3.1 내덕1동 상수도관망
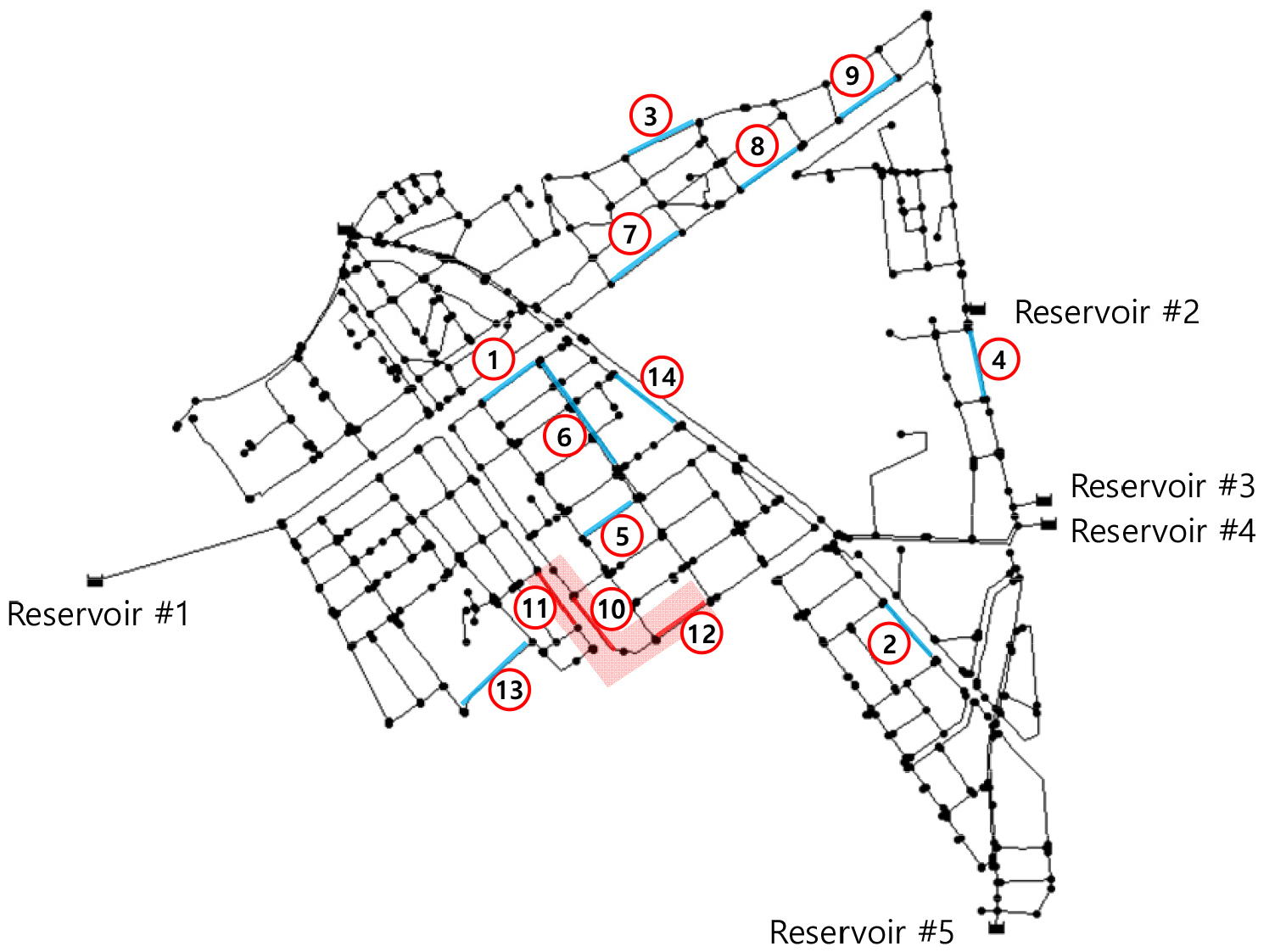
본 연구에서는 개발된 누적피해도 산정모형을 청주시의 실제 상수도 관망에 적용하여 시간에 따른 피해도를 분석하였다. 대상 관망은 청주시 내덕1동 상수관망으로 1.48 km2의 면적과 급수인구 약 10,000명이 거주하고 있으며, 배수유량 2,491 m3/day, 805개의 절점과 912개의 파이프로 구성되어있는 중·대규모 블럭이다. 연구에서는 피해도를 분석하기 위해 시간 경과에 따라 부식 특성이 발생하는 DCIP 재질로 구성되어있고 관 직경 200 mm이상, 관 길이 100 m이상인 상수도관을 선별하여 개별파이프의 매설경과년수에 따른 대상관의 누적피해도를 분석하였으며, 이후 단위관망 전체의 누적피해도를 산정하였다. 상수도관 선별결과 대상 파이프의 개수는 총 14개 이고 대상파이프의 매설년도는 1991년도부터 2008년도까지 다양하게 분포되어 있으며, 정수두압은 평균 45.04 m로 확인되었다. Fig. 4는 선별된 14개 파이프를 표시한 내덕1동 상수도관망이고 누적피해도가 가장 높은 10번, 11번, 12번 파이프를 붉은색으로 표시하였다. Table 3은 대상관의 제원이다.
Table 3.
Specification of each pipe
3.2 개별 파이프의 누적피해도() 분석결과
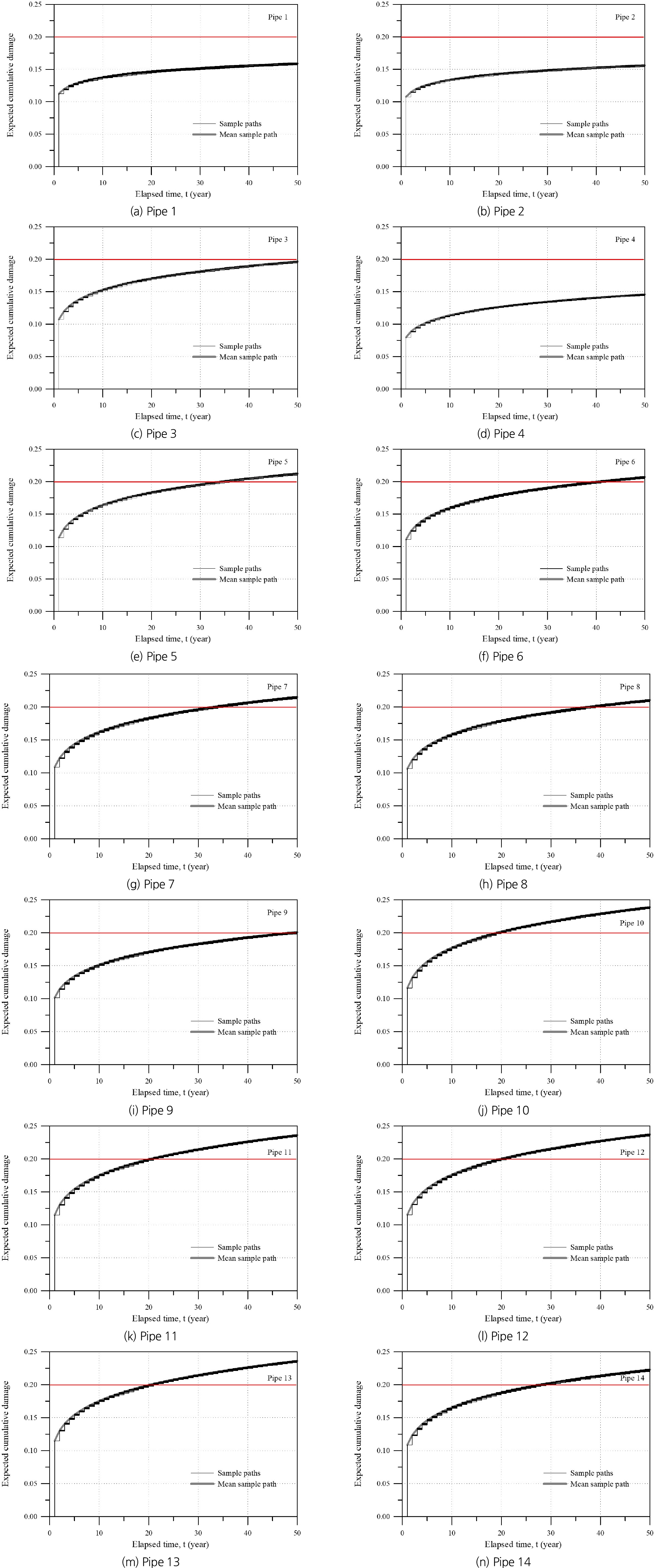
매설 경과년수에 따른 개별파이프의 누적피해도 분석결과 Fig. 5에서 확인할 수 있듯이 매설 경과년수 19년이 경과하였을 경우 10번 파이프에서 가장 먼저 Failure 기준치인 0.2를 초과하는 것으로 확인되었고, 뒤를 이어 12번, 11번 13번 파이프 순으로 Failure 기준을 초과하는 것을 확인할 수 있었다. 반면 매설 경과년수 증가에 따른 누적피해도가 가장 낮은 파이프는 4번 파이프인 것으로 나타났다. 파이프의 압력지수 및 노후지수를 통해 대상 상수관망의 누적피해도를 분석한 결과 파이프의 상용압력 크기가 크더라도 사용년수 증가에 따른 누적피해도는 동일하게 증가하지 않는 것으로 확인되었다. 마찬가지로 초기 매설년도가 오래된 파이프여도 사용연수 증가에 따른 누적피해도는 동일하게 증가하지 않는 것으로 확인되었다. Table 4는 대상 파이프의 누적피해도 위험순위이다.
Table 4.
Rank of damage rate
| Rank of damage rate | Pipe No. | Destruction year | Rank of damage rate | Pipe No. | Destruction year |
| 1 | 10 | 19 | 8 | 8 | 33 |
| 2 | 12 | 20 | 9 | 6 | 33 |
| 3 | 11 | 21 | 10 | 9 | 43 |
| 4 | 13 | 21 | 11 | 3 | 43 |
| 5 | 14 | 26 | 12 | 1 | - |
| 6 | 5 | 28 | 13 | 2 | - |
| 7 | 7 | 29 | 14 | 4 | - |
3.3 단위관망의 누적피해도 분석결과
개별파이프의 누적 피해도() 분석결과를 통해 내덕1동 상수도관망 전체의 누적피해도를 산정하였다. 본 연구에서 누적피해도의 기준은 개별파이프의 피해도 값이 0.2를 초과 하는 것으로 결정하였으며, 기준을 초과하면 1, 기준 미만이면 0으로 결정하여, 파이프 14개에 대해 분석하였다. 이후 매설 경과년도별 Failure가 발생한 파이프 개수를 전체 파이프 개수인 14개로 나누어주어 관망 전체의 누적피해도를 산정하였다. 그 결과 Fig. 6에서 확인할 수 있듯이 매설경과년도가 20년, 30년, 40년, 50년으로 증가할 경우 누적피해도는 각각 0.071, 0.429, 0.643, 0.786으로 나타났으며, 계단식 형태로 피해가 누적되는 것을 확인할 수 있다.
4. 결 론
본 연구에서는 사용연수 경과에 따른 상수도관의 노후도를 정량적으로 산정하기 위해 추계학적 방법을 사용하여 피해도산정 모형을 개발하였다. 먼저 관망의 피해도에 가장 큰 영양을 미치는 인자인 관내압력과 노후도를 결정하였다. 관두께에 영향을 받는 노후지수는 MCS를 이용해 난수를 발생시켜 얻은 데이터를 통해 분석을 진행하였다. 이를 통해 실제 상수도관망의 시간에 따른 개별파이프의 누적피해도를 확인할 수 있었으며, 단위관망(중블럭, 소블럭)의 피해도를 산정할 수 있었다.
1. 사용연수 증가에 따른 개별파이프의 누적 피해도 분석결과 내덕1동 상수도관망의 경우 10번 파이프에서 사용연수 19년이 지났을 때 피해도는 0.2로 나타났으며, 가장 먼저 Failure 기준치를 초과하는 것을 확인할 수 있었다. 또한 사용연수 20년 경과 시 12번 파이프, 21년 경과 시 11번과 13번 파이프의 순서로 Failure 기준치를 초과하는 것을 확인하였다. 반면 사용연수 증가에 따른 누적피해에 가장 안전한 파이프는 4번 파이프인 것으로 확인되었으며, 뒤를 이어 2번, 1번, 3번 파이프의 순서로 안전한 파이프인 것으로 나타났다.
2. 내덕1동 상수도관망 전체의 누적피해도 산정결과, 사용연수 20년 경과 시 약 7%의 누적피해도가 나타나는 것으로 확인되었으며, 사용연수 30년 경과 시 누적피해도가 약 43%까지 급증하는 것을 확인할 수 있었다. 또한 50년 동안 유지보수 없이 사용할 경우 누적피해도는 79%까지 증가하는 것을 확인하였다.
3. 파이프의 압력지수 및 노후지수를 통해 대상 상수관망의 누적피해도를 분석한 결과 파이프의 상용압력이 크거나 매설년도가 오래된 파이프라도 사용년수 증가에 따른 누적피해도는 동일하게 증가하지 않는 것으로 확인되었다. 이는 지역마다 다른 압력조건 및 다양한 매설환경에 기인한 것으로 판단된다. 따라서 향후 상수관망의 안전도 분석 시 압력과 매설년도는 물론 다양한 매설환경 등을 종합적으로 고려해야 할 것으로 판단된다.
본 연구에서 개발된 상수관망의 사용연수 증가에 따른 누적피해도 분석결과를 실제 관로 교체사업에 활용한다면 개선 우선순위를 보다 명확하게 판단할 수 있으며, 경제적이고 효과적인 상수도관망 유지관리 기술이 될 것으로 판단된다.