1. 서 론
2. 홍수경보를 위한 홍수위 및 강수량 산정절차
3. 모형의 기본이론
3.1 지형학적 순간단위유량도(GIUH)
3.2 한계유량 산정방법
4. 대상 유역 및 특성
5. 결 과
5.1 GIUH 매개변수 및 첨두홍수량 산정
5.2 경보수위 설정
5.3 산정방법별 한계유량 비교
6. 요약 및 결론
1. 서 론
하천 인근 지역에서는 홍수로 인하여 지난 수년간 다양한 피해가 발생하고 있으며, 우리나라에서는 이러한 홍수피해를 경감시키기 위해 구조적 및 비구조적 대책들을 세우고 있다. 중요한 비구조적 대책 중의 하나가 홍수경보시스템을 구축하는 것이다. 일반적으로 홍수경보시스템을 구축하기 위하여 홍수경보 기준지점의 수위를 설정하며 이에 대응하는 한계유량을 산출하고 강우-유출모형을 통하여 한계유량에 대응하는 경보강수량을 산정하는 방식을 택하고 있다. 홍수경보시스템을 위한 강우-유출모형을 지형학적 순간단위유량도가 일반적으로 사용되어지고 있다(Kim et al., 2018; Sahoo and Jain, 2018; Mohammadi et al., 2019; Bamufleh et al., 2020).
특히, 한계유량을 산출하는 경우, 측량성과의 부재 영향으로 다양한 과업 및 연구에서 Manning 공식을 통하여 한계유량을 산출하고 있다(Kim et al., 2003; Ahn et al., 2005; Oh et al., 2006; Kim et al., 2018). 하지만 Manning식은 하천 상류에서의 흐름에 대한 정보 없이 단순히 하천 특정지점의 정보만을 활용하여 유량의 정확한 산출에는 한계가 있다.
따라서 본 연구에서는 Manning식에 의해서 산출되는 한계유량의 적정성을 확인하고, 보다 정확한 산출 방식을 제시하기 위해 HEC-RAS 모형을 통하여 한계유량을 계산하였고 Manning식에서 나온 값과 비교 분석하였다.
이를 위해 본 논문을 다음과 같이 구성하였다. 먼저 홍수경보를 위한 홍수위 및 강수량 산정절차를 2장에서 설명하고 본 연구에서 적용되는 모형의 이론을 3장에서 설명하며 대상 유역 및 특성을 4장에서, 결과 및 결론을 5장과 6장에 나타내었다.
2. 홍수경보를 위한 홍수위 및 강수량 산정절차
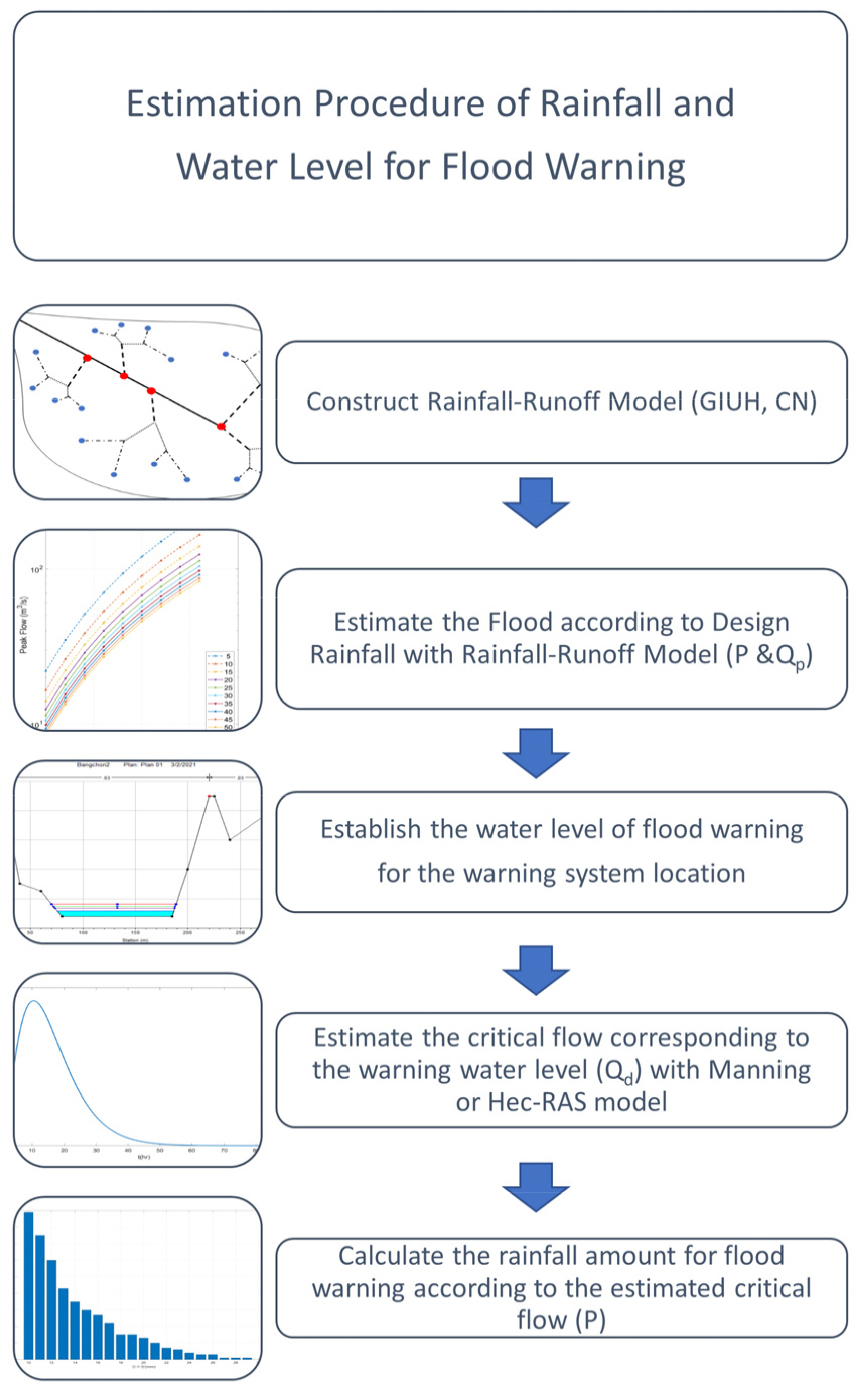
Fig. 1에서 보는 바와 같이 홍수경보를 위한 강수량 및 경보 수위를 산정하기 위한 절차는 다음과 같다.
1) 먼저 강우-유출모형을 구축한다. 일반적으로 홍수경보를 위한 강우-유출모형은 지형학적 특성을 반영하는 것이 중요하게 다루어져 지형학적 순간단위유량도(Geomorphological Instantaneous Unit Hydrograph, GIUH)를 적용한다. 또한, 유효강우량 산정을 위해서 Curve Number (CN)를 이용하게 된다.
2) 구축된 강우-유출모형을 바탕으로 다양한 설계강우량(P, mm)별 첨두홍수량(Qp, m3/s)을 산정한다. 이때 사용되는 강우량은 CN값을 통하여 유효강우량을 산정하며 선행강우를 가정하여 CN (III) 상태의 값을 적용한다. 또한, 홍수에 취약한 상태를 고려하기 위해 초기손실을 무시한 상태 (i.e. Ia=0)로도 홍수량을 산정한다.
3) 다음으로, 홍수경보를 실시하는 수위관측지점에서 경보발령 수위를 설정한다. 일반적으로 경보 발령 수위는 제방의 범람 및 붕괴 상황에 대비하거나, 또는 인명의 안전 확보를 위해 하천의 수심이 50 cm이상으로 증가할 때를 기준으로 하고 있다.
4) 설정된 경보발령 수위에 대응되는 한계유량(Qd, m3/s)을 산출한다. 한계유량을 산출하기 위해서는 수위관측지점의 경사 및 단면을 반영한 Manning 공식을 사용하거나 유량에서 수위를 구할 수 있는 수문모형(e.g. HEC-RAS)을 사용하여 경보발령 수위에 대응하는 유량을 구할 수 있다.
5) 마지막으로, 산정한 한계유량(Qd, m3/s)과 대응되는 첨두홍수량(Qp, m3/s)를 가지는 경보발령 강수량(P, mm)값을 구하게 된다.
3. 모형의 기본이론
3.1 지형학적 순간단위유량도(GIUH)
지형학적 순간단위유량도를 산정하기 위해서는 하천망을 Horton이 제시한 방법에 따라 구분하여야 한다. 유역의 최대 하천차수(Ω)를 가지는 하천망 구분방법은 다음의 원칙을 준수하여 분류하게 된다(Strahler, 1952).
1) 유역 표면상의 흐름을 통해 하천을 시작하는 하도는 일차하천망으로 정의된다.
2) 차수가 동일한 w인 두 하천이 합류하게 되면 합류된 하류의 하천차수는 w+1이 된다.
3) 다른 차수의 두 하천이 합류하게 되면 하류의 하천차수는 합류된 두 개의 하천차수 중 큰 차수를 가진다.
GIUH에는 하천특성을 반영한 Horton의 법칙에서 기인한 변수들이 들어가게 되는데 이는 하천의 분기비(RB), 길이비(RL), 면적비(RA)이며 다음과 같이 정의된다.
여기서 Nw, 는 w 차수에서의 하도 개수, 평균 길이 및 평균면적을 의미한다. 여기서 분기비, 길이비, 면적비의 값을 산정하기 위해서는, 로그스케일로 치환된 값을 차수별로 도시하여 경사값을 구하고, 경사값들로부터 RB, RL, RA를 구할 수 있다.
산정되어진 Horton의 계수 값을 바탕으로 홍수경보에 사용되는 첨두홍수량(Qp, m3/s) 및 첨두도달시간(Tp, hr)을 아래와 같이 구할 수 있다(Rodríguez-Iturbe and Valdés, 1979; Valdés et al., 1979; Rodríguez-Iturbe et al., 1982).
여기서, 은 Eq. (6)으로 나타낼 수 있으며, 는 Eq. (7)에 의해 구할 수 있다.
여기서, n은 Manning의 조도계수를 나타내며 는 최대차수(Ω)의 경사 및 하천 폭(m)을 의미한다. ir 및 tr은 유효강우강도(mm/hr) 및 지속시간(min)을 의미한다. 유효강우강도(ir)는 설정된 강우량을 바탕으로 CN (III)방법을 가지고 유효강우량을 구하고 이를 지속시간(tr, min)으로 나누어 유효강우강도(ir, mm/hr)를 구하게 된다.
Eqs. (4) and (5)에 나타난 첨두홍수량 및 첨두도달시간은 균등한 유효강우강도(ir)를 가지는 강우에 대해서 삼각형 형태의 GIUH를 가정하고 Convolution 곱을 취하여 유도한 것이며, 이는 기존의 특성속도를 이용한 GIUH 식에서 특성속도를 제외시켜 유도된 것이다(Rodríguez-Iturbe et al., 1982).
3.2 한계유량 산정방법
홍수경보를 발령하기 위해서는 하천 수위관측지점의 경보발령 수위를 정하고 이에 대응하는 한계홍수량을 결정하여야 한다. 이를 위하여, 일반적으로 아래의 Manning 공식을 이용하게 된다.
여기서 Qd는 한계유량(m3/s), Y는 수심(m), B는 하폭(m), m은 형상계수(구형일 경우 0), S0는 경사로 표현된다.
또 다른 방법으로는 유역에 하천의 횡단면도 관측이 이루어진 상황에서 유출분석프로그램을 사용할 수 있다. 우리나라에서는 일반적으로 미공병단에서 개발한 HEC-RAS를 사용하고 있다. HEC-RAS 모형은 HEC-2 모형의 후속 프로그램으로 1995년 7월에 미공병단 수리연구소에 의해 보급된 윈도우용 프로그램으로서 입출력 기능을 크게 향상시켰으며, 자료저장 및 관리, 계산 결과의 그래픽처리 기능 등이 추가되었다.
계산과정은 마찰손실을 고려한 일차원 에너지방정식의 해에 근거하며 마찰손실은 Manning의 공식을 이용하여 구하게 되며, 부등류를 표준축차계산법(Standard Step Method)에 의해 계산되는 방식이다.
이는 아래의 식을 풀어 해당 수위를 계산하게 된다.
여기서 H는 기준면에서 수면까지의 높이(EL.m)를 의미하며, V는 평균유속(m/s), he는 에너지 손실수두(m)를 나타낸다. 그리고 L은 1번 2번 단면 간의 거리, C는 단면의 확대축소계수, 는 에너지 보정계수를 의미한다.
본 연구에서는 Eq. (8)의 Manning 공식과 HEC-RAS를 이용한 한계유량을 산정하고 이에 대응하는 첨두홍수량을 구하고 이를 발생시킨 강우량 및 강우지속시간을 산정하여 그 적정성을 판별하였다.
4. 대상 유역 및 특성
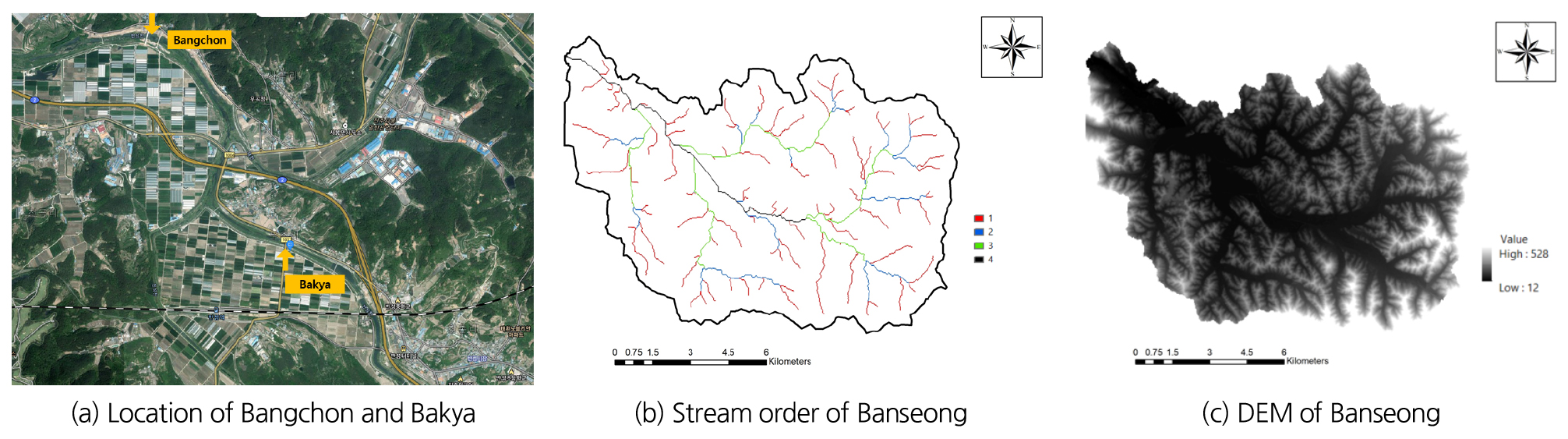
본 연구에서는 진주시의 반성천에 두 개의 지점에 대해서 홍수경보시스템을 구축하는 연구에 대해 실시하였다. 대상 유역의 위치, 하천차수와 DEM 자료를 Fig. 2에 나타내었다. 진주시 반성천의 경우 지난 2019년 10월 태풍 미탁이 경남을 관통하면서 평균강수량 201 mm를 기록하며, 다양한 피해를 주었는데 특히, 반성천에는 하천이 범람하며 일가족이 고립된 후 구조된 바 있다. 특히, 사봉면 무촌리 지사로 440 m가량은 수심이 0.5 m ~ 1.5 m로 차량 및 사람의 통행이 불가능한 상태였고 수난구조보트를 이용해 주택에 접근해 주민을 구조하였다.
반성천은 경상남도 진주시 이반성면에 위치하며, 낙동강 합류점으로부터 약 48 km 상류에서 남강 우안으로 유입되는 지방하천이다. 유역면적은 125.28 km2, 유로연장 20.60 km, 하천연장 17.0 km의 중소하천이다. 평균 표고는 EL.98.29 m, 평균 경사는 약 15.91도로 분석되었다.
전체적인 분석은 남강 합류부를 기준으로 반성천(Banseong) 전체와 수위관측소 및 홍수경보시설이 설치되는 방촌교(Bangchon) 및 백야교(Bakya)를 중심으로 산정되었다.
5. 결 과
5.1 GIUH 매개변수 및 첨두홍수량 산정
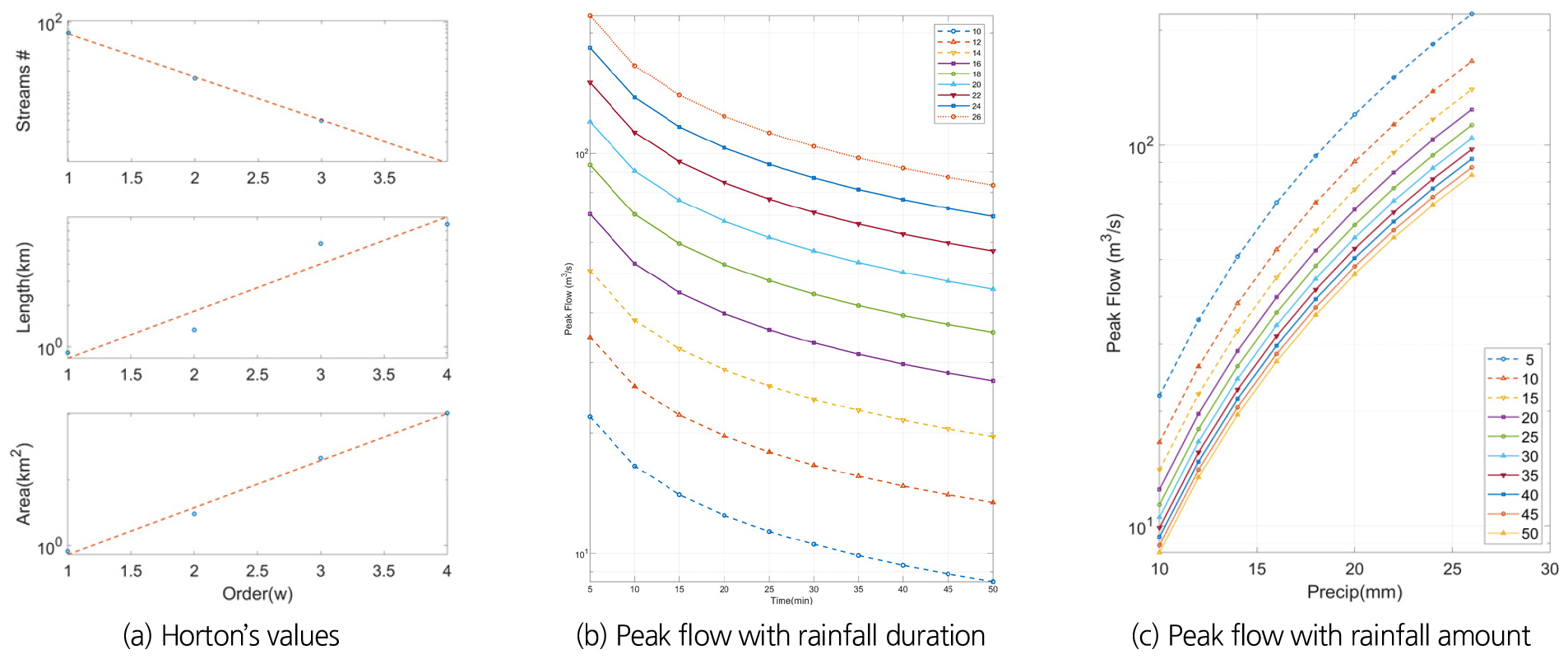
GIUH모형의 매개변수를 계산하기 위해 유역을 차수별로 구분하고 Table 1과 같이 차수별 하도개수(Nw), 하도거리(Lw), 유역면적(Aw)을 산정하였다. 이를 바탕으로 Fig. 3의 그래프에 도식하고 Eqs. (1) ~ (3)에 있는 하천의 분기비(RB), 길이비(RL), 면적비(RA)를 산정하였다(Fig. 3(a)). 특히 RB는 형태로 나타나므로 log (Nw)를 (Ω‒w) 형태로 도시하여 기울기를 구하면 그 기울기 값의 역로그(antilog)값이 기울기가 되어 쉽게 구할 수 있다. 이렇게 산정된 지형학적 특성 인자들이 Table 2에 나타나 있다.
Table 1.
Calculated geomorphologic characteristics
Table 2.
Calculated geomorphologic characteristics for study area
| RB | RL | RA | LΩ (km) | AΩ (km2) | n | CN (III) | |
| Banseong | 4.333 | 2.572 | 5.296 | 13.249 | 128.107 | 0.03 | 85 |
| Bangchon | 4.1086 | 2.209 | 5.187 | 7.817 | 103.284 | ||
| Bakya | 3.288 | 1.889 | 4.277 | 5.346 | 52.088 |
산정된 매개변수들을 바탕으로 다양한 지속시간 및 강우량을 가정하고 이에 대한 첨두홍수량 및 첨두도달시간 값을 Eqs. (4) and (5)을 통하여 구할 수 있다. 구해진 강우지속시간별 첨두홍수량이 Fig. 3(b)에 표시되어 있다. 사용된 강우지속시간(min)은 [5, 10, 15, 20, 25, 30, 35, 40, 45, 50]이며 표현된 강우(mm)는 [10, 12, 14, 16, 18, 20, 22, 24, 26]이다. Fig. 3(b) and 3(c)에서 보는 바와 같이 동일 강우에서 지속시간이 짧을수록 첨두홍수량은 증가하며 동일 지속시간에서 강우량이 클수록 첨두홍수량은 증가하게 되는 경향을 볼 수가 있다.
5.2 경보수위 설정
홍수경보지점에서 하천수위 설정은 하천 내와 하천범람 시 인명피해를 막고 대피시간을 주기 위하여 매우 중요한 사항이다. 일반적으로 친수활동(물놀이 및 낚시)이 발생하는 지역의 경우에는 하천 내(제외지) 활동하는 인명피해를 막기 위한 경보설정을 포함하여야 하며, 주로 하천범람시를 기준으로 할 경우에는 홍수위를 기준으로 경보 수위를 설정하는 것이 적정하다. 본 연구대상지인 반성천의 경우 하천 내의 친수활동이 발생하고 있어 제외지에서의 인명피해를 막기 위한 경보 수위를 산정하였다.
이를 위해서 본 연구에서는 주의(Yellow) 0.6 m, 경계(Orange) 0.75 m, 심각(Red) 1.0 m로 설정하였다. 이는 주위의 기존 영천강 하천경보시스템 구축 시 사용한 0.5 m, 0.7 m, 1.0 m와 유사하게 진행되었다. 또한, 강우의 대표 지속시간 또한 기존에 10분으로 할 경우 과도한 경보가 발령되어 20분으로 조정한 것을 바탕으로 본 연구에서도 20분 지속시간을 기준으로 강우량을 산정하였다.
5.3 산정방법별 한계유량 비교
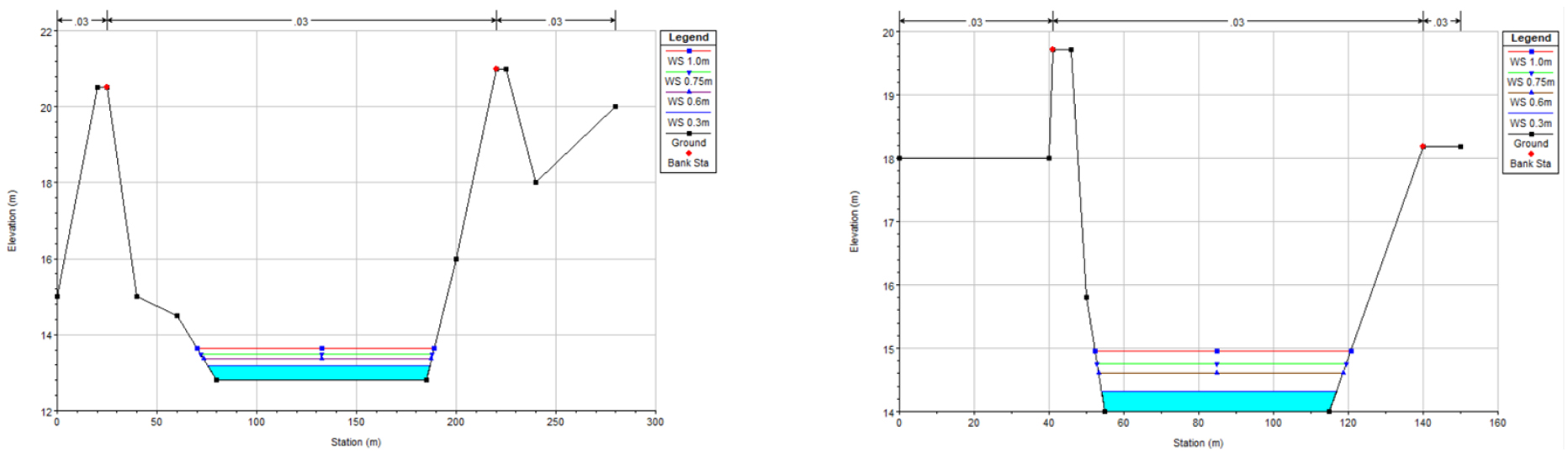
본 연구의 주요 내용인 한계유량 산정방법별 한계유량의 비교를 위해 한계유량 산정공식인(Manning 공식을 변수로 사용) Eq. (8)과 HEC-RAS (Eq. (9))을 이용하였다. 사용 단면은 직접 현장방문을 통해 GPS 측량을 통해 얻었으며 Fig. 4에 나타난 바와 같다. 보다 정확한 HEC-RAS 모형을 위해 반성천 하천기본계획(GyeongNam, 2016)에 나온 보고서를 통해 얻은 설계도를 통해 상류부 하천 단면도를 포함하여 HEC-RAS 모형을 구축하였다.
최종 결과는 Table 3에 나온 바와 같다. 나온 결과에서는 Manning 식이 방촌에서 134 ~ 312 m3/s로 HEC-RAS를 통해 산정된 값(22 ~ 55 m3/s)에 비해 약 6배 가까이 크게 나타났다. 백야에서는 Manning 공식을 통해 나온 값이 HEC-RAS에서 계산된 값보다 약 4배 이상의 한계유량으로 계산되었다. 만일 Manning 식을 통해 산출된 값을 통해 경보강수량을 산정하게 될 경우, Table 4에 나타난 바와 같이 20분 강수량이 28 ~ 40 mm로 반성천 하천기본계획에 나타난 80년 빈도 1시간 강우량인 78 mm에 절반 이상에 해당되는 강우량으로 명백히 과도하게 산정되었다는 것을 확인할 수 있다.
본 연구에서 한계유량 산정공식(Manning 식을 변수로 사용)에서의 과도한 한계유량을 피하기 위해 최상위 차수의 평균 하천폭을 사용하거나 조도계수를 증가시키는 방법 등을 확인하였으나 대부분의 결과가 크게 차이를 보이지 않고 과도한 강수량 산정이 나타남을 확인하였다.
Table 3.
Estimated critical flow (Qd, m3/s)
| Manning | HEC-RAS | |||
| Bangchon | Bakya | Bangchon | Bakya | |
| Yellow (0.6 m) | 134 | 73 | 22 | 18 |
| Orange (0.75 m) | 194 | 105 | 35 | 30 |
| Red (1.0 m) | 312 | 169 | 55 | 45 |
Table 4.
Estimated peak flow (Qp, m3/s) from GIUH
이에 비해 HEC-RAS를 통해 산정된 한계유량을 통하여 계산된 경보강우량은 방촌교에서 13, 15, 18 mm로 확인되었으며 백야교의 경우에는 15, 17, 19 mm로 확인되었다.
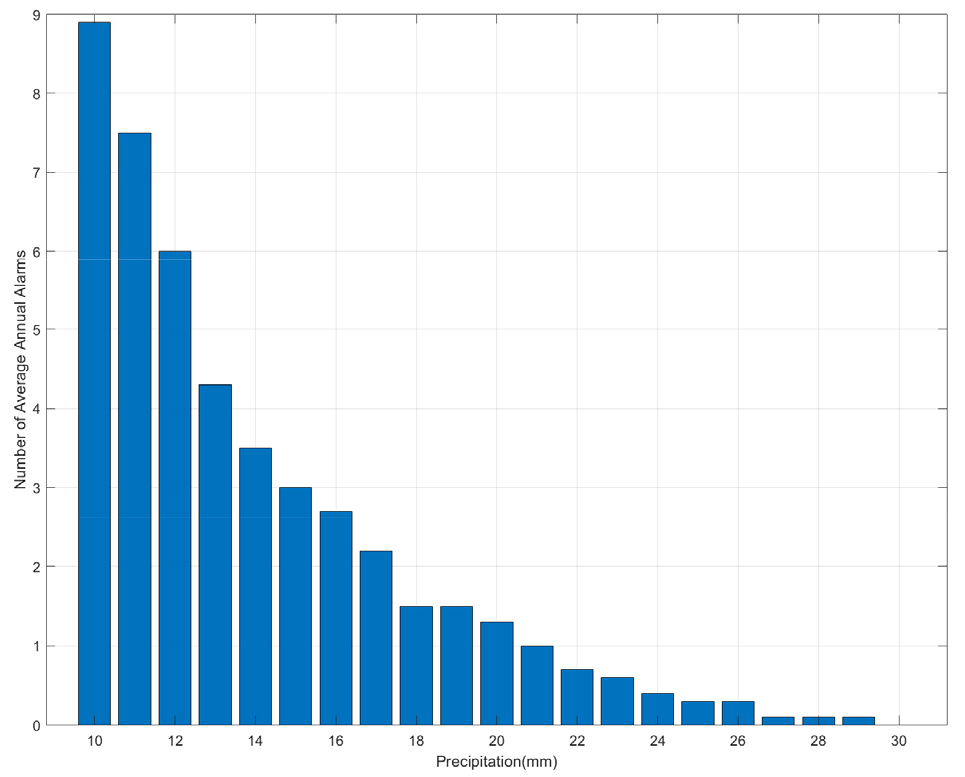
이를 진주관측소의 강우량 자료를 바탕으로 연평균 알람 횟수를 확인하였다(Fig. 5). 확인결과, 13 ~ 17 mm는 연 3 ~ 4회의 알람 횟수를 가지며, 18 ~ 20 mm의 경우는 연 1 ~ 2회의 알람 횟수를 가지는 것을 확인하였다.
기존의 영천강 유역에서 자동경보시스템의 경우 자주 경보시스템이 작동하여 민원 문제 및 실제 위험 상황에서 대처능력이 떨어지는 효과가 발생하는 것으로 알려져 있다. 그리고 기존의 연구(CNU, 2004)에서도 경보발령은 연 3, 4회 정도 발령되는 것으로 산정되었다. 또한, 국립재난연구원(NDMRI, 2016)에서는 일반적으로 한국의 경보횟수는 연 2회 정도로 보고하고 있으며 미국의 경우 연 1회 정도 경보하고 있는 것으로 보고 있다.
만일 Manning 식을 바탕으로 산정된 경보강우량을 보면 연 0.1회 이하가 되는 것으로 판단되어 거의 경보발령이 발생하지 않을 것(10년/1회 이하)으로 판단된다.
6. 요약 및 결론
본 연구에서는 반성천 자동경보시스템을 구축하기 위하여 경보발령의 기준이 되는 수위 및 강수량 설정 시 한계유량을 산정하는 방법을 비교하였다. 일반적으로 측량성과가 없는 지역에 사용되는 한계유량 산정공식(Manning 식을 변수로 사용)과 측량이 되어있는 지역에서 사용할 수 있는 HEC-RAS를 통한 한계유량 값을 비교하였다.
비교결과 반성천의 경우 Manning 식을 통해 산정된 한계유량 값에 대응하는 경보발령 강우량 자체가 지나치게 과도하게 산정되는 것을 확인하였다. 또한, 이를 HEC-RAS로 대체할 경우 산정된 강우량은 경보발령기준(연 3 ~ 4회 발령)에 적절하게 산출되는 것을 확인할 수 있었다.
본 연구를 통해 자동경보시스템 구축을 위한 한계유량 산정 시, HEC-RAS를 통하여 산정하는 값이 Manning 식에 의해 산정된 값보다 더 적절함을 확인할 수 있었다. HEC-RAS 모형을 구축하기 위해서는 하천의 측량값이 필수적으로 존재하여야 한다.
지난 십여년 동안 홍수를 대비하기 위한 다양한 하천사업을 통해 대부분의 지역에서 하천측량이 이루어져 있으며, 자료는 국가수자원관리종합정보시스템(wamis.go.kr)을 통해 받아볼 수 있다. 따라서, 이제는 Manning 식에 의한 한계유량 산정보다는 HEC-RAS를 통하여, 보다 정확한 한계유량 산정을 통해 홍수경보발령 기준이 마련되어야 할 것으로 보인다.