Preview
Research Article

Journal of Korea Water Resources Association. 31 July 2022. 481-494
https://doi.org/10.3741/JKWRA.2022.55.7.481

Evaluation of the future monthly groundwater level vulnerable period using LSTM model based observation data in Mihostream watershed

LSTM을 활용한 관측자료 기반 미호천 유역 미래 월 단위 지하수위 관리 취약 시기 평가
Jae-Beom Leea
,
Amos Agossoub
,
Jeong-Seok Yangc*
이 재범a
,
아거쑤 아모스b
,
양 정석c*
aPh.D Candidate, Department of Civil Engineering, Kookmin University, Seoul, Korea
bPh.D Student, Department of Civil Engineering, Kookmin University, Seoul, Korea
cProfessor, Department of Civil Engineering, Kookmin University, Seoul, Korea
a국민대학교 건설시스템공학과 박사수료
b국민대학교 건설시스템공학과 박사과정
c국민대학교 건설시스템공학부 교수
*Corresponding Author

ABSTRACT

This study proposed a evaluation of the monthly vulnerable period for groundwater level management in the Miho stream watershed and a technique for evaluating the vulnerable period for future groundwater level management using LSTM. Observation data from groundwater level and precipitation observation stations in the Miho stream watershed were collected, LSTM was constructed, predicted values for precipitation and groundwater levels from 2020 to 2022 were calculated, and future groundwater management was evaluated when vulnerable. In order to evaluate the vulnerable period of groundwater level management, the correlation between groundwater level and precipitation was considered, and weights were calculated to consider changes caused by climate change. As a result of the evaluation, the Miho stream watershed showed high vulnerability to underground water management in February, March, and June, and especially near the Cheonan Susin observation well, the vulnerability index for groundwater level management is expected to deteriorate in the future. The results of this study are expected to contribute to the evaluation of the vulnerable period of groundwater level management and the derivation of preemptive countermeasures to the problem of groundwater resources in the basin by presenting future prediction techniques using LSTM.

Keywords
Groundwater level management
Evaluation of vulnerable period
LSTM
Precipitation-groundwater interactions
Miho stream watershed

본 연구는 미호천 유역의 월 단위 지하수위 관리 취약 시기 평가와 LSTM을 이용한 미래 지하수위 관리 취약 시기 평가 기법을 제안하였다. 미호천 유역 내의 지하수위 및 강수량 관측소 관측자료를 수집하고, LSTM을 구성한 후 강수량과 지하수위에 대한 2020~2022년 예측 값을 산정하고, 미래 지하수위 관리 취약시기 평가를 수행하였다. 지하수위 관리 취약시기 평가를 위하여 지하수위와 강수량 간의 상관관계를 고려한 가중치와 기후변화로 인한 관측자료의 변동을 고려하기 위한 가중치를 산정한 후, 이를 조합하여 최종 가중치를 산정하였다. 평가 결과 미호천 유역은 2월, 3월, 6월에 지하수위 관리 취약성이 높게 나타났고, 특히 천안수신 관측소 인근은 미래에 지하수위 관리 취약성 지수가 악화 될 것으로 분석되어 추가 관리 방안 도입이 필요할 것으로 나타났다. 본 연구의 결과는 지하수위 관리 취약 시기 평가 및 LSTM을 활용한 미래 예측 기법을 제시함으로써 발생할 수 있는 유역 내 지하수자원 문제에 선제적인 대응방안 도출에 기여할 것으로 기대된다.

키워드
지하수위 관리
취약 시기 평가
LSTM
강수-지하수 상관관계
미호천

MAIN

  • 1. 서 론

  • 2. 연구 방법

  •   2.1 연구순서

  •   2.2 평가 지표 선정 및 자료 수집

  •   2.3 LSTM Model (Long Short-Term Memory Model)

  •   2.4 표준화 방법

  •   2.5 가중치 산정

  •   2.6 월 단위 지하수위 관측정 별 지하수위 관리 취약성 지수 산정 방법

  • 3. 연구지역

  • 4. 연구결과

  •   4.1 LSTM 모형을 활용한 지하수위 및 강수량 산정 결과

  •   4.2 가중치 산정 결과

  •   4.3 지하수위 관측소 별 월 단위 지하수위 관리 취약 시기 평가 결과

  • 5. 결 론

1. 서 론

최근 전 세계적인 추세와 마찬가지로 국내 역시 기후변화로 인하여 최근 강수강도가 증가하고, 극한 강수사상 발생 일수가 증가하는 등 국내 수자원 환경이 변화하고 있다(NIMS, 2018). 강수강도 및 극한 강수사상 발생의 증가는 강수로 내린 물의 과도한 유출을 야기하기 때문에 물이 지표면 저류 및 지하대수층 유입에 대한 시간을 단축시킴으로써 지표수 및 지하수를 포함한 가용 수자원의 절대량을 감소시킨다(Jeong et al., 2018). 이러한 수자원 환경의 변화에도 기존의 국내 수자원 확보 및 관리 방안은 하천, 호소 등으로 대표되는 지표수 위주의 양적 확보에 치우쳐져 있었으나 최근 지하수자원을 통한 안정적 수량 확보 및 가뭄·홍수 등 수재해 피해의 저감에 대한 연구가 진행되고 있다(Kim et al., 2018; Lee et al., 2020).

수문 순환의 측면에서 지구상에 존재하고 있는 물은 존재하고 있는 형태와 공간적인 차이에 의해 대기 중의 수증기, 해수, 지표수, 지하수 등으로 구분되어 있다. 하지만 각각의 물순환 요소들은 타 물순환 요소에 밀접한 영향을 미칠 수 있기 때문에 물순환 요소의 전반적인 관측이 매우 중요한 상황이다. 그러나 현실적인 문제로 인하여 물순환 요소의 관측자료 확보가 쉽지 않기 때문에 제한된 관측자료를 통한 물순환 요소의 거동을 파악하는데 다양한 방법이 적용되었다. 특히 관측 자료 확보가 상대적으로 어려운 지하수의 경우 과거 관측자료를 통한 지하수위 분포 및 거동을 파악하기 위하여 관측자료의 통계적 분석을 통한 연구가 수행되었고(Cheong et al., 2003; Reghunath et al., 2005; Yang et al., 2011), 지하수 유동 해석 모형을 통하여 지형, 지층 별 지하수 흐름 매개변수, 강수에 의한 함양 등을 고려한 내륙 및 연안 지역의 지하수위 분포 및 흐름 특성 분석에 대한 연구가 수행되었다(Jia and Liu, 2002; Zume and Tarhule, 2008).

지구 상의 수문순환 요소 중 정량적인 평가가 어려운 지하수의 경우, 유역 단위의 자연재해에 대한 잠재적 피해량 또는 대응할 수 있는 능력으로 정의되는 취약성의 개념(IPCC, 2007)을 이용한 평가 연구가 다수 수행되었다. 기존의 지하수자원에 대한 취약성 개념을 적용한 연구는 공간적인 특성의 변화에 대한 연구(Cai et al., 2017)와 지하수자원의 오염에 대한 취약성을 평가하는 연구(Leal et al., 2012; Li et al., 2017)가 수행되었다. 최근 지하수자원의 효율적인 개발 및 지속가능성 확보를 위하여 기존의 공간적 특성 변화와 함께 시간적 특성의 변화를 고려한 시공간적 지하수자원 관리 취약성 평가 연구가 수행된 바 있다(Kim et al., 2018; Lee et al., 2019).

기존의 연구들은 신뢰도 있는 관측자료의 확보가 필수적인데 관측자료의 결측 및 신규 자료의 확보가 어려운 상황을 극복하고 발생할 수 있는 다양한 수자원 문제를 해결하기 위하여 최근 인공신경망을 이용한 연구가 다수 수행되고 있다. Jung et al. (2018)은 LSTM (Long Short-term Memory) 모형을 이용하여 한강 잠수교를 대상으로 감조하천의 수위 예측 연구를 수행하였고, Lee et al. (2018)은 LSTM 모형을 이용하여 Kratie 지점의 유출량 산정 연구를 수행하였는데 메콩강 상류 10개 수위 관측소를 이용한 유출량과 SWAT 모형 구축을 통해 산정된 유출량의 비교 결과 물리적 유역 유출 모형인 SWAT에 비하여 LSTM의 결과가 더 정확하게 나타남을 보였다. 또한, 홍수기 및 이수기의 수자원 관리를 위한 댐 운영의 효율성 제고를 위하여 LSTM 모형을 이용한 댐 유입량 예측 연구가 수행되었으며(Han et al., 2021), 홍수 시 도시 침수 범위 예측을 위하여 LSTM 모형을 적용한 사례가 있었다(Kim et al., 2020). 지하수 유동은 수문기상적 특성, 수리지질적 특성 등의 조건 뿐만아니라 인위적 양수 등 지표수에 비하여 흐름의 특성을 분석하기 매우 어렵다(Alley et al., 2002; Sahoo et al., 2017). Park and Chung (2020)은 관측 지하수위 자료를 입력하고, 예측 자료와 기 관측 자료의 비교를 통해 LSTM 모형의 지하수위 예측 정확도를 평가하였다. 지하수위와 관련된 선행 연구의 경우 결측 자료의 처리 기법 또는 지하수위 예측에 대한 연구가 수행되었는데, 예측된 수문 자료를 활용한 연구의 경우 최근 Lim and Yang (2020)이 수행한 LSTM 모형을 이용한 미래 가뭄 발생 가능성 분석 연구가 수행되었다.

지속가능한 수자원 확보를 위하여 지하수에 대한 관심이 높아지고 있는 가운데, 지하수에 직접적인 영향을 미칠 수 있는 지하수 이용량 등의 관측자료는 상대적으로 부족한 실정이다. 이러한 한계점을 극복하기 위하여 비교적 관측이 충실히 수행되고 있는 지하수위 및 강수량 관측자료 기반의 연구 지역 내 관정 별 지하수위 관리 취약 시기 평가 연구를 수행하였다. LSTM 모형의 적용을 통해 연구 대상 유역의 강수량 및 지하수위 관측 자료를 예측하고, 현재 상태(지하수위 및 강수량 2019년 기준)의 관정 별 지하수위 관리 취약 시기 평가 결과와 예측 된 자료를 이용한 미래의 관정 별 지하수위 관리 취약 시기 평가 결과의 변화를 비교하였다.

2. 연구 방법

2.1 연구순서

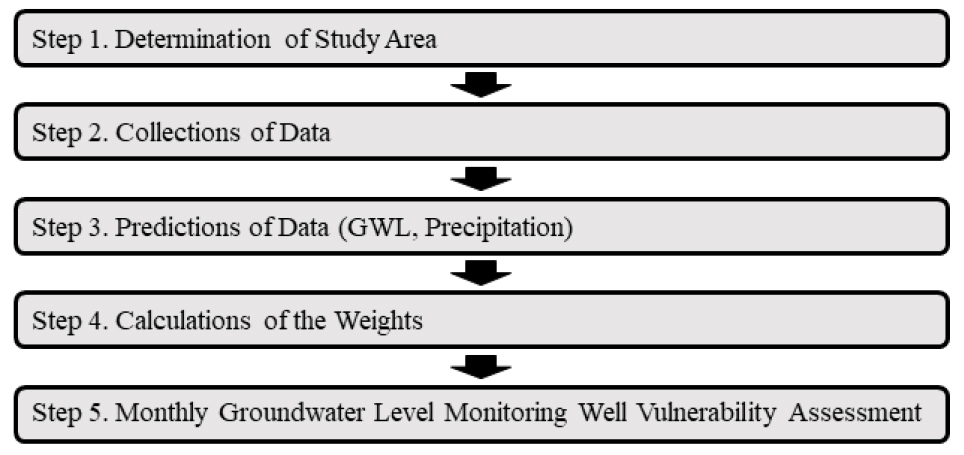
유역 내 지하수자원의 거동을 대표할 수 있는 지하수위의 예측 및 평가는 지속가능한 수자원 관리 및 확보 측면에서 중요하다. 이번 연구에서는 지하수위에 영향을 미칠 수 있는 강수의 관측자료와 함께 유역 내 지하수위 관측자료를 통해 관정 별 월 단위 지하수위 관리 취약 시기 평가를 수행하였다. 그리고 과거 자료를 통한 현재 상태의 지하수위 관리 취약 시기 평가와 함께 LSTM 모형을 적용하여 미래 강수 및 지하수위 관측자료를 예측함으로써 미래의 지하수위 관리 취약 시기 평가를 수행하였다. 연구의 수행을 위하여 연구 대상 유역을 선정하고, 유역 내 강수 및 지하수위 관측자료를 수집한 후 LSTM 모형을 통한 학습 및 예측을 통하여 관측소 별 미래 강수 및 지하수위를 예측하였다. 예측된 미래 강수 및 지하수위 자료를 이용하여 현재 상태(지하수위 및 강수량 2019년 기준)와 예측 자료 기반 월 단위 지하수위 관리 취약 시기를 평가하였다.

Fig. 1은 월 단위 지하수위 관리 취약 시기 평가 연구의 순서를 나타내고 있다.

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550701/images/kwra_55_07_01_F1.jpg
Fig. 1.

Procedure of this study

2.2 평가 지표 선정 및 자료 수집

지하수위 관측소 별 지하수위 관리 취약 시기를 평가하기 위하여 연구 대상 유역을 선정하고, 유역 내의 지하수위 및 강수량 관측소를 선정하였다. 선정된 관측소 별 일 단위 관측자료를 수집하였다. 관측 자료를 바탕으로 시간의 변화에 따른 지하수위 관측소의 취약 시기를 평가하기 위하여 평가 기준을 선정하였다. 평가 기준은 지하수위와 강수량 수집 자료의 수집 기간 전체에 대한 추세(Total Trend, TT), 최근 9년간의 추세(Recent 9years, R9), 최근 기후변화로 인한 국내 강수량 패턴의 변화를 고려하기 위하여 최근 7년 대비 과거 11년간의 추세 변화(Trend Difference from Recent 7years and 11years, R7-P11), 최근 4년 대비 과거 14년간의 추세 변화(Trend Difference from Recent 4years and 14years, R4-P14) 등 네 가지 평가 기준을 선정하였다. 지하수위 관측자료는 국가 지하수 정보센터(National Groundwater Information Center, GIMS)에서 국가지하수위관측망의 관측자료를 수집하였고, 강수량 자료는 국가 수자원 관리 종합 정보시스템(Water Resources Management Information System, WAMIS)에서 수집하였다.

Table 1은 이번 연구에서 수집한 자료의 수집 범위, 출처를 나타내고 있다.

Table 1.

Lists of collected data

Groundwater Level Observation Data
No. Observation Station Name Data Length Reference
G1 Eumseong Daeso (ES-DS) 1998~2019 GIMS
G2 Jincheon Jincheon (JC-JC) 2000~2019
G3 Jeungpyeong Jeungpyeong (JP-JP) 2000~2019
G4 Cheongju Naesu (CJ-NS) 1998~2019
G5 Cheonan Bukmyeon (CA-BM) 2001~2019
G6 Cheonan Susin (CA-SS) 2002~2019
G7 Sejong Jochiwon (SJ-JCW) 2001~2019
Precipitation Observation Data
No. Observation Station Name Data Length Reference
P1 Daeso Health Center (OR) 1990~2019 WAMIS
P2 Jincheon Girls Middle School (JC) 1990~2019
P3 Byeongcheon Elementary School (BC) 1990~2019
P4 EPIS (JCW) 1993~2019
P5 Bantan Bridge (JP) 1990~2019
P6 Cheongju (CJ) 1990~2019
P7 Gadeok Elementary School (GD) 1990~2019

2.3 LSTM Model (Long Short-Term Memory Model)

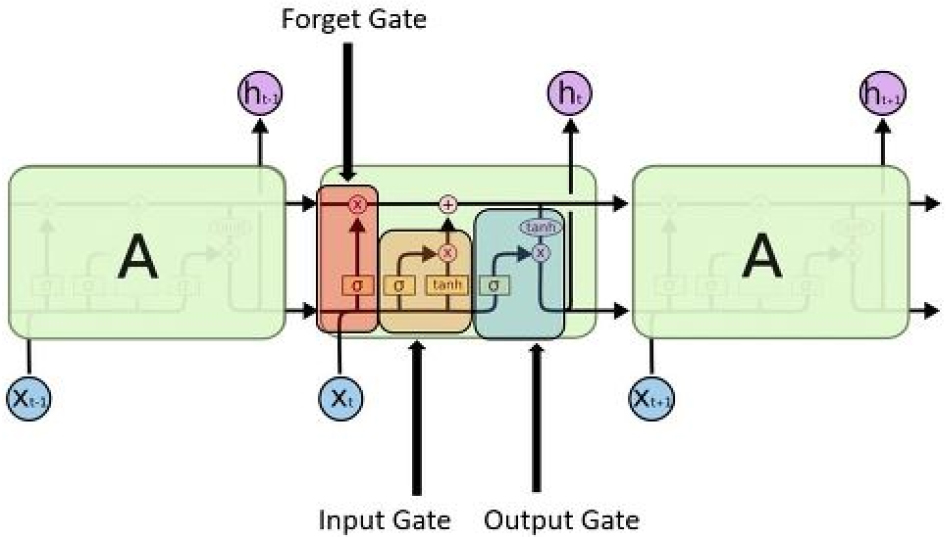
LSTM 모형은 Hochreiter and Shimidhuber (1997)이 개발한 RNN (Recurrent Neural Network)의 한 종류로 시퀀스 간 정보 전달 기능을 갖추고 있다. LSTM 모형은 망각게이트, 입력게이트 및 출력게이트 등 3가지 프로세스로 구분되어 있으며, Fig. 2는 LSTM 모형의 구성도를 나타내고 있다.

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550701/images/kwra_55_07_01_F2.jpg
Fig. 2.

LSTM model structure (Lim and Yang, 2020)

망각게이트(Forget gate, ft)는 정보의 삭제 여부를 결정하는 과정이며 아래 Eq. (1)과 같이 표현된다.

(1)
ft=σwfht-1,xt+bf

여기서 σ는 활성화 함수, wf는 게이트의 가중치, bf는 편향값, xt는 현재 상태의 입력을 나타낸다.

입력게이트(it)는 입력 정보의 저장 과정을 정의하고 다음의 Eqs. (2) and (3)을 통해 표현할 수 있다.

(2)
it=σwiht-1,xt+bi
(3)
Ct~=tanhwcht-1,γt+bC
(4)
Ct=ft×Ct-1+it×Ct~

여기서 Ct는 셀 상태, ht-1는 특정 시점의 출력값, bc, bi는 편향값, Ct~는 활성화함수를 통해 만들어진 새로운 셀 상태, wc는 셀 상태의 가중치를 나타낸다.

마지막으로 출력 게이트(ot)는 Eqs. (5) and (6)에 따라 출력 값을 계산하는 단계이다.

(5)
ot=σwoht-1,xt+bo
(6)
ht=ot×tanhCt

여기서 ωo는 출력게이트의 가중치, h는 특정 시점의 상태, bo는 편향, Ct는 셀 상태, xt는 현재 상태의 입력을 나타내고 있다.

이번 연구에서 LSTM 모형을 이용하여 수집한 강수량 및 지하수위의 자료를 학습하고 미래의 일단위 시계열 자료를 예측하였다. 구글의 오픈 라이브러리인 Tensorflow를 이용하여 LSTM 모형을 구축하였고, 평균제곱근오차(Root Mean Square Error, RMSE)와 결정계수(Coefficient of Determination, R2)를 이용하여 모형을 검증하였다. 이번 연구에서의 RMSE와 R2는 관측 수문 자료 값과 모형을 통해 산정된 수문 자료 값의 비교를 통해 Eqs. (7) and (8)에 따라 LSTM 모형의 모의 능력을 평가하였다.

(7)
RMSE=1n∑i=1nQobs,i-Qcal,i2
(8)
R2=MSSTSS=TSS-RSSTSS

Eq. (7)에서, n은 적용한 시계열 자료의 수, Qobs와 Qcal은 관측 수문자료 값과 모형을 통해 산정된 수문 자료 값, i는 시계열 자료의 시간 단위를 나타내고 있다. Eq. (8)에서 MSS (Model Sum of Squares)는 선형회귀분석에서 해당 변수의 평균을 뺀 예측 제곱의 합이며, TSS (Total Sum of Squares)는 결과 변수와 관련된 제곱의 합이며, RSS (Residual Sum of Squares)는 측정값의 제곱합에서 선형회귀분석의 예측값을 뺀 잔차제곱합이다.

또한, 모형의 보정과정에서 Optimizer, Active function, Epoch와 같은 중요한 매개변수가 수정된다. 모형의 보정 과정 동안 모형이 최상의 성능을 나타낼 때 까지 단일 매개변수를 수정하고 모델의 성능을 평가하였다. 본 연구는 Adam optimizer를 적용하여 신경망의 매개변수를 얻었는데, 여기서 Adam optimizer는 Kingma and Ba (2015)가 도입한 SGD (Stochastic Gradient Descent) 기반의 최적화 알고리즘이다. 이 알고리즘은 각 신경망 매개 변수에 개별적으로 적응형 개별 학습률을 할당하고, Gradient의 첫 번째와 두 번째 순간의 추정치를 기반으로 업데이트 한다는 점에서 기존의 SGD 알고리즘과 다른 특징을 나타내고 있다.

구축된 LSTM 모형 중 강수량 및 지하수위 기존 관측 자료와 산정된 강수량 및 지하수위 자료 값을 비교하였을 때 검증 결과가 우수한 모형을 선정하였고, 강수량 및 지하수위의 예측 결과에 따른 지하수위 관측 관정 별 지하수위 관리 취약 시기 평가에 활용하였다.

2.4 표준화 방법

지하수위 관측 관정 인근의 지하수위 및 강수량 관측소의 관측자료를 이용한 월 단위 지하수위 관리 취약 시기 평가를 위해서는 수집한 자료의 상이성을 고려하여 표준화가 필수적이다. 다기준의사결정 기법을 이용한 취약시기 평가를 위하여 이번 연구에서는 평가 지표의 극값 범위를 기반으로 하는 표준화 방법을 이용하였고, 표준화 방법은 아래와 같다(Nardo et al., 2005).

(9)
rij=maxixij-xijmaxixij-minixij,i=1,2,⋯,n,j∈Ideal

여기서, i는 관정 별 지하수위 관리 취약 시기를 평가하는 각각의 평가 기준이고, j는 평가 대상이다.

2.5 가중치 산정

다기준 의사 결정 기법의 적용에서 평가 기준 선정뿐만 아니라 각 평가 기준의 가중치 결정이 필수적이다. 이번 연구에서 가중치 산정은 각 관측소의 관측자료 기반의 엔트로피 가중치 산정 기법을 통한 엔트로피 가중치(Weights by Entropy method, We), 평가 대상 지하수위 관측 관정과 각 지하수위 및 강수량 관측소와의 피어슨 상관계수 산정 결과를 활용한 상관관계 가중치(Weights by Pearson Correlation Coefficient, Wc)를 이용하여 0~1 범위의 최종 가중치를 산정하였다.

Fig. 3은 엔트로피 방법과 피어슨 상관계수를 이용한 가중치 산정 순서를 나타내고 있다.

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550701/images/kwra_55_07_01_F3.jpg
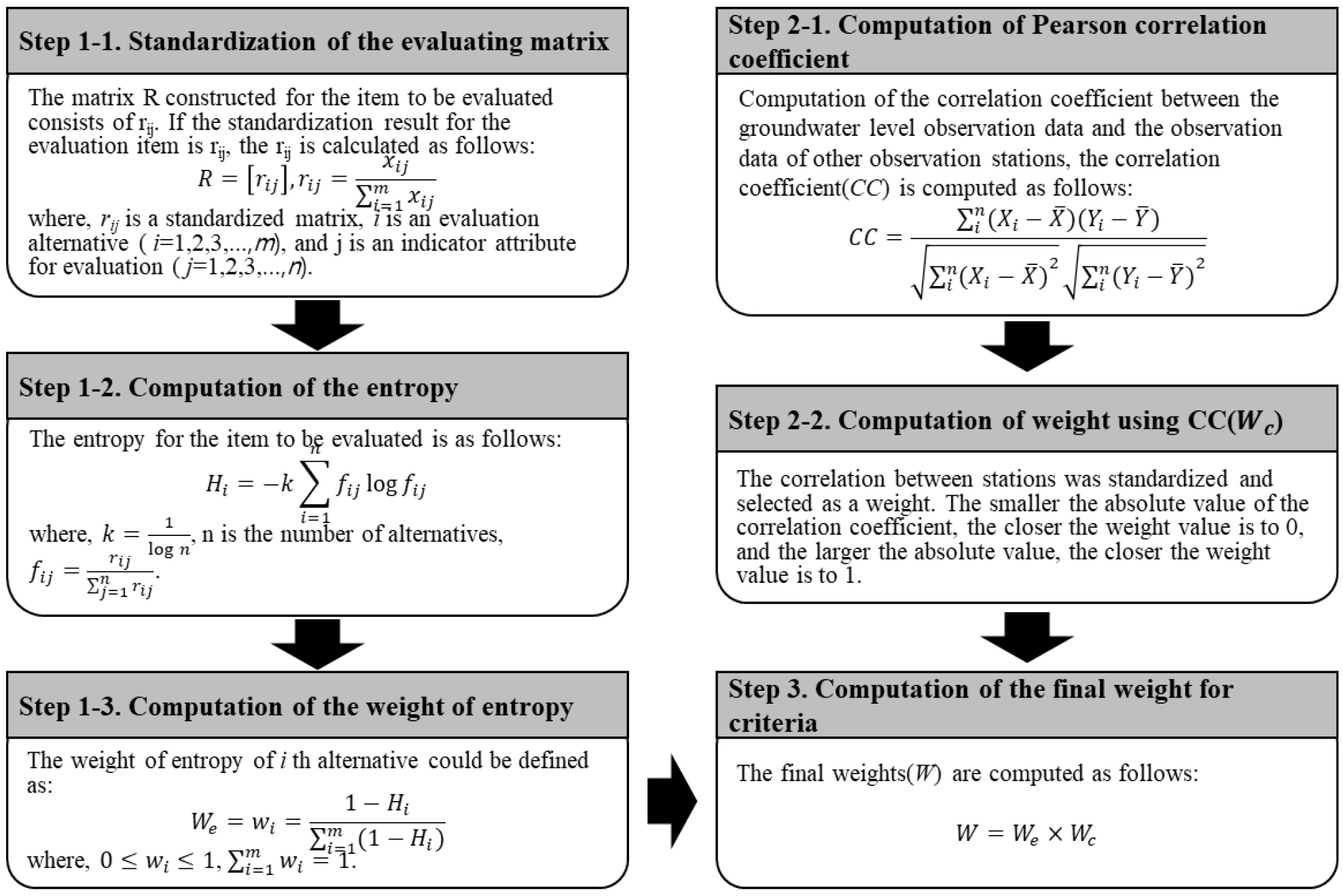
Fig. 3.

Procedure of weights computation using entropy method (Shannon, 1949), pearson correlation coefficient (Benesty et al., 2009)

2.6 월 단위 지하수위 관측정 별 지하수위 관리 취약성 지수 산정 방법

이번 연구에서는 지하수위 관측정 별 지하수위 관리 취약성 지수 산정을 위하여 관측정 자체의 관측자료와 함께 해당 관측정의 지하수위에 영향을 미칠 수 있는 인근의 지하수위 및 강수량 관측소의 관측자료를 활용한 연구를 수행하였다. 기존의 연구에서는 수문순환 요소의 관측자료를 기반으로 유출량 해석, 모델링 해석 등을 이용하여 유역 전반의 지하수위 변동을 해석 또는 예측하기 위한 연구가 수행되었다. 지하수 전공자가 아닌 지하수 관련 담당자가 지하수위 및 강수량 등 수문순환 요소의 관측자료를 활용하여 직관적으로 분석 대상 지역의 지하수위 관리 취약성을 평가하기 위한 연구가 최근에서야 진행되었다(Lee et al., 2019). 다양한 기법을 통하여 취약성 지수를 산정할 수 있는데, 이번 연구에서는 수문순환 요소 간의 상관관계와 관측자료의 변동을 함께 고려하여 단순가중치법(Simple Additive Weighting, SAW)을 이용한 월 단위 지하수위 관측정 별 지하수위 관리 취약성 지수를 산정하였다. 단순가중치법을 활용한 취약성 지수는 아래 Eq. (10)과 같이 산정될 수 있다.

(10)
Fj=∑i=1nwirij,,i=1,2,⋯,n

여기서, i는 지하수위 관리 취약 시기를 평가하는 각각의 평가 기준, j는 평가 대상, rij는 i, j에 대한 표준화된 값, wi는 관측자료의 변동과 관측소 간의 상관관계를 고려하여 산정한 가중치를 의미한다.

3. 연구지역

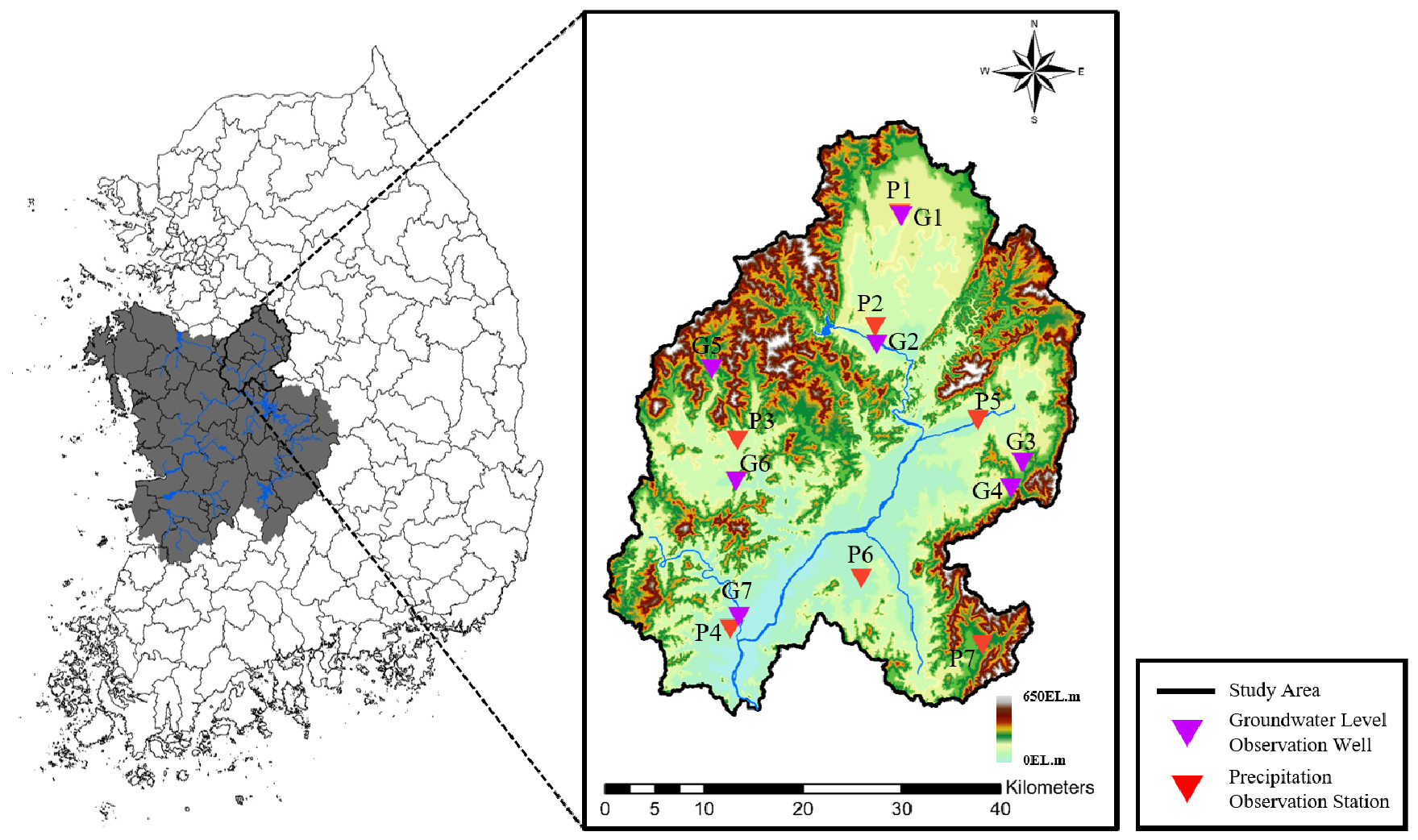
유역 내 지하수위 및 강수량 관측소의 관측자료를 이용하여 지하수위 관측 관정 별 지하수위 관리 취약 시기를 평가하기 위하여 중권역 단위의 연구지역을 선정하였다. 수문학적 측면에서 강수의 형태로 내린 물이 지하수위에 영향을 미칠 수 있기 때문에 연구 지역은 유역 단위로 선정하게 되었고, 자료 수집의 용이성을 고려하여 국내 중권역 중 금강 권역의 미호천 중권역을 선정하였다. 미호천 중권역 내 지하수위 및 강수량의 관측자료를 이용하여 LSTM 모형을 구축하고, 지하수위 및 강수량을 산정하기 위하여 7개 지하수위 관측소와 7개 강수량 관측소를 선정하여 자료를 수집하였다. 각각의 지하수위 관측소의 지하수위 관리 취약 시기는 연구 지역 내의 모든 지하수위 및 강수량 관측소의 관측자료 간 상관관계, 자료의 변동을 고려하여 평가되었다.

Fig. 4와 Table 2는 연구지역 내 수집한 지하수위 및 강수량 관측소의 위치 및 목록을 나타내고 있다.

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550701/images/kwra_55_07_01_F4.jpg
Fig. 4.

Study area and locations of observation stations

Table 2.

Lists of groundwater level and precipitation observation stations

No. Groundwater Level Observation Well No. Precipitation Observation Station
G1 Eumseong Daeso (ES-DS) P1 Daeso Health Center (OR)
G2 Jincheon Jincheon (JC-JC) P2 Jincheon Girls Middle School (JC)
G3 Jeungpyeong Jeungpyeong (JP-JP) P3 Byeongcheon Elementary School (BC)
G4 Cheongju Naesu (CJ-NS) P4 EPIS (JCW)
G5 Cheonan Bukmyeon (CA-BM) P5 Bantan Bridge (JP)
G6 Cheonan Susin (CA-SS) P6 Cheongju (CJ)
G7 Sejong Jochiwon (SJ-JCW) P7 Gadeok Elementary School (GD)

4. 연구결과

본 연구는 연구지역 내 지하수위 관측소 별 지하수위 관리 취약 시기 평가를 위하여 유역 내의 지하수위 및 강수량 관측자료를 바탕으로 다기준의사결정 기법을 활용하였다. 또한 LSTM 모형을 구축하여 지하수위 및 강수량 관측자료 기반 미래 자료를 산정하고, 현재 상태의 지하수위 관리 취약시기와 산정된 미래 지하수위 및 강수량 자료를 적용하였을 때의 지하수위 관리 취약 시기를 평가하였다.

4.1 LSTM 모형을 활용한 지하수위 및 강수량 산정 결과

위의 연구방법에서 설명한 LSTM 모형은 7개의 지하수위 관측소에서 수집한 월 단위 지하수위와 7개의 관측소의 월 단위 강수량을 예측하는 데 사용되었다. 본 연구는 지하수위와 강수량을 하나의 모델에서 개별적으로 예측하기 때문에 하나의 입력 셀과 하나의 출력 셀을 적용하였다.

미래 지하수위 예측의 경우, 구성한 LSTM 모형은 평균 17년의 자료를 이용하여 보정하였고, 최근 2년 데이터를 사용하여 검증하였다. 검증 후, 2020~2022년까지 미래 월 단위 지하수위를 예측하였다. 강수량의 경우 모형 학습에 평균 25년의 데이터를 이용하였고, 강수량 예측 모델은 최근 3년 동안의 데이터를 검증한 후, 2020~2022년의 미래 월 단위 강수량을 예측하는데 사용하였다.

이번 연구에서 구성한 LSTM 모형은 구성 초기 단일 Hidden Layer와 100개의 Cell로 구성하였고, 각 지하수위 관정 별 지하수위 예측 정확도를 위하여 모형의 최적화 결과 Cell의 개수가 200개 일 때, 가장 모형 정확도가 높게 나타났다. 또한, 모델 레이어의 Dropout은 초기 0.2에서 0.3으로 변경 시 최적화 되었으며, Epoch의 경우 1000~2000의 범위로 수정하였을 경우 모형의 신뢰도가 가장 높게 나타났다. Table 3은 이번 연구에서 구성한 LSTM 모형의 초기 설정과 최적화 이후의 설정값의 변화를 나타내고 있다.

Table 3.

Model conditions of LSTM model

Model Conditions Number of Cells Hidden Layer Dropout Epoch
Initial 100 1 0.2 100
After Optimization 200 1 0.3 1000~2000

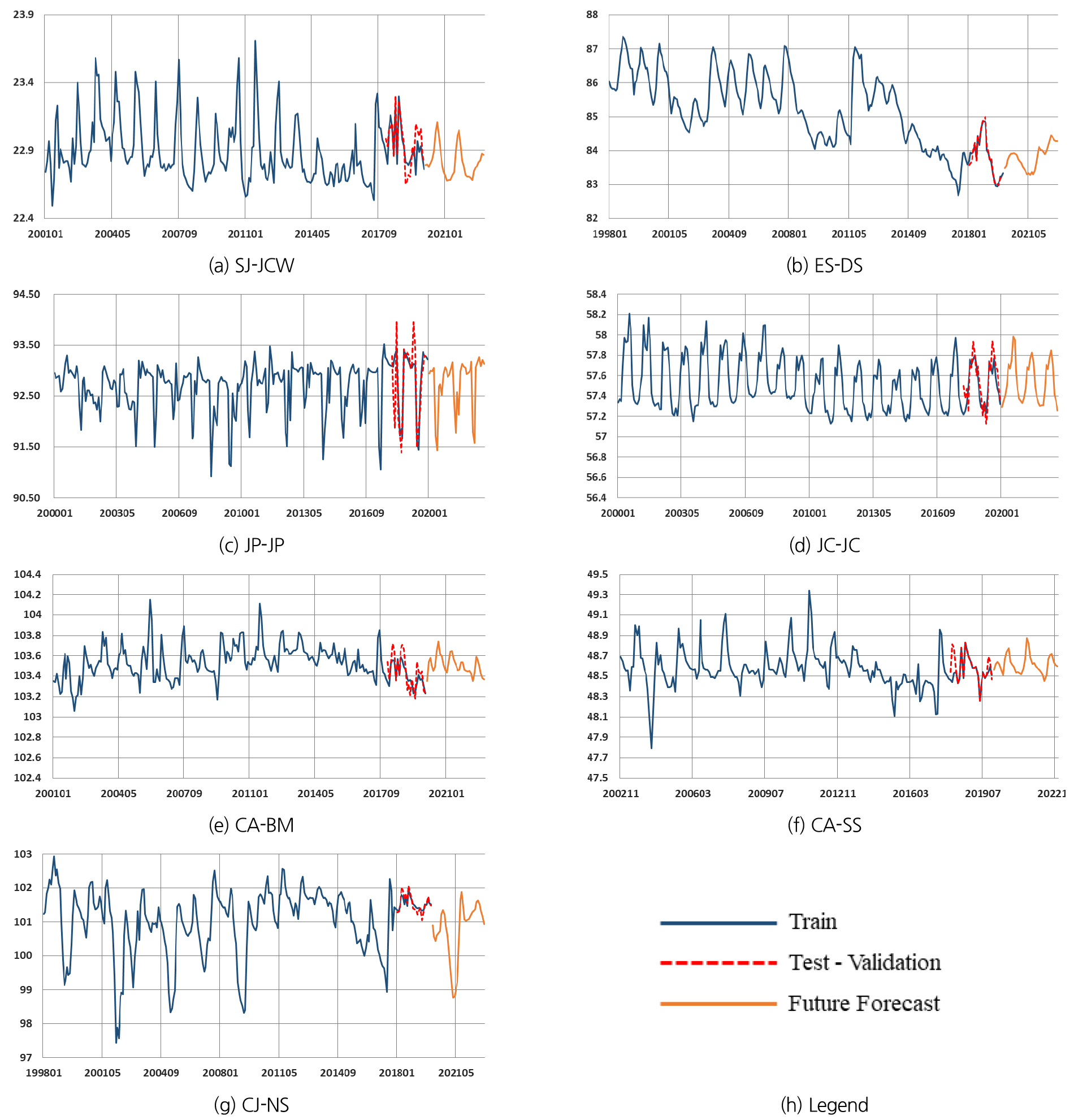
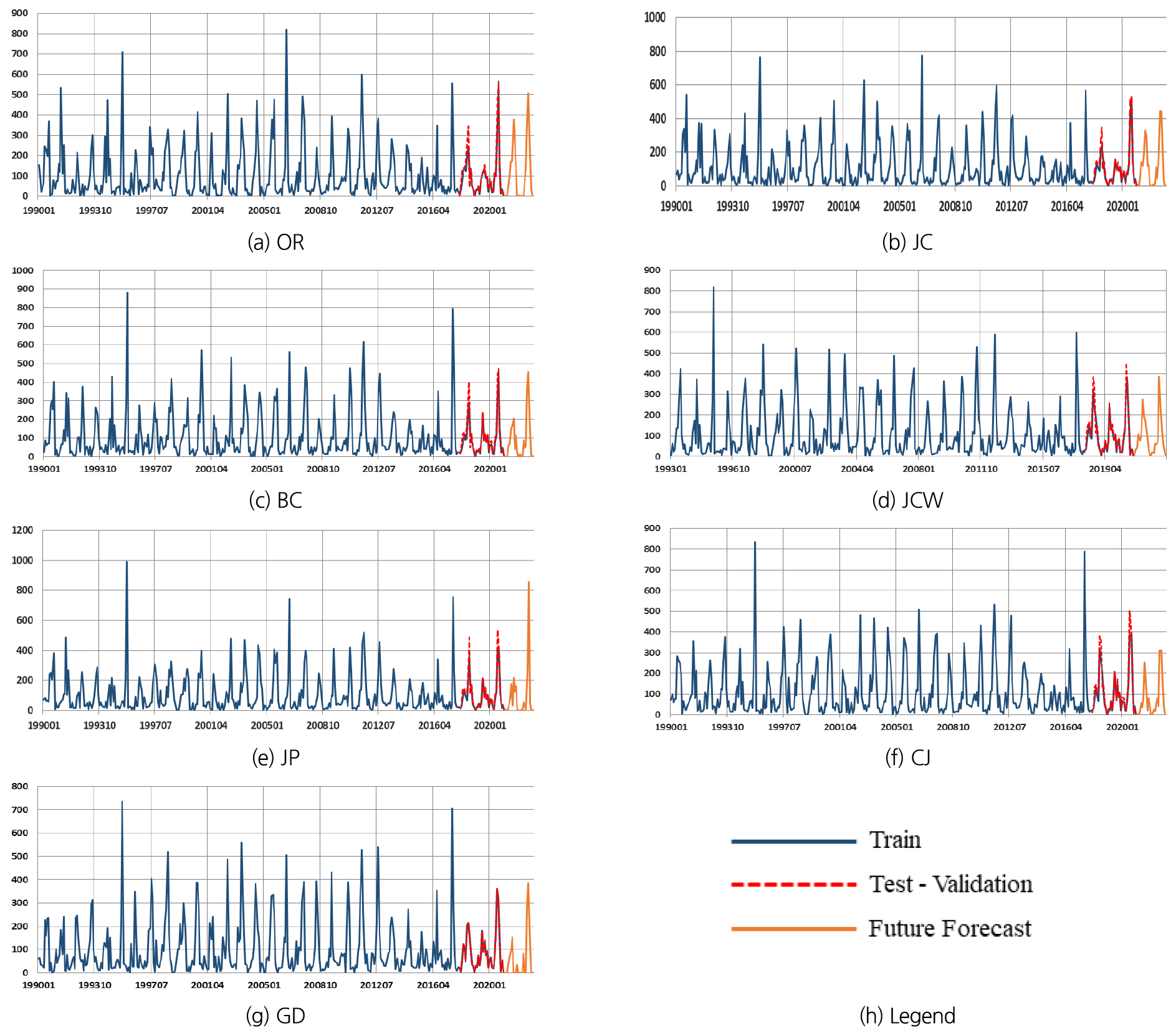
이번 연구에서 지하수위와 강수량에 대한 모델의 성능을 검증하기 위하여 RMSE와 R2를 산정하여 검증하였다. 7개 지하수위 관측소에 대한 모형 보정 결과 Table 4와 같이 0.021~0.055의 RMSE가 산정되었고, R2는 0.847~0.983의 범위로 산정되었다. 7개 강수량 관측소에 대한 월 단위 강수량 예측 결과 Table 5와 같이 0.023~0.037의 RMSE가 산정되었고, R2는 0.852~0.953의 범위로 산정되었다. 지하수위에 비하여 강수량의 예측 성능이 더욱 고르게 나타났는데, 이는 강수량의 경우 지하수위에 비하여 높은 계절적 변동과 더 긴 학습 길이에 의한 차이로 판단되었다. 지하수위의 경우 전체 학습 자료의 계절적 변동이 강수량에 비하여 확연하게 나타나지 않았고, 학습에 활용할 수 있는 관측 자료의 길이가 짧기 때문에 LSMT 모형 예측 결과와 실측 결과의 차이가 나타난 것으로 보인다. RMSE와 R2 산정 결과를 바탕으로 모형의 정확도를 평가하였을 때, 구성된 LSTM 모형은 지하수위와 강수량의 예측 측면에서 비교적 높은 정확도를 나타내고 있는 것으로 평가되었고, 계절 변동이 있는 시계열 데이터의 예측에 적용할 수 있음을 확인하였다.

Figs. 5 and 6은 월 단위 지하수위 및 강수량에 대한 모델 결과를 나타내고 있다.

Table 4.

Monthly average groundwater level train and test results

Wells Input Data Period (Train Data) Test Data Test RMSE (m) Test Coefficient of Determination (R2)
SJ-JCW 2001 - 2017 2018 - 2019 0.055 0.847
ES-DS 1998 - 2017 0.041 0.871
JP-JP 2000 - 2017 0.035 0.976
JC-JC 2000 - 2017 0.026 0.983
CA-BM 2001 - 2017 0.021 0.956
CA-SS 2002 - 2017 0.022 0.848
CJ-NS 1998 - 2017 0.033 0.930
Table 5.

Monthly precipitation train and test results

Wells Input Data Period (Train Data) Test Data Test RMSE (m) Test Coefficient of Determination (R2)
OR 1993 - 2017 2018 - 2020 0.027 0.952
JC 1990 - 2017 0.030 0.912
BC 1990 - 2017 0.037 0.936
JCW 1993 - 2017 0.023 0.930
JP 1990 - 2017 0.031 0.911
CJ 1990 - 2017 0.033 0.953
GD 1990 - 2017 0.036 0.852

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550701/images/kwra_55_07_01_F5.jpg
Fig. 5.

LSTM model results using groundwater level observation data

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550701/images/kwra_55_07_01_F6.jpg
Fig. 6.

LSTM model results using precipitation observation data

4.2 가중치 산정 결과

본 연구는 지하수위 관측소 자체의 자료 뿐만 아니라 타 지하수위 관측소의 관측자료와 강수량 관측소의 관측자료를 이용하여 유역 내 수문순환 요소 간의 상관관계를 적용함으로써 취약 시기 평가 시 유역 내 수문순환을 고려하고자 하였다. 또한 최근 기후변화로 인한 국내 수자원 환경의 변화에 따라 지하수위 관리 현황 및 미래 지하수위 관리 취약 시기 평가를 위한 평가 기준을 선정하였다. 기후변화로 인한 유역 내 수자원 환경의 변화와 수문순환을 고려한 취약시기 평가 기법 적용에는 이를 모두 고려할 수 있는 평가 기준 및 가중치 산정이 필수적이다.

연구지역의 지하수위 및 강수량 자료 수집 후 분석 결과, 지하수위와 강수량 모두 감소하는 추세를 나타내고 있는 것으로 분석되었다. 이번 연구에서는 유역 내 지하수자원의 변화를 대표할 수 있는 대표 인자로 지하수위를 선정하였고, 지하수위에 영향을 미칠 수 있는 강수량 관측 자료의 변동을 함께 고려하여 향후 관측정 별 지하수위의 변동이 어떻게 나타날 수 있는지에 대한 분석을 수행하였다. 지하수위 및 강수량 관측자료의 변화에 따른 취약성을 평가하기 위하여 관측소 별 수집 자료 전체의 변동 추세(TT), 최근 9년간의 변동 추세(R9), 최근 7년과 과거 11년 간의 변동 추세 차이(R7-P11), 최근 4년과 과거 14년 간의 변동 추세 차이(R4-P14) 등 4개 평가 기준을 선정하였다. 선정된 평가 기준을 이용하여 지하수위 및 강수량 각 관측소의 월 단위 시계열 자료의 변동을 평가하고, 엔트로피 방법을 이용하여 각 관측소의 평가 기준 별 가중치를 산정하였다. 또한, 각 관측소 간 상관관계를 고려하기 위하여 각 지하수위 관측소를 기준으로 타 지하수위 관측소, 강수량 관측소의 시계열 관측 자료 간 Pearson 상관계수 산정을 통해 해당 지하수위 관측소의 지하수위 관리 취약 시기 평가 시 어떤 관측소의 관측자료를 더 반영하여 평가할 것인지에 대한 가중치를 산정하였다. 지하수위와 강수량 관측소 간 산정되는 상관계수에 따라 상관계수가 높은 관측소의 관측자료에 대한 가중치를 높게 부여하기 위하여, 기준 지하수위 관측소와 타 관측소 간 상관계수를 표준화 방법을 통해 0~1의 값으로 재 산정하여 적용하였다.

지하수위 자료는 2019년까지, 강수량 자료는 2020년까지의 자료를 수집할 수 있었기 때문에 지하수위 자료는 2020~2022년까지의 자료를 LSTM 모형을 통해 예측하였고, 강수량 자료는 2021~2022년까지의 자료를 LSTM 모형을 통해 예측한 값을 적용하였다. 따라서 연구 결과를 도출하기 위한 연구 Case는 2019년(지하수위 및 강수량 관측값), 2020년(지하수위 예측값, 강수량 관측값), 2021년(지하수위 및 강수량 예측값), 2022년(지하수위 및 강수량 예측값) 등 관측 자료와 예측 자료 활용 측면에서의 4가지 Case로 구분하여 가중치를 산정하였다.

각 Case 별 상관관계에 따른 가중치(Wc) 산정 결과 연구 지역의 산계 및 수계 분포에 따라 소유역이 구분되기 때문에 지하수위 관측소 간 상관관계가 높게 나타나지 않았으나 세종 조치원(SJ-JCW) 지하수위 관측소와 진천 진천(JC-JC) 지하수위 관측소의 관측 자료 간 상관관계가 비교적 높게 나타났고, 두 지하수위 관측소 모두 미호천 중권역 내 강수 관측소의 관측 자료와 상관관계가 높게 나타나 강수량의 변동이 두 관측소의 지하수위에 영향을 미치고 있음을 알 수 있었다. 그러나 SJ-JCW의 경우 2020년부터 LSTM 모형 결과를 추가할 경우 타 관측소와의 상관관계가 줄어듦을 나타내고 있으나 JC-JC의 경우 타 관측소와의 상관관계가 소폭 증가함을 알 수 있었다.

각 Case에 따른 관측소 별 엔트로피 가중치(We) 산정 결과, 모든 관측소에서 실제 관측 자료를 이용한 경우 보다 지하수위 및 강수량 예측 값을 이용한 경우에 최근 7년과 과거 11년 간의 변동 추세 항목에서 가중치가 평균 약 0.054 증가한 것으로 나타났고, 반면 전체의 변동추세, 최근 9년 변동, 최근 4년 대비 과거 14년간의 변동 차이 항목에서 평균 약 -0.01, -0.003, -0.041의 가중치의 감소가 나타났다.

Table 6은 각 기준 지하수위 관측소와 타 지하수위 관측소 및 강수량 관측소 관측자료 간의 상관계수 산정에 따라 산정되는 Wc를 나타내고 있고, Table 7은 각 관측소 별 관측 자료의 변동에 따라 산정된 We의 산정 결과를 나타내고 있다.

Table 6.

Computation results of Wc by the study cases

2019 SJ-JCW ES-DS JP-JP JC-JC CA-BM CA-SS CJ-NS GD BC OR JCW JP JC CJ
SJ-JCW 1.000 0.000 0.074 0.500 0.432 0.029 0.247 0.650 0.643 0.647 0.658 0.622 0.651 0.653
ES-DS 0.225 1.000 0.157 0.062 0.259 0.137 0.236 0.006 0.005 0.037 0.000 0.003 0.026 0.001
JP-JP 0.430 0.330 1.000 0.000 0.460 0.333 0.453 0.295 0.307 0.303 0.284 0.292 0.298 0.288
JC-JC 0.692 0.255 0.000 1.000 0.412 0.323 0.378 0.715 0.711 0.714 0.725 0.697 0.707 0.712
CA-BM 0.406 0.000 0.084 0.002 1.000 0.012 0.439 0.366 0.387 0.388 0.358 0.344 0.370 0.373
CA-SS 0.128 0.000 0.028 0.013 0.152 1.000 0.101 0.190 0.199 0.239 0.217 0.194 0.202 0.196
CJ-NS 0.254 0.023 0.120 0.000 0.468 0.008 1.000 0.082 0.103 0.099 0.089 0.075 0.074 0.098
2020 SJ-JCW ES-DS JP-JP JC-JC CA-BM CA-SS CJ-NS GD BC OR JCW JP JC CJ
SJ-JCW 1.000 0.000 0.056 0.501 0.435 0.028 0.252 0.649 0.639 0.637 0.657 0.620 0.642 0.649
ES-DS 0.224 1.000 0.145 0.046 0.246 0.119 0.240 0.005 0.002 0.029 0.002 0.001 0.016 0.000
JP-JP 0.421 0.325 1.000 0.000 0.457 0.335 0.447 0.284 0.299 0.294 0.276 0.283 0.291 0.279
JC-JC 0.694 0.247 0.000 1.000 0.424 0.330 0.383 0.718 0.717 0.719 0.728 0.701 0.712 0.715
CA-BM 0.419 0.000 0.089 0.032 1.000 0.028 0.444 0.377 0.400 0.397 0.371 0.357 0.381 0.385
CA-SS 0.143 0.000 0.043 0.036 0.167 1.000 0.113 0.201 0.209 0.244 0.226 0.204 0.211 0.205
CJ-NS 0.257 0.027 0.103 0.000 0.463 0.000 1.000 0.084 0.105 0.100 0.093 0.078 0.075 0.101
2021 SJ-JCW ES-DS JP-JP JC-JC CA-BM CA-SS CJ-NS GD BC OR JCW JP JC CJ
SJ-JCW 1.000 0.000 0.025 0.488 0.407 0.008 0.265 0.645 0.631 0.627 0.648 0.613 0.623 0.639
ES-DS 0.233 1.000 0.130 0.032 0.232 0.097 0.273 0.022 0.012 0.018 0.000 0.011 0.002 0.017
JP-JP 0.417 0.321 1.000 0.000 0.459 0.334 0.437 0.279 0.289 0.282 0.273 0.274 0.279 0.275
JC-JC 0.694 0.244 0.000 1.000 0.422 0.340 0.386 0.722 0.720 0.727 0.733 0.704 0.720 0.715
CA-BM 0.408 0.000 0.096 0.036 1.000 0.033 0.395 0.377 0.397 0.380 0.368 0.353 0.374 0.383
CA-SS 0.157 0.000 0.055 0.063 0.177 1.000 0.115 0.214 0.224 0.261 0.244 0.217 0.231 0.219
CJ-NS 0.295 0.090 0.096 0.016 0.419 0.000 1.000 0.112 0.124 0.125 0.110 0.105 0.078 0.120
2022 SJ-JCW ES-DS JP-JP JC-JC CA-BM CA-SS CJ-NS GD BC OR JCW JP JC CJ
SJ-JCW 1.000 0.016 0.008 0.467 0.409 0.000 0.245 0.618 0.595 0.587 0.626 0.539 0.580 0.616
ES-DS 0.244 1.000 0.115 0.031 0.240 0.090 0.256 0.021 0.014 0.018 0.004 0.014 0.000 0.020
JP-JP 0.408 0.312 1.000 0.000 0.449 0.336 0.433 0.286 0.293 0.282 0.273 0.285 0.283 0.277
JC-JC 0.681 0.246 0.000 1.000 0.425 0.339 0.388 0.726 0.724 0.733 0.736 0.694 0.725 0.720
CA-BM 0.402 0.000 0.068 0.026 1.000 0.012 0.371 0.369 0.385 0.365 0.363 0.321 0.359 0.377
CA-SS 0.156 0.000 0.062 0.066 0.176 1.000 0.120 0.215 0.223 0.258 0.242 0.206 0.229 0.220
CJ-NS 0.276 0.072 0.090 0.017 0.403 0.000 1.000 0.111 0.121 0.124 0.106 0.093 0.080 0.118
Table 7.

Computation results of We by the study cases

2019 SJ-JCW ES-DS JP-JP JC-JC CA-BM CA-SS CJ-NS GD BC OR JCW JP JC CJ
TT 0.291 0.281 0.242 0.258 0.254 0.186 0.237 0.270 0.293 0.315 0.295 0.296 0.299 0.283
R9 0.288 0.238 0.264 0.249 0.261 0.275 0.268 0.286 0.286 0.323 0.304 0.285 0.319 0.275
R7-P11 0.218 0.220 0.251 0.228 0.238 0.274 0.237 0.168 0.140 0.184 0.172 0.153 0.137 0.160
R4-P14 0.202 0.261 0.242 0.266 0.247 0.265 0.259 0.275 0.281 0.178 0.229 0.267 0.245 0.281
2020 SJ-JCW ES-DS JP-JP JC-JC CA-BM CA-SS CJ-NS GD BC OR JCW JP JC CJ
TT 0.280 0.244 0.257 0.252 0.251 0.189 0.236 0.248 0.281 0.287 0.260 0.282 0.306 0.253
R9 0.288 0.313 0.238 0.253 0.258 0.216 0.266 0.285 0.280 0.300 0.285 0.268 0.332 0.279
R7-P11 0.192 0.169 0.262 0.237 0.229 0.294 0.248 0.214 0.148 0.213 0.202 0.188 0.187 0.194
R4-P14 0.240 0.275 0.244 0.258 0.262 0.301 0.251 0.252 0.292 0.201 0.254 0.262 0.174 0.275
2021 SJ-JCW ES-DS JP-JP JC-JC CA-BM CA-SS CJ-NS GD BC OR JCW JP JC CJ
TT 0.276 0.220 0.248 0.248 0.254 0.199 0.192 0.287 0.262 0.307 0.282 0.304 0.289 0.279
R9 0.276 0.261 0.216 0.246 0.269 0.244 0.292 0.320 0.306 0.326 0.310 0.326 0.318 0.321
R7-P11 0.238 0.249 0.286 0.266 0.264 0.281 0.287 0.201 0.242 0.214 0.209 0.226 0.210 0.210
R4-P14 0.209 0.270 0.250 0.240 0.213 0.275 0.229 0.192 0.190 0.154 0.199 0.144 0.183 0.190
2022 SJ-JCW ES-DS JP-JP JC-JC CA-BM CA-SS CJ-NS GD BC OR JCW JP JC CJ
TT 0.290 0.235 0.248 0.252 0.250 0.207 0.232 0.271 0.252 0.320 0.266 0.282 0.299 0.257
R9 0.290 0.292 0.242 0.244 0.238 0.233 0.187 0.298 0.290 0.345 0.288 0.300 0.336 0.290
R7-P11 0.280 0.275 0.299 0.255 0.263 0.286 0.305 0.259 0.269 0.167 0.220 0.254 0.149 0.261
R4-P14 0.140 0.198 0.210 0.249 0.249 0.274 0.276 0.171 0.189 0.168 0.226 0.165 0.216 0.192

4.3 지하수위 관측소 별 월 단위 지하수위 관리 취약 시기 평가 결과

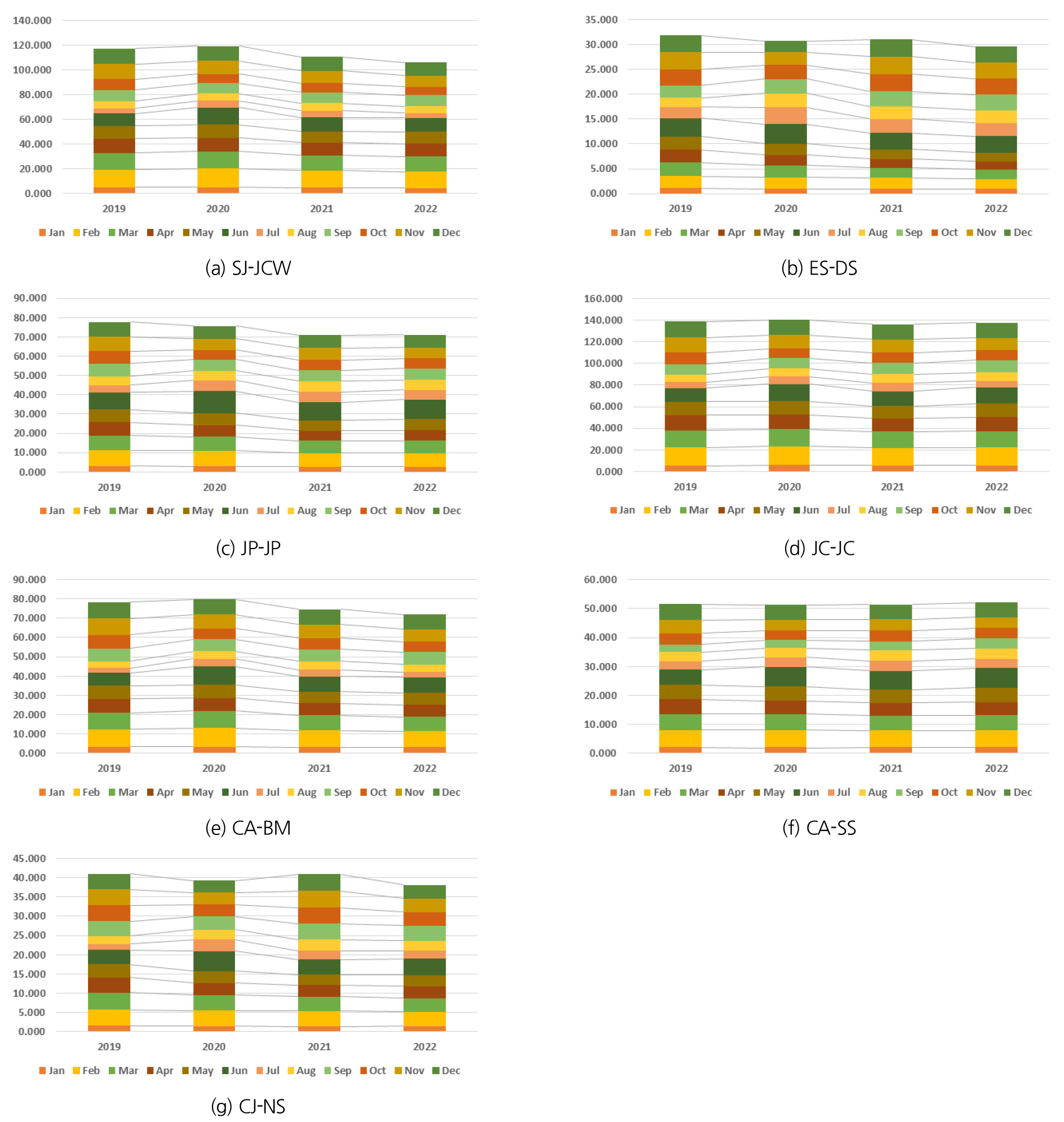
이번 연구에서 지하수위 및 강수량 관측자료를 기반으로 LSTM 모형을 통해 자료를 생산하였고, 기존의 관측자료에 생산된 자료를 추가하였을 때 각 지하수위 관측정 별 취약성 지수의 변화를 분석하였다. 앞서 산정된 가중치를 바탕으로 단순가중치법을 이용하여 지하수위 관측정 별 지하수위 관리 취약 시기 평가 지수(Groundwater Level Management Vulnerability Index by the Groundwater Level Observation Well, GVI)를 산정하였다.

각 지하수위 관측소 별 GVI 산정 결과 진천 진천 지하수위 관측소의 평균 GVI가 11.516으로 나타나 미호천 유역 내에서 지하수위 관리에 가장 취약한 지하수위 관측소로 나타났다. 그 뒤를 이어 세종 조치원 관측소가 평균 9.443, 천안 북면 관측소가 평균 6.346으로 GVI가 높게 나타났다. 미호천 중권역의 월 별 평가 결과는 대부분의 지하수위 관측소에서 2, 3, 6월이 취약한 시기로 평가되었는데, 음성 대소 관측소의 경우 6월이 GVI 3.558로 가장 취약한 것으로 나타났고, 10월, 11월이 2순위, 3순위로 나타났다. 대부분의 지하수위 관측소에 2, 3월에 강수량이 감소하였고, 비교적 풍수기로 나타난 6월의 경우 과거 대비 강수량이 감소하고 있는 경향을 나타내고 있기 때문인 것으로 분석되었다.

연구 Case 별 GVI 산정 결과로, 천안 수신 지하수위 관측소를 제외한 타 관측소에서는 2019년 실제 관측자료만 적용했을 때와 지하수위 2020년 자료 예측 및 강수량 2020년 실제 관측자료를 조합했을 때에 가장 GVI가 높게 나타났다. 반면 천안 수신 관측소의 경우 LSTM 모형을 이용하여 지하수위와 강수량 자료를 2022년까지 예측한 평가 Case에서 GVI가 가장 높게 나타났다. 천안 수신 관측소의 경우 타 관측소와의 상관계수가 높지 않아 천안 수신 관측소 자체의 관측 자료를 주로 이용하여 GVI 평가를 수행하여야 하는데, 예측 지하수위가 실제 관측 지하수위 중 2000년대 중반 지하수위 상승 추세에 비하여 크게 감소할 것으로 예측되었기 때문인 것으로 분석되었다.

Fig. 7은 각 자료 적용 Case 에 따른 지하수위 관측소 별 GVI 변화를 나타내고 있다.

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550701/images/kwra_55_07_01_F7.jpg
Fig. 7.

Analysis of GVI variation by groundwater level observation wells based on prediction of observation data using LSTM model

5. 결 론

기후변화로 인한 수자원 환경의 변화로 안정적인 수자원 확보를 위하여 지하수자원 관리 및 확보에 대한 중요성이 높아지는 가운데 유역 내 지하수자원의 부존 및 지속가능성을 평가하기 위한 다양한 연구들이 수행되고 있다. 본 연구는 유역 내 지하수자원의 현황을 평가하고, 미래 지하수자원의 변동을 예측하기 위하여 자료 기반의 지하수위 관리 취약 시기를 평가하는 연구를 수행하였다. 지하수위 관리 취약 시기 평가 시 유역 내의 수문순환 요소 간 상호 영향성을 고려하기 위하여 지하수위와 강수량 관측자료를 수집하고, 지하수위 관측소를 기준으로 관측 자료의 분석을 통한 지하수위 관리 취약 시기 평가 기법을 제안하였다. 또한, 현황 파악뿐만 아니라 미래 발생 가능한 지하수위의 변동에 따른 취약 시기의 변화를 분석하기 위하여 LSTM 모형을 구성하고, 지하수위 및 강수량의 예측 자료를 생성한 후 미래 지하수위 관측소 별 지하수위 관리 취약 시기를 평가하였다.

강수량과 지하수위 관측 자료의 변동 특성을 고려하기 위한 평가 지표를 선정한 후 강수-지하수 간 상관관계를 고려할 수 있는 가중치와 각 자료의 변동을 고려하기 위한 가중치를 산정하였다. 산정된 가중치를 통하여 이번 연구의 목적인 월 단위 지하수위 관리 취약 시기를 평가하였다. 평가 결과 미호천 유역은 2월, 3월, 6월에 지하수위 관리 취약성 지수가 높게 나타나 해당 시기에 지하수위 관리를 위한 보다 면밀한 조사 및 대응 방안 도출이 필요할 것으로 나타났다. 관정 별 지하수위 관리 취약 시기 평가 결과 평균 취약성 지수는 진천 진천 지하수위 관측소에서 가장 높게 나타났고, 뒤를 이어 세종 조치원, 천안 북면 지하수위 관측소의 취약성 지수가 높게 나타났다. 또한, 2019년까지의 실제 관측 자료를 바탕으로 LSTM 모형을 통해 산정된 2022년까지의 예측 자료를 추가하여 분석하였다. 미호천 유역 내 대부분의 관측소에서 미래 지하수위 관리 취약성 지수가 점차 개선될 것으로 기대되었다. 그러나 천안 수신 관측소의 경우 미래 지하수위 관리 취약성 지수가 더욱 악화될 것으로 분석되었다. 이는 천안 수신 관측소의 경우 타 지하수위 및 강수량 관측소의 관측자료와 상관관계가 낮게 나타나 천안 수신 관측소의 관측자료를 주로 이용하여 평가를 수행할 수 밖에 없는 상황에서, 천안 수신 관측소의 미래 지하수위가 2000년대 중반 지하수위가 높았던 시점보다 큰 폭으로 하강하기 때문에 미래 지하수위 관리 취약성 지수가 높게 산정 된 것으로 판단된다.

LSTM 모형을 활용한 지하수위 관리 취약 시기 평가 기법의 제안은 관측자료의 분석으로도 지하수위 관리 방안의 우선 적용 시기를 결정할 수 있다는 점에서 국내 수자원 관리 효율성 제고에 기여 할 수 있을 것으로 판단된다. 또한 이번 연구 결과는 유역 물 관리의 주체가 될 수 있는 지자체 및 공공기관 등 물 전담 부서 및 기관의 담당자에게 관측 자료를 통한 평가 기법을 제공함으로써 지하수위 관리의 전문성을 함양하여 지하수위 관리 방안을 도출하는데 기여할 것으로 기대된다. 현재 단계의 연구는 유역 내 지하수위 및 강수량 관측소의 개소수에 따라 평가 지수의 총 합이 달라지기 때문에 인접한 다수의 유역 또는 보다 큰 범위의 유역에 적용하기 부적합 할 수 있다. 추후 연구에서는 관측소의 개소수가 다른 인접한 유역의 취약 시기 평가 지수를 정량화 하여 비교 평가할 수 있는 기법에 대하여 추가로 연구를 수행할 예정이다.

Acknowledgements

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2021R1A2C2007595).

Conflicts of Interest

The authors declare no conflict of interest.

References

1
Alley, W.M., Healy, R.W., LaBaugh, J.W., and Reilly, T.E. (2002). "Flow and storage in groundwater systems." Science, Vol. 296, No. 5575, pp. 1985-1990. 10.1126/science.106712312065826
2
Benesty, J., Chen, J., Huang, Y., and Cohen, I. (2009). Pearson correlation coefficient. Noise Reduction in Speech Processing, Springer, Berlin, Heidelberg, Germany, pp. 1-4. 10.1007/978-3-642-00296-0_5
3
Cai, J., Varis, O., and Yin, H. (2017). "China's water resources vulnerability: A spatio-temporal analysis during 2003-2013." Journal of Cleaner Production, Vol. 142, pp. 2901-2910. 10.1016/j.jclepro.2016.10.180
4
Cheong, J.Y., Hamm, S.Y., Kim, H.S., Son, K.T., Cha, Y.H., Jang, S., and Baek, K.H. (2003). "Characteristics of waterlevel fluctuation in riverside alluvium of Daesan-myeon, Changwon City." The Journal of Engineering Geology, Vol. 13, No. 4, pp. 457-474.
5
Han, H.C., Choi, C.H., Jung, J.W., and Kim, H.S. (2021). "Application of sequence to sequence learning based LSTM model (LSTM-s2s) for forecasting dam inflow." Journal of Korea Water Resources Association, Vol. 54, No. 3, pp. 157-166. 10.3741/JKWRA.2021.54.3.157
6
Hochreiter, S., and Schmidhuber, J. (1997). "Long short-term memory." Neural Computation, Vol. 9, No. 8, pp. 1735-1780. 10.1162/neco.1997.9.8.17359377276
7
Intergovernmental Panel on Climate Change (IPCC) (2007). Climate change 2007:The physical science synthesis report. Cambridge University Press, Cambridge, UK. 10.1017/CBO9780511546013
8
Jeong, W.C., Yang, J. -S., and Kim, I.H. (2018). "A plan to improve sustainability in management of groundwater resources." Water for Future, Vol. 49, No. 4, pp. 14-18.
9
Jia, J.S., and Liu, C.M. (2002). "Groundwater dynamic drift and response to different exploitation in the North China Plain: A case study of Luancheng County Hebei Province." Acta Geographica Sinica, Vol. 57, No. 2, pp. 201-209.
10
Jung, S.H., Cho, H.S., Kim, J.Y., and Lee, G.H. (2018). "Prediction of water level in a tidal river using a deep-learning based LSTM model." Journal of Korea Water Resources Association, Vol. 51, No. 12, pp. 1207-1216. 10.3741/JKWRA.2018.51.12.1207
11
Kim, H.I., Han, K.Y., and Lee, J.Y. (2020). "Prediction of urban flood extent by LSTM model and logistic regression." Journal of the Korean Society of Civil Engineering, Vol. 40, No. 3, pp. 273-283.
12
Kim, I.-H., Lee, J.-B., and Yang, J.-S. (2018). "Development of vulnerable period assessment method for efficient groundwater resources management in upstream of Nakdong river basin using entropy method." Journal of Korea Water Resources Association, Vol. 51, No. 9, pp. 761-768. 10.3741/JKWRA.2018.51.9.761
13
Kingma, D., and Ba, J. (2015). "Adam: A method for stochastic optimization." Proceedings of the 3rd International Conference on Learning Representations, ICLR, San Diego, CA, U.S.
14
Leal, J.A.R., Silva, F.O.T., and Montes, I.S. (2012). "Analysis of aquifer vulnerability and water quality using SINTACS and geographic weighted regression." Environmental Earth Sciences, Vol. 66, No. 8, pp. 2257-2271. 10.1007/s12665-011-1447-4
15
Lee, G.H., Jung, S.H., and Lee, D.E. (2018). "Comparison of physics-based and data-driven models for streamflow simulation of the Mekong river." Journal of Korea Water Resources Association, Vol. 51, No. 6, pp. 503-514. 10.3741/JKWRA.2018.51.6.503
16
Lee, J.-B., Kim, I.-H., and Yang, J.-S. (2019). "Development of the vulnerable period assessment method for the weekly groundwater resources management in Yeongsan river basin considering the critical infiltration concept and the correlation between hydrological data sets." Journal of Korea Water Resources Association, Vol. 52, No. 3, pp. 195-206. 10.3741/JKWRA.2019.52.3.195
17
Lee, J.-B., Kim, J.-S., and Yang, J.-S. (2020). "A proposal for regional customization and optimal operation management of groundwater resources through analysis of water resources research trends in Korea." Journal of Korea Water Resources Association, Vol. 53, No. S-1, pp. 743-753.
18
Li, M.H., Tseng, K.J., Tung, C.P., Shih, D.S., and Liu, T.M. (2017). "Assessing water resources vulnerability and resilience of southern Taiwan to climate change." Terrestrial, Atmospheric and Oceanic Sciences, Vol. 28, No. 1, pp. 67-81. 10.3319/TAO.2016.08.23.02(CCA)
19
Lim, J.D., and Yang, J.S. (2020). "Possibility analysisof future droughts using long short term memory and standardized groundwater level index." Journal of Korea Water Resources Association, Vol. 53, No. 2, pp. 131-140.
20
Nardo, M., Saisana, M., Saltelli, A., and Tarantola, S. (2005). Tools for composite indicators building. European Commission. EUR 21682 EN, Institute for the Protection and Security of the Citizen, Joint Research Centre Ispra, Italy.
21
National Institute of Meteorological Sciences (NIMS) (2018). 100 Years of Climate Change on the Korean Peninsula.
22
Park, C.H., and Chung, I.-M. (2020). "Evaluating the groundwater prediction using LSTM model." Journal of Korea Water Resources Association, Vol. 53, No. 4, pp. 273-283. 10.3741/JKWRA.2020.53.4.273
23
Reghunath, R., Murthy, T.R., and Raghavan, B.R. (2005). "Time series analysis to monitor and assess water resources: A moving average approach." Environmental Monitoring and Assessment, Vol. 109, No. 1, pp. 65-72. 10.1007/s10661-005-5838-416240189
24
Sahoo, M.M., Patra, K.C., Swain, J.B., and Khatua, K.K. (2017). "Evaluation of water quality with application of Bayes' rule and entropy weight method." European Journal of Environmental and Civil Engineering, Vol. 21, No. 6, pp. 730-752. 10.1080/19648189.2016.1150895
25
Shannon, C.E. (1949). "Communication theory of secrecy systems." The Bell System Technical Journal, Vol. 28, No. 4, pp. 656-715. 10.1002/j.1538-7305.1949.tb00928.x
26
Yang, J.S., Kim, N.K., Nam, J.J., Lee, M.E., and Chung, E.S. (2011). "Trend analysis of groundwater level in Nakdong River watersheds." Proceedings of the Korea Water Resources Association Conference, pp. 234-234.
27
Zume, J., and Tarhule, A. (2008). "Simulating the impacts of groundwater pumping on stream-aquifer dynamics in semiarid northwestern Oklahoma, USA." Hydrogeology Journal, Vol. 16, No. 4, pp. 797-810. 10.1007/s10040-007-0268-8
페이지 상단으로 이동하기