Long-term runoff simulation using rainfall LSTM-MLP artificial neural network ensemble

Sungwook An; Dongho Kang; Janghyun Sung; Byungsik Kim

doi:10.3741/JKWRA.2024.57.2.127

Preview

Research Article

Journal of Korea Water Resources Association. 29 February 2024. 127-137
https://doi.org/10.3741/JKWRA.2024.57.2.127

Long-term runoff simulation using rainfall LSTM-MLP artificial neural network ensemble

LSTM - MLP 인공신경망 앙상블을 이용한 장기 강우유출모의

Sungwook An^a

Dongho Kang^b

Janghyun Sung^c

Byungsik Kim^d^*

안 성욱^a

강 동호^b

성 장현^c

김 병식^d^*

^aMaster’s Student, Department of Urban Environmental Disaster Management, Kangwon National University, Samcheok, Korea

^bResearch Professor, Department of Urban Environmental Disaster Management, Kangwon National University, Samcheok, Korea

^cAssistant Professor. Department of Urban Environmental Disaster Management, Kangwon National University, Samcheok, Korea

^dProfessor. Department of AI Software, Kangwon National University, Samcheok, Korea

^a강원대학교 방재전문대학원 도시환경재난관리전공 석사과정

^b강원대학교 방재전문대학원 도시환경재난관리전공 연구교수

^c강원대학교 도시환경재난관리전공 조교수

^d강원대학교 AI소프트웨어학과 교수

^{*Corresponding Author}

ABSTRACT

Physical models, which are often used for water resource management, are difficult to build and operate with input data and may involve the subjective views of users. In recent years, research using data-driven models such as machine learning has been actively conducted to compensate for these problems in the field of water resources, and in this study, an artificial neural network was used to simulate long-term rainfall runoff in the Osipcheon watershed in Samcheok-si, Gangwon-do. For this purpose, three input data groups (meteorological observations, daily precipitation and potential evapotranspiration, and daily precipitation - potential evapotranspiration) were constructed from meteorological data, and the results of training the LSTM (Long Short-term Memory) artificial neural network model were compared and analyzed. As a result, the performance of LSTM-Model 1 using only meteorological observations was the highest, and six LSTM-MLP ensemble models with MLP artificial neural networks were built to simulate long-term runoff in the Fifty Thousand Watershed. The comparison between the LSTM and LSTM-MLP models showed that both models had generally similar results, but the MAE, MSE, and RMSE of LSTM-MLP were reduced compared to LSTM, especially in the low-flow part. As the results of LSTM-MLP show an improvement in the low-flow part, it is judged that in the future, in addition to the LSTM-MLP model, various ensemble models such as CNN can be used to build physical models and create sulfur curves in large basins that take a long time to run and unmeasured basins that lack input data.

Keywords

LSTM

MLP

Long-term runoff

Machine learning

Artificial neural network

수자원 관리를 위해 주로 사용되는 물리 모형은 입력자료의 구축과 구동이 어렵고 사용자의 주관적 견해가 개입될 수 있다. 최근 수자원 분야에서 이러한 문제점을 보완하기 위해 기계학습과 같은 자료기반 모델을 이용한 연구가 활발히 진행되고 있다. 본 연구에서는 관측자료만을 이용하여 강원도 삼척시 오십천 유역의 장기강우유출모의를 수행했다. 이를 위해 기상자료로 3개의 입력자료군(기상관측요소, 일 강수량 및 잠재증발산량, 일 강수량 – 잠재증발산량)을 구성하고 LSTM (Long Short-term Memory)인공신경망 모델에 각각 학습시킨 결과를 비교 및 분석했다. 그 결과 기상관측요소만을 이용한 LSTM-Model 1의 성능이 가장 높았으며, 여기에 MLP 인공신경망을 더한 6개의 LSTM-MLP 앙상블 모델을 구축하여 오십천 유역의 장기유출을 모의했다. LSTM 모델과 LSTM-MLP 모형을 비교한 결과 두 모델 모두 대체적으로 비슷한 결과를 보였지만 LSTM 모델에 비해 LSTM-MLP의 MAE, MSE, RMSE가 감소했고 특히 저유량 부분이 개선되었다. LSTM-MLP의 결과에서 저유량 부분의 개선을 보임에 따라 향후 LSTM-MLP 모델 이외에 CNN등 다양한 앙상블 모형을 이용해 물리적 모델 구축 및 구동 시간이 오래 걸리는 대유역과 입력 자료가 부족한 미계측 유역의 유황곡선 작성 등에 활용성이 높을 것으로 판단된다.

키워드

LSTM

MLP

장기유출

기계학습

인공신경망

MAIN

1. 서 론
2. 연구 방법 및 모델 개요
2.1 연구 방법
2.2 모델 개요
3. 모형의 적용
3.1 대상유역 및 자료수집
3.2 기상 및 유출량 자료 구축
3.3 LSTM 및 LSTM-MLP 모델 학습결과
4. 결 론

1. 서 론

지구온난화로 인해 발생한 기후변화는 지역별 강수량, 유출량 및 증발산량을 변화시켜 예외적이던 홍수 및 가뭄 등의 발생빈도 및 강도를 증가시켰다. 이에 우리나라는 기후변화로 인한 수재해 대응을 위하여 국가하천 및 다목적 댐 등의 유출량과 유입량을 관측하고 유황곡선(Flow-Duration-Curve)등을 만들어 평상시의 수자원 관리 및 가뭄 시 하천수 사용 조정 등에 활용하고 있다(MOLIT, 2000). 일반적으로 강우-유출 모형으로부터 도출된 30년 이상의 일 유량 자료를 이용하여 유량지속곡선을 산정하고 있으며, 미계측 유역의 경우 비유량법 및 강우-유출 모델 매개변수의 지역화 등의 방법론을 사용하여 추정한다(KRIHS, 2020; Choi et al., 2021b).

유역 기반의 강우-유출 모델으로는 대표적으로 Soil and Water Assessment Tool (SWAT), Tank, Hydrological Simulation Program-FORTRAN (HSPF)등이 있으며(Han et al., 2016) 최근에는 기존의 강우-유출 모델 이외에 시계열 데이터의 특성을 학습하여 예측하는 딥러닝 오픈소스 라이브러리가 공개됨에 따라 수자원 분야에서도 이를 이용한 시계열 예측 연구가 활발히 진행되고 있다(Lee and Jung, 2018; Lee et al., 2020). 딥러닝 알고리즘의 하나인 LSTM (Long Short-Term Memory)은 기존의 RNN (Recurrent Neural Network)의 시간 의존성 문제를 개선한 모형으로 구글의 텐서플로우와 결합하여 수문 분야에서 많이 사용되고 있다(Mok et al., 2020).

국내에서 Han et al. (2021)과 Mok et al. (2020)은 각각 소양강댐과 용담댐을 대상으로 댐 유입량을 예측했다. Choi et al. (2021a)은 SWAT 물리모델의 매개변수 보정 결과 중 일 최고기온과 강수량을 LSTM 모델에 이용해 유출모의를 진행 했다. 해외에서는 Xu et al. (2020)이 기상자료를 LSTM 모델에 학습하여 Hun강과 Yangtze강의 유출량을 예측했으며 Sahoo et al. (2019)은 LSTM을 이용하여 인도 Mahanadi 강 유역의 저유량 기간 동안 일 유출량을 예측하여 LSTM의 높은 신뢰도를 검증하였다. Jiang et al. (2021)은 LSTM과 MLP를 결합한 HAL (Hybrid ANN-LSTM)을 개발하여 실내온도를 예측한 결과 LSTM으로 온도 패턴을 모델링하고 MLP로 변수와의 관계를 동시에 학습할 수 있음을 확인했다.

본 연구에서는 강원도 삼척시 오십천을 대상유역으로 하였으며 입력자료 구축의 한계점을 극복하고자 LSTM 인공신경망에 관측자료만을 사용하여 유출모의를 수행했다. 또한 강수량 외 요소들이 결과에 어떻게 영향을 미치는지 확인하고자 3개의 입력자료군(기상관측요소, 일 강수량 및 잠재증발산량, 일 강수량 - 잠재증발산량)을 구성해 LSTM (Long Short-term Memory)모델에 각각 학습한 후 비교하여 최적 모형을 선정했다. LSTM 모델에 MLP (Multi Layer Perceptron) 모델을 병렬로 결합하면 LSTM에서 파악하지 못하는 특징들을 학습해 성능이 향상 될 수 있고 구축이 용이한 장점이 있어(Jiang et al., 2021) 선정된 최적 LSTM 모델에 MLP신경망을 결합한 6개의 LSTM-MLP 앙상블 모델을 구축하고 실측값과 비교하여 수자원 분야에서 LSTM-MLP 모델의 가능성을 평가했다.

2. 연구 방법 및 모델 개요

2.1 연구 방법

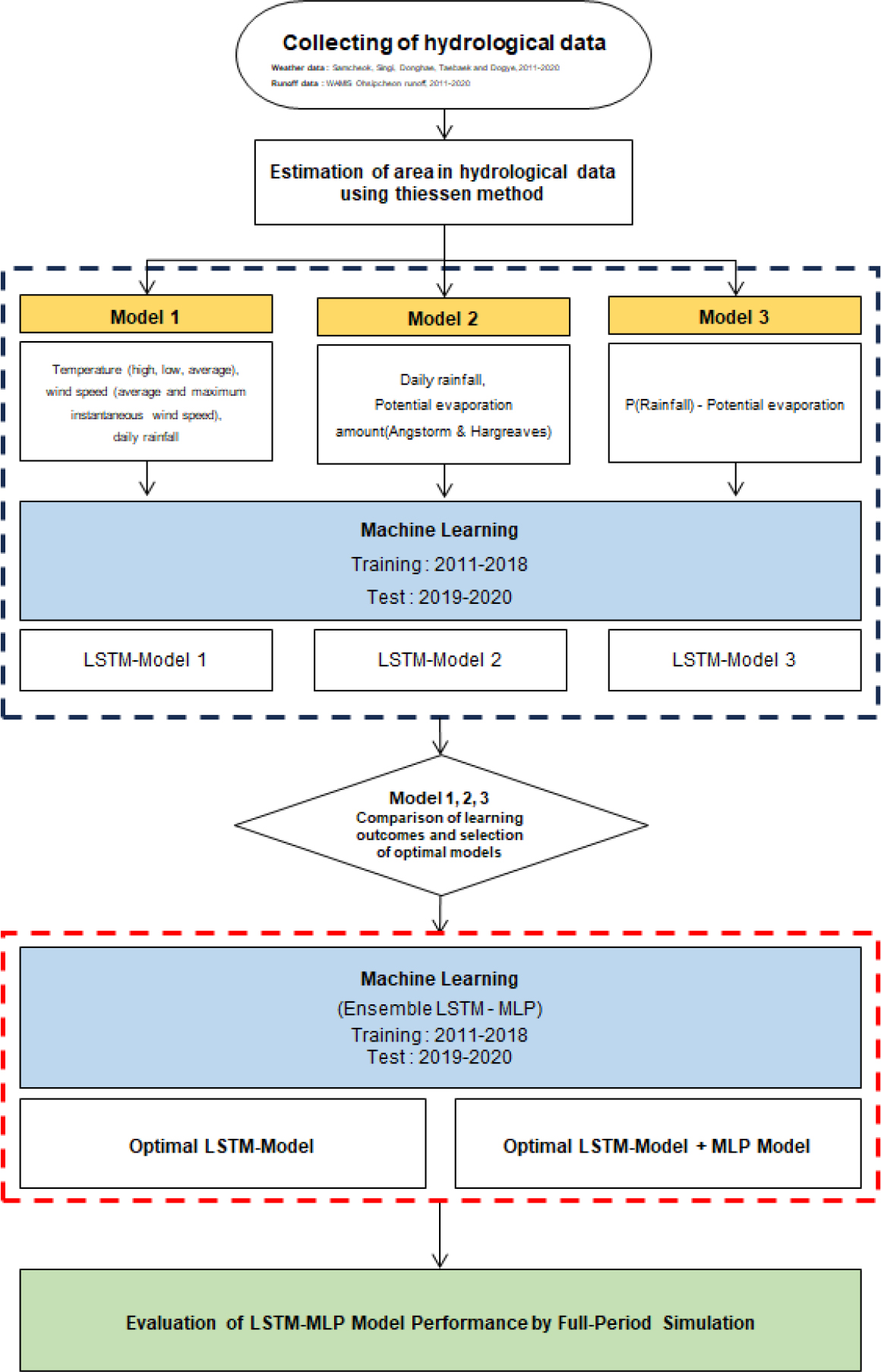
삼척 오십천 유역의 일 유출량을 모의하는데 있어서 5개 기상관측소의 일 단위의 기상자료를 이용해 Hargreaves & Angstrom 공식으로 잠재증발산량을 산정한 후 티센 면적비를 적용했으며 이를 이용해 3개의 자료군을 구성한 뒤 2011년부터 2018년 까지를 Training 기간으로, 2019년부터 2020년까지를 Test 기간으로 사용하여 각각 3개의 LSTM 모델에 학습시켜 최적 모형을 선정했다. 이후 입력데이터의 구성이 자유롭고 데이터가 여러 레이어를 거치면서 발생하는 정보의 손실이 없으며 LSTM 모델에 병렬로 결합했을 때 LSTM 모델에서 파악하지 못하는 특징들을 학습하여 성능이 향상 될 수 있는 장점을 가진 MLP 모델을 결합하여 6개의 LSTM-MLP 앙상블모델(평균값 이용)을 구축 및 학습한 뒤 전체기간(2011년~2020년)의 일 유출량을 모의한 결과를 분석했다(Fig. 1).

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057205/images/kwra_57_02_05_F1.jpg

Fig. 1.

Flowchart of the study

2.2 모델 개요

2.2.1 LSTM 기반 딥러닝 기법

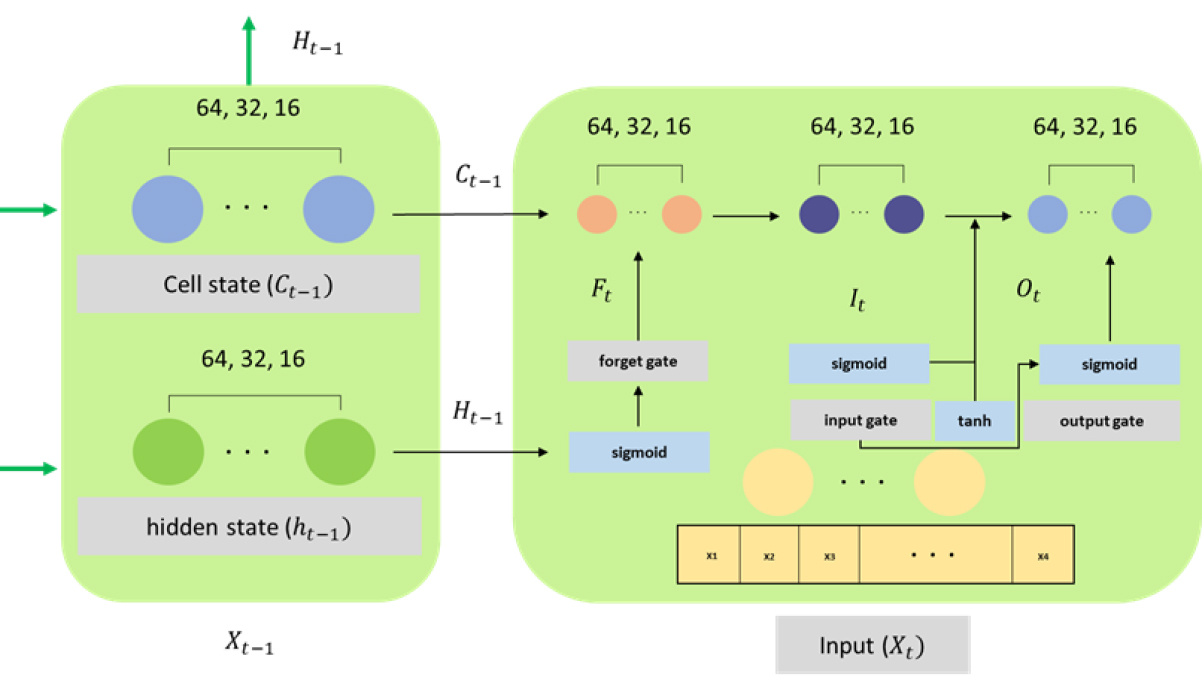
LSTM은 시계열 데이터 처리에 효과적인 딥러닝(Deep Learning) 기법인 순환신경망(Recurrent Neural Network, RNN)이 가지고 있는 기울기 소실과 폭주(Vanishing and Exploding gradient)의 문제를 해결하기 위해 Hochreiter and Schmidhuber (1997)가 제안하였다. LSTM은 여러개의 셀(cell)로 구성되어 있으며, 각 셀에는 데이터 흐름을 조절하기 위한 입력 게이트(Input Gate, $i_{t}$ ), 망각 게이트(Forget Gate, $f_{t}$ ) 및 출력 게이트(Output Gate, $o_{t}$ )로 구성된다(Fig. 2).

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057205/images/kwra_57_02_05_F2.jpg

Fig. 2.

LSTM structure

망각 게이트( $f_{t}$ )는 이전 셀( $c_{t - 1}$ )에서 들어온 정보를 매개변수와 시그모이드 함수(Sigmoid Function, 𝜎)를 이용해 얼마나 잊을지 결정하게 된다(Eq. (1)).

(1)

f_{t} = σ (W_{f} x_{t} + U_{f} h_{t - 1} + b_{f})

여기서, $f_{t}$ 는 (0, 1) 범위의 값을 가진 결과 벡터, 𝜎는 Sigmoid 활성 함수, $W_{f}, U_{f}, b_{f}$ 는 망각 게이트에 대한 매개변수 집합, $x_{t}$ 는 현재 입력, $h_{t - 1}$ 는 이전 스텝의 상태이다. 입력 게이트( $i_{t}$ )에서는 하이퍼볼릭 탄젠트(Hyperbolic Tangent, tanh)를 이용하여 새로운 셀의 업데이트시 사용되는 후보 셀( $\tilde{c}$ )을 생성하고(Eq. (2)), 시그모이드 함수(𝜎)를 이용해 어떤 정보를 업데이트 할지 결정하여(Eq. (3)), 최종적으로 현재의 셀 상태( $c_{t}$ )를 업데이트 한다(Eq. (4)).

(2)

{\tilde{c}}_{t} = \tanh (W_{\tilde{c_{t}}} x_{t} + U_{\tilde{c_{t}}} h_{t - 1} + b_{\tilde{c_{t}}})

(3)

i_{t} = σ (W_{i} x_{t} + U_{i} h_{t - 1} + b_{i})

(4)

c_{t} = f_{t} ⊙ c_{t - 1} + i_{t} ⊙ \tilde{c_{t}}

여기서, ${\tilde{c}}_{t}$ 는 범위(-1, 1)의 값을 가진 벡터, $W_{c}$ 와 $U_{c}$ 는 각각 $x_{t}$ 와 이전 스텝의 가중치, ${\tilde{b}}_{c}$ 는 학습 가능한 매개변수 집합이다. 또한, $i_{t}$ 는 범위 (0, 1)의 값을 가진 벡터, $W_{i}, U_{i}, b_{i}$ 는 입력게이트에 대해 정의된 학습 가능한 파라미터 집합이며, ⊙는 요소 곱 이다. 마지막으로 출력 게이트( $o_{t}$ )의 시그모이드 함수(𝜎)를 거쳐 출력하고(Eq. (5)), 하이퍼볼릭 탄젠트(Hyperbolic Tangent, )를 이용하여 특정 시점의 상태( $h_{t}$ )를 업데이트하게 되어 기울기의 소실과 폭주 문제를 해결할 수 있다(Eq. (6)).

(5)

o_{t} = σ (W_{o} x_{t} + U_{o} h_{t - 1} + b o)

(6)

h_{t} = \tanh (c_{t}) ⊙ o_{t}

여기서, $o_{t}$ 는 범위(0, 1)의 값을 가진 벡터이며, $W_{o}, U_{o}$ 및 $b_{o}$ 는 출력 게이트에 대해 정의된 학습 가능한 파라미터의 집합이다(Hochreiter and Schmidhuber, 1997).

2.2.2 모형의 평가 방법

본 연구에서는 실측값과 모델 예측값의 오차범위 확인에 있어서 MAE (Mean Absolute Error)와 RMSE (Root Mean Square Error)를 사용했으며, PBIAS (Percent Bias)와 VE (Volume Efficiency)를 이용해 모형에서 도출된 총합 값의 범위를 확인했고, NSE (Nash-Sutcliffe Efficiency)와 결정계수 (Coefficient of Determination)를 이용해 모델의 적합도를 확인했다. 평균절대오차(MAE)와 평균제곱근오차(RMSE)는 수문 모형의 예측값과 실측값 간의 오차를 비교하는 지표로 각각 Eqs. (7) and (8)와 같으며, 0에 근접할수록 실측값과의 오차가 적어 최적값을 보인다. PBIAS와 체적효율(VE)은 수문 모형의 참값과 예측값 간의 총합의 크기를 비교하는 지표로 각각 Eqs. (9) and (10)과 같이 계산되며, 0%의 값에 가까울수록 최적값을 보인다. NSE와 결정계수( $R^{2}$ )는 각각 모형의 경향성 및 적합도를 비교하는 지표로 Eqs. (11) and (12)과 같이 계산되며, 1에 가까울수록 최적의 값을 보인다(Choi et al., 2021b).

(7)

M A E = \frac{\sum_{i = 1}^{n} | Q_{i} - S_{i} |}{n}

(8)

RMSE = \sqrt{\frac{\sum_{i = 1}^{n} (Q_{i} - S_{i})^{2}}{n}}

(9)

P B I A S = \frac{[\sum_{i = 1}^{n} (S_{i} - O_{i})]}{[\sum_{i = 1}^{n} (O_{i})]} \times 100

(10)

V E = \frac{\sum_{i = 1}^{n} Q_{i} - \sum_{i = 1}^{n} S_{i}}{\sum_{i = 1}^{n} Q_{i}} \times 100

(11)

N S E = 1 - \frac{(\sum_{i = 1}^{n} (Q_{i} - S_{i})^{2})}{(\sum_{i = 1}^{n} (Q_{i} - \bar{O})^{2})}

(12)

Ｒ^{2} = {(\frac{\sum_{i = 1}^{n} (Q_{i} - \bar{Q}) (S_{i} - \bar{S})}{\sqrt{\sum_{i = 1}^{n} (Q_{i} - \bar{Q})^{2})} \sqrt{\sum_{i = 1}^{n} (S_{i} - \bar{S})^{2})}})}^{2}

3. 모형의 적용

3.1 대상유역 및 자료수집

본 연구에서는 한강권역 삼척오십천수계에 속하는 강원도 삼척시의 오십천을 대상유역으로 선정했으며 인근의 삼척, 동해, 신기, 도계, 태백 ASOS 및 AWS 기상자료와 오십천 유량자료를 활용해 오십천 유출모의 및 분석을 수행했다. 삼척 오십천 유역면적은 394.20 km²이며 유출모의 지점으로 선정한 삼척오십천 하구의 설계빈도와 계획홍수량은 100년, 2,764 m³/s이다. 대상 유역 및 관측소 현황을 Fig. 3과 Table 1과 같이 나타냈다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057205/images/kwra_57_02_05_F3.jpg

Fig. 3.

Location map of the target basin and stations

Table 1.

Weather and flow station

Station name	Station code	Observation start date	X (N)	Y (E)	Note
Donghae	106	1992-05-01	447418	387813	Weather station
Taebaek	216	1985-08-01	409787	376664
Singi	696	2002-12-24	429528	384830
Samcheok	876	2003-06-16	441157	391301
Dogye	878	2010-07-08	415918	386018
Samcheok Osipcheon	1303680	2006	537671	214614	Flow station

3.2 기상 및 유출량 자료 구축

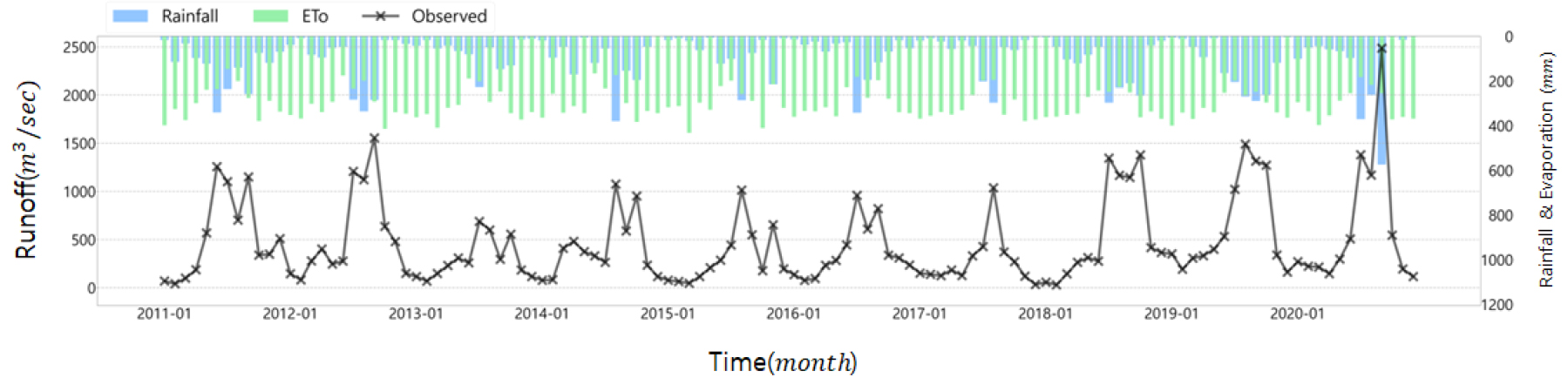
본 연구에서는 인공신경망을 이용한 삼척 오십천 유역의 장기유출모의 입력자료로 일 단위 유출량과 기상자료를 활용했다. WAMIS에서 2011년~2020년 까지의 강원도 삼척 오십천 유역의 일 유출량 자료를, 기상청에서 같은 기간의 AWS (삼척, 신기, 도계) 및 ASOS (동해, 태백) 일 기상자료(강수량, 최고 및 최저기온, 평균기온, 최대 순간 풍속, 평균풍속, 일조시간)를 수집한 후 Hargreaves & Angstorm 공식을 이용해 잠재증발산량을 산정하여 Table 2와 같이 3개의 입력자료군을 구성했다. 2011년~2020년 삼척 오십천 유역의 연 평균 유량은 5,539.68 m³이며 강수량과 증발산량은 각각 1,239.96 mm, 3,652.04 mm이고 Fig. 4와 같이 그래프로 나타냈다.

Table 2.

LSTM model input data

LSTM-Model 1	LSTM-Model 2	LSTM-Model 3
P: Daily precipitation (mm)	P: Daily precipitation (mm)	P - ET: Daily precipitation (mm) - Potential evapotranspiration (mm)
Tmax: Maximum temperature (°C)
Wmax: Max instantaneous wind speed (m/s)
Tmin: Minimum temperature (°C)	ET: Potential evapotranspiration (mm)
Wmean: Average wind speed (m/s)
Tmean: Average temperature (°C)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057205/images/kwra_57_02_05_F4.jpg

Fig. 4.

Monthly time series of flow, precipitation and evapotranspiration in Samcheok Osipcheon watershed

본 연구에서는 LSTM 인공신경망에 대상 유역의 기상자료를 학습하여 유출모의를 진행했을때 강수량 외 요소들이 결과에 어떻게 영향을 미치는지 확인하고자 3개의 입력자료군을 Table 1과 같이 구성하여 각각 LSTM-Model 1에는 6개의 기상요소, LSTM-Model 2에는 일 강수량과 잠재증발산량 2개의 요소, LSTM-Model 3에는 일 강수량에서 잠재증발산량을 뺀 1개의 요소로 입력자료를 구성하여 학습했다. 세 LSTM 모델의 입력자료 모두 유역면적평균을 반영하기 위해 5개의 기상관측소(삼척, 도계, 신기, 동해, 태백)를 기준으로 하여 티센 면적비를 적용하였다. 그 후 3개의 LSTM 모델 학습결과 중 가장 높은 성능을 보인 모델을 선정한 후 MLP 신경망을 더해 LSTM-MLP 앙상블 모델을 구축하여 2011년부터 2020년 까지의 삼척 오십천의 유출 모의 및 분석을 수행했다.

3.3 LSTM 및 LSTM-MLP 모델 학습결과

3.3.1 모델 구축

앞서 기술한 Table 1과 같이 총 3개의 LSTM 모델을 학습함에 있어 총 자료 기간 중 2011년부터 2018년 까지를 Training 기간으로, 2019년부터 2020년 까지를 Test 기간으로 정하여 학습한 후 최적 모델을 선정했다(Table 2, Fig. 5(a)). 모델의 학습횟수는 2000번의 학습 중 Training Loss와 Validation Loss가 최소가 되는 시기를 선정했으며(Table 3) 모델 학습에 12분 27초가 소요되었다. Hidden Layer는 모델 은닉층을 의미하며 Optimizer는 모델 학습 중 오차에 대한 최적화 알고리즘, Sequence Length는 입력자료 길이, Epoch는 학습횟수 이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057205/images/kwra_57_02_05_F5.jpg

Fig. 5.

Model configuration of LSTM and LSTM-MLP

Table 3.

Model parameter setting of LSTM and LSTM-MLP

Model structure		Setting	Note
Input data		Training	2011-01-01 ~ 2018-12-31
Input data		Test	2019-01-01 ~ 2020-12-31
Hidden Layer	LSTM	3 Layer	Layer 1 : 64, Layer 2 : 32, Layer 3 : 16
Hidden Layer	MLP	3 Layer	Layer 1 : 128, Layer 2 : 64, Layer 3 : 32
Optimize		Adam	Learning Rate : 0.00003
Sequence Length		30	-
Epoch	LSTM	973	-
Epoch	LSTM - MLP	1200	-

3.3.2 LSTM 및 LSTM-MLP 모델 학습결과(Test)

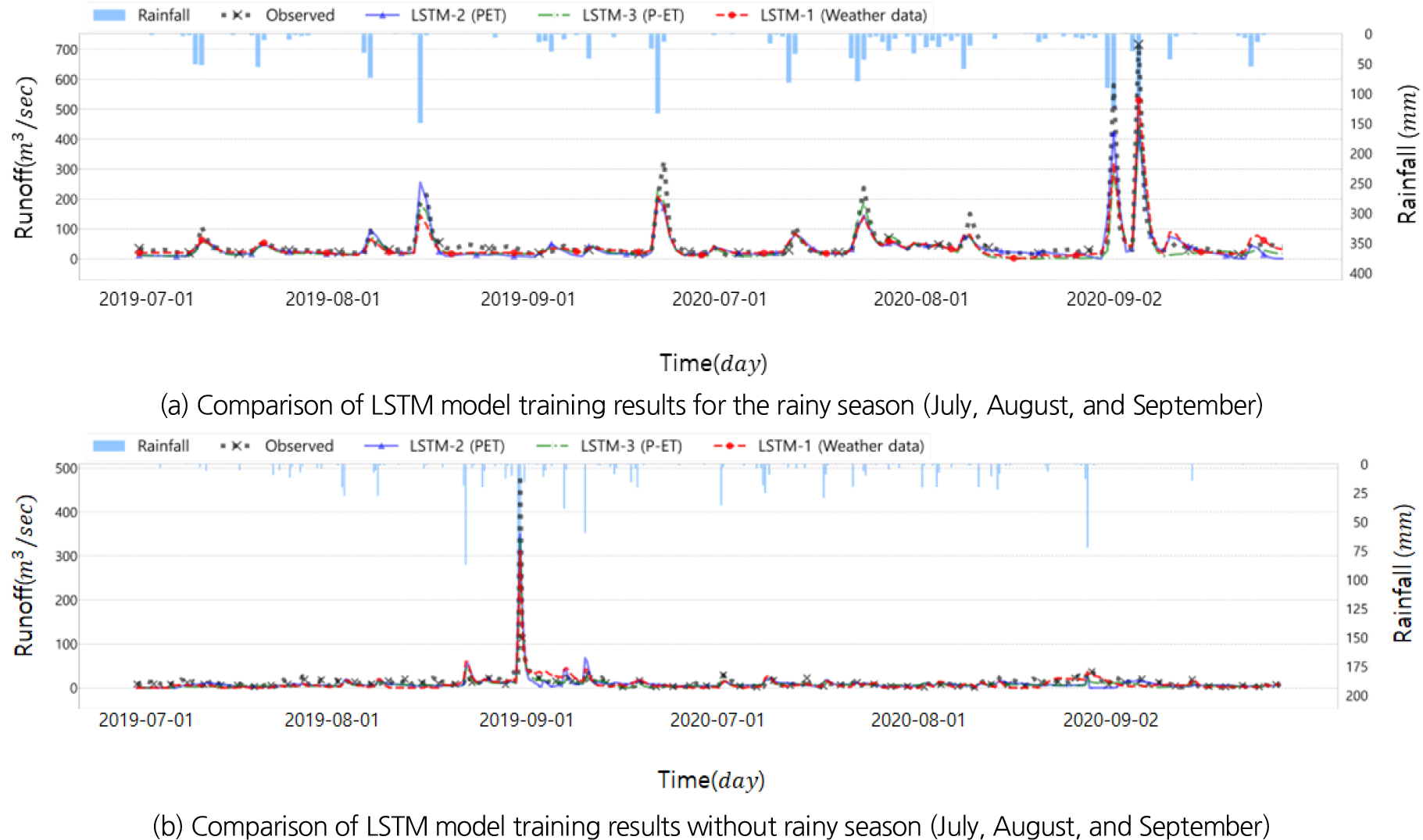
3개의 LSTM 모델 학습 결과는 Fig. 6, Table 4와 같으며 모두 예측모형의 정확도를 정량적으로 평가할 수 있는 지표인 NSE가 0.7 이상으로 준수한 성능(Very good: NSE ≥ 0.7, Good: 0.5 ≤ NSE < 0.7, Satisfactory: 0.3 ≤ NSE < 0.5, and Unsatisfactory: NSE < 0.3)임을 알 수 있다(Kalin et al., 2010).

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057205/images/kwra_57_02_05_F6.jpg

Fig. 6.

LSTM model training results time series (Test)

Table 4.

LSTM model training results metrics (Test)

	Model 1	Model 2	Model 3
MAE	8.75	8.86	8.51
MSE	381.63	384.5	400.68
RMSE	19.54	19.61	20.02
PBIAS %	-19.2	-20.5	-27.7
NSE	0.81	0.81	0.8
rNSE	0.89	0.85	0.89
R2	0.85	0.84	0.87
KGE	0.68	0.69	0.6
VE	0.58	0.58	0.59

강우가 많은 여름철(7월, 8월, 9월)과 여름철을 제외한 기간으로 나누어 세 LSTM 모델을 비교했을때 여름철기간의 결과에서는 Model 1의 PBIAS가 가장 낮았고, 여름철기간을 제외했을때는 Model 2가 가장 낮았다(Table 5). 여름철 기간을 제외했을때 Model 3의 NSE가 가장 높았고 오차를 나타내는 RMSE가 가장 낮게 나타났다. 세 LSTM 모델이 유사한 결과를 보여 예측에 있어 편향의 정도를 나타내는 PBIAS가 가장 낮은 Model 1을 최적 모델로 선정했고(Table 4), LSTM-Model 1을 이용해 Fig. 5(b)와 같이 총 6개의 LSTM-MLP을 구축하여 학습한 후 평균값을 사용하여 전체기간(2011년~2020년)에 대한 유출량을 모의했다.

Table 5.

LSTM model training results metrics for the rainy season

	Rainy season			Without rainy season
	Model 1	Model 2	Model 3	Model 1	Model 2	Model 3
MAE	16	17.12	17.65	6.31	6.09	5.43
MSE	1115.16	1112.67	1299	134.89	139.56	98.5
RMSE	33.39	33.36	36.04	11.61	11.81	9.92
PBIAS %	-17.1	-20.6	-27.5	-22.1	-20.3	-28
NSE	0.80	0.80	0.77	0.73	0.72	0.8
rNSE	0.93	0.90	0.91	0.82	0.76	0.83
R2	0.85	0.85	0.85	0.74	0.73	0.85
KGE	0.67	0.67	0.58	0.68	0.72	0.62
VE	0.67	0.64	0.63	0.46	0.48	0.54

3.3.3 LSTM 및 LSTM-MLP 모의결과 비교(Simulation)

LSTM 및 LSTM-MLP 모델을 이용해 전체기간(2011년~2020년)에 대해 삼척 오십천의 유출량을 모의한 결과는 Fig. 7과 같다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057205/images/kwra_57_02_05_F7.jpg

Fig. 7.

LSTM and LSTM-MLP model simulation results time series

LSTM-Model 1과 비교했을때 LSTM-MLP 모델의 정확도 측면에서 여름철 및 여름철 제외기간에서는 각각 NSE 0.76, 0.72로 약간 감소했으며, PBIAS는 각각 -12.6, -8.5로 개선됐음을 알 수 있다(Table 6). 특히 전체기간(2011년~2020년)에 대한 통계비교를 했을때(Table 7) 25%에 해당하는 저유량 부분이 개선되어 이는 LSTM-MLP 앙상블 모델을 이용해 유출량을 모의했을 때 더 높은 성능을 보였다고 판단된다.

Table 6.

LSTM and LSTM-MLP models results metrics

	LSTM-MLP (rainy season)	LSTM-MLP (without rainy season)	LSTM-MLP (2011-2020 simulation)
MAE	16.08	5.43	8.11
MSE	1363.76	136.53	445.44
RMSE	36.93	11.68	21.11
PBIAS %	-12.6	-8.5	-10.9
NSE	0.76	0.72	0.78
rNSE	0.94	0.75	0.85
R2	0.77	0.74	0.79
KGE	0.73	0.7	0.74
VE	0.67	0.54	0.61

Table 7.

Results of comparing observed vs. predicted (2011~2020)

	Observed runoff	LSTM-MLP	LSTM-Model 1
mean	461.64	448.05	421.70
std	431.59	425.60	429.40
min	30.40	1.57	0.00
25%	151.14	126.59	114.05
50%	308.78	342.39	266.54
75%	573.89	633.21	601.56
max	2486.17	2478.85	2385.82

LSTM-MLP 모델의 모의 결과에 대해 고유량과 저유량에 대한 비교를 위해 Fig. 8과 같이 월별 시계열로 나타내었다. 관측 유출량과 비교시 저유량 부분과 고유량 부분에서 과대 및 과소추정하는 경향을 보였는데, 여러 선행연구에서 정확도 개선을 위한 방법으로 입력데이터의 특징 파악에 강점을 가지고 있는 CNN (Convolution Neural Network)을 LSTM에 결합한 ConvolutionLSTM 등 다양한 모델이 제안되고 있다. 이에 향후 연구에서 ConvolutionLSTM 등 다양한 모델을 이용한다면 보다 관측값에 유사한 결과를 도출 할 수 있을 것으로 기대된다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057205/images/kwra_57_02_05_F8.jpg

Fig. 8.

Observed and simulated(LSTM-MLP) runoff monthly time series

4. 결 론

기후변화로 인한 수재해 대비 및 대응을 위해 일반적으로 사용되는 물리적 기반의 강우-유출 모형의 입력자료 구축 및 구동에 시간이 오래 걸리며 모형의 매개변수 검·보정에 사용자의 높은 이해도가 요구되는 등 한계가 있다. 반면 자료기반 모델의 경우 입력자료가 간단하며, 모델 구동 시간이 비교적 짧은데 비해 예측력이 높은 장점이 있다. 본 연구에서는 LSTM (Long Short-Term Memory) 신경망과 MLP (Multi Layer Perceptron) 신경망을 활용해 유출량을 모의했으며 연구의 결과 및 시사점은 다음과 같다.

(1) 기존 물리적 강우-유출 모형의 구동에 있어서 모형의 입력자료와 매개번수 검·보정에 대한 사용자의 높은 이해도가 필요하며 모형의 구동시간이 오래 걸리지만 데이터 기반의 딥 러닝 기법은 손쉽게 입력자료 구축을 할 수 있으며 물리적 강우-유출 모형에 비해 구동시간이 짧다.

(2) 강원도 삼척 오십천 유역을 대상으로 2011년부터 2020년 까지 총 10년의 일단위 유출량과 기상자료(삼척, 동해, 태백, 신기, 도계)를 수집했고, Hargreaves & Angstorm 공식을 이용해 잠재증발산량을 산정한 후 티센 면적비를 적용해 3개의 입력자료군(6개 기상관측요소, 일 강수량 및 잠재증발산량, 일 강수량 - 잠재증발산량)을 구축해 각각 LSTM 모델에 학습시켰다.

(3) 3개의 LSTM 모델 중 6개의 기상관측요소(일 강수량, 최고 및 최저기온, 평균기온, 평균 풍속, 최대 순간 풍속)를 이용해 학습한 LSTM-Model 1을 최적 모델로 선정했으며, LSTM-Model 1에 MLP를 더한 LSTM-MLP 모델 6개를 구축하고 학습하여 각 모델의 평균값을 이용해 전체기간(2011-2020)까지의 유출량을 모의했다.

(4) LSTM-MLP 모델을 이용해 유출량을 모의한 결과 LSTM 모델의 결과와 대체적으로 비슷했으나 LSTM 모델에 비해 LSTM-MLP 모델이 약간의 오차가 감소했으며 특히 저유량 부분의 분산이 개선되었음을 확인했다.

(5) 본 연구에서는 관측자료만을 이용하여 삼척 오십천 유역의 장기유출 모의를 진행했으며 ConvolutionLSTM 등으로 저유량 부분의 정확도를 개선하여 지형자료 수집이 어려운 미계측 유역등에 활용성이 높을 것으로 기대된다.

Acknowledgements

본 연구는 행정안전부 지능형 상황관리 기술 개발사업의 연구비지원(과제번호 2021-MOIS37-001)에 의해 수행되었습니다.

Conflicts of Interest

The authors declare no conflict of interest.

References

Choi, J.R., An, S.W., Choi, J.Y., and Kim, B.S. (2021a). "A study on the derivation and evaluation of flow duration curve (FDC) using deep learning with a long short-term memory (LSTM) networks and soil water assessment tool (SWAT)." Journal of Korea Water Resources Association, Vol. 54, No. S-1, pp. 1107-1118. doi: 10.3741/JKWRA.2021.54.S-1.1107 10.3741/JKWRA.2021.54.S-1.1107

Choi, J.R., Yoon, H.C., Won, C.H., Lee, B.H., and Kim, B.S. (2021b). "A study on the estimation and evaluation of ungauged reservoir inflow for local government's agricultural drought forecasting and warning." Journal of Korea Water Resources Association, Vol. 54, No. 6, pp. 395-405. doi: 10.3741/JKWRA.2021.54.6.395 10.3741/JKWRA.2021.54.6.395

Han, H.C., Choi, C.H., Jung, J.W., and Kim, H.S. (2021). "Application of sequence to sequence learning based LSTM model (LSTM-s2s) for forecasting dam inflow." Journal of Korea Water Resources Association, Vol. 54, No. 3, pp. 157-166. doi: 10.3741/JKWRA.2021.54.3.157 10.3741/JKWRA.2021.54.3.157

Han, J.H., Ryu, T.S., Lim, K.J., and Jung, Y.H. (2016). "A review of baseflow analysis techniques of watershed-scale runoff models." Journal of the Korean Society of Agricultural Engineers, Vol. 58, No. 4, pp. 75-83. doi: 10.5389/KSAE.2016.58.4.075 10.5389/KSAE.2016.58.4.075

Hochreiter, S., and Schmidhuber, J. (1997). "Long short-term memory." Neural Computation, Vol. 9, No. 8, pp. 1735-1780. doi: 10.1162/neco.1997.9.8.1735 10.1162/neco.1997.9.8.17359377276

Jiang, L., Wang, X., Wang, L., Shao, M., and Zhuang, L. (2021). "A hybrid ANN-LSTM based model for indoor temperature prediction." 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, doi: 10. 1109/ICIEA51954.2021.9516151 10.1109/ICIEA51954.2021.9516151

Kalin, L., Isik, S., Schoonover, J.E., and Lockaby, B.G. (2010). "Predicting water quality in unmonitored watersheds using artificial neural networks." Journal of Environmental Quality, Vol. 39, No. 4, pp. 1429-1440. 10.2134/jeq2009.044120830930

Korea Research Institute for Human Settlements (KRIHS) (2020). A proposal to establish the reference discharges for rational river management.

Lee, D.E., Lee, G.H., Kim, S.W., and Jung, S.H. (2020). "Future runoff analysis in the mekong river basin under a climate change scenario using deep learning." Water, Vol. 12, No. 6, 1156. doi: 10.3390/w12061556 10.3390/w12061556

Lee, G.H., and Jung, S.H. (2018). "Comparison of physics-based and data-driven models for streamflow simulation of the mekong river." Journal of Korea Water Resources Association, Vol. 51, No. 6, pp. 503-514. doi: 10.3741/JKWRA.2018.51.6.503 10.3741/JKWRA.2018.51.6.503

Ministry of Land, Infrastructure and Transportation of Korea (MOLIT) (2000). The long-term comprehensive water resource plan.

Mok, J.Y., Choi, J.H., and Moon, Y.I. (2020). "Prediction of multipurpose dam inflow using deep learning." Journal of Korea Water Resources Association, Vol. 53, No. 2, pp. 97-105. doi: 10.3741/JKWRA.2020.53.2.97 10.3741/JKWRA.2020.53.2.97

Sahoo, B.B., Jha, R., Singh, A., Kumar, D. (2019). "Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting." Acta Geophys, Vol. 67, pp. 1471-1481. doi: 10.1007/s11600-019-00330-1 10.1007/s11600-019-00330-1

Xu, W., Jiang, Y., Jhang, X., Li, Y., Zhang, R., and Fu, G. (2020). "Using long short-term memory networks for river flow prediction." Hydrology Research, Vol. 51, No. 6, pp. 1358-1376. doi: 10.2166/nh.2020.026 10.2166/nh.2020.026

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Long-term runoff simulation using rainfall LSTM-MLP artificial neural network ensemble

ABSTRACT

MAIN

Fig. 1.

Flowchart of the study

Fig. 2.

LSTM structure

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

Fig. 3.

Location map of the target basin and stations

Table 1.

Weather and flow station

Table 2.

LSTM model input data

Fig. 4.

Monthly time series of flow, precipitation and evapotranspiration in Samcheok Osipcheon watershed

Fig. 5.

Model configuration of LSTM and LSTM-MLP

Table 3.

Model parameter setting of LSTM and LSTM-MLP

Fig. 6.

LSTM model training results time series (Test)

Table 4.

LSTM model training results metrics (Test)

Table 5.

LSTM model training results metrics for the rainy season

Fig. 7.

LSTM and LSTM-MLP model simulation results time series

Table 6.

LSTM and LSTM-MLP models results metrics

Table 7.

Results of comparing observed vs. predicted (2011~2020)

Fig. 8.

Observed and simulated(LSTM-MLP) runoff monthly time series

Acknowledgements

Conflicts of Interest

References