1. 서 론
2. 연구방법
2.1 집중형 및 준분포형 GR4J 강우-유출 모형
2.2 순차자료동화 방법
2.3 연구 지역 및 입력 자료 구축
2.4 모의 성능 평가 지표
2.5 실험 조건 설정
3. 결과 및 분석
3.1 수문자료동화 결과 분석
3.2 자료동화 하이퍼-매개변수 영향 분석
3.3 보정기간 길이에 따른 영향 분석
4. 결 론
1. 서 론
기후변화로 인한 홍수 발생빈도, 강도가 증가함에 따라 이를 사전에 대비하고 피해를 최소화하는 수문예측시스템의 정확한 예측이 어려워지고 있다. 수문예측시스템은 기상변화와 수문학적 조건을 분석하여 수문현상을 예측하는 시스템으로, 수문모형을 이용한 정확한 예측 및 해석 기술이 중요한 요소이다. 하지만, 수문모의 정확성은 1) 수문모형의 구조 및 모형 매개변수(model parameters)의 추정, 2) 예측 시작 시점에서의 수문모형 상태량(state variables) 초기 조건, 3) 기상 강제력(weather forcings) 조건, 4) 인간 활동의 물 순환 개입(예: 저수지 운영, 관개 등) 등 다양한 요소로부터 불확실성이 발생한다(Noh et al., 2014). 따라서, 수문 예측 시스템의 정확성을 높이기 위해 결정론적 예측에서 다양한 불확실성 요소를 고려하는 확률론적 예측 방법론의 활용이 증가하고 있다(Alfieri et al., 2012; Cloke and Pappenberger, 2009). 자료동화(Data Assimilation, DA)는 대표적인 확률론적 방법으로, 실시간 관측 정보를 이용하여 현재시간에서의 모형 상태정보를 갱신(update)함으로써 최적의 모형 상태량을 추정하여 수문모의 불확실성을 최소화 하고 수문예측의 정확성을 향상시킬 수 있는 기법이다(Lee et al., 2022).
자료동화 기술은 수자원 분야에 활발히 적용되고 있으며 주요 연구사례는 다음과 같다. Ricci et al. (2011)는 Saint-Venant 방정식 기반 1차원 수리 모형을 적용하여 프랑스의 Adour 유역과 Marne Vallage 유역에 대해 칼만 필터를 적용하여 하천수위를 동화(assimilation)하여, 홍수 시 상류 유량의 보정 및 자료동화는 수위와 유량의 예측 성능을 향상시켰다. Lee et al. (2012)는 미국 국립기상청(NWS)에서 사용하는 SAC-SMA (Gridded Sacramento Soil Moisture Accounting) 분포형 모형과 운동파 추적 모형을 사용하여 Oklahoma 와 Texas 지역의 대상유역에 대해 변분법 기반 자료동화(variational assimilation)를 적용한 결과, 유역 출구뿐만 아니라 유역 내부의 하천 유량 자료를 기반으로 자료동화 적용시 더 정확한 예측이 가능하였다. Rakovec et al. (2012)는 HBV-96 분포형 모형을 사용하여 벨기에 아르덴의 Upper Ourthe 유역에 대해 앙상블 칼만 필터를 적용한 결과, 유역 내 자료동화 적용을 통해 갱신 빈도를 늘리는 것보다 유량 예측을 더 효과적으로 향상시켰다. Liu et al. (2016)는 SWAT (Soil and Water Assessment Tool) 준분포형 모형을 사용하여 중국 Huai 강 상류 유역에 앙상블 칼만 필터를 적용하여 하천유량을 동화한 결과, 유역내 자료동화 적용은 유역 출구의 자료동화 적용 보다 전체유역의 예측정확성을 향상시켰다. Choi and Kim et al. (2021)의 연구에서는 하천유량 관측자료와 파티클 필터 기법을 이용하여 수문모형의 시간에 따라 변화하는 매개변수 추정과 월 유출 예측 성능을 분석한 결과, 월 유출 예측 성능은 자료동화를 적용한 시간변동 매개변수에 의한 모의가 더 우수하였지만 우기에서의 예측 성능 향상은 제한적이었다. 또한, 본 연구에 사용된 modèle du Génie Rural à 4 paramètres Journalier (GR4J) 수문모형의 자료동화 적용 사례는 다음과 같다. Leach and Coulibaly (2019)는 집중형 GR4J 수문모형과 앙상블 칼만 필터를 이용하여 SNODAS (Snow Data Assimilation System)의 적설 수분량(snow water equivalent)과 SMOS (Soil Moisture and Ocean Salinity)의 토양 수분 추정을 하천 유량 동화에 적용하여 앙상블 예측 성능을 개선하였다. Aubert et al. (2003)는 프랑스 Serein 유역에 대해 집중형 GR4J 수문모형과 확장 칼만 필터(extended Kalman filter)를 연계하여 토양 수분과 하천 유량의 자료동화를 수행하였으며, 토양 수분 자료동화는 홍수기, 하천 유량 자료동화는 갈수기 유량 예측 개선에 효과적이었다고 보고하였다. Lee et al. (2022)의 연구에서는 앙상블 칼만 필터와 파티클 필터를 집중형GR4J 수문모형에 적용하여 순차자료동화 기법이 모의 성능에 미치는 영향을 분석한 결과, 자료동화 적용 후 일 유출 모의 정확도 향상이 가능하였지만 홍수기 예측 정확도 향상은 제한적이었다.
한편, 수문모형은 공간상세화 방법에 따라 집중형, 준분포형, 분포형으로 나뉜다. Nayak et al. (2021)의 연구에서는 수문모형의 구조적 특징이 수문자료동화 효율성에 영향을 분석하였다. 집중형 모형은 전체 관심영역을 단일유역으로 단순화하여 모의를 수행하며, 준분포형과 분포형 모형은 공간적으로 세분화된 각 하위 유역의 상관관계를 고려하여 모의를 수행한다. 따라서, 준분포형과 분포형 모형은 유역내 지점에서 검․보정 및 자료동화를 적용할 수 있는 장점을 가지고 있으며, 이는 유역 출구에서의 예측정확성에 영향을 줄 수 있다(Ercolani and Castelli, 2017). 집중형 모형은 비교적 빠르고 간단하게 적용할 수 있는 장점을 가지고 있으나 각 유역내 복잡한 물의 흐름과 여러 하위 유역 간의 공간적 상관관계를 고려하지 못하여, 집중형 모형의 자료동화 적용시 고유량에서의 예측성능 향상에 한계가 존재하였다.
본 연구의 목표는 집중형과 준분포형 수문모형에 대해 순차자료동화기반 앙상블 칼만 필터와 파티클 필터 기법을 적용하여 모형 구조에 따른 모의유량의 특성을 비교하는 것이다. 구체적으로는 GR4J모형의 집중형 및 준분포형 방식 수문모형을 남강댐 유역에 적용하여 강우-유출 모형 구조가 자료동화 성능에 미치는 영향 분석 및 불확실성을 정량적으로 평가한다. 또한, 자료동화와 관련된 하이퍼-매개변수 중 기상강제력(강수, 잠재증발산) 불확실성 범위와 보정기간 길이가 두 수문모형의 예측 성능에 미치는 영향을 분석하여 최적 성능을 얻기 위한 방법을 제시한다. 논문의 구성은 2장에서 연구 방법 및 자료 등 순차자료동화 기법의 이론적 배경에 대해 기술하고, 3장에서는 자료동화 하이퍼 매개변수의 영향 분석 및 수문자료동화 모의 결과에 대해 기술한다. 마지막 4장에서는 결론에 대해 논의한다.
2. 연구방법
2.1 집중형 및 준분포형 GR4J 강우-유출 모형
본 연구에서는 집중형과 준분포형 GR4J 모형을 사용하여 일 유출 모의를 수행하며, 본 절에서는 각 모형의 개요 및 구성에 대해 설명한다.
2.1.1 집중형 GR4J 강우-유출 모형
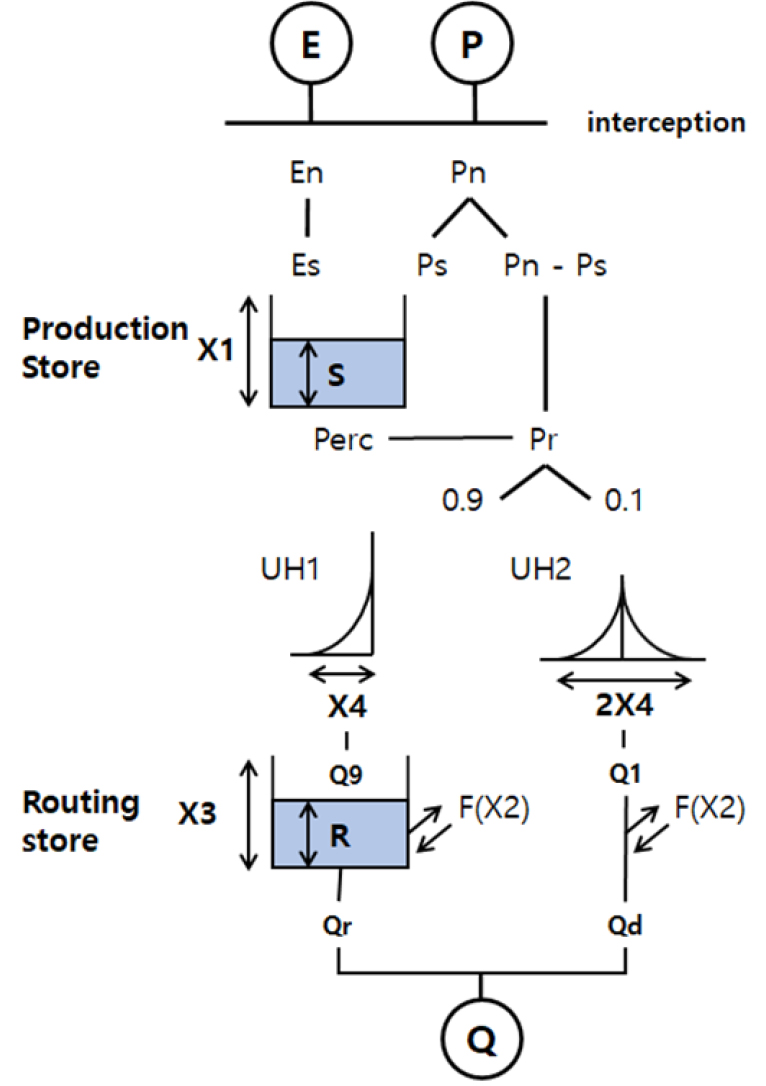
GR4J 수문모형은 Perrin et al. (2003)에 의해 개발된 개념적 강우-유출 모형으로, 유역의 공간적 상관관계를 고려하지 않고 단일 유역 모의를 수행한다. 2개의 저류지, 2개의 단위유량도, 4개의 매개변수(Table 1)를 가지고 있으며(Fig. 1), 비교적 적은 매개변수와 단순한 구조로 적용이 용이하다는 장점을 가지고 있다(Im et al., 2012). 첫번째 저류지인 토양수분 저류지(production store)에서는 입력자료인 강우(Pn)와 잠재증발산(En)의 유출(Pn-Ps)과 침루(Ps)를 고려하고, 두번째 저류지(routing store)에서는 단위유량도(unit hydrograph)를 통해 흘러온 직접 유출량의 90%는 하천으로 유입되고, 10%는 지표면을 통해 유출된다 하천으로부터 유출되는 유량과 지표면을 통해 유출되는 유량은 인접 유역 간 교환계수인 X2 (mm/d)에 의해 하천에서의 지체 및 지하수 유출이 계산되며 최종적으로 위의 두 과정, 즉 하도와 지하수 유출 유량을 합산하여 산정된다(Noh et al., 2023).
Table 1.
Descriptions of lumped and semi-distributed GR4J model parameters
2.1.2 준분포형 GR4J 강우-유출 모형
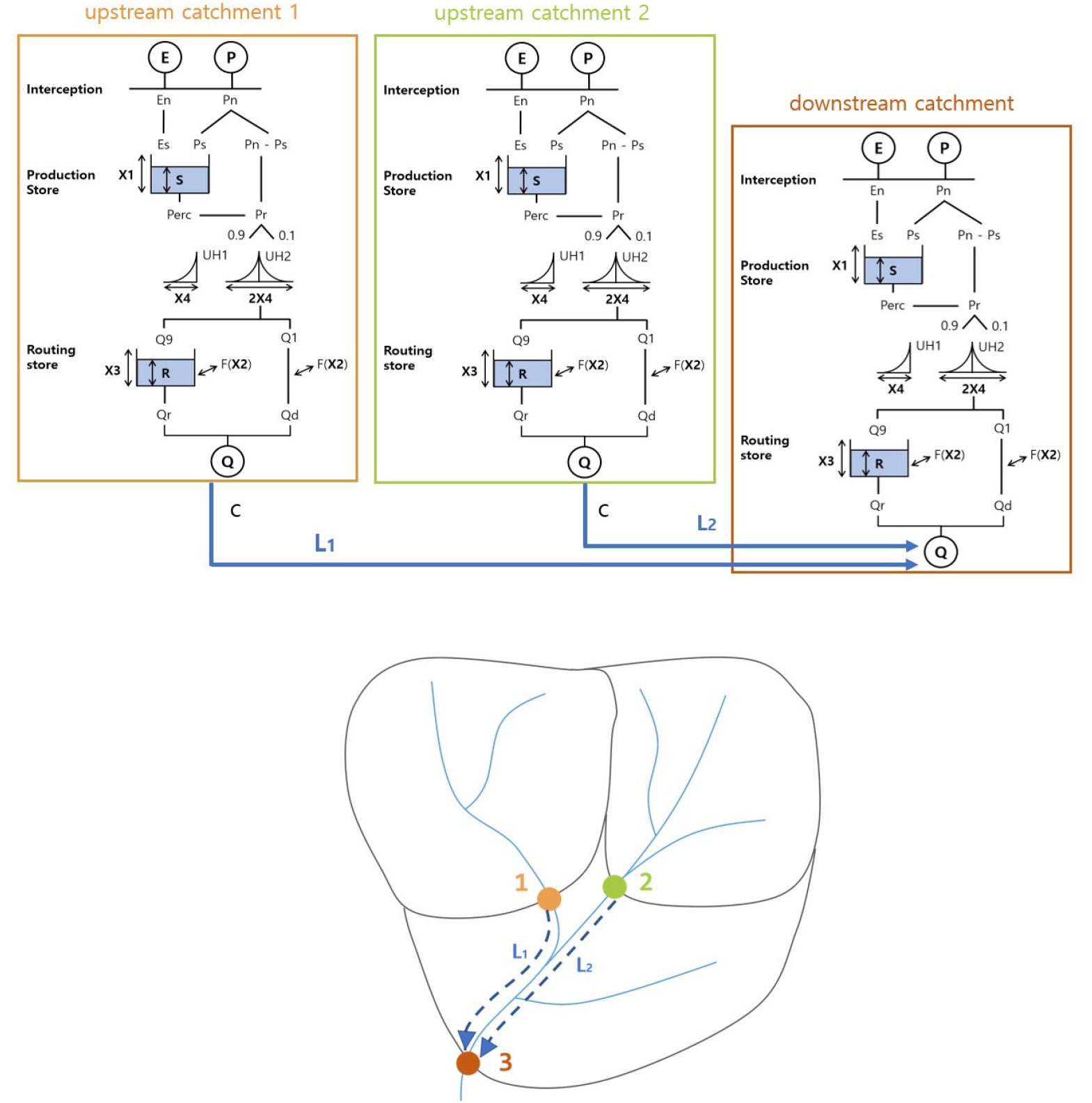
준분포형 GR4J 수문모형은 전체유역을 여러 하위 유역 또는 수문 반응 단위(Hydrologic Response Unit, HRU)로 분할하여, 각 하위 유역 유출량을 집중형 GR4J모형 방식으로 모의한다(Lee, 2024). 각 유역에서의 모의된 유출량은 Muskingum 방법을 통해 상류 유역의 유출량이 하위 유역 출구로 추적된다(Fig. 2). Muskingum 라우팅 방법은 k와 𝜔, 2개의 매개변수가 필요하다. 여기서 k는 도달 길이(L)와 파동 속도(C)에 의해 결정되고 𝜔는 무차원 가중치 계수이다. 파동 속도(C)는 매개변수 차원을 줄이기 위해 본 연구에서는 모든 하위 유역에서 일정하다고 가정하였다. 준분포형 GR4J 수문모형 적용시, 각 하위 유역에 대한 X1부터 X4까지의 4개의 모형 매개변수와 2개의 라우팅 매개변수(Table 1)는 유역별 공간적 특성을 반영한 최적화된 매개변수로 설정해야 한다. 본 연구에서는 R 소프트웨어 패키지인 airGR을 이용하여 집중형 GR4J 모형을 구축하고, airGR 패캐지의 lag model을 활용하여 준분포형 GR4J 모형을 구축하였다.
2.2 순차자료동화 방법
본 연구에서는 순차자료동화 방법 중 앙상블 칼만 필터(Fig. 3(a))와 파티클 필터(Fig. 3(b)) 기법을 적용한다. Fig. 3은 두 기법의 개념을 비교한 것으로, 노란색 선은 관측에 대한 우도, 검은색 선은 모의 상태량의 사전 정규분포, 초록색 선은 모의 상태량의 사후 정규분포이다. 두 기법은 모의 상태량의 사전 및 사후 분포 형태에 따라 나뉜다. 관측에 대한 우도를 정규분포로 동일하게 가정하더라도 앙상블 칼만 필터(Fig. 3(a))는 사전 및 사후 분포를 정규분포로 근사하고, 파티클 필터는 사전 및 사후 분포가 정규분포가 아닌 것이 두 기법의 가장 큰 차이점이다(Lee et al., 2022). 각 자료동화 방법에서 상태량의 사후 분포를 추정하는 방법은 다음 절에서 설명한다.
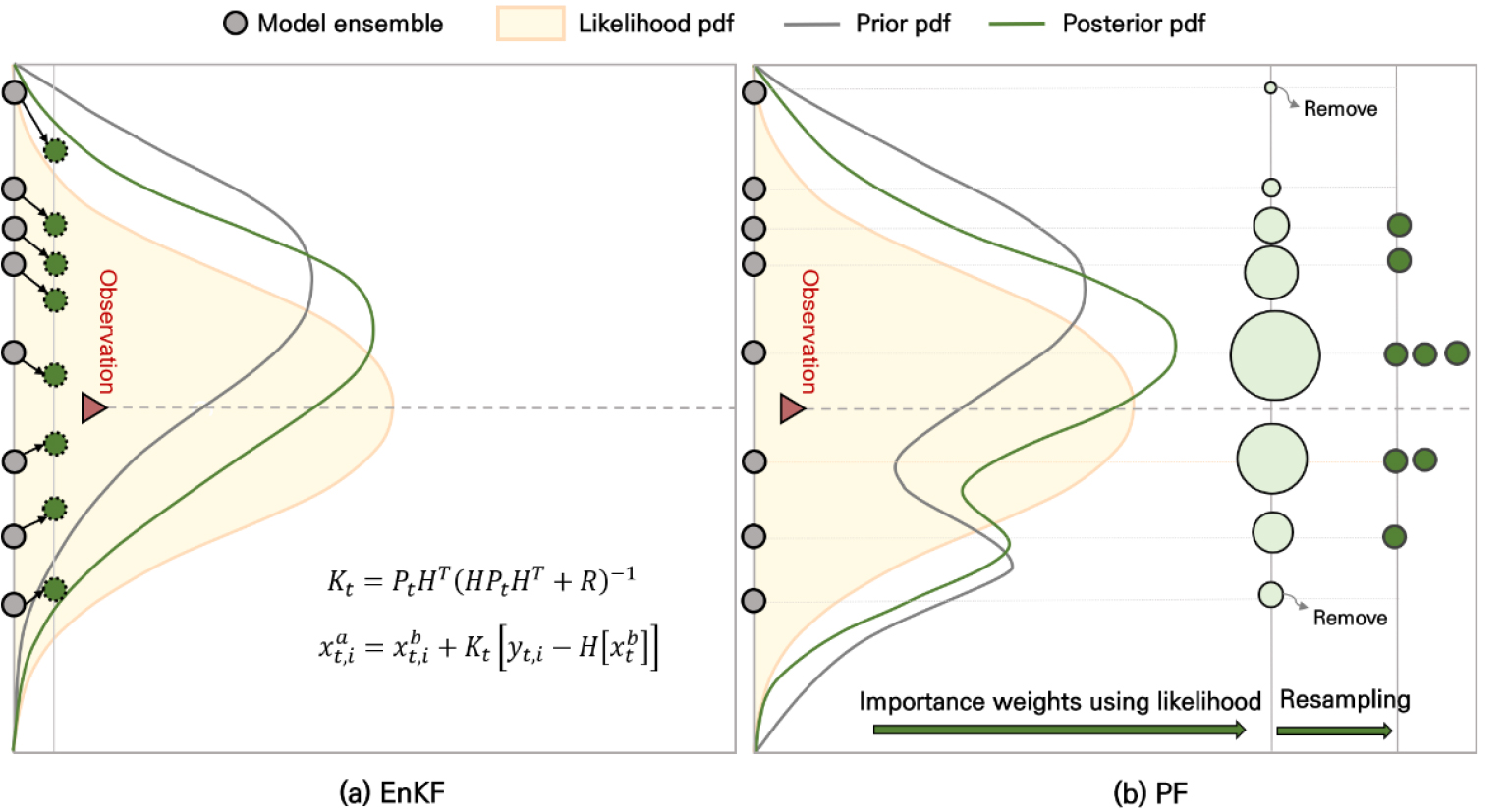
Fig. 3.
Schematic diagram of data assimilation methods: (a) the ensemble Kalman filter and (b) the particle filter (adapted from Lee et al,, 2022)
2.2.1 앙상블 칼만 필터
앙상블 칼만 필터(Ensemble Kalman Filter, EnKF)는 새로운 관측정보가 가용할 때마다 모의(앙상블)와 관측의 상대적인 오차를 고려하여 최적의 상태량을 추정한다. 최적 상태량 추정을 위해 개의 관측치의 분포로부터 개의 앙상블을 생성하여 모형 상태를 갱신(update)한다. 이때의 분포는 평균과 분산으로 생성된 정규분포로 근사하기 때문에 비교적 적은 앙상블 수로도 다차원 문제를 추정할 수 있어 다양한 예측 응용 문제에 적용되고 있다.
시간 t의 i 번째 앙상블의 갱신 이후 모형 분석 상태 추정식은 다음과 같다.
는 i 번째 앙상블의 백그라운드 상태량(갱신 전 상태량, 크기 ), 는 i 번째 앙상블의 관측정보(변수길이 ), H는 관측가능한 수문요소를 추정하는 관측 방정식(크기 ), 는 칼만이득(Kalman gain)을 나타내며 다음 식과 같다.
는 칼만 이득(Kalman gain)으로, 최적의 업데이트를 위한 가중치로 모의, 관측 정보로부터 산정된 오차 공분산 행렬의 조합이며, 는 관측 값의 오차 공분산 행렬(크기 ), 는 모의 값의 오차 공분산 행렬로, 자세한 내용은 Lee (2024)를 참고할 수 있다.
2.2.2 파티클 필터
파티클 필터(Particle Filter, PF)는 칼만 필터 계열 자료동화 기법과 달리 정규분포나 선형화 가정을 하지 않고 사전 및 사후 분포를 추정하는 방법으로, 비선형(non-linear), 비가우시안(non-Gaussian)의 복잡한 구조 모형에도 적용 가능하다는 장점이 있다. 순차 중요도 샘플링(Sequential Importance Sampling, SIS) 기법에서는 사후 확률 분포를 근사하기 위해 파티클을 무작위로 발생시켜 샘플링 하고, 관측정보를 가용할 수 있을 때마다 관측된 파티클의 가중치가 재귀적으로 갱신된다. 이에 따라 베이즈 이론(Bayes' theorem) 기반 사전 분포와 우도 함수의 최적 조합을 통해 사후 분포를 추정하고, 시간 t에서의 사후 확률은 다음과 같이 근사 될 수 있다.
여기서, 는 가중치, 𝛿는 Dirac delta 함수, 는 주요 확률 밀도이다. 모든 파티클의 가중합은 상태 변수의 추정값을 나타내며, 특정 파티클이나 하나의 파티클에서만 모든 가중치를 가지는 경우 퇴화현상이 발생할 수 있다. 이러한 문제를 해결하기 위해 SIS기법에 리샘플링 과정을 추가한 SIR (Sequential Importance Resampling) 기법이 일반적으로 적용된다. SIR 기법은 리샘플링 과정을 통해 낮은 확률을 가진 파티클을 제거하고 높은 확률을 가진 파티클을 복제하여 파티클의 총 개수를 일정하게 유지하며, 특히 파티클의 가중치가 높을수록 해당 파티클은 더 많이 복제되므로 실제와 가까운 파티클은 다시 리샘플링 될 가능성이 높다, 각 파티클의 가중치()는 관측에 대한 우도를 기반으로 산정되었으며, 다음 식과 같다.
여기서, 𝛿는 관측자료의 표준편차로, 본 연구에서는 관측 유량의 10%를 관측 분포의 표준편차로 적용하였다.
2.3 연구 지역 및 입력 자료 구축
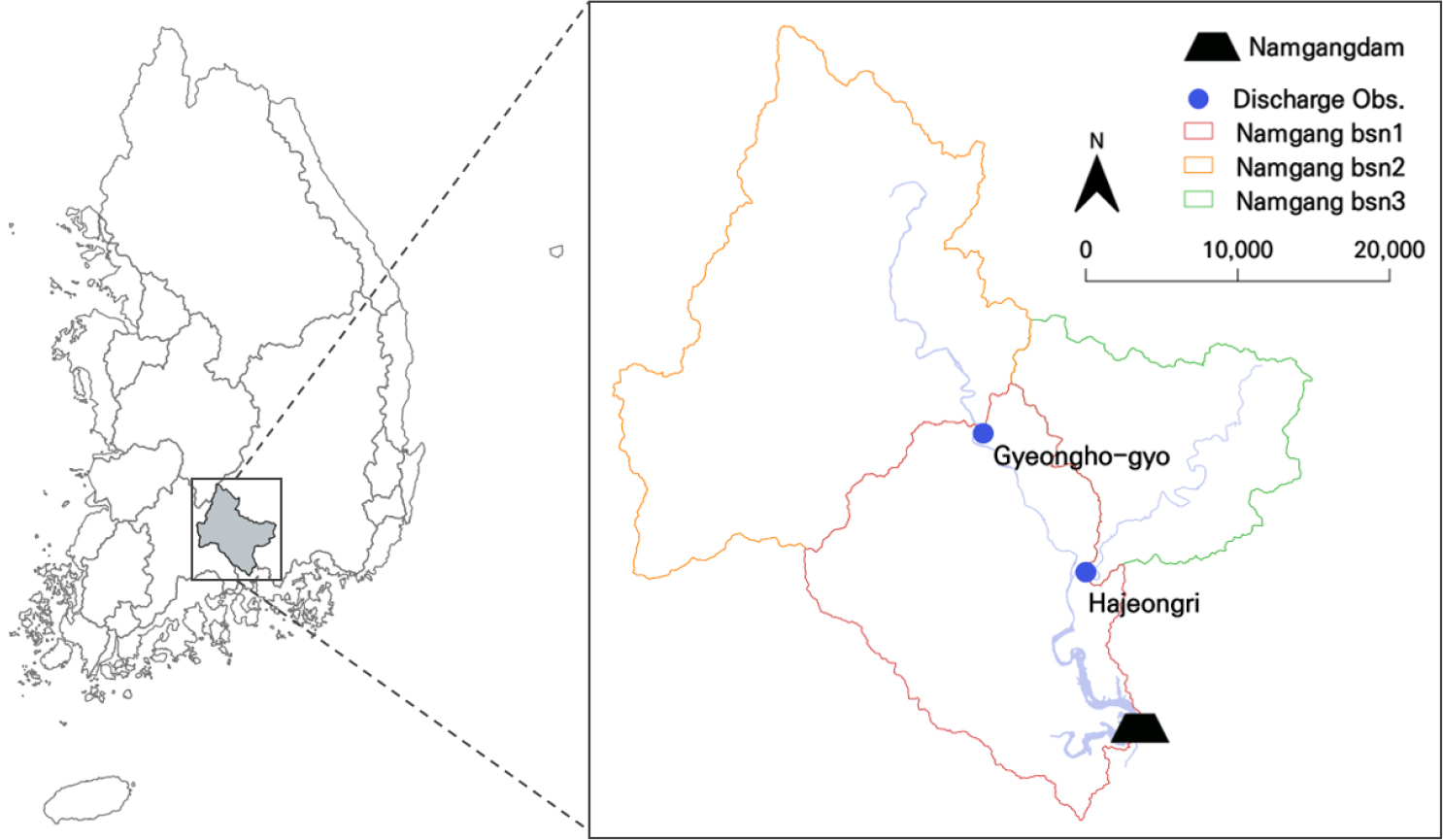
연구지역으로는 진양호를 포함하는 남강댐 상류유역(약 2,300 km2)을 선정하였다. 준분포형 GR4J 모형에서는 소유역별 관측정보를 활용하여 검․보정 및 자료동화를 적용하기 위해 유량 관측지점이 있는 곳을 기준으로 소유역을 설정하였으며, 남강댐 상류유역에 대해 하정리(3번 유역), 경호교(2번 유역), 남감댐(1번 유역)의 3개의 소유역으로 구분하였다(Fig. 4). 또한, 각 하위 유역에 대한 강우 및 기온자료를 구축하였고, 모형의 강우 입력자료는 국가수자원관리종합 정보시스템(WAMIS)에서 제공하는 일 단위 면적 평균 강수량, 기온 입력자료는 기상자료개방포털(http://data.kma.go.kr)에서 제공하는 일 단위 평균 기온을 사용하였다.
준분포형 및 집중형 수문모형에 적용된 전체 및 소유역의 연평균 강우와 표준편차는 다음과 같다. 집중형 GR4J모형은 연평균 강우와 표준편차가 각각 1,640.1 mm, 394.3 mm, 준분포형 GR4J모형의 1번 유역은 연평균 강우와 표준편차가 각각 1,675.5 mm, 456.6 mm, 2번 유역은 각각 1,431.2 mm, 360.2 mm, 3번 유역은 각각 1,364.8 mm, 399.1 mm로 산정되었다. 집중형 모형의 연평균 강우는 35.4 mm 차이로 준분포형 모형의 1번 유역과 가장 유사하였고, 집중형 모형의 연도별 강우 편차는 4.8 mm 차이로 준분포형 모형의 3번 유역과 유사하게 나타났다.
GR4J 모형의 입력자료 중 잠재증발산은 Oudin et al. (2005)이 제시한 기온 기반 방정식을 사용하여 산정하였다.
여기서 는 태양복사에너지이고, T는 2m 높이에서의 평균기온(℃)이다(Oudin et al., 2005; 2010). 본 연구에서는 Eq. (5)의 온도자료를 모형의 온도자료와 동일하게 적용하였으며 유역의 경위도는 유역 중앙지점을 기준으로 사용하였다.
2.4 모의 성능 평가 지표
모의 성능 평가 지표로는 Kling-Gupta Efficiency (KGE), Nash-Sutcliffe Efficiency (NSE)를 사용하였다. 모형의 보정 및 검정 기간 성능에 대해서는 KGE, NSE 지표를 모두 적용하였고, 민감도 분석 등은 KGE 지표를 중심으로 검토하였다.
2.4.1 KGE
KGE는 관측과 모형의 예측 간의 유사성을 측정하는 평가 지표로, 식은 다음과 같다.
여기서 𝛾은 관측 값과 모의 값 사이의 선형 상관계수, 𝛼는 관측 값의 변동성과 모의 값의 변동성 간의 비율로 변동성은 표준편차로 측정된다. 𝛽는 관측 평균과 모의 평균 간의 비율이다. KGE 값은 1에 가까울수록 관측과 모의 사이의 유사도가 높다는 것을 의미하며, KGE가 1이면 모의 값과 관측 값의 일치를 나타낸다. Nash-Sutcliffe efficiency (NSE) 등의 지표가 전체 자료기간 중 일부 홍수기간의 모의 결과에 지배적으로 영향을 받는데 비해, KGE는 𝛼, 𝛽 등에 대한 고려를 통해 비강우 기간에 대한 모의 성능 비교가 가능하기 때문에 평가 지표 적용하였다.
2.4.2 NSE
NSE는 수문 예측정확도를 평가하는 무차원 지표로, 다음 식과 같다.
여기서 는 시간 t에서 관측, 는 시간 t에서 예측, 는 관측의 평균, N은 총 관측의 수를 나타낸다. NSE가 1에 가까울수록 관측과 모의가 완벽하게 일치함을 의미한다.
2.5 실험 조건 설정
모의 실험의 시간적 범위는 유량 및 우량 관측 자료에 대한 사전 검토를 통해 자료 품질이 양호하고 가용한 기간으로 선정하였으며, 총 10년의 일단위 시계열 자료(2006-2015)를 검정 및 보정기간으로 구분하였다. 보정은 2006~2011년(6년), 검정은 2012~2015년(4년) 기간에 대해 수행하였다(Table 2). 이때의 보정기간은 매개변수와 자료동화 하이퍼-매개변수 보정을 수행한다. Warm-up기간은 두 유역 모두 검․보정 기간 모의 시 1년간을 설정하여 모의 초기 조건의 영향을 최소화하고, 검정기간에 대해서만 평가하였다.
Table 2.
Modeling periods for parameter, DA calibration and validation
| Basin | Calibration | Validation |
| Namgang Dam | 2006 - 2011 | 2012 - 2015 |
모형 매개변수 보정 시 목적함수(objective function)를 KGE로 적용하여 두 수문모형에 대해 최적 보정된 매개변수는 Table 3과 같다. 이때의 최적 보정된 KGE 지표는 집중형 GR4J모형의 경우 0.868, 준분포형 GR4J모형의 경우 0.920 로 나타났다. 따라서, 두 수문모형은 KGE 0.85 이상으로 수문사상을 재현하기 적합한 것으로 확인되었다.
Table 3.
Optimized parameter values of GR4J
| Basin | Rainfall-runoff model | Objective function | Optimized parameter values | |||
| X1 | X2 | X3 | X4 | |||
| Namgang Dam | Lumped GR4J | KGE | 21.400 | 1.026 | 22.891 | 1.262 |
| Semi-distributed GR4J | KGE | 132.155 | 4.529 | 13.364 | 1.392 | |
모형 구조가 모의성능에 미치는 영향을 평가하기 위해 준분포형 GR4J 모형은 2번과 3번 유역의 관측 자료를 활용하여 검․보정 및 자료동화 기법을 적용하였으며, 이를 하류 유역 출구에서 집중형 GR4J 모형과 모의정확도를 비교 및 분석하였다. 자료동화 적용시 모형 상태량 섭동 및 갱신 조건은 Lee et al. (2022) 연구에서 가장 성능이 높았던 토양 수분 저류량(production store), 하도 저류량(routing store), 단위유량도(unit-hydro graph)를 모두 섭동 및 갱신하는 조건을 본 연구에 적용하였다. 자료동화와 관련된 하이퍼-매개변수로는 기상강제력(강수, 잠재증발산) 앙상블 생성의 영향을 모의 실험을 통해 사전 검토하였다. 앙상블 수는 앙상블 칼만 필터와 파티클 필터 기법 모두 100개를 적용하였으며, 앙상블 수에 따른 큰 변화가 없어 분석에 포함하지 않았다. 시간 상관 가중치는 Lee et al. (2022) 연구에서의 조건과 동일하게 시간 역상관 길이는 강수 1 일, 잠재 증발산은 2일로 적용하였다.
3. 결과 및 분석
3.1 수문자료동화 결과 분석
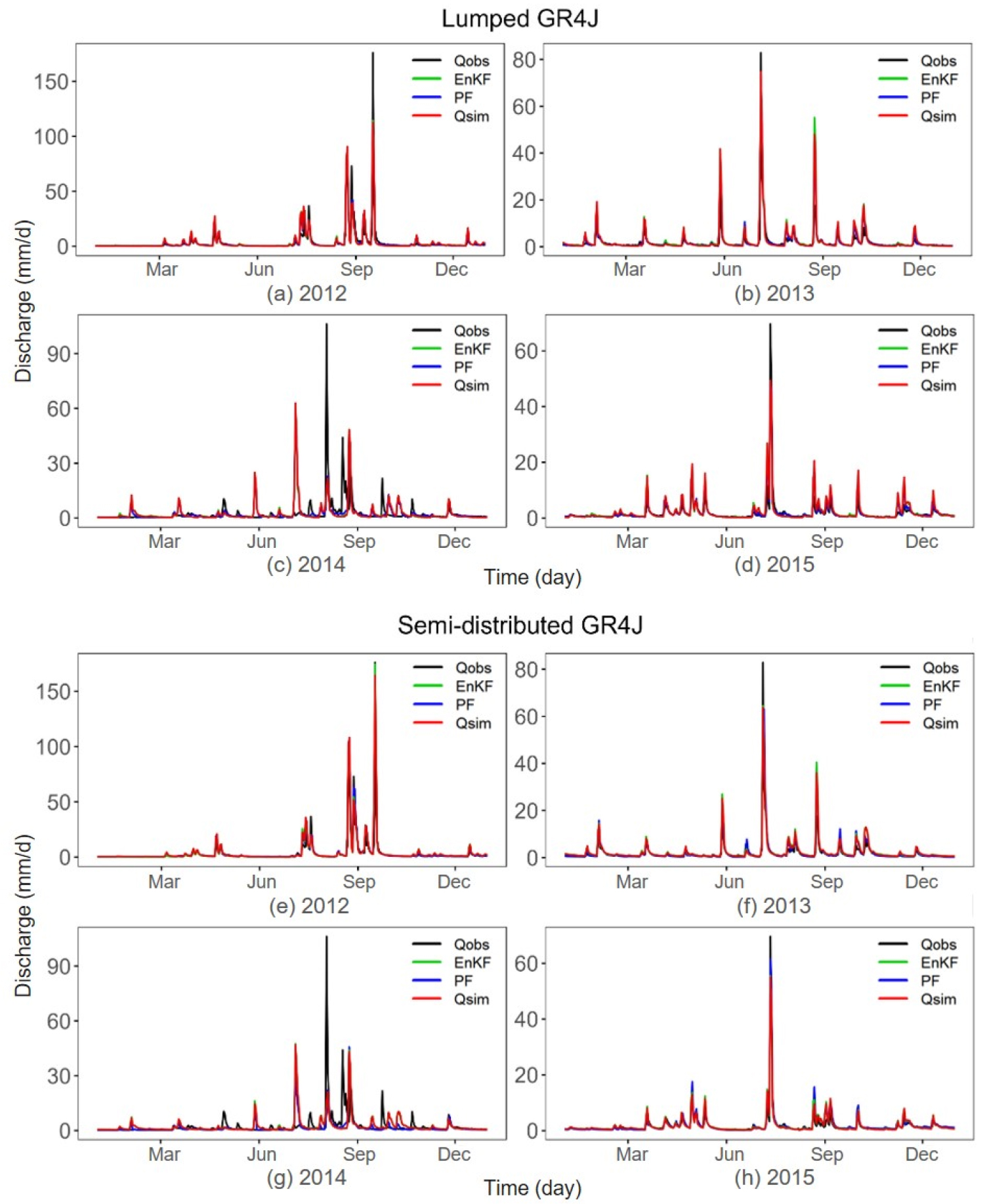
집중형과 준분포형 GR4J 모형에 대해 앙상블 칼만 필터와 파티클 필터 기법을 적용하여 일단위 수문모형 구조가 자료동화 전후 모의성능에 미치는 영향을 분석하였다. Fig. 5는 남강댐 유역의 자료동화 검정기간에 대해 모의된 일 유량을 관측 자료와 연도별로 비교한 그래프이다. 자료동화 결과는 보정기간에 대해 기상강제력 민감도 평가 후, 최적 하이퍼-매개변수를 선정하여 검정기간의 모의를 수행하였다. 남강댐 유역의 2014년(Figs. 5(c) and 5(g)) 결과는 첨두유량이 발생한 8월 3일을 기준으로 앞뒤 15일간 유출율이 150% 이상으로 나타났으며, 관측자료 이상으로 판단되어 해당년도는 제외하고 분석하였다.
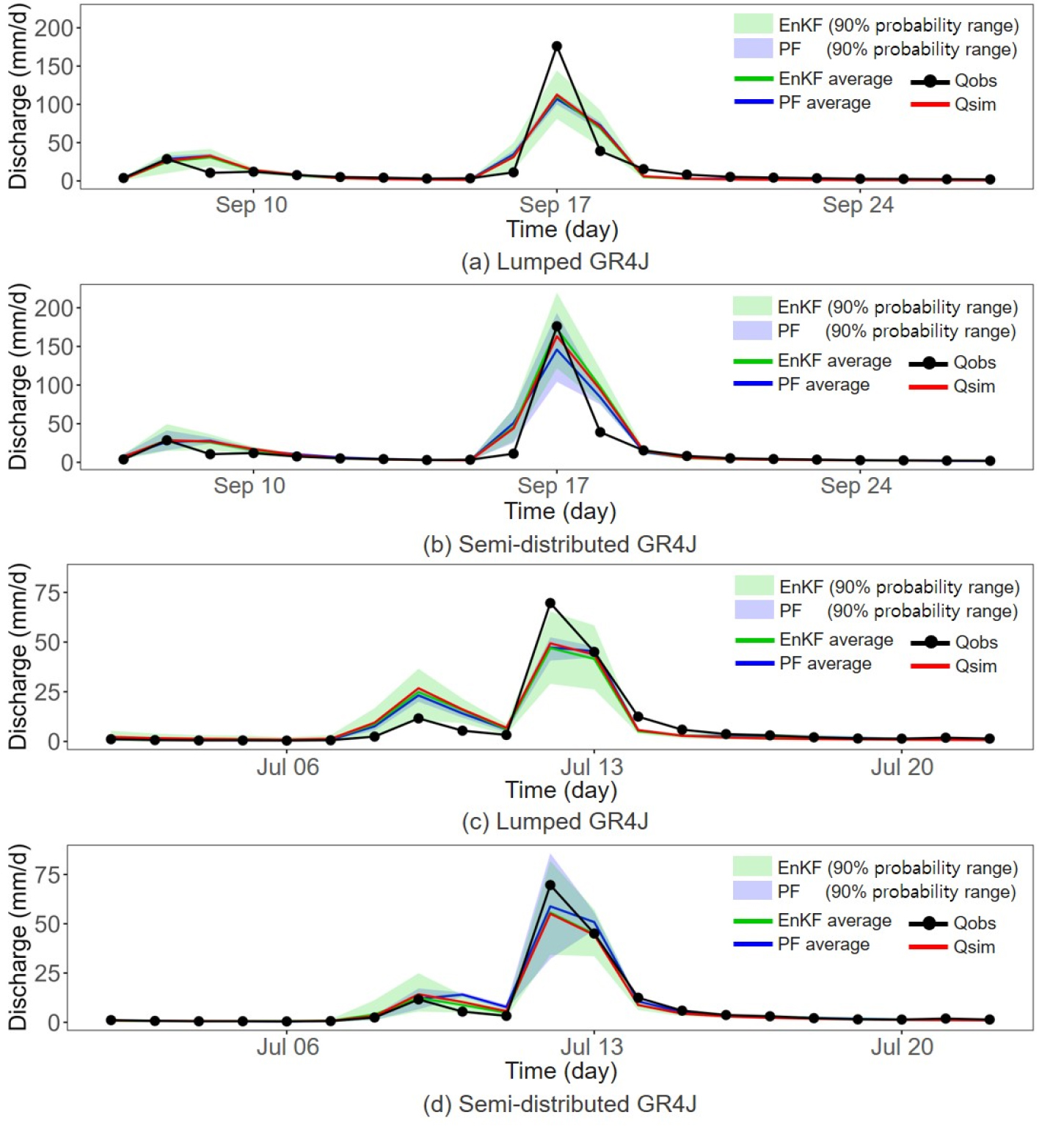
수문모형 구조가 모의성능에 미치는 영향을 비교한 결과, 두 수문모형은 2012년(Figs. 5(a) and 5(e))과 2015년(Figs. 5(d) and 5(h)) 기간의 홍수기에서 모의성능 차이가 나타났다. 홍수기 모의성능 및 자료동화 예측성능 차이를 현격하게 비교하기 위해 2012년(Figs. 6(a) and 6(b))과 2015년(Figs. 6(c) and 6(d)) 기간에 대해 첨두유량이 발생한 기준 앞뒤 10일간 모의를 수행하였다(Fig. 6). Fig. 6에서 검은색 선은 관측 유량(Qobs), 빨간색 선은 모의 유량(Qsim), 초록색 선은 앙상블 칼만 필터(EnKF)의 평균, 파란색 선은 파티클 필터(PF)의 평균, 초록색과 파란색 상자는 앙상블 칼만 필터와 파티클 필터의 90% 확률 분포 범위이다. 앙상블의 수는 각각 100개를 적용하였다.
두 수문모형의 홍수기 모의성능을 비교해 보면, 집중형 GR4J모형(Figs. 6(a) and 6(c))은 빨간색 선인 모의유량이 검은색선인 관측유량에 비해 홍수기에서 과소모의 되었다. 반면, 준분포형 GR4J 모형(Figs. 6(b) and 6(d))은 집중형 모형에서 과소모의된 유량 보다 관측과 가깝게 모의성능이 향상되었다. 이는 공간적 상관관계를 고려하지 않는 집중형 모형의 구조적 특징과 상반된, 상류 유역의 유입량까지 고려하는 준분포형 모형의 구조적 특징이 홍수기의 모의성능을 향상시키는 것으로 판단된다.
자료동화 적용 후 예측성능을 비교해 보면, 준분포형 GR4J 모형(Figs. 6(b) and 6(d))은 집중형 GR4J 모형(Figs. 6(a) and 6(c))보다 자료동화 예측성능이 향상되었다. 2012년 준분포형 GR4J 모형(Fig. 6(b))은 초록색 선인 앙상블 칼만 필터의 평균이 빨간색 선인 모의유량 보다 관측 첨두유량과 가깝게 예측 성능이 향상되었다. 반면, 2012년 집중형 GR4J 모형(Fig. 6(a))의 자료동화 적용 후 모의성능은 여전히 관측 첨두유량에 보다 과소모의 되었다. 이는 2015년 결과에서도 비슷한 양상을 보였다. 2015년 준분포형 모형(Fig. 6(d))의 결과를 보면, 파란색 선인 파티클 필터의 평균은 집중형 모형(Fig. 6(c))의 자료동화 적용 결과 보다 상대적으로 관측 첨두유량과 가깝게 예측성능이 향상되었다. 반면, 2015년 집중형 모형(Fig. 6(c))의 자료동화 적용 후 모의성능은 시각적으로 차이를 확인하기 어려웠다. 즉, 자료동화 적용 후 홍수기 모의성능은 집중형 모형 보다 준분포형 모형에서 예측성능이 향상되었으며, 이는 유역 출구에서만 자료동화를 적용하는 집중형 모형에 비해 여러 하위유역의 공간적 상관관계를 고려하여 유역내 자료동화 적용하는 준분포형 모형의 구조적 특징이 홍수기 예측정확성을 향상시키는데 효과적인 것으로 판단된다. 따라서, 공간적 상관관계를 고려하지 않는 집중형 모형과 공간적 상관관계를 고려하는 준분포형 모형의 구조적 특징은 모의성능 및 자료동화 예측성능에 영향을 미치는 요소로 분석된다.
두 수문모형의 앙상블 확률 분포 범위를 비교해 보면 다음과 같다. 집중형 GR4J 모형(Figs. 6(a) and 6(c))의 경우, 초록색으로 표시된 앙상블 칼만 필터(EnKF)의 범위는 넓었고, 파란색으로 표시된 파티클 필터(PF)의 범위는 상대적으로 좁았다. 준분포형 GR4J 모형(Figs. 6(b) and 6(d))의 경우, 앙상블 칼만 필터와 파티클 필터의 확률 분포 범위에 대한 차이는 없었다. 즉, 집중형 모형은 수문자료동화 기법별 앙상블 확률 분포 범위에 대한 차이가 나타났으며, 준분포형 모형에서는 수문자료동화 기법별 앙상블 확률 분포 범위에 대한 차이가 상대적으로 적었다.
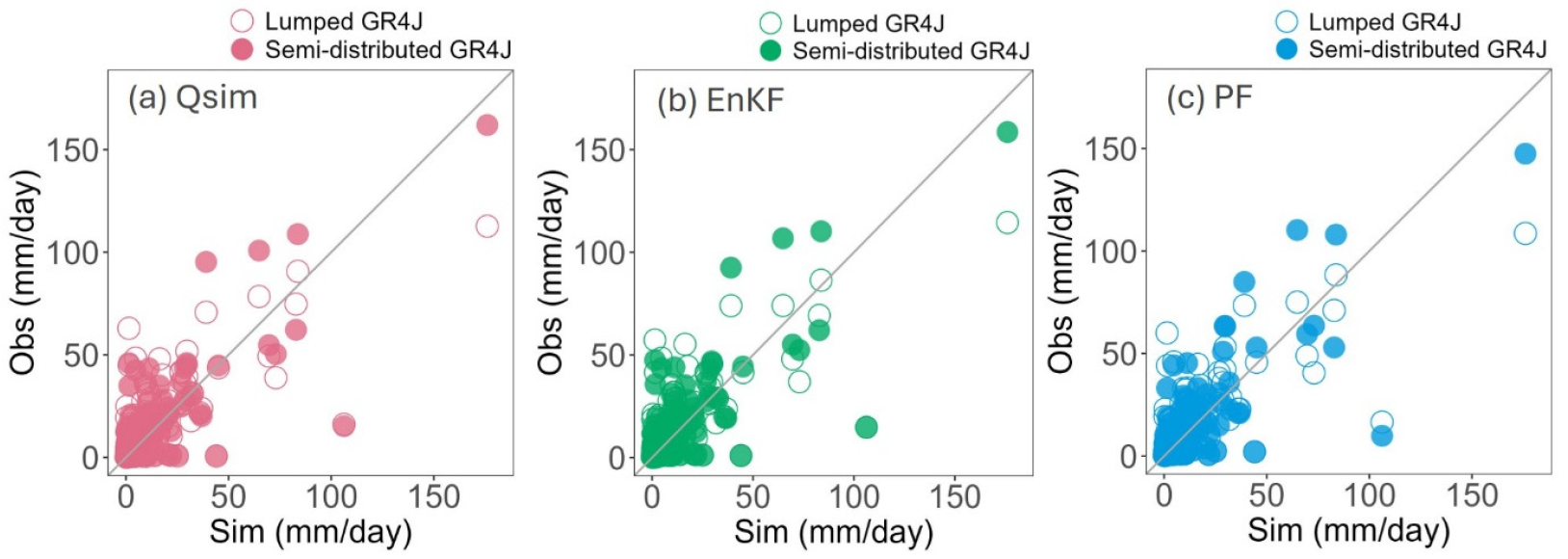
Fig. 7은 집중형과 준분포형 GR4J 모형의 검정기간에 대해 앙상블 칼만 필터, 파티클 필터, 모의유량을 모의와 관측유량의 1:1 그래프를 통해 비교한 결과이며, 이때의 KGE 지표를 막대그래프를 통해 두 수문모형을 비교하였다(Fig. 8). Fig. 7(a)는 모의유량, Fig. 9(b)는 앙상블 칼만 필터, Fig. 9(c)는 파티클 필터에 대한 결과이다. 준분포형GR4J 모형 적용시 모의유량이 약 150 mm/day 이상인 고유량 일 때, Figs. 9(a)~9(c) 모두 집중형 GR4J 모형 보다 관측 모의 일대일 선에 가까워졌다. 또한, 파티클 필터(Fig. 7(c))는 약 75~100 mm/day 모의유량 사이에서 자료동화 전 모의유량(Fig. 7(a))보다 관측 모의 일대일 선에 가까워졌으며, 이는 자료동화를 통해 관측과 더 가깝게 모의되었다.
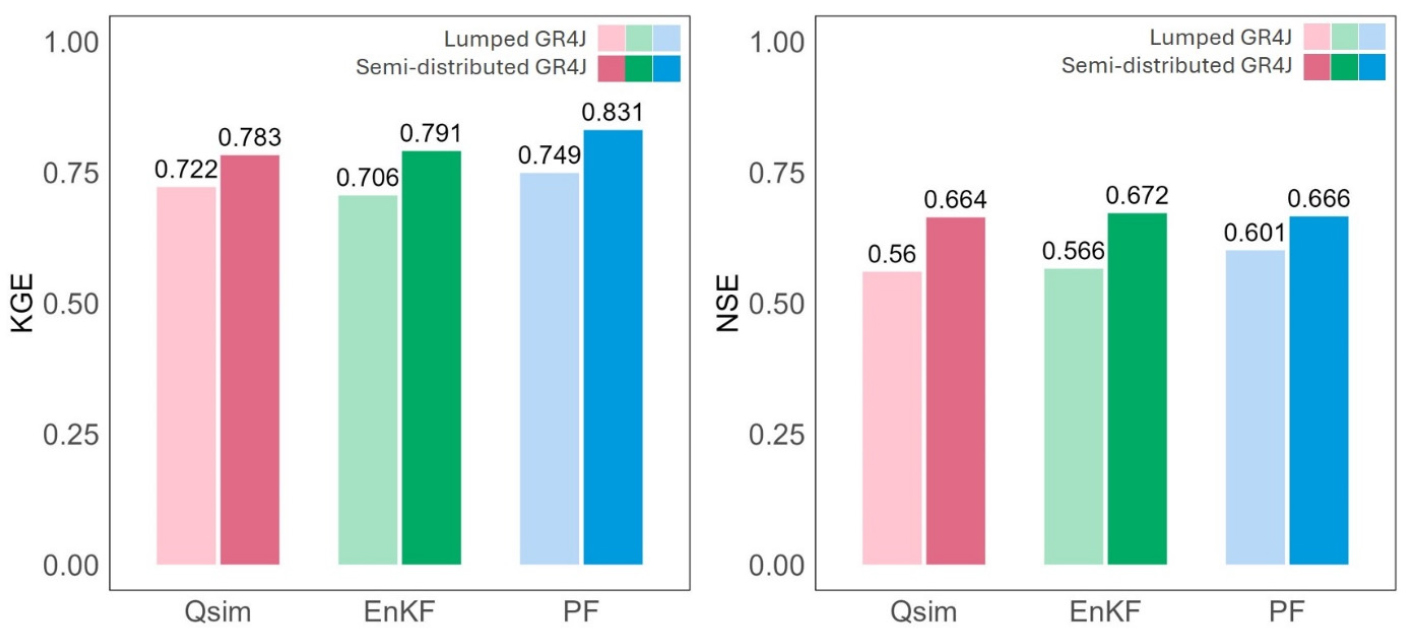
Table 4는 검보정 기간에 대해 자료동화 전후 모형 성능을 KGE, NSE 지수로 평가한 결과이다. 검정기간 결과는 Fig. 8에 비교하였다. 집중형 모형 경우, 자료동화 미적용시 KGE 지표는 0.722에서 파티클 필터 적용후 0.749로 0.027(3.74%) 향상되었다. 준분포형 모형의 경우, 자료동화 전 KGE값이 0.783에서 앙상블 칼만 필터 적용 후 0.791로 0.008(1.02%), 파티클 필터 적용 후 0.831로 0.048(6.13%) 향상되었다. 즉, 두 수문모형은 파티클 필터 적용시 자료동화 적용 전보다 KGE 지표가 가장 높게 나타났다. NSE 지표로도 집중형보다 준분포중형 우수하고, 자료동화를 통해 모형 성능이 향상되는 경향은 KGE와 비슷하게 분석되었다. 다만, NSE 기준으로는 준분포형 모형의 자료동화 성능은 앙상블 칼만 필터가 파티클 피터보다 우수하였다.
Table 4.
Comparison of the performance metrics (KGE and NSE) between the calibration and validation periods for the Namgang Dam basin
두 수문모형의 자료동화 적용 전 KGE 지표를 비교하면 집중형 모형은 0.722, 준분포형 모형은 0.783으로, 집중형 모형 보다 준분포형 모형에서 0.061(8.45%) 높았다. 앙상블 칼만 필터 적용시 KGE 지표는 집중형 모형은 0.706, 준분포형 모형은 0.791로, 집중형 모형 보다 준분포형 모형에서 0.085 (12.03%) 높았다. 파티클 필터 적용 시 집중형 모형은 0.749, 준분포형 모형은 0.831로, 집중형 모형 보다 준분포형 모형에서 0.082(10.95%) 높았다. 즉, 자료동화 전후 KGE 지표는 집중형 모형보다 준분포형 모형에서 높았으며, 이는 상류유역의 자료동화 적용이 가능한 준분포형 모형의 구조적 특징이 전체유역의 모의성능을 향상시키는 것으로 추정된다.
3.2 자료동화 하이퍼-매개변수 영향 분석
본 절에서는 보정기간에 대해 자료동화와 하이퍼 매개변수 중 기상강제력(강수, 잠재증발산) 불확실성 범위가 집중형과 준분포형 모형의 예측성능에 미치는 영향을 분석하여 최적 하이퍼-매개변수를 선정하였다. 기상강제력의 불확실성 범위를 분석하기 위해 강수()와 잠재증발산() 오차 매개변수 범위를 0.1에서 1 사이, 0.1 단위로 변경하며 모의성능을 분석하였다(Fig. 9). Fig. 9에서 x축은 강수 오차 매개변수, y축은 잠재증발산 오차 매개변수, z축은 평가지표 KGE를 나타내며, 검은색 네모 박스는 최적 강수 및 잠재증발산 오차 매개변수의 KGE 값을 표시하였다.
집중형 모형의 최적 오차 매개변수는 다음과 같다. 앙상블 칼만 필터는 = 0.3, = 0.5일 때 KGE값이 0.857, 파티클 필터는 = 0.1, = 0.4일 때 KGE값은 0.858로 최적 모의성능을 보였다. 집중형GR4J 모형의 기상강제력 불확실성을 분석해 보면, 앙상블 칼만 필터(Fig. 9(a))와 파티클 필터 기법(Fig. 9(b))은 기상강제력 중 강수 오차 매개변수가 상대적으로 작을수록 KGE가 향상되었다. 최적 오차 매개변수 범위에 대해 두 기법을 비교해 보면, 앙상블 칼만 필터(Fig. 9(a))는 최적 강수 및 잠재증발산 오차 매개변수 범위가 넓게 나타났고, 파티클 필터(Fig. 9(b))는 상대적으로 좁게 나타났다. 이는 집중형 GR4J모형에 대해 자료동화 적용시, 앙상블 칼만 필터는 강수 및 잠재증발산 오차 매개변수의 영향을 적게 받으며, 파티클 필터는 강수 오차 매개변수가 작을수록 모의 성능이 향상되는 것으로 분석되었다. 따라서, 집중형 GR4J모형의 파티클 필터 모의시 기상강제력 오차 매개변수를 과도하게 설정하지 않는 것이 권고된다.
준분포형 모형의 최적 오차 매개변수는 다음과 같다. 2번 유역의 앙상블 칼만 필터는 = 1.0, = 0.4, 파티클 필터는 = 0.1, = 0.7, 3번 유역의 앙상블 칼만 필터는 = 0.6, = 0.1, 파티클 필터는 = 0.5, = 0.2일 때 최적 모의성능을 보였다. 이는 최적 성능을 얻기 위해 각 하위유역에 따라 기상강제력 불확실성 조건이 다르다는 것을 의미한다. 준분포형 GR4J 모형의 기상강제력 불활실성을 분석해 보면, 2번 유역의 앙상블 칼만 필터(Fig. 9(c))는 강수 오차 매개변수가 클수록, 파티클 필터(Fig. 9(d))는 강수 오차 매개변수가 작을수록 모의정확도가 향상되었다. 3번 유역은 앙상블 칼만 필터(Fig. 9(e))와 파티클 필터(Fig. 9(f)) 모두 강수 오차 매개변수가 클수록 모의정확도가 향상되었다. 최적 오차 매개변수 범위를 비교해 보면, 2번 유역(Figs. 9(c) and 9(d))은 앙상블 칼만 필터와 파티클 필터 모두 최적 강수 및 잠재증발산 범위가 좁게 나타났고, 3번 유역(Figs. 9(e) and 9(f))은 앙상블 칼만 필터와 파티클 필터 모두 상대적으로 넓게 나타났다. 즉, 준분포형 모형의 자료동화 적용시 유역 별 최적 성능을 얻을 수 있는 불확실성 범위가 유사하게 나타났으며, 2번 유역은 강수 오차 매개변수가 커지거나 작을수록 모의성능이 향상되고, 3번 유역은 강수 및 잠재증발산 오차 매개변수의 영향을 적게 받는 것으로 분석되었다. 따라서, 남강댐 유역에 대해 준분포형 GR4J 모형의 자료동화 적용시 2번 유역의 앙상블 칼만 필터는 기상강제력 오차 매개변수를 과도하게 설정하는 것이, 파티클 필터는 기상강제력 오차 매개변수를 과도하게 설정하지 않는 것이 권고된다.
집중형 GR4J 모형은 수문자료동화 기법에 따라, 준분포형 GR4J 모형은 하위유역에 따라 최적 성능을 얻기 위한 불확실성 조건이 달랐다. 따라서, 집중형 GR4J 모형은 자료동화 적용시 최적 성능을 발휘하기 위해서는 자료동화 기법별, 준분포형 GR4J 모형은 각 소유역별 하이퍼-매개변수의 적절한 조정이 필요하다.
3.3 보정기간 길이에 따른 영향 분석
보정기간 길이에 따른 모의정확도 변동 정도를 분석하기 위해 남강댐 유역의 구축된 총 10년 기간 중 보정 4년, 검정 6년(Case 1), 보정 3년, 검정 7년(Case 2), 보정 2년, 검정 8년(Case 3)으로 모의 실험을 구성하였다(Table 5). 이때의 보정기간은 모형 매개변수 보정만 수행하였고, 자료동화 하이퍼-매개변수 보정은 따로 수행하지 않았다. 모의 앙상블 수는 두 기법 모두 30개를 적용하였다.
Table 5.
Modeling periods for calibration and validation according to the length of the calibration period
| Basin | Calibration | Validation | |
| Case 1 | Namgang Dam | 2006-2009 | 2010 - 2015 |
| Case 2 | Namgang Dam | 2006-2008 | 2009 - 2015 |
| Case 3 | Namgang Dam | 2006-2007 | 2008 - 2015 |
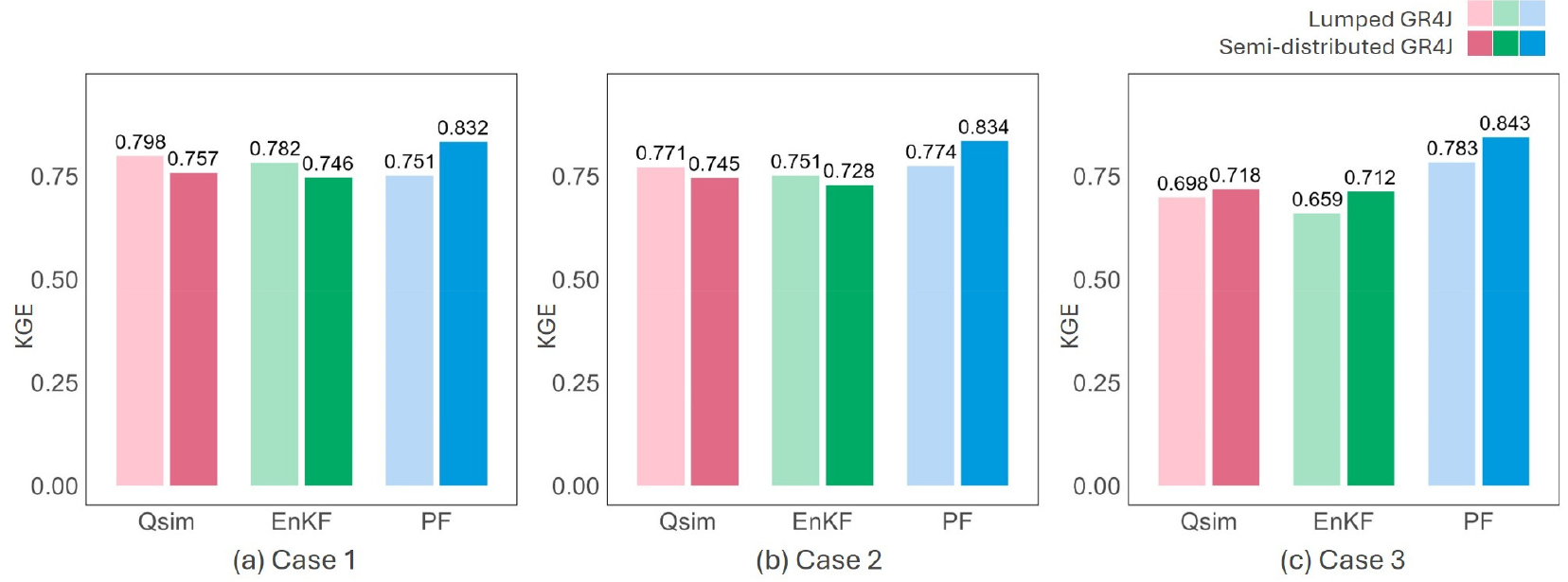
Fig. 10은 모형 매개변수 보정기간 기간을 4년(Case 1), 3년(Case 2), 2년(Case 3)으로 설정하여 모의정확도 변동 정도를 KGE 지표로 분석하였다. 집중형 모형의 KGE값은 0.798 (Case 1), 0.771(Case 2), 0.698(Case 3)로, 준분포형 모형은 0.757(Case 1), 0.745(Case 2), 0.718(Case 3)로, Case 3(보정기간 2년)일 때 Case 1, 2보다 모의성능이 낮아졌다. 이때의 자료동화 모의성능 분석 결과, 앙상블 칼만 필터 적용시 집중형 모형의 KGE 값은 0.782(Case 1), 0.751(Case 2), 0.659 (Case 3)로, 준분포형 모형의 KGE 값은 0.746(Case 1), 0.728 (Case 2), 0.712(Case 3)로, Case 3(보정기간 2년)일 때 Case 1, 2보다 모의성능이 낮아졌다. 반면, 파티클 필터 적용시 집중형 모형의 KGE값은 0.751(Case 1), 0.774(Case 2), 0.783(Case 3)로 0.7이상, 파티클 필터 적용시 준분포형 모형의 KGE값은 0.832(Case 1), 0.834(Case 2), 0.843(Case 3)로 0.8이상으로 나타났다. 즉, 파티클 필터 적용시 보정기간 길이는 자료동화 모의성능에 미치는 영향이 상대적으로 적었다. 반면, 앙상블 칼만 필터 적용시 보정기간 길이는 모의성능에 미치는 영향이 상대적으로 컸으며, 일정기간 이상 보정기간 설정이 필요한 것으로 분석되었다.
4. 결 론
본 연구에서는 집중형과 준분포형 GR4J 수문모형에 대해 앙상블 칼만 필터와 파티클 필터 기법을 적용하여 일단위 수문모형 구조가 홍수기 모의성능에 미치는 영향을 정량적으로 평가하고, 자료동화와 관련된 하이퍼-매개변수의 불확실성이 모형 성능에 미치는 영향을 분석하였다. 주요 연구결과는 다음과 같다.
(1) 집중형 및 준분포형 수문모형의 자료동화 예측성능을 비교한 결과, 파티클 필터 적용시 KGE 지표는 각각 0.749(집중형), 0.831(준분포형)로, 집중형 모형 보다 준분포형에서 0.082(11.0%) 향상되었다. 이는 상류유역의 자료동화 적용이 가능한 준분포형 모형의 구조적 특징이 전체 유역의 모의정확성에 영향을 미치는 것으로 판단된다.
(2) 기상강제력(강수, 잠재증발산) 불확실성이 집중형과 준분포형 GR4J 수문모형의 예측성능에 미치는 영향을 분석한 결과, 집중형 모형은 수문자료동화 기법별, 준분포형 모형은 각 소유역별 최적성능을 얻기 위한 불확실성 조건이 달랐다. 집중형 모형은 자료동화 기법에 따라 기상강제력 오차 크기에 민감하게 반응하며, 준분포형 모형은 각 소유역별 하이퍼-매개변수의 적절한 조정이 필요하다.
(3) 보정기간 길이에 따른 모의정확도 분석 결과, 앙상블 칼만 필터 적용시 집중형 모형의 KGE 지표는 0.782(Case 1), 0.751(Case 2), 0.659(Case 3)로, 준분포형 모형의 KGE 값은 0.746(Case 1), 0.728(Case 2), 0.712(Case 3)로, Case 3(보정기간 2년)일 때 Case 1, 2보다 모의성능이 낮아졌다. 즉, 앙상블 칼만 필터는 보정기간 길이에 따라 모의성능에 영향을 미치며, 일정기간 이상 보정기간 설정이 필요하다.
본 연구에서는 집중형과 준분포형 GR4J 모형을 앙상블 기반 순차자료동화를 적용하여 일 유출 모의 정확도가 향상되는 것을 확인하였다. 특히 집중형 모형의 경우 자료동화 적용시 홍수기의 예측 성능 향상이 제한적이었으나 준분포형 모형의 자료동화 적용을 통해 모의 정확도 향상이 가능하였다. 또한, 최적 성능을 얻기 위해서는 일정기간 이상의 보정기간과 집중형 GR4J 모형은 자료동화 기법별, 준분포형 GR4J 모형은 각 소유역별 하이퍼-매개변수의 적절한 조정이 요구됨을 확인하였다. 후속 연구로는 일 단위 이하 시간 단위 유량 예측으로 확장하여 수문반응시간이 상대적으로 짧은 중소규모에 대한 준분포형 모형의 자료동화 적용 연구가 가능할 것으로 판단된다.