1. 서 론

전 세계 주요 하천 시스템의 대부분은 댐과 저수지의 영향을 받고 있으며, 효율적인 댐 운영으로 수력발전, 물공급, 재난예방을 위한 수자원 관리를 실시하고 있다(Dynesius and Nilsso, 1994; WCD, 2000; Lehner et al., 2011; Shang et al., 2018).

댐 저류량 또는 방류량에 대한 적절한 모의 및 예측, 분석을 포함한 효율적인 댐 운영방안은 댐 본연의 이수, 치수, 친수 기능을 달성하고 인간과 하천 생태계에 대한 위험을 방지하는데 필수적이다. 특히, 2020년에는 예년보다 높은 강우량으로 남부지방에 수재해로 인한 많은 피해가 발생하였으며 이에 따라 정확도 높은 홍수 예보 및 댐 운영의 고도화가 더욱 요구되고 있는 실정이다.

우리나라의 홍수예보는 적기에 홍수특보(홍수주의보, 홍수경보)를 발령하여 홍수피해를 경감시키고자 하는 방재활동의 일환이며 여기에는 댐의 방류량 결정 등과 같은 홍수조절과정을 포함한다. 즉, 댐의 안전성을 최우선으로 하여 댐으로 유입하는 홍수량을 저류하고 효율적으로 조절방류함으로써 홍수 분산에 따른 하류 하천의 홍수피해를 최소화하고 있다. 그리고 이러한 댐의 홍수조절의 경우, 강우예측모형과 강우-유출모형, 의사결정모형, 홍수추적모형 등이 서로 연계되어 운영된다.

댐 및 저수지의 효율적 운영을 위해 1980년대부터 물리기반의 모형(예: HEC-ResSim, WEAP21 등)이 개발되고 활용되어왔으며, 이러한 모형은 일반적으로 rule curve에 근거하여 과거 수문학적 통계량을 기반으로 운영방안을 모의하고 결정한다(Klipsch and Hurst, 2003; Yates et al., 2005).

그러나 댐 운영에 실제 적용되는 운영규칙 또는 시나리오는 수리수문학적 또는 사회경제학적으로 매우 복잡한 유역특성을 반영함은 물론 시간적 스케일에 따라 그 운영 방법이 달라질 수 있다.

예를 들어, 물 공급을 효율적으로 관리하고 경제적 이익을 최적화하기 위해서는 중장기적 (계절 및 월별) 운영이 필요하며, 전력망 부하, 물 수요, 홍수 및 가뭄 등과 같은 재난 예방 등을 위해서는 단기(일 및 시간) 비상 운영이 요구된다. 이러한 시간적 스케일 문제 및 강우-유출 등의 자연조건, 물과 전력 수요-공급 등 인간활동의 영향을 받는 강력한 비선형 상호 작용을 가진 여러 요인의 결과에 따라 실제 댐의 운영은 최초 운영계획에서 벗어날 수 있으며, 내재된 불확실성 때문에 기 계획된 특정 규칙에 기반한 상기 모형은 때때로 방류량을 예측하고 제어하는데 제약이 있을 수 있다(Johnson et al., 1991; Oliveira and Loucks, 1997). 또한 댐 운영 모형을 새로운 시간 스케일을 반영한 규칙으로 재구성해야 하는 경우, 댐 운영자의 전문지식에 대한 요구가 높고, 모형의 계산시간이 단기 비상운영의 요구사항을 충족할 수 없는 상황이 발생할 수도 있다.

위와 같은 근거들을 토대로 효율적 댐 운영에 관한 다양한 연구가 수행되어왔으며 그 중 댐 방류량 결정 및 홍수조절을 위한 연구로 Chang and Chang (2001)은 GA와 ANFIS 알고리즘을 이용한 최적 댐 방류량을 추정하여 기존 M-5 rule curve와 비교하여 그 정확도를 검증하였으며, Chaves et al. (2004)는 댐 수질 및 수량의 효율적 운영을 위하여 DP, Markov chain, GA, ANN 등을 통합한 FSDP 기법을 제시하고 실제 저수지 운영에 적용하여 해당 기법의 적합성을 분석한 바 있다. 또한 Woo et al. (2008)는 댐의 수문 제어를 위하여 동적 퍼지 추론 기법을 이용하고 현업 적용 시의 적정 수위 유지 방안 및 방류량 제어 방안을 제시하였다. 그리고 Kang et al. (2015)은 댐의 홍수조절을 위해 홍수 지침 곡선을 활용하고 댐 수위 상황에 따른 방류량 결정 방법으로 남강댐 유역의 실제 홍수사상에서의 적절성을 평가하였으며, 그 결과 실제 남강댐 상·하류를 고려한 효과적인 댐 운영에 기여할 것으로 분석되었다. Kwak (2021)은 빈도대응법을 이용하여 댐의 홍수조절을 위한 저수량과 목표수위를 추정하였으며 이를 통하여 실제 댐에서의 홍수조절 효과를 확인하였다.

그리고 전술한 물리기반 모형을 사용한 댐 운영 연구로 Yi et al. (2015)는 HEC-ResSim을 활용하여 비상방류설비를 고려한 방류량을 모의하였으며 크기에 따라 구분된 3개의 댐을 예시로 비상방류 설계기준의 적정성을 검토하고 제시하였다. Kim and Kim (2018)은 강우조건과 토양함수상태를 고려하고 강우-유출 모형인 NWS-PC를 사용하여 자연하천과 댐 방류량 조건별 도달시간 산정공식을 개발하였으며 기개발된 산정공식과 함께 황강댐의 방류량 조건에 따른 임진강 수위관측소 도달시간을 산정하고 하류지역의 홍수피해 방지를 위한 적절성을 평가하였다.

물리적 및 통계적 모형 이외에도 최근 인공지능(Artificial Intelligence, AI) 및 빅데이터 기술의 발달로 데이터 기반 AI 모형이 다양한 분야에서 활용되고 있으며, 해당 모형은 복합적인 요인의 영향을 받는 비선형 모의 및 예측 문제를 해결하는 데 적합한 것으로 알려져 있다. 그리고 물리 기반 모형과 달리 AI 모형은 다량의 수문자료와 실시간 댐 운영자료에서 다양한 운영규칙을 자율적으로 학습할 수 있으며, 운영자의 전문적인 요구사항이 낮고 응답속도가 매우 빠른 장점이 있다(Hejazi and Cai, 2009). ANN (Artificial Neural Network) 모형은 역전파알고리즘(back propagation, BP)을 활용하여 신경망을 훈련시킴으로써 우수한 비선형 예측 능력을 제공할 수 있으며, 이미 많은 댐 운영 관련 연구에서 활용된 바 있다(Thirumalaiah and Deo, 1998; Jain et al., 1999; Chaves and Chang, 2008). 최신 딥러닝 기술의 댐 운영사례로써 Zhang et al. (2018)은 BP 기반의 ANN, SVR (Support Vector Regression), LSTM (Long Short-Term Memory) 모형별 댐 운영 모의결과를 소개하고 이 중 LSTM이 가장 적합한 것으로 평가하였다.

국내에서 AI를 활용한 댐 방류 의사결정지원에 대한 연구는 국외보다 다소 미비한 실정이며 이에 본 연구에서는 남강댐을 대상으로 딥러닝 기반 LSTM 모형을 활용하고자 한다. 현재 환경부와 한국수자원공사는 홍수관리를 위하여 지자체, 지역주민이 댐의 수문 방류를 사전에 대비할 수 있도록 1일(24시간) 전 수문방류예고제를 시범 운영 중이며, 이를 토대로 댐 운영에 필요한 기초자료들을 활용하여 댐 직하류 수위관측소의 수위를 최대 24시간까지 선행시간(lead time)별로 예측하였다. 그리고 예측된 수위자료를 기반으로 홍수조절을 위한 방류량 결정 등 댐 운영에서의 딥러닝 기술의 활용성을 평가하고자 한다.

2. 대상 유역

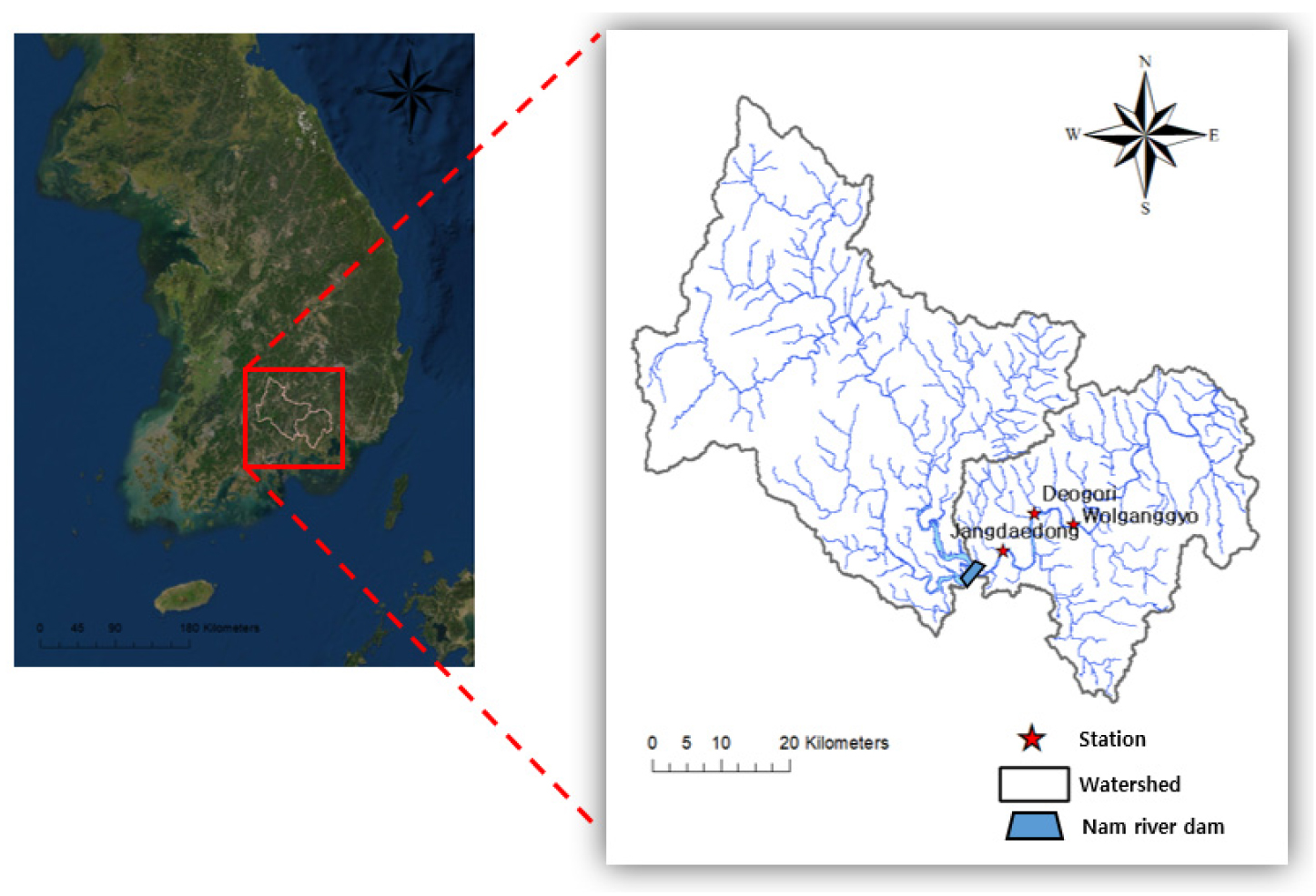
남강은 경상남도 함양군 서상면의 남덕유산(EL 1,507 m)에서 발원하여 남쪽으로 유하하면서 남강댐으로 유입되고, 진주시 지점에서 유로를 동북쪽으로 바꾸어 의령군에서 낙동강 본류와 합류하는 낙동강의 제1지류이며 해당 유역도는 Fig. 1에 도식화하였다.

남강댐 유역은 낙동강 합류점으로부터 80 km 상류지점에 위치하고 유역면적은 2,285 km², 유로연장은 108 km, 유역의 평균 폭은 약 21 km이며 남강 유역의 면적은 3,468 km², 유로연장은 189.93 km, 유역 평균 폭은 18.27 km이다.

남강 유역에 건설된 남강댐은 홍수피해 방지 및 경상남도 서부지역에 생공용수를 공급하기 위한 목적으로 1969년 축조되었고, 이후 기상이변에 등에 대응하기 위해 1999년 댐 규모를 보강한 바 있다. 수문지형학적으로 남강댐은 지리산, 덕유산 등에 둘러싸인 높은 산지 비율과 급한 하상경사로 인하여 수량이 일시에 유입되며, 남강 하류는 완만한 하도경사와 낙동강 본류의 배수 영향으로 홍수위가 장기간 지속되는 특징을 가지고 있다. 또한 댐의 저수용량에 비해 유역규모가 매우 크며 이는 일시에 내리는 집중호우에 대하여 댐에서 홍수조절을 하기에 매우 불리한 여건이다. 그리고 댐 직하류부터 낙동강 본류에 이르는 구간의 상습적인 홍수피해 방지를 위해 대부분의 홍수량을 방수로를 통하여 사천만으로 방류되도록 계획되었으며 Choi et al. (2012)에 따르면 분포형 강우-유출모형인 GRM을 사용한 결과, 사천만 방수로가 남강댐 하류 홍수량 저감에 큰 영향을 미치는 것으로 분석된 바 있다. 또한 장대동 수위관측소는 남강댐으로부터 약 7 km 떨어진 진주시에 위치해 있으며 이는 남강댐 방류에 따른 홍수파가 직접적으로 영향을 미치는 지점이므로 재난 방지를 위해 정확도 높은 수위 예측을 통한 방류량 결정이 필요하다. 2020년의 경우, 장마전선과 3개의 태풍으로 인한 이례적인 강우가 기록되었으며 남강댐 하류지역의 경우, 홍수범람으로 인한 피해가 발생한 바 있다.

Fig. 1.

Location of the study area

3. 방법론

3.1 LSTM

딥러닝은 복잡한 비선형 관계인 자연계 특성을 추출하거나 표현하여 보정 및 예측 정보를 생산할 수 있으며 현재까지도 다양한 분야에서 활발하게 연구가 진행 중이다. 이에 따라 딥러닝 기술은 수자원 분야에서도 실행가능한 효율적인 옵션으로 활용될 수 있다. Sit et al. (2020)에 따르면 대규모 관측 네트워크의 구축으로 이전 세대보다 자료의 수집이 용이해지고, 컴퓨팅 자원의 급속한 발전으로 수자원 관리, 재난 대응 등에 더욱 다양한 딥러닝 기술이 적용될 것으로 전망하였다.

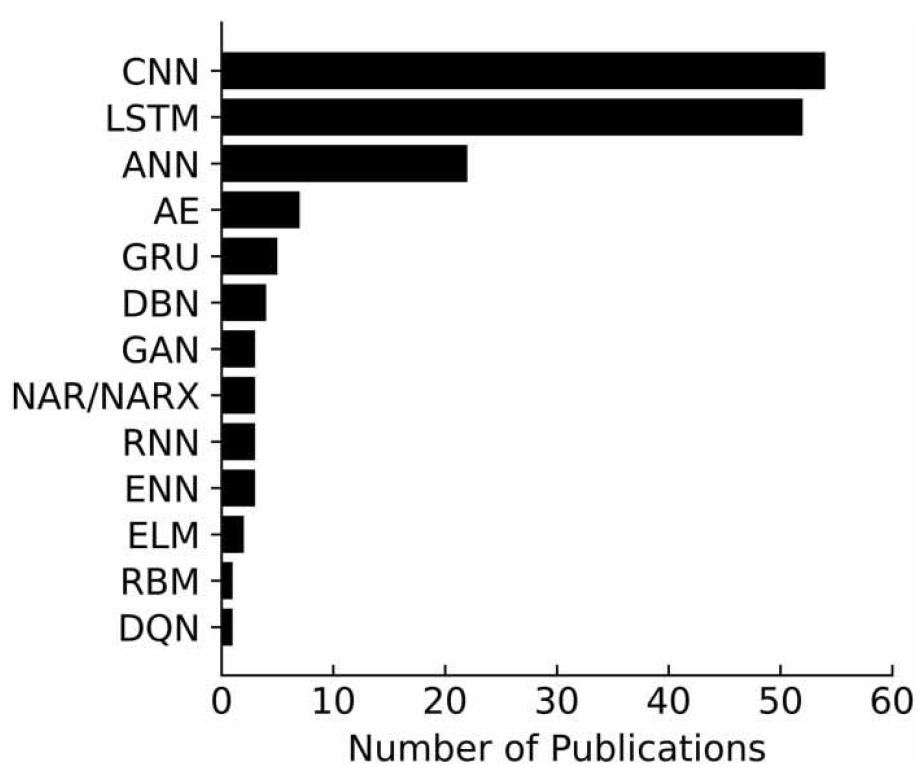
그중 2018년부터 2020년까지 수행된 수자원 분야에서의 딥러닝 활용 연구 중 2차원 이미지 자료처리에 강점을 보이는 CNN (Convolutional Neural Network) 모형과 시계열 자료 처리에 강점을 보이는 LSTM 모형의 활용도가 가장 높게 나타났다(Fig. 2).

Fig. 2.

The frequency of utilization of deep learning algorithms (Sit et al., 2020)

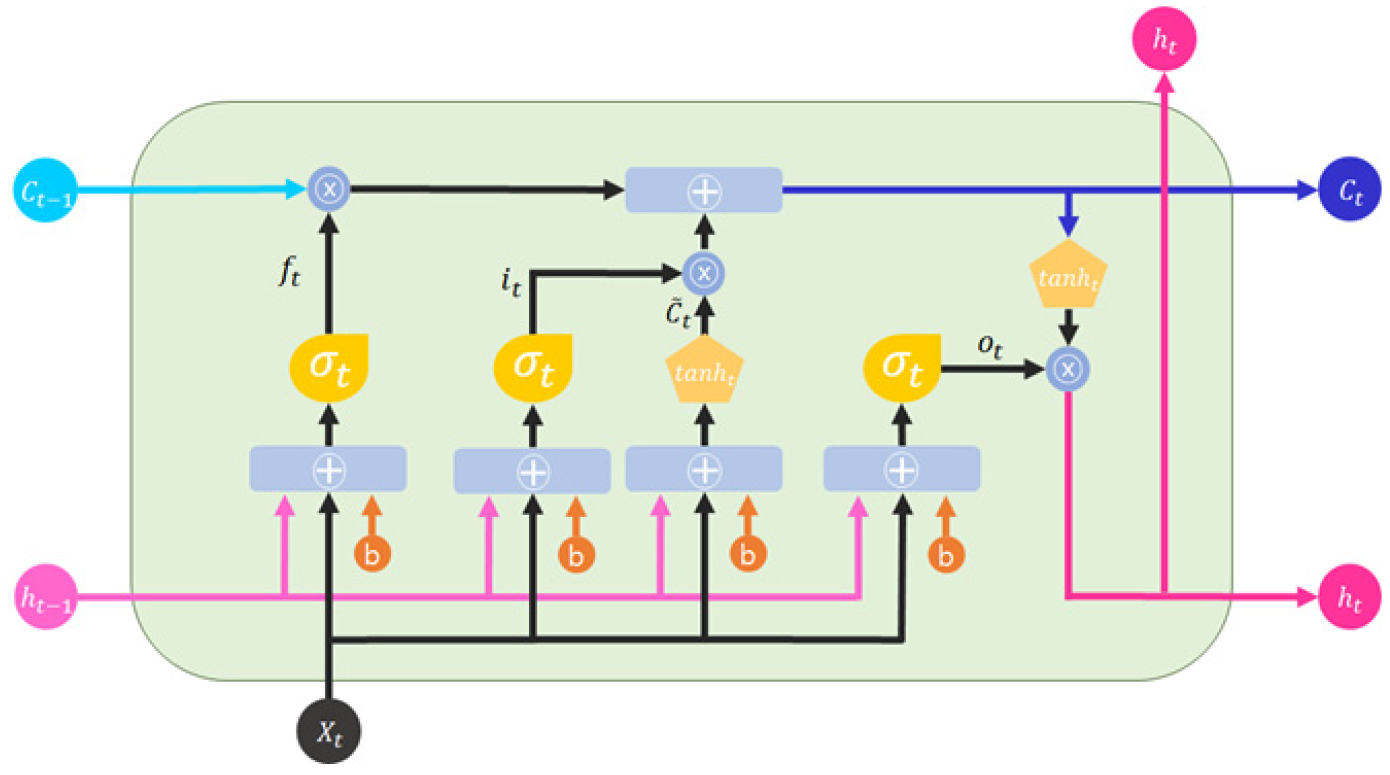
LSTM 알고리즘은 순환신경망(Recurrent Neural Network, RNN)의 가중치 소실 문제를 해결하기 위하여 개발되었으며 Eq. (1)의 망각게이트(forget gate, f_t), Eq. (2)의 입력게이트(input gate, i_t), Eqs. (3) and (4)의 장기기억메모리(cell state, C_t), Eqs. (5) and (6)의 출력게이트(output gate, o_t)로 이루어져 있고 해당 구조를 도식화하면 Fig. 3과 같다. 순환신경망과 LSTM의 차이점은 특정 시점의 상태값(h_t)을 업데이트하기 위해 장기기억메모리 개념을 도입하여 내부에 가지고 있는 정보를 업데이트할 것인지 아닌지를 판단하게 되며 이로 인하여 이전의 시계열 자료 정보를 활용할 수 있는 장점이 있다. 즉, 순환신경망보다 더 많은 자료간의 변동량을 기억하는 특성으로 인하여 장기적인 시간의 종속성을 포착하는데 효율적이므로 여러 가지 시계열 데이터와 관련된 학습문제에 확장 가능한 모형으로 이미 음성인식, 언어모델링, 번역뿐만 아니라 다른 신경망과의 결합을 통한 다양한 분야에서 활용되고 있다(Jung et al., 2018).

Fig. 3.

LSTM model structure

여기서, σ는 시그모이드 활성화 함수, tanh는 하이퍼볼릭탄젠트 활성화 함수, W_f, W_i, W_c, W_o는 각 게이트의 가중치, b_f, b_i, b_c, b_o는 각 게이트의 편향, C_t―1는 과거의 셀 상태, Ct는 후보 셀 상태, C_t는 해당 시점의 셀 상태를 나타낸다.

3.2 입력자료 구축

전술한 LSTM 모형을 적용하기 위한 기초자료로는 댐 수위, 유역 면적평균강우량, 댐 유입량, 발전 방류량, 여수로 방류량, 진주시 방류량(발전 방류량+여수로 방류량), 장대동과 덕오리 관측소 수위까지 총 8개의 시 단위 자료를 구축하였다(Table 1). 남강댐의 경우 2절에서 전술한 바와 같이 남강 본류 진주시의 홍수피해방지를 위하여 홍수기 대부분의 방류량을 사천만으로 방류하도록 계획되어 있다. 그러므로 댐 방류량에 따른 직하류 수위 관측소의 수위를 예측하기 위하여 남강 본류로 방류되는 발전 방류량과 여수로 방류량의 합을 진주시 방류량으로 산정하였다. 자료 활용에 앞서 생성과정에서 발생한 이상치(outlier)들은 모형의 학습과 결과에 불확실성을 초래할 수 있으므로 발생 시간의 전·후 자료, 타 자료와의 상관성을 파악하여 전처리를 수행하였다. 그리고 Table 1에 나타나 있듯이 모형 학습에 이용하기 위해서는 개별 변수간의 표준화가 필요하다. 따라서 Python의 MinMaxScaler 변환를 활용하여 자료가 모형에 입력될 때 0과 1 사이의 값으로 정규화(normalization)되도록 구성하였다.

수집된 입력자료 중 2009년부터 2018년의 10년간의 자료는 모형의 학습과 검증에 활용하였으며 각 80%(학습)와 20% (검증)로 구분하였다. 그리고 2019년부터 2021년 7월까지는 모형의 시험 자료로 활용하여 예측 정확도를 비교·분석하였다(Fig. 4). 또한 무방류 기간을 포함한 전 기간에 대하여 가용한 8개 자료 간의 상관관계를 분석하고 Table 2에 나타내었다. 진주시 방류량은 발전 방류량과 여수로 방류량의 합으로 산정되었으므로 두 변수를 제외하고 장대동 수위관측소와 가장 상관관계가 높은 자료는 진주시 방류량, 덕오리 수위관측소 수위, 댐 유입량 순으로 분석되었으며 각 상관계수는 0.69, 0.6, 0.36으로 나타났다. 그리고 댐 방류량 결정 시 LSTM 모형의 활용성 평가를 위하여 댐 운영에 있어서 수집되는 기초 자료인 댐 수위, 유역 면적평균강우량, 댐 유입량, 진주시 방류량을 기본 변수로 사용하고, 예측 목표지점의 하류 관측소인 덕오리 수위관측소 및 발전 방류량과 여수로 방류량을 학습에 반영하는 여부에 따라 4가지 Case로 Table 3과 같이 구분하였으며 이를 토대로 선행시간별 예측 정확도를 비교·분석하였다.

Fig. 4.

Time series data sets for LSTM applications

예측 정확도의 정량화를 위해 MAE (Mean Absolute Error), RMSE (Root Mean Square Error), NSE (Nash-Sutcliffe Efficiency)를 모형 평가지수로 선정하였으며, 개별 수식은 Eqs. (7)~(9)과 같다.

여기서 N은 자료의 개수, O_t와 P_t는 시간 t에서의 관측 수위와 예측 수위, O는 관측 수위의 평균값을 나타낸다.

4. 모의 결과 및 분석

본 연구에서는 남강댐 유역을 대상으로 댐 운영 자료 및 하류 수위 관측소 자료를 LSTM 모형에 학습 후 댐 직하류 진주시 장대동 수위 관측소의 수위를 7개의 선행시간(1, 3, 6, 9, 12, 18, 24시간)에 대하여 수위를 예측하였다. LSTM 모형은 Block-box 모형으로 학습과 예측의 계산과정을 직접 확인할 수 없으며, 학습 전 사용자가 조절가능한 매개변수로는 sequence length, number of unit, batch size, number of epoch, learning rate 등이 존재한다. 해당 매개변수들은 연구자의 경험적 방법을 토대로 선정되었다. 본 연구에 사용된 sequence length는 학습 시에 입력되는 자료의 길이를 뜻하며 LSTM cell의 time step과 같다. 시 단위 자료에서 1시간 뒤 예측을 수행할 때 sequence length가 4일 경우 4시간(t-3~t)의 자료를 학습에 사용하고 1시간 후(t+1)의 예측값을 생성함을 의미한다. 그리고 number of unit은 LSTM cell 안에서의 노드(node)의 개수를 의미하며, batch size는 모형에 입력되는 자료의 크기, number of epoch는 모형 학습 시 반복 횟수, learning rate는 모형 학습률(속도)을 의미한다. 또한 모형 학습 시 과적합을 방지하기 위하여 2가지 기능을 사용하였다. 첫 번째로는 학습 시 은닉층 노드를 확률적으로 제거하여 학습자료 의존성을 낮춰주는 dropout 기능으로 매개변수인 drop_rate를 0.2로 설정하였다. 두 번째로는 모형별 최적의 반복 횟수를 찾기 위해 early_stopping 기능을 사용하여 최저 오차값 기준 100회 이후까지 학습을 진행하였을 때 오차의 개선이 없을 시 학습이 중단되도록 하여 산정된 최저 오차값을 기준으로 결과를 도출하여 비교·분석하였다.

우선, Table 3에서 분류한 4가지 Case에 대하여 동일한 매개변수 하에 LSTM 모형의 선행시간별 수위 예측을 수행하였으며 예측된 수위를 정량적으로 평가하기 위해 MAE, RMSE 및 NSE를 산정하고 Table 4에 나타내었다.

Table 4와 같이 Case 1부터 4까지 MAE는 0.09 m~0.117 m, RMSE는 0.019 m~0.196 m 그리고 NSE는 0.852~0.999로 안정적으로 예측하는 것을 볼 수 있으며, LSTM 모형의 예측 선행시간이 길어질수록 전반적으로 정확도는 낮아지고 있는 것으로 나타났다. 그중 1시간과 3시간의 예측 결과는 MAE, RMSE 및 NSE 모두 낮은 오차를 보이고 예측 정확도는 매우 우수한 것으로 분석되었다.

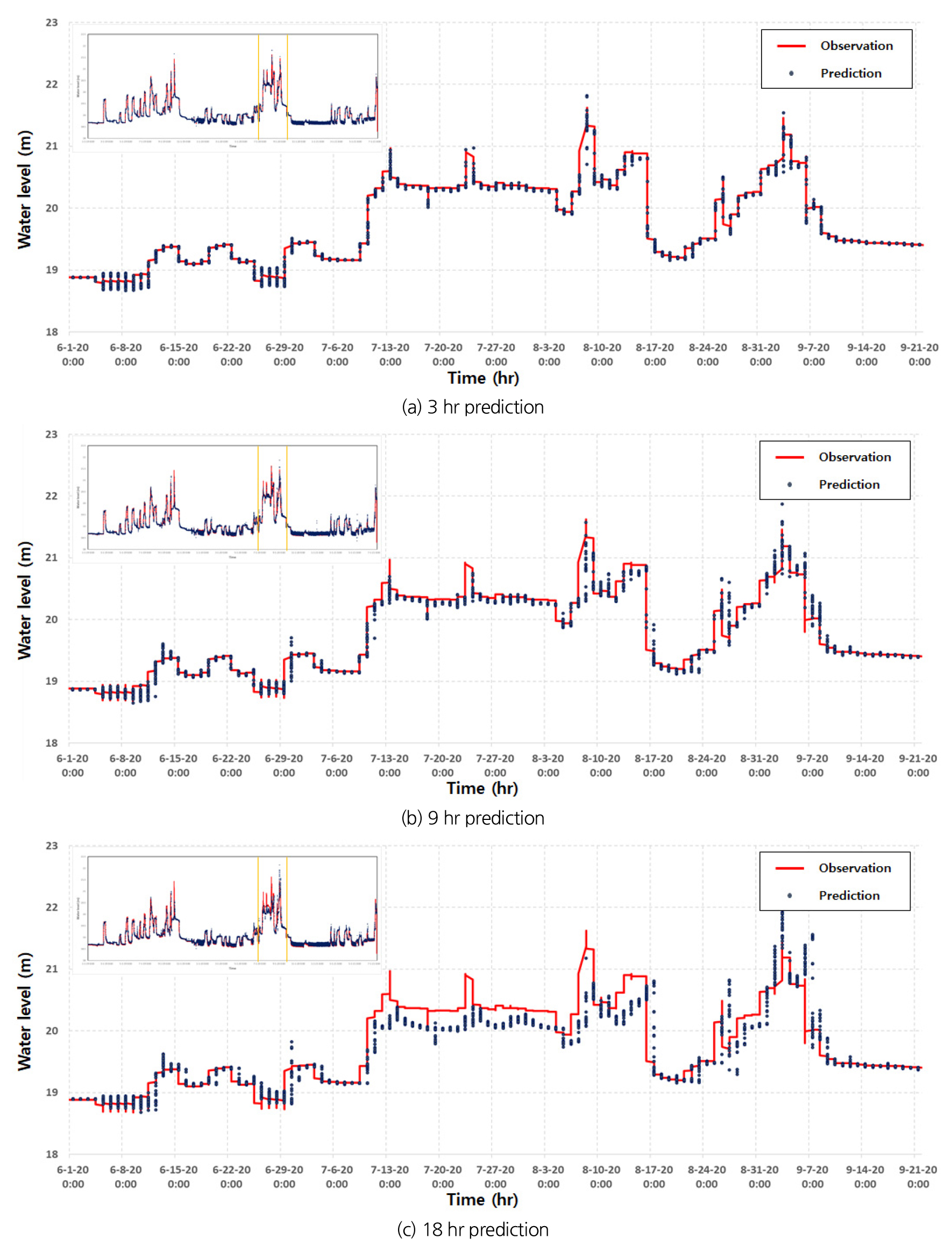
또한 Table 4에서 분석한 시나리오 중 가장 정확도가 높은 Case 2의 시나리오를 선정하여, 선행시간 3시간, 9시간, 18시간의 예측 결과 그래프를 Fig. 5에 도시하였다. Fig. 5를 보면 LSTM 모형은 댐 운영규칙에 따른 일정 방류량에 의한 수위 변화도 매우 안정적으로 예측하는 것으로 분석되었다. 특히, LSTM 모형은 해당 사상의 첨두수위 뿐만 아니라 저수위에 대해서도 관측 수위와의 오차가 크게 발생하지 않고 비교적 높은 정확도를 나타내고 있다. 다만, 선행시간이 길어질수록 관측 수위의 시간적 패턴은 유사하게 모의하고 있으나, Fig. 5(c)와 같이 고수위에서는 예측 수위가 과소 추정하는 것을 확인할 수 있으며 최대 오차는 1 m 이내인 것으로 분석되었다.

추가적으로, LSTM 모형의 매개변수 변화에 따른 예측정확도 분석을 진행하였으며, 그 결과는 Table 5와 같다. Table 5에서 num_unit는 2가지(16, 32) 경우, batch_size는 4가지(16, 32, 64, 128) 경우로 구분하고 선행시간별 8개의 예측 결과를 검증 기간과 예측 기간으로 나누어 정량적으로 도시하였다. 먼저, 검증 기간과 예측 기간의 모의 결과를 비교하면 시험 기간의 예측 정확도가 비슷하거나 선행시간에 따라 근소한 차이로 산정되었다. 이는 LSTM 모형의 학습이 성공적으로 수행되었으며 학습 자료에 과적합되지 않고 예측 자료에 대해서도 안정적인 결과를 제공하였음을 나타낸다.

Fig. 5.

Comparison of water level for the specific rainfall events in case 2

또한 개별 모형의 결과마다 반복횟수(num_epoch)가 다른 것은 전술한 early_stopping 기능에 의한 최적 반복횟수로 설정된 것이며 유닛의 수(num_unit) 매개변수에 따른 예측 정확도의 차이는 미미한 것으로 분석되었다. 그리고 긴급하게 댐 방류량을 결정해야 하는 상황의 경우, 모형의 구동(학습 및 예측)시간 또한 모형 선택에 있어 매우 중요한 인자이다. batch_size와 선행시간에 따라 모형의 학습에 걸리는 시간은 다르게 측정되었으며, 예측 선행시간에 따라 짧게는 약 2분(1시간 예측)에서 길게는 약 20분(18시간 예측)으로 측정되었다. 하지만 사용자의 프로그래밍 기술(병렬처리 등) 및 가용한 컴퓨팅 자원의 용량과 기술 수준에 따라 단축시킬 수 있으며, 딥러닝 기술의 핵심은 학습된 모형을 저장하여 예측이 필요한 자료가 모형에 입력될 시 저장된 모형은 추가적인 학습 없이 바로 예측값을 추정할 수 있는 장점이 있다.

결론적으로 LSTM 모형은 댐의 다양한 운영규칙 조건에서 댐 하류 수위를 정확하게 예측할 수 있음을 보여주었다. 또한, 안정성 및 계산속도의 측면에서 상당한 이점이 있고, 강력한 시계열 예측 능력을 가지고 있어 기학습된 LSTM 모형을 이용하여 사전에 방류량에 대한 직하류 영향성 검토 등이 가능하므로 현재 시범 운영 중인 수문방류예고제와 같은 댐 운영 모의에 있어 매우 유용할 것으로 판단된다.

5. 결 론

본 연구는 딥러닝 기반의 LSTM 모형을 활용하여 댐 직하류 수위관측소의 수위를 각 선행시간별로 예측하고, 예측되는 수위 자료를 활용하여 댐 방류량 결정 시 딥러닝 기술의 활용 가능성을 평가하고자 한다. 남강댐을 대상으로 LSTM 모형을 적용하였으며, 모형의 학습과 검증, 예측에 사용된 기초자료로 댐 수위, 유역 면적평균강우량, 댐 유입량, 발전 방류량, 여수로 방류량, 진주시 방류량, 장대동 관측소 수위, 덕오리 관측소 수위까지 총 8개의 시 단위 자료를 수집하였으며 남강댐 직하류에 위치한 장대동 관측소의 수위를 예측하고 결과에 대한 비교·분석을 수행한 후, 다음과 같은 결론을 도출하였다.

Case 1부터 4의 예측 결과 최적의 성능을 내는 결과는 기초자료로 발전 방류량과 여수로 방류량을 제외한 나머지 자료를 활용하여 LSTM 모형을 학습하는 것으로 분석되었으며, 선행시간 1시간에 대한 평균 예측 결과는 MAE는 0.010 m, RMSE는 0.015 m, NSE는 0.999로 이는 관측 수위와 매우 근접한 예측 결과를 도출하였다. 반면에 선행시간이 길어질수록 그 예측 정확도는 저수위 흐름에서는 비교적 안정적이나 고수위 흐름에서는 첨두 수위와의 오차가 증가하는 것으로 분석되었다. 하지만 Fig. 5(c)의 18시간 예측의 결과에서도 관측 수위의 시간적 패턴을 유사하게 추정하므로, 여러 선행시간별 예측 결과를 기반으로 댐 방류량 의사 결정 시에 활용 가능할 것으로 판단된다.

또한 LSTM 모형의 매개변수에 따른 선행시간별 8개의 예측 결과를 검증 기간과 예측 기간으로 나누어 정량적으로 분석한 결과, 예측 기간의 오차가 검증 기간의 오차와 비교하여 미세하게 과소추정되거나 유사하게 산정되었다. 이는 구축된 모형이 학습 자료에 과적합되지 않고 추가적으로 입력되는 자료에 대해 안정적인 예측값을 제공할 수 있을 것으로 판단된다.

결론적으로, 딥러닝 기반의 LSTM 모형은 댐 운영과 같이 인위적인 운영규칙이 반영되었을 경우에도 안정적인 결과를 제공해줄 수 있으며, 전처리된 가용한 모든 자료들을 학습 후 기학습된 모형을 이용하여 새로운 입력자료가 주어졌을 때 빠른 속도로 안정적인 댐하류 수위 예측 정보를 생산할 수 있다. 즉, 댐의 비상 운영 시 운영자가 기존의 댐 운영 모형과 연계하여 정보를 생산하고 의사결정을 함으로써 댐 하류지역 홍수피해 예방을 위한 24시간 전 수문방류예고제와 같은 재해관리 측면에서 보조적 수단으로 활용이 가능할 것으로 판단된다.

본 연구에서 활용한 LSTM 모형 이외에도 AI 기반 딥러닝 기술은 빠른 속도로 발전하고 있으며, 비선형의 복잡한 자연계 특성을 추출하여 예측 모형을 생성함으로써 댐 운영 모의뿐만 아니라 수자원 분야에서 실행 가능한 효율적인 옵션으로 활용될 수 있다. 더욱이 수자원 분야에서의 딥러닝 기술 확대와 활용성 증가를 위해서는 수자원 데이터의 표준화 및 접근성을 획기적으로 증대할 수 있는 방안을 고려하는 것이 필요하다.