A review of transient storage modeling for analyzing one-dimensional non-fickian solute transport in rivers

Byunguk Kim; Il Won Seo; Jun Song Kim; Hyoseob Noh

doi:10.3741/JKWRA.2024.57.4.263

Preview

Research Article

Journal of Korea Water Resources Association. 30 April 2024. 263-276
https://doi.org/10.3741/JKWRA.2024.57.4.263

A review of transient storage modeling for analyzing one-dimensional non-fickian solute transport in rivers

1차원 Non-Fickian 하천혼합 해석을 위한 하천 저장대 모델링 연구 동향

Byunguk Kim^a

Il Won Seo^b^c

Jun Song Kim^d

Hyoseob Noh^e^*

김 병욱^a

서 일원^b^c

김 준성^d

노 효섭^e^*

^aPh.D. Student, Department of Civil and Environmental Engineering, Seoul National University, Seoul, Korea

^bProfessor Emeritus, Department of Civil and Environmental Engineering, Seoul National University, Seoul, Korea

^cPrincipal Researcher, Institute of Construction and Environmental Engineering, Seoul National University, Seoul, Korea

^dAssistant Professor, Department of Civil and Environmental Engineering, Hankyong National University, Anseong, Korea

^ePostdoctoral Researcher, Institute of Construction and Environmental Engineering, Seoul National University, Seoul, Korea

^a서울대학교 건설환경공학부 박사과정

^b서울대학교 건설환경공학부 명예교수

^c서울대학교 건설환경종합연구소 책임연구원

^d한경대학교 건설환경공학부 조교수

^e서울대학교 건설환경종합연구소 박사후연구원

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by/4.0):

©It is identical to the Creative Commons Attribution Non-commercial License (https://creativecommons.org/licenses/by/4.0)

ABSTRACT

Since the first introduction of one-dimensional transient storage modeling in the field of solute transport analysis in rivers, its application has notably expanded for various purposes, including for hydrology and geobiology over the past few decades. Despite strides in refining transient storage models, there remain unresolved challenges in simplifying complex river transport dynamics into concise formulas and a limited set of parameters. This review paper is dedicated to cataloging and assessing existing transient storage models, outlining the difficulties associated with model structures, parameters, and data, and suggesting directions for future research. We seek to enhance understanding of transient storage by highlighting the importance of continuously evaluating residence time distribution modeling, integrating hydrodynamic models, and using data with minimal assumptions. This paper would contribute to advance our comprehension of the transient storage process, offering insights into sophisticated modeling techniques, pinpointing uncertainty in parameters, and suggesting the necessary avenues for further study.

Keywords

River mixing

Transient storage model

Tracer test

Breakthrough curve

Residence time distribution

지형구조가 복잡한 자연하천에서의 오염물질의 혼합과 이송 현상을 해석하기 위해 개발된 1차원 저장대 모형은 1970년대에 처음으로 제시된 이후 하천 내 오염물질의 정체 현상의 정확한 분석을 목적으로 다양한 형태로 개선되어 왔으며, 지난 수년간 지표수 및 지하수 분야에서 오염물질의 거동 및 체류시간을 예측하는 도구로써 활발히 활용되어 왔다. 그럼에도 불구하고 1차원 저장대 모형은 복잡한 자연하천의 혼합 기작을 제한된 매개변수를 통해 단순화하기 때문에 아직 해결되지 않은 숙제가 남아 있다. 본 리뷰 논문에서는 현재까지 개발된 저장대 모형의 장·단점을 설명하고, 모형의 구조적, 비구조적 불확실성에 대한 문제를 제기하고, 이를 극복하기 위해 필요한 연구의 방향성을 제시하였다. 본 연구 결과, 지속적인 정체시간분포 모델링에 대한 개선, 동수역학 해석 모형과 저장대 모형과의 결합, 그리고 추적자 실험 자료 수집 과정에서 불확도 개선을 통해 저장대 모형의 정확도를 향상시킬 수 있음을 알 수 있다. 모형의 복잡성을 증가시켜 정확도를 강화하는 방안은 지양하여야 하며, 모형 매개변수를 통한 하천의 정체특성 해석에는 수리·지형학적 근거와 추적자 실험 자료와 매개변수 추정 방식의 신뢰성이 함께 제시되어야 한다. 본 연구의 분석 결과와 제언은 저장대 모형을 통한 정밀한 하천 혼합 해석의 향후 연구에 토대가 될 것으로 기대한다.

키워드

하천 혼합

저장대 모형

추적자 실험

모형 매개변수 추정

농도 곡선

체류 시간 분포

MAIN

1. 서 론
2. 하천 저장대 모형의 이론적 배경 및 동향
2.1 하천 저장대 모형의 특성
2.2 하천 저장대모형의 고도화
3. 저장대 모형의 검증 및 매개변수 결정
3.1 저장대 농도자료 계측
3.2 저장대 매개변수 결정 방법
4. 하천 저장대 모델의 전망
5. 결 론

1. 서 론

하천 혼합 모형중에서 가장 기초적인 1차원 모형은 하천의 평균 유속에 의해 이송하고 난류 및 전단류에 의해 물질이 확산되는 혼합거동은 Fick의 법칙을 기반으로 해석하는 1차원 이송-분산 모형(One-Dimensional Advection Dispersion Equation, 1D ADE)이다(Elder, 1959). 하지만, 실제 하천에 유입된 물질의 거동을 살펴보면 여울 및 웅덩이, 식생, 수공 구조물, 하상재료 등의 정체영역에 의해 물질의 일부가 지체되는 현상이 강하게 나타나며(Fig. 1), 그 결과 오염운의 형태가 긴 꼬리를 가지는 것으로 관측된다(Kwon et al., 2021; Park and Seo, 2018). 이러한 정체현상을 야기하는 다양한 크기와 특징을 갖는 하천 내 정체영역 및 구조를 저장대(storage zone)라고 한다. 저장대의 영향을 받은 물질의 시계열 농도 자료는 음의 방향으로 왜곡되는 non-Fickian 거동이 나타나는데 이는 1D ADE로는 정확한 재현이 불가능하다. 이를 극복하고자 저장대 효과를 고려한 1차원 저장대 모형이 Thackston and Schnelle (1970)에 의해 처음으로 제시되었으며, Bencala and Walters (1983)와 Bencala (1983)에 의하여 단기 저장대 모형(Transient Storage Model, TSM)으로 발전되었다. 그들은 자연하천은 단조로운 하나의 개수로가 아니며 다양한 수리·지형학적 구조를 가진 저장대를 내포하고 있기 때문에 정확한 혼합해석을 위해서는 이러한 저장대 메커니즘을 고려해야 함을 강조하였다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-04/N020057403/images/kwra_57_04_03_F1.jpg

Fig. 1.

Various storage zones in a natural stream

하천에서의 오염물질 혼합에 대한 이해는 하천공학자가 끊임없이 해결하고자 하는 숙제이다. 그동안 많은 연구에서 하천 흐름내에서 수동적으로 거동하는 물질(passive scalar)을 추적함으로써 장구간의 하천에서 1차원적인 용존 물질의 확산과 희석, 그리고 최종 귀착(fate)에 대한 이해와 예측을 시도하였다(ASCE Task Committee on Hydraulic Engineering Advocacy, 1996). 특히, 최근 연구들은 하천 흐름과 하도의 물질 교환, 물질 고유의 반응성 등 추적자 물질 이송에 미치는 다양한 수리환경적 요인을 고려하는 연구가 활발하게 수행되고 있으며, 이러한 하천에서의 오염물질 확산 해석에 있어 1차원 저장대 모형의 중요성이 강조되고 있다(Knapp and Kelleher, 2020).

TSM은 지난 40년동안 수많은 실제 하천 현장에 적용되어 타당성이 입증되었으며, TSM 매개변수는 하천의 대상 구간이 갖는 정체현상의 정도를 정량적으로 나타내는 수단으로 활용되어 왔다. 나아가서 TSM을 이용한 하천 혼합 해석, TSM 지배방정식의 개선, 매개변수 결정 방법론, 복합 기작을 고려한 고도화 등이 다양한 분야에서 활발히 연구가 이루어지고 있다. 본 논문에서는 1차원 저장대 모형이 활용된 지난 40년 동안의 연구결과가 하천 혼합에 대한 이해를 어떻게 증진시켰는지에 대해 분석하였다. 여러가지 형태로 제안된 저장대 모형의 장단점을 설명하고, 모형의 구조적, 비구조적 불확실성에 대한 문제를 분석하고, 이를 극복하기 위해 필요한 향후 연구의 방향성을 제시하였다.

2. 하천 저장대 모형의 이론적 배경 및 동향

2.1 하천 저장대 모형의 특성

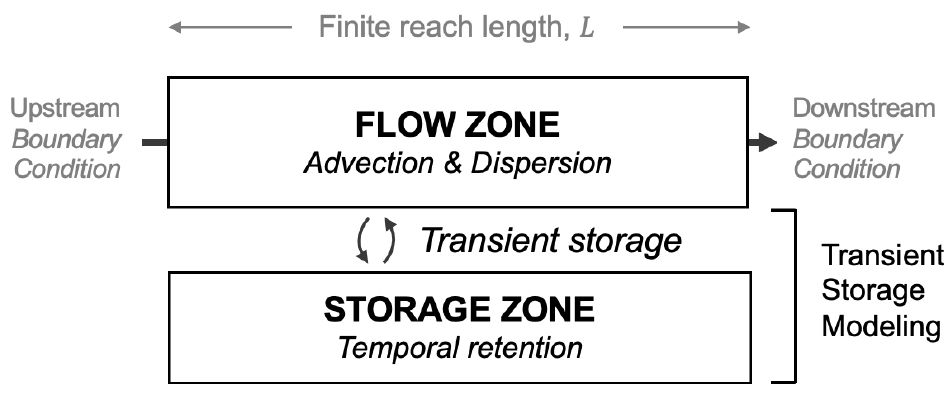
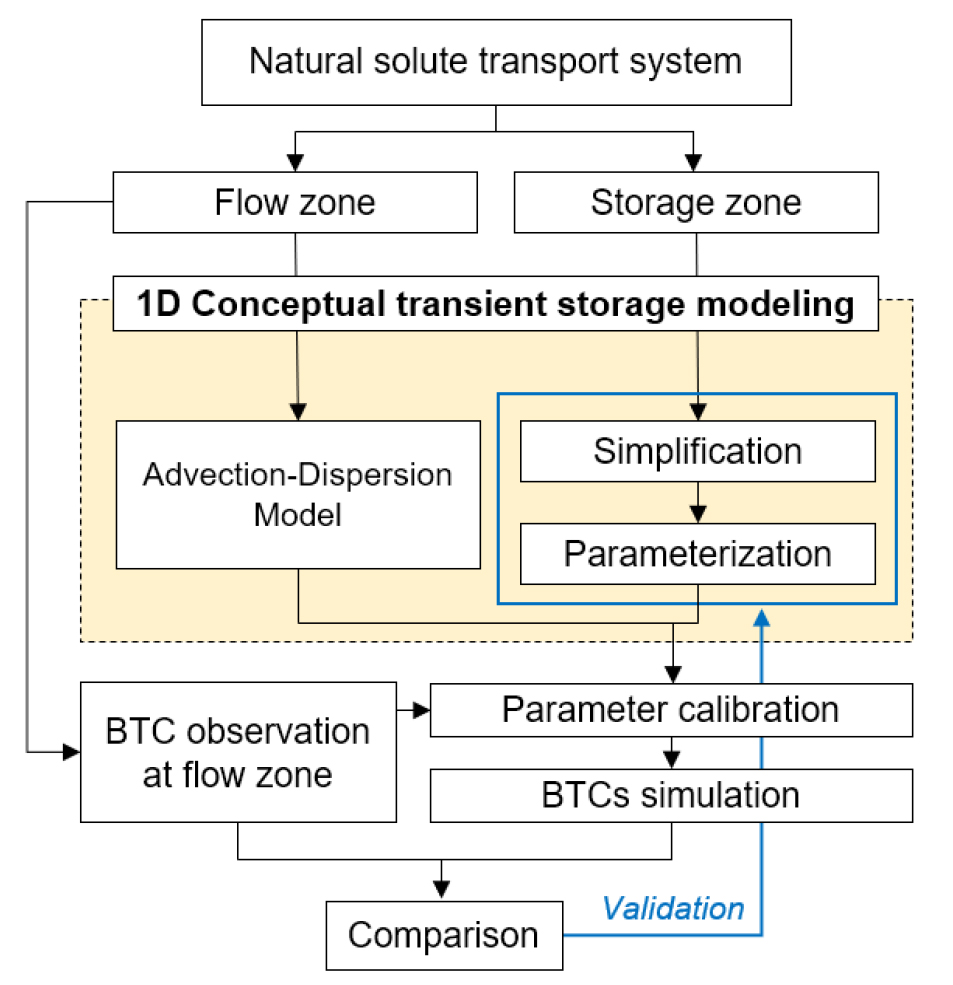
Fig. 2는 일반적인 저장대 모형의 개념도를 나타낸다. 저장대 모형에서는 자연하천의 1차원 물질 이송 과정에서 흐름영역 혹은 본류대(flow zone)에서의 혼합 현상뿐만 아니라, 흐름이 느리거나 정체된 저장대 영역과의 물질 교환 현상이 추가로 고려된다. 흐름 영역에서 물질의 이송은 보편적인 1차원 이송-분산 방정식으로 해석되며, 저장대 영역에서는 이송 메커니즘 없이 확산만을 고려한다. 여기에 추가하여 본류대와 저장대간의 물질 교환을 고려하는데, 이를 해석하기 위한 다양한 현상학적 모형이 정체현상의 시공간 스케일의 기하학적․운동학적 매개변수와 함께 제시되고 있다(Bencala and Walters, 1983). 하지만, 단순화된 매개변수와 달리 실제 자연하천의 정체 현상은 시공간적으로 매우 이질적(heterogeneous)이고 변칙적(anomalous)이다(Yeh et al., 2015). 또한 모래와 자갈 하천의 경우, 하상혼합대(hyporheic zone)로 불리는 하상간극수역에서 발생하는 하도와 하상 간의 물질교환 현상은 육안으로 확인하기 어렵기 때문에, 해당 과정을 직접 관측하기 어려우며 해석적인 접근법은 과도한 가정을 필요로 한다(Choi et al., 2000a). 이에 따라 경험적인 방법으로 주 흐름영역인 본류대에서의 추적자 실험(tracer test)을 통해 취득한 자료를 기반으로 저장대 모형의 매개변수를 결정하고 모델링하는 방식에 의존하고 있다(Tsai et al., 2022). 즉, 저장대 모델링은 Fig. 3와 도시한 바와 같이 본류대에서 추적자의 거동에 최적화된 매개변수를 기반으로 산출된 모의 정확도로 타당성이 입증되고 있다(Kim et al., 2023a).

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-04/N020057403/images/kwra_57_04_03_F2.jpg

Fig. 2.

Schematic of 1D transient stroage models

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-04/N020057403/images/kwra_57_04_03_F3.jpg

Fig. 3.

Process of typical 1D conceptual transient storage modeling

전술한 바와 같이 1차원 저장대 모형은 흐름영역에서 하천의 평균 흐름에 의해 이송되고, 전단류에 의해 물질이 분산되는 가우시안 형태의 혼합 거동을 나타내는 질량 보존 방정식에 저장대와의 물질 교환을 재현하기 위한 생성․소멸 항이 추가된 형태이다. 단기 저장대 모형(TSM)의 지배방정식은 Haggerty et al. (2000)의 일반식을 참고하여 Eq. (1)과 같이 표현할 수 있다.

(1)

\frac{\partial c}{\partial t} = \frac{\partial}{\partial x} (- U c + K \frac{\partial c}{\partial x}) + Γ (x, t)

여기서, c(ML^-3)는 단면 평균 농도, U(LT^-1)는 단면 평균 유속, K(L²T^-1)은 종분산계수, 그리고 𝛤(ML^-3T^-1)는 생성․소멸 항이다. 본 논문에서는 상류에서 유입된 물질이 일정 거리의 하천 구간을 유하하며 발생하는 혼합 기작을 해석하는 문제 중에서 균일 농도 주입 초기조건 $c (x, t = 0) = c_{0}$ 에 대하여 검토하였다. 물질이 초기에 일정 거리 L의 하천구간에 유입되어 본류대에서 높은 농도를 보이는 초기 구간 $t ≪ L ⁄ U$ 에서는 $Γ < 0$ 으로 본류대의 농도가 감소하고, 이후 본류대에서의 농도가 일정 농도 이하로 떨어지는 후기 구간 $t ≫ L ⁄ U$ 에서는 $Γ > 0$ 로 저장대의 지체효과의 정도에 따라 본류대의 농도가 서서히 증가한다.

TSM은 $Γ (t)$ 를 저장대에서의 평균 농도 $c_{s}$ 와 본류대 농도와의 차이에 선형적으로 비례한다고 가정하고, 비례상수로서 물질교환계수 α를 도입하여 Eq. (2)와 같이 단순한 형태로 나타낸다.

(2a)

Γ (t) = α (c_{s} - c)

(2b)

\frac{\partial c_{s}}{\partial t} = \frac{α}{ϵ} (c - c_{s})

여기서, ε는 본류대에 대한 저장대 영역의 부피 비이다. 상기의 모델링은 저장대에서의 물질은 완전 혼합 상태이고, 물질 교환 속도는 균질(homogeneous)하여 단일 α로 대표될 수 있으며, 하천 전역에 걸쳐 ε가 일정(uniform)하다는 가정을 필요로 한다. TSM 모형에 포함되어 있는 매개변수 α와 ε을 통하여 하천구간이 갖고 있는 평균적인 정체 특성을 정량적으로 나타낼 수 있지만(Ward et al., 2017), 복잡한 하천 특성을 과도하게 단순화했다는 측면에서 매개변수가 갖는 물리적 의미에 대해서는 논쟁의 여지가 있다(Knapp and Kelleher, 2020).

선형적인 물질 교환 문제에 대해 더 편리하고 일반적인 해석으로, Eq. (3)과 같이 단일 물질교환계수를 가정하지 않고 흔히 기억함수(memory function)로 불리는 전달함수(transfer function)와의 합성곱(convolution) 형태로 나타낼 수 있다. Haggerty et al. (2000)가 제시한 일반적 모형인 Multi-rate Mass Transfer (MRMT) 모델에서의 𝛤의 형태는 Eq. (3)과 같다.

(3)

Γ (t) = \int \frac{\partial c (t - τ)}{\partial τ} g (τ) d τ = \frac{\partial c}{\partial t} * g

여기서, $g$ (T^-1)는 기억함수로 물질이 저장대에 갇힌 이후 다시 본류대로 나오기까지 소요되는 정체시간의 확률밀도함수를 의미하며, 이후 정체시간분포(retention time distribution)라고 칭한다. τ는 합성곱 연산을 위한 시간 스케일의 가변수이며, *는 합성곱 연산을 나타낸다. TSM은 기억함수 $g$ 가 지수함수 형태를 갖는 경우이다(Kim et al., 2021b). 지수함수 형태의 기억함수에 기반한 TSM은 체류시간이 짧은 경우에는 정확한 정체 현상 모의를 보이는 반면에, 일반적인 하천에서는 체류시간이 길기 때문에 정체현상을 일관되게 과소평가하는 경향을 보이는 것으로 알려져 있다(Marion and Zaramella, 2005). 이에 따라서 강한 정체현상으로 인한 오염물질의 시간-농도 곡선(breakthrough curve, BTC)의 꼬리 부분의 확장과 상대적 고농도 발생으로 대변되는 두꺼운 꼬리(late-time tailing) 현상을 더욱 정확하게 모의하기 위해 로그정규 분포, 멱함수 분포, 감마 분포 등 다양한 기억함수 형태가 제시되고 있다(Haggerty et al., 2000).

전술된 바와 같이 Eq. (3)의 기억함수를 모델링하는 것을 넘어서, 새로운 형태의 지배방정식 또한 제시되고 있다. Boano et al. (2007)은 연속시간 랜덤워크(Continuous Time Random Walk, CTRW) 이론을 접목하여 이와 유사한 구조를 갖는 모형을 Eq. (4)와 같이 제시하고, 멱함수 형태의 정체시간분포를 적용하여 모형의 타당성을 입증한 바 있다. 이는, Eq. (3)과 마찬가지로 다양한 기억함수를 허용하여 넓은 영역의 시간 스케일의 정체현상을 해석할 수 있는 장점이 있다.

(4)

\frac{\partial c (t; x)}{\partial t} = \int_{0}^{t} g (t - τ) (- U \frac{\partial c (τ; x)}{\partial x} + K \frac{\partial^{2} c (τ; x)}{\partial x^{2}}) d τ

Advective Storage Path (ASP) 모형(Wörman et al., 2002)은 하천의 흐름영역과 하상간극수역 경계층에서 발생하는 물질교환 현상을 고려하기 위하여 𝛤에 불규칙한 하상을 따라 흐르는 흐름에 의해 발생한 하천 바닥면의 압력 차로 의한 혼합대 물질교환(hyporheic exchange) 현상을 이송 펌핑 이론(Elliott and Brooks, 1997)을 적용하여 표현하였다. 그래서 이러한 항에 본류대와 저장대 간의 물질교환 기작에 하상의 지형과 흐름 조건의 영향을 반영하고자 하였다.

Fractional Advection-Dispersion Equation (FRADE) 모형(Deng et al., 2004)의 경우, 자연하천의 이질적인 특성을 반영하고자 Fick의 법칙에 기반한 확산항의 차수(fractional power)를 모수화하여 아래와 같이 제시되었다.

(5)

\frac{\partial c}{\partial t} + U \frac{\partial c}{\partial x} = K_{F} \frac{\partial^{F} c}{\partial x^{F}}

여기서 $F$ 는 ‘Fractor’라고 칭하는데, 자연하천의 이질적인 특성으로 인해 $F$ 를 2로 고정하지 않고 하천구간에 따라 변화하는 것으로 제안하였다. FRADE 모형은 분수차 미적분을 도입하여 분산 항에 작용하는 편미분 연산자의 분수 차수를 경험적 데이터에 기반하여 조정함으로써 자연하천에서 관찰되는 긴 꼬리의 BTC로 대표되는 non-Fickian 혼합 과정을 보다 정확하게 모의한다. 이 모형의 장점 중 하나는 자연하천의 지형적 복잡성에 따른 이질적인 특성을 고려할 수 있다는 것이며, 해석해를 유도하기 어렵다는 단점이 있다.

두 개의 서로 다른 정체시간분포 함수를 합성곱으로 연산하는 Solute Transport in River (STIR) 모형(Marion et al., 2008; Marion and Zaramella, 2005)은 하천 표면흐름의 재순환(recirculation) 영역(Shin et al., 2023) 등 상대적으로 짧은 체류시간을 갖는 저장대를 위한 지수함수 형태의 기억함수와 긴 체류시간을 갖는 하상간극수역과의 물질 교환을 위한 이송-펌핑 모형을 확률론적 접근법으로 동시에 적용시킨 모형으로, 이렇게 함으로써 모의 정확도를 증진시킨 것으로 평가되고 있다.

전술한 모형의 특징을 Table 1에 요약하였다. 상술한 방법의 공통의 목표는 BTC의 꼬리 거동을 정확하게 재현하는 것이다. 하지만 Fig. 1에 도시한 바와 같이 저장대의 종류와 형태에 따라 체류시간의 스케일이 다르며(Boano et al., 2014), 지역적 특성이 강하기 때문에 BTC의 꼬리부 예측에 가장 강건하다고 평가되는 전역적인 모형은 아직까지 제시된 바가 없다.

Table 1.

Features of existing transient storage models

Model	First release	Key focus	Pros	Cons
TSM	1983	Mass transport in pool-and-ripple stream	Widely applied, simple conceptualization	Simplification of physical processes, parameter uncertainty, limited for fast storage zone
MRMT	2000	Late-time behavior of tracer breakthrough curves	Provides insights into rate-limited mass transfer and tracer test interpretation	Requires detailed understanding of underlying processes for interpretation
FRADE	2004	Long-tailed dispersion processes	Accurately simulates long-tailed dispersion, adaptable	Difficult in analytical interpretation
STIR	2005	Interactions with multiple storage zones	Physically based, flexible and modular	Complexity and, parameter uncertainty
CTRW	2007	Hyporheic exchange	Applicable for wide range of retention time scale	Complexity and, parameter uncertainty

2.2 하천 저장대모형의 고도화

최근 저장대 모형의 개발 방향성 중 하나는, 모형의 복잡성을 증대시켜 하천에서 발생하는 물질 이송과 관련된 다양한 물리현상들을 반영하려는 노력이다. 예를 들어, 자연하천에 존재하는 저장대의 공간적 이질성(heterogeneous)을 고려하여 두개 이상의 정체시간분포 모형을 적용하여 정확도를 증대시킬 수 있다. 대표적으로 빠른 교환 영역(빠른 저장대)과 느린 교환 영역(느린 저장대)으로 구분하는 방식이며, 이 방식에서는 Eq. (1)의 지배방정식에 Eq. (2)의 형태를 갖는 두개의 생성-소멸항을 추가하고 저장대별로 서로 다른 매개변수를 적용하거나(Briggs et al., 2009; Choi et al., 2000b), 서로 다른 두개의 기억함수를 적용하는 방식이다(Zaramella et al., 2016; Marion et al., 2008). 두 가지의 접근 방식의 차이는 유연성과 적용성에서 서로 다른 특징을 보인다. 첫번째 방식은 단순히 단일 저장대를 두 영역으로 확장하여 간결함을 유지하되 정확도를 향상할 수 있으며, 이를 통해 정체 시스템을 충분히 설명할 수 있는 경우에 적합하다. 반면에 서로 다른 기억함수를 사용하는 두번째 방식의 경우, 다양한 정체시간 스케일을 반영할 수 있는 유연성과 더 높은 정확도를 보일 수 있지만, 근본적인 패턴뿐만 아니라 노이즈까지도 포착하는 과적합(overfitting)으로 인해 최적화된 모형은 일반성을 잃기 쉽고, 최적화된 매개변수의 물리적 의미가 모호해질 우려가 있다. 결국, 연구 대상의 구체적인 요구와 대상지 특성에 따라 적절한 모형을 활용해야 한다.

저장대 모형을 고도화하여 반응성 용존 물질의 혼합 거동을 해석하고자 하는 모형 또한 지속적으로 개발되어 왔다. Gooseff et al. (2005)는 흡착으로 인한 질량 손실을 모형에 반영하였으며, Liao et al. (2013)은 보존성 추적자와 선형 감쇠 추적자의 BTC 분석을 위한 수학식을 제시하였다. Bottacin-Busolin et al. (2021)은 두 개의 저장대 모형을 고려한 STIR 모형의 지배방정식을 반응성 추적자(reactive tracer)에 대한 모형으로 고도화하였다. Runkel (1998)은 TSM 모형에 흡착성과 선형 감쇠항을 추가한 모형을 제안하였고, Kim et al. (2021a)은 이를 고도화하여 물질 고유의 휘발성, 흡착성, 생분해성을 모두 고려할 수 있는 모형을 개발하였으며, 이를 활용하여 톨루엔, 벤젠과 같은 독성 물질에 대한 모의를 수행하였다.

상기의 연구들을 통하여 실제 하천에서의 혼합 기작에 더욱 근접하게 모의할 수 있다는 장점이 있지만, 모형의 복잡성을 증가시킬 수 있다는 단점을 유의하여야 한다. 특히, 저장대 모형을 활용한 모의에서 가장 큰 불확도는 매개변수 결정에서 기인되는 만큼, 추정해야 하는 매개변수 수의 증가는 모의 결과의 정확도는 높일 수 있으나 모형의 신뢰성을 낮출 우려가 있다. 더욱이, 독립적인 물리적 기작을 내포하는 매개변수의 결정을 최적화 방법에 의존하는 저장대 모형에서 매개변수의 증가는 과적합(overfitting)을 초래할 수 있으며, 이 경우 결정된 매개변수의 의미가 모호할 수 있다. 이에 대한 대안으로 Kim et al. (2022)는 물질의 유하거리만으로 BTC의 시공간적 변화를 예측할 수 있는 방법을 제시하고 TSM 모형을 활용한 예측과 비교하여, 단순한 형태의 모형이 더 높은 예측 정확도를 보일 수 있음을 제시하기도 하였다. 즉, 모형의 복잡성과 신뢰성을 모두 고려하여 복잡함과 간결함 간의 균형을 찾거나, 모형의 차원(dimensionality)을 증가시키기 위해서는 저장대 매개변수 결정에서의 불확실성을 충분히 최소화한 신뢰성 확보가 선행되어야 한다.

3. 저장대 모형의 검증 및 매개변수 결정

3.1 저장대 농도자료 계측

전술한 바와 같이 다양한 형태의 정체시간분포 모형이 제시되어 왔는데, 자연하천에서의 저장대는 그 형태와 규모가 다양하고, 흐름영역과의 경계가 모호하며, 저장대 내의 완전 혼합이 보장되지 않고, 일부 형태의 저장대는 가시성과 접근성이 낮아 정체시간분포를 실측하여 모형을 검증하는 것은 어렵다. 이에 따라 정체시간분포 모델링의 타당성은 본류대에서 관측한 추적자의 거동을 통하여 본류대에서의 모의 결과와 비교함으로써 간접적으로 평가하는 것이 일반적이다. 특히, 저장대에 의한 정체현상의 시간 스케일은 본류대에서 일어나는 혼합 메커니즘의 시간 스케일보다 길기 때문에 Fig. 4의 추적자 실험에서 나타난 바와 같이 추적자 운(tracer cloud)이 긴 꼬리를 갖고 추적자의 BTC가 왜곡된다(Kim et al., 2020). 왜곡된 추적자 운의 형태는 고정된 지점에서 측정한 추적자 농도의 시계열 자료로부터 관측될 수 있으며(Haggerty et al., 2000), BTC의 꼬리부를 얼마나 정확히 재현하는지를 통해 저장대 모델링의 정확도를 평가한다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-04/N020057403/images/kwra_57_04_03_F4.jpg

Fig. 4.

Tracer cloud shape flowing along a river channel at Gam Creek, South Korea

일부 연구에서는 저장대 내에서 추적자의 정체현상을 실험적으로 계측하고자 하였다. Weitbrecht et al. (2008)은 수제(groin)가 설치된 인공 수로에서 수제의 기하학적 특성과 경사각에 따른 흐름과 추적자의 정체현상을 조사하였으며, Mignot et al. (2017)에서는 측벽 캐비티(lateral cavity)가 설치된 인공 수로에서의 흐름과 추적자의 정체현상을 조사하여, 캐비티의 수평적 특성보다 수심과 레이놀즈수가 본류대와 저장대 간의 물질교환계수에 더 큰 영향을 미침을 밝혔다. 최근에 Jung and Seo (2021)은 노치형 위어(notched weir)에 대한 실험실 수로 실험을 수행하여 물질교환계수를 분석한 결과, 수제나 캐비티에 의한 저장대의 물질교환계수보다 10배정도 크게 나타나는 것으로 보고하였다. 그는 실험에서 추적자를 저장대 내에 주입하고 시간에 따른 저장대에서의 농도 변화를 직접 측정하여 물질교환계수를 산정하였다. 상술한 실험실 수로 실험에서는 우선적으로 유속장을 측정하여 저장대 영역을 선정하고 이후 추적자 실험을 수행하였기에 저장대 내에서의 추적자의 정체특성을 직접 분석할 수 있는 것으로 판단된다.

자연하천에서는 실험실 수로와 달리 저장대를 판별하기 어렵기 때문에 저장대에서의 농도를 측정하는 것이 매우 어려우나, NaCl 등의 추적자를 주입하고 수표면에서 확인할 수 있는 정체영역에서 체류 현상을 계측하고자 하는 연구가 수행된 바 있다(Gooseff et al., 2011; Jackson et al., 2012; Sandoval et al., 2019). 이러한 연구는 특정 형태의 저장대 영역에서 물질의 정체 현상에 대한 이해를 높이지만, 그들의 연구는 제한된 시공간적 스케일과 조사 가능한 표면에서의 저장대 형태에 제한되기 때문에, 일반적인 하천의 장구간 규모(reach-scale)의 정체현상에 대한 해석으로 확장하기에는 한계가 있다.

전술한 이유 때문에 저장대에서의 정체현상에 관한 연구는 주로 본류대에서 측정한 추적자의 거동으로부터 저장대의 정체특성을 역으로 추정하는 방향으로 수행되고 있다. 이를 위한 최근의 해석방법 중, 합성곱으로 연산되는 저장대 모형을 기반으로 역합성곱(deconvolution) 기법을 적용한 정체시간분포의 자료 기반 모델링이 수행되었다. 역합성곱 기법은 관측된 신호로부터 알고 있는 성분을 제외하여 신호에 내재되어 있는 숨겨진 정보를 추출하는데 활용된다(Krishnan and Fergus, 2009; Kundur et al., 1996). Payn et al. (2008)은 상류 및 하류의 경계에서 측정된 BTC를 이용하여 구간 전체에서의 체류시간분포를 산정하여 비모수적 모델링을 수행하였는데, 자연하천의 흐름과 지형학적 복잡성에서 기인하는 높은 주파수의 농도 변동성으로 인해 직접적인 합성곱 모형의 역산은 불가능하여 통계학적 역산의 대안을 적용하였다. 이후, 최대 엔트로피 역합성곱(maximum entropy deconvolution) 기법(Guymer and Stovin, 2011; Sonnenwald et al., 2014)이나, 필터링 기법을 접목한 역합성곱 기법(Gooseff et al., 2011; Kim et al., 2023b)이 제시된 바 있다. 이러한 역합성곱 기법은 엄격한 핵심 조건이 요구되는데, 저장대 효과가 내포된 본류대에서의 추적자 BTC로부터 효과적으로 저장대에서의 정체시간분포가 분리되어야 하며, 고주파 신호 차단으로 수반되는 데이터의 왜곡의 정도가 허용가능한 수준이여야 한다. 또한, 푸리에 급수에서 처리되는 역합성곱 프로세스는 유한하고 주기적이지 않은 농도곡선을 근사하는 과정에서 왜곡되는 깁스 현상(Gibbs phenomenon)(Duchon, 1979)에 취약하며 이를 최소화하여야 한다. 다만, 잡음(noise)이 있는 데이터로부터 이러한 조건을 모두 만족시키기 어려운 한계가 있다.

3.2 저장대 매개변수 결정 방법

전술한 바와 같이, 저장대 모형의 범용적 활용성에서 불구하고, 현상학적 모델링의 산물인 하천 저장대 모형의 매개변수는 직접 계측이 거의 불가능하다. 저장대의 형태가 다양하고 경계가 모호하여 저장대의 크기를 측정하기 어렵고, 본류대와 저장대간의 물질 교환을 정량적으로 관측할 수 없기 때문이다. 이에 따라서 가장 일반적이고 현실적인 대안은 추적자 실험을 통하여 본류대에서 취득한 농도자료에 저장대 모형을 적용하여 최적의 저장대 매개변수를 찾는 방법이다. 추적자 실험을 통하여 대상 구간에서 변화하는 추적자의 BTC 변화를 관측하고, 이를 가장 정확하게 모의할 수 있는 매개변수를 역으로 찾아내는 경험적 방식이다.

대표적인 역산모형(inverse model)으로는 미국의 USGS에서 개발한 OTIS-P (Runkel, 1998)가 있는데, 이 모형에서는 비선형 최소자승법을 이용해 TSM의 매개변수를 최적화 한다. OTIS-P는 매개변수 최적화 과정에서 추출된 매개변수 값들의 표준편차를 제시해줌으로써 불확도에 대한 정보를 제공해주는 장점이 있다. Seo and Cheong (2021)과 Cheong and Seo (2003)은 BTC의 통계학적 모멘트를 목적함수로 설정한 최적화 기법과 오염운 추적법(routing procedure)을 통한 매개변수 산정법을 제안한 바 있다, 최근에는 저장대 매개변수 결정을 위한 다변량 최적화에서 목적함수가 1개 이상의 최적값(Optima)을 갖는 비볼록성(non-convexity) 문제를 해결하기 위하여 Noh et al. (2019)은 전역최적화 기법인 SC-SAHEL을 이용해 매개변수를 결정하는 모형을 개발하고, 저장대 매개변수 평가에 가장 효과적인 알고리즘을 제시하였다. 또한, Ward et al. (2017)은 Monte Carlo 모의를 활용한 매개변수 결정법을 제시하고 민감도를 분석하였으며, Choi et al. (2020)은 BTC의 구간에 따른 불확도 산정 기법을 적용하고 정형 우도(formal likelihood) 기반의 베이지안 추론(Bayesian inference)을 적용하여 불확도를 고려한 매개변수 결정법을 제안했다. 하지만, 이러한 최적의 매개변수를 찾으려는 최근 연구의 노력에도 불구하고 저장대 매개변수 결정의 불확도를 완전히 해소하지 못 하고 있는 실정이다. 일례로, 추적자 운이 하중도나 여러 갈래로 나뉘는 하천 구조에서 발생하는 왜곡된 BTC의 형태는 정확한 매개변수 규명이 어렵다고 보고되었으며(Noh et al., 2021), 본류대-저장대간의 물질교환율(Da_I)이 작은 경우에도 저장대 매개변수의 불확도가 크게 증가할 수 있는 것으로 알려져 있다(Wagner and Harvey, 1997). 여기서 Da_I는 저장대로 인한 교환율과 흐름에 의한 이송율의 비로서 다음 식과 같이 정의된다.

(6)

D a_{I} = \frac{α (1 + \frac{1}{ϵ}) L}{U} .

상기에 서술된 추적자의 거동을 파악하여 저장대 모형의 매개변수를 역으로 추정하는 역산모형 방식의 경우 추적자 실험 자료가 있는 경우에만 적용 가능하다는 한계가 있으며, 이 경우 하천구간이나 흐름특성이 달라진다면 추정된 매개변수를 활용할 수 없는 단점이 있다. 이러한 지역성 문제를 극복하기 위해, 상대적으로 측정하기 용이한 하천의 수리․지형학적 인자로부터 매개변수를 추정하기 위한 경험식이 개발되어 왔다. 초기 연구인 Thackston and Schnelle (1970)에서는 회귀적 접근 방식으로 TSM 매개변수 중 ε과 수리량과의 관계를 찾는데 중점을 두었다. 이와 같이 2000년 이전의 대부분의 저장대 매개변수 연구에서는(Seo and Yu, 2000; Thackston and Schnelle, 1970; Bencala and Walters, 1983) 기존의 ADE 모형에서의 분산계수와 TSM의 분산계수를 동일하다고 가정하여 경험식에 분산계수를 포함하지 않고, 저장대 매개변수인 저장대 비와 물질교환계수(α)에 대한 산정식을 제시하였다. 하지만, 저장대 효과는 기존의 이송-분산 프로세스에 선형적으로 작용하지 않고 분산계수와 종속적인 상관관계를 갖고 있으며, 이에 일반적으로 TSM의 분산계수가 ADE의 분산계수보다 더 낮게 산정되는 경향이 있어, 독립적인 매개변수로 둘 수 없다고 제시되고 있다(Cheong and Seo, 2003). 이는 다수의 선행 연구들을 통해 입증되었으며, 두 모형의 평균 유속은 유사하게 결정될 수 있지만, 분산계수는 저장대의 영향으로 인해 1에서 3 오더까지 차이가 날 수 있다(Deng et al., 2002). Cheong and Seo (2003)에서 흐름특성을 대표할 수 있는 변수로 평균유속과 전단유속 $U_{*}$ 의 비 $U ⁄ U_{*}$ 와 수심대 하폭비를 제시한 이후 매개변수 경험식은 두 무차원수를 입력변수로 포함하여 제시되었다(Cheong et al., 2007; Sahay, 2012; Noh et al., 2021). 이에 더하여, 이송율과 분산율의 비인 $P e = U L ⁄ K$ 와 사행도가 추가로 고려된 바 있으며(Ehteram et al., 2021), Femeena et al. (2019)은 유속, 수심, 하폭을 이용해 K, α, 그리고 ε을 산정할 수 있는 효율적인 회귀식을 제시하였고, 이후 Noh et al. (2021)은 저장대의 영향으로 인해 TSM 모의를 위한 평균 흐름도 달라질 수 있다는 측면에서 다중 유전자 유전 프로그래밍(multi-gene genetic programming)과 주성분 회귀분석을 적용해 4개의 매개변수(U, K, α, ε)를 산정할 수 있는 경험식을 제시하였다.

전술한 바와 같이 저장대 매개변수를 결정하는 두 가지 방법 모두 경험적 접근법에 의존하고 있다. 대상지에서의 추적자 실험 자료가 있다면 첫번째 방법인 역산모델링을 통해 최적의 매개변수를 결정할 수 있지만, 추적자 실험 당시의 흐름조건에서만 적용 가능한 매개변수이기 때문에 활용성에 제한이 있다. 다만, 이러한 최적화 방식은 하천의 복잡성을 반영할 수 있기 때문에 대상구간의 하천 혼합 및 정체 특성을 분석(diagnostics)하기 위해 활용될 수 있다. 반면에 두번째 방법인 경험식의 경우, 다양한 조건에서의 축적된 자료를 기반으로 산정식을 유도하기 때문에 낮은 정확도의 한계를 보이지만, 추적자 실험 없이 즉각적으로 매개변수를 추정할 수 있기에 하천의 정체현상을 반영한 물질 이송을 예측(prediction)하기 위해 활용될 수 있다. 다만, 대상지에서 구조물, 사행구간, 지류 유입과 같은 불연속점이 있는 경우(Shin et al., 2021a), 이를 충분히 고려한 경험식 구축이 선행되지 않는 한 낮은 정확도가 예상되기에 활용이 지양되어야 한다. 이와 같이, 연구 목표와 적용 환경에 따라 매개변수 결정을 위한 적절한 접근 방식과 방법론이 선정되어야 한다. Table 2에 두 방식에 대한 개요와 장단점을 요약하여 수록하였다.

Table 2.

Methods of determining TSM parameters

Depending on whether tracer data is available	Method	Pros and cons	Examples
Observing Method	Direct measurement	Exact but not possible	None
	Inverse modeling	Accurate but case-specific	- Numerical solution method Runkel, 1998; Runkel and Broshears, 1991; Noh et al., 2019
			- Analytical solution method Hart, 1995; Cheong and Seo, 2003
			- Moment matching method Schmid, 1995; Wörman and Wachniew, 2007; Seo and Cheong, 2001
Predicting Method	Theoretical estimation	Difficult to derive	None
Predicting Method	Empirical estimation	Highly applicable and accessible but less accurate	Thackston and Schnelle, 1970; Cheong et al., 2007; Rowiński et al., 2005; Rowiński and Piotrowski, 2008; Sahay, 2012; Madadi et al., 2020; Noh et al., 2021; Femeena et al., 2019; Ehteram et al., 2021

4. 하천 저장대 모델의 전망

하천 저장대 모형은 하천의 물질 이송 능력 및 정체 특성에 대한 해석 도구로서의 가치를 입증해왔지만, 미지의 하천 구간에 대한 시공간적 물질 혼합 예측에 활용하는 데는 어려움이 있다(Kim et al., 2022). 이에 대한 원인으로는 모형의 구조적 불확실성, 매개변수 결정의 불확실성, 그리고 계측 자료의 불확실성으로 구분할 수 있다.

모형의 구조적 불확실성은 저장대 모형의 개념적 모형 구축 시 복잡한 하천의 수리학적, 지형학적 특성을 과도하게 단순화시키는 과정에 기인한다. 3차원적인 하천 흐름을 1차원으로 차원을 축소하는 과정(Fischer et al., 1979)에서도 하천 규모와 이차류 특성에 따라 정당성을 얻지 못할 수 있으며(Kim et al., 2021c; Shin et al., 2021b; Park et al., 2020), 저장대 모형에서 가정하는 구간 전체에서의 일정한 하천 단면, 저장대에서는 흐름이 존재하지 않고 물질은 완전 혼합 상태, 그리고 저장대의 형태, 규모와 상관없이 일정한 물질교환계수 가정이 실제 하천특성에는 위반되는 경우가 대부분이다. 하상 형태에 따라서 수 초부터 수 일까지의 시간 스케일을 갖는 정체현상(Boano et al., 2014; Kim, 2022)을 특정 수식으로 정체시간분포를 모수화시키는 과정에서도 불확도가 발생할 수 있다. 예를 들어, 지수함수 형태를 갖는 TSM의 정체시간분포 모형은 구조적으로 정체현상이 강하게 발생하는 하천 구간에서의 두꺼운 꼬리를 갖는 non-Fickian 거동을 재현하지 못하는 것으로 알려져 있다(Kim et al., 2023b). 따라서 TSM 이후 제시된 다양한 정체시간분포 모델링을 비교하고, 넓은 영역의 시공간적 매개변수 공간(parameter space)에서 모델링 타당성을 입증하고 제약조건을 규명하기 위한 노력이 지속적으로 필요하다. 동시에 앞서 언급되었던 것처럼, 이러한 한계를 극복하기 위해 최근의 저장대 모델링 연구에서는 모형의 복잡성이 증가하는 경향이 나타나고 있다. 하지만, 모형의 복잡성 증가는 추정해야 하는 매개변수의 증가를 수반하며, 모의 결과의 신뢰성 감소와 오차 원인 규명에 어려움을 초래한다. 이에, 실제 현상에 최대한 근접하게 접근하되 신뢰할 수 있는 하천 혼합 해석 모델링을 위해서는 복잡함과 간소함 사이의 균형을 찾아야 한다.

하천 저장대 모형의 매개변수의 불확도의 경우에도 보다 정량적인 연구가 필요하다. 저장대 모형의 매개변수는 많은 연구자에게 하천에서 물질 이송의 정체현상을 정량적으로 파악하는데 기여하지만, 저장대 모형이 제시된 이후 지금까지 현상학적 해석의 결과인 저장대 매개변수가 실제로 어떤 물리적 의미를 가지며 결정된 값은 어떠한 하천 특성의 근사치인지에 대해 명확하게 밝혀진 바 없다. TSM 모형이 포함하고 있는 저장대의 크기를 나타내는 기하학적 매개변수 ε은 하천 길이에 따라 가산적(additive)이지 않으며(Gooseff et al., 2013), 본류대와 저장대의 물질 교환량(flux)이 레이놀즈수에 비례한다는 보고는 있지만(Kim et al., 2023c), 물질교환 속도를 나타내는 운동학적 매개변수 α는 유량에 따라 증가하거나 감소하는 어떠한 경향성도 발견되지 않았다고 보고되고 있다(Zarnetske et al., 2007). 일반적으로 저장대 매개변수는 일정 하천 구간에서의 추적자 실험 자료로부터 최적값이 산정되며, 해당 하천구간의 평균적인 특성을 나타내는 것으로 해석되는데, 정체 현상이 국부적으로 발생하는 경우 작은 공간 스케일의 현상을 하천 전체에서의 현상으로 해석하는 것이 대한 타당성이 불충분할 수 있다. 저장대 매개변수의 민감도 및 불확도에 대한 평가는 많은 연구에서 제시되고 있으나(Harvey et al., 1996; Kelleher et al., 2019; Knapp and Cirpka, 2017; Choi et al., 2020), 그럼에도 불구하고 많은 연구에서 매개변수에 대한 의미와 불확실성에 대한 별다른 주의 없이 해석과 결론을 내리곤 한다. 다시 말해, 저장대 매개변수를 통한 하천특성 분석에는 하천의 수리학적 및 지형학적 특성과 함께 보수적으로 해석되어야 한다.

하천 특성을 보다 정확하게 대표할 수 있는 매개변수를 찾는 다른 방법으로는 모의 구간을 세분화하는 것이다. 세분화된 구간에 따라 다른 매개변수를 적용한다면 흐름 방향에 따라 비균일(non-uniform)한 하천 특성을 반영하여 더욱 정확한 모의결과를 예상할 수 있다. 매개변수의 불확도는 추정 추정 방식에서도 기인한다. 물리적으로 모호한 의미를 갖는 저장대 매개변수의 결정은 다변량 최적화 방식에 의존하고 있으나, 매개변수들은 서로 종속적이기에 비선형적이며, 등결과성(equifinality) 혹은 비볼록성(non-convexity) 문제 해결을 위해 더욱 견고한 최적화 기법이 제시되고 있다(Knapp et al., 2017; Noh et al., 2021; Madadi et al., 2020; Ehteram et al., 2021). 최근 다양한 알고리즘이 적용되고 있는 가운데, 이들을 엄격하게 비교하여 그 차이를 규명하고 가장 신뢰성 높은 매개변수 결정 방법을 찾을 필요가 있다. 이와 동시에, 추적자 실험 자료의 부재로 최적화 기법을 적용할 수 없는 조건에서 하천의 특성을 통하여 매개변수를 추정하기 위한 해석적 및 경험적 산정식이 제시되고 검증되었지만, 지역성 문제를 극복하기 위한 평가가 지속적으로 필요한 상황이다.

추적자실험 자료의 불확도 개선은 저장대 모형의 매개변수의 불확도를 최소화하고 모델 예측의 정확도를 제고하기 위해 반드시 필요하다. 다양한 형태의 저장대 모형은 결정된 매개변수를 기반으로 모의되며, 매개변수는 하천에서 수행되는 추적자 실험의 결과에 대한 최적값으로 결정되기 때문에, 추적자 실험 자료에서의 불확실성은 모델링의 불확실성으로 이어진다. 추적자 실험에서 경계해야하는 요인 중 하나는 추적자의 반응성이다. 예시로, 염화 나트륨(sodium chloride)는 높은 용해도와 탐지성, 다른 물질과 쉽게 반응하지 않는 화학적 안정성을 갖지만, 다중 발생원의 우려가 있으며 BTC 꼬리 분석을 위한 기저 농도(background concentration) 분리에 어려움이 있을 수 있고, 높은 농도에서 생태계에 위협이 될 수 있다. 많은 연구에서 높은 탐지성으로 낮은 농도에서도 측정할 수 있다는 장점으로 형광염료인 로다민 WT (Rhodamine WT)를 활용했는데, 하천 흐름이 느리거나 혼합대에서의 정체현상 등 분석 대상의 시간 스케일이 클 경우, 추적자의 흡착성을 무시할 수 없다(Runkel, 2015). 이러한 반응성은 종종 주입량과 검출량의 질량 차이에서 나타나며, 대부분의 연구에서는 단순히 검출량을 주입량으로 보상하는 질량 회복(mass recovery) 전처리를 수행하는데, 이러한 반응성이 시간 스케일의 영향이 있을 수 있음에 유의하여야 한다. 또한 반응성 추적자(Haggerty et al., 2009; Knapp et al., 2018)의 활용과 이를 위한 모형(Bottacin-Busolin et al., 2021)이 제시되기도 하였는데, 이들의 연구를 통해 물리적 정체 현상과 대사적 특성을 함께 고려함으로써 생화학적 반응에 대한 정체현상의 영향을 이해하고 기여도를 파악할 수 있다. 또한, 하천수의 온도 측정을 추적자 실험과 병행하여 추적자 실험의 타당성을 효율적으로 향상시킬 수 있다(Neilson et al., 2010). 이러한 개선된 추적자 실험 방법은 하천의 정체현상에 대한 이해의 강화와 저장대 모형의 정확도 및 신뢰성 개선에 도움이 될 것으로 예상된다.

5. 결 론

하천 저장대 모형은 복잡한 하천 흐름이 갖고 있는 정체 특성을 간접적으로 해석할 수 있는 유용한 도구이며, 다양한 분야에서 활용되고 있으며, 동시에 더욱 정확한 모델링을 위한 노력이 지속되고 있다. 특히, 물질의 정체현상을 정량적으로 나타내어 하천 구간 간 비교분석하거나, 정체 구역에서 발생할 수 있는 생물학적 반응에 대한 정량적 평가를 가능하게 한다. 하지만, 이러한 복잡한 하천특성을 1차원의 단순한 구조를 갖는 모형과 제한된 수의 매개변수로 특징짓는 과정에서 많은 불확실성을 내포하고 있으며, 여전히 해결되지 않은 한계를 가지고 있다. 본 논문에서는 현재까지 하천 저장대 모형이 어떻게 개선되고 고도화되었는지를 파악하고, 현재까지도 해결되지 않은 문제를 규명하였으며, 이를 극복하기 위한 연구의 방향성을 제시하였다.

하천 저장대 모형이 가지고 있는 불확실성을 극복하기 위해서, 현재까지 제시된 저장대 모형들의 적용에 따라 다른 적합성을 지속적으로 평가하고 비교할 필요가 있다. 현재의 저장대 모형이 과도하게 단순화되어 실제 현상을 정확하게 반영하지 못하는 문제를 해결하기 위해, 저장대 모형을 실제에 가깝게 고도화하는 연구가 요구된다. 현재의 대표적인 고도화 방법으로는 하천의 저장대를 빠른 교환 영역(빠른 저장대)과 느린 교환 영역(느린 저장대)으로 구분하여 저장대별로 서로 다른 매개변수를 적용하거나, 서로 다른 두개의 기억함수를 적용하는 방식이다. 그러나 이러한 고도화 과정에서 증가되는 매개변수가 모호한 물리적 의미를 가질 수 있으므로, 모형의 복잡성을 증가시켜 정확도를 강화하는 방식에서는 주의가 필요하다.

저장대 매개변수를 결정하는 두 가지 방법 중, 첫 번째 방법은 역산모델링을 통한 최적화 방식인데, 이 방법에 의해 추정된 매개변수는 추적자 실험 시점의 흐름조건에서만 유효하기 때문에 활용성에 제한이 있다. 그러나 이러한 최적화 방식은 하천의 복잡성을 반영할 수 있기 때문에 대상구간의 하천 혼합 및 정체 특성을 분석하기 위해 활용될 수 있다. 두 번째 방법은 다양한 조건에서의 축적된 자료를 기반으로 경험식을 유도하는 방식인데, 이 방법은 낮은 정확도의 한계를 보이지만, 추적자 실험 없이 즉각적으로 매개변수를 추정할 수 있기에 하천의 정체현상을 반영한 물질 이송을 예측하기 위해 활용될 수 있다는 장점이 있다. 다만, 대상지에서 구조물, 사행구간, 지류 유입과 같은 불연속점이 있는 경우, 이를 충분히 고려한 경험식 구축이 선행되지 않는 한 낮은 정확도가 예상되기에 활용이 지양되어야 한다. 이와 같이, 적용하고자 하는 연구 목적에 따라 물질 혼합의 분석(diagnostics) 혹은 예측(prediction)으로 구분하고 적용 환경에 따라 매개변수 결정을 위한 적절한 접근 방식과 방법론이 선정되어야 한다.

마지막으로 하천 저장대 모형의 비구조적 불확실성 측면에서 매개변수를 통한 하천의 정체 특성 해석에 있어서는 물리적 근거가 뒷받침되지 않은 결론은 신뢰하기 어려우며, 매개변수를 통한 정량적 분석에는 추적자 실험 자료의 신뢰성, 매개변수 추정 방식의 신뢰성, 그리고 유속 특성과 같은 수리학적 인자와의 비교분석이 함께 제시되어야 한다. 본 연구에서 분석된 연구 동향과 이에 따른 제언은 향후 하천 현상의 물리적 이해를 바탕으로 저장대 모형을 개선하고, 더욱 정확한 하천 혼합 해석을 위한 연구의 토대가 될 것으로 기대한다.

Acknowledgements

본 연구는 환경부 국토교통과학기술진흥원의 지원(22DPIW- C153746-04)과, 환경부 미세플라스틱 측정 및 위해성평가 기술개발사업(2021003110003)의 연구비 지원에 의하여 연구되었으며 이에 감사드립니다. 또한, 서울대학교 건설환경종합연구소의 지원에도 감사드립니다.

Conflicts of Interest

The authors declare no conflict of interest.

References

ASCE Task Committee on Hydraulic Engineering Advocacy (1996). "Environmental hydraulics: New research directions for the 21st century." Journal of Hydraulic Engineering, ASCE, Vol. 122, No. 4, pp. 180-183.

10.1061/(ASCE)0733-9429(1996)122:4(180)

Bencala, K.E. (1983). "Simulation of solute transport in a mountain pool‐and‐riffle stream with a kinetic mass transfer model for sorption." Water Resources Research, Vol. 19, No. 3, pp. 732- 738. doi: 10.1029/WR019i003p00732

10.1029/WR019i003p00732

Bencala, K.E., and Walters, R.A. (1983). "Simulation of solute transport in a mountain pool‐and‐riffle stream: A transient storage model." Water Resources Research, Vol. 19, No. 3, pp. 718- 724. doi: 10.1029/WR019i003p00718

10.1029/WR019i003p00718

Boano, F., Harvey, J.W., Marion, A., Packman, A.I., Revelli, R., Ridolfi, L., and Wörman, A. (2014). "Hyporheic flow and transport processes: Mechanisms, models, and biogeochemical implications." Eos, Transactions American Geophysical Union, Vol. 52, pp. 603-679. doi: 10.1029/88EO01108

10.1029/88EO01108

Boano, F., Packman, A.I., Cortis, A., Revelli, R., and Ridolfi, L. (2007). "A continuous time random walk approach to the stream transport of solutes." Water Resources Research, Vol. 43, No. 10, pp. 1-12. doi: 10.1029/2007WR006062

10.1029/2007WR006062

Bottacin-Busolin, A., Dallan, E., and Marion, A. (2021). "STIR- RST: A Software tool for reactive smart tracer studies." Environmental Modelling and Software, Vol. 135, 104894. doi: 10.1016/j.envsoft.2020.104894

10.1016/j.envsoft.2020.104894

Briggs, M.A., Gooseff, M.N., Arp, C.D., and Baker, M.A. (2009). "A method for estimating surface transient storage parameters for streams with concurrent hyporheic storage." Water Resources Research, Vol. 46, No. 4, pp. 1-13. doi: 10.1029/2008WR006959

10.1029/2008WR006959

Cheong, T.S., and Seo, I.W. (2003). "Parameter estimation of the transient storage model by a routing method for river mixing processes." Water Resources Research, Vol. 39, No. 4, 1074. doi: 10.1029/2001WR000676

10.1029/2001WR000676

Cheong, T.S., Younis, B.A., and Seo, I.W. (2007). "Estimation of key parameters in model for solute transport in rivers and streams." Water Resources Management, Vol. 21, No. 7, pp. 1165-1186. doi: 10.1007/s11269-006-9074-7

10.1007/s11269-006-9074-7

Choi, J., Harvey, J.W., and Conklin, M.H. (2000a). "Characterizing multiple timescales of stream and storage zone interaction that affect solute fate and transport in streams." Water Resources Research, Vol. 36, No. 6, pp. 1511-1518.

10.1029/2000WR900051

Choi, J., Harvey, J.W., and Conklin, M.H. (2000b). "Characterizing multiple timescales of stream and storage zone interaction that affect solute fate and transport in streams." Water Resources Research, Vol. 36, No. 6, pp. 1511-1518. doi: 10.1029/2000 WR900051

10.1029/2000WR900051

Choi, S.Y., Seo, I.W., and Kim, Y.O. (2020). "Parameter uncertainty estimation of transient storage model using Bayesian inference with formal likelihood based on breakthrough curve segmentation." Environmental Modelling and Software, Vol. 123, 104558. doi: 10.1016/j.envsoft.2019.104558

10.1016/j.envsoft.2019.104558

Deng, Z.-Q., Bengtsson, L., Singh, V.P., and Adrian, D.D. (2002). "Longitudinal dispersion coefficient in single-channel streams." Journal of Hydraulic Engineering, Vol. 128, No. 10, pp. 901- 916.

10.1061/(ASCE)0733-9429(2002)128:10(901)

Deng, Z.-Q., Singh, V.P., and Bengtsson, L. (2004). "Numerical solution of fractional order advection-reaction-diffusion equation." Journal of Hydraulic Engineering, Vol. 130, No. 5, pp. 422-431. doi: 10.2298/TSCI170624034D

10.2298/TSCI170624034D

Duchon, C.E. (1979). "Lanczos filtering in one and two dimensions." Journal of Applied Methorology, Vol. 18, No. 8, pp. 1016-1022.

10.1175/1520-0450(1979)018<1016:LFIOAT>2.0.CO;2

Ehteram, M., Sharafati, A., Asadollah, S.B.H.S., and Neshat, A. (2021). "Estimating the transient storage parameters for pollution modeling in small streams: A comparison of newly developed hybrid optimization algorithms." Environmental Monitoring and Assessment, Vol. 193, No. 8, 475. doi: 10. 1007/s10661-021-09269-7

10.1007/s10661-021-09269-734231083

Elder, J. (1959). "The dispersion of marked fluid in turbulent shear flow." Journal of Fluid Mechanics, Vol. 5, No. 4, pp. 544-560. doi: 10.1017/S0022112059000374.

10.1017/S0022112059000374

Elliott, H., and Brooks, N.H. (1997). "Transfer of nonsorbing solutes to a streambed with bed forms: Theory." Vol. 33, No. 1, pp. 123-136.

10.1029/96WR02784

Femeena, P.V., Chaubey, I., Aubeneau, A., McMillan, S., Wagner, P.D., and Fohrer, N. (2019). "Simple regression models can act as calibration-substitute to approximate transient storage parameters in streams." Advances in Water Resources, Vol. 123, pp. 201-209. doi: 10.1016/j.advwatres.2018.11.010

10.1016/j.advwatres.2018.11.010

Fischer, H.B. (1979). Mixing in inland and coastal waters. Academic Press, Cambridge, MA, U.S.

Gooseff, M.N., Benson, D.A., Briggs, M.A., Weaver, M., Wollheim, W., Peterson, B., and Hopkinson, C.S. (2011). "Residence time distributions in surface transient storage zones in streams: Estimation via signal deconvolution." Water Resources Research, Vol. 47, No. 5, pp. 1-7. doi: 10.1029/2010WR009959

10.1029/2010WR009959

Gooseff, M.N., Briggs, M.A., Bencala, K.E., McGlynn, B.L., and Scott, D.T. (2013). "Do transient storage parameters directly scale in longer, combined stream reaches? Reach length dependence of transient storage interpretations." Journal of Hydrology, Vol. 483, pp. 16-25. doi: 10.1016/j.jhydrol.2012. 12.046

10.1016/j.jhydrol.2012.12.046

Gooseff, M.N., LaNier, J., Haggerty, R., and Kokkeler, K. (2005). "Determining in-channel (dead zone) transient storage by comparing solute transport in a bedrock channel-alluvial channel sequence, Oregon." Water Resources Research, Vol. 41, No. 6, pp. 1-7. doi: 10.1029/2004WR003513

10.1029/2004WR003513

Guymer, I., and Stovin, V.R. (2011). "One-dimensional mixing model for surcharged manholes." Journal of Hydraulic Engineering, Vol. 137, No. 10, pp. 1160-1172. doi: 10.1061/(asce)hy.1943- 7900.0000422

10.1061/(ASCE)HY.1943-7900.0000422

Haggerty, R., Martí, E., Argerich, A., Von Schiller, D., and Grimm, N.B. (2009). "Resazurin as a "smart" tracer for quantifying metabolically active transient storage in stream ecosystems." Journal of Geophysical Research - Biogeosciences, Vol. 114, No. G3, G03014. doi: 10.1029/2008JG000942

10.1029/2008JG000942

Haggerty, R., McKenna, S.A., and Meigs, L.C. (2000). "On the late- time behavior of tracer test breakthrough curves." Water Resources Research, Vol. 36, No. 12, pp. 3467-3479. doi: 10. 1029/2000WR900214

10.1029/2000WR900214

Hart, D.R. (1995). "Parameter estimation and stochastic interpretation of the transient storage model for solute transport in streams." Water Resources Research, Vol. 31, No. 2, pp. 323-328. doi: 10.1029/94WR02739

10.1029/94WR02739

Harvey, J.W., Wagner, B.J., and Bencala, K.E. (1996). "Evaluating the reliability of the stream tracer approach to characterize stream‐subsurface water exchange." Water Resources Research, Vol. 32, No. 8, pp. 2441-2451. doi: 10.1029/96WR01268

10.1029/96WR01268

Jackson, T.R., Haggerty, R., Apte, S.V., Coleman, A., and Drost, K.J. (2012). "Defining and measuring the mean residence time of lateral surface transient storage zones in small streams." Water Resources Research, Vol. 48, No. 10, pp. 1-20. doi: 10.1029/2012WR012096

10.1029/2012WR012096

Jung, S.H., and Seo, I.W. (2021). "Investigation of effects of weir on the pollutant mixing in rivers." In Proceedings of the Korea Water Resources Association Conference, KWRA, pp. 20-20.

Kelleher, C., Ward, A., Knapp, J.L., Blaen, P.J., Kurz, M.J., and Drummond, J.D. (2019). "Exploring tracer information and model framework trade‐offs to improve estimation of stream transient storage processes." Water Resources Research, Vol. 55, No. 4, pp. 3481-3501. doi: 10.1029/2018WR023585

10.1029/2018WR023585

Kim, B., Kwon, S., and Seo, I.W. (2023a). "An explicit solution for characterizing non-Fickian solute transport in natural streams." Water, Vol. 15, No. 9, 1702. doi: 10.3390/w15091702

10.3390/w15091702

Kim, B., Kwon, S., Noh, H., and Seo, I.W. (2022). "Surrogate prediction of the breakthrough curve of solute transport in rivers using its reach length dependence." Journal of Contaminant Hydrology, Vol. 249, 104024. doi: 10.1016/j.jconhyd. 2022.104024

10.1016/j.jconhyd.2022.10402435667323

Kim, B., Seo, I.W., Kwon, S., and Baek, D. (2023b). "Estimating net retention time of solute in storage zones of a stream." Water Resources Research, Vol. 59, No. 5, e2022WR032243. doi: 10.1029/2022WR032243

10.1029/2022WR032243

Kim, B., Seo, I.W., Kwon, S., Jung, S.H., and Choi, Y. (2021a). "Modelling one-dimensional reactive transport of toxic contaminants in natural rivers." Environmental Modelling and Software, Vol. 137, 104971. doi: 10.1016/j.envsoft.2021.104971

10.1016/j.envsoft.2021.104971

Kim, B., Seo, I.W., Kwon, S., Jung, S.H., and Yun, S.H. (2021b). "Analysis of solute transport in rivers using a stochastic storage model." Journal of Korea Water Resources Association, Vol. 54, No. 5, pp. 335-345. doi: 10.3741/JKWRA.2021.54.5.335

Kim, J.S. (2022). "Numerical analysis of the hyporheic flow effect on solute transport in surface water." Journal of Korea Water Resources Association, Vol. 55, No. 1, pp. 23-32. doi: 10. 3741/JKWRA.2022.55.1.23

Kim, J.S., Kang, P.K., He, S., Shen, L., Kumar, S.S., Hong, J., and Seo, I.W. (2023c). "Pore-scale flow effects on solute transport in turbulent channel flows over porous media." Transport in Porous Media, Vol. 146, No. 1-2, pp. 223-248. doi: 10.1007/ s11242-021-01736-6

10.1007/s11242-021-01736-6

Kim, J.S., Seo, I.W., Baek, D., and Kang, P.K. (2020). "Recirculating flow-induced anomalous transport in meandering open- channel flows." Advances in Water Resources, Vol. 141, 103603. doi: 10.1016/j.advwatres.2020.103603

10.1016/j.advwatres.2020.103603

Kim, J.S., Seo, I.W., Shin, J., Jung, S.H., and Yun, S.H. (2021c). "Modeling 2D residence time distributions of pollutants in natural rivers using RAMS+." Journal of Korea Water Resources Association, Vol. 54, No. 7, pp. 495-507. doi: 10. 3741/JKWRA.2021.54.7.495

Knapp, J.L., and Cirpka, O.A. (2017). "Determination of hyporheic travel time distributions and other parameters from concurrent conser- vative and reactive tracer tests by local‐in‐global optimization." Water Resources Research, Vol. 53, No. 6, pp. 4984-5001. doi: 10.1002/ 2017WR020734

10.1002/2017WR020734

Knapp, J.L., González‐Pinzón, R., and Haggerty, R. (2018). "The resazurin‐resorufin system: Insights from a decade of "smart" tracer development for hydrologic applications." Water Resources Research, Vol. 54, No. 9, pp. 6877-6889. doi: 10. 1029/2018WR023103

10.1029/2018WR023103

Knapp, J.L.A., and Kelleher, C. (2020). "A perspective on the future of transient storage modeling: Let's stop chasing our tails." Water Resources Research, Vol. 56, No. 3, pp. 1-7. doi: 10. 1029/2019WR026257

10.1029/2019WR026257

Knapp, J.L.A., Gonzalez-Pinzon, R., Drummond, J.D., Larsen, L.G., Cirpka, O.A., and Harvey, J.W. (2017). "Tracer-based characterization of hyporheic exchange and benthic biolayers in streams." Water Resources Research Research, Vol. 53, pp. 1575-1594.

10.1002/2016WR019393

Krishnan, D., and Fergus, R. (2009). "Fast image deconvolution using hyper-laplacian priors." Advances in Neural Information Processing Systems 22 - Proceedings of the 2009 Conference, Vancouver, British Columbia, Canada, pp. 1033-1041.

Kundur, D., Hatzinakos, D.K., and Hatzinakos, D. (1996). "Blind image deconvolution." IEEE Signal Processing Magazine, Vol. 13, No. 3, pp. 43-64.

10.1109/79.489268

Kwon, S., Noh, H., Seo, I.W., Jung, S.H., and Baek, D. (2021). "Identification framework of contaminant spill in rivers using machine learning with breakthrough curve analysis." International Journal of Environmental Research and Public Health, Vol. 18, No. 3, pp. 1-28. doi: 10.3390/ijerph18031023

10.3390/ijerph1803102333498931PMC7908193

Liao, Z., Lemke, D., Osenbrück, K., and Cirpka, O.A. (2013). "Modeling and inverting reactive stream tracers undergoing two- site sorption and decay in the hyporheic zone." Water Resources Research, Vol. 49, No. 6, pp. 3406-3422. doi: 10.1002/wrcr. 20276

10.1002/wrcr.20276

Madadi, M.R., Akbarifard, S., and Qaderi, K. (2020). "Improved Moth-Swarm Algorithm to predict transient storage model parameters in natural streams." Environmental Pollution, Vol. 262, 114258. doi: 10.1016/j.envpol.2020.114258

10.1016/j.envpol.2020.11425832193080

Marion, A., and Zaramella, M. (2005). "A residence time model for stream-subsurface exchange of contaminants." Acta Geophysica Polonica, Vol. 53, No. 4, pp. 527-538.

Marion, A., Zaramella, M., and Bottacin-Busolin, A. (2008). "Solute transport in rivers with multiple storage zones: The STIR model." Water Resources Research, Vol. 44, No. 10, pp. 1-10. doi: 10.1029/2008WR007037

10.1029/2008WR007037

Mignot, E., Cai, W., Polanco, J.I., Escauriaza, C., and Riviere, N. (2017). "Measurement of mass exchange processes and coefficients in a simplified open-channel lateral cavity connected to a main stream." Environmental Fluid Mechanics, Vol. 17, No. 3, pp. 429-448. doi: 10.1007/s10652-016-9495-7

10.1007/s10652-016-9495-7

Neilson, B.T., Stevens, D.K., Chapra, S.C., and Bandaragoda, C. (2010). "Two‐zone transient storage modeling using temperature and solute data with multiobjective calibration: 2. Temperature and solute.: Water Resources Research, Vol. 46, No. 12, W12521. doi: 10.1029/2009WR008759

10.1029/2009WR008759

Noh, H., Baek, D., and Seo, I.W. (2019). "Analysis of the applicability of parameter estimation methods for a transient storage model." Journal of Korea Water Resources Association, Vol. 52, No. 10, pp. 681-695. doi: 10.3741/JKWRA.2019.52.10.681

Noh, H., Kwon, S., Seo, I.W., Baek, D., and Jung, S.H. (2021). "Multi-gene genetic programming regression model for prediction of transient storage model parameters in natural rivers." Water (Switzerland), Vol. 13, No. 1, 76. doi: 10.3390/ w13010076

10.3390/w13010076

Park, I., and Seo, I.W. (2018). "Modeling non-Fickian pollutant mixing in open channel flows using two-dimensional particle dispersion model." Advances in Water Resources, Vol. 111, pp. 105-120. doi: 10.1016/j.advwatres.2017.10.035

10.1016/j.advwatres.2017.10.035

Park, I., Seo, I.W., Shin, J., and Song, C.G. (2020). "Experimental and numerical investigations of spatially-varying dispersion tensors based on vertical velocity profile and depth-averaged flow field." Advances in Water Resources, Vol. 142, 103606. doi: 10.1016/j.advwatres.2020.103606

10.1016/j.advwatres.2020.103606

Payn, R.A., Gooseff, M.N., Benson, D.A., Cirpka, O.A., Zarnetske, J.P., Bowden, W.B., McNamara, J.P., and Bradford, J.H. (2008). "Comparison of instantaneous and constant-rate stream tracer experiments through non-parametric analysis of residence time distributions." Water Resources Research, Vol. 44, No. 6, pp. 1-10. doi: 10.1029/2007WR006274

10.1029/2007WR006274

Rowiński, P.M., and Piotrowski, A. (2008). "Estimation of parameters of the transient storage model by means of multi-layer perceptron neural networks." Hydrological Sciences Journal, Vol. 53, No. 1, pp. 165-178. doi: 10.1623/hysj.53.1.165

10.1623/hysj.53.1.165

Rowiński, P.M., Piotrowski, A., and Napiórkowski, J.J. (2005). "Are artificial neural network techniques relevant for the estimation of longitudinal dispersion coefficient in rivers?" Hydrological Sciences Journal, Vol. 50, No. 1, pp. 175-187. doi: 10.1623/ hysj.50.1.175.56339

10.1623/hysj.50.1.175.56339

Runkel, R.L. (1998). One-dimensional transport with inflow and storage (OTIS): A solute transport model for streams and rivers. US Department of the Interior, US Geological Survey. Vol. 98, No. 4018, District of Columbia, U.S. doi: 10.3133/ wri984018

Runkel, R.L. (2015). "On the use of rhodamine WT for the characterization of stream hydrodynamics and transient storage." Water Resources Research, Vol. 51, pp. 6125-6142. doi: 10. 1111/j.1752-1688.1969.tb04897.x

10.1002/2015WR017201

Runkel, R.L., and Broshears, R.E. (1991). One-dimensional transport with inflow and storage (OTIS): A solute transport model for small streams. Center for Advanced Decision Support for Water and Environmental Systems (CADSWES), Department of Civil Engineering, University of Colorado, Boulder, CO, U.S.

Sahay, R.R. (2012). "Predicting transient storage model parameters of rivers by genetic algorithm." Water Resources Management, Vol. 26, No. 13, pp. 3667-3685. doi: 10.1007/s11269-012-0092-3

10.1007/s11269-012-0092-3

Sandoval, J., Mignot, E., Mao, L., Pastén, P., Bolster, D., and Escauriaza, C. (2019). "Field and numerical investigation of transport mechanisms in a surface storage zone." Journal of Geophysical Research: Earth Surface, Vol. 124, No. 4, pp. 938-959. doi: 10.1029/2018JF004716

10.1029/2018JF004716

Schmid, B.H. (1995). "Temporal moments accounting for the effects of first-order decay: Sur les équations de stockage du transport longitudinal de soluté dans des canaux à surface libre: Moments temporels tenant compte des effets de décroissance du premiére ordre." Journal of Hydraulic Research, Vol. 33, No. 5, pp. 595-610. doi: 10.1080/00221689509498559

10.1080/00221689509498559

Seo, I.W., and Cheong, T.S. (2001). "Moment-based calculation of parameters for the storage zone model for river dispersion." Journal of Hydraulic Engineering, Vol. 127, No. 6, pp. 453-465.

10.1061/(ASCE)0733-9429(2001)127:6(453)

Seo, I.W., and Yu, D. (2000). "Characterization of pool-riffle sequences in solute transport modeling of streams." Water Engineering Research, Vol. 1, No. 3, pp. 171-185.

Shin, J., Lee, S., and Park, I. (2021a). "Analysis of storage effects in the recirculation zone based on the junction angle of channel confluence." Applied Sciences (Switzerland), Vol. 11, No. 24. doi: 10.3390/app112411607

10.3390/app112411607

Shin, J., Lee, S., and Park, I. (2023). "Influences of momentum ratio on transverse dispersion for intermediate-field mixing downstream of channel confluence." International Journal of Environmental Research and Public Health, Vol. 20, No. 4, 2776. doi: 10.3390/ijerph20042776

10.3390/ijerph2004277636833473PMC9957352

Shin, J., Rhee, D., and Park, I. (2021b). "Applications of two-dimensional spatial routing procedure for estimating dispersion coefficients in open channel flows." Water (Switzerland), Vol. 13, No. 10, pp. 1-21. doi: 10.3390/w13101394

10.3390/w13101394

Sonnenwald, F., Stovin, V., and Guymer, I. (2014). "Configuring maximum entropy deconvolution for the identification of residence time distributions in solute transport applications." Journal of Hydrologic Engineering, Vol. 19, No. 7, pp. 1413- 1421. doi: 10.1061/(asce)he.1943-5584.0000929

10.1061/(ASCE)HE.1943-5584.0000929

Thackston, E.L., and Schnelle, K.B. (1970). "Predicting effects of dead zones on stream mixing." Journal of the Sanitary Engineering Division, Vol. 96, No. 2, pp. 319-331.

10.1061/JSEDAI.0001078

Tsai, C.H., Rucker, D.F., Brooks, S.C., Ginn, T., and Carroll, K.C. (2022). "Transient storage model parameter optimization using the simulated annealing method." Water Resources Research, Vol. 58, No. 7, e2022WR032018. doi: 10.1029/2022WR032018

10.1029/2022WR032018

Wagner, B.J., and Harvey, J.W. (1997). "Experimental design for estimating parameters of rate‐limited mass transfer: Analysis of stream tracer studies." Water Resources Research, Vol. 33, No. 7, pp. 1731-1741.

10.1029/97WR01067

Ward, A.S., Kelleher, C.A., Mason, S.J.K., Wagener, T., McIntyre, N., McGlynn, B., Runkel, R.L., and Payn, R.A. (2017). "A software tool to assess uncertainty in transient-storage model parameters using Monte Carlo simulations." Freshwater Science, Vol. 36, No. 1, pp. 195-217. doi: 10.1086/690444

10.1086/690444

Weitbrecht, V., Socolofsky, S.A., and Jirka, G.H. (2008). "Experiments on mass exchange between groin fields and main stream in rivers volker." Journal of Hydraulic Engineering, Vol. 134, No. 2, pp. 173-183. doi: 10.1061/(ASCE)0733-9429(2008)134

10.1061/(ASCE)0733-9429(2008)134:2(173)

Wörman, A., and Wachniew, P. (2007). "Reach scale and evaluation methods as limitations for transient storage properties in streams and rivers." Water Resources Research, Vol. 43, No. 10, pp. 1-13. doi: 10.1029/2006WR005808

10.1029/2006WR005808

Wörman, A., Packman, A.I., Johansson, H., and Jonsson, K. (2002). "Effect of flow-induced exchange in hyporheic zones on longitudinal transport of solutes in streams and rivers." Water Resources Research, Vol. 38, No. 1, pp. 2-1-2-15. doi: 10.1029/ 2001wr000769

10.1029/2001WR000769

Yeh, T.C., Khaleel, R., and Carroll, K.C. (2015). Flow through heterogeneous geologic media. Cambridge University Press, Cambridge, UK.

10.1017/CBO9781139879323

Zaramella, M., Marion, A., Lewandowski, J., and Nützmann, G. (2016). "Assessment of transient storage exchange and advection-dispersion mechanisms from concentration signatures along breakthrough curves." Journal of Hydrology, Vol. 538, pp. 794-801. doi: 10.1016/j.jhydrol.2016.05.004

10.1016/j.jhydrol.2016.05.004

Zarnetske, J.P., Gooseff, M.N., Brosten, T.R., Bradford, J.H., McNamara, J.P., and Bowden, W.B. (2007). "Transient storage as a function of geomorphology, discharge, and permafrost active layer conditions in Arctic tundra streams." Water Resources Research, Vol. 43, No. 7, pp. 1-13. doi: 10.1029/2005WR004816

10.1029/2005WR004816

Journal of Korea Water Resources AssociationISSN:2799-8746(Print) 2799-8754(Online)한국수자원학회

Preview

A review of transient storage modeling for analyzing one-dimensional non-fickian solute transport in rivers

ABSTRACT

MAIN

Fig. 1.

Various storage zones in a natural stream

Fig. 2.

Schematic of 1D transient stroage models

Fig. 3.

Process of typical 1D conceptual transient storage modeling

(1)

(2a)

(2b)

(3)

(4)

(5)

Table 1.

Features of existing transient storage models

Fig. 4.

Tracer cloud shape flowing along a river channel at Gam Creek, South Korea

(6)

Table 2.

Methods of determining TSM parameters

Acknowledgements

Conflicts of Interest

References