A simple approach to simulate the size distribution of suspended sediment

Minhyuck Kwon; Jisun Byun; Minwoo Son

doi:10.3741/JKWRA.2024.57.5.347

Preview

Research Article

Journal of Korea Water Resources Association. 31 May 2024. 347-357
https://doi.org/10.3741/JKWRA.2024.57.5.347

A simple approach to simulate the size distribution of suspended sediment

부유사 입경분포 모의를 위한 간편법

Minhyuck Kwon^a

Jisun Byun^b

Minwoo Son^c^*

권 민혁^a

변 지선^b

손 민우^c^*

^aGraduate Student, Department of Civil Engineering, Chungnam National University, Daejeon, Korea

^bSenior Researcher, K-water Research Institute, Korea Water Resources Corportation, Daejeon, Korea

^cProfessor, Department of Civil Engineering, Chungnam National University, Daejeon, Korea

^a충남대학교 토목공학과 석사과정

^b한국수자원공사 K-water 연구원 선임연구원

^c충남대학교 토목공학과 교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by/4.0):

©It is identical to the Creative Commons Attribution Non-commercial License (https://creativecommons.org/licenses/by/4.0)

ABSTRACT

Numerous prior studies have delineated the size distribution of noncohesive sediment in suspension, focusing on mean size and standard deviation. However, suspensions comprise a heterogeneous mixture of sediment particles of varying sizes. The transport dynamics of suspended sediment in turbulent flow are intimately tied to settling velocities calculated based on size and density. Consequently, understanding the grain size distribution becomes paramount in comprehending sediment transport phenomena for noncohesive sediment. This study aims to introduce a straightforward modeling approach for simulating the grain size distribution of suspended sediment amidst turbulence. Leveraging insights into the contrast between cohesive and noncohesive sediment, we have meticulously revised a stochastic flocculation model originally designed for cohesive sediment to aptly simulate the grain size distribution of noncohesive sediment in suspension. The efficacy of our approach is corroborated through a meticulous comparison between experimental data and the grain size distribution simulated by our newly proposed model. Through numerical simulations, we unveil that the modulation of grain size distribution of suspended sediment is contingent upon the sediment transport capacity of the carrier fluid. Hence, we deduce that our simplified approach to simulating the grain size distribution of suspended sediment, integrated with a sediment transport model, serves as a robust framework for elucidating the pivotal bulk properties of sediment transport.

Keywords

Grain Size Distribution

Stochastic approach

Sediment Transport

Turbulence

많은 연구에서 비점착성 부유사의 입경분포를 평균입경와 표준편차를 이용해 묘사한다. 그러나 부유사는 크기가 다른 많은 입자의 혼합물로 구성되어 있다. 난류조건에서 부유사의 이동은 크기와 밀도로부터 계산된 침강속도에 영향을 받는다. 따라서 비점착성 부유사의 이동을 이해하려면 입경분포를 보다 정량적으로 고려하는 것이 중요하다. 본 연구의 목적은 난류조건에서 부유사의 입경분포를 모의할 수 있는 간편한 모형화 방법을 제시하는 것이다. 점착성 유사와 비점착성 유사의 차이에 대한 이해를 바탕으로, 점착성 부유사를 위한 추계학적 응집 모형을 비점착성 유사의 입경분포 모의에 적합하도록 수정하였다. 본 연구에서 제안하는 간편법의 적용성을 살펴보기 위해 선행연구의 실험자료에 적용하여 모의 결과와 비교하였다. 수치 모의의 결과를 통해 본 연구에서 제안한 모형이 실험값에서 나타나는 주요한 특성을 모사할 수 있다는 점을 확인하였다. 이를 바탕으로 유사 이동 모형을 사용하여 부유사 입경분포를 모의하는 접근 방식이 부유사 입경분포의 중요한 특성을 이해하기에 효과적이라는 결론을 얻었다.

키워드

입경분포

추계학적 접근

유사이동

난류

MAIN

1. 서 론
2. 방법론
2.1 유사 이송 모형에 대한 간략한 설명
2.2 유사 입경분포 모형의 바닥 경계 조건
2.3 부유 모래에 대한 Floc 입경분포 모형의 수정
3. 모형의 적용 및 결과
4. 결 론

1. 서 론

점착성 유사와 비점착성 유사의 주요한 차이점은 크기와 밀도 같은 유사 물성치의 가변성이다. 63 ㎛보다 작은 입자 크기는 실트와 점토 등의 점착성 유사로 분류된다(Law et al., 2008). 점착성 유사는 입자의 크기가 작기 때문에 지속적인 응집 과정을 거친다. 주로 van der Waals 인력으로 인해 발생하는 전기화학적 인력은 1차 입자 또는 더 작은 플럭(Floc)을 응집하게 한다(Mehta, 2013). 형성된 플럭은 유체의 난류 운동으로 인해 더 작은 파편으로 깨진다(Hunt, 1954). 응집과 파괴 과정(Flocculation Process)에 따라 플럭의 크기는 지속적으로 변하게 된다. 전통적으로 플럭은 프랙탈 구조를 가지는 것으로 가정하며 플럭의 밀도는 플럭 크기에 의존된다(Son and Hsu, 2011). 점착성 유사의 침강속도는 응집 과정에 따라 결정되며 점착성 유사는 응집체의 형태로 변화한다. 반면, 모래나 자갈 같은 비점착성 유사는 응집되는 경우가 거의 없다. 이는 입자의 관성 크기가 입자 표면에 작용하는 전기화학적 인력에 비해 상대적으로 크기 때문이다. 따라서 비점착성 유사의 물성치는 거의 일정하게 유지된다.

유사 입자는 크기와 밀도에 따라 침강속도가 다르며, 재부유나 퇴적 거동은 주로 침강속도에 따라 결정된다. 비점착성 부유사는 고정된 밀도를 가지는 것으로 가정되나 다양한 크기가 혼재되어 이동하므로 침강속도 또한 다양하다. 따라서 비점착성 부유사의 이동을 더 명확하게 이해하기 위해서는 입경분포를 확인할 필요가 있다(Gelfenbaum and Smith, 1986; Wright and Parker, 2004). 이전의 많은 연구에서 부유사 입경분포를 누가대수분포를 이용하여 분석하였다(e.g., Friedman, 1962; Tanner, 1964; Visher, 1969; Samaga et al., 1986; Kuhnle, 1993). Visher (1969)는 다른 정규분포를 나타내는 입경분포가 혼재하는 경우에 대수지에서 분포곡선의 단절이 나타난다는 점을 살펴보았다. 단봉형과 다봉형 분포 모두 일반적으로 하천조건에서 관찰된다. Sun et al. (2002)은 부유사가 균질한 물질로 구성되어 있을 때 단봉형 입경분포를 나타냄을 발견하였다. 입경분포의 특성은 일반적으로 대수정규분포로 가정된다(e.g., Beverage and Culbertson, 1964; Friedman, 1962; Purkait, 2002; Sun et al., 2002; Wu et al., 2004). Purkait (2002)는 Usri 강의 측정자료를 이용하여 부유사의 입경분포 특성을 조사하였다. Purkait (2002)에서 부유사의 입경분포가 다른 분포 함수보다 대수정규분포에 가까운 것을 밝혀냈다. 이러한 관찰은 Sengupta (1975)의 발견과 유사성이 있다. 또한 Sengupta (1975)는 닫힌 순환 수로 내 부유사의 입경분포가 대수정규분포를 따르지만, 하상재료는 대수정규분포를 따르지 않음을 밝혀냈다. 다봉형 분포는 일반적으로 대수정규분포의 포락선으로 가정된다(e.g., Sundborg, 1956; Visher, 1969; Middleton, 1976). 부유사의 다양한 입경분포가 존재하는 이유는 유사를 구성하는 원료, 기계적 파손, 선택적 이송에 따른 분류를 기반으로 이해할 수 있다(Sundborg, 1956; Middleton, 1976; Shi et al., 2012). 이상에서 언급한 이유 중 선택적 이송의 영향이 가장 설득력 있는 가설이라고 여겨진다(Middleton, 1976). Middleton (1976)은 부유사와 하상재료(원료)를 비교하여 관찰된 부유사의 입경분포를 분석하였다. 유사 입자는 전단 속도가 입자의 침강속도를 초과할 때 부유를 시작한다는 이론에 기초하여 측정된 유사의 입경분포는 두 개의 하위 집단(견인력과 간헐적 부유)으로 나뉜다. Middleton (1976)은 입자의 각 하위 집단이 서로 다른 이송 메커니즘에 의해 발생한다고 주장한다.

하상재료의 침식은 하상 전단 응력이 유사 입자의 한계소류력을 초과할 때 시작된다. van Rijn (1984)과 Bagnold (1966)에 따르면, 침식된 유사 입자는 난류 속도의 상승 성분이 입자의 침강속도를 초과할 때 부유하게 된다. 난류와(Turbulent Eddy)의 상승 속도와 전단 속도 사이의 관계를 고려할 때, 하상 전단 응력에 기초하는 전단 속도가 유사 입자의 침강속도를 초과할 때 유사의 부유가 발생한다고 가정한다(van Rijn, 1984). 따라서 유사 입자의 부유 거동은 하상재료의 한계소류력에 크게 의존된다. 균일한 크기로 구성된 하상의 경우 유사 입자의 한계소류력은 일반적으로 Shields Diagram에 의해 결정된다(e.g., Graf, 1984; Cao et al., 2006). 하상이 불균일한 유사로 구성된 경우 차폐 효과로 인해 입경이 다른 유사 개별 크기의 한계소류력을 개별적으로 추정하기 어렵다(Kleinhans and van Rijn, 2002). 그러나 실험실 실험 결과에서는 혼합 모래(< 1 mm)의 한계소류력이 거의 일정한 것으로 나타났다(Kuhnle, 1993). 하상은 모래-자갈 혼합물로 구성되어 있지만 모래 크기 범위에서는 모든 크기에서 동일한 이동성이 관찰된다(e.g., Kleinhans and van Rijn, 2002). 여기서 동일한 이동성은 불균일 유사의 한계소류력이 혼합 유사의 평균 직경이 가지는 한계소류력과 유사함을 의미한다(Miller et al., 1977; Kuhnle, 1993; Kleinhans and van Rijn, 2002).

부유사의 입경분포에 대한 유사 및 유동의 특성을 조사하기 위해 많은 실험실 또는 수치 실험이 수행되었다. Kuhnle and Wren (2009)은 다양한 유형의 하상재료를 사용하여 실험실 실험을 수행했다. Kuhnle and Wren (2009)에서는 하상재료 입경분포의 표준편차가 조립사의 부유에 영향을 미친다는 것을 알 수 있다. 하상의 퇴적이 증가하면 조립질 부유사의 비율이 하상재료의 표준편차에 비해 더 급격히 감소한다(Kuhnle and Wren, 2009). 하상층의 깊이가 증가함에 따라 부유사의 조립사 비율이 감소하는 것은 Sengupta (1975)의 실험 결과에서도 나타난다. 또한 Sengupta (1975)에서 유속이 감소할 때 유사 크기의 최빈값이 조립사에서 사립사로 점진적 이동한다고 밝혀졌다. Sengupta (1979)는 부유사의 입경분포에 대한 하상재료와 유속의 상대적 중요성을 연구하기 위해 수로 실험을 수행했다. Sengupta (1979)는 수로 실험에 근거하여 부유사의 입경분포는 하상재료가 아니라 소류사의 입경분포에 큰 영향을 받는다는 점을 제시하였다. Sengupta (1979)에서 이용한 하상재료는 다봉형 분포를 보이지만, 부유사에서 관찰된 입경분포는 전형적인 대수정규분포를 나타낸다. 이 결과로부터, 다봉형 분포에 나타난 각 분포가 반드시 다른 유사 이송 방식을 나타내는 것이 아님을 알 수 있다(Sengupta, 1979). 실험실 실험 결과에 따르면 흐름 속도, 하상재료의 구성, 측정 높이 등이 부유사 입경분포에 영향을 주는 것으로 나타났다(Kuhnle and Wren, 2009; Sengupta, 1975, 1979).

부유사의 입경분포를 예측하기 위해 수치 모형이 제안되었다(e.g., Ghosh et al., 1981; Ghosh and Mazumder, 1981; Mazumder, 1994; Pal and Ghoshal, 2014a, 2014b). Ghosh et al. (1981)은 소류사 공식과 부유사에 대한 Hunt의 확산 방정식을 통합하여 흐름 내 부유사의 입경분포 모형을 개발하였다. 소류사 공식은 Sengupta (1979)의 실험자료와 비교할 때 합리적인 결과를 모의하였다. Mazumder (1994)는 Ghosh et al. (1981)의 모형을 바탕으로 부유사에 대한 수정된 입자 입경분포 모형을 제안했다. 소류사 공식을 하상물질의 이동 속도 개념으로 대체하여 Ghosh et al. (1981)의 결과를 비교할 때 수치 모의 결과가 향상되었다. 모의 결과로부터 소류사 계산이 필요하지 않으므로 하상재료의 이동 속도를 활용하는 것이 더 현실적인 방법임이 주장되었다(Mazumder, 1994). Pal and Ghoshal (2014b)은 부유사의 입경분포를 재현하기 위해 수학적으로 수치 모형을 제안하였다. Pal and Ghoshal (2014a)의 수치 모형은 간섭침강과 성층(Stratification) 영향을 고려하도록 수정되었다. 입경분포 모형에서 요구되는 지수는 Mazumder et al. (2005)이 개발한 지수법칙 멱함수를 사용하여 계산된다. 모의 결과를 바탕으로 추가적인 효과를 고려하면 수치 모형 결과가 개선된다는 결론을 얻었다(Pal and Ghoshal, 2014b). 앞서 언급한 수치 연구는 부유사의 입경분포 특성에 대한 흐름의 속도, 하상재료의 크기가 주는 영향에 초점을 맞췄다. 일반적으로 부유사의 입경분포는 하상재료, 흐름의 유동특성, 하상층의 깊이에 의해 큰 영향을 받는 것으로 알려져 있다(Sengupta, 1979; Mazumder, 1994; Kuhnle and Wren, 2009). 그러나 유사 입자를 부유시키는 직접적인 원인은 난류섭동(Turbulent Velocity Fluctuation)이다(van Rijn, 1984; Bagnold, 1966). 난류섭동이 상대적으로 크면 입자는 빈번한 하상 접촉 없이 부유 상태를 유지한다. 따라서 부유사의 이동과 입경분포를 연구할 때 난류에 대한 고려가 필요하다. 이 연구에서는 Byun and Son (2020)에서 제안한 점착성 부유사(부유 플럭)의 입경분포 모의모형을 수정하여 비점착성 부유사(모래유사)의 입경분포 모의모형을 제안한다. 이를 위해서 추계학적 접근법이 활용된다. 추계학적 또는 무작위적 접근법(random approach)은 유사 특성 모의서 널리 사용되는 방법이다(e.g., Kleinhans and van Rijn, 2002; Lisle et al., 1998; Shaw et al., 2008). 부유사의 입경분포는 크기 변화를 계산하고 그 결과를 규정된 확률 함수를 기반으로 분석하여 산정된다. 본 연구에서는 선행연구를 바탕으로 대수정규분포를 부유사의 입경분포로 가정한다(e.g., Visher, 1969; Sengupta, 1979; Ghosh and Mazumder, 1981; Kuhnle, 1993; Purkait, 2002; Mazumder et al., 2005). 이 연구의 주요한 목적은 유사의 특성과 유동특성을 고려하여 부유사의 입경분포를 모의하는 모형 개발을 위한 간편법을 제안하는 것이다.

2. 방법론

부유사의 거동을 보다 정확하게 이해하기 위해서는 흐름의 평균속도성분(Mean Component of Velocity), 난류섭동(Turbulent Fluctuation) 등 유동 특성 이외에 부유사의 입경분포 등 유사의 물성치 특성을 함께 살펴보는 과정이 필요하다. 이는 유사 입자의 재부유 및 퇴적을 결정하는 가장 지배적인 요인인 침강속도가 유사 특성(입자의 크기 및 밀도)의 함수이기 때문이다. 유사 입자의 재부유 거동은 난류 운동 에너지(Velocity Fluctuation)을 주요 인자로 한다. 그러므로 퇴적에 대한 난류의 영향과 부유사의 추가 입경분포를 포함하는 것이 필수적이다. 이 연구에서는 난류에 의해 부유되는 유사의 입경분포 모형을 제시한다. 2.1절에서는 Son and Hsu (2011)의 부유사 거동을 고려한 유사 이송 모형을 간략하게 소개한다. 비점착성 부유사의 입경분포를 모의하기 위한 입경분포 모형에 대한 설명과 절차는 2.2절과 2.3절에서 제시한다.

2.1 유사 이송 모형에 대한 간략한 설명

본 절에서는 부유사 입경분포 모형을 적용하기에 앞서 Son and Hsu (2011)가 제안한 유사 이송 모형의 특성을 간략하게 소개한다. 유사 이송 모형은 주로 이송와 확산 과정을 나타내는 두 항으로 구성된다. 부유사 입자의 침전에 의한 난류 및 이송에 의한 연직 혼합을 고려한다(Son and Hsu, 2011).

(1)

\frac{\partial ϕ_{s}}{\partial t} = \frac{\partial}{\partial z} (ϕ_{s} W_{s} + \frac{ν_{t} + ν}{σ_{c}} \frac{\partial ϕ_{s}}{\partial z})

여기서 $ϕ_{s}$ = 부유사의 부피농도, $t$ = 시간, $W_{s}$ = 부유사의 침강속도, 𝜈 = 동점성 계수, $𝜈_{t}$ = 와점성 계수, $σ_{c}$ = 슈미트수이다. $σ_{c}$ 값은 유사 입자의 특성과 관련이 있지만(Son et al., 2016), 정상 흐름 조건에서 문제를 간단히 하기 위해 비점착성 유사 이송에 대한 선행 연구(Hsu et al., 2007)를 바탕으로 0.5의 고정된 값을 활용했다. Son and Hsu (2011) 모형에서 $W_{s}$ 는 간섭침강효과(Hindered Settling Effect)를 고려한 Stokes의 법칙에 의해 계산된다(Richardson and Zaki, 1954). Stokes 법칙은 비교적 작은 입자에 대해 유효한 반면, 본 연구에서 고려하는 유사 입자는 모래 크기 범위를 갖는다. 따라서 부유 입자의 침강속도를 얻기 위해서는 보다 일반적인 공식이 필요하며, 모래 입자의 침강속도를 계산하기 위해서는 입경 조건에 Newtown의 법칙이 적용되기도 한다.

(2)

W_{s} = {[\frac{4}{3} \frac{D}{C_{D}} g (s_{s} - 1)]}^{1 / 2} {(1 - ϕ_{s})}^{4}

여기서 $D$ = 부유사 입경, $C_{D}$ = 무차원 항력계수, $s_{s}$ = 부유사 비중, $g$ = 중력가속도이다. ${(1 - ϕ_{s})}^{4}$ 항은 간섭침전효과(Hindered Settle Effect)를 나타낸다(Richardson and Zaki, 1954). Eq. (2)은 유사의 중량, 항력, 부력 간 힘의 균형으로부터 유도된다. $C_{D}$ 는 모든 부유사 입자가 구형이라는 가정하에 0.5로 설정하였다(Man and Tsai, 2007). Eq. (1)의 우변 첫 번째 항은 중력가속도와 입자의 침강에 의한 이송이고, 두 번째 항은 유사 입자의 연직 확산을 나타낸다. 여기서 유사 입자의 연직 방향 확산은 난류 확산에 의해 발생하며 유사 농도 $\partial ϕ / \partial t$ 의 연직 구배 항을 통해서는 높은 유사 농도에서 낮은 유사 농도로 발생하는 이동을 재현한다. 난류 흐름에서 유사 입자의 확산 강도는 유효점성 $𝜈 + 𝜈_{t}$ 와 $σ_{c}$ 의 비율로 정량화된다. 이송-확산 방정식에서 연직 이동을 계산하려면 흐름 운동량 방정식과 난류의 닫힘 문제에 대한 지배 방정식이 필요하다. Eq. (1)의 $𝜈_{t}$ 를 구하기 위해 본 연구에서는 표준 $k - ε$ 모형이 채택한다(Son and Hsu, 2011).

(3)

\begin{aligned} (1 - ϕ_{s}) \frac{\partial k}{\partial t} = & ν_{t} [{(\frac{\partial u}{\partial z})}^{2} + {(\frac{\partial v}{\partial z})}^{2}] + \frac{\partial}{\partial z} [(ν + \frac{ν_{t}}{σ_{k}}) \frac{\partial (1 - ϕ_{s}) k}{\partial z}] - (1 - ϕ_{s}) ϵ + (s_{s} - 1) g \frac{ν_{t}}{σ_{c}} \frac{\partial ϕ_{s}}{\partial z} \end{aligned}

(4)

\begin{aligned} (1 - ϕ_{s}) \frac{\partial ϵ}{\partial t} = & C_{ϵ 1} \frac{ϵ}{k} ν_{t} [{(\frac{\partial u}{\partial z})}^{2} + {(\frac{\partial v}{\partial z})}^{2}] + \frac{\partial}{\partial z} [(ν + \frac{ν_{t}}{σ_{ϵ}}) \frac{\partial (1 - ϕ_{s}) ϵ}{\partial z}] - C_{ϵ 2} (1 - ϕ_{s}) \frac{ϵ^{2}}{k} + C_{ϵ 3} \frac{ϵ}{k} (S_{s} - 1) g \frac{ν_{t}}{σ_{c}} \frac{\partial ϕ_{s}}{\partial z} \end{aligned}

여기서 $C_{ϵ 1}$ , $C_{ϵ 2}$ , $C_{ϵ 3}$ , $σ_{k}$ , $σ_{\in}$ = 수치적 계수, $k$ = 난류 운동 에너지, 𝜖 = 에너지 소산율, $u$ 및 $v$ = 각각 유선 방향과 흐름 횡단 방향의 흐름 속도이다. Eqs. (3) and (4)의 우변 마지막 항은 유사의 존재로 인해 이송 흐름의 난류 감소 효과(Turbulence Damping Effect)를 나타낸다. Eq. (3) and (4)에 표시된 수치 계수는 Table 1에 나타냈다. $𝜈_{t}$ 는 $k$ 와 𝜖의 계산값을 사용하여 얻는다.

(5)

ν_{t} = C_{μ} \frac{k^{2}}{ε} (1 - ϕ_{s})

여기서 $C_{μ}$ = 모형 계수(0.09)이다. Eqs. (3), (4), (5)에서 보이는 $1 - ϕ_{s}$ 는 유사 입자에 난류가 거의 존재하지 않는다는 가정을 나타낸다. 흐름 속도는 유체와 부유물의 다상위상 방정식(Multi-phase Equation)을 단순화하여 유도된 운동량 방정식으로 계산한다.

(6)

\begin{aligned} \frac{\partial u}{\partial t} = & - \frac{1}{ρ_{w}} \frac{\partial p}{\partial x} + \frac{1}{ρ_{w} (1 - ϕ_{s})} \frac{\partial τ_{x z}^{w}}{\partial x} + \frac{1 + (s_{s}^{w} - 1) ϕ_{s}}{1 - ϕ_{s}} g \sin α_{s} \end{aligned}

여기서 $p$ = 압력, 𝛼 = 하상 기울기, $τ_{x z}^{w}$ 는 계산된 난류 흐름에서의 분명한 레이놀즈 응력이다.

(7)

τ_{x z}^{w} = ρ_{w} (ν + ν_{t}) \frac{\partial u}{\partial z}

여기서 𝜈 = 물의 동점성계수이다.

Table 1.

Standard values of the numerical coefficients for $k$ -𝜖 model (Launder and Sharma, 1974)

Coefficient	$C_{μ}$	$C_{ϵ 1}$	$C_{ϵ 2}$	$C_{ϵ 3}$	$σ_{k}$	$σ_{ϵ}$
Value	0.09	1.44	1.92	0.00	1.00	1.30

2.2 유사 입경분포 모형의 바닥 경계 조건

하상으로부터 침식하는 부유사의 입경분포를 모형화하기 위해서는 하상에서의 침식에 대한 경계 조건을 결정하여야 한다. Son and Hsu (2011)에서 이용한 연속적 침식 공식은 다음과 같다.

(8)

E = M a x [β_{e} (\frac{τ_{b}}{τ_{c}} - 1), 0]

여기서 $τ_{b}$ = 하상 전단응력, $τ_{c}$ = 한계소류력, $β_{e}$ = 경험적인 침식 flux 계수, $E$ = 침식 flux를 의미한다. 하상 전단응력은 마찰 속도( $u$ *)를 이용하여 구하고 매 시간단계마다( $dt$ ) 갱신한다.

(9)

τ_{b} = ρ_{w} u_{*}^{2}

유사 이동 모형의 하상 경계는 유사 입자의 소류와 부유 사이에 위치한다. 여기서 하상재료(하상층)에서 소류사까지의 이송 효과는 본 연구의 모형에 포함되지 않는다. 바닥 경계에서 유사 입자의 초기 운동은 부유사의 입경분포에 즉시 영향을 미치는 것으로 가정한다. 경계에서 유사 입자의 초기 운동에 대한 기준은 Shields 방정식(Graf, 1984)을 사용하여 결정된다.

(10)

τ_{c} = 0.06 g (ρ_{s} - ρ_{w}) D_{50}

여기서 $D_{50}$ = 바닥 경계에 위치한 혼합 유사의 평균 직경이다. 본 연구에서는 선행 실험 결과에 대한 내용을 바탕으로 혼합 유사의 이동성이 동일하다고 가정한다(Miller et al., 1977; Kuhnle, 1993; Kleinhans and van Rijn, 2002).

2.3 부유 모래에 대한 Floc 입경분포 모형의 수정

본 연구의 부유사 입경분포 모형은 Byun and Son (2020)에서 개발한 점착성 유사(플럭) 입경분포 모형으로부터 개념적으로 도출된다. Byun and Son (2020)는 Son and Hsu (2011)가 제안한 점착성 유사에 대한 응집모형을 응용하여 플럭 입경분포 모형을 제시하였다. Son and Hsu (2011)는 플럭의 순간적인 평균 직경을 모의하는 플럭 응집모형을 개발하였다. Son and Hsu (2011)의 모형에서 플럭의 구조는 프랙탈 기하학을 따르며 플럭 크기에 따라 플럭 밀도가 변하게 된다.

(11)

\frac{d D_{f}}{d t} = \frac{G d^{β}}{β l n \frac{D}{d} + 1} \{(\frac{κ'_{A}}{3} d^{F - 3} D^{- F + 4 - β} - \frac{κ'_{B}}{3} {(\frac{μ G}{B_{1}})}^{q} d^{- p + \frac{2 q}{3} F} D^{1 - β + \frac{2 q}{3} (3 - F)} (D - d)^{p})\}

여기서 $D_{f}$ = 응집 과정에서 형성된 플럭의 평균 크기, $d$ = 1차입자의 크기, $c$ = 질량 농도, $ρ_{s}$ = 1차입자의 밀도, $B_{1}$ = 플럭의 항복강도와 관련된 경험적 매개변수, $G$ = 난류전단률(Turbulent Shear Rate, $G = \sqrt{ε ∕ ν}$ ), 𝜇 = 점성계수, $p$ 및 $q$ = 경험적 계수는 각각 1.0, 0.5로 설정된다. Floc( $F$ )의 프랙탈 차원은 Khelifa and Hill (2006)이 제안한 거듭제곱 관계를 사용하여 추정된다.

(12)

F = α {(\frac{D_{f}}{d})}^{β}

Eq. (12)에서 𝛼는 3.0으로 설정되었고 𝛽는 floc 크기와 프랙탈 차원 특성을 기초로 결정된다(Khelifa and Hill, 2006). 플럭의 프랙탈 차원은 플럭의 크기가 1차입자의 크기와 동일해지고 플럭의 밀도가 1차 입자의 밀도와 유사해지면 3.0에 가까워진다.

(13)

ρ_{f} = ρ_{w} + (ρ_{s} - ρ_{w}) {(\frac{D_{f}}{d})}^{F - 3}

여기서 $ρ_{w}$ = 물의 밀도, $ρ_{f}$ = 플럭의 밀도이다. Eq. (8)에서 $k_{A}^{'}$ 은 응집을 일으키는 효율 매개변수이고 $k_{B}^{'}$ 는 난류 전단으로 인한 플럭 파괴를 의미하는 파괴 매개변수이다. 플럭의 파괴 과정은 이송 유체의 난류 운동에 의해 발생하므로 응집체의 파괴는 무작위적로 발생한다고 가정한다. 파괴 과정의 무작위 운동 개념에서 $k_{B}^{'}$ 는 규정된 확률 함수에서 추출된 난수로 가정한다. 플럭 응집모형에 대한 추계학적 접근 방식을 채택함으로써 플럭 크기의 변동을 얻는다(Eq. (11)). 플럭 응집모형의 추계학적 과정을 모의하기 위해서 Monte Carlo 방법을 사용한다. 수집된 크기 변동 데이터는 Byun and Son (2020)에서 규정된 확률 함수를 따르는 플럭 입경분포를 나타낸다.

본 연구에서는 플럭의 입경분포를 살펴본 선행연구(Byun and Son, 2020)의 수치모형(Eq. (11))을 비점착성 부유사 입경분포를 모의하도록 수정하였다. 비점착성 유사는 유사의 특성, 유사 입자의 크기와 밀도가 일정하다는 점에서 점착성 유사와 구분된다. 부유사의 입경분포를 모의하기 위해 유사 특성의 변화와 관련된 매개변수를 수정하였다. 첫째, 점착성 유사의 밀도는 가변 프랙탈 차원으로 정량화하며 크기에 따라 달라진다. 비점착성 유사를 고려하기 위해 프랙탈 차원을 3.0으로 설정하였다. 따라서 모든 부유사는 동일한 밀도를 가지며 더 이상 유사 크기의 함수가 아니다. 둘째, 점착성 유사의 크기는 전기-화학적 결합력과 난류 전단력에 의해 지속적으로 변화한다. 플럭 입경분포 모형에서는 재부유된 응집성 유사 입자가 응집(크기 증가)과 파괴(크기 감소)를 겪는 것은 자연스럽다. 하지만 비점착성 유사의 경우는 유사 크기가 고정적이다. 서로 다른 크기를 갖는 비점착성 유사의 부유는 하상 퇴적물의 재부유와 퇴적 거동에 의해 발생한다. 하지만 플럭 응집모형은 두 가지 가정을 기반으로 모래 부유사의 입경분포를 모의하는데 활용될 수 있다. 즉, 바닥 경계의 정의와 모래의 이동성이 동일하다고 가정한다. 2.2절에서 언급한 것과 같이, 실제 퇴적층으로부터 소류사의 유입은 모형에서 고려하지 않는다. 유사 혼합물의 재부유 및 퇴적 거동은 Shields 방정식 기준에 따라 바닥 경계에서 발생한다. 모래 크기에 해당하는 유사의 동일한 이동성은 많은 실험실 실험에서 확인되었다(e.g., Miller et al., 1977; Kuhnle, 1993; Kleinhans and van Rijn, 2002). 이는 중간 크기보다 큰 혼합물의 유사 입자가 균일한 하상재료의 동일한 입자보다 더 이동성이 높다는 것을 의미한다(Kleinhans and van Rijn, 2002). 더 작은 입자는 균일한 하상재료의 같은 입자가 더 큰 한계소류력 조건에서 움직이기 시작한다. 바닥 경계에서 동일 이동성 개념을 채택함으로써 크기 변동에서 응집과 파괴가 각 하상으로부터의 모래의 재부유 및 퇴적과 부합한다. 동적 평형 상태에 도달한 후 크기의 변화는 모래의 재부유 및 퇴적을 의미한다. 따라서 플럭과 관련된 계수는 수치 계수로 간주한다. 본 연구에서 고려한 유사 입자는 이동성을 채택하기 위해 모래 크기로 제한된다. 결과적으로 밀도가 일정한 유사 입자가 모인 크기 변동 모의값은 부유사의 입경분포를 나타낸다. 부유사의 크기 변동을 모의하기 위해 퇴적 거동과 관련된 자유 매개변수는 난수로 간주된다. 추계학적 과정(또는 무작위적 과정, random process)을 갖는 입경분포 모형을 모의하기 위해 Monte Carlo (MC) 방법이 사용된다(Gentle, 2003).

(14)

p_{d} = \exp [\begin{array}{l} \log (\frac{m^{2}}{\sqrt{\frac{v}{m^{2}} + 1}}) + \sqrt{(\log \frac{v}{m^{2}} + 1)} \times \sqrt{- 2 \log A} \cos (2 π B) \end{array}]

여기서 $m$ = 대수정규분포의 평균, $v$ = 대수정규분포의 분산, $A$ 및 $B$ = 균일하게 분포된 난수이다.

이전 측정값과 실험자료를 기반으로 대수정규분포를 모의하기 위해 대수정규함수에서 대수정규분포 난수( $p_{d}$ )를 산정한다(Visher, 1969; Sengupta, 1979; Ghosh and Mazumder, 1981; Kuhnle, 1993; Purkait, 2002; Mazumder et al., 2005). 단순화를 위해 Box-Muller 방법을 사용하여 $p_{d}$ 를 생성한다(Box and Muller, 1958). 규정된 시간 단계( $Δ t$ )를 기준으로 매시간 단계마다 $p_{d}$ 가 생성된다. $Δ t$ 동안 $p_{d}$ 는 상수로 유지되며 유사 입경분포는 $p_{d}$ 의 상수값을 기반으로 크기 변동을 계산한다. 크기 변동 모형은 Eq. (14)로부터 생성된 난수 $p_{d}$ 를 사용하여 모래의 크기 변동을 계산한다.

(15)

\frac{d D}{d t} = \frac{r_{1} G D^{r_{2}}}{\ln (\frac{D}{D_{s}}) + 1} [+ p_{r} c - p_{d} (D - D_{s})]

여기서 $r_{1}$ , $r_{2}$ = Eq. (11)로부터 도출된 경험적 무차원 계수, $D_{s}$ = 바닥 경계에 있는 하상재료의 최소입경, $D$ = 부유사 입경, $c$ = 부유사의 질량 농도, $p_{r}$ = 유사 재부유와 관련된 무차원 매개변수, $p_{d}$ = 유사 퇴적과 관련된 무차원 매개변수(퇴적계수)이다. Eq. (15)에서 모의한 부유사의 입경분포는 동적 평형 상태에 도달한 후 유효하다. 음의 부호는 침강으로 인해 퇴적된 입자의 제거 효과를 의미하며 양의 부호는 재부유로 인한 추가 입자의 효과를 의미한다. 평형 상태 후 응집된 크기 변동값( $c$ and $G$ )은 부유한 비점착성 유사의 입경분포를 나타낸다.

각 계산 주기가 시작될 때, 비점착성 유사의 입경분포 모형은 생성된 난수(Eq. (14))를 사용하여 먼저 계산한다(Eq. (15)). 유사 입자의 침강속도는 갱신된 유사입경을 사용하여 Eq. (2)에 의해 결정된 다음 이송-확산 방정식으로 계산한다(Eq. (1)). 이후 $k$ -𝜖 모형을 계산하고 Eq. (3)과 Eq. (5)를 통해 와점성계수와 난류에 대한 정보를 얻는다. 흐름의 운동량 방정식은 각 계산 주기가 끝날 때 갱신된 난류 정보를 기반으로 흐름 속도를 얻기 위해 구해진다(Eq. (6)). 따라서 부유한 비점착성 유사의 입경분포는 난류와 유체역학적 특성을 고려하여 구해진다. 입자 크기에 기초한 이송-확산 방정식을 계산하면 질량 보존을 증명할 수 있다. 여기서 각 계산 주기의 시간 간격( $Δ t$ )은 Courant-Friedrichs-Lewy 조건에 의해 결정된다. 초기조건을 위해서는 자연적 1차입자의 크기로 고려되는 4 ㎛를 적용하였고 상하류 등의 구체적 경계조건은 요구되지 않는 수치해석에 해당된다.

3. 모형의 적용 및 결과

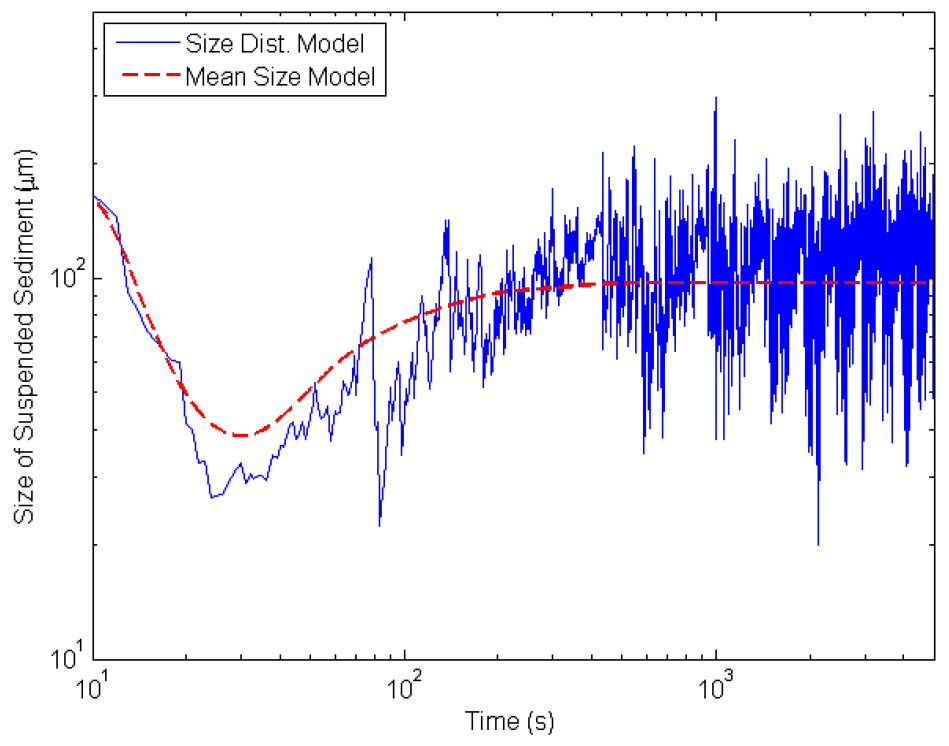
이 장에서는 개발된 부유사 입경분포 모형(Eqs. (14) and (15))의 기능과 한계를 검증하였다. 이를 위해서는 선행 연구사례에서 수집 가능한 실험값을 이용하였다. Eqs. (14) and (15)에서 알 수 있듯이 수치 모형은 주로 질량 농도 $c$ , 난류전단률 $G$ , 최소 입경 $D_{s}$ , 재부유 계수 $p_{r}$ , 평균 $m$ 및 편차 $v$ , 퇴적계수 $p_{d}$ 에 의존된다. 무차원 계수 $r_{1}$ 및 $r_{2}$ 는 점착성 유사의 가변 밀도 개념에서 제안되었다. 본 연구의 모형 개발을 위해서 $r_{1}$ 및 $r_{2}$ 를 상수로 고정하였으며 선행 연구(Byun and Son, 2020)와 동일한 값을 사용하였다. $D_{s}$ 는 크기 변동이 계산될 때 부유사의 가능한 최소 크기를 지정한다. 다양한 유사 크기를 모의하기 위해 $D_{s}$ 값은 이전 연구를 따라 4 ㎛로 지정하였다(Son and Hsu, 2011; Winterwerp, 1998; Byun and Son, 2020). Son and Hsu (2011)의 모형은 초기 유사 크기에 의존하지 않고 점착성 유사의 평균 크기를 계산한다(Son and Hsu, 2008). 여기에서 비점착성 유사의 초기 크기는 $D_{s}$ 값에 따라 결정된다. 따라서 동적 평형 상태에서 모의되는 크기 편차는 $D_{s}$ 값에 의존하지 않는다. $c$ 및 $G$ 는 기존 실험에서 입증된 유체역학적 조건을 재현하기 위해 유체역학적 모형에 의해 결정된다. 마지막으로 $p_{r}$ , $m$ 및 $v$ 는 각 실험값을 기초로 보정된 자유 매개변수이다. 부유사의 중앙값은 퇴적( $m$ ) 및 재부유( $p_{r}$ ) 사이의 균형에 의해 결정되며, 분포의 변화는 난수( $v$ )의 변화에 의해 보정된다. 모의된 입경분포 모양은 난수의 확률 함수( $p_{d}$ )에 의해 결정된다. 따라서 이 세 가지 경험 계수는 각 실험에 대해 보정된다. 비점착성 유사의 입경분포는 동적 평형 상태에 도달한 후 크기 편차에 대한 자료를 이용하여 구한다(Fig. 1). 마지막 3000개 시간 단계의 크기 변동값은 입자 입경분포 모형이 2000개 시간 단계 이전에 동적 평형상태에 접근한다는 가정하에 활용된다. 동적 평형 상태에 도달한 후, 일정한 질량 농도 및 난류 전단 속도 조건에서 특정 높이에서의 크기 변동이 얻어진다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-05/N020057504/images/kwra_57_05_04_F1.jpg

Fig. 1.

The comparison of transient mean size from deterministic model and simulated size fluctuation from grain size distribution model adopted stochastic approach

Samaga et al. (1986)은 부유사의 입경분포에 대한 하상재료의 입경분포 효과를 조사하기 위해 비균질적인 하상재료를 사용하여 수로 실험을 수행했다. 본 연구에서 사용한 실험값은 하상재료가 M2인 시리즈 1(S1)과 하상재료가 M3인 시리즈 4(S4)이다. 부유된 M2와 M3의 입경분포는 중앙값이 각각 0.5 mm와 0.42 mm인 단봉형 분포를 나타낸다. 실험실 실험에 사용된 모든 유사는 비중이 2.65이다. Samaga et al. (1986) 에서 측정된 유사의 입경분포는 0.5 $ϕ$ 단위 간격으로 이격된 각 등급의 개별 분율로 설명된다. 모의 결과와 측정된 데이터를 비교하기 위해 개별 분율을 부피 비율로 조정한다. 측정된 S1과 S4의 질량 농도는 각각 0.8397 g/l와 1.4228 g/l이다. 실험은 수로의 기울기가 0.00496(S1)과 0.00542(S4)로 수행되었다. S1 실험의 수심과 수평속도는 각각 0.072 m와 0.525 m/s이다. S4 실험의 수심과 수평속도는 각각 0.066 m와 0.599 m/s이다. Samaga et al. (1986)에서 제시하지 않는 질량농도의 연직분포는 수심이 얕고 유속이 빠른 조건을 고려하여 균일하게 분포되어 있는 것으로 가정한다. S1과 S4에 대한 수치 실험 조건은 Table 2로 만들었다. 수치 모형을 실험실 실험에 사용하기 위해 수로 기울기의 효과는 중력가속도( $g$ )를 흐름 방향( $g_{x}$ )과 연직 방향( $g_{z}$ )으로 분해하여 적용한다. 하상재료의 등이동성 개념 하에서 하상재료의 중앙값 크기를 사용하여 Shield 방정식으로부터 구한다. 따라서 하상재료의 초기 운동은 동시에 발생되고, 계산된 한계소류력은 하상재료를 나타내는 것으로 가정한다(Kleinhans and van Rijn, 2002). 연직 방향으로 평균 질량 농도와 속도를 재현하기 위해 수치 모형의 경계 조건으로 인한 수심과 수평속도의 수정이 필요하다.

Table 2.

Condition for numerical experiment (Samaga et al., 1986)

Test No.	$H^{'}$ (m)	$u 0$ (m/s)	Re	$g_{x}$ (m/s²)	$g_{z}$ (m/s²)	$τ_{c}$ (Pa)	$p_{r}$	$p_{d}$
Test No.	$H^{'}$ (m)	$u 0$ (m/s)	Re	$g_{x}$ (m/s²)	$g_{z}$ (m/s²)	$τ_{c}$ (Pa)	$p_{r}$	$m$	$v$
S1	1.92	0.925	1.78×10⁶	0.0531	9.8099	0.408	31.50	4.8510^-5	9.610^-9
S4	1.8	0.815	1.47×10⁶	0.0487	9.8099	0.418	31.50	4.4510^-5	9.9810^-9

본 연구에서 사용된 수치 모형은 유사 농도의 수면에서 경계조건을 갖는다. Figs. 2(a) and 2(c)는 각각 S1과 S4의 부유사 농도 및 유속에 대한 연직분포 결과를 보여준다. 수치 실험을 위한 수심( $H'$ )과 흐름 방향(x방향) 유속의 수심적분값( $u 0$ )을 보정하여 실험 결과를 재현하였다. 계산된 0.072 m 이하 평균 흐름방향 평균유속은 0.525 m/s (S1) 이다. S4의 평균 흐름방향 유속은 약 0.066 m 수심 내에서 0.599 m/s로 산정된다. Figs. 2(b) and 2(d)는 Figs. 2(a) and 2(c)에서 나타나는 질량농도와 흐름방향 유속 조건에서 모의된 모형결과와 측정값을 보여준다. 모의 결과가 측정값과 잘 일치하는 것이 Fig. 2에서 확인된다. Son and Hsu (2011)의 모형에서는 난류 경계층에서 수평속도의 연직 구조를 모사하기 위해 유속 연직분포의 로그법칙(logarithmic law of the wall)을 채택한다. 흐름방향 유속의 연직분포는 규정된 수심적분유속과 relaxation 시간 방법을 기초로 생성된다(Son and Hsu, 2011).

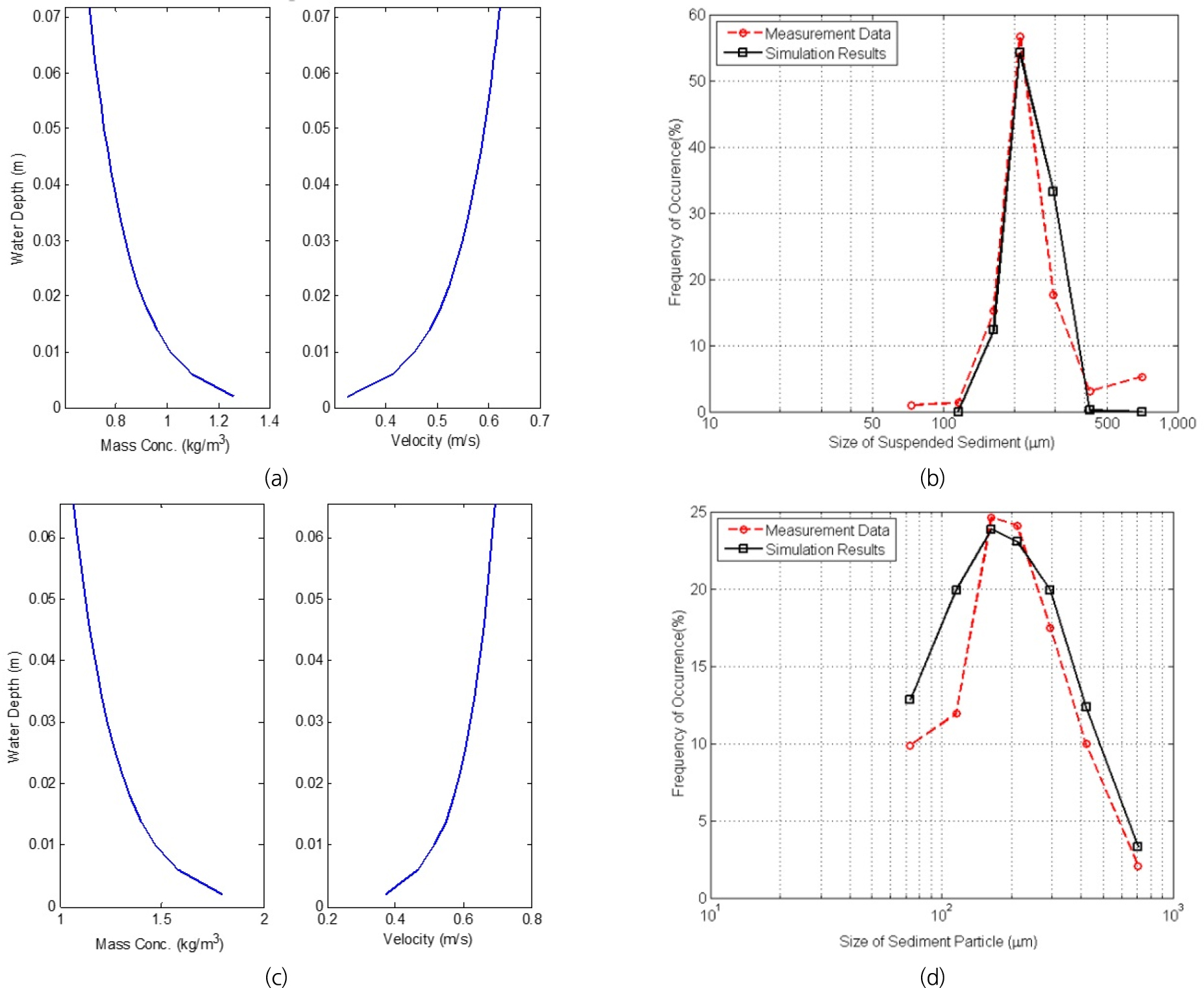
https://cdn.apub.kr/journalsite/sites/kwra/2024-057-05/N020057504/images/kwra_57_05_04_F2.jpg

Fig. 2.

Experimental results of equilibrium sedimentation and hydrodynamics (Samaga et al., 1986) and model results by the present model. Figs. 2(a) and 2(c) show the vertical profiles of sediment concentration and horizontal velocity of S1 and S4, respectively. Figs. 2(b) and 2(d) represent size distribution of suspended sediment under the condition of identical size interval (b: S1, d: S4). The mid-point of each class interval is based on -scale described in Samaga et al. (1986)

Fig. 3은 Sengupta (1975, 1979) 흐름방향 유속 측정값과 모의결과를 보여준다. 유속 모의값이 실험 결과와 합리적으로 일치함을 알 수 있다(Fig. 3). Sengupta (1975, 1979)는 폐회로 수로 내 부유사의 입경분포에 대한 실험 역시 수행했다. Sengupta (1975, 1979)에서 활용된 하상재료는 이봉형 분포를 나타내지만 부유사의 입경분포는 정형적인 모습에 가까운 대수정규분포를 나타낸다(Sengupta, 1975; 1979). 따라서 하상층(Bed 2 및 Bed 3)의 한계소류력을 얻기 위해 하상재료의 중앙값을 추정하였다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-05/N020057504/images/kwra_57_05_04_F3.jpg

Fig. 3.

Simulated results and measured data from Sengupta (1975, 1979). The vertical profiles of horizontal velocities of Bed 2 (a) and Bed 3 (b). The vertical profile of velocities is assumed to follow logarithmic law of turbulent boundary layer

본 연구에서는 두 가지 하상재료의 실험값을 활용한다. 유사 상부의 다른 높이에서 측정된 부유사의 입경분포 중, Bed 2(B2)가 있는 하상의 상부 2.33 cm, Bed 3(B3)이 있는 하상의 상부 17.5 cm의 입경분포가 본 연구에서 개발한 모형의 검증에 사용된다. 하상재료의 중간 크기는 0.172 mm (B2)와 0.236 mm (B3)이다. 수치실험을 위한 조건과 계산된 한계소류력은 Table 3에 요약되어 있다. 유사 입자의 밀도는 2,650 ㎏/m³로 가정한다. 위에서 언급한 바와 같이, 수심과 수심적분유속을 보정하는 과정이 필요하다(Table 3). 실험에 대한 정확한 정보가 부족하기 때문에 부유사의 질량 농도는 바닥 경계 조건(Shields 방정식)에 의해 재현될 수 있다고 가정한다. Fig. 4는 부유한 유사의 입경분포에 대한 수치 및 실험 결과를 보여준다. B2와 B3의 실험 결과를 비교할 때 본 연구에서 제안한 부유사 입경분포모형이 합리적인 모의 결과를 산정한다는 점을 알 수 있다(Fig. 4).

Table 3.

Condition for numerical experiment (Sengupta, 1975; 1979)

Test No.	$H^{'}$ (m)	$u 0$ (m/s)	Re	$g_{x}$ (m/s²)	$g_{z}$ (m/s²)	$τ_{c}$ (Pa)	$p_{r}$	$p_{d}$
Test No.	$H^{'}$ (m)	$u 0$ (m/s)	Re	$g_{x}$ (m/s²)	$g_{z}$ (m/s²)	$τ_{c}$ (Pa)	$p_{r}$	$m$	$v$
B2	1.9	1.07	2.03×10⁶	0.0177	9.8099	0.1672	6.8536	1.83×10^-4	2.56×10^-7
B3	2.4	1.30	3.12×10⁶	0.0487	9.8099	0.2293	10.50	1.25×10^-4	2.75×10^-8

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-05/N020057504/images/kwra_57_05_04_F4.jpg

Fig. 4.

Simulation results and experiment data from Sengupta (1975, 1979). The size distribution of noncohesive sediment in suspension with Bed 2 (a) and Bed 3 (b). The median sizes of suspended sediment are calculated as 0.074 mm (Bed 2), 0.109 mm (Bed 3), respectively. The mid-point of each class interval is based on 𝜙-scale described in Sengupta (1975, 1979)

4. 결 론

본 연구에서는 기개발된 점착성 유사(플럭)의 입도분포 모형을 수정, 보완하여 비점착성 부유사의 입경분포를 모의할 수 있는 모형을 개발하였다. 비점착성 유사의 밀도가 일정하다는 단순한 개념을 기본으로 하는 접근법이 적용되어 계산에 필요한 정량적 비용을 절감하고자 하였다. 본 연구의 모형은 몇 가지 장점과 한계를 가지고 있다. 가장 주목할 특징은 모형 개발을 위한 접근법의 간편함이다. 매개변수 중 하나를 특정 확률 분포를 갖는 난수로 간주하여 부유사의 입경분포를 모의하였다. 부유사 입경분포에 대한 모의는 이론적으로 유동 및 유사이동 모형을 기반으로 한다. 본 연구에서 제안하는 모형은 하상재료의 상세한 입경분포 정보를 필요로 하지 않는다. 이는 본 연구의 모형이 기반하는 플럭 응집모형이 응집을 시작하는 때의 플럭 초기 크기에 의존하지 않기 때문이다. 하상재료의 특성은 하상재료의 중간 크기에 기초한 한계소류력에 의해서만 정량화된다. 크기가 다양한 하상재료의 등가 이동성(Equal Mobility) 개념에서 동적 평형 상태에 도달한 후 부유사의 크기 변동을 모의할 수 있다. 그리고 계산되는 크기 변동값을 취합하여 비점착성 부유사의 입경분포를 모의할 수 있다. 본 연구의 입경분포 모형에서 부유사의 재부유(및 퇴적) 거동은 하상재료로부터 순간적으로 발생하는 것으로 가정한다. 본 연구의 모형은 다양한 유동 및 퇴적 조건에 따른 부유사의 입경분포를 모의한다. 여기서 유동을 운동량 방정식과 난류 모형을 사용하여 모사한다. 난류 모형을 통해 유사의 재부유에 대한 난류의 영향과 부유사의 추가 입경분포에 미치는 영향을 이해할 가능성을 가진다. 또한 유사 입자의 존재로 인한 난류감소효과와 간섭침강효과 역시 모의할 수 있다. 부유사의 존재와 유체흐름(난류)은 서로 상호적인 영향을 미친다고 잘 알려져 있다. 따라서 다양한 유체역학적 조건에서 난류강도감소가 모래의 입경분포에 미치는 영향에 대한 향후연구가 필요하다.

Acknowledgements

이 논문은 2024년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(2021R1I1A3060354).

Conflicts of Interest

The authors declare no conflict of interest.

References

Bagnold, R.A. (1966). An approach to the sediment transport problem from general physics. US Government Printing Office, Washington, D.C., U.S.

10.3133/pp422I

Beverage, J.P., and Culbertson, J.K. (1964). "Hyperconcentrations of suspended sediment." Journal of the Hydraulics Division, Vol. 90, No. 6, pp. 117-128.

10.1061/JYCEAJ.0001128

Box, G.E., and Muller, M.E. (1958). "A note on the generation of random normal deviates." The Annals of Mathematical Statistics, Vol. 29, No. 2, pp. 610-611.

10.1214/aoms/1177706645

Byun, J., and Son, M. (2020). "On the relationship between turbulent motion and bimodal size distribution of suspended flocs." Estuarine, Coastal and Shelf Science, Vol. 245, 106938.

10.1016/j.ecss.2020.106938

Cao, Z., Pender, G., and Meng, J. (2006). "Explicit formulation of the Shields diagram for incipient motion of sediment." Journal of Hydraulic Engineering, Vol. 132, No. 10, pp. 1097-1099.

10.1061/(ASCE)0733-9429(2006)132:10(1097)

Friedman, G.M. (1962). "On sorting, sorting coefficients, and the lognormality of the grain-size distribution of sandstones." The Journal of Geology, Vol. 70, No. 6, pp. 737-753.

10.1086/jg.70.6.30066373

Gelfenbaum, G., and Smith, J.D. (1986). "Experimental evaluation of a generalized suspended-sediment transport theory." Shelf Sands and Sandstones, Edited by Knight, R.J., and Mclean, J.R., Canadian Society of Petroleum Geologists Memoir II, Alberta, Canada, pp. 133-144.

Gentle, J.E. (2003). Random number generation and Monte Carlo methods. Springer Science & Business Media, NY, U.S.

Ghosh, J.K., and Mazumder, B.S. (1981). Size distribution of suspended particles-unimodality, symmetry and lognormality. Proceedings in Statistical Distributions in Scientific Work, Springer, Dordrecht, Netherlands, pp. 21-32.

10.1007/978-94-009-8555-1_2

Ghosh, J.K., Mazumder, B.S., and Sengupta, S. (1981). "Methods of computation of suspended load from bed materials and flow parameters." Sedimentology, Vol. 28, No. 6, pp. 781-791.

10.1111/j.1365-3091.1981.tb01942.x

Graf, W.H. (1984). Hydraulics of sediment transport. Water Resources Publication, CO, U.S.

Hsu, T.J., Traykovski, P.A., and Kineke, G.C. (2007). "On modeling boundary layer and gravity‐driven fluid mud transport." Journal of Geophysical Research: Oceans, Vol. 112, No. C4, C04011.

10.1029/2006JC003719

Hunt, J.N. (1954). "The turbulent transport of suspended sediment in open channels." Proceedings of the Royal Society of London, Vol. 224, No. 1158, pp. 322-335.

10.1098/rspa.1954.0161

Khelifa, A., and Hill, P.S. (2006). "Models for effective density and settling velocity of flocs." Journal of Hydraulic Research, Vol. 44, No. 3, pp. 390-401.

10.1080/00221686.2006.9521690

Kleinhans, M.G., and van Rijn, L.C. (2002). "Stochastic prediction of sediment transport in sand-gravel bed rivers." Journal of Hydraulic Engineering, Vol. 128, No. 4, pp. 412-425.

10.1061/(ASCE)0733-9429(2002)128:4(412)

Kuhnle, R.A. (1993). "Fluvial transport of sand and gravel mixtures with bimodal size distributions." Sedimentary Geology, Vol. 85, No. 1-4, pp. 17-24.

10.1016/0037-0738(93)90072-D

Kuhnle, R.A., and Wren, D.G. (2009). "Size of suspended sediment over dunes." Journal of Geophysical Research: Earth Surface, Vol. 114, No. F2, F02020.

10.1029/2008JF001200

Launder, B.E., and Sharma, B.I. (1974). "Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc." Letters in Heat and Mass Transfer, Vol. 1, pp. 131-138.

10.1016/0094-4548(74)90150-7

Law, B.A., Hill, P.S., Milligan, T.G., Curran, K.J., Wiberg, P.L., and Wheatcroft, R.A. (2008). "Size sorting of fine-grained sediments during erosion: Results from the western Gulf of Lions." Continental Shelf Research, Vol. 28, No. 15, pp. 1935-1946.

10.1016/j.csr.2007.11.006

Lisle, I.G., Rose, C.W., Hogarth, W.L., Hairsine, P.B., Sander, G.C., and Parlange, J.Y. (1998). "Stochastic sediment transport in soil erosion." Journal of Hydrology, Vol. 204, No. 1-4, pp. 217-230.

10.1016/S0022-1694(97)00123-6

Man, C., and Tsai, C.W. (2007). "Stochastic partial differential equation-based model for suspended sediment transport in surface water flows." Journal of Engineering Mechanics, Vol. 133, No. 4, pp. 422-430.

10.1061/(ASCE)0733-9399(2007)133:4(422)

Mazumder, B.S. (1994). "Grain size distribution in suspension from bed materials." Sedimentology, Vol. 41, No. 2, pp. 271-277.

10.1111/j.1365-3091.1994.tb01405.x

Mazumder, B.S., Ghoshal, K., and Dalal, D.C. (2005). "Influence of bed roughness on sediment suspension: experimental and theoretical studies." Journal of Hydraulic Research, Vol. 43, No. 3, pp. 245-257.

10.1080/00221680509500119

Mehta, A.J. (2013). An introduction to hydraulics of fine sediment transport (Vol. 38). World Scientific Publishing Company, Singapore.

10.1142/8708

Middleton, G.V. (1976). "Hydraulic interpretation of sand size distributions." The Journal of Geology, Vol. 84, No. 4, pp. 405-426.

10.1086/628208

Miller, M.C., McCave, I.N., and Komar, P. (1977). "Threshold of sediment motion under unidirectional currents." Sedimentology, Vol. 24, No. 4, pp. 507-527.

10.1111/j.1365-3091.1977.tb00136.x

Pal, D., and Ghoshal, K. (2014a). "Mathematical model on grain-size distribution in suspension over sand-gravel bed." Journal of Hydrology, Vol. 511, pp. 640-647.

10.1016/j.jhydrol.2014.01.035

Pal, D., and Ghoshal, K. (2014b). "Effect of bed roughness on grain-size distribution in an open channel flow." Journal of Hydro-environment Research, Vol. 8, No. 4, pp. 441-451.

10.1016/j.jher.2013.09.001

Purkait, B. (2002). "Patterns of grain-size distribution in some point bars of the Usri River, India." Journal of Sedimentary Research, Vol. 72, No. 3, pp. 367-375.

10.1306/091001720367

Richardson, J.F., and Zaki, W.N. (1954). "Sedimentation and fluidisation, Part 1." Transactions of American Institute of Chemical Engineers, Vol. 31, pp. 35-53.

Samaga, B.R., Ranga Raju, K.G., and Garde, R.J. (1986). "Suspended load transport of sediment mixtures." Journal of Hydraulic Engineering, Vol. 112, No. 11, pp. 1019-1034.

10.1061/(ASCE)0733-9429(1986)112:11(1019)

Sengupta, S. (1975). "Size‐sorting during suspension transportation-lognormality and other characteristics." Sedimentology, Vol. 22, No. 2, pp. 257-273.

10.1111/j.1365-3091.1975.tb00293.x

Sengupta, S. (1979). "Grain‐size distribution of suspended load in relation to bed materials and flow velocity." Sedimentology, Vol. 26, No. 1, pp. 63-82.

10.1111/j.1365-3091.1979.tb00338.x

Shaw, S.B., Makhlouf, R., Walter, M.T., and Parlange, J.Y. (2008). "Experimental testing of a stochastic sediment transport model." Journal of Hydrology, Vol. 348, No. 3-4, pp. 425-430.

10.1016/j.jhydrol.2007.10.014

Shi, Z.H., Fang, N.F., Wu, F.Z., Wang, L., Yue, B.J., and Wu, G.L. (2012). "Soil erosion processes and sediment sorting associated with transport mechanisms on steep slopes." Journal of Hydrology, Vol. 454, pp. 123-130.

10.1016/j.jhydrol.2012.06.004

Son, M., and Hsu, T.J. (2008). "Flocculation model of cohesive sediment using variable fractal dimension." Environmental Fluid Mechanics, Vol. 8, No. 1, pp. 55-71.

10.1007/s10652-007-9050-7

Son, M., and Hsu, T.J. (2011). "The effects of flocculation and bed erodibility on modeling cohesive sediment resuspension." Journal of Geophysical Research: Oceans, Vol. 116, No. C3, C03021.

10.1029/2010JC006352

Son, M., Byun, J., Kim, S.U., and Chung, E.S. (2016). "Effect of particle size on calibration of Schmidt number." Journal of Coastal Research, Vol. 75, No. sp1, pp. 148-152.

10.2112/SI75-30.1

Sun, D., Bloemendal, J., Rea, D.K., van den berghe, J., Jiang, F., An, Z., and Su, R. (2002). "Grain-size distribution function of polymodal sediments in hydraulic and aeolian environments, and numerical partitioning of the sedimentary components." Sedimentary Geology, Vol. 152, No. 3-4, pp. 263-277.

10.1016/S0037-0738(02)00082-9

Sundborg, Å. (1956). "The river Klarälven a study of fluvial processes." Geografiska Annaler, Vol. 38, No. 2-3, pp. 125-316.

10.1080/20014422.1956.11880887

Tanner, W.F. (1964). "Modification of sediment size distributions." Journal of Sedimentary Research, Vol. 34, No. 1, pp. 156-164.

10.1306/74D70FF6-2B21-11D7-8648000102C1865D

van Rijn, L.C. (1984). "Sediment transport, part II: Suspended load transport." Journal of Hydraulic Engineering, Vol. 110, No. 11, pp. 1613-1641.

10.1061/(ASCE)0733-9429(1984)110:11(1613)

Visher, G.S. (1969). "Grain size distributions and depositional processes." Journal of Sedimentary Research, Vol. 39, No. 3, pp. 1074-1106.

10.1306/74D71D9D-2B21-11D7-8648000102C1865D

Winterwerp, J.C. (1998). "A simple model for turbulence induced flocculation of cohesive sediment." Journal of Hydraulic Research, Vol. 36, No. 3, pp. 309-326.

10.1080/00221689809498621

Wright, S., and Parker, G. (2004). "Flow resistance and suspended load in sand-bed rivers: Simplified stratification model." Journal of Hydraulic Engineering, Vol. 130, No. 8, pp. 796-805.

10.1061/(ASCE)0733-9429(2004)130:8(796)

Wu, B., Molinas, A., and Julien, P.Y. (2004). "Bed-material load computations for nonuniform sediments." Journal of Hydraulic Engineering, Vol. 130, No. 10, pp. 1002-1012.

10.1061/(ASCE)0733-9429(2004)130:10(1002)

Journal of Korea Water Resources Association 한국수자원학회 논문집 ISSN:2799-8746(Print) 2799-8754(Online)

Preview

A simple approach to simulate the size distribution of suspended sediment

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Table 1.

Standard values of the numerical coefficients for k-𝜖 model (Launder and Sharma, 1974)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

Fig. 1.

The comparison of transient mean size from deterministic model and simulated size fluctuation from grain size distribution model adopted stochastic approach

Table 2.

Condition for numerical experiment (Samaga et al., 1986)

Fig. 2.

Fig. 3.

Simulated results and measured data from Sengupta (1975, 1979). The vertical profiles of horizontal velocities of Bed 2 (a) and Bed 3 (b). The vertical profile of velocities is assumed to follow logarithmic law of turbulent boundary layer

Table 3.

Condition for numerical experiment (Sengupta, 1975; 1979)

Fig. 4.

Acknowledgements

Conflicts of Interest

References

Standard values of the numerical coefficients for $k$ -𝜖 model (Launder and Sharma, 1974)