Prediction of real-time data in water distribution systems using LSTM

Eunyoung Cho; Seonhong Choi; Hanna Jung; Dongwoo Jang

doi:10.3741/JKWRA.2024.57.12.1003

Preview

Research Article

Journal of Korea Water Resources Association. 31 December 2024. 1003-1014
https://doi.org/10.3741/JKWRA.2024.57.12.1003

Prediction of real-time data in water distribution systems using LSTM

LSTM을 이용한 상수도 시스템 실시간 데이터 예측

Eunyoung Cho^a

Seonhong Choi^b

Hanna Jung^c

Dongwoo Jang^d^*

조 은영^a

최 선홍^b

정 한나^c

장 동우^d^*

^aMaster’s Course, Department of Civil and Environmental Engineering, Incheon National University, Incheon, Korea

^bMaster’s Course, Department of Civil and Environmental Engineering, Incheon National University, Incheon, Korea

^cMaster’s Course, Department of Civil and Environmental Engineering, Incheon National University, Incheon, Korea

^dAssociate Professor, Department of Civil and Environmental Engineering, Incheon National University, Incheon, Korea

^a인천대학교 건설환경공학과 석사과정

^bMaster’s Course, Department of Civil and Environmental Engineering, Incheon National University, Incheon, Korea건설환경공학과 석사과정

^c인천대학교 건설환경공학과 석사과정

^d인천대학교 건설환경공학과 부교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by/4.0):

©It is identical to the Creative Commons Attribution Non-commercial License (https://creativecommons.org/licenses/by/4.0)

ABSTRACT

The domestic water supply coverage rate exceeds 99%, and as aging water pipes increase, the risk of hydraulic and water quality incidents in water pipelines is rising, making it urgent to establish countermeasures. To prepare for various incidents in water supply systems, such as red water and larval accidents, real-time monitoring devices have recently been installed in pipelines. Consequently, the importance of research utilizing the measured data is gradually increasing. In this study, the Long Short-Term Memory (LSTM) method was used to predict future hydraulic and water quality data within water pipelines. Two months of hourly real-time measurement data, including flow discharge, hydraulic pressure, residual chlorine, and pH, were collected from a small block in Seo-gu, Incheon. The predictive accuracy of the LSTM technique was evaluated using the coefficient of determination (R²) and Root Mean Square Error (RMSE). The results of predicting water supply factors over the next seven days showed a high correlation, with R² reaching up to 0.91 for flow discharge. Electrical conductivity, water temperature, and residual chlorine also demonstrated high accuracy, with R² values exceeding 0.8. However, hydraulic pressure showed a low R² value of 0.019, suggesting that the predictive accuracy of the LSTM model is influenced by the continuity of the data used. The prediction results of real-time measurement data through LSTM can serve as crucial information for water supply management and incident prevention, and are expected to improve the ability to respond to incidents effectively.

Keywords

Data prediction

LSTM

Machine learning

Real-time data

Water supply systems

국내 수도관의 보급률은 99% 이상이며, 이에 노후 수도관이 증가하고 있고, 상수관로 내 수리 및 수질 사고의 발생 위험을 높여 대책 마련이 시급한 실정이다. 적수 및 유충 사고 등 상수도에서 발생할 수 있는 다양한 사고에 대비하기 위하여 최근 실시간 모니터링 계측기가 관로에 설치되고 있고, 계측된 데이터를 활용한 연구의 중요성이 점차 증가하고 있다. 본 연구에서는 LSTM (Long Short-Term Memory) 방법을 이용하여 미래 상수도관 내 수리 및 수질 데이터를 예측하고자 하였다. 인천광역시 서구 소블럭의 유량, 수압, 잔류염소, pH 등 2개월의 시 단위 실시간 계측 데이터를 수집하였고, 결정계수와 RMSE (Root Mean Square Error)를 이용하여 LSTM 기법의 예측 정확도를 평가하였다. 장래 7일간의 상수도 인자별 데이터를 예측한 결과, 유량의 경우 R²가 최대 0.91로 높은 상관성을 보이는 것으로 나타났으며, 전기전도도, 수온, 잔류염소의 경우 0.8 이상의 값으로 높은 정확도를 보여주었다. 반면 수압의 경우 0.019의 낮은 값을 보여주었는데, 이는 LSTM 모델은 활용하는 데이터의 연속성 유무에 따라 예측 정확도에 영향을 받는 것으로 시사된다. LSTM을 통한 실시간 계측 데이터의 예측 결과는 상수도 관리와 사고 예방에 중요한 정보로 활용될 수 있으며, 사고 발생 시 대응 능력을 향상시키는 데 도움이 될 것으로 기대된다.

키워드

데이터 예측

LSTM

머신러닝

실시간 데이터

상수도

MAIN

1. 서 론
2. LSTM (Long Short-Term Memory) 이론
3. 대상 지역 선정 및 모델 구축
3.1 대상 지역 소개 및 자료 수집
3.2 모델 구축
4. 모델 적용 결과
4.1 상수도 인자 예측 결과
5. 고 찰
6. 결 론

1. 서 론

상수도의 목적은 깨끗한 수돗물을 안정적으로 공급하는 데 있고, 이러한 목적을 달성하기 위한 다양한 기술이 개발되어 적용되고 있다. 특히 2019년 인천 상수도 적수 사고, 2020년 유충 발생 등으로 수돗물에 대한 신뢰가 낮아지고 있고, 안정적인 상수도 관리와 사고 대응을 위한 관망 내 수리 및 수질 계측기 설치와 효과적인 운영이 필요하다. 상수관망 내 실시간 계측 데이터를 활용한 유지관리 시스템과 모니터링 기술을 기반으로 한 수리, 수질 및 관로 사고 예측 시스템의 중요성도 점차 강조되고 있다. 유량의 변동성과 수질 상태의 변화는 다양한 요인들에 의해 영향을 받는데, 이러한 동적 변동성을 정확하게 예측하고 관리하는 것은 물 자원 관리의 효율성과 안정성을 보장하는 데 결정적인 역할을 하며 최근 AI (Artificial Inteligence) 기술을 기반으로 한 연구도 다양하게 진행되었다.

전통적으로 수리 분야에서의 수질과 유량의 예측은 통계 모델링, 시스템 동역학, 회귀 분석 등의 방법을 사용되었다(Caissie et al., 2005). 최근에는 AI와 관련하여 인공신경망 (Artificial Neural Network)과 그 하위 분야인 딥러닝을 활용하여 상수관망 내 실시간 유량 및 수질 데이터를 예측하는 방법인 LSTM (Long Short-Term Memory) 모델을 중점적으로 활용되어 왔다. LSTM은 장기적인 의존성을 학습할 수 있는 인공신경망의 한 종류로, 시간적 순차성을 가진 데이터에 대해 높은 예측 성능을 보이는 모델로 알려져 있다(Hochreiter and Schmidhuber, 1997).

LSTM은 유량 방면에서 실시간 하천 유량 예측을 수행하는 연구에 사용되고 있으며(Mehedi et al., 2022), 하수처리에서 유입 유량과 유입 성분을 예측하기 위해, 인공신경망인 LM (Levenberg-Marquart) 알고리즘을 사용하여 신경망을 훈련하고 학습시키는 연구가(Moon et al., 2008) 진행되었다.

Park et al. (2018)는 댐의 유입량을 예측하는 모델을 LSTM을 사용하여 개발하였다. 소양강댐 및 충주댐의 빅데이터를 활용하여 인공신경망과 엘만 순환 신경망 모델을 구축하였으며, 이 모델은 기존 인공신경망 모델보다 예측 성능이 우수하거나 비슷하였다. Mok (2019)은 금강 상류에 위치한 용담 다목적댐의 유입량 예측에 LSTM 모델을 사용했다. 이 모델은 텐서플로우와 파이썬 언어를 활용하여 구축되었으며, 단일 및 다중 입력 자료에 따른 예측 결과를 분석하여 댐 운영의 기초 자료의 적용성을 판단하였다. Li et al. (2021)는 이 연구에서는 강우-유출(RR) 예측의 정확도를 향상시키기 위해 동기화된 시퀀스 입력 및 출력 LSTM 네트워크 구조를 제안하였다. 광범위한 실험을 통해 제안된 방법의 효율성을 다양한 통계 및 수문학 관련 평가 메트릭으로 검증하였다.

Tran and Song (2017)은 도시 홍수 피해 방지를 위한 침수 예측에 딥러닝을 적용하였다. 시계열 데이터 분석을 위하여 Recurrent Neural Networks (RNNs)을 강의 수위 관측 데이터를 학습하고, 침수 가능성을 분석하였다. 15분 단위의 시계열 데이터를 입력 조건으로 사용하고, 30분과 60분 후의 강 수위를 예측하였다. 실험에 사용된 딥러닝 모델들 중 LSTM이 Nash Efficiency (NE)가 0.98로 가장 높은 정확도를 보여, LSTM 모델이 다른 RNN 기반 모델들보다 높은 성능 향상을 보였다.

수질 분야에서는 Liu et al. (2019)이 복잡하고 불확실한 수질 영향 요인을 고려하여 LSTM 심층 신경망을 기반으로 하천의 수질 예측 모델을 구축하여 분석하였다. 이 모델은 심층적으로 학습된 수질 모니터링 데이터를 이용하여 미래 6개월 동안의 COD, pH, DO 등 하천 수질을 예측하였다. Hu et al. (2019)은 스마트 양식업에서 중요한 이슈인 가두리 양식의 수질 예측을 위한 LSTM 기반 모델을 개발하였다. 전 처리된 데이터와 상관관계 정보를 사용하여 모델을 구성하였으며, 이를 통해 pH와 수온에 대한 예측을 수행하였다. Dong et al. (2019)은 복잡한 환경 조건하에서 수질 지표를 효과적으로 예측하기 위해 Savitzky-Golay 필터와 LSTM (Long Short Term Memory) 기반 Encoder-Decoder 신경망을 결합한 통합 예측 방법을 제안하였다. 수질 시계열 데이터는 먼저 Savitzky-Golay 필터를 통해 처리되고, 그 후 LSTM이 이 복잡한 시계열 데이터에서 유효한 정보를 추출한다. 실험 결과, 이 통합 모델은 일반적인 예측 방법보다 더 우수한 예측 결과를 도출할 수 있음을 입증하였다.

하천 수위 예측과 관련하여 LSTM을 이용한 연구도 다양하게 진행되었다. Jung et al. (2018)은 감조하천에서의 수위 예측에 딥러닝 기반의 순환 신경망(recurrent neural network, RNN) 모델을 활용하였고, 한강 잠수교의 수위 예측을 위해 TensorFlow의 LSTM 알고리즘을 사용하였다. LSTM 모형의 예측 선행 시간을 6개(1~24시간)로 구분하여 실측 수위와 예측 수위를 비교하였고, 시퀀스 길이가 1시간일 때 가장 정확도가 높은 것으로 나타났다.

LSTM을 이용하여 수자원과 하천 분야에서 수리 및 수질 인자 데이터를 활용한 장래 예측 연구가 국내외에서 다양하게 수행됐으나 상수도 관망 분야 내 활용은 미흡한 것으로 나타났다. 본 연구에서는 실제 운영 중인 상수도 관망에서 계측되고 있는 유량, 수압 데이터뿐만 아니라 pH, 잔류염소, 탁도, 전기전도도 등의 수질 데이터에 대하여 LSTM 기술을 이용하여 장래 기간에 대한 인자별 예측 정확도를 판별하고자 하였다.

연구 대상 지역으로 적수 및 유충 사고가 발생했었던 인천 서구지역을 선정하였으며 장래 예측을 위한 수리 및 수질 데이터를 수집하였다. 수집된 데이터를 이용하여 LSTM 학습 모델을 구축하였고, 미래의 유량 및 수질 상태를 예측하도록 하였다. 최종적으로 모델을 통해 산정된 예측 결과와 실제 측정 결과를 비교하여 모델의 성능을 평가하였다.

2. LSTM (Long Short-Term Memory) 이론

시계열 예측은 금융, 교통 및 다양한 분야에서 중요한 통계 및 머신러닝 연구 주제로 자리 잡고 있다(Kong et al., 2024). 과거부터 RNN (Recurrent Neural Network)은 시퀀스 데이터의 시간적 의존성을 포착하는 데 효과적이었으며, 그중에서도 LSTM (Long Short-Term Memory) 네트워크는 RNN의 기울기 소실 및 폭발 문제를 해결하여 긴 시퀀스에서 더욱 우수한 성능을 발휘하는 대표적인 알고리즘으로 인정받고 있다(Hochreiter and Schmidhuber, 1997).

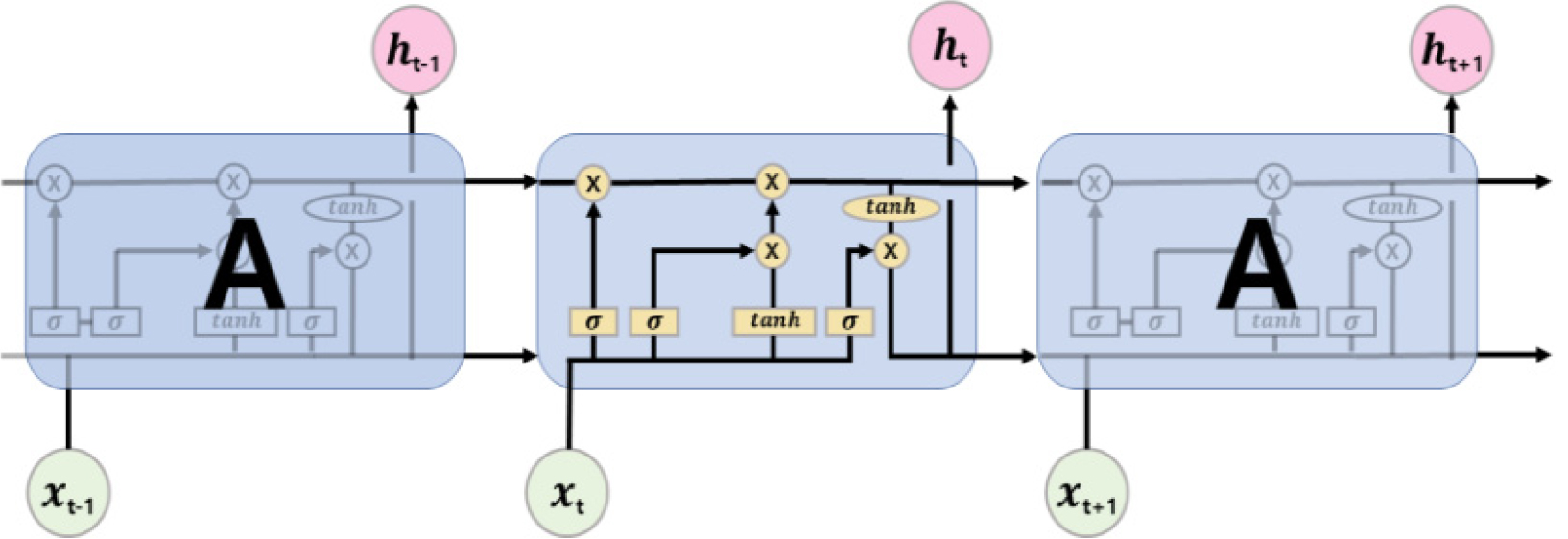
LSTM은 하나의 셀(Cell) 안에 여러 개의 게이트(Gate)가 존재하며 체인 형태를 이룬다. 게이트는 셀을 제어 및 보호하고 망각(Forget Gate Layer), 입력(Input Gate Layer), 출력(Output Gate Layer) 게이트로 나눌 수 있다(Mok, 2019). Fig. 1은 LSTM의 구조를 보여준다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-12/N0200571203/images/kwra_57_12_03_F1.jpg

Fig. 1.

Structure of LSTM (Hochreitere and Schmidhuber, 1997)

망각게이트( $f_{t}$ )에서는 이전 셀에서 들어온 데이터 정보를 얼마나 제거 및 유지할지 결정하는 역할을 한다. 입력게이트( $i_{t}$ )에서는 새로운 데이터 정보 중 어떤 정보를 저장할지 결정하는 역할을 한다. 마지막으로, 출력게이트( $o_{t}$ )에서는 셀에 저장된 정보 중 출력할 최종 결과물을 결정한다(Han et al., 2021). 이러한 과정을 기반으로 LSTM 모형은 Eqs. (1), (2), (3), (4), (5), (6)의 과정을 통해 작동된다.

(1)

f_{t} = σ (W_{f} ∙ [h_{t - 1}, x_{t}] + b_{f})

(2)

i_{t} = σ (W_{i} ∙ [h_{t - 1}, x_{t}] + b_{i})

(3)

o_{t} = σ (W_{o} ∙ [h_{t - 1}, x_{t}] + b_{o})

(4)

\bar{C_{t}} = \tanh (W_{c} ∙ [h_{t - 1}, x_{t}] + b_{c})

(5)

C_{t} = f_{t} ∙ C_{t - 1} + i_{t} ∙ \bar{C_{t}}

(6)

h_{t} = o_{t} ∙ \tanh (C_{t})

여기서, 𝜎는 활성화 함수, $W_{f}$ , $W_{i}$ , $W_{o}$ 는 게이트 가중치, $h_{t - 1}$ 는 전 단계 출력값, $x_{t}$ 는 입력값, $b_{f}$ , $b_{i}$ , $b_{o}$ , $b_{c}$ 는 편향값, $\bar{C_{t}}$ 는 활성화 함수를 통해 만들어진 새로운 셀 상태, $W_{c}$ 는 셀 상태의 가중치, $C_{t}$ 는 셀 상태, $C_{t - 1}$ 은 이전 단계의 셀 상태, $h_{t - 1}$ 는 셀에서의 출력값, tanh는 활성화함수를 나타낸다.

3. 대상 지역 선정 및 모델 구축

3.1 대상 지역 소개 및 자료 수집

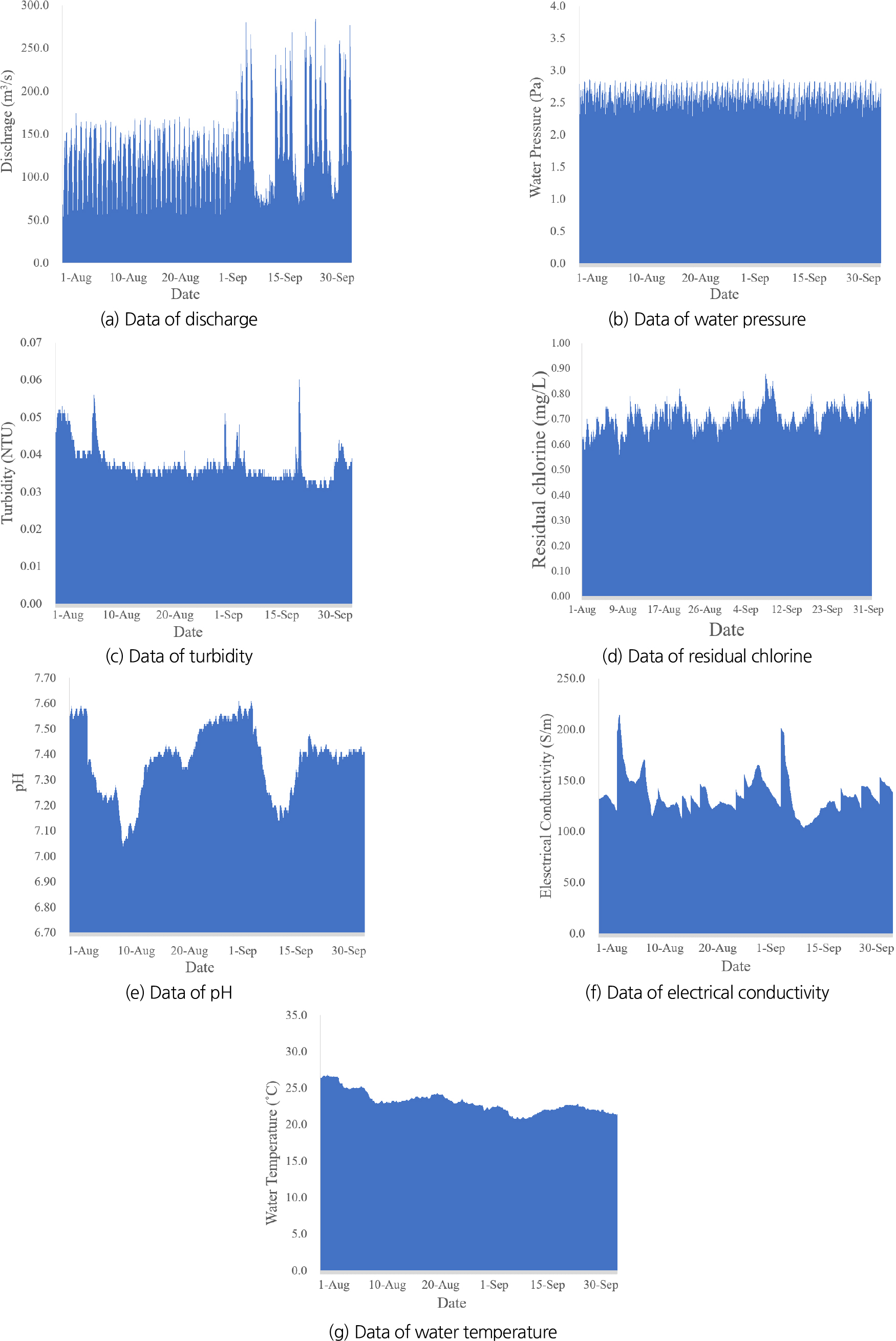
대상 연구지역으로 2019년 적수사고가 발생했었던 인천광역시 서구로 선정했으며, 조사를 위해 서구 석남동 ‘A 소블록’의 계측기에서 유량과 수질(탁도, 잔류염소, pH, 전기전도도, 수온), 수압은 ‘B 소블럭’의 계측기에서 실시간 데이터를 수집하였다. 데이터는 인천광역시상수도사업본부에서 제공한 자료를 사용하였으며, 수집 기간은 2022년 8월 1일부터 9월 30일까지 1시간 단위로 총 1,416개의 데이터를 사용하였다. Figs. 2(a)~2(g)은 연구에 사용된 유량, 수압, 탁도, 잔류염소, pH, 전기전도도, 수온 데이터를 각각 나타내고 있다.

Fig. 2(a)와 같이 관측 유량의 경우 일 단위 패턴이 관측되는 것으로 나타났다. 이는 유량이 사용자의 수요량에 따라 결정되는 수리적 인자이기 때문에 나타나는 것으로 보인다. Fig. 2(b)에서 수압은 유량과 같이 수리적 인자이지만 비교적 작은 변동폭을 보였다. Fig. 2(c)에서 보이는 탁도는 수질 인자로 정수장에서의 방류 수질, 관 상태에 따른 영향을 받으며 일 단위의 패턴이 생성되지 않았고, 변동 폭이 작은 것으로 나타났다. Fig. 2(d)는 잔류염소 농도이며 기준치보다 작은 값을 가질 경우 소독이 충분히 되지 않고 높은 값을 가질 경우 소독부산물과 냄새 측면에서 문제가 될 수 있지만 수질 기준인 1 mg/l 이하로 나타나 수질 기준을 초과하지 않는 것으로 나타났다. Fig. 2(e)는 pH 변화를 나타내며 하한값과 상한값 모두 수질 기준 이내의 범위로 나타났다. Fig. 2(f)은 전기전도도이며 다른 수질 인자에 비하여 불규칙적이고 변동폭이 큰 것으로 나타났다. Fig. 2(g)은 관내 수온을 나타내며 계절적 영향을 많이 받는 것이 특징으로 시간이 지날수록 수온이 내려가고 있는 경향을 보인다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-12/N0200571203/images/kwra_57_12_03_F2.jpg

Fig. 2.

Real-time measurement data

3.2 모델 구축

3.2.1 입력자료 구축

LSTM 모형의 학습과 검증 자료는 인천광역시 서구 2022년 8월부터 9월 기간에 대하여 ‘A 소블록’의 계측기와 ‘B 소블럭’의 관측자료를 이용하였다. 계측 데이터 중 결측 구간에 대해서는 LSTM 모델의 정확도를 낮출 수 있어서 보정이 필요하다. 한 시간 단위의 유량 데이터 중 결측된 유량에 대해서는 한 시간 전·후 값의 평균값을 사용하였다. 결측이 발생한 시간을 n이라고 하였을 때 n-1 시간의 유량과 n+1시간의 유량 평균값으로 보정하였다.

신경망 모형이 넓은 범주의 자료를 학습할 때는 함숫값이 발산할 수 있고, 예측 성능을 저하하므로 활용하기 좋은 정보로 가공하여야 하며, 이러한 과정을 전처리(pre-processing)라 한다(Mok, 2019). 인천광역시 서구의 시간당 유량, 수압, 수질 데이터들의 이상치를 제거하고 MinMaxScaler를 통해 데이터 정규화를 실시하였다. MinMaxScaler는 모든 데이터의 값을 0과 1 사이에 위치하도록 변경하는 것으로 2차원 데이터셋일 경우에는 모든 데이터가 x축의 0과, y축의 0과 1 사이의 영역에 담기게 된다. MinMaxScaler 식은 Eq. (7)과 같이 나타낼 수 있다.

(7)

Y = \frac{(X - X_{\min})}{X_{\max} - X_{\min}}

여기서, $Y$ 는 정규화된 변수값, $X$ 는 실제 변수값, $X_{\min}$ 는 변수의 최소값, $X_{\max}$ 는 변수의 최대값이다.

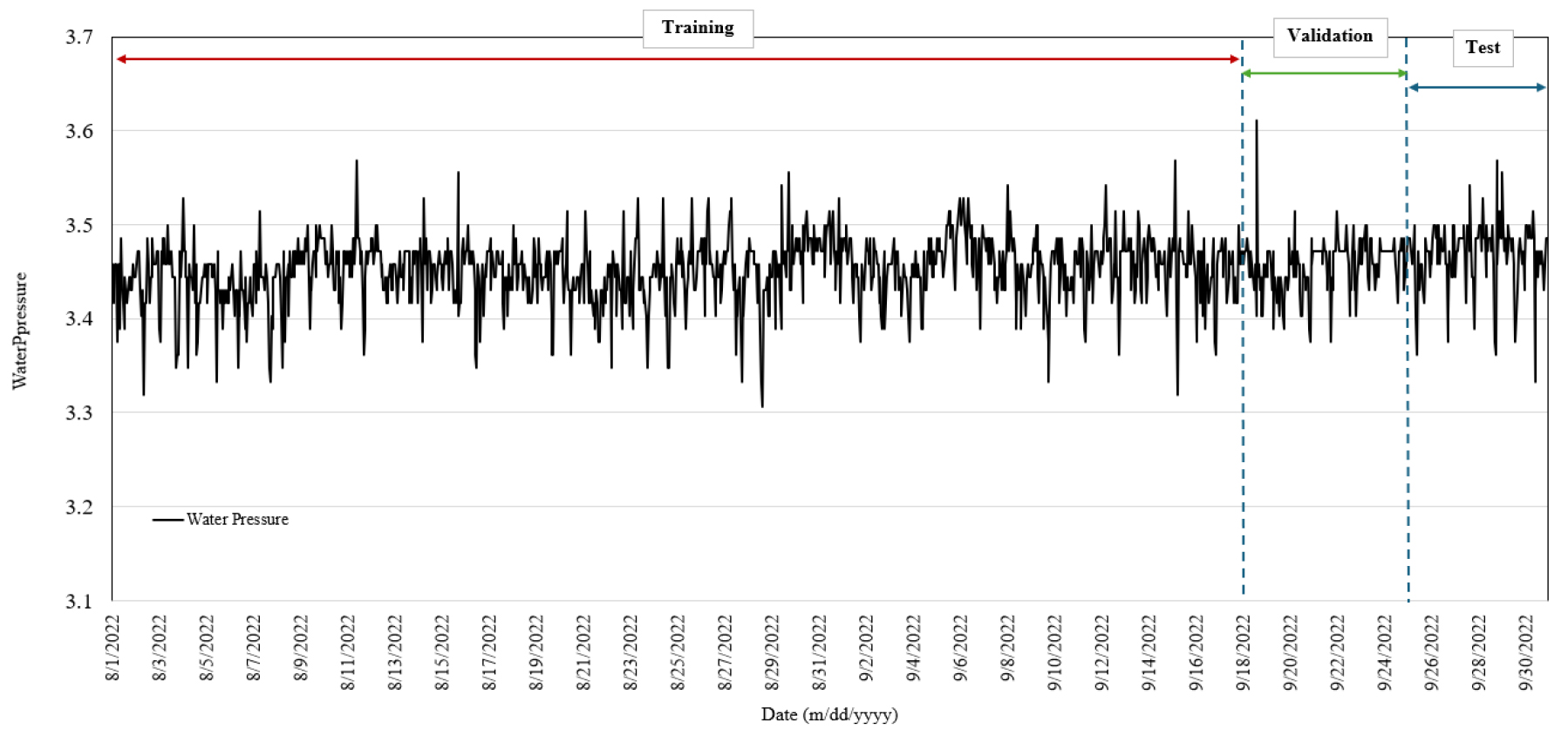
전처리 후 모델의 학습과 시험에 따른 데이터 누수를 막기 위해 일정 비율로 자료를 분류했다. 전체 자료의 80%는 학습자료(training data)로 분류했고 나머지 20% 중 10% 비율은 검증자료(validation data), 남은 10%는 시험자료(test data)이다. 자료는 1시간 단위 time stamp로 기록되었으며 총 개수는 1459개이다. 하지만 본 연구에서는 모델이 예측하는 부분인 시험자료를 일주일 분량의 자료(24*7 = 168)로 맞추기 위해 미세 비율을 조정했다. 이는 Table 1과 같이 구분하여 나타냈다. Fig. 3는 모델의 학습, 검증, 시험에 대하여 수압 데이터를 예시를 구분하여 나타내고 있다.

Table 1.

Ratio and volum for train, validation and test data

Classification	Ratio	Volume
Training	77%	1123
Validation	11.49%	168
Test	11.51%	168

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-12/N0200571203/images/kwra_57_12_03_F3.jpg

Fig. 3.

Input data classification

3.2.2 모형 적용 및 분석

본 연구에서는 2022년 8월 1일부터 9월 30일까지의 데이터로 9월 24일부터 9월 30일까지의 유량, 수압, 수질을 예측하며, 이는 여름철 수질 인자 데이터를 예측하는 것이다. LSTM 기법은 학습 방식에 따라 예측 성능에도 영향을 끼친다. 본 연구에서는 선행 연구(Li et al., 2021)를 기반으로 가장 적합한 모형의 변수를 사용하였다. 모형의 정확도를 판단하기 위한 지표로 평균 제곱근 오차(Root Mean Square, RMSE)와 결정계수( $R^{2}$ )을 사용하였으며, RMSE 산정식은 Eq. (8)로 나타낼 수 있다.

(8)

R M S E = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}}

(9)

R^{2} = \frac{S S E}{S S T} = 1 - \frac{S S R}{S S T}

(10)

S S T = \sum_{i = 1}^{n} (y_{i} - \bar{y})^{2}

(11)

S S E = \sum_{i = 1}^{n} ({\hat{y}}_{i} - \bar{y})^{2}

(12)

S S R = \sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}

여기서 $n$ 은 데이터 수, $y_{i}$ 는 참값, ${\hat{y}}_{i}$ 는 모형 예측값, $\bar{y}$ 는 관측값의 평균을 의미한다. $R^{2}$ 의 산정식은 Eqs. (9), (10), (11), (12)이며, $S S T$ 는 관측값에서 관측값의 평균을 뺀 결과의 총합, $S S E$ 는 추정값에서 추정값의 평균을 뺀 결과의 총합, $S S R$ 는 관측값에서 추정값을 뺀 값, 즉 잔차의 총합이다.

3.2.3 LSTM 모델 파라미터 선정

LSTM 모델에 사용할 파라미터들을 결정하기 위해 학습변수들의 값을 변화시키며 정확도를 측정하고 경험적으로 최적의 파라미터를 구성하였다. LSTM 모델의 은닉층(Hidden Layer)과 뉴런수는 선행연구를 참조하였고, 이는 다음 Table 2(a)와 같다. 또한 본 연구에서 개발된 LSTM 모델의 파라미터는 다음 Table 2(b)와 같다. 아래는 각 파라미터에 대한 설명이다.

Table 2.

Overview of the structure of LSTM models and the parameters of this study

(a) Overview of the structure of LSTM models and the data volume entering them
Reference	Data volume	Number of hidden layer	Neurons of each hidden layer
Zhou et al. (2018)	2592	1	8
Wang et al. (2020)	3672	2	55, 25
Park et al. (2022)	4715	3	50, 50
Jiang et al. (2021)	12600	3	50, 50, 50
Ghimire et al. (2021)	41979	6	100, 40, 5, 30, 20, 10
Zhang et al. (2022)	16368	3	30, 30, 30
* 26. Accurate prediction of water quality in urban drainage network with integrated EMD-LSTM model 2022
(b) Training parameters
Parameter	Value	Parameter	Value
Activation function	tanh	Optimization algorithm	Adam optimizer
Loss function	Mean squared error	Hidden layer	1
Sequence length	5	Learning rate	0.001
Max epochs/Patient	300/30	Batch size	32

데이터 양에 따라 은닉층 수가 보수적으로 증가하는 경향이 보였고, 본 연구의 데이터 양이 1,123개 이기 때문에 은닉층 수는 1개로 정하였다. 뉴런의 개수는 데이터 수에 비해 높은 수인 30을 실험적 방법으로 채택하였다. 본 연구는 데이터의 개형이 계절성과 주기성이 연속적이지 않아 단순한 모델보다 복잡한 모델이 정확도가 높게 나왔고, 과적합 문제는 일정 학습 횟수(epoch)동안 검증데이터(validation data)의 정확도 계산 결과가 낮아지면 학습을 종료하는 조기 종료(Early Stopping)로 방지하였다.

활성화 함수(Activation function)로는 비선형 함수인 탄젠트 하이퍼볼릭 함수(Tanh)가 쓰였는데, 탄젠트 하이퍼볼릭 함수는 -1과 1 사이의 값을 출력하여 평균적으로 0을 중심으로 분포하게 만드는 중심화(Centering) 과정이 이루어지게 하고, 이는 시계열 데이터에서 유리하기 때문에 채택하였다.

손실함수(Loss function)는 학습 결과의 정확도 측정 시 사용되는 지표이며, 종류로는 이진 교차 엔트로피 오차(Binary Cross Entropy Error), 범주형 교차 엔트로피 오차(Categorical Cross Entropy Error), 평균 제곱 오차(Mean Squared Error) 등이 있다(Lin et al., 2017). 그중에서 평균 제곱 오차는 예측한 값과 실제 값 사이의 평균 제곱 오차로 수치형 회귀 문제에 자주 사용되며 본 연구에서도 사용하고자 하였다.

시퀀스 길이(Sequence length)는 입력데이터의 연속적인 요소들의 수를 나타내며 5로 설정하여 입력자료가 직전 5시간 동안의 데이터를 참조할 수 있도록 하였다. 반복 횟수(Epoch)는 총 데이터 샘플 수/배치 크기 학습 반복 횟수(N/ batch size training iterations)를 나타내며, 전체 데이터셋을 얼마나 사용해서 학습을 진행할 것인지를 의미한다. Patient는 조기종료(Early stopping)의 파라미터이다. 과적합 방지를 위해 검증데이터의 손실 값으로 조기종료를 진행하였으며 Patient만큼 손실이 줄어들지 않으면 학습이 종료된다. 따라서 데이터별로 실제 학습 반복 횟수가 다르며 최대 반복 횟수는 조기 종료가 적용되지 않을 때의 최댓값이다. 최적화 알고리즘은 학습 진행 방식을 결정하며, 종류로는 확률적 경사 하강법(SGD), 모멘텀(Momentum), 적응적 학습률 경사 하강법(Adagrad), 평균 제곱근 전파법(RMS-Prop), 적응적 모멘텀 추정(Adam)이 있다. 본 연구에서는 대규모 데이터셋에 적합하며 계산 효율이 높은 적응적 모멘텀 추정을 사용하였다. 학습률(Learning rate)은 모델이 손실함수의 기울기(Gradient)를 얼마나 빠르게 지나갈지 결정하는 요소이며 모델의 가중치를 어떻게 업데이트할지 결정한다. 이는 모델 성능과 학습 속도와 안정성 사이의 균형을 찾기 위해 실험적인 방법으로 결정하였다.

배치사이즈(Batch size)는 한 번의 배치마다 주는 데이터 샘플 사이즈를 의미하며(Smith, 2017), 32로 설정하였다. 작은 배치사이즈는 메모리 사용 효율이 떨어지지만, 너무 큰 배치 사이즈는 메모리 부족 문제를 일으킬 수 있다. 32 라는 배치사이즈 값은 메모리 효율과 학습속도, 일반화 성능을 고려하여 실험적으로 결정하였다.

4. 모델 적용 결과

4.1 상수도 인자 예측 결과

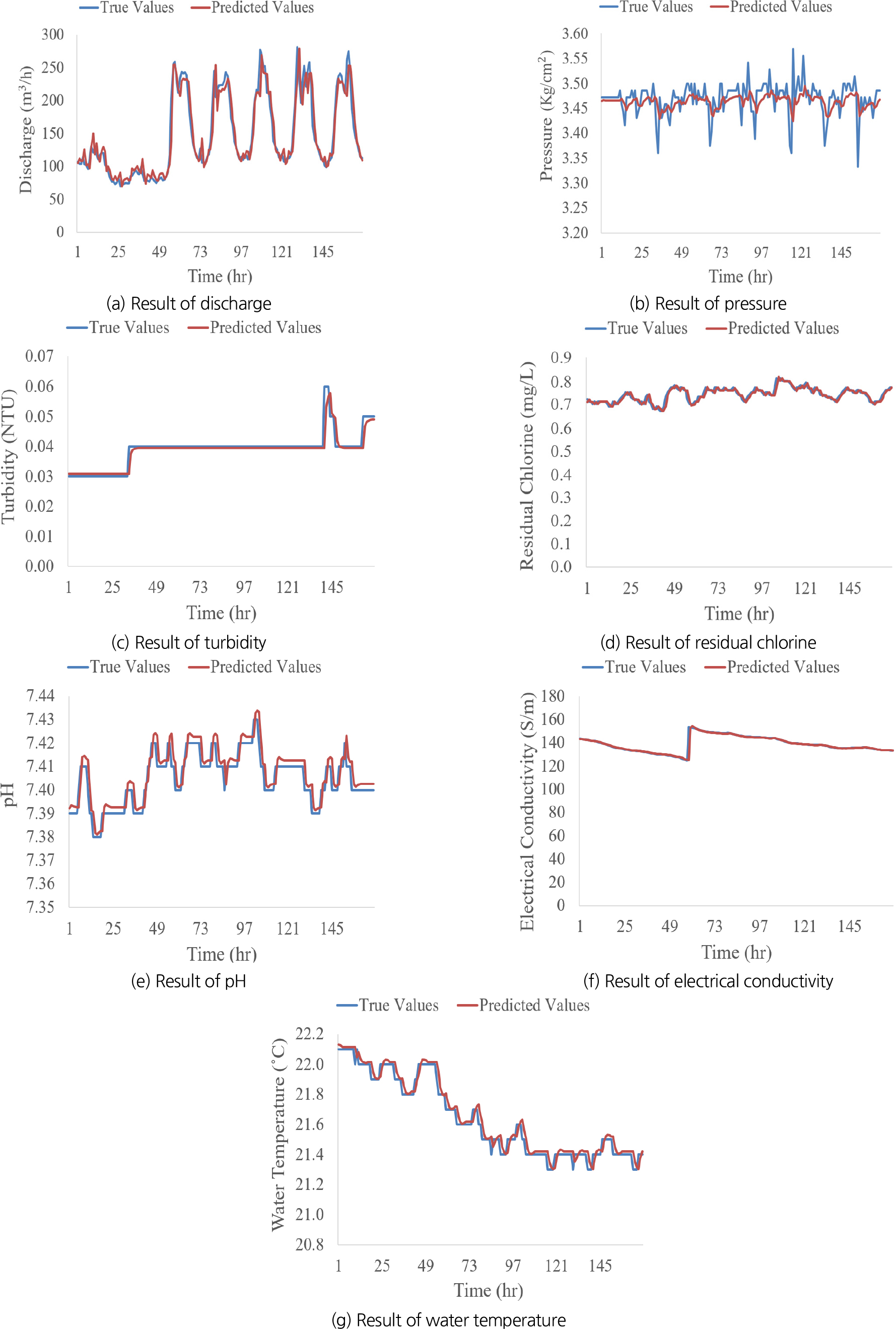
상수도 주요 인자인 유량, 수압, 탁도, 잔류염소, pH, 전기전도도, 수온을 예측하기 위해서 2022년 8월 1일부터 9월 30일까지 1시간 단위의 계측 데이터를 사용하였다. 다음 Figs. 4(a)~4(g)은 9월 24일부터 9월 30일까지 7일 동안 계측된 데이터와 LSTM을 통해 7일 동안 예측된 데이터의 비교 결과를 보여준다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-12/N0200571203/images/kwra_57_12_03_F4.jpg

Fig. 4.

Comparison of measured data and predicted data

7일 예측에 대하여 수리 인자인 유량이 24시간 패턴을 잘 나타내고 있고, 수질 인자인 탁도에 대해서도 대체적인 예측 정확도가 높은 것으로 나타났다. 잔류염소와 pH, 전기전도도, 수온의 경우에도 일간 변화폭이 크지 않으며, 실제 데이터와 예측 데이터의 유사도가 높은 것으로 나타났다. 수압의 경우 인자 중에서 유일하게 다소 낮은 예측 정확도가 나타났다.

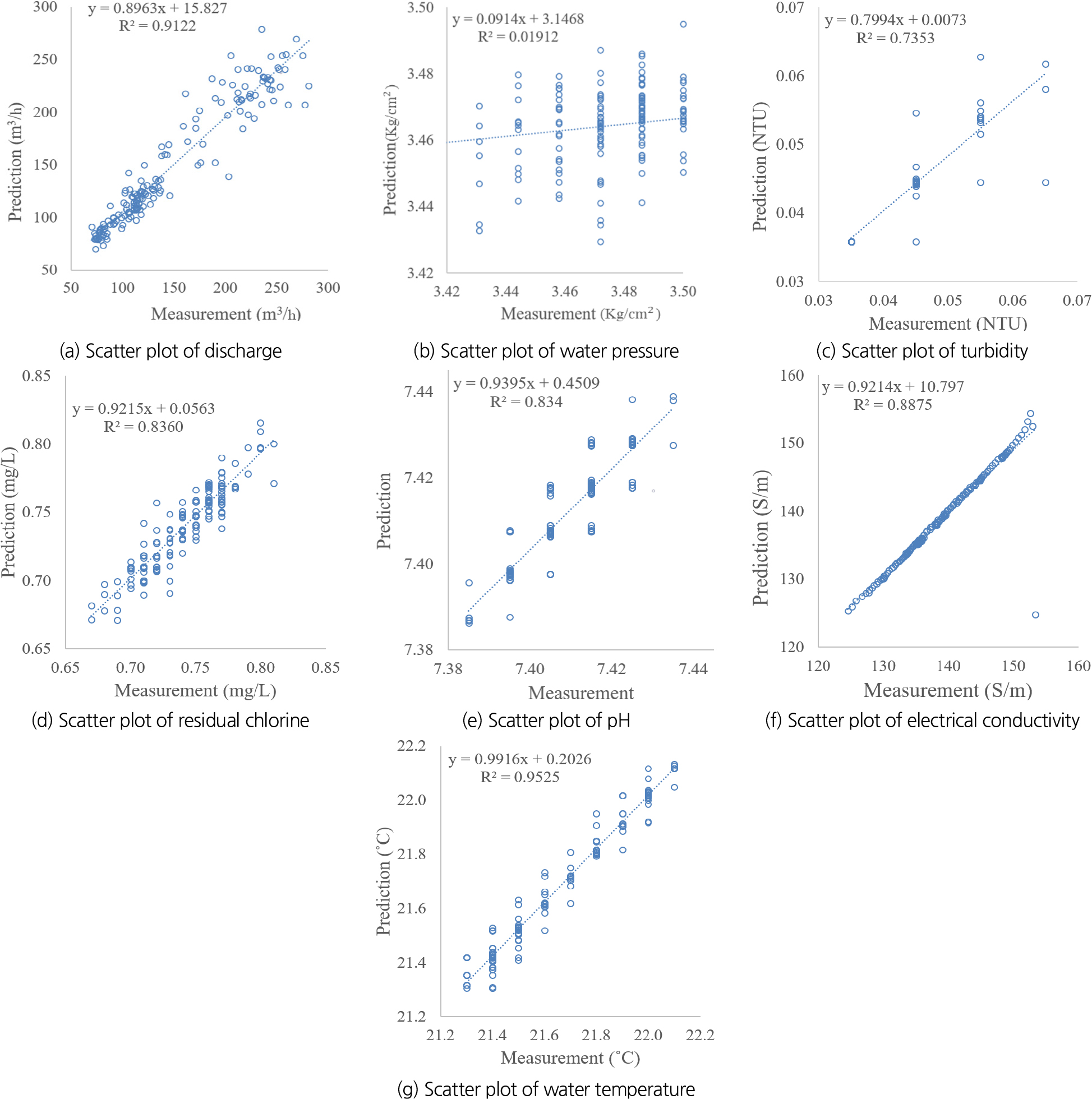
Figs. 5(a)~5(g)는 유량, 수압, 탁도, 잔류염소, pH, 전기전도도, 수온의 실측 데이터와 LSTM 결과와의 비교 산점도를 보여준다.

Fig. 5(a)은 유량 예측에 대한 산점도 그래프로 이상적인 예측 정확도를 보여주고 있다. 특히 50~150 범위의 값들에 대해서 관측값과 예측값의 유사도가 높은 것으로 보인다. Fig. 5(b)는 수압 예측에 대한 산점도 그래프로 모델이 시험 데이터를 잘 해석하고 있지 않는 것으로 보인다. 이는 연속적이지 않은 수압 데이터에 대해서 모델은 손실을 줄이기 위해 중앙값으로 회귀하는 성질을 보이기 때문이라고 해석된다. 반면 이외 Figs. 5(c)~5(g)와 같은 연속적인 데이터에 대해서는 값이 갑작스러운 변화가 있지만 높은 예측 정확도를 보여주고 있다. Fig. 4(c)과 같이 그래프가 갑작스러운 변화에도 예측값과 관측값 사이의 정확도가 높은 것으로 보이는 것은 LSTM이 실시간으로 입력 값을 시퀀스 길이에 따라 업데이트하는 특성으로 판단된다(Van Houdt et al., 2020).

Figs. 5(a)~5(g)와 같이 전체적으로 수리 및 수질 인자 모두 실측값 범위 내 예측이 잘 이루어지는 것으로 나타났다. 유량, 잔류염소, 전기전도도 그리고 수온의 경우 실측값의 유사 범위로 예측이 되었다. 수압의 경우 데이터가 연속적이지 않아 예측 정확도가 낮았다. 이로써 LSTM모델은 갑작스러운 변화에 대한 시점은 예측하지 못하나 지속적으로 모델의 입력데이터를 업데이트하기 때문에 모든 시험 값에 대해 예측 정확도 평균을 내면 연속적인 데이터에서는 예측 정확도가 높게 나오는 것을 확인할 수 있었다. pH, 전기전도도, 수온의 경우 실측값의 변화가 적었고, 예측값이 실측값의 범위로 나타난 것을 확인할 수 있다.

Table 3은 상수도 인자별로 RMSE, $R^{2}$ 를 보여준다.

Table 3.

RMSE, $R^{2}$ by water supply factor

Factor	RMSE	$R^{2}$
Discharge	0.0779	0.9118
Pressure	0.1061	0.0191
Turbidity	0.0813	0.7353
Residual Chlorine	0.0344	0.8360
pH	0.0094	0.7656
Electrical Conductivity	0.0216	0.8839
Water Temperature	0.0080	0.9525

유량, 수압, 탁도, 잔류염소, pH, 전기전도도, 수온 7개의 상수도 인자 중에서 유량, 전기전도도, 수온의 정확도가 높은 것으로 나타났다. 유량의 RMSE는 0.0779, $R^{2}$ 는 0.9118로 높은 정확도를 보였고, 전기전도도의 RMSE는 0.0216, $R^{2}$ 는 0.8839, 수온의 RMSE는 0.0080, $R^{2}$ 는 0.9525로 높은 정확도를 보였다. 탁도, 잔류염소, pH의 경우 예측값이 실측값 범위로 나타났고, RMSE는 0.01이하로 오차가 적은 반면 수압의 $R^{2}$ 는 값이 낮아 정확도가 떨어짐을 확인할 수 있었다.

5. 고 찰

Figs. 4(a)~4(g)의 결과는 예측값과 실제값 사이의 높은 일치성을 보여주며, 특히 갑작스러운 변동에도 정확한 예측 성능을 유지한 것으로 나타났다. 이러한 결과는 LSTM 모델의 특성에 기인하며, LSTM이 시계열 데이터의 특성을 효과적으로 학습하는 이유는 그 구조적인 강점 덕분이다.

LSTM 모델의 핵심은 과거 정보를 잊지 않고 유지하면서도 현재 데이터와 함께 장기의존성을 학습하는 능력이다. Gers et al. (1999)이 제안한 연구에 따르면, LSTM은 기존의 RNN과 달리 게이트 구조를 사용하여 필요한 정보를 적절히 기억하고 불필요한 정보를 잊는 방식으로 데이터를 처리한다. 이를 통해 시계열 데이터의 패턴을 정확하게 학습하고, 이전 시간대의 정보가 중요한 상황에서도 이를 효과적으로 반영하여 예측 성능을 향상시킨다.

또한, Van Houdt et al. (2020)의 연구에 따르면, LSTM은 게이트 구조를 통해 단기적인 변동과 장기적인 추세를 동시에 학습할 수 있다. 이를 바탕으로 갑작스러운 상승과 같은 이벤트가 발생했을 때도 LSTM 모델은 학습한 패턴에 따라 이러한 변동을 예측에 반영하며, 실제값과 유사한 결과를 도출할 수 있다. 이는 LSTM이 데이터의 연속적인 변화에도 민감하게 반응하여 예측 정확도를 유지할 수 있는 이유를 설명한다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-12/N0200571203/images/kwra_57_12_03_F5.jpg

Fig. 5.

Scatter data analysis

특히 LSTM의 또 다른 장점은 새로운 데이터가 지속적으로 입력되는 상황에서 실시간으로 정보를 반영하며 예측을 업데이트할 수 있다는 점이다. Van Houdt et al. (2020)이 언급한 바와 같이, LSTM은 시계열 데이터가 연속적으로 들어올 때도 즉각적인 반응을 보이며, 이를 통해 예측값이 갑작스러운 변동에도 신속하게 조정될 수 있다. 이러한 특성 덕분에, LSTM은 갑작스러운 변화에 대한 예측에서도 우수한 성능을 발휘하며, 실제값과의 높은 일치도를 유지하게 된다.

따라서, 본 연구에서 사용된 LSTM 모델이 예측 정확도가 높은 이유는 모델이 장기의존성과 단기 변동성을 동시에 학습할 수 있으며, 실시간으로 데이터를 반영해 예측을 업데이트할 수 있는 능력 덕분이라고 할 수 있다.

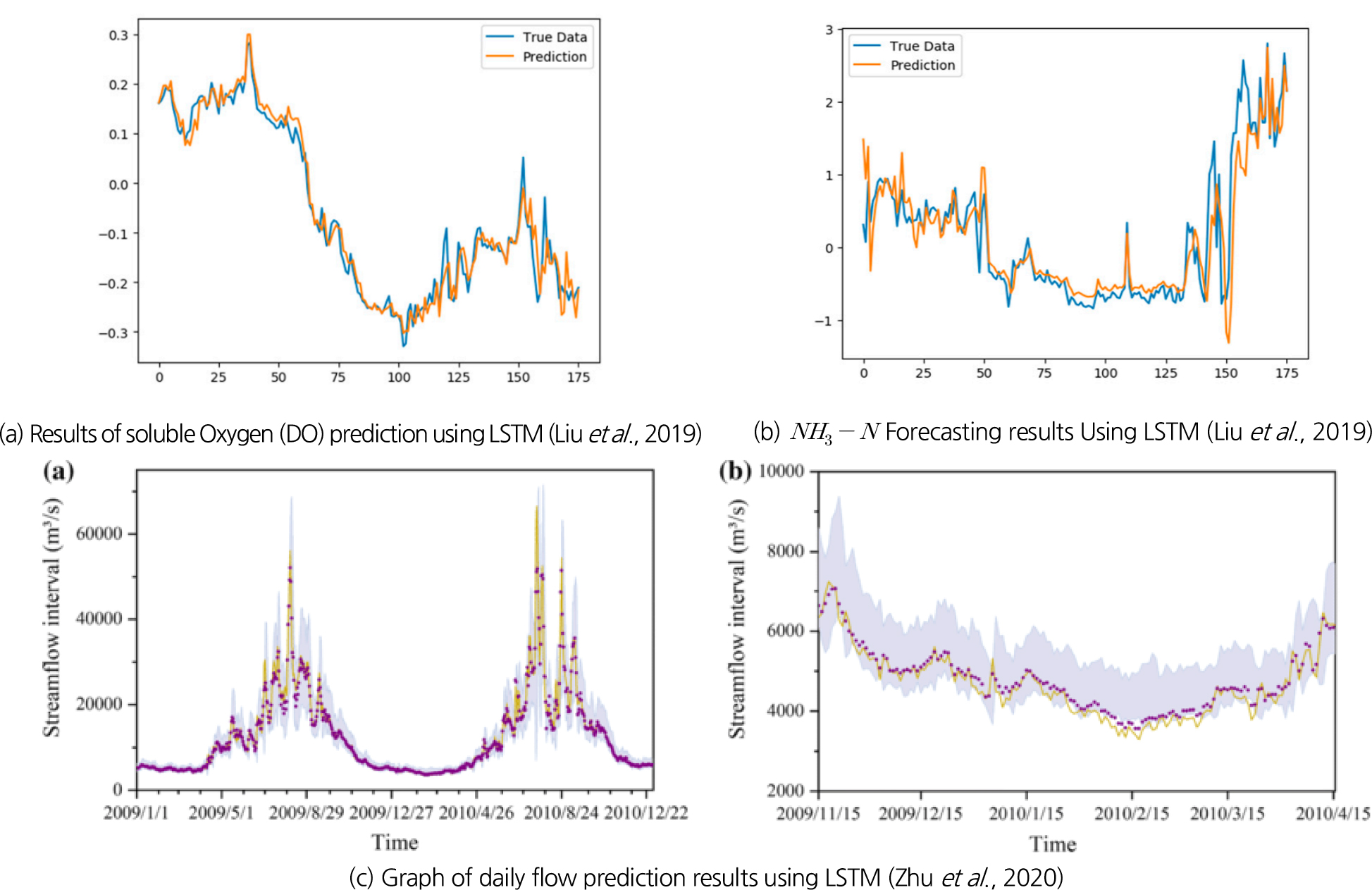
이러한 특성은 선행연구에서도 확인할 수 있다. Figs. 6(a) and 6(b)은 Liu et al. (2019)이 LSTM 모델을 사용하여 양쯔강의 수질관측소의 데이터로 수질 변수인 용존산소(DO)와 $N H_{3} - N$ 를 예측한 결과이다.

Fig. 6(c)는 Zhu et al. (2020)이 양쯔강의 일일 유량을 LSTM 모델을 사용하여 예측한 결과를 보여준다. 노란 실선은 관측값, 빨간 점은 예측값, 회색 블록은 예측구간을 나타내고 있다.

Fig. 6(c)은 LSTM이 실시간으로 데이터를 반영하면서도 갑작스러운 하락에 대해 예측함을 나타낸다. 특히 예측값과 실제값의 일치성이 높으면서도 변동성이 큰 시점에서는 변동 값에 대한 예측 지연성을 보인다. 이는 LSTM 모델이 시계열 데이터의 패턴을 학습하면서, 갑작스러운 변동에 대해 유연하게 반응하지만, 시계열 특성상 약간의 시간 지연이 발생할 수 있음을 시사한다. 이러한 경향은 복잡한 시계열 데이터에서 흔히 발생하는 현상으로, LSTM 모델이 실시간 데이터를 반영하며 높은 예측 정확도를 유지하는 동시에, 변화에 대한 반응 속도에서 약간의 지연이 발생할 수 있다는 점을 Abbasimehr and Paki (2022)이 연구에서 증명하였다. Abbasimehr and Paki (2022)의 연구에서는 LSTM 모델이 장기적 패턴을 잘 학습하면서도 급격한 변동에 대해 반응하는 데 약간의 지연이 발생할 수 있음을 보여주었으며, 이는 복잡한 시계열 데이터의 특성에 기인한다. 본 연구에서도 이와 유사한 경향이 나타났으며, LSTM 모델이 예측값과 실제값의 일치도를 높게 유지하는 한편, 갑작스러운 변화에 대한 예측에서는 미세한 지연이 관찰되었다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-12/N0200571203/images/kwra_57_12_03_F6.jpg

Fig. 6.

Graph of results of previous studies showing the characteristics of LSTM model

따라서, 본 연구는 Abbasimehr and Paki (2022)의 연구 결과와 일치하며, LSTM 모델이 실시간 데이터 처리에 뛰어난 성능을 보이면서도 일부 변화에 대한 반응에서 지연이 발생할 수 있음을 확인하였다. 이러한 결과는 복잡한 시계열 데이터를 다룰 때 LSTM 모델이 가지는 한계와 특성을 잘 보여주고 있다고 판단된다.

6. 결 론

본 연구에서는 인천광역시 서구를 대상으로 LSTM 모형을 이용하여 상수도 수리 및 수질 인자를 예측하는 연구를 수행하였다. 2022년 8월에서 9월까지 한 시간 단위의 데이터 수집하여 LSTM 모델을 학습시켰고, 장래 1일에 대하여 검증을 시행하였다. 모델 예측 결과를 실측자료와 비교하여 RMSE와 $R^{2}$ 를 통해 정확도를 판단하였고, 연구를 통한 결론은 다음과 같다.

상수관망 내 주요 수리 및 수질 인자 예측을 위한 LSTM 모델을 구축하였다. 모델 해석의 정확도를 높이기 위한 적정 윈도우 사이즈, 은닉층 수, 반복횟수, 배치사이즈를 결정하였고, 관측된 수리 및 수질 인자 데이터를 이용하여 장래 예측이 가능한 것으로 나타났다.

LSTM 적용 결과 수온의 RMSE는 0.0080, $R^{2}$ 는 0.9525, 유량의 RMSE는 0.0779, $R^{2}$ 는 0.9118, 전기전도도의 RMSE는 0.0216, $R^{2}$ 는 0.8839으로 수온, 유량, 전기전도도의 예측 정확도가 높은 것을 확인할 수 있었다. 하지만 수압의 RMSE는 0.1061, $R^{2}$ 는 0.0191로 낮은 정확도를 보였다. 이는 LSTM모델의 예측정확도가 훈련데이터의 연속성에 영향을 받는 것을 시사한다.

탁도, pH의 경우 수온, 유량, 전기전도도에 비해 RMSE의 값이 크고, $R^{2}$ 의 값이 작게 예측되었지만, 데이터의 최소, 최대값의 범위와 일간 변화량이 크지 않고, 학습데이터 범위 내로 예측된 것으로 볼 때 변화량이 큰 인자에 대하여 활용성이 높을 것으로 판단되었다.

본 연구에서 사용된 LSTM 모형은 상수도 인자 예측에 있어 활용성이 높은 것으로 판단되며, 다수의 계측기 데이터를 수집하고, 계절 또는 연간 시뮬레이션 수행, LSTM 해석 인자의 조정 등을 통한 추가 연구를 통하여 예측 정확도를 향상할 수 있을 것으로 판단된다. 또한, 본 연구 결과와 개발 모델을 실제 지자체 상수도 시스템에 적용한다면 관망의 유지관리와 사고 대응에 도움이 될 수 있을 것으로 기대된다.

Acknowledgements

본 과제는 행정안전부 지역맞춤형 재난안전 연구개발 사업의 지원을 받아 수행된 연구입니다(20019334).

Conflicts of Interest

The authors declare no conflict of interest.

References

Abbasimehr, H., and Paki, R. (2022). "Improving time series forecasting using LSTM and attention models." Journal of Ambient Intelligence and Humanized Computing, Vol. 13, No. 1, pp. 673-691.

10.1007/s12652-020-02761-x

Caissie, D., Satish, M.G., and El‐Jabi, N. (2005). "Predicting river water temperatures using the equilibrium temperature concept with application on Miramichi River catchments (New Brunswick, Canada)." Hydrological Processes: An International Journal, Vol. 19, No. 11, pp. 2137-2159.

10.1002/hyp.5684

Dong, Q., Lin, Y., Bi, J., and Yuan, H. (2019). "An integrated deep neural network approach for large-scale water quality time series prediction." 2019 IEEE International Conference on Systems, Man, and Cybernetics (SMC), IEEE, Bari, Italy, pp. 3537-3542.

10.1109/SMC.2019.8914404

Gers, F.A., Schmidhuber, J., and Cummins, F. (1999). "Continual prediction using LSTM with forget gates." In Neural Nets WIRN Vietri-99: Proceedings of the 11th Italian Workshop on Neural Nets, Vietri Sul Mare, Salerno, Italy, Springer London, pp. 133-138.

10.1007/978-1-4471-0877-1_10

Ghimire, S., Yaseen, Z.M., Farooque, A.A., Deo, R.C., Zhang, J., and Tao, X. (2021). "Streamflow prediction using an integrated methodology based on convolutional neural network and long short-term memory networks." Scientific Reports, Vol. 11, No. 1, 17497.

10.1038/s41598-021-96751-434471166PMC8410863

Han, H., Choi, C., Jung, J., and Kim, H.S. (2021). "Application of sequence to sequence learning based LSTM model (LSTM- s2s) for forecasting dam inflow." Journal of Korea Water Resources Association, Vol. 54, No. 3, pp. 157-166.

Hochreiter, S., and Schmidhuber, J. (1997). "Long short-term memory." Neural Computation, Vol. 9, No. 8, pp. 1735-1780.

10.1162/neco.1997.9.8.17359377276

Hu, Z., Zhang, Y., Zhao, Y., Xie, M., Zhong, J., Tu, Z., and Liu, J. (2019). "A water quality prediction method based on the deep LSTM network considering correlation in smart mariculture." Sensors, Vol. 19, No. 6, 1420.

10.3390/s1906142030909468PMC6470961

Jiang, Y., Li, C., Sun, L., Guo, D., Zhang, Y., and Wang, W. (2021). "A deep learning algorithm for multi-source data fusion to predict water quality of urban sewer networks." Journal of Cleaner Production, Vol. 318, 128533.

10.1016/j.jclepro.2021.128533

Jung, S., Cho, H., Kim, J., and Lee, G. (2018). "Prediction of water level in a tidal river using a deep-learning based LSTM model." Journal of Korea Water Resources Association, Vol. 51, No. 12, pp. 1207-1216.

Kong, Y., Wang, Z., Nie, Y., Zhou, T., Zohren, S., Liang, Y., and Wen, Q. (2024). "Unlocking the power of LSTM for long term time series forecasting." arXiv preprint, arXiv:2408.10006.

Li, W., Kiaghadi, A., and Dawson, C. (2021). "Exploring the best sequence LSTM modeling architecture for flood prediction." Neural Computing and Applications, Vol. 33, pp. 5571-5580.

10.1007/s00521-020-05334-3

Lin, T.Y., Goyal, P., Girshick, R., He, K., and Dollar, P. (2017). "Focal loss for dense object detection." Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, pp. 2980-2988.

10.1109/ICCV.2017.324

Liu, P., Wang, J., Sangaiah, A.K., Xie, Y., and Yin, X. (2019). "Analysis and prediction of water quality using LSTM deep neural networks in IoT environment." Sustainability, Vol. 11, No. 7, 2058.

10.3390/su11072058

Mehedi, M.A.A., Khosravi, M., Yazdan, M.M.S., and Shabanian, H. (2022). "Exploring temporal dynamics of river discharge using univariate long short-term memory (LSTM) recurrent neural network at East Branch of Delaware River." Hydrology, Vol. 9, No. 11, 202.

10.3390/hydrology9110202

Mok, J.-Y. (2019). Construction of LSTM model and prediction of dam inflow using deep learning. Master's Dissertation, University of Seoul.

Moon, T., Choi, J., Kim, S., Cha, J., Yoom, H., and Kim, C. (2008). "Prediction of influent flow rate and influent components using artificial neural network (ANN)." Journal of Korean Society on Water Environment, Vol. 24, No. 1, pp. 91-98.

Park, K., Jung, Y., Seong, Y., and Lee, S. (2022). "Development of deep learning models to improve the accuracy of water levels time series prediction through multivariate hydrological data." Water, Vol. 14, No. 3, 469.

10.3390/w14030469

Park, M.K., Yoon, Y.S., Lee, H.H., and Kim, J.H. (2018). "Application of recurrent neural network for inflow prediction into multi-purpose dam basin." Journal of Korea Water Resources Association, Vol. 51, No. 12, pp. 1217-1227.

Smith, S.L. (2017). "Don't decay the learning rate, increase the batch size." arXiv preprint, arXiv:1711.00489.

Tran, Q.K., and Song, S.K. (2017). "Water level forecasting based on deep learning: A use case of Trinity River-Texas-The United States." Journal of the Korean Institute of Information Scientists and Engineers, Vol. 44, No. 6, pp. 607-612.

10.5626/JOK.2017.44.6.607

Van Houdt, G., Mosquera, C., and Nápoles, G. (2020). "A review on the long short-term memory model." Artificial Intelligence Review, Vol. 53, No. 8, pp. 5929-5955.

10.1007/s10462-020-09838-1

Wang, H.,, Mu, L.,, Shi, F., and Dou, H. (2020). "Production prediction at ultra-high water cut stage via Recurrent Neural Network." Petroleum Exploration and Development, Vol. 47, No. 5, pp. 1084-1090.

10.1016/S1876-3804(20)60119-7

Zhang, Y., Li, C., Jiang, Y., Sun, L., Zhao, R., Yan, K., and Wang, W. (2022). "Accurate prediction of water quality in urban drainage network with integrated EMD-LSTM model." Journal of Cleaner Production, Vol. 354, 131724.

10.1016/j.jclepro.2022.131724

Zhou, J., Wang, Y., Xiao, F., Wang, Y., and Sun, L. (2018). "Water quality prediction method based on IGRA and LSTM." Water, Vol. 10, No. 9, 1148.

10.3390/w10091148

Zhu, S., Luo, X., Yuan, X., and Xu, Z. (2020). "An improved long short-term memory network for streamflow forecasting in the upper Yangtze River." Stochastic Environmental Research and Risk Assessment, Vol. 34, pp. 1313-1329.

10.1007/s00477-020-01766-4

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Prediction of real-time data in water distribution systems using LSTM

ABSTRACT

MAIN

Fig. 1.

Structure of LSTM (Hochreitere and Schmidhuber, 1997)

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 2.

Real-time measurement data

(7)

Table 1.

Ratio and volum for train, validation and test data

Fig. 3.

Input data classification

(8)

(9)

(10)

(11)

(12)

Table 2.

Overview of the structure of LSTM models and the parameters of this study

Fig. 4.

Comparison of measured data and predicted data

Table 3.

RMSE, R2 by water supply factor

Fig. 5.

Scatter data analysis

Fig. 6.

Graph of results of previous studies showing the characteristics of LSTM model

Acknowledgements

Conflicts of Interest

References

RMSE, $R^{2}$ by water supply factor