Estimating time-varying parameters for monthly water balance model using particle filter: assimilation of stream flow data

Jeonghyeon Choi; Sangdan Kim

doi:10.3741/JKWRA.2021.54.6.365

Preview

Research Article

Journal of Korea Water Resources Association. 30 June 2021. 365-379
https://doi.org/10.3741/JKWRA.2021.54.6.365

Estimating time-varying parameters for monthly water balance model using particle filter: assimilation of stream flow data

입자 필터를 이용한 월 물 수지 모형의 시간변화 매개변수 추정: 하천유량 자료의 동화

Jeonghyeon Choi^a

Sangdan Kim^b^*

최 정현^a

김 상단^b^*

^aPh.D Candidate, Division of Earth Environmental System Science (Major of Environmental Engineering), Pukyong National University, Busan, Korea

^bProfessor, Department of Environmental Engineering, Pukyong National University, Busan, Korea

^a부경대학교 지구환경시스템과학부 (환경공학전공) 박사과정

^b부경대학교 환경공학과 교수

^{*Corresponding Author}

ABSTRACT

Hydrological model parameters are essential for model simulation and can vary over time due to topography, climatic conditions, climate change and human activity. Consequently, the use of fixed parameters can lead to inaccurate stream flow simulations. The aim of this study is to investigate an appropriate method of estimating time-varying parameters using stream flow observations, and how the simulation efficiency changes when stream flow data are assimilated into the model. The data assimilation method can be used to automatically estimate the parameters of a hydrological model by adapting to a variety of changing environments. Stream flow observations were assimilated into a two parameter monthly water balance model using a particle filter. The simulation results using the time-varying parameters by the data assimilation method were compared with the simulation results using the fixed parameters by the SCEM method. First, we conducted synthesis experiments based on various scenarios to investigate if the particle filter method can adequately track parameters that change over time. After that, it was applied to actual watersheds and compared with the predictive performance of stream flow when using parameters that change with time and fixed parameters. The conclusions obtained through this study are as follows: (1) The predictive performance of the overall monthly stream flow time series was similar between the particle filter method and the SCEM method. (2) The monthly runoff prediction performance in the period except the rainy season was better in the simulation by the periodically changing parameters using the data assimilation method. (3) Uncertainty in the observational data of stream flow used for assimilation played an important role in the predictive performance of the particle filter.

Keywords

Data assimilation

Monthly water balance model

Particle filter

Time-varying parameter

수문 모형 매개변수는 모형 모의에 필수적이며, 지형, 기후조건, 기후변화와 인간 활동으로 인해 시간에 따라 달라질 수 있다. 결과적으로 고정된 매개변수의 사용은 부정확한 하천유량 모의로 이어질 수 있다. 본 연구의 목표는 하천유량 관측자료를 이용하여 시간에 따라 변하는 매개변수를 추정하는 방법을 살펴보고, 하천유량 자료가 모형에 동화될 때 모의 효율성이 어떻게 변하는지 분석하는 것이다. 자료 동화 방법은 변화하는 다양한 환경에 적응하여 수문 모형의 매개변수를 자동으로 추정하기 위하여 사용될 수 있다. 입자 필터를 이용하여 하천유량 관측치를 2개 매개변수 월 물 수지 모형에 동화했다. 자료 동화 방법으로 시간변화 매개변수를 사용한 모의 결과는 SCEM 방법으로 고정 매개변수를 사용한 모의 결과와 비교되었다. 먼저 다양한 시나리오에 기반한 합성 실험을 수행하여 입자 필터 방법이 시간에 따라 변화하는 매개변수를 적절하게 추적할 수 있는지를 살펴보았다. 이후 실제 유역에 적용하여 시간에 따라 변화하는 매개변수와 고정된 매개변수를 사용하였을 때의 하천유량 예측성능과 비교하였다. 본 연구를 통해 얻은 결론은 다음과 같다. (1) 전체적인 월 하천유량 시계열의 예측성능은 입자 필터 방법과 SCEM 방법이 서로 비슷하였다. (2) 우기를 제외한 시기의 월 유출고 예측성능은 자료 동화 방법을 이용한 주기적으로 변화하는 매개변수에 의한 모의가 더 우수하였다. (3) 동화에 사용되는 하천유량 관측자료의 불확실성은 입자 필터의 하천유량 예측성능에 중요한 역할을 하였다.

키워드

자료 동화

월 물 수지 모형

입자 필터

시간변화 매개변수

MAIN

1. 서 론
2. 연구 방법
2.1 월 물 수지 모형
2.2 입자 필터
2.3 성능 평가
3. 사례 연구
3.1 수치 실험
3.2 연구 유역 및 자료
3.3 입자 필터 매개변수 설정
4. 결 과
4.1 수치 실험 결과
4.2 시간변화 매개변수의 성능 평가
5. 입자 필터 매개변수의 민감도
6. 결 론

1. 서 론

수문 모형 매개변수는 모형 모의에서 중요한 역할을 한다. 일반적으로 제한된 자료로 보정된 모형 매개변수가 미래에 적용될 수 있다고 가정한다. 즉, 수문 모형의 매개변수는 상수로 처리되는 반면 모형 입력은 시간이 지남에 따라 달라진다. 그러나 이 가정은 기후의 시간적인 변화와 인간 활동으로 인해 모의한 하천유량에 큰 오차를 포함할 수 있다. 모형 매개변수를 시간에 따라 변하는 것으로 간주할 필요성에 대한 인식이 증가하고 있다(Brigode et al., 2013; Thirel et al., 2015; Patil and Stieglitz, 2015). 매개변수 보정은 모형 구조와 관측자료 사이에 상호보완작용을 포함하므로, 모형 매개변수는 기후의 시간적 변화에 따라 달라질 가능성이 있다(Wagener et al., 2003). 다른 한편, 도시화 및 물순환 건전성 프로젝트와 같은 인간 활동은 지표면의 변화를 초래하므로 변화하는 유역 특성을 반영하여 일부 매개변수는 그것에 맞게 변경해야 할 수도 있다(Legesse et al., 2003; Brown et al., 2005). 따라서 수문 모형의 매개변수의 시간적인 변동성을 연구하는 것은 하천유량의 예측에서 매우 중요하다(Xiong et al., 2019).

기후의 시간적 변화와 인간 활동에 대한 반응으로 시간에 따라 변하는 모형 매개변수를 얻기 위해 몇 가지 접근법이 사용되어왔다(Deng et al., 2016). 하나는 선택된 시간변화 모형 매개변수의 수학적인 형식을 설정하는 것이다(Marshall et al., 2006; Jeremiah et al., 2013). Westra et al. (2014)는 계절성, 연간 변동성 및 장기 추세의 함수에 따라 매개변수가 시간에 따라 변한다고 설정하여 수문 모형의 비정상성을 진단하고 해석하는 전략을 제안하였다. 또 다른 방법은 자료를 여러 연속적인 하위 집합으로 나누고 최적화 알고리즘을 이용하여 각 하위 집합의 모형 매개변수를 추정하는 것이다(Seibert et al., 2010; de Vos et al., 2010; Gharari et al., 2013; Vaze et al., 2010). 이러한 방법으로 Merz et al. (2011)은 모형 매개변수의 시간적 변화를 분석하기 위해 오스트리아의 273개 유역에 대해 1976년과 2006년 사이에 6개의 연속 5년 기간 동안 개념적 강우 유출 모형의 매개변수를 추정하였다. 이러한 접근 방식의 단점은 식별된 매개변수 시간변화를 추정하기 위해 사전에 수학적인 형식 또는 기간에 대한 설정이 필요하여 다양한 상황에 대한 모의 환경을 개별적으로 조정해야 한다는 것이다(Pathiraja et al., 2018).

자료 동화 방법은 변화하는 조건에 따라 자동으로 수문 모형의 매개변수를 추정할 수 있다. 자료 동화의 기본 개념은 수문 모형과 관측자료 모두에서 오류를 정량화하고 모형 출력변수를 관측자료와 최적으로 결합하여 수문 모형의 상태변수를 갱신하는 것이다(Clark et al., 2008). 자료 동화 방법은 실시간으로 모형의 상태변수와 매개변수를 갱신하는 데 사용되어왔다(Moradkhani et al., 2005b; Wang et al., 2009; Abbaszadeh et al., 2018). 그러나 일부 연구만이 자료 동화 방법을 이용하여 시간변화 매개변수를 생성하는 데 집중했다(Smith et al., 2008; Moradkhani et al., 2012; Vrugt et al., 2013; Feng et al., 2017; Pathiraja et al., 2018). 국내에서도 하천유량 모의를 위한 자료 동화 연구들이 진행된 바 있으나(Lee and Bae, 2011; Choi et al., 2020), 일부 연구만이 시간변화 매개변수를 다루고 있다(Choi et al., 2011; Lee et al., 2017).

본 연구의 핵심 연구 방법인 입자 필터와 하천유량 자료 동화에 관한 최신 문헌을 살펴보면 아래와 같다. Moradkhani et al. (2005a)는 수문 모델의 상태 및 매개변수의 불확실성 평가를 위하여 입자 필터를 사용한 순차적 자료 동화를 수행하였으며, Noh et al. (2011)도 순차적 몬테카를로 필터, 즉 입자 필터를 사용하여 개념적 수문 모델에 대한 이중 상태-매개변수 갱신에 관한 연구를 수행하였다. Moradkhani et al. (2012)는 입자 필터와 Markov chain 몬테카를로 방법을 결합한 자료 동화 기법을 개발하여 불확실성을 정량화하고자 하였으며, Fan et al. (2017)도 앙상블 칼만 필터와 입자 필터 방법을 결합하여 수문학적 자료 동화를 위한 통합 접근법을 개발하였다. 이후 Abbaszadeh et al. (2018)은 Moradkhani et al. (2012)의 연구를 기반으로 수문 자료의 동화를 위하여 Markov chain 몬테카를로와 결합한 진화된 입자 필터를 개발한 바 있으며, Cao et al. (2019)는 댐 홍수 침수 모의를 위하여 조도의 시공간적 변동성을 고려한 고정밀 2차원 유체 역학 모델에 수정된 입자 필터 기반 자료 동화 방법을 적용하였다.

본 연구의 목적은 하천유량 관측자료를 이용하여 시간에 따라 변화하는 매개변수를 추정하는 방법을 살펴보고, 하천유량 자료가 모형에 동화될 때 모의 효율성이 어떻게 변하는지 분석하는 것이다. 입자 필터 방법이 하천유량을 수문 모형에 동화시키는 데 적용되었다. 먼저 다양한 시나리오를 설정한 가상의 합성 수치 실험을 수행하여 입자 필터 방법이 시간에 따라 변화하는 매개변수를 적절하게 추적할 수 있는지를 살펴보았다. 이후 실제 유역에 적용하여 시간에 따라 변화하는 매개변수를 추정한 후, 고정된 매개변수를 사용하였을 때의 하천유량 예측성능과 비교하였다.

2. 연구 방법

2.1 월 물 수지 모형

여러 목적의 수자원 계획을 수립할 때 그 유역의 수자원 부존량을 계산할 필요가 있으며, 이때 월 기상 자료와 유출고 사이의 관계(즉, 월 물 수지 모형)가 수립되어 있다면 월별 기상 자료를 이용하여 월 유출고 및 연 유출고를 구할 수 있다(Lee, 2006). Xiong and Guo (1999)가 개발한 2개 매개변수로 구성된 월 물 수지 모형은 모형 구조가 단순하고 모의 정확도가 비교적 높아서 월 유출고 모의에 널리 사용된다(Guo et al., 2002; Xiong and Guo, 2012). 모형의 입력은 월 강수량(P, mm/month) 및 월 기준증발산량(E_o, mm/month)이며, 출력은 월 유출고(Q, mm/month) 및 실제 증발산량(E, mm/month)이다. 실제 증발산량 E는 아래와 같이 계산된다.

(1)

E [t] - c \cdot E_{o} [t] \cdot \tanh (\frac{P [t]}{E_{o} [t]})

여기서 c는 월 물 수지 모형의 첫 번째 매개변수(무차원)로서, 강수량과 기준증발산의 변동을 포괄적으로 반영하게 되며 0.2에서 2.0 사이의 값을 갖는다.

월 유출고는 토양수분(s)과 아래와 같은 관계가 있는 것으로 설정된다.

(2)

Q [t] = s [t] \cdot \tanh (\frac{s [t]}{s c})

여기서 sc는 유역의 물 저장 용량을 나타내기 위해 사용되는 월 물 수지 모형의 두 번째 매개변수이다. 매개변수 sc는 토양수분의 단위와 같은 길이의 단위를 가지며, 200 mm에서 2,000 mm의 범위에서 결정된다.월 단위로 모형이 구동되는데, t번째 월에 토양에 남아있는 물의 양(즉, 토양수분) $s [t]$ 은 $s [t - 1] + P [t] - E [t]$ 이므로, 월 유출고는 아래와 같이 계산된다.

(3)

Q [t] = (s [t - 1] + P [t] - E [t]) \cdot \tanh (\frac{s [t - 1] + P [t] - E [t]}{s c})

마지막으로 t번째 월말의 토양수분은 물 수지 방정식에 의하여 아래와 같이 계산된다.

(4)

s [t] = s [t - 1] + P [t] - E [t] - Q [t]

2.2 입자 필터

입자 필터(Particle Filter)는 정규분포를 따르지 않는 시스템에도 적용 가능한 비선형 필터이다(Gordon et al., 1993). 입자 필터도 큰 틀에서는 (앙상블) 칼만 필터 알고리즘과 비슷하게 예측과 갱신 과정을 반복한다(Moradkhani et al., 2005a). 즉, 예측 과정에서는 모형을 이용하여 현재의 예측값을 구하고, 갱신 과정에서는 이 예측값과 관측값을 이용해 최종 상태변수를 갱신한다. 하지만 입자 필터는 칼만 필터에서와 같은 칼만 이득을 사용하지 않는다. 대신에 상태변수를 갱신할 때 입자의 분포로부터 오차 공분산을 직접 산정하게 된다. 입자 필터에서는 입자의 가중치를 반영한 모든 입자의 가중 합이 상태변수의 추정값이다. 다만, 입자 필터는 재샘플링이라는 절차가 추가된다(Moradkhani et al., 2012). 입자 필터 알고리즘을 정리하면 아래와 같다.

1) Step 1: 상태변수 입자 $s_{k}^{i}$ 의 초기화

(5)

s_{k}^{i}, i = 1, \dots, N_{p}

여기서 N_p는 운용할 입자의 개수이다. 월 물 수지 모형에서 상태변수는 토양수분 s이다. 편의상 k는 시간, i는 입자를 지칭한다.

2) Step 2: 매개변수 입자의 표본추출

(6)

θ_{k}^{i}, i = 1, \dots, N_{p}

월 물 수지 모형에서 매개변수 $θ$ 는 c와 sc이므로, 매개변수 $θ$ 는 이변량으로 취급된다.

3) Step 3: 입자 가중치 초기화

(7)

w_{k}^{i} = \frac{1}{N_{p}}, i = 1, \dots, N_{p}

4) Step 4: 입력값 섭동(Perturbation)

(8)

u_{k + 1}^{i} = u_{k + 1} + ξ_{k + 1}^{i}, ξ_{k + 1}^{i} ~ N (0, Σ_{k + 1}^{u}), Σ_{k + 1}^{u} = {(α \cdot u_{k + 1})}^{2}

여기서 $α$ 는 0.1과 같이 관측된 입력의 일정 분율로서, 입력값의 분포는 관측된 값 u가 평균이며, 관측된 값의 10%( $α$ 가 0.1일 때)가 표준편차인 정규분포(N)를 따른다고 가정할 수 있다. 월 물 수지 모형에서 입력값은 강수량 P과 기준증발산량 E_o이다.

5) Step 5: 상태변수 및 출력변수 예측

(9)

[Q_{k + 1}^{i}, s_{k + 1}^{i -}] = M (x_{k}^{i +}, θ_{k}^{i}, u_{k + 1}^{i}), i = 1, \dots, N_{p}

여기서 M ( ‧ )는 월 물 수지 모형이며, $s_{k + 1}^{i -}$ 는 상태변수 입자의 예측값, $Q_{k + 1}^{i}$ 는 입자 i에 의한 출력변수 예측값이다.

6) Step 6: 입자 우도 추정

(10)

L^{i} = n o r m p d f (Q_{k + 1}^{i}, Q_{k + 1}, β Q_{k + 1})

여기서 $n o r m p d f (x, μ, σ)$ 는 평균 $μ$ , 표준편차 $σ$ 인 정규분포에서 $x$ 에 해당하는 정규분포함수 값이다. 즉, 평균은 관측값 $Q_{k + 1}$ 이고 표준편차는 $β Q_{k + 1}$ 인 정규분포에서 입자 i에 의한 출력값이 대응하는 정규분포함수 값이 입자 i에 대한 우도 Lⁱ가 된다. 여기서 $β$ 는 0.1과 같이 관측자료의 일정 분율로 설정될 수 있다.

7) Step 7: 입자 가중치 갱신

(11)

w_{k + 1}^{i} = \frac{w_{k}^{i} L^{i}}{\sum_{i = 1}^{N_{p}} (w_{k}^{i} L^{i})}

즉, 입자 i의 출력변수 예측값 $Q_{k + 1}^{i}$ 와 관측자료 $Q_{k + 1}$ 의 차이가 작을수록 입자 가중치는 커지게 된다.

8) Step 8: 순차적 중요도 재샘플링(Sequential Importance Resampling, SIR)

(1) 0에서 1 사이의 구간을 입자의 개수(N_p)만큼 나누는데, 각 구간은 해당 입자의 가중치에 비례한 길이로 할당한다. 즉, n번째 구간의 길이는 n번째 입자의 가중치를 나타낸다.

(2) 0에서 1 사이 균등분포 난수를 N_p개 생성

(3) (1)에서 할당한 구간마다 (2)에서 생성한 값이 몇 개 들어 있는지 센다. 가중치가 클수록 구간의 길이가 길어서, (2)에서 생성한 값이 해당 구간에 들어가 있을 확률(개수)은 가중치에 비례하게 된다.

(4) 각 구간에 포함된 값의 개수만큼 해당 입자의 개수를 재샘플링한다. 만약 해당 구간에서 (2)에서 생성한 값이 하나도 들어가 있지 않다면 해당 입자는 버린다. 즉, 이 입자는 다음 예측 과정에서 사용되지 않는다. 여러 개의 값이 포함되어 있다면 해당 입자는 그 개수만큼 중복해서 재샘플링한다( $x_{k - r e s a m p}^{i}$ 또는 $θ_{k - r e s a m p}^{i}$ ).

(5) 상태변수 갱신

(12)

x_{k + 1}^{i} = x_{k - r e s a m p}^{i}

9) Step 9: 매개변수 입자 섭동

(13)

θ_{k + 1}^{i} ~ N (θ_{k - r e s a m p}^{i}, γ \cdot Σ_{k}^{θ})

여기서 $γ$ 는 입자 필터 알고리즘의 초 매개변수(hyper-parameter)이며, $Σ_{k}^{θ}$ 는 $θ_{k}$ 의 분산(즉, 재샘플링 이전의 $θ$ 의 분산)이다.

10) Step 10: k = k + 1로 설정한 후, Step 3으로 돌아가서 반복

2.3 성능 평가

모형 예측성능평가는 세 가지 통계량(R², NSE, KGE을 이용하여 수행되었다. R²는 관측자료와 모의 자료의 선형회귀분석에 의한 결정계수이며, 0.6 이상이면 모형의 예측성능(즉, 관측자료와의 일치성)이 만족스러운 것으로 제시되어 있다(Engel et al., 1993). NSE는 Nash-Sutcliffe 모형 효율 계수로서 아래와 같다(Nash and Sutcliffe, 1970).

(14)

N S E = 1 - \frac{\sum_{j = 1}^{N} {(Q_{j}^{s} - Q_{j}^{o})}^{2}}{\sum_{j = 1}^{N} {(Q_{j}^{o} - Q^{o})}^{2}}

여기서 N은 하천유량 관측자료의 개수, Q^s는 예측된 유출고, Q^o는 관측된 유출고, $Q^{o}$ 는 Q^o의 평균이다. NSE가 1에 가까울수록 사용된 모형의 효율성이 높다는 것을 의미한다. 충분한 품질의 모형을 나타내는 임계값은 0.5에서 0.65의 범위로 제안되어있다(Ritter and Munoz-Carpena, 2013).

KGE는 Gupta et al. (2009)이 제안한 계수로서 아래와 같이 산정된다.

(15)

K G E = 1 - \sqrt{(r' - 1)^{2} + (α' - 1)^{2} + (β' - 1)^{2}}

여기서, $r'$ 은 관측자료와 모의 자료의 선형 상관계수, $α'$ 는 모의 자료의 표준편차와 관측자료의 표준편차의 비, $β'$ 는 모의 자료의 평균과 관측자료의 평균 비이다. KGE가 1에 가까울수록 모의 자료가 관측자료를 높은 수준으로 모의하고 있음을 의미한다. Patil and Stieglitz (2015)는 KGE가 0.6 이상이면 충분히 만족스러운 모의 결과로 간주할 수 있음을 제시하였다.

수치 실험에서 시간변화 매개변수의 재현성능은 RMSE를 이용하여 평가되었다.

(16)

R M S E = \sqrt{\frac{1}{N} \sum_{j = 1}^{N} {(θ_{j}^{s} - θ_{j}^{o})}^{2}}

여기서 $\bar{θ^{s}}$ 는 매개변수의 앙상블 평균 추정값이며, $θ^{o}$ 는 설정된 매개변수(참값)이다.

3. 사례 연구

3.1 수치 실험

수치 실험은 모형 매개변수의 시간적 변화를 식별하기 위한 입자 필터의 성능을 평가하기 위해 설계되었다. 모형 매개변수는 추세 및 주기성이 포함되어 주어졌다. 2001년 1월부터 2019년 12월까지 안동댐 유역의 강수량 및 기준증발산량을 입력자료로 삼아서 월 물 수지 모형을 사용하여 하천유량 관측자료를 생성했다. 입자 필터가 시간에 따라 변하는 매개변수를 식별하는 수치 실험은 다음과 같이 설계되었다.

1) 시나리오 설정. 월 간격으로 다양한 시간적인 변화를 가진 매개변수(즉, 시나리오)를 생성한 후에 월 물 수지 모형을 사용하여 하천유량 자료를 생성한다. 수치 실험에 적용된 시나리오는 아래와 같다. 1) 시나리오 1: 고정된 c와 고정된 sc, 2) 시나리오 2: 감소 추세가 있는 c와 감소 추세가 있는 sc, 3) 시나리오 3: 증가 추세가 있는 c와 증가 추세가 있는 sc, 4) 시나리오 4: 감소 추세가 있는 c와 증가 추세가 있는 sc, 5) 시나리오 5: 증가 추세가 있는 c와 감소 추세가 있는 sc, 6) 시나리오 6: 감소 추세와 주기성이 있는 c와 감소 추세가 있는 sc. 시나리오 1은 고정된 매개변수를 입자 필터가 잘 추정하는지를, 시나리오 2와 3은 증가 및 감소 추세가 있는 매개변수를 잘 추정하는지를 검토할 목적으로 설정되었다. 시나리오 4와 5는 어떤 매개변수는 증가 추세가 있고 다른 매개변수는 감소 추세가 있을 때, 매개변수의 시간변화 효과가 상쇄될 수 있으므로, 입자 필터가 이를 효과적으로 추적할 수 있는지를 검토하기 위하여 설정되었다. 시나리오 6은 증발산에 관여하는 매개변수 c에 계절성이 있을 때 입자 필터가 이를 잘 반영하는지를 검토할 목적으로 설정되었다. 매개변수 sc는 유역의 물 저장 용량을 표현하므로 개발 환경에서는 감소 추세가 될 가능성이 있음을 반영한 설정이다.

2) 초기화. 입자 개수 N_p와 동화 시간 단계 N을 설정한다. 첫 번째 시간 단계에서 매개변수와 상태변수 앙상블은 균등분포에 의해 생성되었다.

3) 자료 동화. 매개변수 및 상태변수를 초기화한 후, 모형 매개변수 및 상태변수는 step (1)에서 얻은 하천유량 관측자료를 사용하여 갱신되었다. 마지막으로 입자 필터의 성능을 평가하기 위해 동화된 모형 매개변수와 실제 모형 매개변수를 비교했다.

즉, 수치 실험에서 모형은 하천유량 관측자료를 완벽하게 구현하는 것으로 설정된다. 따라서 모든 오차는 입력자료 및 출력자료가 자체적으로 가지고 있는 불확실성과 매개변수 추정 방법에서 발생하는 것으로 간주할 수 있을 것이다.

3.2 연구 유역 및 자료

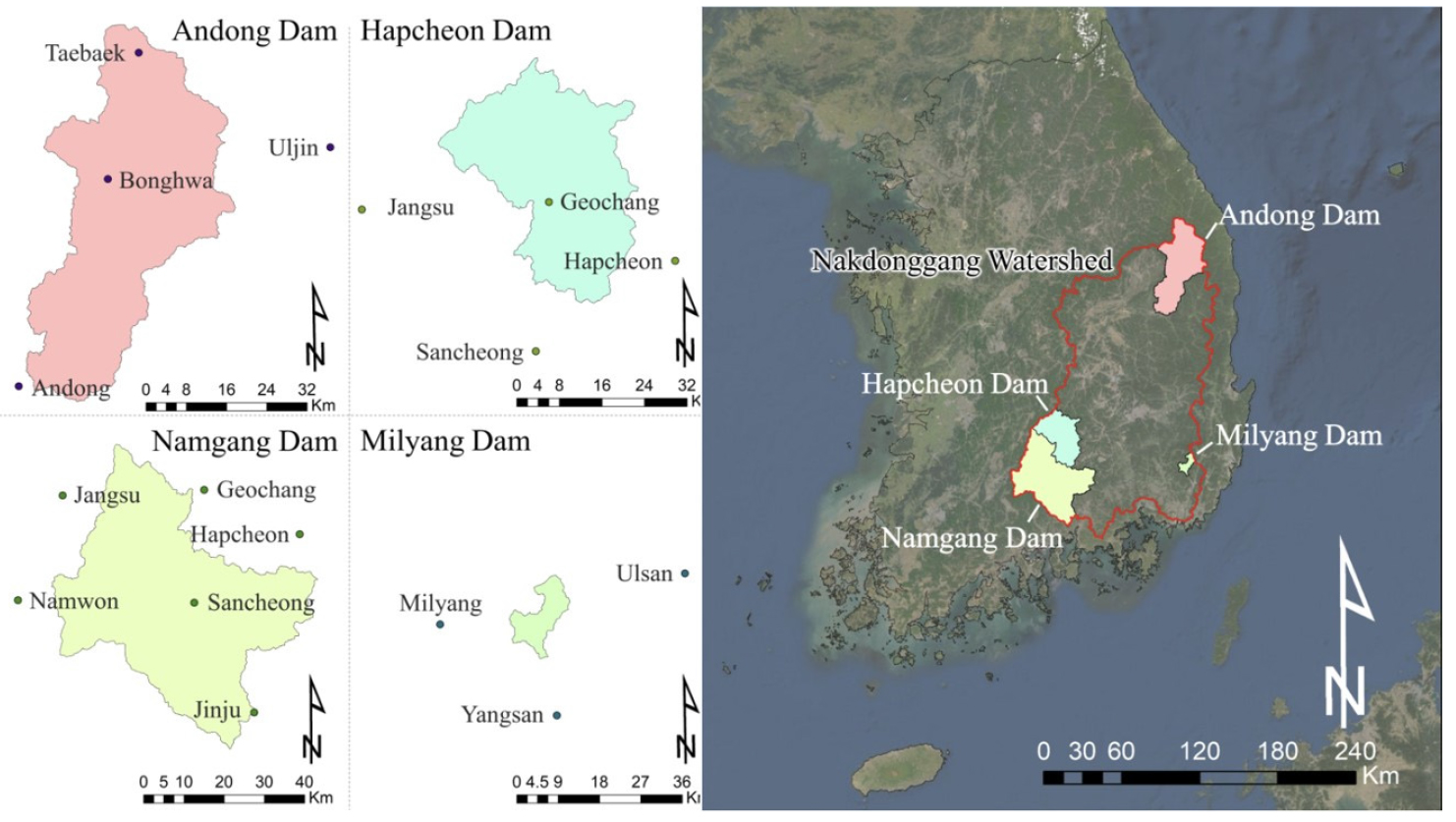
본 연구는 한반도 남동부에 있는 안동댐 유역, 합천댐 유역, 남강댐 유역, 밀양댐 유역의 자료를 사용하여 수행되었다(Fig. 1). 수문 기상 자료에는 2001 ~ 2019년 기간의 월 강수량, 월 기준증발산량, 월 하천유량이 포함된다. 강수량과 기준증발산량은 Fig. 1에 나타난 기상관측지점의 자료를 티센 가중평균하여 적용하였다. 기준증발산량은 Penman-Monteith 방법으로 일 단위로 계산된 후, 월 단위로 합산하였다(Allen et al., 1998, Won et al., 2020). 하천유량 자료는 국가 수자원 관리 종합정보시스템(wamis.go.kr)에서 제공하는 일 단위 댐 유입량 자료를 사용하였다. Table 1에 2001년부터 2019년 기간의 강수량, 기준증발산량, 유출고로 환산된 하천유량의 연평균 값과 유역 면적을 나타내었다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540602/images/kwra_54_06_02_F1.jpg

Fig. 1.

Study area and location of meteorological observation sites

Table 1.

Annual mean values of precipitation, reference evapotranspiration, and runoff depth, and areas for four watersheds

Watershed	Precipitation (mm/year)	Reference evapotranspiration (mm/year)	Runoff depth (mm/year)	Area (km²)
Andong Dam	1,167	1,001	579	1,627
Hapcheon Dam	1,307	1,064	677	929
Namgang Dam	1,494	1,075	998	2,281
Milyang Dam	1,235	1,122	832	103

3.3 입자 필터 매개변수 설정

운용되는 입자의 개수가 입자 필터의 성능과 계산속도에 영향을 미칠 수 있다(Moradkhani et al., 2005a; Dechantcm and Moradkhani, 2012). 일반적으로 입자의 개수가 증가할수록 성능은 개선되지만, 계산시간이 길어지고 더 많은 저장 공간이 필요하게 된다. 10에서 100,000까지 다양한 개수의 입자가 실험되었으며, 최종적으로 3,000개의 입자를 운용하기로 하였다. 입력변수인 강수량과 기준증발산량에 도입된 잡음의 표준편차는 변수의 크기에 비례하게 설정하였다(Leisenring and Moradkhani, 2012). 즉, Eq. (8)의 $α$ 는 강수량과 기준증발산량 모두 0.1을 적용하였다. 출력변수인 하천유량에 도입된 잡음의 표준편차도 변수의 크기에 비례하여 $β$ = 0.1로 설정하였다. 재샘플링된 매개변수의 섭동을 위한 초 매개변수 $γ$ 는 0.1에서 1.0까지 0.1 간격으로 실험하여 유역별로 최적의 모의 성능을 보인 값을 선택하도록 수동 조정하였다.

4. 결 과

4.1 수치 실험 결과

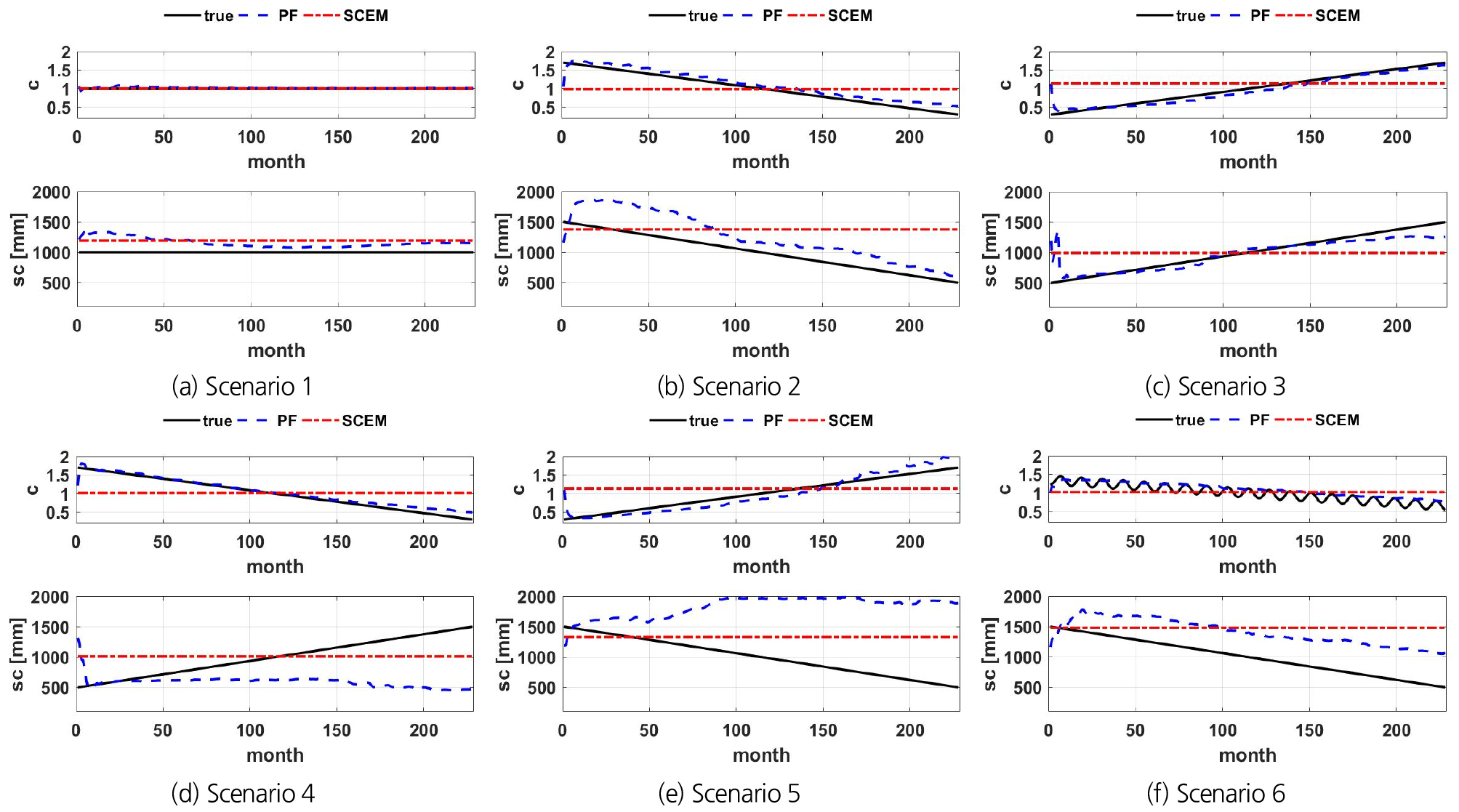
입자 필터를 이용한 자료 동화 방법의 성능을 평가하기 위해 다양한 시나리오에서 동화된 모형 매개변수와 실제 모형 매개변수의 비교를 수행하여 Fig. 2에 도시하였다. Fig. 2에서 ‘true’는 3.1에서 설명된 시나리오에 따른 매개변수의 값이다. 이들 매개변수의 값을 이용하여 하천유량을 생성한 후, 생성된 하천유량에 맞춰 입자 필터를 이용한 자료 동화 방법으로 매개변수를 시간별로 추정한 결과가 ‘PF’이다. 제안된 방법과의 비교를 위하여 고정된 매개변수를 추정하는 방법의 하나인 SCEM (Shuffled Complex Evolution Metropolis) 알고리즘(Vrugt et al., 2003)을 이용한 매개변수 및 하천유량 모의 성능도 같이 제시하였다. Table 2는 매개변수 및 하천유량에 대한 성능 평가 수치를 보여준다.

시나리오 1(고정된 c와 고정된 sc)에서는 입자 필터와 SCEM이 모두 고정된 매개변수를 잘 추정하고 있으나(Fig. 2(a)), 하천유량 예측성능은 SCEM이 약간 더 우수함을 보여준다(Table 2). 그러나 그 차이가 크지 않기 때문에 입자 필터를 이용한 자료 동화 방법은 고정된 매개변수를 잘 추정할 수 있다고 말할 수 있다. 이때, Fig. 2의 거의 모든 그림에서 살펴볼 수 있듯이 입자 필터에 의한 자료 동화 방법은 방법의 특성상 초기에 안정화를 위한 시기가 필요하다. 짧게 보면 12개월, 길게 보면 48개월의 안정화 시기가 지난 이후에는 고정된 매개변수를 잘 추정하였다. 안정화 시기는 자료의 특성 및 모형의 구조, 적용 유역과 같은 다양한 구동 환경에 따라 달라질 것이므로, 적용된 환경에 맞는 적절한 선택이 요구된다. Table 2의 성능 평가 수치는 더 엄격한 관점에서 안정화 시기를 12개월로 간주하여 2002년 1월부터 2019년 12월까지의 결과를 바탕으로 계산되었다. 참고로 안정화 시기를 24개월 또는 48개월로 설정하여 하천유량 예측성능을 평가하면 입자 필터에 의한 방법의 성능 수치가 더 우수하게 계산된다.

시나리오 2와 3에서는 입자 필터가 감소하는 선형 추세를 나타내며 변화하는 매개변수를 비교적 잘 구현해내고 있음을 발견할 수 있다(Figs. 2(b) and 2(c)). 상대적으로 매개변수 c의 감소 추세를 더 잘 재현하고 있다. 이는 매개변수 sc와 비교할 때 매개변수 c가 하천유량 모의에 미치는 영향이 더 크기 때문이다. SCEM은 방법의 특성상 고정된 매개변수를 추정할 수밖에 없다. 따라서 추정된 매개변수의 오차가 SCEM에서 더 커지게 되며, 하천유량 예측성능도 입자 필터를 이용한 자료 동화 방법의 성능에 미치지 못하게 된다(Table 2).

시나리오 4와 5에서는 매개변수의 추세 방향이 다른 경우를 설정한 합성 실험의 결과이다(Figs. 2(d) and 2(e)). 즉, 이 실험은 어떤 매개변수는 하천유량이 증가하는 방향으로 선형 추세가 있으며, 다른 매개변수는 하천유량의 감소하는 방향으로 선형 추세가 있는 상황에 기반한다. 두 개의 실험 모두 매개변수 c의 추세는 증가하든 감소하든 입자 필터가 잘 추적하고 있었으나, 매개변수 sc의 추세는 제대로 추정할 수 없었다. 이는 매개변수 c가 월 유출고 모의에 있어서 매개변수 c의 민감도가 매개변수 sc의 민감도보다 훨씬 크기 때문으로 분석될 수 있다. Table 2의 시나리오 2와 3의 하천유량 예측성능을 보면, 입자 필터의 하천유량 예측성능은 비교적 양호함을 발견할 수 있으며, 이는 월 유출고 모의에 있어서 매개변수 sc가 중요한 역할을 하지 못하고 있다는 사실을 의미한다. 매개변수 sc의 추세를 적절하게 추정할 수 없었던 다른 한 가지 원인으로는 유출에 미치는 영향을 서로 다른 방향으로 진행되는 매개변수를 입자 필터에 동시에 추적하기에는 부족한 면이 있을 수도 있다는 가설이다. 이 가설의 입증을 위한(또는 반증을 위한) 더 정확한 분석을 위해서는 유출에 미치는 민감도가 서로 비슷한 매개변수를 이용한 가상의 수치 합성 실험이 필요하나, 이는 본 연구에서 사용된 월 유출고 모형으로는 불가능하므로 추후 연구로 남겨두도록 하겠다.

Fig. 2(e)는 시나리오 6(추세와 주기 특성이 있는 매개변수 c와 추세 특성이 있는 매개변수 sc)의 매개변수 추정 결과를 보여준다. Table 2에 나타낸 바와 같이 두 방법 모두 하천유량 예측성능은 최소 기준 이상을 확보하고 있으나(사실 입자 필터의 성능은 매우 우수), 추정된 매개변수는 참값과는 거리가 있다. 입자 필터는 매개변수 c의 주기 성분을 매우 제한적인 범위에서만 반영하고 있다. 또한 입자 필터 방법의 한계로 인하여 동화된 c 추정값과 참값 사이에 시간 지연이 있다는 사실에 유의해야 한다. 입자 필터에서 매개변수는 예측값과 관측값을 기반으로 갱신되는데, 매개변수 및 출력변수를 추정할 때 시간 지연이 발생할 수 있다(Clark et al., 2008).

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540602/images/kwra_54_06_02_F2.jpg

Fig. 2.

Model parameter assimilated by PF and estimated by SCEM, and its true value

Table 2.

Scheme performance for parameter estimation and stream flow prediction in numerical experiments

Scenario	Scheme	Parameter c	Parameter sc	Q
Scenario	Scheme	RMSE	RMSE	R²	NSE	KGE
1	PF	0.02982	175.2	0.9931	0.9879	0.9221
1	SCEM	0.00280	193.9	0.9968	0.9919	0.9287
2	PF	0.13251	292.3	0.9839	0.9602	0.8344
2	SCEM	0.40623	474.3	0.5672	0.4979	0.7522
3	PF	0.10055	130.7	0.9978	0.9965	0.9426
3	SCEM	0.42875	290.0	0.8668	0.7860	0.6151
4	PF	0.08648	542.6	0.9534	0.9368	0.8898
4	SCEM	0.40633	290.2	0.7800	0.7544	0.8700
5	PF	0.16242	932.3	0.9823	0.9803	0.9297
5	SCEM	0.42675	439.6	0.8878	0.8021	0.6221
6	PF	0.14493	428.4	0.9757	0.9676	0.8970
6	SCEM	0.22191	561.0	0.8438	0.8261	0.9029

4.2 시간변화 매개변수의 성능 평가

다음으로 입자 필터를 이용하여 과거 하천유량 관측자료를 월 물 수지 모형에 동화하는 실제 사례를 살펴보았다. 입자 필터의 성능은 안동댐 유역, 합천댐 유역, 남강댐 유역, 밀양댐 유역으로부터 2001년 1월부터 2019년 12월까지 19년 동안의 월 강수량, 월 기준증발산량, 월 유출고 자료를 이용하여 평가되었다. 참고로 본 연구에서 모의값은 자료 동화 직후의 결과이다. 자료 동화 후 1개월 선행 예측(예를 들어, one-month ahead forecasting)의 결과가 아니다.

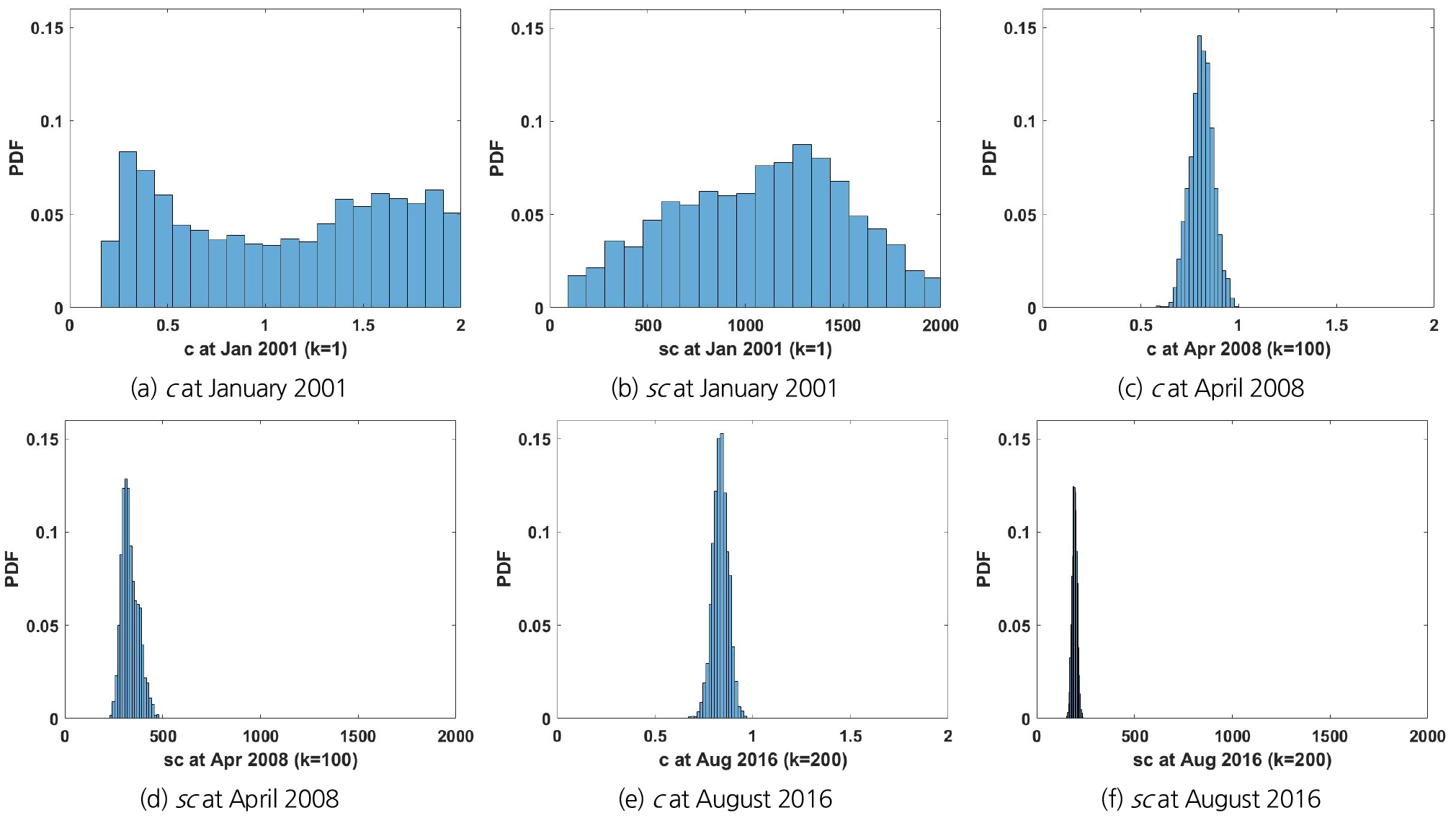
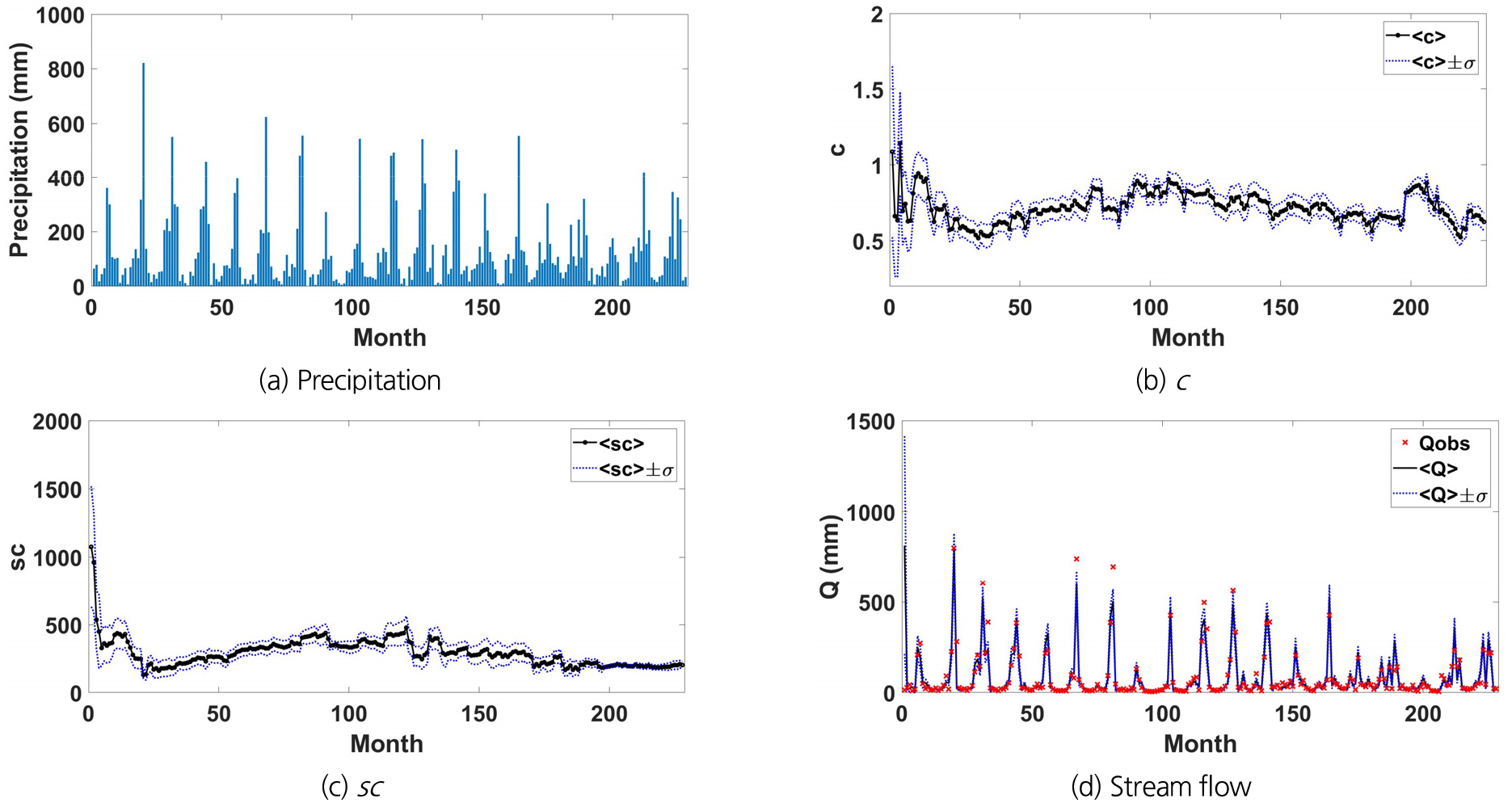
매개변수 추정이 초기 조건에 민감하지 않게 만들기 위해 초기 상태변수(즉, 토양수분 s)에 대해 3,000개의 균일하게 분포된 값의 입자를 생성하였다. 매개변수의 사전분포도 균등분포에서 시작하였다. 매개변수 c는 0.2에서 2.0의 범위이며, 매개변수 sc의 범위는 200 mm에서 2,000 mm로 사전 설정되었다. 따라서 초기 매개변수 입자는 균일하게 미리 정의된 범위 내에서 표본 추출하였다. Fig. 3은 매개변수 공간에서 입자 필터가 3개의 시간 단계에서 추정한 매개변수의 사후분포를 보여준다. Fig. 3의 히스토그램 bin의 개수는 모두 20개로 고정하여 사후분포로부터 표본 추출된 앙상블을 나타내었다. 자료 동화가 진행됨에 따라 매개변수 사후분포의 분산이 줄어들고 있음을 살펴볼 수 있다. 이는 자료 동화 초기에는 추정된 매개변수의 불확실성이 크게 형성되지만, 자료 동화가 진행되면서(즉, 새로운 하천유량 관측자료가 축적되면서) 추정된 매개변수의 불확실성이 일정 수준으로 작아지고 있음을 의미한다. 그러나 매개변수 sc의 경우에서 살펴볼 수 있듯이, 추정된 매개변수의 불확실성이 작아진다는 것이 반드시 추정된 매개변수가 일정한 값으로 수렴된다는 것을 의미하지는 않는다. 2008년 4월과 2016년 8월의 매개변수 sc의 앙상블 평균값이 다름을 발견할 수 있다. 매개변수의 앙상블 평균의 시간에 따른 변화를 Fig. 4에 도시하였다. 자료 동화 방법을 이용하여 추정된 매개변수는 하천유량 관측자료가 갱신될 때마다 그에 적응하여 새로운 매개변수 사후분포를 형성하게 되기 때문에 엄밀하게 말하자면 시간에 따라 연속적으로 변화되는 매개변수 앙상블 평균을 갖게 된다. Fig. 4에서 Q_obs는 하천유량 관측치이며, < >는 사후분포에서 추출된 매개변수(c 또는 sc) 및 그로부터 예측된 하천유량(Q)의 앙상블 평균, $σ$ 는 각 변수의 앙상블 표준편차이다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540602/images/kwra_54_06_02_F3.jpg

Fig. 3.

Time evolution of posterior parameter distributions at three different time segments by assimilation of stream flow for Namgang Dam watershed

Fig. 4에서 볼 수 있듯이 시계열의 시작 부분은 매개변수 입자를 올바른 영역으로 유도하는 데 큰 도움이 되지 않는다. 즉, 시계열 시작 부분의 정보만으로는 시간변화 매개변수를 제대로 식별하기에 충분하지 않다. 자료 동화에 기반한 입자 필터 방법은 재귀 방정식의 구조로 되어 있어서 새로운 자료의 정보에 의존한다. 새로운 정보는 Eq. (10)의 우도함수를 통하여 상태변수와 매개변수에 반영된다. 월 물 수지 모형의 2개 매개변수는 약 12개월(또는 24개월) 후 불확실성이 현저하게 감소하고 있다. 매개변수 입자의 수렴 이유는 매개변수 입자의 갱신 과정에서 하천유량 관측자료가 연속적으로 관여하기 때문이다.

Table 3은 자료 동화 방법을 이용한 입자 필터와 SCEM의 하천유량 예측성능을 보여준다. SCEM은 고정된 매개변수를 추정하는 반면에, 입자 필터는 시간변화 매개변수를 추정한다. 입자 필터는 새롭게 추가된 하천유량 관측자료를 모형에 동화시켜 현재의 사용되고 있는 매개변수를 갱신하기 때문에, 시간 단계가 k = 1에서부터 진화될수록 매개변수의 값이 변화된다. Fig. 4에서 알 수 있듯이 시간변화 매개변수에서 특별한 추세가 있다고 보기는 어려웠다. 대신에, 갱신된 매개변수를 1월부터 12월까지 월별로 따로 모아서 살펴봄으로써 매개변수에 주기 성분이 있는지를 파악할 수 있다. Table 3에서 PFm은 1월부터 12월까지 매월별로 매개변수 앙상블을 별도로 모아서 구한 평균값으로 모형을 구동시킨 결과를 의미한다. PF는 2001년 1월부터 2019년 12월까지 228개월에 걸쳐 연속적으로 변하는 매개변수를 이용한 결과이며, SCEM은 고정된 매개변수를 이용한 하천유량 예측성능이다. 참고로 Table 3의 성능 평가 통계량은 초기 안정화 기간(12개월)을 고려하여 2002년 1월부터 2019년 12월 기간의 자료를 이용하여 계산되었다. 세 가지 방법 모두 월 유출고를 양호하게 모의하고 있으나, 안동댐 유역, 합천댐 유역, 밀양댐 유역에서는 PFm이 상대적으로 우수하며, 남강댐 유역에서는 SCEM이 상대적으로 더 우수함을 살펴볼 수 있다. 성능 평가 통계량별로 가장 우수한 방식을 밑줄로 표기하였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540602/images/kwra_54_06_02_F4.jpg

Fig. 4.

Uncertainty bound tracking of parameters in two parameter monthly water balance model for 19 years assimilation of historical stream flow at Namgang Dam watershed

Table 3.

Performance metrics for monthly stream flow prediction

Watershed		Andong Dam	Hapcheon Dam	Namgang Dam	Milyang Dam
PF	R²	0.8858	0.8679	0.9023	0.7962
	NSE	0.8741	0.8513	0.9018	0.7866
	KGE	0.9191	0.8922	0.9172	0.7648
SCEM	R²	0.8851	0.9153	0.9254	0.8001
	NSE	0.8779	0.9023	0.9184	0.7919
	KGE	0.9352	0.9136	0.8697	0.7762
PFm	R²	0.8961	0.9313	0.9072	0.8217
	NSE	0.8909	0.9270	0.9062	0.8052
	KGE	0.9331	0.8838	0.9108	0.7549

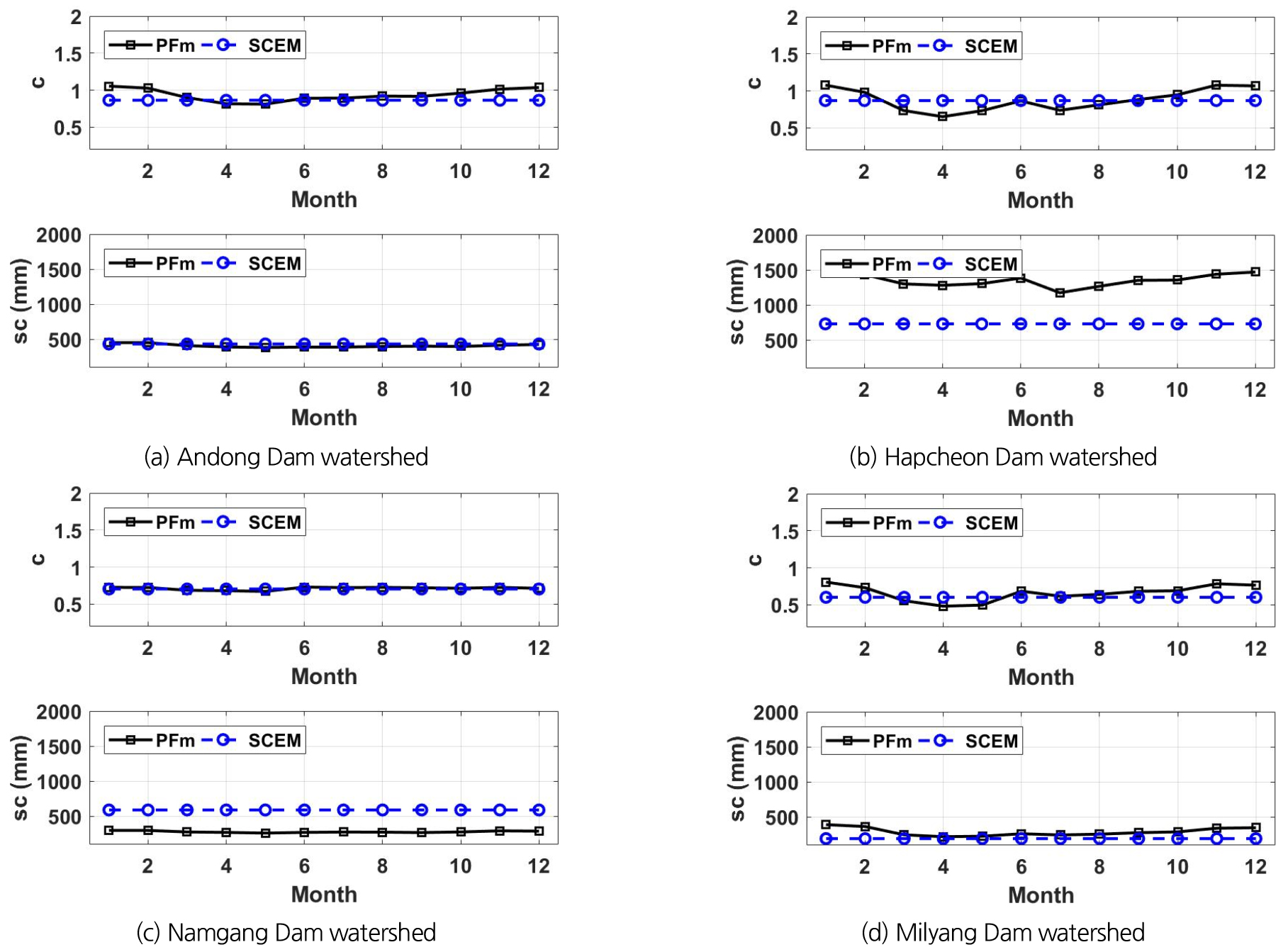
Fig. 5는 시간변화 매개변수 앙상블을 월별로 별도로 모아서 평균값을 추정한 결과를 보여준다. 매개변수 c는 PFm과 SCEM 방법 모두 비슷한 값으로 추정되지만, 두 방법으로부터의 추정된 매개변수 sc는 편차가 있음을 발견할 수 있다. 일차적인 원인으로는 sc가 c에 비하여 하천유량 예측에 미치는 민감도가 상대적으로 작다는데 원인을 찾아볼 수 있을 것이다. 즉, 적용된 월 물 수지 모형에서 입자 필터는 주로 c를 갱신하여 새로 추가된 하천유량 관측자료를 동화시키기 때문이다. 적용된 네 개 유역별로 정도 차이는 있지만, 입자 필터로 갱신된 매개변수 c는 겨울에 큰 값을 가지며, 봄에 작은 값을 보인다. 이러한 사실은 고정된 매개변수를 사용하여 하천유량을 예측하면 겨울에는 과대추정, 봄에는 과소추정의 가능성이 있음을 말해준다.

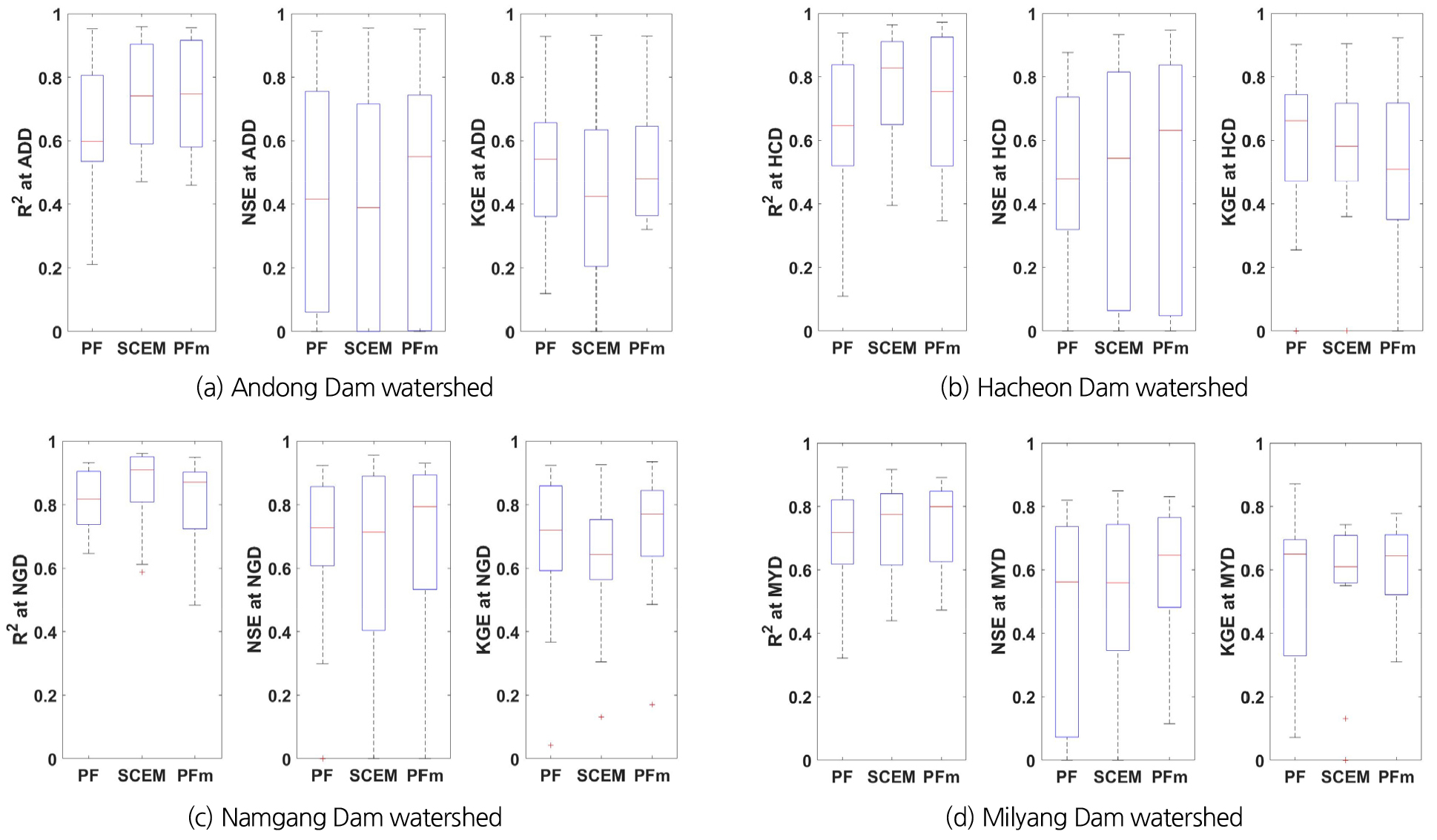
PFm 방식의 매개변수 추정 방법의 적용 가능성은 Fig. 6으로부터 살펴볼 수 있다. Table 3은 2002년 1월부터 2019년 12월까지 전체 월 유출고 시계열을 대상으로 하천유량 예측성능을 평가한 결과이나, Fig. 6은 1월부터 12월까지 매월별로 하천유량 예측성능을 평가한 결과이다. 즉, Fig. 6에서 하나의 box는 1월부터 12월까지의 12개의 하천유량 예측 통계량으로부터 작성된다. Box의 중간값을 기준으로 살펴보면, 안동댐 유역, 남강댐 유역, 밀양댐 유역에서는 PFm 방식이 상대적으로 우수하였으나, 합천댐 유역에서는 세 가지 방법의 우열을 가리기 어려웠다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540602/images/kwra_54_06_02_F5.jpg

Fig. 5.

Monthly parameter ensemble average estimate

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540602/images/kwra_54_06_02_F6.jpg

Fig. 6.

Monthly performance metrics for stream flow prediction

5. 입자 필터 매개변수의 민감도

본 장에서는 입자 필터의 매개변수에 대해서 살펴보았다. 입자 필터를 이용한 자료 동화 방법을 수행할 때, 크게 세 가지 종류의 매개변수가 사전에 결정되어야 한다. 1) 운용할 입자의 개수 N_p, 2) 입력변수의 불확실성 매개변수 $α$ 및 출력변수의 불확실성 매개변수 $β$ , 3) 매개변수 입자 섭동을 위한 초 매개변수 $γ$ .

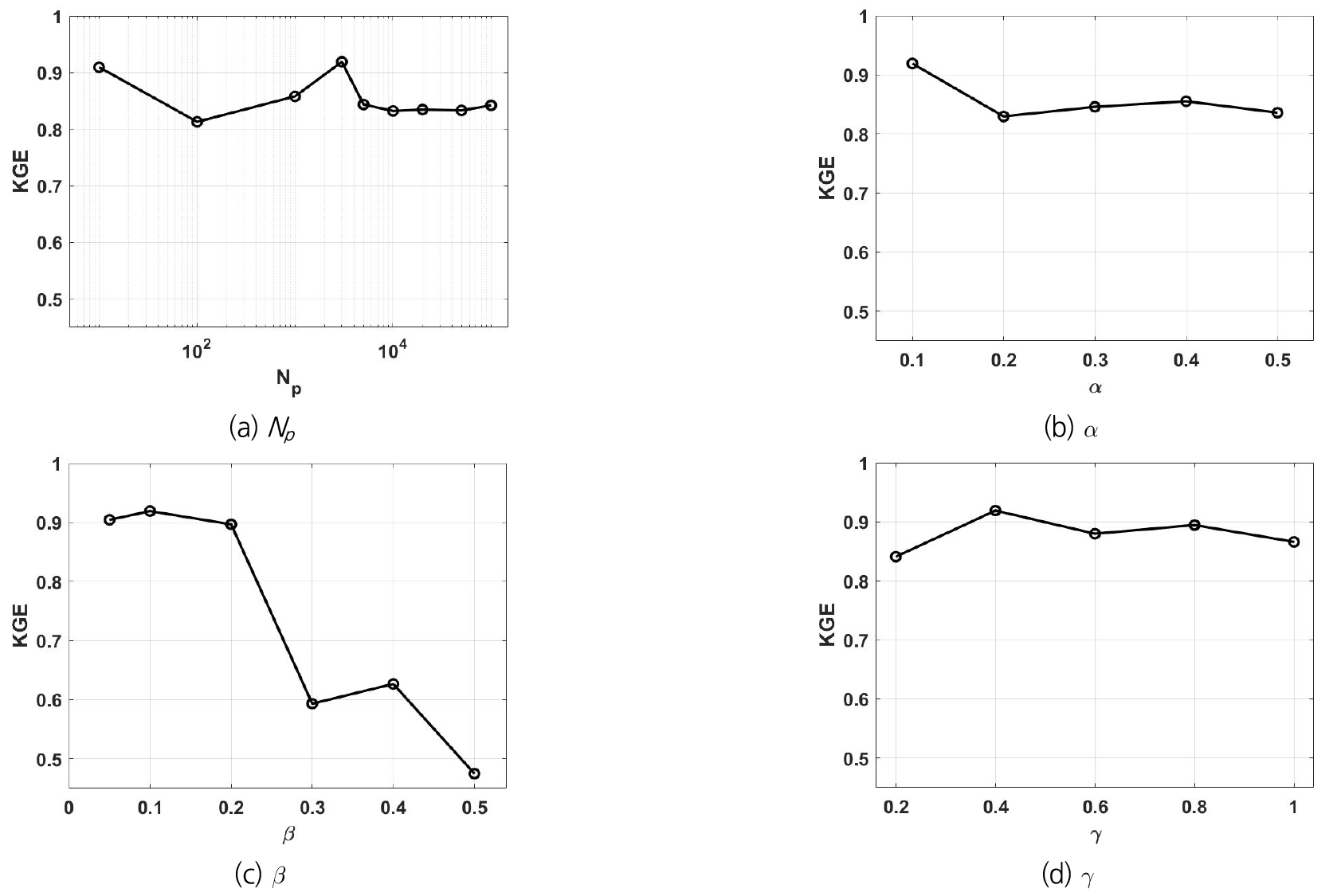
Fig. 7은 다양한 매개변수의 값에 대한 하천유량 예측성능을 보여준다. 하천유량 예측성능은 KGE로 나타내었다. 기준 매개변수 조합은 N_p = 3,000, $α$ = 0.1, $β$ = 0.1, $γ$ = 0.1이며, 다른 매개변수의 값은 고정해두고 하나의 매개변수의 값을 변경해가면서 실험을 진행하였다. 시험 유역은 안동댐 유역이다.

운용되는 입자 개수 N_p을 10개부터 100,000개까지 실험해보았지만, 하천유량 예측성능에 큰 영향을 미치지는 않는 것으로 나타났다(Fig. 7(a)). 안동댐 유역의 경우 3,000개 정도의 입자 개수가 가장 좋은 하천유량 예측성능을 보였지만, 적용 유역에 따라서 또는 입자 필터가 적용되는 기간에 따라서 달라질 수 있는 것으로 분석되었다. 입력자료의 불확실성을 의미하는 $α$ 을 변경시켜 실험한 결과는 Fig. 7(b)에 나타내었다. 입력자료의 불확실성은 입자 필터를 이용한 하천유량 예측성능에 큰 영향을 미치지 않는 것을 알 수 있다. 하지만 출력자료(즉, 하천유량 관측자료)의 불확실성을 의미하는 $β$ 은 예측성능에 많은 영향을 미치고 있음을 발견할 수 있다(Fig. 7(c)). 입자 필터는 하천유량의 새로운 관측정보를 모형에 동화시킴으로써 하천유량을 예측하기 때문에 하천유랑 관측자료의 불확실성은 방법의 성능에 큰 영향을 미치게 된다. 수문 모형의 구축에서 하천유량 관측자료 신뢰도의 중요성을 입자 필터를 통하여 정량화할 수 있을 것이다. 마지막으로 매개변수 입자 섭동과 관련된 초 매개변수 $γ$ 는 하천유량 예측성능에 대한 민감도는 높지 않은 것을 발견할 수 있다(Fig. 7(d)). 참고로 다른 유역의 민감도 분석 결과도 하천유량 관측자료의 불확실성이 입자 필터의 성능에 큰 영향을 미친다는 관점에서 안동댐 유역의 결과와 큰 차이를 보이지는 않았다.

본 연구에서는 입자 필터에 의한 시간변화 매개변수 적용을 하천유량 예측성능을 중심으로 살펴보고, 입자 필터 적용을 위한 매개변수의 민감도 또한 하천유량 예측성능을 위주로 분석하였다. 하지만, 자료 동화 방법을 적용할 때 살펴보아야 하는 또 다른 중요한 특성은 하천유량 예측 및 추정된 매개변수의 불확실성이다. 불확실성은 추정된 매개변수 및 예측된 하천유량의 앙상블을 통하여 살펴볼 수 있을 것이며, 다양한 유역 및 기후조건에서 보정 및 검증을 수행하여 분석될 수 있을 것이다. 이는 추후 연구로 남겨둔다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540602/images/kwra_54_06_02_F7.jpg

Fig. 7.

Sensitivity of Particle filter parameter to stream flow prediction performance

6. 결 론

본 연구에서는 입자 필터 방법을 이용하여 하천유량을 월 물 수지 모형에 동화함으로써 시간에 따라 변하는 매개변수를 식별하고자 하였다. 한반도 동남부 4개 유역(안동댐 유역, 합천댐 유역, 남강댐 유역, 밀양댐 유역)에 대한 수치 실험과 실제 사례 연구 결과를 바탕으로 다음과 같은 결론을 도출했다.

1) 입자 필터 방법을 이용한 시간변화 모형 매개변수 추정은 모형 매개변수의 시간적 변화를 식별하고 월 유출고에 대한 우수한 예측성능을 보여주었다. 하천유량 관측자료의 동화에 의해 추정된 시간변화 모형 매개변수는 시간 불변 접근 방식 기반의 모형 매개변수보다 상대적으로 우수한 월 유출고 예측성능을 나타내었다.

2) 2개 매개변수로 구성된 월 물 수지 모형의 매개변수 중에서 매개변수 c는 겨울에 큰 값을 가지며, 봄에 작은 값을 보이는 주기 성분이 있음을 파악하였으며, 이러한 주기 성분의 반영이 하천유량 예측성능을 개선하는 데 역할을 하고 있음을 발견할 수 있었다.

3) 입력자료의 불확실성이나 매개변수 입자 섭동과 관련된 매개변수와 비교해볼 때, 하천유량 관측자료의 불확실성이 입자 필터의 하천유량 예측성능에 가장 큰 영향을 미치고 있음을 파악하였다.

본 연구에서는 시간에 따라 변하는 매개변수를 추정하는 방법을 제시하고 하천유량 예측성능을 중심으로 적용된 방법의 타당성을 살펴보았다. 하이퍼 매개변수를 미세 조정하거나 입력 및 관측자료의 불확실성을 조정한다면 적용된 방법을 이용하여 더 좋은 하천유량 예측성능을 얻을 수 있을 것이라는 사실을 알 수 있었다. 다음에는 제시된 방법에서의 시간변화 매개변수 및 예측된 하천유량의 불확실성에 관한 연구 및 선행 월 후의 물 수지 예측에 관한 연구도 필요할 것으로 판단된다.

Acknowledgements

본 결과물은 환경부의 재원으로 환경산업기술원의 지능형 도시수자원 관리사업의 지원을 받아 연구되었습니다(2019002950004).

References

Abbaszadeh, P., Moradkhani, H., and Yan, H. (2018). "Enhancing hydrologic data assimilation by evolutionary particle filter and Markov chain Monte Carlo." Advances in Water Resources, Vol. 111, pp. 192-204. doi: 10.1016/j.advwatres.2017.11.011 10.1016/j.advwatres.2017.11.011

Allen, R., Pereira, L., Raes, D., and Smith, M. (1998). Crop evapotranspiration - Guidelines for computing crop water requirements. FAO Irrigation and drainage paper 56, Food and Agriculture Organization of the United Nations, Rome, Italy.

Brigode, P., Oudin, L., and Perrin, C. (2013). "Hydrological model parameter instability: A source of additional uncertainty in estimating the hydrological impacts of climate change?" Journal of Hydrology, Vol. 476, pp. 410-425. doi: 10.1016/j.jhydrol.2012.11.012 10.1016/j.jhydrol.2012.11.012

Brown, A., Zhang, L., McMahon, T., Western, A., and Vertessy, R., (2005). "A review of paired catchment studies for determining changes in water yield resulting from alterations in vegetation." Journal of Hydrology, Vol. 310 No. 1-4, pp. 28-61. doi: 10.1016/j.jhydrol.2004.12.010 10.1016/j.jhydrol.2004.12.010

Cao, Y., Ye, Y., Liang, L., Zhao, H., Jiang, Y., Wang, H., Yi, Z., Shang, Y., and Yan, D. (2019). "A modified particle filter-based data assimilation method for a high-precision 2D hydrodynamic model considering spatial-temporal variability of roughness: Simulation of dam-break flood inundation." Water Resources Research, Vol. 55, pp. 6049-6068. doi: 10.1029/2018WR023568 10.1029/2018WR023568

Choi, D., Yang, J., Chung, G., and Kim, S. (2011). "A conceptual soil water model of catchment water balance: Which hydrologic components are needed to calibrated the model?" Journal of the Korean Society of Civil Engineers, Vol. 31, No. 3B, pp. 211-220. doi: 10.12652/Ksce.2011.31.3B.211 (in Korean) 10.12652/Ksce.2011.31.3B.211

Choi, J., Lee, O., Won, J., and Kim. S. (2020). "Stochastic simple hydrologic partitioning model associated with Markov chain Monte Carlo and ensemble Kalman filter." Journal of Korean Society on Water Environment, Vol. 36, No. 5, pp. 353-363. doi: 10.15681/KSWE.2020.36.5.353 (in Korean) 10.15681/KSWE.2020.36.5.353

Clark, M., Rupp, D., Woods, R., Zheng, X., Ibbitt, R., Slater, A., Schmidt, J., and Uddstrom, M. (2008). "Hydrological data assimilation with the ensemble Kalman filter: Use of streamflow observations to update states in a distributed hydrological model." Advances in Water Resources, Vol. 31, No. 10, pp. 1309-1324. doi: 10.1016/j.advwatres.2008.06.005 10.1016/j.advwatres.2008.06.005

de Vos, N., Rientjes, T., and Gupta, H. (2010). "Diagnostic evaluation of conceptual rainfall-runoff models using temporal clustering. Hydrological Processes, Vol. 24, No. 20, pp. 2840-2850. doi: 10.1002/hyp.7698 10.1002/hyp.7698

Dechantcm, M., and Moradkhani, H. (2012). "Examining the effectiveness and robustness of data assimilation methods for calibration and quantification of uncertainty in hydrologic forecasting." Water Resources Research, Vol. 48, W04518. doi: 10.1029/2011WR011011. 10.1029/2011WR011011

Deng, C., Liu, P., Guo, S., Li, Z., and Wang, D. (2016). "Identification of hydrological model parameter variation using ensemble Kalman filter." Hydrology and Earth System Sciences, Vol. 20, No. 12, pp. 4949-4961. doi: 10.5194/hess-20-4949-2016 10.5194/hess-20-4949-2016

Engel, B., Srinivasan, R., Arnold, J., Rewerts, C., and Brown, S. (1993). "Nonpoint-source (NPS) pollution modeling using models integrated with geographic information systems (GIS)." Water Science and Technology, Vol. 28, pp. 685-690. doi: 10.2166/wst.1993.0474 10.2166/wst.1993.0474

Fan, Y., Huang, G., Baetz, B., Li, Y., Huang, K., Chen, X., and Gao, M. (2017). "Development of integrated approaches for hydrological data assimilation through combination of ensemble Kalman filter and particle filter methods." Journal of Hydrology, Vol. 550, pp. 412-426. doi: 10.1016/j.jhydrol.2017.05.010 10.1016/j.jhydrol.2017.05.010

Feng, M., Liu, P., Guo, S., Shi, L., Deng, C., and Ming, B. (2017). "Deriving adaptive operating rules of hydropower reservoirs using time-varying parameters generated by the EnKF." Water Resources Research, Vol. 53, No. 8, pp. 6885-6907. doi: 10.1002/2016wr020180. 10.1002/2016WR020180

Gharari, S., Hrachowitz, M., Fenicia, F., and Savenije, H. (2013). "An approach to identify time consistent model parameters: sub-period calibration." Hydrology and Earth System Science, Vol. 17, No. 1, pp. 149-161. doi: 10.5194/hess-17-149-2013 10.5194/hess-17-149-2013

Gordon, N., Salmond, D., and Smith, A. (1993). "Novel approach to nonlinear and non-Gaussian Bayesian state estimation." IEE Proceeding F (Radar and Signal Processing), Vol. 140, pp. 107-113. doi: 10.1049/ip-f-2.1993.0015 10.1049/ip-f-2.1993.0015

Guo, S., Wang, J., Xiong, L., Ying, A., and Li, D. (2002). "A macro-scale and semidistributed monthly water balance model to predict climate change impacts in China." Journal of Hydrology, Vol. 268, No. 1-4, pp, 1-15. doi: 10.1016/s0022-1694(02)00075-6 10.1016/S0022-1694(02)00075-6

Gupta, H., Kling, H., Yilmaz, K., and Martinez, G. (2009). "Decomposition of the mean squared error and NSE performance criteria: implications for improving hydrological modelling." Journal of Hydrology, Vol. 377, pp. 80-91. doi: 10.1016/j.jhydrol.2009.08.003 10.1016/j.jhydrol.2009.08.003

Jeremiah, E., Marshall, L., Sisson, S.A., and Sharma, A. (2013). "Specifying a hierarchical mixture of experts for hydrologic modeling: Gating function variable selection." Water Resources Research, Vol. 49, No. 5, pp. 2926-2939. doi: 10.1002/wrcr.20150 10.1002/wrcr.20150

Lee, B., and Bae, D. (2011). "Streamflow forecast model on Nakdong river basin." Journal of Korea Water Resources Association, Vol. 50, No. 4, pp. 241-252. doi: 10.3741/JKWRA.2011.44.11.853 (in Korean) 10.3741/JKWRA.2011.44.11.853

Lee, D., Kim, Y., Yu, W., and Lee, G. (2017). "Evaluation on applicability of on/off-line parameter calibration techniques in rainfall-runoff modeling." Journal of Korea Water Resources Association, Vol. 50, No. 4, pp. 241-252. doi: 10.3741/JKWRA.2017.50.4.241 (in Korean) 10.3741/JKWRA.2017.50.4.241

Lee, J. (2006). Hydrology. Gumiseogwan.

Legesse, D., Vallet-Coulomb, C., and Gasse, F. (2003). "Hydrological response of a catchment to climate and land use changes in Tropical Africa: Case study South Central Ethiopia." Journal of Hydrology, Vol. 275, No. 1-2, pp. 67-85. doi: 10.1016/s0022-1694(03)00019-2 10.1016/S0022-1694(03)00019-2

Leisenring, M., and Moradkhani, H. (2012). "Analysing the uncertainty of suspended sediment load prediction using sequential data assimilation." Journal of Hydrology, Vol. 468, pp. 268-282. doi: 10.1016/j.jhydrol.2012.08.049 10.1016/j.jhydrol.2012.08.049

Marshall, L., Sharma, A., and Nott, D. (2006). "Modeling the catchment via mixtures: Issues of model specification and validation." Water Resources Research, Vol. 42, No. 11, W11409. doi: 10.1029/2005wr004613 10.1029/2005WR004613

Merz, R., Parajka, J., and Bloeschl, G. (2011). "Time stability of catchment model parameters: Implications for climate impact analyses." Water Resources Research, Vol. 47, No. 2, W02531. doi: 10.1029/2010wr009505 10.1029/2010WR009505

Moradkhani, H., DeChant, C., and Sorooshian, S. (2012). "Evolution of ensemble data assimilation for uncertainty quantification using the particle filter-Markov chain Monte Carlo method." Water Resources Research, Vol. 48. No. 12, doi: 10.1029/2012wr012144. 10.1029/2012WR012144

Moradkhani, H., Hsu, K., Gupta, H., and Sorooshian, S. (2005a). "Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using particle filter." Water Resources Research, Vol. 41, W05012. doi: 10.1029/2004WR003604 10.1029/2004WR003604

Moradkhani, H., Sorooshian, S., Gupta, H., and Houser, P. (2005b). "Dual state-parameter estimation of hydrological models using ensemble Kalman filter." Advances in Water Resources, Vol. 28, No. 2, pp. 135-147. doi: 10.1016/j.advwatres.2004.09.002 10.1016/j.advwatres.2004.09.002

Nash, J., and Sutcliffe, J. (1970). "River flow forecasting through conceptual models part I - A discussion of principles." Journal of Hydrology, Vol. 10, pp. 282-290. doi: 10.1016/0022-1694(70)90255-6 10.1016/0022-1694(70)90255-6

Noh, S., Tachikawa, Y., Shiiba, M., and Kim, S. (2011). "Dual state-parameter updating scheme on a conceptual hydrologic model using sequential Monte Carlo filters." Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering), Vol. 67, pp. I_1-I_6. 10.2208/jscejhe.67.I_1

Pathiraja, S., Anghileri, D., Burlando, P., Sharma, A., Marshall, L., and Moradkhani, H. (2018). "Insights on the impact of systematic model errors on data assimilation performance in changing catchments." Advances in Water Resources, Vol. 113, pp. 202-222. doi: 10.1016/j.advwatres.2017.12.006 10.1016/j.advwatres.2017.12.006

Patil, S., and Stieglitz, M. (2015). "Comparing spatial and temporal transferability of hydrological model parameters." Journal of Hydrology, Vol. 525, pp. 409-417. doi: 10.1016/j.jhydrol.2015.04.003 10.1016/j.jhydrol.2015.04.003

Ritter, A., and Munoz-Carpena, R. (2013). "Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments." Journal of Hydrology, Vol. 480, pp. 33-45. doi: 10.1016/j.jhydrol.2012.12.004 10.1016/j.jhydrol.2012.12.004

Seibert, J., McDonnell, J., and Woodsmith, R. (2010). "Effects of wildfire on catchment runoff response: A modelling approach to detect changes in snow-dominated forested catchments." Hydrology Research, Vol. 41, No. 5, pp. 378-390. doi 10.2166/nh.2010.036 10.2166/nh.2010.036

Smith, P., Beven, K., and Tawn, J. (2008). "Detection of structural inadequacy in process-based hydrological models: A particle-filtering approach." Water Resources Research, Vol. 44, No. 1. doi: 10.1029/2006wr005205 10.1029/2006WR005205

Thirel, G., Andreassian, V., Perrin, C., Audouy, J., Berthet, L., Edwards, P. Folton, N., Furusho, C., Kuentz, A., Lerat, J., Lindstrom, G., Martin, E., Mathevet, T., Merz, R., Parajka, J., Ruelland, D., and Vaze, J. (2015). "Hydrology under change: An evaluation protocol to investigate how hydrological models deal with changing catchments." Hydrological Sciences Journal, Vol. 60, No. 7-8, pp. 1184-1199. doi: 10.1080/02626667.2014.967248 10.1080/02626667.2014.967248

Vaze, J., Post, D., Chiew, F., Perraud, J., Viney, N., and Teng, J. (2010). "Climate non-stationarity-validity of calibrated rainfall-runoff models for use in climate change studies." Journal of Hydrology, Vol. 394, No. 3-4, pp. 447-457. doi: 10.1016/j.jhydrol.2010.09.018 10.1016/j.jhydrol.2010.09.018

Vrugt, J., Gupta, H., Bouten, W., and Sorooshian, S. (2003). "A shuffled complex evolution metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters." Water Resources Research, Vol. 39, No. 8. doi: 10.1029/2002WR001642 10.1029/2002WR001642

Vrugt, J., ter Braak, C., Diks, C., and Schoups, G. (2013). "Hydrologic data assimilation using particle Markov chain Monte Carlo simulation: Theory, concepts and applications." Advances in Water Resources, Vol. 51, pp. 457-478. doi: 10.1016/j.advwatres.2012.04.002 10.1016/j.advwatres.2012.04.002

Wagener, T., McIntyre, N., Lees, M., Wheater, H., and Gupta, H. (2003). "Towards reduced uncertainty in conceptual rainfall-runoff modelling: dynamic identifiability analysis." Hydrological Process, Vol. 17, No. 2, pp. 455-476. doi: 10.1002/hyp.1135 10.1002/hyp.1135

Wang, D., Chen, Y., and Cai, X. (2009). "State and parameter estimation of hydrologic models using the constrained ensemble Kalman filter." Water Resources Research, Vol. 45, No. 11, W11416. doi: 10.1029/2008wr007401 10.1029/2008WR007401

Westra, S., Thyer, M., Leonard, M., Kavetski, D., and Lambert, M. (2014). "A strategy for diagnosing and interpreting hydrological model nonstationarity." Water Resources Research, Vol. 50, No. 6, pp. 5090-5113. doi: 10.1002/2013wr014719 10.1002/2013WR014719

Won, J., Choi, J., Lee, O., and Kim, S. (2020). "Copula-based joint drought index using SPI and EDDI and its application to climate change." Science of Total Environment, Vol. 744, 140701. doi: 10.1016/j.scitotenv.2020.140701 10.1016/j.scitotenv.2020.14070132755772

Xiong, L., and Guo, S. (1999). "A two-parameter monthly water balance model and its application." Journal of Hydrology, Vol. 216, No. 1-2, pp. 111-123. doi: 10.1016/s0022-1694(98)00297-2 10.1016/S0022-1694(98)00297-2

Xiong, L., and Guo, S. (2012). "Appraisal of Budyko formula in calculating long-term water balance in humid watersheds of southern China." Hydrological Process, Vol. 26, No. 9, pp. 1370-1378. doi: 10.1002/hyp.8273 10.1002/hyp.8273

Xiong, L., Liu, P., Cheng, L., Deng, C., Gui, Z., Zhang, X., and Liu, Y. (2019). "Identifying time-varying hydrological model parameters to improve simulation efficiency by the ensemble Kalman filter: A joint assimilation of streamflow and actual evapotranspiration." Journal of Hydrology, Vol. 568, pp. 758-768. doi: 10.1016/j.jhydrol.2018.11.038 10.1016/j.jhydrol.2018.11.038

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Estimating time-varying parameters for monthly water balance model using particle filter: assimilation of stream flow data

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

Fig. 1.

Study area and location of meteorological observation sites

Table 1.

Annual mean values of precipitation, reference evapotranspiration, and runoff depth, and areas for four watersheds

Fig. 2.

Model parameter assimilated by PF and estimated by SCEM, and its true value

Table 2.

Scheme performance for parameter estimation and stream flow prediction in numerical experiments

Fig. 3.

Time evolution of posterior parameter distributions at three different time segments by assimilation of stream flow for Namgang Dam watershed

Fig. 4.

Uncertainty bound tracking of parameters in two parameter monthly water balance model for 19 years assimilation of historical stream flow at Namgang Dam watershed

Table 3.

Performance metrics for monthly stream flow prediction

Fig. 5.

Monthly parameter ensemble average estimate

Fig. 6.

Monthly performance metrics for stream flow prediction

Fig. 7.

Sensitivity of Particle filter parameter to stream flow prediction performance

Acknowledgements

References