Comparison of MIROC5 and MIROC6 projections for precipitation over South Korea

Seung Taek Chae; Young Hoon Song; Eun-Sung Chung

doi:10.3741/JKWRA.2021.54.4.229

Preview

Research Article

Journal of Korea Water Resources Association. 30 April 2021. 229-240
https://doi.org/10.3741/JKWRA.2021.54.4.229

Comparison of MIROC5 and MIROC6 projections for precipitation over South Korea

MIROC5와 MIROC 6의 우리나라 미래 강수량 예측 비교

Seung Taek Chae^a

Young Hoon Song^b

Eun-Sung Chung^c^*

채 승택^a

송 영훈^b

정 은성^c^*

^aMaster course, Department Civil Engineering, Seoul National University of Science and Technology, Seoul, Korea

^bPh.D. Student, Department Civil Engineering, Seoul National University of Science and Technology, Seoul, Korea

^cProfessor, Department Civil Engineering, Seoul National University of Science and Technology, Seoul, Korea

^a서울과학기술대학교 건설시스템공학과 석사과정

^b서울과학기술대학교 건설시스템공학과 박사과정

^c서울과학기술대학교 건설시스템공학과 교수

^{*Corresponding Author}

ABSTRACT

This study projected the monthly precipitation for RCP4.5 and RCP8.5 of the MIROC5 and SSP2-4.5 and SSP5-8.5 of MIROC6 GCMs using observations of the historical period (1970 to 2005) of 21 stations in Korea, and then compared the performance before and after bias correction using 6 evaluation indicators. In addition, using the bias corrected GCM’s scenarios, annual precipitation, summer precipitation and winter precipitation in near future period (2021-2060) and far future period (2061-2100) were calculated. Furthermore, the variability of future projection was quantified using the standard deviation and interquartile range values of future precipitation. As a result the rate of change of precipitation was greater in the northern region than in the southern region and in the far future rather than the near future. The variability in the projection were also concluded to be larger in the northern region than that in the southern regions.

Keywords

General circulation model

MIROC5

MIROC6

Quantile mapping

본 연구에서는 MIROC5와 MIROC6 GCM을 대상으로 우리나라 21개의 관측소의 과거 기간(1970년 ~ 2005년) 관측 값을 이용하여 과거 월 강수량을 모의한 뒤 6개의 평가 지표를 사용하여 편이보정 전후의 성능을 비교하였다. 또한 편이 보정된 GCM의 RCP4.5, RCP8.5 그리고 SSP2-4.5, SSP5-8.5 시나리오를 이용하여 가까운 미래 기간(2021년 ~ 2060년)과 먼 미래 기간(2061년 ~ 2100년)별로 연 강수량, 여름철 강수량, 겨울철 강수량 변화율을 산정하였다. 더 나아가 산정된 미래 강수량의 표준편차와 사분범위 값을 이용하여 미래 예측 값의 변동성을 확인하였다. 분석 결과 강수의 변화율은 남부 지역보다는 북부 지역에서 그리고 가까운 미래보다는 먼 미래에서 크게 나타났다. 변동성의 경우도 가까운 미래와 먼 미래 모두 남부 지역보다는 북부 지역에서 크게 나타남을 확인하였다.

키워드

전지구모형

MIROC5

MIROC6

분위사상법

MAIN

1. 서 론
2. 연구방법
2.1 대상 관측소
2.2 전지구모형
2.3 GCM 공간보간
2.4 분위사상법
2.5 평가지표
2.6 변동성 분석
3. 결 과
3.1 GCM 성능 평가
3.2 편이보정 결과
3.3 GCM 공간적 재현성 평가
3.4 GCM 월 강수량 변화율 분석
3.5 변동성 분석
4. 결 론

1. 서 론

전 세계적으로 기후 변화에 따른 인명 및 재산 피해는 중요한 문제 중 하나이다. 따라서 기후 변화를 발생시키는 기후 요소들의 변화를 파악하고 이에 따라 대비하는 것은 기후 변화 연구에서 중요한 목적 중 하나이다. 많은 기후변화 연구에서 강수, 온도 등과 같은 기후 요소들의 변동을 연구하기 위하여 전지구적모형(General Circulation Models, GCMs)을 사용하고 있다(Hwang, 2014; Hong et al., 2018). CMIP (Coupled Model Intercomparison Project)는 전 세계 50개 이상의 기관에서 개발한 GCM의 산출물을 연구하기 위해 개발되었다(Meehl et al., 2000). CMIP는 지속적으로 발전되어 왔으며 최근 6^th Assessment Report (AR6)의 시나리오를 위해 CMIP6가 개발되었다. Intergovernmental Panel on Climate Change (IPCC)에서는 6차보고서에서 새롭게 Shared Socioeconomic Pathway (SSP) 시나리오를 제시하였다. SSP 시나리오는 온실가스 배출 시나리오인 Representative Concentration Pathway (RCP) 시나리오의 복사 강제력을 기반으로 미래 사회 및 환경 변화를 고려한 시나리오로서 기후 변화에 대한 완화(새로워진 기후환경에 대응)와 적응(온실가스 배출량을 저감)에 따른 5개의 시나리오(SSP1, SSP2, SSP3, SSP4, SSP5)로 구분된다(O’Neill et al., 2014).

SSP 시나리오가 개발되면서 기존 RCP 시나리오에 대해 기후를 예측한 전세계 연구소 및 기관에서는 새롭게 기후를 예측하고 있다. 이에 따라 많은 연구에서 다양한 GCM에 대해 지역별로 예측한 기후를 비교하였다(Chen et al., 2020; Scoccimarro and Gualdi, 2020). 더 나아가 기존에 적용되었던 RCP 시나리오와 SSP 시나리오의 여러 GCM의 과거 및 미래 기후예측 결과를 비교한 연구들도 활발하게 진행되고 있다(Wu et al., 2019; Xin et al., 2020; Song et al., 2021).

GCM의 경우 격자 형식으로 기후 자료들이 저장되어 있으며 각 격자간의 거리는 250 ~ 600 km 사이로 격자간의 거리가 매우 넓은 편이다. 이러한 GCM 자료를 이용하여 기후변화를 연구하기 위해서는 격자 자료를 관측지점의 자료로 공간적 보간, 상세화(downscaling)를 실시한다. 또한 관측 자료와 상세화한 자료 사이에는 값의 차이, 편이(bias)가 발생하는데 이를 보정하기 위해 편이보정(bias correction) 방법이 사용되며 대표적으로 분위사상법(quantile mapping)이 사용된다. Kim et al. (2021)은 분위사상법을 이용하여 ACCESS-CM2의 SSP2-4.5와 ACCESS 1-3의 RCP4.5 시나리오를 편이보정하고 청미천 유역의 가뭄지수를 산정하였다. Mishra et al. (2020)은 CMIP6 GCM에 대하여 Empirical Quantile Mapping (EQM)방법을 이용하여 상세화를 수행하여 SSP시나리오 별 남아시아 지역의 기후 변화를 예측하였다.

GCM의 원자료로부터 공간적 상세화 및 편이보정방법을 이용하여 미래기후자료를 생성하는 과정에서 다양한 불확실성이 존재한다. 이러한 불확실성은 연구 결과의 신뢰성을 낮출 수 있다. GCM을 이용하여 미래 기후를 예측할 때 발생하는 불확실성의 원인은 대표적으로 기후 모델 자체의 불확실성, 편이 보정 방법에 따른 불확실성, 기후 시나리오의 불확실성이 있다(Hawkins and Sutton, 2009; Kim et al., 2015). 이에 따라 GCM 자료를 활용하는 과정의 변동성을 정량화하고 이를 줄이려는 노력의 연구가 지속적으로 수행되었다. Schepen and Wang (2013)은 multi-models ensemble (MME) 방법을 이용하여 불확실성을 줄이려 노력하였으며, 실제로 MME방법을 사용하여 예측된 강우 자료가 GCM 모의 강우 자료보다 개선되었음을 확인하였다. Jung et al. (2018)은 평가지표를 이용하여 여러 GCM의 과거 관측 자료에 대한 재현성과 미래 예측자료의 불확실성을 비교하여 가장 신뢰성 있는 GCM들을 선정하였다.

본 연구에서는 여러 GCM 중 Song et al. (2020)에서 강수 모의 시 높은 성능을 보였던 MIROC (Model for Interdisciplinary Research On Climate) GCM을 사용하였으며, 우리나라의 21개의 관측소에 대해 RCP 시나리오를 제공하는 MIROC5 GCM과 SSP 시나리오를 제공하는 MIROC6 GCM을 사용하여 과거기간(1970년 ~ 2005년)의 월 강수량을 공간적 상세화 및 편이보정방법을 통해 모의한 뒤 과거 관측값과 비교하여 GCM의 성능을 비교하였다. 편이보정방법에는 가장 대표적으로 사용되는 방법 중 하나인 분위사상법 중에서 비모수변환법인 스플라인 평활(Smoothing Spline)방법을 사용하여 편이보정을 수행하였다. 편이보정결과를 토대로 MIROC5의 RCP4.5, RCP8.5 시나리오와 이들 시나리오와 유사한 탄소배출경로를 가진 MIROC6의 SSP2-4.5, SSP5-8.5시나리오에 대해 가까운 미래(2021년 ~ 2060년)와 먼 미래(2061년 ~ 2100년)로 기간을 나누어 월 강수량을 모의하였다. 모의된 미래 강수량을 사용하여 과거 동일한 기간에 대해 강수량 변화율을 계산하여 시나리오별로 비교하였다. 또한 모의된 미래 강수량에 대해 표준편차(STDEV)와 사분범위(Interquartile range, IQR) 값을 사용하여 GCM을 통해 모의된 미래 월 강수 예측 값의 변동성을 시나리오 별로 정량화하여 비교하였다.

2. 연구방법

2.1 대상 관측소

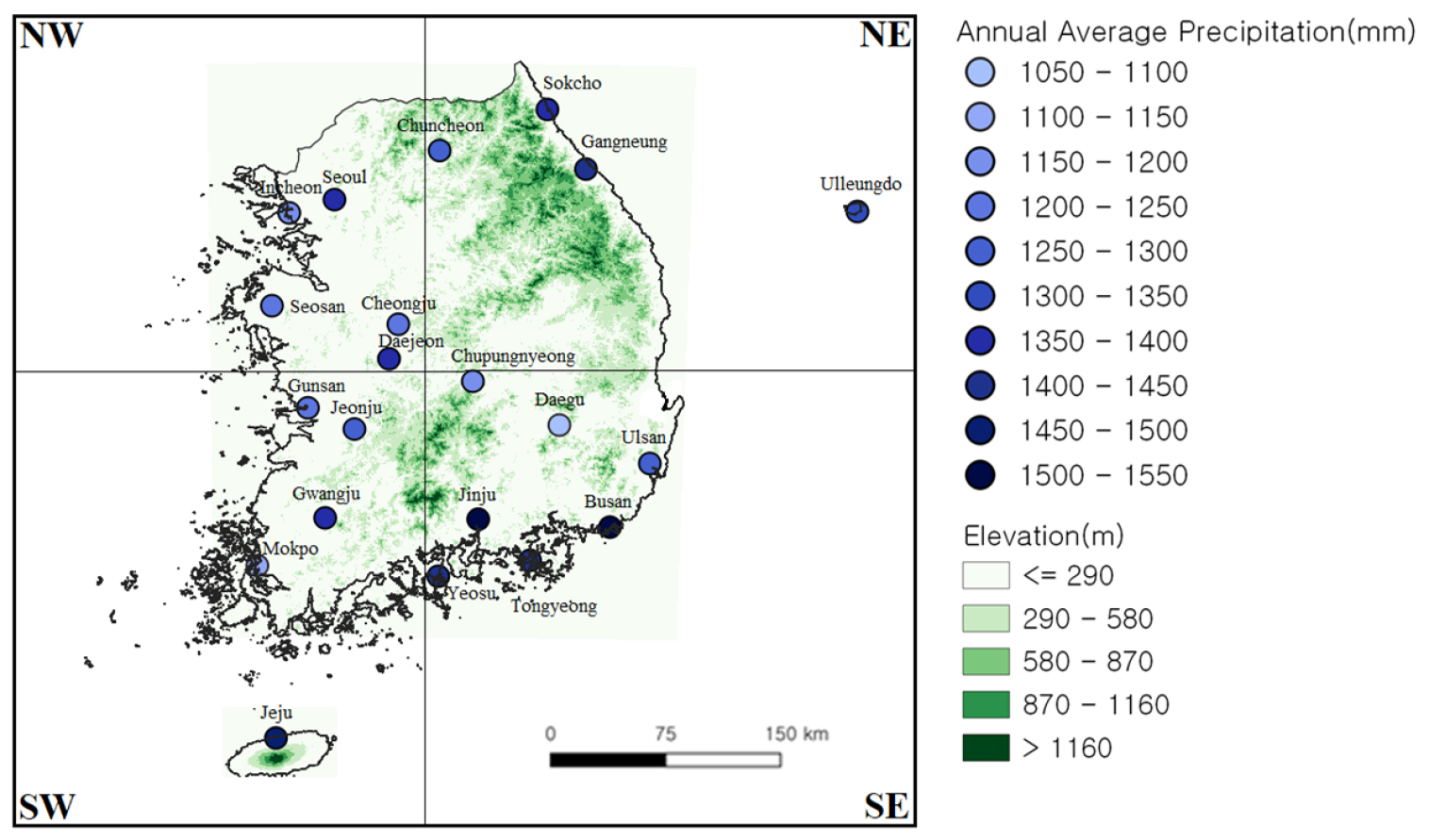
본 연구에서는 우리나라 과거기간(1970년 ~ 2005년) 동안 월 강수량 관측 자료가 충분히 존재하는 21개의 관측소를 대상으로 연구를 진행하였으며, 21개의 관측소는 4개의 지역(북동부(NE), 북서부(NW), 남동부(SE), 남서부(SW))으로 구분하였다. 북서부 지역에는 서울, 인천, 서산, 청주, 대전의 기상 관측소, 북동부 지역에는 춘천, 속초, 강릉, 울릉도의 기상관측소, 남서부 지역에는 군산, 전주, 광주, 목포, 제주의 기상 관측소, 남동부 지역에는 추풍령, 대구, 울산, 부산, 통영, 진주, 여수의 기상관측소가 위치해 있다. 각 관측소는 한국을 기준으로 지역적으로 고르게 분포되어 있어서 우리나라의 강수량을 분석하는데 유용하다. 한국은 지리적으로 산악 지형이 많으며 여름철(6월 ~ 8월)에 대부분의 강수가 내리며 겨울철(12월 ~ 2월)에 강수량이 현저하게 줄어든다. 우리나라의 연간 총 강수량은 1000 ~ 1600 mm이며 여름철에 400 ~ 850 mm가 발생하고 겨울철에 60 ~ 300 mm의 강수량이 발생한다. 본 연구에서 사용한 21개의 관측소의 위치는 Fig. 1과 같이 분포되어 있다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F1.jpg

Fig. 1.

Location of weather stations used in this study

2.2 전지구모형

GCM은 대기, 해양, 빙하 및 지표면의 물리적 과정을 포함하고 있어서, 온실가스 농도 증가에 따른 기후의 변화 및 미래 기후예측을 분석하는데 유용하다. 본 연구에서는 RCP 시나리오와 SSP 시나리오를 제공하며 Song et al. (2020)에서 강수량 모의 시 높은 성능을 보였던 MIROC (Model for Interdisciplinary Research On Climate)의 GCM 결과(Khan et al., 2018; Homsi et al., 2020)를 사용하여 과거 및 미래기간의 강수량 자료를 산정하였다. MIROC는 일본의 동경대학교와 Japan Agency for Marine-Earth Science and Technology에서 개발하였고 격자 간격은 1.4° × 1.4°이다. 본 연구에서는 온실가스 저감 정책이 어느 정도 실현되는 경우인 RCP4.5 시나리오와 현재 추세로 저감 없이 온실가스가 배출되는 경우인 RCP8.5 시나리오와 두 RCP 시나리오와 탄소 배출 경로가 유사하면서 완화와 적응 정도가 모두 중간 단계인 SSP2-4.5 및 완화는 높고 적응은 낮은 SSP5-8.5시나리오를 사용하였다.

2.3 GCM 공간보간

GCM의 모의자료는 매우 큰 격자를 가지고 있으므로 대상유역의 관측값과 비교하였을 때 매우 큰 차이를 보인다. 이러한 차이는 연구결과의 신뢰성을 떨어뜨리므로 이를 해결하기 위하여 공간적 보간법인 역거리 가중치(Inverse Distance Weight) 방법을 사용하였다. 역거리 가중치법은 상대적으로 가까운 거리의 값이 먼 거리의 값보다 관련성이 높다는 Tobler의 첫 번째 법칙의 개념을 이용한 보간법이다(Tobler, 1970). 미계측 지점의 강수량 산정을 위하여 대상 지점에서 가장 가까운 4개의 GCM 격자로부터 미계측 지점의 거리와 GCM 4개 격자의 모의 강수량에 대해 Eqs. (1) and (2)를 사용하였다.

(1)

P_{i} = \sum_{i = 1}^{N} \frac{w_{s} (x)}{\sum_{i = 1}^{N} w_{s} (x)} P_{i} (x_{s})

(2)

w_{s} (x) = \frac{1}{D_{(x, x_{x})}^{c}}

여기서 P_i는 미계측 지점의 강수량, w_s (x)는 보간 가중치, $D_{(x, x_{s})}^{c}$ 는 두 격자 간의 거리, P_i (x_s)는 미계측 지점 주변의 GCM 자료의 모의 강수량이다.

2.4 분위사상법

공간적 상세화 이후에도 관측소와의 값을 비교하였을 때 큰 차이가 발생하는 경우가 많은데 이를 해결하기 위하여 편이보정방법이 사용된다. 본 연구에서는 여러 편이보정방법 중 분위사상법을 사용하였다. 분위사상법은 관측값과 예측 값 사이의 편이를 제거하기 위하여 경험적 확률 분포를 사용하며 관측값과 예측 값의 누적확률분포를 이용하여 모의값의 확률분포를 관측값의 확률분포에 사상시키는 방법이다(Hashino et al., 2006). 분위사상법에서 관측값과 모의값의 누적분포를 생성하기 위한 분위 함수 산정식은 Eq. (3)과 같고 이를 기반으로 관측된 강수량의 산정식은 Eq. (4)와 같다.

(3)

P_{0} = h (P_{m})

(4)

P_{0} = F_{0}^{- 1} (F_{m} (P_{m}))

여기서 P₀는 관측된 강수량, P_m은 모의된 GCM의 강수량, h는 변환함수, F_m은 모의된 GCM 강수량의 누적분포함수, $F_{0}^{- 1}$ 는 F_m의 역함수이다. 본 연구에서는 편이보정을 수행하는데 높은 성능을 나타내는 분위사상법의 비모수변환법(Non-Parametric Transformation) 중 하나인 스플라인 평활방법을 사용하였다(Koenker and Schorfheide, 1994; Gudmundsson et al., 2012). 평활 방법은 Quantile-Quantile Plot에서 스플라인 평활함수를 사용하여 모의값을 산정하는 방법이다.

2.5 평가지표

본 연구에서는 21개의 관측소의 과거기간(1970년 ~ 2005년)에 대해 MIROC5와 MIROC6 GCM의 성능 평가를 수행하였다. 평가 시에는 과거 기간 36년의 관측값과 GCM을 사용한 모의값의 월별 평균 강수량에 대해 6개의 평가지표를 사용하여 GCM의 과거 기후 재현성을 비교하였다. 평가지표에는 Normalized Root Mean Square Error (NRMSE), Percent bias (Pbias), Nash-Sutcliffe Efficiency (NSE), PRCP100, PRCP200, PRCP300을 사용하였다. 이 지표들은 모델의 성능 평가를 위해 다양한 연구에서 자주 사용된다(Getirana and Peters-Lidard, 2013; Moriasi et al., 2015; Golmohammadi et al., 2014). NRMSE의 경우 모델의 모의값과 관측값의 차이를 나타내는 척도인 RMSE의 값을 관측값의 평균으로 나누어 자료의 규모 차이를 제거한 지표이며 값이 0에 가까울수록 높은 정확도를 나타내낸다. 식은 Eq. (5)와 같다.

(5)

N R M S E = \frac{\sqrt{\frac{\sum_{i = 1}^{n} {(x_{i} - x)}^{2}}{n}}}{x}

여기서 x_i는 GCM 모의값, x는 관측값, $x$ 는 관측값의 평균이다.

Pbias는 모의된 값이 관측된 값에 대해 크거나 작은 경향을 나타내며 Eq. (6)를 통해 계산된다. Pbias의 값이 0일 때 최적의 값을 나타내며 양의 값일 때 모델의 과대평가 경향을 나타내고 음의 값일 때 과소평가 경향을 나타낸다.

(6)

P e r c e n t B i a s = \frac{\sum_{i = 1}^{n} (x_{i} - x)}{\sum_{i = 1}^{n} x} \times 100

NSE는 Nash and Sutcliffe (1970)에 의해 제안된 평가 지표로서 수문학적 모델의 예측 평가지표로 많이 사용되어지며 Eq. (7)과 같이 계산된다. NSE 값의 범위는 -∞에서 1 사이이며 값이 1일 때 최적의 값을 나타낸다. 만약 NSE값이 음수일 경우 평균 관측값이 모의값보다 더 나은 예측 변수임을 나타낸다.

(7)

N S E = 1 - \frac{\sum_{i = 1}^{n} {(x_{i} - x)}^{2}}{\sum_{i = 1}^{n} {(x - x)}^{2}}

PRCP100, PRCP200, PRCP300지표는 모의값과 관측값의 월 강수량이 100 mm, 200 mm, 300 mm를 초과하는 월 수의 절댓값 차이로 나타내었다. 본 연구에서 사용된 PRCP지표는 물과 관련된 재난의 최소 강수량인 100 mm 이상의 강수량과 강수량의 극한값을 식별할 수 있는 300 mm 이상의 강수량이 발생하는 일수를 확인하기 위해 사용하였다(Song and Chung, 2020).

2.6 변동성 분석

표준편차와(STDEV)와 사분범위(IQR) 값은 GCM의 변동성을 정량화하여 확인하기 위해 여러 연구에서 사용되었다(Greve et al., 2018; Lee et al., 2018; Song and Chung, 2020). 본 연구에서는 GCM자료를 이용하여 산정된 미래기간의 강수 모의값의 변동성을 정량화 하는데 사용되었다. 표준편차의 경우 모의값이 평균에서 떨어져 있는 정도를 나타내기 위하여 사용하였으며 표준편차의 값이 클수록 모의값의 평균으로부터 분산 정도가 커짐을 의미한다. 사분범위 값의 경우 모의값 집합의 중간 50%에 포함되는 값들의 산포도를 나타낸다. 사분범위 값의 경우 제 1사분위수(25%)와 제 3사분위수(75%)의 차이를 의미한다. 본 연구에서 표준편차는 모의된 강수 분포의 전체 변동성을 정량화하기 위하여 사용되었으며, 사분범위 값의 경우 모의 강수값 중 1사분위와 3사분위 간격의 변동성을 정량화하기 위하여 사용되었다.

3. 결 과

3.1 GCM 성능 평가

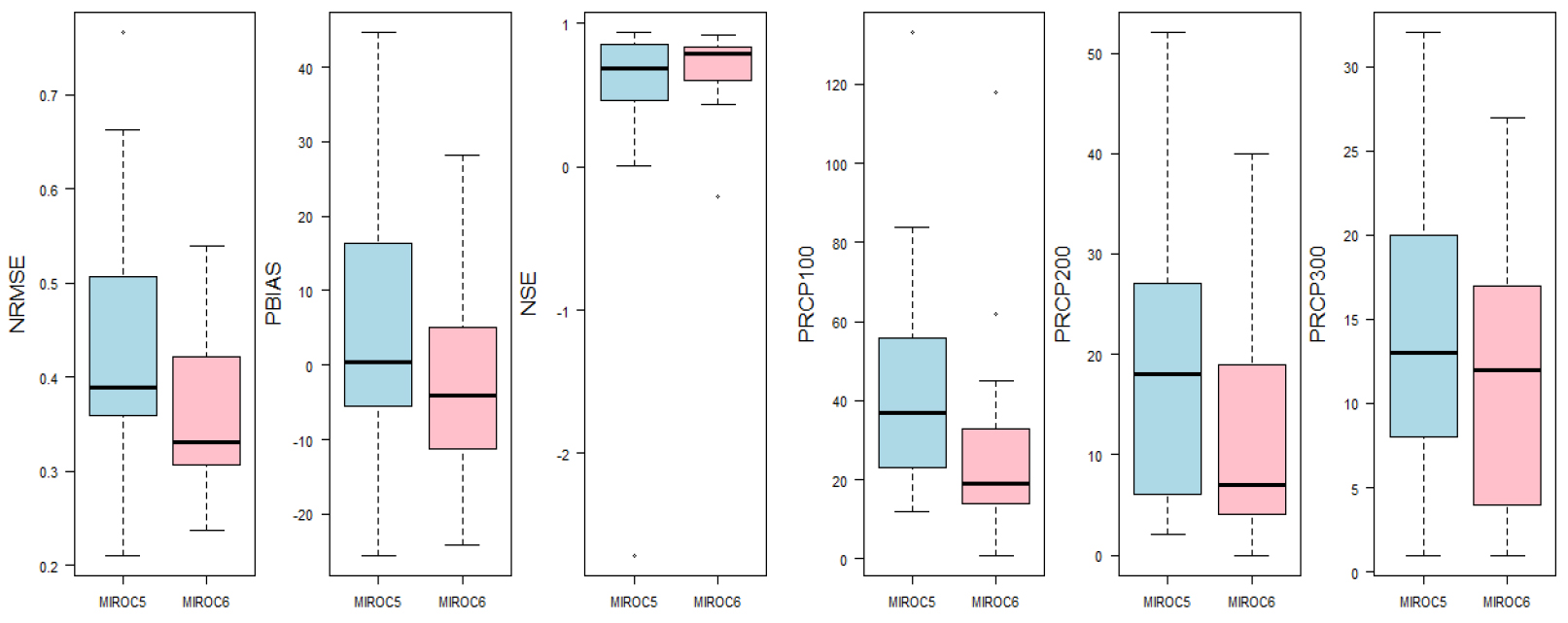
본 연구에서 사용된 GCM의 성능 평가를 위해 21개의 관측소의 과거 기간 관측값과 공간적 상세화를 수행한 GCM의 모의값을 이용하여 GCM의 성능을 평가하였다. GCM 성능 평가 시 6개의 평가 지표가 사용되었으며 평가 지표에 따른 GCM의 성능 평가결과를 Fig. 2와 같이 나타냈다. NRMSE의 경우 MIROC6의 중앙값(0.33)이 MIROC5의 중앙값(0.39)보다 0.06만큼 더 작게 산정되어 MIROC6의 성능이 더 좋게 산정되었다. Pbias의 경우 MIROC5의 중앙값(0.4)과 MIROC6의 중앙값(-4)을 통해 과거 관측값에 대해 MIROC5는 과소평가, MIROC6는 과대평가하는 경향을 확인하였다. NSE의 경우 MIROC6의 중앙값(0.79)이 MIROC5의 중앙값(0.68) 1에 가까우므로 MIROC6가 더 좋은 성능을 나타냄을 확인하였다. 관측값과 모의값의 총 강수량이 100 mm, 200 mm, 300 mm를 초과하는 월 수의 절대 차이를 나타내는 PRCP지표의 경우 PRCP100, PRCP200, PRCP300 순으로 MIROC5의 중앙값(37, 18, 13)이 MIROC6의 중앙값(19, 7, 12)보다 대체로 크게 산정되었으며, 값의 분포 또한 MIROC6 값의 분포가 MIROC5 값의 분포보다 상대적으로 최적값에 가까운 분포를 보임으로 MIROC6의 성능이 더 좋게 산정되었다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F2.jpg

Fig. 2.

Model evaluation results of the raw GCM precipitation data using Boxplot

3.2 편이보정 결과

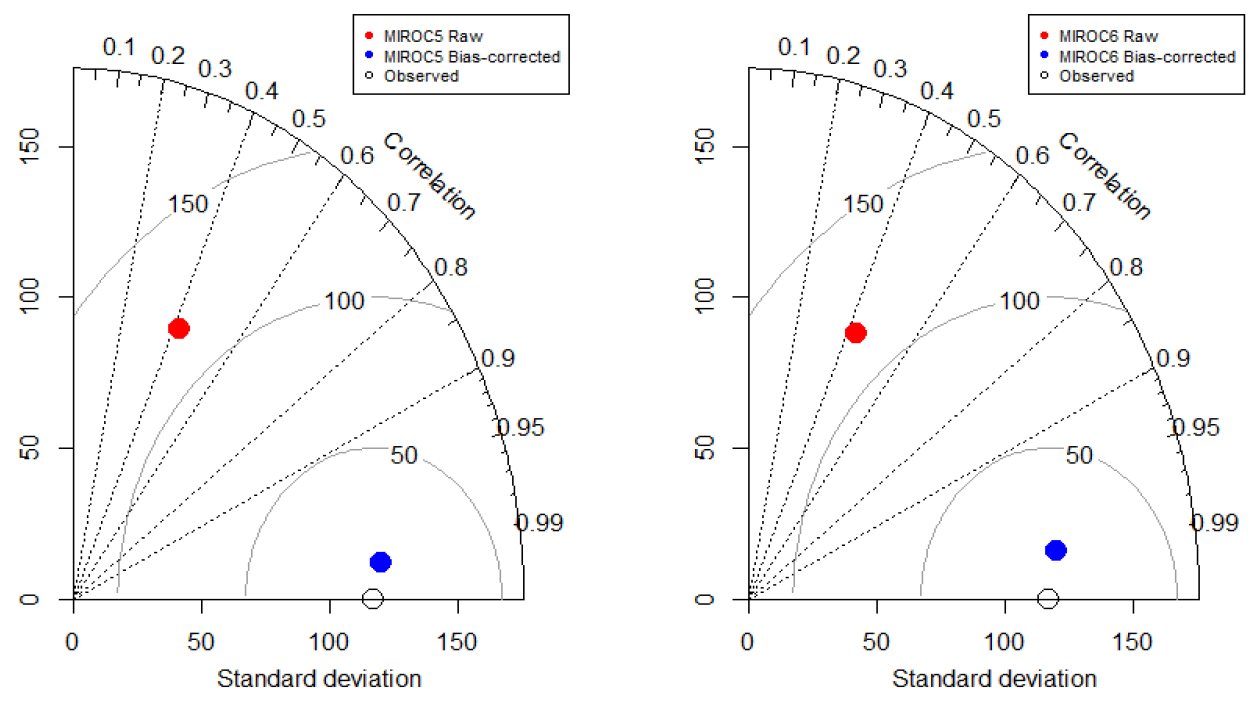
본 연구에서는 역거리 가중치법을 통해 공간적 상세화를 수행하여 과거 기간에 따른 모의값을 추출하였지만 GCM의 넓은 격자 거리와 여러 요인으로 인해 관측값과 모의값 사이에 여전히 차이가 존재하였다. 이를 해결하기 위하여 분위사상법 중 스플라인 평활방법을 이용하여 과거 기간(1970년 ~ 2005년)에 대해 GCM 결과에 대한 편이보정을 수행하였다. 편이보정 방법의 성능을 확인하기 위해 평가 지표에 따른 결과를 Fig. 3과 같이 나타냈으며, 동일 과거 기간의 관측값을 이용하여 편이보정 이전 및 이후 GCM 모의값의 결과를 Fig. 4와 같이 Taylor Diagram으로 나타내었다. Taylor Diagram은 본 연구에서 관측값과 모의값 사이의 표준편차, Pearson 상관관계, RMSE의 값을 나타내기 위해 사용되었다(Taylor, 2001).

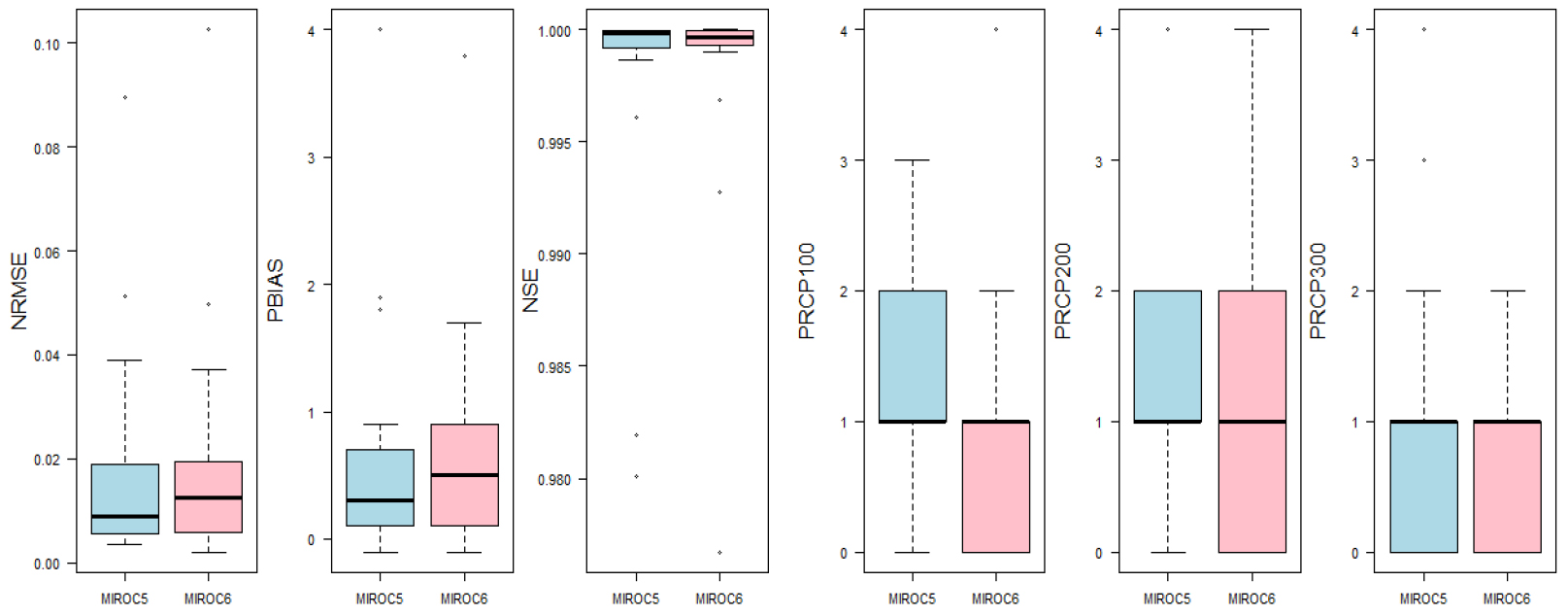
https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F3.jpg

Fig. 3.

Model evaluation results of the bias-corrected GCM precipitation data using Boxplot

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F4.jpg

Fig. 4.

Comparison between raw and bias-corrected GCM data against observed data using Taylor diagram

NRMSE 값의 경우 MIROC5의 중앙값(0.01), MIROC6의 중앙값(0.012) 모두 0에 가까운 높은 성능을 보였다. Pbias의 경우 MIROC5의 중앙값(0.3)이 MIROC6의 중앙값(0.5)보다 최적의 값을 나타내었다. NSE값의 경우 MIROC5와 MIROC6 모두 0.99이상의 값을 확인하였다. PRCP지표의 경우 100 mm, 200mm, 300 mm 순으로 MIROC5의 중앙값(1, 1, 1)과 MIROC6의 중앙값(1, 1, 1)을 확인하였으며, 값의 분포의 경우 두 GCM모두 편이보정 전보다 후에서 최적값에 가까운 분포를 보였다. 편이보정 전의 GCM 모의값과 비교하였을 때 6개의 지표 모두 편이보정된 GCM의 모의값이 편이보정 전 모의값보다 상당히 향상되었음을 알 수 있다.

Taylor diagram의 결과를 통해 편이보정 전 GCM 모의값의 경우 Pearson 상관계수의 범위가 MIROC5와 MIROC6 모두 0.4 ~ 0.45 정도로 나타났으며, 표준 편차의 경우 두 GCM 모두 100 ~ 150 사이의 값을 확인하였다. RMSE 값의 경우 두 데이터 모두 100 ~ 150 사이의 값을 보였다.

편이보정 후의 모의값의 경우 편이보정 이전의 모의값에서보다 상당히 향상된 결과를 확인하였으며, 특히 MIROC5와 MIROC6 모두 Pearson 상관 계수의 경우에서 편이보정 이전의 모의값의 범위인 0.4 ~ 0.45 보다 상당히 향상된 0.99 이상의 값을 보여주었다. RMSE 값 범위의 경우 편이보정 이전의 모의값의 범위인 100 ~ 150에서 0 ~ 50 사이까지 향상된 범위를 보였다.

3.3 GCM 공간적 재현성 평가

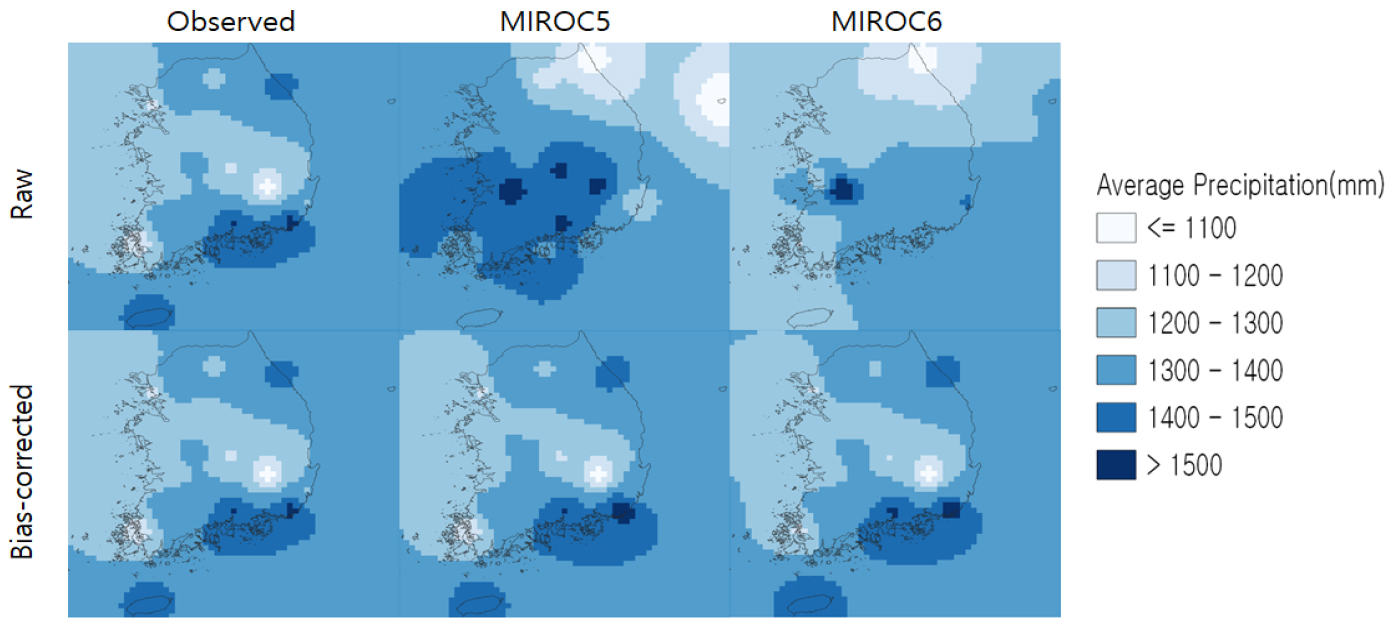
관측 자료와 동일한 과거 36년(1970년 ~ 2005년) 기간의 연 평균 강수량의 분포를 이용하여 MIROC5와 MIROC6 GCM의 편이보정 이전의 모의값과 편이보정 된 모의값의 공간적 재현성을 Fig. 5와 같이 나타내었다. 편이보정 전후 모의값 모두 남쪽에서 북쪽으로 갈수록 강수량이 줄어드는 우리나라 기후를 유사하게 재현함을 확인하였으며, 특히 MIROC6의 경우 남해안과 동해안 지역에서 내륙지방보다 많은 강수량이 발생하는 우리나라 기후를 보다 유사하게 재현함을 확인하였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F5.jpg

Fig. 5.

Spatial distribution of Annual Average Precipitation compared to the historical data

3.4 GCM 월 강수량 변화율 분석

본 연구에서는 가까운 미래 기간(2021년 ~ 2060년, near future)과 먼 미래 기간(2061년 ~ 2100년, far future)의 강수 변화를 확인하기 위하여 21개 관측소의 과거 40년 기간(1970년 ~ 2009년)과 동일한 길이의 관측 자료를 이용하였다. 본 연구에서는 RCP4.5, RCP8.5 시나리오와 SSP2-4.5, SSP5-8.5 시나리오 별로 연간, 여름철, 겨울철 강수량의 변화추이를 확인하였다.

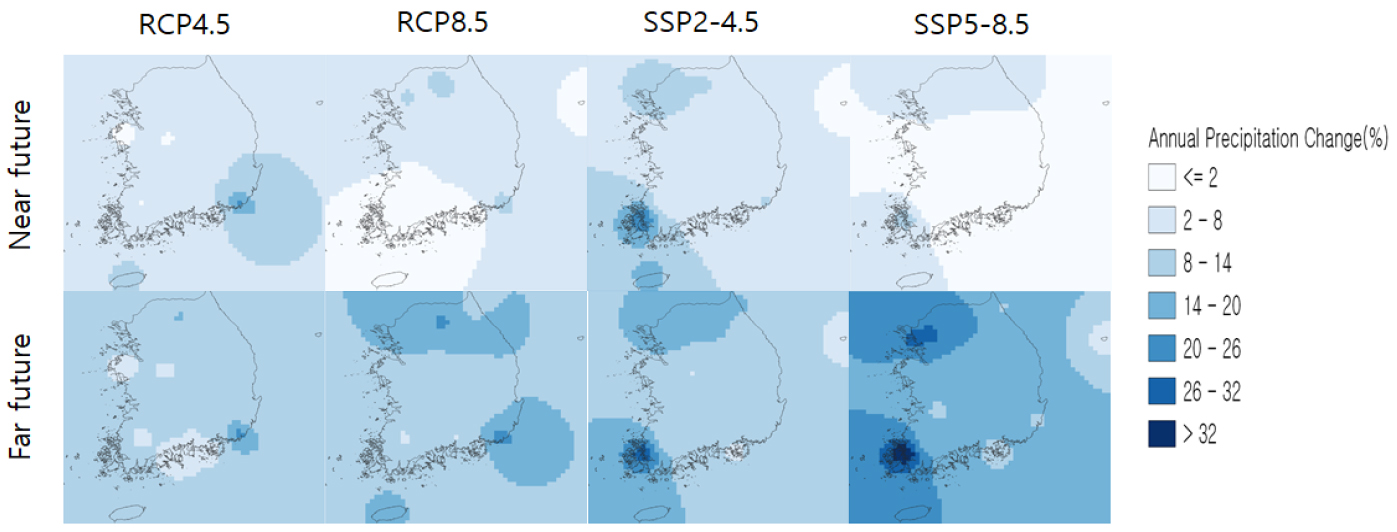
연 강수량의 평균 강수 변화 추이를 Table 1에서와 같이 가까운 미래 기간(2021년 ~ 2060년)과 먼 미래기간(2061년 ~ 2100년)에 대해 지역별(북동부, 북서부, 남동부, 남서부), GCM 시나리오(RCP4.5, RCP8.5, SSP2-4.5, SSP5-8.5)별로 정리하였다. 연간 강수량 변화율의 경우 4개의 시나리오 모두 가까운 미래보다 먼 미래에서 강수의 변화율이 증가하였다. RCP4.5, RCP8.5 시나리오의 경우 먼 미래에서 가까운 미래보다 각각 4.3%, 9.9% 증가된 강수 변화율을 보였으며, SSP2-4.5, SSP5-8.5 시나리오의 경우 먼 미래에서 가까운 미래보다 각각 5.8%, 16.7% 증가된 변화율을 보였다.

MIROC5의 RCP4.5, RCP8.5 시나리오와 MIROC6의 SSP2-4.5, SSP5-8.5 시나리오에 따른 과거 기간 대비 연 강수량의 변화를 공간적으로 보간한 결과를 나타내면 Fig. 6과 같다.

Table 1.

Spatial and temporal averages of future annual precipitation changes (%) estimated by GCMs compared to the base period 1970-2009

Region	Near Future				Far Future
Region	RCP4.5	RCP8.5	SSP2-4.5	SSP5-8.5	RCP4.5	RCP8.5	SSP2-4.5	SSP5-8.5
NE	4.93	4.99	3.50	2.36	10.81	15.15	12.50	14.21
NW	2.86	5.17	6.55	1.84	8.84	13.73	12.36	21.66
SE	8.94	2.82	6.38	-2.01	10.47	12.91	10.12	14.87
SW	5.03	0.43	10.96	2.58	8.76	11.40	15.43	20.99
Average	5.44	3.35	6.85	1.19	9.72	13.3	12.6	17.93

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F6.jpg

Fig. 6.

Spatial distribution of annual precipitation changes (%) compared to the base period 1970-2009

RCP4.5 시나리오와 SSP2-4.5 시나리오의 경우 북부 지역보다 남부 지역에서 강수량의 변화율이 평균적으로 크게 증가하였으며, RCP8.5 시나리오와 SSP5-8.5 시나리오의 경우 남부 지역보다 북부 지역에서 강수량이 크게 증가하였다. 또한 RCP 시나리오의 경우 서부 지역보다 동부 지역에서 상대적으로 강수량이 크게 증가하였으며, SSP 시나리오의 경우 반대 결과를 보였다. 가까운 미래의 경우 SSP2-4.5 시나리오에서 남서부 지역의 변화율이 가장 높게(10.96%) 나타났으며, SSP5-8.5 시나리오에서 남동부 지역이 가장 높은 감소율(-2.01%)을 보였다. 먼 미래의 경우 SSP5-8.5 시나리오에서 북서부 지역이 가장 많이(21.66%) 증가하였으며, RCP4.5 시나리오에서 남서부 지역에서 가장 적게(8.76%) 증가하였다.

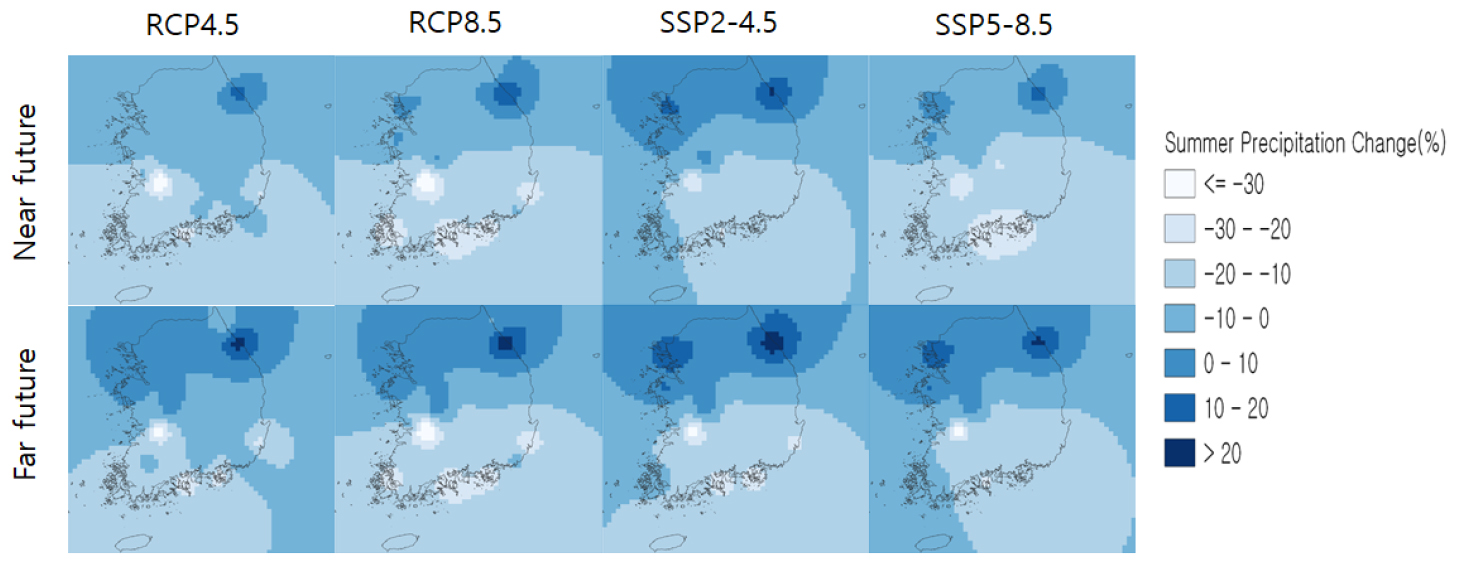
여름철 강수량의 평균 강수 변화 추이를 나타내면 Table 2와 같다. 여름철 강수량의 경우 전체 평균적으로 감소하는 추세를 확인하였으며, RCP4.5, RCP8.5, SSP2-4.5, SSP5-8.5 시나리오 순으로 각각 가까운 미래에서 먼 미래보다 증가된(4.2%, 3.32%, 0.61%, 6.23%) 감소율을 보였다.

MIROC5의 RCP4.5, RCP8.5 시나리오와 MIROC6의 SSP2-4.5, SSP5-8.5 시나리오에 따른 과거 기간 대비 여름철 강수량의 공간적 변화를 나타내면 Fig. 7과 같다. 여름철 강수량의 평균 강수 추이는 가까운 미래와 먼 미래 기간 모두 4개의 시나리오에 대해 북부 지역에서 대체로 증가하는 추세를 보였으며, 남부 지역에서 감소하는 추세를 보였다. 가까운 미래의 경우 SSP2-4.5 시나리오에서 북서부 지역이 가장 높은(6.51%) 증가율을 보였으며, RCP8.5 시나리오에서 남서부 지역이 가장 높은(-22.71%) 감소율을 보였다. 먼 미래의 경우 SSP2-4.5 시나리오에서 북동부 지역이 가장 높은(10.73%) 증가율을 보였으며, RCP8.5 시나리오에서 남서부 지역이 가장 높은(-21.85%) 감소율을 보였다.

Table 2.

Spatial and temporal averages of future summer precipitation changes (%) estimated by GCMs compared to the base period 1970-2009

Region	Near Future				Far Future
Region	RCP4.5	RCP8.5	SSP2-4.5	SSP5-8.5	RCP4.5	RCP8.5	SSP2-4.5	SSP5-8.5
NE	-1.27	1.98	5.40	1.14	4.61	7.40	10.73	5.34
NW	-3.30	0.09	6.51	-0.42	5.67	7.20	9.71	8.96
SE	-11.74	-17.45	-15.85	-20.73	-11.64	-17.56	-18.83	-16.75
SW	-18.57	-22.71	-12.71	-19.47	-16.72	-21.85	-15.81	-12.10
Average	-8.72	-9.52	-4.16	-9.87	-4.52	-6.20	-3.55	-3.64

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F7.jpg

Fig. 7.

Spatial distribution of summer precipitation changes (%) compared to the base period 1970-2009

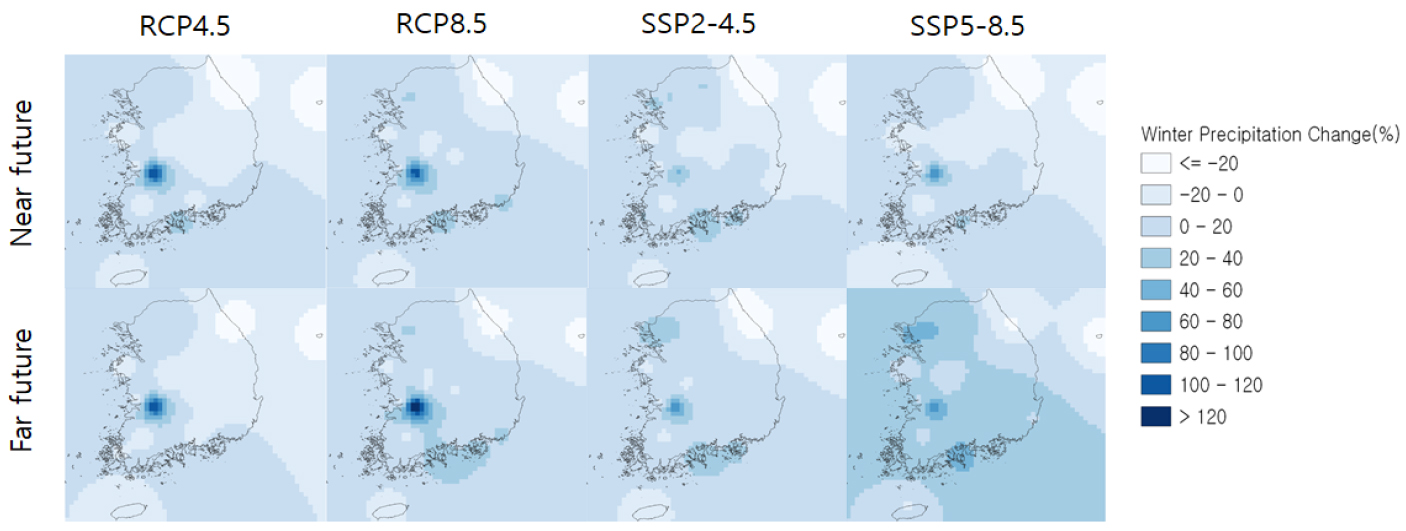
겨울철 강수량의 평균 강수 변화 추이를 나타내면 Table 3과 같다. 겨울철 강수의 변화는 전 지역 평균적으로 증가하는 추세를 보였으며, 가까운 미래보다는 먼 미래에서 더 높은 강수 변화율을 보였다. RCP4.5 시나리오의 경우 먼 미래에서 가까운 미래보다 0.16% 증가된 감소율을 보였으며, 이외 시나리오(RCP8.5, SSP2-4.5, SSP5-8.5)에서 먼 미래에서 가까운 미래보다 각각 3.91%, 3.69%, 21.28% 증가 된 변화율을 보였다.

MIROC5의 RCP4.5, RCP8.5 시나리오와 MROC6의 SSP2-4.5, SSP5-8.5 시나리오에 따른 과거 기간 대비 겨울철 강수량의 공간적 변화를 나타내면 Fig. 8과 같다. 겨울 강수량의 평균 강수 추이는 북동부(NE)지역에서 가까운 미래와 먼 미래 기간 모두 4개의 시나리오에 대해 감소하는 추세를 보였으며, 이외 지역(NW, SE, SW)에서 대체로 증가하는 추세를 보였다. 가까운 미래의 경우 RCP8.5 시나리오에서 남서부 지역이 가장 높게(18.47%) 증가하였으며, SSP5-8.5 시나리오에서 북동부 지역이 가장 높게(-24.47%) 감소하였다. 먼 미래의 경우SSP5-8.5 시나리오에서 남동부 지역이 가장 많이(33.03%) 증가하였으며, SSP2-4.5 시나리오에서 북동부 지역이 가장 많이(-20.46%) 감소하였다.

Table 3.

Spatial and temporal average of future winter precipitation changes (%) estimated by GCMs compared to the base period 1970-2009

Region	Near Future				Far Future
Region	RCP4.5	RCP8.5	SSP2-4.5	SSP5-8.5	RCP4.5	RCP8.5	SSP2-4.5	SSP5-8.5
NE	-23.71	-19.49	-21.97	-24.47	-19.27	-16.44	-20.46	-8.58
NW	-1.42	4.39	5.18	-0.02	1.27	5.91	9.20	24.61
SE	4.45	11.59	8.88	5.78	-2.38	14.33	15.40	33.03
SW	18.42	18.47	9.45	7.88	17.46	26.81	12.17	25.22
Average	-0.57	3.74	0.39	-2.71	-0.73	7.65	4.08	18.57

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F8.jpg

Fig. 8.

Spatial distribution of winter precipitation changes (%) compared to the base period 1970-2009

3.5 변동성 분석

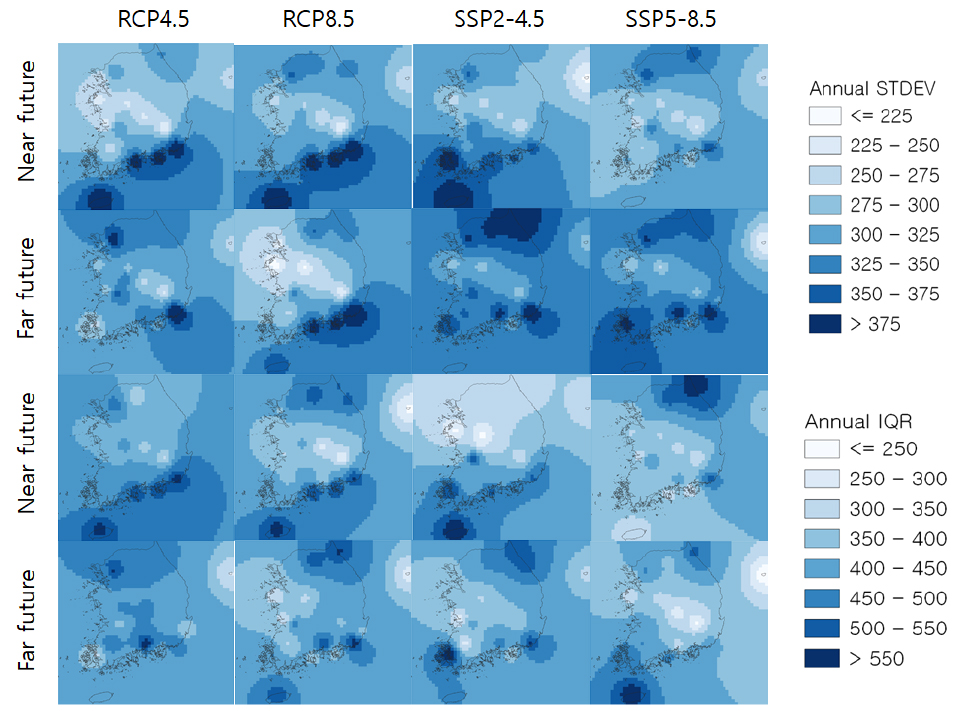
4개의 GCM 시나리오를 이용하여 가까운 미래기간과 먼 미래기간으로 나누어 산정한 미래 강수 모의값에 대해 연 강수량, 여름철 강수량, 겨울철 강수량에 따른 공간적 변동성을 표준편차(STDEV)와 사분범위(IQR)값을 사용하여 정량화한 결과를 나타내면 Table 4와 같다.

표준편차와 사분범위 값을 이용하여 공간적으로 보간된 연 강수량에 대한 GCM 모의값의 변동성을 나타내면 Fig. 9와 같다. 표준편차와 사분범위 값 모두 대체로 가까운 미래가 먼 미래보다 높은 수치를 나타내었다. 연 강수량의 경우 대체적으로 가까운 미래보다 먼 미래의 변동성이 높았으며, 지역적으로 가까운 미래와 먼 미래 모두 북부 지역보다 남부 지역에서의 변동성이 컸다. 가까운 미래의 경우 표준편차는 RCP8.5 시나리오의 값이 SSP5-8.5 시나리오의 값 보다 크게 산정되었으며, SSP2-4.5 시나리오의 값이 RCP4.5 시나리오의 값보다 크게 산정되었다. RCP4.5, RCP8.5 시나리오의 값이 각각 SSP2-4.5, SSP5-8.5 시나리오의 사분범위값보다 크게 산정되었다. 먼 미래의 표준 편차는 SSP2-4.5, SSP5-8.5 시나리오의 값이 각각 RCP4.5, RCP8.5 시나리오의 값보다 높게 산정되었으며, 사분범위 값의 경우 RCP4.5, RCP8.5 시나리오의 값이 각각 SSP2-4.5, SSP5-8.5 시나리오의 값보다 높게 산정되었다.

Table 4.

Variability of GCM monthly precipitation in four regions for different scenarios

Variable	Region	Near Future				Far Future
Variable	Region	RCP4.5	RCP8.5	SSP2-4.5	SSP5-8.5	RCP4.5	RCP8.5	SSP2-4.5	SSP5-8.5
Annual STDEV	NE	298	312	284	324	319	332	375	329
	NW	269	301	295	304	328	246	318	315
	SE	333	336	323	301	321	341	337	341
	SW	309	322	358	294	310	307	349	354
Annual IQR	NE	371	448	328	519	418	468	475	398
	NW	410	403	276	380	464	364	375	370
	SE	452	424	435	382	446	439	428	365
	SW	438	425	485	369	411	420	410	476
Summer STDEV	NE	216	252	186	186	211	221	228	248
	NW	238	243	204	228	203	213	214	231
	SE	242	203	203	181	228	190	212	249
	SW	220	206	218	191	224	192	213	265
Summer IQR	NE	296	333	224	276	275	328	261	349
	NW	352	385	250	312	297	355	254	337
	SE	311	302	233	228	322	256	322	342
	SW	294	305	293	265	306	269	285	414
Winter STDEV	NE	32	65	37	31	37	45	43	57
	NW	9	31	20	13	12	18	30	43
	SE	55	81	48	49	32	53	52	77
	SW	56	68	54	49	46	55	50	80
Winter IQR	NE	34	23	30	32	44	49	30	72
	NW	9	7	19	14	12	16	15	50
	SE	31	25	47	36	32	41	46	67
	SW	44	39	50	42	48	58	55	77

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F9.jpg

Fig. 9.

Spatial distributions of STDEVs and IQRs in monthly precipitation for all seasons

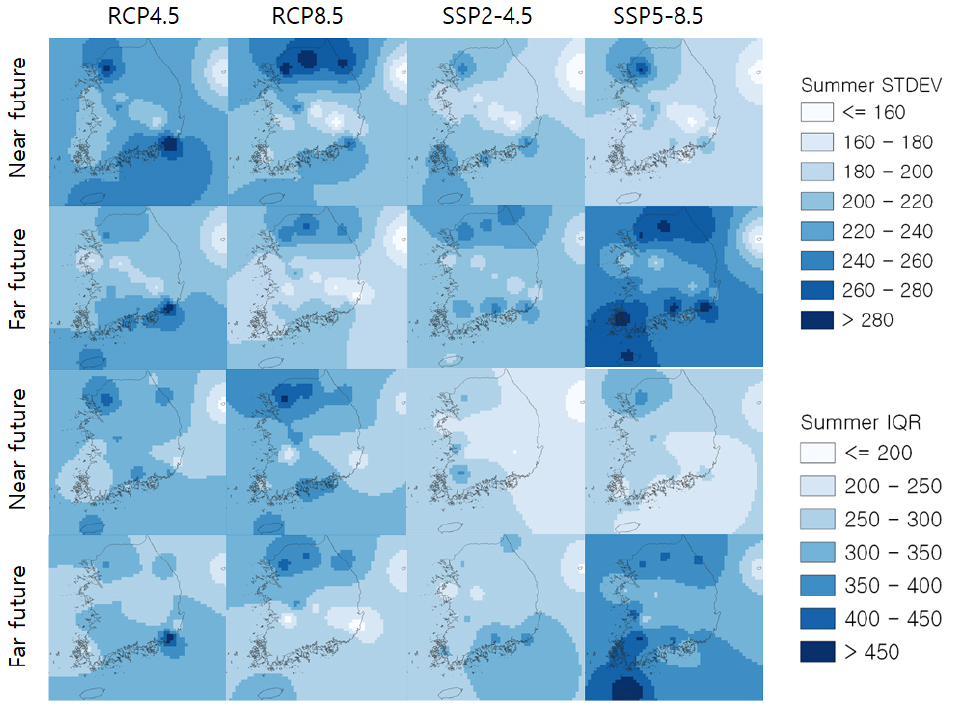
표준편차와 사분범위 값을 이용하여 공간적으로 보간 된 여름철 강수량에 대한 GCM 모의값의 변동성을 나타내면 Fig. 10과 같다. 여름철 강수량의 경우 대체적으로 가까운 미래보다 먼 미래에서 변동성이 높았으며, 지역적으로 가까운 미래에서 북부 지역, 먼 미래에서 남부 지역이 높은 변동성을 보였다. 가까운 미래의 경우 표준편차는 RCP4.5, RCP8.5 시나리오의 값이 각각 SSP2-4.5, SSP5-8.5 시나리오의 값보다 높게 산정되었으며, 사분범위의 값도 같은 결과를 보였다. 먼 미래의 경우 표준편차는 SSP2-4.5, SSP5-8.5 시나리오의 값이 각각 RCP4.5, RCP8.5 시나리오의 값보다 높게 산정되었으며, 사분범위 값의 경우 RCP4.5 시나리오의 값이 SSP2-4.5 시나리오의 값보다 높게 산정되었고, SSP5-8.5 시나리오의 값이 RCP8.5 시나리오의 값보다 높게 산정되었다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F10.jpg

Fig. 10.

Spatial distributions of STDEVs and IQRs in monthly precipitation for summer season

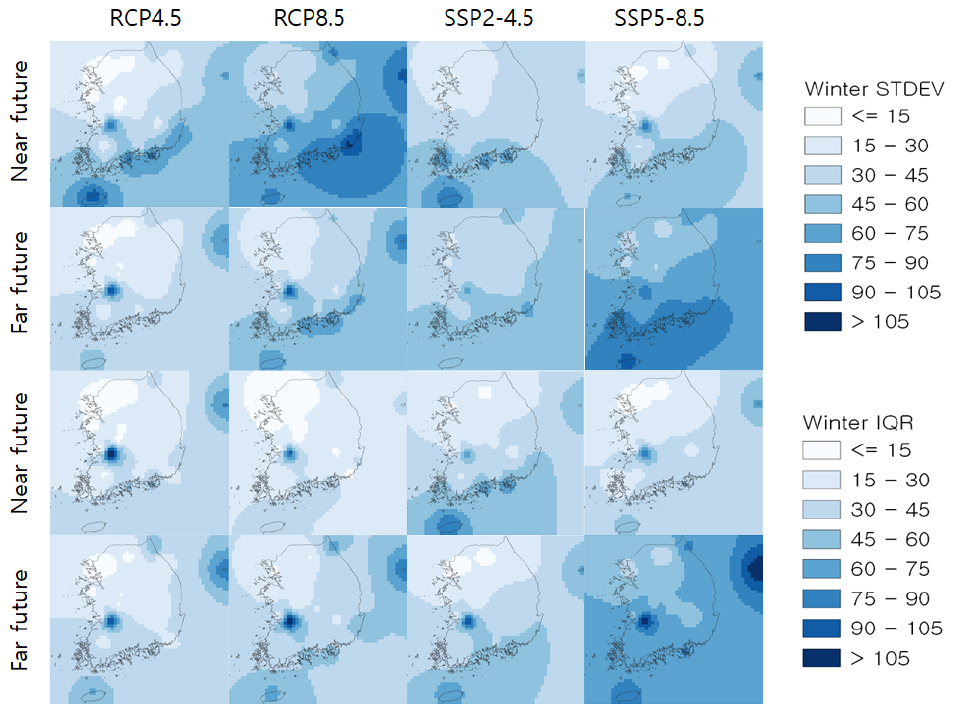
표준편차와 사분범위 값을 이용하여 공간적으로 보간된 겨울철 강수량에 대한 GCM 모의값의 변동성을 나타내면 Fig. 11과 같다. 겨울철 강수량의 경우 대체로 가까운 미래보다 먼 미래에서 높은 변동성을 보였으며, 가까운 미래와 먼 미래 모두 북부 지역보다 남부 지역에서 변동성이 높았다. 가까운 미래의 경우 표준편차는 SSP2-4.5 시나리오의 값이 RCP4.5 시나리오의 값보다 높았으며, RCP8.5 시나리오의 값이 SSP5-8.5 시나리오의 값보다 높았다. 사분범위 값의 경우 SSP2-4.5, SSP5-8.5 시나리오의 값이 각각 RCP4.5, RCP8.5 시나리오의 값보다 높게 산정되었다. 먼 미래의 경우 표준편차와 사분범위 값 모두 SSP2-4.5, SSP5-8.5 시나리오의 값이 각각 RCP4.5, RCP8.5 시나리오의 값보다 높게 산정되었다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-04/N0200540402/images/kwra_54_04_02_F11.jpg

Fig. 11.

Spatial distributions of STDEVs and IQRs in monthly precipitation for winter season

4. 결 론

본 연구에서는 MIROC5의 RCP4.5, RCP8.5 시나리오와 MIROC6의 SSP2-4.5, SSP5-8.5 시나리오를 대상으로 우리나라 21개의 관측소의 과거기간(1970년 ~ 2005년)의 관측값을 이용하여 과거 월 강수량에 대해 편이보정 전후의 성능을 평가하였다. 또한 편이 보정된 MIROC5의 RCP4.5, RCP8.5와 MIROC6의 SSP2-4.5, SSP5-8.5 시나리오를 이용하여 가까운 미래 기간(2021년 ~ 2060년)과 먼 미래 기간(2061년 ~ 2100년) 별로 과거 기간 대비 연 강수량, 여름철 강수량, 겨울철 강수량 변화율을 산정하였다. 더 나아가 과거 기간 대비 강수량 변화율의 표준편차와 사분범위 값을 이용하여 미래 예측 값의 변동성을 확인하였다.

평가지표를 이용한 편이보정 전의 GCM 성능은 Pbias 지표를 제외한 모든 지표에서 MIROC5보다 MIROC6의 성능이 더 좋게 산정되었으며, 편이보정 후의 GCM의 성능은 MIROC5가 MIROC6보다 미세하게 높은 성능을 보였다. Taylor diagram을 이용하여 편이보정의 성능을 확인한 결과 두 GCM 모두 편이보정을 수행하기 전보다 편이보정 후에 향상된 성능을 보임을 확인하였다.

전체적인 강수 변화 추세는 대체로 연 강수량과 겨울철 강수량에서 증가하는 추세를 보였으며, 여름철 강수량에서 감소하는 추세를 보였다. 과거 기간 대비 미래 강수량 변화의 경우 연 강수량과 여름철 강수량에서 남부 지역보다 북부 지역에서 강수량이 증가하는 추세를 보였으며, 겨울철 강수량의 경우 동부 지역보다 서부 지역에서 강수량이 크게 증가하였다.

연 강수량의 경우 4개의 시나리오 모두 가까운 미래보다 먼 미래에서 높은 강수량 증가율을 확인하였다. 여름철 강수량의 경우 4개의 시나리오 모두 가까운 미래에서 먼 미래보다 높은 강수 감소율을 보였다. 겨울철 경수량의 경우 RCP4.5 시나리오에서 가까운 미래보다 먼 미래에서 높은 강수 감소율을 보였으며, RCP8.5, SSP2-4.5, SSP5-8.5 시나리오에서 가까운 미래보다 먼 미래에서 높은 강수 증가율을 보였다.

변동성의 경우 가까운 미래와 먼 미래 모두 연 강수량과, 겨울철 강수량은 대체적으로 남부 지역이 북부 지역보다 변동성이 높았고, 여름철 강수량에서 반대의 결과를 보였다. 연 강수량의 경우 표준편차는 RCP8.5 시나리오에서 먼 미래보다 가까운 미래가 높게 산정되었으며, RCP4.5, SSP2-4.5, SSP5-8.5 시나리오에서 반대의 결과를 확인하였고 사분범위 값도 똑같은 결과가 나타났다. 여름철 강수량의 경우 표준편차는 RCP 시나리오에서 가까운 미래에서 먼 미래보다 높게 산정되었으며, SSP 시나리오에서 반대의 결과를 확인하였으며 사분범위 값도 똑같은 결과를 확인하였다. 겨울철 강수량의 경우 표준편차는 RCP 시나리오에서 가까운 미래에서 먼 미래보다 높게 산정되었으며, SSP 시나리오에서 반대의 결과를 보여주었다. 사분범위 값의 경우 4개의 시나리오 모두 대체로 먼 미래에서 가까운 미래보다 높게 산정되었다.

본 연구에서는 동일기관에서 개발한 GCM을 사용하여 연구를 수행하였으며, 이런 경우 산정된 결과 값이 단일 GCM의 모의 특성에 전적으로 영향을 받는다. 향후 연구에서는 여러 GCM을 추가적으로 사용한다면 보다 다양한 미래 기후에 대해 예측할 수 있을 것이며, 단일 GCM을 사용하였을 때 발생하는 불확실성 또한 고려할 수 있을 것이다. 또한 본 연구에서 GCM을 이용하여 미래 강수량을 산정하였을 때 복사강제력을 토대로 구성된 RCP 시나리오의 결과와 복사강제력과 다양한 사회적 요소까지 고려하여 생성된 SSP 시나리오의 강수 변화 추세나 변동성에 차이가 있었다. 따라서 향후 연구 결과의 다양성을 위해 CMIP5의 RCP 시나리오와 CMIP6의 SSP시나리오의 결과를 비교할 필요가 있다.

Acknowledgements

본 연구는 4단계 BK21 사업의 지원을 받아 수행되었습니다.

References

Chen, Z., Zhou, T., Zhang, L., Chen, X., Zhang, W., and Jiang, J. (2020). "Global land monsoon precipitation changes in CMIP6 projection." Geophysical Research Letters, Vol. 47, pp. 1-9. 10.1029/2019GL086902

Getirana, A.C.V., and Peters-Lidard, C. (2013). "Estimating water discharge from large radar altimetry datasets." Hydrology and Earth System Sciences, Vol. 17, pp. 923-933. 10.5194/hess-17-923-2013

Golmohammadi, G., Prasher, S., Madani, A., and Rudra, R. (2014). "Evaluating three hydrological distributed watershed models: MIKE-SHE, APEX, SWAT." Hydrology, Vol. 1, No. 1, pp. 20-39. 10.3390/hydrology1010020

Greve, P., Kahil, T., Mochizuki, J., Schinko, T., Satoh, Y., Burek, P., Fischer, G., Tramberend, S., Burtscher, R., Langan, S., and Wada, Y. (2018). "Global assessment of water challenges under uncertainty in water scarcity projections." Nature Sustainability, Vol. 1, pp. 486-494. 10.1038/s41893-018-0134-9

Gudmundsson, L., Bremnes, J.B., Haugen, J.E., and Engen-Skaugen, T. (2012). "Technical note: Downscaling RCM precipitation to the station scale using statistical transformations-a comparison of methods." Hydrology and Earth System Sciences, Vol. 16, No. 9, pp. 3383-3390. 10.5194/hess-16-3383-2012

Hashino, T., Bradley, A.A., and Schwartz, S.S. (2006) "Evaluation of bias-correction methods for ensemble streamflow." Hydrology and Earth System Scieces Discussion, Vol. 3, No. 2, pp. 561-594. 10.5194/hessd-3-561-2006

Hawkins, E., and Sutton, R. (2009). "The potential to narrow uncertainty in reginal climate predictions." Bulletin of the American Meteorological Society, Vol. 90, pp. 1095-1108. 10.1175/2009BAMS2607.1

Homsi, R., Shiru, M,S., Shahid, S., Ismail, T., Harun, S.B., Al-Ansar, N., Chau, K.W., and Yaseen, Z.M. (2020). "Precipitation projection using a CMIP5 GCM ensemble model: A regional investigation of Syria." Engineering Applications of Computational Fluid Mechanics, Vol. 14, No. 1, pp. 90-16. 10.1080/19942060.2019.1683076

Hong, H.P., Park, S.Y., Kim, T.W., and Lee, J.H. (2018). "Assessment of CMIP5 GCMs for future extreme drought analysis." Journal of Korea Water Resources Association, Vol. 51, No. 7, pp. 617-627.

Hwang, S.W. (2014). "Assessing the performance of CMIP5 GCMs for various climatic elements and indicators over the southeast US." Journal of Korea Water Resources Association, Vol. 47, No. 11, pp. 1039-1050. 10.3741/JKWRA.2014.47.11.1039

Jung, I.G., Eum, H.I., Lee, E.J., Park, J.H., and Cho, J.P. (2018). "Development of representative GCMs selection technique for uncertainty in climate change scenario." Journal of Korean Society of Agricultural Engineers, Vol. 60, No. 5, pp. 149-162.

Khan, N., Shahid, S., Ahmed, K., Ismail, T., Nawaz, N., and Son, M. (2018). "Performance assessment of general circulation model in simulating daily precipitation and temperature using multiple gridded datasets." Water, Vol. 10, pp. 1793-1811. 10.3390/w10121793

Kim, J.H., Ivanov, V.Y., and Fatichi, S. (2015). "Climate change and uncertainty assessment over a hydroclimatic transect of Michigan." Stochastic Environmental Research and Risk Assessment, Vol. 30, pp. 923-944. 10.1007/s00477-015-1097-2

Kim, J.H., Sung, J.H., Chung, E.S., Kim, S.U., Son, M., and Shiru, M.S. (2021). "Comparison of projection in meteorological and hydrological droughts in the Cheongmicheon watershed for RCP4.5 and SSP2-4.5." Sustainability, Vol. 13, No. 4, 2066. 10.3390/su13042066

Koenker, R., and Schorfheide, F. (1994). "Quantile spline models for global temperature change." Climate Change, Vol. 28, pp. 395-404. 10.1007/BF01104081

Lee, S.H., Yoo, S.H., Choi, J.Y., and Hwang, S.W. (2018). "GCM-related uncertainty in forecasting irrigation and design water requirement for paddy rice fields." International Journal of Climatology, Vol. 38, pp. 1298-1313. 10.1002/joc.5244

Meehl, G.A., Boer, G.J., Covey, C., Latif, M., and Stouffer, R.J. (2000). "The coupled model intercomparison project (CMIP)." Bulletin of the American Meteorological Society, Vol. 81, No. 2, pp. 313-318. 10.1175/1520-0477(2000)081<0313:TCMIPC>2.3.CO;2

Mishra, V., Bhatia, U., and Tiwari, A.D. (2020). "Bias-corrected climate projections for South Asia from coupled model intercomparison project-6." Scientific Data, Vol. 7, pp. 338-369. 10.1038/s41597-020-00681-133046709PMC7550601

Moriasi, D.N., Gitau, M.W., Pai, N., and Daggupati, P. (2015). "Hydrologic and water quality models: Performance measures and evaluation criteria." American Society of Agricultural and Biological Engineers, Vol. 58, No. 6, pp. 1763-1785. 10.13031/trans.58.10715

Nash, J.E., and Sutcliffe, J.V. (1970). "River flow forecasting through. Part I. A conceptual models discussion of principles." Journal of Hydrology. Vol. 10, pp. 282-290. 10.1016/0022-1694(70)90255-6

O'Neill, B.C., Kriegler, E., Riahi, K., Ebi, K.L., Hallegatte, S., Carter, T.R., Mathur, R., and van Vuuren, D.P. (2014). "A new scenario framework for climate change research: The concept of shared socioeconomic pathways." Climate Change, Vol. 122, pp. 387-400. 10.1007/s10584-013-0905-2

Schepen, A., and Wang, Q.J. (2013). "Toward accurate and reliable forecasts of Australian seasonal rainfall by calibrating and merging multiple coupled GCMs." Monthly Weather Review, Vol. 141, pp. 4554-4563. 10.1175/MWR-D-12-00253.1

Scoccimarro, E., and Gualdi, S. (2020). "Heavy daily precipitation events in the CMIP6 worst-case scenario: Projected twenty-first-century changes." Journal of Climate, Vol. 33, pp. 7631-7642. 10.1175/JCLI-D-19-0940.1

Song, Y.H., and Chung, E.S. (2020). "Intercomparison of uncertainty to bias correction methods and GCM selection in precipitation projections." Journal of Korea Water Resources Association, Vol. 53, No. 4, pp. 249-258.

Song, Y.H., Chung, E.S., and Shiru, M.S. (2020). "Uncertainty analysis of monthly precipitation in GCMs using multiple bias correction methods under different RCPs." Sustainability, Vol. 12, No. 18, 7508. 10.3390/su12187508

Song, Y.H., Nashwan, M.S., Chung, E.S., and Shahid, S. (2021). "Advances in CMIP6 INM-CM5 over CMIP5 INM-CM4 for precipitation simulation in South Korea." Atmospheric Research, Vol. 247, pp. 1-14. 10.1016/j.atmosres.2020.105261

Taylor, K.E. (2001). "Summarizing multiple aspects of model performance in a single diagram." Journal of Geophysical Research, Vol. 106, No. 7, pp. 7183-7192. 10.1029/2000JD900719

Tobler, W.R. (1970). "A computer movie simulating urban growth in the detroit region." Economic Geography, Vol. 46, pp. 234-240. 10.2307/143141

Wu, T., Lu, Y., Fang, Y., Xin, X., Li, L., Li, W., Jie, W., Zhang, J., Liu, Y., Zhang, L., Zhang, F., Zhang, Y., Wu, F., Li, J., Chu, M., Wang, Z., Shi, X., Liu, X., Wei, M., Huang, A., Zhang, Y., and Liu, X. (2019). "The Beijing climate center climate system model (BCCCSM): The main progress from CMIP5 to CMIP6." Geoscientific Model Development, Vol. 12, pp. 1573-1600. 10.5194/gmd-12-1573-2019

Xin, X., Wu T., Zhang, J., Yao, J., and Fang, Y. (2020). "Comparison of CMIP6 and CMIP5 simulations of precipitation in China and the East Asian summer monsoon." International Journal of Climatology, Vol. 40, pp. 6423-6440. 10.1002/joc.6590

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Comparison of MIROC5 and MIROC6 projections for precipitation over South Korea

ABSTRACT

MAIN

Fig. 1.

Location of weather stations used in this study

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Fig. 2.

Model evaluation results of the raw GCM precipitation data using Boxplot

Fig. 3.

Model evaluation results of the bias-corrected GCM precipitation data using Boxplot

Fig. 4.

Comparison between raw and bias-corrected GCM data against observed data using Taylor diagram

Fig. 5.

Spatial distribution of Annual Average Precipitation compared to the historical data

Table 1.

Spatial and temporal averages of future annual precipitation changes (%) estimated by GCMs compared to the base period 1970-2009

Fig. 6.

Spatial distribution of annual precipitation changes (%) compared to the base period 1970-2009

Table 2.

Spatial and temporal averages of future summer precipitation changes (%) estimated by GCMs compared to the base period 1970-2009

Fig. 7.

Spatial distribution of summer precipitation changes (%) compared to the base period 1970-2009

Table 3.

Spatial and temporal average of future winter precipitation changes (%) estimated by GCMs compared to the base period 1970-2009

Fig. 8.

Spatial distribution of winter precipitation changes (%) compared to the base period 1970-2009

Table 4.

Variability of GCM monthly precipitation in four regions for different scenarios

Fig. 9.

Spatial distributions of STDEVs and IQRs in monthly precipitation for all seasons

Fig. 10.

Spatial distributions of STDEVs and IQRs in monthly precipitation for summer season

Fig. 11.

Spatial distributions of STDEVs and IQRs in monthly precipitation for winter season

Acknowledgements

References