Data collection strategy for building rainfall-runoff LSTM model predicting daily runoff

Dongkyun Kim; Seokkoo Kang

doi:10.3741/JKWRA.2021.54.10.795

Preview

Research Article

Journal of Korea Water Resources Association. 31 October 2021. 795-805
https://doi.org/10.3741/JKWRA.2021.54.10.795

Data collection strategy for building rainfall-runoff LSTM model predicting daily runoff

강수-일유출량 추정 LSTM 모형의 구축을 위한 자료 수집 방안

Dongkyun Kim^a^*

Seokkoo Kang^b

김 동균^a^*

강 석구^b

^aAssociate Professor, Department of Civil and Environmental Engineering, Hongik University, Seoul, Korea

^bAssociate Professor, Department of Civil and Environmental Engineering, Hanyang University, Seoul, Korea

^a홍익대학교 건설환경공학과 부교수

^b한양대학교 건설환경공학과 부교수

^{*Corresponding Author}

ABSTRACT

In this study, after developing an LSTM-based deep learning model for estimating daily runoff in the Soyang River Dam basin, the accuracy of the model for various combinations of model structure and input data was investigated. A model was built based on the database consisting of average daily precipitation, average daily temperature, average daily wind speed (input up to here), and daily average flow rate (output) during the first 12 years (1997.1.1-2008.12.31). The Nash-Sutcliffe Model Efficiency Coefficient (NSE) and RMSE were examined for validation using the flow discharge data of the later 12 years (2009.1.1-2020.12.31). The combination that showed the highest accuracy was the case in which all possible input data (12 years of daily precipitation, weather temperature, wind speed) were used on the LSTM model structure with 64 hidden units. The NSE and RMSE of the verification period were 0.862 and 76.8 m³/s, respectively. When the number of hidden units of LSTM exceeds 500, the performance degradation of the model due to overfitting begins to appear, and when the number of hidden units exceeds 1000, the overfitting problem becomes prominent. A model with very high performance (NSE=0.8~0.84) could be obtained when only 12 years of daily precipitation was used for model training. A model with reasonably high performance (NSE=0.63-0.85) when only one year of input data was used for model training. In particular, an accurate model (NSE=0.85) could be obtained if the one year of training data contains a wide magnitude of flow events such as extreme flow and droughts as well as normal events. If the training data includes both the normal and extreme flow rates, input data that is longer than 5 years did not significantly improve the model performance.

Keywords

Long short-term memory

Rainfall-runoff model

Deep learning

Artificial neural network

Artificial intelligence

Flow discharge

Soyang river dam

Flow prediction

본 연구는 소양강댐 유역을 대상으로 LSTM 기반의 일유출량 추정 딥러닝 모형을 개발한 후, 모형구조 및 입력자료의 다양한 조합에 대한 모형의 정확도를 살폈다. 첫 12년(1997.1.1-2008.12.31) 동안의 유역평균 일강수량, 일기온, 일풍속 (이상 입력), 일평균 유량 (출력)으로 이루어진 데이터베이스를 기반으로 모형을 구축하였으며, 이후 12년(2009.1.1-2020.12.31) 동안의 자료를 사용하여 Nash-Sutcliffe Model Efficiency Coefficient (NSE)와 RMSE를 살폈다. 가장 높은 정확도를 보인 조합은 64개의 은닉유닛을 가진 LSTM 모형 구조에 가능한 모든 입력자료(12년치의 일강수량, 일기온, 일풍속)를 활용한 경우로서 검증기간의 NSE와 RMSE는 각각 0.862와 76.8 m³/s를 기록하였다. LSTM의 은닉유닛이500개를 초과하는 경우 과적합으로 인한 모형의 성능 저하가 나타나기 시작했으며, 1000개를 초과하는 경우 과적합 문제가 두드러졌다. 12년치의 일강수만 입력자료로 활용한 경우에도 매우 높은 성능(NSE=0.8~0.84)의 모형이 구축되었으며, 한 해의 자료만을 활용하여 학습한 경우에도 충분히 활용 가능한 정확도(NSE=0.63~0.85)를 가진 모형을 구축할 수 있었다. 특히 유량의 변동성이 큰 한 해의 자료만을 활용하여 모형을 학습한 경우 매우 높은 정확도(NSE=0.85)의 모형이 구축되었다. 학습자료가 중유량과 양극한의 유량을 모두 포함한 경우라면 5년 이상의 입력자료는 모형의 성능을 크게 개선시키지 못했다.

키워드

LSTM

강우-유출 모형

딥러닝

인공신경망

인공지능

유량

소양강댐

유량예측

MAIN

1. 서 론
2. 방법론
2.1 연구지역
2.2 자료
2.3 모형 설명
2.4 모형 학습
3. 결과 및 토의
3.1 기본 모형의 성능
3.2 LSTM의 은닉 유닛의 개수에 따른 모형의 정확도
3.3 훈련 자료에 대한 모형의 정확도
3.4 다양한 입력자료의 조합에 따른 모의 정확도
4. 결 론

1. 서 론

뇌가 세상을 인식하는 메커니즘을 개념화한 다중층 퍼셉트론(Multi-Layer Perceptron) 이론은 CPU, GPU, 메모리 등의 반도체를 비롯한 컴퓨터 기술의 비약적인 발달과 함께 심층신경망(deep learning network)으로 진화하여 현실 세계의 다양한 문제들을 풀어내고 있다(Silva et al., 2017).

심층신경망의 가장 중요한 특징 중의 하나는 수십 개에서 수억 개에 달하는 노드들이 선형으로 단순하게 연결된 구조를 통해 복잡한 비선형 시스템을 정확히 모사한다는 점이다. 이러한 독특한 특징으로 인해 지난 수년간 심층신경망을 활용하여 수문학 분야의 문제들을 풀어내려는 다양한 시도들이 있었다(Lee et al., 2019; Sit et al., 2020; Idrees et al., 2021a; Jehanzaib et al., 2021; Idrees et al., 2021b).

심층신경망 알고리즘 중 하나인 Long Short-Term Memory (LSTM, Hochreiter and Schmidhuber, 1997)는 모의하려는 시스템의 이전 상태들을 기억하는 Cell State 라는 독특한 변수를 도입하였는데, 이는 순차적으로 발생하는 다양한 현상들의 연쇄 반응으로 구성된 수문 시스템을 모의하는데 적합하여 강수(Shi et al., 2017; 2015), 증발산(Chen et al., 2020; Yin et al., 2020), 토양수분(Fang et al., 2020; Fang and Shen, 2020), 지하수위(Bowes et al., 2019; Park and Chung, 2020), 하천유량(Kratzert et al., 2018, Hu et al., 2018; Han et al., 2021b), 하천수위(Jung et al., 2018) 등, 다양한 수문변수를 예측하는데 활용되어 전통적인 물리기반의 모형과 유사한 성능을 보였다.

딥러닝 모형은 단순 명료한 수학적 구조로 인해 범용 소프트웨어가 제공되어 모형의 설계와 구현에는 큰 지식과 노력이 불필요한 반면, 오로지 방대한 양의 자료에 기반한 학습을 통해 매개변수들을 교정해야만 모형을 완성할 수 있다. 따라서, 딥러닝 모형의 구축에 필요한 자료의 조합과 그 양을 파악하는 것은 대단히 중요하다. 이러한 정보는 입력 자료 수집을 위해 큰 노력이 소요되는 수문학 분야에서 특히 유용할 것이다.

따라서, 본 연구에서는 소양강 댐 유역에 대하여 딥러닝 기반의 일단위 강우-유출 모형을 구축한 후 다양한 입력자료의 시나리오에 대한 모형 정확도의 변화를 살폈다. LSTM을 활용하여 강우-유출 모형을 구축하고(Kratzert et al., 2018; Hu et al., 2018; Han et al., 2021b) 입력자료 및 모형구조에 대한 정확도를 살핀(Bai et al., 2021, Boulmaiz et al., 2020) 선행연구는 다수 발견되었으나, 우리나라에서 일단위 강우-유출 LSTM 모형 구축 시 필요한 자료 수집방안이라는 구체적인 문제의 해결에 초점을 맞추어 진행된 연구는 드물었다. 특히, 본 연구는 학습/검증 기간에 대한 Nash-Sutcliffe Model Efficiency Coefficient가 각각 0.99 및 0.87에 이르는 정확한 모형을 구축한 후 실험에 활용하여, 본 연구의 결과를 다른 지역의 모형 구축에 활용하는 경우에도 이와 유사한 높은 정확도를 기대할 수 있게 하였으며, 12년이라는 긴 기간을 모형의 검증에 활용하여 결과의 신뢰성을 높였다. 이와 아울러, 딥러닝 모형의 핵심 요소인 LSTM의 은닉층의 개수에 따른 모형의 정확도를 분석함으로써 모형의 최적 구조 또한 제시하고자 하였다.

2. 방법론

2.1 연구지역

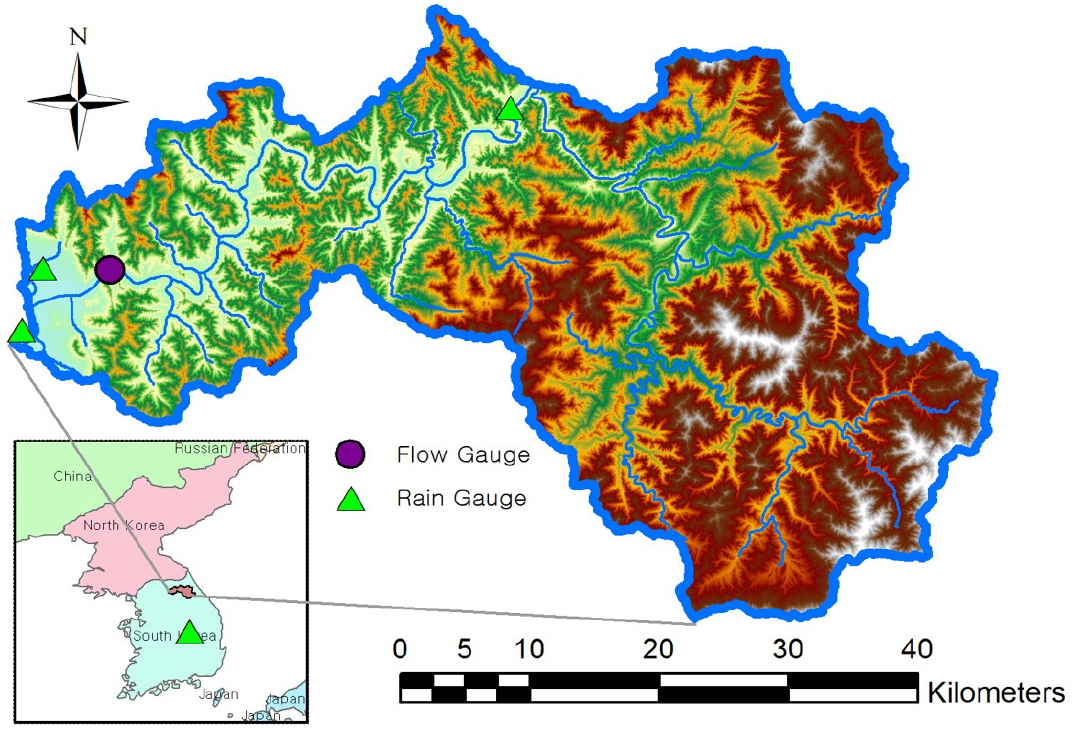
본 연구에서는 Fig. 1에 보인 소양강댐 유역을 연구대상 지역으로 선정하였다. 소양강댐 유역의 면적은 2,703 km², 연평균 강수량은 1,100 mm, 유역평균 유입량은 56 m³/s이다. 소양강댐은 경기, 강원, 수도권의 물 공급을 담당하는 중추적인 국가기간시설로 오랜 기간 동안 유입, 유출, 강수량 등의 수문 변수들이 충실히 기록되어 왔으며, 이는 본 연구가 소양강댐 유역을 연구 대상지역으로 선정한 이유이다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F1.jpg

Fig. 1.

Study area: Soyang River watershed located at the north-eastern part of South Korea

2.2 자료

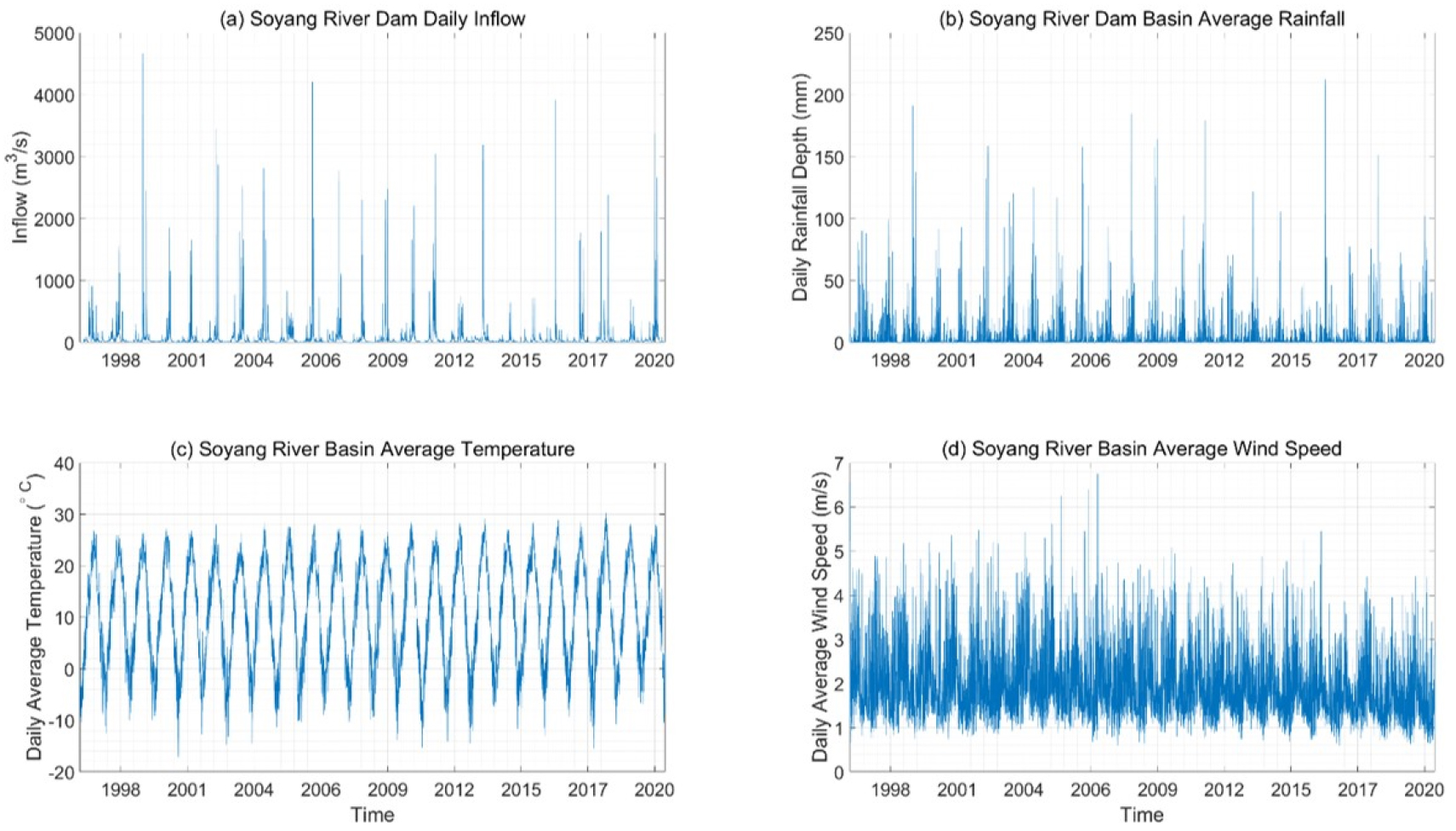
본 연구에서 구축한 딥러닝 모형의 입력자료는 유역 평균 일강수량, 일평균 기온, 일평균 풍속이며 출력자료는 일 유입량자료이다. Fig. 2에 각 자료들을 시계열로 그래프로 표현하여 보였다. 1997년 1월 1일부터 2020년 12월 31일까지 총 35,064 개(4종류의 관측자료/일 × 8766일)의 관측자료가 모형의 구축과 검증에 사용되었다.

유입 일유량은 관측수위를 수위-저수량 곡선에 근거하여 구하였으며(링크 : http://hrfco.go.kr/sumun/makeImageWaterlevel.do?type=Waterlevel&bbsncd=17), 유역평균 강수량, 기온, 풍속은 기상청에서 기상자동관측시스템(ASOS, Fig. 1의 녹색 세모)에서 관측한 시단위 관측치를 하루 단위로 누적(강수량) 혹은 평균(기온, 풍속) 한 후 티센다각형 방법으로 면적 평균하여 구하였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F2.jpg

Fig. 2.

Input and output data used to develop the inflow estimation deep learning model of this study. (a) Daily inflow (output), (b) Daily rainfall (input), (c) Daily average temperature (input), (d) Daily average wind speed (input)

2.3 모형 설명

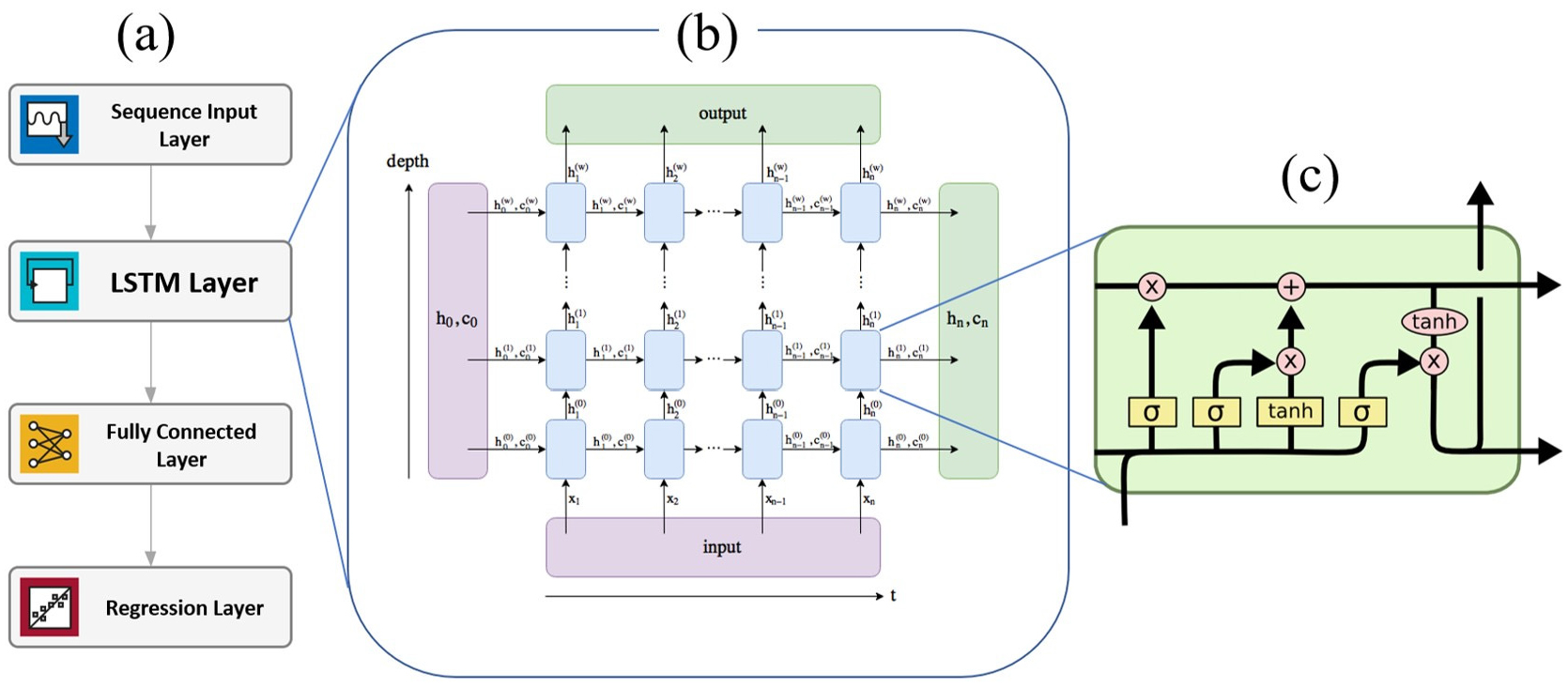
본 연구에서 활용한 딥러닝 모형의 개념도를 Fig. 3에 보였다. Fig. 3(a)는 다양한 딥러닝 레이어 들로 구성된 네트워크를 보였다. 첫번째 블록은 입력 레이어로서 일강수량, 일평균기온, 일평균풍속을 입력 값으로 받아들인 후, 이들을 평균과 표준편차를 사용하여 정규화한 값을 두번째 블록으로 전달한다. 두번째 블록은 장단기 기억신경망(Long Short-Term Memory, LSTM) 레이어로 현재 시간 단계에서의 입력 값(일강수량, 일평균기온, 일평균 풍속), 이전 시간단계에서의 출력 값 및 셀 상태(cell state) 값을 선형 조합하여 여러 개의 값을 출력한다. 세번째 블록은 완전연결(fully connected, FC) 레이어로 이전의 LSTM 레이어에서 산출된 여러 개의 출력 값을 선형으로 조합하여 해당 시간 단계에서의 유량 값을 산출한다. 마지막 레이어는 회귀(regression) 레이어로 모형에서 산출한 유량 시계열과 관측 유량 시계열의 평균제곱근오차(RMSE)를 출력한다. 컴퓨터는 이 레이어가 지시한 바에 따라 모의한 유량과 관측유량의 RMSE가 최소화되도록 매개변수를 조절한다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F3.jpg

Fig. 3.

Schematic of the deep learning model developed in this study. (a) Network diagram of the deep learning blocks. (b) LSTM block composed of multiple hidden blocks (source: https://towardsdatascience.com/animated-rnn-lstm-and-gru-ef124d06cf45, obtained on 2021.6.27)

2.3.1 LSTM 레이어

딥러닝을 활용한 시계열 예측에서 가장 중요한 레이어는 두번째에 위치한 LSTM 레이어이다. 이는 유량, 토양수분과 같은 수문 변수의 예측에 특히 유용한데, 그 이유는 특정 이벤트(예: 강수)에 따른 수문 변수(예: 유출량)들은 이전의 이벤트들(예: 강수, 기온, 풍속)에 의해 결정되는 유역의 상태(예: 토양수분)에 큰 영향을 받으며, LSTM은 순차적으로 발생하는 이벤트들의 특성을 오랫동안 기억할 수 있는 매우 특별한 능력을 가지고 있기 때문이다. 그 개념도를 Fig. 3(b)에 보였다. 이 그림에서 C는 모형 상태변수(cell state), h는 출력 값, X는 입력 값을 의미한다. 각 변수의 아래 첨자는 시간을 의미한다. 본 연구에서 설계한 LSTM 레이어의 입력 값 X는 각 시간대에서의 강수량, 평균 기온 및 평균 풍속이며, 상태변수 C는 물리기반 유역모형의 상태변수인 증발산, 토양수분 등을 직접적으로 의미하지는 않지만 이들을 간접적으로 반영한다고 간주할 수 있다. 레이어의 출력 값인 h는 각 시간 단계마다 여러 개의 값으로 산출되며 이들을 선형으로 결합한 값이 딥러닝 모형의 최종 출력 값인 일 유입 유량이다. 본 연구의 LSTM레이어에 대한 간단한 설명은 다음과 같다.

(1) 망각의 문(Forget Gate)

이 모듈에서는 이전 시간 단계에서 산출된 LSTM의 출력인 $\vec{h_{t - 1}}$ 와 현 시간 단계의 입력 값인 $\vec{x_{t}}$ 를 선형으로 결합한 값을 시그모이드(sigmoid) 함수를 사용하여 0과 1사이의 값으로 전환한 후, 이를 이전 단계의 상태변수 $\vec{C_{t - 1}}$ 에 곱하여 준다. 이를 벡터식으로 표현하면 다음과 같다.

(1)

\vec{C_{1}} = σ (W_{f} \cdot \vec{x_{t}} + U_{f} \cdot \vec{h_{t - 1}} + \vec{b_{f}}) ° \vec{C_{t - 1}}

여기에서 $\vec{C_{1}}$ 는 망각의 문을 통과한 셀의 상태변수 벡터, $σ$ 는 시그모이드 활성화 함수, W_f, U_f는 망각의 문의 가중치의 행렬, $\vec{b_{f}}$ 는 상수항의 벡터를 의미한다. 연산자 “∙”는 벡터곱(vector product), “∘”는 아다마르곱(hadamard product)을 의미한다.

이 모듈에서는 이전 시간 단계에서 산출된 토양수분, 증발산 등 유역의 상태와 연관된 값들을 이전 시간 단계에서의 유량과 현 시간 단계에서의 강수, 기온, 풍속에 근거하여 어느 정도를 기억할 것인지를 결정한다.

(2) 입력의 문(Forget Gate)

이 모듈에서는 $\vec{h_{t - 1}}$ 와 $\vec{x_{t}}$ 를 선형으로 결합한 값을 시그모이드(sigmoid) 함수를 사용하여 0과 1사이의 값으로 전환한 값( $\vec{I_{σ}}$ )와, $\vec{h_{t - 1}}$ 와 $\vec{x_{t}}$ 를 선형으로 결합한 값을 쌍곡탄젠트(hyperbolic tangent) 함수를 사용하여 -1과 1사이의 값으로 전환한 값( $\vec{I_{t}}$ )를 아다마르곱 하여, 망각의 문을 통과한 셀상태 벡터인 $\vec{C_{f}}$ 에 더해준다. 이 과정을 벡터식으로 표현하면 다음과 같다.

(2)

\vec{I_{σ}} = σ (W_{I σ} \cdot \vec{x_{t}} + U_{I σ} \cdot \vec{h_{t - 1}} + \vec{b_{I}}) \vec{I_{t}} = t a n h (W_{I t} \cdot \vec{x_{t}} + U_{I t} \cdot \vec{h_{t - 1}} + \vec{b_{t}}) \vec{C_{t}} = \vec{I_{σ}} ° \vec{I_{t}} + \vec{C_{1}}

여기에서 $\vec{C_{t}}$ 는 입력의 문을 통과한 후 업데이트 된 다음 시간 단계에서의 상태변수 벡터, W_I $σ$ , U_I $σ$ , W_It, U_It는 입력의 문의 가중치 행렬, $\vec{b_{I}}, \vec{b_{t}}$ 는 입력의 문의 상수항 벡터를 의미한다.

이 모듈에서는 이전 시간 단계에서 산출된 유량 관련 변수들과 현 시간 단계에서의 강수, 기온, 풍속에 근거하여 유역의 현재 상태변수(토양수분, 증발산 등)과 관련한 값들을 업데이트 한다.

(3) 출력의 문

이 모듈에서는 이 모듈에서는 $\vec{h_{t - 1}}$ 와 $\vec{x_{t}}$ 를 선형으로 결합한 값을 시그모이드 함수를 사용하여 0과 1사이의 값으로 전환한 값( $\vec{O_{σ}}$ )과 $\vec{C_{2}}$ 를 쌍곡탄젠트 함수를 사용하여 ‒1과 1사이로 전환한 값을 아다마르곱 하여 출력값으로 내보낸다. 이 과정을 벡터식으로 표현하면 다음과 같다:

(3)

\vec{O_{σ}} = σ (W_{o} \cdot \vec{x_{t}} + U_{o} \cdot \vec{h_{t - 1}} + \vec{b_{o}}) \vec{h_{t}} = \vec{O_{σ}} ° \tanh (\vec{C_{t}})

이 모듈에서는 과거 및 현재의 강수, 기온, 풍속에 근거하여 업데이트된 유역의 현재 상태변수들( $\vec{C_{t}}$ )을 기반으로 이전 시간 단계에서 산출된 유량 관련 변수들( $\vec{h_{t - 1}}$ )과 현재 시간 단계의 강수, 기온, 풍속( $\vec{x_{t}}$ )을 활용하여 현 상태에서의 유량 관련 변수들( $\vec{h_{t}}$ )을 산출한다.

2.4 모형 학습

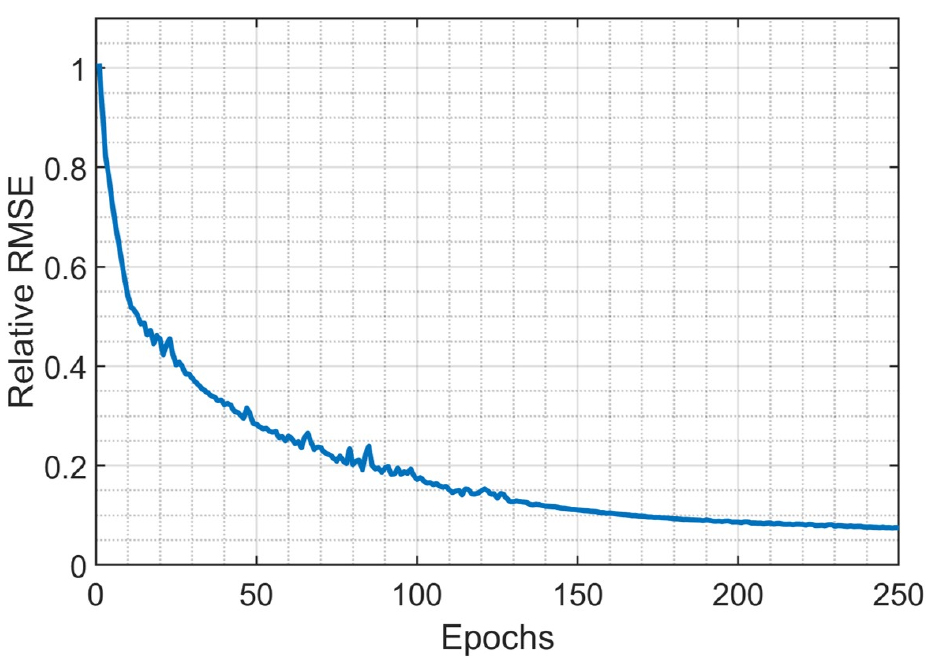
모형의 학습이란 2.3.1장에 보인 가중치 행렬들과 다음 레이어인 완전연결계층의 가중치 행렬의 각 요소들의 값을 모의 유량과 관측유량의 RMSE가 최소화되도록 교정하는 과정을 의미한다. 총 24년(8766일) 중 첫 12년(1997.1.1 ~ 2008.12.31, 4,322일)의 자료를 모형 학습에 사용하였으며, 이 자료를 250번 반복하여 행렬의 가중치를 지속적으로 개선하였다(Epoch =250). Fig. 4에 학습과정 반복에 따라 개선되는 모의-관측유량 사이의 RMSE 값을 보였다. 첫 수십번의 학습 동안에는 모형의 정확도가 크게 향상되었으며, 반복학습이 200회를 초과하는 경우 모형의 정확도가 더 이상 개선되지 않았다. 따라서, 본 연구에서는 250회의 반복학습이 모형 매개변수의 교정에 충분히 큰 값이라 가정하였다. 모형의 교정에는 Intel i9-7980XE CPU와 두 개의 NVIDIA 1080Ti 가 장착된 PC가 사용되었으며, 총 39초가 소요되었다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F4.jpg

Fig. 4.

Relative RMSE value between the observed and the simulated inflow improving as the training epoch increases

3. 결과 및 토의

3.1 기본 모형의 성능

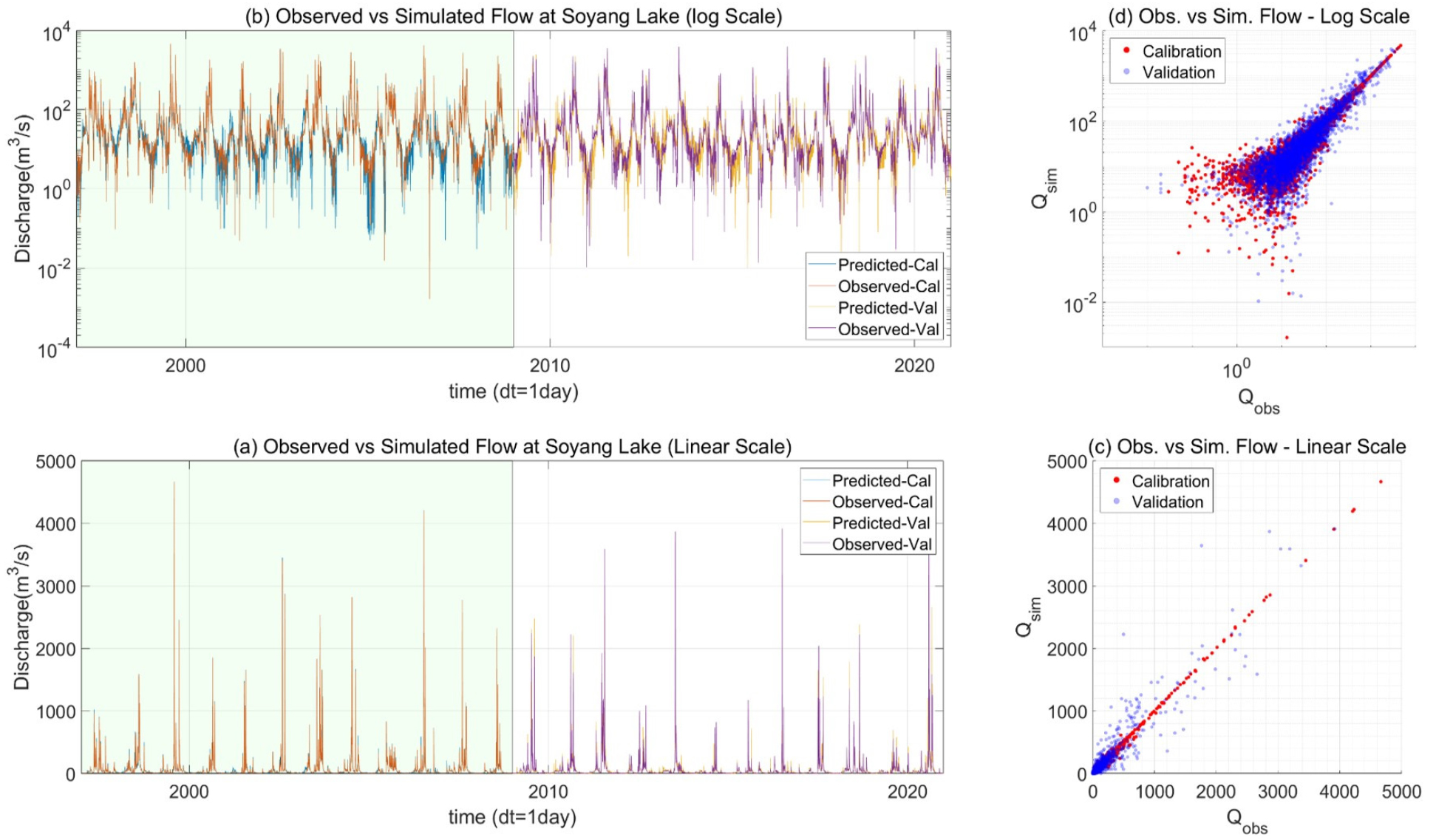
Fig. 5(a)에 기본 모형(LSTM 은닉 유닛 128개, 첫 12년 자료로 모형 학습, 입력자료: 일 강수량, 일평균 기온, 일평균 풍속)에서 산출한 유량을 관측 유량과 비교하였다. 학습자료(1997.1.1 ~ 2008.12.31)와 독립적인 검증기간(2009.1.1 ~ 2020.12.31)에 대하여 비교를 수행하였다. 학습 및 검증기간에 대한 RMSE와 Nash Sutcliffe Coefficient (NSE)를 Table 1에 보였다.

학습기간에 대한 NSE는 0.996이었다. 이는 모형이 완벽에 가깝게 학습되었다는 점을 의미한다. RMSE도 16.2 m³/s 로 매우 양호한 성능을 보였다. 검증기간에 대한 모형의 성능(RMSE= 76.8 m³/s, NSE=0.86)은 학습기간의 성능보다 떨어졌으나, 동일한 유역에 대하여 더욱 정확한 격자형 강수자료를 입력으로 하여 구축된 분포형 지표수문모형의 성능(예: Lee et al., 2017, NSE=0.90)과 유사하였다. 시계열에서 유량을 나타내는 y축을 로그 스케일로 표시한 Fig. 5(b)는 본 연구의 딥러닝 모형이 강우-유출 모의의 도전과제 중 하나인 고유량과 저유량의 동시 예측에 있어서도 매우 뛰어난 성능을 나타냄을 보인다.

Figs. 5(c) and 5(d)에 관측유량(x)과 모의유량(y)을 (c) 선형 및 (d) 로그 스케일로 비교하였다. 선형 축으로 비교한 경우, 학습기간에 대해서는 유량의 전 범위에 걸쳐 매우 정확한 모의결과가 산출되었음을 알 수 있다. 그러나 검증기간에 대해서는 그래프의 오른쪽의 파란색 점들이 나타내는 바와 같이 초 고유량대에서의 모의 값이 관측치를 수십 퍼센트 이상 과소/과대 평가하고 있음을 알 수 있다. 극한현상 재현과 관련한 딥러닝 모형의 한계는 본 연구에만 국한된 것이 아닌 강우-유출 모형의 전형적인 문제로, 모형의 학습에 충분히 많은 극한 현상이 활용되지 않았기 때문이다. 이러한 문제의 해결을 위해 극한 현상에 해당하는 자료를 학습자료 내에 여러 번 반복하는 방안을 시도해 볼 수 있을 것이다. 이러한 방안은 타 분야에서도 자주 시도되었다(Lee et al., 2017).

저-중 유량을 로그함수로 펼쳐 관측/모의 유량을 비교한 Fig. 5(d)의 경우, 평상시 유량인 1 m³ - 100 m³의 구간에서는 검증기간에 해당하는 푸른 점들이 학습기간에 해당하는 붉은 점들보다 오히려 1:1 선에 더 밀착되어 있음을 관찰할 수 있는데, 이는 딥러닝 모형이 관측자료의 대부분을 차지하는 평유량을 완벽에 가깝게 모의하고 있음을 의미한다. 이는 충분한 데이터만 주어진다면 복잡한 수문현상도 딥러닝 모형을 통해 매우 정확히 예측할 수 있음을 의미한다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F5.jpg

Fig. 5.

Time series of observed vs. simulated flow at Soyang Lake shown in (a) linear and (b) log scale. The shaded area is the calibration period. Scatter plot of observed (x) vs. simulated (y) flow shown in (c) linear and (d) log scale

Table 1.

The RMSE and the N-S coefficient of the deep learning model for the training and validation period

	Training (1997.1.1-2008.12.31)	Validation (2009.1.1-2020.12.31)
RMSE (m³/s)	16.2	76.8
NSE	0.996	0.862

3.2 LSTM의 은닉 유닛의 개수에 따른 모형의 정확도

Fig. 3(b)와 앞 절의 방정식들을 살펴보면 LSTM의 출력 값인 $\vec{h_{t}}$ 와 셀 상태 값인 $\vec{C_{t}}$ 가 단일 변수가 아닌 여러 변수로 이루어진 벡터이며, 모의가 진행됨에 따라 이들 변수들이 선형적으로 결합되어 유기적으로 진화함을 알 수 있다. 이러한 독특한 알고리즘을 통해 LSTM은 시스템의 다양한 상태변수들의 서로 다른 시간적 지속성과 이들의 상호작용을 반영할 수 있게 된다. 이러한 다중은닉은 토양수분, 증발산, 지하수위, 하천유량 등의 서로 다른 시간적 지속성을 갖는 다양한 인자들이 역동적으로 상호작용을 하는 수문시스템의 정밀한 모의를 가능케 한다. 또한, LSTM의 은닉유닛의 개수가 많아질 수록 딥러닝 모형이 고려할 수 있는 물리적 메커니즘의 개수가 또한 많아진다는 점을 유추할 수 있다. 다만, 이는 수문현상 모의에 있어 양날의 검으로 작용할 수 있는데, 은닉유닛의 개수가 너무 적으면, 모형이 고려할 수 있는 수문현상의 개수가 적어지므로 정확한 모의를 할 수가 없고, 반대로 은닉유닛의 개수가 너무 많으면 모형이 학습자료에 과적합되어 학습자료의 범위 밖의 입력 값에 따른 모형의 출력 값이 부정확하게 예측된다. 본 연구에서는 이를 더욱 자세히 살펴보기 위하여 은닉 유닛의 개수를 2, 4, 8, 16, 32, 64, 128, 512, 1024개로 늘려가며 모형의 정확도를 살폈다.

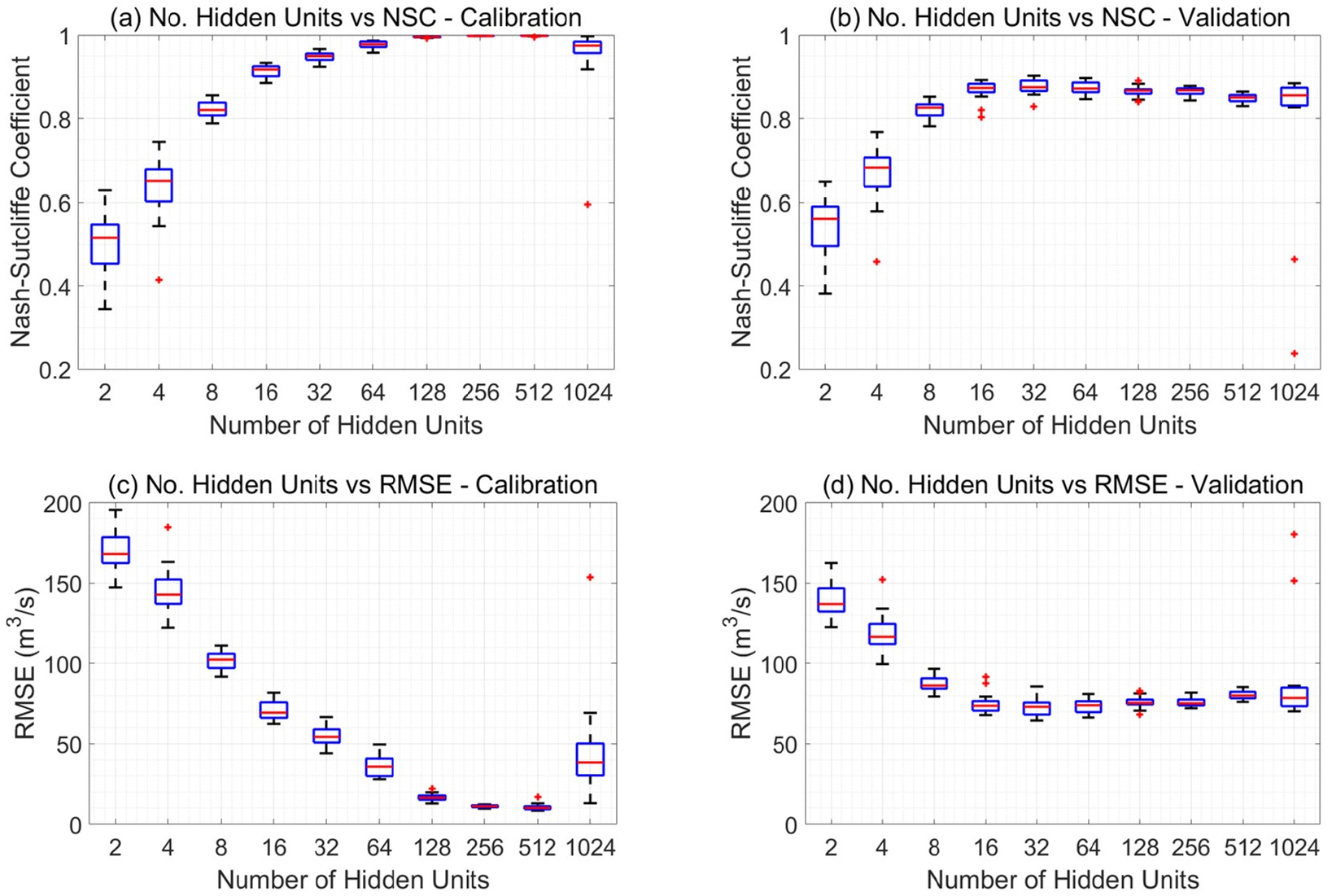
Fig. 6에 은닉유닛의 개수에 따른 훈련 및 검증기간에 따른 NSE(a, b) 와 RMSE(b, d)를 보였다. 동일한 조건에 대하여 학습의 결과가 미세하게 달라질 수 있는데 이는 매개변수 도메인에 무작위로 흩뿌려진 입자들을 시작점으로 하여 학습이 진행되기 때문이다. 이에 따른 불확실성을 고려하기 위하여 동일한 은닉유닛의 개수에 대하여 20회의 학습을 반복한 후 각 케이스에 대한 정확도의 박스플롯을 보였다.

은닉 유닛의 개수가 매우 적은 경우에는 검증기간의 성능이 학습기간의 성능보다 좋았으며, 은닉 유닛의 개수가 늘어날수록 학습기간의 성능이 검증기간의 성능보다 월등히 좋았다. 은닉 유닛의 개수가 64개(RMSE 기준) 혹은 32개(NSE 기준)일 때 검증기간의 성능이 가장 좋았으며, 이 보다 은닉 유닛이 많아지면 오히려 성능이 저하됨이 관측되었다. 은닉 유닛의 개수가 1024개로 매우 많은 경우 앞서 언급되었던 모형의 과적합과 관련한 문제가 뚜렷하게 보였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F6.jpg

Fig. 6.

Root mean square error (RMSE) and Nash-Sutcliffe Model Efficiency Coefficient (NSE) of the flood prediction model varying with the number of the hidden units of the deep learning model. The result for the calibration period (a, c) and the validation period (b, d) are shown separately

3.3 훈련 자료에 대한 모형의 정확도

딥러닝 모형과 같은 데이터 기반 모델은 학습에 활용된 자료의 양과 질에 따라 모형의 정확도가 크게 달라진다. 따라서 본 연구에서는 Table 2에 보인 입력자료의 시나리오에 따른 모형의 정확도를 살펴보았다. 모형의 검증에는 후반기(2009.1.1 ~ 2020.12.31)의 일유량 자료가 모든 시나리오에 대하여 동일하게 사용되었다.

Table 2.

The scenarios of the training data used to investigate the sensitivity of the deep learning model accuracy to the training data wetness and dryness

Scenario Name	Description
L-N	Train using the first n-year's data over the training period
D1	Train using the data of the driest year (1999) over the training period
W1	Train using the data of the wettest year (2001) over the training period
D2	Train using the data concatenating the driest 2 years (1999, 2003) over the training period
W2	Train using the data concatenating the wettest 2 years (2001, 2000) over the training period
D1W1	Train using the data concatenating the driest year (1999) and the wettest year (2001)
D2W2	Train using the data concatenating the driest 2 years (1999, 2003) and the wettest 2 years (2001, 2000)

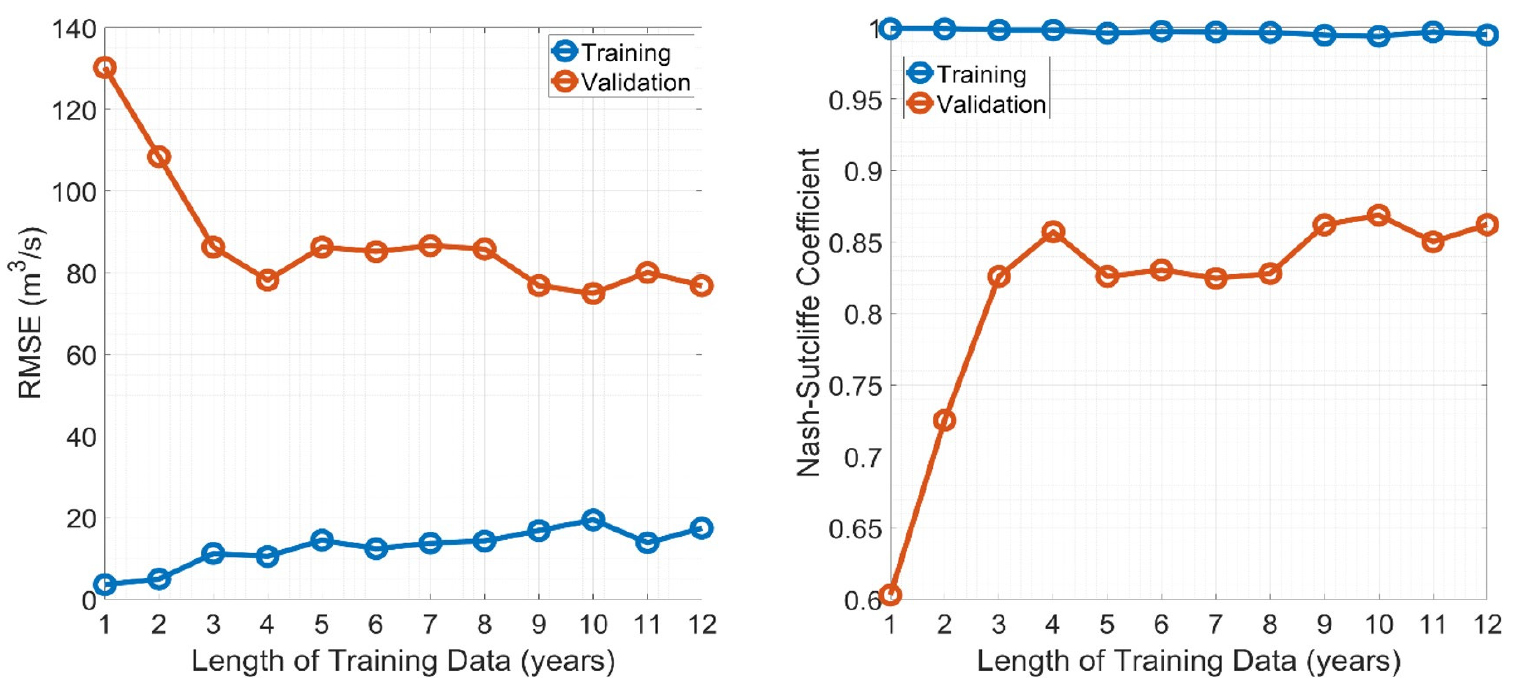
Fig. 7에 보인 두 그래프의 푸른 실선은 학습자료의 길이(1년-12년)에 따른 학습기간에 대한 모형의 RMSE와 NSE를 나타낸다. 학습기간에 대해서는 학습 자료의 길이에 상관없이 모든 시나리오에 대하여 0.99 이상의 NSE를 보여 완벽에 가까운 학습이 이루어진 것으로 나타났다. 다만, 학습자료의 길이가 늘어날수록 학습기간에 대한 RMSE는 꾸준히 증가하는 경향을 보였는데, 이는 학습자료가 길어질수록 홍수/가뭄에 해당하는 유량의 극한값을 향해 모형이 교정되며 평상시의 자료들에 대한 오차가 증가하기 때문으로 추측된다. 두 그래프의 붉은 실선은 검증기간에 대한 학습자료의 길이에 따른 모형의 RMSE와 NSE를 나타낸다. 학습자료의 길이가 길어질수록 모형의 성능이 대체적으로 개선되는 경향을 보였으며, 개선의 정도는 첫 4년 동안 두드러졌다. 학습자료의 길이가 4년을 초과하는 경우 검증기간에 대한 모형의 성능이 크게 개선되지는 않거나, 오히려 성능이 저하되는 경우도 발생하였다. 이는 태풍 루사(2002, 6년차)나 매미(2003, 7년차)와 같은 극한 홍수가 학습자료에 포함됨에 따른 모형의 편향 교정에 의한 문제로 추측된다.

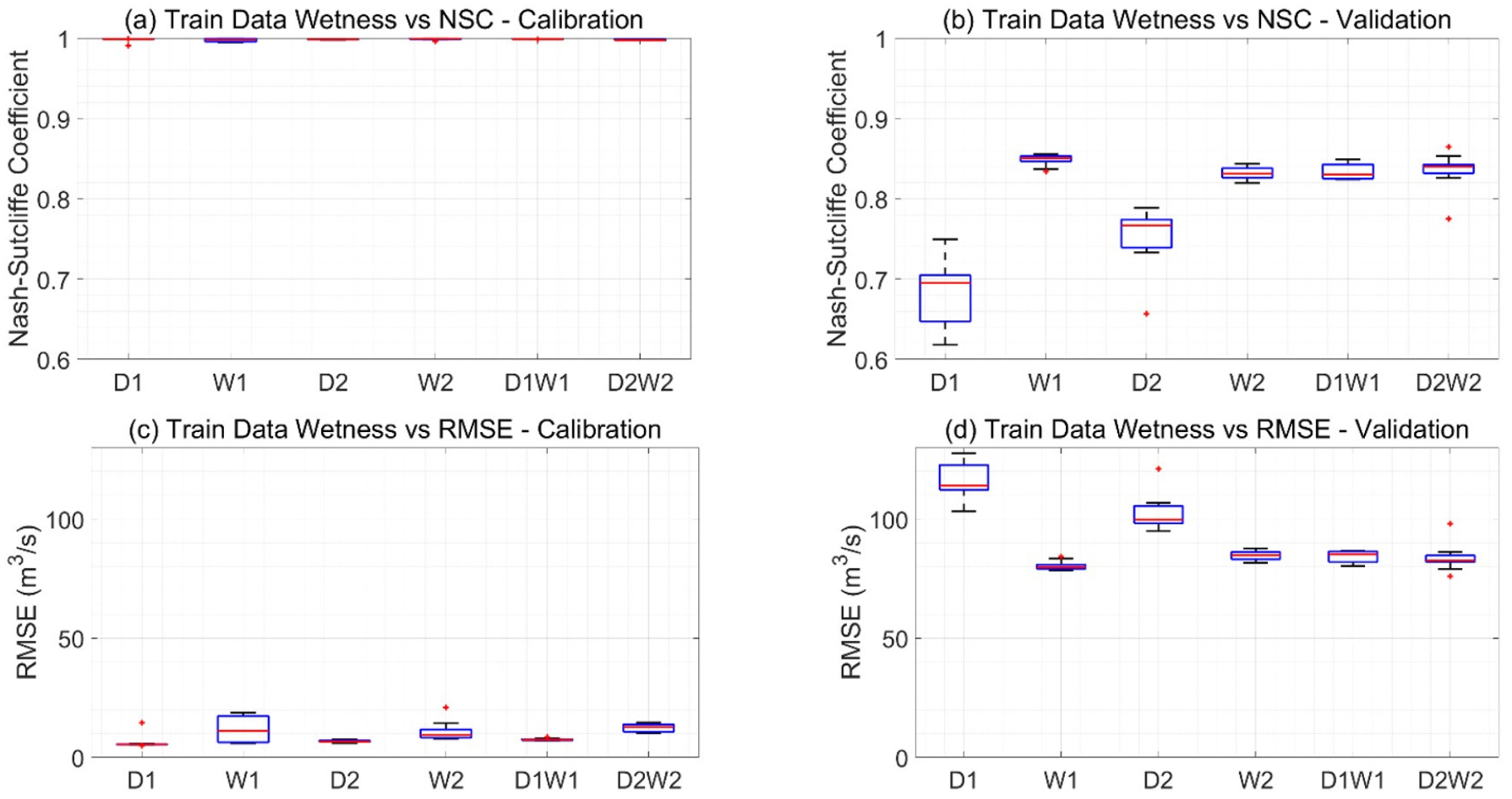
Fig. 8은 Table 1에 보인 입력자료의 다양한 Wetness/Dryness 시나리오에 따른 모형의 NSE (a, b)와 RMSE (c, d)를 보인다. 학습(a, c) 및 검증(b, d) 기간에 대한 결과를 따로 보였으며, 20회의 독립적인 학습-검증에 대한 결과를 박스플롯으로 보였다. Fig. 8(a)는 모든 시나리오에 대하여 학습기간의 NSE 가 0.99 내외의 매우 높은 값을 가지며 모형의 학습이 완벽에 가깝게 수행되었음을 보인다. Figs. 8(b) and 8(d)는 평균 유량이 가장 높았던 한 해(2001)의 자료만을 사용하여 학습하였을 때 가장 정확한 모형(평균 NSE=0.85, 평균 RMSE= 80.41 m³/s)이 구축되었음을 보인다. 이는 십 년 이상의 자료를 학습에 활용한 경우 보다 오히려 더 높은 값이다. 이러한 결과는 딥러닝의 학습에 반드시 방대한 양의 자료가 필요한 것이 아니며, 보통의 값과 극한의 값을 골고루 포함한 적은 양의 데이터로도 충분히 좋은 학습이 가능하다는 점을 의미한다.

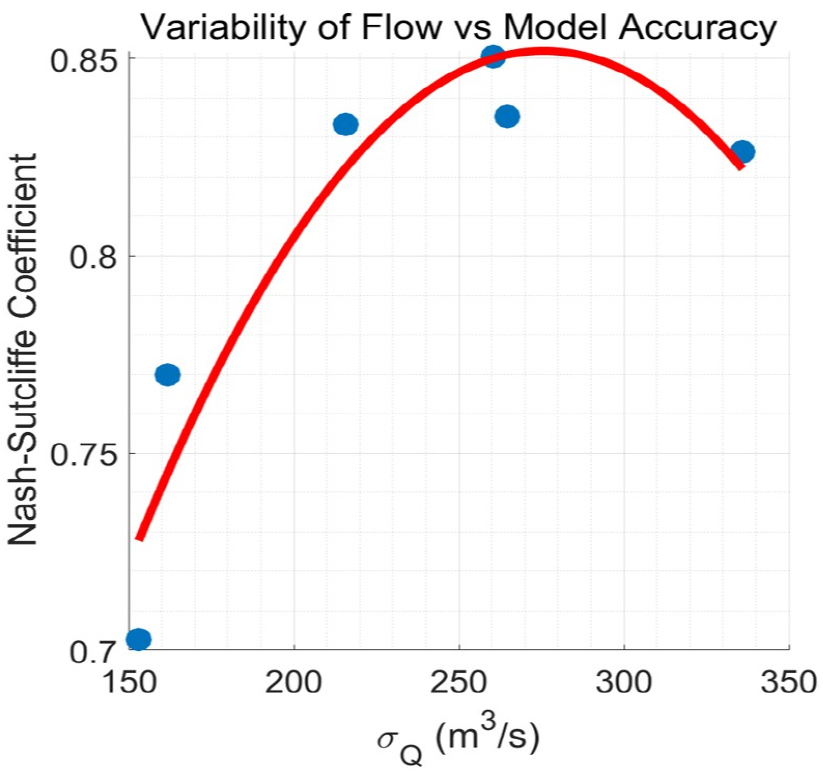
이러한 가정을 더욱 자세히 살펴보기 위해 각 시나리오에 대한 유량의 표준편차와 모형의 평균 정확도의 상관관계를 Fig. 9의 푸른색 점들로 보였다. 붉은 선은 이 점들의 2차(2^nd order) 회귀선이다.

학습자료의 변동성이 커질수록 모형의 성능이 점진적으로 개선되는 것을 볼 수 있다. 한편, 특정 값을 초과하며 다시 성능이 감소되는 추세 또한 관측되었는데, 이는 모형의 교정이 표준편차 증가의 주원인인 극한 값의 재현에 초점을 맞추어 진행되었기 때문으로 추측된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F7.jpg

Fig. 7.

(a) Root mean square error (RMSE) and (b) Nash-Sutcliffe Model Efficiency Coefficient (NSE) of the flow prediction model varying with the L-N scenarios (Table 1)

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F8.jpg

Fig. 8.

Root mean square error (RMSE) and Nash-Sutcliffe Model Efficiency Coefficient (NSE) of the flood prediction model varying with training data wetness scenarios (Table 1). The result for the calibration period (a, c) and the validation period (b, d) are shown separately

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F9.jpg

Fig. 9.

Relationship between the standard deviation of the flow discharge and the mean accuracy of the input data scenarios shown in Table 1

3.4 다양한 입력자료의 조합에 따른 모의 정확도

강수, 기온, 풍속 자료를 동시에 확보하기 어려운 경우가 많으므로, 본 연구에서는 강수, 강수-기온, 강수-풍속 자료만 획득이 가능한 경우를 가정하여 모의의 정확도를 살폈다. 또한, 토양수분의 간접적 지표로 활용되는 지난 5일간의 강수량을 추가적인 입력자료로 하여 모의의 정확도를 살폈다. Table 3에 본 연구에서 시도한 입력자료의 조합을 요약하였다.

Fig. 10에 Table 2에 보인 다양한 입력자료의 조합에 대한 NSE (a, b) 와 RMSE (c, d)를 학습(a, c)및 검증(b, d)기간으로 분류하여 박스플랏을 보였다. 모든 경우에 대하여 학습기간의 NSE는 0.99 내외로 완벽에 가까운 학습이 이루어졌으며(Fig. 10(a)), 검증기간의 결과는 NSE는 0.8 - 0.9 사이(Fig. 10(b)), RMSE는 60 - 95 m³/s (Fig. 10(d))사이로 크게 다르지 않았다. 이는 유량에 직접적인 영향을 미치는 강수자료가 모든 입력자료의 조합에 포함되어 있기 때문이다. 일평균 기온이나 일평균 풍속만을 입력자료로 활용한 경우, 검증기간의 NSE는 각각 -0.13과 -0.14로 매우 낮다는 점은 이러한 주장을 방증한다. 일강수, 일평균기온, 및 일평균풍속을 함께 입력자료로 활용한 경우 모형의 성능이 대체로 좋았으나, 가장 높은 성능은 일강수와 일평균기온을 입력자료를 활용한 모형에서 나타났다. 토양수분의 척도로 활용되는 지난 5일간의 강수량을 추가적인 입력자료로 활용한 경우, 뚜렷한 모의 정확도의 향상은 나타나지 않았다.

Table 3.

The scenarios of the training data used to investigate the sensitivity of the deep learning model accuracy to input data type

Scenario Name	Description
R	Train using the first 12 years of daily rainfall data
RT	Train using the first 12 years of daily rainfall and daily average temperature data
RH	Train using the first 12 years of daily rainfall and daily average wind speed data
RR5	Train using the first 12 years of daily rainfall and past 5-day rainfall data
RTH	Train using the first 12 years of daily rainfall, daily average temperature and daily average wind speed data
RTHR5	Train using the first 12 years of daily rainfall, daily average temperature, daily average wind speed data, and past 5-day rainfall data

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541005/images/kwra_54_10_05_F10.jpg

Fig. 10.

Root mean square error (RMSE) and Nash-Sutcliffe Model Efficiency Coefficient (NSE) of the flood prediction model varying with various combinations of input variables (Table 2). The result for the calibration period (a, c) and the validation period (b, d) are shown separately

4. 결 론

본 연구에서는 소양강댐 유역의 유입량을 추정하는 LSTM 기반의 딥러닝 모형을 구축한 후 다양한 입력자료의 시나리오에 대하여 모형의 성능을 살펴, 미계측 유역 등의 타지역에서 유사한 모형을 구축하는 경우 필요한 입력 자료의 종류와 양을 제시하고자 하였다. 그 결과는 다음과 같다:

1) 32개에서 64개의 다중은닉유닛을 가진 LSTM을 적용한 경우 모형의 성능이 가장 좋았다. 다중은닉유닛의 개수가 512개를 초과하는 모형의 경우 과적합으로 인한 문제가 나타났다.

2) 일강수량과 일유량은 반드시 수집되어야 한다. 다음 우선순위로 확보해야 하는 자료는 일평균 풍속, 일평균 기온이다. 둘 중 하나만 확보하여도 모형의 정확도를 미세하게 개선할 수 있다(NSE 개선도 0.05 내외).

3) 1년치의 학습자료 세트(일강수, 일유량, 일평균기온, 일평균풍속)만 확보하여도 검증기간 기준 NSE 0.63 - 0.85 내외의 정확도를 가진 일유량추정 딥러닝 모형을 구축할 수 있다.

4) 극한 유량이 포함된 한 해의 자료를 활용하여 학습하는 경우가 평유량만을 포함한 한 해의 자료를 활용하여 학습한 경우보다 월등히 좋은 성능을 보였다. 그 둘의 차이는 NSE = 0.2에 육박할 정도로 컸다. 관측 수행 기간 동안 극한 이벤트가 발생하지 않았다면 추후에 1-2개의 극한 홍수 이벤트에 해당하는 자료를 원수집자료에 함께 더해 학습한다면 모형의 성능향상을 기대할 수 있다.

5) 학습자료에 극한 이벤트들이 충분히 포함되어 있다면 5년 이상의 학습자료는 모형 성능 개선에 크게 기여하지 못한다.

이러한 결과를 원격탐사 기반의 강수(Hou et al., 2014; Han et al., 2021a), 기온(Tomlinson et al., 2011) 및 유량자료(Ahmad and Kim, 2019; Jung et al., 2014; Seo et al., 2018)와 결합하여 활용한다면, 개발도상국 등 관측자료가 풍부하지 않은 지역에서도 자료 수집에 큰 노력 없이 딥러닝 기반의 정확한 유량추정 모형을 개발할 수 있을 것이며, 이는 가용 수자원 추정, 기후변화에 따른 수자원 변동성 분석 등의 현안 해결에 도움이 될 수 있을 것이다.

Acknowledgements

이 논문은 2021년도 과학기술정보통신부 재원 한국연구재단의 이공분야기초연구사업(NRF-2021R1A2C2003471)과, 환경부 재원 환경산업기술원의 물관리연구사업(과제번호 127557)의 지원을 받았습니다.

References

Ahmad, W., and Kim, D. (2019). "Estimation of flow in various sizes of streams using the Sentinel-1 Synthetic Aperture Radar (SAR) data in Han River Basin, Korea." International Journal of Applied Earth Observation and Geoinformation, Vol. 83, 101930. 10.1016/j.jag.2019.101930

Bai, Y., Bezak, N., Zeng, B., Li, C., Sapač, K., and Zhang, J. (2021). "Daily runoff forecasting using a cascade long short-term memory model that considers different variables." Water Resources Management, Vol. 35, No. 4, pp. 1167-1181. 10.1007/s11269-020-02759-2

Boulmaiz, T., Guermoui, M., and Boutaghane, H. (2020). "Impact of training data size on the LSTM performances for rainfall-runoff modeling." Modeling Earth Systems and Environment, Vol. 6, pp. 2153-2164. 10.1007/s40808-020-00830-w

Bowes, B.D., Sadler, J.M., Morsy, M.M., Behl, M., and Goodall, J.L. (2019). "Forecasting groundwater table in a flood prone coastal city with long short-term memory and recurrent neural networks." Water, Vol. 11, No. 5, 1098. 10.3390/w11051098

Chen, Z., Zhu, Z., Jiang, H., and Sun, S. (2020). "Estimating daily reference evapotranspiration based on limited meteorological data using deep learning and classical machine learning methods." Journal of Hydrology, Vol. 591, 125286. 10.1016/j.jhydrol.2020.125286

Fang, K., and Shen, C. (2020). "Near-real-time forecast of satellite-based soil moisture using long short-term memory with an adaptive data integration kernel." Journal of Hydrometeorology, Vol. 21, No. 3, pp. 399-413. 10.1175/JHM-D-19-0169.1

Fang, K., Kifer, D., Lawson, K., and Shen, C. (2020). "Evaluating the potential and challenges of an uncertainty quantification method for long short‐term memory models for soil moisture predictions." Water Resources Research, Vol. 56, No. 12, e2020WR028095. 10.1029/2020WR028095

Han, J., Olivera, F., and Kim, D. (2021a). "An algorithm of spatial composition of hourly rainfall fields for improved high rainfall value estimation." KSCE Journal of Civil Engineering, Vol. 25, No. 1, pp. 356-368. 10.1007/s12205-020-0526-z

Han, H., Choi, C., Jung, J., and Kim, H.S. (2021b). "Application of sequence to sequence learning based LSTM model (LSTM-s2s) for forecasting dam inflow." Journal of Korea Water Resources Association, Vol. 54, No. 3, pp. 157-166.

Hochreiter, S., and Schmidhuber, J. (1997). "Long short-term memory." Neural Computation, Vol. 9, No. 8, pp. 1735-1780. 10.1162/neco.1997.9.8.17359377276

Hou, A.Y., Kakar, R.K., Neeck, S., Azarbarzin, A.A., Kummerow, C.D., Kojima, M., Oki, R., Nakamura, K., and Iguchi, T. (2014). "The global precipitation measurement mission." Bulletin of the American Meteorological Society, Vol. 95, No. 5, pp. 701-722. 10.1175/BAMS-D-13-00164.1

Hu, C., Wu, Q., Li, H., Jian, S., Li, N., and Lou, Z. (2018). "Deep learning with a long short-term memory networks approach for rainfall-runoff simulation." Water, Vol. 10, No. 11, 1543. 10.3390/w10111543

Idrees, M., Jehanzaib, M., Kim, D., Kim, T. (2021a). "Comprehensive evaluation of machine learning models for suspended sediment load inflow prediction in a reservoir." Stochastic Environmental Research and Risk Assessment, Vol. 35, pp. 1805-1823. doi: 10.1007/s00477-021-01982-6. 10.1007/s00477-021-01982-6

Idrees, B.M., Lee, J.-Y., Kim, D., Kim., T.-W. (2021b) "Complementary modeling approach for estimating sedimentation and hydraulic flushing parameters using artificial neural networks and RESCON₂ Model." KSCE Journal of Civil Engineering, Vol. 25, pp. 3766-3778. doi: 10.1007/s12205-021-1877-9 10.1007/s12205-021-1877-9

Jehanzaib, M., Idrees, M.B., Kim, D., and Kim, T. (2021). "Comprehensive evaluation of machine learning techniques for hydrological drought forecasting." Journal of Irrigation and Drainage Engineering, Vol. 147, No. 7. doi: 10.1061/(ASCE) IR.1943-4774.0001575 10.1061/(ASCE)IR.1943-4774.0001575

Jung, S., Cho, H., Kim, J., and Lee, G. (2018). "Prediction of water level in a tidal river using a deep-learning based LSTM model." Journal of Korea Water Resources Association, Vol. 51, No. 12, pp. 1207-1216.

Jung, Y., Kim, D., Kim, D., Kim, M., and Lee, S.O. (2014). "Simplified flood inundation mapping based on flood elevation-discharge rating curves using satellite images in gauged watersheds." Water, Vol. 6, No. 5, pp. 1280-1299. 10.3390/w6051280

Kratzert, F., Klotz, D., Brenner, C., Schulz, K., and Herrnegger, M. (2018). "Rainfall-unoff modelling using long short-term memory (LSTM) networks." Hydrology and Earth System Sciences, Vol. 22, No. 11, pp. 6005-6022. 10.5194/hess-22-6005-2018

Lee, G., Kim, D., Kwon, H., and Choi, E. (2019). "Estimation of maximum daily fresh snow accumulation using an artificial neural network model." Advances in Meteorology, Vol. 2019, 2709351. doi: 10.1155/2019/2709351 10.1155/2019/2709351

Lee, Y.O., Jo, J., and Hwang, J. (2017). "Application of deep neural network and generative adversarial network to industrial maintenance: A case study of induction motor fault detection." 2017 IEEE International Conference on big data (big data), IEEE, Boston, MA, U.S., pp. 3248-3253. doi: 10.1109/BigData.2017.8258307 10.1109/BigData.2017.8258307

Park, C., and Chung, I.M. (2020). "Evaluating the groundwater prediction using LSTM model." Journal of Korea Water Resources Association, Vol. 53, No. 4, pp. 273-283.

Seo, M., Kim, D., Ahmad, W., and Cha, J.H. (2018). "Estimation of stream flow discharge using the satellite synthetic aperture radar images at the mid to small size streams." Journal of Korea Water Resources Association, Vol. 51, No. 12, pp. 1181-1194.

Shi, X., Chen, Z., Wang, H., Yeung, D.Y., Wong, W.K., and Woo, W.C. (2015). "Convolutional LSTM network: A machine learning approach for precipitation nowcasting." Advances in Neural Information Processing Systems, pp. 802-810.

Shi, X., Gao, Z., Lausen, L., Wang, H., Yeung, D.Y., Wong, W.K., and Woo, W.C. (2017). "Deep learning for precipitation nowcasting: A benchmark and a new model." arXiv Preprint, arXiv:1706.3458.

Silva, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., Hubert, T., Baker, L., Lai, M., Bolton, A., Chen, Y., Lillicrap, T., Hui, F., Sifre, L., van den Driessche, G., Graepel, T. and Hassabis, D. (2017). "Mastering the game of go without human knowledge." Nature, Vol. 550, No. 7676, pp. 354-359. 10.1038/nature2427029052630

Sit, M., Demiray, B.Z., Xiang, Z., Ewing, G.J., Sermet, Y., and Demir, I. (2020). "A comprehensive review of deep learning applications in hydrology and water resources." Water Science and Technology, Vol. 82, No. 12, pp. 2635-2670. 10.2166/wst.2020.36933341760

Tomlinson, C.J., Chapman, L., Thornes, J.E., and Baker, C. (2011). "Remote sensing land surface temperature for meteorology and climatology: A review." Meteorological Applications, Vol. 18, No. 3, pp. 296-306. 10.1002/met.287

Yin, J., Deng, Z., Ines, A.V., Wu, J., and Rasu, E. (2020). "Forecast of short-erm daily reference evapotranspiration under limited meteorological variables using a hybrid bi-directional long short-term memory model (Bi-LSTM)." Agricultural Water Management, Vol. 242, 106386. 10.1016/j.agwat.2020.106386

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Data collection strategy for building rainfall-runoff LSTM model predicting daily runoff

ABSTRACT

MAIN

Fig. 1.

Study area: Soyang River watershed located at the north-eastern part of South Korea

Fig. 2.

Input and output data used to develop the inflow estimation deep learning model of this study. (a) Daily inflow (output), (b) Daily rainfall (input), (c) Daily average temperature (input), (d) Daily average wind speed (input)

Fig. 3.

Schematic of the deep learning model developed in this study. (a) Network diagram of the deep learning blocks. (b) LSTM block composed of multiple hidden blocks (source: https://towardsdatascience.com/animated-rnn-lstm-and-gru-ef124d06cf45, obtained on 2021.6.27)

(1)

(2)

(3)

Fig. 4.

Relative RMSE value between the observed and the simulated inflow improving as the training epoch increases

Fig. 5.

Time series of observed vs. simulated flow at Soyang Lake shown in (a) linear and (b) log scale. The shaded area is the calibration period. Scatter plot of observed (x) vs. simulated (y) flow shown in (c) linear and (d) log scale

Table 1.

The RMSE and the N-S coefficient of the deep learning model for the training and validation period

Fig. 6.

Root mean square error (RMSE) and Nash-Sutcliffe Model Efficiency Coefficient (NSE) of the flood prediction model varying with the number of the hidden units of the deep learning model. The result for the calibration period (a, c) and the validation period (b, d) are shown separately

Table 2.

The scenarios of the training data used to investigate the sensitivity of the deep learning model accuracy to the training data wetness and dryness

Fig. 7.

(a) Root mean square error (RMSE) and (b) Nash-Sutcliffe Model Efficiency Coefficient (NSE) of the flow prediction model varying with the L-N scenarios (Table 1)

Fig. 8.

Root mean square error (RMSE) and Nash-Sutcliffe Model Efficiency Coefficient (NSE) of the flood prediction model varying with training data wetness scenarios (Table 1). The result for the calibration period (a, c) and the validation period (b, d) are shown separately

Fig. 9.

Relationship between the standard deviation of the flow discharge and the mean accuracy of the input data scenarios shown in Table 1

Table 3.

The scenarios of the training data used to investigate the sensitivity of the deep learning model accuracy to input data type

Fig. 10.

Root mean square error (RMSE) and Nash-Sutcliffe Model Efficiency Coefficient (NSE) of the flood prediction model varying with various combinations of input variables (Table 2). The result for the calibration period (a, c) and the validation period (b, d) are shown separately

Acknowledgements

References