Two-dimensional numerical experiment considering cohort size and wood jam characteristic on driftwood

Taeun Kang; Chang-Lae Jang

doi:10.3741/JKWRA.2021.54.6.407

Preview

Research Article

Journal of Korea Water Resources Association. 30 June 2021. 407-418
https://doi.org/10.3741/JKWRA.2021.54.6.407

Two-dimensional numerical experiment considering cohort size and wood jam characteristic on driftwood

유목의 유입규모와 군집특성을 고려하는 2차원 수치모의 실험

Taeun Kang^a

Chang-Lae Jang^b^*

강 태운^a

장 창래^b^*

^aPostdoctoral researcher, Department of Civil Engineering, Korea National University of Transportation, Chungju, Korea

^bProfessor, Department of Civil Engineering, Korea National University of Transportation, Chungju, Korea

^a한국교통대학교 토목공학과 박사후연구원

^b한국교통대학교 토목공학과 교수

^{*Corresponding Author}

ABSTRACT

In this study, the two-dimensional flow model, Nays2DH, and driftwood dynamics model were combined to analyze the flow and driftwood behavior depending on the characteristics of the inflow of driftwood and the length of the driftwood stem. In particular, the Dashpot-spring model was added to the driftwood dynamics model to simulate the collision motion of the driftwood, and the wood jam characteristics by the collision of the driftwood were compared. As a result of the simulation, the pass rate of the obstacle section, the travel distance of wood jam, and the mean position of the wood pieces were respondent sensitively by the length of the driftwood stem, but the cohort size of the driftwood supply was insignificant excepting for the pass rate. Through this study, we could understand the interaction between hydraulic structures and driftwood, and through this, it is believed that it will be helpful in establishing a durable maintenance plan for hydraulic structures by predicting the transport and jam formation phenomena of driftwood in advance.

Keywords

Driftwood

Large wood

Driftwood modelling

Driftwood dynamics model

Wood jam

Dashpot-spring model

본 연구에서는 유목의 유입량의 특성과 유목줄기의 길이에 따른 하천흐름과 유목거동을 분석하기 위해 2차원 흐름모형인 Nays2DH와 유목동역학모형을 결합하고 이를 활용하여 장애물 근처에서의 유목의 군집특성과 거동을 분석하였다. 또한 유목의 충돌거동을 모의하기 위해 유목동역학모형에 Dashpot-spring 모형을 추가하여 유목의 충돌에 따른 군집특성도 비교하였다. 모의결과 유목줄기의 길이에 따라 장애물구간의 통과율, 유목의 군집이송, 유목들의 평균위치가 민감하게 반응하였고 유목의 유입규모에 대해서는 통과율 이외에는 미미한 반응을 나타냈다. 본 연구를 통해 수공구조물과 유목의 상호작용을 이해할 수 있었으며 이를 통해 유목의 이송과 군집현상 등을 사전에 예측함으로써 수공구조물의 내구성 유지방안 구축에 도움이 될 것으로 사료된다.

키워드

유목

거목

유목모델링

유목동역학모형

유목군집

MAIN

1. 서 론
2. 흐름모형과 유목동역학모형
2.1 흐름모형의 지배방정식
2.2 유목동역학모형(Driftwood dynamics model)의 지배방정식
2.3 Dashpot-spring 충돌모형
3. 수치실험 계산조건
4. 유목의 유입규모와 군집특성에 대한 수치실험
4.1 모형의 검보정
4.2 수치실험 시나리오
4.3 수치실험 결과 및 고찰
5. 결 론

1. 서 론

최근 기후변화로 인해 예측이 어려운 국지성 호우가 빈번하게 발생하고 있으며 이로 인하여 인명 및 재산피해가 해매다 증가하고 있는 실정이다. 더군다나, 국지성 호우는 대량의 홍수를 일으키고 산사태와 제방붕괴를 야기할 수 있다. 또한, 산지나 하천에서 발생한 홍수로 말미암아 인근의 초목과 식생들로부터 유목(driftwood)이 발생하기도 한다.

유목은 대체적으로 견고하며, 큰 규모의 체적과 질량을 가지고 있어, 홍수와 함께 떠내려 오게 되면 수류의 운동에너지를 증폭시키게 되며, 수공구조물과 주택가옥 등에 충돌하게 되면 큰 손상을 주기도 한다. 또한 유목이 수공구조물 인근 하상에 군집하면 통수능을 저하시키기도 하며 식생효과와 마찬가지로 유목주변으로 유속이 증가(Kang and Kimura, 2018)하면서 세굴현상이 발생하게 되는데, 이는 하상저하를 일으키며 수공구조물의 안정성에 지속적으로 피해를 줄 수 있다.

이미 일본과 유럽 등의 국가에서는 유목거동과 하천유역의 상호작용에 대해 많은 관심을 기울이고 있으며 이를 위해 활발한 학술적 교류와 연구 활동을 수행 중이다(Swanson et al., 2020). 특히, 일본의 경우, 하천유역의 경사가 급하기 때문에 홍수발생시 산사태가 빈번하게 일어나고 있으며 그에 따라 대량의 유목들이 하천으로 유입되어 하천의 수공구조물과 주거지역에 심각한 피해를 주고 있다고 보고되고 있다(Kang et al., 2018).

국내의 유목에 대한 피해는 구체적으로 문서화 된 경우가 국외보다는 드물며, Choi et al. (2003)의 연구에 의하면 2001년에 집중호우로 인한 중북부 지역의 21개 피해 교량 중 62%가 부유잡목에 의한 영향이 직간접적으로 피해원인을 제공한 것으로 조사되었다. 또한, 2020년에는 수 십 차례의 태풍과 국지성 호우로 인해 소하천의 교량붕괴 피해가 발생하였으며 그 원인 중에 하나로 유목의 영향을 지적하기도 하였다. 유목들이 교각에 충격을 주면서 흐름방향으로 외력을 증가시켰고 군집된 유목들이 다른 유목들을 연쇄적으로 포착하는 동시에 흐름을 방해하여 수위상승을 야기하고 유목주변으로 세굴을 발생시켜 교량의 붕괴를 촉진한 것으로 보여진다(Fig. 1).

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540605/images/kwra_54_06_05_F1.jpg

Fig. 1.

Bridge collapse and deposition of driftwood around bridge piers (KBS news, 2020).

이러한 상황을 예측하고 대응하고자 하천과 유목의 상호작용 및 물리적 거동에 대한 연구들이 활발하게 수행되어 왔다. 현재는 유목의 2차원 및 3차원 거동을 모의할 수 있는 수치해석모형(e.g., Ruiz-Villanueva et al., 2014; Kimura, 2018; Kang and Kimura, 2018; Kang et al., 2020a, 2020b; Ruiz-Villanueva et al., 2020)이 개발되었고 수리실험(Kang and Kimura, 2018)과 실제하천적용(Kang et al., 2020b; Kimura et al., 2020) 등을 통해 모형의 재현성과 실무적 검증을 활발히 논의하고 있다.

유목의 거동에 관한 대표적인 연구로는 Braudrick, et al. (1997)과 Braudrick and Grant (2000)가 있다. 이 연구들에서는 유목의 형태를 실린더(cylinder)로 가정하여 이에 상응하는 유목의 부력과 뿌리효과(rootwad effect) 등을 고려한 물리적 거동을 수학적으로 도출하였다. 또한, 실내실험 및 관측을 통해 유목의 거동에 따른 하천의 흐름 및 하상변동을 분석하였다. 이를 기반으로 수치해석의 측면에서는 Ruiz-Villanueva et al. (2014)가 2차원 수심적분 흐름모형에 유목거동모형을 결합하여 수리실험과 비교검증 하였고 Ruiz-Villanueva et al. (2020)가 실제하천을 대상으로 하는 유목의 거동과 군집특성을 실내실험과 수치해석을 통해 분석하였다.

또 다른 수치해석 연구인 Kang and Kimura (2018)의 경우에는 Kimura (2018)가 개발한 입자법기반의 유목모형을 하천흐름 계산페키지인 iRIC (2021) 소프트웨어의 Nays2DH (Shimizu et al., 2014)에 결합하였다. 또한 유목의 뿌리효과 및 유목의 부력과 중량으로 인한 유목운동의 임계흘수(critical draft for wood motion, CDM) 계산을 통해 유목의 부유(floating)뿐만 아니라 미끄러짐(sliding)과 퇴적(deposition), 구름운동(rolling motion)에 대해서도 재현될 수 있도록 수치적 모듈을 추가하였으며 이를 수리실험과 비교하여 검증하였다(Kang and Kimura, 2018). 더 나아가 Kang et al. (2020b)의 경우 Bertoldi et al. (2014)의 유목거동 수리실험을 재현하여 모형의 민감도와 정확도 검증을 수행하였다.

최근에는 3차원 흐름상에서의 유목거동을 수치모의하기도 하였다. Kimura and Kitazono (2020)의 경우에는 RANS (Reynolds-averaged Navier-Stokes equations) 흐름모형에 2차원 유목동역학모형(Kang and Kimura, 2018)과 Dashpot-spring 모형을 결합하여 유목의 충돌거동까지 고려하는 실험 및 수치해석을 수행하였다.

전술한 연구들을 종합해보면 유목의 거동과 군집특성을 연구한 경우에는 세부적인 유목의 유입량과 유목의 충돌을 고려하지 않은 것으로 판단된다. 유목의 시간별 유입량의 경우에는 하천에 큰 영향을 미칠 수 있다(Manners and Doyle, 2008). 유목의 총유입량이 같더라도 시간별 유목의 유입량에 따라 유목의 퇴적이 달라질 수 있으며 이는 흐름과 하상변동에도 영향을 줄 수 있다(Kang, 2018; Kang et al., 2020b). 심지어 극한 상황에서는 수공구조물에도 손상을 줄 수 있을 것으로 판단된다. 더군다나, 유목의 군집형성과 관련하여 유목간의 충돌로 인한 상호작용이 필수적으로 고려되어야 할 것으로 판단된다.

따라서 본 연구는 Kang and Kimura (2018)에서 검증된 실내실험과 수치해석조건을 바탕으로 유목의 크기와 유입량에 따른 장애물 근처에서의 유목군집거동을 수치모의하여 그 결과들을 통해 장애물 통과량(pass rate), 군집이송거리(wood jam travel distance), 유목평균위치(mean position of wood pieces)를 비교분석 하였다. 또한 유목충돌의 수치적 효과를 비교해 보기 위해 Dashpot-spring 모형을 활용하여 모의를 수행하여 군집특성과 통과율을 비교 분석하였다. 이를 위해 2차원 흐름모형인 Nays2DH와 Kang et al. (2020b)이 개발한 2차원 유목동역학모형(driftwood dynamics model)을 활용하였다. 추가적으로, 본 연구는 Kang and Kimura (2018)에서는 고려하지 않았던 수치적 충돌현상을 재현하였다. Kang and Kimura (2018)에서는 수치적 충돌현상을 고려하지 않았기 때문에 수치모의 결과에서 유목간의 겹침현상이 발생하였고 이는 실제 자연현상에서는 나타날 수 없는 현상이므로 개선해야할 필요가 있다.

따라서 본 연구에서는 이러한 문제를 개선하여 수치적 충돌을 모의조건의 측면에서 고려하였고 이를 통해 보다 물리적인 유목의 거동을 수치모의 하였으며 충돌과 비충돌의 수치모의 결과를 비교하였다.

2. 흐름모형과 유목동역학모형

2.1 흐름모형의 지배방정식

2차원 모형은 천수방정식을 기반으로 하는 Nays2DH를 활용했으며 여기서 본 모형은 실제하도의 곡선을 포착하기 위해 곡선좌표계(generalized curvilinear coordinates)가 적용된다. Nays2DH의 지배방정식은 아래와 같다.

연속방정식:

(1)

\frac{\partial}{\partial t} (\frac{h}{J}) + \frac{\partial}{\partial ξ} (\frac{h U_{ξ}}{J}) + \frac{\partial}{\partial η} (\frac{h U_{η}}{J}) = 0

운동량 방정식:

(2)

\frac{\partial U_{ξ}}{\partial t} + U_{ξ} \frac{\partial U_{ξ}}{\partial ξ} + U_{η} \frac{\partial U_{ξ}}{\partial η} + α_{1} U_{ξ} U_{ξ} + α_{2} U_{ξ} U_{η} + α_{3} U_{η} U_{η} = - g [(ξ_{x}^{2} + ξ_{y}^{2}) \frac{\partial H}{\partial ξ} + (ξ_{x} η_{x} + ξ_{y} η_{y}) \frac{\partial H}{\partial η}] - C_{f} \frac{U_{ξ}}{h J} \sqrt{{(η_{y} U_{ξ} - ξ_{y} U_{η})}^{2} + {(- η_{x} U_{ξ} + ξ_{x} U_{ξ})}^{2}} - F_{d w} + D_{ξ}

(3)

\frac{\partial U_{η}}{\partial t} + U_{ξ} \frac{\partial U_{η}}{\partial ξ} + U_{η} \frac{\partial U_{η}}{\partial η} + α_{1} U_{ξ} U_{ξ} + α_{2} U_{ξ} U_{η} + α_{3} U_{η} U_{η} = - g [(ξ_{x} η_{x} + ξ_{y} η_{y}) \frac{\partial H}{\partial ξ} + (η_{x}^{2} + η_{y}^{2}) \frac{\partial H}{\partial η}] - C_{f} \frac{U_{η}}{h J} \sqrt{{(η_{y} U_{ξ} - ξ_{y} U_{η})}^{2} + {(- η_{x} U_{ξ} + ξ_{x} U_{η})}^{2}} - F_{d w} + D_{η}

여기서, x와 y는 각각 직교좌표계의 성분, $ξ$ 와 $η$ 는 각각 곡선좌표계의 성분이다. t는 시간, g는 중력가속도(= 9.81 m/s²), H는 수위(m), h는 수심(m)이다. $D_{η}, D_{ξ}$ 는 각각 곡선좌표계에서 $η$ 와 $ξ$ 방향의 난류점성항이다. $F_{d w}$ 는 유목에 의해 흐름에 작용하는 항력벡터이다. Eqs.(2) and (3)에서 C_f는 하상마찰계수(riverbed shear coefficient)이며 매닝계수(Manning coefficient)를 이용하여 표현(Eq.(4))된다.

(4)

C_{f} = \frac{g n_{m}^{2}}{h^{1 / 3}}

본 모형은 물의 흐름방향에 의존적으로 발생하는 하상전단응력을 계산하기 위해 시간에 대하여 음해법을 이용하고 있다. 또한 음해법이라 하더라도 하상고의 형태가 완만한 곡선이 아닌 변곡 또는 급변하는 경우, 수치진동이 발생하기 쉽기 때문에 본 모형은 이를 저감하기 위해 유동에 따른 유속벡터의 재산정 과정을 수행한다. 또한 본 모형은 압력은 격자내부에서, 유속은 격자의 경계면에서 계산되는 엇갈린 격자(staggered grid)를 이용하고 있으며 연속방정식(Eq. (1))에서 각 격자의 body force를 프아송(Poisson)방정식에 기반하여 축차가속완화법(successive over relaxation)으로 계산한다. 이송항에 대해서는 시간과 공간적으로 양해법에 기반하는 3차 정도의 TVD-MUSCL (Total variation diminishing-monotonic Upwind Scheme for Conservation Laws)기법을 활용하고 있으며 난류는 Zero-equation 모형을 이용한다. 결과적으로, 본 모형에서는 반음해법의 계산과정을 통해 양해법보다 큰 시간간격(0.6 < CFL < 1.5)에서도 수치모의를 안정적으로 수행할 수 있으며 해석결과의 정확성까지 확보하게 된다. 또한 병렬처리를 위해 OpenMP를 이용하여 계산 시간을 저감하고 있다. 흐름에 관한 세부적인 내용은 Shimizu et al. (2014), Lee and Jang (2018), Kang and Jang (2020)에 기술되어있다.

2.2 유목동역학모형(Driftwood dynamics model)의 지배방정식

유목동역학모형은 입자법(particle method)을 기초로 한다. 본 연구에서는 여러 입자뭉치를 하나의 군체로 고려하며 개별군체의 이송 및 회전 등의 거동과 군체끼리의 세부적인 충돌거동을 고려할 수 있는 Discrete element method (DEM)를 활용하였다(Gotoh et al., 2013). 그리고 이 모형을 Euler (또는 격자) 기반 모형인 Nays2DH에 결합하였다. 이는 격자법을 이용하면 물의 압력계산에서 높은 정확도를 확보하게 되며, 하천규모와 같은 큰 영역에서의 흐름계산을 입자법으로 계산할 때보다 적은 시간으로 수행할 수 있기 때문이다. 또한, 입자법을 이용하면 유목의 이송운동에서 높은 정확도를 확보 할 수 있기 때문에 격자법과 입자법을 적절히 결합하게 되면 하천수위와 유목의 거동에 대해 높은 정확도와 효율적인 계산시간을 얻을 수 있다(Kang et al., 2019).

유목동역학모형에서는 유목을 실린더형태로 가정하게 되며 이를 고려하는 이송계산은 아래와 같다(Kang and Kimura, 2018).

1) 매 시간간격 마다 흐름모형으로 수심평균유속과 수위를 계산한다.

2) 각각의 유목입자를 둘러싼 4개의 격자점의 수심평균유속과 수위의 값을 쌍선보간법(bilinear interpolation)을 이용하여 유목위치의 수심평균유속과 수위 등의 값들을 보간산정한다.

3) 유목위치의 보간된 수심과 수심평균유속을 고려하여 유목의 침수체적, 침수단면적, 부력, 항력, 유목의 하상마찰력 등을 계산한다.

4) 유목입자들의 개별적인 속도를 보간된 값을 이용하여 계산하고 각 유목마다 입자들끼리의 값을 평균화하여 각 유목의 속도와 이송거리를 계산한다.

5) 유목의 관성력과 유목입자들의 위치를 통해 무게중심을 계산한 후, 유목입자들의 속도벡터를 고려하여 유목의 회전각속도를 계산한다.

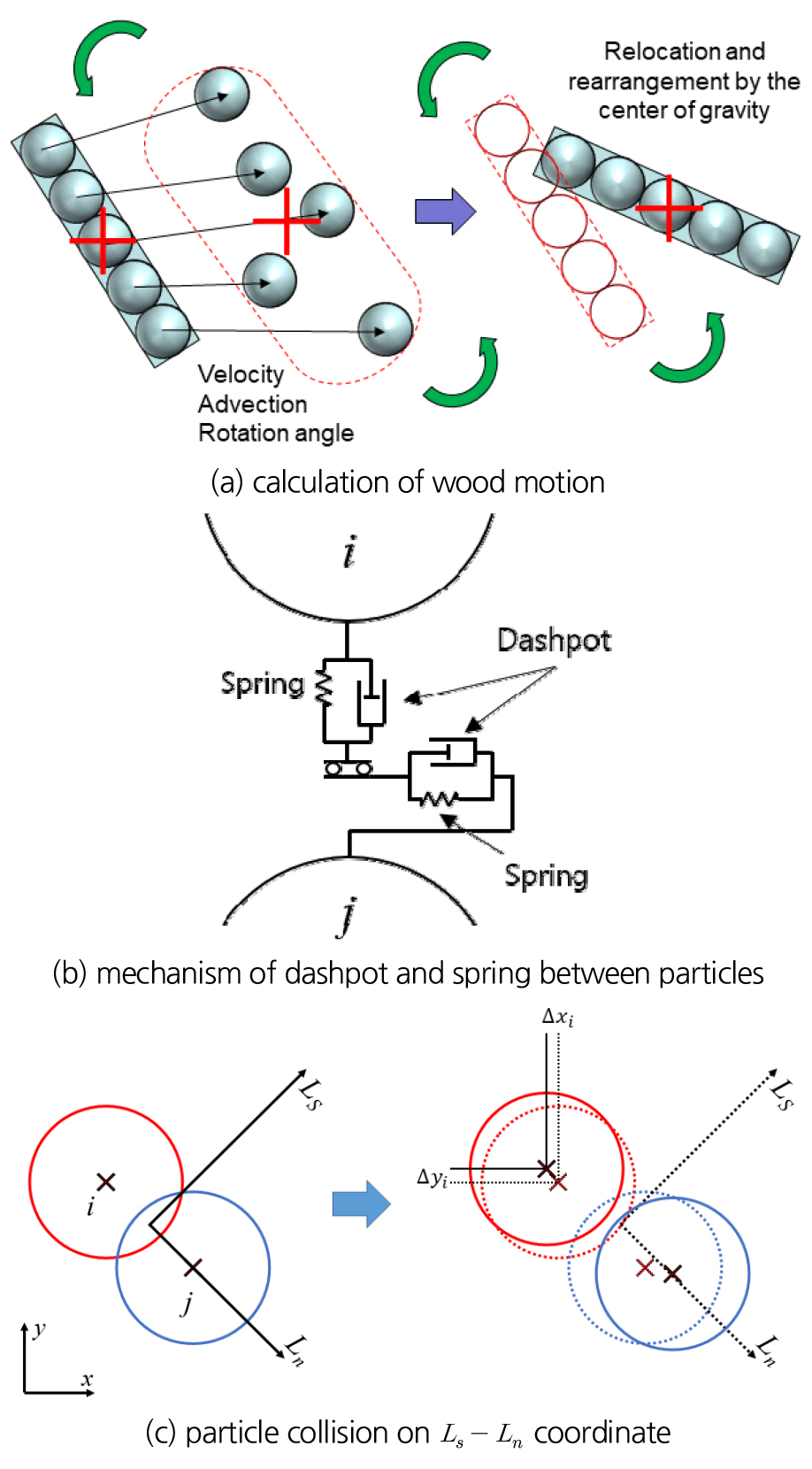
6) 유목의 회전각속도를 계산 후, 회전각속도를 바탕으로 유목의 변화된 줄기각도를 산정하고 유목길이, 무게중심, 산정된 줄기각도를 고려하여 입자들을 재배열한다(Fig. 2(a)).

본 모형에서 유목의 거동을 위해 이용하는 기본적인 입자법 방정식은 아래와 같다(Kang et al., 2020b).

(5)

σ_{d} A_{t} d_{p}^{3} \frac{d u_{p}}{d t} = F_{d} + F_{w a} + F_{a m} + F_{i m p} - F_{b e d}

Eq. (5)는 유목의 CDM에 따라 하상마찰력의 적용여부가 결정되는 것을 나타내고 있으며 여기서, 좌변은 유목입자의 체적력이고 우변은 유목입자에 작용하는 외력( $F_{d}, F_{w a}, F_{a m}, F_{b e d}, F_{i m p}$ )이며 이들 외력은 Eqs. (5a) ~ (5d)로 정의된다.

(5a)

F_{d} = \frac{1}{2} C_{D p} ρ λ_{A - s u b} A_{p} |u - u_{p}| (u - u_{p})

(5b)

F_{w a} = ρ λ_{V - s u b} A_{t} d_{p}^{3} (\frac{d u}{d t})

(5c)

F_{a m} = C_{M} ρ λ_{V - s u b} A_{t} d_{p}^{3} (\frac{d u}{d t} - \frac{d u_{p}}{d t})

(5d)

F_{b e d} = \{\begin{cases} 0, h_{d} > CDM \\ μ A_{t} d_{p}^{3} (σ_{d} - λ_{V - s u b} ρ) g, h_{d} \leq CDM \end{cases}

여기서, $σ_{d}$ 는 유목의 밀도, $A_{t}$ 는 물의 흐름과 유목입자간의 상대속도 벡터에 대한 입자의 투영면적(projection area), $ρ$ 는 물의 밀도(= 1000 kg/m³), C_M은 구형의 유목입자와 외접하는 통제체적(control volume)에 대한 질량계수(본 모형에서는 0.5를 기본으로 함), C_Dp는 물의 흐름에 영향을 받는 유목입자와 물의 레이놀즈수(Reynolds number)를 고려하는 항력계수(유목입자의 크기와 속도에 의해 변함), A_t는 2차원 원주율계수( $π$ /4), $μ$ 는 유목과 하상간의 마찰계수, h_d는 유목의 흘수(draft), CDM은 유목이 부력에 의해 부유하기 직전의 임계흘수(critical draft for wood motion), d_p는 유목입자의 직경(m), $u$ 는 유속벡터, $u_{p}$ 는 유목입자의 속도벡터, $λ_{V - s u b}$ 는 유목입자의 전체체적(volume)과 침수체적(submerged volume)의 비, $λ_{A - s u b}$ 는 유목입자의 투영면적(projection area)과 침수된 투영면적(submerged projection area)의 비, $F_{d}$ 는 유목입자의 투명면적(유속벡터와 유목입자의 속도벡터 의해 변화 됨)에 작용하는 물의 항력, $F_{w a}$ 는 유목의 침수체적 만큼의 물의 체적력, $F_{a m}$ 는 유목입자를 둘러싸고 있는 유체의 추가 체적력(유목입자가 실제로는 실린더 형태임을 고려해야함), $F_{b e d}$ 는 유목입자가 하상에 접촉했을 때의 마찰력, $F_{i m p}$ 는 유목입자간의 충돌력이다. 참고로 유목의 이송은 물의 흐름 따라 지배적으로 발생하기 때문에 본 연구에서는 유목의 속도는 물의 흐름속도를 초과하지 않는 것으로 가정하였다(Ruiz-Villanueva et al., 2020).

본 모형은 유목의 2차원적 수평회전만 재현한다. 이를 곡선좌표계상에서 방정식으로 표현하기 위해서는 매우 복잡하다(Kimura and Kitazono, 2020). 따라서 본 연구에서는 수평회전에 대한 직교좌표계상의 방정식을 Eq. (6)과 같이 표현하였다.

(6)

R = \frac{1}{I} \sum_{n_{p} = 1}^{n_{p m a x}} \{\cos θ (a_{p x}^{n_{p}} L_{x}^{n_{p}}) - \sin θ (a_{p y}^{n_{p}} L_{y}^{n_{p}})\}

여기서 R은 유목의 회전가속도, I는 유목의 관성모멘트, n_p는 유목을 구성하는 입자의 일련번호(serial number), n_pmax는 유목을 구성하는 입자의 개수, $a_{p x}^{n}$ 과 $a_{p y}^{n}$ 는 각각 x와 y방향의 이송가속도, $L_{x}^{n}, L_{y}^{n}$ 는 각각 x와 y방향의 유목의 무게중심과 입자위치(입자중심부) 사이의 거리, $θ$ 는 직교좌표에서 수평축(x축)과 유목줄기 사이의 각도이다. 세부적인 내용은 Kimura and Kitazono (2020)에서 참조할 수 있다.

본 모형에서는 기본적으로 입자의 이송에 대해 시간과 공간적으로 1차 정확도인 전방오일러(Forward Euler)차분법을 이용하고 있으며 이 연구에서는 시간과 공간적으로 2차 정확도를 가지는 Adams-Bashforth 차분법을 고려하였다.

또한 본 연구에서는 흐름과 유목거동의 상호작용을 고려하였다. 여기서 유목이 흐름에 영향을 주지 않으면 one-way 형식이라 하며, 유목과 흐름이 상호작용하게 되면 two-way 형식이라 한다. 본 연구에서는 two-way 형식을 고려하였으며 유목이 흐름에 작용하는 항력은 아래의 식과 같다. 이는 운동량방정식(Eqs. (2) and (3))에서 계산된다.

(7)

F_{d w} = - \frac{1}{2} C_{D p w} \frac{1}{h A_{c e l l}} \sum_{n = 1}^{N_{c e l l}} A_{p n} |u^{n} - u_{p}^{n}| (u^{n} - u_{p}^{n})

여기서 C_Dpw는 물의 흐름에 대한 유목의 항력계수(구형=1.0)이다. A_cell은 각 격자의 넓이(m²)이며 A_pn은 유목입자의 수평면적(m²)이다. N_cell은 A_cell에서의 유목입자의 총 개수이며 n은 해당 셀(격자내부)에 위치하는 유목입자들의 일련번호를 나타낸다.

본 유목동역학모형에 대한 개발과 검증에 대해서는 Kimura (2018), Kang (2018), Kang and Kimura (2018), Kang et al., (2020b), Kimura and Kitazono (2020) 등을 통해 세부사항을 참고할 수 있다.

2.3 Dashpot-spring 충돌모형

Fig. 2(b)는 Dashpot-spring 모형의 모식도를 보여준다. dashpot은 입자간의 충돌로 인해 댐퍼(damper)가 작용하여 속도가 줄어드는 물리체계이며 spring은 입자의 탄성으로 인해 상호적으로 밀어내는 물리체계이다. 본 연구에서는 유목간의 충돌을 고려하기 위해 유목입자를 탄성력을 가지는 고체로 가정하였으며 이에 따른 탄성충돌력을 계산하기 위해 Dashpot-spring 모형을 유목동역학모형에 결합하였다(Gotoh et al., 2013); Kimura and Kitazono, 2020). 여기서, 유목간의 충돌력( $F_{i m p}$ )은 유목입자간의 접촉거리와 탄성계수(Young’s modulus)에 따라 기하급수적으로 증가하게 되며 안정적인 계산을 위해서는 매우 작은 시간간격을 요구하게 된다. 따라서 본 연구에서는 유목의 거동을 계산하는 단계에서는 흐름계산( $∆ t$ = 0.01 sec)보다 더 작은 시간간격( $∆ t$ = 0.0001 sec)을 이용하여 유목거동을 계산하였다.

Dashpot-spring모형의 경우 많은 연구자들에 의해 널리 활용되고 있으며 직교좌표계와 지역좌표계(L_s ‒ L_n)를 기준(Fig. 2(c))하면 지배방정식은 아래와 같다.

(8)

[\begin{matrix} ∆ L_{n}^{i, j} \\ ∆ L_{s}^{i, j} \end{matrix}] = [T_{G L}] [\begin{matrix} ∆ x^{i} - ∆ x^{j} \\ ∆ y^{i} - ∆ y^{j} \end{matrix}]

여기서 유목의 충돌지점을 기준하여 L_s는 충돌운동 법선방향(tangential direction), L_n는 충돌운동 반작용방향(normal direction) 방향이다. L_s방향과 L_n방향으로 지역좌표계를 기준하면 $∆ L_{s}^{i, j}$ 와 $∆ L_{n}^{i, j}$ 는 $∆ t$ 시간 동안의 유목충돌에 의한 이송거리, T_GL은 직교좌표계와 지역좌표계의 변환메트릭스(transformation matrix)이며 i와 j는 상호충돌한 유목입자의 인덱스이다. 본 연구에서는 충돌로 인한 입자의 법선방향 회전은 무시한다.

Dashpot-spring 운동은 유목입자간의의 상대위치와 상대속도 및 입자의 탄성력에 의해 결정되며 이에 대한 충돌력은 지역좌표계를 기준으로 아래와 같이 결정된다.

(8a)

\{\begin{cases} F_{L_{s}} (t) = e_{L_{s}}^{n e w} (t) + p d_{L_{s}} (t) \\ e_{L_{s}}^{n e w} (t) = e_{L_{s}} (t - ∆ t) k s_{L_{s}} ∆ L_{s}^{i, j} \\ p d_{L_{s}} (t) = c_{L_{s}} \frac{∆ L_{s}^{i, j}}{∆ t} \end{cases}

(8b)

\{\begin{cases} F_{L_{n}} (t) = e_{L_{n}}^{n e w} (t) + p d_{L_{n}} (t) \\ e_{L_{n}}^{n e w} (t) = e_{L_{n}} (t - ∆ t) k s_{L_{n}} ∆ L_{n}^{i, j} \\ p d_{L_{n}} (t) = c_{L_{n}} \frac{∆ L_{n}^{i, j}}{∆ t} \end{cases}

여기서 $e_{L_{s}}$ 과 $e_{L_{n}}$ 는 spring force, $p d_{L_{s}}$ 과 $p d_{L_{n}}$ 는 dashpot force, $k s_{L_{s}}$ 과 $k s_{L_{n}}$ 는 spring 상수이다. 또한 유목입자들 간의 미끄러짐 운동은 아래와 같이 결정된다.

(8c)

F_{L_{s}} (t) = μ sign \{e_{L_{n}}^{n e w} (t), e_{L_{s}}^{n e w} (t)\}, w h e n |e_{L_{s}}^{n e w} (t)| > μ e_{L_{n}}^{n e w} (t)

여기서 $μ$ 는 반발계수(= 0.8)이다.

결과적으로 유목입자가 받는 충돌력은 T_GL을 활용하여 직교좌표계에서 아래와 같이 표현된다.

(8d)

[\begin{matrix} F_{p x}^{i} \\ F_{p y}^{i} \end{matrix}] = - \sum_{} {[T_{G L}]}^{- 1} {[\begin{matrix} F_{L_{n}} \\ F_{L_{s}} \end{matrix}]}^{i, j}

여기서 F_px, F_py는 직교좌표계상에서의 유목입자의 충돌가속도이다. Eq. (5)의 $F_{i m p}$ 는 F_px, F_py를 속도벡터로 표현한 값이다. 더 세부적인 내용은 Gotoh et al. (2013), Kang et al. (2019), Kimura and Kitazono (2020)에서 확인 할 수 있다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540605/images/kwra_54_06_05_F2.jpg

Fig. 2.

Schematic diagram for calculation of driftwood motion

3. 수치실험 계산조건

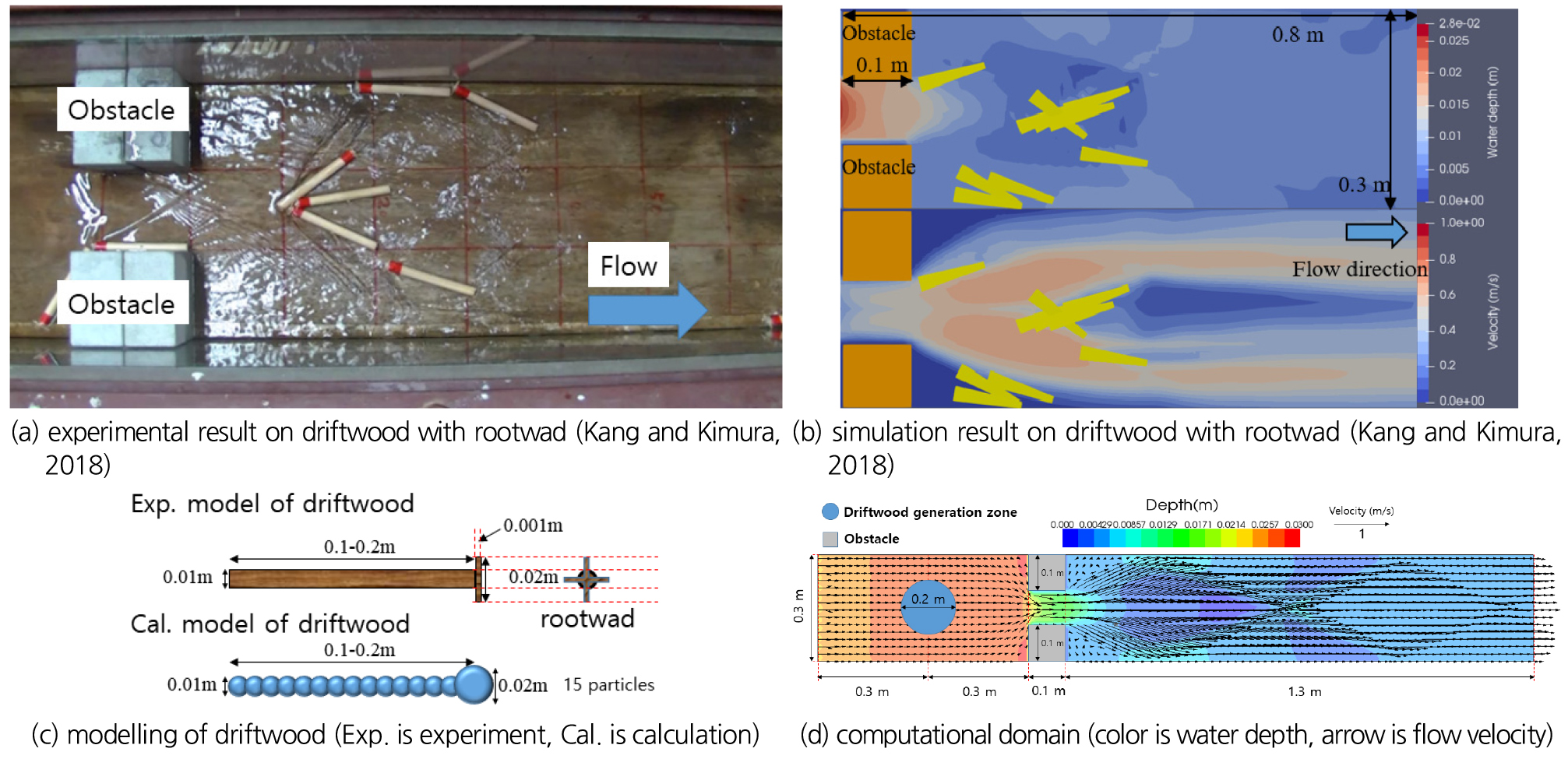
본 연구에서는 Kang and Kimura (2018)의 실내실험(Fig. 3(a))과 수치모형(Fig. 3(b))의 연구를 바탕으로 유목의 유입량에 대한 수공구조물에서의 군집특성을 분석하였다. 유입유량은 0.00065 m³/s로 설정하였고 하도경사는 0.0045 m/m 이며 Manning계수는 매끄러운 바닥을 고려하여 0.006 s/m^1/3으로 결정하였다. 유목의 경우는 Kang and Kimura (2018)의 실험(Fig. 3(c))을 고려하여 650 kg/m³의 밀도를 고려하였으며 유목의 직경은 0.01 m 이다. 또한 Kang and Kimura (2018)는 실린더형 유목의 경우 매끄러운 수로에서는 저수심(일반적으로 유목직경보다 적은 수심) 지역에서도 구름운동으로 인해 유목이 떠내려가기 쉽다고 분석하였으며, 뿌리뭉치가 있는 유목모형의 경우 저수심에서 퇴적이 빈번하게 발생한다고 결론지었다. 따라서 본 연구에서는 유목 모두에 뿌리효과가 있는 것으로 가정하여 수치해석상 유목이 수로에 퇴적하기 용이하도록 설정하였다. 여기서 뿌리뭉치의 직경은 0.02 m 이다(Fig. 3(c)).

계산 도메인 및 흐름의 구조를 나타내기 위해 Fig. 3(d)를 도시하였다. 계산도메인의 크기는 2 m × 0.3 m 이며 0.1 m × 0.1 m의 장애물 2개를 상류로부터 0.6 m 이격된 위치에 배치하여 통수면적에 변화를 주어 장애물 하류단에서 저수심과 도수현상이 발생하도록 하였다.

본 연구에서는 Fig. 3(d)에서 나타난 유목생성지역내부(직경 0.2 m)에서 유목의 발생위치가 무작위적으로 결정된다. 또한 유목줄기의 초기각도는 무작위로 결정되며 초기속도는 0 m/s 이다.

모의조건에 대한 세부내용은 Table 1에 기술되어 있다. 부유운동과 더불어, 유목의 미끄럼운동과 퇴적을 모형을 통해 재현할 수 있도록 하였으며 이를 위해 유목과 수로바닥 사이의 마찰계수들(정적, 동적, 구름)은 Kang and Kimura (2018)의 실험을 기반으로 시행착오를 통해 도출하였다. 구름운동의 경우는 구름운동의 역학을 직접적으로 고려하지 않고 동적마찰계수보다 훨씬 작은 값으로 가정하여 간접적으로 재현하도록 하였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540605/images/kwra_54_06_05_F3.jpg

Fig. 3.

Computational domain and driftwood modelling (Kang and Kimura, 2018)

Table 1.

Computational conditions based on Kang and Kimura (2018)

Parameter	Value
Flow configuration
Flow discharge	0.00065 m³/s
Channel slope	0.0045 m/m
Computational domain size (uniform rectangular shape)	2 m × 0.3 m
Resolution of computational grid length	0.01 m × 0.01 m
Manning roughness coefficient	0.006 s/m^1/3
Time step of water flow in simulation	0.01 sec
Eddy viscosity for zero equation	0.4
Simulation time	60 sec
Driftwood configuration
Input number of driftwood pieces	30 EA
Start time of wood supply	10 sec
Time interval for wood supply	2 sec
Stem (rootwad) diameter of wood pieces	0.01 m (0.02 m)
Length of wood pieces	0.1, 0.15, 0.2 m
Number of wood particles	15 EA
Critical draft for wood motion (trunk particle)	0.006 m
Critical draft for wood motion (rootwad particle)	0.01 m
Static bed friction coefficient	0.5
Kinematic bed friction coefficient	0.2
Rolling bed friction coefficient	0.01
Poisson's ratio	0.3
Young's modulus	0.6 Gpa
Time step of driftwood motion in simulation	0.0001 sec

4. 유목의 유입규모와 군집특성에 대한 수치실험

4.1 모형의 검보정

흐름과 유목의 거동에 관한 수치적 검보정은 Figs. 3(a) and 3(b)와 같이 Kang and Kimura (2018)에서 수행되었으며 유목거동과 흐름을 잘 재현했다고 결론지었다. 여기서 Fig. 3(d)와 같이 장애물 구간에서의 통과유속은 0.47 m/s 이며 장애물 상하류단의 유속은 각각 0.085 m/s, 0.805 m/s 로 나타났다. 수심의 경우에는 장애물 직상류단에서 0.028 m, 장애물 하류단에서는 도수현상이 일어나기 직전부근(장애물로부터 하류방향으로 0.4 m)에서 0.001 m로 나타났다.

한편 Kang and Kimura (2018)은 흐름벡터와 유목줄기 각도로 인해 발생하는 유목의 투영면적변화와 항력변화의 적용을 제안했고 추가적으로 충돌효과를 고려해야한다고 지적했었다. 따라서 본 연구에서는 전술한 투영면적변화 및 항력변화와 충돌효과를 수치적으로 모두 고려하였다.

4.2 수치실험 시나리오

Table 2는 수치실험 시나리오를 나타내며 시나리오별 유목의 길이는 0.1, 0.15, 0.2 m 로 상정하였다(Fig. 3(c)). 유목의 총 유입량은 각각 30개로 동일하며 2 sec 간격으로 유목이 생성된다. 여기서, 2 sec 간격마다 생성되는 유목의 유입규모(cohort size)는 2, 5, 10개 로 상정하였다. 유목모형의 충돌거동이 군집분포에 주는 영향을 분석하기 위해 추가적으로 유목충돌모형을 적용하지 않은 Run 10 을 모의하였다.

본 연구에서는 유목생성의 무작위성을 고려하여 각 Run 당 3회의 수치모의를 수행하였으며 유목은 모의시작 10 sec 후부터(수치모의에서 흐름이 동적평형이 되는 시점) 유목생성영역에서 발생된다. Run 9와 Run 10의 경우에는 충돌효과를 비교하기 위해 Table 2에서 수행한 것 이외에도 모의를 10회 추가 수행하여 유목의 충돌효과를 세부적으로 비교하였다.

Table 2.

Scenario of simulation

No.	Length of trunk (m)	Cohort size (EA)	Dashpot-spring model	Time interval of wood supply	Iteration number of simulations
Run1	0.1	2	Use	2 sec	3 times
Run2	0.1	5	Use
Run3	0.1	10	Use
Run4	0.15	2	Use
Run5	0.15	5	Use
Run6	0.15	10	Use
Run7	0.2	2	Use
Run8	0.2	5	Use
Run9	0.2	10	Use
Run10	0.2	10	No use

4.3 수치실험 결과 및 고찰

4.3.1 유입량과 유목길이에 따른 유목의 장애물 통과율

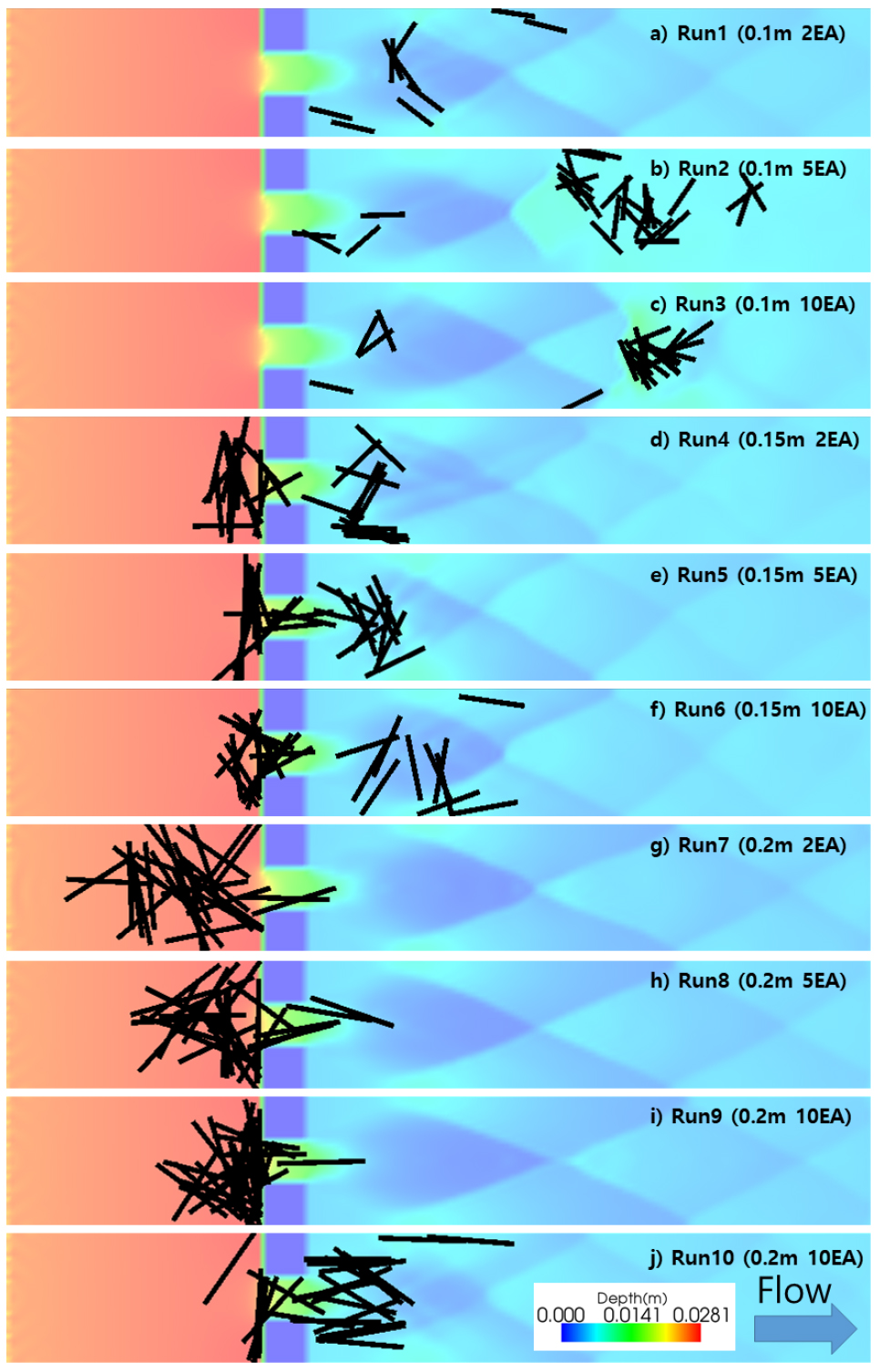
Fig. 4는 유목의 유입에 따른 모의결과를 보여준다. 검정색의 직사각형은 유목을 나타내며 그 외의 색상은 수로 내부에 모의된 수심을 나타낸다. 여기서 Fig. 4는 각 Run 당 3회를 모의한 결과들 중 임의로 선정하여 보여주고 있다.

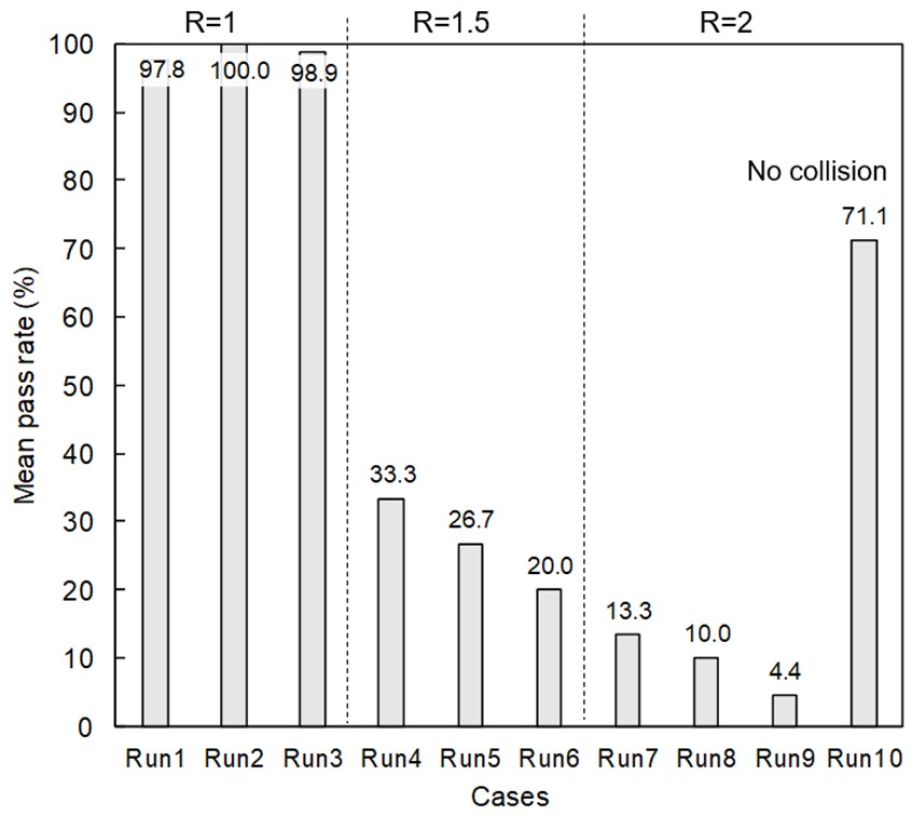
Fig. 5에서는 각 Run 당 3회를 모의하여 산정된 장애물 구간 통과율을 보여주고 있다. 그래프의 세로축은 유목의 장애물구간 통과율(%)을, 가로축은 유목길이와 유입량에 따른 모의유형을 나타낸다. 여기서 R은 유목줄기의 길이(0.1 ~ 0.2 m)와 장애물 경간(0.1 m)의 비율을 나타낸다.

Runs 1 ~ 3 의 경우 유목길이 0.1 m (R = 1)의 유목거동의 결과를 보여주고 있으며 Figs. 4(a) ~ 4(c)에서 나타내는 것과 같이 거의 모든 유목(Fig. 5)이 장애물 하류에 퇴적되거나 일부는 계산영역 밖으로 떠내려갔다. 장애물 하류단에서는 CDM (유목줄기는 0.006 m, 유목뿌리는 0.01 m) 보다 수심이 낮기 때문에 유목의 퇴적이 용이하다(Kang and Kimura, 2018). 또한 Runs 1 ~ 3은 상류단에서 군집이 형성되더라도 장애물사이를 통과하여 하류단으로 쉽게 흘러갔다. Fig. 5에서도 Runs 1 ~ 3의 경우에는 모두 97% 이상의 통과율을 나타냈다. 이는 양쪽 벽에 설치된 장애물의 횡방향 간격은 0.1 m 이며 유목길이도 이와 동일하기 때문에 유목들이 장애물을 통과하기 쉬운 것으로 판단된다.

Runs 4 ~ 9의 경우에는 다른 양상을 보여주었다(Fig. 4). 이들의 경우 장애물 상류단에 유목군집이 형성되었으며 유입량의 일부만 하류단으로 빠져나갔다. Run 9의 경우 평균적으로 4.4% 정도의 유목만이 하류로 빠져나간 것으로 나타났다. 특히, 유목의 줄기가 길어질수록, 유목의 유입규모가 증가할수록 상류단에 형성된 유목의 개수가 평균적으로 증가하였다(Fig. 5). 또한 Runs 1 ~ 3 과 Runs 4 ~ 9 를 비교해봤을 때, 장애물의 간격보다 유목의 줄기가 증가하게 되면 상류단에서 군집형성이 훨씬 용이해지는 것으로 판단된다.

Run 10 의 경우는 Run 9 의 유목의 특성과 동일하며 유목충돌력을 계산하는 Dashpot-spring 모형을 적용하지 않은 모의 결과이다. Run 10 의 평균유목통과율은 71.1% 정도로 나타났다. 또한 이는 유목길이가 장애물의 간격보다 더 큰 Runs 3 ~ 9 의 경우보다 더 큰 통과율을 보였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540605/images/kwra_54_06_05_F4.jpg

Fig. 4.

Simulation results depending on wood length (m) and cohort size (EA)

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540605/images/kwra_54_06_05_F5.jpg

Fig. 5.

Mean pass rate (%) of wood pieces depending on cases (R is L/D; L is length of driftwood (0.1 ~ 0.2 m); D is interval length of obstacles (0.1 m)).

4.3.2 유목의 충돌효과

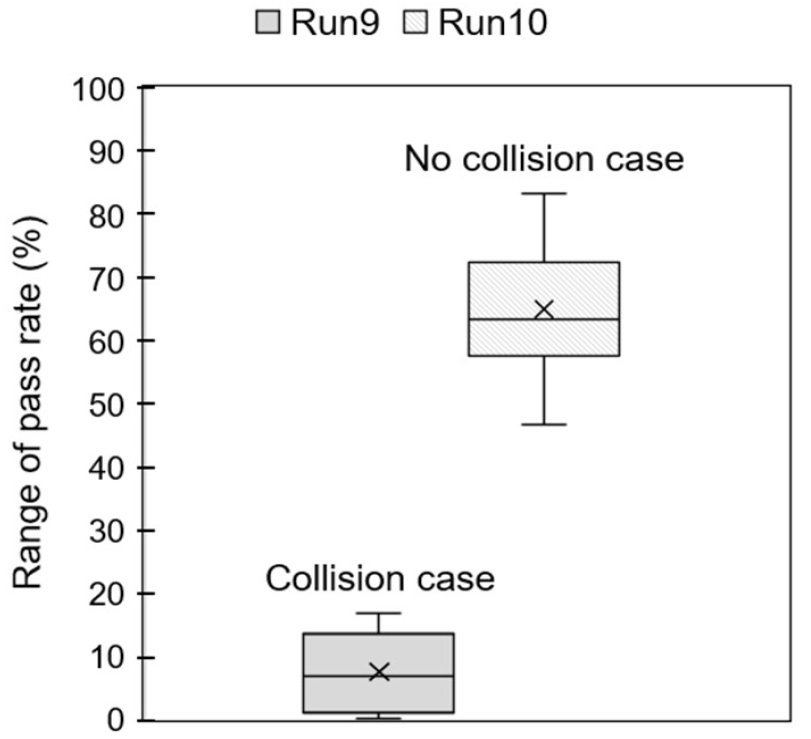
유목충돌의 효과를 더 세부적으로 나타내기 위해 Fig. 6과 같이 Run9와 10의 모의를 추가적으로 10회 수행하여 통과율의 범위를 상자그림(box plot)으로 나타냈다. Run 9의 경우 평균 7.3%의 통과율을 나타냈고 Run10의 경우 Run9보다 8배 이상 큰 65%의 통과율을 나타냈다. 또한 Run10은 최소와 최대의 범위를 Run9 (0 ~ 16.7%)보다 더 넓게(46.7 ~ 83.3%) 보여주었다. 이는 유목의 충돌이 재현되지 않으면 장애물 상류단에서 유목들이 훨씬 쉽게 겹쳐지게 되며, 유목간의 상호작용보다는 흐름에 지배적으로 거동하기 때문으로 판단된다. 반대로, 유목의 충돌이 고려되면 장애물 구간에서 유목들간의 상호충돌로 정체현상이 나타나기 때문에 유목충돌이 없는 경우보다 유목의 통과개수가 줄어들어 통과율의 범위가 더 줄어드는 것으로 판단된다.

충돌효과에 대한 수치모의와 관련하여, Kimura and Kitazono (2020)의 경우에도 만곡부에 설치된 장애물에 유목이 포착되는 실내실험과 수치모의를 수행하였다. 이 연구에서도 Dashpot-spring 모형을 이용한 수치모듈을 적용하였기에 성공적으로 유목의 포착과 장애물구간에서의 군집이 형성되는 과정을 모의할 수 있었다. 본 연구에서도 Kimura and Kitazono (2020)의 실험과 유사한 수치실험결과를 확인 할 수 있었으며 이는 Dashpot-spring 모형이 유목의 충돌효과를 잘 재현할 수 있는 것으로 판단된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540605/images/kwra_54_06_05_F6.jpg

Fig. 6.

Range of pass rate (%) by 10 iterations of Runs 9 and 10

4.3.3 유입량과 유목길이에 따른 유목이송거리와 유목평균위치의 변화

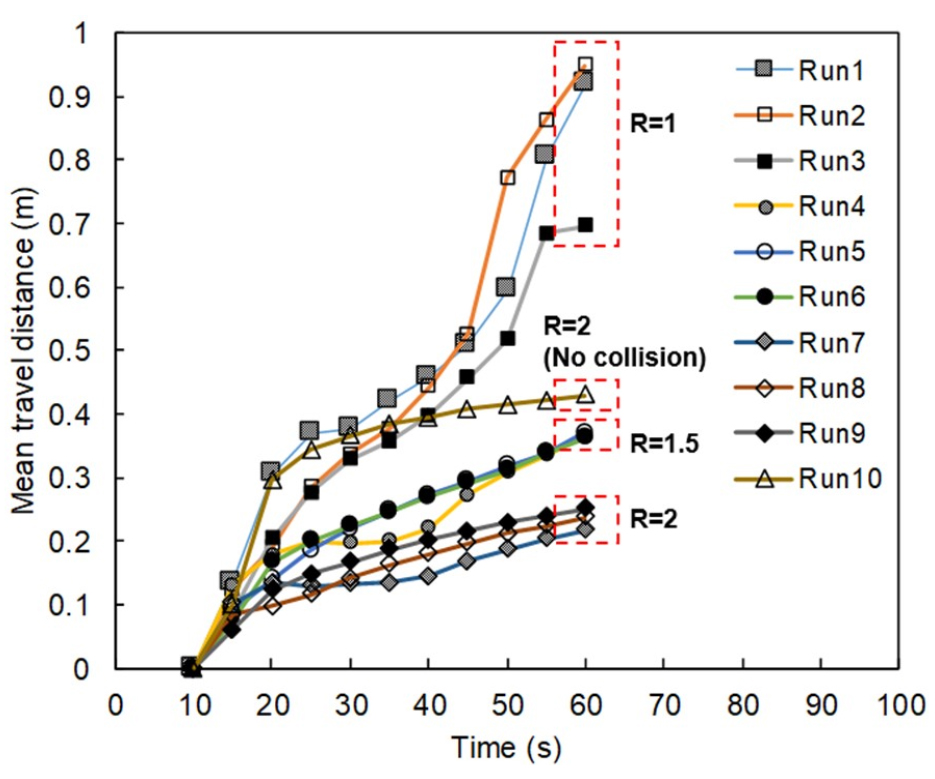
Fig. 7은 유목길이와 유입량에 따른 유목의 이송거리를 5 sec 간격의 시간변화로 나타낸 것이다. 유목은 10 sec 이후에 생성이 되므로 그래프에서는 10 sec 이후에 평균값이 나타난다. Fig. 7에서 유목줄기길이와 장애물구간 간격의 길이비인 R(= 1 ~ 2)에 대해 최종 이송평균거리를 산정하면 각각 0.85, 0.36, 0.23 m 이다.

또한 이 그래프에서는 Runs 1 ~ 3 의 경우 50 sec 이전에는 이송거리의 완만한 증가율을 보여주며 50 sec 이후에는 급경사를 나타낸다. 이는 대량의 유목들이 장애물구간을 통과하여 빠른 유속(> 0.3 m/s)의 영향으로 하류로 급격하게 떠내려가는 거동을 나타냈기 때문이다. Runs 4 ~ 6 의 경우 대체적으로 전체모의시간 동안 완만한 경사를 보여주었지만 Run 4의 경우 30 ~ 40 sec 사이에서 이송의 정체현상을 보여주다가 40 sec 이후에 급격한 경사를 나타내고 50 sec 이후에는 Runs 5 and 6 과 비슷한 경사를 보여주었다. 이는 Run 4 가 장애물구간에서 유목들이 완전히 정체되었다가 40 sec 이후에 한꺼번에 장애물구간을 통과했기 때문이다. Runs 7 ~ 9 는 Runs 1 ~ 6 보다 완만한 경사를 나타내며 60 sec에 장애물구간에서 유목군집의 이송정체현상을 나타냈다. 유목의 줄기에 따라서는 0.2 m (Runs 7 ~ 9) 가 최단이송거리를 보여주었으며 0.1 m (Runs 1 ~ 3) 이 최장이송거리를 나타냈다. 따라서 유목길이가 증가할수록 유목의 이송거리는 줄어드는 것으로 판단된다. 충돌모형을 고려하지 않은 Run 7 의 경우에는 장애물구간에서 정체현상이 일어나지 않았기 때문에 0.2 m 의 유목길이에도 불구하고 0.15 m (Runs 4 ~ 6) 의 유목보다 더 큰 이송거리를 나타냈다. 유목의 유입량의 경우, 동일유목줄기의 모의결과끼리 비교해 봤을 때 유입규모가 증가하더라도 이송거리가 불분명하게 반응하는 것을 알 수 있었다. 따라서 유입규모와 이송거리의 관계를 구체적으로 파악하기 위해서는 추후에 좀 더 폭 넓은 범위의 유입규모(e.g., 100개 이상) 시나리오를 구축하여 수치실험과 실내실험을 수행해야할 것으로 판단된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540605/images/kwra_54_06_05_F7.jpg

Fig. 7.

Time changes in mean travel distance (m) of wood pieces depending on cases (R is L/D; L is length of driftwood (0.1 ~ 0.2 m); D is interval length of obstacles (0.1 m))

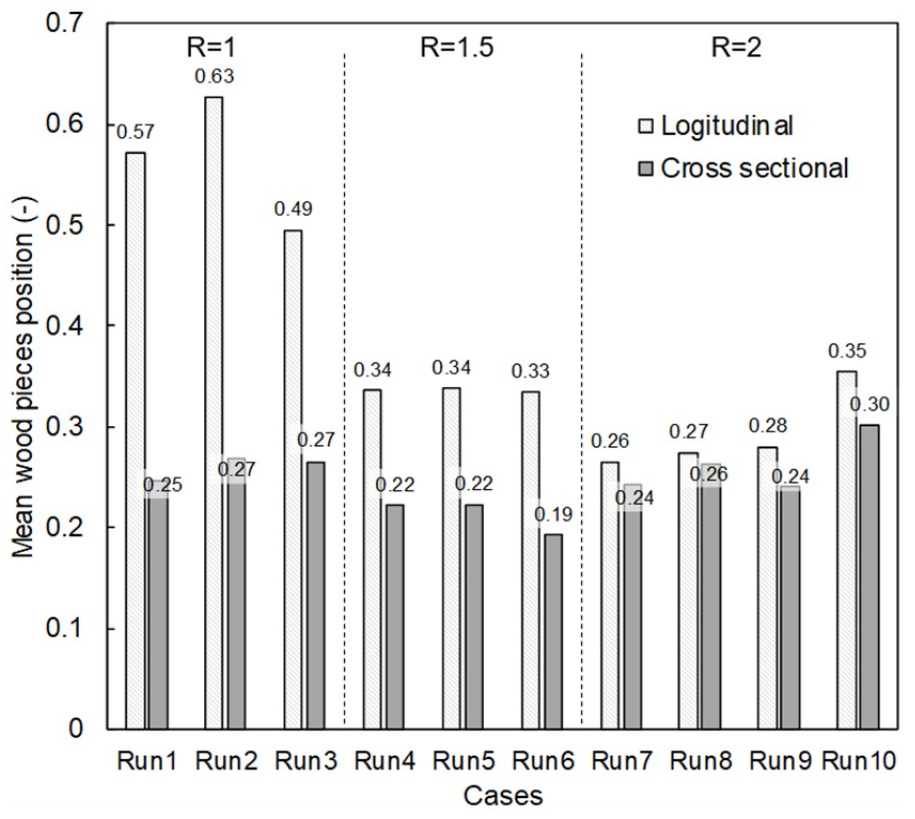
Fig. 8은 계산영역상에 존재하는 유목들의 최종평균위치를 종방향 및 횡방향으로 나타낸 것이다. 종방향 평균위치의 경우 계산영역의 상류단(= 0)과 하류단(= 1)사이의 값을 나타내며 횡방향은 계산영역 횡단면의 중심선(= 0)과 양측 수로벽(= 1)사이의 값을 나타내며 여기서 특정 수로벽에 위치와는 상관없이 항상 양수를 나타낸다. 이 그래프에서도 Fig. 7과 마찬가지로 유목줄기의 길이가 증가할수록 장애물구간에서 정체현상이 일어나기 때문에 종방향 평균위치는 감소하는 것으로 나타났다. 횡방향 평균위치는 불분명하게 나타났으며 이는 주 흐름이 종방향이기 때문에 횡방향 흐름의 효과가 미미하여 유목군집에 영향을 주지 않은 것으로 사료된다. 유목의 유입규모는 Fig. 7과 마찬가지로 유목들의 종방향 및 횡방향의 평균위치에는 큰 영향을 주지는 않는 것으로 판단된다.

한편 본 연구에서는 유목들이 장애물구간에서 군집을 형성하여 정체되는 현상을 주로 고려하여 이송거리와 평균위치를 평가했기 때문에 유목의 유입규모로 인한 이송거리는 장애물이 없는 경우와는 확연하게 달라질 수 있다. 따라서 유입량과 유목의 이송거리의 관계성을 정확히 파악하려면 더 세부적인 연구(e.g., 장거리 수로에서 유목의 미끄러짐과 퇴적이 활발하게 보여질 수 있는 얕은 흐름(수심 < 유목직경)의 실험)가 필요할 것으로 판단된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-06/N0200540605/images/kwra_54_06_05_F8.jpg

Fig. 8.

Final mean wood pieces position (-) of depending on cases (R is L/D; L is length of driftwood (0.1 ~ 0.2 m); D is interval length of obstacles (0.1 m))

4.3.4 모형의 개선사항

본 연구의 경우 2차원 흐름 및 2차원 유목의 거동을 재현하는 수치실험을 수행하였다. 그리고 모의결과는 Kang and Kimura (2018)의 연구와 동일하게 부유운동, 미끄러짐운동, 구름운동, 군집현상 등의 유목거동이 수치적으로 재현된 것으로 판단된다. 2차원 모형으로 재현한 흐름의 경우에는 유목의 최소길이(0.1 m)에 비해 최대수심이 0.028 m 로 깊지 않기 때문에 유목의 수심방향의 거동까지는 고려하지 않아도 무리가 없을 것으로 판단된다. 또한 Fig. 6에 나타난 것처럼 유목의 충돌효과는 장애물구간에서의 유목군집형성에 핵심적인 역할을 하는 것으로 사료된다. 하지만 본 연구의 모의결과에서 유목의 겹침효과(overlapping effect)가 나타나는 것을 확인할 수 있었다(Fig. 4). 여기서, 군집된 유목의 경우 유목이 정체되어 있는 상태이기 때문에 유목을 구성하는 입자의 속도가 유목의 이송에 영향을 미치지 않을 만큼 매우 작다. 이때는 Dashpot-spring 모형의 특성상, 매우 작은 속도에서는 매우 작은 충돌력이 계산되기 때문에 유목의 이송 운동력보다 유목의 충돌력이 더 작아져서 유목이 하류로 매우 천천히 이송되어진다. 결과적으로 Fig. 4와 같이 유목의 겹침효과를 초래하게 된다. 이를 방지하게 위해서는 Dashpot-spring 모형에 경험상수(최소입자속도, 최소겹침길이, 최소반발력 등)를 적용하여 겹침효과를 저감할 수는 있으나, 이를 검증하기 위해서는 추가적인 실내실험이 수행되어야할 것으로 판단된다.

5. 결 론

본 연구에서는 2차원 흐름 모형인 Nay2DH와 유목동역학 모형에 대해 기술하였고 이를 이용하여 유목길이와 유입특성에 따른 장애물 근처에서의 유목거동과 군집특성을 수치모의를 통해 실험 및 분석하였다. 본 연구에서 더 나아가 교각과 소규모 보 등의 실제 수공구조물을 대상으로 유목동역학모형을 통해 모의실험 하게 되면 유목의 이송과 군집현상 등을 사전에 예측할 수 있으며 이는 수공구조물의 내구성 유지방안의 구축에도 도움이 될 것으로 사료된다. 본 연구에 대한 결론은 아래와 같다.

1) 본 연구에서 활용된 유목동역학모형이 유목의 부유, 미끄러짐, 충돌, 군집형성 등을 잘 재현하였음을 확인할 수 있었다. 특히, 충돌모형(i.e., Dashpo-spring 모형)을 적용한 경우 평균 7.3%의 통과율을 나타냈고 충돌모형을 적용하지 않은 경우에는 큰 65%의 통과율을 나타내며 이는 충돌모형이 장애물구간에서의 군집형성에 큰 영향을 미치는 것으로 판단된다.

2) 유목줄기의 길이가 장애물의 간격보다 클수록 장애물 상류단에서 유목군집이 보다 활성화되었다. 세부적으로, 유목줄기와 장애물의 간격의 비가 R = 1인 경우, 97% 이상의 장애물 통과율을 나타내며 모든 유목이 하류로 흘러갔으며, R값이 1.5, 2로 증가할수록 유목은 장애물구간을 통과하지 못하고(통과율: 4.4 ~ 33.3%) 직상류단에 군집되어 있는 현상을 보여주었다.

3) 유목의 유입규모의 특성은 장애물 통과율에는 영향을 주었다. R = 1의 경우, 유목줄기크기가 통과율에 크게 영향을 주었기 때문에 유입규모에 따른 효과는 보여지지 않았으나, R이 1.5 와 2 일 경우에는 유입규모가 클수록 각각 13.3, 8.9 %정도 통과율이 줄어든 것으로 나타났다. 이송거리에 대해서는 유입규모보다는 장애물구간 하류단의 흐름의 영향을 많이 받게 되어, 본 연구에서는 유입규모와 이송거리와의 관계는 불분명한 것으로 나타났다. 이를 파악하기 위해서는 좀 더 폭 넓은 범위의 유입규모(e.g., 100개 이상) 시나리오를 구축하여 실내실험과 수치실험을 수행해야할 것으로 사료된다.

4) 유목의 줄기길이와 종방향 군집위치에 관해서는 R = 1의 경우 평균 0.85 m 이며 R = 1.5, 2의 경우 각각의 평균값은 0.36, 0.23 m 로 나타났다. 이는 유목의 이송거리와 종방향 군집위치는 유목의 길이가 감소할수록 증가한다는 것을 보여준다. 특히 유목줄기가 증가할수록 장애물구간을 통과하지 못하여 이송거리는 더욱 감소하게 된다. 하지만 유목의 유입규모의 변화는 종방향 군집위치와 횡방향 유목평균위치(0.19 ~ 0.3; 무차원 수 임)에 대해 불분명한 효과를 나타났다.

5) 본 연구는 Kang and Kimura (2018)의 실내실험을 바탕으로 수치모의를 수행하였으며 유목의 크기와 유입규모에 대해서만 연구를 수행하였다. 향후 연구에서는 Kang and Kimura (2018)에서 고려했던 수리조건(유량조건과 하도경사의 변화)을 반영하여 추가적인 수치실험을 한다면 흐름에 따른 보다 세부적인 유목의 수치적 거동을 확인할 수 있을 것으로 판단된다. 또한 본 연구는 Kang and Kimura (2018)에서 수행한 실내실험을 응용하여 수치실험을 수행하였기에 보다 구체적인 검보정을 위해서는 유목의 크기와 유입규모에 따른 실내실험도 향후 수행되어야할 것으로 사료된다.

Acknowledgements

이 논문은 2020년도 정부(과학기술정보통신부)의 재원으로 한국 연구재단의 지원을 받아 수행된 해외고급과학자초빙(BP, Brain Pool)의 연구 임(No. 2020H1D3A1A04105845).

References

Bertoldi, W., Welber, M., Mao, L., Zanella, S., and Comiti, F. (2014). "A flume experiment on wood storage and remobilization in braided river systems." Earth Surface Processes Landforms, Vol. 39, pp. 804-813. 10.1002/esp.3537

Braudrick, C.A., and Grant, G.E. (2000). "When do logs move in rivers?" Water Resources Research, Vol. 36, No. 2, pp. 571-583. 10.1029/1999WR900290

Braudrick, C.A., Grant, G.E., Ishikawa, Y., and Ikeda, H. (1997). "Dynamics of wood transport in streams: A flume experiment." Earth Surface Processes and Landforms, Vol. 22, pp. 669-683. 10.1002/(SICI)1096-9837(199707)22:7<669::AID-ESP740>3.0.CO;2-L

Choi, G., Kim, K., and Park, Y. (2003). "Changes in water depth and velocity by debris around piers." Journal of Korea Water Resources Association, Vo. 36, No. 2, pp. 273-284. (in Korean) 10.3741/JKWRA.2003.36.2.273

Gotoh, H., Okayasu, A., and Watanabe, Y. (2013). Computational wave dynamics. Advanced Series on Ocean Engineering, 87, World Scientific, Singapore. 10.1142/8714

International River Interface Cooperative (iRIC) (2021). Japan, accessed 13 January 2021, <http://i-ric.org/en>

Kang, T. (2018). Studies on morphodynamics in shallow rivers with effects of vegetation and large wood using computational models. Ph. D. dissertation, Hokkaido University, Japan.

Kang, T., and Jang, C.L. (2020). "An Experiment on flow simulation depending on opening configuration of weir using a numerical model." Journal of Ecology and Resilient Infrastructure, Vol. 7, No. 3 pp. 218-226. doi: 10.17820/eri.2020.7.3.218. (in Korean)

Kang, T., and Kimura, I. (2018). "Computational modeling for large wood dynamics with root wad and anisotropic bed friction in shallow flows." Advances in Water Resources, Vol. 121, pp. 419-431. 10.1016/j.advwatres.2018.09.006

Kang, T., Kimura, I., and Onda, S. (2019) "Computational modeling for driftwood collision dynamics in shallow flows considering projection area, root wad and anisotropic bed friction." E-proceedings of the 38th IAHR World Congress, Panamá City, Panamá, pp. 103-109. doi: 10.3850/38WC092019-0150 10.3850/38WC092019-0150

Kang, T., Kimura, I., and Onda, S. (2020a). "Congestion patterns of driftwood by a wood supply interval and a collision on sand bars." E-proceedings of River Flow Conference 2020, Netherlands, pp. 1685-1693. 10.1201/b22619-236

Kang, T., Kimura, I., and Shimizu, Y. (2018). "Study on advection and deposition of driftwood affected by root in shallow flows." Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering), Vol. 74, No. 4, pp. I_757-I_762. 10.2208/jscejhe.74.I_757

Kang, T., Kimura, I., and Shimizu, Y. (2020b). "Numerical simulation of large wood deposition patterns and responses of bed morphology in a braided river using large wood dynamics model." Earth Surface Processes and Landforms, Vol. 45, pp. 962-977. doi: 10.1002/esp.4789 10.1002/esp.4789

KBS news (2020). South Korea, accessed on January 13 2021, <https://news.kbs.co.kr/news/view.do?ncd=5001887>. (in Korean)

Kimura, I. (2018). NaysCUBE solver manual (updated). accessed January 13 2021, <http://i-ric.org/en>.

Kimura, I., and Kitazono, K. (2020). "Effects of the driftwood Richardson number and applicability of a 3D-2D model to heavy wood jamming around obstacles." Environmental Fluid Mechanics, Vol. 20, pp. 503-525. 10.1007/s10652-019-09709-6

Kimura, I., Kang, T., and Kato, K. (2020). "Computation on submerged large wood behavior around a driftwood trapping facility." Journal of Japan Society of Civil Engineers (JSCE), Ser. B1 (Hydraulic Engineering), Vol. 76, No. 2, pp. I_967-I_972. (in Japanese)

Lee, K., and Jang, C.L. (2018). "Numerical investigation of space effects of serial spur dikes on flow and bed changes by using Nays2D." Journal of Korea Water Resources Association, Vol. 49, No. 3, pp. 241-252. doi: 10.3741/JKWRA.2016.49.3.241. (in Korean) 10.3741/JKWRA.2016.49.3.241

Manners, R.B., and Doyle, M.W. (2008). "A mechanistic model of woody debris jam evolution and its application to wood-based restoration and management." River Research and Applications, Vol. 24, No. 8, pp. 1104-1123. 10.1002/rra.1108

Ruiz-Villanueva, V., Bladé, E., Sánchez-Juny, M., Marti-Cardona, B., Díez-Herrero, A., and Bodoque, J.M. (2014). "Two-dimensional numerical modeling of wood transport." Journal of Hydroinformatics, Vol. 16, No. 5pp. 1077-1096. 10.2166/hydro.2014.026

Ruiz‐Villanueva, V., Gamberini, C., Bladé, E., Stoffel, M., and Bertoldi, W. (2020) "Numerical modeling of instream wood transport, deposition, and accumulation in braided morphologies under unsteady conditions: Sensitivity and high-resolution quantitative model validation." Water Resources Research, Vol. 57, No. 7, pp.1-22. doi: 10.1029/2019WR026221 10.1029/2019WR026221

Shimizu, Y., Takebayashi, H., Inoue, T., Hamaki, M., Iwasaki, T., and Nabi, M. (2014). Nays2DH solver manual, accessed January 13 2021, <http://i-ric.org/en>.

Swanson, F.J., Gregory, S.V., Iroumé, A., Ruiz-Villanueva, V., and Wohl, E. (2020). "Reflections on the history of research on large wood in rivers." Earth Surface Processes Landforms, Vol. 46, No.1, pp.55-66. doi: 10.1002/esp.4814 10.1002/esp.4814

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Two-dimensional numerical experiment considering cohort size and wood jam characteristic on driftwood

ABSTRACT

MAIN

Fig. 1.

Bridge collapse and deposition of driftwood around bridge piers (KBS news, 2020).

(1)

(2)

(3)

(4)

(5)

(5a)

(5b)

(5c)

(5d)

(6)

(7)

(8)

(8a)

(8b)

(8c)

(8d)

Fig. 2.

Schematic diagram for calculation of driftwood motion

Fig. 3.

Computational domain and driftwood modelling (Kang and Kimura, 2018)

Table 1.

Computational conditions based on Kang and Kimura (2018)

Table 2.

Scenario of simulation

Fig. 4.

Simulation results depending on wood length (m) and cohort size (EA)

Fig. 5.

Mean pass rate (%) of wood pieces depending on cases (R is L/D; L is length of driftwood (0.1 ~ 0.2 m); D is interval length of obstacles (0.1 m)).

Fig. 6.

Range of pass rate (%) by 10 iterations of Runs 9 and 10

Fig. 7.

Time changes in mean travel distance (m) of wood pieces depending on cases (R is L/D; L is length of driftwood (0.1 ~ 0.2 m); D is interval length of obstacles (0.1 m))

Fig. 8.

Final mean wood pieces position (-) of depending on cases (R is L/D; L is length of driftwood (0.1 ~ 0.2 m); D is interval length of obstacles (0.1 m))

Acknowledgements

References