1. 서 론

수리실험 수로의 유입부에서 실험 유량을 균일한 유속분포로 제공하는 것은 유속 측정의 정확도 확보뿐만 아니라 수리 현상을 정확하게 재현하기 위해서 매우 중요한 실험 조건이다(Howes et al., 2009). 고유량 그리고 고유속의 흐름을 대상으로 할 때는 유량 공급관 및 일반적인 타공판(perforated plate)을 이용한 정류장치로에서 공기방울이 유입될 수 있어 이들을 빠르게 제거해야 하며, 흐름의 왜곡 및 난류에너지의 범위를 벗어난 교란을 제어하여야 한다. 이러한 과도한 난류와 공기방울은 수로 실험 구간에서의 유속분포와 수위의 변형에 따른 흐름 현상의 왜곡을 발생시킬 수 있다. 따라서 실험 수로의 상류에서 공급되는 유량은 와(eddy), 소용돌이 흐름(swirling flow), 왜곡된 흐름(distorted flow)을 가능한 짧은 구간에서 제거하여 잘 발달된 균일한 흐름을 효율적으로 제공할 수 있는 정류장치의 개발이 필요하다.

정류장치로는 복수의 타공판을 흐름 방향에 대해서 직렬로 연결하여 적용하는 것이 일반적이다. Spearman et al. (1996)은 90° 만곡관과 S자형 뒤틀린 관수로 하류에 서로 다른 직경의 조합으로 설계된 4가지 천공판(perforated plate)을 이용한 정류장치를 설치하여 흐름 조절 성능을 평가하였다. LDV (laser Doppler velocimetry) 시스템을 이용하여 유속분포 및 난류강도를 측정한 결과를 보면 흐름 왜곡 때문에 발생한 비정상적 유속 변동성분은 빠르게 제거되며 완전히 발달한 흐름 분포는 관수로 직경의 약 11배 하류지점에서 형성되는 것으로 나타났다. Liu and Ting (2007)은 풍동(wind tunnel)에서 등방성 난류를 발생시키기 위해 출구부를 날카롭게 만든 오리피스형 개구(opening)와 유한한 두께의 직선 개구를 가진 천공판 적용하였다. 실험 결과는 오리피스 천공판이 더 잘 정류된 등방성 난류를 생성하는 것을 보여주며, 천공판 구멍 출구부의 각도 조절이 교란 제거와 정류에 역할을 하는 것으로 나타났다. Ouazzane and Benhadj (2007)은 오리피스에서 발생할 수 있는 소용돌이 흐름을 제거하고 완전히 발달된 평균 유속과 난류 분포를 생성하기 위해서 날개(vanes)와 탭(tabs)을 장착하며 등급별로 타공한 평판(graded perforated plate)을 이용하여 제작한 흐름 교정장치를 개발하였다. 실험 결과 이 흐름교정기는 소용돌이 흐름을 제거하며 바로 하류의 짧은 거리 내에서 완전히 발달된 안정한 흐름을 생성하는 것으로 나타났다. Xiang et al. (2019)은 소방용 물대포 노즐로 물이 유입되기 직전의 소방호스에서의 흐름 정류를 최적화하기 위해서 두 개의 동축관(coaxial pipes)와 방사형 날개들(radial blades)로 설계된 흐름 교정기의 성능을 수치해석을 통해 평가하였다.

파이프 관을 병렬로 연결한 벌집(honeycomb) 형태의 정류장치를 대형 풍동(wind tunnel) 시설에 설치하여 성능을 평가하는 연구도 있다. Burley and Harrington (1987)은 마하수(Mach number) 0.2~0.916의 유속을 발생시킬 수 있는 대형 풍동의 안정실(settling chamber)에 벌집 형태의 정류장치와 스크린을 조합한 다양한 정류장치를 설치하고 난류강도(turbulence intensity)를 계측하여 해당 정류장치의 성능을 평가하는 연구를 수행하였다. 이들이 시험 구간의 입구에서 계측한 가장 낮은 난류강도는 1.2%이었으며, 이것은 하나의 벌집 모양 정류장치와 3개의 조밀격자로 구성된 스크린을 이용한 구조에서 발생하였다. Xiong et al. (2003)은 두 개의 천공판 사이에 튜브 다발을 병렬로 묶어 만든 흐름조절기를 관수로 구간에 설치하고 레이놀즈수 10만 구간에서 난류흐름의 유속을 측정하여 흐름조절기의 성능을 평가하였다. 이 연구는 속도분포가 직경의 약 25배 하류지점에서 완전발달된 흐름 형태를 가지게 되며, 천공판이 교란된 흐름을 조절할 때 튜브 다발보다 더 효율이 높음을 보여주었다. Seo (2013)는 공조시스템(heating ventilation and air conditioning, HVAC) 설계기술 개발을 위해서 직경 6 mm의 음료수 빨대를 이용한 정류장치를 이용하여 0.61 m × 0.61 m 사각형 풍동(wind tunnel)에서 발생하는 공기흐름의 난류강도 감소 효과를 연구하였다. 빨대의 길이는 정사각형 덕트 폭의 0.5 배로 설정하여, 서로 다른 공극률과 격자 크기의 스크린(screens)이 난류 감소에 미치는 영향을 분석하는 기술을 제공하였다. Seo (2013)의 연구에서 적용한 빨대를 이용한 정류장치는 규모와 용도 측면에서 본 연구의 대상 장치와 차이는 있지만 접근 방법은 유사하다. Park and Lee (2000)은 버터플라이 밸브 하류에서 속도 경사와 난류강도가 매우 크고 단면 2차류가 현저히 발생하므로 이러한 흐름을 안정화하기 위해서 벌집 모양 병렬관과 격자 스크린을 조합한 정류장치에 대해 수행하였다. 이러한 기존 흐름 조절 및 정류장치에 관한 연구는 대부분 오리피스, 풍동, 급수관 등 관수로 내부에서의 흐름 안정화를 위한 것들이 대부분이다.

개수로 실험수로에 적용되는 흐름 안정화 장치에 관한 연구는 매우 드물다. 수처리 시설의 첨전 공정에서 탁질 제거를 목적으로 흐름을 안정화하는 정류장치(water baffle)에 대한 성능평가 연구가 있다(Cho, 2005). 이 연구에서 적용한 정류장치는 매우 낮은 유속이 대상이므로 일반적인 수리실험에서 공급하는 유량과 유속 범위에서는 적용에 한계가 있다. Howes et al. (2009)는 개수로에서 상류부에 길이 1.0 m, 직경 0.0762 m의 PVC 파이프를 이용한 벌집 모양의 흐름조절기를 설치하여 정류 성능을 평가하였다. 이들은 흐름조절기를 사용할 경우, 실험을 통해 SonTek-SW ADV 장치로 측정한 평균유속과 실제 유속 사이에 단순한 선형관계가 있음을 제시하였으며 일반적인 범위의 실험 유량과 수심 조건에서 유속 측정 정확도를 약 2.2%의 오차범위에서 개선할 수 있음을 보여준다.

개수로 실험 시설에 공급하는 유량은 대부분 다수의 타공판을 흐름방향으로 설치하는 것이 일반적이다. 이러한 장치들은 고유량 조건에서 유속이 빨라지면 타공판 공극 단면에서 흐름분리가 발생하면서 공기방울이 형성된다. 이들 공기방울은 그 하류에 설치된 타공판과 충돌하여 더 작은 공기방울로 분열되기도 하여 실험 구간에서 초음파 또는 전자기파를 이용한 유속 계측장비를 이용한 유속 측정의 정확도를 현저히 떨어트릴 수 있다. 이 연구의 목적은 유속분포 왜곡과 공기방울을 빠르게 제어함으로써 실험수로의 상류 접근 구간의 길이를 줄이고 흐름 측정의 정확도를 높이기 위해 다중병렬관을 이용한 정류장치를 개발하는 것이다. 이를 위해 직경과 길이가 다른 투명 PC (polycarbonate) 재질의 다중병렬관(multiple parallel tubes)을 이용한 정류장치를 제작하였다. 이 연구에서 개발한 정류장치의 개념은 공조시스템 덕트에 음료수 빨대를 이용한 Seo (2013)의 연구 그리고 개수로에서 PVC 파이프를 이용한 Howes et al. (2009)의 연구의 개념과 유사하며, 연구 방향은 실험 개수로에서 적용성이 높은 정류장치를 개발하고자 하는 것이다. 이 연구에서는 내충격성과 내화학성이 우수한 투명 PC관을 이용하며, 다양한 길이와 직경을 조합한 장치의 흐름 정류와 공기방울 제거 성능을 수리실험을 통해 평가하고 최적 성능의 제원과 흐름 제어 특성을 제시하고자 한다.

2. 정류장치

2.1 정류장치 원리

실험수로에서 공급되는 유량이 클 경우 왜곡될 수 있는 유속분포를 직선화하고자 일반적으로 사용하는 타공판보다는 흐름 직선화(straightening)에 효과적인 벌집 형태의 정류장치를 활용한다. 흐름방향으로 길이(판의 두께)가 작은 타공판은 흐름 직선화를 위해서는 다수의 판을 적용한다 해도 흐름 직선화에는 한계가 있으나, 상대적으로 긴 관(튜브)을 사용한다면 흐름 직선화에 도움이 된다. 이와 같이 긴 관을 적층하여 만든 병렬관 다발로 수로 단면 전체를 담당하는 정류장치를 적용한다면 흐름 단면 전체에서의 왜곡된 흐름을 직선화할 수 있다.

실험 수로의 유입 단면에서는 전체 단면에 걸쳐 균일한 유속을 제공하여야 한다. 이 연구에서 개발한 정류장치는 수백 개의 동일한 길이의 관을 흐름 방향에 대해서 병렬로 적층한 다중병렬관 형태이다. 즉, 정류장치의 흐름방향 길이는 적용한 관의 길이가 된다. 유입부 단면 전체에서 흐름이 직선화되더라도 전 단면에 대해서 균일한 유속분포를 발생시키는 것은 전형적인 타공판으로는 효과에 한계가 있다. 이 연구에서 적용하는 정류장치는 다수의 관이 병렬로 구성된 다중병렬관 구조로서 여기에는 일반적인 두 가지 유체역학 원리를 적용할 수 있다. 첫째는 Eq. (1)과 같이 총 유량은 각각의 관에서의 유량을 합한 것과 같다는 것이고 둘째는 Eq. (2)와 같이 정류장치의 상류와 하류 단면 사이에 에너지 방정식을 적용할 때, 수두손실은 경로와 무관하게 동일하다는 것이다(Street et al., 1998).

여기서, Q는 유량이고, hL은 수두손실, 아래첨자 숫자는 관 번호이고 N은 적층한 관의 총개수이다. 이 연구에서 개발한 정류장치에 적용한 병렬관들의 직경과 길이는 모두 동일하다. 따라서, 병렬관의 길이가 충분히 길다면 Eq. (2)와 같이 모든 관을 통과하는 수두손실은 동일하게 된다. 결국 병렬관의 길이가 길수록 유속이 모든 병렬관을 통과하는 유속이 점점 균일화된다는 원리를 적용할 수 있다.

2.2 정류장치 구성

왜곡된 유속분포를 직선화하고 난류의 강도를 합리적인 수준으로 감소시킬 수 있도록 다양한 직경과 길이의 관을 적층하여 제작한 다중병렬관을 이용한 정류장치를 제작하여 그 성능을 평하고자 한다. 정류장치에 적용한 튜브는 투명 PC관으로 전기 절연성, 소화성, 내산성이 있으며, 내후성이 크고 내충격성이 강하여 가벼우면서도 단속적인 충격에 강하다. 정류장치에 적용할 PC관의 직경과 길이는 일반적인 실내 수리실험 수로에 적용 가능한 범위에서 결정하였다. 이 연구에서는 PC관 직경 D가 20 mm, 30 mm, 40 mm의 3가지 그리고 길이 L이 0.1 m, 0.2 m, 0.3 m의 3가지를 조합한 총 9개의 다중병렬관 정류장치를 제작하여 성능을 평가하였다. 각 PC관의 두께는 관들을 적층시 형상이 왜곡되지 않을 정도의 강도를 유지하기 위해서 20 mm는 0.3 mm 그리고 30 mm와 40 mm는 0.5 mm의 두께를 적용하였다. 관의 두께에 의해 통수 단면적이 줄어드는 면적은 전체 단면적 대비 각각 6.0%, 6.6%, 5.0%로 단면 차단효과(blockage effect)는 현저하지 않으며, 각각의 차이는 미미하다. Fig. 1은 이 연구에서 적용한 총 9가지의 PC관을 보여준다.

Fig. 1.

PC (polycarbonate) tubes of three different diameters and lengths in the present flow straightener

전체 9가지 PC관을 병렬로 적층하여 Fig. 2에서 보인 것처럼 카트리지 형태의 정류장치를 제작하여 수리실험을 수행할 때 정류장치의 교체가 쉽게 만들었다. 정류장치는 실험수로의 폭에 맞게 제작한 아크릴판을 이용한 틀 안에 PC관을 적층하였다. 흐름에 의해 병렬관이 변형되지 않도록 각 관의 중앙부에 소량의 접착제를 발라서 병렬관 모두가 일체가 되도록 제작하였다.

Fig. 2.

Bird-eye and front views of the present flow straightener consisting of multiple parallel PC tubes

3. 성능평가 수리실험

3.1 실험 설정

수리실험은 폭 0.6 m 높이 0.6 m, 길이 10 m의 직선 가변경사수로에서 수행하였다. Fig. 3에 보인 것처럼, 실험 수로의 상류부에 있는 유량공급조에는 유량공급관과 총 5개의 타공판을 이용한 정류장치가 있다. 실험시설의 유량공급장치는 최대 0.3 m³/s의 유량을 공급할 수 있다. 실험구간에서의 수심은 수로 하류부에 설치된 연직수문을 이용하여 조절한다. 정류장치는 직사각형 단면의 직선수로 상류단으로부터 2 m 하류 지점에 설치하여 정류 능력을 평가한다.

Fig. 3.

Laboratory experimental rectangular glass channel and experimental setup

타공판이 유량공급수조 내부에(즉 실험수로 상류에) 설치되어 있다고 하더라도 흐름의 후르드수(Froude number, Fr)가 크면 자유수면 변동도 무시할 수 없으며, 흐름이 쉽게 왜곡되고 수로로 공급되는 물속에 작은 공기방울이 포함될 수 있다. 이 연구에서는 흐름 왜곡과 높은 난류강도를 감소시키는 정류 능력을 분명하게 확인하기 위해서 후르드수 약 0.5 조건에서 성능 실험을 수행하였다. PC관의 길이 L과 직경 D를 실험조건으로 설정하여 다양한 L과 D를 가지는 다중병렬관으로 만든 정류장치의 명칭, 무차원 길이 L*를 포함한 제원과 각 실험 조건을 평균유속, 후르드수, 레이놀즈수(Re)의 항으로 정리하면 Table 1과 같다.

주어진 수심과 유량 조건에서 난류 유속 계측은 Nortek사의 초음파 도플러 유속계(Acoustic Doppler Velocimeter, ADV) Vector-300m을 이용하였다. ADV 유속계는, Fig. 4에 보인 것처럼, 다중병렬관의 하류단으로부터 2.0 m 하류 지점의 수로 중앙에 설치하고 수심의 1/2 위치에서 난류 유속을 계측하였다. 유속의 자료추출률(sampling rate)은 64 Hz를 적용하였으며, 모든 유속자료는 300초 동안 계측하여 분석하였다.

Fig. 4.

Velocity measurement using ADV installed 1.0 m downstream of the flow straightener (upstream view)

3.2 결과분석

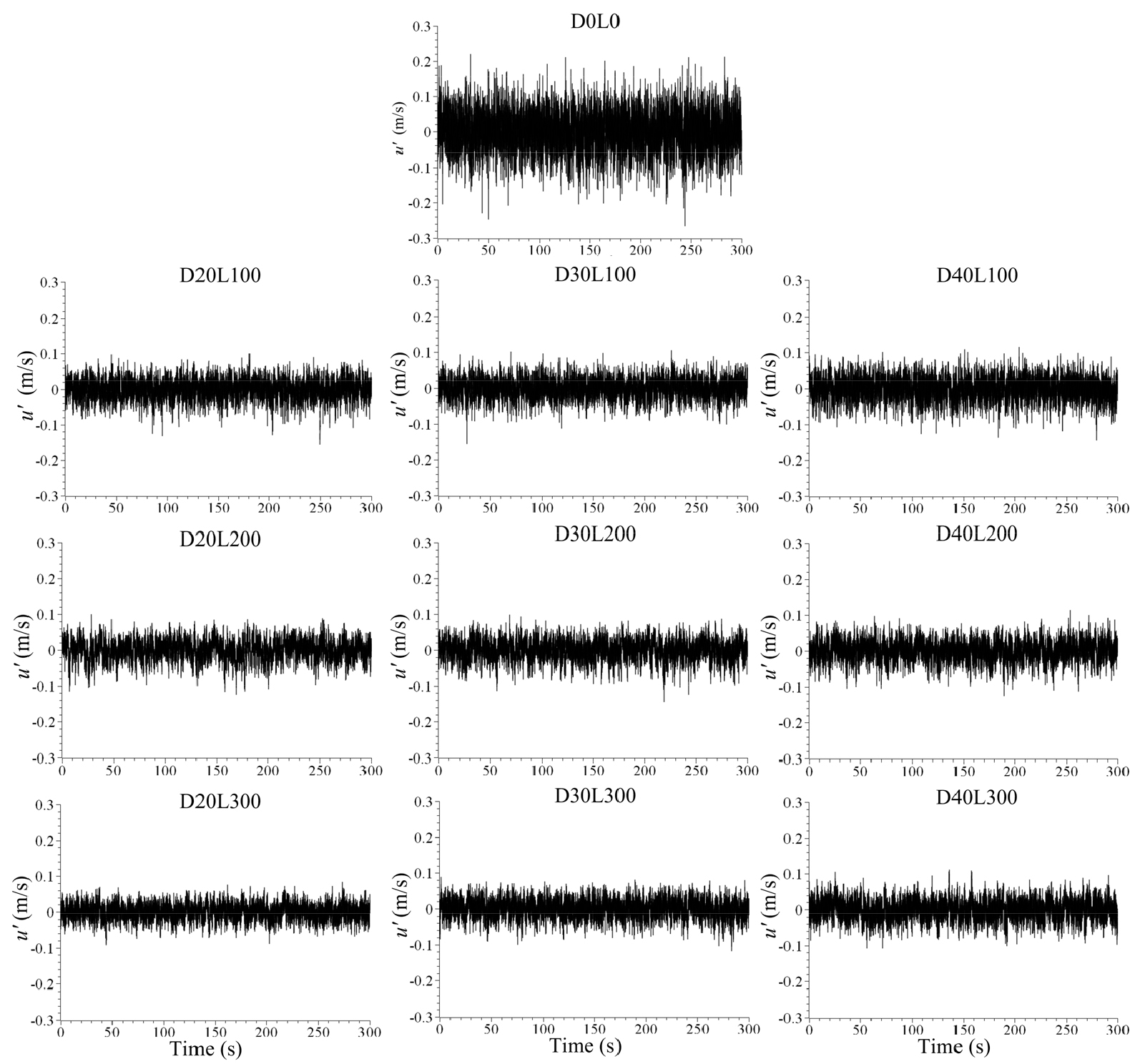
실험수로에서 계측한 유속의 변동성분을 그림으로 나타내면 Fig. 5와 같다. 정류장치를 설치하지 않은 경우인 D0L0의 결과를 보면 유속 변동성분이 대략 -0.2 m/s~0.2 m/s의 범위에 있는 것을 확인할 수 있다. 정류장치를 설치한 경우, 모든 종류의 장치에 대해서 유속 변동성분의 범위가 대략 1/2 수준으로 감소하는 것으로 나타났다. 아울러 길이가 짧은 L100 경우보다 상대적으로 PC관의 길이가 긴 L300의 경우가 미소하게나마 유속 변동성분의 범위가 더 축소되는 것을 확인할 수 있다. 한편, 정류장치를 설치하지 않은 D0L0 경우의 유속 변동성분과 비교해 보면, 이 실험 결과는 실험 수로 상류에 있는 유량공급조 내부에 설치된 기존 타공판은 고유량 조건에서 정류 효과가 떨어짐을 보여준다.

Fig. 5.

Comparison of the fluctuating part of turbulent velocities measured at 0.6 m downstream of the flow conditioners

정량적으로 유속 변동성분의 특성 변화를 분석하기 위해서 난류강도(turbulence intensity, TI)를 비교하였다.

여기서, u'은 난류 변동성분의 평균 제곱근(root mean square)이고 U는 시간평균 유속으로 각각 다음과 같이 정의된다.

여기서, k는 난류운동에너지(turbulence kinetic energy)이며, 아래첨자 x,y,z는 유속의 각 방향 성분을 나타냈다.

공기역학 분야의 연구에서 이용되는 풍동 시험 구간의 유입단면에서 자유흐름(free-stream flow)이 가지는 난류강도는 대부분 2% 이내(Hussein and Martinuzzi, 1996; Damiola et al., 2023)이다. 개수로 흐름의 난류를 연구한 Nakagawa and Nezu (1987)가 매끄러운 개수로에서 수행한 연구 결과에 의하면 바닥 경계층의 영향이 적은 바닥으로부터 떨어진 수심 중앙 부근에서의 난류강도는 약 3% 정도이다. 개수로 흐름에서의 유속 변동성분 u'을 마찰유속(friction velocity) u*로 무차원화한 값을 연구한 Nezu (2005)의 연구 결과를 보면, 경계층의 영향이 적은 바닥으로부터 떨어진 수심 중앙 부근에서의 유속 변동성분을 마찰유속으로 무차원화한 u'/u*는 대략 1.2의 값을 갖는다. Niño et al. (2003)이 매끄러운 개수로에서 수행한 Fr = 0.485~0.626 범위의 실험 자료를 보면 마찰유속 u*의 값은 0.016 m/s~0.023 m/s의 범위에 있으므로, 여기에 Nezu (2005)의 연구 결과를 대입하면 난류강도는 대략 2%~ 2.8%의 범위임을 알 수 있다. 결과적으로 매끄러운 개수로에서의 수행하는 실험에서 접근 흐름의 적절한 난류강도는 3% 이내가 되도록 흐름을 정류하는 것이 필요하다고 볼 수 있다.

본 연구에서 실험을 통해 계측된 유속자료를 이용하여 계산한 난류운동에너지와 난류강도를 정리하면 Table 2와 같다. 정류장치를 설치하지 않은 경우의 난류강도는 6.21%로 산정되었으며, 이 연구에서 개발한 정류장치를 설치한 경우는 전반적으로 난류강도는 절반 이하로 감소하는 것으로 나타났다. 관의 직경이 작을수록 그리고 관의 길이가 길수록 난류강도의 감소 폭은 큰 것으로 나타났다. 관의 직경이 20 mm와 30 mm인 두 경우는 관의 길이가 0.1 m와 0.2 m일 때 난류강도 TI의 크기는 모두 약 50% 정도 유사하게 감소하는 것으로 나타났다. 관의 길이가 0.3 m인 경우 TI의 크기는 관의 직경을 감소시킴에 따라 선형적으로 분명하게 감소하는 것을 볼 수 있다. 즉, 관의 길이 0.3 m이고 직경이 20 mm인 정류장치를 설치할 경우, TI는 약 40%로 감소하여 2.44%의 값을 가지는 것으로 나타났다.

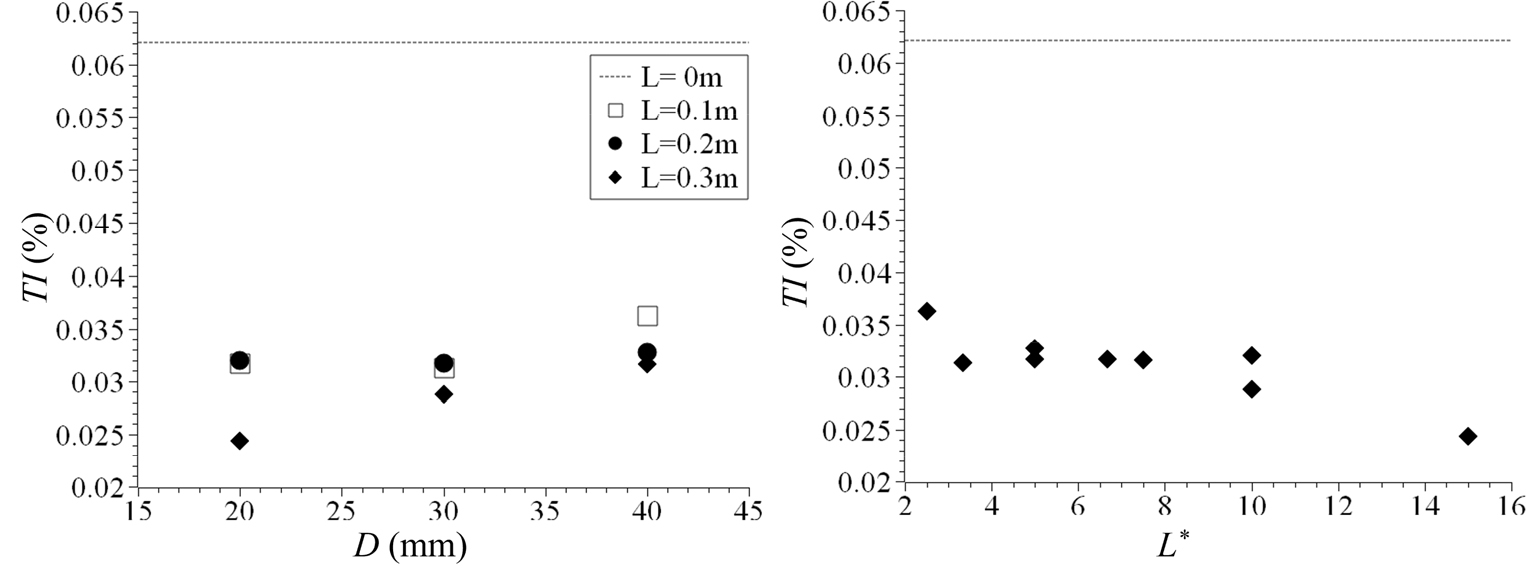
산정한 난류강도 TI와 정류관의 직경 D 그리고 무차원 거리 L*(= L/D)와의 관계를 도시하면 Fig. 6과 같다. 정류관을 설치하지 않은 L = 0 m의 경우에 비하면 정류관을 설치한 모든 경우에 TI가 현저히 감소하는 것을 볼 수 있다. TI와 D의 관계를 보면 L = 0.3 m인 경우 정류관의 직경이 감소할수록 TI가 선형적으로 감소하는 것으로 나타났다. L = 0.2 m와 0.1 m인 경우는 상대적으로 TI감소 추세가 뚜렷하지 않았다. TI와 무차원 길이 L*와의 관계를 보면 L*가 10 이하인 경우는 난류강도의 감소가 유사한 것으로 나타났다. 반면, L*가 15인 경우 TI의 감소 폭이 현저한 것으로 나타났다. 결국, 다중병렬관을 이용한 정류장치는 모든 실험 조건에서 난류강도를 50% 정도 줄일 수 있으며, 결과값은 일반적인 수리실험 조건에서 양호하게 정류된 흐름의 난류강도 수준임을 보여준다. 정류장치의 효과를 분명하게 하기 위해서는 관의 길이를 길게 하는 것이 좋지만, 이 경우 정류장치에 의한 에너지 손실이 클 수도 있다. 본 연구에서 실험을 수행한 실험실 규모 조건에서 확실한 정류 효과를 확보하기 위해서는 정류관의 직경을 20 mm로 유지하는 것이 적합한 것으로 나타났다.

Fig. 6.

Comparisons of turbulence intensities versus the diameter and dimensionless length of flow straighteners

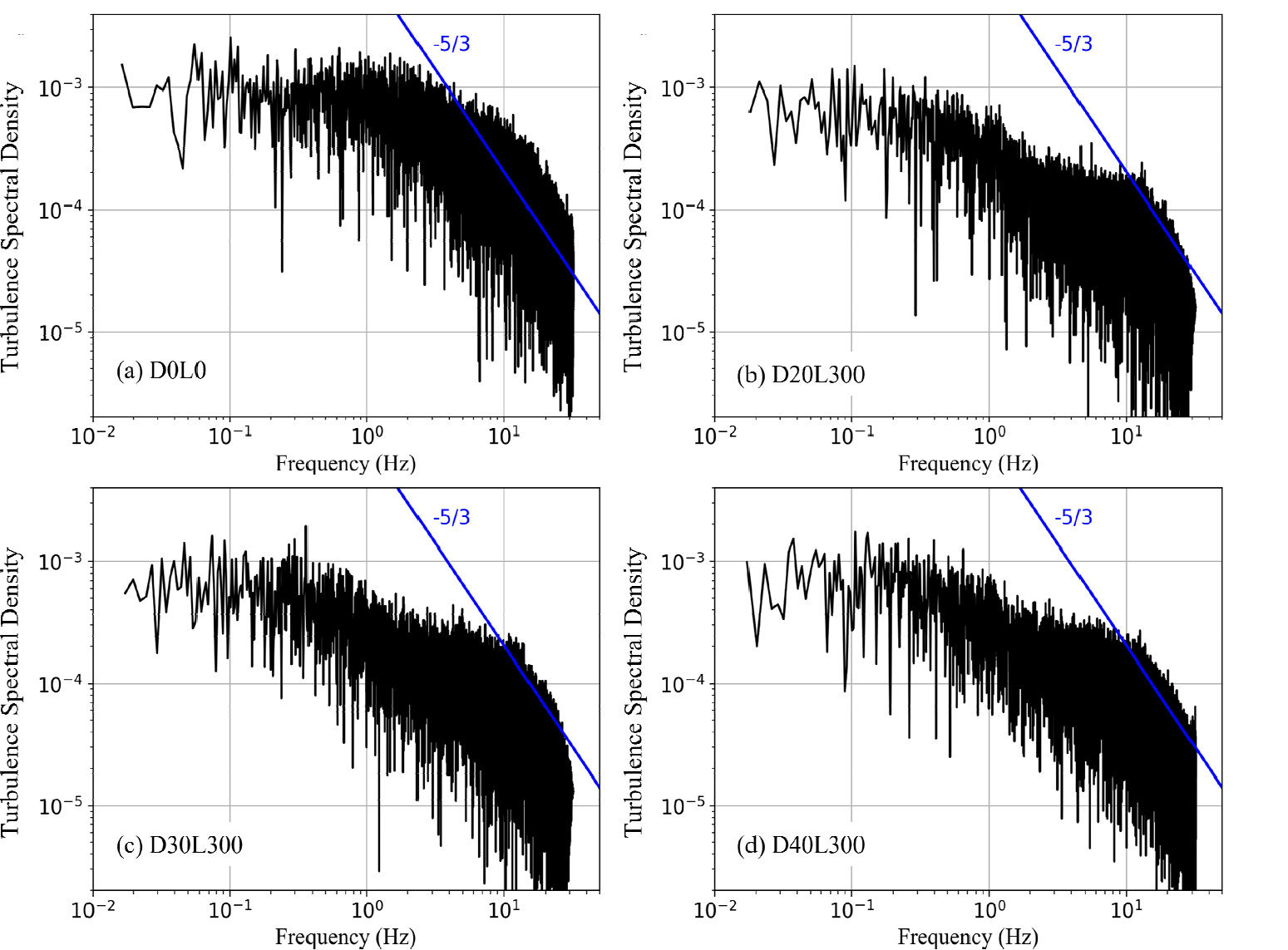
다중병렬관의 길이가 0.3 m인 경우에 계측한 흐름방향 유속성분의 에너지 스펙트럼 변화를 분석하기 위해서 난류 스펙트럼 밀도를 도시하면 Fig. 7과 같다. 지배적인 에너지 스펙트럼 빈도는 f=10-1 정도인 것으로 나타났으며, 정류장치를 이용하여 정류하더라도 이 양상에는 변화가 없는 것으로 나타났다. 정류장치를 설치할 경우 f=5×10-11×101에서의 난류에너지 밀도가 감소하는 것으로 나타났다. 난류에너지는 관성하부영역(inertial subrange)에서 콜모고로프의 벽법칙(Kolmogorov’s power law)으로 -5/3의 경사를 가지며 큰 와(eddy)에서 작은 와로 에너지가 전달된다. 계측된 유속이 가지는 난류에너지 분포에서 관성하부영역을 파악하기 위해서 f-5/3 선을 파란색으로 Fig. 7에 추가하였다. 결과를 보면 관성하부영역은 대략 f=101 빈도 이상에서 발생하면 전반적인 에너지 캐스케이드 양상을 파악하기 위해서는 보다 높은 자료추출률을 가지는 고사양의 유속계를 이용한 유속 계측이 필요함을 볼 수 있다.

Fig. 7.

Turbulence spectra of measured longitudinal velocity component

정류장치 성능평가 실험 사진을 비교하면 Fig. 8과 같다. 이들 사진 분석을 통해 작은 공기방울들이 정류장치를 통과하면서 제거되는 현상을 발견하였다. 실험 전에는 이러한 현상을 예상하지 못했다. 실험수로의 상류에 위치한 유량공급조에서 유량이 증가하면서 다량의 작은 공기방울들이 발생하여, Fig. 8(a)에서 흰색 점선 사각형과 점선 타원형으로 표시한 것처럼, 의도치 않게 실험 구간으로 유입되었다. 발생한 공기방물들은 크기가 작아(즉 부력이 작아서) 빠르게 수면으로 상승하지 못하고 흐름방향 유속이 0.8 m/s 이상으로 빨라서 하류부 실험구간까지 이동하고 있음을 알 수 있다. 공기방울들의 분포는 흰 사선의 사각형 상자 내부에서처럼 흐름방향으로 길게 분포하는 것이 대부분이며 가끔은 흰 타원형에 포함된 것처럼 연직방향으로 분포할 때도 있다. 흥미롭게도 이러한 공기방울들은 정류장치를 통과한 후 빠르게 수면으로 상승하면서 제거되며, 이러한 제거 현상은 정류관의 직경이나 길이에 크게 상관없이 거의 유사하게 발생하는 것으로 나타났다. Figs. 8(b)~8(d)의 기울어진 흰색 점선 사각형 구역에서 보인 것처럼 공기방울이 상승하는 각도는 수평으로부터 약 16°로 모두 유사함을 볼 수 있다. 이렇게 공기방울이 유사한 각도의 사선으로 상승하는 것은 흐름방향 유속이 유사하므로 공기방울의 상승속도(rising velocity)도 모두 유사함을 나타낸다. 즉, 공기방울의 상승속도는 공기방울의 직경과 관계가 있으므로 실험에서 적용한 모든 정류관을 통과한 공기방울의 크기는 유사함을 의미한다. 정류장치를 설치한 실험 구간에서의 흐름 단면 중심부에서 측정한 흐름방향 시간평균유속과 Fig. 8에서 보인 공기방울의 상승 각도를 측정하여 산정한 공기방울의 상승 속도는 약 0.24 m/s인 것으로 나타났다. 즉, 정류장치를 통과한 후 공기방울은 약 0.24 m/s의 속도로 수면으로 상승하여 제거되는 것으로 나타났다.

Fig. 8.

Experimental snapshots of flows in open channel (a) without and (b)-(d) with three different long flow straighteners

물이 공기방울에 작용하는 점성력에 비해 공기방울의 상승속도에 의한 관성력의 크기를 무시할 수 없는 경우에 구형(spherical) 공기방울과 회전타원체(spheroidal) 공기방울의 상승속도는 다음과 같이 각각 산정할 수 있다(Wallis, 1974; Mendelson, 1967).

여기서, vb는 공기방울의 상승속도, g는 중력가속도, ρL과 μL은 액체의 밀도와 점성계수, σL은 액체의 표면장력, de는 공기방울의 부피등가직경(volume-equivalent diameter)이다. 이들 식에서 제시한 바와 같이 공기방울의 상승속도는 매체인 물의 물리적 성질이 일정하다면 공기방울의 직경과 비례관계에 있다. 따라서, 정류장치 상류부에서 거의 수평방향으로 이동하는 작은 공기방울이 정류장치를 통과한 후 상승한다는 것은 공기방울들이 병렬 정류관을 통과하면서 그 크기가 커짐을 의미한다. 공기방울이 병렬 정류관을 통과하면서 공기방울의 크기가 커지는 것은 두 가지 원인이 있을 수 있다. 첫째 Godlieb et al. (2011), Song et al. (2018) 등의 연구 결과에 의하면 압력이 감소함에 따라 공기방울의 크기와 상승속도는 증가한다. 따라서, 흐름이 정류관을 통과할 때 압력흐름(pressurized flow)이 되며, 관중심부에서 유속이 빨라지면서 압력이 낮아져 그만큼 공기방울의 크기가 커진다고 볼 수도 있다. 둘째는 Fig. 9에서 보인 것처럼 실험에서 촬영한 사진을 분석해 보면, Fig. 9(a)에서처럼 다수의 크고 작은 공기방울들이 PC관의 벽면에 달라붙어 있으며, Fig. 9(b)처럼 PC관 벽면 형성된 큰 공기방울들이 흐름에 의해 이탈되어 정류장치를 통과한 후 수면으로 상승하는 것을 볼 수 있었다. 즉 작은 공기방울이 PC관을 통과할 때 PC관 벽면에 붙거나 이미 붙어 있는 공기방울과 접촉하면서 직경이 커지게 되며, 커진 공기방울은 물의 유속에 의해 벽면으로부터 이탈하여 PC관을 통과한 후 부력 증가로 상승하는 것으로 판단된다. 본 연구에서 개발한 정류장치의 공기 제거 능력에 대해서는 추후 특수 촬영 장비 및 압력센서를 이용하여 보다 정확한 분석을 위해서 후속 연구를 통해 진행하고자 한다.

Fig. 9.

Snapshots of (a) bubbles attached on the PC tube wall and (b) bubbles falling off the PC tube wall

4. 결 론

본 연구에서 개발한 다중병렬관을 이용한 정류장치는 다음과 같은 흐름을 안정화하는 특징이 있음을 실험을 통해 확인하였다.

1. 실험수로에서 과도하게 발생한 약 6.2%의 난류강도를 다중병렬관을 이용한 정류장치는 모든 실험 조건에서 난류강도의 크기를 절반 수준으로 줄일 수 있는 것으로 산정되어 유속의 과도한 변동을 제어할 수 있는 것으로 나타났다.

2. 일반적인 개수로 수리실험에서 양호하게 정류된 흐름 수준인 난류강도 3% 내외를 유지하기 위해서는 다중병렬관의 직경은 30 mm 이하가 바람직하며, 직경이 20 mm이고 길이가 0.3 m인 정류관을 사용할 때 난류강도를 약 40%로 감소시켜 약 2.4%의 값을 유지할 수 있는 것으로 나타났다.

3. 관의 길이가 0.3 m인 경우 난류강도의 크기는 관의 직경을 감소시킴에 따라 선형적으로 분명하게 감소하는 것을 볼 수 있으며, 일반적인 실험실 규모 조건에서 확실한 정류 효과를 확보하기 위해서는 정류관의 직경을 20 mm로 유지하는 것이 바람직한 것으로 나타났다.

4. 실험 수로에 고유량을 공급할 경우 발생하는 작은 공기방울은 다중병렬관을 통과하면서 크기가 커짐에 따라 증가한 부력에 의해 약 0.24 m/s의 속도로 수면으로 상승하여 제거 되는 것으로 나타났다. 그리고 정류관의 직경과 길이에 상관없이 정류장치를 통과한 공기방울은 모두 유사한 속도로 수면으로 상승하여 제거되었다.