Development of new artificial neural network optimizer to improve water quality index prediction performance

Yong Min Ryu; Young Nam Kim; Dae Won Lee; Eui Hoon Lee

doi:10.3741/JKWRA.2024.57.2.73

Preview

Research Article

Journal of Korea Water Resources Association. 29 February 2024. 73-85
https://doi.org/10.3741/JKWRA.2024.57.2.73

Development of new artificial neural network optimizer to improve water quality index prediction performance

수질 지수 예측성능 향상을 위한 새로운 인공신경망 옵티마이저의 개발

Yong Min Ryu^a

Young Nam Kim^b

Dae Won Lee^c

Eui Hoon Lee^d^*

류 용민^a

김 영남^b

이 대원^c

이 의훈^d^*

^aPh.D Student, Department of Civil Engineering, Chungbuk National University, Cheongju, Korea

^bPh.D Candidate, Department of Civil Engineering, Chungbuk National University, Cheongju, Korea

^cMaster Student, Department of Civil Engineering, Chungbuk National University, Cheongju, Korea

^dAssociate Professor, School of Civil Engineering, Chungbuk National University, Cheongju, Korea

^a충북대학교 토목공학과 박사과정

^b충북대학교 토목공학과 박사수료

^c충북대학교 토목공학과 석사과정

^d충북대학교 토목공학부 부교수

^{*Corresponding Author}

ABSTRACT

Predicting water quality of rivers and reservoirs is necessary for the management of water resources. Artificial Neural Networks (ANNs) have been used in many studies to predict water quality with high accuracy. Previous studies have used Gradient Descent (GD)-based optimizers as an optimizer, an operator of ANN that searches parameters. However, GD-based optimizers have the disadvantages of the possibility of local optimal convergence and absence of a solution storage and comparison structure. This study developed improved optimizers to overcome the disadvantages of GD-based optimizers. Proposed optimizers are optimizers that combine adaptive moments (Adam) and Nesterov-accelerated adaptive moments (Nadam), which have low learning errors among GD-based optimizers, with Harmony Search (HS) or Novel Self-adaptive Harmony Search (NSHS). To evaluate the performance of Long Short-Term Memory (LSTM) using improved optimizers, the water quality data from the Dasan water quality monitoring station were used for training and prediction. Comparing the learning results, Mean Squared Error (MSE) of LSTM using Nadam combined with NSHS (NadamNSHS) was the lowest at 0.002921. In addition, the prediction rankings according to MSE and R² for the four water quality indices for each optimizer were compared. Comparing the average of ranking for each optimizer, it was confirmed that LSTM using NadamNSHS was the highest at 2.25.

Keywords

Water quality index

Long Short-Term Memory

Novel Self-adaptive Harmony Search

Improved optimizer

하천과 저수지의 수질을 예측하는 것은 수자원관리를 위해 필요하다. 높은 정확도의 수질 예측을 위해 많은 연구들에서 인공신경망이 활용되었다. 기존 연구들은 매개변수를 탐색하는 인공신경망의 연산자인 옵티마이저로 경사하강법 기반 옵티마이저를 사용하였다. 그러나 경사하강법 기반 옵티마이저는 지역 최적값으로의 수렴 가능성과 해의 저장 및 비교구조가 없다는 단점이 있다. 본 연구에서는 인공신경망을 이용한 수질 예측성능을 향상시키기 위해 개량형 옵티마이저를 개발하여 경사하강법 기반 옵티마이저의 단점을 개선하였다. 본 연구에서 제안한 옵티마이저는 경사하강법 기반 옵티마이저 중 학습오차가 낮은 Adaptive moments (Adam)과 Nesterov-accelerated adaptive moments (Nadam)를 Harmony Search (HS) 또는 Novel Self-adaptive Harmony Search (NSHS)와 결합한 옵티마이저이다. 개량형 옵티마이저의 학습 및 예측성능 평가를 위해 개량형 옵티마이저를 Long Short-Term Memory (LSTM)에 적용하여 국내의 다산 수질관측소의 수질인자인 수온, 용존산소량, 수소이온농도 및 엽록소-a를 학습 및 예측하였다. 학습결과를 비교하면, Nadam combined with NSHS (NadamNSHS)를 사용한 LSTM의 Mean Squared Error (MSE)가 0.002921로 가장 낮았다. 또한, 각 옵티마이저별 4개 수질인자에 대한 MSE 및 R²에 따른 예측순위를 비교하였다. 각 옵티마이저의 평균 순위를 비교하면, NadamNSHS를 사용한 LSTM이 2.25로 가장 높은 것을 확인하였다.

키워드

수질인자

Long Short-Term Memory

Novel Self-adaptive Harmony Search

개량형 옵티마이저

MAIN

1. 서 론
2. 연구방법
2.1 Long Short-Term Memory (LSTM)
2.2 경사하강법 기반 옵티마이저
2.3 Harmony Search (HS) 및 Novel Self-adaptive Harmony Search (NSHS)
2.4 개량형 옵티마이저
2.5 데이터 전처리(Data pre-processing)
2.6 대상 유역 및 자료 구축
3. 연구결과
3.1 학습결과
3.2 예측결과
4. 결 론

1. 서 론

하천 및 저수지는 인간이 음용할 수 있는 식용수를 취수하기 위해 사용되는 중요한 장소이다. 최근 도시화 및 산업화로 인해 하천 또는 저수지를 포함한 많은 지역에서 과거에 비해 수질오염에 대한 문제가 증가하고 있다(Park et al., 2006). 높은 정확도 기반의 하천 및 저수지의 수질예측은 수자원 관리와 수질오염 방지를 위해 필수적이다(Lu and Ma, 2020).

수질을 예측하기 위해 사용된 전통적인 기법은 선형방법을 기반으로 한 Auto-regressive, Moving average 및 Auto-regressive integrated moving average (Cai et al., 2015; Babu and Reddy, 2014; Faruk, 2010). 그러나, 선형방법 기반의 수질예측 기법은 수질인자 간의 비선형 관계를 해석할 수 없기 때문에 한계가 있다(Xiang and Jiang, 2009). 선형방법 기반 수질예측 기법의 단점을 개선하기 위해 수질 인자들의 비선형성을 해석할 수 있는 인공신경망(Artificial Neural Network, ANN)을 활용한 연구가 진행되었다. ANN은 수질 자료 간의 비선형성을 고려하여 예측을 진행하기 때문에 선형방법 기반의 예측기법보다 높은 정확도를 나타냈다(Zhang et al., 2017; Li et al., 2019).

ANN은 기계학습(Machine learning) 중 하나로 인간의 두뇌에서 신호를 처리하는 방식을 모방하여 제안된 기법이다. McCulloch and Pitts (1943)는 수학적 기법을 활용하여 ANN의 기초 논리를 제시하였으며, Rosenblatt (1958)은 Perceptron의 개념을 도입하였다. 이후, Rumelhart et al. (1986)은 ANN을 활용한 학습 및 예측과정에서 Back propagation through time을 이용하는 Recurrent Neural Network (RNN)를 제안하였다. RNN은 시계열 자료 분석에 좋은 성능을 보였다. 그러나 RNN은 자료의 길이가 길어질수록 과거의 자료를 반영하기 어려운 기울기 소실이 발생한다. RNN의 기울기 소실을 해결하기 위해 Hochreiter and Schmidhuber (1997)는 Long Short-Term Memory (LSTM)를 제안하였다. 이후, ANN의 학습과정 중 저장구조의 부재 등 구조적 단점을 개선하기 위해 새로운 ANN에 대한 연구가 진행되었다. Lee and Lee (2022a)는 저장구조의 부재 및 지역해로의 수렴가능성을 개선하고자 ANN과 메타휴리스틱 최적화 알고리즘을 직렬적으로 연결한 새로운 ANN을 제시하였다.

다양한 모형의 ANN은 수집된 데이터의 인자별 비선형성을 고려할 수 있다는 장점으로 인해 많은 분야에서 적용되었다(Ryu and Lee, 2022). Dogan et al. (2008)은 ANN을 활용하여 생물학적 산소요구량(Biochemical Oxygen Demand, BOD) 예측을 위한 민감도 분석 및 예측을 실시하였다. 예측결과는 화학적 산소요구량(Chemical Oxygen Demand, COD)을 활용한 BOD 예측이 가장 우수한 방법임을 보였다. Wang et al. (2008)은 엽록소-a (Chlorophyll-a, Chl-a)를 예측하기 위해 Multi Layer Perceptron (MLP)을 활용하였으며, MLP가 Chl-a 예측에 효과적임을 확인하였다. Akkoyunlu and Akiner (2010)는 용존산소량(Dissolved Oxygen, DO)을 예측하기 위해 ANN을 활용하였다. 예측결과를 통해 ANN이 비선형 회귀법(Nonlinear regression method)보다 좋은 성능을 나타냄을 확인하였다.

ANN은 학습 및 예측과정에서 옵티마이저를 선택하는 것이 중요하다(Zare et al., 2011). 옵티마이저는 복잡한 비선형적 입출력 관계를 근사화하는 ANN의 연산자이다. 옵티마이저는 ANN의 계산값과 출력자료 간의 오차가 가장 작은 매개변수(가중치 및 편향)를 탐색한다. 기존의 연구들에서 사용된 옵티마이저는 수학적 기법인 수치미분을 기반으로 매개변수를 탐색하는 경사하강법 기반 옵티마이저이다. 경사하강법 기반 옵티마이저는 기존에 생성된 매개변수를 기반으로 손실함수(Loss function)에 대한 기울기와 학습률을 통해 새로운 매개변수를 탐색한다.

그러나 경사하강법 기반 옵티마이저는 두 가지의 단점이 존재한다. 첫 번째 단점은 지역 최적해로의 수렴 가능성이다. 경사하강법 기반 옵티마이저는 ANN의 출력값과 데이터 간의 오차가 최소가 되는 상관관계를 탐색하는 과정에서 지역탐색만을 고려한다. 경사하강법 기반 옵티마이저는 전역탐색을 고려하지 않기 때문에 전역 최적값을 찾지 못할 가능성이 있다(Sedki et al., 2009). 두 번째 단점은 해 저장공간의 부재이다. 경사하강법 기반 옵티마이저는 학습을 진행하는 과정에서 기존에 생성된 매개변수에 대한 저장공간이 없다. 매개변수 저장공간의 부재로 인해 기존에 생성된 매개변수의 오차가 새로운 매개변수의 오차보다 작아도 강제적으로 매개변수가 갱신된다(Lee and Lee, 2022b). 따라서, 경사하강법 기반 옵티마이저는 학습이 진행되어도 최적의 매개변수를 탐색하지 못할 가능성이 있다.

두 가지의 단점이 존재하는 경사하강법 기반 옵티마이저의 탐색성능을 개선하기 위해서는 전역탐색이 가능하며, 알고리즘 내 해의 저장공간이 존재하는 메타휴리스틱 최적화 알고리즘을 적용할 수 있다. 메타휴리스틱 최적화 알고리즘은 가능해의 범위에서 임의의 해를 선택하는 전역탐색과 기존에 생성된 해집단의 재조합 및 미세조정을 통해 새로운 해를 선택하는 지역탐색을 통해 최적해를 탐색한다. 또한, 메타휴리스틱 최적화 알고리즘은 알고리즘 내의 저장공간을 통해 기존의 해를 저장하고 새롭게 탐색한 해와의 비교가 가능하다.

본 연구는 경사하강법 기반 옵티마이저를 메타휴리스틱 최적화 알고리즘과 결합하여 개량형 옵티마이저(Improved optimizers)를 개발하였다. 개량형 옵티마이저의 탐색성능을 검토하기 위해 LSTM에 적용하였다. 경사하강법 기반 옵티마이저의 단점을 개선하기 위해 메타휴리스틱 최적화 알고리즘 중 Harmony Search (HS) 및 Novel Self-adaptive Harmony Search (NSHS)를 사용하였다. HS는 구조가 단순하고 최적해 탐색성능이 우수하다. NSHS는 HS의 사용성 및 탐색성능을 개선한 알고리즘이다. 개량형 옵티마이저를 적용한 LSTM의 성능을 검토하기 위해 낙동강에 위치한 다산 관측소의 수질인자인 수온(Water Temperature, WT), DO, pH 및 Chl-a를 학습 및 예측하였다.

2. 연구방법

2.1 Long Short-Term Memory (LSTM)

ANN 중 순환구조를 갖는 RNN은 음성 인식, 언어 처리 및 시계열 자료처리에 좋은 성능을 보였다. 그러나 RNN은 장기간의 자료를 사용하는 경우에 오차 경사의 소실이 발생하여 성능이 저하된다. 이러한 RNN의 단점을 개선하기 위해 RNN의 구조에 셀 상태(Cell state) 및 Gate 개념을 추가한 LSTM이 제안되었다(Hochreiter and Schmidhuber, 1997). LSTM은 Input gate, Forget gate 및 Output gate가 있다. LSTM 내 3개의 Gate는 이전 시점의 불필요한 정보는 지우고 필요한 정보를 기억한다. Input gate는 현재 정보를 현재 시점의 정보를 입력하기 위한 Gate이다. Eqs. (1) and (2)는 Input gate의 연산과정이다.

(1)

i_{t} = σ (W_{x i} x_{t} + W_{h i} h_{t - 1} + b_{i})

(2)

\bar{c_{t}} = \tanh (W_{x c} x_{t} + W_{h c} h_{t - 1} + b_{c})

여기서, i_t는 Input gate 계산값, 𝜎는 시그모이드 함수, xt는 현재 시점의 입력값, h_t-1은 이전 시점의 셀 출력값, W_xi와 W_hi는 각각 x_t와 h_t-1에 대한 input gate의 가중치이며, b_i는 input gate의 편향이다. $\bar{c_{t}}$ 는 예비 셀 상태, W_xc와 W_hc는 각각 x_t와 h_t-1에 대한 예비 셀 상태의 가중치이며 b_c는 예비 셀 상태의 편향이다.

Forget gate는 이전 시점으로부터 전달된 정보를 현재시점에서 제거할지 유지할지를 결정한다. Forget gate 값은 0과 1사이의 값을 가지며 0에 가까울수록 정보가 많이 제거된 것이고 1에 가까울수록 많은 정보를 기억한다. Eq. (3)은 Input gate의 연산과정이다.

(3)

f_{t} = σ (W_{x f} x_{t} + W_{h f} h_{t - 1} + b_{f})

여기서, f_t는 Forget gate 계산값 , W_xf와 W_hf는 각각 x_t와 h_t-1에 대한 Forget gate의 가중치이며, bf는 Forget gate의 편향이다.

Output gate는 셀 출력값과 셀 상태 계산값을 결정한다. Output gate에서 계산된 셀 출력값과 셀 상태 계산값은 다음 시점(t+1)의 계산에 영향을 미친다. Eqs. (4)~(6)은 Output gate의 연산과정이다.

(4)

c_{t} = f_{t} \circ c_{t - 1} + i_{t} \circ \bar{c_{t}}

(5)

o_{t} = σ (W_{x o} x_{t} + W_{h o} h_{t - 1} + b_{o})

(6)

h_{t} = o_{t} \circ \tanh (c_{t})

여기서, c_t는 현재 시점의 셀 상태 계산값이며, c_t-1은 이전 시점의 셀 상태 계산값이다. o_t는 Output gate 계산값, W_xo와 W_ho는 각각 x_t와 h_t-1 에 대한 Output gate의 가중치이며, b_o는 Output gate의 편향이다. 또한, h_t는 현재 시점의 셀 출력값이다. Fig. 1은 본 연구에서 사용된 LSTM의 구조이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F1.jpg

Fig. 1.

Structure of long short-term memory used in this study

기존의 수질인자를 예측한 연구 중 Wang et al. (2017)은 LSTM을 이용하여 DO 및 총 인(Total Phosphorus, TP)을 예측하였으며, 은닉층이 1개일 때 뉴런의 개수에 따른 예측성능을 검토하였다. 예측결과는 은닉층의 노드 개수가 15개일 때, 가장 좋은 예측성능을 나타냈다. 따라서, 본 연구는 LSTM의 은닉층 개수를 1개로 설정하였으며, 은닉층의 뉴런 개수는 15개로 설정하였다.

2.2 경사하강법 기반 옵티마이저

ANN의 연산자 중 옵티마이저는 ANN의 출력값과 관측값 간의 오차가 가장 작은 매개변수를 탐색한다. 옵티마이저의 탐색성능은 ANN의 학습 및 예측성능에 직접적인 영향을 미친다(Joo et al., 2020). 옵티마이저 중 가장 기초적인 경사하강법은 수치미분을 통해 얻은 기울기와 학습률을 이용하여 기울기가 0이 되는 지점을 탐색하는 방법이다. Eq. (7)은 경사하강법의 새로운 매개변수 탐색과정을 나타낸 식이다.

(7)

W_{t} = W_{t - 1} - η \frac{\partial L F}{\partial W_{t - 1}}

여기서, W_t는 새로운 매개변수, W_t-1은 이전 학습의 매개변수, 𝜂는 학습률을 의미하며, LF 는 손실함수이다.

경사하강법은 고정된 학습률을 사용하며, 기존에 이동했던 방향을 기억하지 못한다는 단점이 있다. 이러한 경사하강법의 단점을 개선하기 위해 Momentum 및 Adaptive learning rate를 적용하여 다양한 경사하강법 기반 옵티마이저가 제안되었다. Momentum은 과거에 해를 탐색한 방향을 기억하여 같은 방향으로 추가 이동함으로써 경사하강법의 탐색성능 향상시키는 방법이다. Adaptive learning rate는 경사하강법의 학습률이 일정하다는 단점을 개선하기 위해 학습 과정에 따른 유동적인 학습률을 적용하는 방법이다. 경사하강법 기반 옵티마이저에는 Stochastic Gradient Descent (SGD), Adaptive Gradient (Adagrad), Root Mean Squared propagation (RMSprop), Adaptive delta (Adadelta), A variant of Adam based on the infinity norm (Adamax), Adaptive moments (Adam) 및 Nesterov-accelerated adaptive moments (Nadam)가 있다.

다양한 경사하강법 기반 옵티마이저는 Momentum과 Adaptive learning rate의 적용을 통해 개량되었음에도 불구하고 전역탐색이 불가능하다. 경사하강법 기반 옵티마이저는 초기에 생성되는 매개변수에 따라 지역 최적해에 수렴할 수 있다는 단점이 있다. 또한, 경사하강법 기반 옵티마이저는 기존에 생성된 매개변수를 저장하는 구조가 없어 학습이 진행되어도 최적의 매개변수를 찾지 못할 가능성이 있다. 본 연구는 지역탐색 및 전역탐색을 동시에 고려하고 기존의 탐색된 해를 저장하는 구조가 존재하는 메타휴리스틱 최적화 알고리즘을 이용하여 경사하강법 기반 옵티마이저의 단점을 개선하였다.

2.3 Harmony Search (HS) 및 Novel Self-adaptive Harmony Search (NSHS)

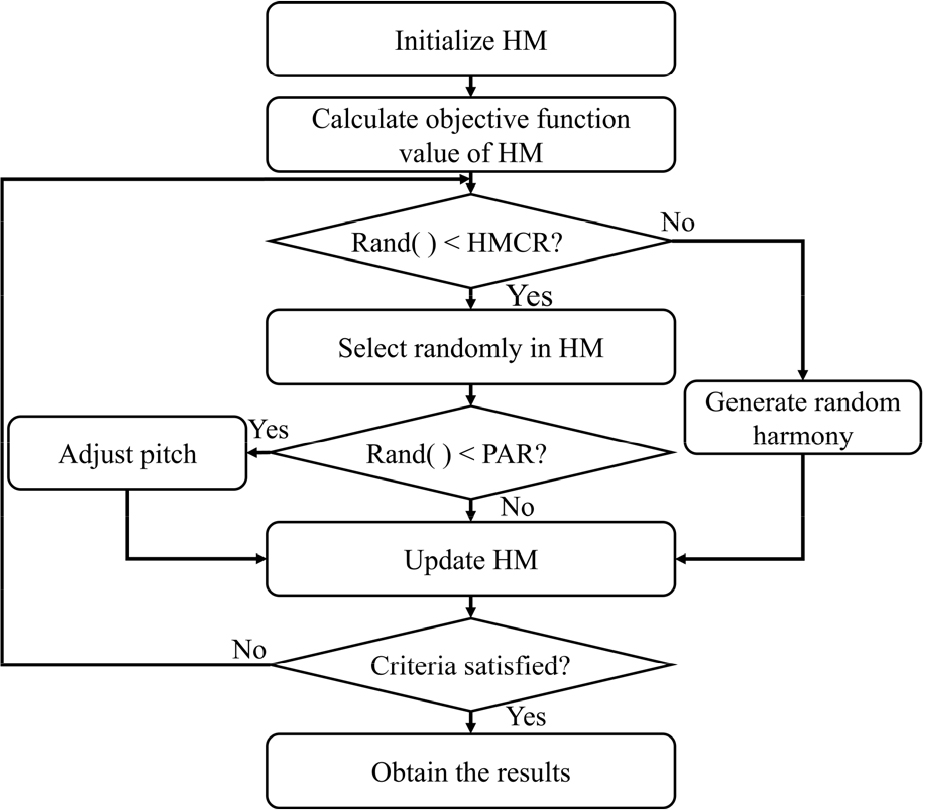
메타휴리스틱 최적화 알고리즘 중 하나인 HS는 악기 연주자들이 즉흥으로 최적의 화음을 찾는 과정을 모방한 알고리즘이다(Geem et al., 2001). HS에서 해(Solution)는 악기 연주자들이 만들어내는 화음에 해당하며, 결정변수(Decision variable)는 악기 연주자들에 해당한다. 또한, 결정변수의 가능해 영역은 악기 연주자들이 연주할 수 있는 음역대에 해당하며, 전역 최적해는 가장 듣기 좋은 화음에 해당한다. HS는 지역탐색과 전역탐색의 반복을 통해 전역 최적해를 탐색한다. Fig. 2는 HS의 탐색과정을 나타낸다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F2.jpg

Fig. 2.

Flowchart of harmony search

HS의 매개변수는 Harmony Memory Size (HMS), Harmony Memory Considering Rate (HMCR), Pitch Adjusting Rate (PAR) 및 Bandwidth (Bw)가 있다. HMS는 해집단인 Harmony Memory (HM)의 크기이며, HMS만큼의 초기 해를 생성한다. HMCR은 전역탐색을 이용한 새로운 해 탐색 또는 HM을 이용한 새로운 해 탐색을 결정한다. HM을 이용하여 새로운 해를 탐색할 경우에는 HM 내의 각 결정변수에 해당하는 임의의 해를 선택한다. PAR은 HM을 이용하여 생성된 새로운 해의 미세조정 여부를 결정한다. 미세조정을 실시할 경우 Bw만큼 미세조정을 실시한다. HS를 통해 생성된 새로운 해는 HM에 저장된 최악의 해와 비교된다. 새로운 해가 최악의 해보다 좋다면 새로운 화음은 HM에 저장되고 최악의 화음은 HM에서 제거된다.

HS는 건설, 설계 및 로봇공학 등 다양한 분야에서 활용되었다(Manjarres et al., 2013). 하지만, HS는 사용자가 직접 매개변수를 설정해야 하며, 매개변수는 HS의 해 탐색성능 및 수렴에 영향을 미친다(Pan et al., 2010). HS의 매개변수 설정에 대한 단점을 개선하기 위해 다양한 알고리즘이 제안되었다. Parameter setting free harmony search, Almost parameter free harmony search 및 NSHS 등 HS의 매개변수 설정에 대한 단점을 개선한 알고리즘 중 NSHS가 수학문제에서 우수한 탐색성능을 보였다(Choi et al., 2019).

NSHS는 Luo (2013)가 제안한 HS 기반 메타휴리스틱 최적화 알고리즘이다. NSHS는 결정변수의 개수에 따라 HMCR이 결정되며, 결정변수가 많은 문제일수록 큰 HMCR을 갖는다. 또한, NSHS는 연주자들이 최적의 화음을 탐색할 때까지 피치를 미세조정하는 것을 착안하여 PAR을 1로 설정한다. Bw는 학습이 진행됨에 따라 감소된다. Eqs. (8) and (9)는 결정변수 개수에 따른 NSHS의 HMCR 및 Bw의 형태이다.

(8)

H M C R = 1 - \frac{1}{n + 1}

(9)

B w_{k} = \{\begin{cases} \frac{u b - l b}{100} \times (1 - \frac{k}{N I}) \\ ; (k = 1, 2, . . . N I) if s t d (f) > 0.0001 \\ 0.0001 \\ ; o t h e r w i s e \end{cases}

여기서, n은 결정변수의 개수, Bw_k는 현재 반복시산의 Bw, k는 현재 반복시산 횟수이다. 또한, ub 와 lb는 결정변수의 최대값 및 최소값이며, NI는 최대 반복시산 횟수이다. std(f)는 현재 반복시산에서 HM내 해집단의 손실함수 계산값에 대한 표준편차를 의미한다.

HS의 전역탐색은 항상 가능해 영역 내에 임의의 실수를 선택한다. NSHS의 전역탐색은 현재 반복시산에서 HM의 손실함수 계산값에 대한 표준편차에 따라 다르게 수행한다. 표준편차가 0.0001보다 작은 경우 NSHS는 빠른 수렴을 위해 좁은 범위 내에서 새로운 임의의 값을 생성한다. 표준편차가 0.0001보다 큰 경우 NSHS는 더 넓은 범위 내에서 새로운 임의의 값을 생성한다. 또한, NSHS는 항상 미세조정을 실시하기 때문에 미세조정을 실시하기 전의 해인 x_i'을 생성한다. NSHS의 x_i'은 Eq. (10)과 같이 생성한다.

(10)

x_{i}' = \{\begin{cases} x_{i}^{j} j \in \{1, 2, . . ., H M S\}; if r n d < H M C R \\ l b + r n d 1 \times (u b - l b); if r n d \geq H M C R and s t d (f) > 0.0001 \\ \min_{j} (x_{i}^{j}) + r n d 1 \times \{\max_{j} (x_{i}^{j}) - \min_{j} (x_{i}^{j})\} \\ ; if r n d \geq H M C R and s t d (f) \leq 0.0001 \end{cases}

여기서, xi'은 미세조정을 실시하기 전의 해, x_i^j는 HM 내 j번째 해의 i번째 결정변수 값이며, min_j(x_i^j) 과 max_j(x_i^j)는 각각 HM 내 i번째 결정변수의 최소값과 최대값이다. 또한, rnd와 rnd1은 0과 1사이의 임의의 실수이다.

Eq. (10)을 통해 생성된 x_i'은 미세조정을 통해 새로운 해인 x_i^new를 생성한다. Eq. (11)은 NSHS의 새로운 해를 생성하는 식이다.

(11)

x_{i}^{n e w} = x_{i}' + r n d 2 \times B w_{k}

여기서, rnd2는 -1과 1사이의 임의의 값이다.

2.4 개량형 옵티마이저

본 연구는 경사하강법 기반 옵티마이저의 지역 최적해 수렴 가능성과 해의 저장공간 부재의 단점을 개선하기 위해 경사하강법 기반 옵티마이저와 HS 또는 NSHS의 결합한 개량형 옵티마이저를 개발하였다. 개량형 옵티마이저는 Gradient descent-based optimizer Conducting Rate (GCR)를 통해 경사하강법 기반 옵티마이저를 실시하거나 HS 또는 NSHS를 실시할지를 결정한다. 개량형 옵티마이저의 해 탐색과정은 Fig. 3과 같다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F3.jpg

Fig. 3.

Flowchart of improved optimizer

Fig. 3을 보면, 개량형 옵티마이저는 경사하강법 기반 옵티마이저를 실시할 경우 기존에 경사하강법 기반 옵티마이저를 통해 생성된 매개변수를 이용하여 매개변수를 탐색하고 결과를 저장한다. HS 또는 NSHS를 실시할 경우 개량형 옵티마이저는 지역탐색 및 전역탐색을 통해 새로운 매개변수를 탐색하고 경사하강법 기반 옵티마이저를 실시한다. 이후 새로운 매개변수와 HM 내 최악의 매개변수를 비교하여 HM을 갱신한다. 본 연구에서 GCR은 Maximum GCR (GCR_max)과 Minimum GCR (GCR_min) 사이에서 반복 학습횟수(Epoch)에 따라 선형으로 감소하는 자가적응형 매개변수를 사용하였다. Eq. (12)는 반복 학습횟수에 따른 GCR의 값이다.

(12)

G C R_{C E} = G C R_{\max} - \frac{G C R_{\max} - G C R_{\min}}{M E} \times C E

여기서, GCR_CE는 현재 반복 학습횟수(Current epoch)의 GCR 값, ME는 최대 반복 학습횟수(Maximum epoch)이며, CE는 현재 반복학습 횟수이다.

본 연구는 개량형 옵티마이저를 제안하기 위해 경사하강법 기반 옵티마이저 중 학습성능이 우수한 옵티마이저를 선정하여 HS 또는 NSHS와 결합하였다. 경사하강법 기반 옵티마이저의 학습결과는 3.1절에 나타냈으며, Adam과 Nadam의 학습오차가 가장 작은 것으로 나타났다. 따라서, Adam combined with HS (AdamHS), Adam combined with NSHS (AdamNSHS), Nadam combined with HS (NadamHS) 및 Nadam combined with NSHS (NadamNSHS)를 이용하여 LSTM을 학습하였으며 Adam 및 Nadam의 학습성능과 비교하였다. 또한, 각 옵티마이저를 이용하여 학습된 LSTM의 예측성능을 비교하였다.

2.5 데이터 전처리(Data pre-processing)

인공신경망의 예측 신뢰도를 높이기 위해서는 자료의 노이즈를 줄이고 범위를 조절하는 등의 데이터 전처리가 필수적이다(Joo et al., 2000). 본 연구는 데이터 전처리 기법 중 Principal Component Analysis (PCA)와 Min-Max Normalization (MMN)을 실시하였다. MMN은 데이터 스케일링을 위한 데이터 전처리 기법인 MMN, Z-score normalization 및 Decimal scaling normalization 중 가장 우수한 성능향상을 보였다(Nawi et al., 2013). PCA는 과적합에 대한 위험성을 감소시킴과 동시에 Chl-a를 예측하는 연구에서 원자료를 사용하는 것보다 좋은 예측성능을 나타냈다(Zheng et al., 2021; Cao et al., 1997).

2.5.1 Min-Max Normalization (MMN)

본 연구에서 취득한 자료는 각각 다른 범위를 갖는다. 하지만, 다른 범위를 갖는 시계열 자료는 학습 및 예측성능에 부정적인 영향을 미친다(Mok et al., 2020). 따라서 ANN의 학습을 실시하기 전에 Data scaling을 실시하는 것이 필요하다. MMN은 최소값과 최대값의 차가 큰 자료를 0과 1사이의 값으로 변환하며 입력 및 출력자료의 범위를 같게 하는 기법이다. MMN은 최대값과 최소값을 기준으로 선형변환을 수행한다. MMN은 원자료간의 관계를 유지하는데 효과적이다(Folorunso et al., 2018). MMN을 실시하기 위한 수식은 Eq. (13)과 같다.

(13)

x_{M M N}^{α} = \frac{x^{α} - x_{\min}}{x_{\max} - x_{\min}}

여기서, x^𝛼_MMN는 MMN을 실시한 α일의 새로운 자료, x^𝛼는 𝛼일의 원자료이며 x_max와 x_min은 각각 원자료의 최대값과 최소값이다.

2.5.2 Principal Component Analysis (PCA)

PCA는 고차원의 자료를 저차원의 자료로 변환시키는 기법이다. PCA는 데이터의 분산(Variance)을 최대한 보존하면서 저차원으로 변환한다. PCA는 주성분(Principal component)을 생성하기 위해 자료를 수직으로 투영하였을 때 분산이 가장 큰 주축(Principal axes)을 결정한다. 이후, 주축에 자료를 수직으로 투영시켜 주성분을 구한다. 이전에 생성된 주축 다음으로 분산이 큰 주축을 정하고 수직으로 투영시켜 다른 주성분을 구한다. 즉, M×N의 자료 X가 있을 때, X의 공분산 행렬을 만들어 공분산 행렬의 고유값(Eigenvalue)와 고유벡터(Eigenvector)을 구한다. 계산한 고유벡터와 X의 내적을 통해 주성분을 생성한다. 고유값이 가장 큰 고유벡터와 내적한 주성분을 PC1이라고 한다. 두번째로 고유값이 큰 고유벡터와 내적한 주성분이 PC2이다.

PCA를 실시함으로써 문제의 복잡성이 감소하여 연산시간을 줄일 수 있다. 또한, PCA는 노이즈의 제거를 통해 과적합에 대한 가능성을 감소시킬 수 있다(Jin et al., 2005). 일반적으로 최적의 PC를 선택하기 위해 PCA를 통해 생성된 각 성분(Component)의 고유값 분산(Eigenvalues variance)의 누적치 비율이 90%인 것을 기준으로 한다(Hasan and Tahir, 2010).

2.6 대상 유역 및 자료 구축

본 연구는 개량형 옵티마이저를 사용한 LSTM의 학습 및 예측성능 평가를 위해 낙동강유역에 위치한 다산 수질관측소의 수질인자를 학습 및 예측하였다. 다산 수질관측소는 경상북도 고령군에 위치하고 있으며, 실시간으로 수질인자를 측정한다. 다산 수질관측소의 하류 4km 지점에는 매곡취수장과 강정취수장이 있다. 취수장의 수질 개선에 대한 선제적 대응을 위해 다산 수질관측소의 일 단위 수질인자 자료를 사용하였다. Table 1은 학습 및 예측을 위해 사용된 LSTM의 입력 및 출력인자이다.

Table 1.

Input and output variables for the LSTM

Input variable (t-1 day)	￭ Meteorological data (Average wind speed, Average temperature, Daily precipitation, Sunshine hours) of Daegu, Gumi, Sangju and Uiseong ￭ Insolation for Daegu ￭ Water level of Seongju-large bridge, Doseong-bridge, Meagok-li ￭ Discharge of Seongju-large bridge, Meagok-li ￭ Water quality index (WT, DO, pH, Chl-a) of Dasan
Output variable (t day)	￭ Water quality index (WT, DO, pH, Chl-a) of Dasan

Chen et al. (2020)은 ANN을 활용하여 수질을 예측한 연구들의 예측선행길이를 분석하였으며, 예측선행길이를 1로 설정하여 관계를 파악하는 것이 이상적임을 확인하였다. 기존의 연구 동향 분석을 바탕으로 본 연구는 예측선행길이를 1로 설정하였다. LSTM의 학습자료는 2014년부터 2020년 까지의 자료를 사용하였다. 2021년의 자료는 LSTM의 예측성능을 평가하기 위한 예측자료로 사용하였다.

수질자료는 물환경정보시스템(https://water.nier.go.kr/)을 이용하여 구축하였다. 수문 및 기상자료는 각각 국가수자원관리종합정보시스템(http://www.wamis.go.kr/)과 기상자료개방포털(https://data.kma.go.kr)을 이용하여 구축하였다. Fig. 4는 유역도 및 자료를 취득한 관측소의 위치를 표시한 그림이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F4.jpg

Fig. 4.

Information about the study area and each station’s location

구축된 자료를 이용하여 PCA를 실시한 후 MMN을 실시하였다. Table 2는 구축된 자료를 이용하여 PCA를 실시한 결과 중 누적치 비율이 약 90%인 7개 주성분의 고유값 분산 및 고유값 분산의 누적치이다.

Table 2.

Results of principal component analysis

Principal components	Eigenvalue
Principal components	Variance (%)	Cumulative (%)
1	27.5494	27.5494
2	22.4036	49.9530
3	14.0788	64.0318
4	11.6316	75.6634
5	7.4199	83.0833
6	4.7877	87.8710
7	2.6762	90.5472

3. 연구결과

본 연구는 경사하강법 기반 옵티마이저의 단점을 개선하기 위해 개량형 옵티마이저를 개발하였다. 개량형 옵티마이저의 성능을 평가하기 위해 LSTM에 적용하여 다산 관측소의 수질인자를 학습 및 예측하였다. 또한, Adam과 Nadam을 적용한 LSTM의 학습 및 예측성능과 비교하였다. Adam 및 Nadam과 결합된 HS 및 NSHS의 매개변수는 우수한 학습성능을 보인 값으로 설정하였다. Table 3은 HS 및 NSHS의 매개변수이다.

Table 3.

Parameters of HS ans NSHS

Parameter	HS	NSHS
Harmony Memory Size	5	5
Harmony Memory Considering Rate	0.9	-
Pitch Adjusting Rate	0.2	-
Bandwidth	0.00001	-

Table 3에 따르면, HMCR 및 PAR은 각각 0.9 및 0.2로 설정하였다. Geem (2006)에 따르면 HMCR은 0.7에서 0.9 사이의 값, PAR은 0.05에서 0.2의 값이 바람직하다고 언급하였다. 개량형 옵티마이저의 GCR_max 및 GCR_min은 각각 1과 0.8로 설정하였다. LSTM의 반복학습 횟수인 Epoch는 수질인자를 예측한 Khatri et al. (2021)의 연구에서 설정한 2,000번으로 설정하였다. 또한, 학습 및 예측의 안정성을 평가하기 위해 10번 반복실행하였다. LSTM의 손실함수는 Mean Squared Error (MSE)를 사용하였다. MSE 수식은 Eq. (14)와 같다.

(14)

M S E = \frac{1}{N} \sum_{i = 1}^{N} (x_{p i} - x_{o i})^{2}

여기서, N은 자료의 개수, x_pi는 관측값, x_oi는 예측값이다.

각 옵티마이저를 적용한 LSTM의 예측성능을 검토하기 위한 성능지표는 MSE 및 R²를 사용하였다. R²의 수식은 Eq. (15)와 같다.

(15)

R^{2} = \frac{\sum_{i = 1}^{n} (x_{o i} - \bar{x})^{2}}{\sum_{i = 1}^{n} (x_{π} - \bar{x})^{2}}

여기서, $\bar{x}$ 는 관측값의 평균이다.

또한, 예측의 안정성을 평가하기 위해 10번 반복실행의 평균값(Average) 및 최대값(Max), 최소값(Min)을 비교하였다.

3.1 학습결과

경사하강법 기반 옵티마이저 중 학습성능이 우수한 옵티마이저를 선정하였다. 선정된 경사하강법 기반 옵티마이저를 HS 또는 NSHS와 결합하여 개량형 옵티마이저를 개발하였다. Table 4는 경사하강법 기반 옵티마이저를 적용한 LSTM의 학습결과이다.

Table 4.

Training results obtained with each LSTM using GD based optimizers

Optimizer	MSE
Optimizer	Average	Max	Min
SGD	0.032474	0.032652	0.032242
Adagrad	0.032655	0.032714	0.032571
RMSprop	0.002985	0.003114	0.002948
Adadelta	0.032692	0.032751	0.032625
Adamax	0.003274	0.003587	0.003074
Adam	0.002933	0.002985	0.002885
Nadam	0.002921	0.002965	0.002888

Table 4를 보면, MSE 최대값과 평균값은 Nadam이 각각 0.002965와 0.002921로 가장 낮았다. MSE 최소값은 Adam이 0.002885로 가장 낮았다. Adam과 Nadam의 MSE 평균값, 최대값 및 최소값이 모두 0.003 이하인 것으로 나타났다. 따라서, Adam과 Nadam을 HS 또는 NSHS와 결합하였다. AdamHS, AdamNSHS, NadamHS 및 NadamNSHS의 성능을 검토하기 위해 Adam 및 Nadam의 학습성능과 비교하였다. Table 5는 Adam, Nadam 및 개량형 옵티마이저를 적용한 LSTM의 학습결과이다.

Table 5를 보면, MSE 평균값 및 최대값이 각각 0.002881 및 0.002889로 NadamHS가 가장 낮았다. MSE 최소값은 AdamNSHS가 0.002836으로 가장 낮았다. 또한, HS 또는 NSHS와 결합한 옵티마이저는 경사하강법 기반 옵티마이저보다 MSE가 낮았다. HS 또는 NSHS를 활용하여 개량된 옵티마이저의 MSE를 비교하면 HS와 결합한 옵티마이저보다 NSHS와 결합한 옵티마이저가 더 낮았다. NSHS는 HS보다 미세조정을 많이 실시하기 때문인 것으로 분석된다. 학습결과를 통해, NadamNSHS을 이용한 학습이 가장 효과적이고 안정적이며 HS와 NSHS의 결합을 통해 경사하강법 기반 옵티마이저의 단점을 개선한 것으로 분석된다. Fig. 5는 학습과정에서 Epoch에 따른 MSE를 나타낸 그림이며, 10번 반복하여 취득한 결과의 평균이다.

Table 5.

Training results obtained with each LSMT using Adam, Nadam and improved optimizers

Optimizer	MSE
Optimizer	Average	Max	Min
Adam	0.002933	0.002985	0.002885
AdamHS	0.002885	0.002915	0.002840
AdamNSHS	0.002884	0.002913	0.002836
Nadam	0.002921	0.002965	0.002888
NadamHS	0.002883	0.002914	0.002842
NadamNSHS	0.002881	0.002899	0.002854

Fig. 5를 보면, 모든 옵티마이저는 비슷한 초기 수렴속도를 보였다. 하지만, 수렴 그래프의 후반부의 경우 개량형 옵티마이저의 MSE값이 더 낮은 것으로 나타났다. Adam과 Nadam의 경우 MSE값이 증가와 감소가 반복되지만, 개량형 옵티마이저는 계단식으로 감소한다. 개량형 옵티마이저의 해 저장 및 비교 구조의 유무차이인 것으로 분석된다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F5.jpg

Fig. 5.

Conversion shape of MSE by each optimizer

학습성능과 함께 경사하강법 기반 옵티마이저와 개량형 옵티마이저를 활용한 LSTM의 학습시간을 비교 및 분석하였다. Table 6은 각 옵티마이저에 따른 평균학습시간을 나타낸 표이다.

Table 6.

Average training time required for LSTM using each optimizer

Optimizer	Adam	AdamHS	AdamNSHS
Trainging times (sec)	180.37	218.45	230.85
Optimizer	Nadam	NadamHS	NadamNSHS
Trainging times (sec)	180.47	218.25	230.08

Table 6을 보면, Adam 및 Nadam이 가장 낮은 학습시간을 나타냈으며, AdamNSHS 및 NadamNSHS가 약 230초로 가장 긴 학습시간을 나타냈다. 개량형 옵티마이저의 경우 HS와 NSHS가 전역 및 지역탐색을 통해 최적의 매개변수를 탐색하게 된다. 개량형 옵티마이저의 특성으로 인해 기존 옵티마이저보다 더 오랜시간이 소요되는 것을 알 수 있다.

3.2 예측결과

AdamHS, AdamNSHS, NadamHS 및 NadamNSHS을 적용한 LSTM의 예측성능을 검토하기 위해 Adam과 Nadam을 적용한 LSTM의 예측성능과 비교하였다. 예측성능 평가하기 위한 지표로는 MSE를 사용하였으며 10번 반복실행의 최대값, 최소값 및 평균값을 비교하였다. Table 7은 각 옵티마이저를 사용한 LSTM의 WT 예측결과이다.

Table 7.

Prediction results of WT obtained with LSTM using Adam, Nadam and improved optimziers

Optimizer	MSE (R²)
Optimizer	Average	Max	Min
Adam	2.69480 (0.96612)	2.88837 (0.96830)	2.56906 (0.96416)
AdamHS	2.65131 (0.96614)	2.83497 (0.96813)	2.49124 (0.96368)
AdamNSHS	2.63876 (0.96618)	2.74623 (0.96848)	2.49435 (0.96483)
Nadam	2.72535 (0.96464)	2.92134 (0.96618)	2.56417 (0.96213)
NadamHS	2.57978 (0.96654)	2.67778 (0.96850)	2.41863 (0.96418)
NadamNSHS	2.61688 (0.96617)	2.69068 (0.96835)	2.51519 (0.96497)

Table 7을 보면, WT 예측의 경우 NadamHS를 적용한 LSTM의 MSE 평균값이 약 2.58로 가장 낮았다. NadamHS를 적용한 LSTM의 MSE 최대값 및 최소값이 가장 낮은 값을 보였다. NadamHS를 적용한 LSTM이 평균 및 최대 R²가 가장 높은 것을 알 수 있으며, 최소 R²의 경우 NadamNSHS가 높은 것을 알 수 있다. Adam 및 Nadam을 사용한 LSTM보다 개량형 옵티마이저를 사용한 LSTM의 MSE 평균값, 최대값, 최소값과 R²의 평균값, 최대값, 최소값 모두 낮았다. 개량형 옵티마이저의 예측 오차가 작은 이유는 경사하강법 기반 옵티마이저보다 안정적이고 비교적 정확한 학습이 진행되었으며, 이를 기반으로 예측을 진행했기 때문인 것으로 분석된다. Table 8은 옵티마이저별 LSTM의 DO 예측결과이다.

Table 8.

Prediction results of DO obtained with LSTM using Adam, Nadam and improved optimziers

Optimizer	MSE (R²)
Optimizer	Average	Max	Min
Adam	0.79803 (0.88278)	0.85015 (0.89099)	0.72987 (0.87646)
AdamHS	0.78499 (0.88309)	0.82892 (0.88699)	0.75830 (0.87658)
AdamNSHS	0.78794 (0.88307)	0.82664 (0.89439)	0.71055 (0.87696)
Nadam	0.82257 (0.87996)	0.89458 (0.88580)	0.78210 (0.87292)
NadamHS	0.80213 (0.88069)	0.83313 (0.88428)	0.77927 (0.87616)
NadamNSHS	0.79195 (0.88227)	0.81051 (0.88893)	0.74611 (0.87943)

Table 8을 보면, DO 예측의 경우 MSE 평균값은 AdamHS를 적용한 LSTM이 약 0.785로 가장 낮았다. MSE 최대값 및 최소값은 각각 NadamNSHS 및 AdamNSHS를 적용한 LSTM이 가장 낮았다. 또한, AdamHS를 적용한 LSTM이 평균 R²가 가장 높은 것을 알 수 있으며, 최대 R²의 경우 AdamNSHS, 최소 R²의 경우 NadamNSHS가 높은 것을 알 수 있다. Tale 8을 통해 AdamHS를 적용한 LSTM의 DO 예측이 비교적 안정적인 것으로 분석된다. Table 9는 옵티마이저별 LSTM의 pH 예측결과이다.

Table 9.

Prediction results of pH obtained with LSTM using Adam, Nadam and improved optimziers

Optimizer	MSE (R²)
Optimizer	Average	Max	Min
Adam	0.04995 (0.89884)	0.05171 (0.90194)	0.04721 (0.89534)
AdamHS	0.05033 (0.89821)	0.05343 (0.90339)	0.04839 (0.88942)
AdamNSHS	0.04965 (0.89875)	0.05173 (0.90419)	0.04706 (0.89236)
Nadam	0.04960 (0.90041)	0.05326 (0.90649)	0.04579 (0.89637)
NadamHS	0.04868 (0.90092)	0.05149 (0.90408)	0.04690 (0.89529)
NadamNSHS	0.04833 (0.90150)	0.05006 (0.90508)	0.04671 (0.89851)

Table 9를 보면, pH 예측의 경우 MSE 평균값 및 최대값은 NadamNSHS를 사용한 LSTM이 각각 약 0.048 및 0.05로 가장 낮았다. MSE 최소값은 Nadam을 사용한 LSTM이 약 0.046으로 가장 낮았으나, NadamNSHS를 적용한 LSTM은 두 번째로 낮은 0.047의 MSE 최소값을 보였다. 또한, NadamHS를 적용한 LSTM이 평균 및 최소 R²가 가장 높은 것을 알 수 있다. 따라서, pH의 예측은 NadamNSHS를 적용한 LSTM의 예측이 비교적 안정적인 것으로 분석된다. Table 10은 옵티마이저별 LSTM의 Chl-a 예측결과이다.

Table 10을 보면, Chl-a 예측의 경우 MSE 평균값은 AdamHS를 적용한 LSTM이 약 65.44로 가장 낮았다. MSE 최대값 및 최소값은 각각 AdamNSHS 및 NadamNSHS를 적용한 LSTM이 가장 낮은 값을 보였다. 평균 R²는 NadamHS 가 가장 높았으며, 최대 R²는 NadamNSHS, 최대 R²는 AdamNSHS가 가장 높았다. Chl-a 예측결과를 보면 경사하강법 기반 옵티마이저보다 개량형 옵티마이저를 적용한 LSTM이 더 좋은 예측결과를 나타내는 것을 알 수 있었다. 본 연구에서 사용된 LSTM은 다중출력 구조로 WT, DO, pH 및 Chl-a를 동시에 예측한다. 따라서 4개의 수질인자에 대한 전체적인 예측성능을 검토하기 위해 각 옵티마이저의 예측성능 순위를 산정하였으며, 순위에 대한 평균을 평가하였다. MSE가 낮을수록, R²가 높을 수록 1순위로 산정하였다. Table 11은 수질인자에 대한 MSE의 순위이며, Table 12는 순위에 대한 평균값이다.

Table 10.

Prediction results of Chl-a obtained with LSTM using Adam, Nadam and improved optimziers

Optimizer	MSE (R²)
Optimizer	Average	Max	Min
Adam	68.71659 (0.82592)	76.43627 (0.84031)	64.39751 (0.81604)
AdamHS	65.44245 (0.83036)	71.99208 (0.84261)	60.02291 (0.81790)
AdamNSHS	65.56830 (0.82984)	67.89993 (0.84031)	63.47448 (0.82346)
Nadam	66.28201 (0.83045)	72.0647 (0.83961)	59.99653 (0.81779)
NadamHS	65.53086 (0.83075)	69.57973 (0.84254)	62.33369 (0.82273)
NadamNSHS	66.10547 (0.82779)	68.94613 (0.84302)	59.34056 (0.82001)

Table 11.

Ranking of the prediction results obtained each LSTM using Adam, Nadam and improved optimizers

Optimizer	Ranking (Average / Max / Min) R² (Average / Max / Min)
Optimizer	WT			DO			pH			Chl-a
Adam	5 (5)	5 (4)	6 (4)	4 (3)	5 (2)	2 (4)	5 (4)	3 (6)	5 (3)	6 (6)	6 (4)	6 (4)
AdamHS	4 (4)	4 (5)	2 (5)	1 (1)	3 (4)	4 (3)	6 (6)	6 (5)	6 (6)	1 (3)	4 (2)	3 (4)
AdamNSHS	3 (2)	3 (2)	3 (2)	2 (2)	2 (2)	1 (1)	4 (5)	4 (3)	4 (5)	3 (4)	1 (4)	5 (1)
Nadam	6 (6)	6 (6)	5 (5)	6 (6)	6 (5)	6 (6)	3 (3)	5 (1)	1 (2)	5 (2)	5 (6)	2 (5)
NadamHS	1 (1)	1 (1)	1 (3)	5 (5)	4 (6)	5 (5)	2 (2)	2 (4)	3 (4)	2 (1)	3 (3)	4 (2)
NadamNSHS	2 (3)	2 (3)	4 (1)	3 (4)	1 (3)	3 (1)	1 (1)	1 (2)	2 (1)	4 (5)	2 (1)	1 (3)

Table 12.

Average of ranking about prediction obtained each models

Optimizer	Adam	AdamHS	AdamNSHS
Average of ranking	4.54	3.83	2.83
Optimizer	Nadam	NadamHS	NadamNSHS
Average of ranking	4.58	2.29	2.25

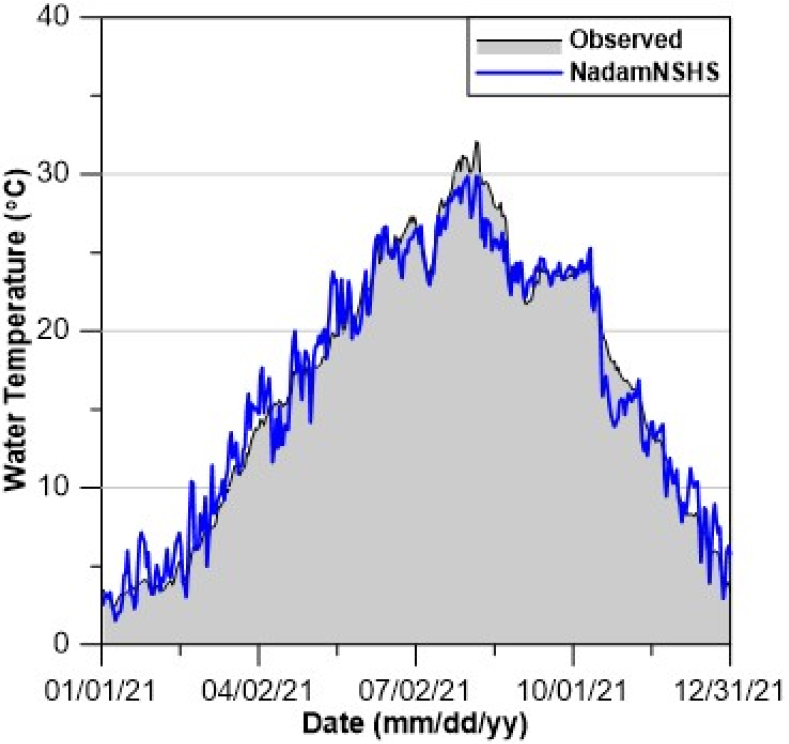
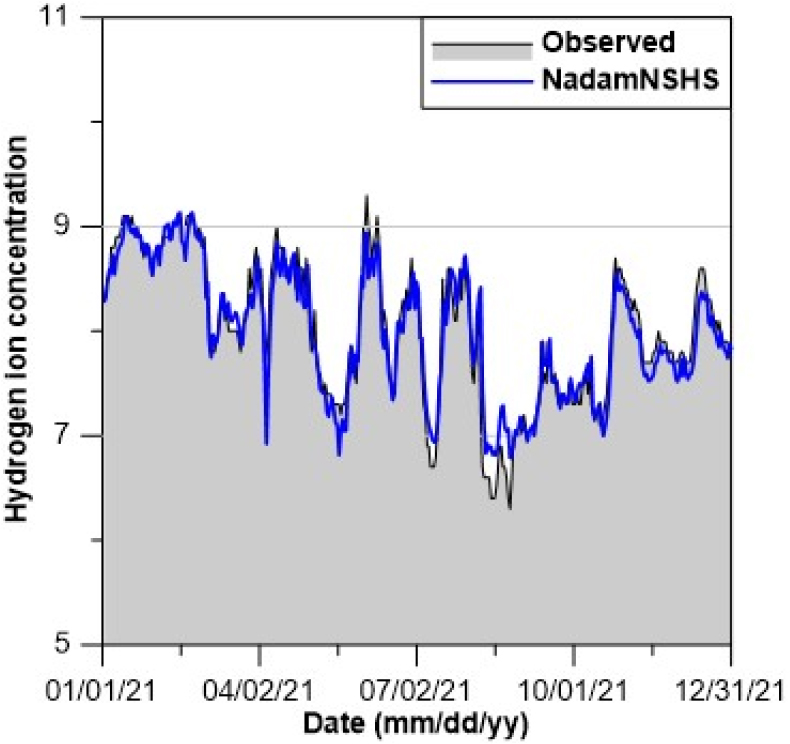
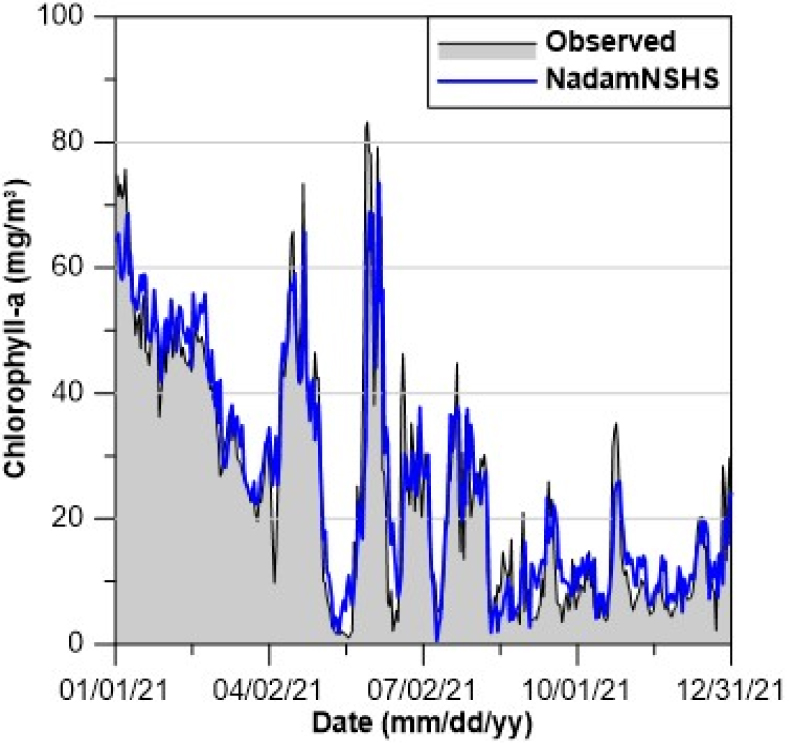
Table 11 및 Table 12를 보면, NadamNSHS을 적용한 LSTM의 순위에 대한 평균이 약 2.14로 가장 높았으며, Nadam을 적용한 LSTM은 약 4.58로 가장 낮았다. 또한, Adam 및 Nadam을 적용한 LSTM보다 개량형 옵티마이저를 적용한 LSTM의 순위에 대한 평균이 높은 것으로 나타났다. 개량형 옵티마이저의 순위에 대한 평균을 비교하면 NadamNSHS 및 AdamNSHS를 적용한 LSTM이 NadamHS 및 AdamHS를 적용한 LSTM보다 높았다. 따라서, NSHS를 이용하여 개량한 옵티마이저의 성능이 비교적 우수한 예측성능을 나타내는 것으로 분석된다. Figs. 6~9는 각각 WT, DO, pH 및 Chl-a에 대한 NadamNSHS를 적용한 LSTM의 예측값과 관측값을 비교한 그래프이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F6.jpg

Fig. 6.

Comparison of the WT prediction results by LSTM using NadamNSHS

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F7.jpg

Fig. 7.

Comparison of the DO prediction results by LSTM using NadamNSHS

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F8.jpg

Fig. 8.

Comparison of the pH prediction results by LSTM using NadamNSHS

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-02/N020057201/images/kwra_57_02_01_F9.jpg

Fig. 9.

Comparison of the Chl-a prediction results by LSTM using NadamNSHS

Figs. 6~9를 보면, 최고 WT에서의 오차는 약 2.2^oC이며, 최저 DO에서의 오차는 약 1.5 mg/L이다. 또한, 최고 pH 및 최고 Chl-a에서의 오차는 각각 약 0.3과 14.3 mg/m³이다. 수질예측결과를 보면, 경사하강법 기반 옵티마이저와 HS 및 NSHS의 결합을 통해 경사하강법 기반 옵티마이저의 단점을 개선한 것으로 분석된다. 특히, NadamNSHS를 적용한 LSTM이 비교적 높은 학습 및 예측 정확도를 보였으며 높은 정확도의 수질인자 예측이 가능할 것으로 분석된다.

4. 결 론

본 연구는 수질예측 성능의 향상을 위해 경사하강법 기반 옵티마이저의 지역 최적해 수렴 가능성과 해의 저장공간 부재의 단점을 개선한 개량형 옵티마이저를 개발하였다. 개발된 개량형 옵티마이저는 경사하강법 기반 옵티마이저 중 학습오차가 낮은 Adam 및 Nadam을 HS 또는 NSHS와 결합하였다. 개량형 옵티마이저의 학습 및 예측성능 검토를 위해 다산 수질관측소의 WT, DO, pH 및 Chl-a를 학습 및 예측하였으며, Adam 및 Nadam의 학습 및 예측성능과 비교하였다.

학습결과를 비교하면, MSE 최대값 및 평균값에서는 NadamNSHS을 이용한 LSTM 각각 약 0.002899와 0.002881로 가장 낮았다. MSE 최소값에서는 AdamNSHS를 이용한 LSTM이 약 0.002836으로 가장 낮았다. 또한, 개량형 옵티마이저를 이용한 LSTM이 Adam 및 Nadam을 이용한 LSTM보다 낮은 MSE를 보였다.

WT, DO, pH 및 Chl-a를 예측한 결과의 MSE 및 R² 평균값을 비교하면, 각각 NadamHS, AdamHS, NadamNSHS와 AdamHS를 사용한 LSTM이 가장 낮은 MSE 및 가장 높은 R²를 보였다. 4개 수질인자에 대한 전체적인 예측성능을 비교하기 위해 MSE가 낮을수록 R²가 높을수록 1순위로 하여 4개 수질인자의 예측 순위에 대한 평균을 산정하였다. 순위에 대한 평균을 비교하면, NadamNSHS을 사용한 LSTM이 2.25로 가장 높은 순위를 보였다. 또한, HS와 NSHS를 이용한 개량형 옵티마이저를 사용한 LSTM의 순위에 대한 평균이 Adam 및 Nadam보다 높았다.

학습 및 예측결과를 통해 개량형 옵티마이저의 학습 및 예측성능이 경사하강법 기반 옵티마이저보다 우수한 것으로 분석된다. 추후 연구를 통해 LSTM의 구조에 따른 학습 및 예측성능의 분석과 함께 학습시간 단축을 위한 계산과정 검토 및 예측선행시간에 따른 ANN의 예측결과를 분석하여 다산 수질관측소의 수질인자 예측을 위한 최적의 LSTM을 구축할 수 있을 것으로 기대된다. 또한, 본 연구에서 사용된 대상유역의 연구결과를 기반으로 추후 국내에 위치하고 있는 수질관측소에 대한 수질예측 연구를 통해 국내에서 범용적으로 사용할 수 있는 개량형 옵티마이저가 적용된 LSTM을 제안할 수 있을 것으로 기대된다.

Acknowledgements

이 논문은 충북대학교 국립대학육성사업(2023)지원을 받아 작성되었음

Conflicts of Interest

The authors declare no conflict of interest.

References

Akkoyunlu, A., and Akiner, M.E. (2010). "Feasibility assessment of data-driven models in predicting pollution trends of Omerli Lake, Turkey." Water Resources Management, Vol. 24, No. 13, pp. 3419-3436. 10.1007/s11269-010-9613-0

Babu, C.N., and Reddy, B.E. (2014). "A moving-average filter based hybrid ARIMA-ANN model for forecasting time series data." Applied Soft Computing, Vol. 23, pp. 27-38. 10.1016/j.asoc.2014.05.028

Cai, Q., Zhang, D., Zheng, W., and Leung, S.C. (2015). "A new fuzzy time series forecasting model combined with ant colony optimization and auto-regression." Knowledge-Based Systems, Vol. 74, pp. 61-68. 10.1016/j.knosys.2014.11.003

Cao, X., Liu, H., and Chen, N. (1997). "Classification of Cm I energy levels using PCA-BPN and PCA-NLM." Chemical Physics, Vol. 220, No. 3, pp. 289-297. 10.1016/S0301-0104(97)00139-0

Chen, Y., Song, L., Liu, Y., Yang, L., and Li, D. (2020). "A review of the artificial neural network models for water quality prediction." Applied Sciences, Vol. 10, No. 17, 5776. 10.3390/app10175776

Choi, Y.H., Eghdami, S., Ngo, T.T., Chaurasia, S.N., and Kim, J.H. (2019). "Comparison of parameter-setting-free and self-adaptive harmony search." Proceedings Harmony Search and Nature Inspired Optimization Algorithms, Singapore, pp. 105-112. 10.1007/978-981-13-0761-4_11

Dogan, E., Ates, A., Yilmaz, C., and Eren, B. (2008). "Application of artificial neural networks to estimate wastewater treatment plant inlet biochemical oxygen demand." Environmental Progress, Vol. 27, No. 4, pp.439-446. 10.1002/ep.10295

Faruk, D.Ö. (2010). "A hybrid neural network and ARIMA model for water quality time series prediction." Engineering Applications of Artificial Intelligence, Vol. 23, No. 4, pp. 586-594. 10.1016/j.engappai.2009.09.015

Folorunso, T.A., Aibinu, A.M., Kolo, J.G., Sadiku, S.O., and Orire, A.M. (2018). "Effects of data normalization on water quality model in a recirculatory aquaculture system using artificial neural network." I-manager's Journal on Pattern Recognition, Vol. 5, No. 3, 21. 10.26634/jpr.5.3.15678

Geem, Z.W. (2006). "Optimal cost design of water distribution networks using harmony search." Engineering Optimization, Vol. 38, No. 3, pp. 259-277. 10.1080/03052150500467430

Geem, Z.W., Kim, J.H., and Loganathan, G.V. (2001). "A new heuristic optimization algorithm: Harmony search." Simulation, Vol. 76, No. 2, pp. 60-68. 10.1177/003754970107600201

Hasan, H., and Tahir, N.M. (2010). "Feature selection of breast cancer based on principal component analysis." In 2010 6th International Colloquium on Signal Processing & its Applications, Malacca, Malaysia, pp. 1-4. 10.1109/CSPA.2010.5545298

Hochreiter, S., and Schmidhuber, J. (1997). "Long short-term memory." Neural Computation, Vol. 9, No. 8, pp. 1735-1780. 10.1162/neco.1997.9.8.17359377276

Jin, L., Kuang, X., Huang, H., Qin, Z., and Wang, Y. (2005). "Study on the overfitting of the artificial neural network forecasting model." Acta Meteorologica Sinica, Vol. 19, No. 2, 216.

Joo, D.S., Choi, D.J., and Park, H. (2000). "The effects of data preprocessing in the determination of coagulant dosing rate." Water Research, Vol. 34, No. 13, pp. 3295-3302. 10.1016/S0043-1354(00)00067-1

Joo, G., Park, C., and Im, H. (2020). "Performance evaluation of machine learning optimizers." Journal of Institute of Korean Electrical and Engineers, Vol. 24, No, 3, pp. 766-776.

Khatri, P., Gupta, K.K., and Gupta, R.K. (2021). "Drift compensation of commercial water quality sensors using machine learning to extend the calibration lifetime." Journal of Ambient Intelligence and Humanized Computing, Vol. 12, pp. 3091-3099. 10.1007/s12652-020-02469-y

Lee, W.J., and Lee, E.H. (2022a). "Runoff prediction based on the discharge of pump stations in an urban stream using a modified multi-layer perceptron combined with meta-heuristic optimization." Water, Vol. 14, No. 1, 99. 10.3390/w14010099

Lee, W.J., and Lee, E.H. (2022b). "Improvement of multi layer perceptron performance using combination of gradient descent and harmony search for prediction of ground water level." Journal of Korea Water Resources Association, Vol. 55, No. 11, pp. 903-911.

Li, L., Jiang, P., Xu, H., Lin, G., Guo, D., and Wu, H. (2019). "Water quality prediction based on recurrent neural network and improved evidence theory: a case study of Qiantang River, China." Environmental Science and Pollution Research, Vol. 26, No. 19, pp. 19879-19896. 10.1007/s11356-019-05116-y31093910

Lu, H., and Ma, X. (2020). "Hybrid decision tree-based machine learning models for short-term water quality prediction." Chemosphere, Vol. 249, 126169. 10.1016/j.chemosphere.2020.12616932078849

Luo, K. (2013). "A novel self-adaptive harmony search algorithm." Journal of Applied Mathematics, Vol. 2013, pp. 1-16. 10.1155/2013/653749

Manjarres, D., Landa-Torres, I., Gil-Lopez, S., Del Ser, J., Bilbao, M.N., Salcedo-Sanz, S., and Geem, Z.W. (2013). "A survey on applications of the harmony search algorithm." Engineering Applications of Artificial Intelligence, Vol. 26, No. 8, pp. 1818-1831. 10.1016/j.engappai.2013.05.008

McCulloch, W.S., and Pitts, W. (1943). "A logical calculus of the ideas immanent in nervous activity." The Bulletin of Mathematical Biophysics, Vol. 5, No. 4, pp. 115-133. 10.1007/BF02478259

Mok, J.Y., Choi, J.H., and Moon, Y.I. (2020). "Prediction of multipurpose dam inflow using deep learning." Journal of Korea Water Resources Association, Vol. 53, No. 2, pp. 97-105.

Nawi, N.M., Atomi, W.H., and Rehman, M.Z. (2013). "The effect of data pre-processing on optimized training of artificial neural networks." Procedia Technology, Vol. 11, pp. 32-39. 10.1016/j.protcy.2013.12.159

Pan, Q.K., Suganthan, P.N., Tasgetiren, M.F., and Liang, J.J. (2010). "A self-adaptive global best harmony search algorithm for continuous optimization problems." Applied Mathematics and Computation, Vol. 216, pp. 830-848. 10.1016/j.amc.2010.01.088

Park, S.Y., Choi, J.H., Wang, S., and Park, S.S. (2006). "Design of a water quality monitoring network in a large river system using the genetic algorithm." Ecological modelling, Vol. 199, No. 3, pp. 289-297. 10.1016/j.ecolmodel.2006.06.002

Rosenblatt, F. (1958). "The perceptron: A probabilistic model for information storage and organization in the brain." Psychological Review, Vol. 65, No. 6, 386. 10.1037/h004251913602029

Rumelhart, D.E., Hinton, G.E., and Williams, R.J. (1986). "Learning representations by back-propagating errors." Nature, Vol. 323, No. 6088, pp. 533-536. 10.1038/323533a0

Ryu, Y.M., and Lee, E.H. (2022). "Application of neural networks to predict Daecheong Dam water levels." Journal of the Korean Society of Hazard Mitigation, Vol. 22, No. 1, pp. 67-78. 10.9798/KOSHAM.2022.22.1.67

Sedki, A., Ouazar, D., and El Mazoudi, E. (2009). "Evolving neural network using real coded genetic algorithm for daily rainfall-runoff forecasting." Expert Systems with Applications, Vol. 36, No. 3, pp. 4523-4527. 10.1016/j.eswa.2008.05.024

Wang, T.S., Tan, C.H., Chen, L., and Tsai, Y.C. (2008). "Applying artificial neural networks and remote sensing to estimate chlorophyll-a concentration in water body." Proceedings of the 2008 2nd International Symposium Intelligent Information Technology Application IITA, Shanghai, China, pp. 540-544. 10.1109/IITA.2008.279

Wang, Y., Zhou, J., Chen, K., Wang, Y., and Liu, L. (2017). "Water quality prediction method based on LSTM neural network." Proceedings 2017 12th International Conference on Intelligent Systems and Knowledge Engineering, Nanjing, China, pp. 1-5. 10.1109/ISKE.2017.8258814

Xiang, Y., and Jiang, L. (2009). "Water quality prediction using LS-SVM and particle swarm optimization." Proceedings 2009 Second International Workshop on Knowledge Discovery and Data Mining, Moscow, Russia, pp. 900-904. 10.1109/WKDD.2009.217

Zare, A., Bayat, V., and Daneshkare, A. (2011). "Forecasting nitrate concentration in groundwater using artificial neural network and linear regression models." International Agrophysics, Vol. 25, No. 2, pp. 187-192.

Zhang, L., Zou, Z., and Shan, W. (2017). "Development of a method for comprehensive water quality forecasting and its application in Miyun reservoir of Beijing, China." Journal of Environmental Sciences, Vol. 56, pp. 240-246. 10.1016/j.jes.2016.07.01728571859

Zheng, L., Wang, H., Liu, C., Zhang, S., Ding, A., Xie, E., Li, J., and Wang, S. (2021). "Prediction of harmful algal blooms in large water bodies using the combined EFDC and LSTM models." Journal of Environmental Management, Vol. 295, 113060. 10.1016/j.jenvman.2021.11306034167054

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Development of new artificial neural network optimizer to improve water quality index prediction performance

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 1.

Structure of long short-term memory used in this study

(7)

Fig. 2.

Flowchart of harmony search

(8)

(9)

(10)

(11)

Fig. 3.

Flowchart of improved optimizer

(12)

(13)

Table 1.

Input and output variables for the LSTM

Fig. 4.

Information about the study area and each station’s location

Table 2.

Results of principal component analysis

Table 3.

Parameters of HS ans NSHS

(14)

(15)

Table 4.

Training results obtained with each LSTM using GD based optimizers

Table 5.

Training results obtained with each LSMT using Adam, Nadam and improved optimizers

Fig. 5.

Conversion shape of MSE by each optimizer

Table 6.

Average training time required for LSTM using each optimizer

Table 7.

Prediction results of WT obtained with LSTM using Adam, Nadam and improved optimziers

Table 8.

Prediction results of DO obtained with LSTM using Adam, Nadam and improved optimziers

Table 9.

Prediction results of pH obtained with LSTM using Adam, Nadam and improved optimziers

Table 10.

Prediction results of Chl-a obtained with LSTM using Adam, Nadam and improved optimziers

Table 11.

Ranking of the prediction results obtained each LSTM using Adam, Nadam and improved optimizers

Table 12.

Average of ranking about prediction obtained each models

Fig. 6.

Comparison of the WT prediction results by LSTM using NadamNSHS

Fig. 7.

Comparison of the DO prediction results by LSTM using NadamNSHS

Fig. 8.

Comparison of the pH prediction results by LSTM using NadamNSHS

Fig. 9.

Comparison of the Chl-a prediction results by LSTM using NadamNSHS

Acknowledgements

Conflicts of Interest

References