investigated and supplemented to eliminate subjectivity in segmental positioning. Appropriateness for the segmentation position was verify in consideration of the physical meaning of the rating curve index (c).1. 서 론
수위-유량관계곡선식은 연속 측정된 수위자료와 다양한 수위에서 측정된 유량자료의 관계를 식으로 표현하는 것으로 이를 이용하여 시계열 유량자료를 취득할 수 있다. 하천에서 연속 유량자료를 취득하는 다른 방법으로 자동유량측정 장치가 있지만 설치비용 및 제한된 설치환경 등의 문제로 대부분 수위-유량관계곡선식을 이용한다.
수위-유량관계곡선식을 개발하려면 GZF (Gauge Height of Zero Flow), 구간분리, 기간분리 등을 결정해야 한다. GZF의 경우 도해법이나 시행착오법을 이용하여 산정하기도 하며 현장조사를 통하여 결정하가도 한다. 기간분리는 주로 홍수 전·후로 하천단면 변화에 의해 발생하며 대부분 현장에서 확인 가능하고 또한 유량측정성과에서 명확하게 구분된다. 즉, GZF와 기간분리는 특징을 조사하여 명확하게 결정이 가능하다고 할 수 있다.
Manfreda (2018)은 하천단면 기하학의 특성에 따라 수위-유량관계곡선식을 세분화하였으며, 일반적으로 수위-유량관계곡선식 구간분리 위치 결정은 실무적으로 하천단면형상, 수위-평균유속, 수위-단면적, 수위- 등 수리적인 요소를 고려하여 결정된다. 이러한 수리적인 요소를 그림으로 도시하여 전체적인 경향을 확인하고 개발자가 구간분리 위치 결정하는 방법이며 이 과정에서 개발자의 주관적인 판단이 많이 개입되기도 한다(Kim et al., 2015). 또한 개발자의 숙련도에 따라 구간분리 위치가 다르게 결정될 수도 있으며 이러한 문제로 수위-유량관계곡선식의 정확도가 논란이 되기도 한다. 잘못된 구간분리는 수위-유량관계곡선식의 오류로 이어지고 이는 내삽구간에서도 오차가 발생하지만, 특히 외삽구간에서 더 큰 오차를 유발하는 경우가 많다.
본 연구에서는 우리나라 실무에서 많이 사용되는 구간분리 위치 결정 방법에 대해 살펴보고, 멱함수 형태의 수위-유량관계곡선식 지수(c)의 이론적 배경을 검토하여 구간분리 위치 결정에 있어서 고려해야 하는 수리적 특성을 살펴보았다. 일본에서 제시된 유량측정성과 검토방법을 응용하여 구간분리 위치 결정방안을 제안하고자 한다.
2. 기존 구간분리 방법
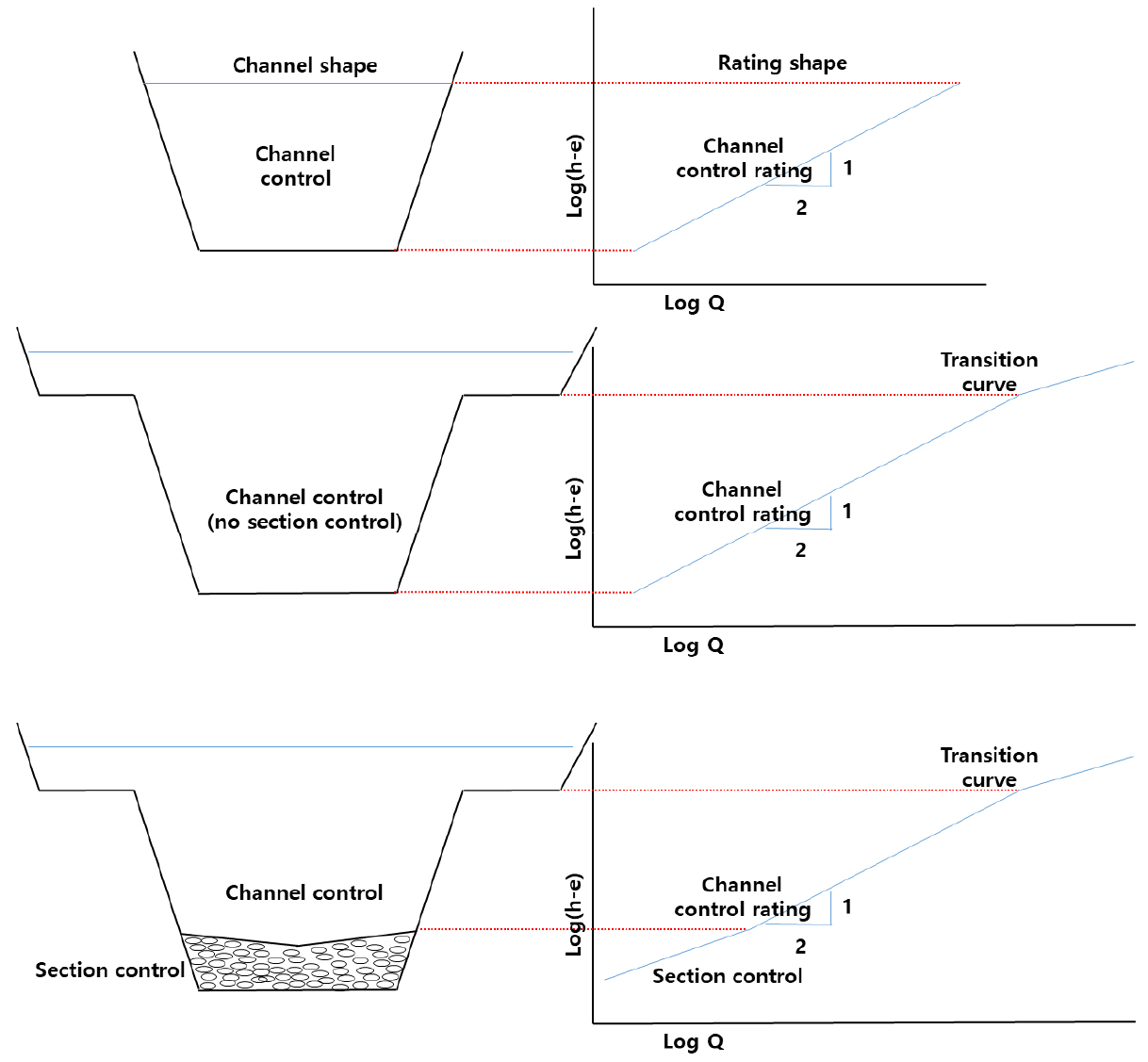
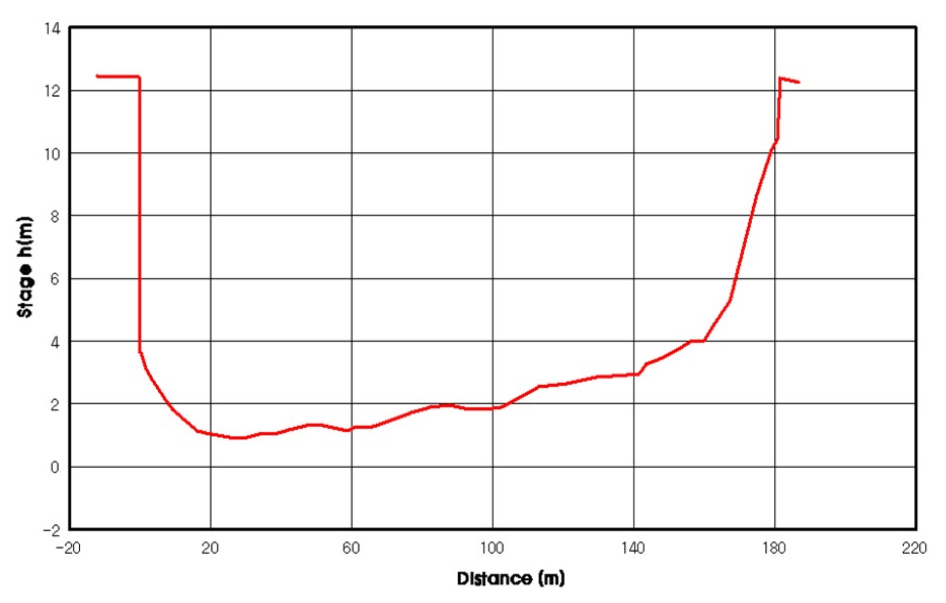
WMO (World Meteorological Organization, 세계기상기구), ISO (International Organization for Standardization, 국제표준화기구), USGS (United States Geological Survey, 미국지질조사국) 등 많은 기관에서 수위-유량관계곡선식 개발에 대한 기준을 제시하고 있다. 하지만 구간분리 위치 결정에 대한 명확한 방법이나 기준은 제시하지 않고 있으며 Fig. 1과 같이 단면형상에 따라 구간분리가 발생한다고 설명하고 있다.
이러한 하천 통제특성에 따른 수위-유량관계곡선식 변화를 고려하여 실무적으로 수위-평균유속, 수위-단면적, 수위 관계 등 수리특성을 검토하여 수위-유량관계곡선식 구간분리를 한다.
기존 구간분리 방법인 위의 세 가지 방법을 이용하여 구례군(송정리)(Guryegun (Songjeongri))와 한덕교(Handeog gyo) 등 두 개소에 대해 분석을 하였다. 분석에 사용된 자료는 섬진강 구례군(송정리) 66개 측정성과와 홍천강 한덕교 지점의 37개 측정성과를 이용하였다. 구례군(송정리)는 자료는 2018년~2020년에 측정된 자료를 이용하였다. 한덕교 자료는 2016년, 2017년, 2019년 측정된 자료를 이용하였다.
2.1 구례군(송정리) 수위관측소
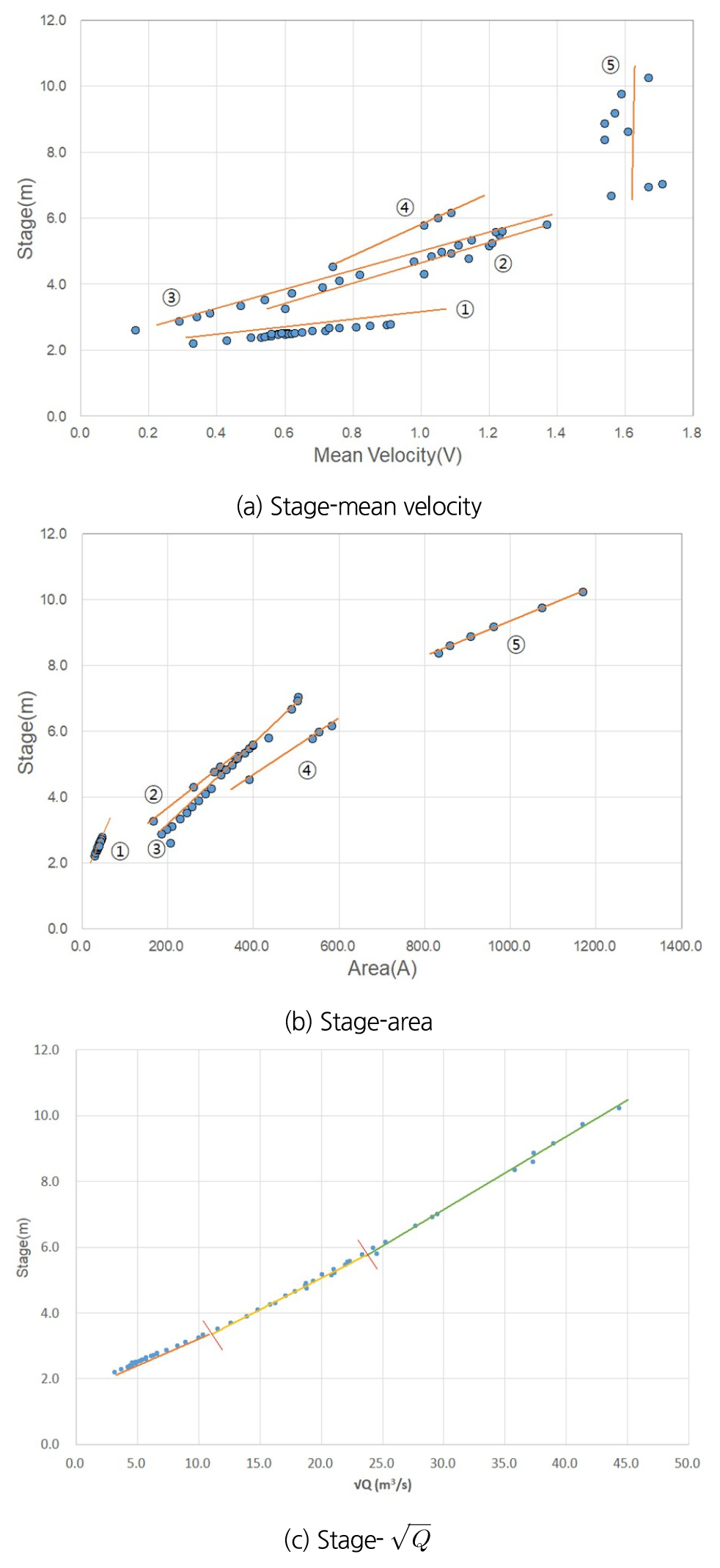
Fig. 2(a)는 구례군(송정리) 관측소의 수위-평균유속 관계를, Fig. 2(b)는 수위-단면적 관계를 보여준다. Fig. 2(c)는 수위-관계를 나타냈다.
Figs. 2(a) and 2(b)에서 구례군(송정리)는 총 5개 위치에서 유량측정이 이루어 진 것을 확인 할 수 있으며 이 그림으로 구간분리를 판단하기란 대단히 어렵다. Figs. 2(a) and 2(b)를 같이 비교하여 분석해보면 수위 약 7.0 m에서 구간분리 가능성이 보이며(단면적은 선형으로 상승하지만 평균유속은 증가하지 않기 때문이다.) 나머지는 판단하기 난해하다. Fig. 2(c)에서 수위 3.0 m와 수위 5.5 m 부근에서 구간분리가 발생하는 것으로 판단되지만 이는 주관적인 관점이며 개발자마다 다르게 판단할 수도 있다.
2.2 한덕교 수위관측소
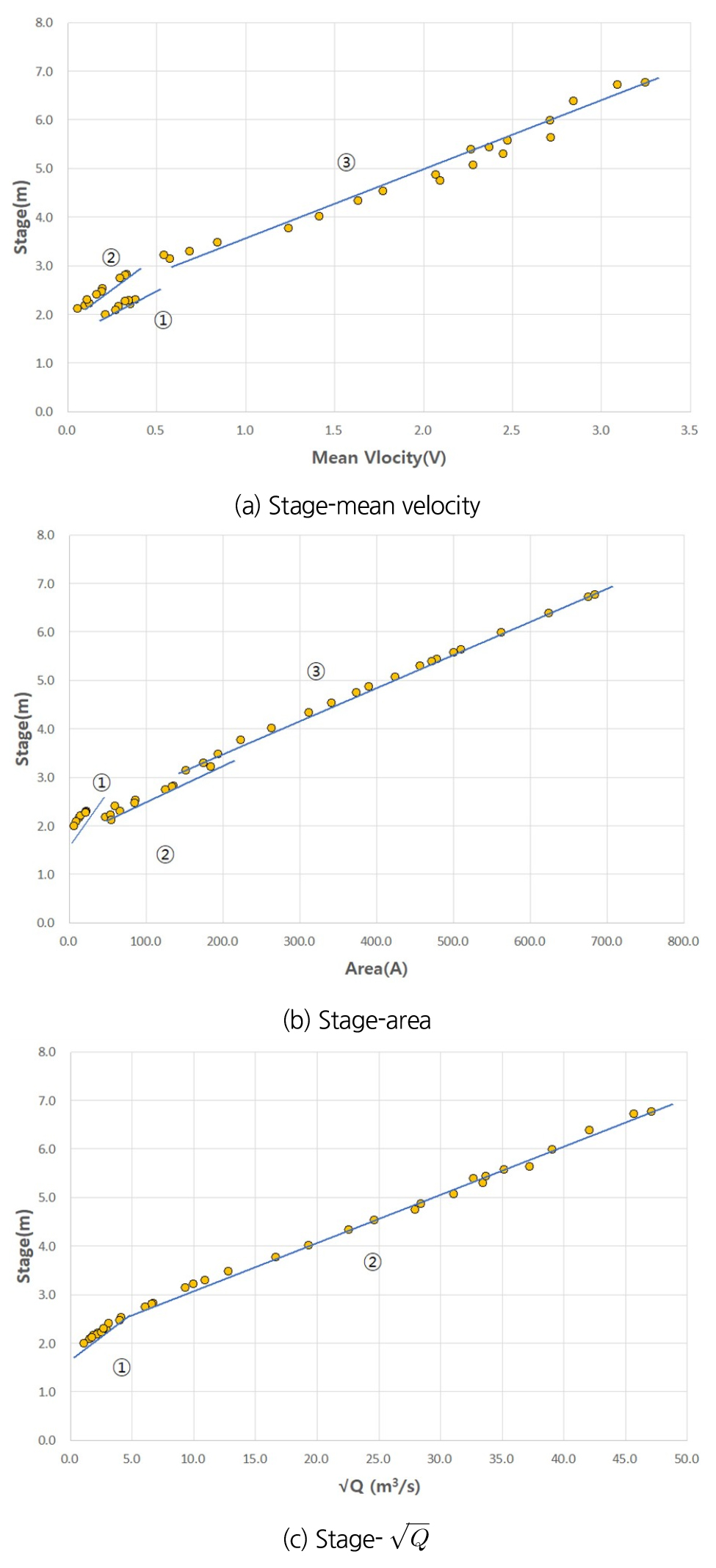
Fig. 3(a)는 한덕교 지점의 수위-평균유속, Fig. 3(b)는 수위-단면적, Fig. 3(c)는 수위- 관계를 보여준다.
Figs. 3(a) and 3(b)에서 모두 세 위치에서 측정이 이루어 진 것을 확인 할 수 있으며 구간분리 위치는 확실하게 나타나지 않는다. 수위 3.5 m 부근에서 구간분리 특징이 보이지만 명확하게 구간분리라고 표현하기는 어렵다. Fig. 3(c) 수위- 그림을 살펴보면 약 수위 2.6 m에서 구간분리 특징이 보이며 나머지 구간분리 위치 확인은 명확하지 않다.
기존 구간분리를 위한 수리특성 검토를 두 지점에 대해 분석한 결과 명확하게 구간분리 특징이 보이기는 쉽지 않으며 이 조차도 개발자에 주관적인 판단이 개입되기 쉽다.
3. 수위-유량관계곡선식(멱함수) 수리적 분석
자연하천에서 구간분리 위치를 특정하기 위해 먼저 수위-유량관계곡선식(멱함수)의 수리적 특징을 살펴볼 필요가 있다.
수위-유량관계곡선식은 매닝공식과 연속방정식에서 다음 Eq. (3)과 같이 멱함수의 형태로 유도된다.
여기서, V = 유속(m/sec), n=조도계수, S=수면경사, R=경심, A=단면적(m2)
여기서, Q = 유량(m3/sec), h = 수위(m), b = GZF (Gauge Height of Zero flow), a, c = 상수
유도과정을 살펴보면 Eq. (2)에서 단면적 A는 수면폭 B와 수심 H의 곱으로 표현하면 다음과 같은 식이 된다(광폭직사각형 단면으로 가정).
조도계수 , 에너지경사(수면경사) S1/2, 수면폭 B를 합쳐서 상수 a로 바꾸면 다음 식과 같이 된다.
수심 H를 수위 h와 이론적인 유효수심 b (또는 GZF)로 표현하고, 통수단면을 광폭직사각형으로 가정하면 R≈H이며 따라서 다음 Eq. (6)과 같이 된다.
또한 단면형태를 광폭포물선 단면으로 가정하면 다음 Eq. (7)와 같이 c = 2.167이 된다.
유도과정에서 상수 a는 조도계수 , 수면경사 S1/2와 수면폭 B로 구성된 것을 기억해야 한다.
지금까지 유도 과정을 살펴보면 단면형상이 단순한 형태일 때의 유도 과정이며 자연하천은 아주 복잡한 형태를 보여 단면형상을 특정하기는 대단히 어렵다. 멱함수의 지수 c는 하천의 단면형상에 따라 변화하며 자연하천에서는 1.3~1.8의 범위를 가지며 최대 2.0을 넘지 않는 것으로 알려졌다(WMO-No. 1044). 광폭사다리꼴과 광폭삼각형 단면형상을 가진 하천은 지수(c)가 각각 2.42, 2.67로 유도되지만(Hamilton et al., 2019) 자연하천에서는 이러한 형태를 찾기 어렵고 조도 등의 영향으로 2.0이 넘지 않는 것이 일반적이다.
또한 이 유도 과정은 하도통제를 받는 상황에서 유도된 식이다. 수위가 낮은 단면통제는 하천바닥의 조도가 큰 영향을 끼치는 것으로 알려져 있으며 이 때의 지수(c)는 2.0을 초과한다. Rantz (1982)은 하천에서 수위 상승에 따라서 단면통제에서 하도통제로 전환되며 그 시점에서 지수(c)는 2가 된다는 것을 증명하였으며, 일반적으로 하천이 수위가 낮은 경우는 단면통제를 받으며 지수(c)는 2보다 커지고, 높은 수위에서는 하도통제를 받으며 지수(c)는 2보다 작아진다고 하였다. 즉, 이는 하천 단면이 단순한 단단면 형태 일지라도 수위가 상승하면 단면통제에서 하도통제로 통제특성이 바뀌면서 수위-유량관계곡선식 지수(c)가 2를 기준으로 바뀐다는 것을 의미한다. 그리고 일반적으로 지수(c)가 변화되는 시점에서는 특별한 단면형태의 변화가 없더라도 수위-유량관계곡선식 구간을 분리 하는 것이 좋다. 따라서 수위-유량관계곡선식 개발에 있어서 지수(c)가 2가 되는 위치(하천수위)를 찾는 것은 필요하다고 할 수 있다.
4. 구간분리 위치 분석 방안
미리 살펴본 바와 같이 기존의 수리적 분석은 구간분리 위치가 명확하게 나타나지 않으며 개발자의 주관이 개입될 여지가 높다. 이를 보완하기 위해 다음의 방법을 추가 분석하여 수위-유량관계곡선식 구간분리 위치를 결정할 것을 제안하고자 한다.
일본은 Eq. (7)에서 지수 c를 2로 고정하고 계수 a, b를 최소자승법으로 구하는 방식으로 수위-유량관계곡선식을 개발한다고 알려져 있다.
또한, Kinoshita (2001)은 매닝식과 Eq. (7)에서 H와 Q의 값과 그 경사(그림상의)가 일치한다고 가정하는 것으로 다음 식을 유도하였다(Kinoshita, 2001).
여기서 , R = 경심(A/B)이며 조도계수와 수면경사는 등류가정에 의해 소거된다.
Eqs. (9) and (10)은 유량측정 성과의 이상치 검토에 활용하는 것으로 알려졌다. 그러나 Eq. (9)를 살펴보면 평균유속 과 단면형상 을 함께 검토가 가능하며 Eq. (10)는 단면형상 요소만으로 검토하는 방식이다. 이 두 식과 앞서 멱함수 유도 과정에서 살펴본 수위-유량관계곡선식의 물리적 의미를 함께 고려하면 다음과 같이 구간분리 위치를 도출할 수 있다.
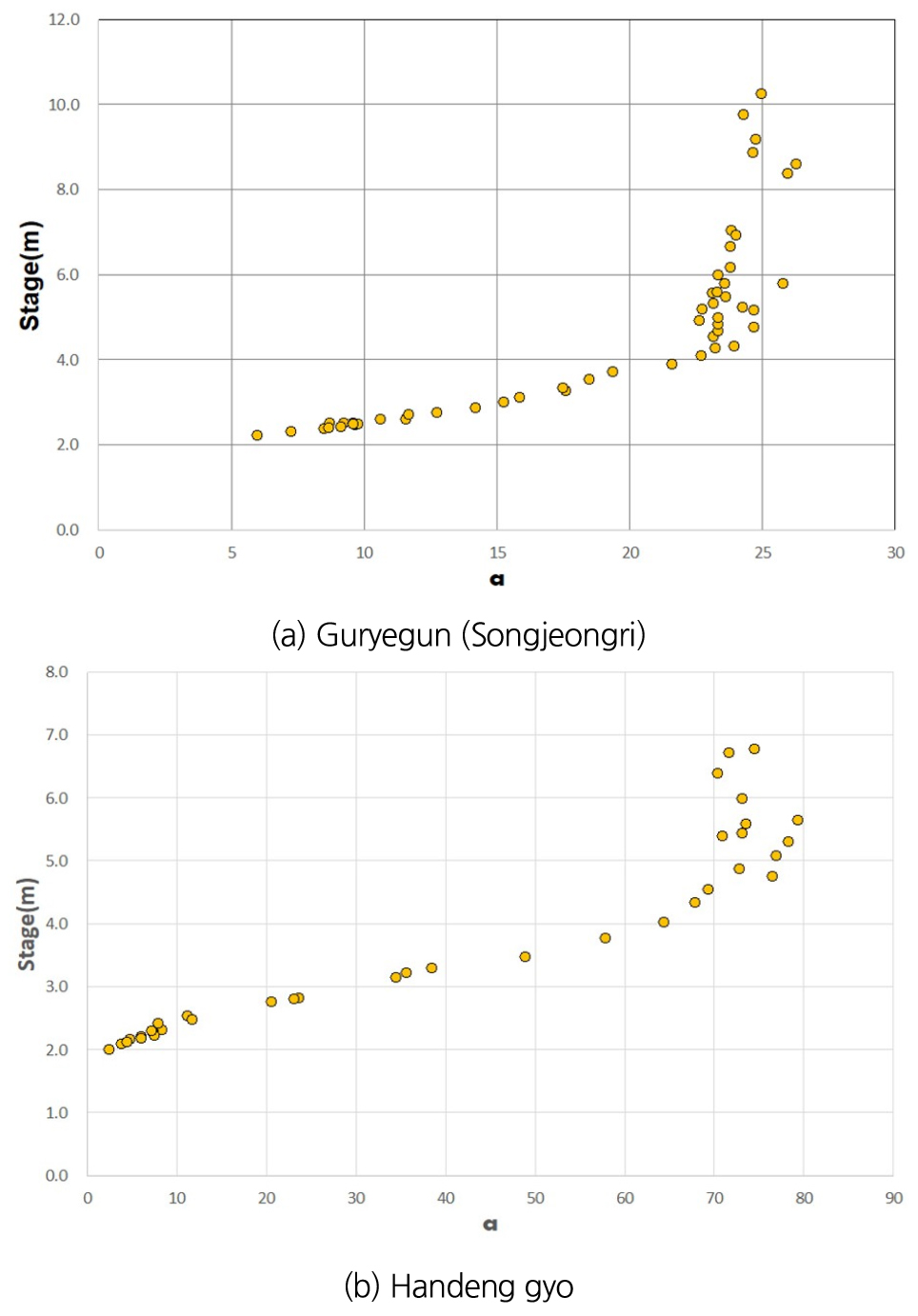
Fig. 4에서 두 지점 모두 계수 a가 상승하다 특정 수위에서 수렴하는 경향을 보인다. 앞서 멱함수 유도과정에서 a는 조도계수에 반비례하고 수면경사에 비례하는 수리적 특징이 있다고 설명하였다. 이를 토대로 분석해 보면 낮은 수위에서 하상에 의한 조도 영향을 크게 받고 수위가 상승 할수록 상대적으로 그 영향이 적어지며 계수 a는 점점 증가하는 것으로 판단된다. 즉, 계수 a가 수렴하는 수위 4.0 m (구례군(송정리))와 4.5 m (한덕교) 부근에서 단면통제에서 하도통제로 바뀌는 시점이라고 할 수 있다. 그리고 이 위치에서 수위-유량관계곡선식 구간을 분리하는 것이 적절한 것으로 판단된다.
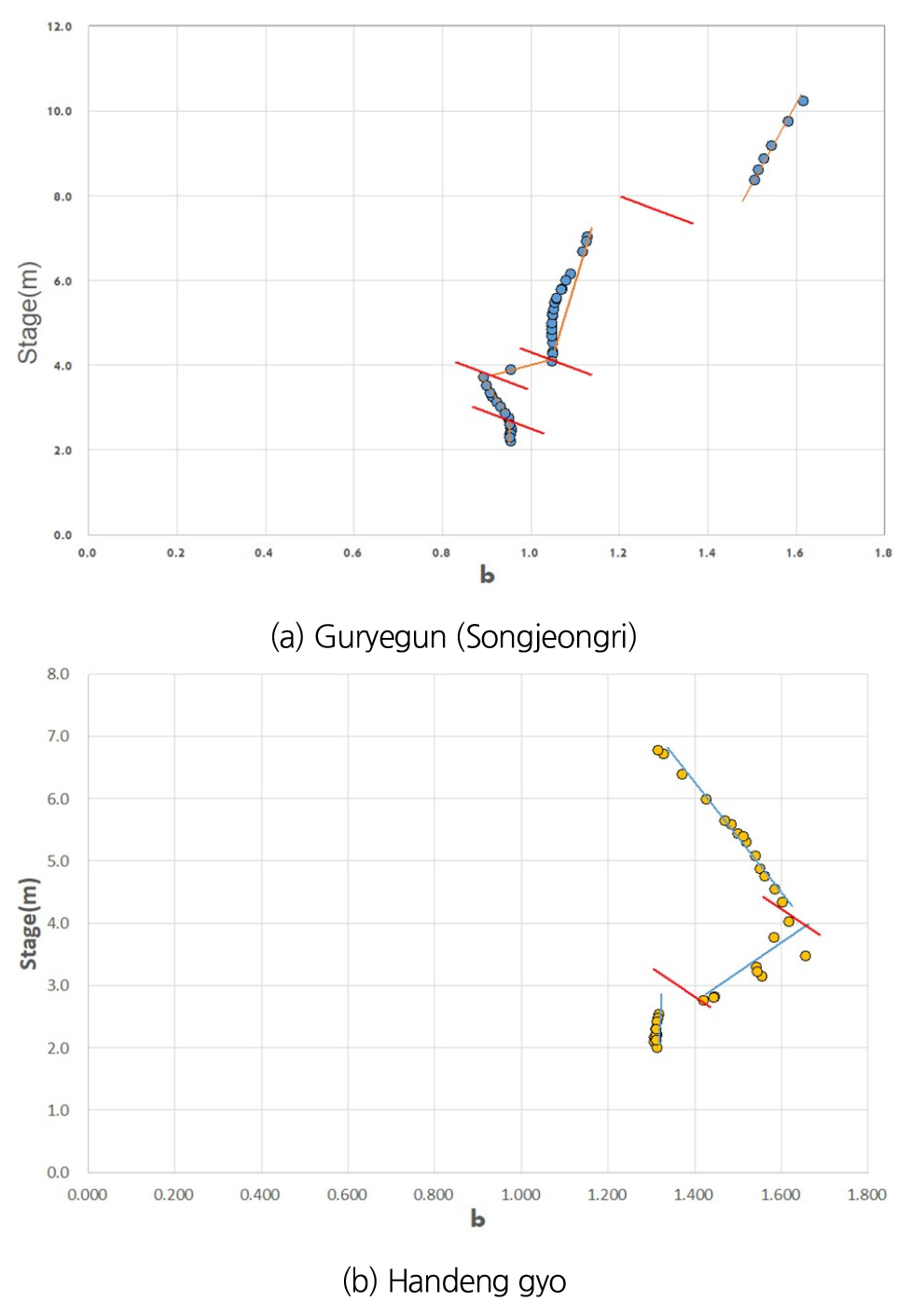
두 번째로 Eq. (10)에 의해 측정성과를 분석하여 다음 Fig. 5에 나타냈다.
Fig. 5(a) 구례군(송정리) 경우 2.5 m, 3.8 m, 4.1 m 7.2 m 등 총 5개로 구간이 분할되는 것으로 나타났다. 그러나 수위 약 3.8 m와 4.1 m의 분할은 그 구간이 약 0.3 m에 불과하여 이런 경우, 실무적으로 하나의 구간분리로 판단하는 것이 합리적이다.
Fig. 5(b) 한덕교의 경우 2.7 m, 4.0 m 등 3개의 구간으로 분할이 가능한 것으로 나타났다.
5. 결 론
앞서 설명한 방법으로 분석된 구간분리 위치를 이용하여 수위-유량관계곡선식 a와 c를 산정하였다(Table 1). GZF b는 각 구간에서 결정계수가 가장 높게 나타나는 값을 취하였다. 산정된 a, b, c는 측정성과를 분석된 구간으로 분류하고 단순하게 회귀분석 된 결과이며 불연속구간 처리 등의 후처리를 하지 않았다.
Table 1.
Rating curve a, b, c
구례군(송정리) 경우 계수 a와 지수 c가 이번 방법으로 구간분리 위치를 결정했을 때 안정적이며 물리적으로도 타당하다. 계수 a는 22.666~69.984의 범위를 보이며 수위가 상승할수록 증가하는 일반적인 경향을 보였다. 지수 c의 경우 2.459~1.578의 범위를 보였으며 수위가 상승할수록 감소하는 경향을 보였다.
일반적으로 단단면의 자연하천에서는 수위가 증가할수록 계수 a는 증가하고 지수 c는 감소하는 경향을 보인다. 계수 a는 하천 바닥 조도 영향이 수위 상승에 따라 상대적으로 감소하므로 증가하고, 지수 c는 단단면 형태의 하천에서 수위가 상승하면 통수단면 형태는 직사각형에 가까워져 감소하는 것이 일반적이다.
한덕교 경우 계수 a는 31.498, 18.081, 297.584로 나타났으며 지수 c는 2.142, 3.255, 2.142로 나타났다. 한덕교 경우 수위 약 2.7 m 부근에서 Fig. 6과 같이 우안 홍수터로 단면이 확대되어 중간 수위-유량관계곡선식에 해당하는 지수 c가 증가하였다. 앞서 설명한 계수 a와 지수 c의 물리적 의미를 고려하면 타당한 것으로 판단된다.
종합해보면 이번에 제안한 구간분리 위치 결정 방법은 계수 a와 지수 c를 산정하여 구간분리 위치를 결정하는 방법으로 간편하면서도 멱함수의 물리적인 의미와 잘 부합되는 것으로 판단된다. 또한 기존의 방법과는 다르게 개발자의 주관적인 판단이 많이 줄어든다.
물론 기존 수리특성 분석 방법이 잘못된 것은 아니다. 그러나 수리특성 분석만으로 구간분리 위치를 결정하는 개발자도 없을 것이다. 단면형태, 수위-윤변 관계, 상·하류검토, 유출분석 등을 많은 요소를 추가로 분석하여 구간분리 위치를 검토하기도 한다. 그러나 기존의 이 방법들은 개발자의 숙련도에 따라서 많은 시행착오를 격기도 한다. 이번에 제안한 방법을 이용한다면 구간분리 위치결정에 대한 시행착오가 상당히 줄어든다.
이번 분석이 이용된 구례군(송정리)와 한덕교 지점은 수위대별로 유량측정성과가 잘 분포되어있고 그 개수도 많은 편이다. 그러나 만약 유량측정성과가 부족하고 분포가 편중되어 있다면 기존의 방법으로 구간분리를 결정하고 수위-유량관계곡선식을 개발하기는 쉽지 않고, 개발된다 하더라도 오류가 발생할 가능성이 있다. 전술하였듯이 이 오류는 특히 외삽구간에서 큰 문제가 된다. 따라서 수위-유량관계곡선식 a와 c의 물 리적 의미를 이해하고 적용하는 것은 정확한 수위-유량관계곡선식 개발에 큰 도움이 된다고 할 수 있다.
기본적으로 수위-유량관계곡선식은 정확하고 충분한 유량측정성과를 토대로 개발되어야 한다. 그러나 현장상황에 따라서 유량측정이 불가능한 경우도 있으며, 예산과 인력의 문제로 충분한 유량측정성과를 확보하지 못하는 경우도 있다. 이런 경우 물리적인 의미를 고려하여 수위-유량관계곡선식을 분할하지 않는다면 기초자료인 유량자료에 큰 오류가 발생한 가능성이 높다고 할 수 있다. 또한 물리적인 방법으로 수위-유량관계곡선식 구간을 분리한다면 개발자의 주관적인 판단이 배제되어 그 신뢰성도 높아진다고 할 수 있다.
