1. 서 론
2. 상수관망시스템의 계층적 수질모의
2.1 EPANET을 이용한 상수관망시스템 모의
2.2 상수관망시스템의 계층적 구조 및 모의방법
3. 상수관망시스템의 공급수질 분석
3.1 잔류염소농도 추정
3.2 수질기준 초과/미달 공급량 분석
4. 적용 및 결과
4.1 적용대상 네트워크
4.2 공급계통의 계층화 결과
4.3 잔류염소농도의 시공간 분석결과
5. 결 론
1. 서 론
국내 상수도 보급률은 1960년대 22% 수준에서 현재 98% 수준에 도달하는 등 수량공급 측면에서 안정적인 서비스 환경을 구축하고 있다. 하지만, 최근 발생한 상수도 내 수질사고로 인해 음용수로서의 신뢰도는 상대적으로 낮은 실정이다. 지난 2013년 환경부(ME, 2013)의 국내 상수도 음용 현황 조사 결과, 수돗물 음용을 기피하는 이유는 주로 녹물이나 이물질, 수돗물의 냄새와 맛, 부정적인 언론보도 등에 따른 우려가 각각 54.4%, 51.4%, 50.7% 인 것으로 조사된 바 있다. 이들 중, ‘녹물이나 이물질’, ‘수돗물의 냄새와 맛’으로 인한 부정적인 인식은 소비자가 직접적으로 체감할 수 있는 요인이며, 상수도 공급계통의 정밀한 수질해석 및 공급수질 개선을 통해 해소가 가능할 것으로 판단된다.
최근 상수도 연구 분야에서는 상수관망 해석 기술을 용수공급 과정에 효과적으로 반영하기 위해 수질해석 정확도를 개선하고, 공급수질을 고려한 최적 운영 방안을 마련하는 등 다양한 연구가 활발히 진행되고 있다. 대표적으로, Chung et al. (2004), K-water (2010), Lee (2019) 등의 연구에서는 실내실험을 통해 수질 반응계수를 추정하였으며, K-water (2017)의 연구에서는 상수관망 수리·수질 해석 모형 중 하나인 EPANET (Rossman et al., 2020)을 활용하여, 실제 수질계측 데이터를 기반으로 수질 반응계수를 추정하고 국내 상수관망 해석에 적용한 바 있다.
앞서 언급된 EPANET 모형은 상수관망시스템의 수질해석 연구에 폭넓게 활용되고 있으며, 특히 Rossman and Boulos (1996)의 연구에서 수질해석 기법에 따른 그 정확도와 효율을 검증한 바 있다. 이후, Sakarya and Mays (2000), Tryby et al. (2002), Prasad et al. (2004)의 연구에서는 EPANET 모형과 최적화 기법을 연계함으로써 최적 수질 공급을 위한 배수펌프의 운영, 정수처리 시설의 배치 및 운영 등의 효율을 극대화할 수 있는 방법을 제시하였다. 또한, Wang et al. (2001), Kang and Lansey (2010)의 연구에서는 공급지역 내 잔류염소농도 등 수질변화에 따른 피드백 제어 방법을 제시하거나, 실시간 최적 정수처리 계획 방안을 제시하는 등 상수관망시스템 내 잔류염소농도를 효율적으로 유지하기 위한 다양한 노력이 계속되고 있다.
이처럼 상수관망시스템 연구분야에서는 컴퓨터 모형을 이용한 해석이 필수적이며, 국내 연구 및 실무 분야에서도 EPANET 모형을 활용한 분석이 활발하게 진행되고 있다. 그러나 컴퓨터 성능이 크게 발달한 현재까지도 대규모 네트워크의 수질해석은 여전히 해결하기 어려운 문제 중 하나이다. 대표적으로, 반복적인 수치해석 기법의 특성상, 수만개 이상의 구성요소가 관여하는 대규모 네트워크의 수질해석은 긴 계산시간으로 인해, 해석이 불가능하거나 다양한 분석을 수행할 수 없는 문제점이 발생한다. 특히, 수질해석에 있어서 실제 용수공급 상태를 나타내는 안정화 상태에 도달하기까지 추가적인 모의기간이 요구되기 때문에 계산효율 문제가 더욱 부각된다. 본 연구에서는 대규모 상수관망시스템의 수질해석에 있어서 계산효율을 개선하기 위해, 공급계통에 따라 네트워크를 송배수구간 및 배급수구간의 두 가지 계층으로 분리하여 해석하는 계층적 모의기법을 제시하였다. 제안된 방법은 국내 대규모 상수도 네트워크를 대상으로 적용되었으며, 다양한 염소투입농도 시나리오에 따른 잔류염소농도 분포를 시공간적으로 분석하였다.
본 연구는 구체적으로 다음과 같이 구성되었다. 2.1절에서는 EPANET 모형의 수리·수질 해석 이론을 소개하였으며, 2.2절에서는 상수관망시스템의 공급계통에 따른 계층적 모의기법을 서술하였다. 3장에서는 상수도 수질 반응계수의 추정방법(3.1절)과 비정상수질 공급량 분석방법(3.2절)을 다루었다. 4장에서는 본 연구의 적용대상 네트워크에 대한 소개 및 계층화 모의, 잔류염소농도 분석 결과를 제시하였으며, 마지막으로 5장을 통해 연구결과를 요약하고 향후 관련 연구의 발전 방향을 소개하였다.
2. 상수관망시스템의 계층적 수질모의
2.1 EPANET을 이용한 상수관망시스템 모의
상수관망의 해석이란 물 공급원으로부터 이용자에게 용수를 공급하는 과정에서 각 시스템 구성요소에 의해 발생하는 수리학적(Hydraulic) 및 수질(Water quality) 상태 변화를 연산하고, 모의하는 과정을 의미한다. 무수히 많은 요소가 관여하는 상수관망시스템의 특성상, 이러한 상수관망의 해석은 다양한 컴퓨터 모형을 바탕으로 수행되고 있으며, 본 연구에서는 EPANET 모형을 활용하여 상수관망시스템의 수리 및 수질해석을 모의하였다. EPANET은 전 세계적으로 가장 폭넓게 활용되고 있는 상수관망해석 모형으로써, 수리·수질 해석 절차는 다음과 같이 간략히 소개할 수 있다.
먼저 EPANET 해석에 따른 수리학적 상태 변화는 관로 내 마찰에 의해 발생하는 수두(Head) 손실과 그 밖의 펌프, 밸브 등에 의해 발생하는 수두 변화를 중심으로 이해할 수 있다. 관마찰 손실수두는 관로의 직경(D), 길이(L), 조도계수 및 유량(Q) 조건을 바탕으로 Darcy-Weisbach, Chezy-Manning, Hazen-Williams 등 산정공식을 통해 계산할 수 있다. 이들 중 Hazen-Williams 공식이 실무에서 가장 대표적으로 활용되고 있으며, 해당 산정식은 Eq. (1)과 같이 표현할 수 있다. EPANET에서는 위와 같은 기본적인 관로 정보 및 각 수요절점에서의 수요량 정보를 바탕으로, 반복적인 수치해석 과정을 거쳐 절점별 실제 용수공급량과 수압, 그리고 관로별 유량과 유속 등의 모의 결과를 도출한다.
여기서, HL: 손실수두(m), L: 관로연장(m), Q: 유량(m3/s), C: Hazen-Williams 조도계수, D: 관경(m).
한편, 상수관망 수질 해석은 시간에 따른 용수 내 반응물질의 농도 변화를 모의하는 과정이며, 따라서 앞서 도출된 수리해석 결과를 바탕으로 시스템 내 용수의 수리학적 거동 및 체류시간 등을 파악하는 것이 필수적이다. 본 연구에서는 수돗물의 소독약으로 널리 사용되는 염소(Chlorine)를 대상으로 수질모의를 수행하였다. EPANET을 이용한 수질해석에서, 용수 내 염소의 반응은 크게 유체용적반응(bulk fluid reactions) 및 관체반응(wall reactions) 과정으로 구분할 수 있다. 먼저 유체 내에서 발생하는 유체용적반응은 반응성분 및 형성물질의 농도, 반응 계수 및 차수의 함수로써 Eq. (2)와 같이 표현할 수 있으며, 반응계수로 수체반응계수(kbulk)를 적용한다. 이때, 반응계수가 양(+)의 값이면 반응물질의 형성(formation), 음(-)의 값이면 감소(decay) 모의를 의미한다.
여기서, (C): M / L3 / T 차원의 반응농도항, C: M / L3 차원의 물질 농도, k: 반응계수, n: 반응의 차수.
또한, 관로 내 송수 과정에서 발생하는 관체반응은 유체용적반응과 동일한 함수를 가지며, 반응계수는 관체반응계수(kwall)를 통해 모의할 수 있다. 그러나, 각 관로의 kwall은 관경 및 유속 등에 의해 서로 상이한 값을 갖게 되며, 무수히 많은 관로 요소를 가진 상수관망 해석에서 이를 모두 산정하고 적용하는 것은 어려운 과정이다. EPANET에서는 이러한 문제점을 해결하기 위해 상수관망 전체에 공통적으로 적용될 수 있는 L / T 차원의 관체반응률(kw) 값을 입력받은 후, 각 관로별로 mass-transfer coefficient (Sherwood et al., 1975) 값을 적용함으로써 각 관로의 관체반응계수(kwall)를 간접적으로 산정한다.
결과적으로 상수관망을 통한 용수의 공급 과정에서는 상술된 유체용적반응과 관체반응이 모두 발생하며, Eq. (3)과 같이 일반적으로 널리 사용되는 1차 반응함수식에서는 kbulk와 kwall 계수가 모두 T‒1로 같은 단위를 갖게 되므로, 수질해석에 적용되는 반응계수 k는 Eq. (4)에 나타난 것과 같이 kbulk와 kwall을 합산하여 산정할 수 있다.
여기서, C0: 초기(t = 0) 염소농도, C(t): 시간 t에서의 염소농도, k: T‒1 차원의 반응계수(즉, kbulk 또는 kwall).
2.2 상수관망시스템의 계층적 구조 및 모의방법
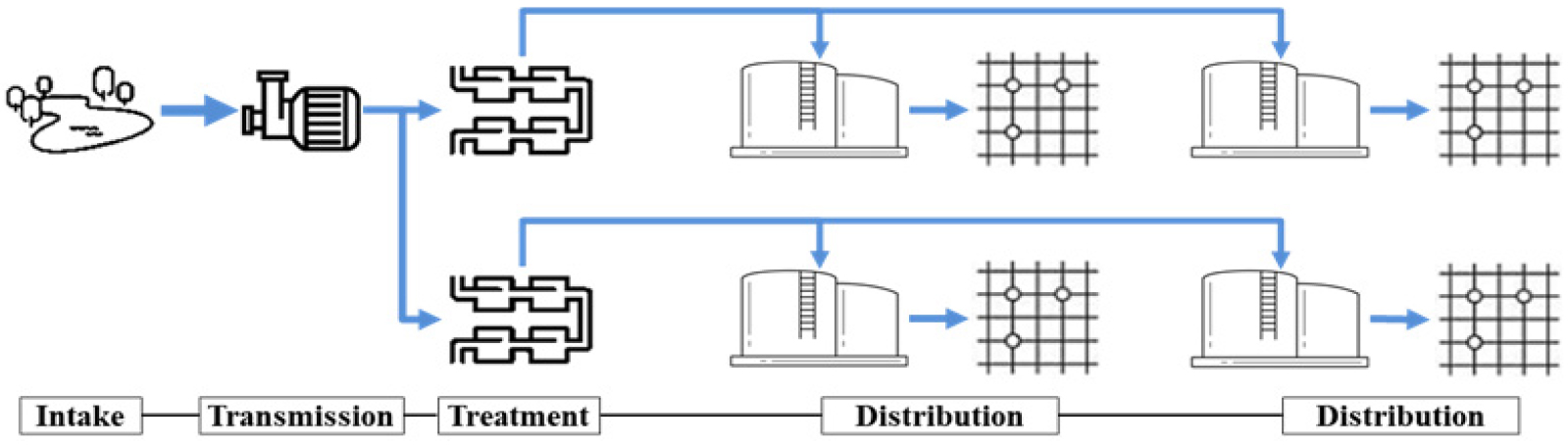
상수도시스템의 공급과정은 공급원에서의 취수, 정수장으로의 도수, 정수장에서의 정수, 배수탱크로의 송수, 배수구획단위의 배수, 급수구획단위의 급수 과정으로 이루어진다(Fig. 1). 여기서 상수관망의 용수공급 구조는 크게 정수장으로부터 공급되는 송수계통과 배수지로부터 공급되는 배급수계통으로 구분되는 일종의 계층적 구조(Hierarchical structure)를 갖는다. 최근에는 대규모 공급계통의 효율적인 운영·관리를 위해, 상수관망을 배수구획 단위로 분할하는 블록화 시스템을 구축하여 운영하고 있으며, 이를 중심으로 상수관망의 계층적 구조를 손쉽게 파악할 수 있다.
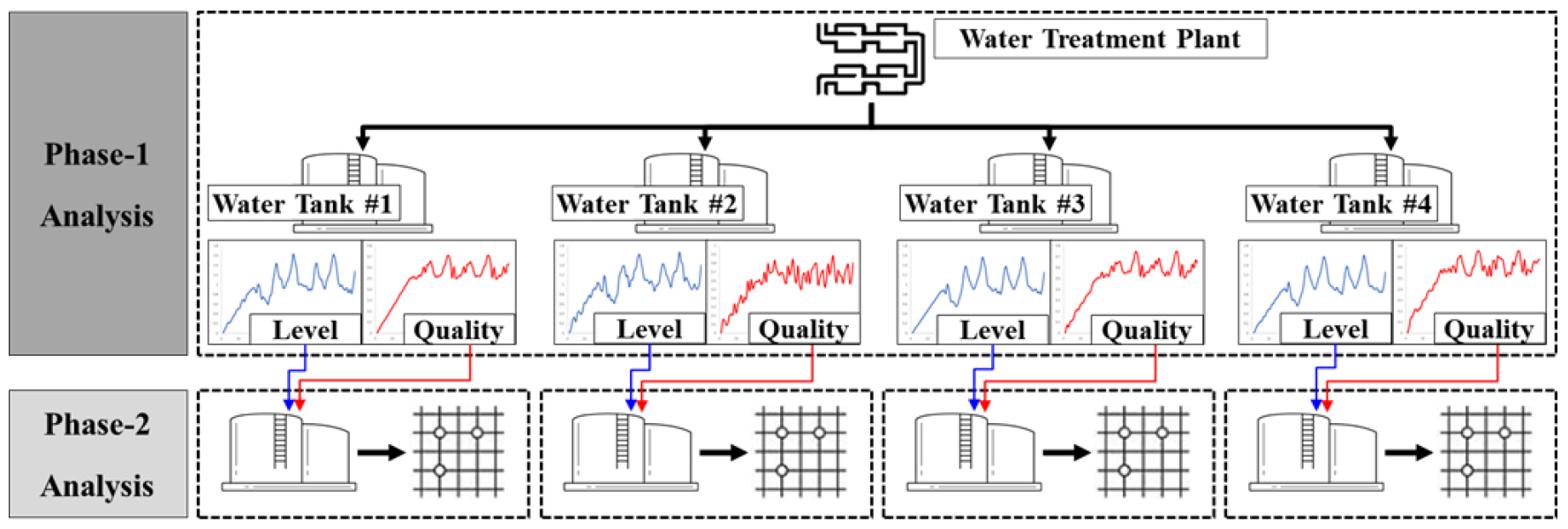
일반적으로 EPANET을 이용한 상수관망의 수리해석(hydraulic analysis)은 대규모 네트워크의 시간변동 모의에서도 계산시간이 길게 소요되지 않는다. 하지만, 수질해석(water qualify analysis)을 위해서는 긴 모의시간(Time duration)과 짧은 시간간격(time step)이 요구되기 때문에 계산시간이 급격히 늘어나는 문제점이 있다. 특히 대규모 네트워크의 정수장에서부터 배수탱크를 거쳐 말단 절점(ending node)까지 한꺼번에 수질모의를 수행할 경우, 수질안정화를 위해 필요한 모의시간이 매우 길어지므로, 네트워크의 규모가 커지게 되면 다양한 수질해석 모의가 현실적으로 어렵게 된다. 본 연구에서는 대규모 상수관망네트워크의 수질해석 효율을 개선하고 정확한 잔류염소농도 추정을 위한 계층적 수질모의기법을 제시하였다. 구체적으로, 제안한 계층적 모의기법에서는 용수공급계통을 크게 1) 정수장에서 배수절점을 포함하는 송배수계통(1-계층)과 2) 배수지에서 급수절점을 포함하는 배급수계통(2-계층)으로 구분한다. 제시한 계층적 모의기법에서의 네트워크 구조는 Fig. 2와 같다.
Fig. 2에 도시한 바와 같이, 계층적 모의기법에서는 먼저 1-계층 네트워크 모의를 통해 각 배수지에서의 수위 및 수질안정화 상태를 도출한다. 1-계층 모의를 통해 배수지의 수위와 염소농도가 안정화 상태에 도달한 후, 해당 정보를 각 2-계층 네트워크의 공급원인 배수탱크의 초기값으로 전달하여 각 배수구역별 모의를 수행한다. 이때, 1-계층 네트워크 해석 결과를 2-계층으로 전달하기에 앞서 다음과 같은 필요조건이 요구된다. EPANET을 이용한 상수관망 해석은 해당 네트워크의 용수공급을 처음부터 개시하는 양상으로 진행되므로, Fig. 2의 1-계층 해석 결과에 나타난 것과 같이 모의기간 초기에는 배수탱크의 수위 및 염소농도 등이 0에서부터 모의되는 것을 확인할 수 있다. 한편, 일정한 모의기간이 지난 후에는 수위 및 염소농도가 안정화 상태에 도달하여 일정한 시간을 주기로 반복적인 양상을 보이는 것을 알 수 있다. 예를 들어, 24시간 주기의 용수사용패턴 및 염소투입 조건을 입력할 경우, 배수탱크 내 수위와 염소농도 또한 24시간을 주기로 반복되는 것으로 이해할 수 있다. 이와 같이, 다양한 상수관망 운영 조건에 따라 최종적으로 수리 및 수질 해석 결과가 주기적으로 반복되는 상태에 도달하였을 때를 네트워크 “안정화” 또는 “패턴화” 상태라고 표현할 수 있으며, 실제 시스템의 상태에 근접하였다고 가정할 수 있다. 따라서, 제안된 계층적 모의방법에서는 1-계층 네트워크 해석에서 모든 배수지가 안정화 상태에 도달한 후, 각 배수지별로 반복주기에 해당하는 기간의 수위, 잔류염소농도 정보를 2-계층의 각 배수지의 초기정보로 입력하고 모의를 수행함으로써 1-계층 및 2-계층 네트워크 간 수리 및 수질해석의 연속성을 확보할 수 있다.
3. 상수관망시스템의 공급수질 분석
3.1 잔류염소농도 추정
상수도 공급과정에서 수돗물의 안전성을 유지하기 위해서는 잔류염소농도(Chlorine residual)를 일정수준으로 유지해야 한다. 본 연구에서는 네트워크 내 잔류염소농도 현황을 바탕으로 상수도 공급수질 서비스를 분석하고자 하였으며, 따라서 EPANET 수질해석에서는 반응물질인 염소의 농도가 시간이 경과함에 따라 감소하는 감소반응 모의를 수행하게 된다. 앞서 2.1절을 통해 소개한 바와 같이 EPANET 수질해석을 위해서는 kbulk 및 kw 등의 반응계수가 요구되며, 이들 반응계수를 정확히 추정할 필요가 있다. 최근 연구에서는 최적화 기법 등을 이용한 매개변수 추정 방법이 적용되고 있으며, 이를 위해서는 많은 양의 실측 수질 데이터가 요구된다.
본 연구에서는 상수관망의 계층적 모의기법을 이용한 수질해석과 잔류염소농도의 시공간적 분석에 집중하고자 하였으며, 따라서 기존 잔류염소의 반응계수 추정 연구를 통해 제시된 반응계수들의 범위를 바탕으로 몇 가지 kbulk 및 kw 값 조합을 적용하였다. 먼저 Lee (2019)의 연구에서는 국내 P-city 광역상수도의 수온별 kbulk 값을 각각 -0.5760(25℃), -0.1872(18℃), -0.1056(4.5℃) d-1 등과 같이 추정하였으며, K-water (2017)의 연구에서는 국내 B-town 지방상수도의 kbulk 값을 3℃부터 30℃까지 –0.1373 ~ -1.4632 d-1의 범위로 추정한 바 있다. 한편 kw 추정과 관련하여, Chung et al. (2004)의 연구에서는 겨울철 국내 S-city 배수계통의 kw 값을 -0.054 ~ -0.115 m/d의 범위로 추정하였으며, K-water (2017)의 연구에서는 -0.05 m/d부터 -10-3 m/d 수준에 이르는 kw 값을 추정한 바 있다. 위와 같은 추정범위를 바탕으로, 본 연구에서는 지중에 매설된 상수관로의 특성을 고려하여 -0.1872(18℃) 및 -0.1056(4.5℃) d-1의 kbulk 조건에서, 관체반응률(kw) 값을 -0.1 m/d부터 -10-4 m/d까지 점진적으로 감소시키는 과정을 통해 잔류염소농도를 모의하고, 해당 모의결과값과 대상 네트워크에서 측정한 실측 잔류염소농도와 비교하여 적정 반응계수값을 추정하였다.
위와 같이 추정된 수질 반응계수를 적용함으로써 EPANET 수질해석을 수행할 수 있으며, 시공간적 상수도 공급수질 분석을 위한 첫 번째 지표로써, 네트워크 내 수요절점별 24시간 잔류염소농도 수질기준 만족 여부를 공간적으로 분석하였다. 여기서 잔류염소농도 수질기준은 다음과 같이 구성하였다. 먼저 잔류염소농도 하한기준은 국내 「수도법 시행령」에 따라 0.1 mg/L를 적용하였다. 반면, 잔류염소농도 상한기준의 경우, 동(同) 시행령에서는 4.0 mg/L를 제시하고 있으나, 실제 상수도시스템 운영에서는 소비자 민원(냄새, 맛 등)에 의해 비교적 낮은 잔류 염소농도를 유지하고 있는 실정이므로, 적용대상지역의 운영 목표를 참고하여 0.6 mg/L를 상한기준으로 설정하였다(대상지역 담당공무원과 논의 후 결정).
3.2 수질기준 초과/미달 공급량 분석
앞서 소개된 절점별 수질기준 만족 여부를 이용한 공급수질 분석은 단점이 존재한다. 예를 들어, 실제 수요량이 낮은 다수의 수요절점에서 잔류염소농도 기준을 벗어나는 경우, 용수공급 서비스가 불량한 것으로 보일 수 있으나, 실제 공급된 용수량이 적으므로 그 위험성은 상대적으로 낮은 것으로 이해할 수 있다. 반면, 수요량이 높은 소수의 수요절점에서 잔류염소농도 기준을 벗어나는 경우에 소비자의 민원이 다수 발생하는 등 오히려 위험성이 큰 것으로 판단할 수 있다.
본 연구에서는 이처럼 수질기준을 만족하지 못하는 용수가 소비자에게 공급되는 규모를 파악하기 위해, 상수도 공급수질 분석의 두 번째 지표로써 아래의 Eqs. (5) and (6)와 같은 산정식을 적용하였다. 즉, 분석대상기간(T)에 걸쳐, 수요절점에서의 매 시간별 수질기준 만족여부를 검토한 후, 수질기준을 만족하지 못한 경우 해당 시간대의 물 사용량을 비정상 수질 공급량으로 분류하여 이를 전체 네트워크 및 분석대상 기간에 대하여 합산한 것을 의미한다. 이때, 분석대상 기간은 네트워크의 안정화가 달성되어 반복성을 보이는 단위 주기에 해당하며, 네트워크 안정화 달성을 위해 용수도달시간이 포함된 EPANET의 전체 모의기간과는 상이한 것으로 이해할 수 있다.
여기서, Slow: 잔류염소농도 하한기준(0.1 mg/L) 미만으로 공급된 용수공급량(m3), : t 시간에 i 절점의 용수사용량(m3/h), : t 시간에 i 절점의 잔류염소농도 하한기준 미달여부를 나타내는 지수값(0 혹은 1), : t 시간에 i 절점의 잔류염소농도(mg/L), N: 상수관망 내 총 절점의 수, T: 총 분석대상기간(hr).
여기서, Shigh: 잔류염소농도 상한기준(0.6 mg/L)을 초과하여 공급된 용수공급량(m3), : t 시간에 i 절점의 잔류염소농도 상한기준 초과여부를 나타내는 지수값(0 혹은 1).
4. 적용 및 결과
4.1 적용대상 네트워크
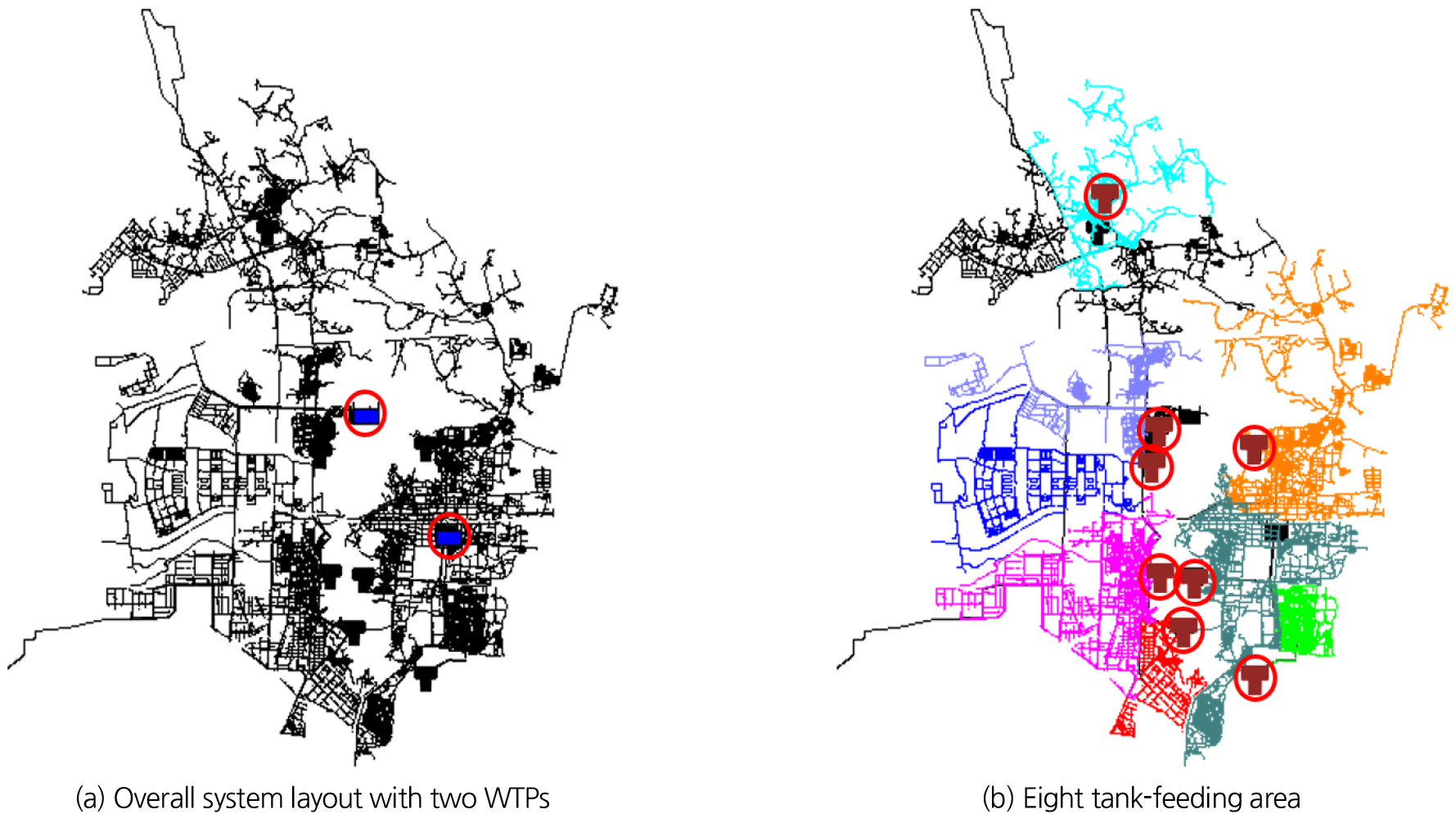
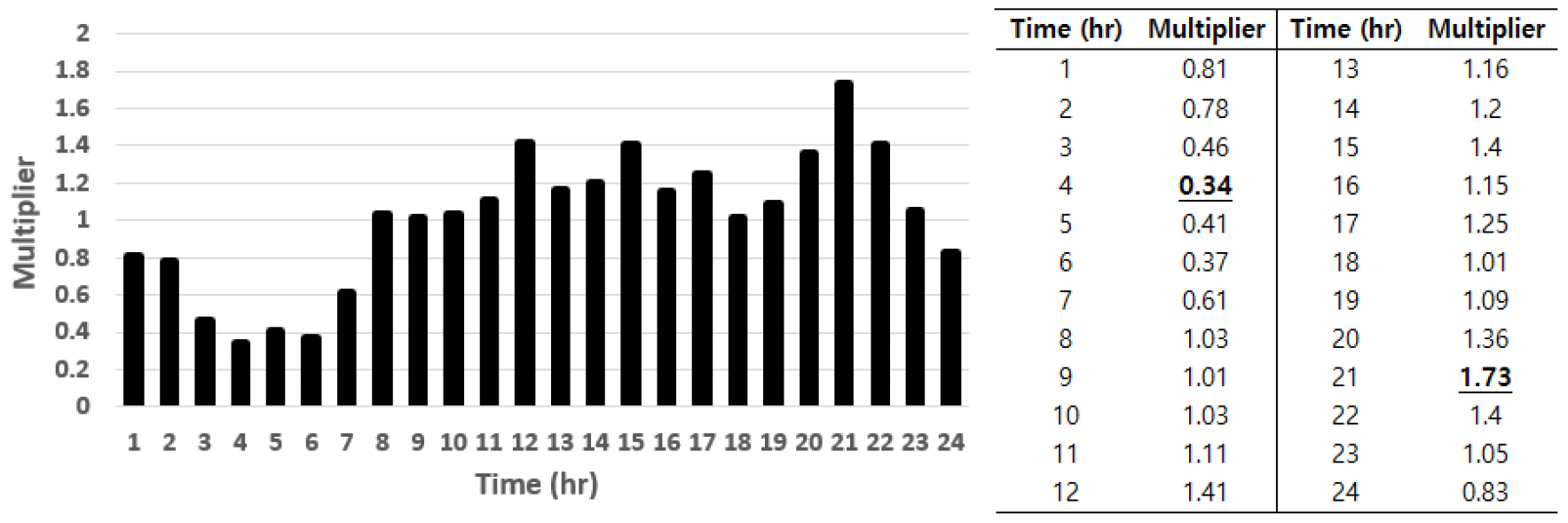
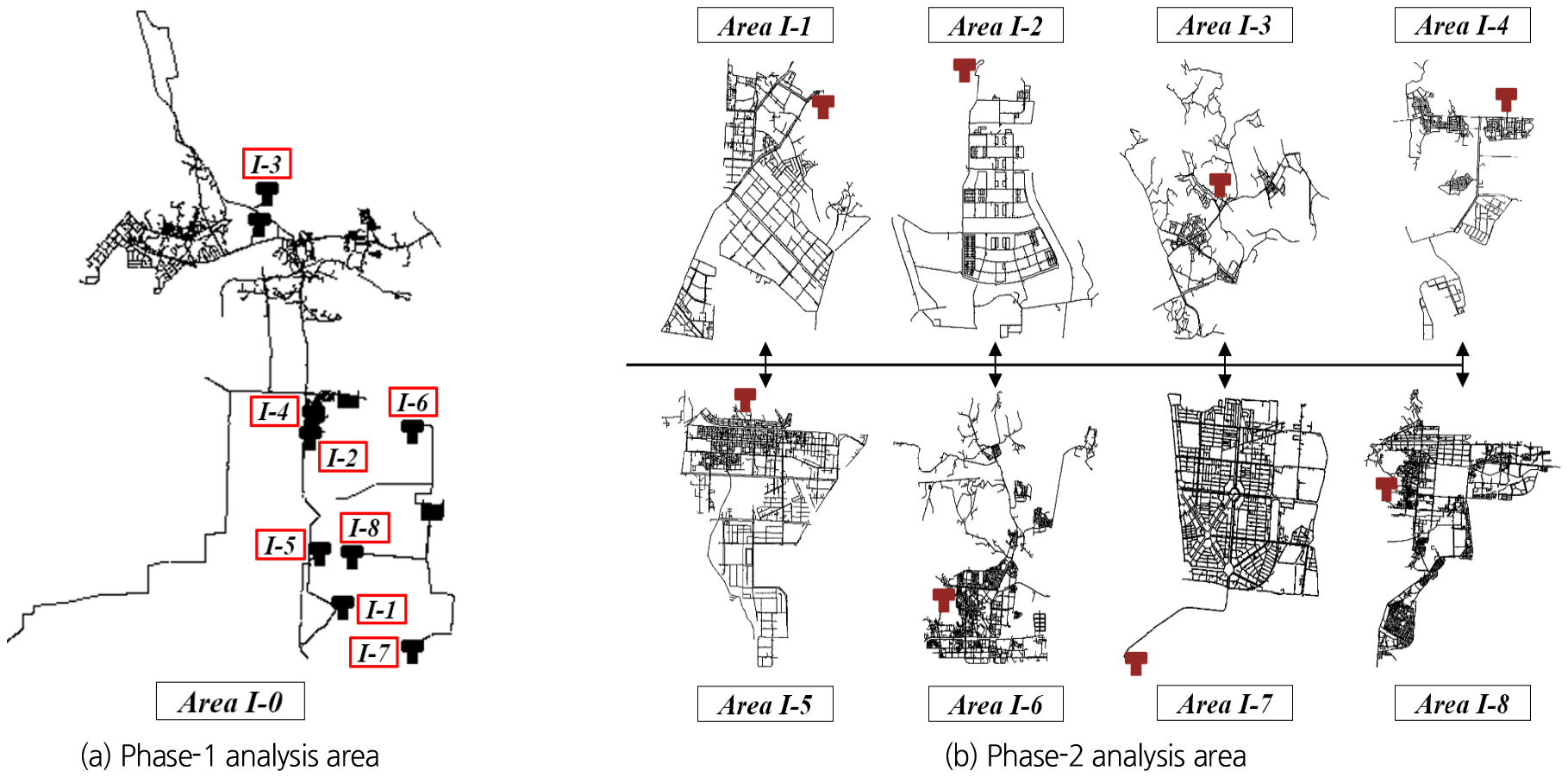
본 연구의 적용대상 네트워크인 국내 I-city 상수관망 구조는 Fig. 3(a)와 같다. Fig. 3(b)에서 검은색으로 표시된 관로는 네트워크 내 2개 정수장으로부터 배수지를 거치지 않고 바로 용수를 공급하는 1-계층 지역이고, 그 외 다양한 색으로 표시된 관로는 네트워크 내 8개의 배수지를 거쳐 각 배급수지역에 용수를 공급하는 2-계층 지역이다. I-city 상수관망은 총 79,943개의 관로를 통해, 전체 76,734개의 절점 중 실제 물 수요가 발생하는 30,457개의 수요절점에 하루 평균 약 409,210 m3 (17,050 m3/h)의 수요량을 공급한다. 전체 공급지역에 대한 24시간 물 사용량 변화는 Fig. 4에 도시하였으며, 따라서 시간당 수요량은 최대 약 29,397 m3/h (21시)부터 최소 약 5,797 m3/h (4시)까지의 범위로 변동한다.
4.2 공급계통의 계층화 결과
네트워크 계층화 방법에 의해 I-city 네트워크를 각각 1-계층 네트워크(I-0 공급지역) 및 2-계층 네트워크(I-1 ~ I-8 공급지역) 구조로 구분하여, Fig. 5에 나타난 것과 같이 계층적 모의를 수행하였다. Fig. 5(a)를 통해 1-계층 네트워크 내 배수지 위치 및 송수계통을 파악할 수 있으며, Fig. 5(b)에서는 2-계층 배급수계통의 구조를 보다 상세하게 나타내고 있다. 즉, 적용대상 지역의 계층적 모의에서는 1-계층 네트워크의 수리·수질 해석을 통해 8개 배수지의 안정화를 모두 달성한 후, 각 배수지의 24시간 수위 및 염소농도 정보를 초기값으로 이용하여 2-계층 네트워크의 수리·수질 해석을 수행하였다. Table 1은 각 공급지역별 네트워크의 절점(수요절점)과 관로의 개수, 그리고 시간당 평균, 최대, 최소 물 사용량 등을 간략히 요약한 표이다.
Table 1.
Sub-network information after hierarchical division
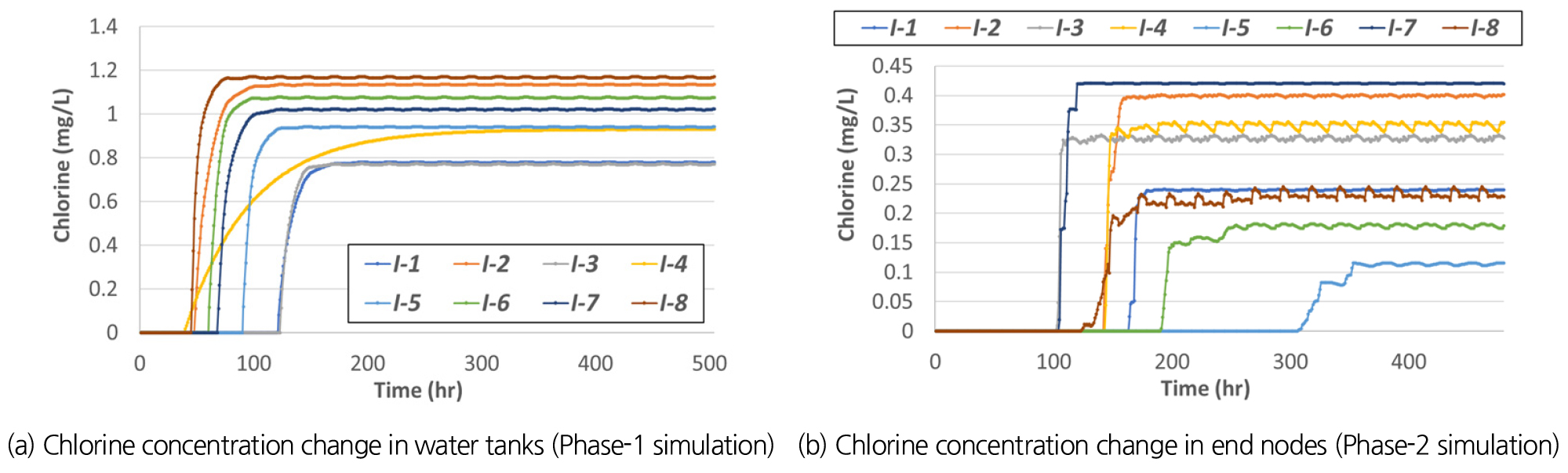
본 연구에서는 위와 같이 계층화된 2-계층 배급수 네트워크들의 수질모의에 앞서, 1-계층 송배수 네트워크의 수질해석 안정화 상태를 모의한 후, 이를 2-계층 배급수 네트워크들의 수질 초기값으로 적용하여 1-계층 및 2-계층 네트워크 간 수질해석 결과의 연속성을 확보하였다. 먼저 1-계층 네트워크의 수질해석 결과, 8개 배수탱크에서의 시간에 따른 잔류염소농도 변화는 Fig. 6(a)과 같이 나타났다. 각 배수탱크의 잔류염소농도는 초기상태(0 mg/L)에서 용수공급 개시 후 일정시간이 지난 후 용수가 도달한 시점부터 농도가 증가하기 시작하여 일정시간이 경과한 후 잔류염소농도가 반복되는 안정화 상태에 도달하는 것을 확인할 수 있다. 이때, 안정화 상태에 도달하는 시간은 배수지별로 상이한 것을 알 수 있다. 예를 들어, I-4 지역의 배수탱크는 가장 긴 안정화 기간이 필요한 것을 알 수 있으며, 따라서 수질해석 안정화를 고려한 1-계층 네트워크의 수질해석 모의기간은 약 504 시간이 소요되는 것으로 분석되었다. 다음으로, 1-계측 수질해석 결과를 각 배수지별 초기값으로 사용하여 2-계층 배급수 네트워크들의 수질모의를 수행한 결과, 각 배급수지역별 최소 잔류염소농도 발생 절점에서의 시간에 따른 잔류염소농도 변화는 Fig. 6(b)와 같이 나타났다. 각 배급수지역의 크기 및 수리학적 여건에 따라, 네트워크별로 수질해석 안정화를 위해 필요한 모의기간은 각각 240시간(I-1), 240시간(I-2), 192시간(I-3), 240시간(I-4), 480시간(I-5), 336시간(I-6), 168시간(I-7), 336시간(I-8)인 것으로 분석되었다. 만약, 제안한 계층적 모의방법을 적용하지 않고 전체 네트워크를 한 번에 모의할 경우, 안정화 소요기간이 가장 긴 I-5 네트워크의 모의기간(즉, 480 시간)을 전체 네트워크에서 고려해야 하므로 수질모의 측면에서 비효율적이다. 반면, 제안된 계층적 모의방법을 적용할 경우, 2-계층에 해당하는 각 배급수 네트워크별로 각각 소요되는 최소 모의기간에 대해서만 분석을 수행하면 되므로, 전체 수질해석에 소요되는 계산시간을 단축시키면서 동일한 수질해석 결과를 도출할 수 있다. 특히 대규모 네트워크의 경우(즉, 절점수가 수십만개에 달하는 지방상수도) 현실적으로 수질해석 자체가 불가능한 상황(개인용 컴퓨터의 메모리 초과로 인한 전산처리 불가능)이 발생하므로, 본 연구에서 제안한 계층적 모의방법은 대규모 네트워크에서 모의결과의 정확도를 유지하면서 수질해석의 부담을 저감하는데 기여할 수 있다.
4.3 잔류염소농도의 시공간 분석결과
I-city 상수관망의 잔류염소농도 분석에 앞서, 수질해석을 위해 사용된 kbulk 및 kw 반응계수는 다음과 같은 과정으로 추정되었다. I-city 내 9개 지점에서 측정한 수질계측 자료를 수집하였으며, 이들 중 상대적으로 말단(즉, 용수공급흐름 상 하류) 절점에 해당하는 것으로 판단되는 I-1, I-2, I-3, I-5 등 네 개 공급지역별 계측지점에서의 잔류염소농도의 범위를 Table 2와 같이 파악하였다. 본 연구에서는 앞서 소개한 바와 같이 기존 반응계수 추정 연구를 통해 제시된 반응계수들의 범위를 기준으로 kbulk 및 kw 값 조합을 적용하였다. 구체적으로, kbulk 는 -0.1872(18℃), -0.1056(4.5℃) d-1 등 두 개의 값을 적용하였고, kw 값을 -0.1 부터 -10-4 m/d까지 점진적으로 감소시키며 수질모의를 수행하였다. 4개의 계측지점별 평균 잔류염소농도의 모의 결과를 Table 3과 같이 정리하였다. 이때, 실측값과의 평균 오차는 반응계수값이 작을수록 더 좋은 결과를 보였으나, 일반적으로 적용되는 kw 값의 범위를 고려하여 kbulk = -0.1056 d-1 그리고 kw = -0.005 m/d의 값을 I-city 상수관망의 수질 반응계수 값으로 적용하였다. 특히, 말단 절점의 계측정보와 함께 송수관로 및 각 배급수지역의 용수공급을 담당하는 배수지의 수질계측 자료를 함께 확보하는 경우, 정수장에서 배수지를 포함하는 1-계층 네트워크와 각 2-계층 네트워크의 잔류염소농도를 보다 정밀하게 모의할 수 있는 반응계수값을 추정할 수 있다.
본 연구에서는 정수장 염소투입농도 변화에 따른 대상 네트워크의 시공간적인 잔류염소농도 범위를 파악하기 위해, 대상지역 내 정수장 염소투입 운영 범위를 바탕으로 수질해석 결과 하한기준에 미달하는 잔류염소농도가 나타나지 않을 때까지 염소투입농도를 점진적으로 증가시킨 네 가지 시나리오(0.8, 1.0, 1.2, 1.5 mg/L)를 분석하였으며, 잔류염소농도가 하한기준(0.1 mg/L)에 못 미치거나, 상한기준(0.6 mg/L)을 초과하는 수요절점의 공간적 분포를 시각화하고 해당 공급량을 분석하였다.
Table 2.
Field observation data of chlorine concentration in the application network
| Observation area | Observed chlorine concentration (mg/L) | ||
| Minimum | Average | Maximum | |
| I-1 | 0.40 | 0.55 | 0.73 |
| I-2 | 0.61 | 0.67 | 0.72 |
| I-3 | 0.50 | 0.61 | 0.76 |
| I-5 | 0.51 | 0.60 | 0.69 |
Table 3.
Simulation results of chlorine concentration in the application network
4.3.1 시나리오 1(정수장 염소투입농도: 0.8 mg/L)
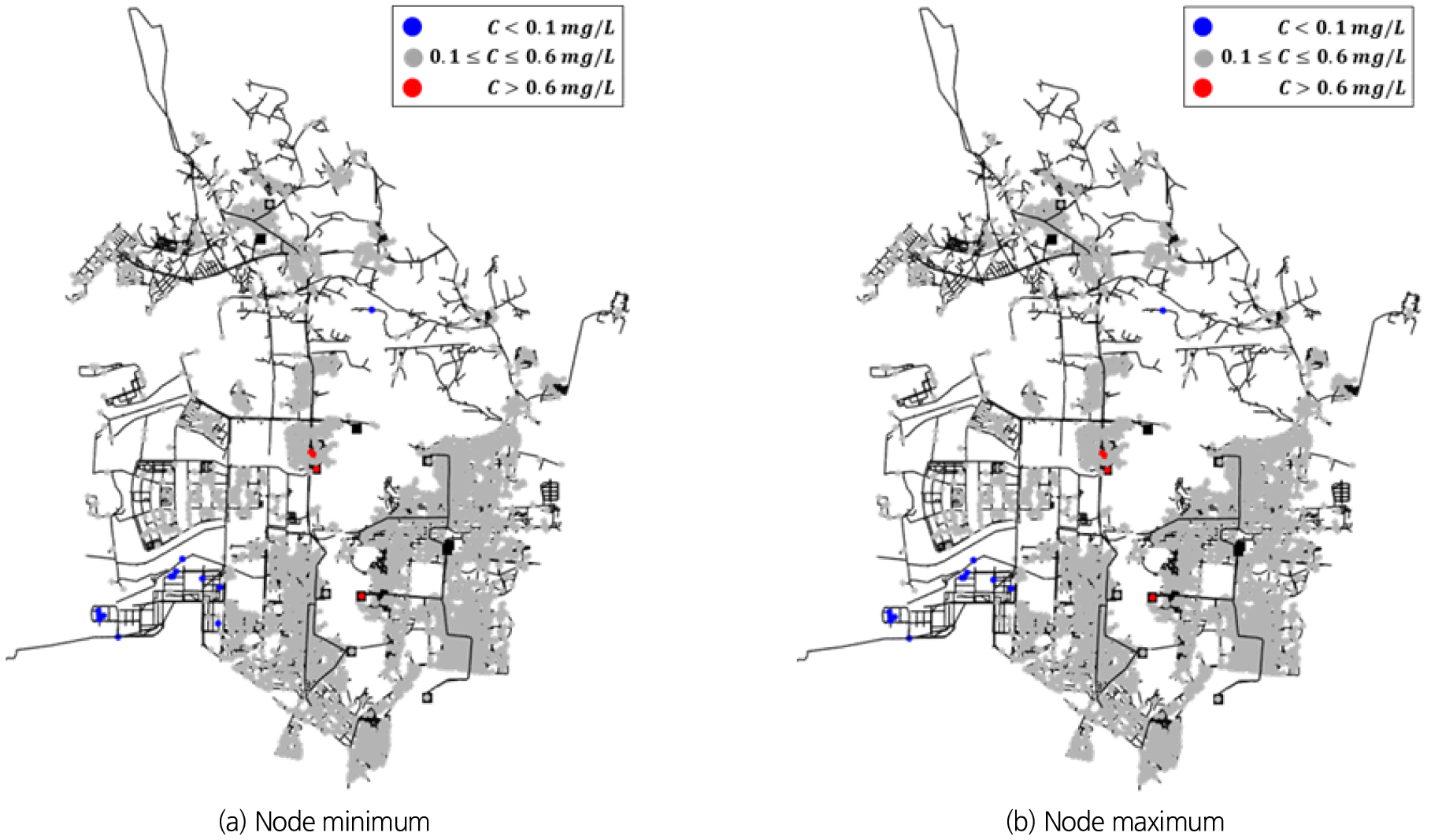
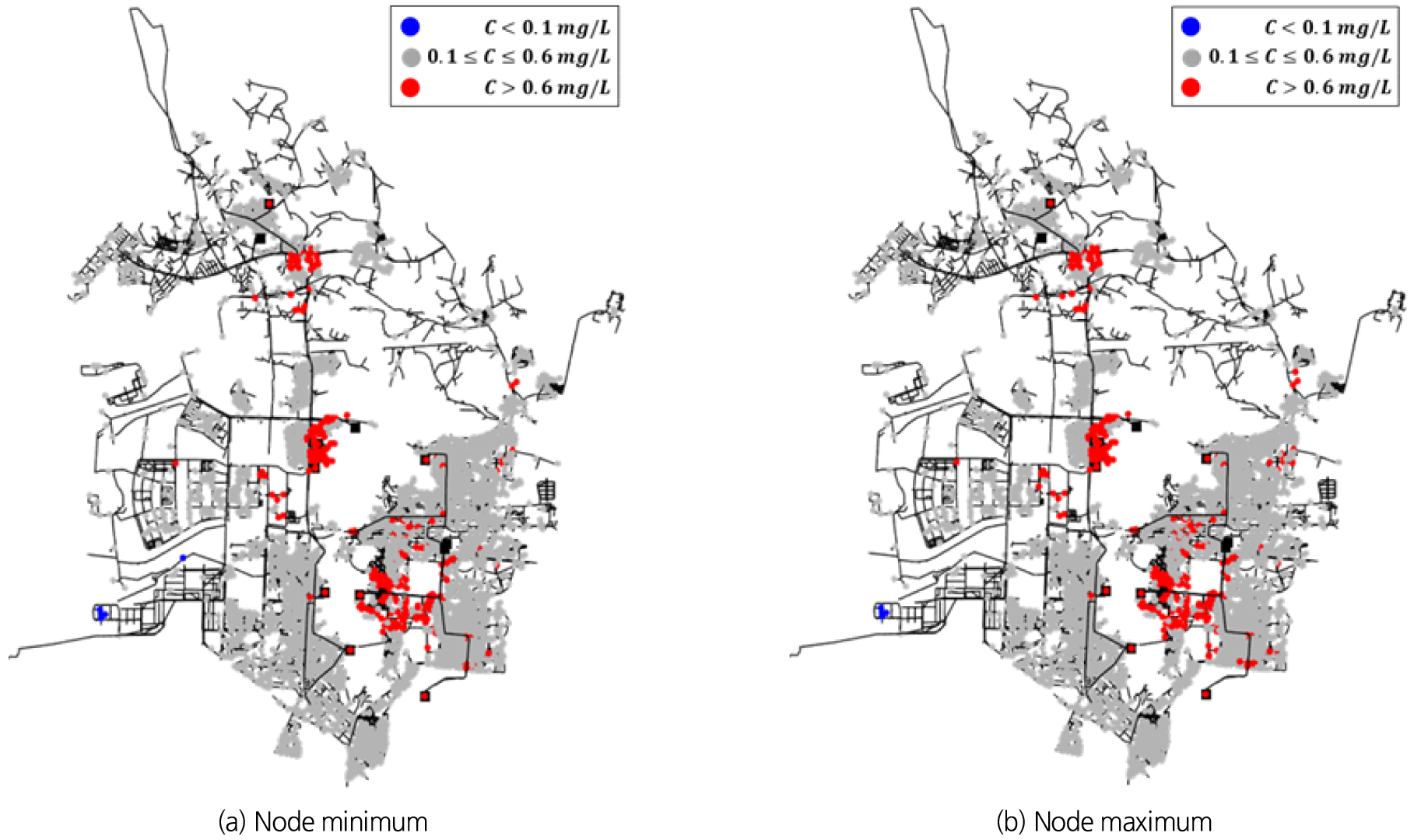
정수장에서 염소투입농도를 0.8 mg/L로 유지할 경우, 각 배급수지역에서의 잔류염소농도 현황은 Table 4와 같이 정리할 수 있으며, 24시간 내 절점별 최소 및 최대 잔류염소농도의 공간적 분포는 Fig. 7과 같이 나타낼 수 있다. Table 4 및 Fig. 7에서 파란색 값 또는 파란색 점으로 표시된 결과는 잔류염소농도 하한기준에 미달하는 용수공급을 의미하며, 붉은색으로 표시된 결과는 상한기준을 초과하는 용수공급을 나타낸다. Fig. 7에서 회색으로 표시된 절점은 기준을 만족하는 절점을 의미한다. 분석 결과, I-5, I-6 배급수지역에서 13개 수요절점(전체 수요절점의 0.2%)이 하한기준 미만의 잔류염소농도를 보이는 것으로 나타났다. 해당 절점에서의 24시간 잔류염소농도 및 수요량 분포를 분석한 결과, 하한기준에 미달하는 수질로 공급된 용수의 양은 약 401 m3/d (전체 수요량의 약 0.13%)에 해당하는 것으로 분석되었다. 반면, 배수지를 거치지 않고 용수를 공급받는 I-0 공급지역에서는 3개 절점(전체 수요절점의 0.05%)이 상한기준을 초과하는 잔류염소농도를 보였으며, 공급량은 약 234 m3/d (전체 수요량의 약 0.07%)에 해당하는 것으로 분석되었다.
Table 4.
Simulation results under Scenario 1(chlorine injection concentration: 0.8 mg/L)
4.3.2 시나리오 2(정수장 염소투입농도: 1.0 mg/L)
정수장에서 염소투입농도를 1.0 mg/L로 유지할 경우, 각 배급수지역에서의 잔류염소농도 현황은 Table 5, 절점별 최소 및 최대 잔류염소농도의 분포는 Fig. 8과 같이 나타났다. 분석 결과, I-5 배급수지역에서 5개 수요절점(전체 수요절점의 0.09%)이 하한기준 미만의 잔류염소농도를 보이는 것으로 나타났으며, 해당 절점에서 하한기준에 미달하는 수질로 공급된 용수의 양은 총 92 m3/d (전체 수요량의 약 0.03%)에 해당하는 것으로 분석되었다. 반면, I-0 및 I-8 지역에서는 70개 수요절점(전체 수요절점의 1.24%)에서 상한기준을 초과하는 잔류염소농도를 보였으며, 해당 공급량은 총 5,757 m3/d (전체 수요량의 약 1.8%)에 해당하는 것으로 분석되었다.
Table 5.
Simulation results under Scenario 2(chlorine injection concentration: 1.0 mg/L)
4.3.3 시나리오 3(정수장 염소투입농도: 1.2 mg/L)
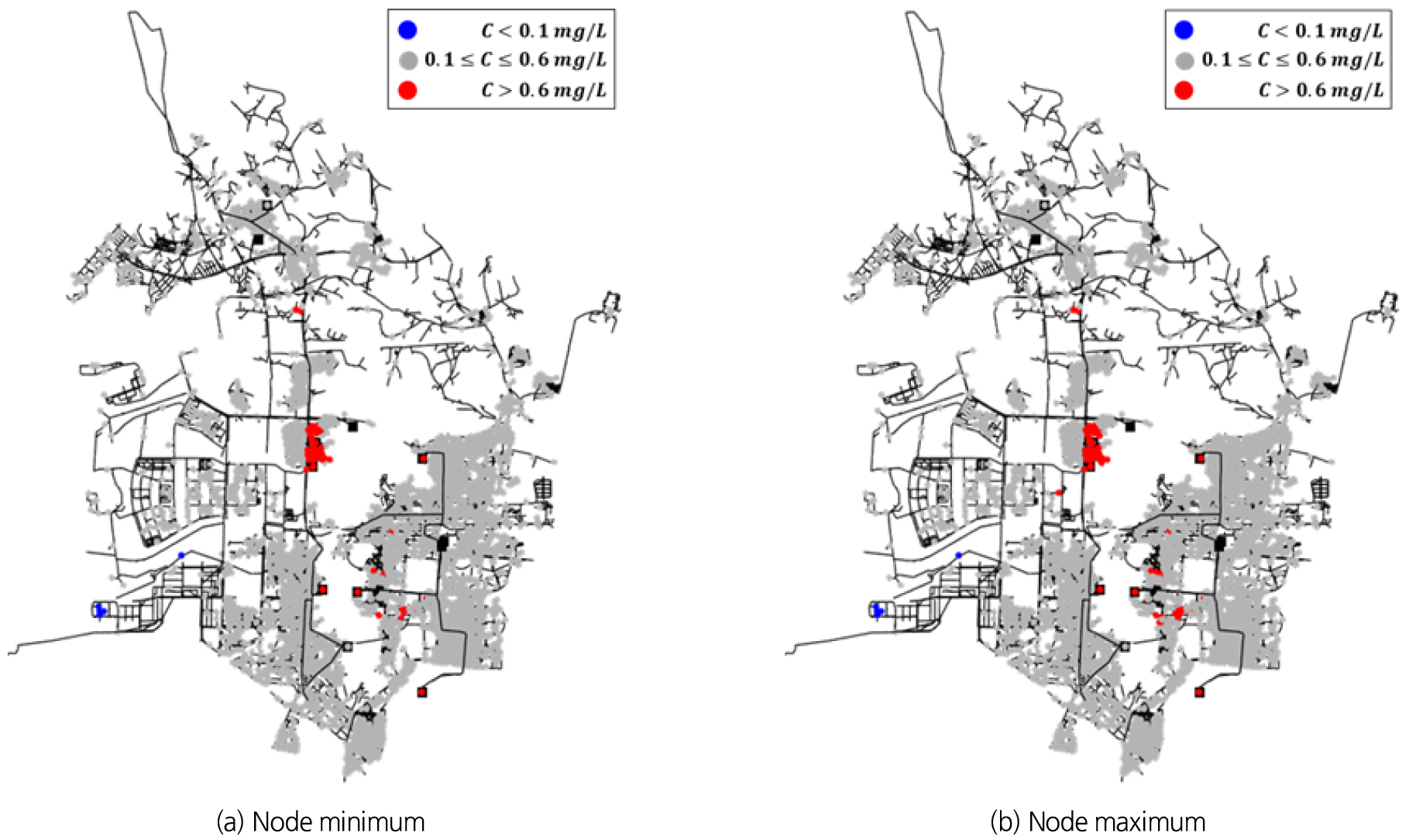
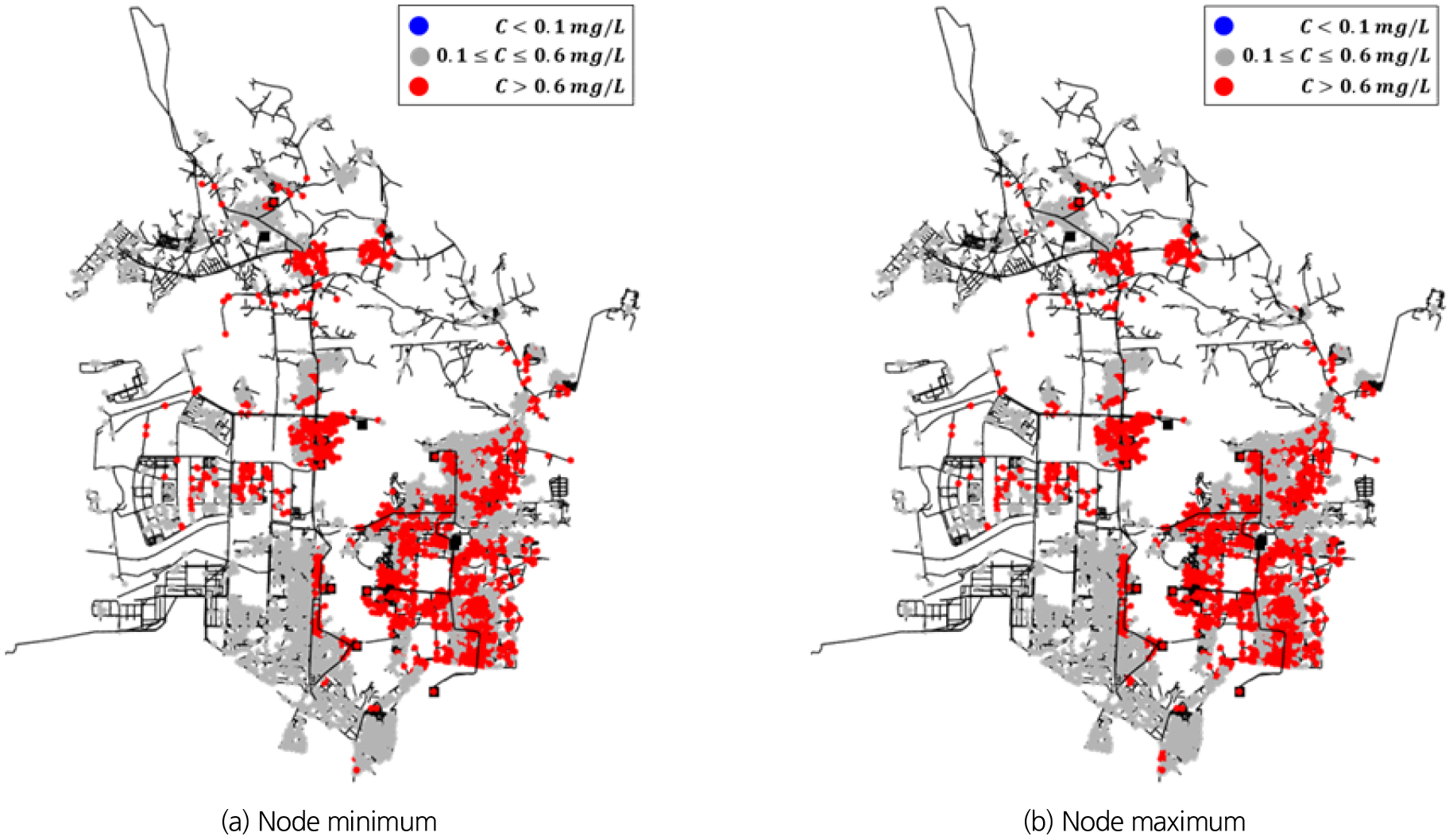
정수장에서 염소투입농도를 1.2 mg/L로 유지할 경우, 각 배급수지역에서의 잔류염소농도 현황은 Table 6, 절점별 최소 및 최대 잔류염소농도의 분포는 Fig. 9와 같이 나타났다. 분석 결과, 시나리오 2와 마찬가지로, I-5 배급수지역에서 5개 절점(전체 수요절점의 0.09%)에서 여전히 하한기준 미만의 잔류염소농도를 보였으나, 해당 절점에서의 24시간 내 잔류염소농도 및 수요량 분포를 분석한 결과, 하한기준에 미달하는 공급시간이 감소하여 해당 공급량은 총 82 m3/d (전체 수요량의 약 0.03%)로 소폭 감소하는 것으로 분석되었다. 반면, I-0 및 I-2, I-4, I-5, I-6, I-7, I-8 지역에서 354개 절점(전체 수요절점의 6.3%)이 상한기준을 초과하는 잔류염소농도를 보였으며, 공급량은 총 37,961 m3/d (전체 수요량의 약 12%)에 해당하는 것으로 분석되었다. 이때, I-5 공급지역의 경우, 잔류염소농도 하한기준 미달과 상한기준 초과가 동시에 나타나며, 따라서 I-5 지역 내 잔류염소농도의 공간적 편차가 크게 발생하는 것을 알 수 있다.
Table 6.
Simulation results under Scenario 3(chlorine injection concentration: 1.2 mg/L)
4.3.4 시나리오 4(정수장 염소투입농도: 1.5 mg/L)
정수장에서 염소투입농도를 1.5 mg/L로 유지할 경우, 각 배급수지역에서의 잔류염소농도 현황은 Table 7, 절점별 최소 및 최대 잔류염소농도의 분포는 Fig. 10과 같이 나타났다. Table 7에 나타난 것과 같이, 시나리오 4에서는 모든 배급수지역에서 더이상 하한기준 미만의 잔류염소농도가 발생하지 않는 것으로 나타났다. 그러나, 상대적으로 높은 투입농도로 인해 잔류염소농도 상한기준을 초과하는 용수의 공급이 급격하게 증가하는 결과를 보였다. 모든 배급수지역에 걸쳐 1,997개 절점(전체 수요절점의 35.4%)이 상한기준을 초과하는 잔류염소농도를 보였으며, 상한기준을 초과하는 수질로 공급된 용수의 양은 시나리오 3 대비 네 배 가까이 증가한 총 142,667 m3/d (전체 수요량의 약 45%)에 해당하는 것으로 분석되었다.
Table 7.
Simulation results under Scenario 4(chlorine injection concentration: 1.5 mg/L)
4.3.5 종합분석
위와 같은 시나리오별 잔류염소농도 분석 결과는 각각 Tables 8 and 9와 같이 요약할 수 있다. 먼저 정수장에서 0.8 mg/L의 염소투입농도를 유지하는 경우, 정수장과 바로 인접한 I-0 공급지역에서 소량(전체 수요량의 0.07%)의 잔류염소농도 기준 초과 공급량이 발생하고, 상대적으로 용수공급 도달시간이 긴 I-5 및 I-6 공급지역에서 소량(전체 수요량의 0.13%)의 잔류염소농도 기준 미달 공급량이 발생하였다. 반면, 하한기준에 미달하는 잔류염소농도를 해소하고자 정수장 염소투입농도를 1.0 및 1.2 mg/L로 증가시킬 경우, 잔류염소농도 기준 미달 공급량의 감소효과(각각 전체 수요량 대비 0.1%p 감소) 대비 기준 초과 공급량의 증가효과(각각 전체 수요량 대비 1.2, 11.9%p 증가)가 더 큰 것으로 나타났다. 특히 염소투입농도를 1.5 mg/L까지 증가시키는 경우 기준 미달 공급량을 완전히 해소할 수 있으나, 전체 수요량의 절반 수준에 해당하는 약 45%의 용수가 기준 초과 상태로 공급되는 것으로 나타났다.
Table 8.
Comparison of minimum and maximum chlorine concentration between the applied scenarios (Unit: mg/L)
Table 9.
Comparison of water supply amount with unsatisfied chlorine concentration between the applied scenarios (Unit: 103 m3/d)
5. 결 론
본 연구에서는 대규모 상수관망의 수질해석 계산효율을 개선하기 위한 계층적 모의기법을 제안하였다. 제안된 모의기법을 국내 I-city의 대규모 상수관망시스템을 대상으로 적용하였으며, 적용대상 네트워크는 한 개의 송배수계통 네트워크와 여덟 개의 배급수계통 네트워크로 계층화되었다. 또한, EPANET 잔류염소농도 모의를 위한 반응계수를 추정하기 위해 I-city 공급지역 내 말단 지점의 수질계측 데이터를 이용하였으며, 모의결과 수체반응계수(kbulk)는 -0.1056 d-1, 관체반응률(kw)은 -0.005 m/d 값을 추정하여 적용하였다. 해당 네트워크의 정수장 염소투입농도를 각각 0.8, 1.0, 1.2, 1.5 mg/L로 가정하여 I-city 수요절점의 잔류염소농도를 시공간적으로 분석한 결과는 다음과 같다.
1) 정수장 염소투입농도를 0.8 mg/L로 유지할 경우, 용수공급량 대부분은 정상 범위에 해당하는 잔류염소농도를 만족하는 것으로 분석되었다(전체 수요량의 약 99.8%).
2) 정수장에서 0.8 ~ 1.0 mg/L 범위의 염소투입농도를 유지하는 경우, 전체 수요량의 약 99%에 해당하는 용수가 정상 범위의 잔류염소농도를 갖는 것으로 나타났다. 이때 염소투입농도를 보다 증가시키는 경우, 잔류염소농도 기준 초과 공급량이 증가하는 부정적인 영향이 더 크게 발생하는 것으로 분석되었다. 따라서, 기준 미달 공급량이 발생하는 배급수지역(I-5, I-6 공급지역)에서의 수질균등화를 위해서는 정수장의 투입농도를 높이기 보다 배수지에서의 염소 재투입 등의 대책이 필요한 것으로 분석되었다.
3) 특히, 정수장 염소투입농도가 1.2 mg/L 이상으로 유지되는 경우, 대부분의 공급지역에서 잔류염소농도 상한 기준을 초과하는 수요절점이 크게 증가하는 것으로 나타났으며, 1.5 mg/L 이상의 염소투입농도에서는 전체 용수수요량의 절반 수준에 해당하는 용수가 잔류염소농도 상한 기준을 초과함으로써 수질 민원이 빈발할 것으로 분석되었다.
본 연구에서 수행된 I-city의 수질 분석에서는 수질모의가 까다로운 대규모 상수관망을 대상으로 계층적 모의기법을 적용하고, 다양한 염소투입농도 시나리오에 따른 잔류염소농도의 분포 및 수질 기준을 만족하지 못하는 용수 공급량을 시공간적으로 비교 분석하는 것에 중점을 두었다. 이러한 수질해석 결과의 신뢰도는 보다 많은 수질 계측자료를 확보하고, 매개변수 추정 기법 등을 활용하여 보다 정확한 반응계수를 추정함으로써 개선시킬 수 있을 것으로 기대된다. 향후 연구에서는 본 연구에서 제안된 계층적 수질모의 기법을 활용하여 1) 잔류염소농도의 시간적 균등화를 위해 정수장에서의 염소투입농도를 공급수량의 변화에 따라 시간대별로 조정하는 기법과 2) 잔류염소농도의 공간적 균등화를 위해 최적의 염소재투입 지점을 선정하는 연구를 수행하고자 한다. 해당 연구는 상수관망시스템의 공급수질 개선을 통해 수질취약 지역을 개선하고 국내 상수도의 공급품질을 향상시킬 수 있을 것으로 기대된다.