Spatial distribution and uncertainty of daily rainfall for return level using hierarchical Bayesian modeling combined with climate and geographical information

Jeonghoona Lee; Okjeong Lee; Jiyu Seo; Sangdan Kim

doi:10.3741/JKWRA.2021.54.10.747

Preview

Research Article

Journal of Korea Water Resources Association. 31 October 2021. 747-757
https://doi.org/10.3741/JKWRA.2021.54.10.747

Spatial distribution and uncertainty of daily rainfall for return level using hierarchical Bayesian modeling combined with climate and geographical information

기후정보와 지리정보를 결합한 계층적 베이지안 모델링을 이용한 재현기간별 일 강우량의 공간 분포 및 불확실성

Jeonghoona Lee^a

Okjeong Lee^b

Jiyu Seo^c

Sangdan Kim^d^*

이 정훈^a

이 옥정^b

서 지유^c

김 상단^d^*

^aResearch Fellow, Department of Environmental Engineering, Pukyong National University, Busan, Korea

^bPost-Doctoral Researcher, Water Resources Management Research Center, K-water Research Institute, Daejeon, Korea

^cMaster Course Student, Division of Earth Environmental System Science (Major of Environmental Engineering), Pukyong National University, Busan, Korea

^dProfessor, Department of Environmental Engineering, Pukyong National University, Busan, Korea

^a부경대학교 환경공학과 전임연구원

^bK-water 유역물관리연구소 수자원연구팀 박사후연구원

^c부경대학교 지구환경시스템과학부 환경공학전공 석사과정

^d부경대학교 환경공학과 교수

^{*Corresponding Author}

ABSTRACT

Quantification of extreme rainfall is very important in establishing a flood protection plan, and a general measure of extreme rainfall is expressed as an T-year return level. In this study, a method was proposed for quantifying spatial distribution and uncertainty of daily rainfall depths with various return periods using a hierarchical Bayesian model combined with climate and geographical information, and was applied to the Seoul-Incheon-Gyeonggi region. The annual maximum daily rainfall depth of six automated synoptic observing system weather stations of the Korea Meteorological Administration in the study area was fitted to the generalized extreme value distribution. The applicability and reliability of the proposed method were investigated by comparing daily rainfall quantiles for various return levels derived from the at-site frequency analysis and the regional frequency analysis based on the index flood method. The uncertainty of the regional frequency analysis based on the index flood method was found to be the greatest at all stations and all return levels, and it was confirmed that the reliability of the regional frequency analysis based on the hierarchical Bayesian model was the highest. The proposed method can be used to generate the rainfall quantile maps for various return levels in the Seoul-Incheon-Gyeonggi region and other regions with similar spatial sizes.

Keywords

Generalized extreme value distribution

Hierarchical bayesian model

Rainfall

Regional frequency analysis

Uncertainty

극한 강우의 정량화는 홍수방어계획의 수립에 대단히 중요하며 극한 강우의 일반적인 척도는 T-년 재현기간으로 표현된다. 본 연구에서는 기후정보와 지리정보가 결합된 계층적 베이지안 모형을 이용하여 재현기간별 일 강우량의 공간 분포 및 불확실성을 추정하는 방법을 제시하고 이를 서울-인천-경기 지역에 적용하였다. 한국 기상청에서 운영 중인 서울-인천-경기 지역의 6개 종관기상관측소의 연 최대 일 강우량이 일반화된 극치 분포에 적합되었다. 지점 빈도해석과 지수 홍수법을 이용한 지역 빈도해석으로부터 도출된 재현기간별 일 강우량과의 비교를 통하여 제안된 방법의 적용성 및 신뢰도를 살펴보았다. 모든 지점과 모든 재현기간에서 지수홍수법에 의한 지역 빈도해석의 불확실성이 가장 큰 것으로 나타났으며, 계층적 베이지안 모형에 의한 지역 빈도해석의 신뢰도가 가장 높은 것을 확인하였다. 제안된 방법은 서울-인천-경기 지역 및 공간적인 크기가 유사한 다른 지역에서 다양한 지속기간에 대한 확률강우량 지도를 생성하는데 사용될 수 있을 것이다.

키워드

일반화된 극치분포

계층적 베이지안 모형

강우

지역 빈도해석

불확실성

MAIN

1. 서 론
2. 연구 방법
2.1 자료
2.2 계층적 베이지안 모형
2.3 지역 빈도해석을 위한 마코프 체인 몬테카를로 알고리즘
3. 결과 및 토론
4. 결 론

1. 서 론

일반적으로 빈도해석 기법은 지점 빈도해석(at-site frequency analysis)과 지역 빈도해석(regional frequency analysis)으로 분류할 수 있다. 지점 빈도해석에서는 주어진 지점의 자료만을 이용하여 확률수문량을 산정하며, 지역 빈도해석에서는 대상 지점을 포함하여 수문학적으로 동질한 것으로 판단되는 주변 지점들의 자료를 모두 포함하여 확률수문량을 산정한다(Heo and Kim, 2019). 지역 빈도해석은 유사한 지점들로부터의 정보를 공유하여 확률분포 추정의 정확성과 신뢰도를 높이는 데 목적이 있다(Liang et al., 2017; Wang et al., 2017). 또한 인접한 지점들에서 발생하는 정보를 전송하여 미계측 혹은 자료 연한이 짧은 지점에서의 확률분포 추정을 가능하게 한다(Renard, 2011).

강우량의 지역 빈도해석은 Dalrymple (1960)의 지수 홍수법(Index flood method, IFM)에서 시작되었으며 Hosking and Wallis (1997)에 의해 광범위하게 연구되었다. IFM에 의한 지역 빈도해석은 크게 다섯 단계로 요약될 수 있다. (1) 균질한 공간 영역을 정의, (2) 지수 홍수(예를 들어, 연 최대 강우량 시계열의 평균)를 사용하여 균질한 영역의 지점 자료들을 정규화, (3) 정규화된 자료들을 하나로 모아서(즉, 자료 풀링) 지역의 공통 확률분포를 추정, (4) 지역 공통 확률분포와 지수 홍수를 연계하여 지점에서의 확률 강우량 추정, (5) 지수 홍수와 지점 특성 사이의 관계를 정립하여 미계측 지역에서의 확률 강우량 추정(Heo and Kim, 2019).

강우량의 지역 빈도해석기법을 개선하기 위한 다양한 연구가 수행된 바 있다. Schaefer (1990)는 미국 워싱턴 주에 대한 지역 빈도해석에서 균질한 지역을 구성하기 위해 연평균 강수량을 사용했다. 지역 빈도해석에서 정보 전송은 계측 지점에서 추정된 지수 홍수와 지점의 특성을 연결하는 회귀 모델에 주로 의존하게 된다. 이에 계측 지점에서 미계측 지점으로의 정보 전송과 관련된 예측 불확실성의 정량화를 목적으로 한 연구가 많은 관심을 받고 있다(Stedinger and Tasker, 1985, 1986; Robson and Reed, 1999; Reis et al., 2005; Kjeldsen and Jones, 2009; Micevski and Kuczera, 2009).

L-모멘트를 사용하여 추정된 매개변수에 대한 불확실성은 일반적으로 부트스트랩 방법을 통해 얻게 된다. L-모멘트의 단점은 공변량을 매개변수에 통합할 수 없다는 것이다(Katz et al., 2002). 매개변수 추정에서 공변량의 포함이 불가능하므로, IFM에서는 지점 자료들을 정규화한 후에 풀링하여 지역 공통의 단일한 확률분포형을 추정하는 절차를 수행하였다고 볼 수 있다.

Cooley et al. (2007)의 연구 이래로 극한 강우사상의 공간 프로세스를 설명하기 위해 고려된 지역의 모든 지점 자료를 하나의 모형으로 통합하는 계층적 베이지안 모형(Hierarchical Bayesian Model, HBM)이 수문학 분야에서 활발하게 적용되고 있다. Aryal et al. (2009)은 HBM을 이용하여 극한 강우의 시공간적 변동성을 설명했으며, Lima and Lall (2009)은 지역 규모에서 강우 발생을 설명하기 위해 HBM을 적용했다. 그 외에도 Ahn et al. (2017)은 저유량의 지역화된 계절 예측을 위해 HBM을 적용하기도 하였다. 국내에서는 Kwon et al. (2013)이 지형 특성과 결합한 HBM에 기초한 강우량 지역 빈도해석모형을 개발하여 전라북도 지역에 적용한 바 있으며, Kwak and Kim (2015)는 HBM을 이용하여 서울, 강릉, 대구, 부산 지점의 확률강우량을 추정하였다.

이러한 선행 연구를 기반으로 본 연구에서는 다양한 공변량 관계를 수용할 수 있는 유연성을 가지고 있으며, 지점에서의 자료를 정규화할 필요가 없는 지역 빈도해석방법을 제안하고 재현기간별 일강우량의 공간 분포 및 불확실성을 살펴보고자 한다. 제안된 방법은 원칙적으로는 분석 초기에 균질한 공간 영역을 정의할 필요는 없지만, 너무 넓은(특성이 상이하거나 불균질한 지역들이 혼합된) 지역에의 적용은 당연히 바람직하지 않을 것이다. 따라서 본 연구의 적용은 한반도 중심부인 서울-인천-경기(이하 수도권) 지역으로 한정하였다.

2. 연구 방법

2.1 자료

한국 기상청에서 운영 중인 수도권 지역의 6개 종관기상관측소(Automated Synoptic Observing System, ASOS)의 일 강우량 자료가 사용되었다. 사용된 관측소 이름은 다음과 같다: 서울, 인천, 수원, 강화, 양평, 이천. 자료 기간은 1973년부터 2017년이다. 사용된 관측소의 기본 정보를 Table 1에 수록하였다.

Table 1.

Site information

Site	Latitude (°)	Longitude (°)	Annual surface air Temperature (℃)
Seoul	37.5714	126.9658	12.5143
Incheon	37.4777	126.6249	12.1155
Suwon	37.2575	126.9830	12.0133
Ghanghwa	37.7074	126.4463	11.1086
Yangpyeong	37.4886	127.4945	11.2806
Icheon	37.2640	127.4842	11.4489

2.2 계층적 베이지안 모형

연 최대 일 강우량 시계열의 빈도해석에서는 주로 일반화된 극치(Generalized Extreme Value, GEV) 분포가 적용된다. GEV 분포의 확률밀도함수 $f (x)$ 는 아래와 같다.

(1)

f (x) = \frac{1}{α} {\{1 - \frac{β (x - x_{o})}{α}\}}^{\frac{1}{β} - 1} \exp [- {\{1 - \frac{β (x - x_{o})}{α}\}}^{\frac{1}{β}}]

여기서 $α$ 은 축척 매개변수, $β$ 은 형상 매개변수, $x_{o}$ 은 위치 매개변수이다. 연 최대 시계열 $x$ 의 범위는 형상 매개변수 $β$ 의 부호에 따라 결정된다. 형상 매개변수가 $β < 0$ 이면 $x$ 은 $x_{o} + α / β < x < \infty$ 의 범위를 가져야 하므로, 연 최대 시계열의 최솟값이 $x_{o} + α / β$ 보다 커야 GEV 분포의 적용이 가능해진다. 만일 $β > 0$ 이면 $x$ 은 $- \infty < x < x_{o} + α / β$ 의 범위를 가지게 되므로, $x_{o} + α / β$ 이 연 최대 시계열의 최댓값보다 훨씬 큰 값이 되어야 GEV 분포를 이용한 빈도해석이 의미를 갖게 된다.

HBM의 첫 번째 단계에서 우도함수는 GEV 분포의 시간과 공간에 대한 곱으로 아래와 같이 표현된다.

(2)

L_{1} = \prod_{j = 1}^{S} \prod_{i = 1}^{T} f (x_{i j} | α_{i j}, β_{i j}, x_{o i j})

여기서 i는 공간(site)을 의미하며, j는 시간(year)을 의미한다.

HBM의 두 번째 단계에서 GEV 분포의 매개변수는 아래와 같은 다변량 정규분포를 갖는 것으로 정의된다.

(3)

ϕ ~ N (μ_{ϕ}, Σ_{ϕ})

(4)

ψ ~ N (μ_{ψ}, Σ_{ψ})

(5)

ζ ~ N (μ_{ζ}, Σ_{ζ})

여기서 $ϕ_{j} = \ln [α_{j}], ψ_{j} = \ln [- β_{j}], ζ_{j} = \ln [\min (x_{j}) - α_{j} / β_{j} - x_{o j}]$ 이다. 따라서 $μ_{ϕ}, μ_{ψ}, μ_{ζ}$ 는 1 × S평균 벡터가 되며, $Σ_{ϕ}, Σ_{ψ}, Σ_{ζ}$ 는 S × S 공분산 행렬이 된다. 축척 매개변수의 평균 $μ_{ϕ}$ 는 아래와 같은 공변량의 함수로 표현된다.

(6)

μ_{ϕ_{j}} = a_{ϕ, 1} + a_{ϕ, 2} {(c o v_{ϕ, 1})}_{j} + a_{ϕ, 3} {(c o v_{ϕ, 2})}_{j}

여기서 $a_{ϕ, k}$ 는 평균 초 매개변수(hyper-parameter)이며, $c o v_{ϕ, k}$ 는 공변량이다. 참고로 공변량은 이슬점, 지표면 기온, 상대습도 등과 같은 기후자료 및 위도, 경도, 고도 등과 같은 지리 자료가 이용될 수 있다. 유사한 방법으로 형상 매개변수 및 위치 매개변수의 평균 $μ_{ψ}$ 와 $μ_{ζ}$ 도 공변량의 함수로 표현할 수 있다. 축척 매개변수의 분산 $Σ_{ϕ}$ 은 아래와 같은 지수 covariogram의 형태로 표현된다.

(7)

Σ_{ϕ} = b_{ϕ, 1} e^{- b_{ϕ, 2} d}

여기서 $b_{ϕ, k}$ 는 공분산 초 매개변수이며, d는 지점들 사이의 거리이다. 유사한 방법으로 형상 매개변수 및 위치 매개변수의 분산 $Σ_{ψ}$ 와 $Σ_{ζ}$ 도 지수 covariogam의 형태로 표현할 수 있다.

HBM의 세 번째 단계에서 초 매개변수 $a_{ϕ, k}$ 와 $b_{ϕ, k}, a_{ψ, k}$ 와 $b_{ψ, k}, a_{ζ, k}$ 와 $b_{ζ, k}$ 의 사전분포는 균등분포로서 정의된다. 본 연구에서는 9개의 평균 초 매개변수와 6개의 공분산 초 매개변수를 적용하였다.

2.3 지역 빈도해석을 위한 마코프 체인 몬테카를로 알고리즘

일반적인 베이지안 추론을 위한 마코프 체인 몬테카를로(Markov Chain Monte-Carlo, MCMC) 방법은 메트로폴리스-해스팅스(Metropolis Hastings, MH) 알고리즘 등이 잘 정형화되어 있어 수치적인 구현이 어렵지 않으나, HBM의 경우에는 수치적인 구현을 위한 적절한 절차가 마련되지 않으면 올바른 사후분포를 샘플링하는 것이 어려운 경우가 많다(Berger et al., 2001).

본 연구에서는 MH 알고리즘에 기초하여 매개변수 및 초 매개변수의 사후분포를 샘플링하였으며 절차는 아래와 같다.

2.3.1. MCMC 초기화(반복 차수 m = 1)

(1) $a_{ϕ, k}$ (여기서 k=1,2,3)의 사전분포에서 $a_{ϕ, k}^{1}$ 을 무작위 샘플링

(2) $b_{ϕ, k}$ (여기서 k=1,2)의 사전분포에서 ${b_{ϕ,}^{1}}_{k}$ 을 무작위 샘플링

(3) Eqs. (6) and (7)를 이용하여 $μ_{ϕ}^{1}$ 과 $Σ_{ϕ}^{1}$ 을 계산

(4) Eq. (3)로부터 $ϕ_{j}^{1}$ (여기서 j=1,2,…, S)을 무작위 샘플링

(5) (1)에서 (4)까지의 과정을 반복하여 $a_{ψ}^{1}$ 과 $b_{ψ}^{1}$ 을 무작위 샘플링하여 $μ_{ψ}^{1}$ 와 $Σ_{ψ}^{1}$ 을 계산한 후, $ψ_{j}^{1}$ 을 무작위 샘플링

(6) 마찬가지 방법으로 $a_{ξ}^{1}$ 과 $b_{ξ}^{1}$ 을 무작위 샘플링하여 $μ_{ξ}^{1}$ 와 $Σ_{ξ}^{1}$ 을 계산한 후, $ξ_{j}^{1}$ 을 무작위 샘플링

2.3.2. MCMC를 이용한 반복 샘플링(반복 차수 m = 2,3,…, M)

(1) $ϕ_{j}$ 의 갱신

- 제안분포 $N (ϕ_{j}^{m - 1}, v Σ_{ϕ}^{m - 1})$ 로부터 $ϕ_{j}^{*}$ 을 무작위 샘플링 수행, 여기서 $v$ 는 샘플링 섭동을 위한 계수

- 매개변수 $ϕ_{j}$ 의 갱신 여부를 위한 $r_{ϕ}$ 계산

(8)

r_{ϕ} = \sum_{j = 1}^{S} \sum_{i = 1}^{T} \ln [f (x | ϕ_{j}^{*}, ψ_{j}^{m - 1}, ζ_{j}^{m - 1})] - \sum_{j = 1}^{S} \sum_{i = 1}^{T} \ln [f (x | ϕ_{j}^{m - 1}, ψ_{j}^{m - 1}, ζ_{j}^{m - 1})] + \sum_{j = 1}^{S} \ln [N (ϕ_{j}^{*} | μ_{ϕ}^{m - 1}, Σ_{ϕ}^{m - 1})] - \sum_{j = 1}^{S} \ln [N (ϕ_{j}^{m - 1} | μ_{ϕ}^{m - 1}, Σ_{ϕ}^{m - 1})]

- $r_{ϕ}$ 와 0 중에서 작은 값이 0에서 1 사이에서 무작위 샘플링한 균등 난수에 자연로그를 취한 값보다 크면 $ϕ_{j}^{m} = ϕ_{j}^{*}$ 로 갱신되며, 아니면 $ϕ_{j}^{m} = ϕ_{j}^{m - 1}$ 로 기존값이 유지됨.

(2) $a_{ϕ, k}$ 의 갱신

- 제안분포 $N (a_{ϕ, k}^{m - 1}, V_{a_{ϕ, k}})$ 로부터 $a_{ϕ, k}^{*}$ 을 무작위 샘플링 수행, 여기서 $V_{a_{ϕ, k}}$ 는 샘플링 섭동을 위한 분산으로 초 매개변수 $a_{ϕ, k}$ 의 사전분포의 분산보다 작은 값으로 설정

- Eq. (6)을 이용하여 $μ_{ϕ}^{*}$ 을 계산

- 초 매개변수 $a_{ϕ, k}^{*}$ 의 갱신 여부를 위한 $r_{a_{ϕ}}$ 계산

(9)

r_{a_{ϕ}} = \sum_{j = 1}^{S} \ln [N (ϕ_{j}^{m} | μ_{ϕ}^{*}, Σ_{ϕ}^{m - 1})] - \sum_{j = 1}^{S} \ln [N (ϕ_{j}^{m} | μ_{ϕ}^{m - 1}, Σ_{ϕ}^{m - 1})]

- $r_{a_{ϕ}}$ 와 0 중에서 작은 값이 0에서 1 사이에서 무작위 샘플링한 균등 난수에 자연로그를 취한 값보다 크면 $a_{ϕ, k}^{m} = a_{ϕ, k}^{*}$ 및 $μ_{ϕ}^{m} = μ_{ϕ}^{*}$ 로 갱신되며, 아니면 $a_{ϕ, k}^{m} = a_{ϕ, k}^{m - 1}$ 및 $μ_{ϕ}^{m} = μ_{ϕ}^{m - 1}$ 로 기존값이 유지됨.

(3) $b_{ϕ, k}$ 의 갱신

- 제안분포 $N (b_{ϕ, k}^{m - 1}, V_{b_{ϕ, k}})$ 로부터 ${b_{ϕ,}^{*}}_{k}$ 을 무작위 샘플링 수행, 여기서 $V_{b_{ϕ, k}}$ 는 샘플링 섭동을 위한 분산으로 초 매개변수 $b_{ϕ, k}$ 의 사전분포의 분산보다 작은 값으로 설정

- Eq. (7)을 이용하여 $Σ_{ϕ}^{*}$ 을 계산

- 초 매개변수 ${b_{ϕ,}^{*}}_{k}$ 의 갱신 여부를 위한 $r_{b_{ϕ}}$ 계산

(10)

r_{b_{ϕ}} = \sum_{j = 1}^{S} \ln [N (ϕ_{j}^{m} | μ_{ϕ}^{m}, Σ_{ϕ}^{*})] - \sum_{j = 1}^{S} \ln [N (ϕ_{j}^{m} | μ_{ϕ}^{m}, Σ_{ϕ}^{m - 1})]

- $r_{b_{ϕ}}$ 와 0 중에서 작은 값이 0에서 1 사이에서 무작위 샘플링한 균등 난수에 자연로그를 취한 값보다 크면 $b_{ϕ, k}^{m} = b_{ϕ, k}^{*}$ 및 $Σ_{ϕ}^{m} = Σ_{ϕ}^{*}$ 로 갱신되며, 아니면 $b_{ϕ, k}^{m} = b_{ϕ, k}^{m - 1}$ 및 $Σ_{ϕ}^{m} = Σ_{ϕ}^{m - 1}$ 로 기존값이 유지됨.

(4) 마찬가지 방법으로 $ψ_{j}, a_{ψ, k}, b_{ψ, k}$ 을 갱신

(5) 마찬가지 방법으로 $ζ_{j}, a_{ζ, k}, b_{ζ, k}$ 을 갱신

3. 결과 및 토론

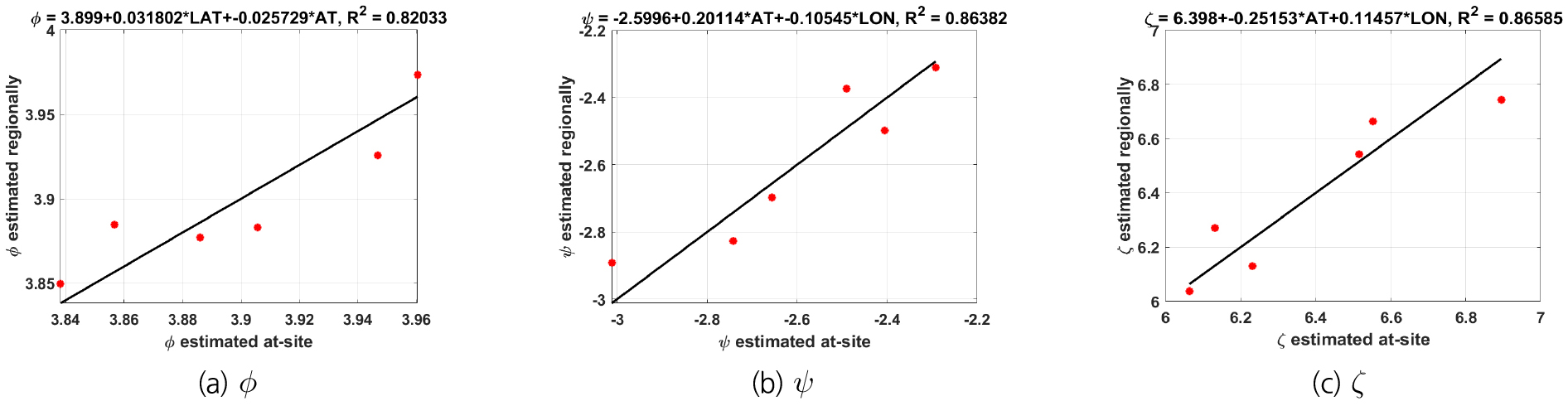
HBM을 구성하기 위해서는 Eq. (6)에 명시된 공변량의 선택이 필요하다. GEV 분포의 매개변수의 평균 $μ_{ϕ}, μ_{ψ}, μ_{ζ}$ 을 위한 공변량을 찾기 위하여 지점별로 MH 알고리즘으로 추정된 매개변수 $ϕ, ψ, ζ$ 와 후보 공변량들 사이의 관계를 탐색하였다(Fig. 1). 축척 매개변수 $ϕ$ 의 경우에는 연평균기온(Annual mean Temperature,, AT)과 위도(Latitude, LAT)가 상관성이 높았으며, 형상 매개변수 $ψ$ 와 위치 매개변수 $ζ$ 는 연평균기온과 경도(longitude, LON)를 사용하는 것이 가장 좋은 상관성을 보여주었다. 따라서 각 매개변수별로 두 개의 공변량을 사용하여 Eq. (6)과 같이 구성하였다. 참고로 Fig. 1에서 연평균기온, 위도, 경도는 모두 표준화 과정을 거친 Z-score 값들(즉, $Z = (X - μ_{X}) / σ_{X}$ )이 적용되었다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F1.jpg

Fig. 1.

Relation between GEV parameters (scale parameter $ϕ$ , shape parameter $ψ$ and location parameter $ζ$ )and covariates (Annual mean surface air temperature, latitude and longitude)

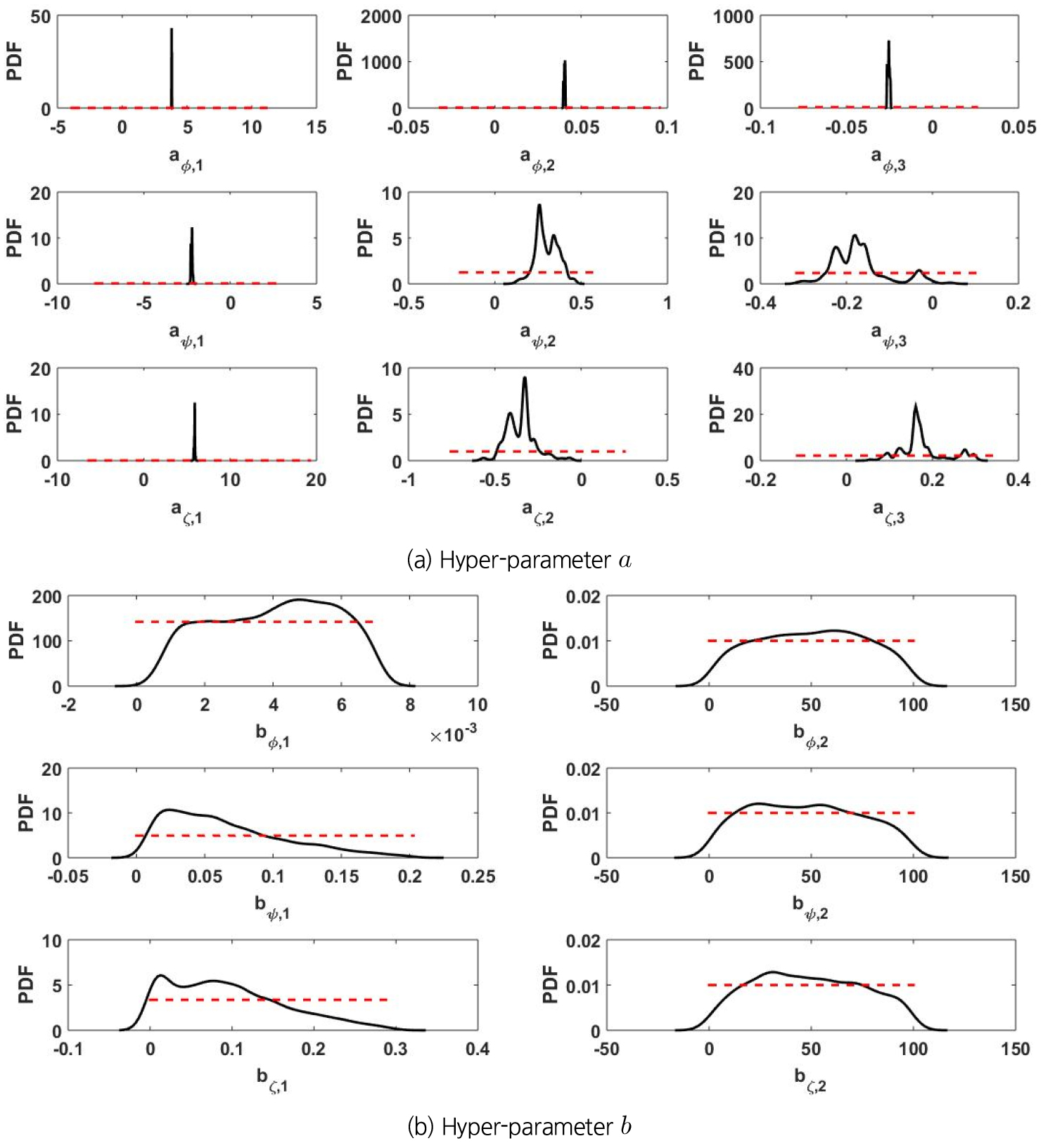
Fig. 2는 초 매개변수들의 사후분포를 보여주고 있다. 그림에서 빨간색 점선은 초 매개변수들의 사전분포를 의미한다. 평균 초 매개변수 a는 사전분포로부터 사후분포가 비교적 양호하게 특정 범위로 수렴되었으나(표준편차가 평균 1.77에서 0.09로 감소), 분산 초 매개변수 b는 사전분포와 거의 동일한 사후분포가 추정되었음을(즉, 매개변수들의 범위가 거의 동일) 알 수 있다(특히 분산 초 매개변수의 감쇠 매개변수 $b_{ϕ, 2}, b_{ψ, 2}, b_{ζ, 2}$ ). 감쇄 매개변수의 사전분포의 범위를 넓히거나 좁혀도 유사한 결과를 얻을 수 있었다. 그러나 감쇄 매개변수의 사전분포의 범위에 대한 최종적인 결과(즉, 확률 강우량의 추정 및 불확실성)의 민감도는 높지 않은 것을 확인할 수 있었다. 이러한 결과는 본 연구와 동일하게 지수 coviogram을 적용하고 감쇄 매개변수의 범위를 0.12에서 3으로 상대적으로 좁게 지정한 Najafi and Moradkhani (2013)의 연구 결과와도 부합된다. Eqs. (6) and (7)의 구조를 살펴보면, GEV 분포 매개변수의 공간 상관성은 평균 초 매개변수 a에 의해 명시적으로 설명될 수 있으며, 평균 초 매개변수 a에 의해 설명되지 않는 공간 상관성은 분산 초 매개변수 b에 의해 부차적으로 설명된다. Fig. 2의 결과와 감쇄 매개변수의 민감도 분석으로부터 GEV 분포 매개변수의 공간 상관성은 주로 평균 초 매개변수 a에 의해 설명된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F2.jpg

Fig. 2.

Posterior distribution of hyper-parameter a and b

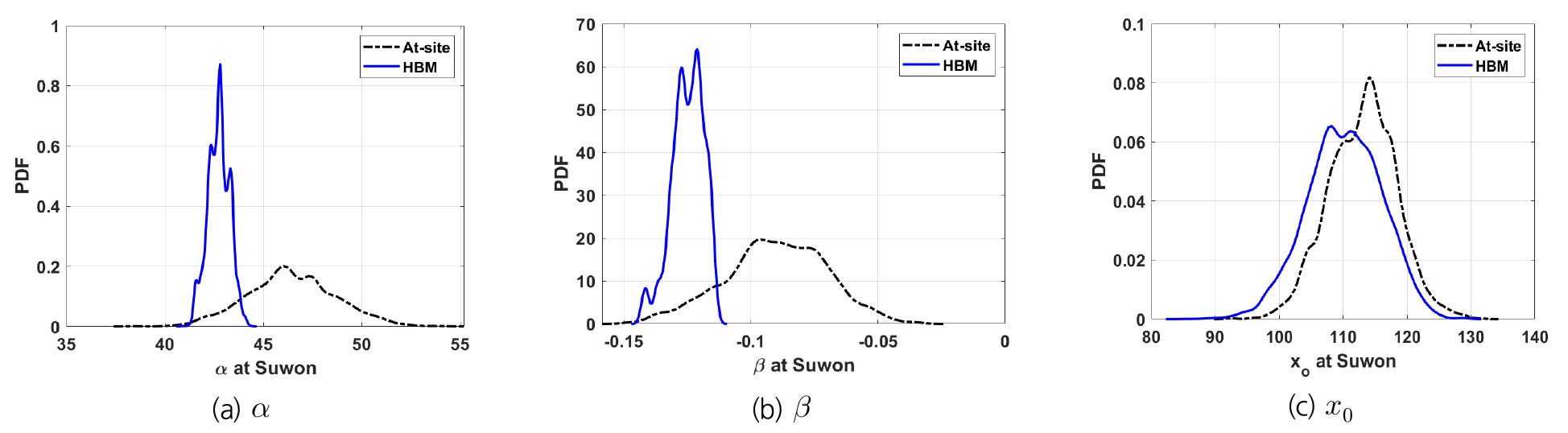
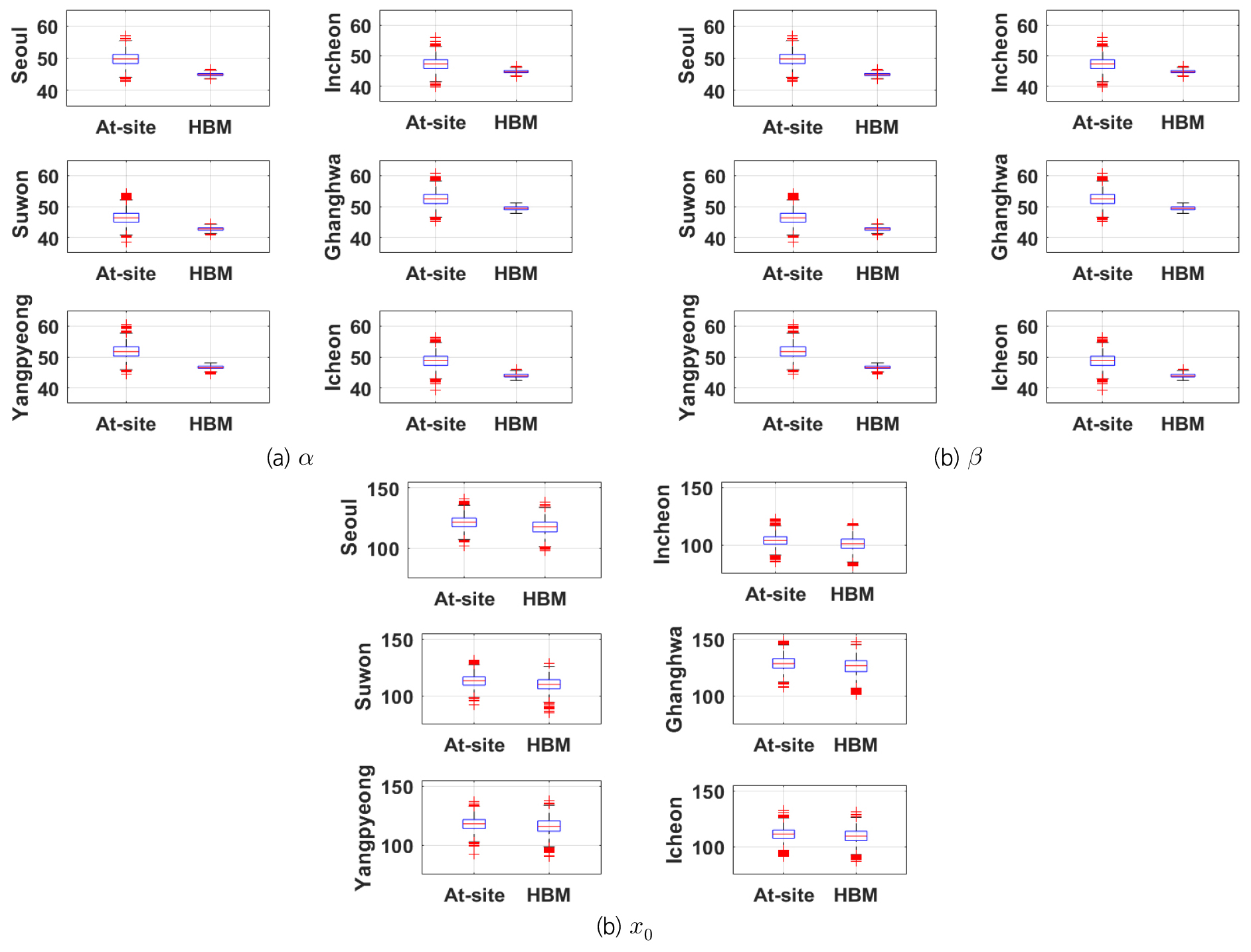
Fig. 3은 수원 지점만을 이용하여 MH 알고리즘으로 추출한 GEV 분포 매개변수의 사후분포(즉, 지점 빈도해석의 결과)와 지역의 모든 자료를 이용하는 HBM으로 샘플링한 수원 지점 GEV 분포 매개변수의 사후분포이다. 위치 매개변수 $x_{0}$ 는 두 방법 모두 유사한 사후분포의 분산도를 보여주고 있지만, 축척 매개변수 $α$ 와 형상 매개변수 $β$ 의 경우에는 HBM으로 샘플링한 사후분포의 분산도가 더 작은 것을 확인할 수 있다. 이는 HBM이 지역의 가용한 모든 자료를 풀링함으로써 불확실성이 더 작은 매개변수 추정치를 제공할 수 있다는 것을 의미한다. Fig. 4는 두 가지 방법에 대한 수도권 지역의 모든 지점들에서 샘플링한 매개변수 앙상블의 box-plot이다. 수원 지점과 유사하게 축척 매개변수 $α$ 와 형상 매개변수 $β$ 는 HBM에 의한 사후분포의 분산도가 더 작게 나타났다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F3.jpg

Fig. 3.

Posterior distribution of parameters of GEV distribution for at-site frequency analysis and HBM-based regional approaches at Suwon site

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F4.jpg

Fig. 4.

Box-plot of GEV parameters for at-site frequency analysis and HBM-based regional frequency analysis

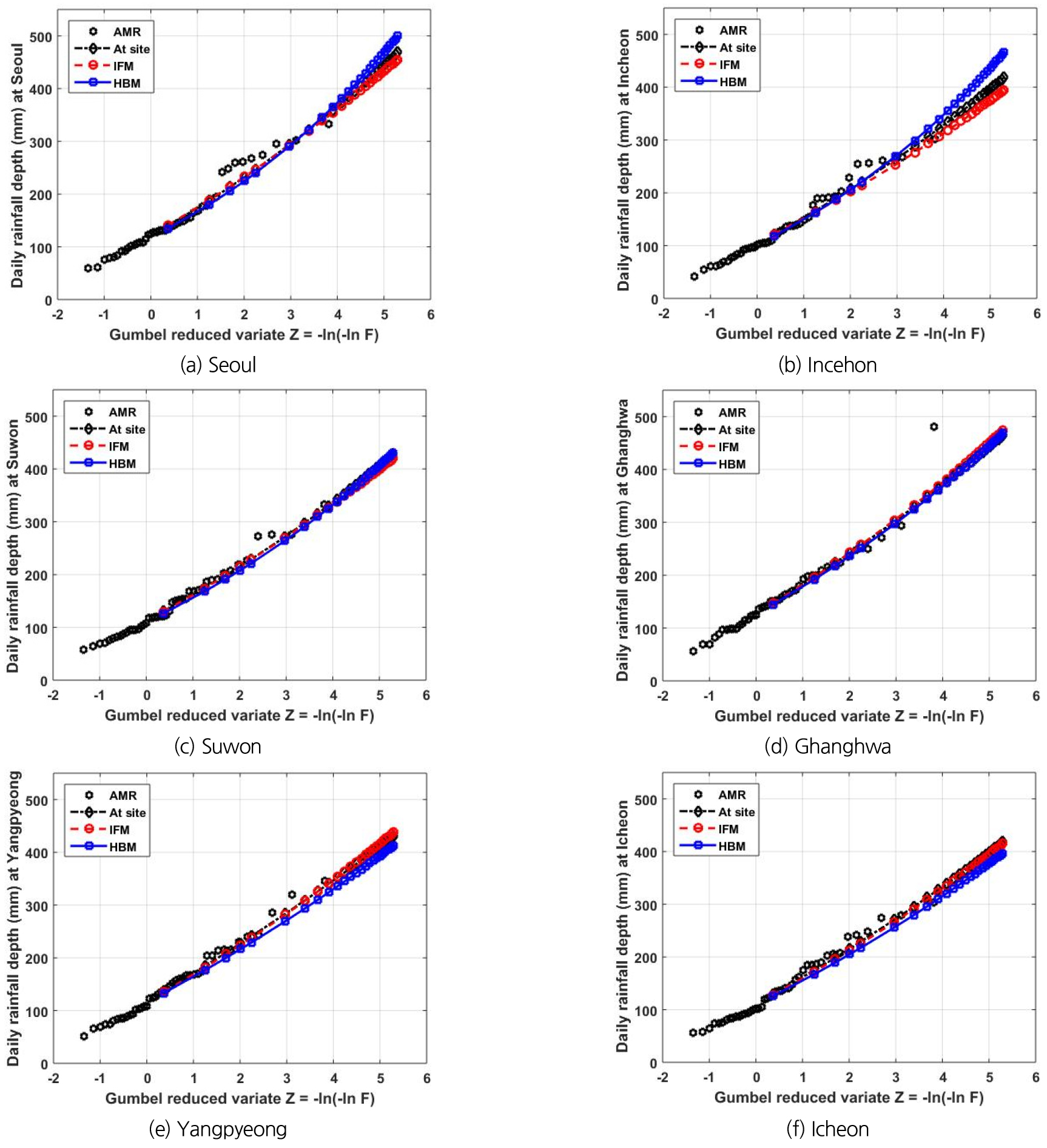
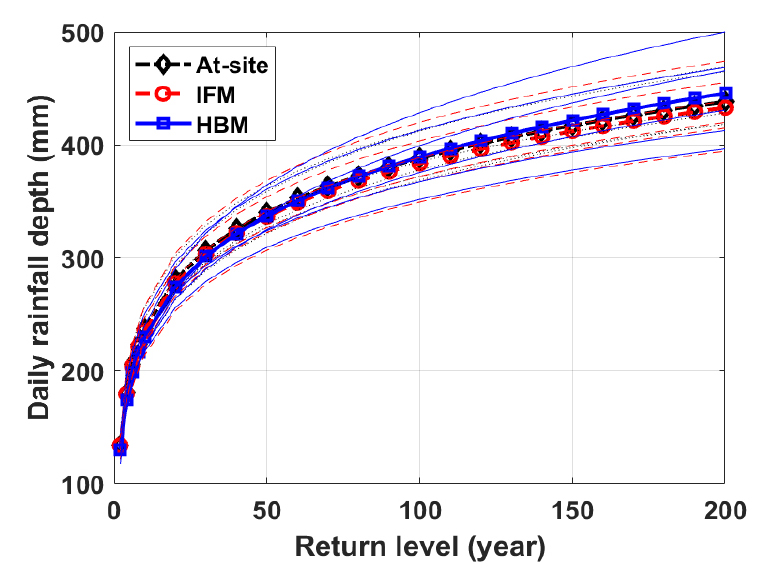
Fig. 5는 지점 빈도해석 및 IFM을 이용한 지역 빈도해석, 본 연구에서 제안된 HBM을 이용한 지역 빈도해석으로 추정한 재현기간별 확률강우량을 보여주고 있다. 추가로 관측자료의 연최대강우량(Annual Maximum Rainfall, AMR)도 비교를 위해 같이 도시하였다. 지점에 따라 차이가 있지만, 세 가지 방법 모두 유사한 확률강우량을 나타낸다. 하지만 인천지점에서 HBM과 IFM에 의한 확률강우량의 평균(Fig. 5의 작성을 위해 사용된 확률강우량의 평균)은 각각 350.37 및 310.79 mm로 약 11% 로 가장 큰 차이를 보였으며, 지점 빈도해석에 의한 확률강우량의 평균은 326.53 mm로 HBM과 약 7% 정도의 차이가 나타났다. 전반적으로 지점 빈도해석을 이용한 확률강우량이 가장 크게 산정되었으며, IFM을 이용한 지역 빈도해석이 가장 작은 확률강우량을 나타내고 있다. 6개 지점에서 확률강우량의 공간적 변동성은 HBM에 의한 지역 빈도해석이 가장 크게 나타났으며, 지점 빈도해석이 가장 작은 공간적 변동성을 보였다(Fig. 6). 전체적으로 HBM에 의한 확률강우량은 IFM에 의한 확률강우량보다는 지점 빈도해석에 의한 확률강우량과 상대적으로 더 유사하였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F5.jpg

Fig. 5.

Daily rainfall quantile for various return levels

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F6.jpg

Fig. 6.

Averaged daily rainfall quantiles at all sites

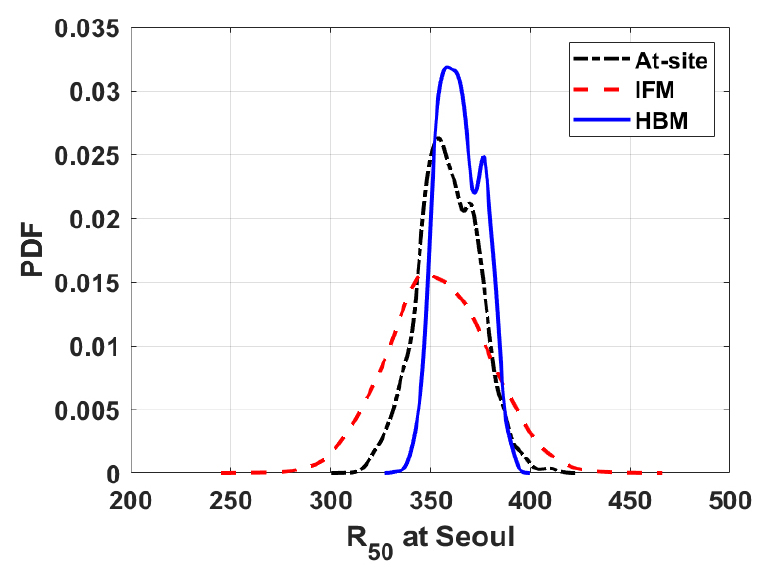
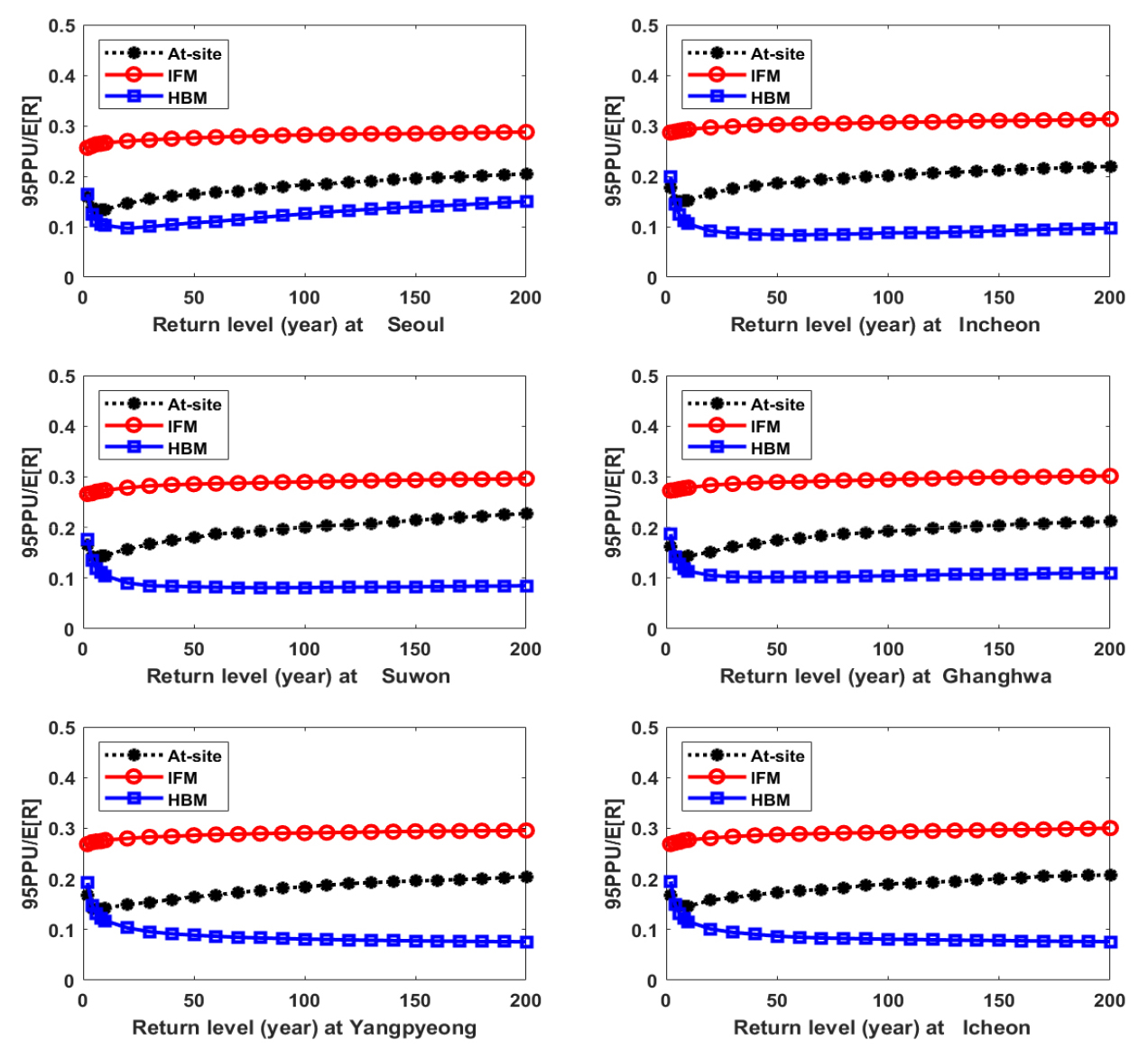
Fig. 7은 지점 빈도해석 및 IFM을 이용한 지역 빈도해석, 본 연구에서 제안된 HBM을 이용한 지역 빈도해석으로 추정한 서울 지점의 재현기간 50년 확률강우량의 사후분포를 보여주고 있다. 서울 지점의 재현기간 50년 확률강우량의 경우, 앙상블 평균의 측면에서는 지점 빈도해석(358.98 mm)과 HBM (364.76 mm)이 유사한 값을 주고 있다. 추정된 확률강우량(즉, 앙상블 평균)의 불확실성 측면에서 살펴보면, HBM에 의한 지역 빈도해석이 가장 작은 불확실성을 보이고 있으며 IFM을 이용한 지역 빈도해석의 불확실성이 가장 큼을 확인하였다. 이러한 개념을 확장하여, 적용된 방법별 재현기간별 확률강우량 앙상블의 불확실성을 정량화하여 지점별로 나타낸 결과는 Fig. 8과 같다. 확률강우량 앙상블의 95% 신뢰구간을 앙상블 평균으로 나눈 값이 95PPU/E[R]이다. 이 값이 클수록 추정된 확률강우량의 불확실성이 크다고 볼 수 있다. 지점 빈도해석과 IFM은 모두 재현기간이 증가할수록 불확실성이 증가하고 있으나, HBM은 재현기간이 증가할수록 불확실성이 감소하다가 재현기간 20년 이상에서 서울 지점에 한정해 다시 증가하고 있음을 파악할 수 있다. 모든 지점과 모든 재현기간에서 IFM에 의한 지역 빈도해석의 불확실성이 가장 큰 것으로 나타났으며, HBM에 의한 지역 빈도해석의 신뢰도가 가장 높은 것을 확인할 수 있다. 재현기간 200년 확률강우량을 기준으로 살펴볼 때, HBM에 의한 지역 빈도해석이 IFM에 의한 지역 빈도해석보다 60% 이상 작은 불확실성이 보이고 있으며, 지점 빈도해석 보다는 50% 이상 불확실성이 저감되었음을 확인할 수 있다.

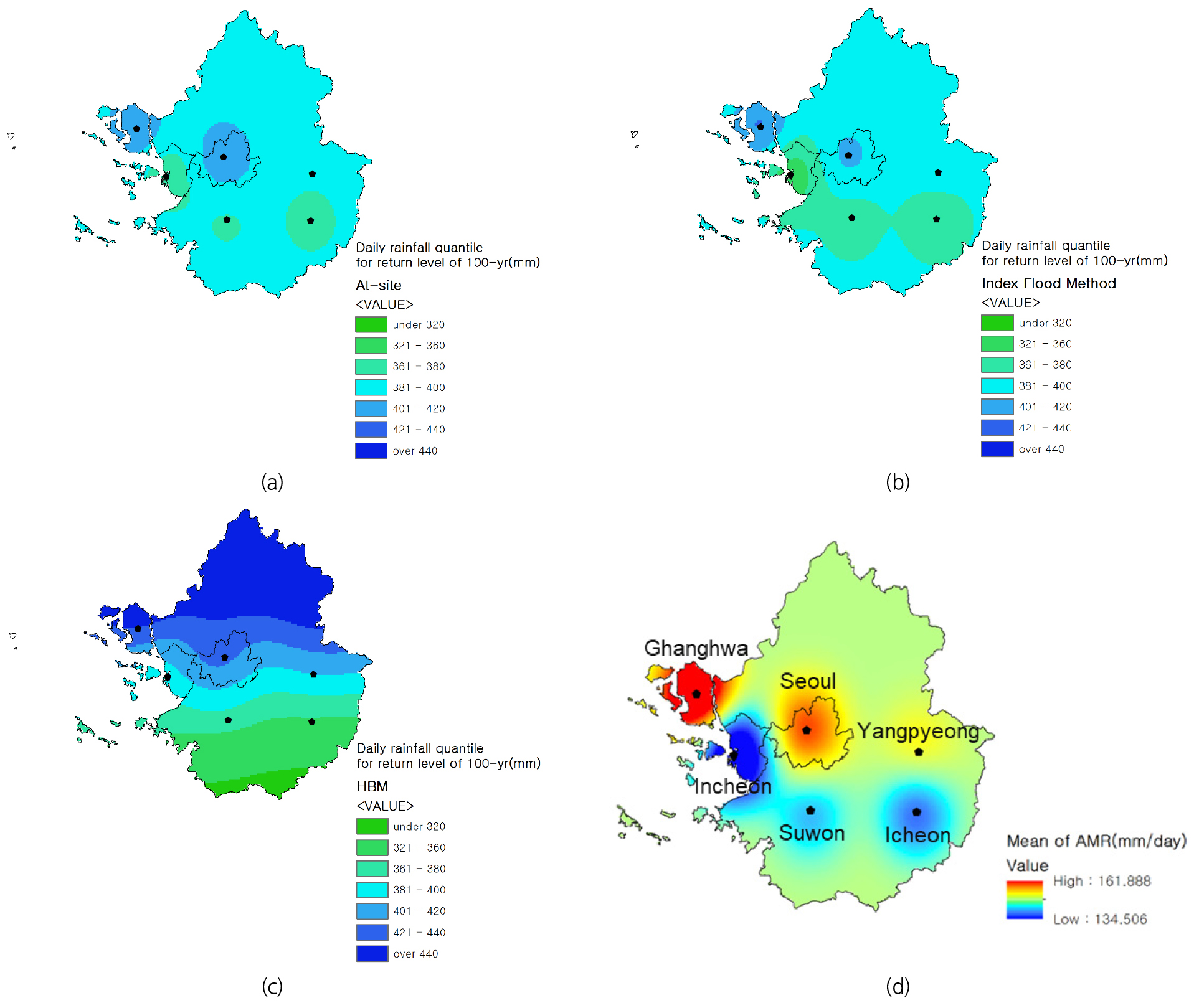
기상정보와 지리정보가 결합된 HBM을 이용한 지역 빈도해석의 장점들 중 하나는 미계측 지역에서의 확률강우량 추정이 가능하다는 것이다. 수도권 지역에 적용된 모델의 경우 연 평균 기온, 위도, 경도에 관한 정보가 주어지면 수도권 임의의 지역에서 확률강우량을 추정할 수 있다. 위도와 경도의 경우 GIS 정보로부터 취득이 가능하나, 연 평균 기온은 관측된 지점에서의 정보만 존재한다. 따라서 6개 지점의 연 평균 기온을 크리깅 방법(Cressie, 1990)을 이용하여 수도권 지역의 격자별(공간 해상도 1 km × 1 km)로 분포시켜 연 평균 기온을 계산하였다. 이들 정보를 이용하여 추정한 수도권 지역의 재현기간 100년 확률강우량을 Fig. 9(c)에 나타내었다. 비교를 위하여 지점 빈도해석과 IFM으로 추정된 지점별 확률강우량의 크리깅 결과를 Figs. 9(a) and 9(b)에 각각 도시하였으며, 지점별 연평균 강우량을 크리깅 기법을 이용하여 공간적으로 분포시킨 결과는 Fig. 9(d)와 같다.

빈도해석 방법별 격자들의 확률강우량의 평균은 지점 빈도해석, IFM, HBM에서 각각 388.73, 383.5, 405.96 mm로 산정되었으며, 지점 빈도해석과 IFM 비슷하며 HBM이 가장 높았다. 최소값은 각각 368.88, 349.23, 299.23 mm였으며, 최대값은 414.12, 420.58, 535.57 mm로 HBM의 공간적 변동성이 가장 큰 것을 확인할 수 있었다. 표준편차도 지점 빈도해석과 IFM은 각각 7.59, 8.94 mm로 비슷했으나 HBM은 52.44 mm로 큰 차이를 보였다. 시각적으로 살펴보더라도 지점 빈도해석과 IFM으로 추정된 크리깅 결과는 수도권지역에 대해 대부분 381-400 mm구간에 속해 공간적인 변동성이 크지 않았다. 단, 서울과 강화지점 부근에서 상대적으로 높은 값을 나타내었으며, 인천, 수원, 이천지점 부근에서는 상대적으로 낮은 값을 나타내었다. IFM은 361-680 mm 구간이 지점 빈도해석 결과에 비해 넓은 지역에서 나타났으며, 인천지역에 대해 가장 낮은 값이 산정되었는데 이는 IFM 방법론에서 사용되는 평균 연최대 일 강수량(Fig. 9(d))의 영향으로 판단된다. HBM을 이용한 지역 빈도해석 결과는 북쪽으로 갈수록 확률강우량이 높아지는 공간적 분포를 보여주었다. 수도권 북부지역은 본 연구에서 사용된 기상관측소와의 거리가 떨어져 있으므로 지점 빈도해석, IFM 및 평균 연최대 일 강수량을 살펴보면 수도권 전체 평균에 해당하는 수치가 분포되어 있다. 하지만 HBM에서는 가장 높은 확률강우량이 나타났는데, 이는 기후정보와 지리정보가 결합되어 확률강우량을 추정할 수 있는 HBM의 장점이 잘 나타난 결과라고 판단된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F7.jpg

Fig. 7.

Posterior distribution of quantile for return level of 50-year at Seoul site

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F8.jpg

Fig. 8.

95PPU/E[R] of variation of quantile ensemble for various return levels

https://static.apub.kr/journalsite/sites/kwra/2021-054-10/N0200541001/images/kwra_54_10_01_F9.jpg

Fig. 9.

Spatially distributed daily rainfall quantile for return level of 100-year. (a) Kriging from at-site frequency analysis, (b) Kriging from Index-flood regional frequency analysis, (c) HBM-based regional frequency analysis, (d) Kriging from at-site annual maximum daily rainfall

4. 결 론

본 연구의 학문적인 기여는 강수량의 지역빈도해석에서 기후정보와 지리정보를 결합한 계층적 베이지안 모형을 개발하고 적용하는 방법론을 제안하는 것에 있다. 외국의 경우에는 확률강우량의 지역적 추정을 위하여 기후정보와 지형 및 지리정보를 결합한 계층적 베이지안 모형을 연구한 사례를 발견할 수 있으며, 국내도 지형 및 지리정보를 결합한 연구사례를 찾아볼 수 있으나, 기후정보와 지리정보를 결합한 지역 빈도해석을 시도한 국내 사례는 찾아보기 어렵다. 기후정보(본 연구에서는 연 평균 기온)와 지리정보(본 연구에서는 위도와 경도)가 결합된 공간분석을 수행함으로써 기존의 IFM에 의한 지역 빈도해석보다 지역적인 차이를 더 잘 설명할 수 있었다.

본 연구에서 제안된 지역 빈도해석은 일반적으로 사용되는 IFM을 이용한 지역 빈도해석과 절차적으로 중요한 차이가 있다. 제안된 절차는 정규화된 연 최대 강우량 시계열을 풀링할 균질한 영역을 미리 결정하는 대신에 여러 지점에서의 연 최대 강우량을 정규화함 없이 결합하는 베이지안 공간모형을 구현한다. 제안된 방법론을 사용하여 다양한 재현기간에 대한 일 강수량을 불확실성과 함께 추정할 수 있었으며, 수도권 지역에 공간적으로 분포된 확률강우량 지도를 제공할 수 있었다. 제안된 방법은 수도권 지역에서 다양한 지속기간에 대한 확률강우량 지도를 생성하는데 사용될 수 있을 것이며, 수도권 지역과 공간적인 크기가 유사한 다른 지역에도 적용될 수 있을 것이다. 더 나아가 연 평균 기온이 GEV 분포 매개변수 추정을 위한 공변량으로 적용되기 때문에, 기후변화를 고려한 지역 빈도해석에도 제안된 방법이 적용될 수 있을 것으로 기대된다.

본 연구에서는 지점 수가 적은 상대적으로 작은 지역을 연구하였기 때문에 GEV 분포의 매개변수를 비교적 간단한 방식(두 개 공변량의 선형 방정식)으로 처리하여 지역 빈도해석을 수행하였다. 더 넓은 지역에 적용하려면 지역 구분에 대한 명시적인 절차가 필요할 것이며, 공변량의 개수와 종류, 표현 방정식도 지역에 맞게 변하는 것이 더 유리할 것이다. 그러나 이를 구현하기 위한 객관적인 방법론이 필요하며, 이를 위한 추가적인 연구가 선행되어야 할 것이다.

Acknowledgements

본 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행되었음 (NRF-2019R1A2C1003114).

References

Ahn, K., Palmer, R., and Steinschneider, S. (2017). "A hierarchical Bayesian model for regionalized seasonal forecasts: Application to low flows in the northeastern United States." Water Resources Research, Vol. 53, pp. 503-521. 10.1002/2016WR019605

Aryal, S., Bates, B., Campbell, E., Li, Y., Palmer, M., and Viney, N. (2009). "Characterizing and modeling temporal and spatial trends in rainfall extremes." Journal of Hydrometeorology, Vol. 10, pp. 241-253. 10.1175/2008JHM1007.1

Berger, J., DeOiveira, V., and Sanso, B. (2001). "Objective Bayesian analysis of spatially correlated data." Journal of the American Statistical Association, Vol. 96, pp. 1361-1374. 10.1198/016214501753382282

Cooley, D., Nychka, D., and Naveau, P. (2007). "Bayesian spatial modeling of extreme precipitation return levels." Journal of the American Statistical Association, Vol. 102, pp. 824-840. 10.1198/016214506000000780

Cressie, N. (1990). "The origins of kriging." Mathematical Geology, Vol. 22, No. 3, pp. 239-252. 10.1007/BF00889887

Dalrymple, T. (1960). Flood-frequency analyses. U.S. Geological Survey Water-Supply paper, 1543-A, Government Printing Office, Washington, D.C, U.S.

Heo, J., and Kim, H. (2019). "Regional frequency analysis for stationary and nonstationary hydrological data." Journal of Korean Water Resources Association, Vol. 52, pp. 657-669.

Hosking, J., and Wallis, J. (1997). Regional frequency analysis: An approach based on l-moments. Cambridge University Press, New York, NY, U.S. 10.1017/CBO9780511529443

Katz, R., Parlange, M., and Naveau, P. (2002). "Statistics of extremes in hydrology." Advances in Water Resources, Vol. 25, pp. 1287-1304. 10.1016/S0309-1708(02)00056-8

Kjeldsen, T., and Jones, D. (2009). "A formal statistical model for pooled analysis of extreme floods." Hydrology Research, Vol. 40, pp. 465-480. 10.2166/nh.2009.055

Kwak, D., and Kim, G. (2015). "Bayesian nonstationary probability rainfall estimation using the Grid method." Journal of Korean Water Resources Association, Vol. 48, pp. 37-44. 10.3741/JKWRA.2015.48.1.37

Kwon, H., Kim, J., Kim, O., and Lee, J. (2013). "A development of regional frequency model based on hierarchical Bayesian model." Journal of Korean Water Resources Association, Vol. 46, pp. 13-24. 10.3741/JKWRA.2013.46.1.13

Liang, Y., Liu, S., Guo, Y., and Hua, H. (2017). "L-Moment-Based regional frequency analysis of annual extreme precipitation and its uncertainty analysis." Water Resources Management, Vol. 31, pp. 3899-3919. 10.1007/s11269-017-1715-5

Lima, C., and Lall, U. (2009). "Hierarchical Bayesian modeling of multisite daily rainfall occurrence: Rainy season onset, peak, and end." Water Resources Research, Vol. 45, W07422. doi: 10.1029/2008WR007485 10.1029/2008WR007485

Micevski, T., and Kuczera, G. (2009). "Combining site and regional flood information using a Bayesian Monte Carlo approach." Water Resources Research, Vol. 45, W04405. doi: 10.1029/2008WR007173 10.1029/2008WR007173

Najafi, M., and Moradkhani, H. (2013). "Analysis of runoff extremes using spatial hierarchical Bayesian modeling." Water Resources Research, Vol. 49, pp. 6656-6670. 10.1002/wrcr.20381

Reis, D., Stedinger, J., and Martins, E. (2005). "Bayesian generalized least squares regression with application to log Pearson type 3 regional skew estimation." Water Resources Research, Vol. 41, W10419. doi: 10.1029/2004WR003445 10.1029/2004WR003445

Renard, B. (2011). "A Bayesian hierarchical approach to regional frequency analysis." Water Resources Research, Vol. 47, W11513. doi: 10.1029/2010WR010089 10.1029/2010WR010089

Robson, A., and Reed, D. (1999). Statistical procedures for flood frequency estimation, in flood estimation handbook. Institute of Hydrology, Wallingford, U.K., p. 338.

Schaefer, M. (1990). "Regional analyses of precipitation annual maxima in Washington State." Water Resources Research, Vol. 26, pp. 119-131. 10.1029/WR026i001p00119

Stedinger, J., and Tasker, G. (1985). "Regional hydrologic analysis: 1. Ordinary, weighted and generalized least squares compared." Water Resources Research, Vol. 21, pp. 1421-1432. 10.1029/WR021i009p01421

Stedinger, J., and Tasker, G. (1986). "Regional hydrologic analysis, 2, Model error estimators, estimation of sigma and log Pearson type 3 distributions." Water Resources Research, Vol. 22, No. 10, pp. 1487-1499. 10.1029/WR022i010p01487

Wang, Z., Zeng, Z., Lai, C., Lin, W., Wu, X., and Chen, X. (2017). "A regional frequency analysis of precipitation extremes in Mainland China with fuzzy c-means and L-moments approaches." International Journal of Climatology, Vol. 37, pp. 429-444. 10.1002/joc.5013

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Spatial distribution and uncertainty of daily rainfall for return level using hierarchical Bayesian modeling combined with climate and geographical information

ABSTRACT

MAIN

Table 1.

Site information

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Fig. 1.

Relation between GEV parameters (scale parameter ϕ, shape parameter ψ and location parameter ζ)and covariates (Annual mean surface air temperature, latitude and longitude)

Fig. 2.

Posterior distribution of hyper-parameter a and b

Fig. 3.

Posterior distribution of parameters of GEV distribution for at-site frequency analysis and HBM-based regional approaches at Suwon site

Fig. 4.

Box-plot of GEV parameters for at-site frequency analysis and HBM-based regional frequency analysis

Fig. 5.

Daily rainfall quantile for various return levels

Fig. 6.

Averaged daily rainfall quantiles at all sites

Fig. 7.

Posterior distribution of quantile for return level of 50-year at Seoul site

Fig. 8.

95PPU/E[R] of variation of quantile ensemble for various return levels

Fig. 9.

Spatially distributed daily rainfall quantile for return level of 100-year. (a) Kriging from at-site frequency analysis, (b) Kriging from Index-flood regional frequency analysis, (c) HBM-based regional frequency analysis, (d) Kriging from at-site annual maximum daily rainfall

Acknowledgements

References

Relation between GEV parameters (scale parameter $ϕ$ , shape parameter $ψ$ and location parameter $ζ$ )and covariates (Annual mean surface air temperature, latitude and longitude)