1. 서 론
2. 연구 방법
2.1 군집분석
2.2 웨이블릿 변환
2.3 Deep Neural Network
2.4 비선형 특성 반영을 위한 KWD Framework 제안
3. 연구 대상 및 결과
3.1 대상지역 현황
3.2 K-means를 이용한 수용가 특성 분석
3.3 Wavelet을 통한 주요 성분 추출
3.4 딥러닝을 알고리즘 적용
3.5 예측 성능 비교
4. 결 론
1. 서 론
상수도 시설은 핵심적인 사회인프라 시설이며, 인간에게 삶의 질을 높여줄 수 있는 필수적인 시설이다. 기존 상수도 시스템에서는 주로 지선·간선에서 통합적으로 계측하거나, 검침원이 직접 확인하는 방식으로 물 사용량을 계측하고 있다. 반면 최근에는 정보통신기술의 발달과 4차 산업 혁명으로 인해 스마트 미터와 같은 IoT 장비를 수자원 시스템에 결합하여 실시간 정보를 제공하는 시스템이 많이 개발되고 있다. 그로 인해 기존에는 파악하지 못했던 개별 수용가 단위의 수요량을 파악할 수 있어 시간적, 공간적으로 고해상도 자료를 수집할 수 있게 되었다. 또한 기존 상수도 시스템에서는 개별 수용가의 수요량을 정확하게 알 수 없었기 때문에 항상 과도한 물을 공급하여 왔다. 그로 인해 에너지 손실이 발생하였었고 특히 펌프에서 가장 큰 에너지 손실이 발생하여 왔다. 상수도 시스템의 전력 사용을 살펴보면, 전체 사용량 중 펌프로 인한 전력 소비량이 80%를 차지하고 있다(Intelligence et al., 2011). 만약 개별 수용가에서 요구하는 물 사용량을 예측 할 수 있다면 펌프를 효율적으로 운영함으로써 전력비용 및 에너지를 절감할 수 있을 것이다.
이와 관련하여 Alvisi et al. (2007)은 효율적인 물 분배 방법을 제안하기 위해서 단기 미래의 물수요량을 예측해야 한다고 언급하였다. 이를 위해 추계학적 또는 선형 시계열 모형인 AR 모형을 적용하였고, 연간, 주간, 일일 수준에서 일반적인 패턴과 주기성을 분석하였다. Atsalakis et al. (2007)도 대규모 물 공급 관리에서 주요 문제는 최적 비용으로 양수 작업을 계획하기 위해서는 수요량을 예측해야 한다고 언급하였다. 또한 선형 시계열 모형에 Neuro-Fuzzy 개념을 적용한 ANFIS (Adaptive Neuro-Fuzzy Inferences System)을 개발하였고, 전통적인 선형 시계열 모형인 자기회귀(AR) 모형과 예측 성능을 비교하였다. 하지만 전통적인 선형 시계열 예측 모형인 AR 모형의 경우 지체시간만큼 이동하여 예측하는 방식으로써, 비교적 단순한 주기 패턴에서 적합하다고 알려져 있다. 다양한 패턴의 주기성분이 복합적으로 결합된 여러 수용가의 물 사용량을 예측하기에는 무리가 있었다.
이에 Koo et al. (2005)는 지역, 용도, 인구밀집 등에 따라 물 사용량 패턴이 상이하기 때문에 군집분석을 통해 지역별 특성을 분류하였고, 각 군집별 회귀모형을 통해 물 사용량 예측 방법을 제안하였다. Lee et al. (2009)는 비 가정용 업종별로 원단위법(면적당 일일 물사용량 등)을 통해 물 사용 패턴 및 특징을 파악하고 분석하였다. 따라서 다양한 업종 및 용도에 따라 다양한 패턴을 예측하기 위해서는 군집 분석을 수행하는 것이 타당하다고 판단된다.
Tabesh and Dini (2009)는 날씨 등의 외적 요인의 영향을 함께 고려하고 비선형적 모형으로 알려진 신경망(artificial neural networks, ANN)을 적용하여 물 사용량 예측을 수행하였다. Choi et al. (2009)는 비선형적 특성을 보이는 물 수요량을 예측하기 위해서는 기존의 시계열 모형인 AR 모형이나 다중회귀모형(multiple regression model, RM)보다 비선형 특성을 더 적절히 모의 할 수 있는 다층 신경망(multi layer perceptron, MLP)등의 머신러닝 모형이 적합하다고 언급하였다. 이를 검증하기 위하여 RM, AR, MLP 모형을 적용하여 물 사용량 예측 성능을 비교한 결과 MLP 모형이 가장 우수한 것으로 나타났다. Firat et al. (2010)도 물 사용량을 예측하기 위하여 GRNN (Generalized Regression Neural Networks), CCNN (Cascade Correlation Neural Network) 등의 신경망 계열 모형을 적용하였다. Kwon et al. (2012)은 비선형적 특성을 반영하기 위해 머신러닝 모형인 SVM (Support Vector Machine)과 시계열을 분해하여 주기별 특징을 파악할 수 있는 웨이블렛 변환(Wavelet transform) 방법을 적용하였다. 그 결과 기존의 AR 모형보다 개선된 예측 결과를 확인하였다. Altunkaynak et al. (2017)도 복잡한 비선형 데이터인 물 사용량을 예측하기 위해 Wavelet을 통해 핵심적인 주기성분을 추출하여 딥러닝(Deep learning) 모형의 적용을 제안하였다. Choi and Kim (2018)은 비선형적 특성을 반영하기 위해 딥러닝 모형을 적용하였고, 최신 IoT 장비인 스마트 수도 미터에서 계측된 개별 수용가의 시간당 물 사용량을 활용하여 물 사용량 예측 모형을 제안하였다.
이처럼 물 사용량 예측은 최적의 수자원 관리와 에너지 절감 측면에서 필수적이기 때문에 많은 연구들에서 정확한 예측을 위해 다양한 방법의 적용을 통해 발전되어져 왔다. 따라서 본 연구에서는 스마트 미터 기반 물 사용량 자료를 활용하여 개별 수용가의 특징에 따라 군집분석을 수행하였고, Wavelet transform을 통해 비선형 자료의 주기 성분을 분해하였다. 또한 딥러닝 모형을 적용해 자료의 비선형성을 학습하여 예측을 수행하였다.
2. 연구 방법
2.1 군집분석
군집분석(cluster analysis)은 불특정 대상이 소유하고 있는 특성을 파악하여 유사한 특성끼리 군집하는 통계적 기법으로 계층적(hierarchical) 군집분석 방법과 비-계층적(non-hierarchical) 군집분석 방법으로 구분된다(Kyoung et al., 2007; Han et al., 2014). 계층적 군집분석 방법은 유사성이 큰 대상끼리 순차적으로 다수의 군집을 만들고 점차적으로 군집을 합쳐 목표 군집을 도출하는 방법이다. 비-계층적 군집화 방법은 군집의 중심(cluster center)을 기준으로 군집의 수(cubic clustering criterion)를 지정하여 군집화하는 방법이다(Nam et al., 2015; Kim et al., 2020b).
비 계층적 군집분석은 계층적 군집분석보다 계산속도가 빠르고 대량의 군집을 발견하는데 효과적인 장점이 있다. 비-계층적 군집분석으로는 대표적으로 K-Means Clustering 알고리즘(이하; K-Means)이 있다(Kwon et al., 2017). K-Means는 특정 성질의 데이터들이 유사성을 기초로 한 군집의 개수(k)를 찾는 알고리즘을 의미한다(Arthur and Vassilvitskii, 2006). 군집의 개수를 설정하기 위하여 군집 내 제곱의 합(total within sum of squares, WSS)과 칼린스키-하라바쯔(Calinski-Harabasz, CH)지수를 활용할 수 있다. 군집 내 제곱의 합은 전체 자료에 대하여 군집 개수 별 제곱 합의 합계이고, CH 지수는 군집 개수의 분산과 전체 자료에 대한 분산의 비율이다.
관측 지점별 유사성을 표현하는 척도로 거리(distance)를 정의해야 한다. 거리를 정의하는 방법 중 가장 일반적으로 사용되는 유클리드 거리(euclidean distance), 모든 변수가 범주형 변수일 때 사용하는 해밍 거리(hamming distance), 한 점에서 다른 점을 얻는데 필요한 수평 및 수직 단위를 맨해튼 거리(manhattan distance), 텍스트 분석에 사용되는 코사인 유사도(cosine similarity)가 있다. 본 연구에서는 정규화한 자료를 이용하므로 유클리드 거리를 사용하여 거리를 계측하였다. 다음 Eq. (1)은 유클리드 거리의 식을 나타냈다.
여기서, x는 변수를 의미하고, p는 총 변수의 개수를 의미한다. 또한 i와 j는 다차원 공간상의 두 개체를 의미하며, dij는 직선 최단 거리인 유클리드 거리를 의미한다.
2.2 웨이블릿 변환
웨이블릿 변환(Wavelet Transform)은 기저함수(basis function)의 스케일(scale)항과 천이항(translation)이라는 두 변수로 표현되고 시계열의 서로 다른 스케일 성분들로 분해 가능하다. 스케일은 주파수 영역에서의 우리가 평가하고자 하는 주파수를 의미한다. 즉, 스케일항을 이용하여 기저함수의 폭을 축소 또는 확대하여 변환시켜 고빈도(high frequency)에서 저빈도(low frequency)에 해당하는 다양한 주파수 영역에서 시계열의 주기를 평가하게 된다. 천이항은 시간에 따른 각 주파수가 가지는 스펙트럼의 강도를 평가하기 위해서 도입된 항이다. 천이항을 우리가 원하는 시간으로 이동시키면서 시간에 따른 주기의 강도를 평가할 수 있다. 이러한 Wavelet Transform의 특성들은 2차원 영역의 복잡성을 효과적으로 분석할 수 있으며 시계열분석에 있어 많이 활용된다(Kwon et al., 2012; Yoo et al., 2019). 다음 Eq. (2)는 Wavelet Transform의 기저 함수를 나타내고 여기서, sc는 스케일을 결정하는 값, sh는 함수의 이동을 결정하는 천이항을 의미한다. 또한 t는 시간을 의미하며 는 기저함수(mother wavelet)를 의미한다.
다음 Eq. (2)와 같이 기저 함수가 될 수 있는 함수 의 스케일과 천이를 통해서 Wavelet Transform을 수행한다. 연속형 웨이블릿 변환(Continuous Wavelet Transform)은 기저함수의 이동 및 확장으로 산정된 웨이블릿 계수를 통해 시간-주파수 분석을 한다. 그러나 무한개의 기저함수를 고려하고 과도한 계산과정으로 인해 중복된 정보가 발생한다는 단점이 있다. 이러한 문제를 해결하기 위하여 전이 및 규모 변수를 무한히 고려하지 않고 이산화하여 과도한 정보를 일정한 비율로 조정된 매개변수 통해 웨이블릿 계수를 샘플링하는 이산형 웨이블릿 변환(Discrete Wavelet Transform)이 있다. 다음 Eq. (3)과 같이 이산형 웨이블릿 변환을 나타냈고, 이산형 웨이블릿 변환에서 기저함수는 Eq. (4)와 같이 나타낸다.
여기서 m은 규모 변수(Scale parameter), j는 전이 변수(shift parameter)를 의미한다.
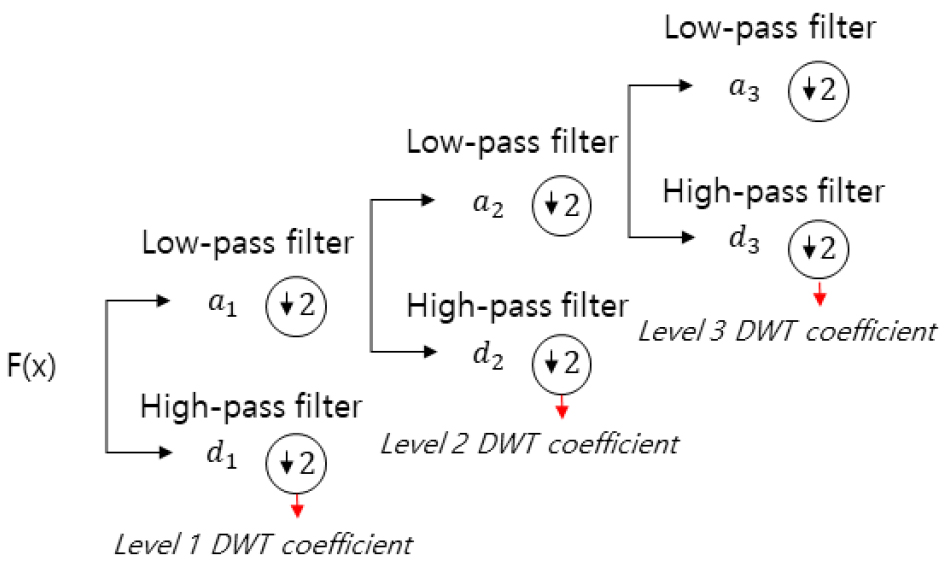
이산형 웨이블릿은 피라미드 원칙에 의해 분석을 수행하며, 기저함수는 고주파수와 저주파수를 구분하는 필터링을 통해 세분화 성분과 근사성분으로 분해된다. 이때 원시자료의 시계열은 최종 단계까지 분리된 근사성분 (an)과 분해 단계별 세분화 성분(d1, d2, …, dn)으로 표현할 수 있다. 이 과정을 Fig. 1에서 그림으로 표현하였다.
2.3 Deep Neural Network
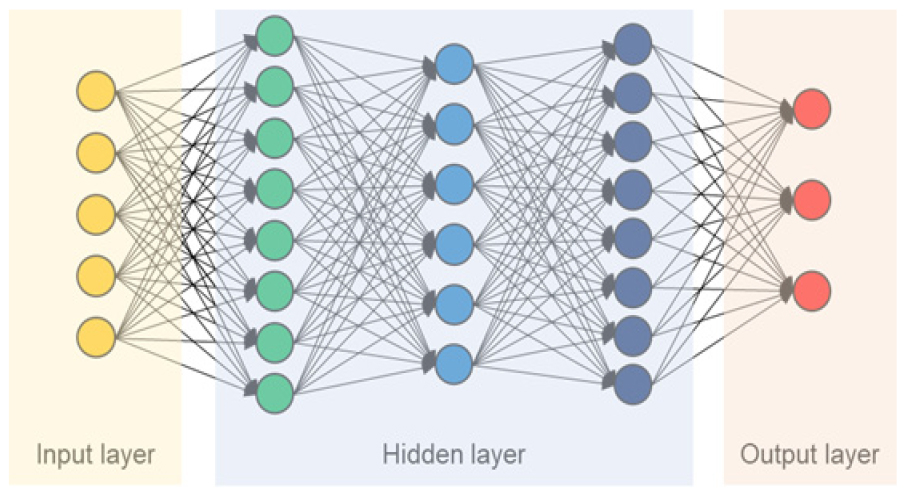
딥러닝(deep neural network, DNN)은 수많은 자료를 분석하고 자료의 패턴을 발견하여 예측하는 점에 있어 효과적이다. 기존의 머신러닝 알고리즘들은 데이터의 양이 많아질수록 모형 예측 성능에 한계가 있으나, 딥러닝은 데이터의 양이 많아질수록 예측 성능이 선형적으로 증가하는 장점이 있다(Kim et al., 2020a). DNN의 구조는 인공신경망(Artificial Neural Network, ANN)과 비슷하지만, Hidden layer에서 2개 이상의 개수를 지니는 차이점이 있다. 또한, 자료의 수가 방대한 경우 과적합(overfitting)이 발생할 수 있는데, 드롭아웃(dropout) 기법을 이용하여 과적합을 해결 할 수 있다(Chun et al., 2020). 드롭아웃은 어떤 노드의 가중치가 특정 데이터에 크게 영향을 받는 현상을 감소시키기 위하여 학습을 진행하는 동안 신경망의 노드를 확률적으로 사용하지 않는다. 즉, 드롭아웃을 이용하여 특정 노드에 크게 의존하지 않도록 과적합 현상을 해결할 수 있다. Fig. 2와 같이 DNN의 구조를 도식화하였다.
2.4 비선형 특성 반영을 위한 KWD Framework 제안
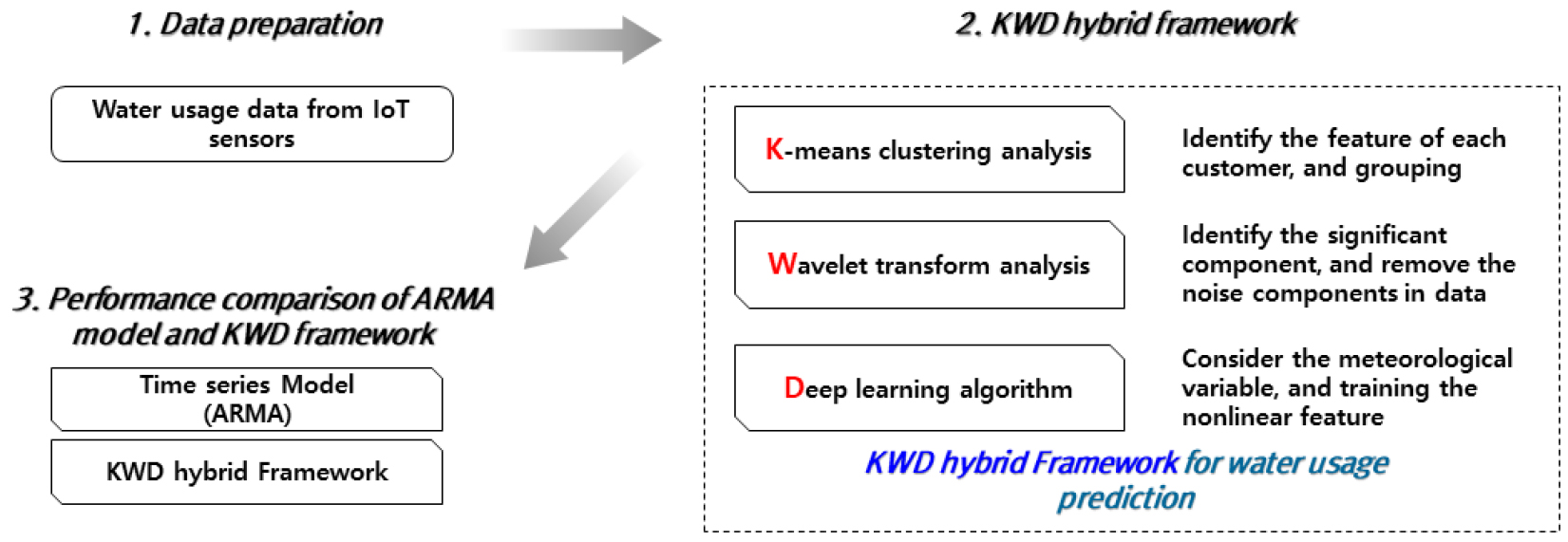
본 연구에서는 물 사용량 자료의 비선형적 특성을 반영하기 위해 선행 연구들에서 제안되었던 K-means Clustering analysis, Wavelet Transform analysis, Deep learning algorithm을 결합하는 방식의 Hybrid Framework 방법을 개발하였고, 다음과 같은 3단계를 통해 진행된다.
첫 번째 K-means Clustering analysis는 개별 수용가의 물 사용 특징을 파악하고, 유사한 특성에 따라 군집을 수행한다. 두 번째 복합적인 주기 성분에 대한 주요 주기 성분을 식별하고 잡음 성분을 제거하기 위하여 Wavelet Transformation analysis를 수행한다. 세 번째 기상요소와 요일과 같은 외적 요인을 고려하고 비선형적 특성을 학습하기 위해 Deep learning algorithm을 적용한다.
본 연구에서는 비선형적 물 사용량 예측을 위해 앞서 설명한 분석 절차를 KWD hybrid framework라고 정의하였고, Fig. 3에서 전체적인 분석 절차를 나타냈다. 마지막으로 전통적인 시계열 예측 모형인 ARIMA 모형과 예측 성능을 비교하였다.
3. 연구 대상 및 결과
3.1 대상지역 현황
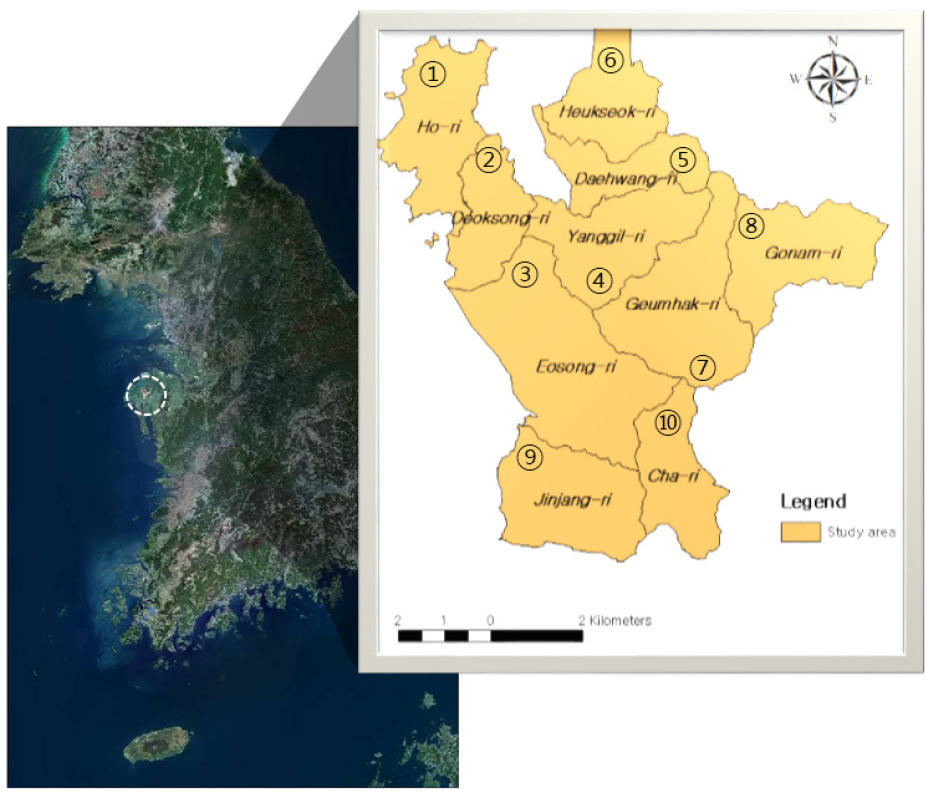
본 연구에서는 물 사용량 예측을 위하여 스마트 수도계량기가 설치된 충청남도 서산시 팔봉면 일대를 대상지역으로 선정하였다. 대상지역은 총 10개의 법정리로 구분되며, 51.37 km2 면적이 포함된다(Fig. 4).
대상지역은 각 사용자의 가구마다(약 1200 가구) 스마트 수도계량기가 설치되어 있으며 초음파 방식으로 실시간 물 사용량을 계량하고 해당 정보를 송·수신 한다. 용도의 경우 가정용(1), 일반용(2)으로 구분되며, 구경은 사용자 마다 13 mm, 15 mm, 20 mm, 25 mm, 32 mm, 40 mm, 50 mm 총 7가지 종류가 있다. 본 연구에서는 한국수자원공사(K-water)로부터 2016년 10월부터 2017년 12월까지 계측된 수용가 단위의 물 사용량 자료를 수집하였다.
3.2 K-means를 이용한 수용가 특성 분석
본 연구에서는 개별 가구의 특징들을 통해 K-means 분석을 수행하고, 유사한 특성을 내포하고 있는 수용가를 군집하였다. 여기서 개별 가구의 특징을 파악하기 위해 위치, 용도, 상수도 구경, 총 사용량 총 4가지 지표를 구축하였다. 특징 변수들은 아래 Table 1에서 자료의 형태를 설명하였다.
Table 1.
The data type of variables
| Variables | Data type |
| 1. Location (Latitude) | Numeric (Double) |
| 2. Location (Longitude) | Numeric (Double) |
| 3. Type of occupancy | Categorical |
| 4. Diameter | Integer |
| 5. Total usage | Numeric (Double) |
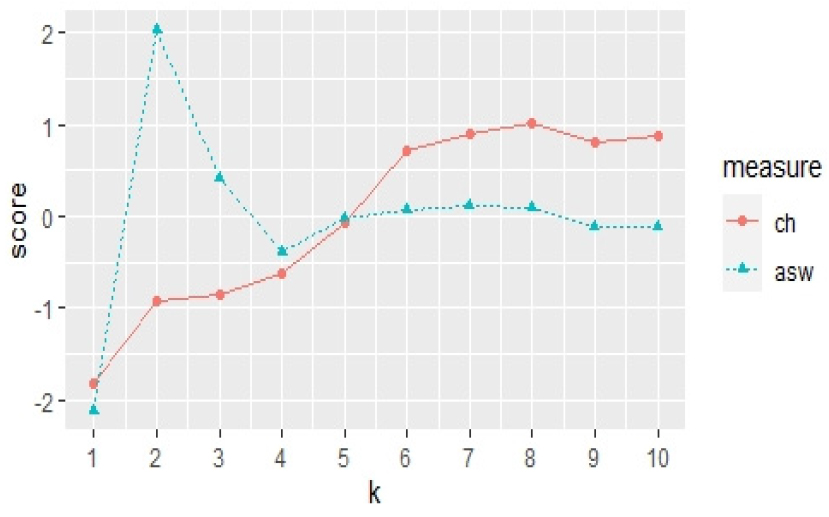
먼저 군집의 개수를 설정하기 위해 군집 내 총 제곱합(Total Within Sum of Squares, 총 WSS)을 계산하고, 곡선에서 곡선에서 첫 번째 “엘보우” 값을 도출하였다. 여기서 총 WSS는 모든 군집의 군집 내 제곱합의 합계이고, “엘보우”란 K값이 증가하다가 첫 번째로 감소하는 구간을 뜻한다. 또한 칼린스키-하라바쯔(Calinski-Harabasz, CH) 지수는 군집 간 분산과 전체 군집 내 분산의 비율이고, 주어진 자료에서 총 제곱합(Total Sum of Squares, TSS)은 자료의 중심에서 모든 자료의 제곱합이다. WSS (k)가 k개 군집의 총 WSS이면, 군집 간 제곱합(Between Sum of Squares, BSS)은 BSS (k) = TSS – WSS (k)로 주어진다. 따라서 Eq. (5)과 같이 나타낼 수 있다. 군집의 중심은 모든 점의 평균값인 점으로 정의하였고, CH 지수를 활용하여 적정한 군집의 개수를 설정하였다.
즉, WSS와 CH의 값이 교차하는 첫 번째 지점이 최적의 군집 개수로 볼 수 있다. Fig. 5와 같이 두 값이 교차하는 그래프를 통해 k = 5 일 때 교차하는 것을 확인하였고, 최적 군집 개수는 5개로 선정하였다.
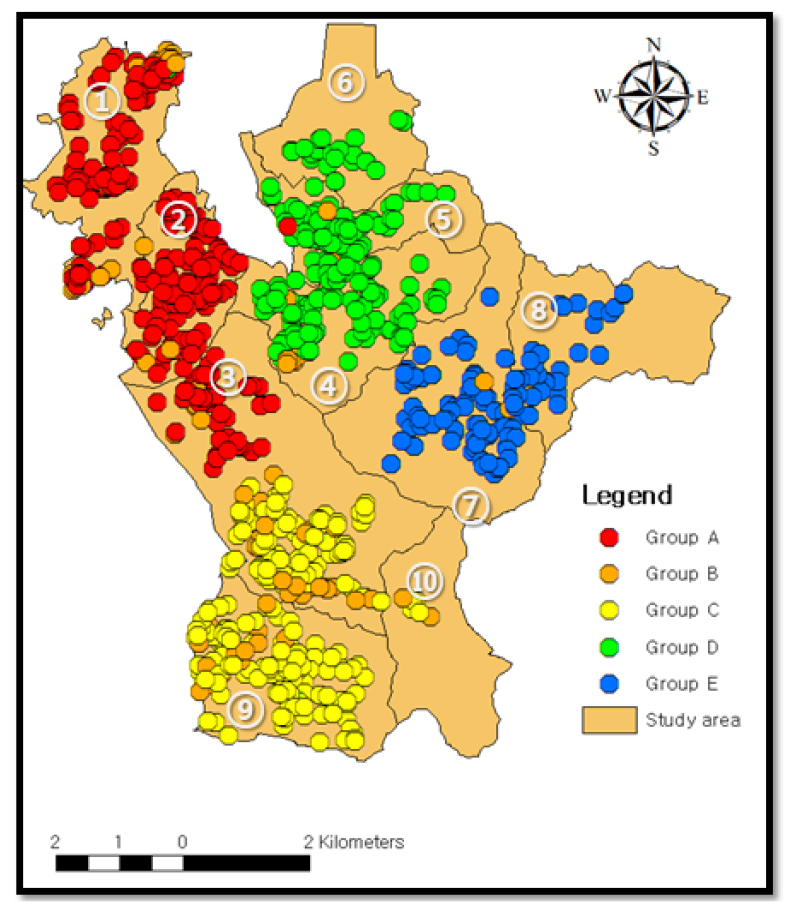
Fig. 6에서 군집 분석 결과를 살펴보면 대부분 근처 위치에 포함되는 수용가별로 군집이 분류된 것을 확인 할 수 있는데, 평균적으로 Group 당 2~3개의 법정리가 포함되었다.
Group A는 ①, ②, ③, Group C는 ③, ⑨, ⑩, Group D는 ④, ⑤, ⑥, Group E는 ⑦, ⑧위치에서 주로 분포하는 것을 확인할 수 있는 반면, Group B는 대상지역 전체에 산재되어 분포하는 것을 확인할 수 있다. 이 결과를 자세하게 살펴보기 위하여 군집 결과에 따른 지표들의 평균을 Table 2에서 정리하였다. 여기서 위치에 대한 정보는 Fig. 6에서 표현하였기 때문에 생략하였다.
Table 2를 살펴보면 용도는 가정용, 구경은 15 mm, 총 사용량은 150 m3~200 m3 로 유사하게 나타나는 것을 확인할 수 있다. 반면 Group B의 경우 일반 용도로써 가정용 보다 구경과 사용량이 훨씬 큰 것을 확인할 수 있다. 즉, 군집분석 결과는 용도나 구경 및 총 사용량은 대부분 유사하기 때문에 위치의 영향으로 분류되었지만, Group B의 경우 일반 용도로서 전 지역에 산재되어 있고 타 Group 보다 물 사용 패턴이 훨씬 많은 것으로 나타난다. 따라서 본 연구에서는 이 결과를 토대로 군집별 물 사용량 자료를 합산하여 재구축하였다.
Table 2.
Average value of diameter and total water usage for each group
| Group | Type of occupancy | Diameter | Total usage |
| A | Household | 15 mm | 190 m3 |
| B | General | 17.84 mm | 734 m3 |
| C | Household | 15 mm | 181 m3 |
| D | Household | 15 mm | 157 m3 |
| E | Household | 15 mm | 156 m3 |
3.3 Wavelet을 통한 주요 성분 추출
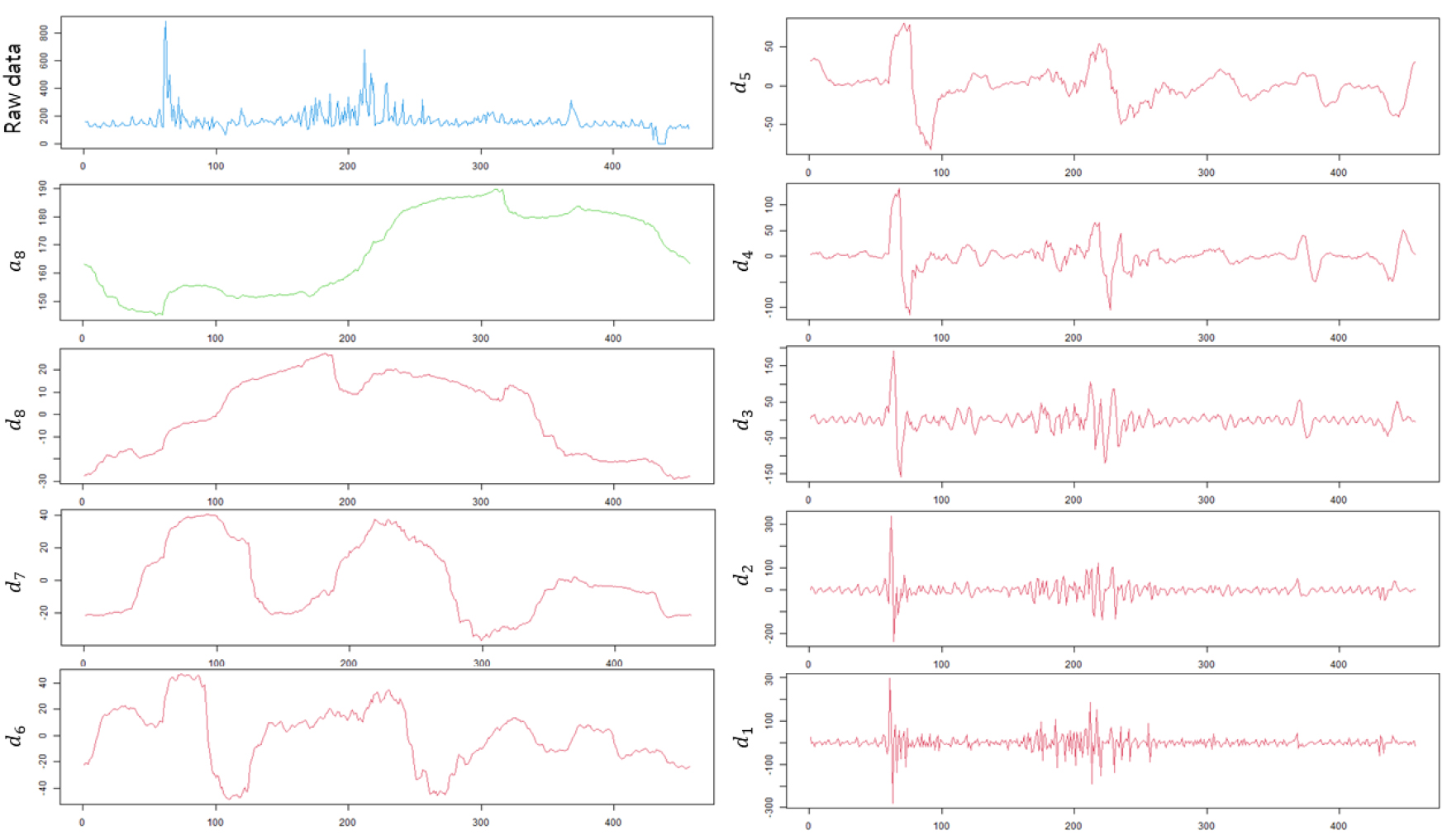
본 연구에서는 물 사용량 자료의 시계열 특성을 파악하여 잡음성분은 제거하고 핵심이 되는 주요 성분을 추출하기 위해 이산형 웨이블릿을 활용하였다. 웨이블릿 변환은 각 군집마다 수행하였으나, 본문에서는 Group A의 분해 결과를 예시로 표현하였다. 웨이블릿 변환시 Daubechies (db), Symlets (sym) 등의 다양한 기저함수가 활용되는데, 본 연구에서는 일반적으로 가장 많이 활용되는 Daubechies (db)를 활용하여 총 8단계로 분해된 결과를 Fig. 7에서 나타냈다.
원시자료의 시계열로부터 분해된 d1 ~ d8은 각 단계별 High pass filter를 통과한 세분화 성분을 나타내며, a8은 최종 근사 성분을 의미한다. 여기서 모든 세분화 성분과 최종 근사 성분을 합하면 원시자료의 시계열이 된다. d1은 가장 큰 주파수 성분으로써 첫 번째로 추출되는 성분, d8은 가장 작은 주파수 성분으로 마지막에 추출되는 성분이며, a8은 마지막으로 d8까지 분해되고 남은 근사성분이다.
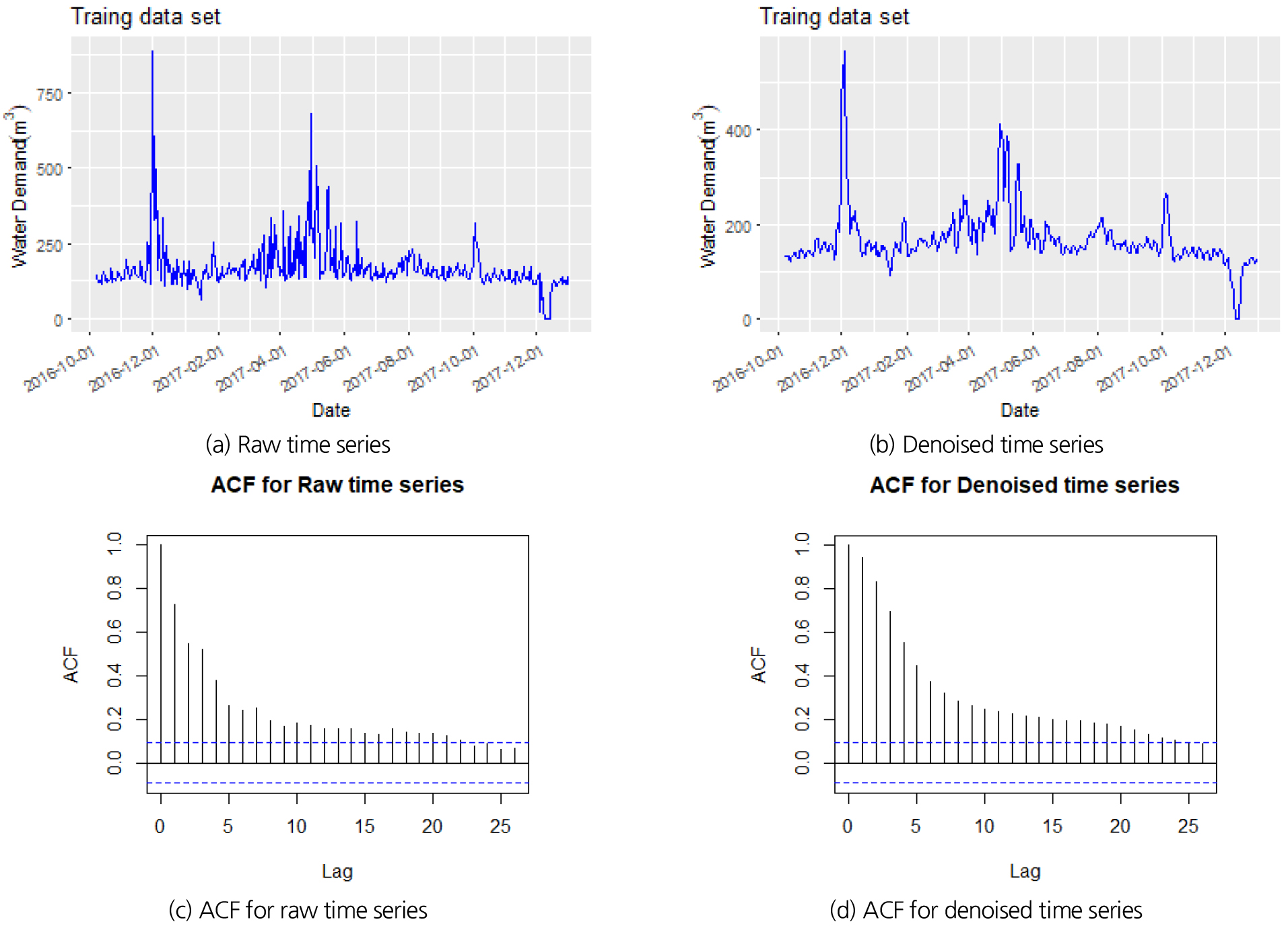
Abbaszadeh (2016)은 일반적인 시계열에서 잡음성분을 분리하기 위하여 고주파수로 분리되는 d1과 d2 성분으로 정의하였다. 또한 잡음성분을 제거한 후 시계열을 인공신경망을 학습 시킨 결과 성능이 개선되는 것을 확인하였다. 이를 참고하여 본 연구에서도 잡음 성분에 해당하는 d1와 d2성분을 제거한 후, d3부터 a8성분까지의 합을 통해 핵심적인 주기 성분을 추출하였다. Fig. 8에서는 원시 자료의 시계열과 잡음성분이 제거된 시계열을 비교하였다. 비교 결과 원시 자료의 시계열의 핵심적인 패턴은 유사하지만, 규칙성 없이 진동하는 형태의 패턴(잡음 성분)은 제거된 것을 확인할 수 있다.
3.4 딥러닝을 알고리즘 적용
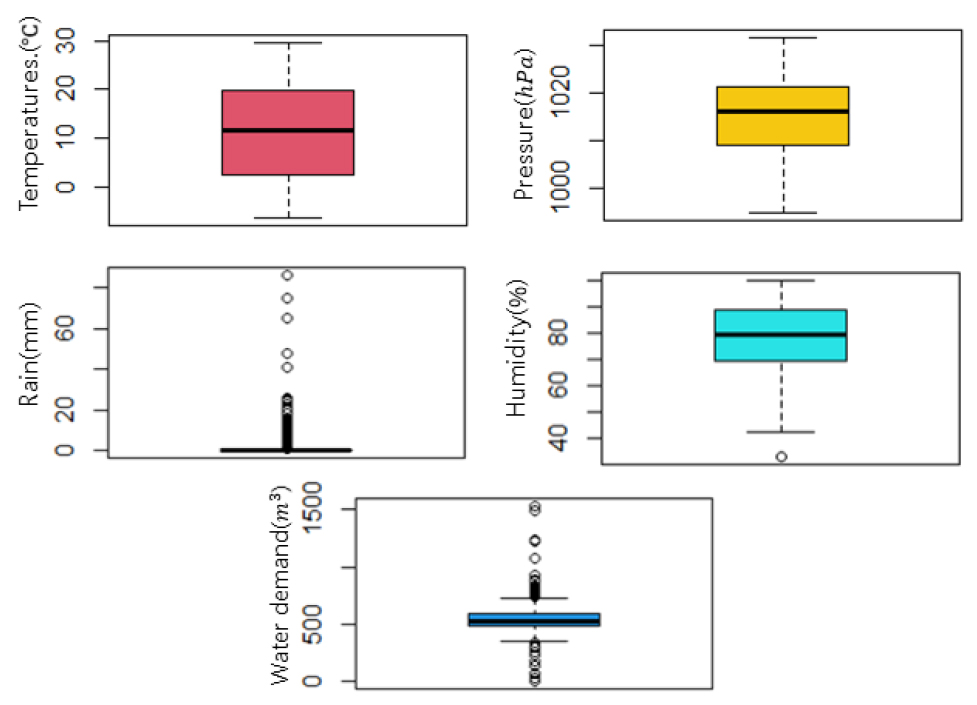
본 연구에서는 물 사용 패턴을 구분하기 위해 일주일 전부터 1일 전까지 수용가의 사용량을 입력 자료로 활용하였으며, 평일과 주말의 사용 패턴이 다르기 때문에 요일 정보도 활용하였다. 또한 외부의 날씨의 영향을 반영하기 위해 기상 요인으로써 기온, 강우, 습도, 기압을 추가로 고려하였다. Fig. 9에서는 입력 자료들의 기초통계량을 확인할 수 있는 Box plot을 나타냈다.
여기서 Box plot은 자료에서 계산된 통계량(최소값, 제 1사분위(Q1), 제 2사분위(Q2), 제 3사분위(Q3), 최대값)을 통해 데이터의 분포를 확인할 수 있는 그래프이다. Q1은 박스의 밑변, Q3은 박스의 윗변을 나타내며, 최소값은 Q1에서 1.5 IQR (Interquartile range)을 뺀값, 최대값은 Q3에서 1.5 IQR을 더한 값으로 표현된다. 또한 최소값과 최대값을 벗어나는 값들은 잠재적 이상치로 표현한다. Fig. 9를 살펴보면 기온과 기압, 습도의 경우 상대적으로 변동성이 크지 않은 것을 확인할 수 있으며, 특히 기온이나 기압은 데이터의 중앙값에서부터 최소값과 최대값의 간격이 일정하기 때문에 정규분포 형태임을 알 수 있다. 강우의 경우 일반적으로 0인 날짜가 훨씬 많기 때문에 0에 가깝게 치우친 지수분포 형태를 띄고 있으며, 다른 변수들에 비해 변동성이 크고 그로 인해 잠재적 이상치 값이 많은 것을 확인할 수 있다. 물 사용량은 강우 보다는 변동성이 적지만 마찬가지로 잠재적 이상치들이 많이 포함되는 것을 확인 할 수 있다.
본 연구에서는 딥러닝 알고리즘에서 가장 기초가 되는 DNN 모형을 적용하였으며, 경험적 방식에 의해 성능이 가장 우수했던 Parameter를 Table 3과 같이 정리하였다. 또한 본 연구에서는 Hidden layer를 총 3개로 구성하였으며, 각 Hidden layer의 Activation function은 Relu로 구성하고 Output layer의 Activation function은 Sigmoid로 망을 구성하였다. 모형의 학습을 위한 Training data set는 2016년 10월 6일부터 2017년 10월 까지를 사용하였고, 모형의 성능 평가를 위한 Test data set는 2017년 11월부터 12월까지 활용하였다.
Table 3.
The parameter of DNN model
| Index | Parameter |
| Activation function 1 | Relu |
| Activation function 2 | Relu |
| Activation function 3 | Relu |
| Activation function 4 | Sigmoid |
| Loss function | MSE |
| Optimizer | Adam |
| Epoch | 30 |
| Batch size | 7 |
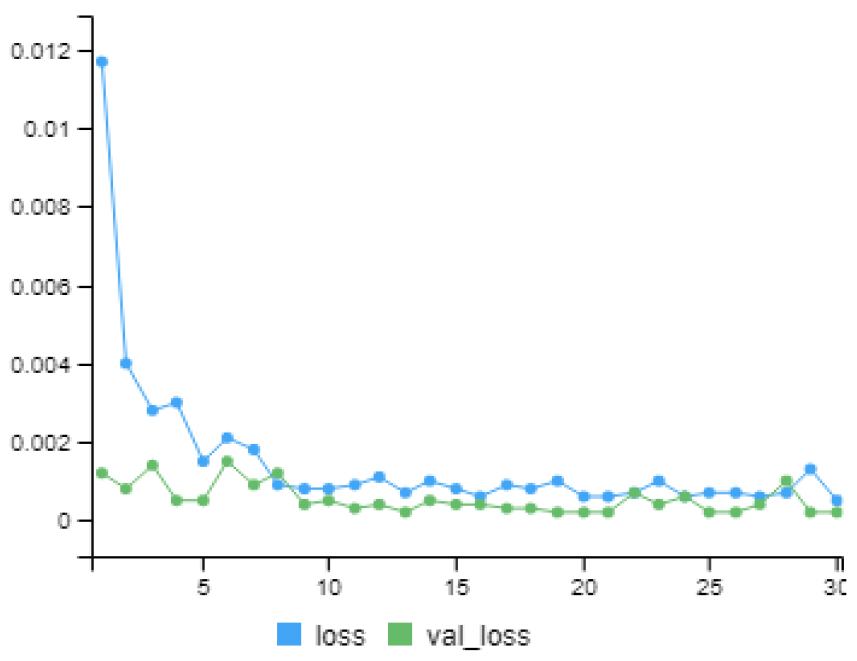
DNN 모형의 학습 과정은 Fig. 10에서 에포크당 Loss (MSE)가 줄어드는 과정을 표현하였다. 딥러닝 알고리즘을 학습할 때 가장 유의해야 할 부분이 과적합이기 때문에, Training data에서 약 20%를 Validation으로 활용하여 에포크 마다의 성능을 검증하였다. 그 결과 지속적으로 에포크가 증가할 때마다 Loss가 감소하는 것을 확인할 수 있었다. 또한 Validation data에서도 Loss가 감소하는 것을 확인할 수 있는데, 이는 모형이 과대 적합되지 않고 올바르게 학습되었음을 알 수 있다.
3.5 예측 성능 비교
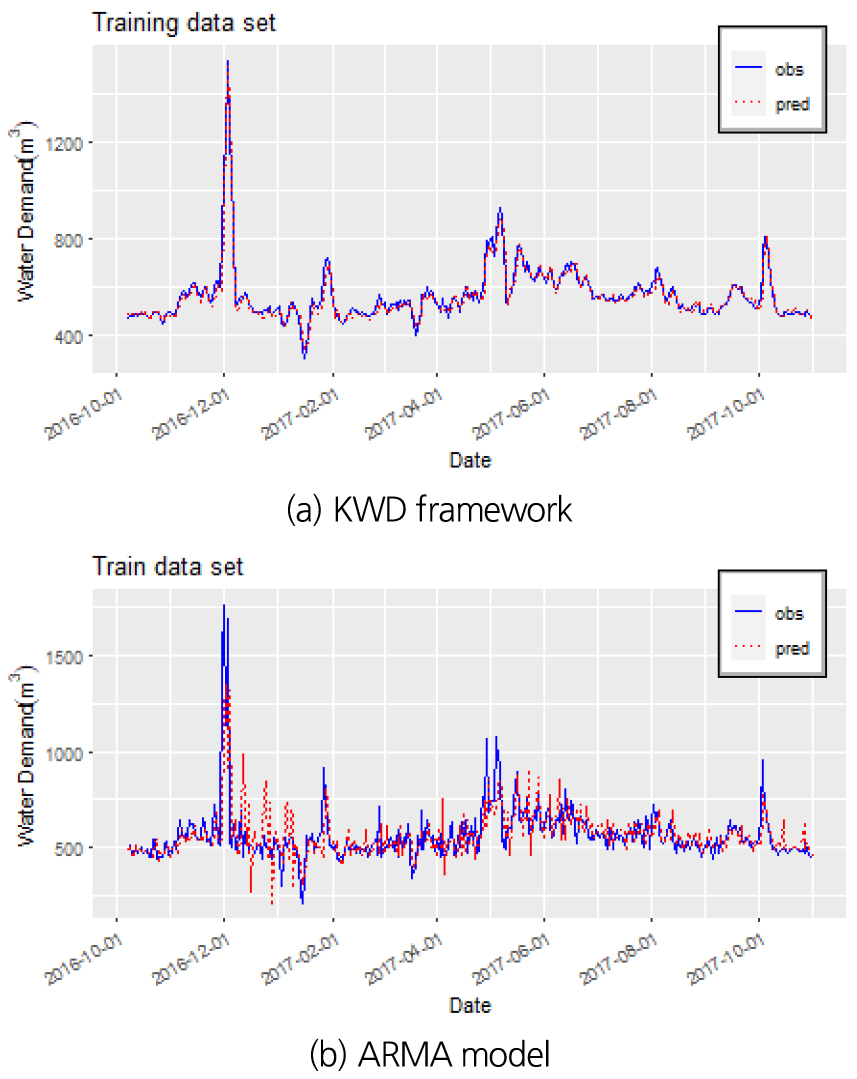
본 연구에서는 K-means, Wavelet, Deep learning 기법을 통해 물 사용량 예측을 위한 방법을 제안하였으며, 이를 KWD Framework라고 정의하였다. 기존에 비해 성능 개선 효과를 확인하기 위해 Fig. 11에서는 KWD Framework와 기존 시계열 예측 모형인 ARMA 모형을 학습한 결과를 표현하였다. 여기서 파랑색 실선은 관측값(obs), 빨강색 점선은 예측값(pred)로 표현하였다.
ARMA 모형은 자기회귀 모형 AR 모형과 이동평균 모형 MA 모형이 결합된 모형이며, 계절성을 추가적으로 고려할 수 있다. 본 연구에서는 Stepwise 방법을 통해 ARMA 모형에 대한 AIC를 최소화하는 AR 차수(p)와 MA 차수(q) 및 계절성을 도출하였다.
Fig. 12에서 Training data set의 시계열을 살펴 보면으로 수정 DNN 모형이 기존의 ARMA 모형보다 훨씬 예측 성능이 우수하게 나타난다. Tables 4 and 5에서는 각 모형의 성능을 정량적으로 비교하였다.
학습 결과를 살펴보면 기존 ARMA 모형의 성능보다 Proposed model의 성능이 개선된 것을 확인할 수 있다. 정밀한 검토를 위해 학습에 활용하지 않은 새로운 데이터 환경(Test data set)에서 모형을 검증하였다.
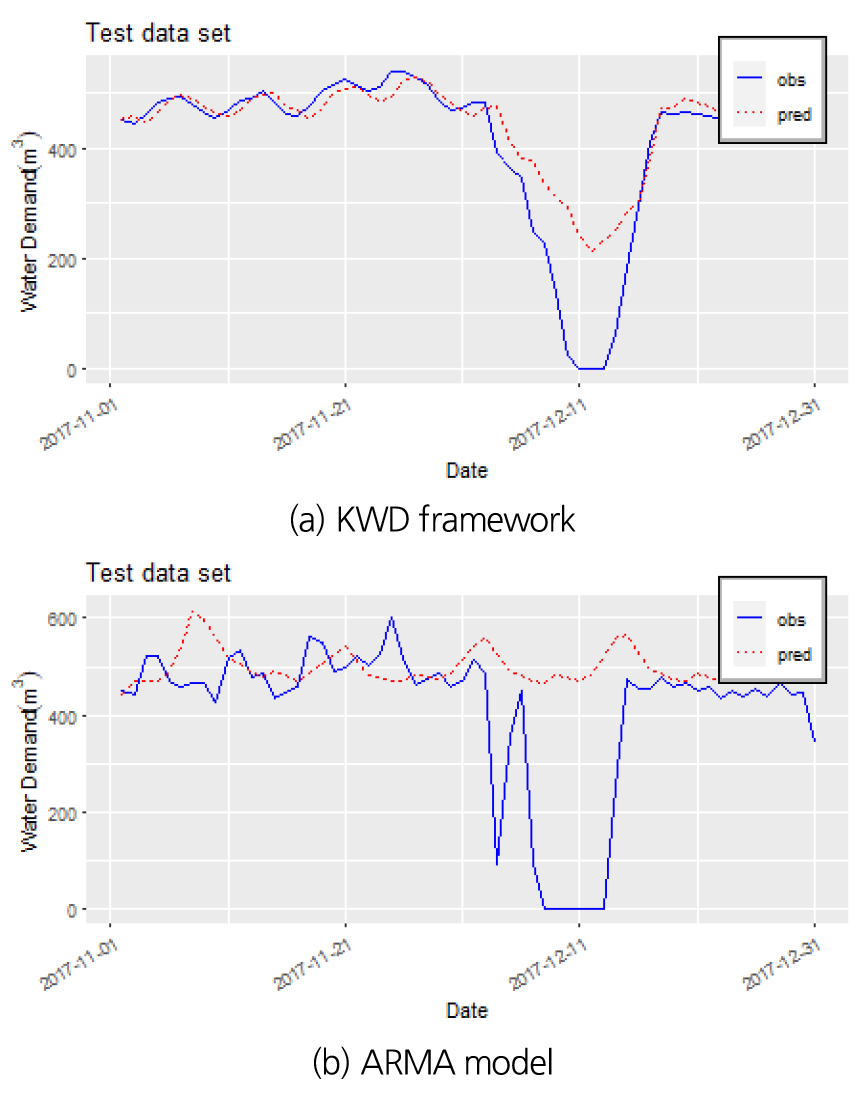
Fig. 13에서 Test data set의 시계열을 살펴보면 으로 수정 본 연구에서 제안한 KWD framework의 성능은 학습 구간과 유사한 성능을 보이는 반면, ARMA 모형은 성능이 현저하게 감소된 것을 확인할 수 있다. 그로 인해 기존 모형 대비 수용가 단위의 물 사용량 예측을 위해서는 본 연구에서 제안하는 모형이 성능이 좋다는 것을 입증하였다.
Table 4.
Evaluation for each model (training data)
| Model | CC | R2 | RMSE (m3) |
| Proposed model | 94.66% | 89.61% | 29.52 |
| ARMA | 62.70% | 39.31% | 121.11 |
4. 결 론
본 연구에서는 비선형적 특성을 내재하고 있는 수용가 단위의 물 사용량을 예측하기 위하여 K-means 군집분석, Wavelet 시계열 분해, Deep learning 알고리즘을 적용하였고, 앞서 언급한 일련의 과정을 KWD framework로 정의하였다. 또한 기존의 시계열 모형과 비교했을 때 성능을 비교하여 개선된 효과를 확인하였다. 분석 결과는 다음과 같이 요약하였다.
첫 번째로 군집분석 결과를 살펴보면 Group은 총 5개로 분류되었으며, Group B를 제외한 나머지 Group들은 모두 특성이 유사하기 때문에 위치기반으로 군집되었다. 반면 Group B는 가정용도가 아닌 일반용 및 학교용도로 등록되어 있으며 상대적으로 많은 양의 물을 사용하고 있기 때문에 타 Group과 특성이 상이한 것으로 나타났다.
두 번째 Wavelet 분석 결과를 살펴보면 원시자료의 시계열에서 총 8개의 시계열로 분해가 되었으며, 선행 연구를 참고하여 고주파수로 볼 수 있는 d1과 d2성분을 잡음성분으로 정의하였다. 또한 분해된 8개의 시계열에서 잡음성분을 빼고 다시 합산하였고, 조정된 시계열과 원시자료의 시계열을 비교하였다. 그 결과 원시자료의 핵심적인 주기패턴을 반영하고 있으며, 잡음성분이 올바르게 제거된 것을 확인하였다.
세 번째 Deep learning 알고리즘을 적용한 결과를 기존 시계열 모형인 ARMA 모형과 비교하였다. 본 연구에서 제안하는 모형은 학습구간에서 상관성이 약 95% 이상 , RMSE는 29.52 m3으로 나타났으며, ARMA 모형은 상관성이 62% , RMSE는 121.11 m3 으로 성능에서 차이가 두드러지는 것을 확인하였다. 추가적으로 새로운 환경에서의 검증을 위하여 Test data set에서 비교했을 때 제안된 모형은 상관성 92%, RMSE가 77.22 m3 로 성능이 유지되는 반면, ARMA 모형은 상관성 39%, RMSE 181.27 m3 로 나타났다. ARMA 모형은 학습 구간 대비 평가 구간에서 성능이 절반 정도로 감소한 것을 확인할 수 있다. 이 결과는 기존의 선형적 특성을 반영한 ARMA 모형이 학습구간에 과도하게 과대적합 되어 새로운 환경에서 예측 성능이 현저하게 감소하는 것으로 볼 수 있다.
본 연구에서는 선행 연구에서 비선형적 특성을 고려하기 위해 수행된 다양한 방법들을 연계하여 하나의 framework로써 제안하였다. 군집 분석은 유사한 수용가 단위의 패턴을 파악하기 위하여 고려하였고 Wavelet은 시계열 분해를 통해 잡음 성분을 제거하기 위하여 고려하였으며 비선형적 패턴을 학습하기 위해 Deep learning 알고리즘을 고려하였다. 그 결과 기존의 시계열 모형 대비 예측 성능이 월등히 개선된 것을 확인할 수 있었고, 이는 앞서 제시한 방식들은 수용가 단위의 비선형적 물 사용량 패턴을 파악하는데 더 용이하다는 결론을 도출할 수 있었다.
본 연구에서 제안하는 모형은 수용가 단위의 예측을 통해 공급량을 알 수 있고 최적의 공급 운영 방안을 수립하는데 활용될 수 있을 것이다. 또한 더 나아가 국가 차원의 전력 소비 및 에너지 절감에도 크게 기여를 할 수 있다고 판단된다.