Development of Life Cycle Carbon Emission Analysis for optimal low-carbon design of water distribution system

Yong Min Ryu; Eui Hoon Lee

doi:10.3741/JKWRA.2024.57.10.711

Preview

Research Article

Journal of Korea Water Resources Association. 31 October 2024. 711-723
https://doi.org/10.3741/JKWRA.2024.57.10.711

Development of Life Cycle Carbon Emission Analysis for optimal low-carbon design of water distribution system

상수관망 저탄소 최적 설계를 위한 Life Cycle Carbon Emission Analysis의 개발

Yong Min Ryu^a

Eui Hoon Lee^b^*

류 용민^a

이 의훈^b^*

^aPh.D. Candidate, Department of Civil Engineering, Chungbuk National University, Cheongju, Korea

^bAssociate Professor, School of Civil Engineering, Chungbuk National University, Cheongju, Korea

^a충북대학교 토목공학과 박사수료

^b충북대학교 토목공학부 부교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by/4.0):

©It is identical to the Creative Commons Attribution Non-commercial License (https://creativecommons.org/licenses/by/4.0)

ABSTRACT

Water distribution systems are important large-scale social infrastructure facilities for maintaining human society. Large-scale social infrastructure facilities are increasing due to urbanization and industrialization. However, one of the problems caused by the progress of urbanization and industrialization is carbon dioxide (CO₂) emissions. In this study, a Life Cycle Carbon Emission Analysis (LCCEA) model was proposed to analyze the amount of CO₂ generated during the life cycle of water distribution systems, such as installation, maintenance, and repair. Based on the proposed LCCEA model, low-carbon optimal design was performed and compared with cost-optimal design. As a result of applying the LCCEA model to domestic and international water distribution systems, the low-carbon optimal design showed a decrease in total and annual CO₂ emissions compared to the cost-optimal design. In addition, when CO₂ emissions were converted to costs and compared, the low-carbon optimal design showed better results in terms of cost. The LCCEA model can be applied to various water distribution systems as well as domestic and international water supply networks used in this study, and it will show good results in the design and operation of water distribution systems.

Keywords

Water distribution system

Life cycle

Carbon dioxide

Life cycle carbon emission analysis

low-carbon optimal design

상수관망은 대규모 사회기반시설물로 인간사회를 유지하기 위한 중요한 시설물이다. 도시화 및 산업화로 인해 대규모 사회기반시설물은 증가하고 있다. 그러나, 도시화 및 산업화의 진행으로 인해 발생하는 문제 중 하나는 온실가스의 배출이다. 본 연구에서는 상수관망을 설치 및 유지ㆍ보수 등 상수관망의 생애주기동안 발생하는 이산화탄소(CO₂)량을 분석하기 위해 Life Cycle Carbon Emission Analysis(LCCEA) 모델을 제안하였다. 제안된 LCCEA 모델을 기반으로 저탄소 최적설계를 진행하였으며, 이를 비용 최적설계와 비교하였다. 국내외 관망에 LCCEA 모델을 적용한 결과, 저탄소 최적설계안은 비용 최적설계안 대비 전체 및 연간 CO₂ 발생량이 감소하였다. 또한, CO₂ 배출량을 비용으로 환산하여 비교한 결과, 비용의 측면에서도 저탄소 최적설계안이 좋은 결과를 나타냈다. LCCEA 모델은 본 연구에서 적용한 국내외 관망뿐만이 아닌 다양한 관망에 적용할 경우, 상수관망 설계 및 운영에 좋은 결과를 나타낼 수 있을 것이다.

키워드

상수관망

생애주기

이산화탄소

Life Cycle Carbon Emission Analysis

저탄소 최적설계안

MAIN

1. 서 론
2. 연구방법
2.1 Life Cycle Carbon Emission Analysis (LCCEA)
2.2 Modified Hybrid Vision Correction Algorithm (MHVCA)
2.3 상수관망 비용 최적설계
2.4 상수관망 저탄소 최적설계
3. 연구결과
3.1 Goyang 관망
3.2 Zhejiang 관망
4. 결 론

1. 서 론

도시화 및 산업화의 진행으로 인해 용수에 대한 수요는 지속적으로 증가하고 있다(Yoon et al., 2012). 상수관망은 생활용수, 공업용수, 농업용수 및 비상용수 등을 공급하는 중요한 역할을 한다(Lee et al., 2015). 국내의 경우 상수관망의 총 연장 중 설치 후 21년 이상이 경과한 관은 약 88,871 km로 전체의 약 36.9%를 차지하고 있으며, 매년 신설 및 교체 등을 진행하고 있다(ME, 2023). 도시화로 인해 개발 및 유지보수가 필요한 상수관망과 같은 대규모 사회기반시설물에 대한 탄소 배출량을 산정 및 분석하는 것은 탄소 배출량 저감을 위해 필수적이다. 상수관망의 설계 목적에 따른 최적 설계안을 도출하기 위해 메타휴리스틱 최적화 알고리즘들을 적용하는 연구가 진행되었다(Reca et al., 2008; Chiplunkar et al., 1986; Geem et al., 2001; Jung et al., 2018; Lee, 2021). 상수관망의 최적 설계안을 도출하는 연구들 중 대부분은 상수관망 설계 시 초기 비용을 최소화하는 연구이다(Lee et al., 2018; Sangroula et al., 2022; Saldarriaga et al., 2020). 또한, 상수관망 내 설계비용 뿐만이 아닌 운영비용, 시스템 유지보수 비용, 시스템 고장지수, 소화를 위한 비상용수, 누수 및 수령(Water age) 등을 목적으로 한 연구가 진행되었다(Jayaram and Srinivasan, 2008; Fu et al., 2013; Shokoohi et al., 2017). 그러나, 기존의 연구들은 설계, 운영에 대한 비용, 용수공급 및 누수 및 수령과 같은 수질에 대해 중점적으로 연구를 진행하였다. 그러나, Intergovernmental Panel on Climate Change 등 전 세계적으로 진행하고 있는 탄소배출 저감과 관련하여 상수관망에 대한 탄소배출 저감 연구는 비용 및 수질을 목적으로 하는 연구보다 미비하다. 예를 들어, 초기 비용을 최소화하는 연구는 관의 비용만을 고려하기 때문에 상수관망의 매설부터 유지ㆍ보수 및 해체 시 발생하는 탄소 배출량 등을 고려하지 않는다. 상수관망을 구축 및 운영하기 위해서는 최초 구축뿐만이 아닌 유지ㆍ보수 및 해체까지 모두 고려하여 최적 설계안을 도출해야 한다. 상수관망 구축을 위해 필요한 자원을 추출, 가공 및 운반하여 시설물의 공사, 운영 및 해체에 사용되는 자원을 최소화하기 위해서는 생애주기에 따른 분석이 필수적이다.

생애주기는 임의의 물품 또는 시설물의 제조단계부터 해체단계까지의 전체 과정을 의미한다(Lee et al., 2015). 상수관망의 생애주기동안 고려해야하는 단계는 제조단계, 유지ㆍ보수단계 및 해체단계가 있다. 제조단계 및 해체단계의 경우 전체 시설물에 대한 정적인 상태를 분석하지만, 유지ㆍ보수단계의 경우 시간에 따라 변하는 관의 노후도를 기반으로 관의 파괴 등을 고려해야 한다. 생애주기를 기반으로 상수관망에 대한 생애주기비용 및 생애주기 분석에 대한 연구가 진행되었다(Kleiner et al., 1998; Lundie et al., 2004). 기존 연구들 중 Filion et al. (2004)의 경우 상수관망의 생애주기 동안 발생하는 에너지를 기반으로 상수관망 교체 빈도에 대한 시나리오를 수립 및 에너지 소비를 정량화하였다. Alsadi and Matthews (2020)은 관종에 따른 상수관망의 설치, 운영 및 폐기단계 동안 발생하는 환경적 영향 및 탄소발생량의 정량화에 대해 연구를 진행하였다. 해당 연구의 경우 PVC관이 다른 관종에 비해 환경에 영향을 적게 미치는 것으로 나타났다. Alsabri and Al-Ghamdi (2020)은 Polyvinylchloride (PVC), Polyethylene (PE) 및 Polypropylene (PP)를 기반으로 플라스틱 생산 공정의 수명주기 평가 및 탄소발생량을 분석하여 탄소발생량이 지구온난화에 미치는 환경적 영향을 분석하였다. 그러나, 기존의 연구들의 경우 상수관망의 생애주기기반 에너지 분석 및 탄소발생량 등에 대해 개별의 연구가 진행되었다. 상수관망과 같은 대규모 사회기반시설물을 운영하는 과정에서 탄소발생량을 감소시키기 위해서는 각 생애주기 단계별로 발생하는 탄소발생량을 분석하는 것이 필수적이다.

본 연구에서는 기존에 제안된 생애주기 단계의 개념을 기반으로 상수관망 저탄소 최적 설계를 위한 Life Cycle Carbon Emission Analysis (LCCEA) 모델을 제안하였다. 제안하는 LCCEA 모델은 상수관망의 설계부터 해체까지의 생애주기 단계에서 발생하는 이산화탄소량을 분석하고 정량화하는 모델이다. 기존의 연구들과 달리 상수관망을 구성하는 관의 관종에 따라 발생하는 이산화탄소량을 분석하는 모델을 통해 상수관망의 최적 생애주기를 분석하고자 한다. 또한, 관의 제작 및 해체 등을 포함하여, 매설시 발생하는 작업에 대한 이산화탄소량을 포함하여 분석하고자 한다. 최적 생애주기를 기반으로 발생하는 전체 및 생애주기 단계별 탄소발생량을 분석할 수 있는 모델을 기반으로 국내외 관망에 적용하여 최적 설계 결과를 비교하였다. 최적 설계안 도출을 위해 기존에 개발된 메타휴리스틱 최적화 알고리즘인 Modified Hybrid Vision Correction Algorithm (MHVCA)을 사용하였다(Ryu and Lee, 2023).

2. 연구방법

2.1 Life Cycle Carbon Emission Analysis (LCCEA)

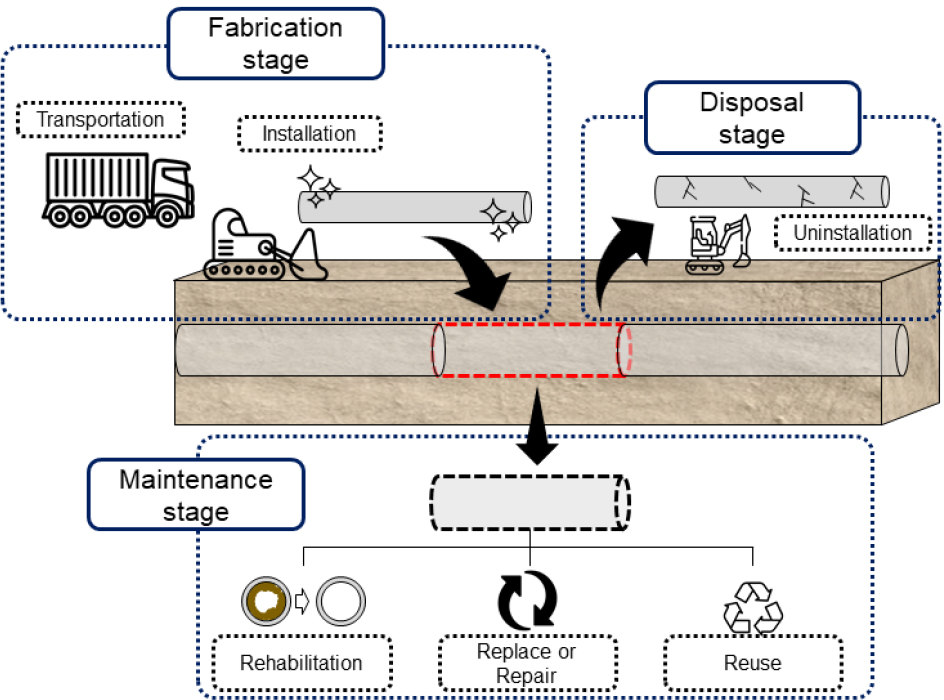
제안하는 LCCEA 모델은 상수관망의 생애주기 단계를 구분하여, 각 단계에 대해서 발생하는 이산화탄소(CO₂)량을 분석하는 모델이다. 상수관망의 생애주기 단계는 총 3가지로 구분하였다. 각 단계는 ① 상수관 제조단계(Fabrication stage), ② 상수관 유지ㆍ보수단계(Maintenance stage) 및 ③ 상수관 해체단계(Disposal stage)이다. Fig. 1은 상수관망 생애주기 단계를 개념적으로 나타낸 그림이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571006/images/kwra_57_10_06_F1.jpg

Fig. 1.

Schema of each stage in water distribution system

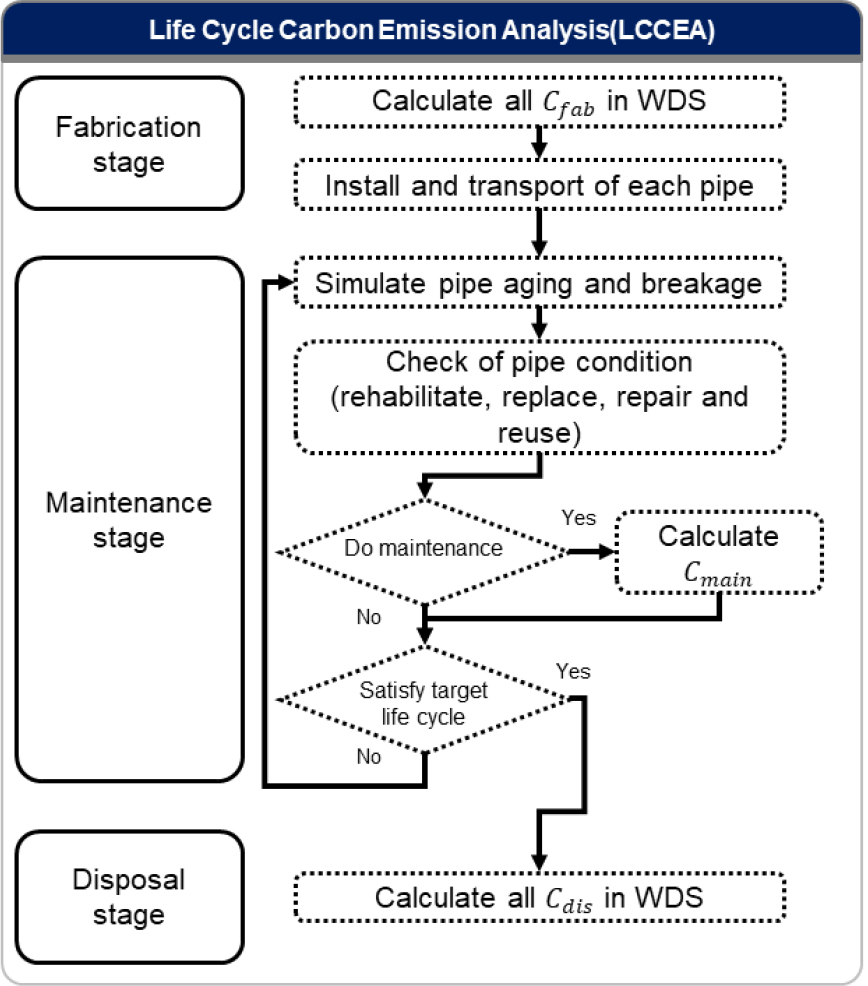
Fig. 1에 따르면, 생애주기의 각 단계는 세부적인 단계로 구성되어 있다. 제조단계의 경우 운송 및 설치 등, 유지ㆍ보수단계의 경우 갱생, 교체 및 재사용 등, 해제단계의 경우 해체가 있다. 생애주기의 각 단계를 LCCEA 모델로 구현하기 위해서 각 단계에 따른 과정을 분석하였다. 각 단계의 세부단계를 기반으로 LCCEA 모델을 구축하였다. Fig. 2는 LCCEA 모델의 흐름도이다.

Fig. 2에 따르면, 제조단계(Fabrication stage)에서는 상수관망에 필요한 각 관의 제조 및 설치 등의 과정에서 발생하는 CO₂ 발생량을 분석한다. 유지ㆍ보수단계(Maintenance stage)에서는 제조단계에서 제작된 관을 기반으로 시간 경과에 따른 모의를 진행한다. 상수관망의 경우 시간 경과에 따라 관의 부식 및 파괴로 인해 관의 갱생 및 교환 등 유지ㆍ보수가 필요하다. 유지ㆍ보수단계에서는 앞서 언급한 부분에 대해 모의를 진행하여, 유지ㆍ보수가 필요할 경우 개별 관에 대한 유지ㆍ보수 과정에서 발생하는 이산화탄소량을 분석한다. 해체단계에서는 상수관망의 생애주기가 끝났을 때 모든 관을 해체한다는 가정을 기반으로 이산화탄소량 분석을 진행한다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571006/images/kwra_57_10_06_F2.jpg

Fig. 2.

Flowchart of LCCEA

2.1.1 제조단계(Fabrication stage)

제조단계는 상수관망을 구성하고 있는 관을 제작 및 설치하는 단계이다. 따라서, 제조단계는 3가지 단계(제작, 운송 및 설치)로 분류할 수 있다. 관을 제조하기 위해서는 관의 내경뿐만이 아닌 관내 압력을 기반으로 관의 두께를 산정해야 한다. Piratla et al. (2012)은 다양한 관종의 파이프를 기반으로 직경에 따른 압력, 외경, 내경 및 관의 평균 두께 등을 나타냈다. Table 1은 관종별 표준 사양을 나타낸 표이다.

Table 1.

Standard specifications of pipes (Piratla et al., 2012)

Pipe material	PVC	PVC-O	HDPE	Ductile iron
Nominal diameter (mm)	200	200	200	200
Pressure (kPa)	1378.95	1620.27	1378.95	2413.16
Mean outside diameter (mm)	229.87	229.87	216.05	229.87
Mean inside diameter (mm)	194.82	215.14	167.39	217.17
Mean thickness (mm)	16.40	7.37	24.33	6.35
Density (kg/m)	17.26	8.18	15.02	31.40

Table 1을 기반으로 Hoop stress 공식을 활용하여 관내 허용 압력을 분석하였다. Eq. (1)은 Hoop stress 공식이다.

(1)

σ_{H o o p} = \frac{P \times D_{m}}{2 t}

여기서, $σ_{H o o p}$ 는 허용응력, $P$ 는 관내 압력, $D_{m}$ 는 관의 직경 및 $t$ 는 관의 두께이다.

본 연구에서는 다양한 관종 중 PVC 관을 사용한다는 가정을 기반으로 진행하였다. Table 1 및 Eq. (1)을 기반으로 PVC관의 관내 허용압력을 분석한 결과 약 8.190 MPa로 나타났다.

관을 제작 후 원하는 지점에 설치하기 위해서는 다양한 장비를 활용하여 작업을 진행해야 한다. Piratla et al.(2012)은 관을 일반적인 매설깊이 1.22 m에 매설하였을 경우 발생하는 작업 현장의 각 장비에 대한 CO₂ 배출량을 분석하였다. 연구결과를 활용하여 단위면적의 단위길이당 약 1,639.11 kg의 CO₂가 발생하는 것을 알 수 있다(Piratla et al., 2012).

2.1.2 유지ㆍ보수단계(Maintenance stage)

유지ㆍ보수단계는 상수관망 내 관이 시간 경과에 따라 노후되는 정도를 기반으로 유지ㆍ보수를 하는 단계이다. 유지ㆍ보수단계에서는 노후도에 따라, 관의 갱생 및 교체 등을 진행한다. Shamir and Howard (1979)는 관의 파괴가 지수함수형태로 발생한다는 것을 확인하였으며, 파손률 공식을 제안하였다. 해당 식은 Walski and Pelliccia (1982), Kleiner et al. (1998), Kleiner and Rajani (1999)에 의해서 식의 타당성을 검증하였다. 또한, 시간에 따라 변하는 관의 노후도에 대해서 Sharp and Walski (1988)는 Hazen-Williams 공식과 Darcy-Weisbach 공식 등을 통해 관의 노후도를 간단한 식으로 유도하였으며, Mononobe (1960)는 기존의 관망자료를 분석하여 노후도 산정 공식을 제안하였다. Lee et al. (2015)은 Mononobe (1960)가 제안한 식을 토대로 Hazen-Williams Coefficient (C)를 정량화하였다. Mononobe (1960)이 제안한 식은 Eq. (2)와 같다.

(2)

C_{y} = C_{0} {(1 - \frac{a \sqrt{y}}{D})}^{b}

여기서, C_y는 시간경과에 따른 Hazen-Williams 계수, C₀는 초기 Hazen-Williams 계수, D는 파이프의 직경(mm), y는 매설 또는 교체 후 경과년도, a 및 b는 파이프의 직경에 따른 계수이다.

Eq (2)의 a와 b는 Baek (2002)이 제안한 식을 통해 계산되었으며, a 및 b에 대한 식은 각각 다음과 같다.

(3)

a = 0.0961659 D + 1.15507

(4)

b = 0.723076 D^{- 0.0660117}

Mononobe (1960) 및 Baek (2002)이 제안한 Eqs. (2), (3), (4)의 경우 강관을 기준으로 제안된 식이다. 본 연구에서 CO₂ 발생량을 분석하기 위해 사용된 관종은 PVC관이다. 기존에 제안된 식의 경우 강관을 기준으로 산출된 실험식 및 계수이다. 본 연구에서는 PVC관과 강관의 시간경과에 따른 노후도 및 파이프 직경에 따른 계수가 동일하다는 가정을 수립하여 적용하였다. 본 연구에서는 다양한 상수관망에 LCCEA 모델을 적용하기 위해 상수관망을 구성하고 있는 관종에 따라 유지ㆍ보수 시기를 분석하였다. 국내 지방공기업법 시행규칙 제 19조 제 1항 제 1호에 따르면, PVC관의 경우 내용년수가 20년으로 규정되어 있다. 따라서, 본 연구에서는 관종의 직경별 시간이 20년 경과되었을 경우의 Hazen-Williams 계수를 기반으로 유지ㆍ보수시기를 선정하였다. 또한, 상수관망 내 관의 Hazen-Williams 계수가 유지ㆍ보수 기준에 부합할 경우 최초 1회에는 갱생을 진행하며, 2회의 경우 관을 교체하는 방법을 적용하였다(Lee et al., 2015). 관의 노후로 인해 최초 1회 갱생을 진행하는 경우, 관의 Hazen-Williams 계수는 초기 계수 대비 약 85% 회복하는 것으로 가정하였다(Lee et al., 2015).

2.1.3 해체단계(Disposal stage)

해체단계는 상수관망을 구성하고 있는 관의 생애주기 종료로 인해 해체하는 단계이다. 해제단계에서는 관을 해체하기 위해서 소비되는 과정에 대한 CO₂ 배출량을 분석한다. 본 연구에서는 해체단계에서 배출되는 CO₂를 관의 제조단계 중 매설하는 과정에서 발생하는 것과 동일하게 산정하였다. 관의 제조단계 중 매설하는 과정에서는 관 제작 시 발생한 CO₂ 및 매설하기 위해 발생하는 CO₂ 배출량을 분석하였다. 해체단계에서는 관을 제조하지 않고 매설과 동일하게 관을 해체 하기 때문에 해체 시 CO₂ 발생량은 관의 매설 시 CO₂ 발생량과 동일하게 가정하였다.

2.1.4 재사용단계(Reuse stage)

본 연구에서 제안한 LCCEA 모델은 상수관망을 하나의 큰 시스템으로 정의하였다. 관의 해체로 인해 발생하는 폐기물을 기반으로 재활용하여 상수관망 시스템 내에서 CO₂ 배출량이 저감되는 부분을 분석하고자 한다. 플라스틱 중 PVC의 재활용 관련 연구는 다양한 측면에서 진행되고 있다(Ditta et al., 2004; Garcia et al., 2006; Ito and Nagai, 2007; Keane, 2007, 2009; Buratet al., 2009; Kameda et al., 2010; Cho et al., 2010). 2017년을 기준으로 PVC 폐기물 총량 약 250 만톤 중 639,648톤이 재활용되었으며, 이는 전체 폐기물의 약 25%이다(VinyPlus, 2018). Janajreh et al. (2015)에 따르면, PVC 폐기물을 기반으로 재활용된 샘플이 원래의 샘플보다 유연성을 일부 잃는 것을 확인하였으나, 원래 샘플보다 더 단단해진다는 것을 확인하였다. 본 연구에서는 상수관망 시스템 내에서 관의 노후로 인해 발생한 PVC 폐기물을 기반으로 재사용을 통해 제조과정에서 CO₂ 발생량의 이득(감소)을 얻는 것으로 가정하였다. 상수관망 시스템에서 재사용을 통해 얻는 이득은 약 25%로 가정하였다.

2.2 Modified Hybrid Vision Correction Algorithm (MHVCA)

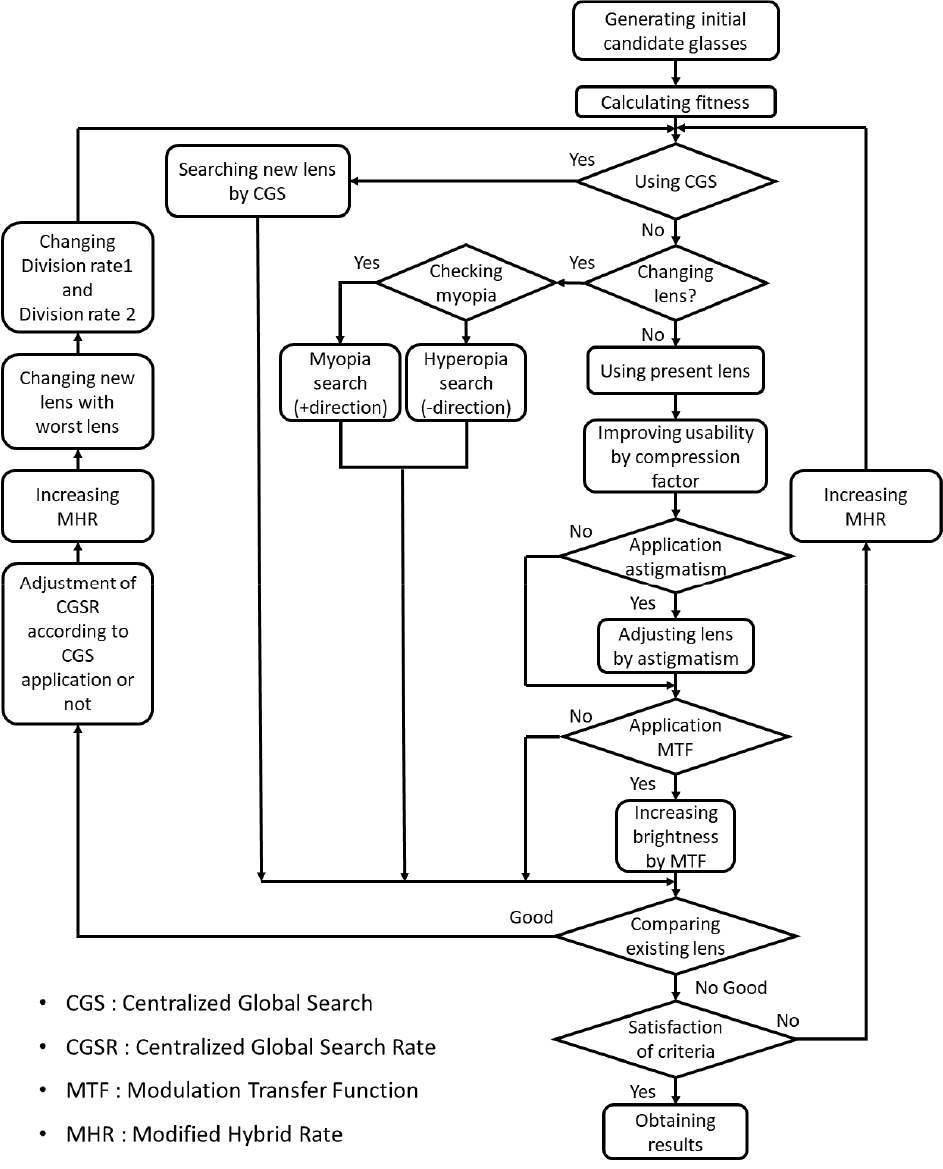
MHVCA는 메타휴리스틱 최적화 알고리즘 중 하나로 상수관망 최적설계에 좋은 성능을 나타낸 알고리즘이다(Ryu and Lee, 2023). Fig. 3은 MHVCA의 연산과정을 나타낸 그림이다.

Fig. 3에 따르면, MHVCA는 중앙집중형탐색(Centralized Global Search) 기반 연산 과정을 활용한 최적해 탐색 및 시력교정과정을 착안한 Vision Correction Algorithm 기반 연산과정을 활용한 최적해 탐색을 진행한다. MHVCA의 가장 큰 특징은 유동적인 탐색방법의 선택이다. MHVCA는 반복시산이 진행되면서 현재 시산의 최적해가 탐색된 연산과정의 선택 확률을 증가시키는 구조로 구성되어 있다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571006/images/kwra_57_10_06_F3.jpg

Fig. 3.

Flowchart of MHVCA

2.3 상수관망 비용 최적설계

상수관망 비용 최적설계는 설계의 목표가 비용 최소화이다. 상수관망을 설계하는 과정에서 관망 내 절점 간 필요한 관의 선택을 통해 최종적으로 상수관망 전체의 비용을 분석한다(Ryu and Lee, 2022). 본 연구에서는 상수관망 비용 최적설계와 함께 상수관망 탄소발생랑 최적설계를 진행한다. 두 가지 최적설계안의 비교를 통해 각 최적설계를 진행하였을 경우에 대한 CO₂ 발생량 결과를 분석하고자 한다. Eq. (5)는 본 연구에서 사용된 상수관망 비용 최적설계 목적함수이다.

(5)

M i n C o s t = \sum_{p i = 1}^{N} C_{c o s t} (D_{p i p}) \times L_{p i p} + \sum_{j = 1}^{M} P_{j} P_{j} = α (h_{\min} - h_{j}) + β, i f h_{\min} > h_{j}

여기서 $C_{c o s t}$ 는 단위 길이당 비용, $L_{p i p}$ 는 $p i p$ 관의 길이, $D_{p i p}$ 는 $p i p$ 관의 직경이다. $N$ 은 관의 수, $M$ 은 절점의 수, $P_{j}$ 은 패널티 함수이다. $h_{j}$ 는 절점 $j$ 의 수압이며, $h_{\min}$ 은 절점의 최소요구수압이다. $P_{j}$ 는 최소요구수압을 만족하지 않는 경우 설계안을 자연적으로 도태시키기 위해 부여하는 패널티이며, 𝛼, 𝛽는 적용하고자 하는 관망별 패널티 함수의 계수이다.

2.4 상수관망 저탄소 최적설계

상수관망 저탄소 최적설계는 설계의 목표가 관망의 생애주기 동안의 CO₂ 발생량 최소화이다. 상수관망의 생애주기동안 초기 설계된 설계안을 기반으로 각 단계별 발생하는 CO₂ 발생량을 분석한다. Eq. (6)은 본 연구에서 사용된 상수관망 저탄소 최적설계 목적함수이다.

(6)

M i n C O_{2} = \sum_{p i = 1}^{N} [C_{f a b} + (C_{m a i n} - C_{r e u}) + C_{d i s}] / L C + \sum_{j = 1}^{M} P_{j} P_{j} = α (h_{\min} - h_{j}) + β, i f h_{\min} > h_{j}

여기서, $C_{f a b}$ 는 제조단계에서 발생한 CO₂ 발생량, $C_{m a i n}$ 는 유지ㆍ보수단계에서 발생한 CO₂ 발생량, $C_{r e u}$ 는 재사용단계에서 발생한 CO₂ 이득량, $C_{d i s}$ 는 해체단계에서 발생한 CO₂ 발생량이다. $P_{j}$ 는 최소요구수압을 만족하지 않는 경우 설계안을 자연적으로 도태시키기 위해 부여하는 패널티이며, 𝛼, 𝛽는 적용하고자 하는 관망별 패널티 함수의 계수이다. 패널티함수의 경우 Eq. (5)에서 사용된 함수와 동일하게 설정하였다.

상수관망 저탄소 최적설계안과 상수관망 비용 최적설계안간의 비교를 위해 각 최적설계안을 탐색하는 과정에서 CO₂ 배출량 및 비용을 산정하였다. 상수관망 저탄소 최적설계안의 도출과정은 상수관망 비용 최적설계안 도출의 과정과 동일하며 과정은 다음과 같다.

① 관종별 내용년수에 따른 Hazen-Williams 계수 분석 및 유지ㆍ보수 시점 선정

② 상수관망의 설계안 탐색

③ 탐색된 설계안 기반 $C_{f a b}$ 산정

④ 매설 경과 년수에 따른 개별 상수관 노후도(Hazen-Williams 계수) 분석

⑤ 매설된 개별 관의 연간 노후도(Hazen-Williams 계수) 및 ①단계에서 분석된 유지ㆍ보수 시점 기반 관 갱생(또는 교체), 재활용 및 해체 모의

⑥ 상수관 노후도(Hazen-Williams 계수)에 따른 연간 $C_{m a i n}$ , $C_{r e u}$ 및 $C_{d i s}$ 산정 및 생애주기 산정(생애주기의 경우, 연간 배출되는 CO₂량을 분석하여, 가장 낮은 CO₂ 배출량이 발생하는 년도를 최적 생애주기로 산정)

⑦ 생애주기에 따른 총 탄소량( $C_{f a b}$ , $C_{m a i n}$ , $C_{r e u}$ 및 $C_{d i s}$ ) 및 설계시 상수관망에 따른 설계 비용 산정

⑧ ②∼⑦과정 반복 및 최적 설계안 제시(저탄소 최적설계의 경우, 목적이 탄소량 최소화이며, 비용 최적설계의 경우, 목적이 비용의 최소화이다.)

총 8단계의 과정을 통해 상수관망 저탄소 최적설계안 및 비용 최적설계안을 도출한 후 결과를 비교하였다. 일반적인 상수관망 비용 최적설계안 도출과정은 최초 설치된 관망을 고려하여 분석 및 비교를 진행한다. 본 연구에서는 상수관망 비용 최적설계안과 상수관망 저탄소 최적설계안을 비교하였다. 각 설계안의 최초 설치시 비용을 비교하였으며, 최초 설치, 유지ㆍ보수, 재활용 및 해체 등으로 인해 발생하는 CO₂량을 검토하였다.

3. 연구결과

본 연구에서 제안된 LCCEA 모델을 기반으로 상수관망 최적설계에 적용하여 상수관망의 생애주기 동안 발생하는 CO₂ 발생량을 분석하였다. 상수관망 비용 최적설계안과 LCCEA 모델 기반 저탄소 최적설계안 간의 생애주기에 대한 CO₂ 발생량을 비교하기 위해 Goyang 관망 및 Zhejiang 관망에 적용하였다. 상수관망 최적설계를 위해 미국 환경청에서 개발한 소프트웨어인 EPANET 2.0과 Visual Basic 6.0을 연동하여 모의하였다(US EPA, 2000).

3.1 Goyang 관망

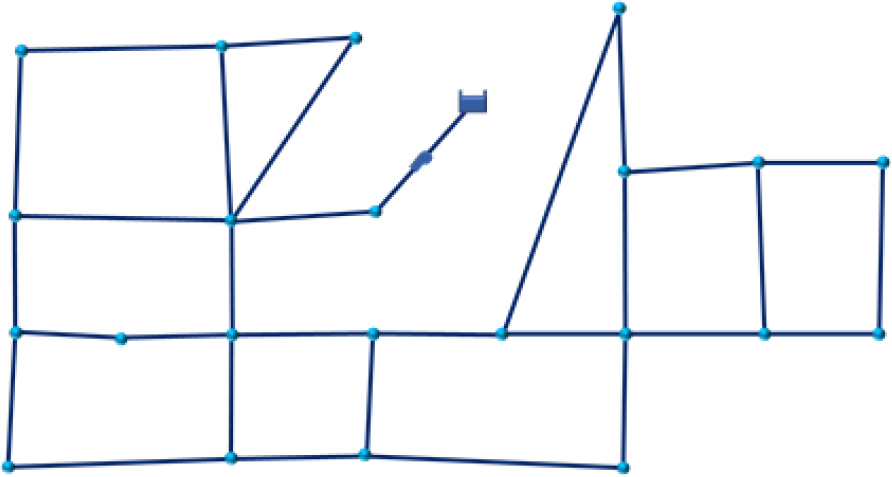
본 연구에서 제안한 LCCEA 모델을 국내에 위치하고 있는 Goyang 관망에 적용하여 CO₂ 배출량을 분석하였다. Fig. 4는 Goyang 관망의 형태이다.

Fig. 4에 따르면, Goyang 관망의 경우 하나의 저류지, 25개의 절점 및 30개의 관으로 구성되어 있다. Table 2는 Goyang 관망 내 절점의 수요량을 나타낸 표이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571006/images/kwra_57_10_06_F4.jpg

Fig. 4.

Layout of Goyang network

Table 2.

Demand by node in Goyang network

Node No.	Demand (l/s)	Node No.	Demand (l/s)
1	0.000	12	0.434
2	1.771	13	0.434
3	0.816	14	0.729
4	0.677	15	5.156
5	0.868	16	1.250
6	0.781	17	0.920
7	0.729	18	0.642
8	0.556	19	1.372
9	0.486	20	1.441
10	0.347	21	0.365
11	0.486	22	9.253

Goyang 관망의 경우 Table 2와 같이 절점별 수요량을 기반으로 생애주기동안 고정된 수요량으로 설정하여 모의하였다. Goyang 관망의 각 절점별 최소요구수압은 15 m이며, Hazen-Williams 계수는 110이다. 각 절점별 최소요구수압을 만족하지 못할 경우 적용하는 패널티함수의 𝛼 및 𝛽는 각각 10²⁰ 및 10⁷로 설정하였다. Goyang 관망의 설계안 중 가장 높은 비용을 나타내는 설계안은 약 329,726$이다. 관망의 절점 중 최소요구수압을 하나의 절점이라도 만족하지 못할 경우 패널티를 부여하여 설계 후보군들에서 도태시키기 위해 최소 약 10,000,000$의 패널티가 부여되게 설정하였다. Table 3은 Goyang 관망을 설계하기 위해 사용된 관의 직경별 단위길이당 비용이다.

Table 3과 Piratla et al. (2012)의 연구결과 및 Hoop stress 공식을 기반으로 Goyang 관망에 필요한 관별 두께를 산정하였다. 관별 두께를 기반으로 단위면적을 산정하였다. Table 4는 Piratla et al. (2012)이 제시한 다양한 관종에 대한 직경에 따른 압력, 외경, 내경, 평균 두께 및 밀도이다.

Table 3.

Cost of pipe per diameter for Goyang network

Internal diameter (mm)	Cost ($/m)	Internal diameter (mm)	Cost ($/m)
80	37.890	200	47.624
100	38.933	250	54.125
125	40.563	300	62.109
150	42.554	350	71.524

Table 4.

Standard specifications of pipe (Piratla et al., 2012)

Pipe material	Pressure (kPa)	Mean outside diameter (mm)	Mean inside diameter (mm)	Mean thickness (mm)
PVC	1,378.95	229.78	194.82	16.40
PVC-O	1,620.27	229.78	215.14	7.37
HDPE	1,378.95	216.05	167.39	24.33
Ductile iron	2,413.16	229.87	217.17	6.35

다음은 Recio et al. (2005)가 제안한 관경에 따른 제원 및 직경에 따른 CO₂ 배출량이다.

Table 5에 따르면, PVC관의 경우 관의 제조시 단위 면적에 따라 약 0.3094g-CO₂ 만큼의 탄소량이 배출된다는 것을 알 수 있다. Table 6은 Goyang 관망을 설계하기 위해 사용되는 관의 직경에 따른 제원을 분석한 표이다.

Table 5.

Characteristics of the standard pipes (Recio et al., 2005)

Pipe material	Inner diameter (mm)	Outer diameter (mm)	Production of pipe (kg-CO₂)
PVC RD315	299.6	315	6.9 (3 m of pipe)

Table 3 및 6을 기반으로 Goyang 관망의 최적설계를 진행하였다. 최적설계안을 도출하기 위해 MHVCA를 사용하였으며 최적설계를 총 30회 진행 및 최적설계안을 선정하였다. MHVCA의 매개변수는 민감도 분석을 통해 적용하였다. Table 7은 Goyang 관망의 최적설계를 위해 설정한 MHVCA의 매개변수를 나타낸 표이다.

Table 6.

Specifications of each pipe for Goyang network

Internal diameter (mm)	External diameter (mm)	Surface area (mm²)	CO₂ emission (kg-CO₂)
80	93.470	1,835.134	0.568
100	116.837	2,867.397	0.887
125	146.046	4,480.308	1.386
150	175.256	6,451.644	1.996
200	233.674	11,469.589	3.549
250	292.093	17,921.234	5.545
300	350.511	25,806.576	7.985
350	408.930	35,125.618	10.868

Table 7.

Parameter setting of MHVCA for optimal design of Goyang network

Parameter	MHVCA
Candidate glasses	190
Centralized global search rate	0
Division rate1	0.1
Division rate2	0.7
Compression factor	50
Astigmatic correction	30

Table 7에 따르면, Candidate glasses는 알고리즘 내 저장공간이며, Centralized global search rate는 중앙집중형 탐색을 실행하는 확률, Division rate는 지역탐색 방향을 설정하는 매개변수, Compression factor 및 Astigmatic Correction은 MHVCA 내 연산과정의 방향 및 범위를 조정하는 매개변수이다. 최적설계 목적에 따라 가장 좋은 결과를 기반으로 비용 최적설계안과 저탄소 최적설계안을 비교하였다. 최적 설계안 간의 전체 CO₂ 배출량(Total CO₂ emission), 연간 CO₂ 배출량(Total CO₂ emission per year), 생애주기(Life cycle), 제조 시 CO₂ 배출량(Carbon emission of fabrication, C_f), 교체 시 CO₂ 배출량(Carbon emission of replacement, C_re), 관 파괴에 따른 수리 시 CO₂ 배출량(Carbon emission of repair, C_rp), 갱생 시 CO₂ 배출량(Carbon emission of rehabilitation, C_reh), 재사용 시 CO₂ 배출량(Carbon emission of reuse, C_reuse) 및 해체 시 CO₂ 배출량(Carbon emission of disposal, C_d)을 비교하였다. 본 연구에서 비교한 비용 최적설계안(Cost optimal design)의 경우, 비용만을 고려하여 최소의 비용이 요 optimal design)의 경우, CO₂ 발생량만을 고려하여 최소의 CO₂발생량이 나타나는 최적설계안이다. Table 8은 Goyang 관망의 최적설계안을 비교한 표이다.

Table 8에 따르면, 연간 CO₂ 배출량의 경우 저탄소 최적설계안이 더 낮은 것을 알 수 있다. 관의 제조단계에서 발생한 C_f 및 C_re에 따르면, 저탄소 최적설계안이 비교적 더 높게 나타난 것을 알 수 있다. 또한, C_reuse이 저탄소 최적설계안이 낮은 것을 알 수 있다. 그러나, 저탄소 최적설계안의 경우 C_reh 및 C_p는 비용 최적설계안보다 낮았다. 이를 통해 저탄소 최적설계안의 경우 비용 최적설계안과 달리 관의 제조시에 약 16.834 kg-CO₂만큼의 CO₂를 많이 배출했으나, 유지ㆍ보수 및 해체단계에서 CO₂ 배출량이 약 83.095kg-CO₂만큼 낮은 것으로 나타났다. 동일한 생애주기 중 저탄소 최적설계안의 경우 매년 약 4.201 kg-CO₂만큼의 CO₂ 배출량이 저감되었으며, 전체 생애주기 동안에는 약 67.218 kg-CO₂만큼의 CO₂ 배출량이 저감되었다.

Table 8.

Comparison between cost-optimal design and low-carbon optimal design (Goyang network)

	Cost optimal design	Low-carbon optimal design
Total CO₂ emission per year (kg-CO₂/yr)	1,450.185	1,445.984
Cost per year ($/yr)	11,063.147	11,066.556
Life cycle (yr)	16	16
C_f (kg-CO₂)	3,350.982	3,367.816
C_re (kg-CO₂)	12,686.213	12,751.867
C_rp (kg-CO₂)	0.000	0.000
C_reh (kg-CO₂)	9,464.305	9,265.972
C_reuse (kg-CO₂)	2,366.076	2,316.493
C_d (kg-CO₂)	67.533	66.577
Total CO₂ emission (kg-CO₂)	23,202.957	23,135.739
Cost ($)	177,010.359	177,064.903

비용의 측면에서는 저탄소 최적설계안이 더 높은 결과를 나타냈다. 비용 최적설계안 대비 저탄소 최적설계안의 CO₂ 저감량을 비용으로 환산하여 결과를 분석하였다. 에너지 경제연구원 및 한국응용통계연구원의 통계 결과를 기반으로, 관망을 설치하기 위해 사용하는 기계 및 기타 에너지를 발산하는 장치의 연료를 유류로 가정하였다. 가정 사항을 기반으로 최적 설계안 간 CO₂ 저감량을 비용으로 환산한 결과, 전체 CO₂ 배출량의 저감으로 인해 약 4,439.56$만큼의 이득이 있었으며, 연간 277,47$만큼의 이득이 있었다.

비용 최적설계안 및 저탄소 최적설계안의 생애주기를 기반으로 제조, 교체, 수리, 갱생, 재사용 및 해체 시 CO₂ 발생량을 분석하였다. Fig. 5는 생애주기를 기반으로 연간 발생하는 제조, 교체, 수리, 갱생, 재사용 및 해체 시 CO₂ 발생량을 나타낸 그림이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571006/images/kwra_57_10_06_F5.jpg

Fig. 5.

CO₂ emissions per year based on life cycle (Goyang)

Fig. 5에 따르면, 제조 및 교체 시에는 저탄소 최적설계안의 CO₂ 발생량이 높았으나, 갱생시 저탄소 최적설계안의 CO₂ 발생량이 비용 최적설계안보다 낮은 것을 알 수 있다. 갱생과정에서 발생하는 CO₂가 저탄소 최적설계를 진행하였을 경우 비용 최적설계안보다 약 2.1%정도 감소되어 상대적으로 낮은 CO₂ 발생량이 나타난 것을 알 수 있다. 갱생과정에서 발생한 CO₂의 감소는 전체 시스템에 대해 갱생 횟수가 적다는 것을 의미한다. Goyang 관망에서 생애주기에 따른 CO₂ 발생량 중 유지ㆍ보수단계의 경우 약 85%를 차지하고 있으며, 갱생의 경우 약 42%를 차지하고 있다. 이를 통해 유지ㆍ보수 단계 중 갱생과정의 경우 CO₂ 발생량에 대한 많은 영향을 미치는 것을 알 수 있다. 따라서, 갱생과정에서 감소된 CO₂ 발생량을 통해 상수관망 저탄소 최적설계안의 경우, 비용 최적설계안보다 유지ㆍ보수 단계를 줄일 수 있다는 장점이 있다.

3.2 Zhejiang 관망

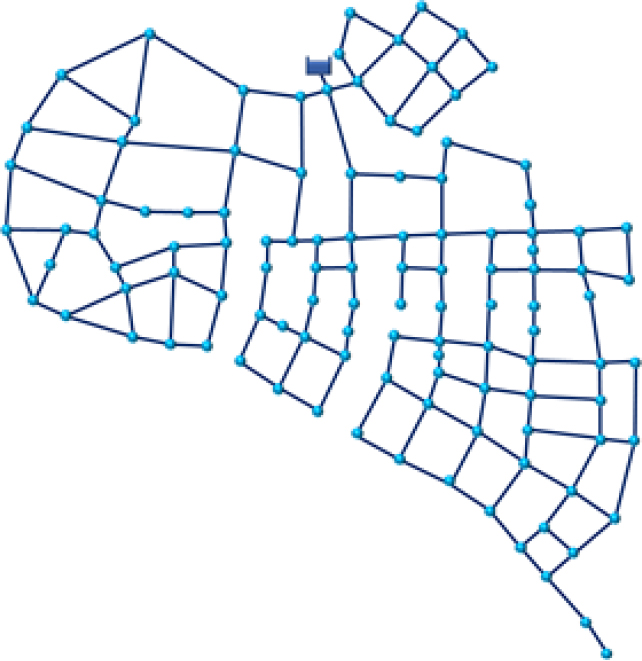
국내 적용 결과를 기반으로 국외 관망에 LCCEA를 적용하기 위해 중국에 위치하고 있는 Zhejiang 관망에 적용하였다. Fig. 6은 Zhejiang 관망의 형태이다.

Fig. 6에 따르면, Zhejiang 관망의 경우 하나의 저류지, 113개의 절점 및 164개의 관으로 구성되어 있다. Table 9는 Zhejiang 관망 내 절점의 수요량을 나타낸 표이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571006/images/kwra_57_10_06_F6.jpg

Fig. 6.

Layout of Zhejiang network

Zhejiang 관망의 경우 Table 9와 같이 절점별 수요량이 나타나있으며, 생애주기동안 고정된 수요량으로 설정하여 모의하였다. Zhejiang 관망의 각 절점별 최소요구수압은 22m이며, Hazen-Williams 계수는 130이다. 각 절점별 최소요구수압을 만족하지 못할 경우 적용하는 패널티함수의 𝛼 및 𝛽는 각각 10²⁰ 및 10¹⁰으로 설정하였다. Zhejiang 관망의 설계안 중 가장 높은 비용을 나타내는 설계안은 약 53,948,977$이다. 관망의 절점 중 최소요구수압을 하나의 절점이라도 만족하지 못할 경우 패널티를 부여하여 설계 후보군들에서 도태시키기 위해 최소 약 10,000,000,000$의 패널티가 부여되게 설정하였다. Table 10은 Zhejiang 관망을 설계하기 위해 사용된 관의 직경별 단위길이당 비용이다.

Table 9.

Demand by node in Zhejiang network

Node No.	Demand (l/s)	Node No.	Demand (l/s)	Node No.	Demand (l/s)
1	25.00	39	22.45	77	29.69
2	34.05	40	31.73	78	38.23
3	32.93	41	59.19	79	98.64
4	30.52	42	46.83	80	68.23
5	73.38	43	33.70	81	45.33
6	55.95	44	22.53	82	87.61
7	119.87	45	22.06	83	27.97
8	28.25	46	24.51	84	50.04
9	40.13	47	21.13	85	95.49
10	32.86	48	20.27	86	94.66
11	52.07	49	36.82	87	80.23
12	33.28	50	56.30	88	85.17
13	124.01	51	59.13	89	245.52
14	27.67	52	35.86	90	63.24
15	61.54	53	28.54	91	30.03
16	18.45	54	44.65	92	23.50
17	73.14	55	18.40	93	133.34
18	39.22	56	53.24	94	34.76
19	13.15	57	34.73	95	55.02
20	25.56	58	58.81	96	35.96
21	86.02	59	77.97	97	86.73
22	58.90	60	61.95	98	47.11
23	42.38	61	70.68	99	36.17
24	65.64	62	21.56	100	72.68
25	57.84	63	17.12	101	39.17
26	39.74	64	31.01	102	40.04
27	102.51	65	21.44	103	50.11
28	24.80	66	49.63	104	92.70
29	23.81	67	30.67	105	57.36
30	37.18	68	25.58	106	17.17
31	40.31	69	15.47	107	4.64
32	35.14	70	17.18	108	18.26
33	50.07	71	31.63	109	47.86
34	55.19	72	30.90	110	0.00
35	43.86	73	16.73	111	73.50
36	75.77	74	30.89	112	46.51
37	37.74	75	34.59	113	105.32
38	69.01	76	96.22	-	-

Table 10.

Cost of pipe per diameter for Zhejiang network

Internal diameter (mm)	Cost ($/m)	Internal diameter (mm)	Cost ($/m)
150	24.530	500	134.024
200	35.200	600	180.158
250	47.388	700	234.740
300	61.160	750	261.228
350	76.450	800	291.742
400	93.610	900	355.322
450	113.784	1,000	426.690

Table 10과 Piratla et al. (2012)의 연구결과 및 Hoop stress 공식을 기반으로 Zhejiang 관망에 필요한 관별 두께를 산정하였다. Table 11은 Zhejiang 관망을 설계하기 위해 관의 직경에 따른 제원을 분석한 표이다.

Table 11.

Specifications of each pipe for Zhejiang network

Internal diameter (mm)	External diameter (mm)	Surface area (mm²)	CO₂ emission (kg-CO₂)
150	175.256	6,451.644	1.996
200	233.674	11,469.589	3.549
250	292.093	17,921.234	5.545
300	350.511	25,806.576	7.985
350	408.930	35,125.618	10.868
400	467.348	45,878.358	14.195
450	525.767	58,064.797	17.965
500	584.185	71,684.934	22.180
600	701.022	103,226.305	31.939
700	817.859	140,502.471	43.472
750	876.278	161,291.102	49.904
800	934.696	183,513.431	56.780
900	1,051.533	232,259.186	71.862
1,000	1,168.370	286,739.736	88.718

Table 10 및 11을 기반으로 Zhejiang 관망의 최적설계를 진행하였다. MHVCA의 매개변수는 민감도 분석을 통해 적용하였다. MHVCA를 활용하여 최적설계를 총 30회 진행하였다. MHVCA의 매개변수는 민감도 분석을 통해 적용하였다. MHVCA를 활용하여 최적설계를 총 30회 진행하였다. Table 12는 Goyang 관망의 최적설계를 위해 설정한 MHVCA의 매개변수를 나타낸 표이다.

Table 12.

Parameter setting of MHVCA for optimal design of Zhejiang network

Parameter	MHVCA
Candidate glasses	190
Centralized global search rate	0
Division rate1	0.1
Division rate2	0.7
Compression factor	50
Astigmatic correction	45

Table 13는 Zhejiang 관망의 최적설계안을 비교한 표이다.

Table 13.

Comparison between cost-optimal design and low-carbon optimal design (Zhejiang network)

	Cost optimal design	Low-carbon optimal design
Total CO₂ emission per year (kg-CO₂/yr)	399,069.996	314,607.083
Cost per year ($/yr)	402,364.516	317,586.848
Life cycle (yr)	16	22
C_f (kg-CO₂)	893,844.674	982,136.944
C_re (kg-CO₂)	3,688,775.272	3,971,561.576
C_rp (kg-CO₂)	0.000	0.000
C_reh (kg-CO₂)	2,380,327.978	2,598,385.235
C_reuse (kg-CO₂)	595,081.994	649,596.309
C_d (kg-CO₂)	17,254.003	18,868.382
Total CO₂ emission (kg-CO₂)	6,385,119.932	6,921,355.828
Cost ($)	6,437,832.258	6,986,910.656

Table 13에 따르면, 연간 CO₂ 배출량의 경우 저탄소 최적설계안이 더 낮은 것을 알 수 있다. 또한, 생애주기의 경우 저탄소 최적설계안이 비용 최적설계안보다 6년 더 긴 것을 확인할 수 있다. 관의 제조단계에서 발생한 C_f 및 C_re, 유지ㆍ보수단계에서 발생한 C_reh 및 해체단계에서 발생한 C_d가 저탄소 최적설계안이 비교적 더 높게 나타난 것을 알 수 있다. 그러나, C_reuse가 저탄소 최적설계안이 높은 것을 알 수 있었다.

전체적인 CO₂ 배출량이 비용 최적설계안이 높았으나, 저탄소 최적설계안은 생애주기가 더 긴 것을 알 수 있다. 생애주기는 상수관망 시스템을 사용할 수 있는 기간이다. 생애주기를 통해 저탄소 최적설계안은 비용 최적설계안보다 더 오랜 기간 사용이 가능하다는 것을 알 수 있다. 생애주기가 긴 저탄소 최적설계안은 비용 최적설계안보다 오래 사용하기 때문에 제조, 유지ㆍ보수 및 해체단계의 CO₂ 배출량이 많은 것을 알 수 있다. 저탄소 최적설계안은 비용 최적설계안보다 연간 약 84,462 kg-CO₂만큼의 CO₂ 배출량이 저감되었으며, 연간 약 84,777$만큼의 비용이 저감되었다.

생애주기에 따른 저탄소 최적설계안의 전체 비용을 분석하기 위해 CO₂ 저감량을 비용으로 환산하여 결과를 분석하였다. Goyang관망의 가정 사항을 동일하게 적용하여 분석하였다. 최적 설계안 간 CO₂ 저감량을 비용으로 환산한 결과, 연간 5,578,568$만큼의 이득이 있었다.

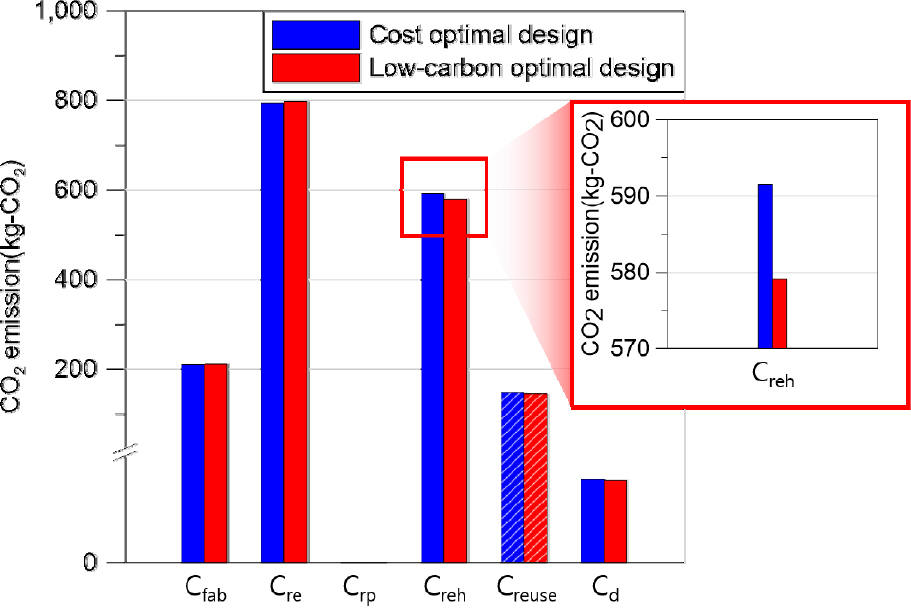
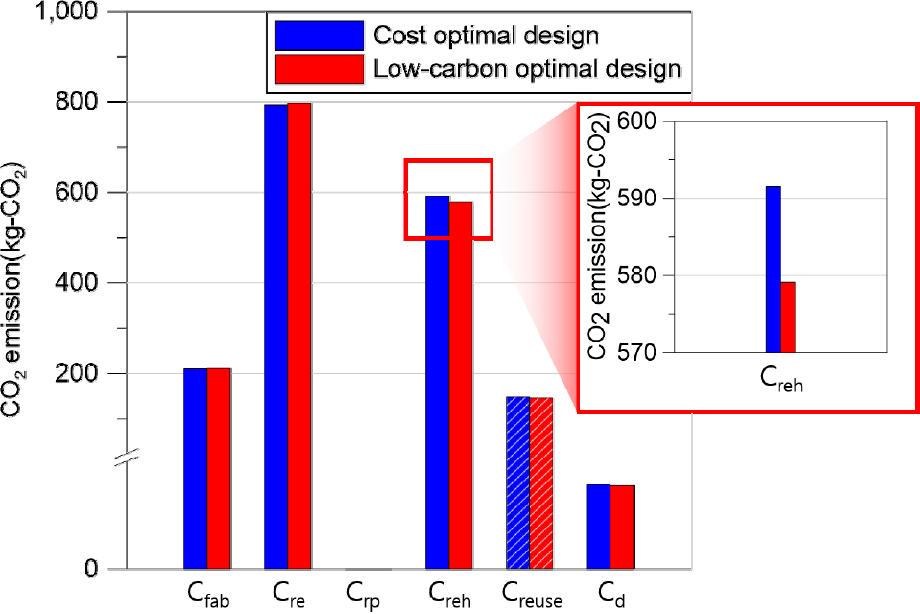
비용 최적설계안 및 저탄소 최적설계안의 생애주기를 기반으로 제조, 교체, 수리, 갱생, 재사용 및 해체 시 CO₂ 발생량을 분석하였다. Fig. 7은 Zhejiang 관망에서 생애주기를 기반으로 연간 발생하는 제조, 교체, 수리, 갱생, 재사용 및 해체 시 CO₂ 발생량을 나타낸 그림이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571006/images/kwra_57_10_06_F7.jpg

Fig. 7.

CO₂ emissions per year based on life cycle (Zhejiang)

Fig. 7에 따르면, 모든 과정에서 저탄소 최적설계안이 비용 최적설계안보다 CO₂ 발생량이 낮은 것을 알 수 있다. Zhejiang관망의 최적설계 결과, 저탄소 최적설계안은 비용 최적설계안보다 생애주기가 6년이 길다. 따라서, 연간 발생하는 CO₂량이 감소하는 것을 알 수 있다. 저탄소 최적설계안은 비용 최적설계안보다 최대 약 50,022 kg-CO₂만큼 더 낮았다. 관의 노후로 인해 관을 교체할 때 발생하는 CO₂량이 약 22% 감소가 되었다.

4. 결 론

본 연구는 대규모 사회기반시설물인 상수관망을 설계하는 과정에서 탄소량 저감을 위해 제안된 LCCEA 모델을 기반으로 최적설계를 진행하였다. 제안된 LCCEA 모델의 적용가능성을 확인하기 위해 LCCEA 모델을 기반으로 메타휴리스틱 최적화 알고리즘인 MVHCA를 활용하여 최적설계를 진행하였다. 국내외 관망을 기반으로 LCCEA 모델을 활용한 저탄소 최적설계결과를 기존 비용 최적설계안과 결과를 비교하였다. 최적 설계안 간의 CO₂ 배출량을 비교 및 분석하기 위해 생애주기의 각 단계별 비교를 진행하였다.

국내 Goyang 관망에서는 동일한 생애주기에서 전체 CO₂ 발생량 및 연간 CO₂ 발생량이 비용 최적설계안 대비 저탄소 최적설계안이 약 0.29% 감소하는 것으로 나타났다. 전체 및 연간 비용의 경우 저탄소 최적설계안이 비용 최적설계안보다 약 0.031% 높게 나타났다. 그러나, CO₂ 배출량 저감에 따른 환산 비용의 경우, 저탄소 최적설계안이 전체 약 4,439$, 연간 277$ 감소하는 것으로 나타났다. 저탄소 최적설계안은 전체 및 연간 CO₂ 배출량이 감소하였으며, 비용의 경우 CO₂ 저감에 따른 환산비용을 고려하게 되면 저탄소 최적설계안이 낮은 비용을 나타내는 것을 알 수 있다. 또한, Goyang 관망의 적용결과를 통해 상수관망 저탄소 최적설계를 적용할 경우 유지ㆍ보수단계에서 관을 갱생하는 횟수를 줄일 수 있다는 것을 알 수 있었다. 국외 Zhejiang 관망에서는 저탄소 최적설계안이 비용 최적설계안보다 긴 생애주기가 나타났다. 저탄소 최적설계안의 긴 생애주기로 인해 전체 CO₂ 배출량은 비용 최적설계안 대비 약 8.153% 만큼 높았다. 그러나, 연간 비용 및 연간 CO₂ 배출량은 약 21.344% 만큼 감소하였다.

제안된 LCCEA 모델 기반 최적설계 적용결과를 통해 LCCEA 모델은 기존 비용 최적설계안보다 생애주기 및 CO₂ 배출량 및 비용(환산 비용 고려시)에 좋은 결과를 나타냈다. 제안된 LCCEA 모델은 상수관망 최적설계에 사용할 경우 유지ㆍ보수단계에 대해서 많은 양의 CO₂ 발생량을 감소시킬 수 있다. 유지ㆍ보수단계의 CO₂ 발생량 감소는 유지ㆍ보수 횟수를 줄일 수 있다는 것을 의미한다. 유지ㆍ보수 횟수의 감소는 CO₂발생량뿐만이 아닌 유지ㆍ보수를 위한 비용 등을 줄일 수 있다는 것을 의미한다. 이를 통해 제안된 LCCEA 모델의 경우 적용한 관망을 포함하여 다양한 관망에 적용할 경우 저탄소를 목적으로 하는 최적설계에 대해서 좋은 결과를 나타낼 것으로 기대된다. 그러나, 제안된 LCCEA 모델의 경우, 생애주기 내 각 단계별 발생하는 CO₂를 산정하기 위해 파이프 직경에 따른 계수에 대한 식 등 수립된 가정사항이 존재한다. 향후 해당 가정사항을 실제 결과값 간의 비교를 통해 연산과정의 구체화 등이 이루어진다면 LCCEA 모델은 사회기반시설물을 설계하는 과정에서 탄소량 저감을 위해 사용될 수 있을 것이다. 또한, 본 연구의 경우, 비용 및 탄소발생량에 대한 단목적 최적설계를 진행하여 최적설계안을 비교 및 분석하였다. 각 최적설계안을 기반으로 생애주기에 대한 세부적 및 전체적 분석을 진행하였다. 단목적 최적설계안을 기반으로 비용 및 탄소발생량을 동시에 고려할 수 있는 다목적 최적설계기법을 적용하게 될 경우 관리자가 선택할 수 있는 다양한 LCCEA 모델을 구축할 수 있을 것으로 예상된다.

Acknowledgements

본 논문은 환경부의 재원으로 한국환경산업기술원의 도시홍수시설의 계획, 운영, 유지관리 최적화 기술개발사업의 지원을 받아 연구되었습니다(RS-2024-00398012).

Conflicts of Interest

The authors declare no conflict of interest.

References

Alsabri, A., and Al-Ghamdi, S.G. (2020). "Carbon footprint and embodied energy of PVC, PE, and PP piping: Perspective on environmental performance." Energy Reports, Vol. 6, pp. 364-370.

10.1016/j.egyr.2020.11.173

Alsadi, A.A., and Matthews, J.C. (2020). "Evaluation of carbon footprint of pipeline materials during installation, operation, and disposal phases." Journal of Pipeline Systems Engineering and Practice, Vol. 11, No. 2, 04020005.

10.1061/(ASCE)PS.1949-1204.0000422

Baek, C.W. (2002). Development of optimal decision-making system for rehabilitation of water distribution systems using ReHS. Master Thesis, Korea University.

Burat, F., Güney, A., and Kangal, M.O. (2009). "Selective separation of virgin and post-consumer polymers (PET and PVC) by flotation method." Waste Management, Vol. 29, No. 6, pp. 1807-1813.

10.1016/j.wasman.2008.12.01819155169

Chiplunkar, A.V. (1986). "Looped water distribution system optimization for single loading." Journal of Environmental Engineering, Vol. 112, No. 2, pp. 264-279.

10.1061/(ASCE)0733-9372(1986)112:2(264)

Cho, M.H., Jung, S.H., and Kim, J.S. (2010). "Pyrolysis of mixed plastic wastes for the recovery of benzene, toluene, and xylene (BTX) aromatics in a fluidized bed and chlorine removal by applying various additives." Energy & Fuels, Vol. 24, No. 2, pp. 1389-1395.

10.1021/ef901127v

Ditta, A.S., Wilkinson, A.J., McNally, G.M., and Murphy, W.R. (2004). "A study of the processing characteristics and mechanical properties of multiple recycled rigid PVC." Journal of Vinyl and Additive Technology, Vol. 10, No. 4, pp. 174-178.

10.1002/vnl.20026

Filion, Y.R., MacLean, H.L., and Karney, B.W. (2004). "Life-cycle energy analysis of a water distribution system." Journal of Infrastructure Systems, Vol. 10, No. 3, pp. 120-130.

10.1061/(ASCE)1076-0342(2004)10:3(119)

Fu, G., Kapelan, Z., Kasprzyk, J.R., and Reed, P. (2013). "Optimal design of water distribution systems using many-objective visual analytics." Journal of Water Resources Planning and Management, Vol. 139, No. 6, pp. 624-633.

10.1061/(ASCE)WR.1943-5452.0000311

Garcia, D., Balart, R., Crespo, J.E., and Lopez, J. (2006). "Mechanical properties of recycled PVC blends with styrenic polymers." Journal of Applied Polymer Science, Vol. 101, No. 4, pp. 2464-2471.

10.1002/app.23484

Geem, Z.W., Kim, J.H., and Loganathan G.V. (2001). "A new heuristic optimization algorithm: harmony search." Simulation, Vol. 76, No. 2, pp. 60-68.

10.1177/003754970107600201

Ito, M., and Nagai, K. (2007). "Degradation behavior and application of recycled PVC sheet made of floor sheet for railway vehicle." Polymer Degradation and Stability, Vol. 92, No. 9, pp. 1692-1699.

10.1016/j.polymdegradstab.2007.06.005

Janajreh, I., Alshrah, M., and Zamzam, S. (2015). "Mechanical recycling of PVC plastic waste streams from cable industry: A case study." Sustainable Cities and Society, Vol. 18, pp. 13-20.

10.1016/j.scs.2015.05.003

Jayaram, N., and Srinivasan, K. (2008). "Performance‐based optimal design and rehabilitation of water distribution networks using life cycle costing." Water Resources Research, Vol. 44, No. 1.

10.1029/2006WR005316

Jung, D., Kang, D., and Kim, J.H. (2018). "Development of a hybrid harmony search for water distribution system design." KSCE Journal of Civil Engineering, Vol. 22, No. 4, pp. 1506-1514.

10.1007/s12205-017-1864-3

Kameda, T., Fukuda, Y., Grause, G., and Yoshioka, T. (2010). "Chemical modification of rigid poly (vinyl chloride) by the substitution with nucleophiles." Journal of Applied Polymer Science, Vol. 116, No. 1, pp. 36-44.

10.1002/app.31452

Keane, M.A. (2007). "Catalytic conversion of waste plastics: Focus on waste PVC." Journal of Chemical Technology & Biotechnology: International Research in Process, Environmental & Clean Technology, Vol. 82, No. 9, pp. 787-795.

10.1002/jctb.1757

Keane, M.A. (2009). "Catalytic transformation of waste polymers to fuel oil." ChemSusChem: Chemistry & Sustainability Energy & Materials, Vol. 2, No. 3, pp. 207-214.

10.1002/cssc.20090000119253926

Kleiner, Y., Adams, B.J., and Rogers, J.S. (1998). "Long-term planning methodology for water distribution system rehabilitation." Water Resources. Research, Vol. 34, No. 9, pp. 2039-2051.

10.1029/98WR00377

Kleiner, Y., and Rajani, B. (1999). "Using limited data to assess future needs." Journal‐American Water Works Association, Vol. 91, No. 7, pp. 47-61.

10.1002/j.1551-8833.1999.tb08664.x

Lee, E.H. (2021) "Application of self-adaptive vision-correction algorithm for water-distribution problem." KSCE Journal of Civil Engineering, Vol. 25, No. 3, pp. 1106-1115.

10.1007/s12205-021-2330-9

Lee, E.H., Lee, H.M., Yoo, D.G., and Kim, J.H. (2018). "Application of a meta-heuristic optimization algorithm motivated by a vision correction procedure for civil engineering problems." KSCE Journal of Civil Engineering, Vol. 22, No. 7, pp. 2623-2636.

10.1007/s12205-017-0021-3

Lee, S.Y., Yoo, D.G., Jung, D.H., and Kim, J.H. (2015). "Optimal life cycle design of water pipe system using genetic algorithm." Journal of the Korea Academia-Industrial Cooperation Society, Vol. 16, No. 6, pp. 4216-4227.

10.5762/KAIS.2015.16.6.4216

Lundie, S., Peters, G.M., and Beavis, P.C. (2004). "Life cycle assessment for sustainable metropolitan water systems planning." Environmental Science & Technology, Vol. 38, No. 14, pp. 3465-3473.

10.1021/es034206m15296294

Ministry of Environment (ME) (2023). 2022 Waterworks Statistics.

Mononobe, N. (1960). Hydraulics. Iwanami, Tokyo, Japan, pp. 155-158.

Piratla, K.R., Ariaratnam, S.T., and Cohen, A. (2012). "Estimation of CO 2 emissions from the life cycle of a potable water pipeline project." Journal of Management in Engineering, Vol. 28, No. 1, pp. 22-30.

10.1061/(ASCE)ME.1943-5479.0000069

Reca, J., Martínez, J., Gil, C., and Baños, R. (2008). "Application of several meta-heuristic techniques to the optimization of real looped water distribution networks." Water Resources Management, Vol. 22, No. 10, pp. 1367-1379.

10.1007/s11269-007-9230-8

Recio, J.M.B., Guerrero, P.J., Ageitos, M.G., and Narváez, R.P. (2005). Estimate of energy consumption and CO2 emission associated with the production, use and final disposal of PVC, HDPE, PP, ductile iron and concrete pipes. Universitat Politécnica de Catalunya, Barcelona, Spain, p. 13.

Ryu, Y.M. and Lee, E.H. (2022). "Optimal design of water distribution system using modified hybrid vision correction algorithm." Journal of Korea Water Resources Association, Vol. 55, No. suppl 1, pp. 1271-1282.

Ryu, Y.M., and Lee, E.H. (2023). "Application of modified hybrid vision correction algorithm for water distribution systems in civil engineering." KSCE Journal of Civil Engineering, Vol. 27, No. 8, pp. 3617-3631.

10.1007/s12205-023-0126-9

Saldarriaga, J., Páez, D., Salcedo, C., Cuero, P., López, L.L., León, N., and Celeita, D. (2020) "A direct approach for the near-optimal design of water distribution networks based on power use." Water, Vol. 12, No. 4, 1037.

10.3390/w12041037

Sangroula, U., Han, K.H., Koo, K.M., Gnawali, K., and Yum, K.T. (2022). "Optimization of water distribution networks using genetic algorithm based SOP-WDN program." Water, Vol. 14, No. 6, 851.

10.3390/w14060851

Shamir, U., and Howard, C.D., (1979). "An analytic approach to scheduling pipe replacement." Journal‐American Water Works Association, Vol. 71, No. 5, pp. 248-258.

10.1002/j.1551-8833.1979.tb04345.x

Sharp, W.W., and Walski, T.M. (1988). "Predicting internal roughness in water mains." Journal‐American Water Works Association, Vol. 80, No. 11, pp. 34-40.

10.1002/j.1551-8833.1988.tb03132.x

Shokoohi, M., Tabesh, M., Nazif, S., and Dini, M. (2017). "Water quality based multi-objective optimal design of water distribution systems." Water Resources Management, Vol. 31, pp. 93-108.

10.1007/s11269-016-1512-6

U.S. Environmental Protection Agency (US EPA) (2000). EPANET 2.0 user's manual. Washington D.C., U.S.

VinyPlus (2018). Belgium, accessed 1 August 2024, <www.vinyplus.eu>.

Walski, T.M., and Pelliccia, A. (1982). "Economic analysis of water main breaks." Journal‐American Water Works Association, Vol. 74, No. 3, pp. 140-147.

10.1002/j.1551-8833.1982.tb04874.x

Yoon, J,S.,, Yoo, D.G.,, Lee, H.M.,, and Kim, J.H. (2012). "Optimal leakage detection model of water distribution systems using semi-pressure driven analysis and harmony search." Journal of Korean Society of Hazard Mitigation, Vol. 12, No. 3, pp. 23-31.

10.9798/KOSHAM.2012.12.3.023

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Development of Life Cycle Carbon Emission Analysis for optimal low-carbon design of water distribution system

ABSTRACT

MAIN

Fig. 1.

Schema of each stage in water distribution system

Fig. 2.

Flowchart of LCCEA

Table 1.

Standard specifications of pipes (Piratla et al., 2012)

(1)

(2)

(3)

(4)

Fig. 3.

Flowchart of MHVCA

(5)

(6)

Fig. 4.

Layout of Goyang network

Table 2.

Demand by node in Goyang network

Table 3.

Cost of pipe per diameter for Goyang network

Table 4.

Standard specifications of pipe (Piratla et al., 2012)

Table 5.

Characteristics of the standard pipes (Recio et al., 2005)

Table 6.

Specifications of each pipe for Goyang network

Table 7.

Parameter setting of MHVCA for optimal design of Goyang network

Table 8.

Comparison between cost-optimal design and low-carbon optimal design (Goyang network)

Fig. 5.

CO2 emissions per year based on life cycle (Goyang)

Fig. 6.

Layout of Zhejiang network

Table 9.

Demand by node in Zhejiang network

Table 10.

Cost of pipe per diameter for Zhejiang network

Table 11.

Specifications of each pipe for Zhejiang network

Table 12.

Parameter setting of MHVCA for optimal design of Zhejiang network

Table 13.

Comparison between cost-optimal design and low-carbon optimal design (Zhejiang network)

Fig. 7.

CO2 emissions per year based on life cycle (Zhejiang)

Acknowledgements

Conflicts of Interest

References

CO₂ emissions per year based on life cycle (Goyang)

CO₂ emissions per year based on life cycle (Zhejiang)